OverviewofRobustAdaptiveCritic ControlDesign

Abstract Adaptivedynamicprogramming(ADP)andreinforcementlearningare quiterelevanttoeachotherwhenperformingintelligentoptimization.Theyareboth regardedaspromisingmethodsinvolvingimportantcomponentsofevaluationand improvement,atthebackgroundofinformationtechnology,suchasartificialintelligence,bigdata,anddeeplearning.Althoughgreatprogresseshavebeenachieved andsurveyedwhenaddressingnonlinearoptimalcontrolproblems,theresearch onrobustnessofADP-basedcontrolstrategiesunderuncertainenvironmenthas notbeenfullysummarized.Hence,thischapterreviewstherecentmainresultsof adaptive-critic-basedrobustcontroldesignofcontinuous-timenonlinearsystems. TheADP-basednonlinearoptimalregulationisreviewed,followedbyrobuststabilizationofnonlinearsystemswithmatcheduncertainties,guaranteedcostcontroldesignofunmatchedplants,anddecentralizedstabilizationofinterconnected systems.Additionally,furthercomprehensivediscussionsarepresented,including event-basedrobustcontroldesign,improvementofthecriticlearningrule,nonlinear H∞ controldesign,andseveralnotesonfutureperspectives.Thisoverviewisbeneficialtopromotethedevelopmentofadaptivecriticcontrolmethodswithrobustness guaranteeandtheconstructionofhigherlevelintelligentsystems.
1.1Introduction
Nowadays,machinelearningbecomesthecoretechniqueofartificialintelligence andplaysanimportantroleinmoderntechnology.Artificialintelligence,bigdata, anddeeplearningareallhottopicsofinformationtechnology.Machinelearning [6, 36]anddeeplearning[51, 85, 111]areextremelyhelpfulforthestudyofbig data[18, 105].In2016,GoogleDeepMinddevelopedaprogramcalledAlphaGo [115]thathasshownperformancepreviouslythoughttobeimpossibleforatleasta decade.Insteadofexploringvarioussequencesofmoves,AlphaGolearnstomakea movebyevaluatingthestrengthofitspositionontheboard.Thiskindofevaluation wasensuredtobepossibleviadeeplearningcapabilitiesofartificialneuralnetworks [31, 39, 181].Duetotheexcellentpropertiesofadaptivity,advancedinput-output
©SpringerNatureSingaporePteLtd.2019
D.WangandC.Mu, AdaptiveCriticControlwithRobustStabilization forUncertainNonlinearSystems,StudiesinSystems,DecisionandControl167, https://doi.org/10.1007/978-981-13-1253-3_1
mapping,faulttolerance,nonlinearity,andself-learning,neuralnetworksarefrequentlyusedforuniversalfunctionapproximationinnumericalalgorithms.Deep neuralnetworksbasedlearninghasplayedavitalroleinAlphaGo’ssuccess[155]. Positionevaluation,aimedatapproximatingtheoptimalcostfunctionofthegame, isthekeyprocedureofAlphaGo.Noticeably,reinforcementlearning[120]isan indispensablecomponentofthisadvancedproduct.
1.1.1ReinforcementLearningandAdaptiveCriticDesigns
Asanimportantbranchofartificialintelligenceandespeciallymachinelearning, reinforcementlearningtacklesmodificationofactionsbasedoninteractionswiththe environment.Theenvironmentcompriseseverythingoutsidetheagent(thelearner andthedecision-maker)andalsointeractswiththeagent.Reinforcementlearning focusesonhowanagentoughttotakeactionsinanenvironmentsoastomaximize thecumulativerewardorminimizethepunishment,wheretheideaofoptimization isinvolved.Infact,peopleoftenareinterestedinmimickingnatureanddesigning automaticcontrolsystemsthatareoptimaltoeffectivelyachieverequiredperformanceswithoutunduelydependingonthelimitedresources.Prescribingasearch trackingbackwardfromthefinalstepandemployingtheprincipleofoptimality therebyfindingtheoptimalpolicy,dynamicprogrammingisausefulcomputational techniquetosolveoptimalcontrolproblems[9, 59].However,duetothedefectof backwardnumericalprocesswhencopingwiththehigh-dimensionaloptimization problems,itiscomputationallyuntenabletorundynamicprogrammingtoobtain theoptimalsolution(i.e.,thewell-known“curseofdimensionality”[9]).What’s worse,thebackwarddirectionofthesearchprocessprecludestheuseofdynamic programminginreal-timecontrol.
Reinforcementlearningishighlyrelatedtodynamicprogrammingtechnique. Classicaldynamicprogrammingalgorithmsareoflimitedutilityinreinforcement learningbecauseoftheirdependenceontheperfectmodelandamassofcomputationalexpense.However,dynamicprogrammingprovidesanessentialfoundation forunderstandingreinforcementlearning.Thereisaclassofreinforcementlearning methodsincorporatingtheactor-critic(oradaptivecritic)structure,whereanactor componentappliesanaction(orcontrollaw)totheenvironmentandacriticcomponentevaluatesthevalueofthataction.Thecombinationofactor-criticstructure, dynamicprogramming,andneuralnetworks,resultsintheadaptive/approximate dynamicprogramming(ADP)algorithm[109, 164, 165, 167],inventedbyWerbos forobtainingapproximateoptimalsolutions.ThecoreideaofADPistheadaptive criticbasedoptimizationanditisregardedasanecessaryoutlettoachievetruly brain-likeintelligence[109, 167].
1.1.2Adaptive-Critic-BasedOptimalControlDesign
Artificialneuralnetworksandfuzzysystemsarealwaysregardedasimportantintelligentcomplementstopracticalcontrolengineering.Actually,theyareoftenusedas fundamentalcomponentsofvariouscomputationalintelligencetechniquesandthe optimizationdesignofcomplexdynamicsbasedonthemisasignificanttopicof decisionandcontrolcommunity[33, 78, 156, 157, 173].Linearoptimalregulators havebeenstudiedbycontrolscientistsandengineersformanyyears.However,it isnotaneasytasktoacquiretheanalyticsolutionoftheHamilton-Jacobi-Bellman (HJB)equationforgeneralnonlinearsystems.Thus,theiroptimalfeedbackdesignis muchtoodifficultbutconsiderableimportant.Remarkably,thesuccessiveapproximationmethod[1, 5, 8, 110]andthecloselyrelatedADPmethodarebothdeveloped toconquerthedifficultyviaapproximatingtheHJBsolution.Ingeneral,ADPisa promisingtechniquetoapproximateoptimalcontrolsolutionsforcomplexsystems [1, 5, 8, 109, 110, 164, 165, 167].Particularly,itisregardedasaneffectivestrategy todesignoptimalcontrollersinonlineandforward-in-timemanners.Amongthem, theadaptivecriticisthebasicframeworkandneuralnetworksareofteninvolvedto serveasthefunctionapproximator.EmployingtheADPmethodalwaysresultsin adaptivenear-optimalfeedbackcontrollersandhenceisusefultoperformvarious nonlinearintelligentcontrolapplications.
ThereareseveralsynonymsusedforADP,andmostofthemarecloselyrelated toneuralnetworks.Theyare“adaptivecriticdesigns”[30, 101, 102],“adaptive dynamicprogramming”[55, 97],“approximatedynamicprogramming”[5, 112, 167],“neuraldynamicprogramming”[76, 113],“neuro-dynamicprogramming” [12],“reinforcementlearning”[112, 120]includingQ-learning[159],and“relaxed dynamicprogramming”[62, 106].Inthebasicframework,therearethreecomponents:critic,model,andaction.Theyareusuallyimplementedvianeuralnetworks andperformthefunctionofevaluation,prediction,anddecision,respectively.Some improvedstructuresarealsoproposed,suchasthegoalrepresentationADP[32, 99, 123, 200]andfuzzyADP[123, 191].Inthelasttwodecades,ADPhasbeen promotedextensivelywhencopingwithadaptiveoptimalcontrolofdiscrete-time systems[21, 24, 34, 35, 68, 71, 77, 90, 91, 95, 118, 143, 153, 161, 163, 174, 175, 187, 197]andcontinuous-timesystems[13, 15, 26, 43, 47, 74, 81, 82, 87, 88, 98, 100, 117, 127, 129, 130, 182, 184, 202].Amongthem,theiterativeADP algorithmbasedonvalueiterationisimportanttotheself-learningoptimalcontrol designofdiscrete-timesystems[5, 91, 143, 153, 187],whilethepolicyiterationis significanttotheadaptiveoptimalcontroldesignofcontinuous-timesystems[1, 74, 88, 127, 130].Theconvergenceoftheseiterativealgorithmsisabasicissuesothat ithasbeensufficientlystudied[1, 5, 43, 47, 74, 77, 81, 88, 91, 95, 117, 118, 127, 130, 143, 153, 187].Forcomprehensivesurveypapersandbooksofrecentdevelopments,pleasereferto[16, 44, 57, 58, 60, 65, 67, 72, 116, 131, 134, 154, 186, 192],includingvarioustopicsintermsoftheory,design,analysis,andapplications. Asemphasizedby[57, 58, 60],theADPtechniqueiscloselyrelatedtoreinforcement learningwhenengagingintheresearchoffeedbackcontrol.Ingeneral,valueand
policyiterationsarefundamentalalgorithmsofreinforcementlearningbasedADP inoptimalcontrol.Itiseasytoinitializethevalueiteration,butonecannotalways guaranteethestabilityofiterativecontrollawsduringtheimplementationprocess. Policyiterationstartswithastabilizingcontroller,butitisdifficulttofindtheinitial admissiblecontrollawinmanysituations.Asaresult,thegeneralizedversionof thesetwoalgorithmshasreceivedgreatattention[57, 58, 60, 68, 72, 163]recently, forintegratingtheiradvantagesandavoidingtheweaknesses.
Therapiddevelopmentofinformationtechnology,especiallyartificialintelligence,bigdata,anddeeplearning,areprofoundlyaffectingoursociety.Nowadays, thedata-drivencontroldesignhasbecomeahottopicinthefieldofcontroltheory andcontrolengineering[37, 38, 152, 158, 177].ThedevelopmentofADPmethods greatlypromotestheresearchofdata-basedoptimalcontroldesign[21, 67, 81, 95, 96, 143, 149, 184, 202].Anoveliterativeneuraldynamicprogrammingalgorithm wasdevelopedin[96, 149],reflectingacombinationofneuraldynamicprogrammingtechniqueandtheiterativeADPalgorithm.Theintegralreinforcementlearning proposedin[52–54]providesanewoutletofachievingthemodel-freeoptimalregulation.Alloftheseresultsarebeneficialtothedevelopmentofartificialintelligence andcomputationalintelligencetechniques.
1.1.3Adaptive-Critic-BasedNonlinearRobustControl Design
ExistingresultsofADPmethodsaremostlyobtainedundertheassumptionthatthere arenodynamicaluncertaintiesinthecontrolledplants.Nevertheless,practicalcontrol systemsarealwayssubjecttomodeluncertainties,exogenousdisturbancesorother changesintheirlifetime.Theyarenecessarilyconsideredduringthecontrollerdesign processinordertoavoidthedeteriorationofnominalclosed-loopperformance.A controllerissaidtoberobustifitworkseveniftheactualsystemdeviatesfromits nominalmodelonwhichthecontrollerdesignisbased.Theimportanceoftherobust controlproblemisevidentwhichhasbeenstudiedbycontrolscientistsformany years(see[19, 49, 50, 56, 63, 64]andthereferencestherein).In[63, 64],therobust controlproblemwashandledbyusingtheoptimalcontrolapproachforthenominal system.1 Thisisaveryimportantresultwhichestablishesaconnectionbetweenthe twocontroltopics.However,thedetailedprocedureisnotdiscussedanditisdifficult tocopewithgeneralnonlinearsystems.Then,anoptimalcontrolschemebasedon theHJBsolutionforrobustcontrollerdesignofnonlinearsystemswasproposedin [3, 4].Thealgorithmwasconstructedbyusingtheleastsquaresmethodperformed offlinewhiletheclosed-loopstabilityanalysiswasnotfullydiscussed.
1 Itrepresentstheportionofsystemwithoutconsideringtheuncertaintyduringthefeedbackcontrol designaimedatguaranteeingthedesiredperformanceofadynamicplantcontaininguncertain elements[19, 63, 64].
Since2013,theregraduallyappearedsomepublicationsofADP-basedrobust controldesigns[75, 119, 133, 138–141, 144, 178, 199].Ingeneral,theproblem transformationisconductedtobuildacloserelationshipbetweentherobustness andoptimality.Moreover,theclosed-loopsystemisalwaysprovedtobeuniformly ultimatelybounded(UUB)thatwillbedefinedlater.In[139],apolicyiteration algorithmwasdevelopedtosolvetherobustcontrolproblemofcontinuous-time nonlinearsystemswithmatcheduncertaintiesandthealgorithmwasimprovedin [141].Thismethodwasextendedtodealwiththerobuststabilizationofmatched nonlinearsystemswithunknowndynamics[144]andwithconstrainedinputs[75]. Incidentally,itisworthmentioningthatatentativeresultofADP-basedrobustcontrol designofdiscrete-timenonlinearsystemswasgivenin[140].Forimprovingthe learningruleofthecriticneuralnetwork,theadaptation-orientednear-optimalcontrol problemwasrevisitedandthentherobuststabilizationofnonlinearsystemswas studiedwithfurtherresults[133].Moreover,therobustcontrolmethodofnonlinear systemswithunmatcheduncertaintieswasderivedin[199].Therobustcontroldesign withmatcheduncertaintiesanddisturbanceswasalsostudiedin[119]asanextension of[141].Notethedata-drivenapproachesarehelpfultotheADP-basedrobustcontrol designsincesystemuncertaintiescansometimesberegardedasunknowndynamics. FordiscussingtheoptimalityoftheADP-basedrobustcontroller,anoveldata-based robustoptimalcontrolmethodofmatchednonlinearsystemswasconstructed[138]. Data-basedrobustadaptivecontrolforaclassofunknownnonlinearsystemswith constrained-inputwasstudiedviaintegralreinforcementlearning[178].Theseresults guaranteethatADPmethodsareapplicabletoalargeclassofcomplexnonlinear systemsunderuncertainenvironment.Hence,theygreatlybroadenstheapplication scopeofADP,sincemanyofpreviouspublicationsdonotfocusontherobustness ofobtainedcontrollers.Subsequently,becauseofpossessingthecommonspeciality ofhandlingsystemuncertainty,thecombinationofslidingmodecontrolwithADP providesanewdirectiontothestudyofself-learningcontroldesign[23, 90].In[90], theapplicationissueonair-breathinghypersonicvehicletrackingwasaddressed byemployinganinnovativecombinationofslidingmodecontrolandADP.Then, theslidingmodecontrolmethodbasedonADPwasusedin[23]tostabilizethe closed-loopsystemwithtime-varyingdisturbancesandguaranteethenearlyoptimal performanceofthesliding-modedynamics.
ForfillingupthegapinmostofADPliteraturewheredynamicuncertaintiesor unmodeleddynamicswerenotaddressed,animportantframeworknamedrobust ADPwasproposedin[14, 25, 41, 42, 45]tocopewiththenonlinearrobustoptimal controldesignfromanotheraspect.AnoverviewofrobustADPmethodforlinear andnonlinearsystemswasgivenin[45],outliningthedevelopmentofrobustADP theorywithpotentialapplicationsinengineeringandbiology.In[42],akeystrategyintegratingseveraltoolsofmodernnonlinearcontroltheory,suchastherobust redesignandbacksteppingtechniquesaswellasthenonlinearsmall-gaintheorem [46],wasdevelopedwithADPformulation.Afterthat,therobustADPmethodwas employedtodecentralizedoptimalcontroloflarge-scalesystems[14]andoutput feedbackcontrolofinterconnectedsystems[25].Therein,theapplicationsofrobust ADPtopowersystemsweregivenspecialattention[14, 25, 41, 42, 45].Generally,
therobustADPdesigncannotonlystabilizetheoriginaluncertainsystem,butalso achieveoptimalityintheabsenceofdynamicuncertainty.Itwasemphasizedthat, undertheframeworkofrobustADP,computationaldesignsforrobustoptimalcontrolcanbecarriedoutbasedonlyontheonlinedataofthestateandinputvariables [45].Inthissense,therobustADPmethodcanberegardedasanonlinearvariant of[40],whereacomputationaladaptiveoptimalcontrolstrategywasproposedto iterativelysolvethelinearalgebraicRiccatiequationusingonlineinformationof stateandinput.
However,aswehaveseen,mostofthepreviousresearchonlyconcernswith therobustnessoftheuncertainsystemandtheoptimalityofthenominalsystem [42, 75, 133, 139, 199].Inotherwords,thedirectoptimalcontroldesignofuncertainnonlinearsystemsisverydifficult.Thisisbecausecopingwiththecostfunction oftheuncertainplantisnotaneasytask.Therefore,someresearchershavepaidattentiontothestudyofboundednessofthecostfunctionwithrespecttotheuncertain plant,inadditiontooptimizingit.Theguaranteedcostcontrolstrategy[17]possesses theadvantageofprovidinganupperboundonagivencostandthereforethedegradationofcontrolperformanceincurredbysystemuncertaintiescanbeguaranteedtobe lessthanthisbound.Whendiscussingtheoptimalitywithrespecttotheguaranteed costfunction,itleadstotheoptimalguaranteedcostcontrolproblem.Theguaranteedcostcontroldesignisasomewhatmatureresearchtopicofcontrolcommunity, buttherearesomenewresultswiththeemergingADPformulation[70, 94, 142, 172, 180].UndertheADPframework,weobtainanovelself-learningoptimalguaranteed costcontrolscheme.
Whenstudyingcomplexdynamicalsystems,weoftenpartitionthemintoanumber ofinterconnectedsubsystemsforconvenience.Thecombinationofthesesubsystems canbeseenaslarge-scalesystems.Asoneoftheeffectivecontrolschemesforlargescalesystems,thedecentralizedcontroldesignhasacquiredmuchinterestbecauseof itsevidentadvantages,suchaseasyimplementationandlowdimensionality[66, 69, 92, 107, 114, 136, 141].Itisshownthatthedecentralizedstabilizationforaclassof interconnectednonlinearsystemsiscloselyrelatedtotheADP-basedrobustcontrol design[66, 69, 92, 136, 141].Inthissense,theself-learningdecentralizedcontrol schemecanbeconstructedwithADPformulation.Notethat,therobustnessissueis alsoincludedintheaforementionedguaranteedcostcontrolanddecentralizedcontrol designs.Itwillbeillustratedthatthesethreecontroltopicsarecloselyconnected undertheproposedadaptivecriticframework[134].
Forconsistencyandconvenience,thefollowingnotationswillbeusedthroughout thechapter. R representsthesetofallrealnumbers. Rn istheEuclideanspaceof all n -dimensionalrealvectors. Rn ×m isthespaceofall n × m realmatrices. · denotesthevectornormofavectorin Rn orthematrixnormofamatrixin Rn ×m . In representsthe n × n identitymatrix. λmax (·) and λmin (·) standforthemaximal andminimaleigenvaluesofamatrix,respectively.Let Ω beacompactsubsetof Rn , Ωu beacompactsubsetof Rm ,and A (Ω) bethesetofadmissiblecontrol laws(definedin[1, 8, 127, 130])on Ω ρ istheparameterintheutilitycorrespondingtotheuncertainterm. L2 [0, ∞) denotesaspaceoffunctionswherethe Lebesgueintegraloftheelementisfinite. isthe L2 -gainperformancelevel. i isthe
symbolofthe i thsubsysteminaninterconnectedplant, j isthesamplinginstantofthe event-triggeringmechanism,and k istheiterationindexofthepolicyiterationalgorithm. N+ ={i } N i =1 ={1, 2,..., N } denotesthesetofpositiveintegersbetween1 and N N ={0, 1, 2,... } standsforthesetofallnon-negativeintegers.“T ”isused forrepresentingthetransposeoperationand ∇ (·) ∂(·)/∂ x isemployedtodenote thegradientoperator.
1.2ADP-BasedContinuous-TimeNonlinearOptimal Regulation
Inthissection,wepresentabriefreviewofthecontinuous-timenonlinearoptimal regulationmethodwithneuralnetworkimplementation.ThebasicideaoftheADP methodforoptimalcontrolofcontinuous-timesystemsisinvolvedtherein.
1.2.1BasicOptimalControlProblemDescription
Weconsideraclassofcontinuous-timenonlinearsystemswithcontrol-affineinputs givenby
where x (t ) ∈ Ω ⊂ Rn isthestatevector, u (t ) ∈ Ωu ⊂ Rm isthecontrolvector,and thesystemfunctions f ( ) and g ( ) aredifferentiableintheargumentssatisfying f (0) = 0.Welettheinitialstateat t = 0be x (0) = x 0 and x = 0betheequilibrium pointofthecontrolledplant.Theinternalsystemfunction f ( x ) isassumedtobe Lipschitzcontinuousontheset Ω in Rn whichcontainstheorigin.Generally,the nonlinearplant(1.1)isassumedtobecontrollable.
Inthischapter,weconsidertheundiscountedoptimalcontrolproblemwithinfinite horizoncostfunction.Welet
denotetheutilityfunction,2 wherethescalarfunction Q ( x ) ≥ 0andthe mdimensionalsquarematrix R = R T > 0,andthendefinethecostfunctionas
2 Theselectedstate-relatedutility Q ( x (t )) ismoregeneralthantheclassicalform x T (t ) Qx (t ),where Q = Q T > 0.Thecontrol-relatedutilitycanbechosenasthenon-quadraticform[75, 83, 187, 189]insteadofthetraditionallyquadraticone u T (t ) Ru (t ) whenencounteringinputconstraints.
Forsimplicity,thecost J ( x (t ), u (t )) iswrittenas J ( x (t )) or J ( x ) inthesequel. Whatwealwaysconcernisthecostfunctionstartingfrom t = 0,representedas J ( x (0)) = J ( x 0 ). Duringoptimalcontroldesign,wewanttoderivetheoptimalfeedbackcontrol law u ( x ) tominimizethecostfunction(1.3),where u ( x ) shouldbeadmissible.
Definition1.1 (cf. [1, 8, 127, 130])Acontrollaw u ( x ) issaidtobeadmissiblewith respectto(1.3)on Ω ,denotedby u ∈ A (Ω),if u ( x ) iscontinuouson Ω , u (0) = 0, u ( x ) stabilizessystem(1.1)on Ω ,and J ( x 0 , u ) isfiniteforall x 0 ∈ Ω .
Foranadmissiblecontrollaw u ( x ) ∈ A (Ω),iftherelatedcostfunction(1.3)is continuouslydifferentiable,thentheinfinitesimalversionisthenonlinearLyapunov equation
with J (0) = 0.DefinetheHamiltonianofsystem(1.1)as
UsingBellman’soptimalityprinciple,theoptimalcostfunction J ∗ ( x ),specifically definedas
satisfiestheso-calledcontinuous-timeHJBequation
Basedonoptimalcontroltheory,theoptimalfeedbackcontrollawiscomputedby
Usingtheoptimalcontrolexpression(1.8),theHJBequationturnstobetheform
Wenoticethattheoptimalcontrollawcanbederivediftheoptimalcostfunctioncan beobtained,i.e.,theequation(1.9)issolvable.However,thatisnotthecase.Since thecontinuous-timeHJBequation(1.9)isdifficulttodealwithintheory,itisnot aneasytasktoobtaintheoptimalcontrollaw(1.8)forgeneralnonlinearsystems.
1.2ADP-BasedContinuous-TimeNonlinearOptimalRegulation9
Thispromotestheinvestigationofiterativealgorithms,suchaspolicyiteration.We firstconstructtwosequencesintermsofthecostfunction { J (k ) ( x )} andthecontrol law {u (k ) ( x )},andthenstartiterationfromaninitialadmissiblecontrollerasfollows:
Generally,thepolicyiterationincludestwoimportantiterativesteps[120],i.e.,policy evaluationbasedon(1.4)andpolicyimprovementbasedon(1.8),whichareshown inAlgorithm1.
Algorithm1 PolicyIterationforOptimalControlProblem
1:Initialization
Lettheinitialiterationindexbe k = 0and J (0) ( ) = 0. Giveasmallpositivenumber asthestoppingthreshold. Startiterationfromaninitialadmissiblecontrollaw u (0) .
2:PolicyEvaluation
Usingthecontrollaw u (k ) ( x ),solvethefollowingnonlinearLyapunovequation
with J (k +1) (0) = 0,where x = f (
3:PolicyImprovement
) + g ( x )u (k ) ( x ).
Basedon J (k +1) ( x ),updatethecontrollawvia
4:StoppingCriterion
If | J (k +1) ( x ) J (k ) ( x )|≤ ,stopandobtaintheapproximateoptimalcontrollaw;else,set k = k + 1andgobacktoStep2.
Notethattheabovepolicyiterationalgorithmcanfinallyconvergetotheoptimal costfunctionandoptimalcontrollaw,i.e., J
and
(
) as k →∞.Theconvergenceproofhasbeengivenin[1, 74]andrelatedreferences therein.However,itisstilldifficulttoobtaintheexactsolutionoftheLyapunov equation.Thismotivatesustodevelopanapproximatestrategytoovercomethe difficulty[13, 15, 26, 42, 43, 74, 81, 88, 127, 130, 138, 144],whichresultsin theADP-basedneuralcontroldesign.Besides,theknowledgeofsystemdynamics f ( x ) and g ( x ) isneededtoperformtheiterativeprocess.Actually,someadvanced methodshavebeenproposedtorelaxthisrequirement,suchastheintegralpolicy iterationalgorithm[130],theneuralidentificationscheme[144],andtheprobing signalmethod[40, 42].Asdiscussedinthefollowingsections,greateffortsarestill beingmadeinthisaspect.
1.2.2NeuralControlDesignwithStabilityDiscussion
AsisshowninSect. 1.1,severalneuralnetworksareoftenincorporatedinadaptivecriticdesigns.Amongthem,thecriticnetworkisregardedasthemostfundamentalelement,eventhoughtheremaybeotherelementsinvolved,suchasmodel network[91, 143]andactionnetwork[127, 143].Differentconfigurationsreflect distinctobjectivesofcontroldesigners.Thesinglecriticstructureisoftenemployed toemphasizethesimplicityofthedesignprocedure[75, 139].
Duringtheneuralnetworkimplementation,wetaketheuniversalapproximationpropertyintoconsiderationandexpresstheoptimalcostfunction J ∗ ( x ) onthe compactset Ω as
where ωc ∈ Rl c istheidealweightvector, l c isthenumberofneuronsinthehidden layer, σc ( x ) ∈ Rl c istheactivationfunction,and εc ( x ) ∈ R isthereconstruction error.3 Then,thegradientvectoroftheoptimalcostfunctionis
Sincetheidealweightisunknown,acriticneuralnetworkisdevelopedtoapproximatetheoptimalcostfunctionas
where ˆ ωc ∈ Rl c denotestheestimatedweightvector.Similarly,wederivethegradient vectoras
Notethatthespecificstructureofthecriticnetworkisalwaysanexperimentalchoice withengineeringexperienceandintuitionafternoticingatradeoffbetweencontrol accuracyandcomputationalcomplexity[1].Actually,selectingtheproperneurons forneuralnetworksismoreofanartthanscience[101].Determiningthenumberof neuronsneededforaparticularapplicationisstillanopenproblem.
Consideringthefeedbackformulation(1.8)andtheneuralnetworkexpression (1.13),theoptimalcontrollawcanberewrittenasaweight-relatedform
3 Formostofthegeneralnonlinearcases,theidealvector ωc andtheidealscalar εc areunknown buttheyarebothbounded.
1.2ADP-BasedContinuous-TimeNonlinearOptimalRegulation11
Usingthecriticneuralnetwork(1.15),theapproximateoptimalfeedbackcontrol functionis4
Basedontheneuralnetworkformulation,theapproximateHamiltonianiswrittenas
Noticing(1.9),wedefinetheerroras
sothat ec =
),
andfindthattheset
)).Asgivenin[1, 8, 74, 127],wedefine
islinearlyindependent.
Now,weshowhowtotrainthecriticnetworkanddesigntheweightvector ˆ
c tominimizetheobjectivefunctionnormallydefinedas E c = (1/2)e 2 c .Traditionally, basedon(1.19),wecanemploythenormalizedsteepestdescentalgorithm
totunetheweightvector,wheretheconstant αc > 0isthelearningratewhilethe term (1 + φ T φ)2 isadoptedfornormalization.ThesimplediagramoftheADP-based controllerdesignmethodisdepictedinFig. 1.1,where(1.21)isthebasiclearning criterionoftheneuralnetwork.
Definingtheerrorvectorbetweentheidealweightandtheestimatedvalueas ˜ ωc = ωc −ˆω
,wecaneasilyfindthat
.Here,letusintroducetwonew variables φ1 = φ/(1 + φ T φ) and φ2 =
and φ2 ≥ 1.Then,by usingthetuningrule(1.21),wederivethatthecriticweighterrordynamicscanbe formulatedas
wherethescalarterm ecH representstheresidualerrorduetoneuralnetworkapproximation.
Inadaptivecriticdesigns,weintendtoidentifytheparametersofthecriticnetworksoastoapproximatetheoptimalcostfunction.Ascommonlyrequiredwithin theadaptivecontrolfield[49],thepersistenceofexcitationassumptionisnaturally
4 Thecontrollawfunctionisdirectlycomputedasaclosed-loopexpressionofthecriticweight vectorinthissinglenetworkstructure.Anadditionalactionnetworkisbuiltwhenimplementing thesynchronouspolicyiterationalgorithm[60, 127]toimprovethesequentialupdates[58, 130] intermsofsavingcomputationtimeandavoidingdynamicsknowledge.
Fig.1.1 TheADP-basedlearningprocessandoptimalcontroldesigndiagram.Thesolidline representsthesignalflowwhilethedashedlinedenotestheneuralnetworkback-propagatingpath. Thedottedcomponentindicateswhetherthereisanimprovementmoduleaddedtothelearning criterion.Ifitissetto“N”,thereisnoimprovementanditisactuallythetraditionallearningrule (1.21).Ifitissetto“Y”,therewillbeanimprovedmodule(discussedlater)duringthelearning process
neededduringadaptivecriticlearning.Notethatbasedon[127, 129],thepersistence ofexcitationconditionensuresthat λmin (φ1 φ T 1 )> 0,whichissignificanttoperform theclosed-loopstabilityanalysis.Thefollowingassumptioniscommonlyusedsuch asin[13, 88, 100, 127].
Assumption1.1 Thecontrolmatrix g ( x ) isupperboundedsuchthat g ( x ) ≤ λ g , where λ g isapositiveconstant.Onthecompactset Ω ,theterms ∇ σc ( x ), ∇ εc ( x ),and ecH areallupperboundedsuchthat ∇ σc ( x ) ≤ λσ , ∇ εc ( x ) ≤ λε ,and |ecH |≤ λe , where λσ , λε ,and λe arepositiveconstants.
Definition1.2 (cf. [88, 100, 144])Foranonlinearsystem ˙ x = f ( x (t )),itssolution issaidtobeUUB,ifthereexistsacompactset Ω ⊂ Rn suchthatforall x 0 ∈ Ω ,there existabound Λ andatime T (Λ, x 0 ) suchthat x (t ) x e ≤ Λ forall t ≥ t0 + T , where x e isanequilibriumpoint.
Lemma1.1 (cf. [127]) Forsystem(1.1)andtheconstructedneuralnetwork(1.15), wesupposethatAssumption 1.1 holds.Theapproximateoptimalcontrollawisgiven by(1.18)andthecriticnetworkistunedbasedon(1.21).Then,theclosed-loop systemstateandthecriticweighterrorareUUB.
TheUUBstabilityactuallyimpliesthatafteratransitionperiod T ,thestatevector remainswithintheballofradius Λ aroundtheequilibriumpoint.Notethattheproofof suchUUBstabilityisperformedbyemployingthewell-knownLyapunovapproach. BasedonLemma 1.1,thecriticweighterror ˜ ωc isupperboundedbyafiniteconstant. Then,accordingto(1.17)and(1.18),wecanfindthat
isalsoupperbounded.Thisimpliesthatthenear-optimalcontroller ˆ u ∗ ( x ) canconvergetoaneighborhoodoftheoptimalvalue u ∗ ( x ) withafinitebound.Besides,this boundcanbesetadequatelysmallbyadjustingtherelatedparameterslikethecritic learningrate.
ItisalsoworthmentioningthatthepreviousADP-basedoptimalregulation methodprovidesthebasisforfurtheradaptivecriticcontroldesigns.Notethatthe dynamicaluncertaintiesarenotincludedinsystem(1.1).Consideringtheuniversalityoftheuncertainphenomenon,itisindeednecessarytoextendtheADP-based optimalcontroldesignapproachtorobuststabilizationproblemsandinvestigatethe robustnessofADP-basedcontrollersunderuncertainenvironment.
1.3NonlinearRobustControlDesignwithMatched Uncertainties
ThissectionmainlypresentstheresultsaboutADP-basedrobustcontroldesign formatcheduncertainnonlinearsystems[3, 4, 14, 23, 25, 41, 42, 45, 75, 119, 133, 138–141, 144, 178, 199].ThereareseveralcategoriesofADP-basedrobust controlstrategies,suchastheleast-square-basedproblemtransformationmethod [3, 4],adaptive-design-basedproblemtransformationmethod[75, 119, 133, 139–141, 144, 199],data-basedproblemtransformationmethod[138, 178],thecombined slidingmodecontrolmethod[23],andtherobustADPmethod[14, 25, 41, 42, 45]. Wewillnotonlyexhibittherobustnessoftheoptimalcontrollerwithrespecttothe nominalsystembutalsodiscusstheoptimalityoftherobustcontroller.Actually, someofthesemethods[3, 4, 14, 25, 42, 45, 199]canbeappliedtounmatched robustcontroldesign.
1.3.1ProblemTransformationMethod
Ifdynamicaluncertaintiesarebroughtintosystem(1.1)byvariouschangesduring theoperationofthecontrolledplant,wehavetopayattentiontotherobustnessof thedesignedcontroller.Weconsideraclassofcontinuous-timenonlinearsystems subjectedtouncertaintiesanddescribedby
wheretheterm g ( x )d ( x ) reflectsakindofdynamicaluncertaintiesmatchedwith thecontrolmatrix.Weassume d (0) = 0,soastokeep x = 0asanequilibriumof
thecontrolledplant.Itisoftenassumedthattheterm d ( x ) isboundedbyaknown function d M ( x ),i.e., d ( x ) ≤ d M ( x ) with d M (0) = 0. Consideringtheuncertainnonlinearsystem(1.24),forcopingwiththerobust stabilizationproblem,weshoulddesignacontrollaw u ( x ),suchthattheclosedloopstatevectorisstablewithrespecttodynamicaluncertainties.Inthissection, byadoptingapositiveconstant ρ andspecifying Q ( x ) = ρ d 2 M ( x ),weshowthatthe robustcontrolproblemcanbeaddressedbydesigningtheoptimalcontrollerofthe nominalplant(1.1),wherethecostfunctionisstillgivenby(1.3)andthemodified utilityisselectedas
Notethatinthissituation,theoptimalcontrolfunctioniskeptunchangedevenifthe modifiedutilityisemployed.Forsystem(1.1)andcostfunction(1.3)withmodified utilityfunction(1.25),theHamiltonianbecomes
Observingthemodifiedutilityfunction(1.25)andusingtheoptimalcontrollaw (1.8)again,theHJBequationwithrespecttothemodifiedoptimalcontrolproblem becomes
Wefirstshowthestabilityoftheclosed-loopformofthenominalsystembased ontheapproximateoptimalcontrollaw.
Theorem1.1 (cf.[139]) Forthenominalsystem(1.1)andcostfunction(1.3)with modifiedutilityfunction(1.25),theapproximateoptimalcontrollawobtainedby (1.18)guaranteesthattheclosed-loopsystemstateisUUB.
Then,weshowhowtoguaranteetherobuststabilizationofthematcheduncertain system(1.24)basedonthedesignednear-optimalcontrollaw.
Theorem1.2 (cf.[133]) Forthenominalsystem(1.1)andcostfunction(1.3)with modifiedutilityfunction(1.25),theapproximateoptimalcontrolobtainedby(1.18) guaranteesthattheclosed-loopformoftheuncertainnonlinearplant(1.24)possessesUUBstabilityif ρ>λmax ( R ).
Theorems 1.1 and 1.2 exhibittheclosed-loopUUBstabilityofthenominalplant (1.1)anduncertainplant(1.24),respectively,whenapplyingthedesignednearoptimalcontrollaw(1.18).Oneshouldpayspecialattentiontothefactthatthe closed-loopformoftheuncertainplantisUUBwhenusingtheapproximateoptimal
Another random document with no related content on Scribd:
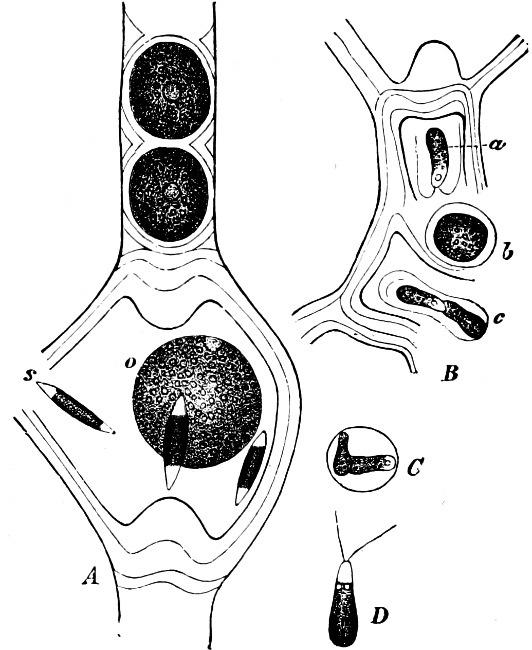
F��. 48. Scenedesmus quadricauda.
Order 5. Protococcaceæ. The cells are motionless, free or affixed on a stalk (e.g. Characium, Fig. 49), either separate or loosely bound to one another; they never form multicellular individuals. Multiplication by division is nearly always wanting. Reproduction takes place by swarmspores, which have 1 or 2 cilia, and sexual reproduction in some by gamete-conjugation. The principal genera are: Chlorococcum, Chlorochytrium, Chlorocystis, Scotinosphæra, Endosphæra, Phyllobium, Characium, Ophiocytium, Sciadium.
F�� 49 Characium strictum A The cell-contents have divided into many swarmspores B Swarmspores escaping
Order 6. Hydrodictyaceæ. The individuals are unicellular but several unite after the zoospore-stage into definitely formed families (cœnobia). Ordinary vegetative division is wanting, but asexual reproduction takes place by zoospores (or by motionless cells without cilia), which unite and form a family similar to the motherfamily, inside the mother-cell, or in a mucilaginous envelope. Where sexual reproduction is found it takes place by gamete-conjugation. The principal genera are: Pediastrum (Fig. 50), Cœlastrum, Hydrodictyon (Fig. 51).
F�� 5O Pediastrum asperum
F��. 51. Hydrodictyou reticulatum. A A cell where the zoospores are on the point of arranging themselves to form a net. B A cell with gametes swarming out.
The cœnobium of Hydrodictyon reticulatum (Water-net) is formed of a large number of cells which are cylindrical, and attached to one another by the ends (Fig. 51). The asexual reproduction takes place by zoospores, which are formed in large numbers (7,000–20,000) in each mother-cell, within which they move about for a time, and then come to rest and arrange themselves into a new net (Fig. 51 A) which is set free by the dissolution of the wall of the mother-cell,
grows, and becomes a new cœnobium. The sexual reproduction takes place by gamete-conjugation. The gametes are formed in the same manner as the zoospores, but in larger numbers (30,000–100,000), and swarm out of the mother-cell (Fig. 51 B). The zygote forms, on germination, 2–5 large zoospores, each with one or two cilia, these generally swarm about for a time, and after a period of rest become irregular thorny bodies (polyhedra); their contents again divide into zoospores, the thorny external coating of the polyhedra is cast off, and the zoospores, surrounded by the dilated internal coating, unite to form a small family, which produces several others in the manner described.
Family 2. Confervoideæ.
The individuals are always multicellular, the cells firmly bound together and united into unbranched or branched filaments, expansions, or masses of cells which grow by intercallary divisions or have apical growth. In the first seven orders the cells are uninuclear, but the cells of the remaining three orders contain several nuclei. Asexual reproduction by zoospores, akinetes or aplanospores. Sexual reproduction by isogamous or oogamous fertilisation.
The Confervoideæ, through the Ulvaceæ, are connected with the Tetrasporaceæ, and from the Coleochætaceæ, which is the most highly developed order, there are the best reasons for supposing that the Mosses have taken their origin. The Cladophoraceæ show the nearest approach to the Siphoneæ.
Order 1. Ulvaceæ. The thallus consists of one or two layers of parenchymatous cells, connected together to form either a flat membrane (Monostroma, Ulva) or a hollow tube (Enteromorpha), and may be either simple, lobed, or branched. Reproduction takes place by detached portions of the thallus; or asexually by zoospores or akinetes. Gamete-conjugation is known to take place in some members of this order, the zygote germinating without any restingstage. The majority are found in salt or brackish water.

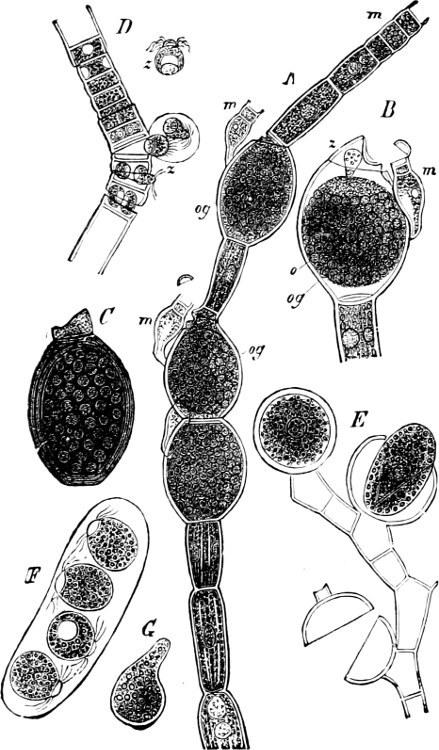
F��. 52. Ulothrix zonata: a portion of a filament with zoospores, which are formed two in each cell (zoosporangium); the dark spots are the red “eye-spots”; 1, 2, 3, 4, denote successive stages in the development of the zoospores; b a single zoospore, v the pulsating vacuole; c portion of a filament with gametes, sixteen are produced in each gametangium; d free gametes, solitary or in the act of conjugation; e the conjugation is completed, and the formed zygote has assumed the resting-stage.
Order 2. Ulothricaceæ. The thallus consists normally of a simple unbranched filament (sometimes a small expansion consisting of one layer of cells is formed, as in Schizomeris and Prasiola which were formerly described as separate genera). Asexual reproduction takes place by means of zoospores (with 1, 2, or 4 cilia), akinetes or aplanospores; the last named may germinate immediately, or only after a period of rest. Sexual reproduction takes place by the conjugation of gametes of about the same size, each having two cilia (Fig. 52 d). The zygote of Ulothrix, on germination, produces a brood of zoospores which swarm for a time and then elongate to become Ulothrix-filaments (alternation of generations). The gametes may also germinate without conjugation in the same manner as the zoospores. The principal genera are: Ulothrix, Hormidium, Conferva, Microspora.—Ulothrix zonata is very common in running fresh water. Nearly all the species of Hormidium occur on damp soil, tree-stems and stones.
Order 3. Chætophoraceæ. The thallus consists of a single, branched, erect or creeping filament of cells, often surrounded by mucilage. The cells have only one nucleus. Asexual reproduction by zoospores with 2 or 4 cilia, by akinetes, or aplanospores. In many,
conjugation between gametes with 2 cilia may be found. They approach on one side, Ulothricaceæ, and on the other, Mycoideaceæ. The principal genera are: Stigeoclonium, Draparnaldia, Chætophora, Entoderma, Aphanochæte, Herposteiron, Phæothamnion, Chlorotylium, Trichophilus, Gongrosira, Trentepohlia. Most of the species of Trentepohlia are coloured red by the presence of a red colouring material, which occurs in addition to the chlorophyll. They are aerial Algæ which live on stones (T. jolithus, “violet stone,” so named on account of its violet-like odour in rainy weather), on bark and old wood (T umbrina), or on damp rocks (T. aurea). Trichophilus welckeri lives in the hair of Bradypus.
Order 4 Mycoideaceæ. The thallus is discoid, consisting of one or more celllayers, and is always attached Asexual reproduction by zoospores with 2 or 4 cilia. Sexual reproduction in some species by the conjugation of gametes with 2 cilia. This order forms the connecting link between Chætophoraceæ and Coleochætaceæ. The species occur in fresh water (Chætopeltis) as well as in salt (Pringsheimia), on the carapace of tortoises (Dermatophyton = Epiclemmydia), or endophytic between the cuticle and the epidermal cells of the leaves of tropical plants, destroying the leaf-tissue (Mycoidea).
Order 5. Cylindrocapsaceæ. The thallus consists of a simple (rarely, in parts, formed of many rows) unbranched filament, attached in the young condition, which has short cells with a single nucleus, and is enveloped in a thick envelope with a laminated structure. Asexual reproduction by zoospores with 2 cilia, which are formed 1, 2, or 4 in each vegetative cell. The antheridia are produced by a single cell, or a group of cells, in a filament, dividing several times without increasing in size. Two egg-shaped spermatozoids, each with 2 cilia (Fig. 53 D), are formed in each antheridium, and escape through an aperture in the side; in the first stages they are enclosed in a bladder-like membrane (Fig. 53 B, C). Other cells of the filament swell out and form oogonia (Fig. 53 A), which resemble those of Œdogonium. After fertilisation, the oospore surrounds itself with a thick wall, and assumes a reddish colour. The germination is unknown. The unfertilised oospheres remain green, divide often into 2–4 daughter-cells, and grow into new filaments.
F��. 53. Cylindrocopsa involuta. A Oogonium with oosphere (o) surrounded by spermatozoids (s). B Two antheridia, each with two spermatozoids. C Spermatozoids surrounded by their bladder-like membrane. D Free spermatozoid.
This order, which only includes one genus, Cylindrocapsa, forms the connecting link between Ulothricaceæ and Œdogoniaceæ. The few species (4) occur only in fresh water.
Order 6. Œdogoniaceæ. The thallus consists of branched (Bulbochæte) or unbranched (Œdogonium) filaments, attached in the early stages. The cells may be longer or shorter, and have one nucleus. Asexual reproduction by zoospores, which have a chaplet of cilia round the base of the colourless end (Fig. 6 a). Sexual reproduction takes place by oogamous fertilisation. On the germination of the oospore, 4 zoospores are formed (Fig. 54 F). They occur only in fresh or slightly brackish water. The division of the cells takes place in quite a peculiar and unusual manner. At the upper end of the cell which is about to divide, a ring-shaped thickening of soft cellulose is formed transversely round the wall; the cell-nucleus of the mother-cell and the protoplasm then divide by a transverse wall into two portions of similar size, and the cell-wall bursts transversely along the central line of the thickened ring. The cell-wall thus divides into two parts—the upper one short, the “cap,” and the lower one much longer, the “sheath.” The portions of the original cell-wall now separate from each other, the cellulose ring extending, and supplying an additional length of cell-wall between them. The cap and sheath will project a little in front of the piece thus inserted. The dividing wall between the two new cells is formed near to the uppermost edge of the sheath, and gradually becomes thicker and firmer. The inserted piece of wall forms the larger part of the wall of the upper cell: the remainder is formed by the cap. This mode of division is repeated exactly in the same way, and new caps are formed close below the first one, one for every division.
F�� 54 A Œdogonium ciliatum A Female plant with three oogonia (og) and dwarf-males (m) B An oogonium with spermatozoid (z) seen entering the oosphere (o)
having passed through an aperture near the summit of the oogonium; m dwarf-male. C Ripe oospore. D Œdogonium gemelliparum F Portion of a male filament from which spermatozoids (z) are emerging E Portion of filament of Bulbochæte; the upper oogonium still encloses the oospore, in the central one the oospore is escaping while the lower one is empty F Four zoospores developed from an oospore G Zoospore germinating
Fertilisation takes place in the following way The oogonium is a large ellipsoidal, swollen cell (og, in Fig. 54 A), whose contents are rounded off into an oosphere with a colourless receptive-spot (see B); an aperture is formed in the wall of the oogonium, through which the spermatozoids are enabled to enter (B). The spermatozoids are produced either directly, as in D (in pairs), in basal cells of the filament, or indirectly. In the latter case a swarmspore (androspore) is formed which comes to rest, attaches itself to an oogonium, germinates, and gives rise to a filament of a very few cells—dwarfmale (A, B, m). The spermatozoids are formed in the upper cell of the dwarf-male (m), and are set free by the summit of the antheridium lifting off like a lid. On the germination of the oospore (C), which takes place in the following spring, 4 zoospores are produced (F) (i.e. the sexual generation); these swarm about for a time, and ultimately grow into new filaments.
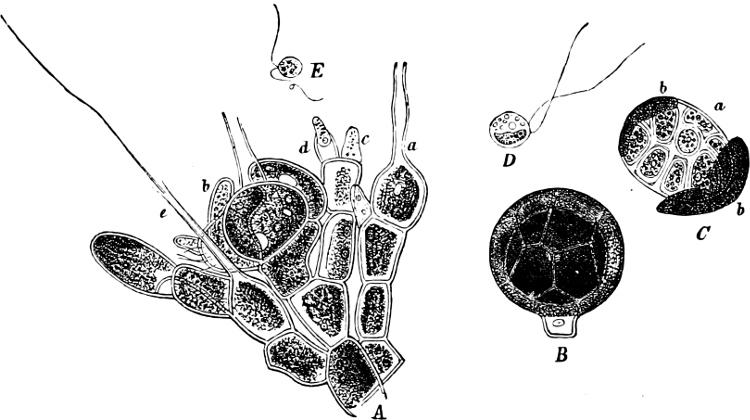
F��. 55.—Coleochæte pulvinata. A A portion of a thallus with organs of reproduction; a oogonium before, b after fertilisation; c an antheridium, closed; d open, with emerging spermatozoid. B Ripe oogonium, with envelope. C Germination of the oospore. D Zoospore. E Spermatozoid.
Order 7. Coleochætaceæ. The thallus is always attached, and of a disc- or cushion-shape, formed by the dichotomous branching of filaments of cells united in a pseudo-parenchymatous manner. Each cell has only one nucleus. Asexual reproduction by zoospores with 2 cilia (Fig. 55 D), which may arise in all the cells. Sexual reproduction by oogamous fertilisation. The spermatozoids resemble the swarmspores, but are smaller (E), and originate singly (in the species figured) in small conical cells (c, d in A). The oogonia are developed at the extremities of certain branches: they are bottleshaped cells with very long and thin necks (trichogyne), open at the end (a in A); at the base of each oogonium is a spherical oosphere. The spermatozoids reach the oosphere through the trichogyne, or through an aperture in the wall when the trichogyne is absent, and fertilisation having taken place, the oogonium becomes surrounded by a cell-layer (envelope), which grows out from the cells near its
base (b in A), and in this way a kind of fruit is formed (B) (spermocarp, cystocarp).
The oospore, next spring, divides and forms a parenchymatous tissue (homologous with the Moss-sporophyte); this bursts open the envelope (C), and a zoospore (homologous with the spores of the Moss-capsule) arises in each of the cells, and produces a new Coleochæte. We have then, in this case, a still more distinct alternation of generations than in Œdogonium. Only one genus, Coleochæte, is known, but it contains several species, all living in fresh water.
Order 8. Cladophoraceæ. This order is probably derived from the Ulothricaceæ. The thallus consists of a single, unbranched or branched filament, generally with an apical cell. The cells have each 2 or more nuclei. Asexual reproduction by zoospores with 2 or 4 cilia, and by akinetes. Conjugation of gametes with 2 cilia is found in some genera. They occur in salt as well as in fresh water. The principal genera are: Urospora, Chætomorpha, Rhizoclonium, Cladophora; of the last named genus the species C. lanosa and C. rupestris are common in salt water; C. fracta and C. glomerata in fresh water.
Order 9. Gomontiaceæ. Gomontia polyrrhiza, the only species hitherto known, is found on old calcareous shells of certain salt water Molluscs.
Order 10. Sphæropleaceæ. The thallus consists of free, unbranched filaments, with very elongated multinuclear cells. The vegetative cells form no zoospores. Sexual reproduction by oogamous fertilisation (see page 13, Fig. 10 B). The oospore has a thick wall (Fig. 10 D) studded with warts, and assumes a colour resembling red lead. It germinates only in the following spring, and produces 1–8 zoospores, each with 2 cilia (Fig. 10 E), which grow into new filaments. Only one species, Sphæroplea annulina, is known.
Family 3. Siphoneæ.
The thallus has apical growth, and in the vegetative condition consists generally of one single (in the Valoniaceæ most frequently
of more) multinuclear cell, which may be much branched, and whose separate parts in the higher forms (e.g. Bryopsis, Fig. 57; Caulerpa, Fig. 59, etc.) may be differentiated to perform the various physiological functions (as root, stem and leaf). Vegetative multiplication by detached portions of the thallus (gemmæ); asexual reproduction by zoospores, akinetes, or aplanospores. Sexual reproduction by gamete-conjugation, rarely by oogamous fertilisation. The zygote or oospore germinates as a rule without any resting-stage.
F��. 56. Botrydium granulatum: a an entire plant forming swarmspores; b swamspores; c an individual with gametangia; d, gamete; e, f, g conjugation; h zygote seen from above; i the same in a lateral view.
Most of the Siphoneæ occur in salt water or on damp soil. Many (e.g. Dasycladaceæ) are very much incrusted with lime, and occur, in the fossilized condition, in the deposits from the Cretaceous period to the present time. The Siphoneæ are connected by their lowest forms (Botrydiaceæ or Valonia) with the Protococcaceæ, but show also, through the Valoniaceæ, points of relationship to the Cladophoraceæ.
Order 1. Botrydiaceæ. The thallus in the vegetative condition is unicellular, club-shaped, with a small single (Codiolum) or repeatedly dichotomously branched system of colourless rhizoids (Botrydium, Fig. 56 a), by which it is attached to objects immersed in salt water
(Codiolum) or to damp clay soil (Botrydium). Asexual reproduction by zoospores with one (Botrydium) or two cilia, and by aplanospores. The sexual reproduction is only known in Botrydium, and takes place in the following manner: in the part of the thallus which is above ground and in an active vegetative condition, several round cells (Fig. 56 c) are formed, which may be green or red according as they grow under water, or exposed to the strong light of the sun. These cells must be considered as “gametangia” as they produce many gametes (d) provided with two cilia. The zygote (h, i) formed by the conjugation (e, f, g) may either germinate immediately, or become a thick-walled resting-cell of an irregular, angular form.
Order 2. Bryopsidaceæ. The thallus in the vegetative condition is unicellular, and consists at the lower extremity of branched rhizoids, while the upper portion is prolonged into a stem-like structure of unlimited growth, producing, acropetally, branches and leaf-like structures The latter have limited growth, and are separated by a cross wall from the stem, and become gametangia, or drop off The gametes have two cilia, and are of two kinds: the female, which are green and large and the male, which are of brownish colour and smaller Zoospores or any other method of asexual reproduction are unknown Only one genus, Bryopsis, living in salt water
F��. 57. Bryopsis plumosa. A the plant, natural size. B A portion (enlarged) which shows the growing point (v), and the leaves derived from it in acropetal succession.
Order 3 Derbesiaceæ. Only one genus, Derbesia, living in saltwater The zoospores, which are formed in a few lateral, swollen zoosporangia, possess one nucleus which has arisen through the coalescence of several, and they resemble the zoospores of Œdogonium by having a circle of cilia attached at the base of the colourless spot.
Order 4. Vaucheriaceæ. The thallus consists, in the vegetative condition, of a single irregularly or dichotomously branched cell, without differentiation into stem or leaf; root-like organs of attachment may however occur Asexual reproduction by zoospores, which are formed singly in the extremity of a branch cut off by a transverse wall. They contain many nuclei, and bear small cilia situated in pairs, which give the appearance of a fine “pile” covering the whole or a great part of the surface. Akinetes, aplanospores, and phytoamœbæ (naked masses of protoplasm, without cilia, which creep like an amœba on a substratum) may occur under certain conditions.
The sexual reproductive organs are formed on short lateral branches, and are separated from the vegetative cell (Fig. 58 A) by
cell-walls. Numerous spermatozoids, each with two cilia, are developed in the coiled antheridium (A, b). The oogonium is a thick, egg-shaped, often oblique cell, with its protoplasm rounded into an oosphere, which has a hyaline “receptive-spot” (A, a) immediately beneath the aperture formed in the wall of the oogonium. A slimy mass, which serves to receive the spermatozoids, is formed in some species in this aperture. The spermatozoids when liberated swim towards and enter the oosphere, which then immediately surrounds itself with a thick cell-wall. The mature oospore (B) contains a large quantity of oil. At germination the outer cell-wall bursts and a new plant is formed. There is only one genus, Vaucheria, with species living in salt as well as in fresh water and on damp soil.
F�� 58 Vaucheria sessilis A Fertilisation; b the antheridia; a the oogonia; a the receptive spot B Oospore
Order 5. Phyllosiphonaceæ are parasites in the leaves and stalks of Flowering-plants.
Order 6. Caulerpaceæ. The thallus has distinct differentiation into root, stem and leaf-like members (Fig. 59); it is unicellular. Within the cell, strong, branched threads of cellulose extend from one side to the other serving as stays to support the thallus. Reproduction takes place by detached portions of the thallus; no other modes of reproduction are known. This order may most approximately be classed with the Bryopsidaceæ. The genus Caulerpa consists of more than seventy species which inhabit the tropical seas.
Order 7. Codiaceæ. The thallus has various forms, but without distinct differentiation in stem- or leaf-structures, sometimes (e.g. Halimeda) it is very much incrusted with lime. In the early stages it is unicellular (later, often multicellular), very much branched, with the branches, at any rate partly, so united or grown in amongst one another (Fig. 60) that an apparently parenchymatous cellular body is formed. Akinetes or aplanospores are wanting; zoospores (or gametes?) may be developed in some species, however, in special swollen sporangia. Fertilisation similar to that in Bryopsis occurs perhaps in Codium. They are all salt water forms.
Order 8. Valoniaceæ. The thallus is generally multicellular, without differentation into stem- or leaf-structures, but the cells are sometimes united together and form a leaf-like reticulate expansion (e.g. Anadyomene). Zoospores are known in some, and they are then formed directly in the vegetative cells. In others (e.g. Valonia), a mass of protoplasm, which maybe separated through the damaging of a cell, can surround itself with a cell-wall, and grow into a new plant. No other modes of reproduction are known. The most important genera are: Valonia, Siphonocladus, Chamædoris, Struvea, Microdictyon, Anadyomene They are all salt water forms
F��. 59.—Caulerpa prolifera (natural size).
As already pointed out, the Valoniaceæ occupy a somewhat central position among the Siphoneæ, and present points of similarity and contrast with the Botrydiaceæ and the Bryopsidaceæ through Valonia, with the Dasycladaceæ through Chamædoris, and also with the Cladophoraceæ through Siphonocladus, and Struvea
Order 9. Dasycladaceæ. The thallus consists of an axile longitudinal cell, destitute of transverse walls, attached at the base by root-like organs of attachment, and producing acropetally whorls of united, single or branched, leaf-like structures with limited growth. Asexual reproduction is wanting. Sexual reproduction by conjugation

































