INGENIERÍA MECÁNICA
AUTOMOTRIZ



NO TE ESTRESES!!!!!
EDITOR : Rafael



Instituto de Ingeniería Mecánica Automotriz

EDITOR : Rafael Navarro Mancilla
DIRECTOR: Mitzy Karen Gonzáles Salazar
Dirección: Calle Paseo Tollocan PTE. #2915 Col. Nueva Oxtotitlán, C.P. 50100 Toluca, Estado de México Junio 2
31/05/2025
Agradecimientos
En esta revista agradezco al docente quien me brindo conocimiento y un buen acompañamiento quien si no fuera por ella no fuera posible crear esta revista ya que nos dijo que podíamos exentar gracias a una revista bien hecha , esto me hizo presentar esta revista con temas relevantes a la materia de probabilidad y estadística cada pagina conlleva un poco de toda la información que hay sobre estos temas y agradezco a la institución de ingeniería mecánica automotriz por los talleres de computo para poder elaborar esta revista de una forma mas practica y sencilla .
1.MODELO MATEMÁTICO

2.FENÓMENOS PROBABÍLISTICOS
3.NATURALEZA Y OBJETIVOS DE LA ESTADÍSTICA
4.EL MÉTODO ESTADÍSTICO Y LA FRECUENCIA RELATIVA
5.ESTADÍSTICA DESCRIPTIVA
6.ORGANIZACIÓN Y PRESENTACIÓN DEL CONJUNTO DE DATOS
7.ORDENACIÓN Y TABLAS DE FRECUENCIA
8.LA SUMATORIA Y SUS PROPIEDADES
9.CONSTRUCCIÓN NUMÉRICA DE LA TABLA DE FRECUENCIA
10.DISTRIBUCIÓN DE FRECUENCIA RELATIVA ACUMULADA
11.MEDIDAS DESCRIPTIVAS PARA UN CONJUTO DE DATOS
12.MEDIDAS DE CENTRALIZACIÓN O DE TENDENCIA CENTRAL
13.MEDIDAS DE DISPERSIÓN O ESPARCIMIENTO
14.MOMENTOS DE ORDENAR
15.MEDIDAS DE FORMA
16.FUNDAMENTOS DE PROBABILIDAD 17.DEFINICIÓN DE PROBABILIDAD
18.REGULARIDAD ESTADÍSTICA 19.POSTULADOS DE PROBABILIDAD
20.ESPACIOS MUESTRALES FINI
21.ESPACIOS MUESTRALES EQUIPROBABLES
22.CÁLCULO DE PROBABILIDAD
23.TÉCNICA PARA LA NUMERACIÓN DE PUNTOS MUESTRALES
24.EVENTOS INDEPENDIENTES
25.NOCIÓN DE VARIABLE ALEATORIA
26.VARIABLES DISCRETAS Y SUS DISTRIBUCIONES DE PROBABILIDAD
27. DEFINICÓN
28.LA DISTRIBUCIÓN DE PROBABILIDAD
29.DIFERENTES DISTRIBUCIONES DE PROBABILIDAD DISCRETAA
30.UNIFORME DISCRETA
31.BINOMIAL
32.GEOMÉTRICA
33.BINOMIAL NEGATIVA
34.HIPERGEOMÉTRICA
35.POISSON

MODELOS MATEMÁTICOS
El proceso de calcular el volumen de una naranja, suponerla de forma esférica o considerarla seccionada y cada sección inscrita en un cilindro, se corresponde con una simplificación y abstracción de la realidad. Este es un ejemplo de modelo estático
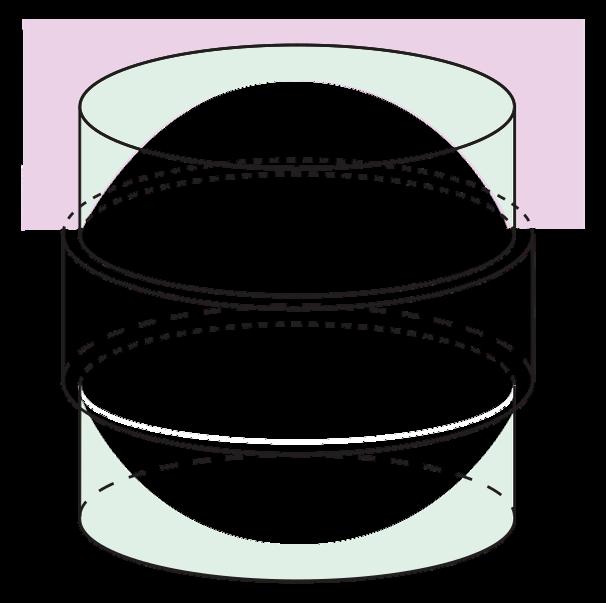

Una definición de modelo matemático es la siguiente: un modelo matemático es una construcción matemática abstracta y simplificada relacionada con una parte de la realidad y creada para un propósito particular. Así, por ejemplo, un gráfico, una función o una ecuación pueden ser modelos matemáticos de una situación específica

Las bondades de un modelo dependerán de la situación a ser modelada y del problema planteado Diferentes modelos de una misma situación producirán diferentes simplificaciones de la realidad y, en consecuencia, dan lugar a distintos resultados También, un mismo modelo puede servir para distintas situaciones. Por ejemplo, la función f(t)= Kert puede modelar tanto el crecimiento durante el tiempo t de una población que posea inicialmente K individuos con una tasa instantánea relativa de crecimiento r; así como puede modelar la capitalización continua de una suma de dinero K colocada
a col rn%st adnutreasn tye veal rtiiaebmlepso dt,e p aacrau elord cou aall bcaosntt
Existen diferentes tipos de modelos matemáticos: discretos, continuos, dinámicos, estáticos,
Un esquema que representa bastante bien el proceso de modelado matemático es el siguiente: De igual forma, el grafo creado por Euler, presentado antes para esquematizar el problema de los 7 puentes, es un ejemplo de modelo matemático: es una abstracción de la ciudad y de los puentes y una simplificación del fenómeno real. El modelo refleja, sin embargo, los aspectos sustanciales que son relevantes a la situación en estudio
Situación real
Interpretación
Contrastación
Evaluación
Resultados
Si los resultados no son satisfactorios afinamos el modelo
Especificación del problema (puede ser en lenguaje natural)
Matematización
Uso de herramientas algoritmos,...) Modelo matemático




Vivimos en un mundo regido tanto por leyes deterministas como por eventos inciertos. Los fenómenos probabilísticos pertenecen a este segundo grupo: son situaciones donde, aunque se conocen los posibles resultados, no se puede predecir con certeza cuál ocurrirá En estos contextos, el estudio de la probabilidad permite entender, modelar y tomar decisiones en escenarios donde domina la incertidumbre.
La probabilidad, tal como la conocemos hoy, tiene raíces en los juegos de azar del siglo XVII Matemáticos como Blaise Pascal y Pierre de Fermat establecieron las bases del cálculo de probabilidades en su correspondencia sobre problemas de apuestas Desde entonces, su desarrollo ha evolucionado hasta convertirse en una disciplina esencial en la estadística, la física, la economía, la biología, la inteligencia artificial y muchas otras áreas.

1 Fenómenos aleatorios simples
Eventos con pocos resultados posibles, como lanzar una moneda, sacar una carta o lanzar un dado.
2 Fenómenos aleatorios compuestos
Situaciones que resultan de la combinación de múltiples eventos simples, como lanzar dos dados o analizar secuencias genéticas
3. Fenómenos probabilísticos continuos
Modelan variables que pueden tomar infinitos valores dentro de un rango, como el peso de una persona o el tiempo que tarda un proceso industrial
4. Fenómenos estocásticos
Procesos evolutivos donde el resultado depende del azar y se desarrolla a lo largo del tiempo, como el crecimiento bursátil o la propagación de una enfermedad.

Interpretaciones de la probabilidad
Existen varias escuelas de pensamiento sobre cómo interpretar la probabilidad:
Frecuentista: define la probabilidad como la frecuencia relativa de un evento al repetir un experimento muchas veces.
Bayesiana: considera la probabilidad como una medida subjetiva del grado de creencia o conocimiento sobre un evento.
Clásica: basada en casos equiprobables, como en los juegos de azar
Importancia en la toma de decisiones
Comprender los fenómenos probabilísticos permite:
Reducir la incertidumbre en decisiones empresariales, científicas y personales
Optimizar estrategias en entornos complejos y variables
Prever comportamientos colectivos en sistemas sociales o naturales
Simular escenarios futuros para evaluar posibles resultados y riesgos


Estadística descriptiva. La estadística descriptiva comprende las técnicas que se emplean para resumir y describir datos numéricos. Son sencillas desde el punto de vista matemático y su análisis se limita a los datos coleccionados sin inferir en un grupo mayor. El estudio de los datos se realiza con representaciones gráficas, tablas, medidas de posición y dispersión.
Estadística inferencial. El problema crucial de la estadística inferencial es llegar a proposiciones acerca de la población a partir de la observación efectuada en muestras bajo condiciones de incertidumbre. Ésta comprende las técnicas que aplicadas en una muestra sometida a observación, permiten la toman de decisiones sobre una población o proceso estadístico. En otras palabras, es el proceso de hacer predicciones acerca de un todo basado en la información de una muestra. La inferencia se preocupa de la precisión de los estadígrafos descriptivos ya que estos se vinculan inductivamente con el valor poblacional.
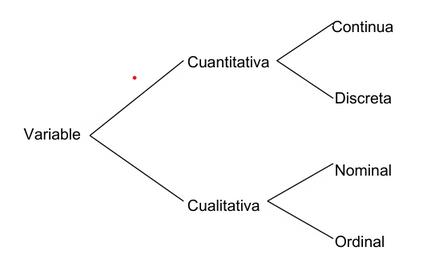
Variable. Se llama variable a una característica que se observa en una población o muestra, y a la cual se desea estudiar. La variable puede tomar diferentes valores dependiendo de cada individuo. Una variable se puede clasificar de la siguiente manera.
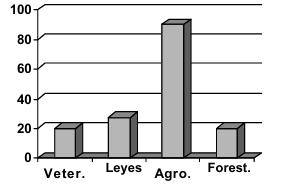
BARRAS Es un procedimiento gráfico para representar los datos nominales u ordinales Para cada categoría se traza una barra vertical en que la altura es la frecuencia absoluta de la categoría. El ancho de la barra es arbitrario.

Población. Es el conjunto de todos los elementos que presentan una característica común determinada, observable y medible. Por ejemplo, si el elemento es una persona, se puede estudiar las características edad, peso, nacionalidad, sexo, etc. Los elementos que integran una población pueden corresponder a personas, objetos o grupos (por ejemplo, familias, fábricas, emprersas, etc). Las características de la población se resumen en valores llamados parámetros.
Muestra La mayoría de los estudios estadísticos, se realizan no sobre la población, sino sobre un subconjunto o una parte de ella, llamado muestra, partiendo del supuesto de que este subconjunto presenta el mismo comportamiento y características que la población. En general el tamaño de la muestra es mucho menor al tamaño de la población Los valores o índices que se concluyen de una muestra se llaman estadígrafos y estos mediante métodos inferenciales o probabilísticos, se aproximan a los parámetros poblacionales.


El manejo de la información requiere de la ordenación de datos de tal forma que permita la obtención de una forma más fácil la obtención de conclusiones acerca de la muestra. Una primera ordenación se realiza mediante el manejo de tablas, en las que se ordenan los datos de acuerdo a ciertas características de los datos.
LafrecuenciarelativaacumuladaH :eslasumadelosvalores acumuladosdelafrecuenciarelativa i ∑nfi ∑Frecuenciarelativaacumulada=H =h = i i
i= N1 lasumadelasfrecuenciasrelativasquesehanacumulado,incluyendola clasesobrelaquese estacalculandolafrecuenciarelativa
Frecuencia
La frecuencia absoluta f(xi) se determina como el número de veces que se repite un dato xi

La frecuencia absoluta acumulada F: Para un determinado valor se considera como la frecuencia de cada dato x mas la suma de los valores anteriores a dicha suma i i
La frecuencia relativa h : es el cociente h =f/N , en algunas ocasiones se representa como n/N, donde N es el número total de datos, corresponde a la suma de todas la frecuencias individuales de cada clase, y n o f los datos en cada clase. Las frecuencias relativas representan el porciento de veces en que ocurre un dato. Como veremos en teoría de probabilidades, el concepto de frecuencia relativa nos conduce a un concepto de probabilidad i i i i i i
Frecuencias
Los gráficos son útiles porque ponen en relieve y aclaran las tendencias que no se captan fácilmente en la tabla, ayudan a estimar valores con una simple ojeada y brinda una verificación gráfica de la veracidad de las soluciones.
Histograma:
Esta formado por rectángulos cuya base es la amplitud del intervalo y tiene la característica que la superficie que corresponde a las barras es representativa de la cantidad de casos o frecuencia de cada tramo de valores, puede construirse con clases que tienen el mismo tamaño o diferente (intervalo variable) La utilización de los intervalos de amplitud variable se recomienda cuando en alguno de los intervalos, de amplitud constante, se presente la frecuencia cero o la frecuencia de alguno o algunos de los intervalos sea mucho mayor que la de los demás, logrando así que las observaciones se hallen mejor repartidas dentro del intervalo
DISTRIBUCIÓN DE FRECUENCIAS
Organización de datos agrupados
Definiciones
Los intervalos contienen los límites de clase que son los puntos extremos del intervalo Se denominan intervalos cerrados, cuando contienen ambos límites e intervalos abiertos si incluyen solo un límite
Limites Reales: Sirven para mantener la continuidad de las clases
Anchura o tamaño del intervalo: es la diferencia entre los límites reales de una clase
Número de clases: es el número total de grupos en que se clasifica la información, se recomienda que no sea menor que 5 ni mayor que 15
Marca de Clase: Es el punto medio del intervalo de clase, se recomienda observar que los puntos medios coincidan con los datos observados para minimizar el error
Frecuencia: es el número de veces que aparece un valor
Frecuencia Acumulada: Indica cuantos casos hay por debajo o arriba de un determinado valor o límite de clase.
Frecuencia Relativa: Indica la proporción que representa la frecuencia de cada intervalo de clase en relación al total, es útil para comparar varias distribuciones con parámetros de referencia uniformes.


ESTADÍSTICA DESCRIPTIVA
ESTADÍSTICA DESCRIPTIVA. GRÁFICOS. La estadística descriptiva o análisis exploratorio de datos ofrece modos de presentar y evaluar las características principales de los datos a través de tablas, gráficos y medidas resúmenes. En este capítulo presentaremos formas simples de resumir y representar gráficamente conjuntos de datos. El objetivo de construir gráficos es poder apreciar los datos como un todo e identificar sus características sobresalientes. El tipo de gráfico a seleccionar depende del tipo de variable que nos interese representar por esa razón distinguiremos en la presentación gráficos para variables categóricas y para variables numéricas.
POLÍGONO DE FRECUENCIAS El polígono de frecuencias es similar al histograma en muchos aspectos, pero pretende dar una imagen aproximada de la “curva” definida por la distribución de la variable. Para cosntruirlo se usan los mismos ejes que en el histograma. Se indica en la escala horizontal el punto medio de cada intervalo y en la escala vertical la escala densidad para ese intervalo, esto define pares (x, y) en el gráfico que se unen con tramos de líneas rectas. Se marcan además los puntos medios del intervalo que precede al primero y del que sigue al último.
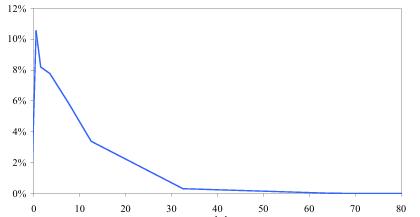
MEDIANA DE LAS DESVIACIONES
ABSOLUTAS (MAD) La MAD (median absolute deviations) es otra medida de dispersión que pretende dar una idea resumen de “distancias a un punto central” tal como ocurre con el desvío estándar. Pero, ¿en qué difiere del desvío estándar? - - - Considera la mediana como punto central de la distribución para calcular las desviaciones. Toma el valor absoluto de las desviaciones para eliminar el signo (en vez de elevar al cuadrado como hacemos al calcular el desvío estándar). Toma la mediana de las distancias (en vez de promediar como hacemos con s).
DESVIACIÓN ESTÁNDAR Y VARIANZA MUESTRAL
La desviación estándar mide cuan lejos se encuentran los datos de la media muestral. Un modo de medir la variabilidad de los datos de una muestra sería tomar algún valor central, por ejemplo la media, y calcular el promedio de las distancias a ella. Mientras mayor sea este promedio, más dispersión deberían presentar los datos. Sin embargo, esta idea no resulta útil, ya que las observaciones que se encuentran a la derecha de la media tendrán distancias (o desviaciones) positivas, en tanto que las observaciones menores que la media tendrán distancias negativas y la suma de las distancias a la media será inevitablemente igual a cero. Un modo de evitar este inconveniente es elevar las distancias al cuadrado y de este modo tener todos sumandos positivos.



Los datos estadísticos son el producto de las observaciones efectuadas en las personas y objetos en los cuales se produce el fenómeno que queremos estudiar. Dicho en otras palabras, son los antecedentes (en cifras) necesarios para llegar al conocimiento de un hecho o para reducir las consecuencias de este.
En el mundo de la investigación, la recolección de datos constituye uno de los pilares fundamentales del proceso científico Sin embargo, la utilidad real de los datos no depende únicamente de su obtención, sino también y especialmente de cómo son organizados, estructurados y presentados La forma en que se gestiona un conjunto de datos puede marcar la diferencia entre una investigación confusa y una que aporte conclusiones claras, sólidas y valiosas
Presentación de los Datos



Para lograr una presentación clara y comprensible de la información, se recurrió a distintos métodos visuales y tabulares:
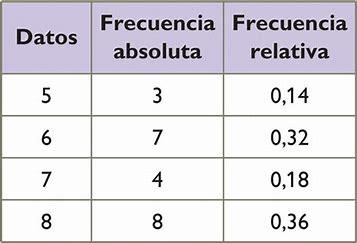
Tablas de frecuencia: utilizadas para mostrar la distribución de las variables discretas
Gráficos de barras y diagramas de pastel: empleados para ilustrar la proporción de categorías dentro de variables cualitativas.
Histogramas y polígonos de frecuencia: aplicados en el análisis de variables cuantitativas continuas, revelando la forma de la distribución de los datos
Diagramas de dispersión: útiles para explorar relaciones entre variables numéricas, como correlaciones entre edad e ingreso
Adicionalmente, se calcularon medidas estadísticas clave como la media, mediana, moda, así como desviación estándar y varianza, que permiten resumir y comprender de forma más profunda el comportamiento general del conjunto de datos
La presentación cuidadosa de los datos no solo permite visualizar patrones, sino que también facilita la toma de decisiones basada en evidencia, objetivo central de este estudio.
El conjunto de datos fue obtenido a través de [método de recolección: encuestas estructuradas, dispositivos de medición, registros administrativos, etc ], aplicados entre los meses de [fechas] a una muestra de [número de individuos o unidades] El instrumento de recolección fue diseñado para capturar tanto variables cualitativas (sexo, ocupación, nivel educativo) como cuantitativas (edad, ingresos mensuales, horas trabajadas) El diseño del cuestionario se sometió a una validación de contenido por expertos y se aplicó una prueba piloto para asegurar su claridad y fiabilidad
Una organización cuidadosa y una presentación clara del conjunto de datos no solo hacen más accesible la información, sino que constituyen la base para un análisis riguroso y replicable Esta fase no debe subestimarse, ya que prepara el terreno para interpretar correctamente los resultados y extraer conclusiones válidas y relevantes






En un mundo cada vez más guiado por la información, saber organizar y entender los datos se ha vuelto fundamental Dos herramientas básicas para lograrlo son la ordenación y las tablas de frecuencia Ambas forman parte de los primeros pasos en el análisis estadístico, y permiten visualizar patrones, identificar tendencias y tomar decisiones informadas
Ordenar datos significa organizarlos siguiendo un criterio, como de menor a mayor (orden ascendente) o de mayor a menor (orden descendente) Esto facilita su análisis, ya que permite identificar rápidamente valores extremos (el mínimo y el máximo), detectar repeticiones o agrupar datos similares. Por ejemplo, si tenemos las edades de los estudiantes de una clase: 12, 14, 13, 12, 15, 14, 13, ordenarlas nos da: 12, 12, 13, 13, 14, 14, 15.
Tipos de Frecuencia
1 Frecuencia absoluta (f): número de veces que aparece un valor.
2 Frecuencia relativa (fr): proporción respecto al total. Se calcula como
3 fr = f / total de datos.
4.Frecuencia acumulada (F): suma progresiva de las frecuencias absolutas.
¿Qué es una Tabla de Frecuencia?
Una tabla de frecuencia es una forma organizada de resumir datos Se utiliza para mostrar cuántas veces se repite cada valor en un conjunto de datos
Esta herramienta es muy útil en estadística para entender mejor la información y detectar patrones de manera rápida.
¿Para qué sirve?
Para ordenar los datos de forma clara.
Para saber qué valores son más frecuentes
Para facilitar la creación de gráficos (como diagramas de barras o histogramas)
Para resumir grandes cantidades de datos sin perder información importante

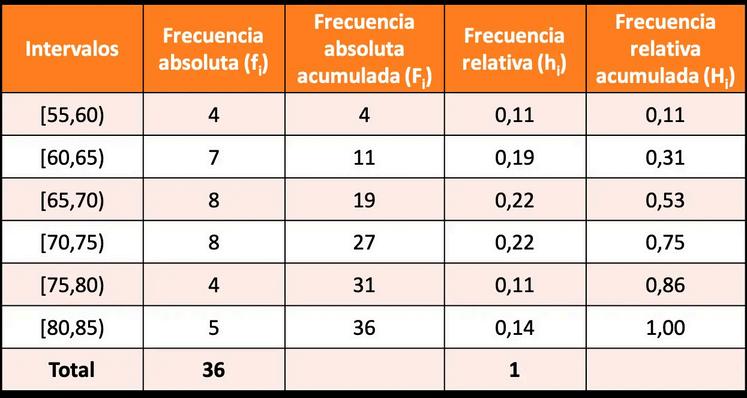
1.valores o categorías: Son los diferentes valores o categorías que se están analizando en la variable. Por ejemplo, si se está analizando la altura de las personas, los valores o categorías podrían ser «bajo», «medio» y «alto»
2.Frecuencia absoluta: Es el número de veces que cada valor o categoría ocurre en el conjunto de datos Esta columna muestra el recuento de ocurrencias para cada valor.
3 Frecuencia relativa: Es la proporción o porcentaje de veces que cada valor o categoría ocurre en el conjunto de datos. Se calcula dividiendo la frecuencia absoluta de cada valor entre el tamaño total de la muestra y se expresa como un decimal o un porcentaje
4.Frecuencia acumulada: Es la suma acumulada de las frecuencias absolutas o relativas a medida que se avanza a través de los valores o categorías en la tabla. Puede ser ascendente (sumando desde el valor más bajo hasta cada valor sucesivo) o descendente (sumando desde el valor más alto hacia abajo)

La sumatoria es una forma compacta y elegante de representar una suma de términos que siguen un patrón. En lugar de escribir todos los términos uno por uno, usamos el símbolo Σ acompañado de una expresión que describe cómo varían esos términos
Esto se lee como:
"La suma de f(i) desde i = a hasta i = b"
Σ es el símbolo de suma
i es el índice de la sumatoria (puede ser cualquier letra)
a es el valor inicial del índice.
b es el valor final del índice.
f(i) es la expresión que depende del índice i.
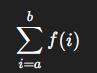

La sumatoria es mucho más que un símbolo matemático
Es una herramienta fundamental para analizar, modelar y resolver problemas en múltiples áreas del conocimiento
Dominar su uso y entender sus propiedades no solo agiliza los cálculos, sino que también te prepara para enfrentar desafíos más complejos en el mundo de la ciencia y la tecnología.
La sumatoria tiene aplicaciones vastas en diversos campos de las matemáticas y áreas relacionadas En el ámbito de la estadística, es fundamental para calcular promedios, varianzas y desviaciones estándar. La sumatoria proporciona un método sistemático para trabajar con datos agrupados y ayudar a los analistas a obtener conclusiones sobre un conjunto de datos.
¿Dónde se Usa la Sumatoria?
La notación de sumatoria se utiliza en muchas ramas de las matemáticas y la ciencia:
En estadística, para calcular promedios, varianza y desviación estándar
En álgebra, para expresar series numéricas
En cálculo, como paso previo a la integral definida.
En física, para representar sumas de fuerzas, energías, etc
En programación y ciencia de datos, para recorrer listas o conjuntos de datos.

Notación de la sumatoria
La notación de la sumatoria es una forma concisa y clara de representar sumas largas o complejas. En esta notación se especifican varios elementos clave:
El símbolo de sumatoria (Σ): Indica que se va a realizar una suma.
Límite inferior (i=1): Representa el valor inicial del índice de la suma
Límite superior (n): Representa el valor final del índice de la suma.
La expresión a sumar: Es el término que se va a sumar en cada iteración Puede ser una variable o una función de esa variable.

Para construir una tabla de frecuencias, sigue estos pasos:

1.Organiza los datos en diferentes categorías y construye una tabla en la que cada fila corresponda a una categoría
2.Calcula la frecuencia absoluta de cada categoría en la segunda columna de la tabla de frecuencias.
3.Calcula la frecuencia absoluta acumulada de cada categoría en la tercera columna de la tabla de frecuencias
4.Los componentes básicos de una tabla de frecuencia incluyen:
5.Categoría: Los distintos valores o grupos en los que se clasifica la información.
6.Frecuencia absoluta: El número total de veces que aparece cada categoría.
7 Frecuencia acumulada: La suma de las frecuencias absolutas hasta cierto punto en la tabla
8.Frecuencia relativa: La proporción de cada categoría respecto al total de observaciones.
¿Qué es una tabla de frecuencias?
Una tabla de frecuencias es una herramienta estadística que organiza y resume la información sobre la distribución de datos. Consiste en una estructura de columnas que muestra las distintas categorías o valores de una variable, junto con el número de veces que cada categoría ocurre en un conjunto de datos Esta tabla proporciona una visión general y ordenada de la frecuencia con la que aparecen los valores en una muestra o población, lo que permite analizar patrones, identificar tendencias y extraer conclusiones significativas.
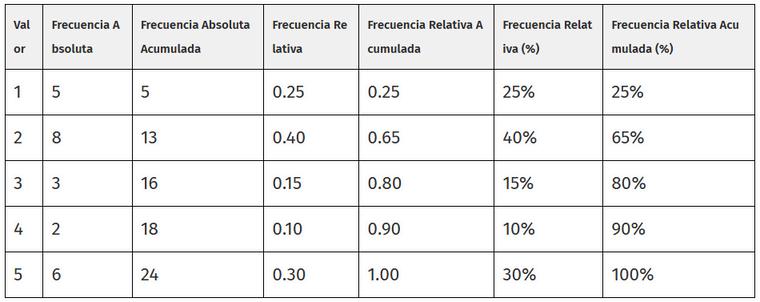
Calcula las frecuencias relativas

Interesante
Cuenta las ocurrencias
Cómo hacer una tabla de frecuencias
Recopila tus datos.
Identifica los valores únicos
Al construir una tabla de frecuencia, somos capaces de organizar datos de manera sistemática y visualizar la distribución de valores, lo que nos permite comprender mejor la variabilidad y la estructura de nuestros datos Además, nos brinda la capacidad de identificar valores atípicos, evaluar la simetría de la distribución y realizar comparaciones entre diferentes conjuntos de datos

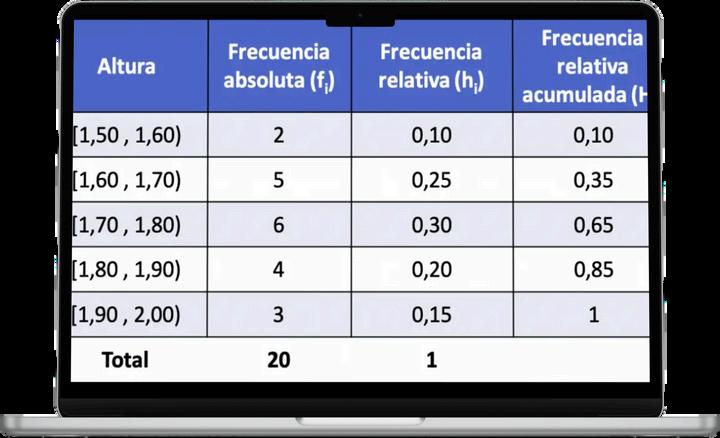
¿Qué es?

La frecuencia relativa acumulada es una forma de expresar cuántos datos han o cierto punto dentro de un conjunto de datos, en relación con el total Se obtiene sumando progresivamente las frecuenci n

¿Por qué es útil?

Nos permite acumulan los aumentan. Ideal para responder preguntas como: ¿Qué porcentaje de estudiantes obtuvo una nota de 8 o menos?

Se usa en estadística descriptiva, análisis de datos y gráficos de ojiva
Para calcular la frecuencia relativa acumulada, es necesario seguir algunos pasos básicos:
1 Determinar la Frecuencia Absoluta (fi): Identifica cuántas veces se repite cada valor en los datos.
2 Calcular la Frecuencia Relativa (hi): Divide la frecuencia absoluta de cada valor entre el total de observaciones.
3 Acumular las Frecuencias Relativas: Suma las frecuencias relativas de manera secuencial, comenzando desde la primera clase hasta llegar a la última.

En el ámbito educativo, el uso de la frecuencia relativa acumulada ayuda a los educadores a evaluar la distribución del rendimiento académico de los estudiantes. Esto permite identificar no solo cuántos estudiantes alcanzaron un cierto nivel de competencia, sino también analizar cuántos están por debajo o por encima de ella De esta manera, se pueden implementar estrategias personalizadas de enseñanza y mejorar los métodos pedagógicos
En el ámbito del marketing y la investigación de mercado, analizar la frecuencia relativa acumulada permite a las empresas segmentar a los consumidores según comportamientos de compra, preferencias o características demográficas Por ejemplo, una empresa puede descubrir que un 70% de sus clientes prefieren un determinado producto, lo que les permitirá enfocar sus esfuerzos de marketing de manera más efectiva
Las instituciones financieras utilizan las frecuencias relativas acumuladas para evaluar el riesgo crediticio, permitiendo una toma de decisiones más informada sobre la concesión de créditos Al entender cómo se distribuyen las calificaciones de riesgo entre los solicitantes, se pueden establecer políticas de otorgamiento que minimicen los impagos y maximicen la rentabilidad.
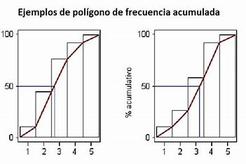



La desviación estándar siempre es cero cuando todos los datos son iguales.
Esto ocurre porque no hay variabilidad: todos los valores están exactamente en el mismo punto, por lo tanto, no se dispersan respecto a la media.


¿Qué son las estadísticas descriptivas?
Medidas de las estadísticas descriptivas
Todas las estadísticas descriptivas son medidas de tendencia central o medidas de variabilidad, también denominadas medidas de dispersión. Las medidas de tendencia central se especializan en los valores típicos o medios de los conjuntos de conocimientos; mientras que las medidas de variabilidad se especializan en la dispersión de los conocimientos Estas dos medidas utilizan gráficos, tablas y discusiones generales para ayudar a las personas a comprender el significado de los datos analizados
Las estadísticas descriptivas son coeficientes descriptivos breves que resumen un conjunto de datos determinado, que puede ser una representación del conjunto o una muestra de una población. Las estadísticas descriptivas se debilitan en medidas de tendencia central y medidas de variabilidad (difusión). Las medidas de tendencia central incluyen la media, la mediana y la moda, mientras que las medidas de variabilidad incluyen la desviación de la calidad, la varianza, las variables mínima y máxima y, por consiguiente, la curtosis y las escenas.
Las medidas descriptivas de un conjunto de datos son las siguientes:
Media: es el promedio de todos los datos de la muestra
Mediana: es el valor del medio de todos los datos ordenados de menor a mayor.
Moda: es el valor que más se repite del conjunto de datos
Tendencia central: es la medida que describe cómo todos los valores de los datos se agrupan en torno a un valor central.
Variación: es la cantidad de disgregación o dispersión de los valores con respecto a un valor central
Forma: es el patrón de distribución de los valores desde el menor hasta el mayor.




¿Qué son las medidas de tendencia central?
Las medidas de tendencia central nos proporcionan información esencial sobre los valores centrales o medios de un conjunto de datos, ayudándonos a identificar el valor "típico" en torno al cual tienden a conglomerarse los puntos de datos.
Media: el promedio de los valores individuales de un conjunto de datos
Mediana: el número en el medio de un conjunto de datos con un número igual de valores superiores e inferiores
Moda: el número o valor que ocurre con mayor frecuencia en un conjunto de datos
A menudo se incluye el rango al encontrar las medidas de tendencia central. Sin embargo, el rango es en realidad una medida de variación Una medida de variación describe la variabilidad de los datos, o qué tan dispersos están los datos en un conjunto de datos.
DATO INTERESANTE
Las medidas de tendencia central son útiles, pero no lo dicen todo.
Por ejemplo, si dos empresas tienen el mismo salario medio, podrías pensar que pagan lo mismo Pero si una tiene todos los sueldos parecidos y otra tiene unos muy altos y otros muy bajos, la historia cambia
Para analizar mejor estas medidas, es recomendable combinar las medidas de tendencia central con medidas de dispersión
Nos ofrecen información sobre la variabilidad de una determinada variable

¿Para qué sirven?
Sirven para mucho más que resumir Algunas de sus utilidades más comunes son: Detectar desigualdades: si la media y la mediana son muy distintas, es posible que haya muchos extremos o valores atípicos
Identificar lo típico o habitual dentro de un grupo de datos
Comparar grupos entre sí, como la media de notas entre diferentes clases
Estudiar la evolución de una variable a lo largo del tiempo (por ejemplo, el sueldo medio año tras año).
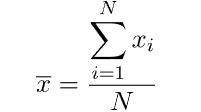
MEDIDAS DE DISPERSIÓN O ESPARCIMIENTO

¿Qué son las medidas de dispersión?
Las medidas de dispersión o de variación, en estadística, miden cuánto se aleja una distribución de datos del valor de una medida central, como puede ser la media o promedio aritmético Su valor
siempre es positivo y normalmente distinto de 0, salvo en el caso de datos idénticos

La desviación estándar es, con mucho, la medida de dispersión más utilizada, por eso vale la pena destacar sus principales características:
La desviación estándar indica cuánto se alejan los datos de la media
Siempre es positiva, pero puede ser 0 si todos los datos son idénticos
A mayor valor de la desviación estándar, más dispersos están los datos
Las unidades de la desviación estándar son las mismas que las de la variable en estudio
Su valor cambia rápidamente cuando uno de los datos (o más), tiene un valor muy diferente al resto
Los valores de la desviación estándar son sesgados, es decir, los promedios de la desviación estándar no se distribuyen alrededor de la media, en contraste con la varianza, que es no sesgada
Ejemplo de varianza
El cálculo de la varianza requiere hallar la media Tomando los datos del número de huracanes, la media se calcula mediante:
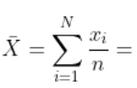
Desviación estándar
Para subsanar el problema de la falta de concordancia entre las unidades, se define la desviación estándar σ, como la raíz cuadrada de la varianza:


Principales medidas de dispersión
Las principales son: rango, varianza, desviación estándar y coeficiente de variación
Rango
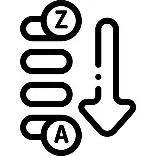
Se define el rango R de un conjunto de datos a la diferencia entre el valor máximo xmax y el valor mínimo xmin del conjunto:
Rango = R = Valor máximo – valor mínimo = xmax xmin
Varianza
Esta medida se utiliza para comparar a cada uno de los datos con la media del conjunto, y se calcula sumando las diferencias, elevadas al cuadrado, entre cada valor con la media y dividiendo entre el número total de valores
Sea:
-La media: μ
-Un valor cualquiera, perteneciente al conjunto de datos: xi
-El número total de observaciones: N
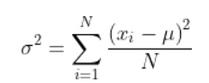


Primer momento:
El término “momento” en estadística se refiere a una medida cuantitativa que captura varias características de una distribución de probabilidad Los momentos son esenciales para comprender la forma y el comportamiento de los datos Los momentos más comunes son el primer momento (media), el segundo momento (varianza), el tercer momento (asimetría) y el cuarto momento (curtosis) Cada uno de estos momentos proporciona información única sobre la distribución de los puntos de datos, lo que permite a los analistas resumir e interpretar conjuntos de datos complejos de manera eficaz
El primer momento, también conocido como media, es el promedio de un conjunto de valores. Se calcula sumando todos los puntos de datos y dividiendo por el número de puntos La media sirve como punto central alrededor del cual se agrupan los valores de los datos, lo que la convierte en una estadística fundamental en análisis de los datosComprender la media es crucial para identificar tendencias y hacer predicciones basadas en datos históricos

Tercer momento: asimetría

Segundo momento: varianza
El segundo momento, o varianza, mide la dispersión de los puntos de datos en torno a la media. Se calcula promediando las diferencias al cuadrado entre cada punto de datos y la media Una varianza alta indica que los puntos de datos están muy dispersos, mientras que una varianza baja sugiere que están agrupados en torno a la media. La varianza es un componente fundamental en varios métodos estadísticos, incluidas las pruebas de hipótesis y el análisis de regresión.
El tercer momento, conocido como asimetría, cuantifica la asimetría de una distribución de probabilidad. Una distribución puede ser sesgada positivamente (cola larga a la derecha) o negativamente (cola larga a la izquierda). La asimetría ayuda a los analistas a comprender la dirección y el grado de asimetría en los datos, lo que puede afectar significativamente el modelado y la interpretación estadística Reconocer la asimetría es vital para elegir pruebas y métodos estadísticos adecuados.

Cuarto momento: curtosis
El cuarto momento, o curtosis, mide la “cola” de una distribución de probabilidad Indica qué proporción de los datos se encuentra en las colas en comparación con el centro de la distribución Una curtosis alta sugiere que los datos tienen colas pesadas o outliers, mientras que una curtosis baja indica colas ligeras Comprender la curtosis es esencial para la evaluación de riesgos en finanzas y para evaluar la confiabilidad de los modelos estadísticos


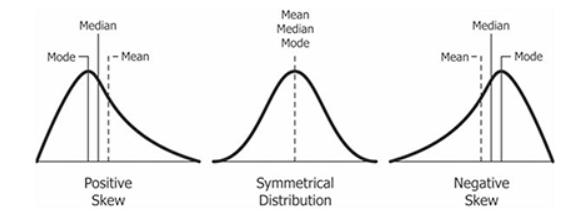
En estadística, las medidas de forma son unos indicadores que permiten describir una distribución de probabilidad según la forma que tiene Es decir, las medidas de forma sirven para determinar cómo es una distribución sin necesidad de representarla gráficamente
Existen dos tipos de medidas de forma: la asimetría y la curtosis La asimetría indica el grado de simetría de una distribución, mientras que la curtosis indica el grado de concentración de una distribución alrededor de su media.
Cuáles son las medidas de forma?
Vista la definición de medidas de forma, en este apartado se muestran cuáles son este tipo de parámetros estadísticos.
En estadística, se distinguen dos medidas de forma:
Asimetría: indica si una distribución es simétrica o asimétrica.
Curtosis: indica si una distribución es escarpada o achatada.
Asimetría
Hay tres tipos de asimetría:
Asimetría positiva: la distribución tiene más valores diferentes a la derecha de la media que a su izquierda.
Simetría: la distribución tiene el mismo número de valores a la izquierda que a la derecha de la media
Asimetría negativa: la distribución tiene más valores diferentes a la izquierda de la media que a su derecha

Hay tres tipos de curtosis:
Curtosis
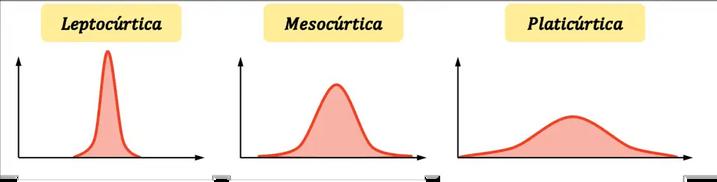
La curtosis, también llamada apuntamiento, indica el grado de concentración de una distribución alrededor de su media. Es decir, la curtosis muestra si una distribución es escarpada o achatada En concreto, cuanto mayor sea la curtosis de una distribución más escarpada (o apuntada) es.
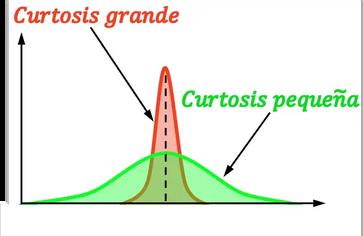
Leptocúrtica: la distribución es muy apuntada, es decir, los datos están muy concentrados alrededor de la media. En concreto, las distribuciones leptocúrticas se definen como aquellas distribuciones más apuntadas que la distribución normal
Mesocúrtica: la curtosis de la distribución es equivalente a la curtosis de la distribución normal Por tanto, no se considera ni apuntada ni achatada
Platicúrtica: la distribución es muy achatada, es decir, la concentración en torno a la media es baja Formalmente, las distribuciones platicúrticas se definen como aquellas distribuciones más achatadas que la distribución normal
Fundamentos de probabilidad

La probabilidad es una herramienta matemática que se utiliza para estudiar la aleatoriedad y proporcionar predicciones sobre la posibilidad de que algo ocurra. Hay varias reglas básicas de la probabilidad que pueden utilizarse para ayudar a determinar la posibilidad de que varios sucesos ocurran juntos, por separado o de forma secuencial En este artículo se tratan los fundamentos de la probabilidad, que son importantes tanto a la hora de realizar o interpretar los resultados de los ensayos clínicos, como a la hora de tomar decisiones clínicas para los pacientes en función de la probabilidad de los distintos resultados

Fórmula para calcular la probabilidad
El cálculo de las probabilidades se lleva a cabo según la siguiente fórmula:
Probabilidad = Casos favorables / casos posibles x 100 (para llevarlo a porcentaje)
Tipos de probabilidad
Probabilidad es una herramienta matemática que se utiliza para estudiar la aleatoriedad y proporcionar predicciones sobre la posibilidad de que algo ocurra
Abreviaturas:
La probabilidad se abrevia como P(evento)
Ejemplo: P(A) se refiere a la probabilidad de que ocurra el evento A
Los tipos de probabilidad incluyen:
Probabilidad teórica: modelos matemáticos y no observaciones
Frecuencia relativa: observaciones y/o mediciones
Probabilidad personal o subjetiva: nada más que sentimientos personales
Existen diferentes tipos de probabilidad, de acuerdo al tipo de recurrencia que expresan:
Frecuencial. Determina la cantidad de veces que un fenómeno puede ocurrir, considerando un número determinado de oportunidades, a través de la experimentación.
Matemática Pertenece al ámbito de la aritmética y aspira al cálculo en cifras de la probabilidad de que determinados eventos aleatorios tengan lugar, a partir de la lógica formal y no de su experimentación Binomial. Estudia el éxito o fracaso de un evento, o cualquier otro tipo de escenario probable que tenga dos posibles resultados únicamente.
Objetiva Conoce de antemano la frecuencia de un evento, y simplemente da a conocer los casos probables de que ocurra dicho evento
Subjetiva. Se sustenta en ciertas eventualidades que permiten inferir la probabilidad de un evento, aunque alejada de una probabilidad certera o calculable De allí su subjetividad
Hipergeométrica Se obtiene gracias a técnicas de muestreo, creando grupos de eventos según su aparición
Lógica Posee como rasgo característico que establece la posibilidad de ocurrencia de un hecho a partir de las leyes de la lógica inductiva
Condicionada Se emplea para comprender la causalidad entre dos hechos distintos, cuando puede determinarse la ocurrencia de uno tras la ocurrencia del otro



Ejemplo de Probabilidad
¿Qué es la probabilidad?
Dicho de una manera mucho más simple, la probabilidad es la medida de qué tan seguros podemos estar de que un evento sucederá. Imagina que es una forma de expresar nuestras expectativas sobre algo en el futuro, usando números del 0 al 100%, donde 0% significa que algo definitivamente no va a pasar, y 100% significa que estamos seguros de que sucederá.

Un ejemplo de probabilidad sería lanzar una moneda al aire La probabilidad de que caiga cara o cruz es del 50% para cada resultado, ya que hay dos posibilidades igualmente probables.


Tipos de probabilidad
Los tipos de probabilidad son:
Probabilidad objetiva: se basa en criterios objetivos para determinar la probabilidad de un evento.
Probabilidad subjetiva: se basa en la experiencia de una persona para predecir la probabilidad de ocurrencia de un evento, es decir, se basa en criterios subjetivos
Probabilidad clásica: se basa en la lógica para calcular la probabilidad de un evento, es decir, hace un cálculo teórico de la probabilidad
Probabilidad frecuencial: es la frecuencia relativa esperada a largo plazo para un suceso elemental de un experimento aleatorio.
Probabilidad condicional: indica la probabilidad de que ocurra un evento A si otro evento B ha sucedido
Probabilidad de Poisson: es la probabilidad de que ocurra un número determinado de eventos durante un cierto periodo de tiempo
Probabilidad binomial: sirve para definir matemáticamente eventos en los que solamente existen dos posibles resultados, los cuales se llaman «éxito» y «fracaso».
Probabilidad hipergeométrica: indica la probabilidad del número de casos de éxito en una extracción aleatoria y sin remplazo de n elementos de una población.
Probabilidad simple: es la probabilidad de que ocurra un evento simple del espacio muestral
Probabilidad conjunta: indica la probabilidad de que dos o más sucesos ocurran al mismo tiempo.



Conclusión
Lejos de ser un simple concepto teórico, la regularidad estadística es una herramienta para comprender el mundo. Nos enseña que, bajo el manto del azar, existe una lógica profunda y predecible Es la clave que permite a la ciencia hacer inferencias, estimar probabilidades, y diseñar políticas basadas en evidencia. En definitiva, como dijo el matemático Persi
Diaconis:
"El azar es solo la apariencia externa del orden "

Regularidad estadística es una noción en estadística y teoría de probabilidad según la cual los eventos aleatorios exhiben regularidad cuando se repiten suficientes veces o que suficientes eventos aleatorios suficientemente similares exhiben regularidad Es un término general que cubre la ley de los grandes números, todos los teoremas del límite central y los teoremas ergódicos.
Si uno lanza un dado una vez, es difícil predecir el resultado, pero si uno repite este experimento muchas veces, verá que el número de veces que ocurre cada resultado dividido por el número de lanzamientos eventualmente se estabilizará hacia un valor específico valor

Aplicaciones prácticas
La regularidad estadística no es solo un concepto abstracto. Se aplica en múltiples campos:
Medicina: Para evaluar la eficacia de un tratamiento a través de ensayos clínicos.
Economía: Para prever tendencias de consumo o inflación.
Meteorología: Para predecir el clima a partir de grandes volúmenes de datos
Calidad industrial: En el control de calidad de productos fabricados en masa
Aunque la regularidad estadística es poderosa, también tiene límites. No garantiza resultados exactos en muestras pequeñas, y puede ser malinterpretada. Además, si los datos no son verdaderamente aleatorios o independientes, las conclusiones pueden ser engañosas.

¿Qué son los postulados de la probabilidad?
Los postulados de la probabilidad son reglas matemáticas básicas que permiten asignar valores numéricos al grado de certeza o posibilidad de que ocurra un evento Estos principios fueron establecidos formalmente por el matemático soviético Andréi Kolmogórov en 1933, en su obra Fundamentos de la Teoría de la Probabilidad.
Kolmogórov planteó tres axiomas o postulados que son aceptados universalmente y que forman el núcleo de la probabilidad clásica o axiomática.

Postulado 3: Aditividad
Postulado 1: No negatividad
Para cualquier evento A, su probabilidad es un número real no negativo:
P(A) ≥ 0
Este postulado dice que ninguna probabilidad puede ser negativa. Tiene sentido: no se puede tener "menos que cero" posibilidades de que algo ocurra Este principio es la base más simple y lógica del sistema probabilístico
Postulado 2: Probabilidad total La probabilidad del espacio muestral (el conjunto de todos los eventos posibles) es 1:
P(S) = 1
Este postulado significa que algo debe suceder En cualquier experimento aleatorio, el resultado pertenece al espacio muestral. Por eso, la suma de las probabilidades de todos los posibles resultados debe ser igual a 1 (o 100%)
Por ejemplo, al lanzar un dado:
P(1) + P(2) + P(3) + P(4) + P(5) + P(6) = 1
Si A y B son eventos mutuamente excluyentes (no pueden ocurrir al mismo tiempo), entonces:
P(A ∪ B) = P(A) + P(B)
Esto significa que si dos eventos no pueden suceder simultáneamente, la probabilidad de que ocurra uno u otro es la suma de sus probabilidades individuales
Ejemplo clásico:
En una baraja de 52 cartas, la probabilidad de sacar un rey (P(K)) es 4/52
La probabilidad de sacar una reina (P(Q)) también es 4/52
Como no puedes sacar ambas a la vez, P(K ∪ Q) = P(K) + P(Q) = 8/52
¿Por qué son importantes?
Estos postulados parecen simples, pero son extremadamente poderosos. Todo, desde los seguros hasta la inteligencia artificial, se basa en estos principios Nos permiten modelar fenómenos complejos, hacer predicciones y tomar decisiones informadas bajo incertidumbre Además, son consistentes, universales y ampliables. A partir de ellos se derivan reglas más avanzadas, como:
La probabilidad condicional
El teorema de Bayes
La regla del complemento
La independencia de eventos


ESPACIOS MUESTRALES FINITOS
¿Qué es el Espacio Muestral Finito?
El espacio muestral es el el grupo de todos los resultados específicos que se pueden obtener tras una experimentación de carácter aleatorio. A cada uno de sus componentes de un espacio muestral, también conocido como espacio de muestreo, se los define como puntos muestrales o, simplemente, muestras.
El espacio muestral finito es una herramienta crucial para el análisis de la probabilidad en situaciones donde los resultados son claramente definidos y limitados en número. Es como un conjunto cerrado de posibles resultados que se pueden enumerar de manera completa.

¿Cuándo Usar un Espacio Muestral Finito?
El espacio muestral finito se utiliza cuando se enfrenta a situaciones donde los resultados son finitos y claramente definidos Por ejemplo, al lanzar un dado de seis caras o al seleccionar una carta de una baraja de cartas estándar, el espacio muestral es finito porque los resultados son limitados y conocidos.
Aplicaciones
Aunque son simples, los espacios muestrales finitos tienen aplicaciones prácticas importantes, como en:
Juegos de azar (dados, cartas, ruleta).
Estadística elemental
Simulaciones computacionales básicas.
Análisis de riesgos en situaciones discretas
portancia en la probabilidad
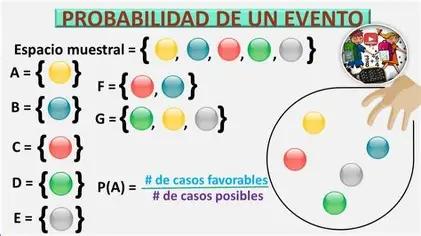
Los espacios muestrales finitos son la base de muchos modelos probabilísticos sencillos Gracias a que sus resultados pueden enumerarse, es posible calcular probabilidades utilizando reglas básicas, como la regla de Laplace:
Si todos los resultados son igualmente probables, la probabilidad de un evento es igual al número de casos favorables dividido entre el número total de casos posibles. Esto hace que los espacios muestrales finitos sean ideales para introducir conceptos de probabilidad en la educación básica y media.
Tipos de espacios muestrales
Existen dos grandes tipos de espacios muestrales:
Espacios muestrales finitos: tienen un número limitado y contable de resultados. Espacios muestrales infinitos: tienen un número ilimitado de resultados posibles
Ejemplos clásicos:
1 Lanzamiento de una moneda
Espacio muestral: Ω = {cara, cruz}
Cardinalidad: 2 resultados posibles
2.Tiro de un dado de seis caras
Espacio muestral: Ω = {1, 2, 3, 4, 5, 6}
Cardinalidad: 6
3.Extracción de una carta de una baraja española sin comodines
Espacio muestral: 40 cartas posibles
Ω = {1♥, 2♥, , Rey♠} (representación abreviada)

En teoría de probabilidades, un espacio muestral equiprobable es el conjunto de sucesos de un experimento aleatorio en el cual todos los resultados tienen la misma probabilidad de suceder. Por lo tanto, la probabilidad de que ocurra cada suceso en un espacio muestral equiprobable es igual a uno partido por el número total de sucesos del espacio muestral
Los espacios muestrales equiprobables tienen las siguientes propiedades:
La probabilidad de suceder de cada elemento de un espacio muestral equiprobable es mayor o igual a cero
La suma de las probabilidades de todos los sucesos elementales de un espacio muestral equiprobable es igual a 1
¿Por qué es importante?
Trabajar con espacios equiprobables permite aplicar la regla clásica de Laplace, una de las fórmulas más conocidas y sencillas en probabilidad:
P(A)=Nu ˊ mero de casos favorables al evento ANu ˊ mero total de casos posiblesP(A) = \frac{\text{Número de casos favorables al evento A}}{\text{Número total de casos posibles}}P(A)=Nuˊ mero total de casos posiblesNu ˊ mero de casos favorables al evento AEsta fórmula solo es válida si todos los resultados del experimento tienen la misma probabilidad de ocurrir, es decir, cuando el espacio muestral es equiprobable


Aplicaciones de los espacios equiprobables
Juegos de azar (dados, ruleta, loterías).
Modelos básicos en estadística
Simulaciones por computadora. Diseño de experimentos simples
Educación matemática inicial, por su claridad y simplicidad.

¿Qué es la probabilidad?
La probabilidad es una rama de las matemáticas que se encarga de estudiar el azar Nos permite calcular qué tan probable es que ocurra un evento Desde lanzar una moneda hasta predecir el clima, la probabilidad está presente en nuestra vida diaria
El estudio formal de la probabilidad comenzó en el siglo XVII, cuando matemáticos como Blaise Pascal y Pierre de Fermat buscaron resolver problemas relacionados con los juegos de azar. A partir de sus trabajos, la probabilidad se transformó en una herramienta matemática rigurosa que más tarde evolucionaría con aportes de Jacob Bernoulli, Pierre-Simon Laplace y Andrey Kolmogórov, quien en el siglo XX formuló los axiomas modernos de la probabilidad.

El cálculo de probabilidad es una herramienta matemática poderosa para comprender el azar, tomar decisiones y analizar riesgos. Saber calcular probabilidades nos ayuda a mirar el mundo con más lógica y menos incertidumbre.



¿Cómo se calcula?
Cuando todos los resultados posibles de un experimento tienen la misma probabilidad de ocurrir (caso equiprobable), usamos la siguiente fórmula:
Curiosidad matemática
El estudio formal de la probabilidad comenzó en el siglo XVII gracias a los matemáticos Pierre de Fermat y Blaise Pascal, quienes buscaban resolver problemas de juegos de azar. Lo que comenzó como un juego, ¡se convirtió en una ciencia!

¿Qué es un punto muestral?
En probabilidad, un punto muestral es un resultado individual de un experimento aleatorio El conjunto de todos estos puntos se llama espacio muestral, y se representa con la letra griega Ω (omega). Por ejemplo, al lanzar un dado, los puntos muestrales son:
Ω = {1, 2, 3, 4, 5, 6}
¿Por qué numerar los puntos muestrales?
La numeración de puntos muestrales es una técnica que permite organizar, representar y analizar de manera clara todos los posibles resultados de un experimento. Es especialmente útil cuando:
El experimento es complejo o involucra múltiples variables.
Se quiere representar el espacio muestral de forma ordenada.
Se necesita identificar rápidamente casos favorables
Técnica paso a paso
1
2
Definir claramente el experimento
Debemos entender qué estamos analizando.
Ejemplo: Lanzar dos dados
Determinar todos los resultados posibles
Listamos todos los puntos muestrales posibles
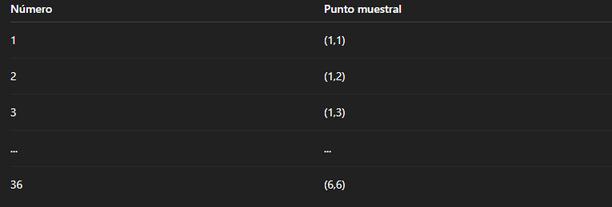
Para dos dados, cada resultado es un par ordenado (uno por cada dado):
Ω = {(1,1), (1,2), ..., (6,6)} → hay 36 combinaciones posibles.
Asignar un número a cada punto muestral
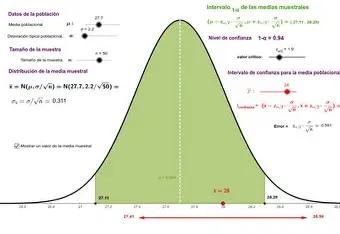
3
Este paso consiste en numerar los elementos del espacio muestral, para facilitar su identificación

4
Usar diagramas si es necesario
Cuando el número de puntos es alto o el experimento es complejo, es útil usar tablas de doble entrada, diagramas de árbol o diagramas de Venn para representar los puntos muestrales visualmente.
EVENTOS INDEPENDIENES

Los eventos independientes son resultados de un experimento aleatorio cuya probabilidad de ocurrencia no dependen entre sí. Es decir, dos eventos A y B son independientes si la probabilidad de que suceda el evento A no depende de que ocurra el evento B y viceversa.
Los eventos independientes también se llaman sucesos independientes


¿Qué significa que dos eventos sean Independientes y cuál es su relevancia en la probabilidad?
Cuando dos eventos son Independientes, la ocurrencia o resultado de uno no tiene ninguna influencia en la probabilidad de que el otro ocurra Esto es esencial en la probabilidad y permite calcular la probabilidad conjunta de eventos en situaciones complejas.
¿Cuál es la importancia de entender la independencia de eventos en el análisis de datos y la toma de decisiones?
Entender la independencia de eventos es fundamental en el análisis de datos y la toma de decisiones, ya que permite evaluar correctamente la probabilidad de que múltiples eventos ocurran juntos Esto es esencial en campos como la estadística, la economía y la ciencia
¿Cómo se calcula la probabilidad conjunta de dos eventos Independientes?
La probabilidad conjunta de dos eventos Independientes se calcula multiplicando las probabilidades individuales de cada evento. Es decir, si A y B son eventos Independientes, P(A y B) = P(A) * P(B).



variable aleatoria, que se entiende como el resultado numérico de un experimento aleatorio y se la llama así porque justamente el resultado se desconoce a priori, o dicho en otras palabras, es el resultado del azar.
Por ejemplo, arrojar simultáneamente dos monedas una sola vez, o bien lanzar una moneda dos veces, podría tener los siguientes resultados, denotando la aparición de una cara como C y la de un sello como S:
(C, C) = dos caras.
(C, S) = cara y sello en ese orden.
(S, S) = dos sellos.
(S, C) = sello y cara en ese orden. Se pueden definir muchas variables para un experimento aleatorio, para este en particular podría definirse el “número de caras”, y su resultado es enteramente al azar.
Tipos de variables aleatorias
Las variables aleatorias pueden ser de dos tipos: Discretas. Continuas.
Es importante distinguir entre uno y otro tipo, ya que de esto depende la forma de tratamiento de la variable.
Dos eventos son independientes cuando la ocurrencia de uno no influye en la probabilidad de que ocurra el otro.


DATO INTERESANTE
¿Qué es una variable discreta?
En el campo de la estadística y la probabilidad, las variables aleatorias permiten modelar fenómenos inciertos. Dentro de estas, las variables discretas son fundamentales por su aplicación en numerosos contextos reales y teóricos.
Una variable discreta es aquella que puede tomar un número finito o numerable de valores distintos. Estos valores suelen ser enteros y separados unos de otros, como el número de hijos en una familia, el número de autos que pasan por una intersección en una hora, o la cantidad de llamadas que recibe una central telefónica.
A diferencia de las variables continuas que pueden asumir infinitos valores dentro de un intervalo—, las variables discretas se caracterizan por su "cuantificabilidad" exacta.

Distribución de probabilidad de una variable discreta
La distribución de probabilidad de una variable discreta asigna una probabilidad a cada uno de los posibles valores que puede tomar dicha variable. Esta asignación debe cumplir dos condiciones:
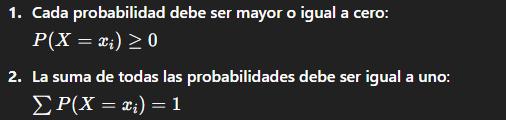
Aplicaciones
Las variables discretas y sus distribuciones se utilizan ampliamente en:
Estadística aplicada
Control de calidad
Finanzas
Biología
Ingeniería
Ciencias sociale


La distribución de probabilidad es una de las herramientas esenciales de la estadística y la ciencia de datos. Nos ayuda a convertir la incertidumbre en conocimiento útil y aplicable. En un mundo cada vez más guiado por la información, comprender cómo se comportan los datos es tan valioso como saber interpretarlos.

Tipos de distribuciones
Existen dos grandes categorías:
1. Distribución de probabilidad discreta
Se aplica a variables discretas, que solo pueden asumir valores específicos y contables (como el número de personas en una sala)
Ejemplo clásico:
La distribución binomial, que calcula la probabilidad de obtener cierto número de éxitos (como caras al lanzar una moneda varias veces).
2 Distribución de probabilidad continua
Se utiliza para variables continuas, que pueden tomar un número infinito de valores dentro de un intervalo (como la altura de una persona o el tiempo que tarda en llegar un autobús).
Ejemplo clásico:
La distribución normal (también llamada curva de Gauss), famosa por su forma de campana y su aplicación en fenómenos naturales, sociales y psicológicos

¿Qué es una distribución de probabilidad?
La distribución de probabilidad describe cómo se distribuyen los posibles resultados de un experimento aleatorio Es una función matemática que asigna una probabilidad a cada valor posible que puede tomar una variable aleatoria.
Esta herramienta permite no solo conocer qué resultados son más probables, sino también modelar y anticipar comportamientos en campos tan variados como la física, la biología, la economía y la inteligencia artificial
¿Por qué es importante?
Comprender las distribuciones de probabilidad es fundamental para: Estimar riesgos y tomar decisiones informadas.
Analizar grandes volúmenes de datos
Realizar inferencias estadísticas (como intervalos de confianza y pruebas de hipótesis).
Simular escenarios futuros en modelos computacionales.
Características clave
Una distribución de probabilidad debe cumplir lo siguiente: No negatividad: Ninguna probabilidad puede ser menor que cero.
Totalidad: La suma de todas las probabilidades posibles debe ser igual a 1
Forma: Cada distribución tiene una forma específica (simétrica, sesgada, uniforme, etc.) que influye en la interpretación de los datos

DIFERENTES DISTRIBUCIONES DE PROBABILIDAD DISCRETA

Las distribusiones de probabilidad discreta permiten modelar eventos aletorios que pueden contraerse desde numeros de llamadas de una linea de emergencia hasta cuantas veces necesitas lanzar un dado para obtener 6, estas herramientas son fundamentales en estadisticas, ciencia de datos e ingenoeria.
Caracteristicas principales

Se aplica a situaciones como lanzar un dado .

Dato curioso
Conjunto de resultados finito ó numerable
Cada resultado tiene una probabilidad especifica
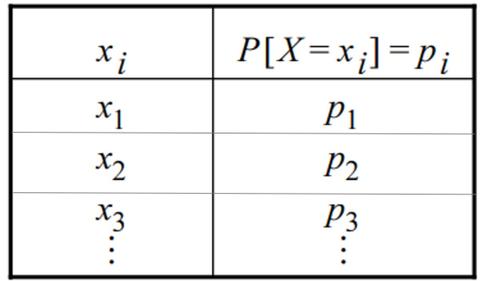


EnelsigloXVII,el matemáticoBlaise Pascalsecomunicaba porcartaconPierre deFermatpara resolverproblemas relacionadoscon juegosdeazar.¡Esa correspondenciafue elorigenformaldela teoríadela probabilidadque usamoshoy!


¿Qué es una distribución uniforme discreta?
La distribución uniforme discreta es una distribución de probabilidad en la que todos los valores posibles de una variable discreta tienen la misma probabilidad de ocurrir Es decir, se asigna una probabilidad igual a cada uno de los resultados en un conjunto finito de valores
Ejemplo clásico:
El lanzamiento de un dado justo de seis caras Cada número del 1 al 6 tiene la misma probabilidad:

Características
Equiprobabilidad: Todos los valores posibles tienen la misma probabilidad.
Variable discreta: Los resultados posibles son finitos y contables.
Función de probabilidad: Si la variable aleatoria XXX puede tomar nnn valores (por ejemplo, de aaa a bbb), entonces:
Gráfica de la distribución uniforme discreta Como la distribución uniforme discreta solo puede tomar algunos valores dentro de un intervalo, su representación gráfica son puntos. Además, todos las probabilidades son iguales, por lo tanto, todos los puntos de la distribución uniforme discreta tienen la misma coordenada vertical.
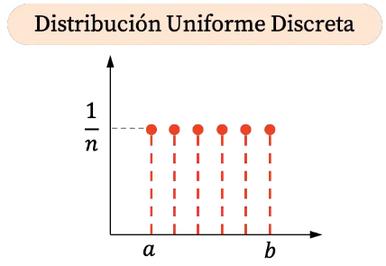
La distribución uniforme discreta no solo es una de las más simples en teoría de probabilidad, sino también una de las más versátiles. Su concepto de igualdad de probabilidades es clave para entender cómo se construyen sistemas justos y aleatorios. Desde lanzar un dado hasta simular escenarios complejos en la inteligencia artificial, esta distribución sigue siendo una piedra angular en el estudio del azar.

BINOMIAL ÉXITO
La distribución binomial es un modelo que se usa cuando se hacen varios experimentos con solo dos resultados posibles.
EJEMPLO ESTADÍSTICA


¿Cuál es la probabilidad de obtener exactamente 3 caras al lanzar una moneda 5 veces?

FRACASO

Un binomio es una expresión algebraica que consta de dos términos unidos por una suma o una resta. Es un caso particular de los polinomios y se usa frecuentemente en operaciones algebraicas y en fórmulas como el famoso binomio de Newton.




Geométrica
Las progresiones geométricas no solo son una herramienta matemática; son una forma de describir fenómenos reales que se expanden, se reducen o se transforman de manera multiplicativa. Desde la tecnología hasta la naturaleza, las progresiones geométricas modelan comportamientos que no crecen linealmente, sino que se duplican, triplican o se fraccionan rápidamente.
¿Qué es una progresión geométrica?
Una progresión geométrica es una sucesión de términos en la que cada uno se obtiene multiplicando el anterior por una constante fija (la razón rrr). Es decir:

La probabilidad es un valor numérico que muestra la probabilidad de que suceda algún evento en particular. La probabilidad geométrica es el cálculo de la probabilidad de que golpee un área particular de una figura. Se calcula dividiendo el área deseada por el área total.


El resultado de un cálculo de probabilidad geométrica siempre será un valor entre 0 y 1. Si un evento nunca puede suceder, la probabilidad es 0. Si siempre sucede, la probabilidad es 1. Si está tratando de golpear un área muy pequeña relativa al tamaño de todo el tablero, entonces la probabilidad es más cercana a 0. Si está tratando de golpear un área grande en relación con el tamaño de todo el tablero, entonces la probabilidad es más cercana a 1.

¿Qué es la distribución binomial negativa?
La distribución binomial negativa es una distribución de probabilidad que describe el número de ensayos de Bernoulli necesarios para obtener un número determinado de resultados con éxito. Por lo tanto, una distribución binomial negativa tiene dos parámetros característicos: r es el número de resultados con éxito deseado y p es la probabilidad de éxito de cada experimento de Bernoulli realizado.

La diferencia entre una distribución binomial negativa y una distribución binomial es que la distribución binomial negativa cuenta el número de veces que se necesitan para conseguir un determinado número de resultados con éxito, en cambio, la distribución binomial cuenta el número de casos de éxito de una serie de ensayos de Bernoulli.
La distribución binomial negativa queda definida por dos parámetros característicos: r es el número de resultados con éxito deseado y p es la probabilidad de éxito de cada experimento de Bernoulli realizado.
Fórmula general
La probabilidad de que se necesiten exactamente xxx ensayos para obtener rrr éxitos se calcula mediante:
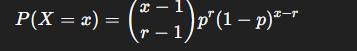
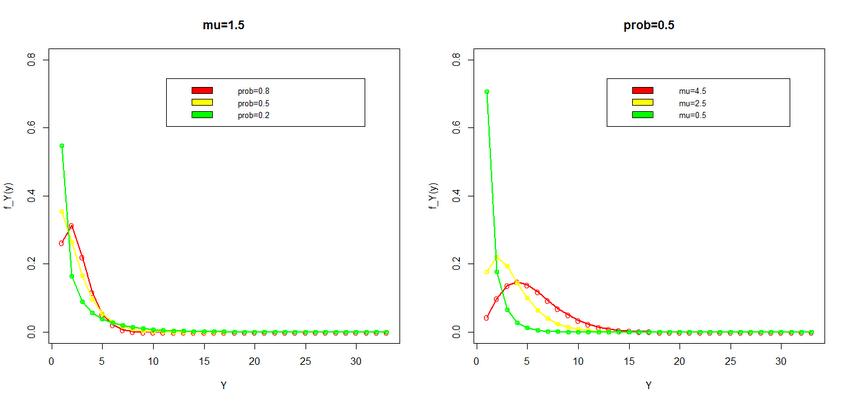

La distribución hipergeométrica es una función estadística discreta, adecuada para calcular la probabilidad en experimentos aleatorios con dos resultados posibles. La condición que se requiere para aplicarla es que se trate de poblaciones pequeñas, donde las extracciones no se reemplazan y las probabilidades no son constantes.
Por lo tanto, cuando se elige un elemento de la población para saber el resultado (verdadero o falso) de cierta característica, ese mismo elemento no puede elegirse de nuevo. Ciertamente, el siguiente elemento elegido tiene así mayor probabilidad de obtener un resultado verdadero, si el elemento anterior tuvo resultado negativo. Esto significa que la probabilidad varía en la medida que se extraen elementos de la muestra.
Las aplicaciones principales de la distribución hipergeométrica son: control de calidad en procesos con poca población y el cálculo de probabilidades en los juegos de azar.
Fórmula de distribución hipergeométrica
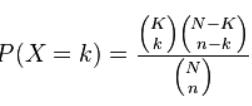
K es el número de éxitos en la población
k es el número de éxitos observados
N es el tamaño de la población
n es el número de sorteos
Aplicaciones en el mundo real
Control de calidad: inspección de productos sin dañar o alterar los lotes
Biología: estudios de genética y muestreo de poblaciones naturales. Ciencias sociales: encuestas donde no se permite repetir participantes. Juegos de azar: cartas extraídas de un mazo sin devolverlas.
POISSON
La distribución de Poisson es una distribución de probabilidad discreta y se emplea para describir procesos que pueden ser descritos con una variable aleatoria discreta. Describe situaciones en las cuales los clientes llegan de manera independiente durante un cierto intervalo de tiempo y el número de llegadas depende de la magnitud del intervalo

La fórmula de Poisson se utiliza para calcular la probabilidad de que ocurra un número determinado de eventos en un intervalo fijo de tiempo o espacio. La ecuación que representa esta distribución es:
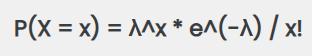
Donde:
P(X = x): es la probabilidad de que ocurra el evento x veces.
λ (lambda): representa el número promedio de ocurrencias en el intervalo considerado.
e: es la base de los logaritmos naturales, aproximadamente igual a 2.71828.
x!: es el factorial de x, que es el producto de todos los enteros positivos hasta x.

La Distribución de Poisson se llama así en honor a Simeón Dennis Poisson (1781-1840), francés que desarrolló esta distribución basándose en estudios efectuados en la última parte de su vida.
La distribución de Poisson tiene varias característic distintivas que la diferencia de otras distribuciones probabilidad. En primer lugar, es importante destac que es una distribución de probabilidad discreta, que significa que solo toma valores enteros negativos. Esto es fundamental para eventos q ocurren en cantidades contadas.
Otra característica clave es que la media y la varianza de la distribución de poisson son iguales y ambas son representadas por el parámetro λ Esto se traduce en que la concentración de los eventos aumenta a medida que λ se incrementa, reflejando una mayor probabilidad de observar más eventos en el intervalo considerado.

FUENTESDEINFORMACIÓN
Paula N. R.27 (febrero 2024) ¿Qué es un modelo matemático? Tipos, propiedades y elementos.
profesores dcb (15 de enero del 2019)ibro indd
Ramos R Julio, del Águila, Víctor y Bazalar B , Ana Estadística básica para los negocios. Universidad de Lima, 2017.
Cristina O (16 de marzo del 2025)frecuencia relativa: Qué es, usos y ejemplos
Cristina O. (16 de marzo del 2025)Estadística descriptiva: Qué es, objetivo, tipos y ejemplos
Vargas Sabadías, Antonio. Estadística descriptiva e inferencial, Universidad de Castilla La Mancha, 1996
Blanco, A. (2018). Probabilidad y estadística para ingeniería y ciencias. McGraw-Hill Education
Montgomery, D. C., & Runger, G. C. (2014). Probabilidad y estadística aplicadas a la ingeniería (5.ª ed.). Wiley