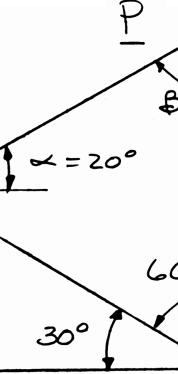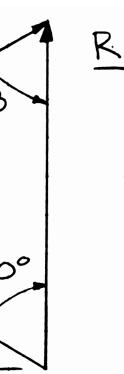CHAPTER 2
Copyright © McGraw-Hill Education. Permission required for reproduction or display. Vector Mechanics for Engineers Statics Full Download: http://testbanktip.com/download/vector-mechanics-for-engineers-statics-and-dynamics-11th-edition-beer-solutions-manual/ Download all pages and all chapters
Copyright © McGraw-Hill Education. Permission required for reproduction or display.
SOLUT (a) P (b) T W
ION arallelogram l riangle rule: e measure:



















BLEM 2.1 forces are a itude and dir e triangle rul
pplied as sho ection of thei e.
wn to a hoo r resultant us
k. Determine ing (a) the pa
graphically rallelogram la
the w,
139 R =
1kN,47 α =
.8°
1391 N = R
47.8°
PRO Two magn (b) th law: Copyright © McGraw-Hill Education. Permission required for reproduction or display.
OBLEM 2.2 forces are hically the the parallelo




applied as s magnitude gram law, (










hown to a b and directio b) the triang






ort. Determi esultant usi
°
e
90 R =
6lb, 2 α =
6.6
906 R =
lb 26.6°
SOLUT (a) P (b) T W ION arallelogram l riangle rule: Copyright © McGraw-Hill Education. Permission required for reproduction or display.
measure:
PR Two grap (a) law:
racket supp n of their r le rule.
ne ng
SOLUTION (a) Parallelogram law: (b) Triangle rule:
PROBLEM 2.3
Two structural members B and C are bolted to bracket A. Knowing that both members are in tension and that P = 10 kN and Q = 15 kN, determine graphically the magnitude and direction of the resultant force exerted on the bracket using (a) the parallelogram law, (b) the triangle rule.




We measure: 20.1kN, R = 21.2 α = ° 20.1kN = R 21.2° Copyright © McGraw-Hill Education. Permission required for reproduction or display.
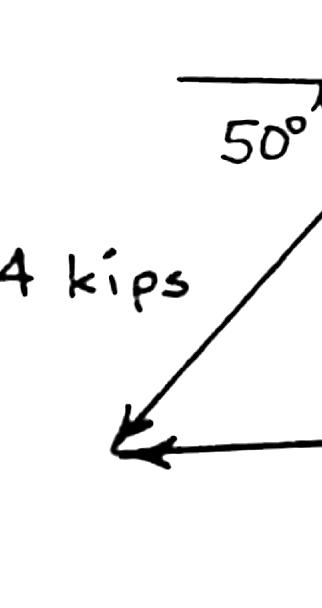
PROBLEM 2.4
Two structural members B and C are bolted to bracket A. Knowing that both members are in tension and that P = 6 kips and Q = 4 kips, determine graphically the magnitude and direction of the resultant force exerted on the bracket using (a) the parallelogram law, (b) the triangle rule.




SOLUTION (a) Parallelogram law: (b) Triangle rule: We measure: 8.03kips,3.8 R α = =° 8.03kips = R 3.8° Copyright © McGraw-Hill Education. Permission required for reproduction or display.
SOLUTION
PROBLEM 2.5
A stake is being pulled out of the ground by means of two ropes as shown. Knowing that α = 30°, determine by trigonometry (a) the magnitude of the force P so that the resultant force exerted on the stake is vertical, (b) the corresponding magnitude of the resultant.
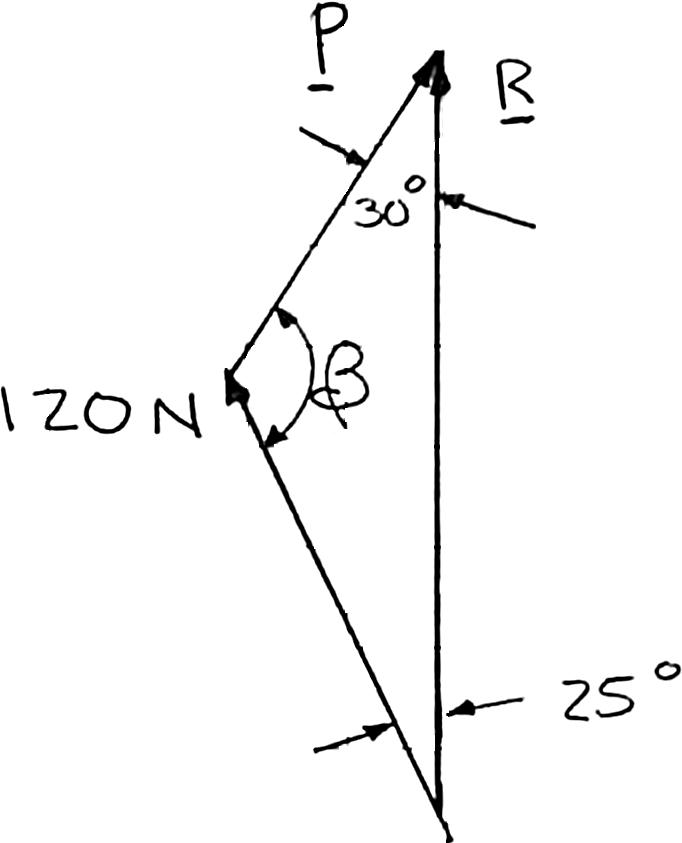
Using the triangle rule and the law of sines:

(a) 120N sin30sin25 P = °° 101.4N P = (b) 3025180 1802530 125 β β °++°=° = °−°−° =° 120N sin30sin125 = °° R 196.6N = R Copyright © McGraw-Hill Education. Permission required for reproduction or display.
SOLUTION
PROBLEM 2.6
A telephone cable is clamped at A to the pole AB. Knowing that the tension in the left-hand portion of the cable is T1 = 800 lb, determine by trigonometry (a) the required tension T2 in the right-hand portion if the resultant R of the forces exerted by the cable at A is to be vertical, (b) the corresponding magnitude of R.

Using the triangle rule and the law of sines:

(a) 7540180 1807540 65 α α °+°+=° = °−°−° =° 2 800lb sin65sin75 T = °° 2 853 lb T = (b) 800lb sin65sin40 R = °° 567 lb R = Copyright © McGraw-Hill Education. Permission required for reproduction or display.
SOLUTION
PROBLEM 2.7
A telephone cable is clamped at A to the pole AB. Knowing that the tension in the right-hand portion of the cable is T2 = 1000 lb, determine by trigonometry (a) the required tension T1 in the left-hand portion if the resultant R of the forces exerted by the cable at A is to be vertical, (b) the corresponding magnitude of R.
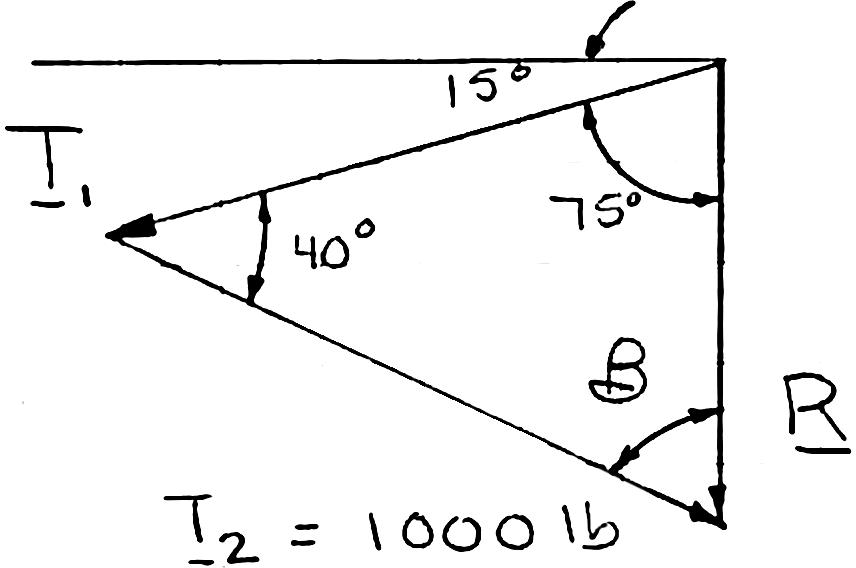
Using the triangle rule and the law of sines:

(a) 7540180 1807540 65 β β °+°+=° = °−°−° =° 1 1000 lb sin75°sin65 T = ° 1 938 lb T = (b) 1000 lb sin75°sin40 R = ° 665 lb R = Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 2.8

A disabled automobile is pulled by means of two ropes as shown. The tension in rope AB is 2.2 kN, and the angle α is 25°. Knowing that the resultant of the two forces applied at A is directed along the axis of the automobile, determine by trigonometry (a) the tension in rope AC, (b) the magnitude of the resultant of the two forces applied at A.


SOLUTION Using the law of sines: 2.2 kN sin30°sin125 sin25 TAC R == ° 2.603 kN 4.264 kN TAC R = = (a) 2.60 kN TAC = (b) 4.26 kN R = Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 2.9

A disabled automobile is pulled by means of two ropes as shown. Knowing that the tension in rope AB is 3 kN, determine by trigonometry the tension in rope AC and the value of α so that the resultant force exerted at A is a 4.8-kN force directed along the axis of the automobile.



Using the law of cosines: 222 (3 kN)(4.8 kN)2(3 kN)(4.8 kN)cos 30° 2.6643 kN AC AC T T =+− = Using the law of sines: sinsin30 3 kN2.6643 kN 34.3 α α ° = =° 2.66 kN AC = T 34.3° Copyright © McGraw-Hill Education. Permission required for reproduction or display.
SOLUTION
nowing that (a) the requir the support is Copyright © McGraw-Hill Education. Permission required for reproduction or display.




ed to


SOLUT Using th (a) (b) ION e triangle rule e and law of s si 5 s α β + + sin117 R
a magnitude
angle α
horizonta ines: insin25 0 N35 N in0.6037 α α ° = = 37.138 α = 25180 180 117.862 β °=° = °− = 35 N .862sin 2 = ° 2.10 re applied
f P
R
l, (b) the corre 4 8° 2537.138 °−° ° 5°
PROBLEM Two forces
o
if the be
as
is 35 N, d resultant
o
shown to a ho etermine by f the two forc sponding mag 37.1 α =° 73.2 N R =
ok support. K trigonometry es applied to nitude of R. the

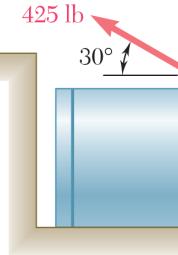



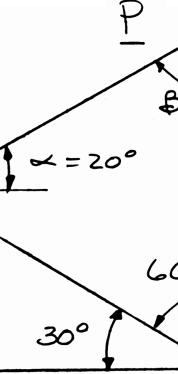
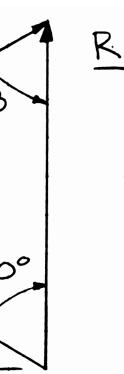
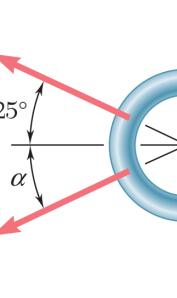
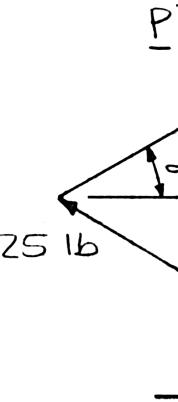
SOLUT Using th (a) (b) ION e triangle rule e and the law 50 β + ° 4 s 4 s P A th m fo m of sines: 60180 180 70 β +°=° = ° = ° 25 lb sin70sin6 P = ° 25 lb sin70sin5 R = ° ROBLEM steel tank is at α = 20°, d agnitude of rces applied agnitude of R 5060 −°−° 0° 0° 2.11 to be position etermine by the force P i at A is to be v . ed in an excav trigonometry f the resultan ertical, (b) th ation. Knowi (a) the requir t R of the t e correspondi 392 lb P = 346 lb R = ng ed wo ng Copyright © McGraw-Hill Education. Permission required for reproduction or display.






SOLUT Using th (a) (b) ION e triangle rule e and the law ( 3 α + sin P A th tr th c of sines: 30)60 sin(90) 425 lb β β β α °+°+ °− 90 α °− (42.59830 R °+
steel tank is at the mag igonometry ( e two force orresponding 180 180( 90 sin60 500 lb α α =° = °−+ =°− ° = 47.402 =° 500 lb )sin60 = °° 2.12 to be position nitude of P a) the require s applied at magnitude of 30)60°−° ed in an excav is 500 lb, d angle α if th A is to be v R. ation. Knowi determine e resultant R ertical, (b) 42.6 α =° 551 lb R = ng by of the Copyright © McGraw-Hill Education. Permission required for reproduction or display.
ROBLEM
to R. ROBLEM
2.13 is to be p trigonometr smallest forc orces applied magnitude of

ositioned in y (a) the e P for which at A is v R






an excavati magnitude a the resultant ertical, (b)

SOLUT The sma (a) P (b) R ION llest
P w (425 lb)co = (425 lb)sin =
os30° n 30°
force
will be perpen
P A D 368 lb = P 21 R = on. nd R the 13 lb Copyright © McGraw-Hill Education. Permission required for reproduction or display.
d o c dicular
steel tank etermine by irection of the f the two f orresponding
mine by trigo rce P for wh pport is hor

) ich the result
(b)



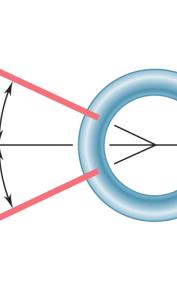

SOLUT The sma (a) P (b) R ION llest force P w (50 N)sin = (50 N)cos =
F
will be perpen 25° 25°
2.14
nometry (a
P izontal,
m R c 21.1 N = P 45.3 N R = the ant the Copyright © McGraw-Hill Education. Permission required for reproduction or display.
ROBLEM or the hook s agnitude and of the two orresponding dicular to R.
upport of Pro direction of t forces appli magnitude of
b. 2.10, deter he smallest fo ed to the su R
PROBLEM 2.15
For the hook support shown, determine by trigonometry the magnitude and direction of the resultant of the two forces applied to the support.


SOLUTION Using the law of cosines: 222 (200 lb)(300 lb) 2(200 lb)(300 lb)cos(4565) 413.57 lb R R =+ −+° = Using the law of sines: sinsin(4565) 300 lb413.57 lb 42.972 α α + ° = =° 902542.972 β = +−° 414lb = R 72.0° Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 2.16
Solve Prob. 2.1 by trigonometry.


PROBLEM 2.1
Two forces are applied as shown to a hook. Determine graphically the magnitude and direction of their resultant using (a) the parallelogram law, (b) the triangle rule.


SOLUTION
Using the law of cosines: 222 (900N)(600N) 2(900N)(600 N)cos(135)

Using the law of sines:

1390.57N R R =+ −° =
600N1390.57N 3017.7642 47.764 α α α ° = =° = 1391N = R 47.8° Copyright © McGraw-Hill Education. Permission required for reproduction or display.
sin(30)sin(135)
members ers are in ten
the ma e bracket usin

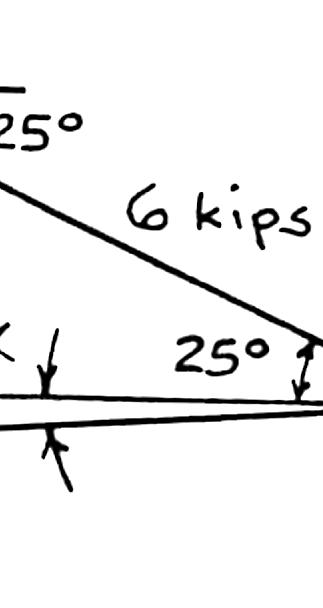

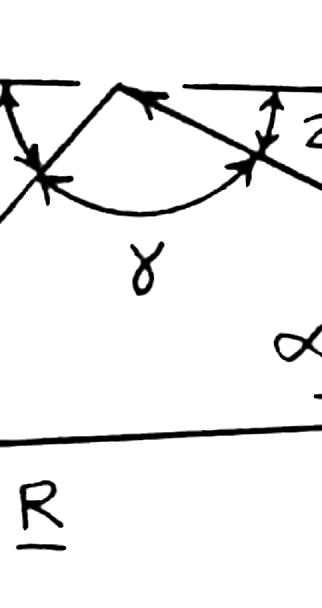


SOLUT Using th We hav Then And ION e force triang e: P So PR A Q re (b gle and the law 180 105 γ = = 2 (4 64 8.0 R R = = = 4kip sin(25 sin(25 25 ° ° ° ROBLEM
lve Problem 2 OBLEM 2.4 Knowing tha = 4 kips, de sultant force ) the triangle r s of cosines a (5025°−°+ ° ° 2 2 kips)(6kip .423kips 264kips + s8.0264 )sin1 )0.4813 28.775 3.775 α α α α = + += += =° .17 .4 by trigono
exerted on th ule. nd sines: ) 2 s)2(4kip kips 05 7 ° ° ° metry. ral
s)(6kips)cos 1
C
05° 8.03 k = R olted to brac P = 6 kips
direction of allelogram la ips 3.8° ket nd the w, Copyright © McGraw-Hill Education. Permission required for reproduction or display.
2
Two structu t both memb termine graph
ically
B and
are b sion and that gnitude and g (a) the par
a
SOLUTION
PROBLEM 2.18
For the stake of Prob. 2.5, knowing that the tension in one rope is 120 N, determine by trigonometry the magnitude and direction of the force P so that the resultant is a vertical force of 160 N.

PROBLEM 2.5 A stake is being pulled out of the ground by means of two ropes as shown. Knowing that α = 30°, determine by trigonometry (a) the magnitude of the force P so that the resultant force exerted on the stake is vertical, (b) the corresponding magnitude of the resultant.


Using the laws of cosines and sines: 222(120N)(160N)2(120N)(160N)cos25 72.096N P P =+−° = And sinsin25 120N72.096N sin0.70343 44.703 α α α ° = = =° 72.1N = P 44.7° Copyright © McGraw-Hill Education. Permission required for reproduction or display. Vector Mechanics for Engineers Statics Full Download: http://testbanktip.com/download/vector-mechanics-for-engineers-statics-and-dynamics-11th-edition-beer-solutions-manual/ Download all pages and all chapters