Applied Statistics in Business and Economics
5th Edition Doane Seward
0077837304 9780077837303
Download solution manual at:
https://testbankpack.com/p/solution-manual-for-appliedstatistics-in-business-and-economics-5th-edition-doaneseward-0077837304-9780077837303/
Download full test bank at :
https://testbankpack.com/p/test-bank-for-applied-statistics-inbusiness-and-economics-5th-edition-doane-seward0077837304-9780077837303/
Chapter 10
Two-Sample Hypothesis Tests
True / False Questions
1. A pooled proportion is calculated by giving each sample proportion an equal weight.
True False
2. The difference between two sample proportions p1 - p2 may be assumed normally distributed if each sample has at least 10 "successes" and 10 "failures."
True False
3. When testing the difference between two population proportions, it is necessary to use the same size sample from each population.
True False
© 2016
4. When using independent samples to test the difference between two population means, a pooled variance is used if the population variances are unknown and assumed equal.
True False
5. In comparing the means of two independent samples, if the test statistic indicates a significant difference at α = .05, it will also be significant at α = .10.
True False
6. The degrees of freedom for the t-test used to compare two population means (independent samples) with unknown variances (assumed equal) will be n1 + n2 - 2.
True False
7. When using independent samples to test the difference between two population means, it is desirable but not necessary for the sample sizes to be the same.
True False
8. The Welch-Satterthwaite test is more conservative than the pooled variance test to compare two population means with unknown variances in independent samples.
True False
9. When sample data occur in pairs, an advantage of choosing a paired t-test is that it tends to increase the power of a test, as compared to treating each sample independently.
True False
10. A paired t-test with two columns of 10 observations in each column would use d.f. = 18.
True False
11. In conducting a paired t-test of the difference between two population means, the usual null hypothesis is that the mean of the population of paired differences is zero.
True False
12. The t-test for two samples of paired data will use n differences, making it a one-sample t-test.
True False
13. The F test is used to test for the equality of two population variances.
True False
14. The F distribution is never negative and is always skewed right.
True False
15. In an F test for the ratio of two population variances, the degrees of freedom in both the numerator and the denominator must be equal.
True False
10-2
Copyright © 2016 McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
16. The critical value in an F test for equal variances is the ratio of the sample variances.
True False
17. The test statistic in an F test for equal variances is the ratio of the sample variances.
True False
18. We could use the same data set for two independent samples (i.e., two columns of data) either to compare the means (t-test) or to compare the variances (F test).
True False
19. The Welch-Satterthwaite t-test for two means has the same degrees of freedom as the pooled samples t-test for two means.
True False
20. When the variances are known, a test comparing two independent sample means would use the normal distribution.
True False
21. When the variances are unknown, a test comparing two independent sample means would use the Student's t distribution.
True False
22. If the sample proportions are p1 = 15/60 and p2 = 20/90, normality may be assumed in a test comparing the two population proportions.
True False
23. If the sample proportions are p1 = 6/90 and p2 = 4/100, normality may be assumed in a test comparing the two population proportions.
True False
24. A paired t-test with two columns of 8 observations in each column would use d.f. = 7.
True False
25. If the population variances are exactly equal, the sample F test statistic will be zero.
True False Multiple Choice Questions
10-3
Copyright © 2016 McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
26. In a right-tailed test comparing two proportions, the test statistic was zcalc = +1.81. The p-value is:
A. .9649
B. .0351
C. .4649
D. Must know n to answer.
27. In a left-tailed test comparing two means with unknown variances assumed to be equal, the test statistic was t = -1.81 with sample sizes of n1 = 8 and n2 = 12. The p-value would be:
A. between .025 and .05.
B. between .01 and .025.
C. between .05 and .10.
D. Must know α to answer.
28. In a left-tailed test comparing two means with variances unknown but assumed to be equal, the sample sizes were n1 = 8 and n2 = 12. At α = .05, the critical value would be:
A. -1.960
B. -2.101
C. -1.734
D. -1.645
29. In a right-tailed test comparing two means with known variances, the sample sizes were n1 = 8 and n2 = 12. At α = .05, the critical value would be: A. 1.960
30. In a test for equality of two proportions, the sample proportions were p1 = 12/50 and p2 = 18/50. The test statistic is approximately:
A. -1.44.
B. -1.31.
C. -1.67.
D. Must know α to answer.
31. In a test for equality of two proportions, the sample proportions were p1 = 12/50 and p2 = 18/50. The pooled proportion is:
C. .36
D. .30
10-4
Copyright © 2016 McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
32. If the sample proportions were p1 = 12/50 and p2 = 18/50, the 95 percent confidence interval for the difference of the population proportions is approximately:
A. [-.144, +.244].
B. [-.120, +.120].
C. [-.298, +.058].
D. [-.011, +.214].
33. John wants to compare two means. His sample statistics were and
. Assuming equal variances, the 95 percent confidence interval for the difference of the population means is approximately:
A. [2.44, 6.19].
B. [1.17, 5.08].
C. [0.08, 4.32].
D. [-0.09, 3.19].
34. John wants to compare two means. His sample statistics were and
. Assuming equal variances, the pooled variance is:






A. 4.5
B. 4.9
C. 5.1
D. 3.8
35. John wants to compare two means. His sample statistics were and
. Assuming equal variances, the test statistic is:
A. 2.37
B. 2.20
C. 1.96
D. Must know α to answer.
36. John wants to compare two means. His sample statistics were and
. Assuming equal variances, the degrees of freedom for his test will be:
A. 16.
B. 18.
C. 9.
D. 8.
Copyright © 2016 McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
37. In a random sample of patient records in Cutter Memorial Hospital, six-month postoperative exams were given in 90 out of 200 prostatectomy patients, while in Paymor Hospital such exams were given in 110 out of 200 cases. In comparing these two proportions, normality of the difference may be assumed because:
A. the populations are large enough to be assumed normal.
B. the probability of success can reasonably be assumed constant.
C. the samples are random, so the proportions are unbiased estimates.
D. nπ ≥ 10 and n(1 - π) ≥ 10 for each sample taken separately.
38. In a random sample of patient records in Cutter Memorial Hospital, six-month postoperative exams were given in 90 out of 200 prostatectomy patients, while in Paymor Hospital such exams were given in 110 out of 200 cases. In a left-tailed test for equality of proportions, the test statistic is:
A. -1.96
B. -2.00
C. -4.00
D. -3.48
39. In a random sample of patient records in Cutter Memorial Hospital, six-month postoperative exams were given in 90 out of 200 prostatectomy patients, while in Paymor Hospital such exams were given in 110 out of 200 cases. In a left-tailed test for equality of proportions, the p-value is:
A. .9772
B. .0228
C. .4772
D. .0517
40. In a random sample of patient records in Cutter Memorial Hospital, six-month postoperative exams were given in 90 out of 200 cases, while in Paymor Hospital such exams were given in 110 out of 200 cases. The pooled proportion is:
A. .50
B. .40
C. .30
D. .20
41. Management of Melodic Kortholt Company compared absenteeism rates in two plants on the third Monday in November. Of Plant A's 800 employees, 120 were absent. Of Plant B's 1200 employees, 144 were absent. To compare the two proportions, the pooled proportion is:
A. .130
B. .140
C. .132
D. .135
10-6
Copyright © 2016 McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
42. Management of Melodic Kortholt Company compared absenteeism rates in two plants on the third Monday in November. Of Plant A's 800 employees, 120 were absent. Of Plant B's 1200 employees, 144 were absent. MegaStat's results for a two-tailed test are shown below.
The test statistic (shown as z = x.xx) is approximately:
A. 2.022
B. 1.960
C. 1.942
D. 1.645
43. Management of Melodic Kortholt Company compared absenteeism rates in two plants on the third Monday in November. Of Plant A's 800 employees, 120 were absent. Of Plant B's 1200 employees, 144 were absent. MegaStat's results for a two-tailed test are shown below.
At α = .05, the two-tailed test for a difference in proportions is:


A. just barely significant.
B. not quite significant.
C. not feasible due to nonnormality.
10-7
Copyright © 2016 McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
44. A new policy of "flex hours" is proposed. Random sampling showed that 28 of 50 female workers favored the change, while 22 of 50 male workers favored the change. Management wonders if there is a difference between the two groups. For a test comparing the two proportions, the assumption of normality for the difference of proportions is:
A. clearly justified.
B. clearly unjustified.
C. a borderline call.
45. A new policy of "flex hours" is proposed. Random sampling showed that 28 of 50 female workers favored the change, while 22 of 50 male workers favored the change. Management wonders if there is a difference between the two groups. What is the test statistic to test for a zero difference in the population proportions?
A. 1.321
B. 1.287
C. 1.200
D. -1.255
46. A new policy of "flex hours" is proposed. Random sampling showed that 28 of 50 female workers favored the change, while 22 of 50 male workers favored the change. Management wonders if there is a difference between the two groups. What is the p-value for a two-tailed test?
A. .3849
B. .1151
C. .2301
D. .3453
47. At Huge University, a sample of 200 business school seniors showed that 26 planned to pursue an MBA degree, compared with 120 of 800 arts and sciences seniors. We want to know if the proportion is higher in the arts and sciences group. The pooled proportion for this test is:
A. .130
B. .140
C. .145
D. .146
48. At Huge University, a sample of 200 business school seniors showed that 26 planned to pursue an MBA degree, compared with 120 of 800 arts and sciences seniors. We want to know if the proportion is higher in the arts and sciences group. For this test, the assumption of normality for the difference of proportions is:
A. clearly unjustified.
B. clearly justified.
C. a borderline call.
10-8
Copyright © 2016 McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
49. At Huge University, a sample of 200 business school seniors showed that 26 planned to pursue an MBA degree, compared with 120 of 800 arts and sciences seniors. We want to know if the proportion is higher in the arts and sciences group. What is the z test statistic?
A. -1.322
B. -1.122
C. -0.716
D. We must first know α
50. At Huge University, a sample of 200 business school seniors showed that 26 planned to pursue an MBA degree, compared with 120 of 800 arts and sciences seniors. We want to know if the proportion is higher in the arts and sciences group. The p-value for a left-tailed test is approximately:
A. .38
B. .48
C. .24
D. .51
51. Two well-known aviation training schools are being compared using random samples of their graduates. It is found that 70 of 140 graduates of Fly-More Academy passed their FAA exams on the first try, compared with 104 of 260 graduates of Blue Yonder Institute. To compare the pass rates, the pooled proportion would be:
A. .500
B. .435
C. .400
D. .345
52. Two well-known aviation training schools are being compared using random samples of their graduates. It is found that 70 of 140 graduates of Fly-More Academy passed their FAA exams on the first try, compared with 104 of 260 graduates of Blue Yonder Institute. To compare the two proportions, the assumption of normality of the test statistic is:
A. justified, but it is a borderline case.
B. clearly justified.
C. clearly not justified.
53. Two well-known aviation training schools are being compared using random samples of their graduates. It is found that 70 of 140 graduates of Fly-More Academy passed their FAA exams on the first try, compared with 104 of 260 graduates of Blue Yonder Institute. The test statistic to test the pass rates for equality is:
A. 2.141
B. 1.298
C. 1.227
D. 1.924
10-9
Copyright © 2016 McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
54. Two well-known aviation training schools are being compared using random samples of their graduates. It is found that 70 of 140 graduates of Fly-More Academy passed their FAA exams on the first try, compared with 104 of 260 graduates of Blue Yonder Institute. To compare the pass rates, find the critical value for a right-tailed test at α = .05.
A. 1.960
B. 1.645
C. 2.326
55. Two well-known aviation training schools are being compared using random samples of their graduates. It is found that 70 of 140 graduates of Fly-More Academy passed their FAA exams on the first try, compared with 104 of 260 graduates of Blue Yonder Institute. To compare the pass rates, the p-value for a right-tailed test is approximately:
A. .054
B. .027
C. .155
D. .013
56. Two well-known aviation training schools are being compared using random samples of their graduates. It is found that 70 of 140 graduates of Fly-More Academy passed their FAA exams on the first try, compared with 104 of 260 graduates of Blue Yonder Institute. In a right-tailed test, the p-value is .0275, so at α = .025 we should:
A. reject the hypothesis of equal proportions.
B. not reject the hypothesis of equal proportions.
C. change the α to .05 to get a rejection.
57. Of 200 youthful gamers (under 18) who tried the new Z-Box-Plus game, 160 rated it "excellent," compared with only 144 of 200 adult gamers (18 or over). The pooled proportion for a test to compare the two proportions would be:
A. .76
B. .72
C. .77
D. Must know α to answer.
58. Of 200 youthful gamers (under 18) who tried the new Z-Box-Plus game, 160 rated it "excellent," compared with only 144 of 200 adult gamers (18 or over). The test statistic to test the two proportions for equality would be:
A. 1.645
B. 1.960
C. 1.873
D. 1.448
10-10
Copyright © 2016 McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
59. Of 200 youthful gamers (under 18) who tried the new Z-Box-Plus game, 160 rated it "excellent," compared with only 144 of 200 adult gamers (18 or over). The p-value for a right-tailed test to compare the two proportions would be approximately:
A. .042
B. .031
C. .054
D. .095
60. Of 200 youthful gamers (under 18) who tried the new Z-Box-Plus game, 160 rated it "excellent," compared with only 144 of 200 adult gamers (18 or over). The 95 percent confidence interval for the difference of proportions would be approximately:
A. [+.013, +.263].
B. [-.014, +.188].
C. [-.003, +.163].
D. [+.057, +.261].
61. Carver Memorial Hospital's surgeons have a new procedure that they think will decrease the time to perform an appendectomy. A sample of 8 appendectomies using the old method had a mean of 38 minutes with a variance of 36 minutes, while a sample of 10 appendectomies using the experimental method had a mean of 29 minutes with a variance of 16 minutes. For a right-tailed test for equal means (assume equal variances), the critical value at α = .10 is:
A. 1.746
B. 1.337
C. 2.120
D. 2.754
62. Carver Memorial Hospital's surgeons have a new procedure that they think will decrease the time to perform an appendectomy. A sample of 8 appendectomies using the old method had a mean of 38 minutes with a variance of 36 minutes, while a sample of 10 appendectomies using the experimental method had a mean of 29 minutes with a variance of 16 minutes. For a right-tailed test of equal means (assume equal variances), the pooled variance is:
A. 14.76
B. 26.00
C. 24.75
D. 27.54
10-11
Copyright © 2016 McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
63. Carver Memorial Hospital's surgeons have a new procedure that they think will decrease the time to perform an appendectomy. A sample of 8 appendectomies using the old method had a mean of 38 minutes with a variance of 36 minutes, while a sample of 10 appendectomies using the experimental method had a mean of 29 minutes with a variance of 16 minutes. For a right-tailed test of means (assume equal variances), the test statistic is:
A. 3.814
B. 2.365
C. 3.000
D. 1.895
64. Based on a random sample of 13 tire changes, the mean time to change a tire on a Boeing 777 has a mean of 59.5 minutes with a standard deviation of 8.4 minutes. For 10 tire changes on a Boeing 787, the mean time was 64.3 minutes with a standard deviation of 12.4 minutes. To test for equal variances in a two-tailed test at α = .10, the critical values are:
A. 3.73 and 0.228
B. 2.51 and 3.67
C. 3.07 and 0.398
D. 3.07 and 0.357
65. A certain psychological theory predicts that men want bigger families than women. Kate asked each student in her psychology class how many children he or she considered ideal for a married couple and obtained the Excel results shown below at α = .05.

What conclusion can you draw in a two-tailed test at α = .05?
A. Men want larger families on average than women.
B. Women want larger families on average than men.
C. We cannot reject the hypothesis of equal population means.
D. The decision depends on whether or not the variances are equal.
10-12
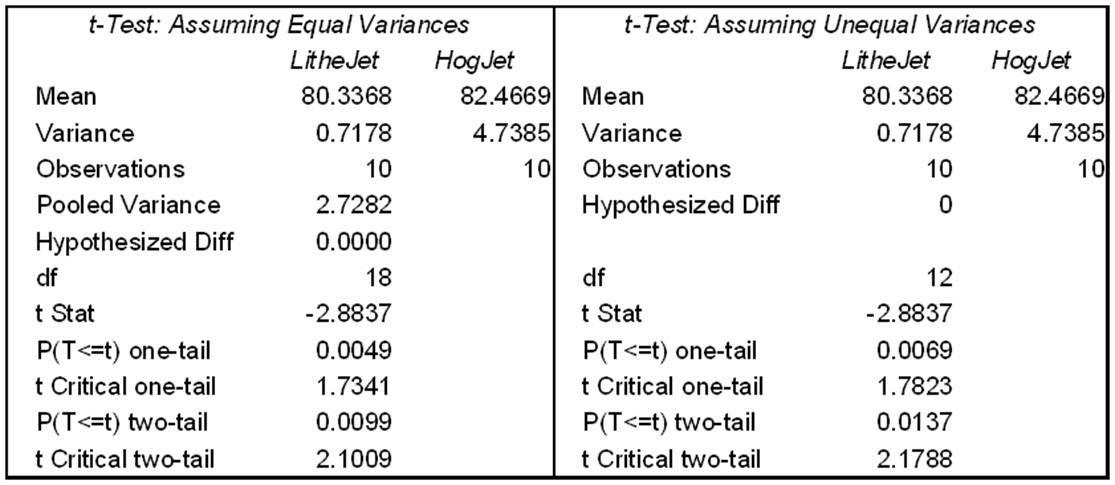
Copyright © 2016 McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
66. Nacirema Airlines is buying a fleet of new fuel-efficient planes. The HogJet and the LitheJet both meet their price and performance needs, and both planes meet EPA noise guidelines. However, the quieter plane is preferred. Each plane is flown through a typical takeoff and landing sequence 10 times, while remote sensors at ground level record the noise levels (in decibels). The table below summarizes the sound level tests using Excel's default level of significance (α = 0.05).
In a left-tailed test comparing the means at α = .05, we would:
A. not reject H0.
B. reject H0.
C. have insufficient information to make a decision.
67. Nacirema Airlines is buying a fleet of new fuel-efficient planes. The HogJet and the LitheJet both meet their price and performance needs, and both planes meet EPA noise guidelines. However, the quieter plane is preferred. Each plane is flown through a typical takeoff and landing sequence 10 times, while remote sensors at ground level record the noise levels (in decibels). The table below summarizes the sound level tests using Excel's default level of significance (α = 0.05).
After inspecting this table, we would most likely:
A. use the test assuming unequal variances.

B. use the test for equal variances.
C. perform another test to determine if the variances are equal before proceeding.
D. realize that the decision isn't affected by our assumptions concerning the variance.
10-13
Copyright © 2016 McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
68. Nacirema Airlines is buying a fleet of new fuel-efficient planes. The HogJet and the LitheJet both meet their price and performance needs, and both planes meet EPA noise guidelines. However, the quieter plane is preferred. Each plane is flown through a typical takeoff and landing sequence 10 times, while remote sensors at ground level record the noise levels (in decibels). The table below summarizes the sound level tests using Excel's default level of significance (α = 0.05).
If we switched from α = .05 to α = .005 in a two-tailed test of means, our assumption about variances (assumed equal or assumed unequal) would:

A. affect the decision.
B. not affect the decision.
C. require a new analysis.
69. A psychology researcher has a theory that predicts women will tend to carry more cash than men. A random sample of Ersatz University students revealed that 16 females had a mean of $22.30 in their wallets with a standard deviation of $3.20, while 16 males had a mean of $17.30 with a standard deviation of $9.60. The researcher's hypothesis would lead us to perform a:
A. right-tailed test.
B. left-tailed test.
C. two-tailed test.
70. A psychology researcher has a theory that predicts women will tend to carry more cash than men. A random sample of Ersatz University students revealed that 16 females had a mean of $22.30 in their wallets with a standard deviation of $3.20, while 16 males had a mean of $17.30 with a standard deviation of $9.60. The test statistic for the researcher's hypothesis is:
A. impossible to determine without knowing α.
B. 1.250.
C. 1.504.
D. 1.976.
10-14
Copyright © 2016 McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
71. A random sample of Ersatz University students revealed that 16 females had a mean of $22.30 in their wallets with a standard deviation of $3.20, while 16 males had a mean of $17.30 with a standard deviation of $9.60. In comparing the population variances at α = .10 in a two-tailed test, we conclude that:
A. the variances are equal.
B. the variances are unequal.
C. the variances are incomparable (different sample sizes).
72. Randomly chosen MBA students were asked their opinions about the ideal number of children for a married couple. The sample data were entered into MegaStat, and the following results were produced.
To compare the means, would it be appropriate to use a test that assumes equal variances?
A. Yes, because by pooling our variances, we can simplify our calculations.
B. Yes, we should assume equal variances when comparing independent samples.

C. No, because the sample statistics show that the variances are unequal at α = .05.
D. No, because the variances will differ because the means differ significantly.
10-15
Copyright © 2016 McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
73. Litter sizes (number of pups) for randomly chosen dogs from two breeds were compared. The sample data were entered into Excel, and the following results were produced.
What is the critical value for a left-tailed test comparing the means at α = .05?

A. -1.645
B. -1.721
C. -1.703
D. -1.699
74. Randomly chosen MBA students were asked their opinions about the ideal number of children for a married couple. The sample data were entered into MegaStat, and the following results were produced.
What conclusion can you draw from this analysis at α = .05?
A. Men want larger families on average than women.
B. Women want larger families on average than men.
C. This is insufficient evidence to suggest a difference in means.
D. We could conclude that men want larger families if we used a two-tailed test.
Copyright © 2016 McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.

75. Litter sizes (number of pups) for randomly chosen dogs from two breeds were compared. The sample data were entered into Excel, and the following results were produced.
What is the p-value for a left-tailed test comparing the means at α = .05?

A. Less than .10
B. More than .10
C. Between .10 and .05
D. Between .05 and .01
76. During a test period, an experimental group of 10 vehicles using an 85 percent ethanol-gasoline mixture showed mean CO2 emissions of 667 pounds per 1000 miles, with a standard deviation of 20 pounds. A control group of 14 vehicles using regular gasoline showed mean CO2 emissions of 679 pounds per 1000 miles with a standard deviation of 15 pounds. At α = 0.05, in a left-tailed test, the critical value to compare the means (assuming equal variances) is:
A. -2.508
B. -2.074
C. -1.321
D. -1.717
77. During a test period, an experimental group of 10 vehicles using an 85 percent ethanol-gasoline mixture showed mean CO2 emissions of 667 pounds per 1000 miles, with a standard deviation of 20 pounds. A control group of 14 vehicles using regular gasoline showed mean CO2 emissions of 679 pounds per 1000 miles with a standard deviation of 15 pounds. Assuming equal variances, the pooled variance is:
A. 296.59
B. 225.00
C. 400.00
D. 522.16
Copyright © 2016 McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
78. During a test period, an experimental group of 10 vehicles using an 85 percent ethanol-gasoline mixture showed mean CO2 emissions of 667 pounds per 1000 miles, with a standard deviation of 20 pounds. A control group of 14 vehicles using regular gasoline showed mean CO2 emissions of 679 pounds per 1000 miles with a standard deviation of 15 pounds. At α = 0.05, in a left-tailed test (assuming equal variances) the test statistic is:
A. -1.310
B. -2.042
C. -1.645
D. -1.683
79. During a test period, an experimental group of 10 vehicles using an 85 percent ethanol-gasoline mixture showed mean CO2 emissions of 240 pounds per 100 miles, with a standard deviation of 20 pounds. A control group of 14 vehicles using regular gasoline showed mean CO2 emissions of 252 pounds per 100 miles with a standard deviation of 15 pounds. A quick comparison of the sample variances suggests that the population variances are:
A. probably equal.
B. probably unequal.
C. incomparable.
80. Mary did an analysis of acute care variances in samples of occupancy rates at two community hospitals and obtained the following results:
Can Mary conclude that the variances are unequal at α = .05?

A. No, there isn't enough evidence to believe the variances are unequal.
B. Yes, the analysis shows that the variances are unequal.
C. You can't tell without knowing the sample sizes.
Copyright © 2016 McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
81. Mary analyzed occupancy rates at two community hospitals and obtained the following Excel results.

Which conclusion is correct in a two-tailed test at α = .05?

A. There appears to be no difference in the mean occupancy rates.
B. HealthPro has a significantly higher mean occupancy rate.
C. There is a significant difference in the mean occupancy rates.
82. A medical researcher wondered if there is a significant difference between the mean birth weight of boy and girl babies. Random samples of 5 babies' weights (pounds) for each gender showed the following:
To test the researcher's hypothesis, we should use the:
A. paired (dependent) samples t-test.
B independent samples t-test.
C. large-sample z-test.
D. t-test for correlation.
Copyright © 2016 McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
83. A medical researcher wondered if there is a significant difference between the mean birth weight of boy and girl babies. A random sample of babies' weights (pounds) showed the following. How many degrees of freedom would be used to test for a zero difference in means?



A. 4
B. 8
C. 10
D. Must know α to say.
84. In a test of a new surgical procedure, the five most respected surgeons in FlatBroke Township were invited to Carver Hospital. Each surgeon was assigned two patients of the same age, gender, and overall health. One patient was operated upon in the old way, and the other in the new way. Both procedures are considered equally safe. The surgery times are shown below:
Which test should we use to test for zero difference in mean times?
A. Paired t-test
B. Independent samples t-test
C. Independent samples z test
D. Cannot be sure without knowing α.
85. In a test of a new surgical procedure, the five most respected surgeons in FlatBroke Township were invited to Carver Hospital. Each surgeon was assigned two patients of the same age, gender, and overall health. One patient was operated upon in the old way, and the other in the new way. Both procedures are considered equally safe. The surgery times are shown below:
The time (in minutes) to complete each procedure was carefully recorded. In a right-tailed test for a difference of means, the test statistic is:
A. 3.162
B. 1.645
C. 1.860
D. 2.132
10-20
Copyright © 2016 McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
86. A corporate analyst is testing whether mean inventory turnover has increased. Inventory turnover in six randomly chosen product distribution centers (PDCs) is shown.


The degrees of freedom for the appropriate test would be:
87. A corporate analyst is testing whether mean inventory turnover has increased. Inventory turnover in six randomly chosen product distribution centers (PDCs) is shown.
The right-tailed critical value at α = 0.005 is:
Copyright © 2016 McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
88. A corporate analyst is testing whether mean inventory turnover has increased. Inventory turnover in six randomly chosen product distribution centers (PDCs) is shown.
The value of the test statistic is:
A. 3.798
B. 2.449
C. 1.225
D. 3.503
89. The table below shows the mean number of daily errors by seven air traffic controller trainees during the first two weeks on the job. We want to perform a paired t-test at α = .05 to see if the mean daily errors have decreased from Week 1 to Week 2.


The right-tailed critical value at α = 0.05 is:
Copyright © 2016 McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
90. The table below shows the mean number of daily errors by air traffic controller trainees during the first two weeks on the job. We want to perform a paired t-test at α = .05 to see if the mean daily errors decreased significantly.
The test statistic is:
A. 1.25
B. 1.75
C. 0.87
D. 0.79
91. The table below shows the mean number of daily errors by air traffic controller trainees during the first two weeks on the job. We want to perform a paired t-test at α = .05 to see if the mean daily errors decreased significantly.


What would be the degrees of freedom for the appropriate test?
A. 14
B. 12
C. 7
D. 6
92. The F-test for equality of variances assumes:
A. normal populations.
B. equal means.
C. equal sample sizes.
D. equal means and sample sizes.
93. Which is not true of the two-tailed F-test for equality of variances?
A. It requires reversing the numerator and denominator d.f. to obtain the left-tail critical value.
B. It can be avoided by "folding" the larger variance into the numerator and adjusting α.
C. It is fairly robust to the presence of nonnormality in the populations being sampled.
10-23
Copyright © 2016 McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
94. Which of the following is not a characteristic of the F distribution?
A. It is a continuous distribution.
B. It is always a positive number.
C. It is a family based on two sets of degrees of freedom.
D. It describes the ratio of two sample means.
95. Carver Memorial Hospital's surgeons have a new procedure that they think will decrease the variance in the time it takes to perform an appendectomy. A sample of 8 appendectomies using the old method had a variance of 36 minutes, while a sample of 10 appendectomies using the experimental method had a variance of 16 minutes. At α = .10 in a two-tailed test for equal variances, the critical values are:
A. 0.272 and 3.29
B. 0.299 and 3.07
C. 0.368 and 2.51
D. -1.645 and +1.645
96. The folded F-test for equality of variances:
A. is rarely used because of its complexity.
B. requires looking up the critical value for α/2.
C. puts the smaller variance in the numerator.
D. requires looking up two critical values of F instead of one.
97. An F-test for equality of variances gives a p-value of .003. At α = .05, what conclusion can be made about the preferred test to compare the means for the same sample?
A. We would prefer a pooled variance t-test for equality of means.
B. We would not wish to pool the variances in a t-test for equality of means.
C. We would prefer a paired t-test for equality of means.
D. The variances have nothing to do with the t-test for equality of means.
98. A random sample of Ersatz University students revealed that 16 females had a mean of $22.30 in their wallets with a standard deviation of $3.20, while 6 males had a mean of $17.30 with a standard deviation of $9.60. At α = .10, to test for equal variances in a two-tailed test, the critical values are:
A. 0.441 and 3.24
B. 0.556 and 2.27
C. 0.345 and 4.62
D. 0.387 and 2.90
10-24
Copyright © 2016 McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
99. A random sample of Ersatz University students revealed that 16 females had a mean of $22.30 in their wallets with a standard deviation of $3.20, while 6 males had a mean of $17.30 with a standard deviation of $9.60. The value of the test statistic for a folded F-test for equal variances is:
A. 0.333
B. 0.111
C. 9.00
D. 3.00
100.Assuming unequal variances in a t-test for a zero difference of two means, we would:

A. sum the degrees of freedom for each sample.
B. use the larger degrees of freedom for simplicity.
C. use a complicated formula for the degrees of freedom.
D. use a z-test to be conservative in the calculation.
101.The z-test for zero difference in two means:
A. is generally the preferred test for means.
B. is rarely suitable for business data.
C. is the most powerful test for means.
D. is not available in Excel's Data Analysis.
102.A confidence interval for the difference of two population means:
A. must pool the sample variances.
B. may or may not pool the sample variances.
C. cannot be used to test for equal population means.
103.A medical researcher compared the variances in birth weights for five randomly chosen babies of each gender, with the MegaStat results shown below.
The population variances:
A. may be assumed equal at any customary α
B. should be assumed unequal at any customary α
C. are not relevant to this paired t-test.
10-25
Copyright © 2016 McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
104.A medical researcher wondered if there is a significant difference between the mean birth weight of boy and girl babies. She weighed a random sample of five babies of each gender. Their weights (pounds) are shown below, along with some MegaStat results.

The population means:
A. may be assumed equal at any customary α.
B. should be assumed unequal at any customary α.
C. are not relevant to this paired t-test.
105.The coach of an adult Master's Swim class selected eight swimmers within each of the two age groups shown below. A 50-yard freestyle time is recorded for each swimmer. The resulting times (seconds) are shown below. Which statistical test would you choose to compare the two groups?

A. t-test for independent samples with known variances
B. t-test for independent samples with unknown variances
C. t-test for paired samples
D. z-test for two independent proportions
Copyright © 2016 McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
106.Jason wants to perform a two-tailed test for equality between two independent sample proportions. Each sample has at least 10 "successes" and 10 "failures." Jason's test statistic is1.44. What is his p-value?
A. .1498
B. .0749
C. .9251
D. Between .01 and .05
107.Does the Speedo Fastskin II Male Hi-Neck Bodyskin competition racing swimsuit improve a swimmer's 200-yard individual medley performance times? A test of 100 randomly chosen male varsity swimmers at several different universities showed that 66 enjoyed improved times, compared with only 54 of 100 female varsity swimmers. To test for equality in the proportions of men versus women who experienced improvement, the test statistic is approximately:
A. 1.73
B. 1.47
C. 2.31
D. Can't tell without knowing the tail of the test.
108.Does the Speedo Fastskin II Male Hi-Neck Bodyskin competition racing swimsuit improve a swimmer's 200-yard individual medley performance times? A test of 100 randomly chosen male varsity swimmers at several different universities showed that 66 enjoyed improved times, compared with only 54 of 100 female varsity swimmers. In comparing the proportions of males versus females, is it safe to assume normality?
A. Yes, clearly.
B. Yes, but just barely.
C. No.
D. Can't tell without knowing α
109.The table below shows two samples taken to compare the mean age of individuals who purchased the iPhone 3G at two AT&T store locations.

What are the critical values for a two-tailed test for equal variances at α = .05?
A. 0.275, 3.14
B. 0.244, 3.37
C. 0.210, 3.95
D. 0.181, 4.32
Copyright © 2016 McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
110.The table below shows two samples taken to compare the mean age of individuals who purchased the iPhone 3G at two AT&T store locations.

At α = .05, can you conclude that the first sample has a larger variance than the second sample?
A. Yes, clearly.
B. Yes, but just barely.
C. No.
111.Group 1 has a mean of 13.4 and group 2 has a mean of 15.2. Both populations are known to have a variance of 9.0 and each sample consists of 18 items. What is the test statistic to test for equality of population means?
A. -1.755
B. -1.643
C. -1.800
D. -1.285
112.Which is not a type of comparison for which you would anticipate a two-sample test?
A. Before Treatment versus After Treatment.
B. Old Method versus New Method.
C. Sample Mean versus Desired Mean.
D. Experimental Group versus Control Group.
Short Answer Questions
Copyright © 2016 McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
113.Random samples of students were compared to see whether or not there was a difference in the proportion favoring the university's proposed switch from MWF (three-day) classes to MW and TR (two-day) classes. The results shown below are from MegaStat. Analyze these results thoroughly.
Copyright © 2016 McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.

114.The table below compares two samples taken to compare the mean age of individuals who purchased the iPhone 3G at two AT&T store locations. Very briefly, what conclusions can you draw?
Copyright © 2016 McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.

115.Random samples of Tuesday and Friday withdrawals from a college-campus ATM were compared to see whether or not there was a difference in the means. The results shown below are from MegaStat. Analyze these results thoroughly.
Copyright © 2016 McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.

