Chapter
Nine
What Makes Some Music Great And Why Does It Matter?


Bach: Prelude in C Major, BWV 846; beginning of 1722 autograph1
The definition of music (“music is a kind of heightened poetry and dance ”) and why it’s so important to us (when, through music, I “come to know me” then “I can become part of we”), the heavenly tuning of the cosmos and the everyday tuning of our violins’ and keyboards’ (that business of half and whole steps with Pythagorean tuning and the different temperaments), the general categories of music (folk, pop, classical), what it means to “swing” (we live in patterns); in the last several hundred pages we’ve covered a lot of ground, from ancient philosophers in both China and Greece to fencing at Versailles to Mari Sandoz on the Nebraska prairies to Stockhausen’s quartet of helicopters. But I’ve left something out. I’ve hinted at it and occasionally we’ve glanced by it. But we haven’t addressed it directly. We need to now. It’s very important, indeed it’s the most important thing we can discuss.
1 Staatsbibliothek, Berlin, Mus.ms.Bach 40; image public domain. https://www.bachdigital.de/receive/BachDigitalSource source_00001361
It’s the question of value. You’ll remember that in our Chapter Five discussion of the three general categories of music we also talked about values within those types.
“Popular music” is the music that’s most popular, and that popularity is tabulated by sales. The best popular music is the music that sells the most. “Folk music” is music of the home. It’s loved. Its metric of value isn’t counted-up but felt. Classical music is distinguished by three characteristics: 1) literary support, 2) artistic quality, and 3) the expressive importance of structure (form). Popular music can be quite artistic, like classical music as we saw with Dolly Parton’s “The Grass Is Green”, and it can become quite important to a culture, like folk music was we saw in the case of Pete Seeger’s and Lee Hay’s “If I Had A Hammer” Folk music, once it’s arranged and copywritten, can be a lucrative piece of popular music as has been the case with the 19th-century Appalachian ballad “Tom Dooley” which was popularized by The Kingston Trio. Their 1958 single topped the Billboard Hot 100 chart on November 17 of that year, selling over three million copies. And a piece of classical music can become a successful piece of popular music as in the case of the aria “Nessun Dorma” from Giacomo Puccini’s 1924 opera Turandot performed by tenors José Carreras, Plácido Domingo, and Luciano Pavarotti on their 1990 “The Three Tenors” concert album It sold over ten and a half million albums.
But the artistic quality of the pop song, or the commercial success of the folk song, are irrelevant to the core characters of the genera. But artistic quality is essential to classical music. If a pop song isn’t at least reasonably profitable, it’s eliminated from the catalogue. Physical copies are literally destroyed. A folk song that isn’t cherished is forgotten.2 Apart from being presented as curiosity or stored in an archive, there’s no justification to perform or to preserve a piece of classical music that isn’t artistically good. It’s lost its raison d’être.
Because it’s an essential part of our category of classical music we’re compelled to know what makes music artistically valuable. Or more simply: what makes music good, and going beyond that, what makes good music great? And then, why is great music important?
2 This has happened to the song “Dixie.” Written by the Ohioan Daniel Emmett as a minstrel song in 1859, it quickly became popular throughout the United States, becoming an anthem of the Confederacy after secession Upon hearing the news of Robert E. Lee’s surrender at Appomattox Court House the previous day, on the afternoon of April 10, 1865 an enormous crowd gathered in front of the White House, clamoring for Lincoln to address them. The President appeared at a window, and after brief congratulations, said: “I see you have a band [Voices: “We have three of them.”] I propose now closing up by requesting you to play a certain piece of music or a tune. I thought ‘Dixie’ one of the best tunes I ever heard. [Laughter]. I heard that our adversaries over the way had attempted to appropriate it. I insisted yesterday that we had fairly captured it. [Cheers and laughter]. I presented the question to the Attorney-General, and he gave his opinion that it is our lawful prize [Laughter and cheers.] I ask the band to give us a good turn upon it.” The bands then played “Dixie” followed by “Yankee Doodle.” In the century and half following that afternoon demonstration, “Dixie” became a core piece of American patriotic folk music, as essential to the American “home” as were “Yankee Doodle,” “The Battle Hymn of the Republic,” and “My Country ‘Tis of Thee,” words and tune. But reflecting changing attitudes of the 1990’s (or possibly engineering those changes), educators began removing it from elementary school song books and the song ceased being taught and sung. At this writing it’s rare for an American under 30 to know the piece. It has been forgotten. Carl Sandburg, Abraham Lincoln, the War Years – IV, New York, Charles Scribner’s Sons, 1939, pp. 207-208.
I’d would be surprised if upon reading that you don’t bristle a bit. It’s not a fashionable question. Once considered a given, the idea that there are broad standards of value shared across a culture, and even between cultures a given idea in the cultures of Confucian China, Hindu India, and Christian Europe for the last several millennia has in the last half century come to be viewed with suspicion, derision, and an almost evangelical opposition in fashionable thinking. Condemned in a litany of nouns and neologisms ending in “ist” (colonialist, racist, sexist, straightist, the list continues), in those circles the question of “good” music, or extended to “good” art, is a slaver’s trap, hiding within itself beliefs of one culture’s superiority over another. For these thinkers, the questions we’re asking are not questions about values, aesthetic or otherwise, but instead posturings, subtle displays of power that demonstrate the ability of one group to force its beliefs upon another. Simply asking the question is an act of hegemony.
In one way we’ve been here before, at the beginning. You’ll remember that in Chapter One, when we began our consideration of the definition of music, we addressed the issue of whether or not a definition could be objective. Through the course of that chapter we saw that music, like just about everything else, could be objectively defined and we came up with a definition. The question here is very much like that. The points raised in the paragraph above shouldn’t be dismissed cavalierly, but I’m going to ask you to put them aside. We’ll touch on them again at the end.
IAs we started our consideration of music’s definition by listening to and thinking about real pieces of music (List I:1) and not speculating about music as a general notion I’d like to anchor our thought here in a real piece of music: the Prelude in C Major, BWV 846,3 with which Johann Sebastian Bach opened the first volume of his Well-Tempered Clavier.[Ex.9.1]. Between 1717 and 1723, Bach was in the service of Leopold, Prince of Anhalt-Köthen. The prince was a devout Calvinist and because Reformed worship did not make use of elaborate music, Bach primarily composed non-liturgical works while in his employ. The suites for unaccompanied cello, the sonatas and partitas for violin, and the Brandenburg concerti, all roughly date from this time. In 1722, he published what he called “The Well-Tempered Clavier” (Das Wohltemperierte Klavier), a collection of twenty-four paired preludes and fugues, written for a keyboard, rising chromatically from C major, to c minor, to C-sharp major, to c-sharp minor, to D major, to d minor, to E flat major, to e-flat minor, and so forth, to a final a prelude and fugue in b minor [Ex.9.]. Bach completed a second volume in 1742. The volumes are universally regarded as
3 BWV stands for Bach-Werke-Verzeichnis, (“Bach Works Catalogue”). Beginning in the 19th century, scholars began the process of cataloguing composers’ works. Mozart’s works are identified by “K Numbers” numbers because they were catalogued by Ludwig von Köchel (1800-1877), Schubert’s by “D Numbers” because they were catalogued by Otto Deutsch (1883-1967), and Domenico Scarlatti’s works by “K Numbers” because they were catalogued by Ralph Kirkpatrick (1911-1984). Beginning in 1850, Bach’s works were first collected in the Bach Gesellschaft (BG) where they are identified by volume number. A third version of his collected works, Neu-BachAusgabe (NBA)(“New Bach Edition”), was fully published in 2007 but identifies works by their BWV number.

monuments of western classical music; their study is a core of all musicians’ training and pianists aspiring to any stature learn the pieces and play them throughout their lives (Frederick Chopin made it a practice to play through a prelude and fugue at the beginning of each day, a discipline that is followed by many pianists). While some of the pieces are quite virtuosic, the first prelude is simple and within the abilities of the beginning keyboard player, as is appropriate since the piece is an expansion of a shorter version Bach wrote for his second child, Wilhelm Friedemann Bach, around 1720, when the boy was ten years old.4 A copy of the score is included at the end of this chapter and before we move on I suggest that you play it. It’s not hard, just stumble through it, nobody is listening except you. Example IX.3 is a rhythmically simplified schematic of the piece, showing the chords. Arabic numbers indicate the measures.
4 This is catalogued as BWV 846A and is included in the collection of teaching pieces known as the Klavierbüchlein.
5 Staatsbibliothek, Berlin, Mus.ms.Bach 40; image public domain

Example IX.3
C Major Prelude Chordal Schematic
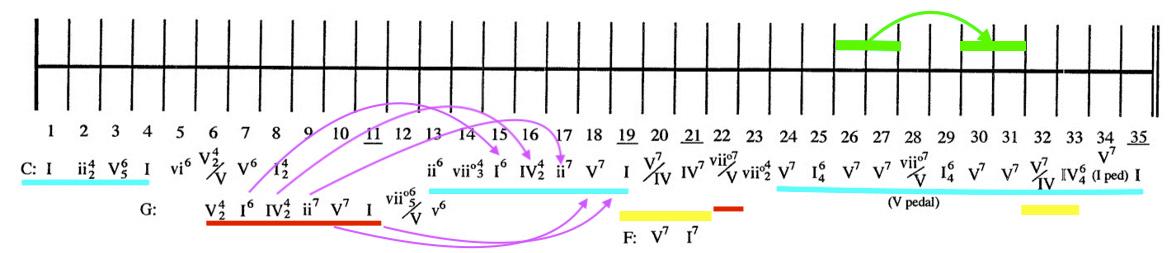
The double bars indicate important sections which are articulated by cadences (a “cadence” is the technical term for the end of a phrase). Bach first cadences in C major in m. 4. That’s the end of Bach’s first section. In the second section he modulates to G major and ends that section with a cadence in G major in measure 11. In the next section Bach modulates back to C major, cadencing in measure 19. After a very short section that suggests F major, Bach begins the last section, the prelude’s longest, with a feign to G major subtly emphasized by an eight measure pedal point on G (measures 24-31) and returns to C major in measure 35 after nod to F major in measures 32 and 33. The pedal point on G is echoed at the end by a four measure pedal point on C. Bach’s harmony is summarized in Ex.IX.4. Sections in C major are underlined in blue, G major in red, and F major in yellow (here and elsewhere technical vocabulary will be used, there’s no way to thoroughly understand the material without it. But if you find it’s opaque don’t worry about it; you can follow the general argument without understanding all the detail).
Example IX.4
C Major Prelude: Harmonic summary
Measures 15 through 19 is an exact transposition of measures 7 through 11 (shown by the purple arrows) in other words Bach modulates back to C Major from G Major in the same way as he modulated earlier from C Major to G Major. Bach’s harmonic rhythm throughout the piece is one chord for each measure with the sole exception of measure 33 where Bach moves from the subdominant six-four to the supertonic four-two on the fourth beat. There are very few dissonances caused by non-chord tones in the piece. There are only two passing-tones: the “C” in measure 23 and the antepenultimate “E” in measure 34. Bach repeats measures 26 through 27 in measures 30 through 31 (shown in green), a passage that includes one four-three suspension between the adjacent measures. And it’s possible to consider the dissonances between measures 8 and 9 and again between measures 16 and 17 as both two - three suspensions, although we can

Example IX.5
Schematic of three different versions of the C Major Prelude. also consider those dissonant sonorities as major chords with major sevenths in third inversion. Although in the last century, major chords with major sevenths, or any kind of chord with a major seventh, have not only become typical in our harmonic practice but even harmonic consonances, in the beginning of the 18th century they were exceedingly rare; composers used chords containing sevenths but the sevenths were typically minor sevenths or diminished sevenths. Bach’s decision to use the major chord with the major seventh three times in the prelude, in measures 8, 16, and again in 21, is startling.
Why did he do it? These are exceedingly odd chords for the time. Are they perhaps mistakes? We’ve already mentioned that the prelude already existed in a shorter form in a version from about 1720. Why did Bach lengthen it here? Was he paid by the measure? That’s not a silly question. Sometimes artists are paid “by the yard,” so to speak. It was customary for novels to be serialized in the 19th century. Charles Dickens’ Oliver Twist appeared in twenty-four installments in the journal Bentley’s Miscellany between April 1838 and October 1839 and Alexandre Dumas’ The Count of Monte Cristo appeared in 139 installments in the Journal des Débats between August 1844 and January 1846; the more chapters the authors wrote the greater their fees. Theater composers regularly have to write music to “cover” certain times. In order to cover the time required for the scene change between the first two acts of his Turandot, in 1924 Puccini inserted a comic trio for the courtiers Ping, Pang, and Pong. Ralph Vaugh Williams did the same thing in his opera Pilgrim’s Progress, twenty-seven years later, inserting a intermezzo for baritone allowing for a scene change between the first two acts and composers for films and video games are always dealing with ways to fill specific time spans with music. Did Bach just need something longer here? Did he need to fill up a page?
And how much longer? Christian Friedrich Gottlieb Schwencke (1767–1822) was a musician and mathematician. As a boy, he sang at Hamburg’s Michaeliskirche under the direction of Bach’s son, Carl Philipp Emanuel Bach (1714-1788). He must have been an extraordinarily talented musician because upon Carl Philipp Emanuel’s death, without previously have held a similar position and having just finished his university studies and being only
twenty-two years old, he was elected to succeed him as Kantor at the Johanneum, the city’s oldest school, and music director of the city of Hamburg (a significant appointment as Hamburg was the third largest city in the Holy Roman Empire, only slightly smaller than Vienna and Berlin and commercially more robust than either). Scholars presume, reasonably, that Schwencke had access to Johann Sebastian’s music both from his boyhood, when he was singing for Carl Philipp Emanuel, and later when he succeeded Carl Philipp Emanuel in Hamburg.
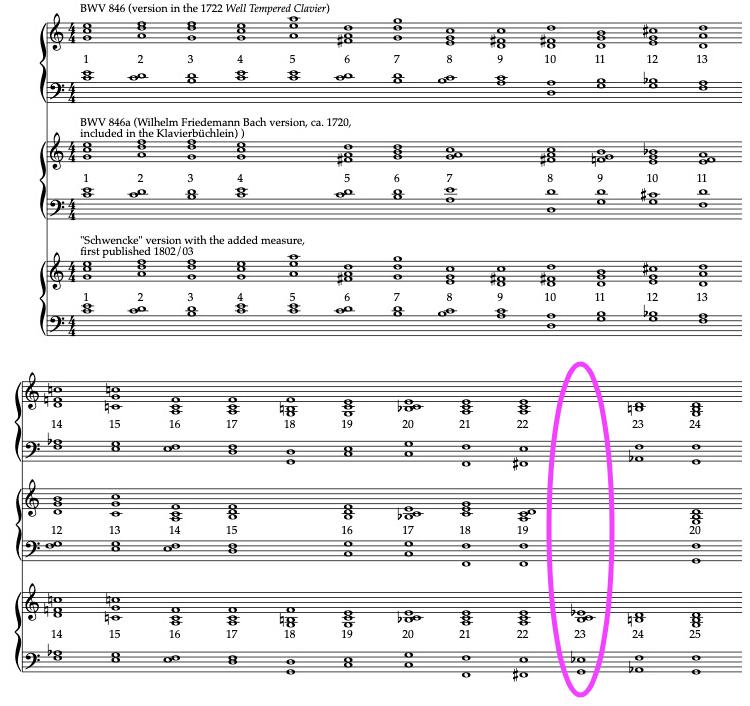
When we say that Well-Tempered Clavier was published in 1722 we don’t mean that it was printed, distributed, and sold through merchants, as things are published today. Music did circulate that way in the 18th century, and earlier, but in the case of the Well-Tempered Clavier we mean that Bach completed a finished score and copies, made by hand, were circulated among cognoscenti. At some point, Schwencke made his own copy of the volume, whether or not that copy came directly from Johann Sebastian or was a copy of a copy, we don’t know, but Schwencke’s version of the prelude had 36 measures, not 35; there’s an additional measure between measures twenty-two and twenty-three. The source of the extra measure is uncertain. It’s reasonable to speculate that Schwencke possibly had access to a Bach manuscript that contained that extra measure. But it’s also plausible that Schwencke, looking at the odd progression between those measures and the leap of the diminished third in the bass (f sharp to a flat), chose to correct what could be considered unstylistic voice-leading. So he added a measure to “smooth it out.”
The cause for the addition isn’t important at the moment. What is important is that when Simrock, a publishing house in Bonn, came to engrave and publish an edition of the WellTempered Clavier in 1801 or 1802, the source of their edition was Schwencke’s manuscript (it’s suspected that Schwencke was the edition’s editor). Possibly as soon as just weeks after the Simrock publication, H.A.Nägeli in Zurich and Hoffmeister & Kühnel published their own editions of the volume, editions that did not contain the extra measure that was included in the Simrock edition. All three editions circulated in the 19th century but the Simrock version was given added authority when Carl Czerny (1791-1857), one of the most import musicians of the century (he began piano and composition studies with Beethoven when he was ten years old and later became the teacher of Liszt) included the extra measure in the version of the WellTempered Clavier he edited for Peters in 1837. It was this version of the prelude that Charles Gounod used which, after versions as an improvisation, apiece for violin and piano, and a song with a French text, finally was wedded to the text of the Ave Maria in 1859, becoming one of the most performed works of the late 19th century.6
We have three versions of the prelude: the earliest written for Wilhelm Friedemann Bach, and two that purportedly date from 1722. They’re all different lengths. Example IX.5 is a schematic of the versions, showing only the chords. The Arabic numerals are the measure numbers of the different versions and the “added” measure is circled.
And we have more questions about the prelude’s length. In measure thirty-one Bach has a dominant-seventh, the resolution of the four-three suspension he prepared in the previous
6 Norbert Müllermann, “On the lookout for the lost measure: Bach’s C-major Prelude from the Well-Tempered Clavier I, posted April 16, 2012. https://blog.henle.de/en/2012/04/16/on-the-lookout-for-the-lost-measure-bach’s-cmajor-prelude-from-the-well-tempered-clavier-i/
measure (and these two measures are a rhetorical repetition of measures twenty-six and twentyseven, shown in green in Ex. IX.4). Bach could have resolved that dominant-seventh directly to a tonic, thus ending the piece in measure thirty-two or continuing the rhythmic flow of his arpeggiations into measure thirty-three, as I have done in Example IX.6. But instead of a tonic in measure thirty-two, Bach has a dominant-seventh of the subdominant, a chord suggesting the key of F Major, and extends the piece for another two or three measures from where he could have ended it. And we can go even further, noticing that Bach could have ended the piece with dominant to tonic cadences in measures nineteen and twenty-eight. Why didn’t he?

Example IX.6
C Major Prelude, Linton alternative ending
At this point you might say, “Well, he just didn’t,” or “he thought it just sounded better” or even “what difference does it make? It sounds good the way it is.” But we need to remember that here we’re thinking about classical music and one of the primary reasons why we value classical music is because of its artistic excellence, its beauty. Just as no executive seated at the table of record label’s board meeting would say “I really don’t care if this release makes us any money,” because making money is the reason they’re all sitting around that table and the purpose of the meeting is to try to figure out how to make more and remember, I’ve been there it’s inadequate here not to think about artistic quality. Just because this piece exists the way it is doesn’t mean that it’s the best it can be. Can it be improved? Bach himself changed it at least once and it’s reasonable for us to think he changed it to improve it. Did it work?
Let’s consider the issue of length by thinking about engineering a bridge (and we’re going to come back to that term: “engineering”). Bridges are wonderful things. By allowing us to pass over some sort of impediment a chasm, a river, another road they make getting places easier and, in that way, bring us together (which is a bit like music). But they’re difficult to build. They must reconcile two opposing requirements: strength and weight. The bridge must be strong enough to both span the length it’s required to cross and to hold the weight it’s required to bear (and be strong enough to withstand winds and earthquakes and so forth). There’s a ballet that needs to be danced here because even though the bridge requires a great deal of strength to keep it up that strength itself carries weight and the bridge can't be too heavy or it will collapse under its own mass. Make it lighter and it can’t hold the load. The bridge has to be “just strong enough.”
Sometimes engineers call this “elegance,” the simplest solution to a problem. For engineers, elegance is aesthetic, it’s beautiful. I call it the “law of just enough.” Not enough, failure. Too much, failure. There just has to be enough.


Example IX.7
New River Gorge Bridge, Fayetteville, West Virginia, 1977
Michael Baker Company, Clarence Wood, lead engineer.

Example IX.8
Millau Viaduct, Tarn River Gorge, France, 2004
Norman Foster, architect; Michel Virlogeux, lead engineer.
The bridges over the Tran River in France and the New River in West Virginia are good examples of this principle of “just enough.” [Ex.IX 7 & 8]. Not too much, not too little. And although their ornamentation might obscure this principal, the Alexander III bridge in Paris and the Pons Fabricius in Rome exemplify it as well (certainly the Roman bridge does; if it didn’t it wouldn’t have survived over two thousand years). And they’re beautiful. Elegant.

Example IX 9
Pont Alexander III, Paris, 1900.
Gaston Cousin & Joseph Cassien-Bernard, architects Jean Résal and Amédée Alby, engineers.

IX.10
Let me give you two other examples, both closer to home. Perhaps you've been the host of a dinner party and it's been a delightful evening but the party is drawing to a close and it's time for the guests to depart. Although the various signs etiquette requires are being given, and most of the guests pick up on them and leave, a few guests remain, oblivious. They stay. And stay. You’re a good host and because etiquette requires that more offers of refreshment are given, you do so, but with giving hints (increasingly less subtle as time draws on) like "how about one final drink before you go home?" But the guests prolong their visit. They just don’leave. What was a delightful dinner party degenerates into a sentence in purgatory. The opposite happens too. We've all had the experience where a meeting with friends was cut short by demands on our time. We would have liked it to go on for just a bit more but it didn’t. And we part with regret. In both cases the rule of "just enough" is broken.
And the last one we’ve all experienced. We’ve all told a joke. And I expect we’ve all probably told a joke badly, to our embarrassment, and heard one told or better, “performed” brilliantly, the way that a great stand-up comedian tells a joke. The difference between our pedestrian joke-telling and the comedian’s isn’t so much in the subject matter as it is in the timing. How it’s told. What’s revealed, what’s left out, and the precise moment of the springing of the punch line.
A successful bridge, a pleasant dinner party, a joke that’s funny, they’re all characterized by the rule of “just enough.” Not too much, not too little. The work uses enough materials whatever those materials might be to accomplish what needs to be done but no more. In regards to a piece of music, one of the areas in which we find the rule of "just enough" is in the piece's length. It lasts just as long as it needs to and no longer. The Russian-American choreographer George Balanchine (1904-1983) once remarked that the composer created time. He meant by this that whereas the thing out of which a sculptor creats his work of art might be clay or stone, the composer creats his work of art out of time, manipulating it in a way analogous to the manner in which the sculptor works with clay. Time is of the greatest importance in a piece of music, it is, as Balanchine said, the work of art's foundational element as we discussed in the previous chapter. In regards to the “law of just enough,” the piece of music must last the just the right amount of time
Which of the versions of the prelude lasts the right amount of time? We have at least four to consider: 1) the first written for Wilhelm Friedemann, BWV 846a; 2) the one from 1722 and catalogued as BWV 846; 3) Schwencke’s version with the extra measure; and 4) the Linton “improvement” that ends in measure 33 or can be shortened to end in measure 32.
We can approach an answer by looking at the key structure of Bach’s prelude. You will remember that we found that Bach shapes his piece into five sections differentiated by keys and articulated by cadences (Example 9.4). But let’s look at that more closely. What do we see and that’s the verb, “see”, and that verb is going to become important.
The measures that anchor the five sections are shown in Example 9.11, measures one, eleven, nineteen, twenty-one, and thirty-two; C major, G major, C major, F major (with the seventh added that we’ve already mentioned and will discuss further later) and back to C major.

Example IX.11
Cadential sections of the prelude
Put let’s now focus only on the bass. What do we see? [Ex.IX.12]
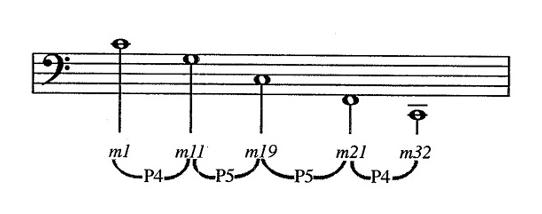
Example IX.12
Prelude bass pitches
We see a pattern. Down a perfect fourth, down a perfect fifth, down another perfect fifth, down a perfect fourth. 4 5 5 4. It’s crucial to note that Bach could have kept the prelude’s harmonic structure and changed the octaves of these pitches. I wrote above that Bach went “back to C major” at the end but that’s not quite right: he went down to C major. And that makes all the difference. Had Bach put that C an octave higher, his pattern would have been broken. Had he begun the prelude with a bass note an octave lower, that patter would have been broken. Had he gone up to C in measure nineteen, instead of going down, the pattern would have been broken. The pattern only works if these precise notes are placed in the precise octaves in which Bach put them.
This mirrored structure, which is the same forwards as it is backwards, is called chiastic, from the Greek letter C, or chi. It is a rhetorical form that the Baroque inherited from classical antiquity in which phrases are related to each other through inversions. This passage from Matthew 19:30 is a simple example.
But many that are first shall be last and the last shall be first.
Example IX.13
Chiastic form of Matthew 19:30
The device was popular both with the writers of Greece and Rome and with peasant Palestinian storytellers (it is the form of many of the parables in Luke).7 Because chi is the first letter of Χριστός, Christos, "Christ" in Greek, the design took-on added significance for Christians since it was understood as an oblique reference both to the Savior’s title and to the means of salvation, the cross. Bach was fond of symmetrical constructions on multiple levels and it’s not surprising to see him carefully construct this symmetrical pattern here. And you’ll remember that I alerted you to the verb “see.” The chiastic design is something that’s more seen than heard. When the way a piece of music looks on the page is part of the composer’s aesthetic it’s called Augenmusik, “eye music.”

Example IX.14
Baude Cordier, “Belle Bonne, Sage”
Example IX.15
Peter Maxwell Davies, 8 Songs for a Mad King Codex Chantilly, MS 564, 1350-1400 Composer’s autograph, 1968, 3rd movement
7 For the use of chiastic forms in Luke’s parables, see: Kenneth Bailey: Poet and Peasant and Through Peasant Eyes: A Literary-Cultural Approach to the Parables in Luke, Grand Rapids: Erdmann’s. 1983.
Although not frequently a part of the western classical music aesthetic, during certain eras and with some composers it has been significant. We find examples of its use in the music cultivated at the famous, or notorious depending on the point of view papal court at Avignon. One of the best known examples is Baude Cordier’s (fl. early 15th century) “Belle Bonne, Sage.”[Ex.9.14]. Here the scribe designed the staves to look like a heart, echoing the text of the rondeaux (“Beautiful, good, wise, lovely, and noble lady, You have brought great pleasure to my heart. . .”). The practice again became popular after World War II. Peter Maxwell Davies (19342016) himself wrote-out the published score of his song cycle Eight Songs for a Mad King. [Ex.9.15]. He designed the score of the third movement to look like a bird cage; the various performers are supposed to be playing in similarly designed birdcages on stage and the text references George III, the “mad” king, talking with birds. We’ll see Bach again using Augenmusik when we look at his St. Matthew Passion in the Addendum but for now it’s enough to note this rhetorical skeleton on which Bach has hung the prelude.
But noticing this skeleton doesn’t help us answer the question of whether or not the piece is the right length. In all four versions we’re considering, that bass movement down a fourth, down a fifth, down another fifth, down a fourth is maintained; the measures in which these events occur are different. We will answer this question about length and the “law of just enough” but before we do we need to go over two things: 1) the mathematical proportion called “the golden mean” and 2) the principle of “concinnity.” We’ll begin with concinnity.
II
Although the concept of concinnity can be seen as early as Cicero’s (106-43 BC) instructions on rhetoric,8 our discussion of concinnity begins with Leon Battista Alberti (14051472).[Ex.9.15] Linguist, architect, mathematician, philosopher, priest, diplomat, horseman, athlete (in his autobiography he boasted that he could throw a coin high enough to hit a cathedral’s ceiling and leap over a standing man’s head), Alberti exemplified what historians later came to call the “Renaissance man.” He’s credited with being one of the inventors of cryptography and his design for the façade of Mantua’s Sant’Andrea Basilica, begun in 1472 (but only finished, in accordance with his original plans, in 1772), is one of the finest exteriors of the early Renaissance design. He could do everything, and apparently told people so.
During the 1440’s, Alberti procured an appointment as a secretary in the Chancery of Pope Eugene IV (the Chancery was an office something like our Department of State combined with the Justice Department). While in Rome he surveyed the city’s ancient ruins and although he was not the first person to do so since Antiquity Petrarch (1304-1374) had studied them a half-century earlier his surveys were the most rigorous and systematic. In 1452, he collected his observations into the ten books of the De re aedificatoria (“On the Art of Building”). Alberti was deeply influenced by Vitruvius’ (ca.80 BC-ca.15 BC) De architectura (“Regarding
8 See particularly Cicero’s 46 BC, De Oratore Book 3, section 173.
Architecture”) which had been rediscovered at the Abbey of St Gall in Switzerland in 1414 (manuscripts had been copied at the court of Charlemagne and were known in the Middle Ages but by the 13th century the Roman work received little attention and it was largely forgotten) and largely based his De re aedificatoria on Vitruvius’ model (we will come again upon Vitruvius when we look at Leonardo di Vinci’s famous “Vitruvian Man”, Ex IX.66). Published in 1485 (the year before Vitruvius’ book was first printed), Alberti’s book became the most important treatise on architecture and city planning for the next three hundred years.

Example IX.15
Example IX.16
Leon Battista Alberti, bronze self-portrait, c. 14359 Façade of Basilica of Sant’Andrea, Mantua
Alberti addresses beauty throughout his treatise, but passages in the sixth and ninth books are particularly important where he defines “beauty” and then gives its primary characteristic. In Book VI Chapter 2, Alberti defines the “concept of beauty as harmony and proportion, where nothing can be added or subtracted without diminishing the whole.10 In Book IX, Chapter 5 he writes: “Concinnity (concinnitas) is the absolute and primary principle of beauty, such that there
9 Leon Battista Alberti, “Self-Portrait” National Gallery of Art, Washington, D.C, #1957.15.125 https://www.nga.gov/artworks/43845-self-portrait
10 “Est autem pulchritude quaedam quasi partium conspiratio, quas nulla res addita, detracta aut immutata possit non peior reddere.” De re aedificatoria, Book VI Chapter 2
is such proportion and arrangement in all parts that nothing can be added or subtracted without violating the harmony of the whole.” 11
In the twentieth century, the American musicologist Jan LaRue (1918-2004) refined Alberti’s definition further and defined concinnity as the “purposeful reinforcement of the various elements of a work of art.”12 Internationally known for his cataloguing of thousands of 18th century symphonies, LaRue came to this insight primarily through careful study of Mozart’s and Haydn’s works. Of the thousands of pieces of music LaRue studied, what tended to set Haydn’s and Mozart’s apart? High levels of concinnity. His idea works like this: Works of art are made up of various elements. A painting is made up of line, color, design, and so forth. A piece of music is made up of rhythm, volume, melody, and so forth. A poem is made up of meter, form, the sounds of the word, and so forth. And in each of these, in the best examples the works’ various are parts are used together for a coherent affect. While LaRue applied his insights primarily to music, as we will, they are applicable to all forms of art. An example can make this clearer.
John Milton’s (1608-1674) Paradise Lost is regarded by many as one of the greatest works in the English language. Published in 1667, Milton’s work is an epic poem in blank verse (blank verse is poetry with a regular meter but unrhymed lines) in 10,565 lines divided into ten books (ten in the first edition, redivided into twelve in the second and all subsequent editions). It’s in iambic pentameter. You’ll remember from the previous chapter that iambic pentameter is a meter where iambs, a weak event followed by a strong one (or long followed by short), are arranged in sets of fives, making a unit of ten “beats” (remember that poetic “beats” are different from musical “beats,” which is very annoying to musicians since sometimes one poetic beat has three musical beats and sometimes it has one as in the example below and I would prefer to call the poetic beats “events” but several thousand years of convention can’t be easily, or wisely, over ridden). In the following example I’ve added the ta DUM lyrics traditional to schoolbooks. [Ex.IX.17]

Example IX.17 Iambic pentameter
Now let’s look at Milton’s poem. I’ve reproduced as Example 9.18 the first twenty-six lines of the poem. I’d like you to take the time now to read them aloud. And it’s essential that
11 “Concinnitas est absoluta primariaque ratio pulchritudinis, ut in omnibul partibus talis sit proportion et collocation, ut nihil possit addi vel detrahi sine totius harmonia violate.” De re aedificatori: Book 9 Chapter 5
12 Jan LaRue, Guidelines for Style Analysis, New York: W.W.Norton & Company, 1970. I studied with LaRue at New York University and the comments in this section are from lessons with him.
you read them aloud, my point and Milton’s genius won’t be understood and experienced if you read them silently. But I don’t want you to just read them aloud, I want you to read these verses backwards, counting-off the syllables as you do so. Begin with line twenty-six. Read it backward, keeping track of each syllable with your fingers. Then read line twenty-five, again keeping track with your fingers. Exaggerate the rhythm.
Of Man’s First Disobedience, and the Fruit
What with no middle flight intends to soar Of that Forbidden Tree, whose mortal tast Above th’ Aonian Mount, while it pursues [15] Brought Death into the World, and all our woe, Things unattempted yet in Prose or Rhime. With loss of Eden, till one greater Man And chiefly Thou O Spirit, that doest prefer Restore us, and regain the blissful Seat, [5] Before all Temples th’ upright heart and pure, Sing Heav’nly Muse, that on the secret top
Instruct me, for Thou know’st; Thou from the first Of Oreb, or of Sinai, didst inspire Wast present, and with mighty wings outspread [20] That Shepherd, who first taught the chosen Seed, Dove-like satst brooking on the vast Abyss In the Beginning how the Heav’ns and Earth And mad’st it pregnant: What in me is dark Rose out of Chaos: Or if Sion Hill [10] Illumin, what is low raise and support; Delight thee more, and Siloa’s Brook that flow’d That to the highth of this great Argument Fast by the Oracle of God; I thence I may assert Eternal Providence, [25] Invoke thy aid to my adventurous Song, And justifie the ways of God to men.
Example IX.18
Beginning of Paradise Lost
I expect your reading sounded like this.[Ex.IX.19].


Example IX.19
Reading Paradise Lost
Of course, reading it backwards is ridiculous because it destroys Milton’s meaning, but, except for an occasional elision (I’ve given one in line 18), it bounces along quite nicely: daDUM da-DUM da-DUM da-DUM da-DUM da-DUM Ten beats, every line.
Until here. “Of Man’s First Disobedience, and the Fruit”[Ex.IX.20]

Example IX.20
Paradise Lost, opening line
It falls apart. It begins well enough with the iambic short - long followed another short but then we have five syllables, dis – oh – bee – dee – ance, followed by the three syllables of “and the fruit” (which you’ll remember is technically called a tribach). It’s awful. But what’s going on here?
A great deal. Milton’s poem is a re-telling of the first chapters of Genesis, the story that’s usually referred to as the creation and fall. God has created and then placed Adam in the Garden Eden and in the garden’s center he has planted two trees, the “Tree of Life” and the “Tree of the Knowledge of Good and Evil.” God warns Adam: “Of every tree of the garden thou mayest freely eat: but of that tree of the Knowledge of Good and Evil, thou shalt not eat of it: for in the day thou eatest thereof thou shalt surely die.”13 God then makes the woman Eve as a companion for Adam. They live in Paradise but a serpent appears and convinces Eve to pick and eat a fruit from the Tree of Life. She does and then convinces Adam to do so also and he does. They disobey God, taste the forbidden fruit, they discover shame, and God condemns them to die and has them driven out of Eden. Adam and Eve have lost Paradise.
They lost paradise because they disobeyed of God’s law. And what is Milton’s law in this poem? It’s iambic pentameter. The five-syllable “disobedience” violates the epics’ poetic “law.” And what was Adam’s and Eve’s means of disobedience? The fruit, a fruit that they thought desirous but was unspeakably bitter when tasted. And when we speek that line and we have to speak it to experience this don’t we notice how odd “fruit” feels in our mouths? Doesn’t it feel distasteful, even repulsive?
“Concinnity” is “purposeful reinforcement of the various elements of a work of art.” What are Milton’s elements in his poem? Rhythm iambic pentameter, the physical sounds of the words, the way it feels to speak these words, the story itself, the story’s theological significance, the form of the epic; these are all things that Milton weaves together to make his poem. In this first line, the metric violation of “disobedience” reinforces the word’s meaning.
Our physical distaste in speaking “fruit” at the line’s end poetically makes us experience Adam’s and Eve’s experience in tasting sin.
It’s important to recognize that the reading of this line has been controversial for a long time. As shown in Ex.IX.21 it’s possible to elide two of the syllables of “disobedience” and in so doing make the line conform to standard iambic pentameter. Many readers read it that way and there are justifications for it. There’s no agreement on whether “disobedience” was pronounced

Example IX 21
Paradise Lost, opening line standard iambic pentameter
with four or five syllables in the 17th century so justifying either reading from history is tricky. If the line is spoken with a four-syllable “disobedience” it becomes a conventional line of iambic pentameter of no particular interest and if someone were to begin reading the poem, knowing it to be in iambic pentameter, then that person very well might launch into the expected da-DUM da-DUM da-DUM pattern, plow through the line and not notice anything about it remarkable at all because reading that way there wouldn’t be.
But I didn’t ask you do to that. I asked you to read the verses backwards. And doing that we crashed when we came to the five syllable “disobedience,” reading it with four syllables would have been completely artificial. In that crash we experienced Milton’s corruption of the meter. And we can go further. Adam and Eve recogniced the catastrophy of their actions only in retrospect. The disaster of Milton’s metric violation is clear only when the line is remembered, read in the knowledge of what followed it.
The 1) violation of the poem’s meter by the five syllable “disobedience” and the distaste which vocalizing “fruit” causes us, work together coherently to reinforce Milton’s subject: the catastrophy of the fall. This is “concinnity.”
I’d like us to look at two pieces of music, “Shennadoah” and “Moon River.” As Milton used the poetic device of meter, we’re going to look at the melodic device appoggiatura Coming from the Italian verb appoggiara, meaning “to lean,” an appoggiaruta is a very important dissonance in western music. The melody leaps, usually up but not always, and lands on a pitch that isn’t part of the chord that silmultaneously sounds with it. For that reason it’s called a “non-chord tone” and is a dissonance. The melody then moves down by step to a pitch that’s part of the chord, resolving the dissonance. The dissonance is always rhythmically strong, meaning that it falls on a strong beat (a “down beat” is a strong beat). [Ex.IX.22] As with most dissonances in this music, it is used to emphasize a place of strong emotional character.

Example IX 21
An appoggiatura
Although it’s one of America’s best known and most beloved folk songs, the history of “Shennadoah” is obscure. Attributed, with varing degrees of plausibility (and fantasy), to French fur trapers, kielboat rivermen on the Ohio and Mississippi rivers, African-American slaves and New England sailors, the tune and text were first discussed by William Alden in his 1882 article on “Sailor Songs,” published in Harper’s New Monthy Magazine. [Ex.IX.22] Alden called it a “windlass” song, or the kind of sea shanty intended to “beguile the men, while getting up the anchor or working the pumps, into temporary forgetfulness of their prosaic labor.” He thought it was of “clearly negro origin.”14 [Ex.IX.22]

Example IX 22
“Shanandore” from Harper’s New Monthly Magazine, 1882
14 The other kind of sea shanty was the “pulling song”, a song used “merely to aid the men, when pulling on a rope, to pull at the same precise instant. Alden believed many of the “sailor songs” to be of negro origin: “Undoubtedly many sailor songs have a negro origin. They are the reminiscences of melodies sung by negroes stowing cotton in the holds of ships in Southern ports. The “Shanty-men,” those bards of the forecastle, have preserved to some extent the meaningless words of negro choruses, and have modified the melodies so as to fit them for salt-water pourposes.” William L. Alden, “Sailor Songs,” Harper’s New Monthly Magazine, Volume 65, July 1882, p.282.
Whatever it’s origin, and the identity of “Shenandoah” the Virginia river or a daughter of the Oneide chief John Skenandoa? after having passed through the hands of generations of anonymous musicians the piece we have today is extraordinary. [Ex.IX.23]



Example IX 23
“Shenandoah” with standard harmonization
In the second measure, the “D” and the “F” are both appoggiaturas. The “D” resolves down to the “C” following and the “F” resolves down to the following E.” The first appoggiatura is approached by the leap of a major third while the second is approached by the more dramatic leap of the perfect fourth. The increasing leaps add urgency to the line and the appoggiaturas enhance the poignancy of the text’s “hear,” “daughter,” and “see.” This is echoed in measure six, the dissonant “G” adding to the saddness of the same three words but these rhythmically strong dissonances are not approached by leap but instead by step. At the end of measure seven we have the “D” on “a-way,” a dissonance similar to an appoggiatura but rhythmically weak (called an échappeé or “escape tone”). The dissonances reinforce the text by making important words more dramatic.
We don’t know who (and that “who” must be a plural because it was re-written over the generations) wrote “Shenendoah” but we do know who wrote “Moon River:” Henry Mancini (1924–1994) and Johnny Mercer (1909 –1976). Written for the 1961 movie Breakfast at Tiffany’s, the song won the 1962 Academy Award for best song as well as the 1962 Grammy Award for “Song of the Year.” Mancini wrote the music first to which Mercer later composed his lyrics and, as we saw with “Shenandoah,” the music and the words reenforce each other.
Example IX.24 is the song’s first seven measures, including a somewhat simplified version of its standard harmonization.

Example IX.24
“Moon River” showing dissonances
Paralleling “Shenandoah,” the opening phrase of “Moon River” is enlivened by two appoggiaturas, one on the downbeat of the second measure (the “D” resolving to the “C”) and the second on the downbeat of the fifth (the “B” resolving to the “A”). Also paralleling “Shenandoah,” the second appoggiatura is approached by a leap greater than the first (a leap of a perfect fourth for the first appoggiatura and a much more dramatic leap of a major seventh for the second). Furthermore, and again paralleling “Shenandoah,” the dissonances strengthen the affect of the words on which they fall. The harmonic “pain” of the appoggiaturas on “River” and “cross-in’” and the accented passing-tone on “wider” all add to the poignancy of the words (the arched melodic line for “crossin’” even looks like a bridge).
The structure of the song reinforces the text. What does the “dream maker” do? It breaks hearts (the melodic repetition shown in blue boxes). Who is “waitin’ round the bend”? It’s “my Huckleberry friend” (the melodic repeition shown in orange boxes). The music of the first seven bars, in which the text introduces the wistful “Moon River” and the journey across it, is repeated in measures seventeen through twenty-three where the text tells who will be making that trip (the parallel shown in yellow).

Example IX 25
“Moon River” structural relationships (boxes) and dissonances (arrows)
Most of the poem is evocative (what, for instance, is a “moon river”?), but one line is almost ridigously unambiguous: “We’re after the same rainbow’s end.” There is no ambiguity in the text and there’s none in the music: the text is paired with an arpeggiation of a C Major chord set with absolute metric clarity: events happen only on beats one and three for the five measures of the text’s duration. But notice how the phrase which is an arch (another example of Augenmusik) peaks on “D,” a pitch which is thirteenth of the “F” chord. In tertian harmony, a “thirteenth chord” is a chord that contains all seven menbers of a traditional scale, arranged in thirds, the last pitch in that series being thirteen steps above the lowest pitch. Here, the “D” is not only the top of the melodic arch but also the top pitch of the “F” thirteenth, it’s almost the “end” of the harmonic rainbow.

Example IX 26
Audry Hepburn singing “Moon River” from Breakfast at Tiffany’s
“Moon River” was written as a part of an entertainment, a musical moment for Breakfast at Tiffany’s heroine Audry Hepburn, and both the film and the song were commercial successes. By the criteria of “pop music,” “Moon River” is a great piece of music. But the interlocking of Mancini’s music with Mercer’s lyrics on every level where one is inconceivable without the other raises this pop song to the level a great work of art. For all its wit and craftsmanship, it’s a level that Dolly Parton’s “The Grass Is Blue” doesn’t reach. Successful as a pop song and, as we saw, Parton’s song is artistically made, but it’s not great art; Mancini’s and Mercer’s piece is.15 The level of concinnity between music and text that we see in “Moon River” we saw earlier in the folk song “Shenandoah.” And as with “Moon River,” that degree of concinnity raises “Shenandoah” to a level of greatness that “We Shall Overcome” a folk song we looked at earlier doesn’t achieve. “We Shall Overcome” is a deeply beloved and historically very significant folk song, but it’s not great art. “Shenandoah” is.
With “Moon River,” “Shenendoah,” and Paradise Lost, we’ve seen examples of “concinnity,” the characteristic of a great work of art where its various elements work together for unified purposes. And we’ve been introduced to the “rule of just enough.” We need to return to the C Major Prelude and answer the questions we’ve raised about it, but before we do we need to add to these an understanding of “the golden mean.”
15 At the first preview screening of Breakfast at Tiffany in 1961, Martin Rackin, head of Paramount, was enthusistic about the film but wanted the song cut. It was retained only at Audrey Hepburn’s insistance. Ironically, twenty-three years earlier, studio executives also wanted “Over the Rainbow” cut from The Wizzard of Oz In 2024, “Moon River” and “Over the Rainbow” were named two of the four most memorable songs in American films by the American Film Institue (the other two were “As Time Goes By” and “Singin’ in the Rain.”
The “golden mean” or the “golden proportion” or “the golden ratio” or even “the divine proportion” (the terms are used interchangeably) is a coherent relationship between parts and a whole. It’s typically designated by the Greek letter j, “phi.” That’s a rather opaque definition but I think you can easily understand it if we go through an exercise in design. You’ll need paper (graph paper helps), pencil, a compass, and a straight edge. You can do it on your own or follow along here.
Draw a line.


Now make the line the base of a square.

Find the midpoint of the base of the square and extend your compass to the upper right corner and draw an arc (we could draw a complete circle but an arc will do)
IX 3


Extend the base line of the square to the point where it intersects the arc, an extension shown here in blue.
Figure IX.4
Now construct an upright from the point where the extended base line intersects the arc to the point where this line now intersects the extension of the top line of the square. Complete the new rectangle (here in blue).
IX.5
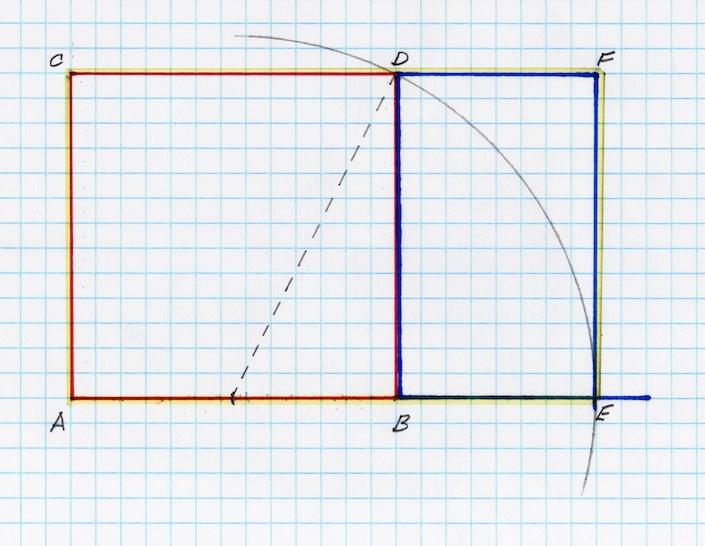
We now have several figures. We have our original square (in red: A, B, C, D), we have a rectangle attached to it (in blue: B, E, D, F) and a larger rectangle made of them both (outlined in yellow: A, E, C, F). What is interesting here is that the proportions of the smaller rectangle (in blue) are the same as the larger rectangle (in yellow).
Figure IX.6
We now take the smaller rectangle and use its base (B-E) to construct a square within it. This in turn creates a third rectangle (G, H, D, F) and the proportions of this third rectangle are the same as the first two.
IX.7



If we take one of the short sides of this third rectangle and use it to construct a third square we find now have a fourth rectangle (D, I, G, J, shown by the pink line) and this rectangle has the same proportions of the previous three.
Figure IX.8
Figure IX 9
If we take this rectangle and repeat the process (taking its short side as the base of a square) we create another rectangle (in light purple: K, L, G, J). Again this rectangle has the same proportions as all of the earlier rectangles. We can create an infinite of number ever smaller rectangles using this same process and all of the rectangles will have the same proportions. These kind of rectangles have been called "golden rectangles" and are defined by the “golden ratio.”
This golden ratio can be defined as "the relationship between two smaller things is the same as they are both together to a larger." Or: "a + b is to a as a is to b"
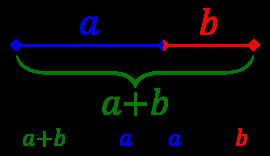


Figure IX.10
Calculations of j
This relationship echoes the “Fibonacci series.” Leonardo Bonacci (c. 1170 – c.12401250), known as “Fibonacci” (for son of Bonacci), is one of the most important mathematicians in our civilization. Born in Pisa to a family of merchants, he studied in present-day Algeria and traveled throughout the Mediterranean on business. In his dealings with the Muslim world he learned what he called the modus Indorum, the “way of the Indians,” (what we commonly call today “Arabic numerals”) and, recognizing it to be superior to the Roman numeral system of counting then used in Latin Europe, he introduced the new way of calculating in his 1202 Liber Abaci (“Book of the Abacus”). Although Fibonacci’s book was primarily about practical matters of doing business (converting currencies, figuring interest, calculating profits, etc.), he did include a riddle about multiplying rabbits in a section dealing with sequences. Supposing that a pair of newborn rabbits, one male, one female, were placed in an enclosed field, and these rabbits took a month to mature, and that pair produced another pair of rabbits, one male and one female, and those rabbits took a month to mature and then also produced a pair of new rabbits, and this pattern continued, and none of the rabbits died, how many rabbits would be in the field after a given number of months? Fibonacci found that the number of pairs followed a pattern in which each successive number is the sum or the two previous numbers. One plus one equals two. Two plus one equals three. Three plus two equals five, five plus three equals eight, and so on. This is the pattern.[Ex.IX.27]
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377. . . etc
Example IX.27
Fibonacci series
In the final decades of the 19th Century, French mathematician Édouard Lucas (18421891) noticed a similarity between the golden ratio and ratios between adjacent numbers of the Fibonacci series, both approaching the ratio 1: 0.618.[Ex.IX.28]
233 ÷ 377 = 0.618037135 3 ÷ 5 = 0.6
144 ÷ 233 = 0.618025751 5 ÷ 8 = 0.625
89 ÷ 144 = 0.6150555555 8 ÷ 13 = 0.61538461538
55 ÷ 89 = 0.61787752808 13 ÷ 21 = 0.6190476190 34 ÷ 55 = 0.61818181818 21 ÷ 34 = 0.6176470588
Example IX.28
Ratios of adjacent Fibonacci numbers
Let’s look again at Figure 9.6 and modify it a bit. This will help us understand the discussion above [Fig.IX.11]
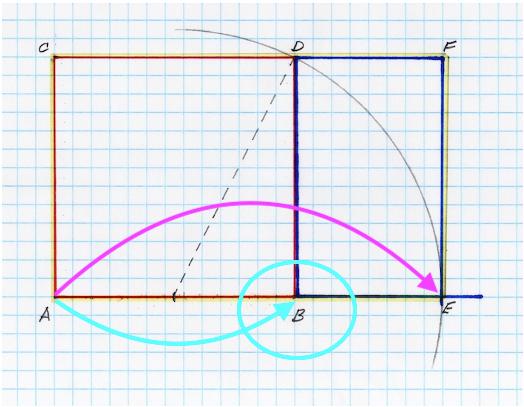
Figure IX 11
Golden ratio of golden rectangle
"B," circled in bright turquoise, is the golden mean from "A - E", if we take "A" as the starting point. If we look at the grid on which this is drawn, we can see the arc, shown in bright violet, extends the thirteen units of "A - B" by eight units (“B – E”). This length of "A - B", 13, divided by the complete length of "A - E", 21, results in .61904 (like Pi, the decimals go on forever).

If we take our compass and construct arcs in each of the squares of our example, we can construct a spiral. As with the repeating rectangles and the numbers of the Fibonacci series, this spiral can, theoretically, go on forever, as long as we continue to make ever smaller rectangles. It’s typically called the “golden spiral” or occasionally the “Fibonacci spiral.” [Fig.IX.12]

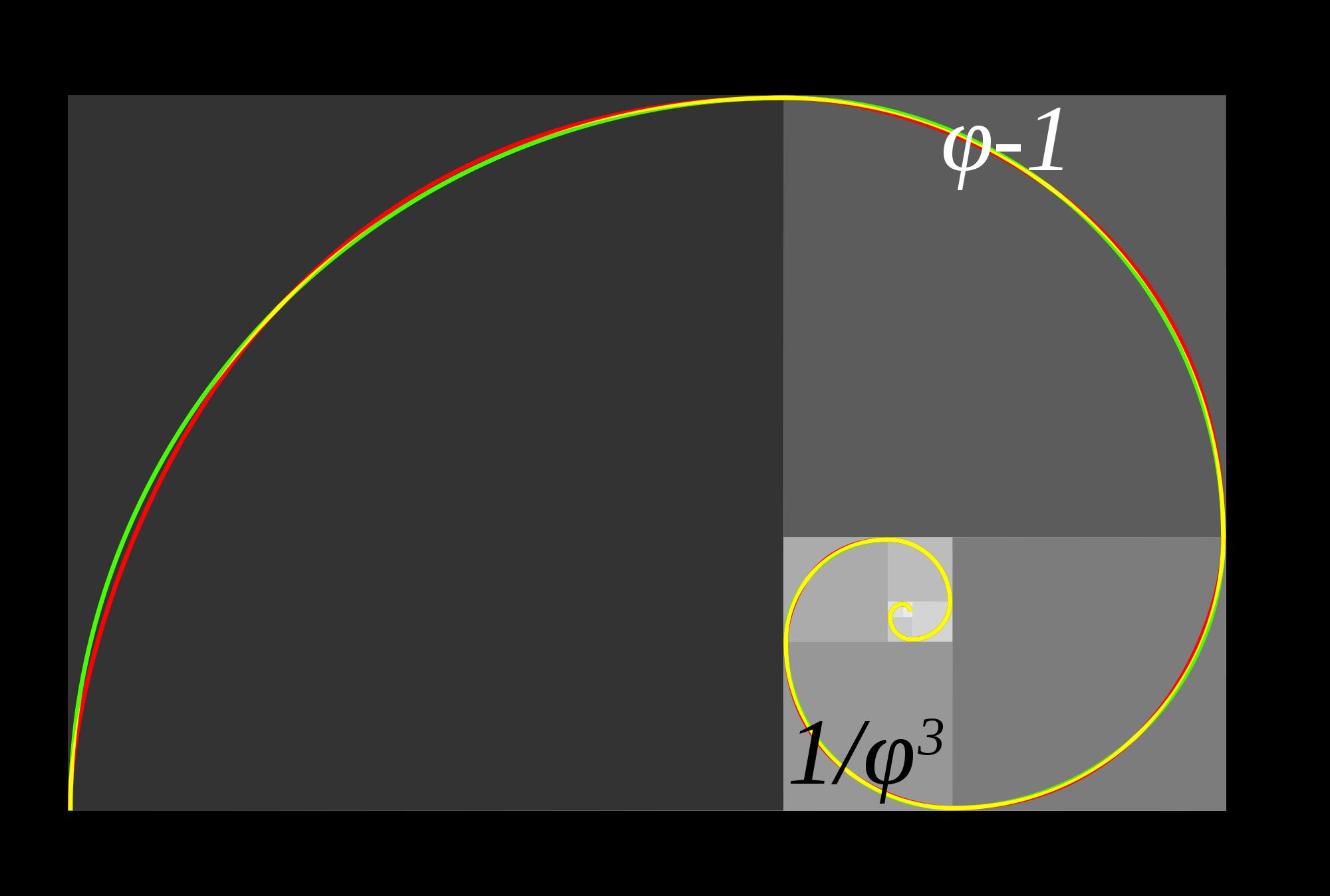
Example IX 30
Comparison of logarithmic spiral and golden rectangle arcs.
But of course, Figure IX 12 isn’t a spiral. It’s a collection of discreet diminishing quartercircles that approximate a spiral. Example IX.29 is a true logarithmic spiral and in Example IX 30 the two spirals are imposed on each other (the green line is the line of the quarter-circles, the logarithmic spiral is in red and the sections that overlap are shown in yellow). In rigorous mathematical contexts the two spirals are not to be confused, but the golden spiral is so close to the logarithmic spiral that in contexts such as ours they are considered interchangeable.
Both golden mean proportions and golden spirals appear in nature. “Phyllotactic” spirals (from the Greek phyllon, meaning “leaf,” and taxis, meaning “arrangement”) are spirals characterized by optimized sun exposure and space for growth. The seeds or pedals or even branches sometimes follow Fibonacci progressions. Pine cones, sunflower heads, pineapples, rose and lily blossoms, the fronds of some ferns, are examples of phyllotactic spirals. Spiral galaxies, hurricanes and tornadoes and nautilus shells can be seen to exhibit characteristics of


Example IX 31 Golden spirals
A) pinecone; B) Queen Ann’s Lace flower; C) dahlia flower D) hurricane from space; E) split nautilus shell; F) fern fond
logarithmic spirals. The spiral appears so frequently in nature that it’s been called “divine” since the Franciscan friar and inventor of double-entry bookkeeping, Luca Pacioli (c.1445–1517) labeled it “divine” in his 1505 De Divina Proportione, a remarkable book with illustrations by Leonardo da Vinci. Not content with just the ratio’s divinity, the German mathematician Martin Ohm (1792-1872) called it “golden” (goldener Schnitt) in his 1835 Die reine ElementarMathematik. In 1970, H.E. Huntley repeated the “divine” appellation in his The Divine Proportion, A study in Mathematical Beauty15 and more recently numerous writers have attributed cosmically metaphysical and even magical powers to the numbers. Scott Olsen’s The Golden Section: Nature’s Greatest Secret, in which he attests that the golden ratio is the “key to the mysteries of life” is typical 16 Whether divine, golden, a key to the cosmos encrypted by the
15 H.D. Hungley: The Divine Proportion, A Study in Mathematical Beauty, New York: Cover, 1970. Frequently cited in literature about the golden mean, the golden mean’s divinity is as mysterious as the author, about whom no biographical material is available.
16 Scott Olsen, The Golden Section: Nature’s Greatest Secret, Bury St. Edwards, England: Wooden Books, 2021 Olsen’s work is circumspect when compared with that of Drunvalo Melchizedek (born Bernard Perona). His The Ancient Secret of the Flower of Life includes extended references to Atlantis which were revealed to him by
Babylonians and held as a secret by magicians for thousands of years but available now in paperback and once understood wherever you find it will provide us the answers for life’s mysteries we don’t have to go that far to see that the proportion is around us a lot. It’s literally stamped on our faces.
I have a tool to help us see this. Nick Taylor is an artisan in Raumati, New Zealand. He makes calipers that extend and contract to show the golden mean between two points.17 However they are extended, the middle prong will also show the point 0.618 between the extremes [Ex.IX.32]


channeling the ancient Atlantis magician “Thoth.” Drunvalo Melchizedek, The Ancient Secret of the Flower of Life, in two volumes, Flagstaff, Arizona: Light Technology Publishing, 1999 17 https://goldenmeancalipers.com
Example IX.33 is Aishwarya Rai Bachchan (b.1973), an Indian actress and model and Miss World 1994. Some people have called her the most beautiful woman in the world, and she might be.


Example IX 33
Aishwarya Rai Bachchan
If we apply our caliper to Bachchan’s face as we look at her straight on, extending the caliper from her chin to her hairline, we see that we find that the vertical golden mean of that distance lies at the center of her nose, between her eyes.[Ex.IX.34] If we shorten the caliper to the distance between her chin and that center of her nose between her eyes, in other words, now finding the golden mean of the golden mean, we find that the golden mean of this distance is roughly the tip of her nose.[Ex.IX.35] If we repeat this once again, now shortening the caliper to the distance between her chin and the middle of her nose, in other words finding a third golden mean, we find that golden mean at the middle of her mouth.[Ex.IX.36]

IX 33
The golden mean of the distance from

Example IX 34
The golden mean of the distance her chin to the her chin to her hairline. center between her eyes, over her noise (the 2nd golden mean)

Example IX.36
The golden mean of the distance from her nose to her chin (the 3rd golden mean)

If we take our calipers and extend them across her face at eye level (which is roughly, as viewed directly from the front, a face's widest position), we find that the golden mean of that distance lies at the edge of the eye, about at the tear duct.[Ex.IX 37]
And if the calipers are reversed, the golden mean of that distance is the opposing eye and its tear duct.
If we take that shorter distance of this measurement, we find that it is also very close to the lengths of the eyebrow ridge, the nose, and the mouth [Ex.IX.38]

Furthermore, if we apply our calipers to her mouth, we find that the golden mean of the distance between the edges of her mouth is one of the cupid's bow of the upper lip (invert the caliper and it's the other).[Ex.IX.39]


Example IX.40 is Adam Ayash (b.1987), a Lebanese/American model, actor, composer and artist. We can apply the same procedures to his face we applied to Bachchan’s: golden mean proportions cascading down the face (A, B, C) and then repeated across the face and the mouth (D, E, F). [Ex.IX 41]


The golden mean isn’t a proportion found only on part of these peoples’ faces, on the length but not its width for instance; it repeats across their faces on multiple levels. The length of the whole face, the face’s width, the similar lengths of the eyebrows and the nose and the mouth, and even the arc of the lip, give these faces a cohesion and appropriateness that we find immediately “right.” And it’s not much of a jump from that sense of “rightness” to thinking “that’s beautiful.”
Here’s Matt Damon (b. 1970) [Ex.IX 42]


Example IX.42
Matt Damon
Matt Damon is one of the most accomplished men of his generation He is an Oscar winning screen writer and Oscar nominated actor, star of dozens of films, producer, philanthropist and apparently a genuinely nice guy (my daughter used to see him at a Starbucks in New York, he was self-effacing and nice to everybody). But look at his nose; it’s too short. He’s a handsome man, but pictures “B” and “C” show that his noise is just a bit off. It needs to be a tad longer and the calipers show that. He’s a brilliant film actor but that “just a bit off” gives him the physical ability to star in both leading-man and comic roles. I don’t think any audience would easily accept Adam Avash as a comic character, he’s too uniformly good looking. Casting directors are highly attuned to the way audiences react subliminally to faces, and that little flaw helps give Damon’s comic acting an edge of credibility which a more uniformly proportioned face might not have. Of course if he weren’t a great actor nothing on, or off, his face would make him one, but that stubby nose is all part of Damon’s successful package.
And speaking of a successful package, we have this. Jay Leno (b. 1950) [Ex IX.43]

Jay Leno is an enormously successful comedian. His success is because of his great intelligence and wit (luck helps too) but it's certainly not hurt by the fact that he literally looks "funny." His nose is too short for the length of his face. It's a bit comic. Yet even here there's a consistency: the relationship between the lengths of the eyebrow and the mouth and nose and the smaller distance of the golden mean across the face are all the same, just like Matt Damon's, but the proportions between the lengths of Leno’s noise and chin are just, well, just funny.
Besides being stamped on our faces, the golden ratio is also found in the relationship between the lengths some of the bones of our hands. The proximal phalanx is about .618 of the length of the metacarpal bone below it. [Ex.IX 44] The middle phalanx is about .618 of the length of the proximal phalanx.[Ex.IX.45] And the distal phalanx is about .618 of the length of the middle phalanx.[Ex.IX.46]





With the golden ratio playing such an important part in the two most visible parts of our bodies, our faces and our hands, it's not surprising that the ratio is found in things we make: sculpture, architecture, painting and drawing. We create works of art that in some way or another reflect our basic characteristics. But we must be careful here not to overstep. A great deal has


been written on the golden ratio in the arts and far too often we find occasions of authors imposing pre-packaged answers upon their questions, conclusions searching for evidence. The Parthenon in Athens is a good example. Frequently, discussions of the golden ratio begin with the Parthenon, writers claiming that it was designed and constructed according to the golden ratio and then present diagrams to support the claim (the examples shown below are typical of examples found on the web). [Ex. IX,49]
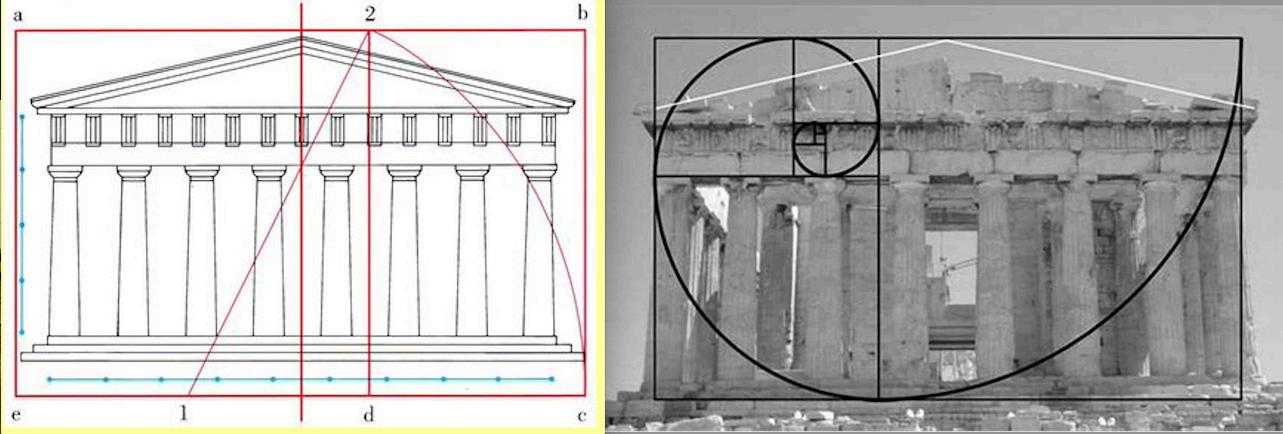

Example IX.49 miscellaneous examples of golden mean analyses superimposed on the Parthenon, from the web.
These assertions go back the beginning of the modern popularization of the golden ratio. In 1914, Theodore Andrea Cook (1867-1928) published The Curves of Life 18 Here he introduced his readers to the spirals of nature, the Fibonacci series, and the golden ratio which he identified with the Greek letter j, “phi,” crediting the idea to the American mathematician Mark Barr (1871-1950), Barr suggesting j to honor the Greek sculptor Phidias (c. 480 BC – 430 BC) who was responsible for much of the Parthenon’s sculpture. Cook presented the Parthenon as the example par excellence of golden ratio design. But this is problematic on several levels. As can be seen from Ex. IX.49, there’s no agreement on what constitutes the building’s “front.” Does it include the platform? And if so, how much? One step? Two steps? And where do the measurements begin? From the exterior of the walls or from the interior? Is the pediment included?
18 Theodore Andrea Cook, The Curves of Life, London: Constable & Company, Ltd, 1914.
When asserting that the Parthenon’s front conforms to the golden ratio there’s no consensus exactly what that “front” is.
Also the Greeks themselves didn’t use the golden ratio as we understand it and didn’t necessarily favor the proportion 1: 0.618 over others. Although Euclid (c. 325 - c. 347 BC) famously twice in his Elements gave instructions for constructing a figure of the proportions of the golden mean,19 the ratio wasn't described as a decimal until 1597 when Michael Maestlin (1550 - 1632) mentioned it in a letter to his friend Johannes Kepler (1571-1630). In any case, the writers of classical antiquity did not have irrational numbers available to them so the ratio they used was 5 : 3 or 13 : 8 (which is the ratio of the golden rectangle we used in Figues.9.3 -11). More recent surveys have found the proportional ratio used across the Parthenon to be 9:4.20 [Ex.IX.50]

Example IX 50
Elevation of the Parthenon showing 9:4 proportions
But there is amble evidence that medieval architects at least intuited golden mean proportions in aspects of their buildings. The cathedrals of Paris (begun 1163) and Chartres (begun 1194) are well known examples.
We’ve seen Chartres before, in Chapter Six, where we looked at sculptures of the Liberal Arts, Music, and Pythagoras on the cathedral’s west front. Example IX.45 is a ground plan of the church. The vertical axis, the “nave,” and the horizontal axis, the “transept”, are clear (both the nave and the transept have aisles on each side). The half-circle at the top is the “apse.” The area where the nave and the transept intersect is called the “crossing.” The “X’s” mark the peaks of the vaults across the spaces. If we take our caliper and place one end at the peak of the vault at the entrance (C) and place the other end at the peak of the vault over the apse (A), we see that the peak of the vault over the crossing is at the golden mean of the distance from the entrance to the apse (B).[Ex.IX.51-54]
19 Elements, Book II, Proposition 11 and Book VI, Proposition 30
20 Susan Woodford, The Parthenon, Cambridge: Cambridge University Press, 1981; also Fangqing Lu, “Architecture as spatial-textile storytelling: Metamorphosis of frieze as a narrative medium mediating the Panathenaia Festival,” Frontiers of Architectural Research, Volume 5, Issue 4, December 2016, pp. 489-498.




Example IX.52
Chartres Cathedral vault over apse. (Ex.IX.45 “A”)
Example IX 53
Chartres Cathedral vault over apse. (Ex.IX.45 “B”)
Example IX.54
Chartres Cathedral vault over apse. (Ex.IX.45 “C”)

Furthermore, the width of the nave and the distances across the transept are also marked by golden ratio relationships (or very close to them). In Example IX.55, “C” and “C1” are piers at the crossing. Both mark golden ratio distances calculated first from the end of the crossing, “A,” to “B”, that “C” marking the golden ratio of the full distance across the nave and then “A” to “B1,” and that “C1” marking the golden ratio of that part of the distance. “C1” to “B1” also mark the nave’s width
In the interior, the height of the nave arcade marks the golden mean of the height of the nave walls.[Ex.IX.56]

The cathedral's late gothic north tower (dating from about 1515) also shows signs of being partially designed according to principals approximating the golden ratio.[Ex.IX.57-58]


The west facade of Notre Dame of Paris shows several proportional relationships that are similar to the golden ratio. As in Chartres, the proportion is found between large sections (as between stories of the facade) and smaller details. And again, we have to remember that these proportions are very similar to the golden ratio, not mathematically precise reproductions of it.


Although we know a few by name and can identify their projects, for the most part the masons and architects and they were frequently the same person of the early Middle Ages were anonymous.21 This is not the case with the Basilica of Santa Maria Novella in Florence The interior of the church was largely finished by the early 1360’s but, with the exception of the lowest story, the front facade remined incomplete for another two hundred years. In about 1456, Alberti the same Alberti with whom we began our discussion of “concinnity” was commissioned to complete the facade. Although Alberti does not explicitly mention the golden mean in his De re aedificatoria, golden mean proportions can be seen across the facade. [Ex.IX.61]


21 Jean de Chelles (active 1258-1265) is a case in point. He is known to have worked on Notre Dame’s south transept and its rose window, but the west facade was completed a generation earlier by unnamed master masons.
And of course, this.

Example IX.62
The “Mona Lisa” on a typical day in its gallery at the Louvre
In his 2008 BBC documentary, The Mona Lisa Curse, critic Robert Hughes (1938-2012) called it the most abused painting in existence, Leonardo da Vinci’s “The Mona Lisa.”22 It inevitably shows-up in discussions of art and the golden mean where charts, almost ad infinitum, are imposed upon it, demonstrating Leonardo’s use of the divine proportion.
The two graphics of Example IX.63, taken from the web, are typical of this kind work. In Ex. IX.63a, a series of golden rectangles are imposed on the painting but there’s no clear reason why the larger rectangle is placed where it is other than the fact it’s centered on the figure’s nose. In Ex. IX.63b another set of geometric shapes within a rectangle is imposed on a different part of the nose (although these figures are not all related by golden ratios). And in Example IX.64 we shouldn’t be surprised that the proportions of the Mona Lisa’s face reflect telescoping golden ratios because all beautiful faces do we saw that with Aishwarya Rai Bachchan. Leonardo simply painted what he saw (or an idealization of what he saw), those ratios across the face are not the result of a significant artistic decision or strategy.
22 Robert Hughes (writer), Mary Chang (director), The Mona Lisa Curse, Oxford Film and Television (for BBC Channel 4), 2008.


Example IX.64
Golden mean relationships down the face of the “Mona Lisa”
But this doesn’t mean that there’s no evidence that Leonardo organized his painting considering golden ratio principles. There is. There are three zones in the painting. First, the zone in which the Mona Lisa sits, in front of a balcony wall. There is a second zone, behind her, of landscape. This landscape is again separated from the sky by a horizon line. With our calipers
along the sides, Example IX.65 shows those three divisions in Leonardo’s painting, with a dotted line highlighting them.

Unlike a face, which is naturally divided by golden mean relationships, there is nothing about nature that dictates where a canvas is to be divided. In this picture any of the divisions could have been higher or lower. Yet here we have a golden mean relationship between them. Did Leonardo calculate this or was his decision intuitive? For our purposes now it doesn’t matter, it’s enough that the phenomenon exists.
Continuing with Leonardo, we have this: his "Vitruvian Man" dating from about 1490, so called because Leonardo drew it to illustrate private notes on Vitruvius' De architectura.23 [Ex. IX.65] We’ve come across Vitruvius before, you’ll remember that Alberti largely based his De re aedificatoria on the Roman’s work. Vitruvius completed it around 15 BC, dedicating it to Caesar Augustus. Vitruvius believed that buildings should be based upon the same proportions as the human body. Here is Vitruvius’ description of the proportions of the human face.
23 Although Giovanni Sulpicio da Veroli had published the first printed edition of De architectura in Rome in 1486, it is probable that Leonardo’s notes were from consulting manuscripts of the book since numerous manuscript copies were available in the courts where he served.
If we take the height of the face itself, the distance from the bottom of the chin to the under side of the nostrils is one third of it; the nose from the under side of the nostrils to a line between the eyebrows is the same; from there to the lowest roots of the hair is also a third, comprising the forehead.24


The ratio here is 3 : 2, which is 0.666, not the golden ratio of 0.618 but not that far from it. Vitruvius also placed the navel at the center of the body. There were no illustrations of how the human body might exemplify those proportions in either the manuscripts that circulated in the Middle Ages or in the 1486 printed edition, so Leonardo’s decision to make one was almost unprecedented 25

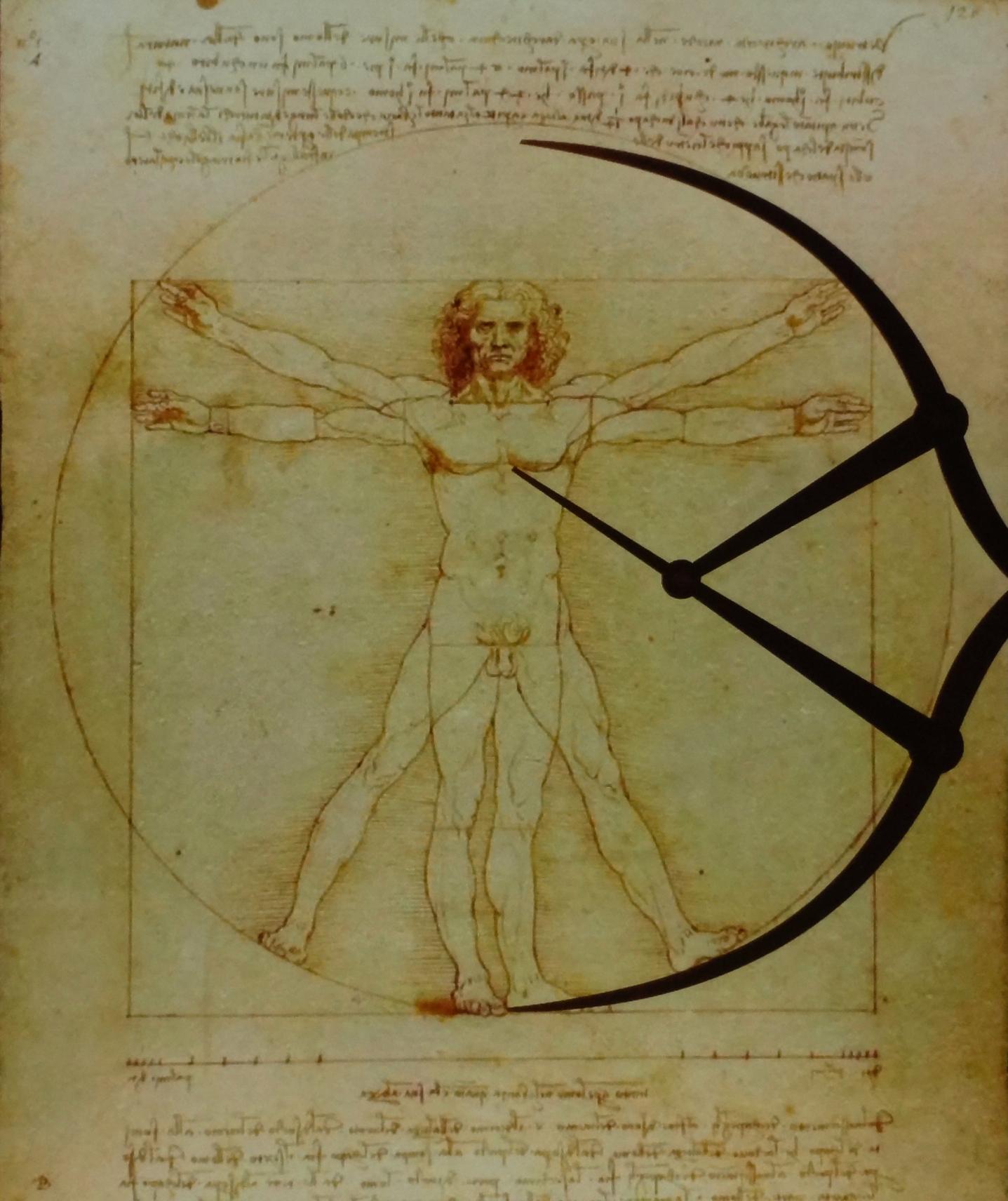
If we place our calipers on Leonardo’s body, we can see that Leonardo changes Vitruvius’ navel as the center of the body. Now the navel is golden mean of the distance from the toes to the crown of the head; the navel marks the golden mean of the figure's height.[Ex.IX.67]
IX.67
And should we extend our caliper to include the circle in which Leonardo places his figure, we see that point of the caliper marks the center of the figure’s chest. As in the case of Leonardo's Mona Lisa, the face also conforms to the near golden ratio relationships we discussed earlier.[Ex.IX.68]
Example IX.68
25We must use the caveat “almost” because Francesco di Giorgio Martini (1439-1505), a contemporary of Leonardo, was including diagrams of human figures superimposed on floor plans of churches as examples of Vitruvian principles in his works of the same period.

The Vitruvian Man is probably Leonardo's most widely known drawing. The David is Michelangelo's most widely known sculpture. Completed in 1504, Michelangelo's figure has similar proportions to Leonardo's. The navel is quite close to the golden mean of the figure's height, going from the feet up to the crown of the head (although figuring the golden mean from a photograph is a barely satisfactory way of finding measurements; we need to be modest in our conclusions).
IX.69
As in the case of the face, we can see that the golden ratio is a close approximation of nature (or at least the nature of English/American model James Dawson Martin) [Ex.IX.70]


Example IX.70
Michelangelo’s “David,” Leonardo’s “Vitruvian Man,” James Dawson Martin

One of the most beautiful architectural ensembles in the United States is the Center Green of New Haven, Connecticut. In Example IX.71, the tallest spire is that of the First Church of Christ (or Center Church), a congregation founded in 1639. The present church was built in 1812 by architect Ithiel Town (1874-1844). The white tower just behind it is The United Church, designed by David Hoadley (1774-1839) in 1814. Between them is the steeple of the First Methodist church, built in 1849 and designed by Henry Austin (1804-1891).

Again, keeping in mind that we need to be circumspect with our findings because we’re not dealing with architectural drawings or surveys but instead photographs, which besides making our analysis imprecise can have an additional possible problem of distortion because of the angle of the photographer, what do we discover about these building when we apply our calipers to them? For simplicity’s sake, I’ll summarize our work, the yellow always indicating the longer part of a line’s golden ratio, the violet the smaller [Ex. IX.73].



We find that all three architects incorporated at least something very close to the golden mean in their steeples and that this proportion doesn’t apply to just one element in the architects’ designs but to multiple elements. The proportion echoes itself.
One block from these churches is the Harkness Tower on the campus of Yale University. Designed by James Gamble Rogers (18971947) and completed in 1921, it was part of Yale’s decision to remodel itself into a Connecticut version of Oxford and Cambridge with a quasi English college structure for undergraduates and medieval “ish” buildings. This tower was the centerpiece of the campus transformation. And while such imitations of past styles often fail to produce lasting architecture, with almost unlimited funds and genius designers, it can work. It worked here. The tower is evocative of medieval bell towers in Rouen and Bruges and part of Rogers’ success is the care he took with the proportions that echo throughout the tower.26
About the same time Rogers was “gothic-sizing” Yale, the great American architect Bertram Goodhue (1869-1924) was designing many of the buildings for the Panama-California Exposition in San Diego. The centerpiece of the exposition was a Spanish-baroque styled
26 A favorite story that’s repeated on the Yale campus, but probably apocryphal, is that when the architect Frank Lloyd Wright (1867-1959) visited Yale he insisted that he have a room from which the Harkness Tower couldn’t be seen, he detested it so much. Even geniuses can have occasional bad taste.

quadrangle, dominated by a domed exposition space, evocative of a colonial Spanish cathedral, and the two-hundred foot “California” bell tower. Completed in 1915 and now part of the city’s Balboa Park, the tower is San Diego’s primary landmark. The four upper stories of the tower,


including the stylized bell at its top and even the weather vane atop that, are series of golden ratios, each one progressively smaller as the tower rises.
I think in all these things the faces, the buildings, the paintings we have a sense that they’re “just right;” it’s intuitive. Our measurements are useful only because they confirm what we already sense about them. They give us a way we can talk about “their rightness.” Conversely, we can have an intuitive sense of when things aren’t right.
Example IX.81 is Edmund Chapel at Wheaton College, outside of Chicago. I went there as an undergraduate and spent a lot of time looking at that tower. It was designed by the architectural firm J. Emil Anderson and Son and completed in 1961. The tower starts off OK but as it goes up something goes wrong. We sense it's not right.


When we take our calipers to the tower we can see what’s not right. The relationship between the upper floors is disjointed. [Ex.IX.82] The “clock” part of the tower is too short for the distance from the bottom of the first woodclad story to the top of the steeple. It should go up to that line marked by the question-mark. As it is, it’s stumpy. We look at it and compare it to the church steeples on the New Haven Green, the towers at Yale and San Diego, we’re disappointed. In fact, the more we look at this the less we want to. Thinking about the faces we looked at earlier, we might call this the “Jay Leno” of steeples.
Before we leave the matter of the golden mean, I’d like us to look at one more picture. It’s “The Great Wave of Kanagawa” by Katsushika Hokusai (1750-1849). [Ex.IX.83] Unlike the “Mona Lisa,” which was painted for an aristocratic patron (but never delivered), or “The David”, which was commissioned by the city of Florence, “The Great Wave” was printed off a woodblock in 1831 as part of the series “Thirty-six Views of Mount Fuji” and mass produced in sets of as many as eight-thousand copies for the growing middle-class culture of urban Edo Japan. It was not a work for limited number of aristocrats. It was cheap, about the same price as a bowl of noodles. Approximately five hundred of the original prints remain, and they are not cheap now. World-wide it’s probably the most recognizable example of Japanese art and one of the greatest pictures I know.
Why is it so good? Why is it legitimately comparable with Leonardo’s painting? Let’s take our calipers to the print. Example IX.84 is a summary of what we find, the yellow always indicating the longer part of a line’s golden ratio, the violet the smaller.

Example IX.83
Katsushika Hokusai: “The Great Wave of Kanagawa,” 1830-3227

Example IX.84
“The Great Wave of Kanagawa” golden ratio analysis
27 New York: The Metropolitan Museum of Art, H. O. Havemeyer Collection, Bequest of Mrs. H. O. Havemeyer, 1929, Object Number: JP1847
Let’s look at the perimeters first. Line “A,” across the top of Hokusai’s work, has a golden section marking the peak of the great waves’ arc, with the shorter portion of the golden ratio line coming first (in purple) followed by the longer part of the line (in yellow). “D” is the right perimeter of the print (“right” as we look at it, “stage left” for an actor). As we go down that line, we see that the golden ratio of that line marks where the top of Hokusai’s wave intersects with the print’s edge, the short section coming first (the red, dotted line shows the intersection of the wave and the print’s edge). We see that the design in both the top and righthand perimeters is articulated by golden relations. “C” is another line going down through Hokusai’s print. It’s the mirror of “D” with “D’s” long and short parts reversed in “C.” The golden section of “C” marks the summit of Mount Fuji. “B” is another line going across Hokusai’s print. It’s the mirror of “A”, the long and short parts of “A” being reversed in “B.” The golden section of this line almost marks Mount Fuji’s summit but it falls short by just a bit. “E” is a right perimeter line marking the distance of “D’s” golden section down to the print’s bottom. The golden section of this line marks where Hokusai’s second wave intersects with the print’s perimeter, being the golden section of the golden section (line “D”).
What is this print about? What story is Hokusai telling us? This is a picture about opposites. The solidity of the great mountain, eternally the same, the fluidity of the great wave, ever changing. The wave is huge, the mountain is small. The mountain is serene, the ocean is tempestuous. The mountain is remote, the ocean is all around us. The mountain’s design is balanced, symmetrical, the huge wave lunges out, chaotic, with claw-like surf. The foam of the wave’s surf becomes snow over the mountain, the opposition of water and ice. Both the wave and Fuji are mountains, but one is a mountain of stone and the other is a mountain of water. And cowering in their boats are the fisherman, caught between the mountain of stone and the mountain of water, the ocean threatening death, the mountain offering life. Everything hangs in the balance.

You’ll remember that concinnity is “the purposeful reinforcement of the various elements of a work of art.” Look at how Hokusai’s design reinforces this drama. Both the mountains water and stone are articulated by golden ratio placements, and the ratios are in opposite directions (shown by turquoise arrows) reinforcing their opposition. The ratio across the top of the print is echoed by the ratio down the side. The summit of Mount Fuji is echoed by the summit of the wave (shown by the green arrows), the inversion again reinforcing the opposition of water and stone. As on a human face, the golden mean doesn’t appear once, it appears multiple times, cascading across the picture.

It isn’t significant that a golden mean relationship can be found here. The spirals of a pine cone have a golden mean relationship and it’s just a pine cone. Example IX.86 is one of many analyses readily available that find golden mean proportions in Hokusai’s print, but the analysis is meaningless.28 It’s just a golden mean diagram imposed on the design, aligning one spiral with another, the alignment in no way enhances the meaning of Hokusai’s work. In fact, it obscures it. It is the multiplicity of the golden mean relationships plural that together propels Hokusai’s work into the highest levels of aesthetic eloquence.
The “rule of just enough,” the golden rectangle, the Fibonacci series, there’s one more thing we must mention before we return to Bach’s prelude: fractals. Simply put, a “fractal” is a geometric shape or mathematical set that is characterized by “self-similarity,” meaning that it contains smaller copies of itself within itself. Figure IX.9 is a fractal in that the large rectangle contains within it four other rectangles identical to it in proportion. Benoit Mandelbrot (1924 –2010) who began his career as a research mathematician at IBM and ended it teaching at Yale, was famous for inventing the term “fractal.” He first noticed fractal-like relationships between large and small elements in nature when looking at the coast line of Great Britain in 1967.29 In the following years he developed his “Mandelbrot Set,” a recursive formula that can be used to create fractals of extreme complexity.30 Fractal relationships have been found from neuron branching (and almost all areas of cell biology), to river formation, to the rings of Saturn.31 The
28 Seamus A. Power and Anthony G Shannon, “Natural Mathematics, the Fibonacci Numbers and Aesthetics in Art,” Journal of Advances in Mathematics, Vol. 17, 2019.
29 Benoit Mandelbrot, “How Long Is The Coast of Britain? Statistical Self-Similarity and Fractional Dimension,” Science, New Series, Vol. 156, No. 3775 (May 5, 1967), pp. 636-638. I’ve always wondered if all architecture Mandelbrot was living amid in New Haven ever influenced his thinking about fractals; I never got a chance to ask him.
30 The Mandelbrot Set is z_(n+1) = z_n² + c:
31 J.H. Smith, et al, “How Neurons Exploit Fractal Geometry to Maximize Physical Connectivity,” Scientific Reports, 11, 2332, 2021; Jun Li, Martin Ostoja-Starzewski, “Edges of Saturn’s rings are fractal,” Springerplus,
golden mean, the Fibonacci sequence, and fractals are examples of things where there is a coherent relationship between the thing’s smallest parts and its largest.

2015, April 1; 4:158; David G Tarboton, et. al, “The fractal nature of river networks,” Water Resources Research, 1988,Vol. 24 (8), 1317.
We’re now ready to return to the C Major Prelude. We left it with two questions. Why is it as long as it is and what is the purpose of those very odd major-major seventh chords which Bach used three times? First question: thinking about the principle of artistic economy or the "rule of just enough" why didn't Bach end the prelude in measure thirty-two, or thirty-three (the “Linton” ending, Ex IX.6) instead of measure thirty-five? Is it too long? Could the prelude be improved by extending it to thirty-six measures, as Czerny believed?
Bach’s prelude is thirty-five measures long. Consider a “measure” like an inch or a meter, a way of marking-off distance. Beginning in measure one, and continuing to measure thirty-five, what is the golden mean of that distance? We take thirty-five and multiply it by 0.618 and get 21.63. Measure twenty-one is the golden mean of the prelude.
But before we go further a caveat: we need to remember that we are not dealing here with mathematics and the exactitude mathematics demands. The golden ratios we saw across “The Great Wave” and echoed over Aishwarya Bachchan’s face were not calculated – and justified –with mathematical precision. They were relationships that we intuited before we recognized their golden mean characteristics. In regards to this measure, we don’t need to be concerned about the decimal digits or whether or not we’re basing our calculations on the first sixteenth-note of the measure or the last (or even slightly into the following measure or the end of the previous one). Here, “twenty-one” is our golden mean.
But is that “twenty-one” important? Not necessarily. Every line has a “golden mean,” the San Diego Freeway has a golden mean, the fact that one exists isn’t significant. What can be significant is what that golden mean marks. This is measure 21. It is important? [Ex.IX.88]

Example IX.88
Bach, C Major Prelude m. 21
This is a very important measure. You’ll remember that the “F” in the bass marks the lowest point in Bach’s descent; from this point Bach has the bass ascend (to “F-sharp,” “A-flat,” and then the “G” that becomes the pedal until Bach reaches the “C” in measure 32). This “F” is also an essential part of the chiastic design we summarized in Example IX.12.
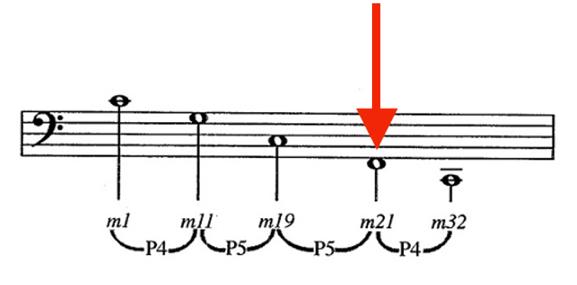
Example IX.89
Phi here reinforces we’ve come across that word before, “reinforces” Bach’s chiastic design. But there’s more. Over the last pages we’ve seen that the golden ratio is a repeated ratio. It’s a kind of fractal that testifies to a coherent relationship between the small parts of things and the larger parts. Think of faces we saw earlier. [Ex.IX.90] A

The golden ratio isn’t just once down the face, but down the face several times, and across the face, and in the width of the mouth, length of eye brows, placement of the cupid’s bow. Phi, j , echoes across the face.
Let’s return to the prelude. We can call the j we just discovered the primary golden ratio of the prelude, going from measure one to the end, measure thirty-five. But measure one to measure twenty-one is another section. If we look at that section, and reverse our direction figuring the golden mean from measure twenty-one to the beginning, we find the golden ratio of that section to be measure eight. That is the prelude’s second j . Now we have a third section,
from measure eight to measure twenty-one. Going forwards, we find that the j of this section is measure sixteen. Forwards, for the first golden section, backwards for the second golden section, forwards again for the third golden section.31 [Ex. IX.91]

Example IX.91
Golden section of the C Major Prelude
We now know that the golden mean in measure 21 helps to emphasize the end of Bach’s descending bass and the beginning of its reversal but are the other two measures of any significance, measures eight and sixteen?

Example IX.92
Major-major seventh chords and the golden ratios
31 5 x .618 = 21.63. This is clearly measure twenty-one. 21.618 x .618 = 13.15. If we count back thirteen measures from the very beginning of measure 21, or even the final moments of measure 20, we’re taken to the measure eight. Between measure eight and measure and measure twenty-one we have fourteen measures. 14 x .618 = 8.652. Although the math with the second and third gold sections of the prelude doesn’t quite give us the centered phi’s that we get with the first golden section, if we take our calipers to the diagram of the prelude we can clearly see that the second and third golden ratios fall in the areas of measures eight and sixteen. As we saw with “The Great Wave”, we’re dealing with reasonable approximations.
Each of the chords on those measures is a major chord with a major seventh, the extraordinarily unusual sonority we discussed earlier, chords that appear nowhere else in the prelude. [Ex.IX.10] The major/major seventh chords articulate the golden ratios of the prelude. But there’s more. All three of the chords are subdominants, the first the subdominant in G Major, the second the subdominant in C Major, and the third a purposefully ambiguous tonic on “F” or a subdominant-seventh in C Major. But there’s more.
The dissonance in these unusual sonorities is caused by the inclusion of the minor second, or major seventh, depending on how the chord is placed. The first two times Bach places it in third inversion, meaning the seventh is in the bass and the dissonance is a minor second above it. The dissonance is also between the first and second pitches presented. Another way of saying this is that the dissonance is as close as it can be vertically the minor second and horizontally it’s the first two events in the measure. What would be the opposites of “as close as can be” and “as soon as can be”? Wouldn’t those opposites be “as far as can be” and “as late as can be”? Look what Bach does in measure twenty-one. The dissonant interval now isn’t a minor second, but major fourteenth and it’s placed as the last note in the pattern. [Ex.IX.93]

Example IX.93
Major-major seventh chords
We’re now able to answer the question about the prelude’s length. It’s thirty-five measures long because it has to be. If it were thirty-six measures, or thirty-two, or thirty-three Bach’s architecture would collapse. It must be precisely thirty-five measures long or none of those proportions that highlight the major seventh chords would align. And our second question: what are the purposes of the major seventh chords? Did Bach throw them in whimsically, capriciously, just because he wanted something a bit different there? No. The chords punctuate prelude’s golden sections. Why are the pitches in the bass in the octaves Bach places them in? Because they must be in those precise octaves to articulate the chiastic structure of Bach’s modulations. And where is the “keystone” of the prelude, the piece’s most dramatic point? It’s where Bach’s two strategies intersect: the strategy of the chiastic structure and the strategy of the
telescoping golden ratios: measure twenty-one. The golden mean of the entire piece intersects with the lowest pitch of Bach’s bass in an octave required by the chiastic form sounding the most dissonant chord in the piece, in root position, and spanning an ambitus greater than any other sonority up to that point.
We began this chapter thinking about bridges and the “rule of just enough.” And you’ll remember that I described the bridges as being “engineered.” We need to return to that. When people think of composers writing music people typically think of the composers being caught in the grip of some emotion and then struggling to express that emotion through their music, their music flowing tempestuously out of their psychic agony (it’s always agony). There is some of that involved in composing, the desire, better the necessity to express something inchoate and we’ll look at this more carefully in the appendix but actually very little. Like the planning of a bridge, our greatest compositions are engineered. A piece is planned, examined, tested, replanned, re-calculated, and revised until the piece is finished. Finished because it’s perfect.
Greatest and perfect. Our greatest pieces of music are perfect. This prelude is perfect.
That’s a stunning assertion. Pause. Let that sink in. This prelude is perfect.
Change anything about the piece, change the octaves in which the piece’s first “C” is placed or the “F” on the downbeat of measure 21, place a major-major seventh chord in any other measure than in the measures Bach placed them or alter any of the three major-major seventh chords he uses to any other kind of chord, extend the piece by one beat, or contract it by one beat change anything about this prelude and it’s ruined.
This prelude is perfect.
We’ve come across “perfect” before. It was with the Pythagoreans and their notion that octaves, fourths, and fifths were “perfect” because their intervals were defined by ratios, and these particular ratios used numbers that could be manipulated to add up to ten and the Pythagoreans considered ten a perfect number with metaphysical and magical properties.32 That was, and is, all nonsense. Ten isn’t any more magical than four, or seven-and-three-quarters, or twelve (and both the ancient Mesopotamians and Egyptians counted in units of twelve) and the sound of a fifth isn’t any more “perfect” than the sound of a seventh; they’re both just sounds. But we also found “perfection” in the general Greek philosophical tradition of “changelessness.” You’ll remember that in this tradition the primary attribute of divinity, or perfection, was its constancy. It didn’t change because it didn’t need to change, it was perfect, it was constant.
Let me suggest another word for “constant:” “integrity.” And let’s go back to engineering and thinking about a bridge. Engineers say that a bridge has “integrity” when it remains stable, safe, and functional throughout its designed lifespan. All parts of the bridge must contribute to that integrity, meaning that some parts of the bridge can't be designed to hold it up while other elements are weak or even designed to bring it down. There’s a specialized kind of engineer who’s called an “integrity engineer” who is tasked with making sure that all parts of the bridge
32 1 + 2 + 3 + 4 = 10. Pythagorean ratio for the “perfect” octave: 2 : 1, “perfect” fourth: 4 : 3, “perfect” fifth: 3 : 2. The notion was also seen in the tetractys. See Chapter Three, footnote forty-five.

will function as intended and that “all” is essential because even the failure of a very small part can bring the entire bridge down. This happened spectacularly and horribly in Connecticut. In 1983 a one-hundred foot span of the bridge across the Mianus River on Interstate 95 one of the most heavily traveled routes in America collapsed in Cos Cob, Connecticut. Three motorists plunged into the river and died. A couple of pins that supported a part of the bridge had failed, weakened (the engineering term is "fatigued") through corrosion from the salt water in nearby Long Island Sound. In this case, the pins lost "integrity" and three lives were lost. Not all the pins failed, just two of them, most of the pins were just fine, yet because of this failure the whole bridge lost its integrity and failed. It wasn't a good bridge any more.
[Ex.IX.94]33
“Greatest,” “perfect,” “integrity,” now I’ve introduced “good.” When it collapsed, I wrote that the bridge "wasn't a good bridge any more." I want to discuss goodness and what is essential about "goodness."
What is the essential character of "goodness"? Let's address this question by turning it around (a technique of thinking about things we’ve done several times before). If goodness is to exist in any sort of a meaningful way it must be different from something else, in other words we need to be able to recognize "goodness" from something else, like "ice bucket" or “toaster” or “loudness.” And if we can tell it apart from something else, what is the most "apart" from goodness? What would goodness be least like?
Goodness would be least like badness. Goodness is the opposite of badness (and of course I'm making that word up, badness, and it's interesting that we don't have a word that describes the category of "bad" that mirrors the use of "goodness" for the large category of "good," but I don't know how significant that is). Let's define "goodness" by first defining its opposite, "badness."
33 Mary Jacobson, “Oral History Project Blog – The Mianus River Bridge Collapse, Greenwich Sentinel, June 24, 2002, https://www.greenwichsentinel.com/2022/06/24/oral-history-project-blog-the-mianus-river-bridge-collapse/ Photo courtesy of Greenwich Historical Society. I was living in Connecticut at the time of the collapse and you could feel a collective shudder going through New England when the news of the bridge’s collapse broke; we all through “I could have been driving over that bridge when it failed.”
Let's think of something that we'd all easily recognize as "bad." Just in our common use of the term, what would most of us agree as being "bad"? How about telling lies? Can we agree, lying is understood as being one of those things that would come under the category of "bad."?
We can say that there are occasions where we might think that telling a lie isn't completely bad, it's justified the whole business of espionage is built on that principle, and when a friend asks us how she looks in a particular outfit we all know it's acceptable to fudge the truth a bit (and we even have a word for that, calling it a "fib"), especially if that friend is your wife yet generally I think we can agree that telling lies is bad.
Let's go further. Let's imagine someone who is a really great liar. Let’s imagine the best liar in the world. What would be his essential quality? What would it be that would make him such a successful liar? Might it be that he was able to tell unusually convincing stories? Certainly, that would be part of it. And it would be essential that he kept track of his lies, so that he wouldn’t get caught in telling different versions of his lie. But when we think more carefully, I think we’ll find that the essential quality of a virtuoso liar is that he doesn’t lie all the time. Indeed, we might go further and say that the essential quality of the virtuoso liar is that he is a very good truth teller. Indeed, his most important characteristic would be that he usually tells the truth. If he lies all the time we would have no problem identifying his lies. He would be easily caught. But, if he lies only rarely, and is careful about his lies, and even lies about only the matters that are most important to him that kind of liar is a virtuoso. We believe him to be always telling the truth, he lies so rarely and he deceives us so skillfully. His virtuosity helps us see the essential character of his deceit, of his "badness:" he cannot lie with integrity. He can’t lie all the time.
He can only be a successful liar if he only rarely lies and has a reputation for honesty. And he can succeed as a deceiver only if he lives in a culture that values truth telling and punishes deception. His success as a liar comes at the expense of his society; he is parasitic upon it and can be eventually deadly to it. He is like a bridge of which some parts of are engineered to support weight but which has other parts that are corroded.
If the lie is "badness", and we're concluding that badness is exemplified by the impossibility of its integrity – the opposite of badness would be goodness and the essential character of goodness would be integrity.
We've come to something very important. The essential character of goodness is integrity and that kind of integrity, like the perfectly engineered bridge, is stable and enduring. It's worthy of trust. We can put our confidence in it. It won't harm us. It’s true. There’s a word for something that exhibits that kind of “trueness” but it’s not in English. But we need to know it.
Schindler's List is a 1993 movie based on the life of Oskar Schindler (1908-1974).
Directed by Steven Spielberg (b. 1946), the film won seven Academy and three Golden Globe awards. In 2007 the American Film Institute ranked it as eighth on its list of the one hundred best American movies.
Schlinder was an amoral, womanizing opportunist of the kind that thrived in the chaos of post-World War I Germany. Using Nazi party connections (he joined in 1939), he acquired an enamelware company in Kraków, Poland where he employed cheap Jewish labor in partnership with the occupying Germans. But witnessing the brutality of the German assault in 1942 upon the Jewish ghetto in Kraków, he had a change of heart. He began to think of ways to protect his Jewish workers. By convincing the German overlords that his workers were essential to the war effort he rescued many of them from being deported to death camps. Late in the war he successfully relocated his entire factory, with workers, to the relative safety of Czechoslovakia.
About an hour and a half into the film there’s a scene where Schindler, played by Liam Neeson (b.1952) is in his office with Itzak Stern (1901-1969), his accountant from the ghetto, played by Ben Kingsley (1943). Together they are assembling names of Jewish workers to be designated “essential,” keeping them from transportation to a death camp and Stern is typing names on a list. This is the dialogue of the scene.[Ex.IX.93]

“The list is an absolute good. The list is life. All around its margins lies the gulf.”

Example IX.95
Still from Schindler’s List, “mitzvot” scene
The word we need to learn is in Hebrew: mitzvah ( מִצְוָה ), plural: "mitzvot" ( מִצְווֹת ) It’s frequently translated “commandment.” The laws God gave to Moses on Mount Sinai are mitzvot. They are completely pure, without fault or error of any sort. They are utterly true. They are perfect. But mitzvot are not traditionally limited to God’s commandments. Prayer, fasting, advocating for justice, acts of kindness, saving a life; these are all examples of mitzvot and they are said to help “repair the world,” tikkun olamתִּיקּוּן
) Schindler’s list is a mitzvah and Spielberg stages the scene to make the meaning explicit. The only light source is hidden, off camera (and the lamp on the desk is purposefully unlit). That light from the unseen source illuminates the list Stern holds and the list throws the light across the room; the list throws back the darkness. Absolute good repels the chaos. It may be the most profoundly theological scene in any film.
We’ve answered this chapter’s first question, “What makes some music great”? It is the music’s integrity. Every part of a great piece is engineered to accomplish its purpose. It is coherent and that coherency makes it thoughtfully expressive. And we’ve now answered our second question, “Why does it matter?” It matters because that kind of piece justifies our civilization's existence.
Like perfect, that’s a startling statement. But let's consider. We all seek meaning in our lives, we want our lives to have purpose. And unless we’re utterly debased and we must acknowledge that such people exist we hope that purpose involves bettering our world, at least in some small way. I think we hope that by the end we will have done more to make the world a
little better than we have done to made it worse and that good that we’ve done might justify our existence. Those ways in which we seek to do so are our attempts at mitzvot. But there are some attempts at making the world that are it’s hard to find the right word more radiant? than others. Schindler’s decision to rescue the Jews who were working for him was untainted by any self-interest. He was twice arrested and had the full extent of his scheme been discovered not only would he have been executed, and his execution probably preceded by torture, but his wife and maybe others killed as well. Schindler was not perfect, but his deed was. Bach was not perfect, but his prelude is. Our mitzvot are better than we are. Absolute goods, they push back against the abyss.
What justification can there be for a civilization unless it pushes back against the abyss? And what justification can there be for a life unless it pushes back against the abyss? The abyss exists. The abyss exists first within ourselves and secondarily in the worlds we live in. Schindler lived in a Germany that had completely given itself over to the abyss and was focused on spreading it across the world, a civilization that paralleled his own hedonism. His decision pushed back the darkness in his own heart before it saved one Jew, but then it saved over a thousand and, in Spielberg’s re-telling, it inspired millions.
I suspect that in the three hundred years since its composition the prelude has inspired millions. It has certainly inspired me and I suspect since you have come this far it inspires you. And knowing what you now know about it, you are a slightly different person than you were when you began this chapter. The prelude has enriched you.
“Enriched.” There’s a reason why I use that word now. You’ll remember that we ended Chapter Five with a discussion of the 1840 “The Old Arm Chair,” Billboard’s first chart of hits in 1947, and the problem faced by BlackRock, Inc., Sony, Universal, and the other corporations that have spent billions of dollars purchasing catalogues of popular music. And although United States copyright law generally extends the copyrights of recordings to ninety-five years after their release, the popularity, and thus commercial viability, of a piece of popular music usually doesn’t extend beyond a generation. Released in May, 2024, “Not Like Us” by Kendrick Lamar (b. 1987) hit one billion streams on Spotify by the end of that year and was a centerpiece of the 2025 Superbowl halftime show.34 It was the most income generating piece of music in 2024, producing an estimated $7.6 million from streaming, sales, and publishing. The song has enriched Interscope Records, which owns the copyright, Universal Music Group, which owns Interscope Records, and of course Mr. Lamar. But as in the cases of most of those pieces on that 1947 chart, there will be an end date on that enrichment and each successive year the piece will produce less and less revenue. The enrichment will diminish until the piece is nothing more than a cultural curiosity, like “The Old Arm Chair” (by August of 2025 “Not Like Us” had already dropped to No. 69 of the Billboard Top 200). The piece will fail to enrich.
34 Rania Aniftos, “Kendrick Lamar’s ‘Not Like Us’ Hits One Billion Spotify Streams,” Billboard, January 1, 2025, https://www.billboard.com/music/rb-hip-hop/kendrick-lamar-not-like-us-one-billion-spotify-streams-1235878578/ ; Gary Trust, “Kendrick Lamar’s ‘Not Like Us” Holds at No. 1 on Billboard Global 200 Chart” Billboard, February 24, 2025, https://www.billboard.com/music/chart-beat/kendrick-lamar-not-like-us-number-1-global-200-chart-fourth-week1235909052/
The prelude is not like that, it does not fail to enrich. All things decay, it's the second law of thermodynamics. But over time the prelude does not become less perfect. It remains the same; what changes is our wonder before it. It grows. Schindler's list is now a part of history. It is past but time similarly does not diminish our wonder before it. The more we consider it, the more we know both of the dangers Schindler and his allies faced and of the connivance and complacency of his fellow Germans people who stood aside and allowed the horrors to happen the deeper our astonishment grows. The mitzvah does not decay, and because it does not decay it testifies to a cosmos with an alternative physics.
Perfect, enriched, alternative physics, justifying our civilization's existence, mitzvah Those are weighty notions to hang on a little piece of music, perhaps outlandish. But they are justified, we are dealing with matters of the greatest possible seriousness. Our greatest works of art, our most selfless acts, our greatest accomplishments, our mitzvot, are our justifications.
I want to make several things clear. First, that "our", the first person plural. Bach wrote the prelude himself, it wasn't the product of a committee. The work is his accomplishment. But Bach's skill to compose it was learned, he had teachers and his teachers had teachers, and he had the occasion to write it because of the support of Prince Leopold of Anhalt-Köthen (1694-1728) who was his employer and enthusiastic patron. Apart from writing-out several copies, Bach didn't preserve the piece. It was further copied and shared with cognoscenti until it was engraved and commercially published 1802. The piece is first Bach's accomplishment, but the training that equipped him with the skills to write it, and the society which husbanded his occasion to write it, and the civilization that honored and has preserved since he wrote it all require that first person plural: "our." The prelude is Bach's mitzvah, honoring it is ours.
But there is an important catch here, and that's my second point and I'd like to return to Spielberg's film to illustrate it. Toward the film's close (and following the historical account), Schindler, having convinced the Nazis that his Jewish prisoners were skilled workers essential for the war effort, has re-located his operations to Brinnlitz, Czechoslovakia, where he has established a new factory producing secretly defective munitions (in an administrative mix-up, in the transfer the men were delivered to Brinnlitz but the women and children were sent to Auschwitz, a mix-up Schindler eventually is able to correct). The Reich has collapsed and Schindler, receiving the news that the Germans have surrendered unconditionally, assembles the Jewish workers and the guards on the factory floor and announces Germany's defeat. The workers are free to go. Reminding the guards of their orders to shoot everyone there, Schindler challenges them not to be murders, and after an initial hesitation they disperse. Schindler reminds the crowd that as a member of the Nazi party, a munitions manufacturer, and a profiteer of slave labor, he will be sought as a war criminal and he must flee.
That night, as Schindler and his wife are getting in a car about to begin their flight from the advancing Soviet army, he's met by a delegation of prisoners. They give him a letter, signed by every worker in the camp, explaining what Schindler had done, in hope that it might help Schindler should he be arrested and tried by the victorious Allies. And they give him a gold ring. A few hours earlier, one of the prisoners had given-up a tooth with its gold filling and another prisoner, an ex-jeweler, had cast the gold into a ring, inscribing it with the Hebrew "Whoever saves one life, saves the world." Looking at the ring, Schindler is struck by the realization that
he could have saved move. He made so much money, he was so rich, he could have saved so many more. He collapses in tears. And although Stern tries to comfort him, reminding him of the thousands he did save, Schindler isn't comforted; he knows he could have saved more. In a final act of kindness, several prisoners exchange clothes with the Schindlers, allowing them to escape the camp in clothes less conspicuous than their Third Reich finery. They drive off into the night, into the dark.

IX.96
Still from Schindler’s List, Oskar Schindler holds the ring he's just been given
The list is a mitzvah. It is a light that throws back the darkness. But it is also a light that shows the darkness's existence. Schindler can't be comforted because it is his own mitzvah that reveals the darkness in his heart. By doing what he did he recognizes that he did not do enough. The list justifies Schindler's existence. It also justifies his condemnation. Spielberg has Schindler exit the narrative in tears, which is also the way we exit the theater.
The mitzvah reminds us of what we are capable. It presents to us what we have done and gestures to what we have chosen not to do. It is the door to self-awareness. Existentially, can there be anything more important than this? Apart from the basic necessities of our existing water, food, shelter, safety can there be anything more crucial to our lives than this knowledge? Pause. Consider the gravity of this moment. Can there?
I think not. The C Major Prelude demonstrates unequivocally that perfection exists, that in its perfection it is a mitzvah and that as a mitzvah it justifies present tense our civilization's existence. It demonstrates and reminds us of what we are capable. And it does more than remind and demonstrate, it calls us to "do likewise."35 And because of this, the piece is of the greatest possible importance. It's not a casual entertainment, or a business opportunity, or even a piece sentimentally loved, any more than Spielburg's film is a summer blockbuster. It is a mitzvah and encountering it thoughtfully can change a life. And this prelude is not alone. Although proportionally rare in relationship to the whole corpus of music, there are many pieces like this of similar thoughtfulness and integrity, from the Middle Ages to recent years, and not just pieces of music but paintings and poems and sculptures and buildings, some of which we've encountered in these pages (Rembrandt's "Aristotle Contemplating the Bust of Homer," Milton's Paradise Lost, Hokusai's "Great Wave"), in-other-words works of art. And as the reference to Hokusai demonstrates, this kind of art isn't limited to Western Civilization, but finds examples in the civilizations of East and South Asia as well. When I wrote "that kind of piece justifies our civilization's existence" I might better written: "justifies humanity's existence." Integrity is not limited by geographical boundaries.
And there's another matter. When we know how important the prelude is and works like it we realize how utterly detestable Duchamp's "Bottle Rack" and Cattelan's "Comedian" (Examples II.1 & 2) and Stockhausen's "Helikopter-Streichquartett" are because their integrity dissolves under almost minimal scrutiny or, in the case of "Comedian," literally rots. Just as Schindler's list condemns every German industrialist who chose to support the Third Reich, so too the Bach prelude and the Hokusai print and the Rembrandt painting illuminate the pretense and deceit of the Duchamps and Cattelans and Stockhausens of our world

There is a story, attributed to Oscar Wilde (1854-1900), where, in one of his greatest fits of aestheticism, Wilde gestures to a table set for afternoon tea and urges his listeners to "live worthy of that tea pot!" The comment is often ridiculed as a paean to the vacuous cult of beauty, an idea that was much discussed in the Oxford of Wilde's day with its emphasis upon sensuality and delight in decadence and is even echoed in Fyodor Dostoevsky (1821-1881) notion of the redemptive power of beauty (frequently, somewhat caricatured, in the motto "beauty will save the world"). But to ridicule it is to misunderstand it. To live "worthy" of the tea pot isn't to live a life of dissipation and sensuality, a life of exquisite taste and passé ethics because if anything to make a tea pot is a lot of hard, dirty, work in front of wheels and molds and kilns and paints and glazes but it is to live a life of integrity, discipline, imagination, and trust worthiness that last one is very important because we have to trust that the teapot's handle is strongly attached because if it is'nt we're in danger of being scalded that results in something beautiful and physically and emotionally nourishing to ourselves and to our community. The tea pot, the prelude, Schindler's list point to us to a way we should be living.
Should be living, but we rarely are. Wilde certainly wasn't, as he himself movingly acknowledged in his 1897 De Profundis. I'm not either. Maybe you too.
VWe're almost at the end. And I'd like us to go back to the beginning. We opened with chapters about the definition of music and why music is important to us. Let’s return there. Do you remember John Baize, sitting at his piano, playing a gospel song in what had been his living room, a tornado having just taken the roof off his house? For him, for us, music is a way we come to understand ourselves emotionally and, having understood ourselves, we’re able to better understand each other. It’s a way I can move from me to we. And you remember William Duckworth of Sandersville, Georgia, who is credited with inventing the chanted choruses that make forced marches if not fun, at least a bit less odious. We use music to make our lives easier that’s music’s utilitarian purpose, and we use music to make our lives more pleasant by making it more beautiful that’s music’s aesthetic purpose. We remember John Cage and his 4' 33" and recognized that “music” is a particular attitude we have to sound and not just sound alone but also silences around and within that sound (and we remember, ironically, that the one piece without any silence is Cage's famous piece). And we recognized that music is intimately related to both poetry and dance, metaphorically containing the DNA of both. We looked at categories of music: pop, folk, and classical, and the traits that united them and traits that separated them. We looked at how our lives and our cosmos are made up of patterns and how these patterns are manifested in musical rhythm. And finally, we looked in some detail at one little piece of music and how, in its perfection, it drives back the darkness in the world, and in us.
And we had Shakespeare, the lines he gave to Duke Orsino that opens Twelfth Night.
If music be the food of love, play on; Give me excess of it, that, surfeiting, That appetite may sicken, and so die. That strain again! it had a dying fall; O, it came o'er my ear like the sweet sound, That breathes upon a bank of violets, Stealing and giving odour!"
Those seven lines in iambic pentameter (yes, the same meter we saw Milton using in Paradise Lost), along with Congreve's "Music hath charms. . ., " are probably the most famous lines about music in our language.36 But before we directly address them I'd like to return to one of the more outlandish claims I've made here. You'll remember that I said that our greatest music, as mitzvoth, does not decay. Its excellence does not fade or diminish or become corrupted. By not decaying it violates the second law of thermodynamics which describes how all things decay, and all means all: suns, solar systems, pine trees, tuning forks, cocker spaniels 37 The perfection of the prelude testifies to an alternative cosmos with an alternative physics.
But what else does not decay? What else refuses to diminish over time, but instead endures and even becomes stronger? What else in these ways points to an alternative physics, to another world? Is there anything else?
Yes. Love.
Love does not diminish. It does not decay. Infatuation, devotion, affection, obsession, these all can wax and wane, but not love. Again, I expect you're surprised. But where else could 36
Line by line scansion:
È ¢ È ¢ È ¢ È ¢ È ¢ If mu- / sic be / the food / of love, / play on;
È ¢ È ¢ È ¢ È ¢ È ¢ Give me / ex - cess / of it, / that, sur - / feit - ing,
È ¢ È ¢ È ¢ È ¢ È ¢ That ap- /pe - tite / may sick - / en, and / so die.
È ¢ È ¢ È ¢ È ¢ È ¢ That strain / a - gain! / it had / a dy - / ing fall;
È ¢ È ¢ È ¢ È ¢ È ¢ O, it / came o'er / my ear / like the / sweet sound,
È ¢ È ¢ È ¢ È ¢ È ¢ That breathes / up - on / a bank / of vi - / o - lets,
È ¢ È ¢ È ¢ Stea - ling / and giv - / ing o - / dour!"
37 Of course nuance is required, and irony. The laws of thermodynamics are "things," yet they don't apparently diminish or decay over time. The "laws" endure. But there is a difference between the perfection of the mitzvah and the perfection of a law, like the laws of physics, in that the laws of physics aren't created but instead discovered and are perfect only in so far as they explain observable phenomenon and when observations become keener laws are revised, whereas a mitzvah is created and is immutable.
we end? Love is where it begins, and in which it ends. And that "it" is everything. We began with creation stories. Do you remember the Hopi's Spider Grandmother, Gogyeng Sowuhti, and the Sun Spirit, Towa, and how the Sun Spirit directed Spider Grandmother to guide to Hopi to another world? Why did Sun Spirit to that? Out of love for the Hopi people, so that they might be preserved and flourish. And do you remember in the Hebrew Scriptures how the Lord God told Job that upon creation "the morning stars sang together"? And why were they singing? They were in the presence of Love. Go back to Chapter Six and look at Example VI.10, the opening of Gafurious' Practica musicae, from 1496, and compare it to this: [Ex. IX.98]

This is a depiction from 1445 of the opening chapters of Genesis that was once a small part of an imposing altar at Siena's Church of San Domenico, showing the world upon its
38 Giovanni di Paolo, "The Creation of the World and the Expulsion from Paradise", Metropolitan Museum of Art, Robert Lehman Collection, Object Number 1975.1.31
creation and God's expulsion of Adam and Eve from the Garden of Eden by Sienese painter Giovanni di Paolo (1398-1482) (this is roughly a generation earlier than the illustration for the Gafurious). Although the cosmos in the illustration for the Gafurious is arranged as a ladder, with the earth at the bottom, and in the di Paolos it's presented as concentric circles, with the earth at its center, we can clearly make-out in both the orbits of the heavenly bodies (di Paolo particularly helps us with a golden sun in the white circle). But it's this detail that concerns us here. [Ex. IX.99]

Example IX.99
di Paolo: "The Creation of the World and the Expulsion from Paradise", detail39
God is placing his finger on the circle of the stars (although a lot of the gold that was used to depict them has flaked off, we can just make-out figures of the zodiac), setting the cosmos spinning, giving it life (and yes, Michelangelo echoes this gesture in his depiction of God giving life to Adam in his fresco on the Sistine Chapel's ceiling). In Canto XXVII of Paradiso of his Divine Comedy, Dante Alighieri (1265-1321) tells us that the Primum Mobile,
39 Ascending from the earth, the rings in di Paolo's cosmos are first, the four elements (earth, water, air, fire in red), the Moon, Mercury, Venus, Sun, Mars, Jupiter, Saturn, the Stellatum (with the zodiac), the Primum Mobile, the Caelum Ipsum (or the Empyrean).
the outmost sphere of the cosmos, is set into motion by God's Love, and this motion is transferred to the rest of creation.40 Existing outside of the cosmos and its laws, with its own physics, Love sets the cosmos spinning. And the morning stars sing together.
Our greatest music, as with our greatest paintings, our greatest stories, our greatest poems, our greatest buildings our greatest lists are examples of Love; they are echoes of that other cosmos, they are bound by that other physics. Shakespeare's Duke Orsino is primarily pining for romance, but Dante showed us that romance carries a glimmer of that larger love in it. And as we've done so many times before in these pages, we can answer the duke's question by turning it around. No, music is not the food of Love. Music does not nourish Love, or strengthen it, or make it grow, not the Love we're talking about here. But instead, Love, the Love that starts the Primum Mobile moving and brings life to our cosmos, nourishes music. With terrible taste, we can keep Shakespeare's iambic pentameter and re-write his line with "Because it is the food of song, love on," terrible because it makes Duke Orsino sound like a 1968 hippie at a picnic and it's not nearly as compelling to begin a play with a statement instead of a question, but the point is made. "Play on" not because our music enhances Love or romance, or patriotism, or finances, or egos but because Love compels us to make music worthy of it.
Play on.

40 We can chide di Paulo slightly here for to be precise he should have placed God's finger on the darker blue ring above where he placed it, the clearly painted Primum Mobile. But artists are granted their liberties.
41 Detail of Example III.13
