Geometry through calculations

This e-book is a collection of works created by students within the etwinning project G.A.M.E. (Growing with Applied Mathematics Experiences)

In the Geometry in real life theme, the students created problems and solved them, collaboratively. The result was the eBook: Geometrythroughcalculations.

Coordinating Teachers:

• Mihaela Git, Jean Monnet High School, Romania

• Ludmila Cojocari, Gaudeamus High School, R.Moldova

• Benedicte Leduc, Broceliande High School, France

• Tugba Varol, Baruthane Secondary School,Turkey

• Vlatka Hizman Trzic, Technical School Virovitica, Croatia

• Maria Roussaki, Othisi High School, Greece

• María Bellver, IES Cristobal Perez Pastor, Spain

• Cîtu Georgiana, Virgil Ierunca High School, Romania

1 TERNARY TOWER IN SHANGHAI, CHINA

1. Find a function that models this skyscraper.

2. Create your own design for a tower using other functions.

Irina, Jean Monnet High School

��(��)=��.������������

with a rotation by ������ around the point O.

https://www.geogebra.org/m/qbrg8fvj

Patrik, Technical School Virovitica, Croatia

FLUIDITY 2.0 HIGH-RISE

is a Mega Luxury Hotel and Office Hybrid Tower in Swiss Alps

1. Insert the picture into a GeoGebra file.

2. Determine 2 functions that describe the silhouettes of this beautiful hotel. You can find several possible models.

Denisa, Jean Monnet High School, Romania

2. - It has a twirling form and a spanning open-air spaces with the surrounding Swiss landscape.

-To extend the green and fresh environment to the upper levels of the Luxury Hotel and Office.

Malala Ramanantsoa and Lily-Rose Leseigneur, Brocéliande High School, France

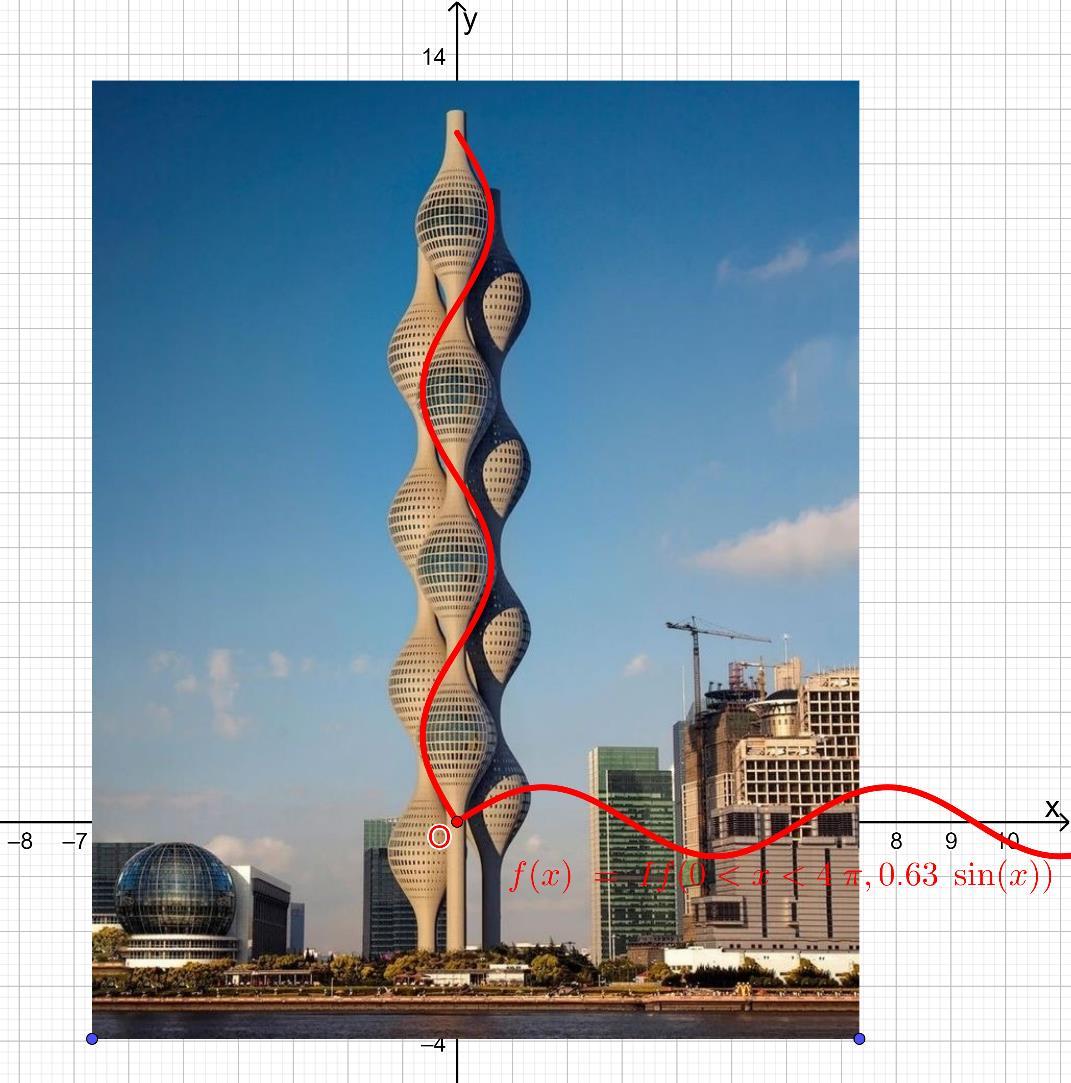
THE LOUVRE PYRAMID

https://www.geogebra.org/m/jgnvkxdwf

The Louvre Pyramid reaches the height of 21.6 metres and its square base has sides of 34 metres.

Calculate:

1. The perimeter of the base

2. The base surface area

3. The total area of the pyramid.

Moldova

Solution:

1. The perimeter is a square, so we can assume that the perimeter is equal 4⋅side ⇔ 4⋅34 = 136.

The Louvre Pyramid have a perimeter of 136 meters.

2. We know that the base is a square, thus we can deduce the formula of the base surface area : side⋅side ⇔ 34⋅34 = 1156 m².

The Louvre Pyramid have a base surface area of 1156 square meters.

3. The Louvre is a pyramid, the formula for the area of a pyramid is :

V = �� �� ⋅���� ⋅��, ����=base area h=height

Thus we can calculate :

Vpyramid = �� �� ⋅��������⋅����.��=��������.�� m3 .

The total area of the Louvre Pyramid is 8323.2 cubic meters.

By Thaïs CLÉMENT Brocéliande High School, France

Mariela D., Gaudeamus High School,

Some of the particulars to this construction are that it is comprised of 18,038 pieces of metal held together by some 2.5 million rivets. The iron from which it was fashioned has a mass of 7300 tonnes. The top of the tower (the sun-facing side) can shift up to 18 cm due to thermal expansion. The density of the wrought iron used to create this tower is 7.70 g/cm3 and was allegedly sourced from Reșița in Romania.

If one were to dismantle the Eiffel Tower and melt it to create an iron sphere, what would be its radius?

IF the top of the Eiffel Tower is seen from a distance of 600 meters at an angle of 30 degrees, find the tower height.

https://opentextbc.ca/intermediatealgebraberg/chapter/chapte r-4-7-mathematics-in-life-the-eiffel-tower/

The situation and the data

The Statue of Liberty, erected in 1886, is 46.50 m high without its base and 93 m high with base. A tourist in the front of a boat is looking at the statue. His eye is 5 m above the sea.

From what angle does the tourist see the Statue of Liberty?

The situation is represented on a GeoGebra worksheet as follows:

- the statue and its base are assimilated to two vertical segments carried by the same line,

- The observer is considered to be a vertical segment representing the height of his eye above sea level.

How does the angle of vision vary as the boat approaches the statue?

Alwena.BP, Brocéliande High School, France

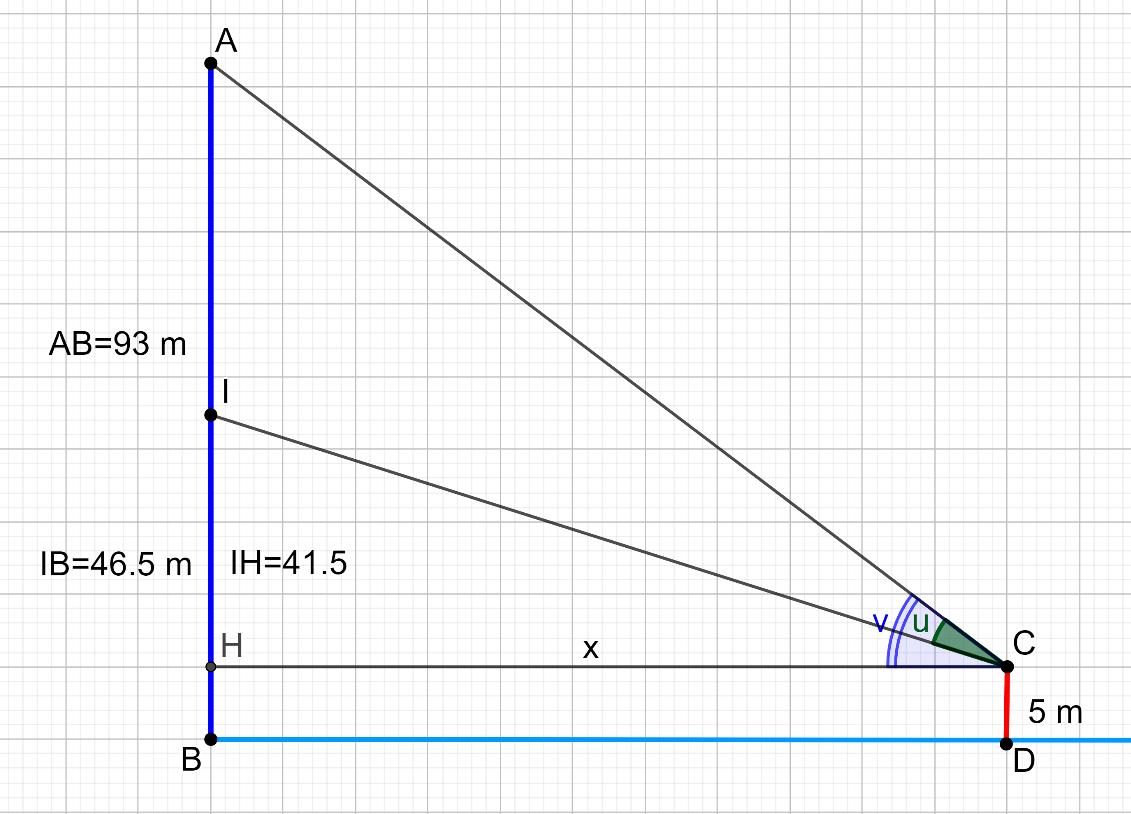
������(∡������)=������(∡��)= ���� �� ,���� =93−5=87⟹������(∡��)=

87 �� .

������(∡������)=������(∡��)=

���� �� = 41.5 ��

������∡(�� ��)=

������(∡��)=

������(∡��)–������(∡��)

��+������(∡��)∙������(∡��)

87 �� –41.5 �� 1+87 �� ∙ 41.5 �� = 45.5 �� ∙ ��2 ��2 +3610.5 ⟹

������(∡��)=

����.���� ����+��������.��.

For example, for �� =100�� ⟹������(∡��)=0.3343 and the angle �� =19°.

For, �� =10�� ⟹������(∡��)=0.1226 and �� =7°.

Daria, Jean Monnet High School, Romania

THE BURJ AL ARAB HOTEL

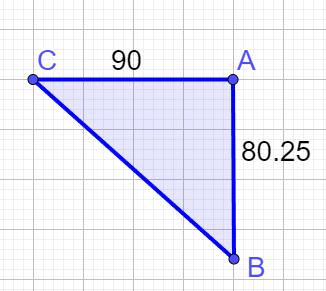
The Burj Al Arab hotel is 321 meters above the ground. Considering that the sides of each of the triangular poles in the body of the hotel are 90 meters, what is the length of the irons used as the hypotenuse?

Sude , Baruthane Secondary School ����

Irina, Jean Monnet High School, Romania

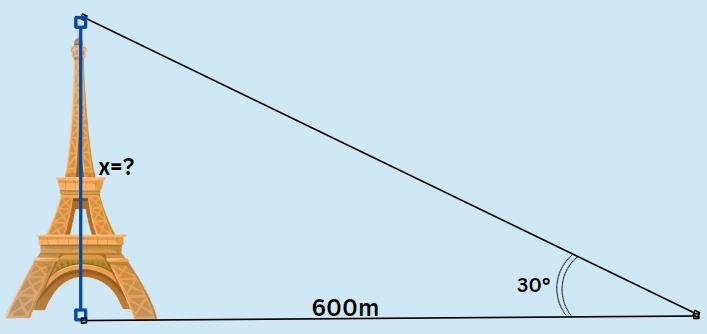
EIFFEL TOWER

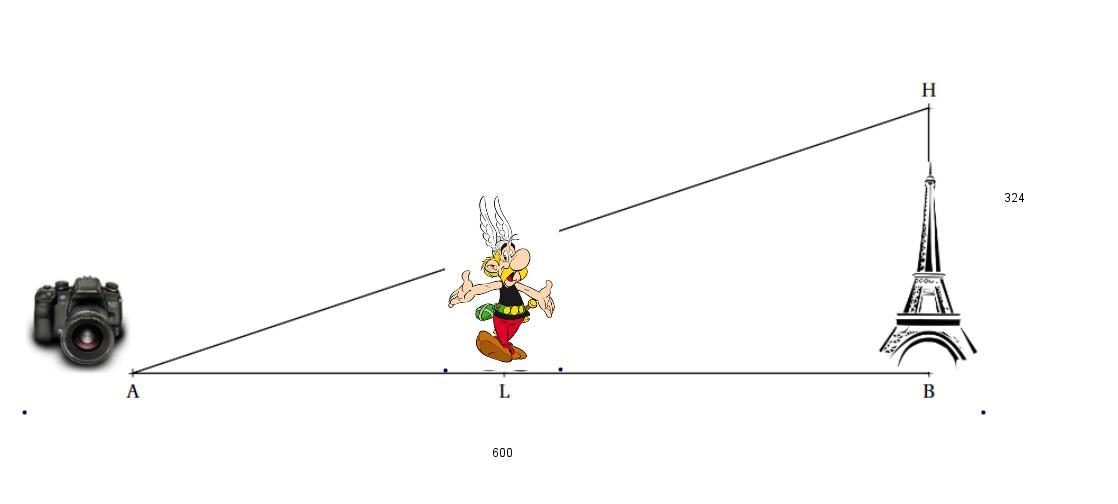
Asterix is on a visit to Paris. Today, he is at the Champs de Mars where he can see the Eiffel tower whose height BH is 324 m.

He places his camera on the ground at a distance AB = 600 m from the monument and programs it to take a photo.

1 What is the measure to the nearest degree of the angle HAB?

2 Knowing that Asterix is 1.70 m tall, at what distance AL must she stand to appear as tall as the Tower Eiffel in his photo?

Give an approximate value of the result to the nearest centimeter.

Jeanne, Brocéliande High School, France

To answer the first question, we can use the Pythagorean Theorem to find the length of the hypotenuse of the right triangle formed by the Eiffel Tower, the camera, and the ground. The hypotenuse is the line connecting the Eiffel Tower and the camera.

We have: ������ +������ =������, we get: �������� +�������� =������

Solving for CH, we find that CH = 675.6 meters.

To find the measure of the angle HAB, we can use the inverse cosine function. In this case, the side adjacent to the angle HAB is AB, and the hypotenuse is CH. Therefore, the cosine of the angle HAB is AB/CH.

We can find the measure of the angle HAB by using the inverse cosine function on the value AB/CH: angle HAB = arccos(AB/CH) = arccos(600/675.6)

Using a calculator, we find that this is approximately 31.7 degrees.

For the second question, we can use similar triangles to find the distance AL. Let's call the distance from the camera to Asterix's feet DL. Then we have the following similar triangles: [Eiffel Tower, camera, ground] ~ [Asterix, camera, DL]

Since the ratios of corresponding sides of similar triangles are equal, we have: BH/AB = HA/AL

Substituting the values given in the problem, we get: 324/600 = HA/AL. Solving for AL, we find that AL = 288 meters.

Since 1 meter is equal to 100 centimeters, the distance AL is approximately 28800 centimeters. To the nearest centimeter, this is 28800 centimeters.

Dino Špondreht, Technical School Virovitica Croatia

TRIANGLES IN OP-ART

This work in GeoGebra was inspired by an op-art painting made by Max Bill.

https://www.geogebra.org/m/n6wry2jg

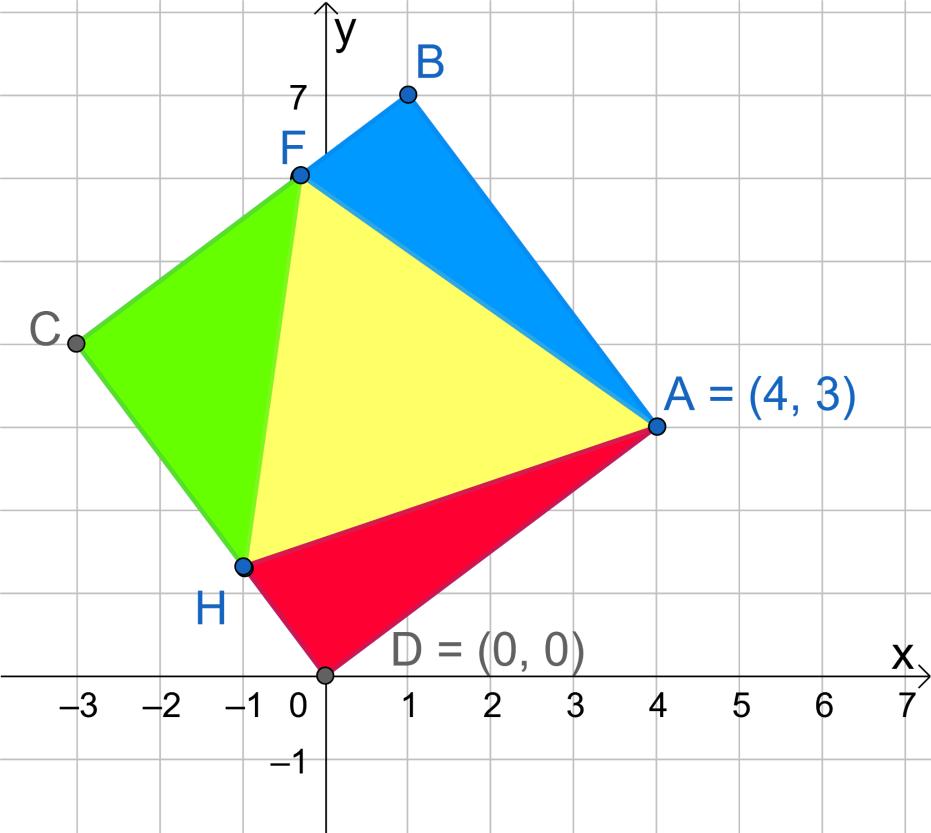
ABCD is a square with A(4; 3) and D(0; 0).

1. Find the equations of AD, AB, BC lines.

2. Calculate AD

3. If BF=DH 1.6 units, calculate the yellow area.

Luca D, Jean Monnet High School, Romania

Solution:

1. ����: ��−���� ���� ���� = ��−���� ���� ���� ⇒ �� �� = �� �� ⇒��= ���� ���� ⇒��= �� ����⇒��= �� �� ��

����: �� ���� ���� −���� = �� ���� ���� −���� ⇒ �� �� −�� = �� �� �� ⇒ ⇒���� ����= ����+��⇒ ��= �� �� ��+ ���� ��

����: �� ���� ���� −���� = �� ���� ���� −���� ⇒ �� �� −�� = �� �� −�� ⇒

⇒−����+����=−����+��⇒��= �� �� ��+ ���� �� .

2. ������ =���� +���� =����⇒ ����=��.

3. ����=����−����=��−��.��=��.��

����=���� ����=�� ��.��=��.�� ���������� = ����⋅���� �� = ��⋅��.�� �� = �� �� =��=�������� ������������ = ����⋅���� �� = ��.��⋅��.�� �� = ����.���� �� =��.���� ���������� =���� =����

�������������� =���� (��.��+��.��+��.����)=���� ����.���� �������������� =����.����

Vlad, Jean Monnet High School, Romania

TRIANGLES IN OP-ART

ABC is a equilateral triangle with AB=8. Each triangle, starting with the second, has a side 0.9 from the side of the previous triangle

https://www.geogebra.org/m/yhey8pkq

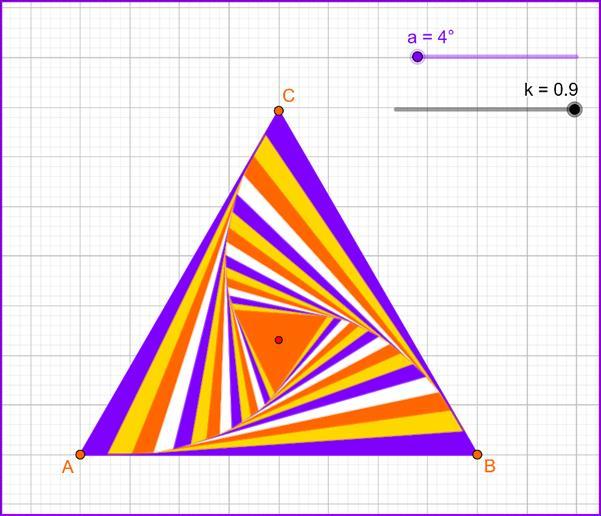
1. Find the area of ABC triangle.

2. Calculate the sum of the perimeters for the first 5 equilateral triangles.

3. Calculate the sum of the areas for the first 5 equilateral triangles.

Florentina, Jean Monnet High School, Romania

Solution:

1. ��= ����√�� �� = ����√�� �� =����√��

2. ���� =��⋅��,��=��,��

���� =��,��⋅��,��=��,����

���� =��,����⋅��,��=��,������

���� =��,������⋅��,��=��,��������

���� =��⋅��=����

���� =��⋅��,��=����,��

���� =��⋅��,����=����,����

���� =��⋅��,������=����,������

���� =��⋅��,��������=����,��������

���� +���� +���� +���� +����

=����+����,��+����,����+����,������+����,�������� =����,��������

3. ���� = ��,����√�� �� =����,����√��

���� = ��,������√�� �� =����,��������√��

���� = ��,��������√�� �� =��,������������√��

���� = ��,����������√�� �� =��,����������������√��

���� +���� +���� +���� +����

=����√��+����,����√��+����,��������√��

+��,������������√��+

+��,����������������√��=����,����������������√��

Buștiuc Arina, Gaudeamus High-School, Moldova

10.

SQUARES&TRIANGLES IN OP-ART

This drawing was made in GeoGebra, after a painting by Max Bill.

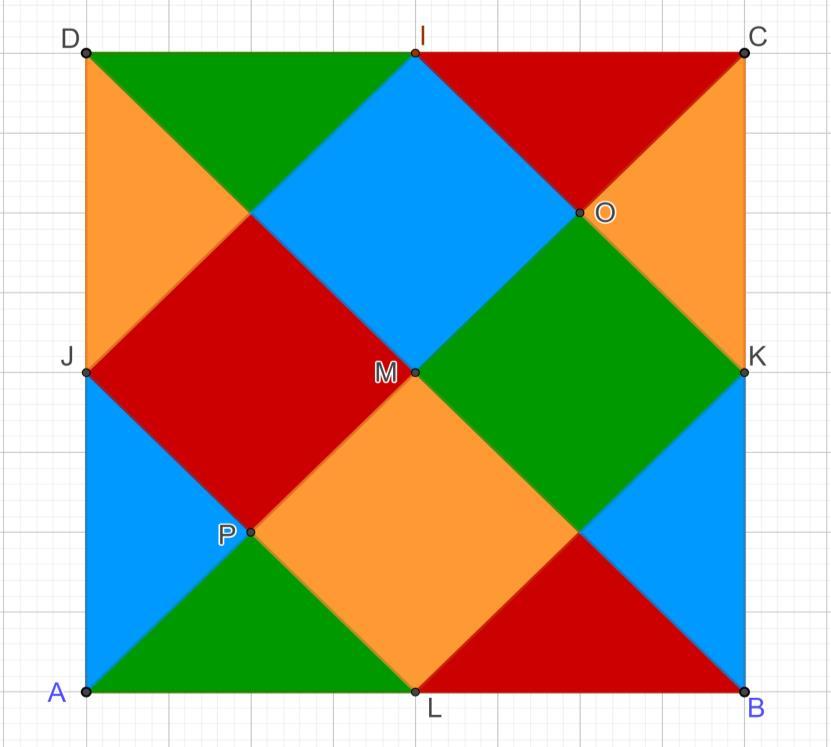
With the notations in the drawing, ABCD is a square with side 8 units and L, K, I, J are the means of sides

AB, BC, CD, respectively DA.

1. Prove that the lines aC, KL, IJ are parallel.

2. Show that ΔAPJ, ΔAPL, Δ KOC are congruent triangles.

3. Prove that the surface colored in red is equal to the surface colored in blue.

4. Calculate the ratio between the area of the orange and the area of the square

Teofil, Jean Monnet High School, Romania

Solution:

1. DIJ=45=DCA (corresp.angles)⇒����||����

ACB=45=LKB (corresp.angles) ⇒����||����

2. ΔAPJ is an isosceles right triangle with hypotenuse equal to half of the side of the square

ΔAPL, isosceles right triangle with hypotenuse equal to half of the side of the square

Δ KOC, isosceles right triangle with hypotenuse equal to half of the side of the square

ΔAPJ≡ΔAPLΔ ≡KOC

3. The red surface has an area equal to the area of two squares with side:

The blue surface has an area equal to the area of two squares with side

4. The orange surface has an area equal to the area of two squares with side

11. Model inspired by a carpet from SINAIA - Romania

In the attached image, ABCD is a rhombus with diagonals of 10u and 8u. Each rhombus, starting with the second, has a side 0.8 of the side of the previous one.

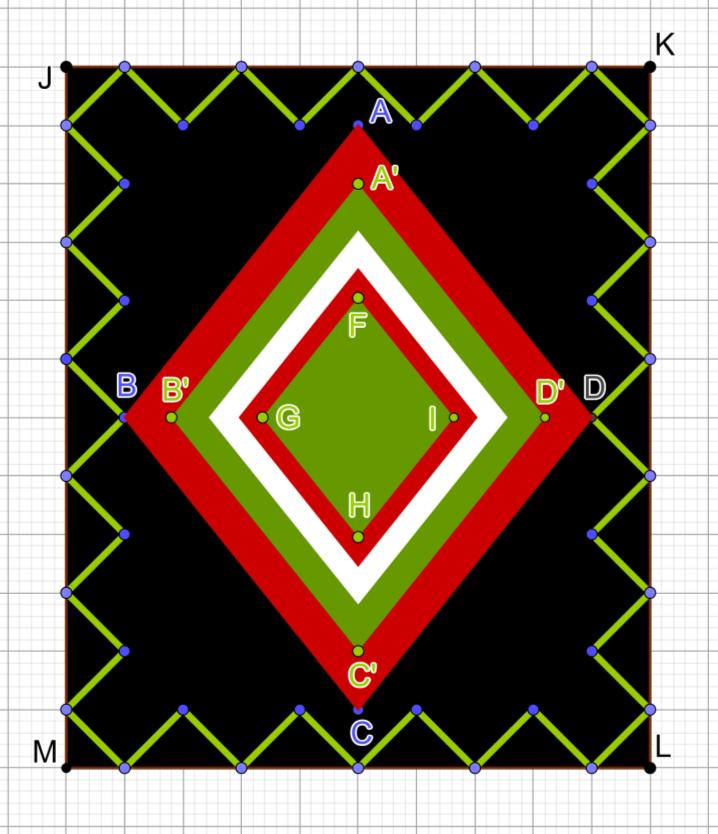
1. Calculate the area of the rhombus FGHI.

2. If the dimensions of the black rectangle are 12u and 10u, find the length of the green polygonal line, formed by segments that describe isosceles right triangles.

Carlos Sanz Ene, Jean Monnet High School, Romania

SPIRALS

Which is larger? The red or the yellow area?

You may draw this design by joining 10 equally spaced dots with semicircles!

GeoGebra shapes:

You may get the shape on the left by cutting this one in half and sliding.

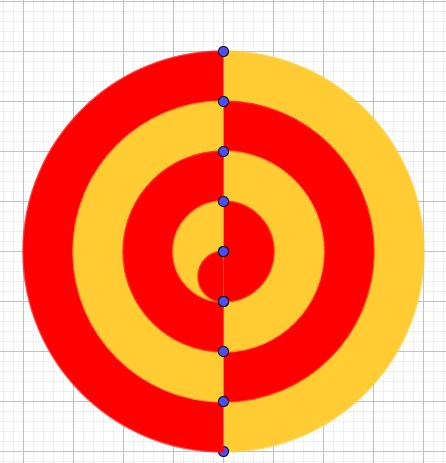
Since everything except the center is symmetric, the larger area is red!

Ellie and Marianna, Othisi High School

Matei, Jean Monnet High School, Romania

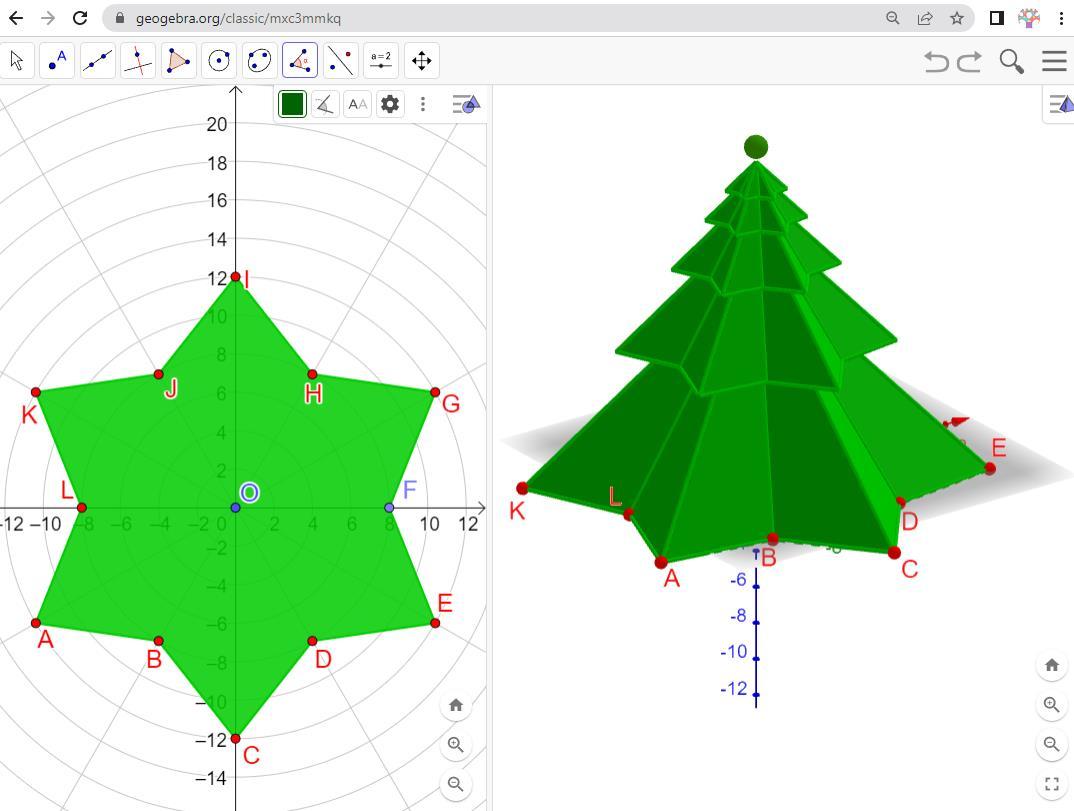
https://www.geogebra.org/m/uddqhtrv

This tree is built as a sequence of 5 regular pyramids in which each pyramid, starting with the second one, has the elements 0.5 of the previous one. The base is a star polygon with 12 sides. IJ=JK=KL=...+HI=6.5 and BHFHJL is a regular hexagon with BD=8. The great high is 16.

Calculate the volume of the third pyramid.

Ana, Jean Monnet High School, Romania

What is the volume of the cube with the largest side length that can fit inside this sphere with a diameter of 78 meters?

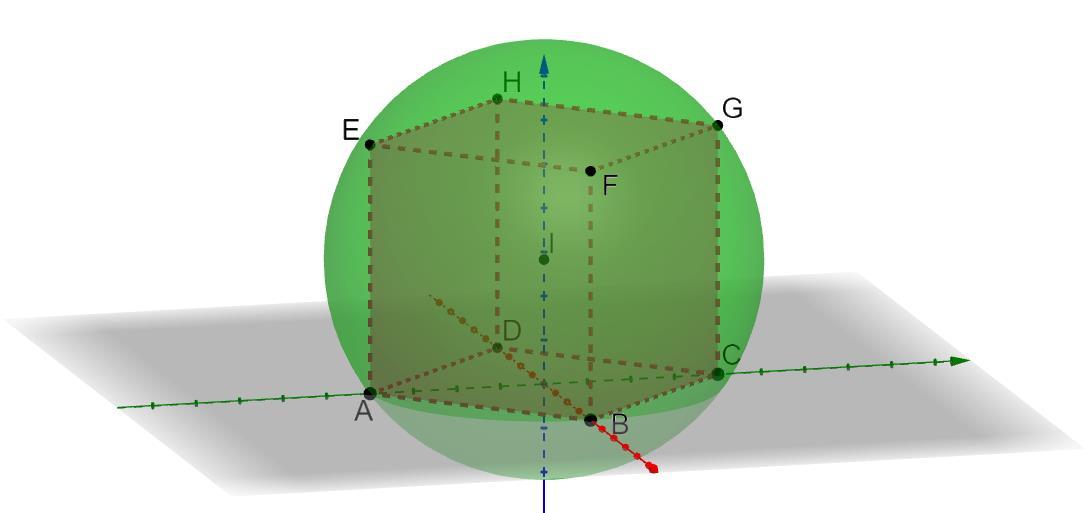
https://www.geogebra.org/3d/dgp27q5w

Beyza, Baruthane Secondary School, Turkey

Miruna, Jean Monnet High School, Romania

15. WHITE HOUSE

The length of the white house is 25 meters and the width is 52 meters, so what is the perimeter and the area of the white house?

Çağan Aras, Baruthane Secondary School, Turkey Solution:

16. CUBS

Natalija and Dijana make a large cube from small cubes. Natalija finished her cube like which we see in the left picture.

How many more small cubes must Diana add to her work that she gets a cube equal to Natalia's?

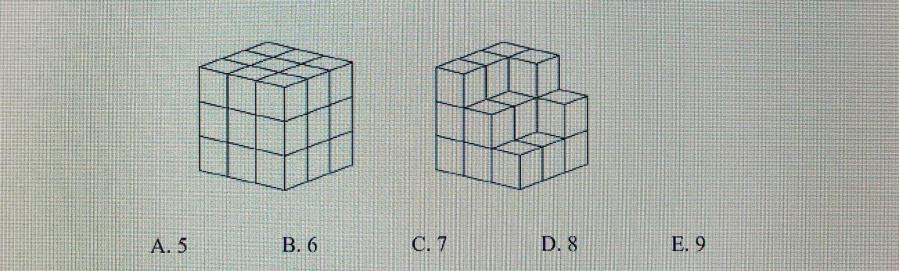
Patrik Živković, Technical School Virovitica, Croatia

We use the formulas for the perimeter and area of the rectangle:

P=2(L+l); A=L ⋅ l

P=2∙(25+52)=2∙77=154⇒

P=154 m

A=25 ⋅ 52 = 1300 ��2

A= 1300 ����

Mara, Jean Monnet High School, Romania

The large cube that Natalija made has 27 cubes and Diana only has 20 in her work, therefore she needs to add 7 more cubes (Answer:C.7).

Mariela D., Gaudeamus High School, Moldova

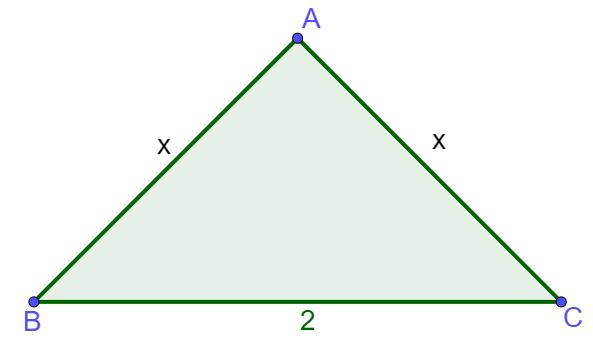
SQUARES

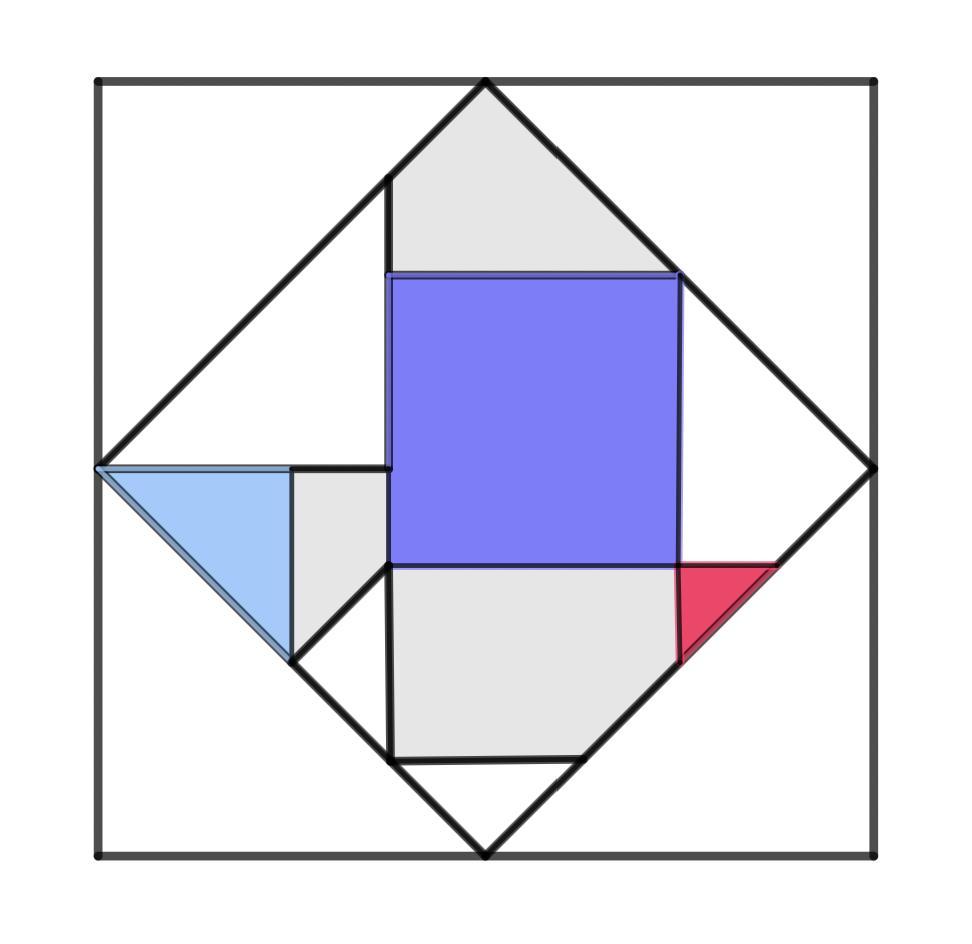
What is the area of the purple square, knowing that a side of the square is 2√3 cm.

Calculate the perimeter of the blue triangle, knowing that it is an isosceles triangle, whose base is 3 cm, and the other two are congruent and are twice the size of the base.

Solution:

We know that the side of the square is 2√3 cm.

So the area of the purple square is 2√3 ∙ 2√3 which is equal to 12cm².

We know that the lenght of the base is of 3 cm and that it’s an isosceles triangle. The other two sides measure twice the size of the base: 3∙2 so 6 cm. The perimeter is the sum of all sides: 3+3+6= 12 cm

Arina B., Gaudeamus High School, Moldova

Jeanne, Brocéliande High School, France

TOWER IN PISA

The tower of Pisa is 56.294 meters high. If the diameter of the leaning tower of Pisa is 15.484 meters, what is volume of the tower in Pisa?

Petar Petrinović.Elementary School of Nikola Andrić.

Vukovar/Croația

Solution:

We use the formula for the volume of the cylinder:

�� =��⋅��2 ⋅ℎ

�� = 1 2 �� = 15,484 2 =7,742(��)

according to the formula, the volume of the pisa tower is:

�� =��⋅7.72 ⋅56.29=59.29⋅56.29��=3337.4341��

�� =3337.4341����3 ≈10479.54��3

Aparatu Maria Magdalena, Gaudeamus High School, Moldova

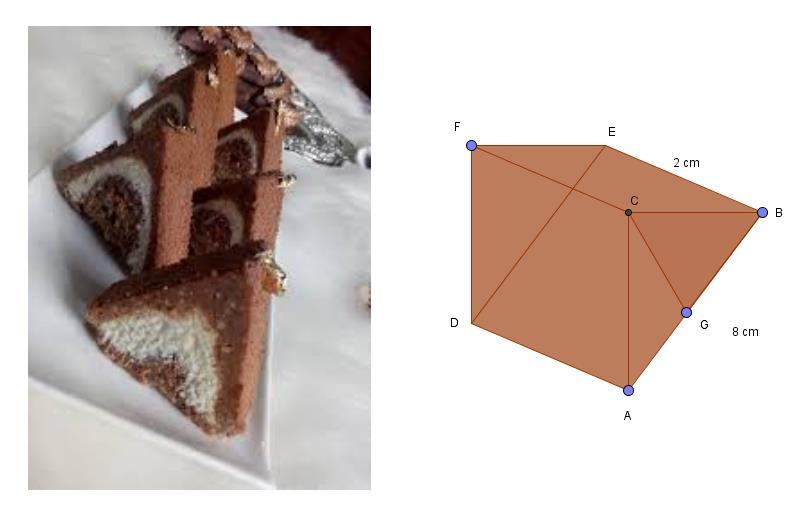
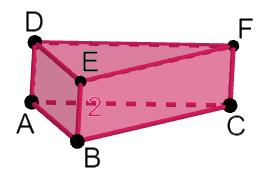
Before eating this cake, we are going to calculate its volume. The length AB equals 8 cm and the length EB equals 2 cm. ABC is an equilateral triangle. CBG is a rectangle triangle in G. The point G intersects the line AB in two.

Louise Wester, Brocéliande High School, France

Matei, Jean Monnet High School, Romania

THE ARC OF TRIOMPHE, PARIS, FRANCE

Listenbourg students are on a trip to Paris, Ella, a student wants to find the volume of the Arc de Triomphe.

The main volume is 50∙45∙22 = 49500m3 .

But Ella can't find the total volume ( without corbels, baseboards, sculptures)...

Task: Find the volume of the main and secondary arch

It's up to you to help Ella and find it !

Manon L, Brocéliande High School, France Solution:

Denisa, Jean Monnet High School, Romania

PLAYING CARDS

Ivan built houses from playing cards. The picture shows the houses that Ivan built, a one-story house, two-story and three-story. How many cards does he need to build a four-story house?

one-story=2 cards two-story=7 cards threestory=15 cards

Explain your solution !

Marko Zalović, Technical School Virovitica, Croatia

Solution:

To know how many cards are needed for a 4 story house we need to use this formula: n∙(3∙n+1)/2

For example:

First story: ��⋅��+ �� �� = �� �� =�� cards

Second story: 2(3⋅2+1)/2 = 2⋅7/2 = 14/2 = 7 cards

Third story: 3(3⋅3+1)/2 = 3⋅10/2 = 30/2 = 15 cards

And now for the fourth story: 4(3⋅4+1)/2 = 4⋅13/2 = 52/2 = 26 cards

Mariela D., Gaudeamus High School, Moldova

Solution:

CAMP NOU STADIUM

What

220 meters wide and 250 meters long?

Eymen,Baruthane Secondary School, Turkey

A = L⋅l= 220m ⋅ 250m= 55000mp

Andreea / Virgil Ierunca High School Romania

is the area of the Camp Nou Stadium, which is