EIFFEL TOWER

To answer the first question, we can use the Pythagorean Theorem to find the length of the hypotenuse of the right triangle formed by the Eiffel Tower, the camera, and the ground. The hypotenuse is the line connecting the Eiffel Tower and the camera.

We have: ������ +������ =������, we get: �������� +�������� =����

Solving for CH, we find that CH = 675.6 meters.

To find the measure of the angle HAB, we can use the inverse cosine function. In this case, the side adjacent to the angle HAB is AB, and the hypotenuse is CH. Therefore, the cosine of the angle HAB is AB/CH.

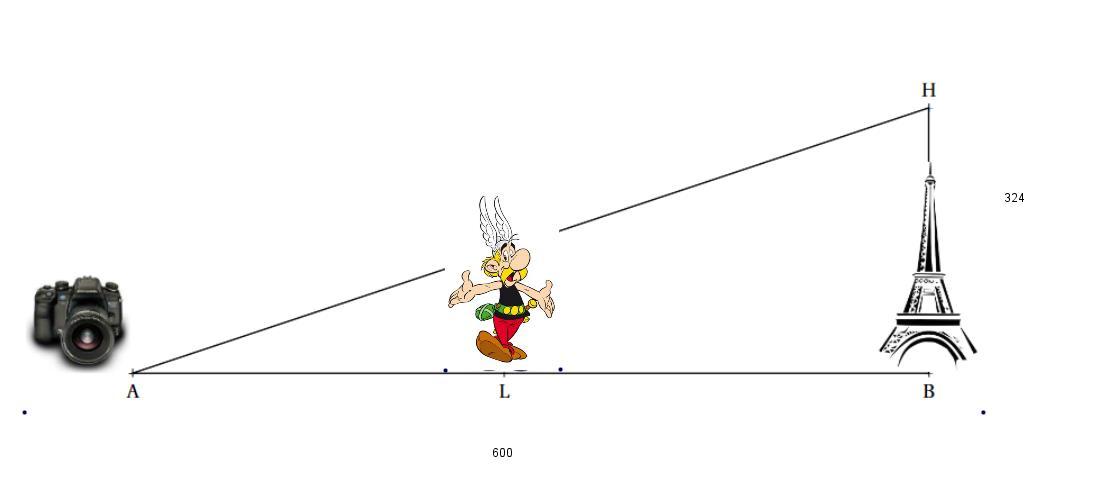
Asterix is on a visit to Paris. Today, he is at the Champs de Mars where he can see the Eiffel tower whose height BH is 324 m.

He places his camera on the ground at a distance AB = 600 m from the monument and programs it to take a photo.

1 What is the measure to the nearest degree of the angle HAB?

2 Knowing that Asterix is 1.70 m tall, at what distance AL must she stand to appear as tall as the Tower Eiffel in his photo?

Give an approximate value of the result to the nearest centimeter.

We can find the measure of the angle HAB by using the inverse cosine function on the value AB/CH: angle HAB = arccos(AB/CH) = arccos(600/675.6)

Using a calculator, we find that this is approximately 31.7 degrees.

For the second question, we can use similar triangles to find the distance AL. Let's call the distance from the camera to Asterix's feet DL. Then we have the following similar triangles: [Eiffel Tower, camera, ground] ~ [Asterix, camera, DL]

Since the ratios of corresponding sides of similar triangles are equal, we have: BH/AB = HA/AL

Substituting the values given in the problem, we get: 324/600 = HA/AL. Solving for AL, we find that AL = 288 meters.

Since 1 meter is equal to 100 centimeters, the distance AL is approximately 28800 centimeters. To the nearest centimeter, this is 28800 centimeters.

Jeanne, Brocéliande High School, France

TRIANGLES IN OP-ART

This work in GeoGebra was inspired by an op-art painting made by Max Bill.

https://www.geogebra.org/m/n6wry2jg

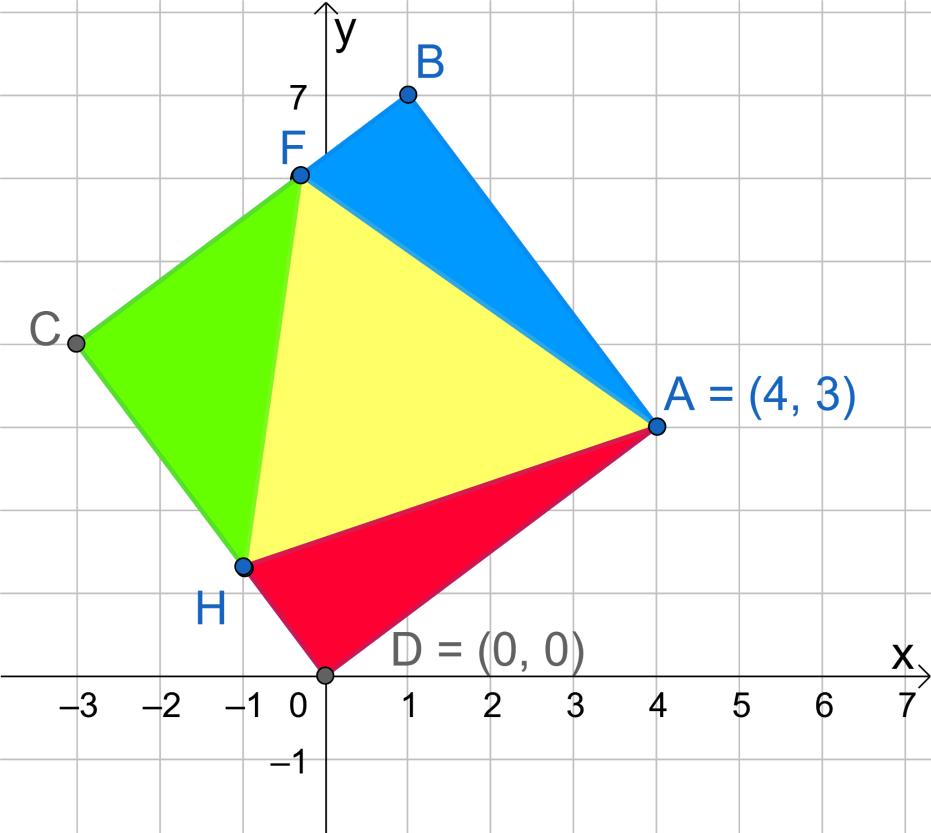
ABCD is a square with A(4; 3) and D(0; 0).

1. Find the equations of AD, AB, BC lines.

2. Calculate AD

3. If BF=DH 1.6 units, calculate the yellow area.

Luca D, Jean Monnet High School, Romania

TRIANGLES IN OP-ART

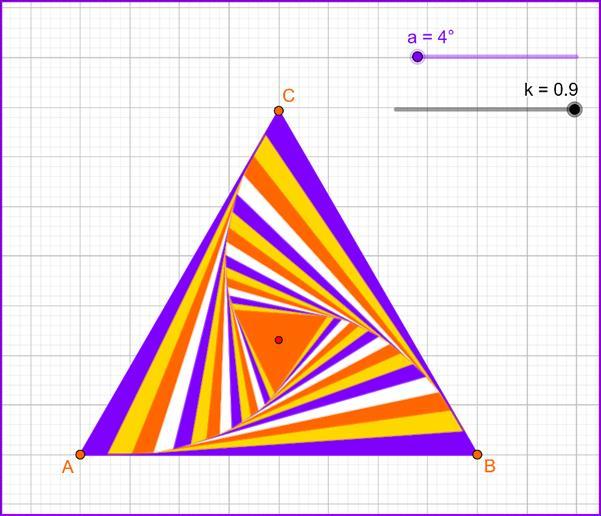
ABC is a equilateral triangle with AB=8. Each triangle, starting with the second, has a side 0.9 from the side of the previous triangle https://www.geogebra.org/m/yhey8pkq

1. Find the area of ABC triangle.

2. Calculate the sum of the perimeters for the first 5 equilateral triangles.

3. Calculate the sum of the areas for the first 5 equilateral triangles.

Florentina, Jean Monnet High School, Romania

SQUARES&TRIANGLES IN OP-ART

This drawing was made in GeoGebra, after a painting by Max Bill.

Solution:

1. DIJ=45=DCA (corresp.angles)⇒����||����

ACB=45=LKB (corresp.angles)

2. ΔAPJ is an isosceles right triangle with hypotenuse equal to half of the side of the square

ΔAPL, isosceles right triangle with hypotenuse equal to half of the side of the square

Δ KOC, isosceles right triangle with hypotenuse equal to half of the side of the square

ΔAPJ≡ΔAPLΔ ≡KOC

3. The red surface has an area equal to the area of two squares with side:

The blue surface has an area equal to the area of two squares with side

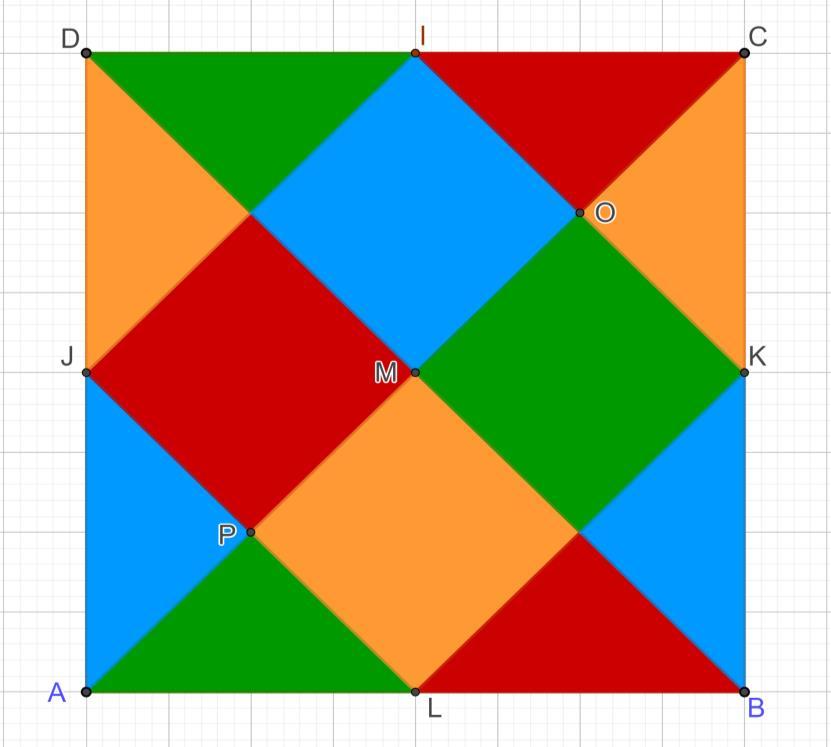
With the notations in the drawing, ABCD is a square with side 8 units and L, K, I, J are the means of sides

AB, BC, CD, respectively DA.

1. Prove that the lines aC, KL, IJ are parallel.

2. Show that ΔAPJ, ΔAPL, Δ KOC are congruent triangles.

3. Prove that the surface colored in red is equal to the surface colored in blue.

4. Calculate the ratio between the area of the orange and the area of the square

Teofil, Jean Monnet High School, Romania

4. The orange surface has an area equal to the area of two squares with side

11. Model inspired by a carpet from SINAIA - Romania

In the attached image, ABCD is a rhombus with diagonals of 10u and 8u. Each rhombus, starting with the second, has a side 0.8 of the side of the previous one.

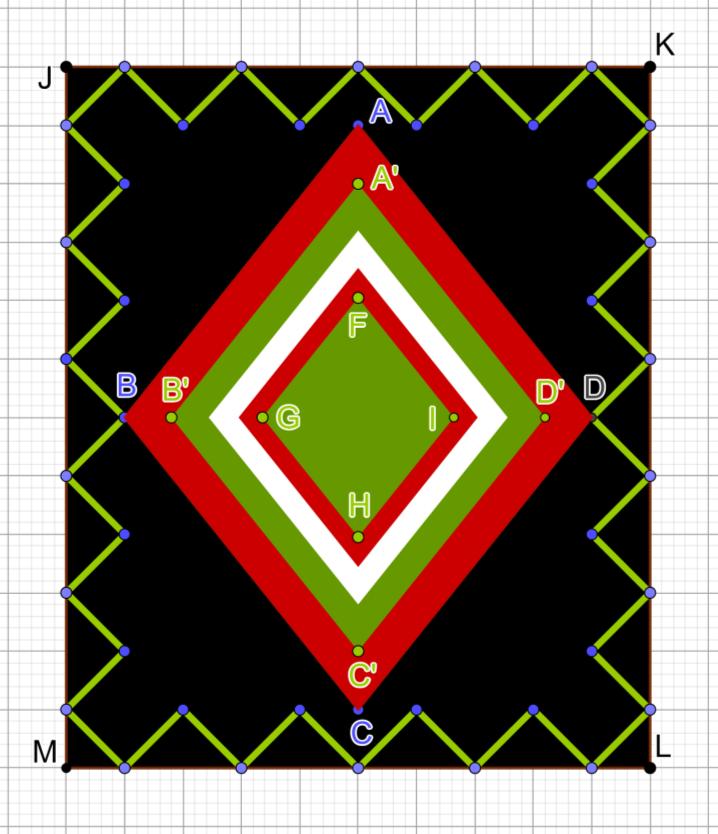
1. Calculate the area of the rhombus FGHI.

2. If the dimensions of the black rectangle are 12u and 10u, find the length of the green polygonal line, formed by segments that describe isosceles right triangles.

Carlos Sanz Ene, Jean Monnet High School, Romania