

UNIVERSIDAD TECNOLÓGICA DE PANAMÁ
FACULTAD DE INGENIERÍA DE SISTEMAS COMPUTACIONALES
DEPARTAMENTO DE COMPUTACIÓN Y SIMULACIÓN DE SISTEMAS

CARRERA LICENCIATURA EN INGENIERÍA DE SISTEMAS Y COMPUTACIÓN
Estructuras Discretas para la Computación
Proyecto #3
Título de la experiencia: Semigrupos y Grupos
Integrantes:
Bravo, Christian 8-1031-1700
Hernández, Jeshuath 20-14-8142
Iglesias, Benjamín 8-1029-142
Aguilar, Alan 8-1015-2455
Profesor:
Ing. Samuel Jiménez
Semestre I, 2025
1. Operaciones
1.1 Definición
1.2 Propiedades generales de las operaciones
1.2.1 Propiedad Cerradura
1.2.2 Asociatividad
1.2.3 Conmutatividad
1.2.4 Elemento Identidad
1.2.5 Elemento Inverso
1.2.6 Distributividad
1.2.7 Propiedad de Cancelación
1.2.8 Elemento Idempotente
1.2.9 Homomorfismos
2. Semigrupos
2.1 Definición
2.2 Teorema de los Semigrupos
2.3 Productos y Cocientes
2.4 Ejemplos Prácticos 3. Grupos
3.1 Definición
3.2 Teoremas Fundamentales
3.3 Productos y Cocientes
3.4 Ejemplos Prácticos
4. Codificación y Detección de Errores 11
4.1 Codificación de información Binaria y detección de Errores
4.2 Decodificación y Corrección de Errores.
Introducción
En este proyecto tuvimos la oportunidad de adentrarnos en uno de los temas más interesantes del curso de Estructuras Discretas: los semigrupos y grupos. Aunque al principio parecía que todo eran solo definiciones, símbolos raros y muchas propiedades, a medida que íbamos avanzando y entendiendo las ideas, nos dimos cuenta de que hay muchísima lógica detrás y que estos conceptos son más útiles de lo que imaginábamos. A lo largo de la investigación pudimosvercómoestructurascomolossemigrupos,quesolonecesitanlapropiedadasociativa, ya tienen aplicaciones reales en la informática y otras áreas. Y ni hablar de los grupos, que con sus propiedades adicionales (identidad, inversos y a veces conmutatividad) se convierten en una herramienta poderosa para resolver problemas complejos de álgebra, simétrica, criptografía, etc.
También fue interesante ver cómo todo está conectado. Desde una operación binaria simple hasta los teoremas más elaborados como el de Lagrange o el de Cayley, hay un hilo lógico que le da forma a todo. Además, aprendimos sobre codificación de información y detección de errores, temas súper importantes en la transmisión de datos y que dependen directamente de las estructuras matemáticas que estudiamos. En general, este trabajo no solo nos sirvió para aprender los conceptos, sino también para desarrollar habilidades como analizar, abstraer y aplicar teorías en situaciones concretas.
Desarrollo del Contenido
En esta revista se realizará una investigación sobre el módulo 3 de la materia Estructuras Discretas para la computación con el tema Semigrupos y Grupos. Los Puntos Investigados con su respectivo desarrollo son los siguientes:
1. Operaciones binarias sobre un conjunto
1.1 Definición
R. Una operación binaria sobre un conjunto es una regla que asigna a cada par ordenado de elementos del conjunto un único elemento también perteneciente al mismo conjunto. Es decir, si tenemos un conjunto A, una operación binaria * sobre A se define como:
∗ :A×A→A.
Esto significa que al tomar dos elementos cualquiera de A, digamos a y b el resultado de a * b también pertenece a A. Un ejemplo típico es la suma de números enteros a + b ∈ Z para cualquier a,b ∈ Z.
1.2 Propiedades generales de las operaciones binarias
R. Las operaciones binarias pueden tener ciertas propiedades que permiten clasificarlas y estudiarlas dentro de estructuras algebraicas como los grupos, semigrupos, y monoidales. A continuación se explican las más importantes:
1.2.1 Propiedad de Cerradura
R. Una operación binaria ∗ sobre un conjunto A cumple la propiedad de cerradura si para todo par de elementos a,b ∈ A, el resultado a ∗ b también pertenece a A.
Ejemplo: La suma de números naturales: si a=3 y b=5, entonces a+b=8, que también pertenece a los naturales.
1.2.2 Asociatividad
R. La asociatividad permite agrupar los elementos sin cambiar el resultado de la operación. Una operación ∗ es asociativa si para todos a, b, c ∈A, se cumple: (a ∗ b) ∗ c = a ∗ (b ∗ c)
Ejemplo: La suma de enteros es asociativa: (2 + 3) + 4 = 2 + (3 + 4)= 9.
1.2.3 Conmutatividad
R. El orden de los elementos no afecta el resultado de la operación. Una operación * es conmutativa si para todos a,b ∈A, se cumple: a * b = b * a
1.2.4 Elemento Identidad
R. Es un elemento que no cambia a los demás cuando se aplica la operación. Un elemento identidad e ∈ A es tal que para todo a ∈ A: a∗ e = e∗ a= a
1.2.5 Elemento Inverso
R. Es el elemento que al operarse con otro da como resultado la identidad.
Dado un elemento a ∈ A, existe un inverso a^−1 ∈ A tal que: a ∗ a^−1 = a^−1 ∗ a = e donde e es el elemento identidad.
1.2.6 Distributividad
R. Es la propiedad que relaciona dos operaciones distintas, permitiendo distribuir una sobre otra.
Una operación * es distributiva respecto a otra operación ∘ si: a∗ (b∘ c)=(a∗ b)∘ (a∗ c) y/o (b∘ c)∗ a=(b∗ a)∘ (c∗ a).
Ejemplo:
La multiplicación es distributiva sobre la suma: 2⋅ (3+4)=2⋅ 3+2⋅ 4=142
1.2.7 Propiedad de Cancelación
R. Permite eliminar elementos comunes de ambos lados de una ecuación si se cumple la operación.
Una operación ∗ tiene la propiedad de cancelación si: a∗ b=a∗ c⇒b=c
Ejemplo: En los números reales sin el 0, si a ⋅ b = a ⋅ c y a ≠ 0 entonces b=c.
1.2.8 Elemento idempotente
R. Es un elemento que al operarse consigo mismo da como resultado el mismo elemento.
Ejemplo: En el conjunto {0,1} con la operación lógica “AND” (∧), se cumple: 1 ∧ 1 = 1, 0 ∧ 0 = 0. Ambos son idempotentes.
1.2.9 Homomorfismo
R.Unhomomorfismoesunafunciónentredosestructurasalgebraicas(comogruposo semigrupos)queconservalaoperación.Esdecir,sif:A→Besunhomomorfismoy*es laoperaciónenA,entonces: f( a∗ b ) = f(a) ∗ f(b), para todo a,b ∈A
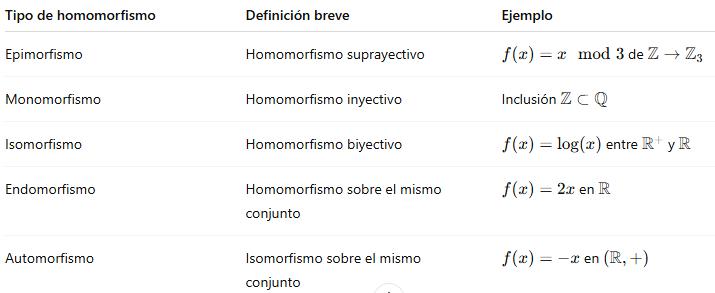
2.9.1 Epimorfismo
R. Un epimorfismo es un homomorfismo que es suprayectivo (es decir, su imagen cubre todo el conjunto de llegada).
Ejemplo: Lafunciónf:Z→Znqueasignaacadaenterosuresiduomódulon,esun epimorfismo.
1.2.9.2 Monomorfismo
R. Un monomorfismo es un homomorfismo inyectivo (no hay dos elementos distintos del dominio que se mapean al mismo del codominio).
Ejemplo: La inclusión de los enteros Z en los racionales Q es un monomorfismo.
1.2.9.3 Isomorfismo
R. Un isomorfismo es un homomorfismo biyectivo (inyectivo y suprayectivo) y tiene una función inversa que también es un homomorfismo.
Ejemplo: El grupo (R+,) y el grupo (R-,) son isomorfos mediante la función logaritmo f(x)=log(x)
1.2.9.4 Endomorfismo
R. Un endomorfismo es un homomorfismo de un conjunto hacia sí mismo.
Ejemplo: La función f(x)=2x en el conjunto R es un endomorfismo si se considera la suma como operación.
1.2.9.5 Automorfismo
R. Un automorfismo es un isomorfismo de un conjunto hacia sí mismo.
Ejemplo: La función f(x)=−x en (R,+) es un automorfismo.
1.2.9.6 Ejemplos de cada una
2. Semigrupos
2.1 Definiciones
Un semigrupo es una estructura algebraica que consiste en un conjunto no vacío S junto con una operación binaria asociativa. Formalmente, se define como:
● Conjunto subyacente:
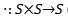
● Operación binaria: (generalmente denotada como multiplicación o simplemente ab).
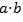
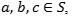
● Asociatividad: Para todo se cumple
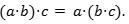
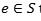
A diferencia de un grupo, un semigrupo no requiere tener elementos neutros ni inversos. Si además existe un elemento tal que para todo entonces S se denomina monoide
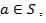
Ejemplo básico:
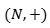
● es un semigrupo (los números naturales bajo la suma), pero no es un monoide porque no tiene elemento neutro en N el 0 no está en N según algunas definiciones).
2.2
Teorema de los semigrupos
Uno de los resultados fundamentales en la teoría de semigrupos es el Teorema de Rees, que describe la estructura de ciertos semigrupos simples. Sin embargo, un teorema más accesible y relevante es el siguiente:
Teorema (Representación de semigrupos)
Todo semigrupo S puede ser incrustado (representado de manera inyectiva) en el semigrupo de todas las transformaciones de un conjunto X. Es decir, existe un conjunto X y un homomorfismo inyectivo donde T(X) es el semigrupo de funciones bajo composición.
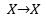
Demostración:
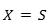
1. Sea (el mismo conjunto del semigrupo).
2. Paracada definimos comolafunciónϕ(a)(x)=a⋅x.
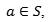
3. La asociatividad de S garantiza que ϕ sea un homomorfismo.
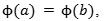
4. Si entonces (si S tiene identidad), o se usa otra técnica en caso contrario.
Este teorema muestra que los semigrupos pueden verse como sistemas de transformaciones, lo que los conecta con áreas como la teoría de grupos y la teoría de categorías.
2.3 Productos y cocientes de los semigrupos
Producto directo de semigrupos
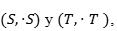
Dados dos semigrupos su producto directo es el conjunto de pares (s.t) con la operación componente a componente:
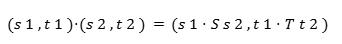
Este nuevo semigrupo hereda la asociatividad de S y T
Ejemplo:
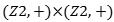
● es un semigrupo con cuatro elementos:
Semigrupos cociente
Dado un semigrupo S y una relación de congruencia ∼ (una relación de equivalencia que satisface el semigrupo cociente ��/∼ consiste en las clases de equivalencia [a]con la operación:
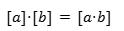
Ejemplo:
● Sea y ~ definida por �� ∼ ��. si tiene dos elementos: [0] (pares) y [1] (impares), y la suma sigue las reglas
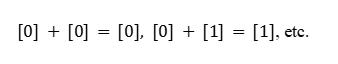
2.4 Ejemplos prácticos
1. Semigrupos en informática (Autómatas y lenguajes formales)
En teoría de autómatas, el conjunto de cadenas sobre un alfabeto con la operación de concatenación forma un semigrupo (de hecho, un monoide si se incluye la cadena vacía ).
2. Semigrupos en biología (Modelado de poblaciones)
Si S representa estados de una población y la operación es la evolución en el tiempo, la asociatividad modela que el desarrollo en etapas sucesivas no depende del paso intermedio.
3. Semigrupos en economía (Procesos de producción)
Si S Son recursos y la operación es su combinación para producir nuevos bienes, la estructura de semigrupo captura la idea de que el orden de combinación no afecta el resultado final.
4. Semigrupos de matrices
El conjunto de matrices bajo la multiplicación forma un semigrupo (y un monoide si se incluye la matriz identidad).
3. Grupos
3.1 Definiciones
La teoría de grupos es una rama fundamental del álgebra abstracta que estudia estructuras donde se pueden definir operaciones internas con propiedades bien determinadas. Un grupo se define formalmente como un par ordenado (G,∗ )(G, \ast), donde GG es un conjunto no vacío y ∗ \ast una operación binaria que satisface las siguientes propiedades:
1. Cerradura: Para todo a,b ∈ G, el resultado de a∗ b ∈ G.
2. Asociatividad: Para todo a,b,c ∈ G, se cumple (a∗ b)∗ c=a∗ (b∗ c).
3. Elemento identidad: Existe un elemento e ∈ G e tal que, para todo a ∈ G, se cumple a∗ e=e∗ a=a.
4. Elemento inverso: Para cada a ∈ G, existe un elemento ∈ G tal que
Si se cumple que la operación es conmutativa, a∗ b=b∗ a para todos los elementos del grupo, se trata de un grupo conmutativo o abeliano, en honor a Niels Henrik Abel, uno de los pioneros del estudio de estas estructuras.
Los grupos aparecen de forma natural en muchas áreas del conocimiento, desde la física teórica (simetrías y conservación de cantidades) hasta la informática, la criptografía, y la teoría de autómatas y lenguajes formales.
3.2 Teorema de los grupos
Uno de los pilares de la teoría de grupos es el Teorema de Lagrange, que se enuncia así:
- Si G es un grupo finito y H es un subgrupo de G, entonces el orden de H (número de elementos) divide exactamente al orden de G: >
Este resultado es crucial para clasificar subgrupos y analizar la divisibilidad estructural. Otros teoremas clave incluyen:
● Teorema del subgrupo normal más pequeño que contiene un subconjunto: Nos permite construir subgrupos normales generados por subconjuntos dados.
● Teoremas de isomorfismo: Conjunto de tres teoremas que describen cómo ciertas construcciones de grupos cocientes y morfismos se relacionan entre sí.
● Teorema de Cayley: Todo grupo es isomorfo a un subgrupo del grupo simétrico Sn, es decir, todo grupo puede representarse por permutaciones.
3.3 Productos y cocientes de los grupos
Dado dos grupos (G,∗ ) y (H, ), se puede construir el producto directo G×H definido como:
● Elementos: Pares (g,h) con g ∈ G y h ∈ H.
● Operación:
Este producto es un grupo cuyo orden es ∣ G∣⋅∣
si ambos grupos son finitos. Se usa para construir nuevos grupos a partir de otros conocidos.
Cociente de Grupos
Sea N un subgrupo normal de G. El grupo cociente G/N está formado por las clases laterales aN={a∗ n:n ∈ N}. La operación está bien definida y hereda la estructura de grupo de G. Este tipo de construcción es fundamental en la simplificación y análisis de grupos más complejos.
3.4 Ejemplos prácticos
Grupo (Z,+): El conjunto de enteros con la suma es un grupo abeliano. El cero actúa como identidad, y cada elemento aa tiene un inverso -a.
Grupo de simetrías de un triángulo equilátero : Tiene 6 elementos: 3 rotaciones y 3 reflexiones. Es un grupo no abeliano, útil en geometría y teoría de grupos de simetría.
Grupo GL(n,R): Conjunto de todas las matrices invertibles n×n con coeficientes reales bajo la multiplicación de matrices. Es no abeliano y relevante en álgebra lineal y física.
Grupo simétrico Sn: Conjunto de todas las permutaciones de un conjunto con n elementos. Tiene n! elementos. Si n > 3, ya no es abeliano. Es fundamental para entender la estructura de todos los grupos finitos.
4. Codificación de información binaria y detección de errores
1. Codificación de información binaria
● Bits Y código Binarios:
● Las cadenas de bits se organizan en palabras (Codwords), que pertenecen a códigos diseñados para maximizar la distancia de haming entre ellas, reduciendo la probabilidad de error.
● Los códigos lineales binarios (n, k, d) permiten definir un espacio vectorial, facilitando la generación y decodificación.
2. Detección de errores
● Paridad (Simple y bidimensional)
● Añade un bit de paridad par o impar para detectar errores de un solo bit
● En la paridad bidimensional, se utilizan filas y columnas, detectando y a veces corrigiendo errores de bits únicos
● Checksum: se suman segmentos de bits en complemento a uno; si el resultado no es cero, hay error.
● Cyclic Redundancy Check: Se realiza una división polinómica y se añade el residuo. Detecta eficazmente errores de ráfagas de bits.
3. Corrección De errores
● Códigos de Hamming: Permiten corregir errores simples y detectar dobles errores. Inventados por Richard hamming en 1950
● Errores en ráfagas: Muy usados en CD, DVDs, QR, Comunicaciones espaciales y 5G
● LDPC: Matrices dispersas ideales para decodificación iterativa
● Códigos convolucionales para la comunicación continua (módems, TV digital)
● Técnicas avanzadas como list decoding mejoran la corrección de errores en códigos como reed-muller y reed-solomon
4 Decodificación y corrección de errores
● Corrección por detección y solicitud retransmisión (ARQ) vs Forward Error Correction (FEC): FEC permite corregir sin retransmitir, usando redundancia programada
● Elradiodecorrecciónestárelacionadoconladistanciamínimade:uncódigo corrigehasta⌊(d–1)/2⌋errores
● Decodificación exige técnicas eficientes: desde búsqueda sencilla hasta algoritmos polinomiales (Viterbi, belief propagation) y aprendizaje automático
Conclusión
Después de realizar este proyecto, nos queda claro que los grupos y semigrupos no son sólo conceptos abstractos que se ven en clase por cumplir. Son parte de un lenguaje matemático que permite entender, modelar y resolver problemas reales en muchas disciplinas, especialmente en ciencias de la computación. Muchas veces en la universidad uno se pregunta ¿para qué me va a servir esto en la vida real? y, en este caso, la respuesta es bastante directa. Estas estructuras están presentes en cosas tan comunes como los algoritmos de encriptación, la corrección de errores en redes de comunicación, y hasta en videojuegos o aplicaciones gráficas que usamos todos los días.
Además, este proyecto fue una buena manera de trabajar en equipo, repartirnos tareas, investigar fuentes confiables y discutir los conceptos para que todos los entendiéramos bien. Como grupo, a varios integrantes del grupo nos ayudó a perderle un poco el miedo al álgebra abstracta, porque vimos que con ejemplos claros y buena explicación, todo tiene sentido. Nos llevamos no solo conocimiento, sino también la experiencia de cómo abordar un tema matemático complejo y volverlo comprensible entre todos. Sin duda, fue un reto, pero también una experiencia valiosa para nuestra formación como futuros ingenieros.
Bibliografía
1.1 Gallian, J. A. (2016). Contemporary Abstract Algebra (9th ed.). Cengage Learning.
https://es.wikipedia.org/wiki/Operación_binaria
1.2.9 Wikipedia. (s.f.). Homomorfismo. Recuperado el 21 de junio de 2025, de https://es.wikipedia.org/wiki/Homomorfismo
1.2 a 1.2.5 Wikipedia. (s.f.). Operación binaria. Recuperado el 21 de junio de 2025, de https://es.wikipedia.org/wiki/Operación_binaria
1.1 a 1.2.9 Khan Academy. (s.f.). Introduction to group theory Recuperado de https://www.khanacademy.org/math/linear-algebra/alternate-bases/grouptheory/v/introduction-to-group-theory
3
D, S. (2024, 19 mayo). Teoría de grupos: propiedades fundamentales y aplicaciones claves. Club de los Teoremas https://www.teoremas.club/teoria-de-grupos-propiedades/
colaboradores de Wikipedia. (2025, 11 marzo). Teoría de grupos.
Wikipedia, la Enciclopedia Libre
https://es.wikipedia.org/wiki/Teor%C3%ADa_de_grupos
colaboradores de Wikipedia. (2025b, marzo 20). Teoremas de isomorfismo
Wikipedia, la Enciclopedia Libre.
https://es.wikipedia.org/wiki/Teoremas_de_isomorfismo
D, S. (2023, 6 octubre). Teorema de Cauchy para Grupos. Club de los Teoremas.
https://www.teoremas.club/teorema-de-cauchy-para-grupos/
Teorema de Lagrange (teoría de grupos) Academia Lab. (s. f.). https://academialab.com/enciclopedia/teorema-de-lagrange-teoria-de-grupos/
Error Correction Zoo. (s.f.). Bits into bits https://errorcorrectionzoo.org/c/bits_into_bits
1. G2. (2023). What is error detection? https://www.g2.com/articles/error-detection
2. Error Correction Zoo. (s.f.). Binary linear codes. https://errorcorrectionzoo.org/list/binary_linear
3. GeeksforGeeks. (2022, October 17). Error detection in computer networks https://www.geeksforgeeks.org/computer-networks/error-detection-in-computer-networks/
4. Wikipedia contributors. (2024, June 1). Error correction code. In Wikipedia. https://en.wikipedia.org/wiki/Error_correction_code
