HOW CAN I...?
Complete the square for the following equation
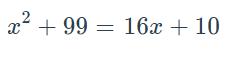
Let’s write the expression in standard form
− 2 16x +99−10 = 0
ax
x
x − 2 16x +89 = 0
+ 2 bx + c 2 b = 2 −16= −8 ( )2 b 2 = (−8)2= 64
x − 2 16x +89 = 0 We are going to add and subtract ( )2 b 2 → 64 x − 2 16x +64−64+89 = 0 Grouping (x − 2 16x +64)−64+89 = 0 (x−)(x−) +25 (x −8)(x −8) +25= 0 (x −8) = 2 −25
Same idea: write in standard form
−6x + 2 64x +8x −222 = 0
−6x + 2 72x −222 = 0
Divide by -6 to have coefficient 1
−6x + 2 72x −222 = 0
−6 −6 −6 −6 x − 2 12x +37 = 0
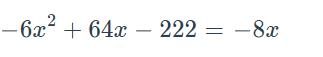
Complete the square for the following expression
Now the same process
( )2 b 2 = ( ) 2 −12 2
(−6) = 2 36 add and subtract 36
x − 2 12x +36−36+37 = 0
(x − 2 12x +36)+1 = 0
(x−)(x−) = −1
(x −6)(x −6) = −1
(x −6) = 2 −1
