Year10
GeometryandProofs TestQuestions
Level1
Copyright©2024MathspacePtyLtd
Allrightsreserved.
Thisdocument,includingbutnotlimitedtoalltests,questions,answers,andanyaccompanying materials,isprotectedbycopyrightlawandisprovidedexclusivelyfortheuseofteachingstaff. Thecontenthereinisintendedtoassessspecificcurriculumoutcomesasoutlinedinthe MathematicsK–10Syllabus(2023)andisalignedwiththesubtopicscoveredwithinthe designatedMathspacetextbook.
PermittedUse:
-ThismaterialistobeusedsolelybytheteachingstaffofaMathspacecustomerschoolforthe purposeofassessingstudentswhoareofficiallyenrolledandhaveprocuredthenecessary textbook.
-Teachersareauthorisedtoedit,copy,andadjustthetestquestionsforthesolepurposeof tailoringtheassessmenttotheirstudents'needs.Allmodificationsmustretaintheoriginalpurpose ofassessingcurriculum-specificoutcomes.
-SharingofthismaterialisrestrictedtoteachingstaffwithinaMathspacecustomerschool.Itmay not,underanycircumstances,bedisclosedordistributedtostudentsoranythirdpartiesoutside theteachingstaff.
ProhibitedUse:
-Reproductionofthismaterial,inpartorwhole,foranypurposesotherthanthoseexplicitly permittedhereinisstrictlyprohibited.
-DistributionofthismaterialtostudentsorindividualsnotemployedbyaMathspacecustomer schoolasteachingstaffisforbidden.
-Useofthismaterialforanycommercialpurposes,orinanysettingoutsideofaMathspace customerschool,isnotallowed.
SpecialNotes:
-Eachtestcontainsatablethatidentifiesthecurriculumoutcomesitaddressesandreferences therelevantsubtopicfromthetextbook.Thisensuresalignmentwiththeeducationalgoalsand facilitateseaseofuseforteachers.
-Fullyworkedsolutionsandmarkingrubricsareincludedtoaidintheaccurateassessmentof studentperformance.
-Atableisprovidedattheendofeachsetofworkedsolutions,indicatingtheoverlapping questionsamongtestsofvaryingdifficultylevels.Thisisintendedtoassistinscalingand equitablyassessingstudentsundertakingdifferentlevelsofdifficulty.
Byusingthismaterial,youagreetoadheretothetermsoutlinedabove.Violationoftheseterms mayresultindisciplinaryactionandcouldleadtolegalproceedings.
Foranyinquiriesorfurtherclarificationonpermitteduse,pleasecontactMathspaceat info@mathspace.com.au
MathspaceYear102024NSWCurriculum
Chapter14:GeometricProofs
Test1 Name:
Remembertoshowallyourworking!
1 Core Foreachofthebiconditionalstatements,explainwhethertheyaretrueorfalse.Iffalse, justifyyouranswerwithacounterexample.
a.Anumberisoddifandonlyifitisnotamultipleoftwo.
b.Aquadrilateralisarectangleifandonlyifithastwopairsofparallelsides.
c.Anglesarecomplementaryifandonlyiftheyareadjacent.
d.Anumberisaperfectsquareifandonlyifitssquarerootisawholenumber.
e.Atriangleisarighttriangleifandonlyifthesumofthesquaresofthetwoshorter sidesisequaltothesquareofthelongestside.
2 Core Completetheproofforthetheorem:
Usingthediagram:
a.Determineifthereisenough informationtojustifytheconclusionthat
Inthediagrambelow,isastraightline.Whatadditionalinformationisneededtoprove ���� andarecongruentby:∆������∆������ a.Rightangle-Hypotenuse-Side congruence? b.Angle-Side-Anglecongruence?
Usingthediagram:
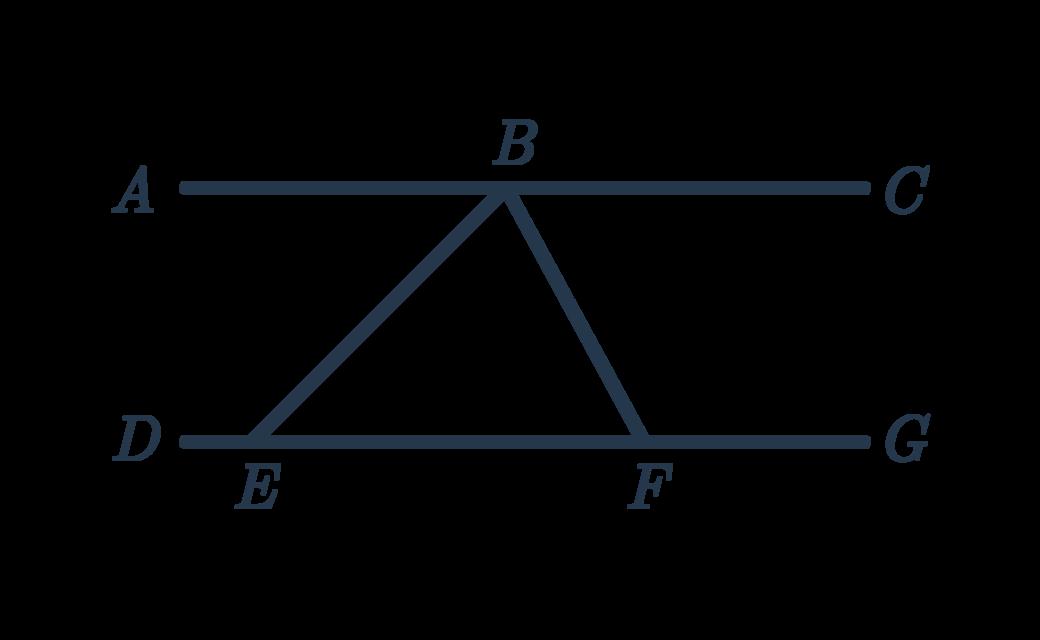
Quadrilateralhasand.Cisthepointatwhichthediagonals ������������||��������||���� ���� andintersect. ����
a.Whattypeofquadrilateralis? ��������
b.Ifcm,findthelengthof. ���� =10 ����
c.If,find: ∠������ =112°
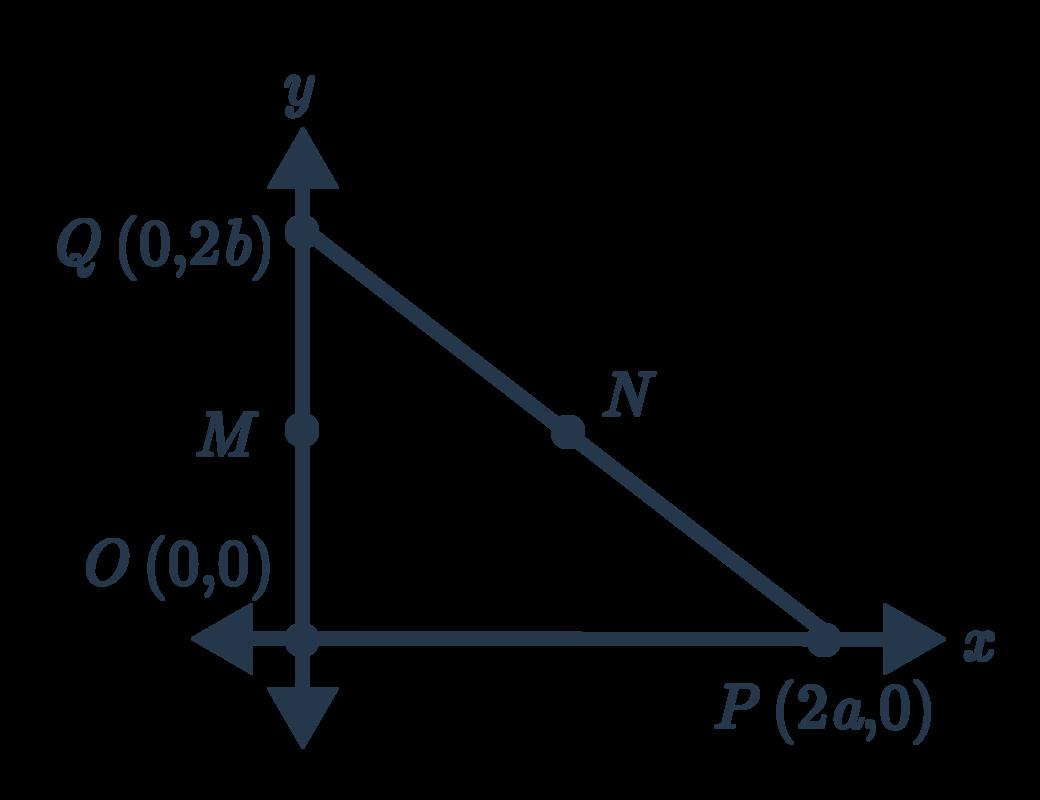
ThediagrambelowshowsarighttriangleonaCartesianplane.Pointisthemidpointof �� andpointisthemidpointof. ����������
a.Findtheco-ordinatesofand. ����
TotalMarks=/70 Copyright©2024MathspacePtyLtd
QuestionSubtopicOutcome
114.01MA5-GEO-P-01.5
214.01MA5-GEO-P-01.5
314.02MA5-GEO-P-02.1
414.02MA5-GEO-P-02.1
514.03MA5-GEO-P-02.1
614.03MA5-GEO-P-02.1
714.04MA5-GEO-P-02.2
814.04MA5-GEO-P-02.2
914.05MA5-CIR-P-01.1
1014.05MA5-CIR-P-01.1
1114.04MA5-GEO-P-02.2
1214.06MA5-CIR-P-01.1
1314.05MA5-CIR-P-01.1
1414.07MA5-CIR-P-01.2
MA5-GEO-P-01.5
ApplylogicalreasoningtonumericalproblemsinvolvingplaneshapesContributesto: MA5-GEO-P-01establishesconditionsforcongruenttrianglesandsimilartrianglesandsolves problemsrelatingtopropertiesofsimilarfiguresandplaneshapes(Path:Ext)
MA5-GEO-P-02.1
Copyright©2024MathspacePtyLtd
ConstructformalproofsinvolvingcongruentandsimilartrianglesContributesto:MA5-GEO-P-02 constructsproofsinvolvingcongruenttrianglesandsimilartrianglesandprovespropertiesof planeshapes(Path:Ext)
MA5-GEO-P-02.2
ApplylogicalreasoningtoproofsinvolvingplaneshapesContributesto:MA5-GEO-P-02 constructsproofsinvolvingcongruenttrianglesandsimilartrianglesandprovespropertiesof planeshapes(Path:Ext)
MA5-CIR-P-01.1
ProveandapplyangleandchordpropertiesofcirclesContributesto:MA5-CIR-P-01applies deductivereasoningtoprovecircletheoremsandsolverelatedproblems(Path:Ext)
MA5-CIR-P-01.1
ProveandapplyangleandchordpropertiesofcirclesContributesto:MA5-CIR-P-01applies deductivereasoningtoprovecircletheoremsandsolverelatedproblems(Path:Ext)
MA5-CIR-P-01.2
ProveandapplytangentandsecantpropertiesofcirclesContributesto:MA5-CIR-P-01applies deductivereasoningtoprovecircletheoremsandsolverelatedproblems(Path:Ext)
Copyright©2024MathspacePtyLtd
GeometryandProofs
WorkedSolutions
Level1
Copyright©2024MathspacePtyLtd
Allrightsreserved.
Thisdocument,includingbutnotlimitedtoalltests,questions,answers,andanyaccompanying materials,isprotectedbycopyrightlawandisprovidedexclusivelyfortheuseofteachingstaff.The contenthereinisintendedtoassessspecificcurriculumoutcomesasoutlinedintheAustralian Curriculumv9andisalignedwiththesubtopicscoveredwithinthedesignatedMathspacetextbook.
PermittedUse:
-ThismaterialistobeusedsolelybytheteachingstaffofaMathspacecustomerschoolforthepurpose ofassessingstudentswhoareofficiallyenrolledandhaveprocuredthenecessarytextbook.
-Teachersareauthorizedtoedit,copy,andadjustthetestquestionsforthesolepurposeoftailoringthe assessmenttotheirstudents'needs.Allmodificationsmustretaintheoriginalpurposeofassessing curriculum-specificoutcomes.
-SharingofthismaterialisrestrictedtoteachingstaffwithinaMathspacecustomerschool.Itmaynot, underanycircumstances,bedisclosedordistributedtostudentsoranythirdpartiesoutsidethe teachingstaff.
ProhibitedUse:
-Reproductionofthismaterial,inpartorwhole,foranypurposesotherthanthoseexplicitlypermitted hereinisstrictlyprohibited.
-DistributionofthismaterialtostudentsorindividualsnotemployedbyaMathspacecustomerschool asteachingstaffisforbidden.
-Useofthismaterialforanycommercialpurposes,orinanysettingoutsideofaMathspacecustomer school,isnotallowed.
SpecialNotes:
-Eachtestcontainsatablethatidentifiesthecurriculumoutcomesitaddressesandreferencesthe relevantsubtopicfromthetextbook.Thisensuresalignmentwiththeeducationalgoalsandfacilitates easeofuseforteachers.
-Fullyworkedsolutionsandmarkingrubricsareincludedtoaidintheaccurateassessmentofstudent performance.
-Atableisprovidedattheendofeachsetofworkedsolutions,indicatingtheoverlappingquestions amongtestsofvaryingdifficultylevels.Thisisintendedtoassistinscalingandequitablyassessing studentsundertakingdifferentlevelsofdifficulty.
Byusingthismaterial,youagreetoadheretothetermsoutlinedabove.Violationofthesetermsmay resultindisciplinaryactionandcouldleadtolegalproceedings.
Foranyinquiriesorfurtherclarificationonpermitteduse,pleasecontactMathspaceat info@mathspace.com.au
MathspaceYear102024NSWCurriculum
Chapter14:GeometricProofs
Test1WorkedSolutions
1 a.True (1mark)
b.False (1mark)
Aparallelogramhastwopairsofparallelsidesbutis notarectangle. (1mark)
c.False (1mark)
Inthediagramsbelow(nottoscale):
● isadjacenttobuttheyarenot∠������∠������ complementary
● iscomplementarytobuttheyarenot∠������∠������ adjacent
(1markforasinglecounterexample)
d.True (1mark)
e.True (1mark)
2 (Given) ∠�� = ∠�� (Complementaryangles)
Statethatitistrue.
Statethatitisfalse. Giveavalidcounterexample.
Statethatitisfalse. Giveavalidcounterexample.
Statethatitistrue.
Statethatitistrue.
=90°
=90° (Substitute)
(Collectliketerms)
=90° (Dividebothsidesby )
=45°
=45°2 (Substitute)
=45° (0.5markforeachcompletedblank) Copyright©2024MathspacePtyLtd
a.(Given) ����||���� (Given) (0.5mark)
∠������ =127° (Co-interiorangles)
∠������ + ∠������ =180° (1mark) (Substitute)
∠������ +127°=180° ∠������ =127° (1mark)
(Subtractfrombothsides)
∠������ =53°127° (0.5mark)
Statetherelevantgiveninformation.
Useparallellinesrelationshipstomake linksbetweenknownandunknown angles.
Useknownangle(s)towriteanequation whichcanbesolvedfor. ∠������ Maketheconclusion.
b.(Given)
∠������ =62°
∠������ + ∠������ + ∠������ =180° (Supplementaryangles) (1mark)
53°+ ∠������ +62°=180° (Substituteand) ∠������ =53° ∠������ =62° (1mark) (Evaluatethesum)
∠������ +115°=180° (0.5mark) (Subtractfrombothsides)
∠������ =65°115° (0.5mark)
4 a. Yes (1mark)
Statetherelevantgiveninformation.
Useanglerelationshipstomakelinks betweenknownandunknownangles.
Useknownangle(s)tofind, ∠������ showingworking.
Maketheconclusion.
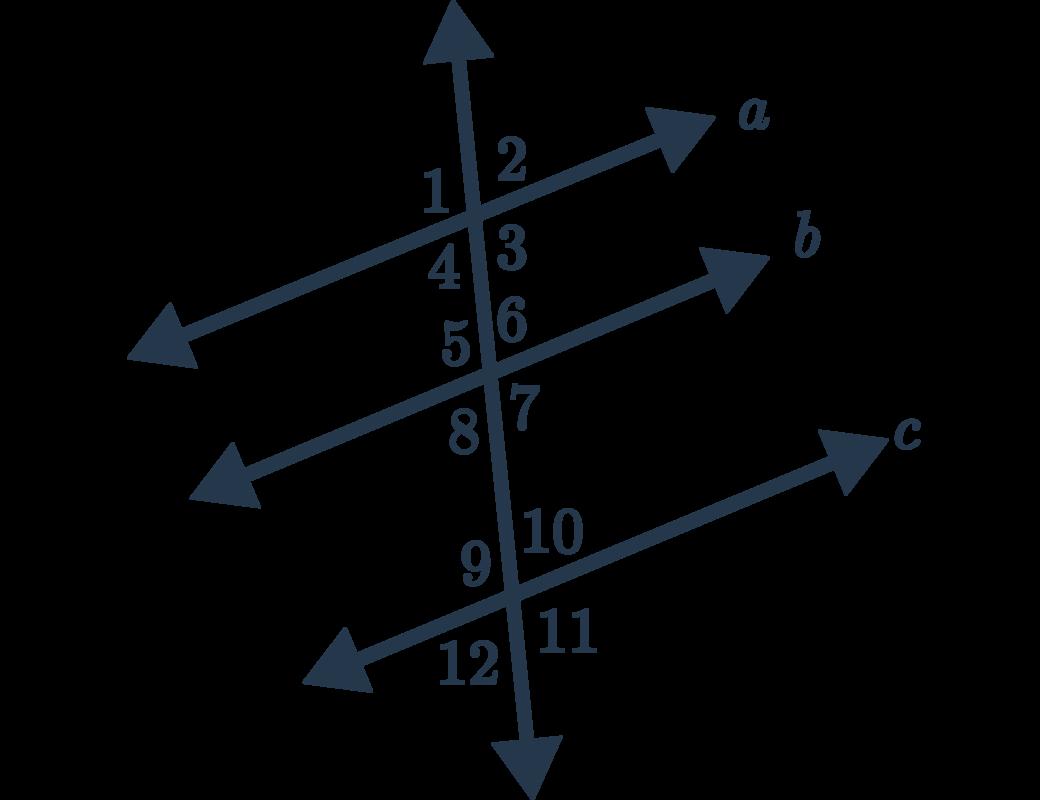
Byoppositeangles ∠2= ∠4. ∠1= ∠5 meansthat(correspondingangles). ��||�� Giventhenand ��||����||��∠4= ∠12 (correspondingangles).Bysubstitution ∠2= ∠12
b.(Given) ��||�� (Given) (0.5mark)
∠3= ∠11 (Correspondingangles) (1mark)
7= ∠11 (Substitute) (1mark)
3= ∠7 ∠7= ∠11 (Correspondingangles) (0.5mark)
5 a. (1mark) ����
(1mark)
Statetherelevantgiveninformation. Useparallellinesrelationshipsandgiven informationtomakelinksbetweenangles. Maketheconclusion.
Fromthediagram ∠������ = ∠������ =90° (R)andiscommon(S),sotosatisfy ���� theRHStestthehypotenusesmustbeof equallength.
Fromthediagram ∠������ = ∠������ =90° (A)andiscommon(S),sotosatisfy ���� theASAtesttheanglesontheotherside ofthecommonsidemustbeequal.
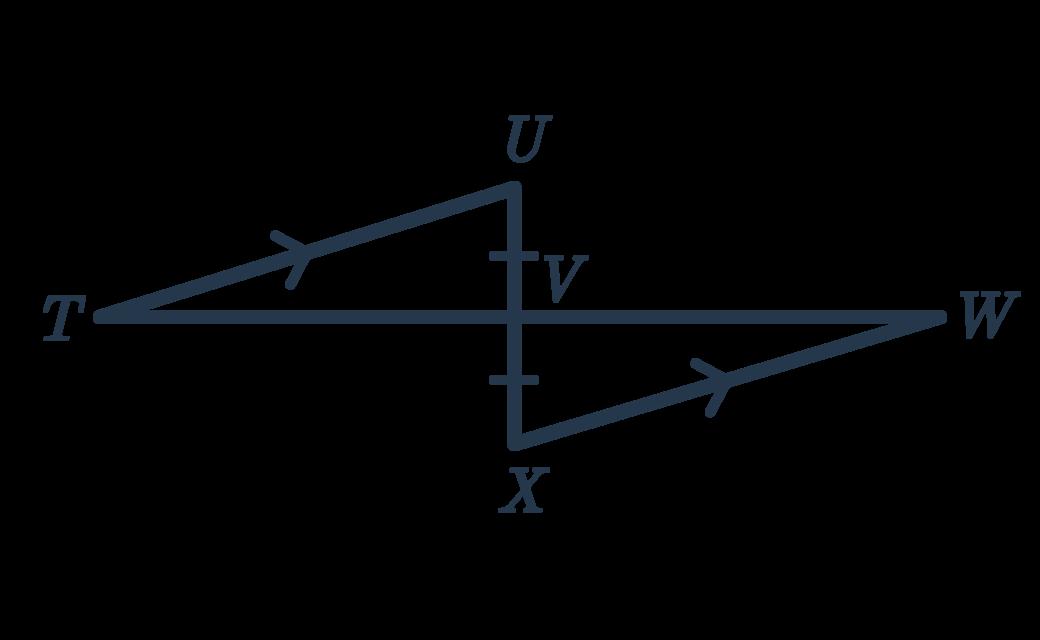
6 (Given) ���� =
(Given) (1mark) ����
(Verticallyoppositeangles)
(1mark) (Alternateangles) (1mark)
Statetherelevantgiveninformation. Useanglerelationshipsandparallellines relationshipstomakelinksbetween angles.
Alternatively,(Alternateangles) ∠������ = ∠������ (AAS) (1mark) ∴∆������≡∆������
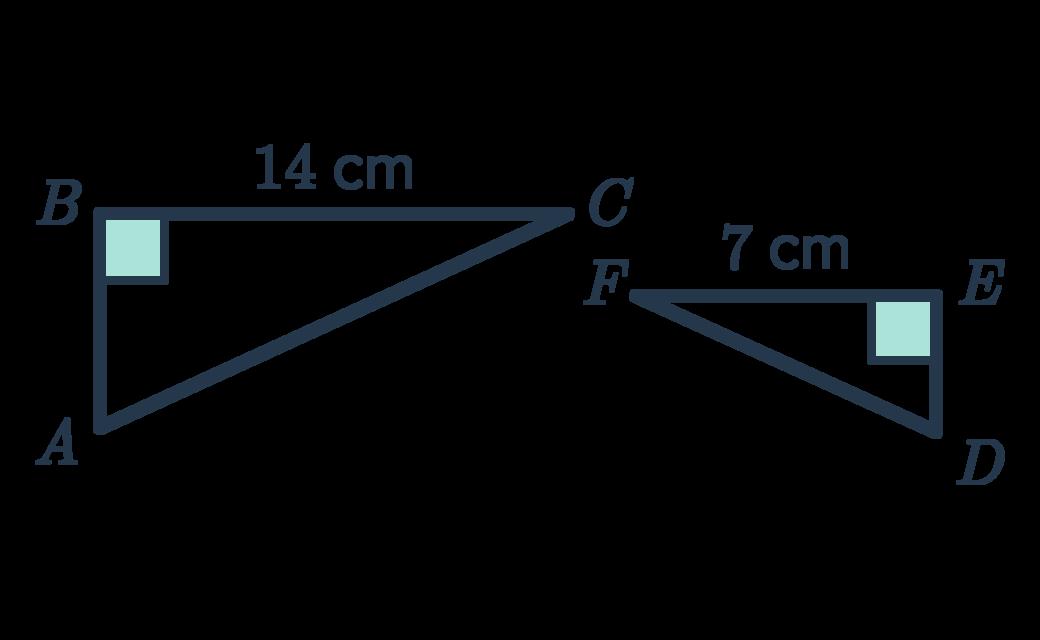
7 a.Thereisinformationgivenforonlyonepairof correspondingsidesandonepairofangles. (1mark)
Eachsimilaritytestrequiresinformationaboutthree pairsofsidesorangles. (1mark)
b.(RHS) ���� ���� =2 (SAS) ���� ���� =2 (AAA) ∠������ = ∠������ (AAA) ∠������ = ∠������ (1markeachforanythreeoftheabove)
8 (1mark) 15 10 =1.5 (1mark)
Concludethatthetrianglesarecongruent, statingtherelevanttest.
Notethatinformationisgivenfor2pairs ofsides/anglesonly.
Notethateachtestrequiresinformation for3pairsofsides/angles.
Findtheratiooftheshortestsides
Findtheratioofthemiddlesides
75 50 =1.5
45 30 =1.5 (1mark)
SothetrianglesaresimilarbySSS. (1 mark)
9 a.Parallelogram (1mark)
b. ���� = 1 2 ���� = 1 2 10() cm (1mark) =5
c. i. (1mark) ∠������ =112° ii. ∠������ =180°112° (1mark) =68° d. ���� = ���� ���� = ����
(1markforanythreeoftheabove)
Findtheratioofthelongestsides Statethesimilaritytest.
Aquadrilateralwithbothpairsofopposite sidesareparallelisaparallelogram.
Diagonalsofaparallelogrambisecteach other
Substitutecm ���� =10
Evaluate
Oppositeanglesinaparallelogramare congruent
Co-interioranglesinaparallelogramare supplementary
Stateanytwoadjacentsidesareequal
Statethediagonalsareperpendicular Stateadiagonalbisectsoneoftheangles itpassesthrough 10
Usethemidpointformulafor ��
Simplify
c.Slopeof
(1mark)
Usethemidpointformulafor ��
Simplify
Usethedistanceformulafor ����
Substitutetheco-ordinates
Simplify
Substitutetheco-ordinatesfor ����
Simplify
Maketheconclusion,linkingtoprevious working
Usethegradientformulafor ����
Substitutetheco-ordinates
Simplify
Statetheslopeof ����
Maketheconclusion,linkingtoprevious working
ishorizontalsoalsohasaslopeof (1mark) ���� 0
Theslopesofandareequalso������������
11 (1mark)
(1mark)
(1mark)
12 (1mark) ∠������ =2(46)=92 (Angleatcentreistwiceangleatcircumference) (1mark)
2�� +92=180 (Anglesumoftriangle)
Writetheratioofonepairofknownsides
Writetheratioofanotherpairofknown sides
Statethattheincludedanglesarethe same
Writethecongruencystatementandtest
Writeanequationfortheratioofthefinal pairofsides
Substitutethevaluesofthesides
Takethereciprocalofbothsides
Multiplybothsidesby 20
Evaluatetheproduct
Subtractfrombothsides 5
Dividebothsidesby 2
Usecentreangletheorem
Identifiesisoscelestriangleanduseangle sumtoequateto180
13
2�� =98 =49 (1mark) �� Solvesforx
Gradientof: ����
(1mark)
Gradientof: ���� (1mark)
(1mark)
andareparallel (0.5mark)
Gradientof: ����
Gradientof: ���� (1mark)
andareparallel (0.5mark)
Bothpairsofoppositesidesareparallel,soisa �������� parallelogram. (0.5mark)
Writethegradientof ����
Usethegradientformulafor ����
Findthegradientof ����
Concludethatandareparallel ��������
Findthegradientof ����
Findthegradientof ����
Concludethatandareparallel ��������
Concludethatisaparallelogram ��������
= ����(����������) (0.5marks)
14 (0.5marks)
= ����(������������������������������������������������) (0.5
∠������ = ∠������ =90(��������������������������������������������������������) marks)
(0.5marks)
Usepropertiestoprovecongruenceofthe twotrianglesusingRHSmethod
=2+ �� =2+10=8
TotalMarks:70 Copyright©2024MathspacePtyLtd
Usecongruenceoftrianglestoequate correspondingsidelengthsandsolvefor x
Equatecorrespondingsidelengthsand substitutextofindFH