UNIVERSIDAD BICENTARIA DE ARAGUA
SAN CRISTOBAL - EDO TÁCHIRA
CARRERA: INGENIERIA DE SISTEMAS
CURSO: MODELAJE Y SIMULACIÓN
Construcción de Modelos de Simulación
Autor: Mariana Vivas M
Dedicamos esta revista a todos los estudiantes, profesionales y entusiastas de la ciencia de datos y la simulación, que buscan entender y construir modelos sólidos para la toma de decisiones. Su curiosidad y empeño en crear soluciones precisas y eficientes para problemas complejos nos inspiran a seguir innovando en el campo de la simulación.
Prólogo
LLa simulación de sistemas es una metodología que permite analizar y entender sistemas complejos mediante la construcción de modelos computacionales que imitan su comportamiento en condiciones controladas. Este enfoque es ampliamente utilizado en diversos campos, como la ingeniería, las finanzas y la investigación operativa, para estudiar sistemas donde la variabilidad y el comportamiento no son fácilmente predecibles mediante métodos analíticos tradicionales.
En el contexto de la simulación, los modelos de Montecarlo representan una técnica clave, ya que permiten explorar posibles escenarios mediante la generación de valores aleatorios dentro de parámetros definidos. Esto resulta especialmente útil en situaciones donde los datos varían de manera impredecible, como en el mercado financiero. Por ejemplo, una empresa que desee proyectar la rentabilidad de una inversión en un año, bajo condiciones de volatilidad del mercado, puede emplear la simulación de Montecarlo para obtener una distribución de resultados posibles. De esta manera, la empresa puede identificar patrones de riesgo y oportunidades, y utilizar estos conocimientos para tomar decisiones fundamentadas.
Esta revista digital, "Construcción de Modelos de Simulación", explora en profundidad la metodología de simulación, herramientas como Montecarlo y su implementación en hojas de cálculo, así como el análisis de variabilidad e impacto en la toma de decisiones. Invitamos al lector a sumergirse en cada artículo y sección, diseñada para ilustrar las bases, aplicaciones y alcances de la simulación en la construcción de modelos.
Introducción a la Simulación
Metodología General de la Simulación
Ejemplo de simulación de Montecarlo
Conceptualización y Definición de Problemas en Simulación
Indicadores y Parámetros en Modelos de Simulación
Impacto de la Variabilidad en la Simulación
Definiciones Clave en la Simulación
Artículos de Interés y Noticias
Conclusiones
Bibliografía
Introducción a la Simulación
La construcción de modelos de simulación es el proceso de crear representaciones matemáticas o computacionales de sistemas complejos para analizar, comprender y predecir su comportamiento en distintos escenarios sin necesidad de experimentar en el sistema real. Esta práctica es clave en áreas donde los sistemas son demasiado costosos, peligrosos, o inviables para pruebas directas, como en finanzas, ingeniería, manufactura, ciencias de la salud y logística.
¿Para qué sirve la construcción de modelos de simulación?
Sirve para: Predecir Comportamientos y Resultados: al simular diferentes escenarios, los modelos permiten prever resultados y patrones de comportamiento del sistema.
Evaluar Impacto de Variables: analizan cómo los cambios en variables específicas afectan el sistema.
Optimizar
Decisiones: permiten probar estrategias y políticas en un entorno virtual antes de implementarlas en la realidad, reduciendo el riesgo.
Capacitar y Educar: los modelos de simulación son herramientas efectivas para la enseñanza y el entrenamiento, ya que replican el comportamiento de sistemas reales.
Características de los Modelos de Simulación
Representación
Realista: los modelos buscan representar las dinámicas del sistema real, incluyendo interacciones y dependencias.
Variabilidad e Incertidumbre: incluyen variabilidad en las variables y condiciones, reflejando la incertidumbre que existe en el sistema real.
Escalabilidad: se pueden ajustar para simular desde situaciones pequeñas y simples hasta sistemas complejos.
Iteratividad: permiten realizar múltiples simulaciones o “corridas” con diferentes valores de variables para observar el rango de resultados posibles.
Estadística y Probabilidad: emplean técnicas estadísticas, como Montecarlo, para generar datos aleatorios y obtener distribuciones de posibles resultados.
Importancia de los Modelos de Simulación
La simulación es fundamental en el análisis de sistemas porque permite:
Minimizar costos y riesgos
Mejorar la toma de decisiones
Anticipar desempeño bajo distintas condiciones
Fomentar la innovación
En resumen, la construcción de modelos de simulación es una herramienta indispensable en la ciencia y la industria moderna, proporcionando una forma segura, flexible y precisa de explorar y entender los sistemas complejos que rodean nuestras decisiones y operaciones.
Metodología general de la simulación
La Metodología General de la Simulación
Es un conjunto de pasos y técnicas que guían el desarrollo y análisis de un modelo de simulación, permitiendo entender y prever el comportamiento de sistemas complejos. Esta metodología es clave para estructurar y asegurar la validez y utilidad de los modelos, y suele seguir una serie de etapas organizadas, que incluyen desde la definición del problema hasta la interpretación de resultados.
Pasos de la Metodología General de la Simulación
Definición del Problema: esta etapa es la base de la simulación. Implica identificar y formular claramente el problema o sistema que se desea estudiar
Especificación del objetivo: determinar los resultados deseados de la simulación.
Diseño del modelo: establecer un modelo conceptual.
Recolección y preparación de datos: selección de datos y fuentes relevantes.
Validación del modelo: evaluar si el modelo representa con precisión la realidad.
Implementación y ejecución: configurar y ejecutar el modelo.
Análisis de resultados y conclusiones: interpretar los datos simulados y tomar decisiones.
Importancia de la Metodología General de la Simulación
La metodología estructurada asegura que el proceso de simulación sea riguroso y replicable, y que los modelos generados sean útiles y fiables. Siguiendo estas etapas, se pueden obtener predicciones más precisas y una comprensión profunda del sistema, minimizando errores y asegurando que la simulación proporcione información relevante para la toma de decisiones.
Ejemplo de simulación tipo Montecarlo
Ejemplo de Simulación de Montecarlo en Hoja de Cálculo
La simulación Montecarlo se basa en generar múltiples escenarios de resultados aleatorios para entender las posibles variaciones. El siguiente ejemplo muestra su implementación en una hoja de cálculo para proyectar el rendimiento de una inversión a lo largo del tiempo.
Pasos de Configuración:
Identificar variables de entrada.
Definir un rango de posibles valores para cada variable.
Usar funciones de probabilidad para simular múltiples resultados.
Ejemplo de problema formulado
Problema:
Una empresa desea evaluar la rentabilidad futura de una inversión en el mercado financiero a lo largo de un período de un año, considerando la volatilidad del mercado. La rentabilidad mensual de esta inversión es incierta y varía de acuerdo con diversos factores económicos y de mercado. La empresa necesita estimar el rendimiento probable al final del año para tomar decisiones estratégicas.
Objetivo de la simulación
Estimar el rendimiento acumulado de la inversión al final de 12 meses, considerando la variabilidad mensual de las tasas de rendimiento. Utilizar la simulación de Montecarlo para modelar los posibles escenarios de rentabilidad al final del año.
Indicadores:
Rentabilidad acumulada anual: rendimiento total al final de los 12 meses.
Tasa de rentabilidad mensual: rentabilidad generada en cada mes, que variará aleatoriamente en cada simulación.
Variación total: rango de rendimientos acumulados, que permitirá observar los extremos y la variabilidad del modelo.
Datos:
Rendimiento mensual promedio esperado: 0.8%
Desviación estándar mensual: 2% (para reflejar la volatilidad).
Número de simulaciones (corridas): 10,000 simulaciones para obtener una distribución confiable de resultados.
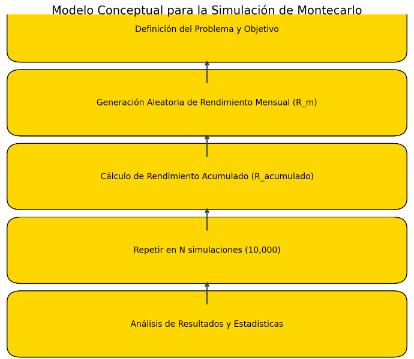
Modelo conceptual para la simulación de Montecarlo
Para visualizar cómo se construye el modelo conceptual de esta simulación, aquí está el flujo de trabajo:
Definición de Variables:
R m: Rendimiento mensual simulado.
R acumulado: Rendimiento total acumulado al final del año.
Paso 1: Generar valores aleatorios de rendimiento mensual usando una distribución normal con una media de 0.8% y desviación estándar de 2% en cada iteración.
Paso 2: Calcular el rendimiento mensual simulado (R m) durante 12 períodos (meses), acumulando el rendimiento al final de cada mes.
Paso 3: Repetir los pasos anteriores en cada simulación para 10,000 corridas, registrando el rendimiento acumulado (R acumulado) al final del año.
Paso 4: Analizar los resultados para obtener la media, mediana, desviación estándar y percentiles del rendimiento acumulado.
Implementación en Hoja de Cálculo
En una hoja de cálculo, la simulación se puede organizar de la siguiente manera:
Columna A: identificador de la simulación (1 a 10,000).
Columnas B a M: rendimiento mensual para cada mes (simulado con la función =NORMINV(RAND(), 0.008, 0.02)).
Columna N: rendimiento acumulado al final del año, calculado multiplicando los rendimientos de cada mes.
Resumen de estadísticas: calcular en la hoja de cálculo los indicadores claves: promedio de rendimiento anual, desviación estándar, mediana y percentiles.
A continuación, un diagrama que muestra visualmente este modelo conceptual para visualizar el flujo de trabajo en la simulación de Montecarlo.
A continuación, ejemplos de gráficos que ilustran la distribución y relación de los resultados de la simulación de Montecarlo:
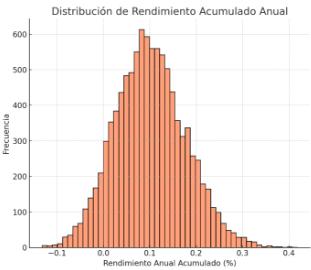
Histograma del rendimiento acumulado anual: muestra la distribución del rendimiento anual proyectado, indicando la frecuencia de ocurrencia de cada rango de rendimiento. La mayoría de los resultados se concentran alrededor del promedio, reflejando la variabilidad esperada.
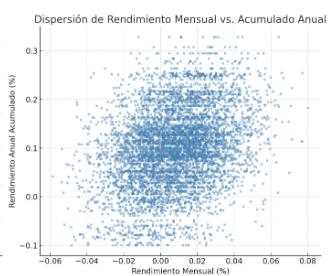
Gráfico de dispersión de rendimiento mensual vs. acumulado anual: este gráfico muestra la relación entre los rendimientos mensuales simulados y el rendimiento acumulado anual. Cada punto representa una simulación específica, permitiendo observar la variabilidad mensual y su impacto en el rendimiento acumulado.
I
Un análisis completo de los resultados nos permite ver cómo los rendimientos proyectados se distribuyen y cuál es el nivel de riesgo y oportunidad en la inversión. Los gráficos y parámetros generados de la simulación ayudan a:
Evaluar la estabilidad y viabilidad de la inversión: observar la media, mediana y los percentiles da una visión clara de la rentabilidad probable.
Tomar decisiones estratégicas basadas en riesgos: con la variabilidad observada, la empresa puede decidir si el rango de posibles rendimientos se alinea con sus objetivos y tolerancia al riesgo.
Comparar escenarios: las herramientas de simulación de Montecarlo facilitan probar diferentes valores en los parámetros de entrada, como cambiar el rendimiento mensual esperado o la desviación estándar, y observar cómo afectan la rentabilidad proyectada.
Definiciones clave en la simulaicon
Réplica
Una réplica es una repetición completa de una simulación bajo las mismas condiciones iniciales y parámetros.
La réplica permite observar la variabilidad en los resultados de una simulación bajo las mismas configuraciones y ayuda a obtener estimaciones más confiables.
Con múltiples réplicas, se puede calcular estadísticos clave (como la media o la desviación estándar) con mayor precisión, mejorando la interpretación de los resultados y garantizando que no dependan de un solo conjunto de resultados.
Corrida
Una corrida es la ejecución de una simulación para un conjunto específico de parámetros, produciendo un resultado particular.
Cada corrida representa un posible comportamiento del sistema en función de las variables aleatorias. Puede observar cómo el sistema se comporta en un escenario único.
Realizar múltiples corridas permite construir un rango de escenarios posibles, importante para entender cómo el sistema responde a diferentes configuraciones y para obtener una distribución de resultados que refleja la variabilidad real.
Estado Transitorio
Es el estado inicial en una simulación en el que el sistema no ha alcanzado todavía su comportamiento estable y puede presentar inestabilidad o variabilidad adicional.
El estado transitorio refleja el tiempo necesario para que el sistema " se acomode" y llegue a una situación de equilibrio o estado estable.
Permite identificar el momento en el que los datos obtenidos en la simulación son representativos del comportamiento normal del sistema. Ignorar el estado transitorio puede sesgar los resultados hacia valores que no reflejan la verdadera dinámica del sistema.
Estado Estable
Es la fase de la simulación en la cual el sistema ha alcanzado un comportamiento regular, y las métricas de interés son constantes o presentan variabilidad controlada.
Indica el momento en que las observaciones se estabilizan y los resultados son consistentes. Es fundamental para el análisis, ya que los resultados en el estado estable reflejan el comportamiento continuo del sistema. Los análisis y decisiones basados en la simulación suelen realizarse a partir de los datos obtenidos en el estado estable.
Condiciones Iniciales
Son los valores y configuraciones de las variables al inicio de la simulación, antes de que comience la corrida.
Las condiciones iniciales establecen el punto de partida del sistema y pueden influir en el tiempo que tarda en llegar al estado estable. Elegir condiciones iniciales adecuadas ayuda a evitar estados transitorios largos y reduce el sesgo en los resultados. Para sistemas complejos, es fundamental que las condiciones iniciales sean representativas del sistema real o que minimicen su impacto en el estado estable.
Reloj de la Simulación
Es el contador o marcador de tiempo que avanza en intervalos durante la simulación, permitiendo registrar eventos y actualizar el estado del sistema en cada paso.
Sincroniza la secuencia de eventos o el progreso en una simulación, registrando en qué momento ocurren los eventos clave.
El reloj permite analizar el sistema a lo largo del tiempo, lo cual es esencial para simulaciones dinámicas donde se estudian los cambios en el sistema en función del tiempo.
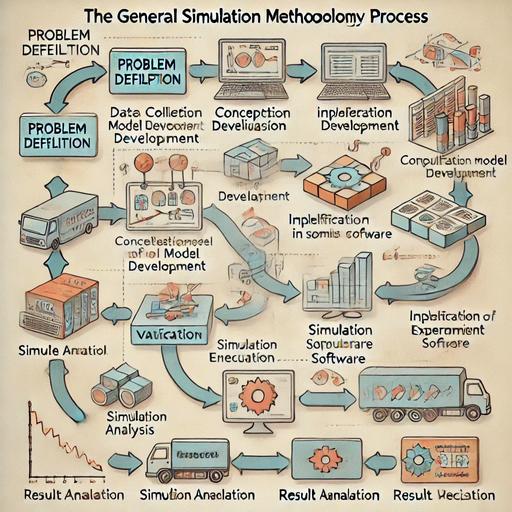
Diagrama que muestra el proceso general de la metodología de simulación, detallando la relación entre cada paso del proceso.
Espacio Publicitario
Mantente al tanto de las últimas noticias. Lee los siguientes artículos:
ModeloNacionaldeSimulación2024-2026:incorporacióndenuevasempresasyvinculación conelsectorforestal
https://diario.uach.cl/modelo-nacional-de-simulacion-2024-2026-incorporacion-de-nuevasempresas-y-vinculacion-con-el-sector-forestal/
El futuro de la ciencia de datos y el aprendizaje automático
https://www.silicon.es/el-futuro-de-la-ciencia-de-datos-y-el-aprendizaje-automatico-2484943
Conclusiones
En conclusión, la simulación de sistemas es una técnica fundamental para comprender y prever el comportamiento de sistemas complejos en un entorno controlado. Al modelar escenarios realistas y ejecutar múltiples iteraciones bajo condiciones variables, la simulación ofrece una perspectiva única sobre la manera en que diferentes factores pueden afectar un sistema. Esto es especialmente útil en áreas donde la incertidumbre y la variabilidad son altas, como en los mercados financieros, donde los modelos de simulación tipo Montecarlo permiten a las empresas evaluar el riesgo y la rentabilidad de posibles inversiones.
La metodología general de simulación sigue un proceso riguroso y estructurado, que comienza con la definición clara del problema y culmina en la interpretación de resultados. Cada paso, desde la construcción y verificación del modelo hasta la ejecución y el análisis de simulaciones, contribuye a asegurar que los resultados sean precisos y útiles para la toma de decisiones. En resumen, la simulación, y en particular los modelos de Montecarlo, proporciona un enfoque integral para analizar sistemas con alto grado de incertidumbre. Desde el análisis de rentabilidad de inversiones hasta la evaluación de procesos industriales, esta herramienta no solo permite a las organizaciones optimizar sus decisiones, sino también prepararse para múltiples escenarios, facilitando así una toma de decisiones más informada y estratégica en contextos complejos y variables.
Sancruz T. (2021). “Construcción de Modelos de Simulación”. Disponible en: https://www.studocu.com/esmx/document/instituto-tecnologico-superior-deacayucan/sistemas-operativos-2/introduccion-a-laconstruccion-de-los-modelos-de-simulacion/14795927
Urquía E. (2018). “Los Modelos de Simulación”. Disponible en:
https://repositorio.uam.es/bitstream/handle/10486/67925 6/EM 32 3.pdf
Ramos R. (2017). “Construcción de Modelos de Simulación”. Disponible en:
https://www.academia.edu/36246730/Unidad 3 Constru ccion de Modelos de Simulacion
Recursos del Aula virtual - Curso: Modelaje y SimulaciónUnidad II