Projektnr.: L-400 med udragende og asfalt
Geometri:
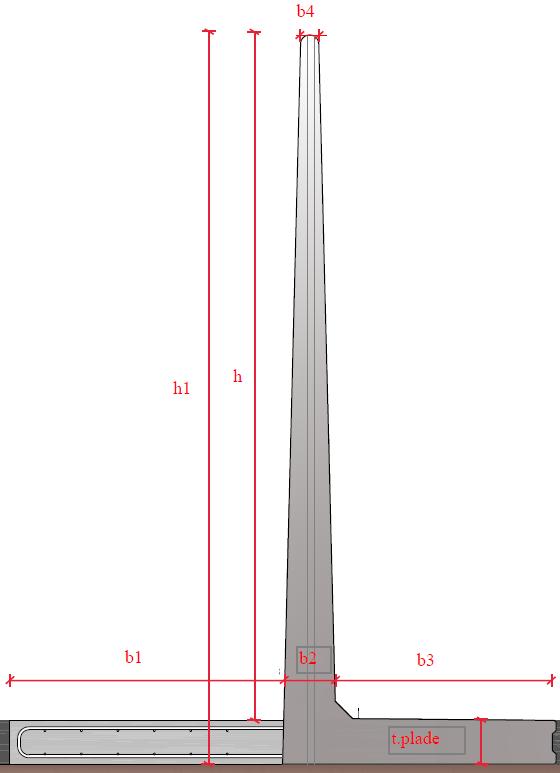
Total højde af elementh1 =4,000m
Tykkelse af vandret del af elementt.plade =0,250m
Netto højde af element: h = h1-t.pladeh =3,750m
Bredde af påstøbt venstre ende af bundpladeb1 =1,155m
Bredde af lodret del af element i bundb2 =0,288m
Bredde af højre del af bundpladeb3 =1,212m
Bredde af lodret del af L-element i topb4 =0,100m
Total bredde af element: b.tot = b1+b2+b3b.tot =2,655m
Projektnr.: L-400 med udragende og asfalt
Forudsætninger:
Element dimensioneres for ensidigt ensilagetryk.
Mht glidning regnes element fastholdt via trækforbindelse under belægning eller lignende
Iht SBI-anvisning 176 skal regnes på to tilfælde:
Tilfælde A: uvejret (dvs ikke tørret) afgrøde, der ikke komprimeres med køretøj.
Tilfælde B: forvejret (dvs tørret) afgrøde inklusive bidrag fra komprimeringskøretøj
Tilfælde hvor uvejret afgrøde komprimeres, kan antages at være dækket, når støttevæggene er dimensioneret for ovennævnte lasttilfælde A og B
Tilfælde A & B regnes for begge retninger (dvs både højre og venstre)
For tilfælde A regnes med følgende partialkoefficienter på laste:
Tilfælde A1: 1.15 på vandret last fra ensilage og 1.00 på øvrige laste
Tilfælde A2: 1.30 på al last fra ensilage og 0.85 på øvrige laste
For tilfælde B regnes med følgende partialkoefficienter på laste:
Tilfælde B1: 1.15 på vandret last fra ensilage, 1.30 på vandret last fra køretøj, 1.00 på øvrige laste
Tilfælde B2: 1.30 på al last fra ensilage & køretøj, 0.85 på øvrige laste
Som en tilnærmelse regnes lodret del af L-element at have lige (90 grader) lodret vinkel med bund
Materialeparametre:
Generelt:
Karakteristisk betontrykstyrkefck =35,0MPa
Karakteristisk armeringstrækstyrkefyk =550,0MPa
Elasticitetsmodul for armeringEs =200000MPa
Middeltrækstyrke, beton: fctm = 0.30*fck 2/3 fctm =3,2MPa
Effektivitetsfaktor for forskydning: v = 0.7-fck/200
v =0,53
Forhold mellem armering & betonen E-modul, kvasi-permanent oo =23
Partialkoefficient for armeringstrækstyrke s = 1,20
Regningsmæssig armeringstrækstyrke: fyd = fyk/ s fyd =458,3MPa
Betonbrudtøjning cu3 =0,35%
Armeringsflydetøjning: yd = fyd/Es yd =0,23%
Balanceret armeringsgrad: bal = 0.8* cu3/(cu3+yd) bal =0,483
Forhold mellem armering & betonen E-modul, kvasi-permanent oo =23
Tilladelig revnevidde(aggressiv miljø)wk.max =0,30mm
Tilladelig lodret spænding under element til =250kN/m2
Element:
Partialkoefficient for betons trykstyrke c1 = 1,40
Regningsmæssig betontrykstyrke: fcd1 = fck/ c1 fcd1 =25,0MPa
Dæklag på armeringc1 =35mm
Vandret påstøbt pladedel:
Partialkoefficient for betons trykstyrke c2 = 1,45
Regningsmæssig betontrykstyrke: fcd2 = fck/ c2 fcd2 =24,1MPa
Dæklag på armeringc2 =35mm
Projektnr.: L-400 med udragende og asfalt
Lodret last & placering af tyngdepunkter:
Lodret last:
Egenlast lodret del af L-element: gk1 = 0.5*(b2+b4)*h*25*1.0gk1 =18,2kN/m
Egenlast vandret del b1: gk2 = b1*t.plade*25*1.0gk2 =7,2kN/m
Egenlast vandret del b2+b3: gk3 = (b2+b3)*t.plade*25*1.0gk3 =9,4kN/m
Totale egenlast element: gk.ele = gk1+gk2+gk3gk.ele =34,8kN/m
Egenlast komprimeringskøretøjGt =120kN
Akselafstand på komprimeringskøretøja =3,00m
Medvirkende væglængde for optagelse af komprimeringslastb.komp =3,00m
Egenlast uvejret ensilage gu = 10,0kN/m3
Egenlast forvejret ensilage gf = 7,5kN/m3
Tyngdepunkter målt ifht nedre, venstre punkt af konstruktion:
Tyngdepunkt af gk1: tgp.gk1 = b1+0.5*b2tgp.gk1 =1,299m
Tyngdepunkt af gk2: tgp.gk2 = 0.5*b1tgp.gk2 =0,578m
Tyngdepunkt af gk3: tgp.gk3 = b1+0.5*(b2+b3)tgp.gk3 =1,905m
Tyngdepunkt af gk.ele: (gk1*tgp.gk1+gk2*tgp.gk2+gk3*tgp.gk3)/gk.ele =1,313m
Tyngdepunkter af Gt, g u & gf beregnes separat i specifikke lasttilfælde
Placering af vandrette snit i lodret elementdel:
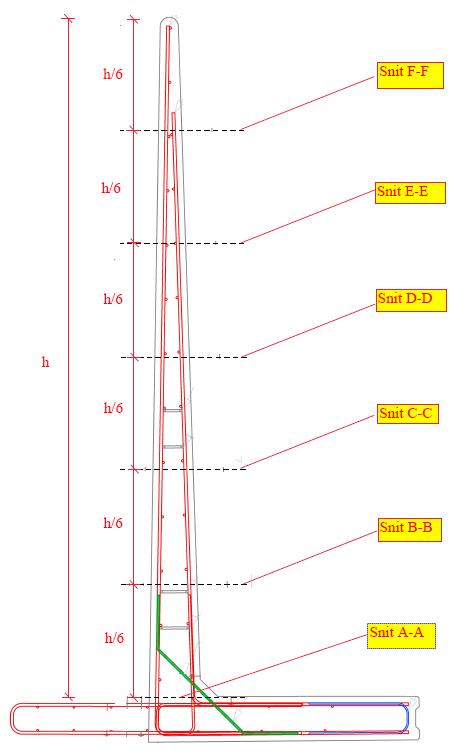
Projektnr.: L-400 med udragende og asfalt
Resultater fra beregninger på efterfølgende sider:
Generelt:
Kontrol af om element er stabilt: Element er stabilt
Maksimal lodret spænding under element:
Udnyttelsesgrad: . = max/til
Påstøbt, vandret pladedel i venstre underside af element:
Udnyttelsesgrad forskydning: .V = VSd/VRd
Udnyttelsesgrad momentoptagelse: .M = MSd/MRd
Udnyttelsesgrad revnevidde: .wk = wk/wk.max
Vandret pladedel i højre underside af element:
Udnyttelsesgrad forskydning: .V = VSd/VRd
Udnyttelsesgrad momentoptagelse: .M = MSd/MRd
Udnyttelsesgrad revnevidde: .wk = wk/wk.max
Lodret vægdel (maksimale udnyttelser for snit A-A t.om. Snit F-F):
Snit A-A:
Maksimal udnyttelsesgrad forskydning
max =248,7kN/m2
= 99% OK
.V = 38% OK
.M = 83% OK
.wk = 83% OK
.V = 62% OK
.M = 88% OK
.wk = 92% OK
.VA-A = 58% OK
Maksimal udnyttelsesgrad momentoptagelse .MA-A = 85% OK
Maksimal udnyttelsesgrad revnevidde .wkA-A = 91% OK
Snit B-B:
Maksimal udnyttelsesgrad forskydning
.VB-B = 48% OK
Maksimal udnyttelsesgrad momentoptagelse .MB-B= 85% OK
Maksimal udnyttelsesgrad revnevidde .wkB-B=
Snit C-C:
Maksimal udnyttelsesgrad forskydning
Maksimal udnyttelsesgrad momentoptagelse
Maksimal udnyttelsesgrad revnevidde
Snit D-D:
Maksimal udnyttelsesgrad forskydning
.VC-C =
.MC-C =
=
.VD-D = 30% OK
Maksimal udnyttelsesgrad momentoptagelse .MD-D= 65% OK
Maksimal udnyttelsesgrad revnevidde
Snit E-E:
Maksimal udnyttelsesgrad forskydning
.wkD-D = 79% OK
.VE-E = 26% OK
Maksimal udnyttelsesgrad momentoptagelse .ME-E= 49% OK
Maksimal udnyttelsesgrad revnevidde
Snit F-F:
Maksimal udnyttelsesgrad forskydning
.wkE-E = 68% OK
.VF-F = 18% OK
Maksimal udnyttelsesgrad momentoptagelse .MF-F= 78% OK
Maksimal udnyttelsesgrad revnevidde
.wkF-F = 27% OK
ingeniørvirksomhed.
Projektnr.: L-400 med udragende og asfalt
Dimensionering af samling mellem påstøbt, vandret pladedel & element:
Beregningsprincip:
Til optagelse af forskydning i støbeskel anvendes dén del af netarmering der er i trykzone, mens dén del af netarmering der er i trækzone anvendes til momentoptagelse
Forskydning i støbeskel:
Valgt armering på tværs af støbeskel: ø16pr.200mm
Armeringsareal på tværs af støbeskelAs =1005mm2/m
Friktionskoefficient (glat støbeskel)
Armeringsforhold: = As/(t.plade*1.0)
Bæreevne af støbeskel: Rd = **fyd
Maksimal bæreevne af støbeskel: Rd,max = 0.5* v*fcd2
Resulterende bæreevne af støbeskel: Rd = MIN (Rd & Rd,max)
= 0,50
= 0,004
Rd =0,92MPa
Rd,max =6,34MPa
Rd =0,92MPa
Maksimal forskydning i snit mellem påstøbning og elementVSd =87,7kN/m
Forskydningsbæreevne: VRd = Rd*t.pladeVRd =230,4kN/m
Udnyttelsesgrad: .V = VSd/VRd
Momentoptagelse:
.V = 38% OK
Valgt armering til optagelse af momentø16pr.200mm
Armeringsareal til optagelse af momentAs =1005mm2/m
Effektiv højde: d = t.plade-c2-0.5*ød =207mm
Armeringsgrad: = As*fyd/(1000*d*fcd2)
Hjælpefaktor: = *(1-0.5* )
= 0,092 OK
= 0,088
Maksimal moment i snit mellem påstøbning og elementMSd =75,3kNm/m
Momentbæreevne: MRd = *1000*d2*fcd2 MRd =91,0kNm/m
Udnyttelsesgrad: .M = MSd/MRd .M = 83% OK
Revnevidder:
Kvasi-permanent momentMk =55,2kNm/m
Højde af trykzone: Ac*0.5*x = *As*(d-x) hvoraf findes følgende 2.gradsligning:
500*x2+*As*x-*As*d = 0 => 500 *x2 + 23121*x -4786138= 0
Disk. d =1,01E+10 => x1 =-124& x2 =77x =77mm
Transformeret inertimoment: It = 1000*x3/3+*As*(d-x)2 It =5,43E+08mm4/m
Armeringsspænding: s = *(Mk/It)*(d-x) s = 303MPa
Effektivt trækpåvirket betonareal omkring armeringen bestemmes med den effektive højde:
hc.ef = MIN(2.5*(t.plade-d) & (t.plade-x)/3 & t.plade/2)hc.ef =58mm
Effek. trækpåvirket betonareal omk. Arm.: Ac.eff = 1000*hc.efAc.eff =57529mm2/m
Tøjningsdifferens #1: #1 = s/Es-(0.4/Es)*(Ac.eff/As+)*fctm #1 =0,100%
Tøjningsdifferens #2: #2 = 0.6* s/Es #2 =0,091%
Tøjningsdifferens: sm -cm = MAKS(#1 & #2) sm -cm =0,100%
Maksimal revneafstand: sr,max = 29*c21/3+0.17*Ac.eff*ø/Assr,max =251mm
Revnevidder: wk = sr,max*(sm -cm)wk =0,25mm
Udnyttelsesgrad: .wk = wk/wk.max .wk = 83% OK
ingeniørvirksomhed. www.vsp.dk
Projektnr.: L-400 med udragende og asfalt
Dimensionering af samling mellem vandret & lodret del af element: Samme materialeparametre og armering som i påstøbt vandret pladedel. Hermed findes følgende:
Forskydning i snit mellem lodret del & vandret del:
Hjælpefaktor k: k = 1+(200/d) 0.5, dog max 2.0 k =1,98
Armeringsforhold: = As/(d*1.0) = 0,005
Regningsmæssig bæreevne: vRd,c = (0.18/1.40)*k*(100* *fck)1/3 vRd,c =0,66MPa
Dog som minimum: vRd,c,min = (0.051/1.40)*k 1.5*fck0.5 vRd,c,min =0,60MPa
Resulterende bæreevne: vRd,c = MAX(vRd,c & vRd,c,min)vRd,c =0,66MPa
Maksimal forskydning i snit mellem lodret del & vandret delVSd =84,6kN/m
Forskydningsbæreevne: VRd = v Rd,c*dVRd =135,7kN/m
Udnyttelsesgrad: .V = VSd/VRd .V = 62% OK
Momentoptagelse i snit mellem lodret del & vandret del:
Maksimal moment i snit mellem vandret og lodret delMSd =79,9kNm/m
Momentbæreevne: MRd = MRd fra beregning af støbeskelMRd =91,0kNm/m
Udnyttelsesgrad: .M = MSd/MRd
Revnevidder:
.M = 88% OK
Generelt som for beregning af påstøbt pladedel, men med følgende ændringer:
Kvasi-permanent momentMk =58,9kNm/m
Armeringsspænding: s = *(Mk/It)*(d-x)
s = 323MPa
Tøjningsdifferens #1: #1 = s/Es-(0.4/Es)*(Ac.eff/As+)*fctm #1 =0,110%
Tøjningsdifferens #2: #2 = 0.6* s/Es #2 =0,097%
Tøjningsdifferens: sm -cm = MAKS(#1 & #2)
sm -cm =0,110%
Maksimal revneafstand: sr,max = 29*c1/3+0.17*Ac.eff*ø/Assr,max =251mm
Revnevidder: wk = sr,max*(sm -cm)wk =0,28mm
Udnyttelsesgrad: .wk = wk/wk.max
.wk = 92% OK
Projektnr.: L-400 med udragende og asfalt
Dimensionering af lodret del af element:
Beregningsprincip:
Der regnes på en række vandrette snit i den lodrette del af elementet: Tykkelsesgradient:
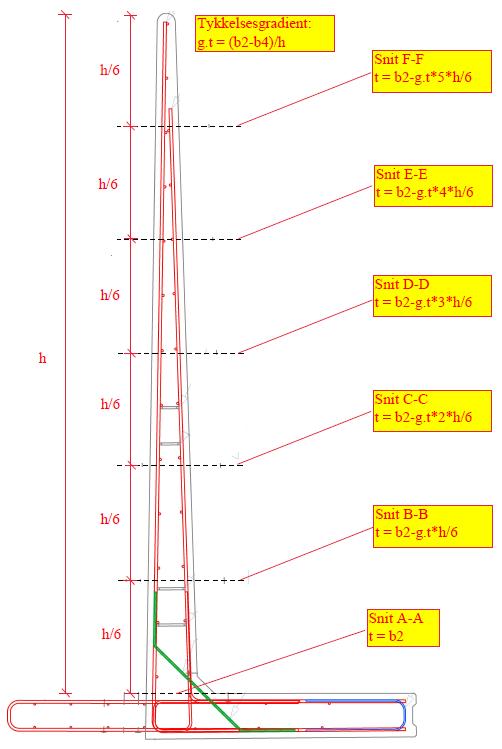
Projektnr.: L-400 med udragende og asfalt
Dimensionering af lodret del af element….fortsat:
Snit A-A:
Fuldt forankret armering:
Fuldt forankret armering i snit:15stk ø16pr.2400mm
Armeringsareal pr. løbende meterAs =1257mm2/m
Momentoptagelse:
Tykkelse af snit: t = b2t =288mm
Effektiv højde: d = t (snit A-A)-c1-0.5*ød =245mm
Armeringsgrad: = As*fyd/(1000*d*fcd1)
Hjælpefaktor: = *(1-0.5* )
= 0,094 OK
= 0,090
Maksimalt moment i snit A-AMSd =114,3kNm/m
Momentbæreevne: MRd = *1000*d2*fcd1 MRd =134,5kNm/m
Udnyttelsesgrad: .M = MSd/MRd
Forskydningsoptagelse:
.M = 85% OK
Hjælpefaktor k: k = 1+(200/d) 0.5, dog max 2.0 k =1,90
Armeringsforhold: = As/(d*1.0)
= 0,005
Regningsmæssig bæreevne: vRd,c = (0.18/1.40)*k*(100* *fck)1/3 vRd,c =0,64MPa
Dog som minimum: vRd,c,min = (0.051/1.40)*k 1.5*fck0.5 vRd,c,min =0,57MPa
Resulterende bæreevne: vRd,c = MAX(vRd,c & vRd,c,min)vRd,c =0,64MPa
Maksimal forskydning i snit A-AVSd =91,4kN/m
Forskydningsbæreevne: VRd = v Rd,c*dVRd =157,0kN/m
Udnyttelsesgrad: .V = VSd/VRd
Revnevidder:
.V = 58% OK
Kvasi-permanent momentMk =87,9kNm/m
Højde af trykzone: Ac*0.5*x = *As*(d-x) hvoraf findes følgende 2.gradsligning:
500*x2+*As*x-*As*d = 0 => 500 *x2 + 28902*x -7080941= 0
Disk. d =1,50E+10 => x1 =-151& x2 =94x =94mm
Transformeret inertimoment: It = 1000*x3/3+*As*(d-x)2 It =9,36E+08mm4/m
Armeringsspænding: s = *(Mk/It)*(d-x) s = 327MPa
Effektivt trækpåvirket betonareal omkring armeringen bestemmes med den effektive højde: hc.ef = MIN(2.5*(h-d) & (h-x)/3 & h/2)hc.ef =65mm
Effek. trækpåvirket betonareal omk. Arm.: Ac.eff = 1000*hc.efAc.eff =64813mm2/m
Tøjningsdifferens #1: #1 = s/Es-(0.4/Es)*(Ac.eff/As+)*fctm #1 =0,116%
Tøjningsdifferens #2: #2 = 0.6* s/Es #2 =0,098%
Tøjningsdifferens: sm -cm = MAKS(#1 & #2) sm -cm =0,116%
Maksimal revneafstand: sr,max = 29*c11/3+0.17*Ac.eff*ø/Assr,max =235mm
Revnevidder: wk = sr,max*(sm -cm)wk =0,27mm
Udnyttelsesgrad: .wk = wk/wk.max
.wk = 91% OK
ingeniørvirksomhed.
Projektnr.: L-400 med udragende og asfalt
Dimensionering af lodret del af element….fortsat:
Snit B-B:
Fuldt forankret armering:
Fuldt forankret armering i snit:11stk ø16pr.2400mm
Armeringsareal pr. løbende meterAs =922mm2/m
Momentoptagelse:
Tykkelse af snit: t = b2-g.t*h/6t =257mm
Effektiv højde: d = t (snit B-B)-c1-0.5*ød =214mm
Armeringsgrad: = As*fyd/(1000*d*fcd1)
Hjælpefaktor: = *(1-0.5* )
= 0,079 OK
= 0,076
Maksimalt moment i snit B-BMSd =74,0kNm/m
Momentbæreevne: MRd = *1000*d2*fcd1 MRd =86,7kNm/m
Udnyttelsesgrad: .M = MSd/MRd
Forskydningsoptagelse:
.M = 85% OK
Hjælpefaktor k: k = 1+(200/d) 0.5, dog max 2.0 k =1,97
Armeringsforhold: = As/(d*1.0)
= 0,004
Regningsmæssig bæreevne: vRd,c = (0.18/1.40)*k*(100* *fck)1/3 vRd,c =0,63MPa
Dog som minimum: vRd,c,min = (0.051/1.40)*k 1.5*fck0.5 vRd,c,min =0,59MPa
Resulterende bæreevne: vRd,c = MAX(vRd,c & vRd,c,min)vRd,c =0,63MPa
Maksimal forskydning i snit B-BVSd =63,5kN/m
Forskydningsbæreevne: VRd = v Rd,c*dVRd =133,6kN/m
Udnyttelsesgrad: .V = VSd/VRd .V = 48% OK
Revnevidder:
Kvasi-permanent momentMk =56,9kNm/m
Højde af trykzone: Ac*0.5*x = *As*(d-x) hvoraf findes følgende 2.gradsligning:
500*x2+*As*x-*As*d = 0 => 500 *x2 + 21195*x -4528591= 0
Disk. d =9,51E+09 => x1 =-119& x2 =76x =76mm
Transformeret inertimoment: It = 1000*x3/3+*As*(d-x)2 It =5,48E+08mm4/m
Armeringsspænding: s = *(Mk/It)*(d-x) s = 328MPa
Effektivt trækpåvirket betonareal omkring armeringen bestemmes med den effektive højde: hc.ef = MIN(2.5*(h-d) & (h-x)/3 & h/2)hc.ef =60mm
Effek. trækpåvirket betonareal omk. Arm.: Ac.eff = 1000*hc.efAc.eff =60120mm2/m
Tøjningsdifferens #1: #1 = s/Es-(0.4/Es)*(Ac.eff/As+)*fctm #1 =0,107%
Tøjningsdifferens #2: #2 = 0.6* s/Es #2 =0,098%
Tøjningsdifferens: sm -cm = MAKS(#1 & #2) sm -cm =0,107%
Maksimal revneafstand: sr,max = 29*c11/3+0.17*Ac.eff*ø/Assr,max =272mm
Revnevidder: wk = sr,max*(sm -cm)wk =0,29mm
Udnyttelsesgrad: .wk = wk/wk.max .wk = 98% OK
ingeniørvirksomhed.
Projektnr.: L-400 med udragende og asfalt
Dimensionering af lodret del af element….fortsat:
Snit C-C:
Fuldt forankret armering:
Fuldt forankret armering i snit:7stk ø16pr.2400mm
Armeringsareal pr. løbende meterAs =586mm2/m
Delvist forankret armering:
Delvist forankret armering i snit:4stk ø16pr.2400mm
Forankringsforhold lb/ø =39
Fuld forankringslængde: lb = ø*lb/ølb =624mm
Effektiv forankringslængde: L.ef = 1500-2*626L.ef =248mm
Armeringsareal pr. løbende meterAs2 =335mm2/m
Effektivt armeringsareal pr. løbende meter: As2.ef = L.ef*As2/lb =133mm2/m
Total effektiv armering:
Effektivt armeringsareal pr. løbende meter: As = As1+As2.efAs =720mm2/m
Momentoptagelse:
Tykkelse af snit: t = b2-g.t*2*h/6t =225mm
Effektiv højde: d = t (snit C-C)-c1-0.5*ød =182mm
Armeringsgrad: = As*fyd/(1000*d*fcd1)
Hjælpefaktor: = *(1-0.5* )
= 0,072 OK
= 0,070
Maksimalt moment i snit C-CMSd =46,3kNm/m
Momentbæreevne: MRd = *1000*d2*fcd1 MRd =58,0kNm/m
Udnyttelsesgrad: .M = MSd/MRd
Forskydningsoptagelse:
.M = 80% OK
Hjælpefaktor k: k = 1+(200/d) 0.5, dog max 2.0 k =2,00
Armeringsforhold: = As/(d*1.0)
= 0,004
Regningsmæssig bæreevne: vRd,c = (0.18/1.40)*k*(100* *fck)1/3 vRd,c =0,62MPa
Dog som minimum: vRd,c,min = (0.051/1.40)*k 1.5*fck0.5 vRd,c,min =0,61MPa
Resulterende bæreevne: vRd,c = MAX(vRd,c & vRd,c,min)vRd,c =0,62MPa
Maksimal forskydning i snit C-CVSd =40,6kN/m
Forskydningsbæreevne: VRd = v Rd,c*dVRd =112,5kN/m
Udnyttelsesgrad: .V = VSd/VRd .V = 36% OK
Revnevidder:
Kvasi-permanent momentMk =35,6kNm/m
Højde af trykzone: Ac*0.5*x = *As*(d-x) hvoraf findes følgende 2.gradsligning:
500*x2+*As*x-*As*d = 0 => 500 *x2 + 16551*x -3017727= 0
Disk. d =6,31E+09 => x1 =-96& x2 =63x =63mm
Transformeret inertimoment: It = 1000*x3/3+*As*(d-x)2 It =3,19E+08mm4/m
Armeringsspænding: s = *(Mk/It)*(d-x) s = 306MPa
Effektivt trækpåvirket betonareal omkring armeringen bestemmes med den effektive højde: hc.ef = MIN(2.5*(h-d) & (h-x)/3 & h/2)hc.ef =54mm
Effek. trækpåvirket betonareal omk. Arm.: Ac.eff = 1000*hc.efAc.eff =54151mm2/m
Tøjningsdifferens #1: #1 = s/Es-(0.4/Es)*(Ac.eff/As+)*fctm #1 =0,090%
Tøjningsdifferens #2: #2 = 0.6* s/Es #2 =0,092%
Tøjningsdifferens: sm -cm = MAKS(#1 & #2) sm -cm =0,092%
Maksimal revneafstand: sr,max = 29*c11/3+0.17*Ac.eff*ø/Assr,max =300mm
Revnevidder: wk = sr,max*(sm -cm)wk =0,28mm
Udnyttelsesgrad: .wk = wk/wk.max .wk = 92% OK
Projektnr.: L-400 med udragende og asfalt
Dimensionering af lodret del af element….fortsat:
Snit D-D:
Fuldt forankret armering:
Fuldt forankret armering i snit:7stk ø16pr.2400mm
Armeringsareal pr. løbende meterAs =586mm2/m
Momentoptagelse:
Tykkelse af snit: t = b2-g.t*3*h/6t =194mm
Effektiv højde: d = t (snit D-D)-c1-0.5*ød =151mm
Armeringsgrad: = As*fyd/(1000*d*fcd1)
Hjælpefaktor: = *(1-0.5* )
= 0,071 OK
= 0,069
Maksimalt moment i snit D-DMSd =25,5kNm/m
Momentbæreevne: MRd = *1000*d2*fcd1 MRd =39,1kNm/m
Udnyttelsesgrad: .M = MSd/MRd
Forskydningsoptagelse:
.M = 65% OK
Hjælpefaktor k: k = 1+(200/d) 0.5, dog max 2.0 k =2,00
Armeringsforhold: = As/(d*1.0)
= 0,004
Regningsmæssig bæreevne: vRd,c = (0.18/1.40)*k*(100* *fck)1/3 vRd,c =0,61MPa
Dog som minimum: vRd,c,min = (0.051/1.40)*k 1.5*fck0.5 vRd,c,min =0,61MPa
Resulterende bæreevne: vRd,c = MAX(vRd,c & vRd,c,min)vRd,c =0,61MPa
Maksimal forskydning i snit D-DVSd =28,1kN/m
Forskydningsbæreevne: VRd = v Rd,c*dVRd =92,7kN/m
Udnyttelsesgrad: .V = VSd/VRd .V = 30% OK
Revnevidder:
Kvasi-permanent momentMk =19,6kNm/m
Højde af trykzone: Ac*0.5*x = *As*(d-x) hvoraf findes følgende 2.gradsligning:
500*x2+*As*x-*As*d = 0 => 500 *x2 + 13488*x -2036614= 0
Disk. d =4,26E+09 => x1 =-79& x2 =52x =52mm
Transformeret inertimoment: It = 1000*x3/3+*As*(d-x)2 It =1,79E+08mm4/m
Armeringsspænding: s = *(Mk/It)*(d-x) s = 250MPa
Effektivt trækpåvirket betonareal omkring armeringen bestemmes med den effektive højde: hc.ef = MIN(2.5*(h-d) & (h-x)/3 & h/2)hc.ef =47mm
Effek. trækpåvirket betonareal omk. Arm.: Ac.eff = 1000*hc.efAc.eff =47419mm2/m
Tøjningsdifferens #1: #1 = s/Es-(0.4/Es)*(Ac.eff/As+)*fctm #1 =0,058%
Tøjningsdifferens #2: #2 = 0.6* s/Es #2 =0,075%
Tøjningsdifferens: sm -cm = MAKS(#1 & #2) sm -cm =0,075%
Maksimal revneafstand: sr,max = 29*c11/3+0.17*Ac.eff*ø/Assr,max =315mm
Revnevidder: wk = sr,max*(sm -cm)wk =0,24mm
Udnyttelsesgrad: .wk = wk/wk.max .wk = 79% OK
Projektnr.: L-400 med udragende og asfalt
Dimensionering af lodret del af element….fortsat:
Snit E-E:
Fuldt forankret armering:
Fuldt forankret armering i snit:5stk ø16pr.2400mm
Armeringsareal pr. løbende meterAs =419mm2/m
Momentoptagelse:
Tykkelse af snit: t = b2-g.t*4*h/6t =163mm
Effektiv højde: d = t (snit E-E)-c1-0.5*ød =120mm
Armeringsgrad: = As*fyd/(1000*d*fcd1)
Hjælpefaktor: = *(1-0.5* )
= 0,064 OK
= 0,062
Maksimalt moment i snit E-EMSd =10,9kNm/m
Momentbæreevne: MRd = *1000*d2*fcd1 MRd =22,2kNm/m
Udnyttelsesgrad: .M = MSd/MRd
Forskydningsoptagelse:
.M = 49% OK
Hjælpefaktor k: k = 1+(200/d) 0.5, dog max 2.0 k =2,00
Armeringsforhold: = As/(d*1.0)
= 0,004
Regningsmæssig bæreevne: vRd,c = (0.18/1.40)*k*(100* *fck)1/3 vRd,c =0,59MPa
Dog som minimum: vRd,c,min = (0.051/1.40)*k 1.5*fck0.5 vRd,c,min =0,61MPa
Resulterende bæreevne: vRd,c = MAX(vRd,c & vRd,c,min)vRd,c =0,61MPa
Maksimal forskydning i snit E-EVSd =18,8kN/m
Forskydningsbæreevne: VRd = v Rd,c*dVRd =72,9kN/m
Udnyttelsesgrad: .V = VSd/VRd .V = 26% OK
Revnevidder:
Kvasi-permanent momentMk =8,4kNm/m
Højde af trykzone: Ac*0.5*x = *As*(d-x) hvoraf findes følgende 2.gradsligning:
500*x2+*As*x-*As*d = 0 => 500 *x2 + 9634*x -1152861= 0
Disk. d =2,40E+09 => x1 =-59& x2 =39x =39mm
Transformeret inertimoment: It = 1000*x3/3+*As*(d-x)2 It =8,25E+07mm4/m
Armeringsspænding: s = *(Mk/It)*(d-x) s = 188MPa
Effektivt trækpåvirket betonareal omkring armeringen bestemmes med den effektive højde: hc.ef = MIN(2.5*(h-d) & (h-x)/3 & h/2)hc.ef =41mm
Effek. trækpåvirket betonareal omk. Arm.: Ac.eff = 1000*hc.efAc.eff =41109mm2/m
Tøjningsdifferens #1: #1 = s/Es-(0.4/Es)*(Ac.eff/As+)*fctm #1 =0,016%
Tøjningsdifferens #2: #2 = 0.6* s/Es #2 =0,056%
Tøjningsdifferens: sm -cm = MAKS(#1 & #2) sm -cm =0,056%
Maksimal revneafstand: sr,max = 29*c11/3+0.17*Ac.eff*ø/Assr,max =362mm
Revnevidder: wk = sr,max*(sm -cm)wk =0,20mm
Udnyttelsesgrad: .wk = wk/wk.max .wk = 68% OK
Projektnr.: L-400 med udragende og asfalt
Dimensionering af lodret del af element….fortsat:
Snit F-F:
Delvist forankret armering:
Delvist forankret armering i snit:4stk ø16pr.2400mm
Forankringsforhold lb/ø =39
Fuld forankringslængde: lb = ø*lb/ølb =624mm
Effektiv forankringslængde: L.ef = 3225-5*626L.ef =95mm
Armeringsareal pr. løbende meterAs =335mm2/m
Effektivt armeringsareal pr. løbende meter: As = L.ef*As2/lb As =51mm2/m
Momentoptagelse:
Tykkelse af snit: t = b2-g.t*5*h/6t =131mm
Effektiv højde: d = t (snit F-F)-c1-0.5*ød =96mm
Armeringsgrad: = As*fyd/(1000*d*fcd1)
Hjælpefaktor: = *(1-0.5* )
= 0,010 OK
= 0,010
Maksimalt moment i snit F-FMSd =1,7kNm/m
Momentbæreevne: MRd = *1000*d2*fcd1 MRd =2,2kNm/m
Udnyttelsesgrad: .M = MSd/MRd
Forskydningsoptagelse:
.M = 78% OK
Hjælpefaktor k: k = 1+(200/d) 0.5, dog max 2.0 k =2,00
Armeringsforhold: = As/(d*1.0)
= 0,001
Regningsmæssig bæreevne: vRd,c = (0.18/1.40)*k*(100* *fck)1/3 vRd,c =0,32MPa
Dog som minimum: vRd,c,min = (0.051/1.40)*k 1.5*fck0.5 vRd,c,min =0,61MPa
Resulterende bæreevne: vRd,c = MAX(vRd,c & vRd,c,min)vRd,c =0,61MPa
Maksimal forskydning i snit F-FVSd =10,8kN/m
Forskydningsbæreevne: VRd = v Rd,c*dVRd =58,7kN/m
Udnyttelsesgrad: .V = VSd/VRd .V = 18% OK
Revnevidder:
Kvasi-permanent momentMk =1,3kNm/m
Højde af trykzone: Ac*0.5*x = *As*(d-x) hvoraf findes følgende 2.gradsligning:
500*x2+*As*x-*As*d = 0 => 500 *x2 + 1173*x -113034= 0
Disk. d =2,27E+08 => x1 =-16& x2 =14x =14mm
Transformeret inertimoment: It = 1000*x3/3+*As*(d-x)2 It =8,87E+06mm4/m
Armeringsspænding: s = *(Mk/It)*(d-x) s = 287MPa
Effektivt trækpåvirket betonareal omkring armeringen bestemmes med den effektive højde: hc.ef = MIN(2.5*(h-d) & (h-x)/3 & h/2)hc.ef =39mm
Effek. trækpåvirket betonareal omk. Arm.: Ac.eff = 1000*hc.efAc.eff =39142mm2/m
Tøjningsdifferens #1: #1 = s/Es-(0.4/Es)*(Ac.eff/As+)*fctm #1 =-0,364%
Tøjningsdifferens #2: #2 = 0.6* s/Es #2 =0,086%
Tøjningsdifferens: sm -cm = MAKS(#1 & #2) sm -cm =0,086%
Maksimal revneafstand: sr,max = 29*c11/3+0.17*Ac.eff*ø/Assr,max =95mm
Revnevidder: wk = sr,max*(sm -cm)wk =0,08mm
Udnyttelsesgrad: .wk = wk/wk.max .wk = 27% OK
Projektnr.: L-400 med udragende og asfalt
Tilfælde A, retning højre:
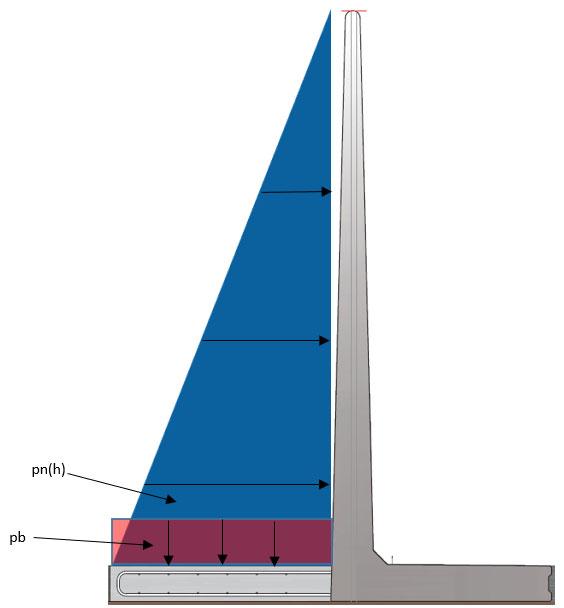
Vandret fladelast ved bund: pn(h) = g u * hpn(h) =37,5kN/m2
Lodret fladelast på vandret del b1 fra ensilage: pb = g u * hpb =37,5kN/m2
Lodret linielast fra ensilage: gk4 = b1*pbgk4 =43,3kN/m
Tyngdepunkt af gk4: tgp.gk4 = 0.5*b1tgp.gk4 =0,578m
Tilfælde A1: faktor 1.15 på vandret last fra ensilage, 1.00 på øvrige laste:
Total lodret linielast: n = 1.00*(gk.ele+gk4)n =78,1kN/m
Tyngdepunkt af n: tgp.n = (gk.ele*tgp.ele+gk4*tgp.gk4)/ntgp.n =0,905m
Vandret lastresultant: vd = 1.15*(0.5*h*pn(h))vd =80,9kN/m
Afstand fra u.k. element til vd: tgp.vd = t.plade+h/3tgp.vd =1,500m
Væltende moment fra vd: m.vd = vd*tgp.vdm.vd =121,3kNm/m
Excentricitet fra m.vd: e.vd = m.vd/ne.vd =1,553m
Placering af n: x.n = tgp.n+e.vdx.n =2,458m
Effektiv trykzone under element: tz = 2*(b.tot-x.n)tz =0,394m
Spænding under effektiv trykzone: = n/tz = 198,2kN/m2
Tilfælde A2: 1.30 på al last fra ensilage og 0.85 på øvrige laste
Total lodret linielast: n = 1.00*gk.ele+1.30*gk4n =91,1kN/m
Tyngdepunkt af n: tgp.n = (1.00*gk.ele*tgp.ele+1.30*gk4*tgp.gk4)/n =0,858m
Vandret lastresultant: vd = 1.30*(0.5*h*pn(h))vd =91,4kN/m
Afstand fra u.k. element til vd: tgp.vd = t.plade+h/3tgp.vd =1,500m
Væltende moment fra vd: m.vd = vd*tgp.vdm.vd =137,1kNm/m
Excentricitet fra m.vd: e.vd = m.vd/ne.vd =1,505m
Placering af n: x.n = tgp.n+e.vdx.n =2,363m
Effektiv trykzone under element: tz = 2*(b.tot-x.n)tz =0,583m
Spænding under effektiv trykzone: = n/tz = 156,2kN/m2
Projektnr.: L-400 med udragende og asfalt
Tilfælde A, retning højre….fortsat: Snitkræfter i lodret del af element:
Forskydningskraftkurvelodretdel,lasttilfældeA1[kNm/m]
Momentkurvelodretdel,lasttilfældeA1[kNm/m]
Projektnr.: L-400 med udragende og asfalt
Tilfælde A, retning højre….fortsat: Snitkræfter i lodret del af element:
Forskydningskraftkurvelodretdel,lasttilfældeA1[kNm/m]
Momentkurvelodretdel,lasttilfældeA1[kNm/m]
Projektnr.: L-400 med udragende og asfalt
Tilfælde A, retning højre….fortsat:
Snitkræfter i vandret, venstre, påstøbt del af element ved overgang til lodret del af element:
Karakteristisk forskydning fra egenlast: V.gk = gk2V.gk =7,2kN/m
Karakteristisk forskydning fra ensilage: V.ek = gk4V.ek =43,3kN/m
Karakteristisk moment fra egenlast: M.gk = gk2*0.5*b1M.gk =4,2kN/m
Karakteristisk moment fra ensilage: M.ek = gk4*0.5*b1M.ek =25,0kN/m
Tilfælde A1: faktor 1.15 på vandret last fra ensilage, 1.00 på øvrige laste:
Overlap mellem plade og effektiv trykzone: L = tz-b2-b3L =0,000m *
Forskydning: VSd = 1.00*(V.gk+V.ek)-L* VSd =50,5kN/m
Moment: MSd = 1.00*(M.gk+M.ek)-0.5*L 2* MSd =29,2kNm/m
Tilfælde A2: 1.30 på al last fra ensilage og 0.85 på øvrige laste
Overlap mellem plade og effektiv trykzone: L = tz-b2-b3L =0,000m *
Forskydning: VSd = 0.85*V.gk+1.30*V.ek-L* VSd =62,4kN/m
Moment: MSd = 0.85*M.gk+1.30*M.ek-0.5*L 2* MSd =36,1kNm/m
Anvendelsesgrænse: 1.00 på al last:
Lodret last & tyngdepunkt af denne som for beregning af tilfælde A1.
Væltende moment: m.vk = m.vd fra A1/1.15m.vk =105,5kNm/m
Excentricitet fra m.vk: e.vk = m.vk/ne.vk =1,351m
Placering af n: x.n = tgp.n+e.vdx.n =2,255m
Effektiv trykzone under element: tz = 2*(b.tot-x.n)tz =0,799m
Spænding under effektiv trykzone: = n/tz = 97,7kN/m2
Overlap mellem plade og effektiv trykzone: L = tz-b2-b3L =0,000m *
Moment: MSk = 1.00*(M.gk+M.ek-0.5*L 2* MSk =29,2kNm/m
* Hvis der ikke er noget overlap sættes L = 0
Snitkræfter i vandret, højre del af element ved overgang til lodret del af element:
Karakteristisk forskydning fra egenlast: V.gk = b3*t.plade*25*1.0 =7,6kN/m
Karakteristisk moment fra egenlast: M.gk = V.gk*0.5*b3M.gk =4,6kN/m
Tilfælde A1: faktor 1.15 på vandret last fra ensilage, 1.00 på øvrige laste:
Udbredelse af effektiv trykzone: L = MIN(tz & b3)L =0,394m
Afstand fra lodret snit til start effektiv trykzone: a1 = b3-La1 =0,818m
Forskydning: VSd = L* -1.00*V.gk VSd =70,5kN/m
Moment: MSd = L* *(a1+0.5*L)-1.00*M.gk MSd =74,7kNm/m
Tilfælde A2: 1.30 på al last fra ensilage og 0.85 på øvrige laste
Udbredelse af effektiv trykzone: L = MIN(tz & b3)L =0,583m
Afstand fra lodret snit til start effektiv trykzone: a1 = b3-La1 =0,629m
Forskydning: VSd = L* -0.85*V.gk
Moment: MSd = L* *(a1+0.5*L)-0.85*M.gk
Anvendelsesgrænse: 1.00 på al last:
VSd =84,6kN/m
MSd =79,9kNm/m
Udbredelse af effektiv trykzone: L = MIN(tz & b3)L =0,799m
Afstand fra lodret snit til start effektiv trykzone: a1 = b3-La1 =0,413m
Moment: MSk = L* *(a1+0.5*L)-1.00*M.gk
MSk =58,9kNm/m
Projektnr.: L-400 med udragende og asfalt
Tilfælde A, retning venstre:
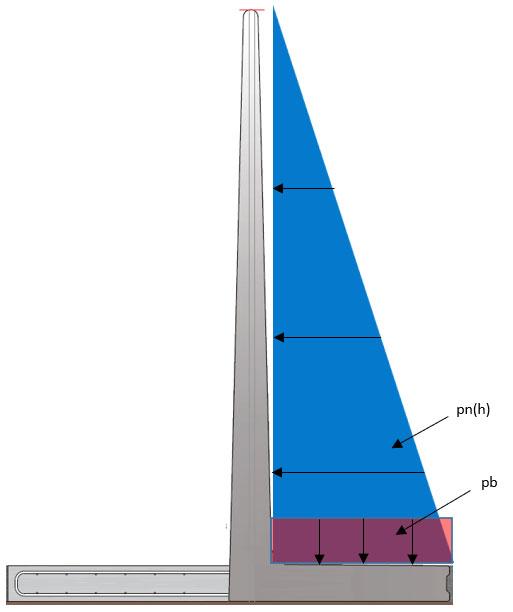
Vandret fladelast ved bund: pn(h) = g u * hpn(h) =37,5kN/m2
Lodret fladelast på vandret del b3 fra ensilage: pb = g u * hpb =37,5kN/m2
Lodret linielast fra ensilage: gk4 = b3*pbgk4 =45,5kN/m
Tyngdepunkt af gk4: tgp.gk4 = b1+b2+0.5*b3tgp.gk4 =2,049m
Tilfælde A1: faktor 1.15 på vandret last fra ensilage, 1.00 på øvrige laste:
Total lodret linielast: n = 1.00*(gk.ele+gk4)n =80,2kN/m
Tyngdepunkt af n: tgp.n = (gk.ele*tgp.ele+gk4*tgp.gk4)/ntgp.n =1,730m
Vandret lastresultant: vd = 1.15*(0.5*h*pn(h))vd =80,9kN/m
Afstand fra u.k. element til vd: tgp.vd = t.plade+h/3tgp.vd =1,500m
Væltende moment fra vd: m.vd = vd*tgp.vdm.vd =121,3kNm/m
Excentricitet fra m.vd: e.vd = m.vd/ne.vd =1,512m
Placering af n: x.n = tgp.n-e.vdx.n =0,218m
Effektiv trykzone under element: tz = 2*x.ntz =0,436m
Spænding under effektiv trykzone: = n/tz = 184,0kN/m2
Tilfælde A2: 1.30 på al last fra ensilage og 0.85 på øvrige laste
Total lodret linielast: n = 1.00*gk.ele+1.30*gk4n =93,9kN/m
Tyngdepunkt af n: tgp.n = (1.00*gk.ele*tgp.ele+1.30*gk4*tgp.gk4)/n =1,776m
Vandret lastresultant: vd = 1.30*(0.5*h*pn(h))vd =91,4kN/m
Afstand fra u.k. element til vd: tgp.vd = t.plade+h/3tgp.vd =1,500m
Væltende moment fra vd: m.vd = vd*tgp.vdm.vd =137,1kNm/m
Excentricitet fra m.vd: e.vd = m.vd/ne.vd =1,461m
Placering af n: x.n = tgp.n-e.vdx.n =0,315m
Effektiv trykzone under element: tz = 2*x.ntz =0,631m
Spænding under effektiv trykzone: = n/tz = 148,8kN/m2
Projektnr.: L-400 med udragende og asfalt
Tilfælde A, retning venstre….fortsat:
Snitkræfter i lodret del af element:
Samme som for tilfælde A, retning højre.
Se snitkraftkurver på forgående sider
Snitkræfter i vandret, venstre, påstøbt del af element ved overgang til lodret del af element:
Karakteristisk forskydning fra egenlast: V.gk = gk27,2kN/m
Karakteristisk moment fra egenlast: M.gk = V.gk*0.5*b1M.gk =4,2kN/m
Tilfælde A1: faktor 1.15 på vandret last fra ensilage, 1.00 på øvrige laste:
Udbredelse af effektiv trykzone: L = MIN(tz & b1)L =0,436m
Afstand fra lodret snit til start effektiv trykzone: a1 = b1-La1 =0,719m
Forskydning: VSd = L* -1.00*V.gk VSd =73,0kN/m
Moment: MSd = L* *(a1+0.5*L)-1.00*M.gk MSd =71,0kNm/m
Tilfælde A2: 1.30 på al last fra ensilage og 0.85 på øvrige laste
Udbredelse af effektiv trykzone: L = MIN(tz & b1)L =0,631m
Afstand fra lodret snit til start effektiv trykzone: a1 = b1-La1 =0,524m
Forskydning: VSd = L* -0.85*V.gk
Moment: MSd = L* *(a1+0.5*L)-0.85*M.gk
Anvendelsesgrænse: 1.00 på al last:
Lodret last & tyngdepunkt af denne som for beregning af tilfælde A1.
VSd =87,7kN/m
MSd =75,3kNm/m
Væltende moment: m.vk = m.vd fra A1/1.15m.vk =105,5kNm/m
Excentricitet fra m.vk: e.vk = m.vk/ne.vk =1,315m
Placering af n: x.n = tgp.n-e.vdx.n =0,415m
Effektiv trykzone under element: tz = 2x.ntz =0,830m
Spænding under effektiv trykzone: = n/tz
= 96,6kN/m2
Udbredelse af effektiv trykzone: L = MIN(tz & b1)L =0,830m
Afstand fra lodret snit til start effektiv trykzone: a1 = b1-La1 =0,325
Moment: MSk = L* *(a1+0.5*L)-1.00*M.gk
MSk =55,2kNm/m
Snitkræfter i vandret, højre del af element ved overgang til lodret del af element:
Karakteristisk forskydning fra egenlast: V.gk = b3*t.plade*25*1.0 =7,6kN/m
Karakteristisk forskydning fra ensilage: V.ek = gk4V.ek =45,5kN/m
Karakteristisk moment fra egenlast: M.gk = V.gk*0.5*b3M.gk =4,6kN/m
Karakteristisk moment fra ensilage: M.ek = gk4*0.5*b3M.ek =27,5kN/m
Tilfælde A1: faktor 1.15 på vandret last fra ensilage, 1.00 på øvrige laste:
Overlap mellem plade og effektiv trykzone: L = tz-b1-b2L =0,000m *
Forskydning: VSd = 1.00*(V.gk+V.ek)-L* VSd =53,0kN/m
Moment: MSd = 1.00*(M.gk+M.ek)-0.5*L 2* MSd =32,1kNm/m
Tilfælde A2: 1.30 på al last fra ensilage og 0.85 på øvrige laste
Overlap mellem plade og effektiv trykzone: L = tz-b1-b2L =0,000m *
Forskydning: VSd = 0.85*V.gk+1.30*V.ek-L*
Moment: MSd = 0.85*M.gk+1.30*M.ek-0.5*L 2*
Anvendelsesgrænse: 1.00 på al last:
VSd =65,5kN/m
MSd =39,7kNm/m
Overlap mellem plade og effektiv trykzone: L = tz-b1-b2L =-0,613m *
Moment: MSk = 1.00*(M.gk+M.ek)-0.5*L 2*
* Hvis der ikke er noget overlap sættes L = 0
MSk =14,0kNm/m
Projektnr.: L-400 med udragende og asfalt
Tilfælde B, retning højre:
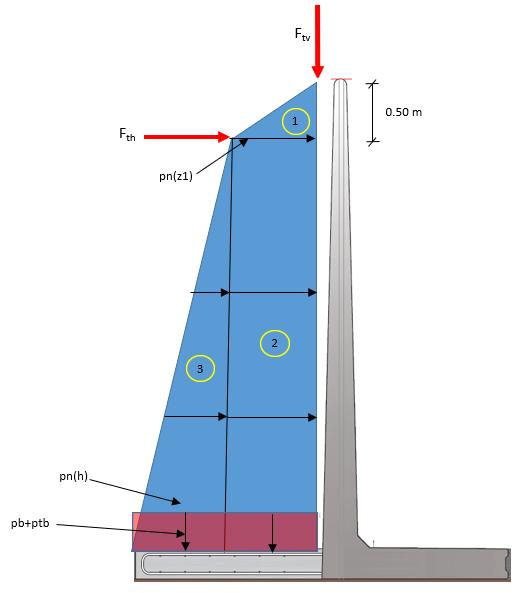
Ensilagebidrag til karakteristisk last:
Vandret fladelast i dybden z1: pn(z1) = (7/3)*g f*0.50pn(z1) =8,75kN/m2
Vandret fladelast ved bund: pn(h) = pn(z1)+(1/3)*g f*(h-z1)pn(h) =16,88kN/m2
Lodret fladelast på vandret del b1: pb = g f * hpb =28,13kN/m2
Vandret resultant for område 1: N1 = 0.5*0.50*pn(z1)N1 =2,2kN/m
Vandret resultant for område 2: N2 = (h-0.50)*pn(z1)N2 =28,4kN/m
Vandret resultant for område 3: N3 = 0.5*(h-0.50)*(pn(h)-pn(z1)) =13,2kN/m
Lodret linielast fra ensilage: gk4 = b1*pbgk4 =32,5kN/m
Afstand fra u.k. element til N1: a.N1 = h1-(2/3)*0.50a.N1 =3,67m
Afstand fra u.k. element til N2: a.N2 = t.plade+0.5*(h-0.50)a.N2 =1,88m
Afstand fra u.k. element til N3: a.N3 = t.plade+(1/3)*(h-0.50)a.N3 =1,33m
Tyngdepunkt af gk4: tgp.gk4 = 0.5*b1tgp.gk4 =0,58m
4.0
Projektnr.: L-400 med udragende og asfalt
Tilfælde B, retning højre….fortsat:
Komprimeringskøretøjets bidrag til karakteristisk last:
Forudsat afstand mellem enkeltkræfters angrebspunktera =3,00m
Vandret punktlast i dybden z1: F th = (1/8)*GtFth =15kN
Lodret punktlast: Ftv = (0.3/8)*(1+2*h/(h+a)-a/(3*h+2*a))*GtFtv =8,7kN
Lodret fladelast på vandret del b1: ptb = (Gt*0.9*a 2/(h+a)2)/a2 ptb =2,37kN/m2
Afstand fra u.k. element til Fth: a.Fth = h1-0.50a.Fth =3,500m
Lodret linielast fra komprimeringskøretøj: gk5 = b1*ptbgk5 =2,7kN/m
Tyngdepunkt af gk5: tgp.gk5 = 0.5*b1tgp.gk5 =0,58m
B1: 1.15 på vandret last fra ensilage, 1.30 på vandret last fra køretøj, 1.00 på øvrige laste:
Total lodret linielast: n = 1.00*(gk.ele+gk4+gk5+F tv/b.komp)n =72,9kN/m
Tgp. af n: tgp.n = (gk.ele*tgp.ele+gk4*tgp.gk4+gk5*tgp.gk5+F tv*b1/b.komp)/n = 0,951m
Vandret lastresultant: vd = 1.15*(N1+N2+N3)+1.30*F th/b.kompvd =56,9kN/m
Afstand fra u.k. element til vd:
a.vd = (1.15*(N1*a.N1+N2*a.N2+N3*a.N3)+1.30*F th*a.Fth/b.komp)/vd =1,995m
Væltende moment fra vd: m.vd = vd*a.vdm.vd =113,5kNm/m
Excentricitet fra m.vd: e.vd = m.vd/ne.vd =1,557m
Placering af n: x.n = tgp.n+e.vdx.n =2,508m
Effektiv trykzone under element: tz = 2*(b.tot-x.n)tz =0,293m
Spænding under effektiv trykzone: = n/tz = 248,7kN/m2
B2: 1.30 på al last fra ensilage og køretøj, 0.85 på øvrige laste:
Total lodret linielast: n = 0.85*gk.ele+1.30*(gk4+gk5+F tv/b.komp)n =79,1kN/m
Tgp. af n: tgp.n = (0.85*gk.ele*tgp.ele+1.30*(gk4*tgp.gk4+gk5*tgp.gk5+F tv*b1/b.komp))/n = 0,880m
Vandret lastresultant: vd = 1.30*(N1+N2+N3+F th/b.komp)vd =63,5kN/m
Afstand fra u.k. element til vd:
a.vd = 1.30*(N1*a.N1+N2*a.N2+N3*a.N3+F th*a.Fth/b.komp)/vd =1,975m
Væltende moment fra vd: m.vd = vd*a.vdm.vd =125,4kNm/m
Excentricitet fra m.vd: e.vd = m.vd/ne.vd =1,584m
Placering af n: x.n = tgp.n+e.vdx.n =2,464m
Effektiv trykzone under element: tz = 2*(b.tot-x.n)tz =0,382m
Spænding under effektiv trykzone: = n/tz = 207,3kN/m2
Anvendelsesgrænse: 1.00 på al last:
Total lodret linielast: n = 1.00*(gk.ele+gk4+gk5+F tv/b.komp)n =72,9kN/m
Tgp. af n: tgp.n = (gk.ele*tgp.ele+gk4*tgp.gk4+gk5*tgp.gk5+F tv*b1/b.komp)/n = 0,951m
Vandret lastresultant: vk = 1.00*(N1+N2+N3+F th/b.komp)vk =48,8kN/m
Afstand fra u.k. element til vd:
a.vk =(N1*a.N1+N2*a.N2+N3*a.N3+F th*a.Fth/b.komp)/vk a.vk =1,975m
Væltende moment fra vk: m.vk = vk*a.vkm.vk =96,4kNm/m
Excentricitet fra m.vk: e.vk = m.vk/ne.vk =1,323m
Placering af n: x.n = tgp.n+e.vkx.n =2,274m
Effektiv trykzone under element: tz = 2*(b.tot-x.n)tz =0,762m
Spænding under effektiv trykzone: = n/tz = 95,7kN/m2
Projektnr.:
Tilfælde B, retning højre….fortsat:
Forskydningskraftkurvelodretdel,lasttilfældeB1[kNm/m]
Momentkurvelodretdel,lasttilfældeB1[kNm/m]
Projektnr.:
Tilfælde B, retning højre….fortsat:
Forskydningskraftkurvelodretdel,lasttilfældeB2[kNm/m]
Momentkurvelodretdel,lasttilfældeB2[kNm/m]
Projektnr.: L-400 med udragende og asfalt
Tilfælde B, retning højre….fortsat:
Snitkræfter i vandret, venstre, påstøbt del af element ved overgang til lodret del af element:
Karakteristisk forskydning fra egenlast: V.gk = gk2V.gk =7,2kN/m
Karakteristisk forskydning fra ensilage: V.ek = gk4V.ek =32,5kN/m
Karakteristisk forskydning fra køretøj: V.kk = gk5+Ftv/1.0V.kk =11,5kN/m
Karakteristisk moment fra egenlast: M.gk = gk2*0.5*b1M.gk =4,2kN/m
Karakteristisk moment fra ensilage: M.ek = gk4*0.5*b1M.ek =18,8kN/m
Karakteristisk moment fra køretøj: M.kk = gk5*0.5*b1M.kk =1,6kN/m
B1: 1.15 på vandret last fra ensilage, 1.30 på vandret last fra køretøj, 1.00 på øvrige laste:
Overlap mellem plade og effektiv trykzone: L = tz-b2-b3L =0,000m *
Forskydning: VSd = 1.00*(V.gk+V.ek+V.kk)-L* VSd =51,2kN/m
Moment: MSd = 1.00*(M.gk+M.ek+M.kk)-0.5*L 2* MSd =24,5kNm/m
B2: 1.30 på al last fra ensilage og køretøj, 0.85 på øvrige laste:
Overlap mellem plade og effektiv trykzone: L = tz-b2-b3L =0,000m *
Forskydning: VSd = 0.85*V.gk+1.30*(V.ek+V.kk)-L* VSd =63,3kN/m
Moment: MSd = 0.85*M.gk+1.30*(M.ek+M.kk)-0.5*L 2* MSd =30,0kNm/m
Anvendelsesgrænse: 1.00 på al last:
Overlap mellem plade og effektiv trykzone: L = tz-b2-b3L =0,000m *
Moment: MSk = 1.00*(M.gk+M.ek+M.kk)-0.5*L 2* MSk =24,5kNm/m
* Hvis der ikke er noget overlap sættes L = 0
Snitkræfter i vandret, højre del af element ved overgang til lodret del af element:
Karakteristisk forskydning fra egenlast: V.gk = b3*t.plade*25*1.0 =7,6kN/m
Karakteristisk moment fra egenlast: M.gk = V.gk*0.5*b3M.gk =4,6kN/m
B1: 1.15 på vandret last fra ensilage, 1.30 på vandret last fra køretøj, 1.00 på øvrige laste:
Udbredelse af effektiv trykzone: L = MIN(tz & b3)L =0,293m
Afstand fra lodret snit til start effektiv trykzone: a1 = b3-La1 =0,919m
Forskydning: VSd = L* -1.00*V.gk VSd =65,3kN/m
Moment: MSd = L* *(a1+0.5*L)-1.00*M.gk MSd =73,1kNm/m
B2: 1.30 på al last fra ensilage og køretøj, 0.85 på øvrige laste:
Udbredelse af effektiv trykzone: L = MIN(tz & b3)L =0,382m
Afstand fra lodret snit til start effektiv trykzone: a1 = b3-La1 =0,830m
Forskydning: VSd = L* -0.85*V.gk VSd =72,7kN/m
Moment: MSd = L* *(a1+0.5*L)-0.85*M.gk MSd =76,9kNm/m
Anvendelsesgrænse: 1.00 på al last:
Udbredelse af effektiv trykzone: L = MIN(tz & b3)L =0,762m
Afstand fra lodret snit til start effektiv trykzone: a1 = b3-La1 =0,450m
Moment: MSk = L* *(a1+0.5*L)-1.00*M.gk MSk =56,0kNm/m
Projektnr.: L-400 med udragende og asfalt
Tilfælde B, retning venstre:
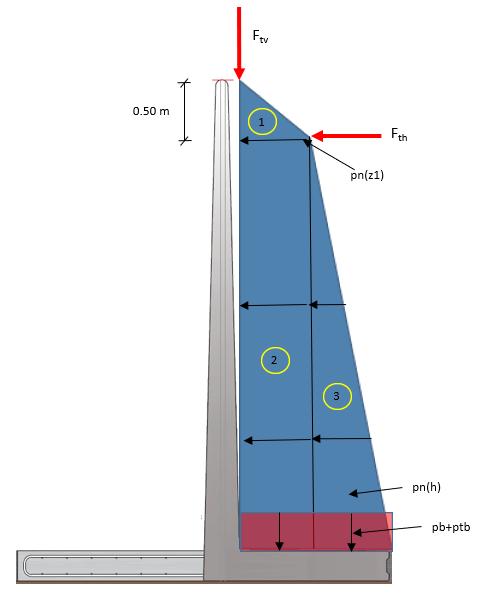
Ensilagebidrag til karakteristisk last:
Vandret fladelast i dybden z1: pn(z1) = (7/3)*g f*0.50pn(z1) =8,75kN/m2
Vandret fladelast ved bund: pn(h) = pn(z1)+(1/3)*g f*(h-z1)pn(h) =16,9kN/m2
Lodret fladelast på vandret del b1: pb = g f * hpb =28,1kN/m2
Vandret resultant for område 1: N1 = 0.5*0.50*pn(z1)N1 =2,2kN/m
Vandret resultant for område 2: N2 = (h-0.50)*pn(z1)N2 =28,4kN/m
Vandret resultant for område 3: N3 = 0.5*(h-0.50)*(pn(h)-pn(z1)) =13,2kN/m
Lodret linielast fra ensilage: gk4 = b3*pbgk4 =34,1kN/m
Afstand fra u.k. element til N1: a.N1 = h1-(2/3)*0.50a.N1 =3,67m
Afstand fra u.k. element til N2: a.N2 = t.plade+0.5*(h-0.50)a.N2 =1,88m
Afstand fra u.k. element til N3: a.N3 = t.plade+(1/3)*(h-0.50)a.N3 =1,33m
Tyngdepunkt af gk4: tgp.gk4 = b1+b2+0.5*b3tgp.gk4 =2,05m
Projektnr.: L-400 med udragende og asfalt
Tilfælde B, retning venstre….fortsat:
Komprimeringskøretøjets bidrag til karakteristisk last:
Forudsat afstand mellem enkeltkræfters angrebspunktera =3,00m
Vandret punktlast i dybden z1: F th = (1/8)*GtFth =15kN
Lodret punktlast: Ftv = (0.3/8)*(1+2*h/(h+a)-a/(3*h+2*a))*GtFtv =8,7kN
Lodret fladelast på vandret del b3: ptb = (Gt*0.9*a 2/(h+a)2)/a2 ptb =2,37kN/m2
Afstand fra u.k. element til Fth: a.Fth = h1-0.50a.Fth =3,50m
Lodret linielast fra komprimeringskøretøj: gk5 = b3*ptbgk5 =2,9kN/m
Tyngdepunkt af gk5: tgp.gk5 = b1+b2+0.5*b3tgp.gk5 =2,05m
B1: 1.15 på vandret last fra ensilage, 1.30 på vandret last fra køretøj, 1.00 på øvrige laste:
Total lodret linielast: n = 1.00*(gk.ele+gk4+gk5+F tv/b.komp)n =74,6kN/m
Tgp.af n: tgp.n = (gk.ele*tgp.ele+gk4*tgp.gk4+gk5*tgp.gk5+F tv*(b1+b2)/b.komp)/n = 1,682m
Vandret lastresultant: vd = 1.15*(N1+N2+N3)+1.30*F th/b.kompvd =56,9kN/m
Afstand fra u.k. element til vd:
a.vd = (1.15*(N1*a.N1+N2*a.N2+N3*a.N3)+1.30*F th*a.Fth/b.komp)/vd =1,995m
Væltende moment fra vd: m.vd = vd*a.vdm.vd =113,5kNm/m
Excentricitet fra m.vd: e.vd = m.vd/ne.vd =1,521m
Placering af n: x.n = tgp.n-e.vdx.n =0,161m
Effektiv trykzone under element: tz = 2*x.ntz =0,323m
Spænding under effektiv trykzone: = n/tz = 231,4kN/m2
B2: 1.30 på al last fra ensilage og køretøj, 0.85 på øvrige laste:
Total lodret linielast: n = 0.85*gk.ele+1.30*(gk4+gk5+F tv/b.komp)n =81,4kN/m
Tgp.af n:tgp.n =(0.85*gk.ele*tgp.ele+1.30*(gk4*tgp.gk4+gk5*tgp.gk5+F tv*(b1+b2)/b.komp))/n = 1,753m
Vandret lastresultant: vd = 1.30*(N1+N2+N3+F th/b.komp)vd =63,5kN/m
Afstand fra u.k. element til vd:
a.vd = 1.30*(N1*a.N1+N2*a.N2+N3*a.N3+F th*a.Fth/b.komp)/vd a.vd =1,975m
Væltende moment fra vd: m.vd = vd*a.vdm.vd =125,4kNm/m
Excentricitet fra m.vd: e.vd = m.vd/ne.vd =1,540m
Placering af n: x.n = tgp.n-e.vdx.n =0,213m
Effektiv trykzone under element: tz = 2*x.ntz =0,426m
Spænding under effektiv trykzone: = n/tz = 191,1kN/m2
Anvendelsesgrænse: 1.00 på al last:
Total lodret linielast: n = 1.00*(gk.ele+gk4+gk5+F tv/b.komp)n =74,6kN/m
Tgp.af n: tgp.n = (gk.ele*tgp.ele+gk4*tgp.gk4+gk5*tgp.gk5+F tv*(b1+b2)/b.komp)/n = 1,682m
Vandret lastresultant: vk = 1.00*(N1+N2+N3+F th/b.komp)vk =48,8kN/m
Afstand fra u.k. element til vk:
a.vk = (N1*a.N1+N2*a.N2+N3*a.N3+F th*a.Fth/b.komp)/vk a.vk =1,975m
Væltende moment fra vk: m.vk = vk*a.vkm.vk =96,4kNm/m
Excentricitet fra m.vk: e.vk = m.vk/ne.vk =1,292m
Placering af n: x.n = tgp.n-e.vkx.n =0,390m
Effektiv trykzone under element: tz = 2*x.ntz =0,781m
Spænding under effektiv trykzone: = n/tz = 95,6kN/m2
Projektnr.: L-400 med udragende og asfalt
Tilfælde B, retning venstre….fortsat:
Snitkræfter i lodret del af element:
Samme som for tilfælde B, retning højre.
Se snitkraftkurver på forgående sider
Snitkræfter i vandret, venstre, påstøbt del af element ved overgang til lodret del af element:
Karakteristisk forskydning fra egenlast: V.gk = gk27,2kN/m
Karakteristisk moment fra egenlast: M.gk = V.gk*0.5*b1M.gk =4,2kN/m
B1: 1.15 på vandret last fra ensilage, 1.30 på vandret last fra køretøj, 1.00 på øvrige laste:
Udbredelse af effektiv trykzone: L = MIN(tz & b1)L =0,323m
Afstand fra lodret snit til start effektiv trykzone: a1 = b1-La1 =0,832m
Forskydning: VSd = L* -1.00*V.gk VSd =67,4kN/m
Moment: MSd = L* *(a1+0.5*L)-1.00*M.gk MSd =70,0kNm/m
B2: 1.30 på al last fra ensilage og køretøj, 0.85 på øvrige laste:
Udbredelse af effektiv trykzone: L = MIN(tz & b1)L =0,426m
Afstand fra lodret snit til start effektiv trykzone: a1 = b1-La1 =0,729m
Forskydning: VSd = L* -0.85*V.gk
Moment: MSd = L* *(a1+0.5*L)-0.85*M.gk
Anvendelsesgrænse: 1.00 på al last:
VSd =75,3kN/m
MSd =73,1kNm/m
Udbredelse af effektiv trykzone: L = MIN(tz & b1)L =0,781m
Afstand fra lodret snit til start effektiv trykzone: a1 = b1-La1 =0,374m
Moment: MSk = L* *(a1+0.5*L)-1.00*M.gk
MSk =52,9kNm/m
Snitkræfter i vandret, højre del af element ved overgang til lodret del af element:
Karakteristisk forskydning fra egenlast: V.gk = b3*t.plade*25*1.0 =7,6kN/m
Karakteristisk forskydning fra ensilage: V.ek = gk4V.ek =34,1kN/m
Karakteristisk forskydning fra køretøj: V.kk = gk5+Ftv/1.0V.kk =11,6kN/m
Karakteristisk moment fra egenlast: M.gk = V.gk*0.5*b3M.gk =4,6kN/m
Karakteristisk moment fra ensilage: M.ek = gk4*0.5*b3M.ek =20,7kN/m
Karakteristisk moment fra køretøj: M.kk = gk5*0.5*b3M.kk =1,7kN/m
B1: 1.15 på vandret last fra ensilage, 1.30 på vandret last fra køretøj, 1.00 på øvrige laste:
Overlap mellem plade og effektiv trykzone: L = tz-b1-b2L =0,000m *
Forskydning: VSd = 1.00*(V.gk+V.ek+V.kk)-L* VSd =53,3kN/m
Moment: MSd = 1.00*(M.gk+M.ek+M.kk)-0.5*L 2* MSd =27,0kNm/m
B2: 1.30 på al last fra ensilage og køretøj, 0.85 på øvrige laste:
Overlap mellem plade og effektiv trykzone: L = tz-b1-b2L =0,000m *
Forskydning: VSd = 0.85*V.gk+1.30*(V.ek+V.kk)-L* VSd =65,8kN/m
Moment: MSd = 0.85*M.gk+1.30*(M.ek+M.kk)-0.5*L 2* MSd =33,0kNm/m
Anvendelsesgrænse: 1.00 på al last:
Overlap mellem plade og effektiv trykzone: L = tz-b1-b2L =0,000m *
Moment: MSk = 1.00*(M.gk+M.ek+M.kk)-0.5*L 2* MSk =27,0kNm/m
* Hvis der ikke er noget overlap sættes L = 0
