Intermediate algebra 12th edition bittinger solutions manual 1

Solution Manual for Intermediate Algebra 12th edition by Bittinger

Beecher and Johnson 0321924711 9780321924711

Full download link at:

Solution manual: https://testbankpack.com/p/solution-manual-for-intermediatealgebra-12th-edition-by-bittinger-beecher-and-johnson-03219247119780321924711/

Test bank: https://testbankpack.com/p/test-bank-for-intermediate-algebra-12thedition-by-bittinger-beecher-and-johnson-0321924711-9780321924711/

Chapter 3 Systems of Equations

Exercise Set 3.1

RC2. True; see page 243 in the text.

RC4. True; see page 245 in the text.

8.

Consistent; independent

Consistent; independent

Consistent; independent

16.

The graphs are the same.There are infinitely many solutions.

Consistent; dependent

18.

20.

Consistent; independent

Consistent; independent

22. Consistent; independent; the pair (1, 1) is a solution ofboth equations in system C and is not a solution of any other systemshown,sosystem C correspondstothisgraph.

24. Consistent; independent;the systemconsistsofalinewith y-intercept (0, 1) and a horizontal line. Both lines pass through (4, 3). System E corresponds to this graph.

26. Consistent; independent; the pair ( 1, 3) is a solutionof both equations in system A and is not a solution ofany othersystemshown,sosystem A correspondstothisgraph.

28. 3 x +2 = 2 x 5

30. 5(10 4x) = 3(7x 4)

50 20x = 21x +12

x = 38

32. ( 0.26, 57.06)

34.

Exercise Set 3.2

RC2. True; we can use the substitution method to solve any system of two equations in two variables.

RC4. False;seeExample3onpage253inthetext.

2. x = 8 4y, (1)

3x +5y = 3 (2)

3(8 4y)+5y = 3

24 12y +5y = 3

24

7y = 3

7y = 21

y = 3

Substitute 3 for y in (1).

Substitutingfor x in(2)

x = 8 4 3 =8 12 = 4

The solution is ( 4, 3).

4. 9x 2y =3, (1)

3x 6= y (2)

9x 2(3x 6) = 3

9x 6x +12= 3

3x +12= 3

3x = 9

x = 3

Substituting for y in (1)

Substitute 3for x in(2).

3( 3) 6 = y 9 6 = y

15= y

The solution is ( 3, 15).

3.2

6. m 2n =3, (1)

4m + n =1 (2)

We solve the first equation for m.

m 2n = 3 (1)

m = 2n +3 (3)

We substitute 2n +3 for m in the second equation and solve for n

4(2n +3)+ n = 1

8n +12+ n = 1 9n +12 = 1 9n = 11 11 n = 9

Now we substitute 11 for n in Equation (3).

9

Substitute 2p 8 for q in Equation (2) and solve for p

5p +7(2p 8)= 1

5p +14p 56 = 1 19p 56 = 1 19p =57 p = 3

Substitute 3 for p in Equation (3).

q =2 · 3 8=6 8= 2

The solution is (3, 2).

14. 3x + y =4, (1) 12 3y = 9x (2)

Solvethefirstequationfor y

8. t =4 2s, (1)

t +2s = 6 (2)

(4 2s)+2s = 6 Substitutingfor t in(2)

4 = 6

We get a false equation. The system has no solution.

10. 5x +6y =14, (1)

3y + x =7 (2)

Wesolvethesecondequationfor x

3y + x = 7 (2)

x = 3y +7 (3)

Substitute3y +7for x inthefirstequationandsolvefor y

5(3y +7)+6y = 14

15y +35+6y =14

21y +35= 14

21y = 21

y = 1

Substitute 1 for y in Equation (3).

12+9x 12= 9x 12 12 = 0 0 = 0

We have a true equation. Any value of x will make this equation true. Thus the system of equations has infinitely many solutions.

16. 5x +3y =4, (1)

x 4y =3 (2)

We solvethe secondequationfor x x 4y = 3 (2)

x = 4y +3 (3)

Substitute4y +3for x inthefirstequationandsolvefor y

5x +3y = 4 (1)

5(4y +3)+3y = 4

20y +15+3y = 4

23y +15 = 4

23y = 11 11 y =

x =3( 1)+7= 3+7=4 11 23

The solution is (4, 1).

12. 4p 2q =16, (1)

5p +7q =1 (2)

Solve the firstequation for q.

4p 2q = 16 (1)

Substitute 23 for y in Equation (3).

11 44 69 25

x =4 23 +3= 23 + 23 = 23

The solution is 25 11 23, 23

Substitute6x +13for y inEquation(1)andsolvefor x. 4x +13(6x +13) = 5

Substitute 2for x inEquation(3).

y =6( 2)+13= 12+13=1

The solution is ( 2, 1).

20. Let l =thelengthand w =thewidth. Solve:

2l +2w =340, l = w +50

Thesolutionis(110, 60),sothelengthis110mandthe width is 60 m.

22. Let x and y representtheangles. Solve:

+ y =90,

= 5x +6

The solution is (14, 76), so the measures of the angles are 14◦ and 76◦ .

24. Let x =thenumberofcoach-classseatsand y =thenumber of first-class seats. Solve: x + y =152, x =5+6y

The solution is (131, 21), so there are 131 coach-class seats and 21 first-class seats. 26.

28. m = 3 ( 4) = 7 2 ( 5) 3

30. 12(2x 3) = 16(4x 5)

24x +36 = 64x 80 116= 88x 29 = x 22

32. 5x + 2y = a,

x y = b

Wemultiplyby2onbothsidesofthesecondequationand then add.

5x + 2y = a

2x 2y =2b Multiplyingby27x + 0 = a +2b Adding 7x = a +2b a +2b

lution. 7 7

34. Let b = the number of ounces of baking soda and v = the number of ounces of vinegar to be used. Solve:

b =4v,

b + v =16

Thesolution is (128, 32), so 12.8 oz of baking soda and 3.2 ozof vinegar should be used.

Exercise Set 3.3

RC2. If a system of equations has no solution, then it is inconsistent.

RC4. Ifthegraphsoftheequationsinasystemoftwoequationsintwovariablesarethesameline,thentheequations are dependent

RC6. Ifthegraphoftheequationsinasystemoftwoequa-tions in two variables intersect at one point, then the equations are independent.

2. x + y = 9, (1)

2x y = 3 (2)

3x = 6 Adding x = 2

Substitute 2for x in(1).

2+ y = 9 y = 7

The solution is (2, 7).

4. 2x 3y = 18, (1)

2x + 3y = 6 (2)

4x = 12 Adding

x = 3

Substitute3for x in(2).

2 3+3y = 6 6+3y = 6 3y = 12 y = 4 x = 7

Next we multiply by 5onbothsidesofthesecondequation and then add.

The solution is (3, 4).

6. 2x + 3y = 9, (1)

5x 6y = 9 (2)

4x +6y = 18 Multiplying(1)by2

5x 6y = 9

9x = 27

x = 3

Substitute 3for x in(1).

2( 3)+3y = 9 The solution is

6+3y = 9

3y = 3 y = 1

The solution is ( 3, 1).

8. 2a + 3b = 11, (1)

4a 5b = 11 (2)

4a 6b = 22 Multiplying (1) by 2

4a 5b = 11 11b = 33

b = 3

Substitute 3 for b in (1).

2a +3 3 = 11

2a +9 =11

2a = 2 a = 1

The solution is (1, 3).

10. 3x 2y = 1, (1)

6x +4y = 2 (2)

6x 4y = 2 Multiplying (1) by 2

6x +4y = 2 (2)

0 = 0 True for all (x, y)

There are infinitely many solutions.

12. 5x + 4y = 2, (1)

2x 8y = 4 (2)

10x + 8y = 4 Multiplying(1)by2

2x 8y = 4

12x = 8

14. 5x + 3y = 25, (1)

3x + 4y = 26 (2)

20x +12y =100 Multiplying(1)by4 9x 12y = 78 Multiplying (2) by 3

11x =22

x = 2

Substitute 2for x in(1).

5 2+3y = 25

10+3y = 25

3y = 15

y = 5

The solution is (2, 5).

16. 3x 5y = 2

3x +5y = 7 Rearranging

0 = 5 Falseequation

There is no solution.

18. 10x + y = 306, (1)

10y + x = 90 (2)

y = 10x +306 (3) Solving(1)for y

10( 10x +306)+ x =90 Substitutingfor y in (2)

100x +3060+ x = 90

99x = 2970

x = 30

Substitute30for x in(3).

y = 10 30+306=6

The solution is (30, 6).

20. 2 x + 1 y = 11,

14x +3y = 231, (1) Multiplyingby21 3x 7y = 210 (2) to clear fractions

98x +21y = 1617 Multiplying(1)by7

9x 21y = 630 Multiplying (2) by 3

Substitute 21for x in(1).

14( 21)+3y = 231

3y = 63

y =21

The solution is ( 21, 21).

22. 2 x + 3 y = 17,

3 5

1 1

2x 3y = 1

Wemultiplythefirstequationby15andthesecondequation by 6 to clear fractions.

10x +9y = 255, (1)

3x 2y = 6 (2)

20x +18y = 510 Multiplying(1)by2

27x 18y = 54 Multiplying (2) by 9

47x = 564

x = 12

Substitute 12for x in(1).

10( 12)+9y = 255 120+9y = 255

9y = 135

y = 15

The solution is ( 12, 15).

24. 4 x + 3 y = 4,

49x 21y =35 Multiplying (1) by 7

12x +21y =39 Multiplying(2)by3

37x =74

x = 2

Substitute 2for x in(2).

4 2+7y = 13

7y = 21

y = 3

The solution is (2, 3).

28. 13x 02y = 12, (1)

04x +17y =89 (2)

13x 2y = 120, (3) Clearingdecimals

4x +170y = 890 (4)

1105x 170y = 10, 200 Multiplying (3) by 85

4x + 170y = 890 (4)

1109x = 11, 090

x = 10

Substitute10for x in(3).

13 10 2y = 120

2y = 10 y = 5

The solution is (10, 5).

3 2 30. Let x = the larger number and y = the smaller number.

5 1 x y = 6

Solve:

6 8 x + y = 2,

We multiply the first equation by 6 and the second equation by 24 to clear fractions.

8x + 9y = 24, (1)

20x 3y = 144 (2)

8x + 9y = 24

60x 9y = 432 Multiplying (2) by 3

68x = 408 x = 6

Substitute 6for x in(1).

8( 6)+9y = 24

48+9y = 24 9y = 72 y = 8

The solution is ( 6, 8).

26. 0.7x 0.3y = 0.5,

04x +07y =13

7x 3y = 5, (1) Clearing decimals

4x + 7y =13 (2) in both equations

The solution is (11, 9), so the numbers are 11 and 9.

32. Let x =thelargernumberand y =thesmaller number.Solve:

x + y = 9, 2x +3y = 2

The solution is (25, 16), so the numbers are 25 and 16.

34. Let x and y represent the measures of the angles. Solve:

x + y =180, x y =22

The solution is (101, 79), so the measures of the angles are 101◦and 79◦

36. Let x =thenumberof two-pointshotsmadeand y = thenumber of foul shots made. Solve:

x + y = 64, 2x + y = 100

The solution is (36, 28), so Chamberlain made 36 two-point shots and 28 foul shots.

38. Let x = the number of redbud trees chosen and y = the number of dogwood trees chosen. Solve:

Exercise Set 3.4

x + y =18, 37x +45y = 754

The solution is(7, 11), so7 customers chose an Eastern Redbud and 11 chose a Kousa Dogwood.

40. f( 1) =3( 1)2 ( 1)+1 =3+1+1=5

42. f(2a)=3(2a)2 2a +1=12a2 2a +1

44. Domain: all real numbers; range: {y|y ≤ 5}, or (−∞ , 5]

46. m = 10 2 = 8 = 1

4 2+3a = 7

3a = 15 a = 5

Thus, a =5and b =2.

Exercise Set 3.4

RC2. 15

RC4. 02(10) = 2 2 ( 10) 8

y y1 = m(x x1)

y 2= 1(x ( 10))

y 2 = x +10 y = x +12

48. x + y x y = 1,

2. Let x =thenumberofsmallstemssoldand y =thenumber of large stems sold. Solve:

x + y =118,

2.50x +3.95y = 376.20

Thesolutionis(62, 56),soKevinsold62sunflowerswith small stems and 56 with large stems. 2 x y + 2

5 x + y = 2 6

Afterclearingfractionswehave:

3x +7y = 10, (1)

2x y = 6 (2)

6x + 14y = 20 Multiplying(1)by2

28x 14y = 84 Multiplying (2) by 14

34x = 64 32 x = 17

Substitute 32 for in (1).

4. Let x and y represent the number of truffles and cream mints, respectively, in each box.The 75 boxes are identi-

cal,soeachsoldfor$1872/75,or$24.96. Solve:

x + y = 12,

295x +179y =2496

The solution is (3, 9), so each box contained 3 truffles and 9 cream mints.

6. Let x = the number of ounces of lemon juice and y = the number of ounces of linseed oil to be used. Solve:

Thesolutionis 1 10

, so 10

3 ozoflinseedoilshould beused.

oz of lemon juice and

8. Let x = the number of pounds of Deep Thought Granola and y = thenumber of pounds of Oat Dream Granola to be used. Solve: x + y = 20,

The solution is 32 38 17, 17 025x +01y = 019(20)

50. There are many correct answers. Find one by expressing the sum of the two numbers:

x + y = 1

52. Substitute 4 for x and 3 for y in both equations and solve for a and b

4a 3b = 26, (1) 4b +3a = 7 (2)

12a 9b = 78 Multiplying (1) by 3

12a 16b = 28 Multiplying (2) by 4

The solution is (12, 8), so 12 lb of Deep Thought Granola

and8lbofOatDreamGranolashouldbeused.

10. Let x =thenumberofpoundsofsoybeanmealand y =the number of pounds of corn meal in the mixture. The amountofproteininthemixture is012(350 lb),or42lb. Solve: x + y = 350, 0.16x +0.09y = 42

Thesolutionis(150, 200),so150lbof soybean meal and200 lb of corn meal should be used.

12. Let x and y representthenumberofAcuminatabulbsand

25b = 50 b = 2

Substitute 2 for b in (2).

Cafe Brun bulbs, respectively, in the assortment. Solve: x + y =12,

485x +950y = 12(795)

The solution is (4, 8), so the assortment contains 4 Acuminata bulbs and 8 Cafe Brun bulbs.

14. Let x =theamountinvestedat4%and y =theamount Solve: 2900 = (r w)5, invested at 6%. Solve:

x + y = 45, 000 2900= w 29 r 2 6

0.04x +0.06y = 2430

The solution is (13, 500, 31, 500), so $13,500 was invested at 4% and $31,500 was invested at 6%.

16. Let x = the number of liters of Arctic Antifreeze that should be used and let y = the number of liters in the mixture. Solve:

x + 7 5 = y

0.18x +0.1(7.5) = 0.15y

Thesolutionis(12.5, 20),so12.5LofArctic Antifreezeshould be used.

18. Let x =theamountborrowedat2.8%interestand y =theamountborrowedat4.5%. Solve: x + y = 31, 000, 0.028x +0.045y =1024.40

The solution is(21, 800, 9200), so $21,800 was borrowed at 2.8% and $9200 was borrowed at 4.5%.

20. Let x and y represent the number of quarters and dollar coins, respectively, used to make change. Note that the change owed is $20 $925= $1075.Solve: x + y = 19,

025x + y = 1075

The solution is (11, 8), sothere were 11 quarters and 8 dol-

The solution is (620,40), so the headwind is 40 mph and the plane’s air speed is 620 mph.

mi.

d =80t,

d =96t(t 1)

We find that d =480 km.

24. Let r =thespeedof theboatinstill water.

Distance Rate Time

Downstream d r +6 3

Upstream d r 6 5

Solve: d =3(r +6),

d =5(r 6)

Wefindthat r =24mph.

26. Let w = the speed of the headwind. Note that 4 hr 50 5 min= 4 6 hr,or 29 6 hr.

Solve: d = 8t, 6 d = 4(1 t)

We find that d =4 km.

40. Let b =thenumberofboysand g =thenumberofgirls.Then Phyllis has b brothers and g 1 sisters, and Phil hasb 1 brothers and g sisters.

Solve: b = 2(g 1), b 1 = g

The solution is (4, 3), so there are 4 boys and 3 girls in the family.

Chapter 3 Mid-Chapter Review

1. False ; see page s 253 and 260 in the text.

2. False ; see page 245 in the text.

3. True ; see page 245 in the text.

4. True; a vertical line x = a and a horizontal line y = b intersect at exactly one point, (a, b).

5. x +2y =3,

y = x 6

x +2(x 6) = 3

x +2x 12 = 3 3x 12 = 3 3x = 15 x = 5

y = 5 6

y = 1

The solution is (5, 1).

6. 3x 2y = 5,

2x + 4y = 14

6x 4y =10

2x + 4y = 14

8x =24

x = 3

2 3+4y = 14 6+4y =14 4y = 8 y = 2

The solution is (3, 2).

7. Graph the lines on the same set of axes.

8. Graphthelinesonthesamesetofaxes.

The solution appears to be (5, 1).

Check:

The solution is (5, 1).

Since the system of equations has a solution, it is consistent. Since there is exactly one solution, the equations are independent.

Thesolutionappearstobe(0, 3).

Check: x + y = 3 3x + y = 3 0+3 ? 3 3 0+3 ? 3

The solution is (0, 3).

Since the system of equations has a solution, it is consistent. Since there is exactly one solution, the equations are independent.

9. Graph the lines on the same set of axes.

The graphs are the same. There is an infinite number of solutions.Since the system of equations has a solution, it isconsistent.Sincethereareinfinitelymanysolutions,the equations are dependent.

10. Graph the lines on the same set of axes.

The lines are parallel. There is no solution. Since the system of equations has no solution, it is inconsistent. Since there is no solution, the equations are independent.

11. x = y +2, (1)

2x 3y = 2 (2)

Substitute y +2 for x in the Equation (2) and solve for y

2(y +2) 3y = 2

2y +4 3y = 2 y +4= 2 y = 6 y = 6

Substitute6for y inEquation(1)andfind x

x =6+2=8

The solution is (8, 6).

12. y = x 5, (1)

x 2y =8 (2)

Substitute x 5 for y in the Equation (2) and solve for x.

x 2(x 5) = 8

x 2x +10 = 8

x +10 = 8

x = 2

x = 2

Substitute2for x inEquation(1)andfind y

y =2 5= 3

The solution is (2, 3).

13. 4x +3y =3, (1)

y = x +8 (2)

Substitute x +8 for y in the Equation (1) and solve for x

4x +3(x +8) = 3

4x +3x +24 = 3 7x +24 = 3

7x = 21

x = 3

Substitute 3for x inEquation(2)andfind y

y = 3+8=5

The solution is ( 3, 5).

14. 3x 2y =1, (1)

x = y +1 (2)

Substitute y +1 for x in the Equation (1) and solve for y

3(y +1) 2y = 1

3y +3 2y = 1 y +3 = 1 y = 2

Substitute 2for y inEquation(2)andfind x

x = 2+1= 1

The solution is ( 1, 2).

15. 2x + y = 2, (1)

x y = 4 (2)

3x = 6 Adding x = 2

Substitute2for x inEquation(1)andsolvefor y

2 2+ y = 2

4+ y = 2 y = 2

The solution is (2, 2).

16. x 2y = 13, (1)

x + 2y = 3 (2)

2x = 10 Adding x = 5

Substitute5for x inEquation(2)andsolvefor y.

5+2y = 3

2y = 8 y = 4

The solution is (5, 4).

17. 3x 4y = 5, (1)

5x 2y = 1 (2)

First multiply by 2 on both sides of Equation (2) and then add.

3x 4y = 5

10x +4y =2

7x = 7

x = 1

Substitute 1for x inEquation(1)andsolvefor y.

3( 1) 4y = 5

3 4y = 5

4y = 8

y = 2

The solution is ( 1, 2).

18. 3x + 2y = 11, (1)

2x + 3y = 9 (2)

Weusethemultiplicationprincipleonbothequationsand then add.

9x + 6y = 33 Multiplying(1)by3

4x 6y = 18 Multiplying (2) by 2

5x =15

x = 3

Substitute3for x inEquation(1)andsolvefor y

3 3+2y = 11 9+2y =11 2y = 2 y = 1

The solution is (3, 1).

19. x 2y = 5, (1)

3x 6y =10 (2)

Firstwe multiply by 3onbothsidesofEquation(1)and then add.

3x +6y = 15

3x 6y =10 0 = 5

We get a false equation. There is no solution.

20. 4x 6y = 2, (1)

2x +3y = 1 (2)

First we multiply by 2 on both sides of Equation (2) and then add. 4x 6y = 2

Substitute8for y inEquation(2)andsolvefor x

Weobtainanequationthatistrueforallvaluesof x and y Thus,if anordered pairisasolution ofoneofthe original equations, it is a solution of the other equation also. The systemof equations hasan infinite number of solutions.

The solution is ( 9, 8).

23. Familiarize Let l = the length of the garden, in feet, and let w = the width.

w = l 2

We have a system of equations. 2

+2w =44, (1)

Solve. We substitute l 2for w inEquation(1)andsolve for l

We multiply both sides of Equation 1 by 6 and both sides of Equation (2) by 20 to clear fractions.

3x + 2y = 6 (3)

4x 15y =220 (4)

We use the multiplication principle on both equations again and then add.

45x + 30y =90

Multiplying(3)by15

Now substitute 12 for l in Equation (2) and find w w =12 2=10

Check Theperimeteris212ft+2 10ft=24ft+20ft=44 ft. Also,thewidth,10ft,is2ftlessthanthelength,12 ft. The answer checks.

8x 30y =440

Multiplying (4) by 2 53x =530 x = 10

Substitute10for x inEquation(3)andsolvefor y.

3 · 10+2y = 6 30+2y = 6 2y = 24

The solution is (10, 12). 22. 02x + 03y =06, (1) 01x 02y = 25 (2)

We could begin by clearing the decimals. Instead, we will multiplyby2onboth sides of Equation (2) and thenadd.

State.Thelengthofthegardenis12ft,andthewidthis 10 ft.

24. Familiarize.Let x and y representtheamountsinvestedat 2% and at 3%, respectively. Then the 2% investment earns0.02x,andthe3%investmentearns0.03y.

x + y = 5000

I `nteres ˛ t ¸ earned x was $129

002x +003y = 129

After clearing decimals, we have the following system of equations.

x + y = 5000, (1)

2x + 3y = 12, 900 (2)

Solve. Multiply both sides of Equation (1) by 2and then add.

2x 2y = 10, 000

2x + 3y = 12, 900

y =2900

Substitute2900for y inEquation(1)andsolvefor x

x +2900 = 5000

x =2100

Check

Totalinvestment:$2100+$2900=$5000

Amountearnedat2%:0.02($2100)=$42

Amountearnedat3%:0.03($2900)=$87

Totalearnings: $42+$87=$129

Theanswerchecks.

State.$2100wasinvestedat2%,and $2900 wasinvested at 3%.

25. Familiarize Let x =thenumberoflitersof20%solution and y =thenumberoflitersof50%solutiontobeused. Themixturecontains30%(84L),or0.3(84L),or25.2L of acid.

Translate We organize the information in a table.

26. Familiarize. Let d = the distance traveled and r = the speed of the boat in still water, in mph. Then when the boattravelsdownstreamitsspeedis r +6,anditsspeed upstream is r 6. The distances are the same.

We organize the information in a table.

We get one equation from the “Number of liters” row of the table.

x + y = 84

The last row of the table yields a second equation.

02x +05y =252

After clearing decimals, we have the following system of equations.

x + y = 84, (1)

2x +5y =252 (2)

Solve Multiply both sides of Equation (1) by 2and then add.

2x 2y = 168

2x + 5y = 252

3y = 84

y = 28

Substitute28for y inEquation(1)andsolvefor x

x +28 = 84

x = 56

Check The total amount of the mixture is 56 L+28 L, or 84 L. The amount of acid in the mixture is 02(56 L) +

0.5(28L)=11.2L+14L=25.2L. Theanswerchecks.

State. 56 L of the 20% solution and 28 L of the 50% solution should be used.

Translate Using d = rt ineachrowofthetable,weget a system of equations.

d = (r +6)5, d = 5r +30, (1) or

d = (r 6)8 d = 8r 48 (2)

Solve. Substitute 8r 48for d inEquation(1)andsolve for r

8r 48 = 5r +30

3r 48 = 30

3

r =78

r = 26

Check When r = 26, then r +6 = 26+6 = 32, and the distance traveled in 5 hr is 32 5, or 160 mi. Also, r 6 = 26 6=20, andthedistance traveledin8hris 20 8, or 160 mi.Since the distances are the same, the answer checks.

State.The speed of the boat in still water is 26 mph.

3 2

27. Graphically: 1. Graph y = 4x +2 and y = 5x 5 and find the point of intersection.The first coordinate of this point is the solution of the original equation.

2.Rewritetheequationas 7 x +7=0. Thengraph 7 20 y = 20 x +7 and find the x-intercept. The first coordinate of this point is the solution of the original equation. Algebraically: 1. Usetheadditionandmultiplicationprinciples for equations.

2. Multiply by 20 to clear the fractions and then use the addition and multiplication principles for equations.

28.

a) Answersmay vary.

x + y = 1,

x y = 7

b) Answersmayvary

x +2y = 5,

3x +6y = 10

c) Answersmayvary.

x 2y = 3,

3x 6y = 9

29. Answers may vary. Form a linear expression in two variables and set it equal to two different constants. See Exercises 10 and 19 in this review for examples.

30. Answersmayvary. Letanylinearequationbeoneequation inthesystem.Multiplybya constant on both sides ofthat equation to get the second equation in the system.See Exercises 9 and 20 in this review for examples.

Exercise Set 3.5

RC2. (c)

RC4. (a)

2. 2x y 4z = 12, (1)

2x + y + z = 1, (2) x + 2y + 4z = 10 (3)

2x y 4z = 12 (1)

2x + y + z = 1 (2)

4x 3z = 11 (4) Adding

4x 2y 8z = 24 Multiplying (1) by 2 x + 2y + 4z = 10 (3)

5x 4z = 14 (5) Adding

16x 12z = 44 Multiplying (4) by 4

15x +12z = 42 Multiplying (5)by 3 x = 2

4( 2) 3z = 11 Substituting in (4)

z = 1

2( 2)+ y +1 = 1 Substitutingin(2)

y 3 = 1 y = 4

The solution is ( 2, 4, 1).

4. x y + z = 4, (1)

3x + 2y + 3z =7, (2)

2x + 9y + 6z = 5 (3)

2x 2y + 2z = 8 Multiplying(1)by2

3x 2y + 3z = 7 (2)

5x + 5z = 15 (4)

9x 9y + 9z = 36 Multiplying(1)by9

2x + 9y + 6z = 5 (3)

11x +15z =41 (5)

15x 15z = 45 Multiplying (4) by 3

11x + 15z = 41

4x = 4

x = 1

5 1+5z = 15

z = 2

Substitutingin(4)

1 y +2 = 4 Substituting in (1)

y = 1

The solution is (1, 1, 2).

6. 6x 4y + 5z = 31, (1)

5x +2y +2z =13, (2)

x + y + z = 2 (3)

6x 4y + 5z = 31 (1)

4x + 4y + 4z = 8 Multiplying(3)by4

10x + 9z = 39 (4)

5x + 2y + 2z = 13 (2)

2x 2y 2z = 4 Multiplying (3) by 2

3x = 9 x = 3

10 3+9z = 39 Substitutingin(4)

z = 1

3+ y +1 = 2

y = 2

Substitutingin(3)

The solution is (3, 2, 1).

8. x + y + z = 0, (1)

2x +3y +2z = 3, (2)

x + 2y 3z = 1 (3)

2x 2y 2z =0 Multiplying (1) by 2

2x + 3y + 2z = 3 (2)

y = 3

x + z = 3

x 3z =5

2z =8

z = 4

x 3 4 = 0

x = 7

Substituting in (1)

Substituting in (3)

Substituting in (1)

The solution is (7, 3, 4).

10. 2x + y 3z = 4, (1)

4x 2y + z = 9, (2)

3x + 5y 2z = 5 (3)

2x + y 3z = 4 (1)

12x 6y + 3z = 27 Multiplying(2)by3

14x 5y = 23 (4)

8x 4y + 2z = 18 Multiplying(2)by2

3x + 5y 2z = 5 (3)

11x + y =23 (5)

14x 5y = 23 (4)

55x +5y =115 Multiplying(5)by5

69x =138 x = 2

11 2+ y = 23 Substitutingin(5)

y = 1

4 · 2 2 · 1+ z = 9 Substitutingin(2)

z = 3

The solution is (2, 1, 3).

12. 2x + y + 2z = 11, (1)

3x + 2y + 2z = 8, (2)

x + 4y + 3z = 0 (3)

2x + y + 2z = 11 (1)

2x 8y 6z =0 Multiplying(3)by 2 7y 4z =11 (4)

3x + 2y + 2z = 8 (2)

3x 12y 9z =0 Multiplying(3)by 3 10y 7z =8 (5)

49y 28z = 77 Multiplying (4) by 7

40y +28z = 32 Multiplying (5)by 4

9y = 45

y = 5 7( 5) 4z = 11 Substituting in (4)

z = 6

x +4( 5)+3 · 6 = 0 Substitutingin(3) x = 2

The solution is (2, 5, 6).

14. 2x + y + 2z = 3, (1)

x + 6y + 3z = 4, (2)

3x 2y + z = 0 (3)

12x 6y 12z = 18 Multiplying(1)by 6

x + 6y + 3z = 4 (2) 11x 9z = 14 (4)

4x + 2y + 4z = 6 Multiplying(1)by2

3x 2y + z = 0 (3)

7x + 5z = 6 (5)

55x 45z = 70 Multiplying (4) by 5

63x + 45z = 54 Multiplying(5)by9

8x = 16

x = 2

7( 2)+5z =6 Substitutingin(5)

z = 4

2( 2)+ y +2 4 = 3 Substituting in (1)

y = 1

The solution is ( 2, 1, 4).

16. 2r + s + t = 6, (1)

3r 2s 5t = 7, (2)

r + s 3t = 10 (3)

4r + 2s + 2t = 12 Multiplying(1)by2

3r 2s 5t = 7 (2)

7r 3t =19 (4)

2r + s + t = 6 (1)

r s +3t =10 Multiplying (3) by 1

r + 4t = 16 (5)

7r 3t = 19

7r 28t = 112 Multiplying (5) by 7

31t = 93

t = 3

r +4 · 3 = 16 Substitutingin(5)

r +12= 16

r = 4

2 4+ s +3 = 6 Substitutingin(1)

8+ s +3 = 6

s +11 = 6

s = 5

The solution is (4, 5, 3).

18. x + 4y z = 5, (1)

2x y + 3z = 5, (2)

4x + 3y + z = 5 (3)

3x + 12y 3z = 15 Multiplying(1)by3

2x y + 3z = 5 (2)

5x + 11y = 10 (4)

x + 4y z = 5 (1)

4x + 3y + z = 5 (3)

5x + 7y =10 (5)

5x + 11y = 10 (4)

5x 7y = 10 Multiplying (5) by 1

4y = 0

y = 0

5x +11 · 0 = 10

5x = 10

x = 2

4 2+3 0+ z = 5

8+ z = 5

Substitutingin(4)

Substitutingin(3)

z = 3

The solution is (2, 0, 3).

in Equation (1). We will use equations(2)and(3)toobtainanotherequationwithno cterms.

The solution is 4, 2, 2 . b = 5

The solution is (2, 5, 3).

28. F = 3ab

F = a Dividing by3b

3b

30. F = 1 t(c d) 2

2F = tc td

2F tc = td

2F tc = d, or t

tc 2F t = d, or

c 2F = d t 32. Ax + By = c

y = B

Exercise Set 3.6

RC2. (d)

RC4. (b)

2. Let x, y, and z represent the fat content of a Big Mac,

a medium order of fries, and a vanilla milkshake, respectively.Solve:

x + y + z =66,

x = z +11,

y + z = x +8

The solution is (29, 19, 18), so a Big Mac has 29 g of fat,

2 5 the fries have 19 g of fat, and the milkshake has 18 g of 34. y = 3x 4

The equation is in slope-intercept form, y = mx + b The fat.

slope is 2 , and the y-intercept is

36. 2x 5y = 10

5y = 2x +10

1 1 ( 5y)= ( 2x +10)

0, 5

4. Let x, y,and z representthemeasuresofangles A, B,and

C,respectively.Solve:

x + y + z = 180,

y =2x,

z =80+ x

Thesolution is (25, 50, 105), so the measures of angles A,

5 5 B,and C are25◦,50◦,and105◦,respectively. 2

y = 5x 2

Theequation is nowin slope-intercept form, y = mx + b. 2

The slope is 5, and the y-intercept is (0, 2).

38. w + x y + z =0, (1)

w 2x 2y z = 5, (2)

w 3x y + z =4, (3)2w

x y + 3z = 7 (4)

Pairingequations(1)and(2),(2)and(3),and(2)and(4) and eliminating z, we have

2w x 3y = 5, (5)

2w 5x 3y = 1, (6)

5w 7x 7y = 8 (7)

2w x 3y = 5 (5)

2w + 5x + 3y = 1 Multiplying (6) by 1

4x = 4 x = 1

Substituting 1for x in(5)and(7),wehave

2w 3y = 6, (8)

5w 7y = 15 (9)

Solving the system composed of (8) and (9), we have w =

3and y =0.

3 1 0+ z = 0

z = 4

Substituting in (1)

The solution is ( 3, 1, 0, 4).

6. Weknowthethousandsdigitmustbe1. TheUnitedStates did not exist as a union until the 1700’s, and the first U. S.transcontinentalrailroadwascompletedbefore2000.

1 x y z

Welet x representthehundredsdigit, y thetensdigit,and z theonesdigit. Since z isamultipleof3,weknowthat z mustbe3,6,or9. Wehavethefollowingpossibilities:

1 x y 3 1 x y 6 1 x y 9

Wealsoknowthat z isonemorethan x

When z = 3, x = 2

When z = 6, x = 5.

When z = 9, x = 8

Now the possibilitiesare:

1 2 y 3 1 5 y 6 1 8 y 9

Only 1 8 y 9 is a reasonable possibility.

1+8+ y +9 = 24 y = 6

Thus, the year is1869.

8. Let x, y, and z represent the number of tall, grande andventi coffeesserved, respectively. Solve:

x + y + z =50,

1.75x +1.95y +2.25z =

9870, 12x +16y +20z = 10(80)

Thesolutionis(12, 26, 12),soBrandieserved12tall coffees, 26 grande coffees, and 12 venti coffees.

10. Let x, y,and z representthepricesofachildren’sbook,a paperback,andahardback, respectively. Solve:

22x +10y +5z = 6350, 12y +15z =52.50, 8x +6z = 29

The solution is (1.75, 1.25, 2.50), so a children’s book costs $1.75,apaperbackcosts$1.25,andahardbackcosts$2.50.

12. Let x, y, and z representthepricesof upgradingtheprocessor, thememory, and the graphics card, respectively. Solve:

480+ x + y = 745, 480+ y + z = 690, 480+ x + z = 805

Thesolutionis(190, 75, 135),sothe processor upgradecosts $190,thememoryupgradecosts$75,andtheup-grade to the graphics card costs $135.

14. Let x, y, and z represent the number of calories in the sandwich,thesoup,andthecookierespectively. Solve:

x + y + z = 580,

x = y + z 20,

z = y +120

Thesolutionis(280,90,210),sothesandwichhas280calories,thesouphas90calories,andthecookiehas210calories.

16. Let x, y, and z representthenumber ofservings ofroast beef,bakedpotato,andasparagus,respectively. Solve:

300x +100y +50

20x + 5y + 5

20y +44

z =800 (Calories)

z = 55 (protein)

z =220 (vitaminC)

9 11 15 1

22. Let x, y,and z representthenumberofordersthatcanbe processedalonebySteven,Teri,andIsaiah,respectively. Solve:

x + y + z =740,

x + y =470,

y + z =520

Thesolutionis(220, 250, 270),soSteven,Teri, and Isaiahcan process220,250,and270orders,respectively,alone.

24.

26. Itispossible for a verticalline to intersectthe graphmore than once, so this is not the graph of a function.

28. There is no vertical line that can intersect the graph more than once, so this is the graph of a function.

30. Let T , G,and H representthe number of tickets Tom,Gary, and Hal begin with, respectively. After Hal gives tickets to Tom and Gary, each has the following number of tickets:

Tom: T + T, or2T,

Gary: G + G, or 2G, Hal: H T G.

After Tom gives tickets to Gary and Hal, each has the

The solution is 8, 4 , 4 3 ,sothemealshouldhave1 8 3 followingnumberoftickets: Gary: 2G +2G, or 4G, servingsofroastbeef,2 4 bakedpotatoes,and3 4 servings of asparagus.

18. Let x, y,and z representtheamount ofthePerkinsloan, theStaffordloan,andthebankloan,respectively. Solve:

x + y + z = 32, 000,

005x +004y +007z =1500,

005x =007z +220

The solution is (10, 000, 18, 000, 4000), so Terrance has a Perkins loan for $10,000, a Stafford loan for $18,000, and a bank loan for $4000.

20. Let x, y,and z representthenumberof2-pointfieldgoals,3pointfieldgoals,and1-pointfoulshotsmade,respec-tively. Thetotalnumberofpointsscoredfromeach ofthese types of goals is 2x, 3y, and z. Solve:

2x +3y + z =92,

x + y + z =50,

x =19+ z

The solution is (32, 5, 13), so the Knicks made 32 twopointfield goals, 5 three-point field goals, and 13 foul shots.

Hal: (H T G)+(H T G), or

2(H T G),

Tom: 2T 2G (H T G), or3T H G

AfterGarygivesticketstoHalandTom, eachhasthe following number of tickets:

Hal: 2(H T G)+2(H T G), or

4(H T G)

Tom: (3T H G)+(3T H G), or

2(3T H G),

Gary: 4G 2(H T G) (3T H G), or7G H T.

Since Hal, Tom, and Gary each finish with 40 tickets, we write the following system of equations:

4(H T G) = 40,

2(3T H G)= 40,

7G H T = 40

Solving the system we find that T = 35, so Tom started with 35 tickets.

32. Let w, x, y, and z representthe ages of Tammy, Carmen, Dennis, and Mark respectively. Solve:

w = x + y, x =2+ y + z, y =4z, w + x + y + z = 42

The solution is (20, 12, 8, 2), so Tammy is 20 years old.

Exercise Set 3.7

RC2. The sentence 4x y < 3 is an example of a linear inequality.

RC4. The ordered pair (1, 6) is a solution of 4x y < 3.

RC6. Todeterminewhichhalf-planetoshadewhengraphing an inequality, we can usea test point.

2. 4x +3y ≥ 0

4 6+3( 8) ? . 0 .

(6, 8) is a solution.

4. 6y x > 2 6( 2) 5 ? . 2 12 5 . 17 FALSE

(5, 2) is not a solution.

6. Graph: y < 3x

Graph y = 3x, using a dashed line.Test (1, 1): 1 < 3 is true.

8. Graph: y ≤ x 3

Graph y = x 3, using a solid line. Test (0, 0): 0 3is false.

10. Graph: y ≥ x +4

Graph y = x +4, using a solid line. Test (0, 0): 0 4is false.

12. Graph: x y ≥ 3

Graph x y = 3, using a solid line. Test (0, 0): 0 3is false.

14. Graph: 2x +3y < 6

Graph 2x +3y = 6, using a dashed line.Test (0, 0):0 < 6 is true.

16. Graph: 2y x ≤ 4

Graph 2y x = 4, using a solid line. Test (0, 0): 0 4is true.

18. Graph:2x 2y ≥ 8+2y 2x 4y ≥ 8

Graph 2x 4y =8, using a solid line. Test (0, 0): 0 8is false.

26. From the graph we see that the related equation is x = 1 andthehalf-planecontaining(0, 0) is not in the solution set.Thus, inequality D corresponds to this graph.

28. Fromthegraphweseethattherelatedequationis y = 3and the half-plane containing (0, 0) is not in the solution set. Thus, inequality E corresponds to this graph.

30. The equation 4y = 8 3x corresponds to the graph of the related equation. The half-plane containing (0, 0) is not shadednoris(0, 0)inthesolutionset of inequality A, sothis inequality corresponds to the given graph.

32. Graph: y ≥ x, y ≤ x +4

Graph y = x and y = x+4 usingsolidlines. Indicatethe regionforeachinequalitybyarrows,andshadetheregion where they overlap.

20. Graph: y ≥ 2

Graph y = 2, using a solid line. Test (0, 0): 0 2is true.

22. Graph: x ≤ 4

Graph x = 4, using a solid line. Test (0, 0): 0 4is false.

To findthe vertex wesolve y = x, y = x +4

The vertex is (2, 2).

34. Graph: y < x, y > x +3

Graph y = x and y = x +3usingdashedlines.Indicatethe region for each inequality by arrows, and shade the region where they overlap.

24. Graph: 7x +2y ≥ 21

Graph 7x +2y = 21, using a solid line. Test (0, 0): 0 21 is false.

To findthe vertex wesolve y = x, y = x +3 3 3

The vertexis 2, 2

36. Graph: x ≥ 2, y ≤ 2x +3

Shade the intersection of the graphs of x ≥ 2 and y ≤ 2x +3.

To find the vertices we solve three different systems of equations.

From(1)and(2)wehave x y = 2, x +2y = 8.

Solving,weobtainthevertex(4, 2).

From(1)and(3)wehave x y = 2, y = 4.

Solving,weobtainthevertex(6, 4).

To findthe vertex wesolve x = 2, y = 2x +3

The vertex is ( 2, 7).

38. Graph: x + y ≤ 3, x y ≤ 4

Shadethe intersection of the graphs of x + y ≤ 3 and x y ≤ 4.

From(2)and(3)wehave x +2y = 8, y = 4

Solving, we obtain the vertex (0, 4).

42. Graph: y x ≥ 1, (1)

y x ≤ 3, (2)

2 ≤ x ≤ 5 (3)

Thinkof (3)astwoinequalities:

2 ≤ x, (4)

x ≤ 5 (5)

Graphthelines y x = 1, y x =3, x =2,and x = 5 usingsolidlines. Indicatetheregionforeachinequalityby arrows,andshadetheregionwheretheyoverlap.

To findthe vertex wesolve x + y = 3, x y = 4

Thevertex is 7 1 2, 2

40. Graph: x y ≤ 2, (1) x +2y ≥ 8, (2) y ≤ 4 (3)

Graph the lines x y = 2, x +2y = 8, and y = 4, usingthe solid lines. Indicate the region for each inequality by arrows,andshadetheregionwheretheyoverlap.

Find theverticesasfollows:

System of equations Vertex

From (1) and (4) (2, 3)

From (1) and (5) (5, 6)

From (2) and (4) (2, 5)

From (2) and (5) (5, 8) 44. 4(3x +

a) Shade the intersection of the graphs of the three inequalities above.

Chapter 3 Concept Reinforcement

1. False; see page 245 in the text.

2. True; see page 245 in the text.

3. Thepoint(0 )isthe -interceptofalinearequation. Ifboth equationscontainthepoint(0, b),thentheequationshave the same y-intercept.

4. The graph of x = 4 is a vertical line and the graph of y = 4 is a horizontal line, so the lines have a point of intersection. Thus the system of equations x = 4 and y = 4isconsistent. Thegivenstatementisfalse.

Chapter 3 Study Guide

1. Graph both lines on the same set of axes.

The solution appears to be (4, 1).

Check:

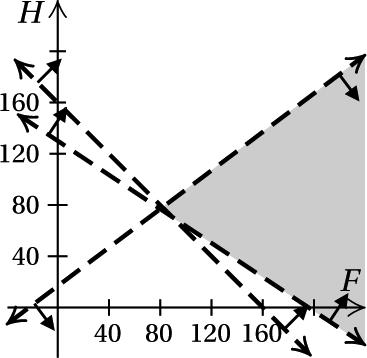
b) The point (80, 80) is not in the shaded region, so it is not dangerous to exercise when F =

80◦and H =80%.

Chapter 3 Vocabulary Reinforcement

1. Asolutionofasystemoftwoequationsintwovariablesis an ordered pair that makes both equations true.

2. Aconsistentsystemofequationshasatleastonesolution.

3. Asolutionofasystemofthreeequationsinthreevariables is an ordered triple that makes all three equations true.

4. If,forasystemoftwoequationsintwovariables,thegraphs oftheequationsaredifferentlines,thentheequa-tions are independent

5. Thegraph of aninequalitylike x > 2y isahalf-plane.

The solution is (4, 1).

Since the system of equations has a solution, it is consistent. Since there is exactly one solution, the equations are independent.

2. 2x + y = 2, (1)

3x + 2y = 5 (2)

We will use the substitution method. First solve Equation (1) fory.

= 2x +2 (3)

Nowsubstitute 2x+2 for y inEquation (2) and solve for x

Substitute 1for x inEquation(3)andfind y

y = 2( 1)+2=2+2=4

The solution is ( 1, 4).

3. 2x + 3y = 5, (1)

3x + 4y = 6 (2)

Wewillusetheeliminationmethod. Usethemultiplication principle on both equations and then add.

8x + 12y = 20 Multiplying(1)by4

9x 12y = 18 Multiplying (2) by 3 x = 2 x = 2

Substitute 2 for x in one of the original equations and solve for y

2( 2)+3y =5 UsingEquation(1)

4+3y = 5

3y = 9 y = 3

The solution is ( 2, 3).

4. Familiarize Welet x and y representtheamountsofthe investments. We will use the simple interest formula,I = Prt

Translate. We organize the information in a table.

5. x y + z = 9, (1)

2x + y + 2z = 3, (2)

4x + 2y 3z = 1 (3)

We will start by eliminating y from two different pairs of equations.

x y + z = 9 (1)

2x + y + 2z = 3 (2)

3x + 3z = 12 (4)

2x 2y + 2z = 18 Multiplying(1)by2

4x + 2y 3z = 1 (3)

6x z = 17 (5)

Now solve the system of Equations (4) and (5).

3x + 3z = 12 (4)

18x 3z = 51 Multiplying (5) by 3 21x =63

x = 3

3 · 3+3z = 12

9+3z = 12

3z = 3

z = 1

Substituting3for x in(4)

2 3+ y +2 1 = 3

Substituting 3for x and 1 for z in (2)

The “Principal” row of the table gives us one equation:

x + y = 23, 000.

The“Interest”rowofthetablegivesusasecondequation:

0.06x +0.05y =1237.

After clearing decinmals, we have the following system of equations.

x + y = 23, 000 (1)

6x +5y = 123, 700 (2)

Solve WemultiplyEquation(1)by 5andthenadd.

5x 5y = 115, 000

6x + 5y = 123, 700

x = 8700

Substitute8700for x inEquation(1)andsolvefor y

8700+ y = 23, 000

y = 14, 300

Check $8700 + $14, 300 = $23, 000 and 006($8700) +

005($14, 300)=$522 + $715=$1237,so the answer checks.

State $8700wasinvestedat6%,and$14,300wasinvested at 5%.

The solution is (3, 5, 1). 6. Graph: 3x

Wefirstgraphtheline

We draw the linedashed since the inequality symbol is > To determinewhich halfplanetoshade,testapointnotontheline.Wetry (0, 0).

Since 0 > 6 isfalse, we shade the half-plane that does not contain (0, 0).

7. Graph: x 2y ≤ 4, (1)

x + y ≤ 4, (2)

x 1 ≥ 0 (3)

Graphthelines x 2y = 4, x + y = 4, and x 1 = 0 (or x =1) using solidlines.Indicate the region for each inequalitybyarrowsandshadetheregionwheretheyoverlap.

2. Graph both lines on the same set of axes.

To find the vertices we solve three different systems of equations. From (1) and (2) we obtain the vertex (4, 0).

From(1)and(3)weobtainthevertex 1, 3 . From(2) and (3) we obtain the vertex (1, 3).

Chapter 3 Review Exercises

1. Graph both lines on the same set of axes.

The graphsare the same.Any solution of oneof the equations is also a solution of the other. Each equation has an infinitenumberofsolutions.Thusthesystemofequations has an infinite number of solutions.

Since the system of equations has a solution, it is consistent. Since there are infinitely many solutions, the equations are dependent.

3. Graph both lines on the same set of axes.

The solution (point of intersection) seems to be the point ( 2, 1).

Check:

4x y = 9 x y = 3

4( 2) 1 ? 9 2 1 ? 3

The lines are parallel. There is no solution.

Since the system of equations has no solution, it is inconsistent. Since there is no solution, the equations are independent.

4. 2x 3y =5, (1)

x =4y +5 (2)

Substitute 4y +5for x inEquation(1) andsolvefor y.

2(4y +5) 3y = 5

8y +10 3y = 5

5y +10= 5 . 9 . TRUE

The solution is ( 2, 1).

Since the system of equations has a solution it is consistent. Since there is exactly one solution, the equations are independent.

5y = 5 y = 1

Substitute 1for y inEquation(2)andfind x x =4( 1)+5= 4+5=1

The solution is (1, 1).

5. y = x +2, (1)

y x =8 (2)

Substitute x +2 for y in the second equation and solve for x

y x = 8 (2)

x +2 x = 8 2 = 8

We get a false equation. There is no solution.

6. 7x 4y =6, (1)

y 3x = 2 (2)

First solve the second equation for y

y 3x = 2 (2)

y = 3x 2 (3)

Nowsubstitute3x 2for y inthefirstequationandsolve for x. 7x 4y = 6 (1) 7x 4(3x 2) = 6

Since (2, 2) checks, it is the solution.

Nextsubstitute 2 for x inEquation(3)andfind y.

We multiply by 9 on both sides of the first equation and by 2 on both sides of the second equation to clear the fractions.

3x + 2y = 9, (1)

3x + y = 12 (2)

NowwemultiplybothsidesofEquation(2)by 1andthen add.

3x + 2y = 9 3x y = 12

Substitute 3for y inEquation(2)andsolvefor x

Since 5, 5 checks, it is the solution.

7. x +3y = 3, (1)

2x 3y =21 (2)

3x = 18 Adding

x = 6

Substitute6for x inEquation(1)andsolvefor y.

+3y = 3 3y = 9 y = 3

The solution is (6, 3).

8. 3x 5y = 4, (1)

5x 3y = 4(2)

We multiply Equation (1) by 3 and Equation (2) by 5 and then add. 9x 15y = 12 25x +15y = 20

16x = 32 x = 2

Nowsubstitute2for x inoneoftheequationsandsolvefor y

Firstwerewritethefirstequationintheform Ax + By = C

1 5x +2y =3, (1)

3x + 4y = 6 (2)

Now multiply Equation (1) by 2 and then add.

3x 4y = 6

3x + 4y = 6 0 = 0

We get an equation that is true for all numbers x and y The system has an infinite number of solutions.

11. Familiarize Let x = the number of less expensive brushes sold and y = the number of more expensive brushes sold.

Translate We organize the information in a table.

The“Numbersold”rowofthetablegivesusoneequation:

x + y = 45

The“Amounttakenin”rowgivesusasecondequation:

8.50x +9.75y =398.75

We havea systemofequations:

x + y =45,

8.50x +9.75y = 398.75

Wecanmultiplythesecondequationonbothsidesby100 to clear the decimals:

x + y = 45, (1)

850x +975y = 39, 875 (2)

Solve We solve the system of equations using the eliminationmethod.BeginbymultiplyingEquation(1)by 850.

850x 850y = 38, 250 Multiplying (1)

850x + 975y = 39, 875

125y = 1625

y = 13

Substitute13for y in(1)andsolvefor x

x +13 = 45

x = 32

Check The number of brushes sold is 32+13, or 45. The amount taken in was $850(32)+$975(13)= $272+ $12675=$39875. Theanswerchecks.

State. 32 of the less expensive brushes were sold, and 13 of the more expensive brushes were sold.

12. Familiarize.Let x and y representthenumberoflitersof Orange Thirst and Quencho that should be used, respectively.Theamountof orangejuicein themixtureis 10%(10 L), or 0.1(10 L), or 1 L.

Translate We organize the information in a table.

5x 5y = 50

15x + 5y = 100

10x =50

x = 5

Nowsubstitute5for x inoneoftheequationsandsolve for y

x + y = 10 (1)

5+ y = 10

y = 5

Check If 5 L of each type of juice are used, then the mixture contains 5 + 5, or 10 L. The amount of orange juiceinthemixtureis015(5)+005(5),or075+025,or 1 L. The answer checks.

State 5 L of Orange Thirst and 5 L of Quencho should be used.

13. Familiarize Wefirstmakeadrawing.

Slow train

d miles . 44mph (t +1) hr✲

From the drawing we see thatthe distancesare the same. We organize the information in a table.

d = r t

d = 44(t+1)

→ d =52t

Translate Using d = rt ineachrowofthetable,weget a system of equations:

d = 44(t +1),

d =52t

Solve Wesolvethesystemof equations.

52t = 44(t +1) Usingsubstitution 52t = 44t +44 8

The first row of the table gives us one equation.

The last row yields a second equation.

0.15x +0.05y =1

After clearing decimals we have the following system of equations.

x + y =10, (1)

15x +5y =100 (2)

Solve We use the elimination method.First we multiply Equation (1) by 5 and then add.

Check. At52mph, in 52 hr the fast train will travel 11 1 1 52 2 , or 286 mi. At 44 mph, in 52 +1, or 62 hr, the slowtraintravels44 13 , or 286 mi. Since the distances are the same, the answ 2 checks. 1

State The second train will travel 52 hr before it overtakes the first train.

14. x + 2y + z = 10, (1)

2x y + z = 8, (2)

3x + y + 4z = 2 (3)

Westartbyeliminating y fromtwodifferentpairsofequations.

x + 2y + z = 10 (1)

4x 2y + 2z = 16 Multiplying(2)by2

5x + 3z = 26 (4)

2x y + z = 8 (2)

3x + y + 4z = 2 (3)

5x + 5z = 10 (5)

Now solve the system of Equations (4) and (5).We multiply Equation (5) by 1 and then add.

5x + 3z = 26 (4)

5x 5z = 10

2z =16

z = 8

5x +3( 8)=26

5x 24 = 26

5x =50

x = 10

3 10+ y +4( 8) = 2

Substituting 8for z in(4)

x +3 3+2( 2) = 6 Substituting3for y and 2for z in(3)

x +9 4 = 6

x +5 = 6

x = 1

x = 1

We obtain ( 1, 3, 2). This checks, so it is the solution.

16. 2x 5y 2z = 4, (1)

7x + 2y 5z = 6, (2)

2x + 3y + 2z = 4 (3)

Westartbyeliminating x fromtwodifferentpairsofequations.

14x 35y 14z = 28 Multiplying (1) by 7

14x 4y +10z =12 Multiplying (2) by 2

39y 4z = 16 (4)

2x 5y 2z = 4 (1)

2x + 3y + 2z = 4 (3) 2y = 0

y = 0

Substitute 0 for y in Equation (4) and solve for z

39 0 4z = 16 4z = 16 z = 4 30+ y 32 = 2

Substituting 10 for x and

We obtain (10, 4, 8). This checks, so it is the solution.

15. 3x + 2y + z = 1, (1)

2x y 3z = 1, (2)

x +3y +2z = 6 (3)

Westartbyeliminating x fromtwodifferentpairsofequations.

3x + 2y + z = 1 (1)

3x + 9y +6z = 18 Multiplying(3)by3 11y +7z =19 (4)

2x y 3z = 1 (2)

2x +6y +4z =12 Multiplying(3)by2 5y + z = 13 (5)

Now we solve the system of Equations (4) and (5).

11y + 7z = 19 (4)

35y 7z = 91 Multiplying (5) by 7

24y = 72 y = 3

5 3+ z = 13

15+ z = 13

Substituting3for y in(5)

Nowsubstitute 0for y and4 for z in one of the original equationsandsolve for x. We use Equation (1).

2x = 4 x = 2

We obtain (2, 0, 4).This checks, so it is the solution.

17. x + y +2z =1, (1)

x y + z =1, (2)

x + 2y + z = 2 (3)

Westartbyeliminating y fromtwodifferentpairsofequations.

x + y + 2z = 1 (1)

x y + z = 1 (2)2x + 3z = 2 (4)

2x 2y + 2z = 2 Multiplying(2)by2

x + 2y + z = 2

3x + 3z = 4 (5)

Now solve the system of Equations (4) and (5).

2x + 3z = 2 (4)

3x 3z = 4 Multiplying (5)by 1

x = 2

x = 2

2 2+3z = 2

Substituting2for x in(4)

x + y + z =49.

Thepriceofthecaramelnutcrunchpopcornwassixtimes thepriceoftheplainpopcornand$16morethantheprice of the mocha choco latte popcorn, so we have

x =6y and x = z +16.

2+ y +2 2 4

= 1 Substituting2for x and 2 3 for z in (1)

We have a systemof equations.

x + y + z =49,

x =6y, 2+ y 3 = 1

x = z +16

Solve Solving the equation we have (30, 5, 14).

Check Thetotalcostwas$30+$5+$14,or$90. $30issix times$5andis$16morethan$14. Theanswerchecks.

We obtain 2, 3, 3 This checks, so it is the solution.

18. Familiarize Let a, b, and c represent the measures of anglesA,B,andC,respectively.Recallthatthesumofthe measuresof theangles ofatriangleis 180◦ . Translate

State.Onebagofcaramelnutcrunchpopcorncosts$30, onebagofplainpopcorncosts$5,andonebagofmocha choco latte popcorn costs $14.

20. Graph: 2x +3y < 12

Firstgraphtheline2x+3y =12.Drawitdashedsincethe inequality symbol is < Test the point (0, 0) to determine if it is a solution. he

Since 0 < 12 is true, we shade the half-plane containing (0, 0) and draw the graph.

Firstgraphtheline y = 0(the x-axis). Drawitsolidsince theinequalitysymbolis Testthepoint(1, 2)todetermine if it is a solution.

A;

morethanthemeasure Since 2 ≤ 0 is false, we shade the half-plane that does not

contain (1, 2) and obtain the graph.

Theanswerchecks.

1 State. The measures of angles A, B, and C are 90◦ , 672 ◦ , 1 ◦ and22 2 ,respectively.

19. Familiarize Let x, y, and z representthepricesof 1bag of caramel nut crunch popcorn, 1 bag of plain popcorn, and1bagofmochachocolattepopcorn,respectively. Translate.Thetotalcostof1bagofeachtypeofpopcorn was $49, so we have

22. Graph: x + y ≥ 1

First graph the line x + y = 1. Draw it solid since the inequality symbol is Test the point (0, 0) to determineif it is a solution.

25. Graph: x y ≤ 3, (1)

x + y ≥ −1, (2) y ≤ 2 (3)

Wegraphthelines x y =3, x + y = 1,and y =2usingsolid lines. We indicate the region for each inequality by arrows at the ends of the lines. Note where the regions overlap, andshade the region of solutions.

Since 0 1 isfalse,we shade the half-plane thatdoesnot contain (0, 0) and obtain the graph.

23. Graph: y ≥ −3, x ≥ 2

Wegraph the lines y = 3 and x =2 using solid lines.We indicate the region for each inequality by arrows atthe endsofthelines.Notewheretheregionsoverlap,andshade the region of solutions.

To find the vertices we solve three different systems of equations. From (1) and (2) we obtain the vertex (1, 2). From (1) and (3) we obtain the vertex (5, 2). From (2) and (3) we obtain the vertex ( 3, 2).

26. Familiarize Let x and y representthenumbers.

Tofindthevertexwesolvethesystemofrelatedequations:

= 3,

We see that the vertex is (2, 3).

24. Graph: x +3y ≥ 1, x +3y ≤ 4

Wegraphthelines x +3y =1and x +3y =4usingsolidlines. Weindicatetheregionforeachinequalitybyarrowsatthe ends of the lines. Note where the regions overlap, and shade the region of solutions.

We have a system of equations. x + y = 2, (1)

Solve. WemultiplybothsidesofEquation(1)by 1and then add.

x y = 2

2x + y = 4

x = 6

Substitute6for x inEquation(1)andsolvefor y.

6+ y

8

Check 6+ ( 8) = 2, and 2 6+( 8)= 12 8 = 4.

Theanswerchecks.

State Thenumbersare6and 8.

Since one number is 6, C is the correct answer.

27. Familiarize.Let t =thetimethecarstravel,andlet d = the distance the first car travels. Then the distance the secondcartravelsis275 d.Weorganizetheinformationin a table.

Translate.Using d = rt ineachrowofthetable,weget a system of equations.

d =50t, 275 d = 60t

Solve

275 50t = 60t Using substitution

275=110t

2.5= t

Check.In2.5hr,thefirstcartravels50(2.5),or125mi,and thesecondcartravels60(2.5),or150mi. Thenthecarsare 125mi+150mi, or275mi, apartafter2.5hr.The answer checks.

State.Thecarswillbe275miapartafter2.5hr.A is the correct answer.

28. Wegraphtheequationsandfindthepointsofintersection.

Since we have only two equations, it is not possible to eliminate z from another pair of equations. However, in Equation (4), note that 5 is a factor of both 5y and 100. Therefore,5 must also be a factor of 19x,and hence of x,since5isnotafactorof19.Thenforsomepositiveinteger n, x = 5n (We require n to be positive, sincethenumber of adults clearly cannot be negative and must also be nonzerosincetheexercisestatesthattheaudienceconsists of adults,senior citizens,and children.) We have:

19

· 5n + 5y = 100

19n + y = 20 Dividingby5

Since n and y must both be positive, n = 1. (If n > 1, then 19n + y > 20.) Then x = 5 · 1, or 5.

19 5+5y = 100 Substitutingin(4)

y = 1

5+1+ z = 100 Substitutingin(1)

z = 94

There were 5 adults, 1 senior citizen, and 94 children in the audience.

4. No; the symbol doesnotalways yielda graphin which the half-plane above the lineis shaded. For the inequality y 3, for example, the half-plane below the line y = 3 is shaded.

Chapter 3 Test

The solutions are (0, 2) and (1,3).

Chapter 3 Discussion and Writing Exercises

1. Answers may vary. One day a florist sold a total of 23 hangingbasketsandflatsofpetunias. Hanging basketscost $10.95 each and flats of petunias cost $12.95 each.The sales totaled $269.85. How many ofeachwere sold?

2. WeknowthatmachinesAandBcanpolish3400lenses,so machineCcanpolish5700 3400,or2300lenses. Machines B and C can polish 4200 lenses, so machine B can polish 4200 2300,or1900lenses.ThenmachineAcanpolish 5700 1900 2300, or 1500 lenses.

3. Let x = the number of adults in the audience, y = the

1. Graph both lines on the same set of axes.

The solution (point of intersection) seems to be the point ( 2, 1).

Check: numberofseniorcitizens,and z =thenumber of children. Thetotalattendanceis100,sowehaveEquation(1),

x + y + z = 100. The amount taken in was $100, so Equation (2) is 10x +3y +05z = 100. There is no other in-

formationthatcanbetranslatedtoanequation. Clearing decimalsinEquation(2)andtheneliminating z givesus Equation(3),95+25y =500.Dividingby5onbothsides, we have Equation (4), 19x +5y =100.

The solution is ( 2, 1).

. TRUE

2. Graph both lines on the same set of axes.

5. x =3y +2, (1)

2x 6y =4 (2)

Substitute 3y +2for x in the secondequation and solve for y.

2(3y +2) 6y = 4

6y +4 6y = 4 4 = 4

We have an equation that is true for all values of x and y The system of equations has infinitely many solutions.

6. x +2y =6, (1)

2x +3y = 7 (2)

The lines are parallel. There is no solution. Since the system of equations has no solution, it is inconsistent. Since there is no solution, the equations are independent.

3. Graph both lines on the same set of axes.

Solvethefirstequationfor x

x +2y = 6

x = 2y +6 (3)

Nowsubstitute 2y +6for x inthesecondequationand solve for y

2( 2y +6)+3y = 7

4y +12+3y =7 y +12= 7

y = 5

y = 5

Nextwesubstitute5for y inEquation3andfind x x = 2 5+6= 10+6= 4

The orderedpair( 4, 5) checks in both equations. It is the solution.

The graphsare the same.Any solution of oneof the equations is also a solution of the other. Each equation has an infinitenumberofsolutions.Thusthesystemofequations has an infinite number of solutions.

Since the system of equations has a solution, it is consistent. Since there are infinitely many solutions,the equations are dependent.

4. 4x +3y = 1, (1)

y =2x 7 (2)

Substitute 2x 7 for y in the first equation and solve for x.

4x +3(2x 7) = 1

4x +6x 21 = 1 10x 21 = 1 10x =20

x = 2

Next we substitute 2 for x in Equation (2) to find y

y =2x 7 = 2 2 7 = 4 7= 3

The ordered pair (2, 3) checks in both equations.It isthe solution.

7. 2x + 5y = 3, (1) 2x + 3y =5 (2)

8y = 8 Adding

y = 1

Nowsubstitute1for y inoneoftheequationsandsolve for x

2x +5y = 3 Equation(1) 2x +5 1 = 3 2x +5 = 3 2x = 2 x = 1

The orderedpair( 1, 1) checks in both equations. It is the solution.

8. x + y = 2, (1) 4x 6y = 3 (2)

MultiplyEquation(1)by6andthenadd.

6x + 6y = 12

4x 6y = 3

10x = 15 3 x = 2

Nowsubstitute 3 for x in one of the original equations the plane traveling against the wind is r 20. We organize and solve for y 2

Theorderedpair is the solution.

, 2 checksinbothequations. It

information in a table.

rstmultiplyeachequationby15toclearthefractions.

Now we multiply Equation (4) by 2 and then add.

We get a false equation. The system of equations has no solution.

10. Familiarize Let l =thelengthand w =thewidth,infeet.

Translate. The width is 42ftlessthan the length, sowe have one equation:

w = l 42.

We use the formula P =2l +2w to get a second equation:

288=2l +2w

We have a system of equations.

w = l 42, (1)

288=2l +2w (2)

Solve Weuse thesubstitution method.

288 = 2l +2(l 42)

288 = 2l +2l 84

288 = 4l 84

372=4l

93 = l

Substitute93for l inEquation(1)andfind w.

w =93 42=51

Check The length, 93 ft, is 42 ft more than the width, 51 ft.Also, 2 93+2 51=288 ft.The answer checks.

State The length is 93 ft, and the width is 51 ft.

11. Familiarize. Let d = the distance traveled and r = the speed of the plane in still air, in km/h. Then with a 20-

Translate Using

ineachrowofthetable,weget a system of equations.

km/h tailwind the plane’s speedis r +20.The speed of