Spis treści
Rozdział 0. Pierwszy ruch
Rozdział 1. Bliski Wschód
1. Tryktrak (backgammon)
2. Królewska gra z Ur
3. Senet
4. Kości do gry
5. Symetryczne kostki
6. Kostka
Rozdział 2. Morze Arabskie
7. Homo ludens
10. Gry konika polnego
11. Szachy
12. Carrom
13. Ludo (chińczyk).
14. Węże i drabiny
15. Karty ganjifa.
16. Zakazane gry Buddy
17. Gra w klasy
20. Gra ultimatum
Dylemat więźnia.
22. Go.
23. Szachy chińskie
24. Bierki (mikado)
25. Domino
26. Madżong (mahjong)
27. Zi pai, khanhoo i początki gry w karty
Rozdział 6. Morze Wschodniochińskie
Karty
28. Wist
29. Brydż
30. Pik, kier, karo, trefl
31. Lady Charlotte i Game of Parliament
32. Tarot
Rozdział 7. Japonia
33. Hanafuda
34. Karty Pokémon
Rozdział 8. Północny Pacyfik
Psychologia gier
35. Dungeons & Dragons
36. MangaHigh.com
37. Cranium
Rozdział 9. Australazja
38. Mu torere
Rozdział 10. Pacyfik Południowy
Gry i sztuka
39. Cluedo.
40. Azad i Gracz
41. Gry i zagadki
42. Gry teatralne
43. Mozart i jego gra w kości
Rozdział 11. Ameryka Południowa i Środkowa
44. Meksykańskie bingo.
45. Jogo do bicho
46. Adugo i komikan
47. Sapo
48. Truco
49. Perudo albo dudo, albo kości oszusta
50. Pitz, gra w piłkę Majów
Rozdział 12. Stany Zjednoczone
51. Kasyno
52. The Mansion of Happiness
53. Monopoly
Scrabble
55. Wordle
56. Papier, kamień, nożyce
57. Wsiąść do pociągu (Ticket to Ride)
Rozdział 13. Ocean Atlantycki
Gry komputerowe
58. Prince of Persia
59. Spacewar!
60. Tetris
61. Gra w życie
62. Kółko i krzyżyk
Rozdział 14. Afryka
63. Mancala
64. Gulugufe i fanorona
65. Achi
66. Bolotoudou
67. Młynek
68. Agram
Rozdział 15. Europa
69. Spiel des Jahres
70. Pandemic (Pandemia)
71. Najlepsza planszówka w historii
72. Ludus latrunculorum
73. Ryzyko.
74. L’Attaque i kobiety w branży gier
75. Szewc, czyli gra w kreski
76. Dobble
77. SET.
78. Mornington Crescent oraz niegry
79. Gry bez końca
80. Gra szklanych paciorków
Dodatek. Jak grać w osiemdziesiąt gier dookoła świata?
Nintendo uzna a, e warto rozwija si w kierunku, jaki podpowiedzia o jej pojawienie si gier komputerowych w latach siedemdziesi tych. Tak oto pocz tki jednego z najwi kszych producentów gier na wiecie wi si z kartami hanafuda, sprzedawanymi w sklepiku po o onym gdzie przy bocznej uliczce, który Yamauchi otworzy w Kioto w 1889 roku.
34. Karty Pokémon
Karty hanafuda, dzi ki którym powsta a rma Nintendo, nie s wprawdzie powszechnie znane na wiecie, jednak Nintendo mo e pochwali si udzia em w wypromowaniu innego zestawu kart do gry, które zrobi y prawdziwie mi dzynarodow karier . Mowa tu o kartach z „kieszonkowymi potworami”, czyli Pocket Monsters, a w skrócie: Pokémon Pierwsza generacja sk ada a si ze stu dwóch kart, które gracze kolekcjonowali, którymi si wymieniali i grali. Karty Pokémon pojawi y si w Stanach Zjednoczonych w 1998 roku –a czterysta tysi cy saszetek, z których ka da zawiera a dziesi kart, sprzedano w mniej ni sze tygodni od momentu ich wej cia na rynek. Rok pó niej dotar y do Wielkiej Brytanii i zanim si obejrza em, razem z synem wystawiali my przeciwko sobie karty Charizard i Squirtle, a tak e chadzali my do naszego miejscowego kiosku, gdzie kupowali my kolejn saszetk z nadziej na to, e wreszcie tra nam si Mewtwo.
Na ka dej karcie widnieje posta , która ma konkretne moce, a tak e okre lone s abe strony. Gracz wybiera kart , która b dzie go reprezentowa a w walce, a nast pnie stara si wykorzysta umiej tno ci swojej postaci w taki sposób, aby zada obra enia postaci widniej cej na karcie przeciwnika. Celem jest zmniejszenie do zera liczby punktów ycia przypisanych do karty oponenta i wyeliminowanie jej z rozgrywki. W grze obowi zuje zasada przeciwprzechodnio ci, umo liwiaj ca stworzenie dobrze zrównowa onej talii –chodzi o to, e podobnie jak w grze papier, kamie , no yce, wa ne jest, aby ka da karta by a silna w walce z niektórymi kartami, nawet je li jest s aba w potyczce z innymi.
Popularno kart Pokémon po cz ci wi za a si z tym, e kolekcjonerzy nie tylko d yli do zebrania wszystkich 102 kart w celu skompletowania zestawu, lecz tak e mogli u y ich w grze przeciwko znajomym. Kiedy jako dziecko zbiera em karty z pi karzami, nikt jeszcze nie wpad na sprytny pomys wykorzystania ich do stworzenia gry.
Z takim po czeniem kolekcjonowania, handlu wymiennego i grania mieli my po raz pierwszy do czynienia w 1993 roku, kiedy to na rynku pojawi si zestaw kart o nazwie Magic: The Gathering. Gracz wciela si w czarodzieja – rzuca zakl cia i wykorzystuje moce magicznych stworze widniej cych na kartach, które ma w r ku, walcz c przeciwko innemu czarodziejowi. Mo na tu wyczu atmosfer przypominaj c t , która towarzyszy rozgrywce w Dungeons & Dragons. I faktycznie, matematyk Richard Gar eld postanowi stworzy gr Magic: The Gathering, gdy us ysza o Dungeons & Dragons, a w miejscowym sklepie tytu ten by niedost pny.
Dla Gar elda gry zawsze by y czym wa nym. W dzieci stwie przez jaki czas mieszka w Bangladeszu i Nepalu. Nie zna lokalnego j zyka, ale komunikowa si z miejscowymi
dzie mi, graj c, na przyk ad w szklane kulki. Kiedy wi c nie móg dosta fascynuj cej nowej gry o nazwie Dungeons & Dragons, stworzy w asn gr osadzon w klimacie fantasy
Zaprojektowa j tak, e rozgrywka wymaga sporej dozy my lenia strategicznego w momencie wyboru kart, za których pomoc b dziemy walczyli. Element losowo ci i szcz cia zwi zany z dobieraniem kart oznacza, e nawet pocz tkuj cy mo e mie szans w starciu z do wiadczonym graczem.
Gar eld zadba te o to, by rozgrywka w Magic: The Gathering wi za a si z pewnym ryzykiem – pocz tkowo gracze musieli wystawia losow kart ze swojej kolekcji jako zap at za gr w razie przegranej. Zasada ta, zwana ante, okaza a si jednak problematyczna tam, gdzie hazard jest zabroniony.
Gra stworzona przez Gar elda ma pewn niezwyk cech . Niedawno wykazano, e jest ona na tyle z o ona, e w kartach da si zakodowa maszyn uniwersaln , co oznacza, e w rozgrywce mo liwa jest symulacja ka dego algorytmu, jaki taka maszyna jest w stanie zaimplementowa . Na przyk ad, jako e mo na napisa algorytm pozwalaj cy znale milionow liczb pierwsz , istnieje te gra w karty, któr mo na interpretowa jako wykonanie takich oblicze . Odbywa si to poprzez u o enie kaskadowych serii kart, które wyzwalaj si nawzajem w taki sposób, e okre lone sekwencje kart wymuszaj kolejno konkretne dzia ania gracza. Jest to wprawdzie bardzo ma o prawdopodobny scenariusz, jednak zasady gry go nie zabraniaj .
Udowodniono, e nie da si rozstrzygn kwestii, czy algorytm realizowany na maszynie uniwersalnej si zatrzyma, co implikuje z kolei, e istniej takie scenariusze, w których niemo liwe jest wskazanie, kto b dzie zwyci zc rozgrywki. Nie istnieje algorytm okre laj cy, czy w niektórych scenariuszach istnieje ruch wygrywaj cy, a nawet czy gra w ogóle si zako czy.
Karty mo na wykorzysta do symulacji sposobu dzia ania komputera dzi ki temu, jak wygl daj instrukcje, które nale y wykona podczas zagrywania karty. Na przyk ad karta Xathrid Necromancer instruuje gracza: „Ilekro Xathrid Necromancer lub inna kreatura typu Human, któr kontrolujesz, zginie, nale y stworzy stapowany token czarnej kreatury Zombie 2/2”*. Polecenie to dzia a przecie dok adnie tak, jak linia kodu: „Je li maszyna jest w stanie s, a ostatnia odczytana komórka to symbol k, zrób to i to”.
Gra Magic: The Gathering odnios a niemal natychmiastowy sukces – nak ad dziesi ciu milionów kart wyprzedano w ci gu zaledwie dwóch miesi cy od premiery. Firma zajmuj ca si produkcj kart nie mog a nad y za popytem i musia a wstrzyma promocj gry. Karty Pokémon powsta y w a nie na bazie sukcesu Magic: The Gathering. Z my l o stworzeniu agodniejszej, milszej w odbiorze gry opartej na kolekcjonowaniu i rywalizacji
* Jest to przek ad podanego przez autora tekstu znajduj cego si na tej karcie: „Whenever Xathrid Necromancer or another Human creature you control dies, create a tapped 2/2 black Zombie creature token”. Nie wydano polskiej wersji gry, wi c nasi rodzimi gracze pos uguj si kartami w j zyku angielskim, ich argon za stanowi mieszank polskiego i angielskiego – co stara am si odda w przek adzie.
61. Gra w życie
Najlepsze w grach jest to, e stanowi one wyabstrahowane wersje ca ego tego zamieszania, jakiego do wiadczamy w yciu codziennym. Dzi ki nim atwiej nam zrozumie , e jeden, okre lony zestaw regu mo e prowadzi do ró nych zako cze . Jest pewna szczególna, ukochana przez matematyków gra, która przepi knie ilustruje, jak to mo liwe, e ycie jako takie powsta o w wyniku niezwykle prostych zasad namna ania komórek.
Gra w ycie – bo o niej mowa – nie jest jednak tak naprawd gr . Niemniej jednak ten stworzony przez matematyka Johna Conwaya program doskonale obrazuje jedn z podstawowych cech dynamiki wspania ych gier, a tak e samego ycia, a mianowicie to, e proste regu y mog prowadzi do niezwyk ej z o ono ci.
Po raz pierwszy zetkn em si z gr w ycie, gdy odwiedzi em Conwaya w Cambridge w 1986 roku. Ko czy em studia i postanowi em zaj si prac naukow w obszarze symetrii w matematyce. Mój tutor z Oksfordu opowiedzia mi o zespole w Cambridge kierowanym przez Conwaya, który w a nie uko czy prac nad niezwyk publikacj opisuj c kluczowe aspekty symetrii. Owa pi knie wydana ksi ka, zatytu owana The Atlas of Finite Simple Groups, jest dla wiata symetrii niczym uk ad okresowy pierwiastków dla chemii. Od lat jest jedn z najbli szych memu sercu pozycji w mojej biblioteczce.
Projekt ów by kulminacj stupi dziesi cioletniej podró y ca ych pokole matematyków, która rozpocz a si od stworzenia nowego j zyka symetrii przez Evariste’a Galois. Ów francuski naukowiec, zanim zgin w pojedynku na tle uczuciowym i politycznym jako zaledwie dwudziestoletni m odzieniec, zaproponowa mianowicie nowy sposób rozumienia symetrii, zak adaj cy, e istniej pewne atomowe struktury symetryczne, z których mo na zbudowa wszystkie inne obiekty symetryczne. Mowa tu mi dzy innymi o wielok tach foremnych, na przyk ad pi ciok cie foremnym. Conway i jego zespó udokumentowali jednak w swoim atlasie, e istniej równie tak egzotyczne bestie jak Monster *, czyli p atek niegu, w którego przypadku mówimy o przestrzeni a 196 883-wymiarowej.
Chc c uczestniczy w kolejnym rozdziale prac, który mia nast pi po publikacji Atlasu, uda em si do Cambridge, aby porozmawia z Conwayem o tym, e przymierzam si do doktoratu z symetrii w matematyce. Kiedy wszed em do pokoju wspólnego, ujrza em grup studentów pochylonych nad siatk 19 na 19 pól i umieszczaj cych na niej bia e kamyki. Rozpozna em te pionki – pochodzi y ze staro ytnej gry go, ale najwyra niej nie grali w go, skoro na planszy by y tylko bia e kamienie.
Okaza o si , e grali w gr w ycie Conwaya. Jak ju wspomnia em, tak naprawd nie jest to w ogóle gra, a raczej przyk ad tak zwanego automatu komórkowego. Zabawa polega na umieszczaniu bia ych kamieni na polach planszy, które staj si dzi ki temu ywymi komórkami. Puste pola s z kolei komórkami martwymi. Obowi zuj jednak pewne regu y,
* Potwór.
okre laj ce, które komórki pozostaj w kolejnej generacji ywe, które umr , a które si narodz . To, jaki los czeka dane pole, zale y od o miu innych pól, które je otaczaj .
Oto regu y gry: przetrwanie – je li komórka jest ywa, to przetrwa do nast pnego pokolenia, o ile w ród o miu otaczaj cych j komórek ma dwóch lub trzech ywych s siadów; mier – komórka umiera, je li jej rodowisko jest zbyt zat oczone, to znaczy je li otaczaj j cztery lub wi cej komórek; albo umiera z powodu izolacji, je li s siaduje tylko z jedn yw komórk lub w ogóle nie ma ywych s siadów; narodziny – nowa komórka rodzi si , je li dane pole graniczy z dok adnie trzema ywymi komórkami.
Zabawa polega tu na wymy laniu coraz to nowych uk adów kamieni, które prowadz do interesuj cych zachowa w toku gry. Jedna wa na uwaga: gra nie ogranicza si do planszy dziewi tna cie na dziewi tna cie u ywanej w go – tak naprawd przeznaczona jest do gry na niesko czenie wielkiej dwuwymiarowej siatce. Plansza do go stanowi a po prostu dla studentów przydatne narz dzie do treningu, dzi ki któremu mogli zapozna si z zasadami. Je li zamiast kamieni go u yjemy czarnych i bia ych pikseli oraz komputera, b dziemy mogli znacznie lepiej przyjrze si , jak ró norodne jest ycie, które rodzi si w tej grze.
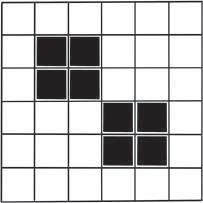
Ze wzgl du na to, jak skonstruowane s regu y, niektóre kon guracje nigdy si nie zmieniaj . Na przyk ad blok czterech ywych komórek z pokolenia na pokolenie pozostaje taki sam. Ka da ywa komórka jest otoczona przez trzy inne ywe komórki i w ten sposób prze ywa do nast pnego pokolenia, przy czym nie rodzi si tu adna nowa komórka. Taki blok czterech komórek nazywa si w grze w ycie martw natur
Istniej te kon guracje, które oscyluj , czyli okresowo si zmieniaj , pomi dzy jednym uk adem a drugim. Kiedy umie cimy obok siebie dwa bloki, ich komórki, które stykaj si naro nikami, umieraj z powodu nadmiaru s siadów, ale potem rodz si ponownie.
Gry to tak e opowie ci, w które zanurzamy si wraz z przyjació mi, co ma pewn przewag nad samotnym oddawaniem si lekturze. Mamy tu tak e mo liwo dzia ania i decydowania o tym, jak potoczy si nasza historia – mo e i powie wzruszy nas do ez, ale to w grze dopadnie nas prawdziwe poczucie winy zwi zane z naszymi w asnymi posuni ciami.
Oto ksi ka, która opowiada o ca ej masie szalonych, fantastycznych, niezwykle wci gaj cych gier, jakie ludzie dotychczas stworzyli w toku swojej bytno ci na ziemi. Gwoli cis o ci inne zwierz ta równie bawi si i graj w dzieci stwie – na przyk ad lwi tka walcz na niby, a na dalszych etapach ycia wykorzystuj w polowaniu zdobyte w ten sposób umiej tno ci. Nasz gatunek, którego równie doros e osobniki zajmuj si graniem, jest chyba jednak wyj tkiem.
Rzecz jasna, nie ka dy doros y lubi gra . Dla niektórych ca e to zamieszanie zwi zane z prowadzeniem rozgrywki i mierzeniem si z zasadami, które przyjmujemy z w asnej woli, aby osi gn jaki wymy lony cel, to zupe na strata czasu. Có , niew tpliwie jest to przyjemno dost pna osobom, które owym czasem dysponuj w pewnym nadmiarze. Wierz jednak, e gdy osi gniemy wreszcie ten utopijny moment, kiedy nie b dziemy musieli pracowa , bo wszystko b d robi y za nas maszyny, nasze ycie zacznie si obraca w a nie wokó grania.
Kocham gry. Uwielbiam je do tego stopnia, e gdziekolwiek jad , staram si tam dotrze do gier szczególnie lubianych przez mieszka ców danego kraju, a mój baga w drodze powrotnej nieodmiennie zawiera kilka z nich. Odkry em bowiem, e – podobnie jak historie opowiadane przez miejscowych pomagaj nam zrozumie inne spo ecze stwa – gry, w które graj ludzie z ró nych miejsc wiata, mog nam sporo powiedzie o ró nicach i podobie stwach mi dzykulturowych. W niektórych kulturach prym wiod gry losowe, a nie strategiczne, co by mo e odzwierciedla tendencj tych grup do przyjmowania fatalistycznej postawy wobec ycia zamiast wiary w mo liwo kszta towania w asnego losu. Podobnie na przyk ad wi ksza popularno gry polegaj cej na d eniu do zaj cia jak najwi kszego terytorium, takiej jak go, ni bardziej bezpo rednio agresywnej gry typu szachy zdaje si zdradza co nieco na temat warto ci piel gnowanych w danej spo eczno ci i jej sposobu postrzegania wiata. Niektóre gry rzeczywi cie uwydatniaj ró nice mi dzy kulturami, inne jednak s na tyle uniwersalne, e w rozmaite ich wersje gra si na ca ym wiecie.
Dzi ki grom i ich historii atwiej jest zrozumie , jak rozwija y si i wyodr bnia y poszczególne kultury. Mo na wr cz powiedzie , e gry s niczym ywe stanowiska archeologiczne, kryj ce w sobie nami tno ci i d enia naszych przodków. Powiedz mi, w co grasz, a powiem ci, kim jeste .
Kiedy siedz w domu i nie mog wyjecha , moja kolekcja gier pozwala mi powróci wspomnieniami do miejsc, z których je przywioz em. Ka da z nich to portal do którego z odwiedzonych niegdy krajów, paszport do innego wiata – czy to historycznego, geogra cznego, czy matematycznego. Zbiór gier otula mnie jak ciep y kokon i niezmiennie przypomina mi o tym, jak dalekie podró e mo emy odbywa we w asnych my lach, nie wychodz c z domu.
Nie jestem jednak historykiem, antropologiem ani psychologiem, lecz matematykiem.
Wydaje mi si , e jest mi z grami tak bardzo po drodze mi dzy innymi dlatego, e maj wiele wspólnego z matematyk – wspania dziedzin , któr pokocha em. Regu y gry s jak aksjomaty matematyczne, a sama rozgrywka przypomina odkrywanie, co z nich wynika. W moim odczuciu, graj c w gr , gramy w matematyk . Niejedna udana gra jest przecie uciele nieniem idei matematycznej. Gry polegaj ce na dopasowywaniu elementów, takie jak Dobble, wykorzystuj niezwyk e struktury geometryczne zbudowane w wielowymiarowej przestrzeni. Planszówki takie jak Wsi do poci gu * sprawdzaj si natomiast dzi ki systemowi punktowania, który równowa y ryzyko podejmowane przez gracza mo liw do uzyskania nagrod . Najlepsze gry maj proste zasady, które umo liwiaj prowadzenie zró nicowanych i z o onych rozgrywek. W staro ytnej grze go gracze na zmian uk adaj czarne i bia e kamienie na planszy 19 na 19 pól. Mimo tak prostego uk adu wyj ciowego mamy tu do czynienia z niesamowitym wr cz wachlarzem kierunków, w jakich gra mo e si potoczy . I to w a nie ma, wed ug mnie, wiele wspólnego z tym, co najpi kniejsze w matematyce. Bo przecie atwo jest okre li , czym s liczby pierwsze – to liczby niepodzielne** – a jednak, cho zajmujemy si nimi od dwóch tysi cy lat, wci potra nas zaskoczy . Jest jeszcze jeden powód, który sprawia, e moim zdaniem to w a nie matematyk dobrze sprawdzi si jako przewodnik po wiecie gier. Otó gracz, który ma w r kawie par sztuczek matematycznych, zazwyczaj ma te szans uzyska dzi ki nim przewag nad rywalem. Gry okre la pewien zbiór zasad wyznaczaj cych granice naszych posuni , matematyka za jest bardzo naturalnym j zykiem, dzi ki któremu mo emy bada implikacje logiczne owych zasad i wytyczy optymaln drog do osi gni cia celu.
Ludwig Wittgenstein uwa a , e nie da si zde niowa gry jako takiej. Termin „gra” by w jego rozumieniu przyk adem s owa, które mo na zrozumie i wyja ni wy cznie poprzez pos ugiwanie si nim, czyli stwierdzanie, e co jest gr , a co ni nie jest. Proces ten nazwa gr j zykow .
Ta ksi ka te jest gr – mo na j wr cz potraktowa jako prób zagrania w Wittgensteinowsk gr j zykow . Kiedy b d opowiada o grach, które uda o mi si zgromadzi podczas podró y dooko a wiata, ka da z nich b dzie stanowi a kolejny ruch w grze wed ug Wittgensteina.
W moim zbiorze gier pró no szuka sportu. Jedyny wyj tek stanowi popularna u Majów gra w pi k zwana pitz – nie mog em si oprze i musia em o niej opowiedzie . Na kartach tej ksi ki nie ma jednak pi ki no nej, koszykówki czy futbolu. Nie twierdz , e futbol to nie gra; ma o tego, uwielbiam go, jednak nie bez powodu okre lamy pewien typ rozgrywek odr bnym terminem, a mianowicie s owem „sport”. Sport to w moim odczuciu gra dla cia a, natomiast mnie interesuj gry dla umys u. Jako dziecko sk ania em si raczej ku nerdom graj cym w karty ni supergo ciom kopi cym pi k , w czym mia a zapewne wydatny
* Oryginalna, angielska nazwa tej gry to Ticket to Ride (wszystkie przypisy pochodz od t umaczki).
** A dok adniej: niepodzielne przez adne inne liczby ni przez 1 i przez same siebie.
udzia moja mikra postura. Takie osobiste preferencje nie umniejszaj , rzecz jasna, znaczenia sportu dla ludzko ci. Odgrywa on przecie podobn do wspomnianej ju rol przygotowawcz , gdy umo liwia trenowanie na wypadek niebezpiecze stwa. Jako przewodnik i matematyk mam jednak znacznie wi cej do powiedzenia na temat gier umys owych ni sportowych, opieraj cych si na brutalnej sile i wytrzyma o ci zycznej. Niektóre gry, o których opowiem, to w zasadzie niemal amig ówki – to zreszt kolejna koncepcja, któr warto wyja ni . W mojej ksi ce amig ówka cz sto awansuje do rangi pe noprawnej gry w momencie, gdy w czane s w ni inne osoby. Wordle przeskoczy o z kategorii amig ówek do gier, i to rozgrywanych w imponuj cej skali, w momencie gdy pojawi a si mo liwo udost pniania swoich statystyk innym. Elementem ró nicuj cym jest tu w a nie komponent zak adaj cy rywalizacj albo wspó prac z innymi. Czym zatem jest, powiedzmy, uk adanie pasjansa? Czy jest to amig ówka, czy gra, skoro aby wygra , trzeba gra przeciwko talii kart? A co z grami komputerowymi, w których gracz mierzy si z kodem? Wittgenstein ma racj : gra wymyka si wszelkim de nicjom. Zabieraj c was w podró w osiemdziesi t gier dooko a wiata, krok po kroku staram si spójnie opowiedzie , co tak naprawd mamy na my li, mówi c „gra”.
Ksi ka ta przypomina gr z jeszcze jednego wzgl du, a mianowicie istnieje mnóstwo sposobów grania w ni . Mo na j czyta od pierwszej do ostatniej strony, w kolejno ci, w jakiej je dla was u o y em, poznaj c ka d z gier w okre lonym porz dku, zgodnie z numerami, którymi s opatrzone. Mam jednak inn sugesti : rzu cie kostk (sze ciocienn ) i zacznijcie od gry oznaczonej wyrzuconym numerem. Kiedy ju si z ni zaznajomicie, rzu cie ponownie, dodajcie wyrzucon liczb oczek do poprzedniej i wykonujcie kolejne ruchy po tek cie, jakby cie grali w planszówk . Po dotarciu do ko ca listy wrócie po prostu do pocz tku. Na ko cu ksi ki znajdziecie tabelk z tytu ami gier – mo ecie odhacza te, które ju poznali cie w trakcie swojej wyprawy. Dzi ki temu ka dy mo e odby swoj podró , rozegra w asn ksi kow gr i w ten sposób stworzy now ksi k . (Mój wewn trzny matematyk nie móg sobie odmówi obliczenia, ile ró nych ksi ek mo e w ten sposób powsta . Dojd cie do tego sami, niech stanie si to dla was jeszcze jedn gr ). Nie jestem pierwszym autorem, który sugeruje ró ne sposoby czytania jednej ksi ki. Powie B.S. Johnsona pod tytu em Nieszcz ni sk ada si z arkuszy lu no umieszczonych w pude ku. Pierwszy i ostatni rozdzia s zszyte, ale to czytelnicy decyduj , w jakiej kolejno ci przeczytaj pozosta e dwadzie cia pi cz ci utworu. Oznacza to cznie 15 511 210 043 330 985 984 000 000 mo liwych, ró ni cych si od siebie ksi ek. Francuski poeta Raymond Queneau, wspó twórca eksperymentalnego ruchu Oulipo, postanowi da swoim czytelnikom jeszcze wi cej opcji i w tym celu skomponowa tomik sonetów, w którym ka dy z czternastu wersów ka dego poematu ma dziesi mo liwych wariantów. Moja ksi ka jest wyrazem zachwytu wobec matematyki, która kusz co wy ania si spod powierzchni wielu moich ukochanych gier. Równolegle do g ównej narracji zamie ciem tu fragmenty opisuj ce owe matematyczne wspania o ci. Zapraszam was do zanurzenia si w te fantastyczne opowie ci matematyczne, bo w ka dej z nich kryje si klucz do tworzenia, a cz sto te wygrywania gier. Je li jednak poczujecie, e robi si za g boko,
mo ecie mia o wróci na powierzchni . By mo e zdecydujecie si zajrze w te miejsca ponownie przy okazji kolejnej podró y przez ksi k .
W trakcie czytania pami tajcie, e ksi ka ta nie jest encyklopedi gier, wyczerpujcym s ownikiem czy kompendium zasad. Na ko cu zamie ci em kilka adresów stron internetowych, na których znajdziecie informacje na temat tego, jak gra w niemal ka d moliw gr . Z pewno ci znajd si tacy, którzy z pretensj zauwa , e nie uwzgl dni em tej czy innej gry. Có , taktownie podkre lam, e przecie to moja w asna, bardzo osobista kolekcja. Wybra em tytu y, które pozwalaj mi mówi o tym, w co gramy, w kategoriach lozo i, kultury, matematyki i socjologii.
Ka dy rozdzia dotyczy innej cz ci globu i zach ca do odkrywania, w co graj jej mieszka cy. Od Indii po Chiny, od Afryki po Ameryk – przemierzymy wiat, zasiadaj c z miejscowymi do gry. Pomi dzy rozdzia ami geogra cznymi znajdziecie moje morskie interludia. Przenosz c si z regionu do regionu, b d zatrzymywa si pomi dzy nimi, aby przyjrze si rozmaitym aspektom lozo cznym, matematycznym czy kulturowym gier, które nie s w oczywisty sposób zwi zane z adnym konkretnym punktem na mapie wiata.
Kiedy zestawi em omawiane tu gry i powi zane z nimi tematy, zupe nie nieoczekiwanie okaza o si , e jest ich dok adnie osiemdziesi t. A poniewa chodzi tu o podró po grach z ca ego wiata zarówno w sensie historycznym, kulturowym, matematycznym, jak i geogra cznym w a nie, nie mog em powstrzyma si od nawi zania do s ynnej opowieci Jules’a Verne’a o podj tej przez Phileasa Fogga próbie okr enia wiata w ci gu osiemdziesi ciu dni i postanowi em wykorzysta jego wypraw jako ram narracyjn mojej historii. Dzi ki opisanym tu grom uda o mi si wyruszy – zupe nie jak Fogg – we w asn podró wokó globu, w ramach której przeprawiam si po morzach i l dach z jednego kontynentu na drugi. Moj nieocenion towarzyszk , biletem wst pu i kluczem do wszystkich drzwi, jakie napotkam, moim Passepartout* b dzie natomiast matematyka – to razem z ni wybieram si w podró w osiemdziesi t gier dooko a wiata.
* U yte przez autora, pochodz ce z j zyka francuskiego s owo passe-partout oznacza „sta y bilet wst pu”, a tak e „klucz uniwersalny”, a jednocze nie nawi zuje do postaci z powie ci Verne’a –Jean Passepartout to kamerdyner towarzysz cy Foggowi w podró y dooko a wiata, bez którego bezpieczne i terminowe zako czenie jej by oby zapewne niemo liwe.