Spistreści
Wstęp9
1.Wybranefaktyzanalizyialgebryliniowej11
1.1.Podstawowepojęciaidefinicje ...................11
1.1.1.SymboleLandaua O i o ..................13
1.2.Macierze ...............................14
1.2.1.Funkcjemacierzy ......................14
1.2.2.Wartościiwektorywłasnemacierzy
1.2.3.Dodatniośćwprzestrzeniachwektorowych ........23
1.2.4.MacierzeMetzleraitwierdzeniePerrona-Frobeniusa..24
1.3.Uogólnieniapojęciaróżniczkowalności
1.4.Rachunekróżniczkowyfunkcjiwieluzmiennych
1.4.1.TwierdzenieTaylora
1.5.Twierdzenieofunkcjiuwikłanej
2.Równaniaróżniczkowei
2.1.Równaniaróżnicowe
2.1.1.Liniowerównanieróżnicowe ................38
2.1.2.Równaniaróżnicowesprowadzalnedorównanialiniowego40
2.2.Przeglądrównańróżniczkowychzwyczajnych mającychjawnerozwiązania ....................44
2.2.1.Równaniaozmiennychrozdzielonych ...........45
2.2.2.Równanialiniowe ......................53
2.2.3.Wybranerównaniawyższychrzędów ...........55
2.2.4.Równaniaredukowalnedorównańpierwszegorzędu..56
3.ZagadnienieCauchy’ego65
3.1.Podstawowepojęcia ........................65
3.2.Twierdzeniaoistnieniuijednoznacznościrozwiązań ......66
3.2.1.Pojęciaiwynikipomocnicze ................66
3.2.2.TwierdzeniePicarda-Lindel¨ofa..............68
3.2.3.Przedłużanierozwiązań... ...............70
3.2.4.Rozwiązalnośćukładówrównańliniowych ........76
3.2.5.Innetwierdzeniaoistnieniurozwiązań ..........86
3.2.6. Ciągłazależnośćrozwiązaniaodwarunkówpoczątkowych iparametrów ........................89
3.2.7.Nieujemnośćrozwiązań ..................92
3.2.8.Nieujemnośćrozwiązańukładówrównańliniowych...93
3.3.Nierównościróżniczkowe ......................94
4.Układydynamiczne107
4.1.Pojęciapodstawowe ........................107
4.2.Długookresowadynamikaukładówliniowych ..........109
4.3.Trajektorie,portretyfazoweizbiorygraniczne .........114
4.3.1.Trajektorieiichwłasności .................114
4.3.2.Elementarnemetodyszkicowaniaportretówfazowych.117
4.3.3.Zbiorygraniczne ......................126
4.4.Stabilnośćrozwiązań ........................130
4.5.Topologicznarównoważnośćukładówdynamicznych ......140
5.FunkcjaLapunowaijejuogólnienia145
5.1.Lokalnastabilnośćpunktustałego ................145
5.2.Globalnastabilnośćpunktustałego ................153
5.3.ZasadaLaSalle’a ..........................157
5.4.Stabilnośćbrzegowychpunktówstałych .............160
5.5.NieróżniczkowalnefunkcjeLapunowa ...............164
5.6. TwierdzeniaodwrotnedotwierdzeniaLapunowaiichzastosowania 172
6.Dalszeaspektyteoriiukładówdynamicznych183
6.1.Rozmaitośćstabilna,niestabilna,centralna ...........183
6.2.OdwzorowaniePoincar´ego.....................203
6.3.TwierdzeniePoincar´ego-Bendixona ................209
6.4.KryteriumBendixonaiuogólnienieDulaca ...........218
6.5.Bifurkacje ..............................225
6.5.1.Bifurkacjelokalne ......................225
6.5.2.BifurkacjaHopfa ......................230
6.5.3.Bifurkacjeglobalne... ..................237
7. Modelewieloskaloweizaburzoneukładyrównańróżniczkowych245
7.1.TwierdzenieTichonowa ......................247
7.2.JednostajnetwierdzenieTichonowa ................252
7.3.Opóźnionawymianastabilności ..................257
7.3.1.Bifurkacjatranskrytyczna .................259
7.3.2.Bifurkacjawidłowa .....................263
7.3.3.Bifurkacjawsteczna... .................264
8.Falewędrujące275
8.1.Falewędrującewkontekścieukładówdynamicznych ......276
8.2.Metodykonstrukcjirozwiązańwpostacifalwędrujących ....294
8.2.1.Metodatangensahiperbolicznegoijejuogólnienia...295
8.2.2.Potrzebneiniepotrzebneuogólnienia ...........300
9.Podstawowa liczbareprodukcyjna305
9.1.DodatkowewłasnościmacierzyMetzlera .............305
9.2.Definicjapodstawowejliczbyreprodukcyjnej ...........306
9.2.1.Macierznastępnegopokolenia ...............306
9.3.MatematycznadefinicjaR0 ....................309
9.4.R0 alokalnaiglobalnastabilnośćDFE ..............322
Rysunek1.1.Widmookresowejmacierzy A (pełnekółka)wjejkolespektralnym ijegoprzesunięciewlewoo ρ(A )(pustekółka).Widzimy,żewartościwłasne otejsamejwartościbezwzględnejco λmax (aniżadneinne)niemogąmiećtej samejczęścirzeczywistejcodominującawartośćwłasnamacierzyMetzlera B = ρ(A )I + A
Definicja1.3. Mówimy,żemacierzMetzlera B jestnieredukowalna,jeślimacierz A jestnieredukowalna.
Oczywiściedefinicja1.3niezależyod z .Istotnie,zgodniezuwagą1.4, współczynnikinaprzekątnejnieodgrywająroliwdefinicjinieredukowalności macierzy A .Widzimyteż,żeklasyfikacjamacierzyMetzlerajestprostszaniż macierzynieujemnych.Jakwidaćnarysunku1.1,jeśli B jestnieredukowalna, toistniejeprostawartośćwłasna λmax macierzy B i,nawetjeśli B jestmacierzą okresową, λmax z> λ dlawszystkichinnychwartościwłasnych λ macierzy B .Dokładniej,zachodzinastępującawersjatwierdzeniaPerrona-Frobeniusa dlamacierzyMetzlera(patrz[76,Theorem2.6]).
Twierdzenie1.3. Załóżmy,że B jestnieredukowalnąmacierząMetzlera.Istniejewartośćwłasna τmax macierzy B ,którajestrzeczywista,prostaoraz spełnia
τmax > λ
dlawszystkich λ ∈ σ (B ), λ = τmax .Wartościwłasnej τmax odpowiadająjedyne, zdokładnościądostałychmnożników,dodatniepraweilewewektorywłasne.
WieleużytecznychwłasnościmacierzyMetzleramożnaudowodnićwstosunkowoprostysposóbprzywykorzystaniumetodteoriiukładówdynamicznych
Rozdział2.Równaniaróżniczkowei różnicowe
Przykład2.3. (Dynamikapopulacyjnawczasieciągłym)Jeślirozważamy populacjebezwyróżniającychsięsezonówrozrodczych,któremogąbyćobserwowanewdowolnymczasie,topowinniśmyrozważaćmodeleopisujące zmianyzachodzącewsposóbciągły.Odpowiednikiemdyskretnegomodelu maltuzjańskiego(2.14)wczasieciągłymjest
Jesttorównanieozmiennychrozdzielonych,któregorozwiązaniemjestfunkcja
gdzie P (t0 )jestwielkościąpopulacjiwchwili t0
Analogiczniedoprzypadkuzczasemdyskretnymmodel (2.20) niejest realistyczny,zwłaszczadladużych t.Argumentującpodobniejakpoprzednio, możemyrozważyćmodellogistycznyzczasemciągłym dP dt = rP 1 P K ,P
gdzie r jestnaturalnymwspółczynnikiemwzrostu,a K jestpojemnością środowiska.Równanietojestteżrównaniemozmiennychrozdzielonych,które przyzałożeniu,że P (t) =0i P (t) = K możnazapisaćjako 1
Całkującobiestronyod t0 do t iwykorzystującwarunekpoczątkowy,otrzymujemy K r P P0 ds s(K s) = t t0 .
Stosującrozkładnaułamkiproste,dostajemy K r P P0 ds (K s)s = 1 r P P0 1 s + 1 K s ds = 1 r ln P P0 K P0 K P .
Możnaudowodnić(patrzprzykład3.2),żejeśli0 <P0 <K ,to P (t) <K dla wszystkich t>t0 .Podobnie,jeśli P0 >K ,todostajemy P (t) >K dla t>t0 .
Zatem(K P0 )/(K P (t)) > 0,więc r (t t0 )=ln P P0 K P0 K P ,
co,pokrótkichrachunkach,daje P (t)= P0 K P0 +(K P0 )e r (t t0 ) . (2.23)
Abyzilustrowaćpowyższewyniki,musimyznaćparametrywobumodelach.Użyjemytutajwartościpodanychwksiążce[15],przytoczonychzaU.S. DepartmentofCommerce.Wedługtychdanychpopulacjanaświeciew1965 rokuwynosiła3,34miliardyiwdekadzie1960–1970wzrastaławprzeciętnym tempie2%rocznie.Zatem P (t0 )= P (1965)=3,34 · 109 , zaś r =0, 02,i(2.21) przyjmujepostać
P (t)=3,34 · 109 e 0,02(t 1965) .
Wmodelulogistycznymobserwowanywspółczynnikwzrostuwchwili t0 możnazapisaćjako r0 = r 1 P (t0 ) K .
Zgodniez[15]przyjmiemy r =0,029,codla P (t0 )=3,34 · 109 daje K =10,76 miliardów.Otrzymamywówczasrówność
P (t)= (3,34 109 )(10,76 109 ) 3,34 · 109 +((10,76 · 109 ) (3,34 · 109 ))e 0,029(t 1965) .
Narysunku2.1jestprzedstawioneporównanieobserwowanychwartościpopulacjiświatazprzewidywaniamiopartyminamodelumaltuzjańskimilogistycznym.
Choćmodellogistycznyjestwciążzbytprosty,abymożnagobyłowykorzystywaćwpoważnychbadaniachdemograficznych,maonwielejakościowych
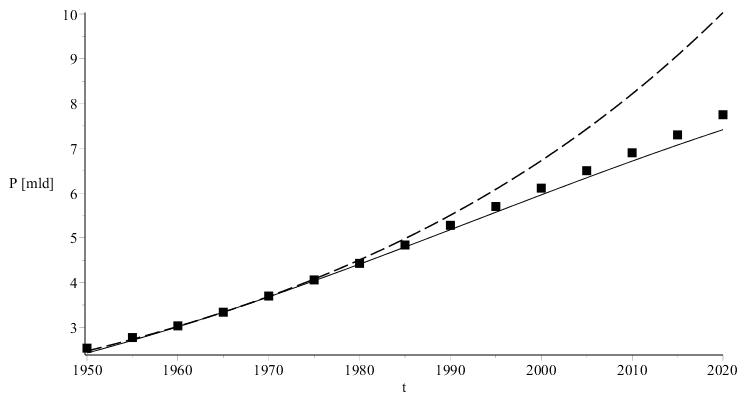
Rysunek2.1.Populacjaświata.Danerzeczywiste(punkty),wzrostmaltuzjański (liniakreskowa)iwzrostlogistyczny(liniaciągła)
6.1.Rozmaitośćstabilna,niestabilna,centralna 193
Zgodnieztwierdzeniem6.1mamywięcdwuwymiarowąrozmaitośćstabilną orazjednowymiarowąrozmaitośćniestabilnąstycznądoprostej
Narysunku6.3możemyzauważyćtrajektorię,którawrazzewzrostemczasu nawijasięna X u corazbardziejzbliżającsiędo X u .Rzuttejtrajektoriina płaszczyznęstyczną X s jestogniskiemasymptotyczniestabilnym(rysunek6.4).

Rysunek6.3.Trajektorieukładu (6.14)

Rysunek6.4.Rzuttrajektoriina płaszczyznęstyczną X s
Przykład6.4. [81,p.261]Rozważmyukładrównań x1 = x1 + x2 +3x2 2 x2 = x2 . (6.15)
Zauważmy,żewpunkcie P =(0, 0)Jakobianmadwiewartościwłasne: 1 oraz1. Ponadtozachodzi X s = L in 1 0 oraz X u = L in 1 2 (porównajrysunek6.5).
Łatwopokazać(zaczynającoddrugiegorównania),żedladowolnegowarunkupoczątkowego(x10 ,x20 )rozwiązaniaukładu(6.15)sąpostaci
x1 (t)= x10 e t + x20 sinh t + x2 20 (e2t e t ) x2 (t)= x20 et . (6.16)
Rysunek6.8.Odwzorowaniepierwszegopowrotu
OdwzorowaniePoincar´egodostarczainformacjiotrajektoriachokresowych.
Jeżeli P (x0 )= x0 ,czyli x0 jestpunktemstałymodwzorowaniaPoincar´ego, totrajektoriategopunktujestokresowa.Odwrotnie,jeśliΓprzecinapewną trajektorięokresowąwpunkcie x0 ,tojestonpunktemstałymodwzorowania Poincar´ego.Ponadtobadaniepochodnejtegoodwzorowaniawpunkcie x0 dostarczainformacjiostabilnościtrajektoriiokresowej γ ,oczymmówiponiższe twierdzenie.
Twierdzenie6.5. [2,Proposition23.5] Jeśli
|σ (JP (x0 ))| < 1, to γ jestasymptotyczniestabilna.
Zauważmy,żezastosowanieodwzorowaniaPoincar´egodoukładówdwóch lubtrzechrównańróżniczkowychznacznieupraszczabadanietychukładów, ponieważwymiarprzestrzeni,wktórejprowadzimyanalizęzmniejszasięo1.
Przykład6.9. Rozważmyukład (4.25),którywewspółrzędnychbiegunowych przyjmujepostać
r = r (1 r ) θ =1 .
Przyjmijmynastępującewarunkipoczątkowe: r (0)= x, θ (0)=0.Wówczas otrzymujemy
r (t,x)= xet 1 x + xet ,θ (t)= t,
