Manifest naukowy
Zanim przejdziemy dalej, oto jedno zdanie, w które naprawdę wierzę i które chcę, żebyście zapamiętali: każdy może być naukowcem. Powiem nawet więcej: każdy jest naukowcem.
Gdy patrzymy wstecz na historię naszej cywilizacji, prędzej czy później zdajemy sobie sprawę, że nikt nigdy nie urodził się ani nie został wyszklony, aby zostać naukowcem lub wynalazcą zmieniającym świat. Pierre de Fermat1), siedemnastowieczny geniusz, którego badania wpływają na matematyków od wielu pokoleń, zarabiał na życie jako prawnik. Albert Einstein zrewolucjonizował całą fizykę, choć pracował w urzędzie patentowym. Problem polega na tym, że w dzisiejszych czasach ludzie są zniechęcani do nauki. Kiedy teorie Einsteina zostały potwierdzone w eksperymentach, stał się celebrytą bardziej rozpoznawalnym niż gwiazdy muzyki. Najważniejsze gazety na świecie ogłosiły konkursy na opisanie teorii względności w najprostszej możliwej formie. Uczestników były tysiące – ludzi różnych profesji, nie tylko fizyków. Świat był naprawdę zafascynowany tym tematem. Obecnie rokrocznie dokonywanych jest więcej odkryć niż w ciągu całych dziesięcioleci w poprzednim stuleciu. Lecz my ich nie dostrzegamy. Albo nie chcemy widzieć. Albo nie mamy na to czasu. Dlaczego?
Pierwszym powodem jest pośpiech. Wyścig z czasem jest po prostu modny. Niestety to samo dzieje się w szkole i w miejscu pracy. Jako nauczyciel akademicki słyszałem już wiele razy: „To mi nie będzie potrzebne. Chcę się nauczyć tylko tego, co będę wykorzystywać w pracy”. A takie podejście to początek końca.
1) Pierre de Fermat (1601–1665) – francuski prawnik i matematyk-amator, fizyk matematyczny, a z wykształcenia lingwista, od 1631 r. radca parlamentu (ówczesna nazwa sądu) w Tuluzie. Zajmował się przede wszystkim teorią liczb, w której sformułował m.in. słynne wielkie twierdzenie Fermata.
x Manifest naukowy
Końca kreatywności. Wiedza kształconych teraz ludzi jest coraz bardziej ograniczona, skierowana tylko na konkretne zadania. Z błyskotliwych, myślących istot powoli zmieniamy się w narzędzia. Ludzie zaczynają unikać teorii i uczą się tylko, jak je stosować w praktyce. Nie ma czasu na zrozumienie kontekstu całej koncepcji – mamy go tylko tyle, aby zastosować rozwiązania, które nam pokazano. Nie mamy czasu zapytać „dlaczego?”, zostajemy wyłącznie z pytaniem „jak?”. Drugim powodem jest jedno z największych kłamstw, które z powodzeniem powtarza się wszędzie coraz młodszym ludziom. Mówi się im, że nie będą w stanie czegoś zrozumieć. Niektórzy są uważani za „humanistów”, więc nie powinni nawet próbować patrzeć na równanie matematyczne (ponieważ mogliby od tego oślepnąć). Ludzie są w jakiś sposób klasyfikowani już po pierwszej próbie zrobienia czegoś. A czy wiecie, że pierwsza wersja pracy doktorskiej Einsteina została odrzucona? Albo że przez ponad dwa lata bezskutecznie szukał pracy jako nauczyciel? Co by mu dziś powiedziano? Prawdopodobnie coś w stylu: „Zostaw to. Po prostu naucz się korzystać z tego oprogramowania. Pracodawca potrzebuje ludzi, którzy to umieją. I do tego dobrze płaci”.
Nie rezygnujcie z wiedzy. Nie patrzcie na widoczne korzyści. Nie rezygnujcie, nawet jeśli szef wam powie, że dana wiedza nie jest niezbędna. Kontakt z nauką nie tylko rozwija wasze umiejętności, ale co ważniejsze, rozwija umysł. Jeśli wyszkolicie swój mózg, żeby unikał wyzwań, prędzej czy później znajdziecie się w sytuacji, w której nie będziecie mieć zielonego pojęcia, co robić. Będziecie mieli w głowie pustkę. Po prostu nauczcie się interesować światem. Porzućcie na chwilę zwyczajowe metody i standardy pracy i spójrzcie na swoje codzienne obowiązki z punktu widzenia obserwatora. Zatrzymajcie się przez chwilę na ulicy i pomyślcie o materiałach, z których jest wykonana. Najlepsze jest to, że nie musicie się uczyć kreatywności. Musicie sobie tylko przypomnieć, jak to jest być twórczym. Dzieci są bardzo kreatywne i zadają tysiące pytań. Niestety tak się składa, że gdy dorastają, mówi się im, że nie muszą znać wszystkich odpowiedzi.
Nigdy nie przestawajcie zadawać pytań. Ciekawość jest jednym z naszych najsilniejszych instynktów. Nie walczcie z nią, traktujcie jak dar. Uczcie się i bądźcie z tego dumni, bez względu na wiek. Podejście naukowe może pomóc znaleźć rozwiązania i w pracy i w życiu osobistym. Ciekawość wspiera aktywność umysłu i zapobiega demencji.
Nie wierzcie nikomu, kto mówi, że nie jesteście w stanie czegoś zrozumieć. Wszyscy rodzimy się z tą samą ciekawością w naszych umysłach i sercach. Podążajcie za nią.
Każdy jest naukowcem.
2. Sztuczna inteligencja: sformułowanie rodem z science fiction, które zmieniło świat
Jak można się spodziewać, problem plecakowy rzadko jest rozważany naukowo w sytuacjach takich jak ta opisana powyżej. Jego realny wpływ można zauważyć w wielu obszarach i aspektach alokacji zasobów, jak w przypadku wyboru najlepszego portfela inwestycyjnego – które akcje kupić (i ile z nich na każdą firmę), w które zainwestować swoje oszczędności w najlepszy dla nas sposób: stabilny, czy w obciążony dużym ryzykiem, lecz z ogromną prognozą zysku. Inny przykład? Jak optymalnie połączyć wiele różnych substancji chemicznych, aby uzyskać lek, który najlepiej eliminuje określone wirusy. Jeśli zastanowić się nad tym głębiej, można dojść do wniosku, że sedno problemu jest dokładnie takie samo jak w przykładzie ze złodziejem. Problem plecakowy jest popularniejszy, niż myślimy. A największym wyzwaniem jest to, o czym już wspomnieliśmy – nie ma szybkiego sposobu na znalezienie rozwiązania. Wystarczy powiedzieć, że jeśli mamy dziesięć elementów do wyboru, musimy sprawdzić ponad tysiąc rozwiązań! Ale tutaj pojawia się światełko w tunelu – do pomocy przychodzi nam technologia słabej sztucznej inteligencji zwana algorytmem genetycznym (patrz rozdział 4). Ta metoda, zainspirowana procesem ewolucji biologicznej, szybko generuje coraz więcej rozwiązań i łączy je ze sobą, aby znaleźć optymalny wynik w rozsądnym czasie.

Tak, to jest pierwsza ramka z cyklu „Ale kosmos!”. Czujecie się trochę przestraszeni lub trochę niekomfortowo? Zupełnie niepotrzebne. Po prostu śledźcie tekst i cieszcie się małym wycinkiem wiedzy informatycznej. Małym, ale niezwykle ważnym. Aby go zrozumieć, musimy sobie przypomnieć, jak działa komputer. Maszyny po prostu postępują zgodnie z komendami przekazanymi przez twórców oprogramowania. Niezależnie od tego, do czego są zaprojektowane (do pokazywania zdjęć, obliczania wydatków, wyświetlania filmów itp.), za graficznym interfejsem użytkownika (GUI) widać, że wszystko, co się dzieje, to operacje matematyczne. Im więcej operacji musi wykonać nasz komputer, tym więcej potrzeba czasu, a nawet najnowszy komputer działa czasami powoli. Podstawową operacją matematyczną jest mnożenie, którego informatycy zwykle używają jako odniesienia do określenia, jak złożony lub czasochłonny jest dany algorytm. Im więcej mnożeń jest niezbędnych, tym większa złożoność. Aby to zrozumieć, grupujemy wszystkie algorytmy (techniki) w różne kategorie. Ich definicje są dość skomplikowane, więc nie będziemy się w to zbytnio zagłębiać. Możemy to uprościć, mówiąc, że istnieją
Algorytm czy heurystyka?
dwie główne kategorie: P (dla szybkich algorytmów) i NP (dla czasochłonnych). Algorytm silni należy do klasy P: dla n! musisz wykonać n – 1 mnożeń, na przykład 5! = 1 * 2 * 3 * 4 * 5, więc mamy 4 mnożenia (5 – 1). Im większa liczba, tym więcej mnożeń trzeba wykonać, lecz nadal liczba obliczeń nigdy nie jest większa od wartości wejściowej, którą oznaczamy jako O(n). „P” oznacza wielomian (ang. polynomial) jako czas potrzebny do wykonania danego zadania – innymi słowy jesteśmy pewni, że algorytm zakończymy w ramach iluś podstawowych operacji będących którąś potęgą danych początkowych, na przykład O(n2), lub O(n3) itp.
Z kolei mamy wspomniany wyżej „problem plecakowy”. Policzmy, ile obliczeń musi wykonać maszyna. Załóżmy, że mamy 10 przedmiotów do wyboru. Każdy element można albo umieścić w plecaku, albo zostawić, co daje nam do sprawdzenia dwie opcje. To daje nam dwie możliwości dla każdego obiektu:
(TV)(laptop)(…)
Przedmiot123 4 5678910
Czy jest w Plecaku?T/NT/NT/N T/NT/NT/NT/N T/N T/N T/N
Liczba możliwości 2 2 22222222
Chociaż na pierwszy rzut oka to niewiele, prawdziwa siła tkwi w liczbie tych alternatywnych możliwości, które muszą być traktowane niezależnie (ponieważ nie możemy oprzeć jednego wyniku na innych – musimy sprawdzić wszystkie).
Tak więc, aby obliczyć ostateczną liczbę możliwości (aby przygotować plecak z najbardziej opłacalnym łupem), musimy pomnożyć wszystkie możliwości dla każdej pozycji: 2 * 2 * … * 2 (dziesięć razy) =210 = 1024. Nadal niewiele? Jeśli mamy do sprawdzenia 20 przedmiotów (co nie jest dużą liczbą), system musiałby sprawdzić ponad milion kombinacji (220), a dla 30 elementów – ponad miliard (230). W przypadku większej liczby przedmiotów liczba ta zaczyna rosnąć jeszcze szybciej: dla 58 elementów (co nie jest dużo w przypadku liczby towarów na przeciętnej półce sklepowej) znalezienie odpowiedzi zajęłoby najsilniejszemu superkomputerowi (takiemu jak Summit firmy IBM® lub TaihuLight chińskiej firmy Sunway) rok. W przypadku 270 elementów liczba możliwości do sprawdzenia znacznie przekroczyłaby liczbę atomów we wszechświecie! Taka liczba jest nie do wyobrażenia. Problem plecakowy (wraz z wieloma innymi) należy do klasy NP, gdzie skrót ten oznacza niedeterministyczny czas wielomianowy. Nie są znane szybkie algorytmy do znalezienia takiego rozwiązania. Problemy pozostałyby nierozwiązane, może na zawsze, chyba że użyjemy heurystyki (takiej jak ta, będąca podstawą technik SI).
„Chcę zagrać w grę”
Istnieje pewna bardzo ładna legenda na temat pochodzenia szachów. Historia rozgrywa się w pałacu króla czy sułtana, gdzieś pomiędzy Azją a Bliskim Wschodem. Pewnego dnia pałac odwiedził wędrowny naukowiec i filozof, który przyszedł zaprezentować monarsze swoją nową grę planszową. Tą grą były oczywiście szachy i po kilku partiach władca był tak zachwycony, że postanowił nagrodzić twórcę czymkolwiek ten tylko zamarzy. Podróżny odmówił, mówiąc, że jest to podarunek, ale król nie przestawał nalegać. Naukowiec zatem powiedział, że ma bardzo szczególne życzenie – chciał dostać pewną określoną liczbę ziaren ze spichlerza władcy, ściśle związaną z ofiarowaną grą (rysunek 2.4).

Rysunek 2.4. 64 pola szachownicy
Chciał dostać jedno ziarno na pierwsze pole na szachownicy, a następnie podwojoną liczbę ziaren na każdy kolejne pole, a więc 2 ziarna, a następnie 4, 8, 16, 32 itd. Władca się zaśmiał i zgodził. Jednak kiedy przybyli matematycy z królewskiej akademii, aby pomóc w obliczeniach, król zdał sobie sprawę, jak bardzo się mylił. Mnożenie przez 2, choć to nie wydaje się dużo, jest bardzo trudną operacją (przykład można również zobaczyć we wcześniejszej ramce „Ale kosmos! Złożoność”).

Rysunek 3.1. Piramida szampanek – po napełnieniu kieliszki „przesyłają” napój do niższych warstw
Ważne, by pamiętać, że sposób działania pojedynczego neuronu jest dość prosty, zatem absolutnie niewystarczający do zarządzania naszymi myślami, nadziejami i lękami. Prawdziwa moc naszych umysłów jest ukryta w połączeniach między neuronami. Każdy neuron jest połączony średnio z około 7000 innych komórek. Można więc błyskawicznie sobie uświadomić, że łączna ilość tych połączeń, zwanych synapsami, wynosi nawet aż 1015, czyli innymi słowy, milion miliardów. Jak ogromna jest ta liczba? Wysokość wieży zbudowanej z takiej liczby monet jednopensowych, ułożonych jedna na drugiej, przekroczyłaby odległość Ziemia – Słońce ponad siedmiokrotnie! Synapsy transmitują sygnał elektryczny, który, o ile jest wystarczająco silny, umożliwia im aktywowanie kolejnych neuronów. Cała struktura jest niezwykle skomplikowana i trudna do szczegółowego monitorowania – wyobraźmy sobie, że nasza piramida kieliszków jest wielkości Ziemi, a nalewanym szampanem są połączone populacje Wielkiej Brytanii i Australii.
7. Przyszłość ze sztuczną inteligencją
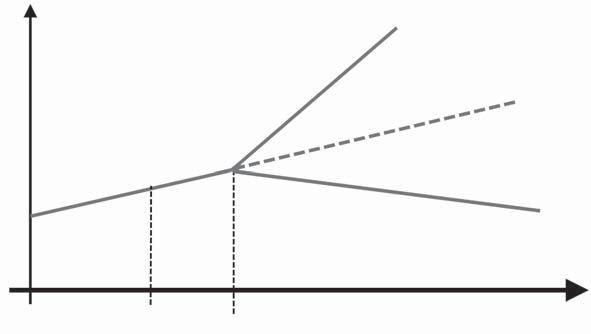
Rysunek 7.3. Przyszłość. Jaką drogę obiorą przyszłe pokolenia?
Wspomniałem wcześniej, że wśród twórców sztucznych sieci neuronowych znacznie bardziej popularne jest naprawianie nieoczekiwanych zachowań systemu poprzez prezentowanie nowszych i bardziej odpowiednich przykładów do nauki niż próby ręcznej zmiany czegokolwiek w strukturze sieci. Stajemy zatem przed nowym wyzwaniem: mamy nie tylko zmodyfikować narzędzie, lecz także zrozumieć, co ono „myśli i planuje zrobić” (niezależnie od tego, co te dwa czasowniki naprawdę tutaj oznaczają). Zrozumienie jest kluczem do przyszłości i musimy zaakceptować fakt, że w miarę jak techniki sztucznej inteligencji stają się coraz bardziej złożone i bliższe silnej sztucznej inteligencji, będziemy w stanie pojmować coraz mniejszą liczbę ich predyspozycji. Po zastanowieniu możemy określić poziomy umiejętności sztucznej inteligencji z perspektywy ludzkich zdolności. Ponumerujmy je od 0 do 4, co będzie odpowiadać przyszłej osi czasu:
Poziom 0 – możemy: większość obecnych aplikacji SI na pewno jest teraz na tym poziomie. Innymi słowy, systemy naśladują niektóre z naszych zdolności i funkcji, więc nie mamy problemu ze zrozumieniem lub powtórzeniem tych zautomatyzowanych działań. Jeśli z jakiegoś powodu aplikacja nie działa, możemy (dzięki naszej wiedzy i umiejętnościom) ją zastąpić; może wolniej, ale nadal jest to dla nas wykonalne. Tak więc, na przykład
