Klar, Parat, Tænk 4 by Alinea

Lone Anesen og Nina Winther

Tænke n de Klasserum

Klar, Parat, Tænk

Klar Parat Tænk

Særtryk © Alinea 2025

Forfattere: Lone Anesen og Nina Winther

Redaktion: Jakob Thomsen

Design: andresen design

Illustrationer: Pernille Mühlbach

Trykt hos: Eurographic 1. udgave, 1. oplag 2025

Denne bog er beskyttet i medfør af gældende dansk lov om ophavsret. Kopiering må kun ske i overensstemmelse med loven. Det betyder f.eks. at kopiering til undervisningsbrug kun må ske efter aftale med Copydan Tekst og Node. Det er ikke tilladt at udføre tekst- og dataminering (TDM) af bogen, herunder til brug for træning af AI-teknologier m.v., uden forlagets forudgående skriftlige samtykke.

Alinea støtter børn og unge

Alinea er en del af Egmont, der som Danmarks største mediekoncern har bragt historier til live i mere end 100 år. Egmont er en dansk fond, som hvert år uddeler 100 millioner kroner til børn og unge, der har det svært.

alinea.dk

Lone Anesen og Nina Winther

Klar, tænk…

Frugtspyd

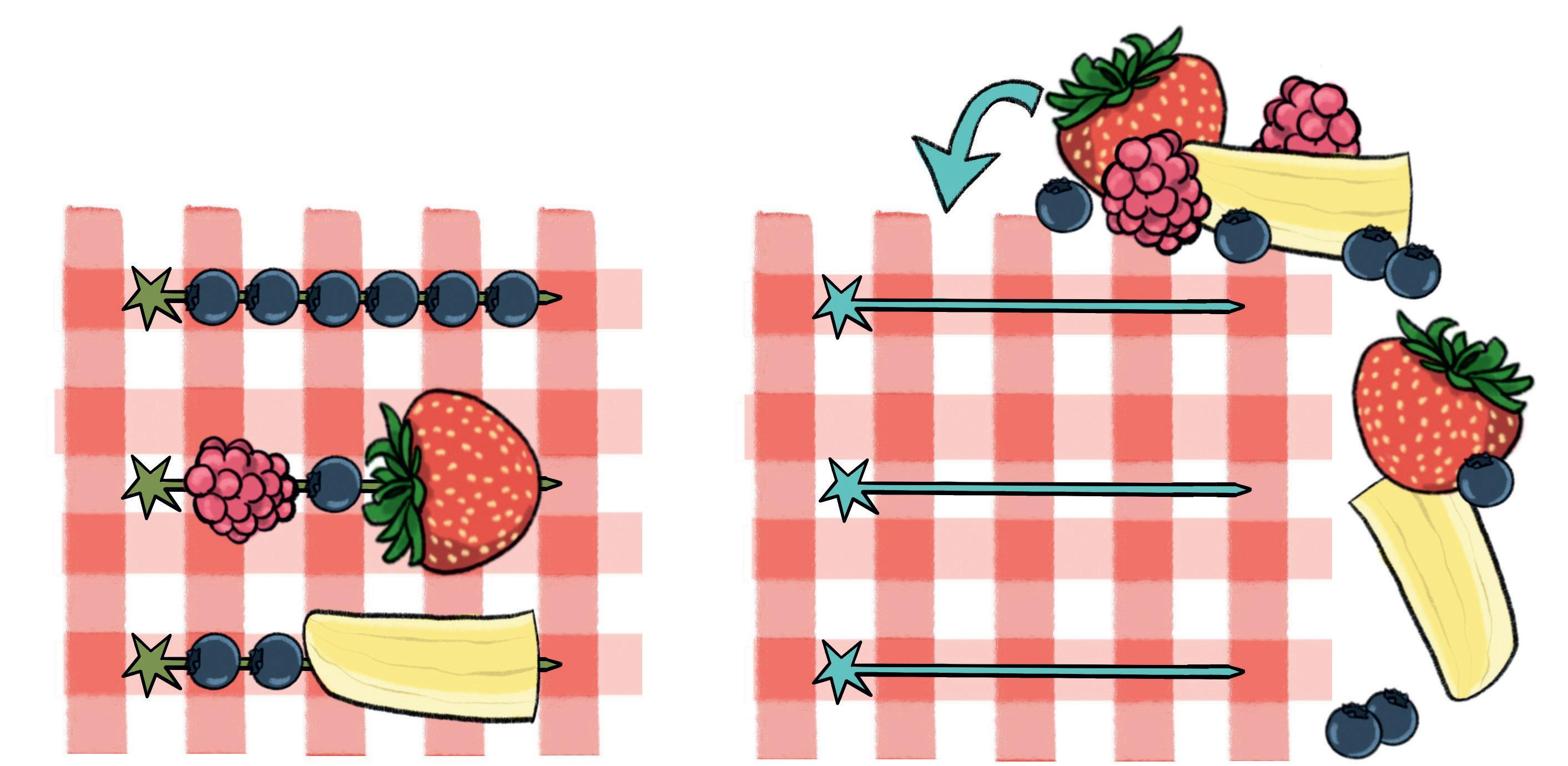
Baggrund

Brøk-veksling: Opgaven omhandler brøker forstået som en længde på en slags tallinje (0-1), her repræsenteret via et frugtspyd. Enhederne på tallinjen svarer til et antal blåbær, i intro opgaven og den første udvidelse svare ét blåbær til sjettedele og i den sidste til tolvtedele. De andre bær svarer til en veksling af blåbær, fx svarer et hindbær til 2 blåbær, altså 2 6 = 1 3

Eleverne kan via frugt få en fornemmelse for sammenligninger af brøkdele, som længder på en tallinje, der tilsammen giver 1 hel. Opgaven kan pege hen imod forkortelser af brøker.

At samme brøk kan skrives som 2 6 og 1 3 og at 1 3 måske giver den bedste forestilling af stor brøken egentlig er.

Opgaven kan derfor give en snak om, hvilket svar (den forkortede udgave), der er smartest at bruge som svar.

Ræsonnement: Eleverne skal anvende ræsonnementer, når de veksler mellem brøkerne.

Udvidelse

Byg så mange forskellige spyd med de blå spyd, og beskriv dem med brøker. Spyddene skal være fyldt helt op uden mellemrum.

Intro

Lærer: Hvad får I øje på?

Elev: Det er noget med nogle frugtspyd.

Lærer: Ja, hvor mange blåbær kan der være på et helt spyd?

Elev: Seks blåbær.

Lærer: Ja, hvor stor en brøkdel fylder et enkelt blåbær på spyddet?

Elev: 1 ud af 6, altså en sjettedel.

Lærer: Ja, de forskellige frugter har forskellige størrelser, så de svarer til forskellige brøker.

Klar, parat, tænk…

I skal nu finde ud af, hvilken brøkdel de andre frugter svarer til.

MATERIALER EFTER BEHOV

Tegneflade med kvadratnet, fx folie eller kopiark i A3

Byg alle de mulige spyd, der er dobbelt så lange, og beskriv dem med brøker. Spyddene skal være fyldt helt op uden mellemrum.

Når eleverne tænker højt

Læg mærke til …

• Om eleverne kan omsætte frugternes længder til brøker

• Om eleverne kan veksle mellem brøkerne/frugterne.

Stil spørgsmål, der får eleverne til at tænke videre:

• Kan I finde flere løsninger?

• Hvilke frugter/brøker kan I veksle mellem?

• Er det muligt, at alle fire frugter/bær kan være på det samme spyd?

• Kan I skrive det som et regnestykke med brøker?

• Kan I tegne jer frem til svaret?

• Hvilke brøker er nemme at lægge sammen? Hvilke er sværere?

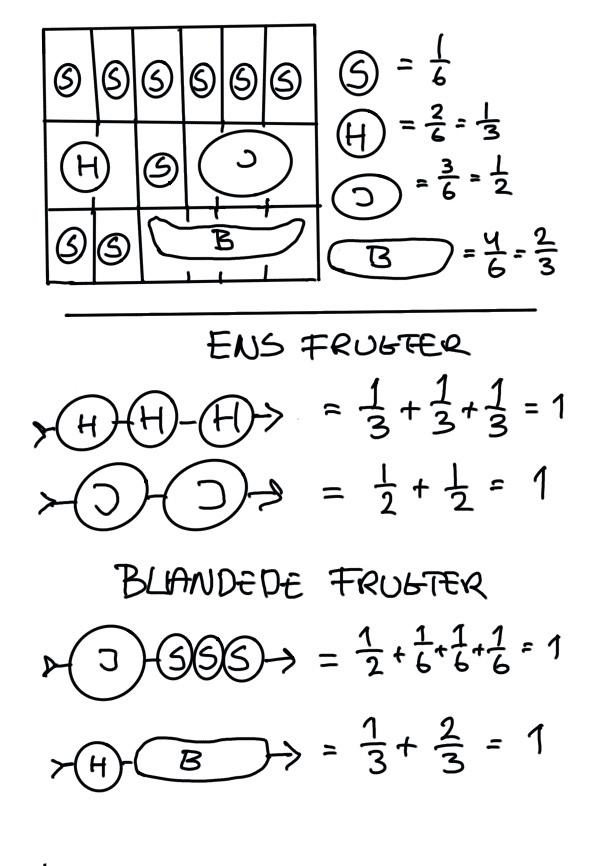
Løsninger

Grønne spyd

Blå spyd

spyd

VIGTIGE ORD

Brøkdel

Hel

En del af en hel Veksle

Fire slags frugt/bær, fx

Hvad ved vi nu?

• Hvilke løsninger er I nået frem til?

• Hvordan fandt I ud af, hvilke spyd I kunne bygge?

• Hvilke smarte måder fandt I, for at finde alle de mulige spyd?

• Hvad skete der med brøkerne, når spyddene blev længere?

• Hvilke smarte måder fandt I, da I lagde brøkerne sammen?

• Hvad ved vi nu om veksling og addition af brøker?

• Hvilke brøker var lette at lægge sammen?

• Kan man lægge alle brøker sammen?

• Hvorfor/Hvorfor ikke?

• Kan alle brøker veksles til andre brøker?

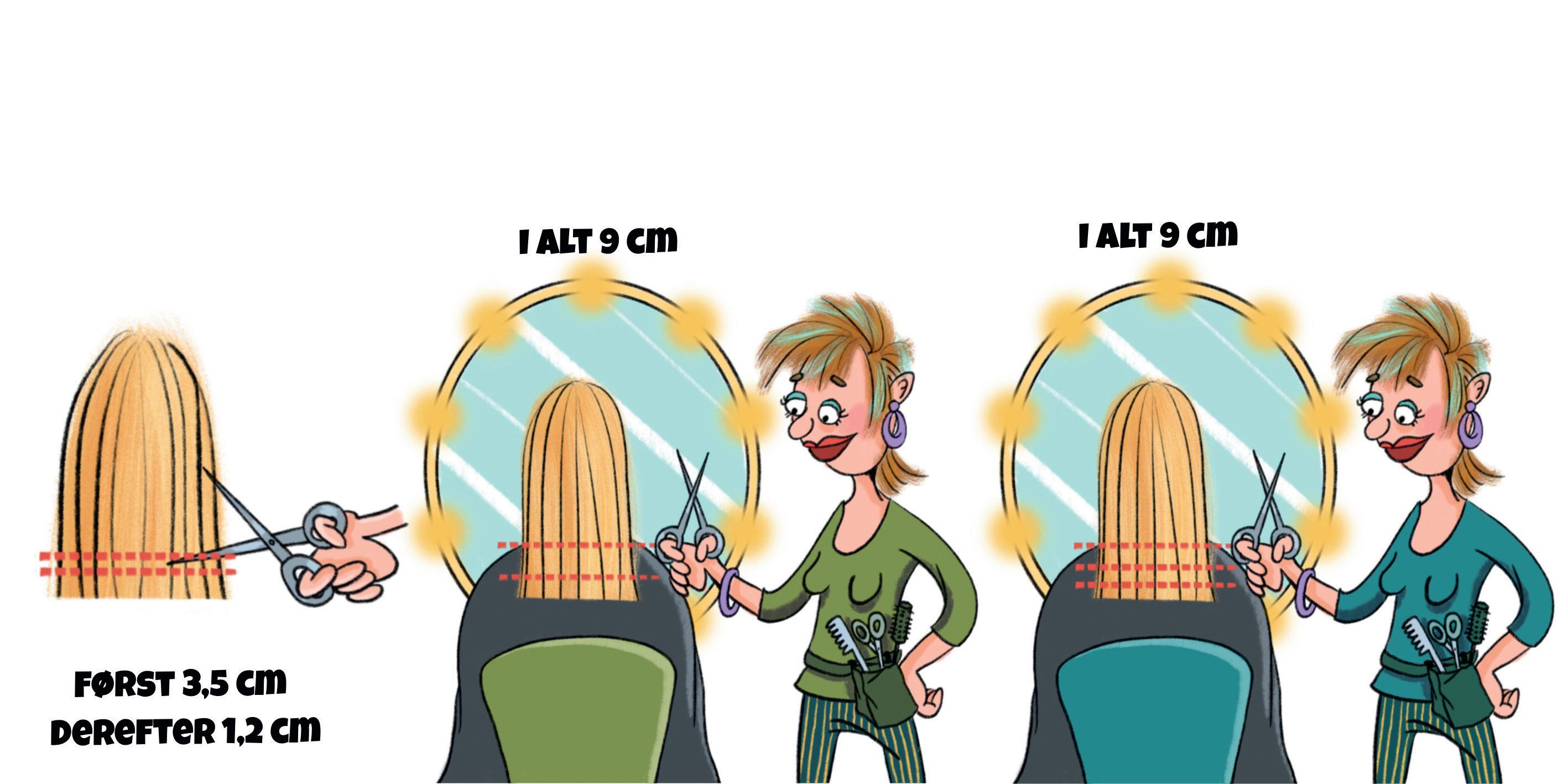
FrisørFrisøren

Addition af decimaltal: Opgaven lægger op til addition af decimaltal med én decimal. Opgaven giver mulighed for at skelne mellem enere og tiendedele via konteksten omkring centimeter og millimeter. Eleverne kommer til at overveje overgangen, når de fx lægger 4 tiendedele og 6 tiendedele sammen. Det åbner op for vigtige samtaler om forskellen på fx 0,10 og 0,1 samt 1,0.

Problembehandling: Opgaven kan have problemløsningskarakter, idet der stilles krav om brug af alle cifre samt omvendte opgaver, der kræver flere afprøvninger og masser af tænkning.

Vær opmærksom på elever, der kan have brug for støtte i at håndtere frustration, hvis løsningerne ikke kommer hurtigt. Tal gerne om, at det er en forventelig reaktion, og at hjerner kan være dovne, men har brug for motion for at blive stærkere og hurtigere. Opmuntring i form af: ’Det skal nok komme’, ’bare bliv ved’ kan hjælpe, men varer det for længe, kan et tip, der hjælper dem på vej, være løsningen.

Udvidelse Baggrund

Frisøren vil være sikker på at ikke at klippe for meget af håret. Så hun klipper de 9 cm af tre omgange. Hvor meget kan hun have klippet af hver gang? Hvert ciffer må kun benyttes én gang.

Intro

Lærer: Hvad ser I?

Elev: Det er noget med hår, der skal klippes. Der er to røde streger på håret. Det er nok der, hvor frisøren vil klippe håret?

Lærer: Ja, først klippede frisøren 3,5 cm af. Det var ikke nok. Kunden ville gerne have klippet 1,2 cm mere af. Hvor meget er håret i alt blevet kortere?

Elev: 4,7 cm.

Lærer: Ja, I skal nu finde ud af, hvad frisøren kan klippe af håret, hvis hun klipper af to omgange, og håret skal ende med at være 9 cm kortere. I må bruge alle cifre, men hvert ciffer kun én gang.

Klar, parat, tænk…

Pigen vil have klippet mere end 10 cm af sit hår. Frisøren kan klippe to eller tre gange. Hvert ciffer må kun benyttes en gang.

Når eleverne tænker højt

Læg mærke til …

• Om eleverne har forstået, at de skal danne decimaltal med cifrene 0-9

• Om eleverne kun benytter hvert ciffer én gang

• Om eleverne forstår, at 10 tiendedele udgør en hel.

Stil spørgsmål, der får eleverne til at tænke videre:

• Er I sikre på, at I kun har brugt hvert ciffer én gang?

• Hvad betyder cifferet før kommaet og cifferet efter kommaet?

• Hvor mange millimeter går der på en centimeter?

• Hvad er forskellen på f.eks. 0,10, 0,1 og 1,0?

• Hvad betyder det, hvis de to decimaler giver mere end 10 tilsammen?

• Kan I mon finde flere løsninger?

• Kan I bygge videre på noget I har i forvejen?

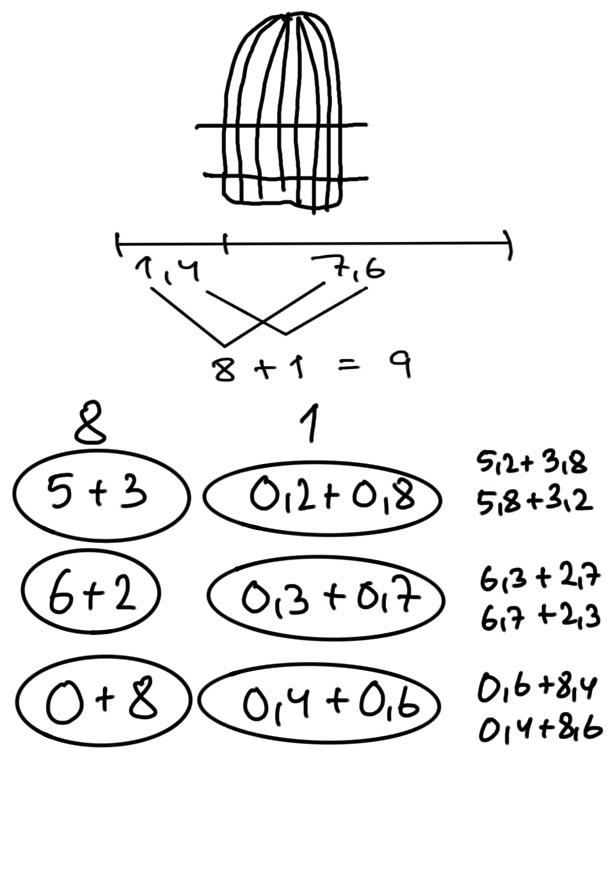
Løsninger

Grøn løsning Fx

1,4 + 7,6 = 9

2,7 + 6,3 = 9

3,1 + 5,9 = 9

Blå løsning Fx

5,2 + 3,1 + 0,7 = 9

4,7 + 2,8 + 1,5 = 9

2,5 + 4,8 + 1,7 = 9

3,2 + 1,8 + 4,0 = 9

VI GTIGE ORD

Decimaltal

En decimal

Tiendedele

Cifre

Centimeter

Millimeter

Rød løsning Fx

7,2 + 8,4 = 15,6

6,2 + 5,0 + 3,7 = 14,9 5,1 + 4,3 + 2,7 = 12,1

Hvad ved vi nu?

• Hvilke løsninger fandt I frem til?

• Hvordan fandt I frem til løsningerne?

• Blev I opmærksomme på smarte måder at tænke på?

• Hvordan kunne jeres tænkning vises på forskellige måder?

• Hvordan kan I nemt lave flere løsninger, når I har fundet én?

• Hvilke regnestykker lagde I særligt mærke til?

• Hvilke regnestykker kan være ”drilske”?

• Fandt I nogle ”smarte” måder at regne med decimaltal?

• Hvad ved vi nu tilsammen om at lægge tal med én decimal sammen?

Kalender

Baggrund

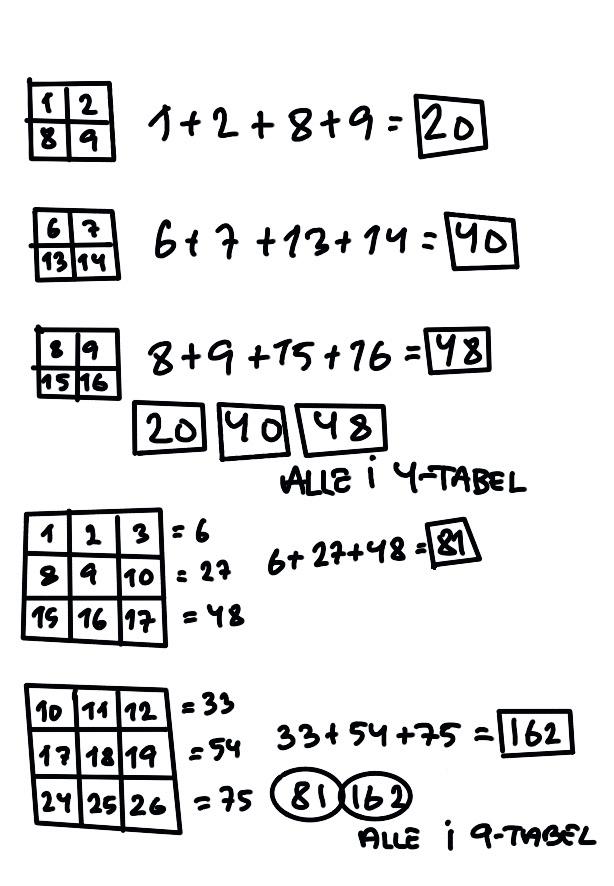
Talmønstre: I opgaven skal eleverne finde summen af tal indrammet i en firkant på en kalender. Eleverne skal undersøge sig frem og finde et system bagved. For de fleste antal af indrammede tal gælder det, at summen er med i tabellen, svarende til antallet af tallene. Dette system gælder dog ikke for alle antal af tal.

Ræsonnement: Opgaven indeholder mulighed for, at eleverne (med lidt hjælp) kan ræsonnere sig frem til forklaringen på, hvorfor systemer henholdsvis virker eller ikke virker (se under Løsninger), fx ”fordi det første tal i alt vokser med…, som er med i tabellen...”.

Intro

Lærer: Hvad tror I det handler om?

Elev: Noget med en kalender og nogle indrammede tal.

Lærer: Ja, på den grønne kalender, er der sat en firkant om fire tal. Hvad er summen?

Elev: Summen er 32.

Lærer: Ja, I skal nu prøve andre steder i den grønne kalender at indramme fire tal i en firkant og finde summen. Prøv at se, om I får øje på noget interessant.

Klar, parat, tænk…

Udvidelse

Hvad sker der, hvis I indrammer ni tal i en firkant i kalenderen og finder summen?

Hvilke andre antal findes der tilsvarende systemer bag? Hvilke duer ikke?

Når eleverne tænker højt

Læg mærke til …

· Om eleverne arbejder systematisk og prøver flere muligheder.

· Om eleverne får øje på et system.

· Om eleverne prøver at finde forklaringer bag systemerne.

Stil spørgsmål, der får eleverne til at tænke videre:

· Gælder det mon altid? I en anden måned?

· Når rammen placeres anderledes?

· Kan I få øje på et system bag det?

· Hvordan kan I beskrive systemet?

· Hvor meget bliver tallet større, hvis I går mod højre eller nedad?

· Hvordan kan det være, at systemet virker?

Løsninger

Grøn kalender

De fire tal som et kvadrat. Summerne er alle i 4-tabellen fordi: 1 + 7 + 8 = 16 som er i 4-tabellen.

xx + 1

x + 7x + 8

De fire tal tegnet som et rektangel på én række vandret eller lodret, gælder dette ikke fordi: 1 + 2 + 3 = 6 som ikke er i 4-tabellen.

xx + 1x + 2x + 3

Hvad ved vi nu?

· Hvad lagde I mærke til?

· Hvilket mønster fik I øje på?

Blå kalender

De ni tal som et kvadrat. Summerne er alle i 9-tabellen fordi:

1 + 2 + 7 + 8 + 9 + 14 + 15 + 16 = 72 som er i 9-tabellen.

xx + 1x + 2

x + 7x + 8x + 9

x + 14x + 15x + 16

· Hvorfor kan det give mening at lede efter mønstre?

· Hvordan kan vi bruge mønstrene til at forudsige andre summer?

· Hvilke sammenhænge fandt i mellem summerne og tabellerne?

· Hvad gør, at et system virker eller ikke virker?

· Hvad ved vi nu tilsammen om at finde talmønstre?

VI GTIGE ORD

Talmønstre System

Dato

Rød kalender Fx

Det gælder også for 3, 5, 7: De ulige tal i et rektangel på en række.

1 + 2 + 3 = 6, er med i 3-tabellen

Det gælder ikke for 2 og 6 tal på en række.

De lige tal i et rektangel på en række.

1 + 2 = 3 er ikke med i 2-tabellen

Klar Parat Tænk er en samling af opgaver, som tilbyder et udtræk af principperne fra Det Tænkende Klasserum, tilsat erfaringer fra undervisningen til mellemtrinnet i Danmark.

Hver aktivitet er bygget omkring en tænkende opgave og varer en lektion. Med bogen i hånden bliver du derfor klædt godt på til at gennemføre en undervisning, hvor eleverne er aktive og tænkende.

Du vil på hvert opslag finde

Strimmel

Visuel præsentation af opgaven, som er klar til at printe ud og sætte på elevernes tavle. Den understøtter eleverne imens de arbejder og hjælper med at fastholde dem i opgaven.

Baggrund

Beskrivelse af den faglige pointe og kompetence, som opgaven bygger på, samt om der er en særlig matematisk opmærksomhed, som opgaven sætter i spil.

Intro

Her får du et eksempel på en mundtlig dialog, som du kan bruge til at introducere opgaven til eleverne.

Klar, parat, tænk…

Udvidelser

Forslag til, hvordan du kan udvide opgaven, når eleverne er klar.

Når eleverne tænker højt

Hvad skal du lytte efter når eleverne arbejder og hvilke spørgsmål du kan stille til eleverne, så de tænker videre i opgaven.

Vigtige ord

Her finder du ord, som kan give mening at lytte efter om eleverne bruger eller tale om deres betydning sammen med eleverne.

Løsninger

Facitter, så du hurtigt kan danne overblik og finde svarmuligheder.

Hvad ved vi nu?

Gode spørgsmål til at samle op på opgaven og til at få eleverne til at forklare deres løsninger.

Derudover vil der på tavlen være 2-3 eksempler på, hvilke strategier eleverne kan have brugt til at løse opgaven.

Klar Parat Tænk til mellemtrinnet er

delt op i 3 bøger på 3 niveauer.

Klar Parat Tænk 4, 5 og 6 indeholder hver 30 opgaver og en beskrivelse af, hvordan du kommer i gang med at arbejde med aktiviteterne. Opgaverne er fordelt på 3 niveauer, hvor 4 er lettest og 6 er sværest. Opgaverne dækker over stofområderne, som eleverne møder fra 4. til 6. klasse, og har fokus på de matematiske kompetencer.

Klar Parat Tænk er perfekt til dig, der ønsker at skabe en kultur i klasserummet, der har fokus på samarbejde og hvor klasserummet summer af nysgerrige elever, som sammen tænker højt. Det vigtigste omdrejningspunkt er elevernes forklaringer og forsøg på løsning af opgaverne.