Portafolio Digital sobre Proyecto Final De Estadística 2

UNIVERSIDAD MARIANO GÁLVEZ DE GUATEMALA

EXTENSIÓN JACALTENANGO

Facultad de Ciencias de la Administración.

Licenciatura en Administración de Empresas.

Estadística II.

Licdo. Carlos Humberto López Ovalle.

Proyecto Final de Estadística.

Luis Enrique Delgado Domingo.

Carné No.7822-20-12836

Jacaltenango, Huehuetenango, junio de 2024.

ABSTRACT

Los temas teóricos y casos prácticos desarrollados en el presente proyecto, tienen como objetivo principal desarrollar la capacidad de estudio y análisis de las diferentes variables y los estudios a los cuales se puede someter una evaluación estadística para cualquier tipo de labor que se nos sea encomendada, siendo así capaces de desarrollar un proyecto estadístico, obteniendo de él resultados reales con información del mundo real para fines de estudio, dependiendo de las condiciones o lo requerido de una población o muestra (por ejemplo) Tales resultados de este tipo de estudio, pueden ser utilizados por nosotros los estudiantes de administración de empresas para campañas publicitarias, lanzamiento de productos, estudios de mercado, análisis en la producción o en el mejoramiento de servicios para una empresa donde laboremos.

INTRODUCCIÓN

El siguiente proyecto pretende dar un acercamiento general hacia los temas de Estadística vistos durante el semestre, que nos da como resultado la comprensión de conceptos de identificación de población y muestra, variables, análisis de datos en general, etc., los cuales nos permiten hallar respuesta a los casos correspondientes, con el fin de analizar la información obtenida para su fácil manipulación, conllevando a la correcta interpretación de sus resultados.

Gran parte de la utilidad que tiene la Estadística, es la de proporcionar un medio para informar basado en datos recopilados, la eficacia con que se pueda realizar tal proceso de información dependerá de la presentación de tales datos, con lo que podemos apoyarnos también de gráficos para una mejor eficiencia al analizar los resultados.

En cada tema teórico y casos prácticos se determinarán conclusiones válidas y con esto podremos tomar decisiones con base a los análisis resultantes, es decir, al deducir de ello gracias al análisis de estos datos, podremos obtener unas previsiones para el futuro con precisión, siempre y cuando se haga el correcto empleo de los métodos estadísticos para cada caso

La adquisición de conocimientos sobre el contenido que a continuación será presentado, nos ayuda en la etapa de formación profesional como estudiantes de administración de empresas, y que, a futuro también nos apoyará al momento de estar en busca de la conceptualización teórica y su correcta aplicación práctica en el campo laboral; teniendo en cuenta que estos casos son aplicables a las diferentes situaciones en las que nos encontremos y que nos puedan auxiliar al dar solución a un problema evidente.

OBJETIVOS

General:

El objetivo principal, es que, por medio de este proyecto investigativo y práctico, se puedan definir y verificar los avances conceptuales y procedimentales para la resolución de cada caso sobre la fundamentación de Estadística II

Específicos:

✓ Comprender la importancia del estudio de la estadística, para lo cual es necesario un recorrido por sus conceptos, métodos e importancia.

✓ Aplicar apropiadamente los métodos estadísticos en la recolección de información y procesos matemáticos básicos en cálculos estadísticos.

✓ Adquirir los conocimientos y habilidades sobre cada tema, ser capaz de reconocer los elementos habituales de la estadística.

✓ Interpretar resultados estadísticos y poder resolver problemas reales

LUIS ENRIQUE DELGADO DOMINGO

DATOS PERSONALES

Fecha de nacimiento: 26 de mayo de 1999.

Edad: 24 años.

CUI: 3202 60658 1307

Dirección: Cantón Hernández zona 4, Jacaltenango, Huehuetenango.

CONTACTO

Teléfonos: 4671-1429 / 5559-9290

Correo Electrónico: masterboss.led117@gmail.com

FORMACIÓN

Escuela Oficial Urbana Mixta, Dr. Epaminondas Quintana. 2006 - 2011

Diploma de Nivel de Educación Primaria.

Instituto Mixto de Educación Básica por Cooperativa Jacaltenango. 2012 - 2014

Diploma de Nivel de Educación Básica.

Liceo Mixto Privado Camposeco. 2015 - 2017

Título de Nivel de Educación Diversificada: “Perito en Computación”.

Diploma de Nivel de Educación Diversificada: “Bachiller Industrial”.

Universidad Mariano Gálvez. 2022 – (Actualidad)

Pensum: “Licenciatura en Administración de Empresas”.

EXPERIENCIA LABORAL

NOVA Sistemas (Técnico) 2017-2020

Asesor de ventas y técnico en reparación y mantenimiento de equipos en general; instalación de redes (internet y/o infraestructura), cámaras de seguridad, configuración de equipos de cómputo y otros dispositivos inteligentes.

Grupo Radial CMM (Técnico) 2019-2022

Manejo y reparación de equipos de cómputo, equipos radiales y redes.

Wiwitz, Sociedad Anónima (Administrador) 2020-(Actualidad)

Administración general; manejo y control financiero de la sociedad, administración de bases de datos (clientes, proveedores, documentos FEL, etc.), supervisión y dirección de personal, auxiliar de puestos.

El Rancho de Don Julián (Administrador) 2020-(Actualidad)

Manejo y control financiero de la entidad, registros contables, supervisión y dirección de personal.

MATERIAL DE APRENDIZAJE: TEMAS TEÓRICOS VISTOS EN EL SEMESTRE

MÓDULO I

Regresión Lineal Múltiple

Lineal es porque las potencias de las variables involucradas van a ser 1. Regresión lineal es una técnica de análisis de datos que predice el valor de datos desconocidos mediante el uso de otro valor de datos relacionado o conocido. Con un modelo matemático porque existe la variable desconocida o dependiente y la variable conocida o independiente como una ecuación lineal.

Utilizamos regresión lineal múltiple como modelo matemático cuando estudiamos la posible relación entre varias variables independientes (predictoras o explicativas) y otra variable dependiente (criterio, explicada, respuesta). Se le llama múltiple porque está conformada por variables representadas por: x, y, z.

Modelos matemáticos de la regresión lineal múltiple:

Sistema de ecuaciones normalizadas:

Sumatorias:

Series Cronológicas

Las series cronológicas son llamadas también series de tiempo, es el conjunto de observaciones obtenidas de una misma variable durante un periodo de tiempo (meses, semestres, trimestres). La importancia de su análisis es porque contando con datos pesados, permite realizar un pronóstico confiable de la actividad futura y tomar decisiones anticipadas. Las series pueden ser negativas o positivas en su comportamiento.

Las series cronológicas se utiliza para realizar proyecciones. Las proyecciones, las vamos hacer con la siguiente fórmula:

Para conseguir estos valores nos vamos apoyar de dos métodos:

Método Directo (origen en el inicio):

Es un sistema de ecuaciones de segundo grado, donde debemos despejar “a” y “b”.

Ecuaciones:

1. ����=����+������

2. ������=������+����²��

Método Abreviado: “a” y “b” se encuentran despejados.

Ecuaciones:

1. ��= ∑�� ��

2. ��= ∑����

MÓDULO II

Números Índices

Son serie de números que miden los cambios relativos de las variables o grupo de variables en el tiempo o en el espacio. Con respecto a una base en el tiempo se establece generalmente un año, pero puede ser un mes, una semana o un día. En el caso de una base espacial, puede ser una región, un país o una ciudad.

Los números índices son medidas que indican algo, por lo general en cuanto han variado ciertas cosas o bien cómo se comportan entre sí.

Se pueden trabajar con tres índices:

Índices de precios:

Índices de cantidades:

Índices de valores:

Simbología:

Ip = Índice de precios

Iq = Índice de cantidades

Iv = Índice de valores.

Pn = Precio de un artículo del año que se compra.

Po = Precio de un artículo del año base

Qn = Cantidad de un artículo del año que se compra

Qo = Cantidad de un artículo del año base.

Probabilidades

Es el cálculo matemático que evalúa las posibilidades que existen de que una cosa suceda cuando interviene al azar.

Propiedades:

1. Que la probabilidad debe ser entre 0 y 1

0 ≤ P(A) = ≤ 1

2. Que la probabilidad de un evento seguro es 1

P(E) = 1

3. Que la probabilidad de un evento que no puede suceder, no es seguro, es decir, improbable

P(∅) = P(E) = ∅

4. Probabilidad del complemento que no ocurra a menos sea = 1, la probabilidad que si ocurra.

P(A) = 1 – P(A)

Eventos en las probabilidades:

Eventos mutuamente excluyentes: Son sucesos que no pueden suceder al mismo tiempo.

Regla de adición: Sean dos eventos “a” y “b” tales que mutuamente sean excluyentes, es decir, que la probabilidad de que ocurran los dos al mismo tiempo va a ser cero (0), en ecuación sería: P(A∩B) = ∅.

Ecuación para el cálculo: P(A∪B) = P(A) + P(B).

Eventos mutuamente no excluyentes:

Son aquellos que sí pueden ocurrir al mismo tiempo.

Regla de adición: Si los eventos “a” y “b” no son mutuamente excluyentes, para la probabilidad de la unión se tiene la ecuación: P(A∩B) ≠ ∅.

Ecuación para el cálculo: P(A∪B) = P(A) + P(B) - P(A∩B).

Distribución de Probabilidades

Es aquella que permite establecer toda la gama de resultados probables de ocurrir en un experimento determinado, es decir, describe la probabilidad de que un evento se realice en el futuro.

Distribución de probabilidades para una variable discreta:

Es discreta cuando solo puede tomar unos ciertos valores enteros (0, 1, 2, 3...).

Distribución de Probabilidades Binomial

Es una distribución de probabilidad discreta que cuenta el número de éxitos en una secuencia de “n” ensayos entre sí con una probabilidad fija “p” de ocurrencia de éxitos entre los dos ensayos. En resumen, decimos que la distribución binomial se van a encontrar dos resultados: éxito o fracaso.

Condiciones para que se cumpla el experimento binomial:

1. El experimento consta de una secuencia de “n” ensayos idénticos.

2. En cada ensayo hay 2 resultados posibles. A cada uno de ellos se le llama éxito y al otro fracaso.

3. La probabilidad de éxito es constante de un ensayo a otro, nunca cambia y se denota por “p”, por ello, la probabilidad de fracaso sería 1-p

4. Los ensayos son independientes, de modo que el resultado de cualquiera de ellos no influye en el resultado de cualquier otro ensayo.

Para un experimento binomial, sea “p” la probabilidad de un “éxito” y “1-p” la probabilidad de un “fracaso” en un solo ensayo; entonces, la probabilidad de obtener “x” éxitos en un “n” ensayos, está dada por la función de probabilidad de f(x) que significa f de x:

F(x) = P(X=x) = (n/x) (p)x (1-p) n-x

Simbología:

f(x) = función de probabilidad binomial.

X = variable aleatoria binomial

x = 0,1, 2…, n el cual son valores enteros

n = número de ensayos.

p = probabilidad de obtener éxito.

1-p = probabilidad de obtener fracaso

(�� ��) = coeficiente binomial.

El número combinatorio de (�� ��) es: ��! ��!(�� ��)!

Distribución de Probabilidades Normal

La distribución normal nos permite crear modelos de muchísimas variables y fenómenos, como, por ejemplo, la estatura de los habitantes de un país, la temperatura ambiental de una ciudad.

Es una distribución de probabilidad continua, porque las variables pueden tomar cualquier valor dentro de un rango dado. Se puede aplicar en fenómenos cuantitativos, así como el muestreo probabilístico.

Fórmula para determinar la variable estandarizada:

��=

Simbología:

Z = Variable estandarizada.

�� = Promedio o media testada

�� = Media normal

�� = Desviación estándar.

Prueba de Hipótesis

¿Qué es una Hipótesis?:

Es una afirmación relativa a un parámetro de la población sujeta a verificación. Una hipótesis es una aseveración o un supuesto o afirmación. En estadística, una hipótesis es una aseveración o afirmación acerca de una propiedad de una población.

¿Qué es una prueba de Hipótesis?:

Es un procedimiento estándar para probar una aseveración acerca de una propiedad de una población. Es un procedimiento el cual sirve para verificar si dichas hipótesis se rechazan o no se rechazan. La prueba de hipótesis comienza con una afirmación o suposición sobre parámetros de la población como podría ser la media población.

Procedimiento para pruebas de Hipótesis:

Paso 1: Se Establece la Hipótesis Nula (Ho) y Alternativa (Ha).

El primer paso consiste en establecer la hipótesis que se debe probar. Esta recibe el nombre de Hipótesis Nula (Ho)

Ho = se lee Hipótesis subíndice cero o bien hipótesis nula.

Ha = se lee Hipótesis subíndice a o bien hipótesis alternativa.

¿Qué es la hipótesis alternativa? Describe lo que se concluirá si se rechaza la hipótesis nula. También se le conoce como hipótesis de investigación. Es el enunciado que se acepta si los datos de la muestra ofrecen suficiente evidencia para rechazar la hipótesis nula.

Paso 2: Se selecciona un nivel de significancia.

Nivel De Significancia O Nivel De Riesgo: Es la probabilidad de rechazar la hipótesis nula cuando es verdadera.

Existen dos errores al utilizar hipótesis nula:

Error tipo 1. Rechazar la hipótesis nula (Ho), cuando es verdadera.

Error tipo 2. Aceptar la hipótesis nula (Ho), cuando es falsa.

Paso 3: Se selecciona el estadístico de Prueba.

Estadístico de Prueba: Es el valor determinado a partir de la información de la muestra, para determinar si se rechaza la hipótesis nula.

Paso 4: Se formula la Regla de Decisión.

La región o área de rechazo define la ubicación de todos esos valores que son tan grandes o tan pequeños que la probabilidad de que ocurran en una hipótesis nula verdadera es muy remota.

Paso 5: Se toma una Decisión.

El quinto y último paso en la prueba de hipótesis consiste en calcular el estadístico de la prueba, comparándola con el valor crítico, y toma la decisión de rechazar o no la hipótesis nula.

MÓDULO III

Muestreo Estadístico

La muestra es, en esencia, un subgrupo de la población. Digamos que es un subconjunto de elementos que pertenecen a ese conjunto definido en sus características al que llamamos población.

El muestreo es “La técnica empleada para la selección de elementos (unidades de análisis o de investigación) representativos de la población de estudio que conformarán una muestra y que será utilizada para hacer inferencias (generalización) a la población de estudio”.

El muestreo estadístico estudia o investiga una muestra y permite inferir esos resultados a una población completa. Por todo lo anterior es una herramienta de la investigación científica.

Ventajas del muestreo:

- Reducción de costos: Los costes de un estudio serán menores si los datos de interés se pueden obtener a partir de una muestra de la población blanco.

- Eficiencia: Al trabajar con un número reducido de sujetos a estudio, representativos de la población blanco; el tiempo necesario para conducir el estudio y obtener resultados y conclusiones será ostensiblemente menor.

- La manipulación de datos es mucho más simple: Si con una muestra de 1,000 personas tengo suficiente, ¿para qué quiero analizar un fichero de millones de registros.

Desventajas del muestreo:

- Inadecuada representación de la población blanco: Esto puede ocurrir si se decide trabajar con muestras pequeñas.

- Introducimos error (controlado) en el resultado: Debido a la propia naturaleza del muestreo y a la necesidad de generalizar resultados.

- Tenemos el riesgo de introducir sesgos debido a una mala selección de la muestra: Por ejemplo, si la forma en que seleccionamos individuos para la muestra no es aleatoria, los resultados pueden verse seriamente afectados.

Utilidad del muestreo:

El muestreo tiene por objetivo estudiar las relaciones existentes entre la distribución de una variable “y” en una población “z” y la distribución de esta variable en la muestra a estudio.

El muestreo es útil gracias a que podemos acompañarlo de un proceso inverso, que llamamos generalización de resultados. Es decir, para conocer un universo lo que hacemos es:

1. Extraer una muestra del mismo.

2. Medir un dato u opinión.

3. Proyectar en el universo el resultado observado en la muestra.

Muestreo Probabilístico:

El muestreo probabilístico analiza y estudia una población utilizando la selección aleatoria, simplemente porque en un grupo de individuos todos tienen la misma oportunidad de ser elegidos.

Tipos:

1. Muestreo aleatorio simple.

2. Muestreo aleatorio estratificado

3. Muestreo aleatorio sistemático

4. Muestreo aleatorio por conglomerados.

5. Muestreo aleatorio polietápico.

Muestreo no Probabilístico:

El muestreo no probabilístico es una técnica que selecciona las personas que harán parte de la muestra de una manera subjetiva, esto quiere decir, según la decisión del investigador, evitando hacerlo al azar.

Tipos:

1. Muestreo por cuotas.

2. Muestreo por juicios, opinático o intencional.

3. Muestro casual, incidental o por conveniencia

4. Muestreo por bola de nieve

5. Accidental o consecutivo.

Cálculo del Tamaño de la Muestra

Tamaño de la Muestra:

El tamaño de muestra es el número determinado de sujetos o cosas que componen la muestra extraída de una población, necesarios para que los datos obtenidos sean representativos de la población.

¿De qué tamaño debe ser una muestra?:

- Una muestra demasiado grande dará lugar a la pérdida de valiosos recursos como tiempo y dinero.

- Una muestra pequeña puede no proporcionar información confiable.

Determinación del tamaño óptimo de muestra:

La determinación del tamaño muestral depende, entre otros, de los siguientes factores:

- Los objetivos del estudio.

- Los conocimientos previstos sobre el comportamiento de la característica en la población.

- Los recursos técnicos y financieros para obtener la información.

- El error máximo que permitirá el analista.

- La confiabilidad de la inferencia esperada por el analista.

Consideraciones estadísticas y no estadísticas:

La selección del tamaño de la muestra depende de consideraciones no estadísticas y estadísticas.

Consideraciones no Estadísticas

• La disponibilidad de recursos.

• Disponibilidad de personal.

• El presupuesto.

• La ética.

• El marco de muestreo.

Consideraciones Estadísticas

• La precisión deseada.

• El nivel de confianza de las conclusiones.

• El tamaño de la población.

• El grado de variabilidad de la población.

Nivel de precisión:

Determina el error de muestreo o error permitido, es el rango en donde se estima que está el valor real de la población.

El margen de error es el porcentaje de variación aceptable que existe en los resultados de la investigación. Puede expresarse también en términos de la variable que se investiga.

Nivel de confianza:

El intervalo de confianza es grado en que se espera que los resultados se encuentren dentro de un rango específico:

Intervalo de confianza

Valor de Z

Medidas Estadísticas:

Dependiendo si se estimará una media o una proporción, se requiere contar con algunos valores estadísticos como:

- Desviación estándar (��): índice de la dispersión de un conjunto de datos

- Probabilidad de éxito (p): proporción de individuos en la población que poseen la característica de interés.

- Probabilidad de fracaso (q): proporción de individuos que no poseen la característica de interés.

Tipo y tamaño de población:

Dependiendo de su tamaño, puede considerarse:

Población Finita:

Cuando se conoce o puede determinarse el número de elementos que la integran y está delimitada.

Por ejemplo:

- Todos los habitantes de una comunidad.

- El número de estudiantes de una institución universitaria.

- El número de obreros de una compañía

- La flota de vehículos de una transportadora.

Población Infinita:

Cuando se desconoce el total de elementos que la conforman, por lo que no existe un registro documental

Por ejemplo:

- La población de insectos en el mundo.

- Número de estrellas en el universo.

- Cantidad de granos de arena.

- Número de gotas de agua en el lago.

ACTIVIDADES: CASOS PRÁCTICOS VISTOS EN EL SEMESTRE

Tema 1: Regresión Lineal Múltiple

Sea un conjunto de datos:

Se pide: Realizar la regresión lineal múltiple de Y sobre X y Z (porque la variable Y va a depender de la variable X y Z).

Solución:

Modelo matemático de la regresión lineal múltiple de Y sobre X y Z: �� ̂ =����+����+�� ��= Punta de flecha estimada. �� ̂ = Y estimada.

Se construye el sistema de ecuaciones normalizadas bajo el modelo matemático de “Y” con las incógnitas a, b y c.

6 ������ = 100

Sistema de ecuaciones normalizadas:

1. 16.50a + 14b + 6c = 54

2. 76.25a + 48b + 16.50c = 243.50

3. 48a + 54b + 14c = 100

Hallazgo de valores:

a = 4 b = -3 c = 5

Y estimado: �� ̂ =����+����+��

Sustituyendo:

�� ̂ =4x 3z+5 �� ̂ =4(2) 3(1)+5

��

̂ =8 3+5 ��

̂ =13 3

=����

Tema 2: Series Cronológicas

Ejemplo: Dada la siguiente serie de tiempo, hacia la proyección del mes de septiembre:

Método Directo:

Ecuaciones:

1. ���� = ���� + ������

2. ������ = ������ + ����²��

7a+21b=81 21��+91�� =246

147�� 441�� = 1,701

147��+637�� =1,722

0 196�� = 21 21 196

b=0.11

21a+91b=246

21a+91(0.11)=246

21a+10.01=246

21a=-10.01+246

21a=235.99

23599 21

Y=a+bx

a=11.24

Y=11.24+0.11(x)

Y=1.24+0.11(8)

Y=11.24+0.88

Y=12.12

Método Abreviado:

a= ∑�� �� = 81 7 =11.57 b= ∑���� ∑��² = �� 28 =0.11

Y=a+bx

Y=11.57+0.11(5)

Y=11.57+0.55

Y=12.12

Resultado: Se proyectarán 12.12 millones de quetzales para septiembre.

Tema 3: Números Índices

Dados los siguientes precios y cantidades de producción de arroz durante los períodos 2015 hasta el 2018. Calcular algunos números índices. Tomar en cuenta que el año base es el año 2015 y año en que se compran los artículos es 2016.

2015 18 1200

2016 20 1450

2017 25 1150

2018 30 1320

Índice de precios:

���� = ���� ���� ∗100

����2016= 20 18 ∗100

����2016=111∗100

������������=������

Interpretación: Esto indica que el precio del arroz en el año 2016, aumentó un 11% con respecto al año 2015 que es nuestro año base.

Tema 4: Probabilidades

Se lanza un dado. Cuál es la probabilidad de:

1. Que caiga más de 8:

P (8) = ∅ cumple la tercera propiedad ya que nunca sucederá que caiga más de 8.

2. Que caiga 2, 3, 4, 5 o 6:

��(1)=1–��(1)

��(1)=1 1/6 =5/6

��(1)=0.83=83%

Eso significa que puede caer 2, 3, 4, 5, ó 6 con un 83% de probabilidad.

Eventos mutuamente excluyentes:

Se tienen los números de 1 al 20. Sea A los números pares mayores que 4, y B los números impares menores que 15. Si se selecciona un número al azar. ¿Cuál es la probabilidad de que sea un número par mayor que 4 o un número impar menor que 15?

٠= {��, ��, ��, ��, ��, ��, ��, ��, ��, ..., ����

P(A∪B) = P(A) + P(B)

P(A∪B) = 8/20 + 7/20

P(A∪B) = 15/20 = 0.75 = 75%

Eventos mutuamente no excluyentes:

En una cafetería el 80% de los clientes toma café, el 65% revisa su teléfono mientras se encuentra en el lugar y solo el 47% de los clientes les gusta tomar café mientras usa su teléfono en el lugar, con esta información si se selecciona un cliente al azar. ¿Cuál es la probabilidad de que tome café o revise su teléfono?

P(C∪T) = P(C) + P(T) - P(C∩T)

P(C∪T) = 0.80 + 0.65 - 0.47

P(C∪T) = 0.98 = 98%

Tema 5: Distribución de Probabilidades

Una encuesta que se haya hecho a personas que leen la Revista P y Personas que leen la Revista T; se encuentra que 15 de ellas leen ambas revistas, 5 solo leen la Revista P, 10 leen la Revista T y 20 que no leen ninguna.

= ����

La probabilidad que sea el evento 1: P(E1) = 5/50 = 0.10 = 10%

La probabilidad que sea el evento 2: P(E2) = 15/50 = 0.30 = 30%

La probabilidad que sea el evento 3: P(E3) = 10/50 = 0.20 = 20%

La probabilidad que sea el evento 4: P(E4) = 20/50 = 0.40 = 40%

Tema 6: Distribución de Probabilidades Binomial

En un restaurante llamado Matehamburguesa. La probabilidad de que aun cliente nuevo le guste la Matehamburguesa es de 0.80. Si llegan 5 clientes nuevos. ¿Cuál es la probabilidad de que solo a 2 de ellos les guste la Matehamburguesa? Defina las variables y sustituya las fórmulas.

X = número de clientes nuevos de 5 a los que les gusta la Matehamburguesa

X ~ B (n, p)

X ~ B (5, 0.80) n = 5

Combinatoria 5 en 2 (�� ��): �� �� = ��!

��)! 5 2 = 5! 2!(5 2)! =

Solución:

��(��)=��(�� =��)=(�� ��)(��)�� (1 ��)�� ��

��(2)=��(�� =2)=(5 2)(0.80)2 (1 0.80)5 2

��(2)=��(�� =2)=10(080)2 (1 080)3

��(2)=��(�� =2)=10∗0.64(0.20)3

��(2)=��(�� =2)=10∗0.64∗0.008

��(2)=��(�� =2)=00512∗100%=�� ����%

Interpretación: La probabilidad que a 2 de 5 personas les guste la Matehamburguesa, es del 5.12%

Tema 7: Distribución de Probabilidades Normal

En Mazatenango, la media de la temperatura en grados Celsius es de 32 grados en cada verano. ¿Cuál será la probabilidad de que sea menor de 28 grados Celsius si su desviación tiene o sea de 4 grados Celsius?

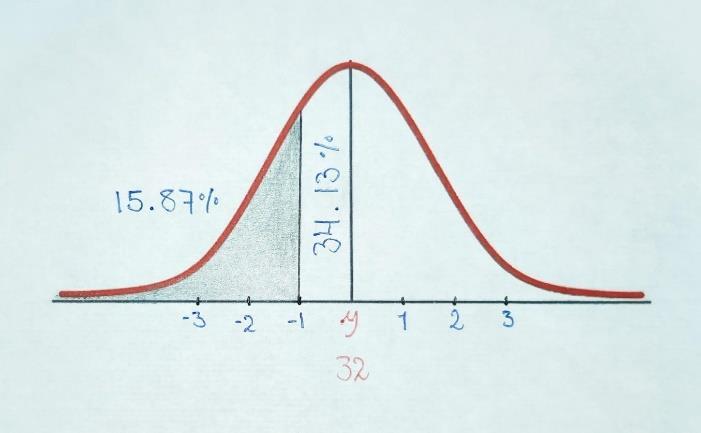
Interpretación: La probabilidad de que la temperatura en la ciudad sea menor a 28° Celsius en toda la región es el 15.87%

Tema 8: Prueba de Hipótesis

Caso de ambas colas:

Una empresa fabrica y arma escritorios y otros muebles para oficina. La producción semanal del escritorio modelo A325 tiene una distribución normal, con una media de 200 y una desviación estándar de 16. Hace poco con motivo de la expansión del mercado, se introdujeron nuevos métodos de producción y se contrató a más empleados. El vicepresidente de fabricación pretende investigar si hubo algún cambio en la producción semanal del escritorio. En otras palabras, ¿la cantidad media de escritorios que se produjeron es diferente de 200 escritorios semanales?, utilice un nivel de significancia de 0.01 en una muestra de 50 semanas la cantidad media de escritorios que se produjeron fue de 203.5.

Datos:

�� = 203.5

µ = 200

�� = 16

n = 50

α = 0.01

Paso 1: Establecer la hipótesis nula (Ho) y la hipótesis alternativa (Ha):

Ho: µ = 200

Ha: µ ≠ 200

Paso 2: Seleccionar el nivel de significancia:

α = 0.01

Paso 3: Seleccionar el estadístico de prueba:

Paso 4: Formular la regla de decisión:

0.50 - 0.005 = 0.495

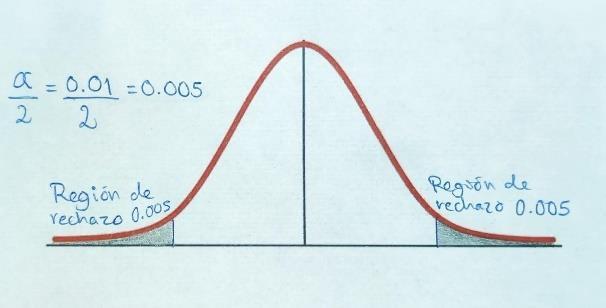
Paso 5. Se toma una decisión y se interpretan los resultados:

No se rechaza la Ho: µ = 200

La µ no es distinta de 200

Interpretación: Basándonos en los datos estadísticos de la muestra podemos responder que no, la media poblacional no es distinta de 200, en otras palabras, no rechazamos la hipótesis nula (Ho) de la media igual a 200 y si rechazamos la hipótesis alternativa (Ha) que menciona que la media es diferente de 200.

Caso cola izquierda:

Un fabricante afirma que el peso mínimo de sus paquetes de galletas es de 50 gramos. Suponemos que la afirmación del fabricante es verdadera y se plantea como hipótesis nula. Con un nivel de significancia de 5%, con una muestra de 36 paquetes arrojo una media de 48 gramos por paquete. Se sabe que la desviación estándar de la población es de 4 gramos. Con los datos anteriores de prueba de hipótesis caso cola izquierda, de solución al mismo, aplicando los 5 pasos señalados y con la regla de decisión de que si el estadístico de prueba es menor que el valor Z crítico entonces rechazamos la hipótesis nula.

Datos:

= 48

= 50

= 4

= 36

= 0.05

Paso 1: Establecer la hipótesis nula (Ho) y la hipótesis alternativa (Ha):

Ho: µ ≥ 50

Ha: µ < 50

Paso 2: Seleccionar el nivel de significancia:

α = 0.05

Paso 3: Seleccionar el estadístico de prueba:

= �� µ ��/√�� = 48 50 4/√36 = ��

Paso 4: Formular la regla de decisión:

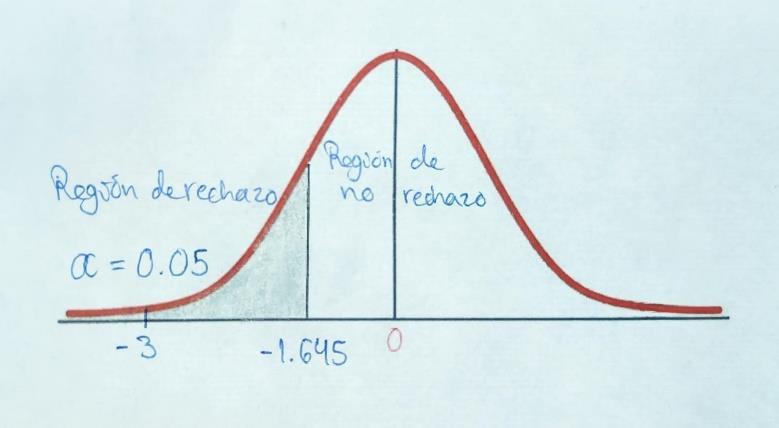
Paso 5: Se toma una decisión y se interpretan los resultados:

= �� µ ��/√�� = 48 50 4/√36 = ��

Ha: µ < 50 = Los paquetes de galletas contienen menos de 50 gramos.

Interpretación: Los paquetes de galleta contienen menos de 50 gramos, es decir, que estamos rechazando que el peso mínimo de los paquetes de galleta sea de 50 gramos y estamos aceptando la hipótesis alternativa de que el peso promedio de las galletas es menor a 50 gramos. En este caso el fabricante está llenando sus paquetes con menos de lo que indica la etiqueta.

Caso cola derecha:

Supongamos que queremos saber si el peso medio de una población de gatos es mayor a 4 kilogramos. Teniendo una muestra de 40 gatos de un refugio, con un nivel de significancia de 2%, con una media muestral de 4.5 kilogramos, con una desviación estándar de 0.80. Con los datos anteriores de prueba de hipótesis caso cola derecha, de solución al mismo, aplicando los 5 pasos señalados y con la regla de decisión de que si el estadístico de prueba es mayor que el valor Z crítico entonces rechazamos la hipótesis nula.

Datos:

�� = 4.50

µ = 4

�� = 0.80

n = 40

α = 0.02

Paso 1: Establecer la hipótesis nula (Ho) y la hipótesis alternativa (Ha):

Ho: µ ≤ 4

Ha: µ > 4

Paso 2: Seleccionar el nivel de significancia:

α = 0.02

Paso 3: Seleccionar el estadístico de prueba: �� = �� µ ��/√�� = 4.5 4 0.8/√40=��.����

Paso 4: Formular la regla de decisión:

Paso 5: Se toma una decisión y se interpretan los resultados:

= �� µ ��/√�� = 4.5 4 0.8/√40=��.����

Ha: µ > 4 = Se rechaza la hipótesis nula a favor de la hipótesis alternativa.

Interpretación: Por lo tanto, con la información obtenida a partir de la muestra de 40 gatos, podemos inferir que, en la población, la media del peso de los gatos es mayor a 4 kilogramos

Tema 9: Cálculo del Tamaño de la Muestra

1. Cálculo del tamaño de muestra para la estimación de la media con población infinita.

Planteamiento: Se desea estimar el ingreso promedio de las familias que viven en el municipio de San Pedro Jocopilas. Un estudio previo mostró que la desviación estándar de los ingresos familiares en comunidades similares era de Q 900.00 ¿Qué tan grande debe ser una muestra para que se tenga 95% de confianza de que el error de estimación no es mayor de Q.100.00?

Datos:

Nivel de confianza: 95% = 1.96

Desviación estándar: Q.900

Margen de error: Q.100

n = 311.17

Interpretación: se necesita aproximadamente una muestra de 312 familias para estimar su ingreso promedio con un intervalo de confianza del 95% y un error máximo de Q 100

2. Cálculo del tamaño de muestra para la estimación de la media con población finita.

Planteamiento: Se desea estimar el ingreso promedio de 5000 familias que viven en el municipio de San Pedro Jocopilas. Un estudio previo mostró que la desviación estándar de los ingresos familiares en comunidades similares era de Q 900 ¿Qué tan grande debe ser una muestra para que se tenga 95% de confianza de que el error de estimación no es mayor de Q.100?

Datos:

Nivel de confianza: 95% = 1.96

Desviación estándar: Q.900

Margen de error: Q.100

Tamaño de población: 5,000

�� = ��2 ∗��2 ∗�� ��2(�� 1)+ ��2 ∗��2

�� = 1.96²∗900²∗5000 100²∗(5000 1)+1.96²∗900² = 3.8416∗810,000∗5000 10,000∗(5000 1)+38416∗810,000

�� = 15,558,480,000 10,000∗4,999+3.8416∗810,000 = 15,558,480,000 49,990,000+3,111,696 = 15,558,480,000 53,101,696

n = 292.99

Interpretación: se necesita aproximadamente una muestra de 293 familias para estimar su ingreso promedio con un intervalo de confianza del 95% y un error máximo de Q 100

3. Cálculo del tamaño de muestra para proporciones con Población (N) desconocida.

Planteamiento: Se desea estimar la proporción de personas que en una comunidad rural no tienen ninguna escolaridad, para lo que se definen los siguientes criterios: Nivel de confianza: 95%. Proporción de personas sin escolaridad: 20%. Error máximo tolerable: 10%.

Datos: Nivel de confianza: 95% = 1.96

p = 0.20

q = 0.80

Margen de error: 0.10

n = 61.46

Interpretación: se necesita una muestra de 62 personas para estimar proporción de aquellas sin escolaridad, con un nivel de confianza del 95% y un error máximo de 10%.

4. Cálculo del tamaño de muestra para proporciones con Población (N) conocida

Planteamiento: Se desea estimar la proporción de 45,000 personas que en una comunidad rural no tienen ninguna escolaridad, para lo que se definen los siguientes criterios: Nivel de confianza: 95%. Proporción de personas sin escolaridad: 20%. Error máximo tolerable: 10%

Datos:

Nivel de confianza: 95% = 1.96

p = 0.20

q = 0.80

Margen de error: 0.10

Tamaño de población: 45,000

Interpretación: se necesita una muestra de 62 personas para estimar proporción de aquellas sin escolaridad, con un intervalo de confianza del 95% y un error máximo de 10%, cuando el tamaño de la población es de 45,000 familias.

MAPA MENTAL SOBRE “LAS FINANZAS”

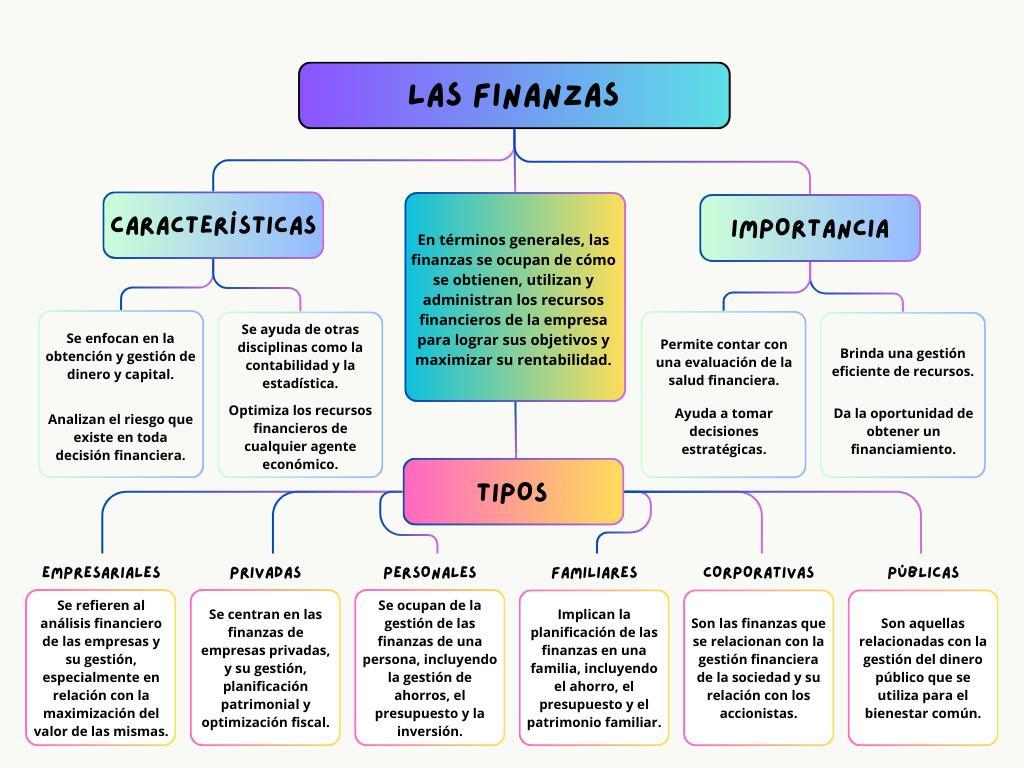
RESUMEN SOBRE EL LIBRO: “EL HOMBRE QUE CALCULABA”

Un hombre que iba camino a Bagdad se encuentra con un hombre que repetía constantemente el numero un millón cuatrocientos veinte tres mil setecientos cuarenta y cinco, el hombre preguntó del porqué de la repetición de este número y el hombre le comenzó a contar su historia que comenzó cuando trabajaba con un rebaño de ovejas y que mientras pastoreaba podía contar cada cosa que miraba en su camino, al ver este su habilidad para los números decidió dedicarse a ser un calculados. El nombre de este personaje era Beremiz Samir.

Beremiz tuvo numerosas aventuras como por ejemplo cuando viajaba, se encontró con un grupo de hombres que discutían acerca de la repartición de la herencia que su padre había dejado, pero eran 35 camellos entre tres personas y este cálculo que era imposible, Beremiz dejó satisfecho a los tres hermanos. Otra ocasión mientras viajaba, se encontró un hombre rico de Bagdad, llamado Salem a quien le habían robado sus pertenencias y habían matado a sus esclavos y a quien Beremiz dio de comer durante todo el camino y al llegar a Bagdad, encontraron a Ibrahim, quien le dio dinero para que pagara a Beremiz, pero éste encontró un error en la repartición del dinero y rectificó la operación dejando impactados a todos, de esta misma manera resuelve el caso de un de un joyero que debía recibir cierta comisión por ventas.

Acudieron un día unos hombres a quienes se les tenía que pagar para poder salvar un hostal, pero al momento de realizar las reparticiones de los bienes que le correspondían a cada una de las personas, la operación era ilógica, pero Beremiz ayudó a resolver este problema dejando impactados a los dueños del Hostal. Posteriormente, Beremiz inicia a impartirle clases de matemáticas y aritmética a Telassim en el palacio de Lezid y le explica que las matemáticas son la base de todas las ciencias.

Un día, Beremiz fue a un café en donde había un hombre que se dedicaba a relatar historias y al reconocer a Beremiz el calculador, decidió ponerlo a prueba poniéndole un problema matemático que pensó que no lo iba a poder resolver, entonces Beremiz con su gran inteligencia procedió a la resolución del problema donde la respuesta de Beremiz era verídica, de esa manera dejó imputadas a las personas del café que le daban numerosos elogios por su gran inteligencia.

La segunda clase de matemática de Telassim, se trató acerca de los diferentes sistemas de numeración como lo era el sistema quinario, que era cuando las unidades se agrupaban de cinco en cinco, otro de los sistemas fue el romano en donde los números estaban representados por las letras como la L, C, D y M. En una prisión sucedió una gran tragedia, se incendió la cárcel y los prisioneros sufrieron mucho en ese momento y los encargados de la cárcel decidieron disminuir las sentencias de los presos a la mitad de los años que vivieran, pero eso iba a ser muy difícil, porque ellos no sabían cuánto iba a vivir cada uno de los presos; entonces llamaron a Beremiz para que pudiera resolver este problema y lo resolvió por medio de una ecuación.

Beremiz fue citado nuevamente en el palacio para platicar con algunos sabios, pero su temor le daba inseguridad, uno de los sabios lo probó haciéndole una pregunta que no era de matemáticas, sino de cultura general y Beremiz la contestó correcta. Otro sabio le preguntó que quién había sido el geómetra que se suicidó al mirar al cielo, y Beremiz les dijo que había sido Eratóstenes y les contó la historia.

Después otra de las historias comentadas por Beremiz, fue la de la princesa Dahizé y sus tres prometidos de los cuales debía escoger al más inteligente. La manera era haciéndoles diversas pruebas de lógica las cuáles se las explicó Beremiz, que también fue aprobada. Uno de los sabios con los que comentaba problemas de lógica y matemáticas le dijo que les explicara un problema que se trataba de ocho perlas de las cuales una de estas era más pesada que las demás; Beremiz haciendo un razonamiento lógico, halló la respuesta correcta y los sabios lo halagaron con un bello poema.

Los sabios le ofrecieron oro y plata para recompensar la sabiduría del calculador, pero él no quiso esa oferta, sino él quería casarse con Telassim, la hija del jeque Lezid. Entonces les ofrecieron mejor a unas esclavas, porque no le podían dar a Telassim, pero las esclavas eran mentirosas y para probarlo Beremiz le pregunta a una de ellas el color de sus ojos y mintió, al preguntarle a la otra también mintió

El jeque Lezid muere en un combate contra los mongoles. La ciudad de Bagdad es destruida y ahora sólo quedan ruinas. Beremiz se casa con Telassim y se entera que Telassim es cristiana; Beremiz decide dejar las creencias de Mahoma y decide seguir a Cristo con su esposa e hijos.

ENSAYO SOBRE EL TEMA:

Autor: Luis Enrique Delgado Domingo.

Tema: “Distribución de Probabilidades Normal”.

La distribución normal, es una distribución de probabilidades muy importante y es frecuentemente utilizada en varias aplicaciones estadísticas Su función de densidad tiene forma de campana; dos parámetros determinan la distribución normal: la media y la desviación estándar. La gráfica de su función de densidad es simétrica respecto de un determinado criterio estadístico, y a dicha densidad se le denomina “Campana de Gauss”.

Debido a su gran aplicación en varios campos, es una de las distribuciones de probabilidad que con más constancia aparece en

casos reales. Su nombre indica su extendida utilización, justificada por la frecuencia con la que los ciertos fenómenos tienden a parecerse en su comportamiento a esta distribución.

En estadística, esta distribución nos puede ayudar a calcular la posibilidad de que algunos eventos dentro de un rango determinado sucedan, por ejemplo, en una ciudad donde queremos evaluar la situación del clima, con ayuda de este tipo de modelo estadístico podríamos calcular dentro un rango de probabilidad las veces en que la temperatura sea muy elevada durante la semana y de esta manera coordinar nuestras actividades cuando salgamos al aire libre.

Para ello nos apoyamos de la fórmula: ��= �� �� �� , en dónde �� equivale a la

variable estandarizada, �� a la media testada, �� a la media normal, �� igual a la desviación estándar

Seguidamente usaremos la tabla general de distribución normal para encontrar el valor que nos acaba de dar �� y dicho valor será ubicado para luego ser multiplicado por 100, el cual sería la probabilidad de los sucesos que estamos hallando, que en este caso sería la temperatura

En resumen, la distribución normal es una herramienta estadística fundamental con propiedades y aplicaciones muy versátiles, esto se debe a que muchos procesos aleatorios siguen aproximadamente este tipo de distribución, lo que la convierte en una herramienta fundamental o pieza clave en el análisis de datos y la toma de decisiones informadas en una amplia gama de campos.

GLOSARIO DE TÉRMINOS

1. Regresión: En estadística, el análisis de la regresión es un proceso estadístico para entender cómo una variable depende de otra variable.

2. Variable: En matemáticas y en lógica, una variable es un símbolo constituyente de un predicado, fórmula, algoritmo o de una proposición.

3. Normalizada: La normalización es el proceso de elaborar, aplicar y mejorar las normas que se emplean en distintas actividades científicas, industriales o económicas, con el fin de ordenarlas y mejorarlas.

4. Cronológica: Es una de las ciencias auxiliares de la historia cuya finalidad es determinar el orden temporal de los acontecimientos históricos y es fundamental para la historia, se asocia al ordenamiento temporal de acontecimientos.

5. Simbología: Se refiere al estudio y uso de símbolos para comunicar ideas, conceptos o significados más allá de su forma literal.

6. Excluyente: El verbo excluir, por su parte, alude a suprimir, apartar o rechazar algo o a alguien, dejándolo fuera de un cierto marco o grupo.

7. Discreta: En matemáticas, una variable que no puede tomar algunos valores dentro de un mínimo conjunto numerable, solamente puede asumir ciertos valores.

8. Binomial: En teoría de la probabilidad y estadística, la distribución binomial se utiliza para predecir la probabilidad de obtener un número específico de éxitos en un número fijo de intentos, cada uno con dos posibles resultados (éxito o fracaso) y donde cada intento es independiente de los demás.

9. Estandarizada: Es la adaptación de un proceso a una serie de normas o reglas de referencia. Se trata de ajustar algo a un estándar, modelo o patrón.

10.Desviación: En matemáticas y estadística, la desviación es una medida de la diferencia entre el valor observado de una variable y algún otro valor, a menudo la media de esa variable.

11.Testada: Al ser un participio, denota siempre tiempo pasado y aspecto perfectivo, es decir, que la acción ya se ha completado

12.Aseveración: Es una afirmación que busca confirmar o ratificar la verdad o certeza de algo. Puede ser evaluada en términos de verdad o falsedad, y puede ser relacionada con otras aseveraciones de modo lógico.

13.Inferencias: En lógica, se denomina inferencia al proceso mediante el cual se obtienen conclusiones determinadas a partir de un conjunto específico de premisas.

14.Sesgos: Es un peso desproporcionado a favor o en contra de una cosa, persona o grupo en comparación con otra, generalmente de una manera que se considera injusta.

15.Estratificado: Denota que algo está formado o dispuesto en estratos, que son capas o niveles. El muestreo estratificado es una forma de representación estadística que muestra cómo se comporta una característica o variable en una población a través de hacer evidente el cambio de dicha variable en subpoblaciones o estratos en los que se ha dividido

16.Sistemático: Es lo que se adapta a un sistema ordenado y reglado o se repite con asiduidad, con partes interrelacionadas.

17.Polietápico: Es un tipo de muestreo, también llamado muestreo por etapas, es un método para seleccionar la muestra de un estudio estadístico

18.Opinático: Es un tipo de muestreo, un método no probabilístico que sirve para seleccionar los individuos que formarán parte de la muestra de un estudio estadístico.

19.Incidental: Se trata de un suceso que aparece en relación a otro que opera como el principal, siendo, por lo tanto, de relevancia menor.

20.Simétrico: Correspondencia exacta que se verifica en la forma, el tamaño y la posición de las partes de un objeto considerado como un todo.

21.Sucesos: Son hechos o acontecimientos que resulta de importancia o interés particular dentro de un contexto determinado.

CONCLUSIONES

✓ Los conceptos ya descritos, han sido analizados de tal manera de hacer más fácil su comprensión y entendimiento ya que la estadística es la ciencia que trata de entender, organizar y tomar decisiones que estén de acuerdo con los análisis efectuados.

✓ En un mundo inundado de datos, la estadística ayuda a discernir entre la información relevante y la aleatoria. Ayuda a evaluar la credibilidad de los estudios y afirmaciones, lo que es crucial para la toma de decisiones en cualquier nivel.

✓ La aplicación de métodos estadísticos es fundamental en diversos campos y disciplinas debido a su capacidad para analizar datos, extraer patrones y conclusiones, y tomar decisiones fundamentadas.

✓ La adquisición de conocimientos y habilidades en estadística es fundamental en diversos campos y sectores debido a su capacidad para extraer información significativa a partir de datos

✓ Desarrollar la habilidad de interpretar los resultados de análisis estadísticos de manera precisa y contextualizada, comprendiendo su significado y relevancia, aplicando los conocimientos estadísticos para resolver problemas del mundo real en campos como la economía y administración.

REFERENCIAS

http://www.librosmaravillosos.com/hombrecalculaba/pdf/El%20Hombre%20que%20Calculaba%20%20Malba%20Tahan.pdf

https://www.matematicasonline.es/BachilleratoCCSS/segundo/archivos/distribucion_normal/DISTRIBUC ION%20NORMAL.htm

https://www.hiru.eus/es/matematicas/distribucion-normal

https://definicion.de/regresion/

https://concepto.de/variable/

https://es.thefreedictionary.com/estandarizada

https://dle.rae.es/binomial

https://www.wordreference.com/definicion/desviaci%C3%B3n

https://economipedia.com/definiciones/muestreo-estratificado.html

https://es.bab.la/diccionario/espanol/sistem%C3%A1tico

https://dle.rae.es/sim%C3%A9trico

https://concepto.de/suceso/