Issuu

Solution 7.1

Fundamentals of Electric Circuits 6th Edition Alexander Full download at: Solution Manual: https://testbankpack.com/p/solution-manual-for-fundamentals-ofelectric-circuits-6th-edition-by-alexander-sadiku-isbn-00780282219780078028229/

prior written consent of McGraw-Hill Education

without

All rights

No reproductionor distribution

reserved

the

(a) =RC = 1/200 For the resistor, V=iR= 56e 200t  8Re 200t x10 3 C  1  1  0.7143F  R  56  7 k 8 200R 200X7X103 (b)  =1/200= 5 ms (c) If value of the voltage at = 0 is 56 . 1 x56  56e 200t 2  e200t  2 200t  ln2  t  1 ln2  3 466 ms o o 200

Solution 7.2

τ = R thC

where R th is the Thevenin equivalent at the capacitor terminals.

R th =120||80 +12 = 60 Ω

τ = 60x0.05 = 3 s.

Solution 7.3

R = 6k +40kx(25k+35k)/(40k+25k+35k) = 6k+2400k/100 = 30 kΩ.

τ = RC = 30kx50x10–12 = 1.5 µs.

reproductionor distribution without the prior written consent of McGraw-Hill Education

Solution 7.4

For t<0, v(0-)=40 V.

For t >0. we have a source-free RC circuit.

τ = RC = 2x103 x10x10 6 = 0.02

v(t) = v(0)e t /τ = 40e 50t V

reproductionor distribution without the prior written consent of McGraw-Hill Education

Solution 7.5

Using Fig. 7.85, design a problem to help other students to better understand source-free RC circuits.

Although there are many ways to work this problem, this is an example based on the same kind of problem asked in the third edition.

Problem

For the circuit shown in Fig. 7.85, find i(t), t>0.

Solution

Let v be the voltage across the capacitor For t <0, v(0 ) = 4 (24) = 16 V

2 + 4

For t >0, we have a source-free RC circuit as shown below.

prior written consent of McGraw-Hill Education

i + 5Ω 24 V 4 Ω 4Ω 1/3 F

2 Ω t=0

Figure 7.85 For Prob. 7.5.

i 5Ω 4 Ω

Copyright © 2017 McGraw-HillEducation All rights reserved No reproductionor distribution without the prior written consent of McGraw-Hill Education v(t) = v(0)e t /τ = 16e t / 3 V i(t) = C dv = 1( 1)16e t / 3 = 1.778e t / 3 A dt 3 3

Solution 7.6

The switch in Fig. 7.85 has been closed for a long time, and it opens at t = 0. Find v(t) for t ≥ 0.

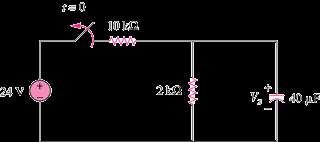
60 V

Solution

v(0) = [2x60/(10+2)] = 10 V and τ = RC = 2,000x40x10–6 = 0.08.

Note, 1/0.08 = 12.5/s

This then leads to v(t) = [10e–12.5t] V for all 0 ≤ t.

v(t) Figure 7.85 For Prob. 7.6.

Assuming that the switch in Fig. 7.87 has been in position A for a long time and is moved to position B at t=0. Then at t = 1second, the switch moves from B to C Find vC(t) for t ≥

Solution

Step 1. Determine the initial voltage on the capacitor. Clearlyit charges to 15 volts when the switch is at position A because the circuit has reached steady state.

This then leaves us with two simple circuits, the first a 500 Ω resistor in series with a 2 mF capacitor and an initial charge on the capacitor of 15 volts. The second circuit which exists from t = 1 sec to infinity. The initial condition for the second circuit will be vC(1) from the first circuit. The time constant for the first circuit is (500)(0.002) = 1 sec and the time constant for the second circuit is (1,000)(0.002) = 2 sec vC(∞) = 0 for both circuits. Step

consent of McGraw-Hill Education Solution 7.7

0. 10 kΩ A 15 V B C 500 Ω 1 kΩ 2 mF Figure 7.87 For Prob.

7.7

2. vC(t) = [15e-t]u(t) volts for 0 < t < 1 sec and = 15e–1e –2(t–1) at t = 1 sec, and = [5.518e–2(t–1)]u(t–1) volts for 1 sec < t < ∞ [15e–t] volts for 0 < t < 1 sec, [5.518e–2(t–1)] volts for 1 sec < t < ∞.

Copyright © 2017 McGraw-HillEducation All rights reserved No reproductionor distribution without the prior written consent of McGraw-Hill Education Solution 7.8 0 1 1 1 (a) 1   RC  4 dv -i  C dt -0.2e-4t  C(10)(-4)e-4t 1  C  5mF R   50  4C 1 (b)   RC  4 1  0.25 s 1 (c) w C (0)  CV2  2 (5 10-3)(100)  250mJ 2 (d) w   CV2  CV2 1 e-2t0   R 0.5  1 e-8t0 2 2  0 2 0 1 e-8t0  2 or e8t0 t0   2 1 ln(2)  86.6 ms 8

Solution 7.9

The switch in Fig. 7.89 opens at t=0. Find vo for t > 0. 2 kΩ t=0

Solution

For t < 0, the switch is closed so that

vo(0) = [4/(2+4)]15 = 10 V.

For t >0, we have a source-free RC circuit where τ = 4,000x0.003 = 12 s.

Thus,

vo(t) = [10e–t/12] V for all t ≥ 0.

prior written consent of McGraw-Hill Education

No reproduction

or distribution without the

–

+ + 15 V vo 4 kΩ 3 mF

Figure 7.89 For Prob. 7.9.

Solution 7.10

For t<0,

+ 9

For t>0, we have a source-free RC circuit

vo(t) = 9e–16.667t V

Let the time be to.

3 = 9e–16 667to or e16.667to = 9/3 = 3

to = ln(3)/16.667 = 65.92 ms.

without the prior written consent of McGraw-Hill Education

reproductionor distribution

v(0 ) = 3 (36V) = 9 V

τ = RC

3x103 x20x10 6 = 0.06s

Solution 7.11

For t<0, we have the circuit shown below.

V +

io(0–) = [2/(2+8)]6 = 1.2 A

For t >0, we have a source-free RL circuit.

τ = L = 4 =1/3 thus,

R 4+8

io(t) = 1.2e–3t A

prior written consent of McGraw-Hill Education

All

No reproductionor distribution without the

rights reserved

4H io 4

Ω 4H

Ω 24

8 Ω

Ω

Ω 4||4= 4x4/8=2

Solution 7.12

Using Fig. 7.92, design a problem to help other students better understand source-free RL circuits.

Although there are many ways to work this problem, this is an example based on the same kind of problem asked in the third edition.

Problem

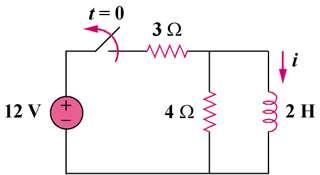
The switch in the circuit in Fig. 7.90 has been closed for a long time. At t = 0, the switch is opened. Calculate i(t) for t > 0.

Solution

When t < 0, the switch is closed and the inductor acts like a short circuit to dc. The 4 Ω resistor is short-circuited so that the resulting circuit is as shown in Fig. (a)

prior written consent of McGraw-Hill Education

Figure 7.90

3 Ω 12 V + i(0-) 4 Ω 2 H (a) (b)

Solution 7.13 12 i(0 ) = 3

= 4 A

Since the current through an inductor cannot change abruptly, i(0) = i(0 ) = i(0+ ) = 4 A

or distribution without the prior written consent of McGraw-Hill Education

reproduction

When t > 0, the voltage source is cut off and we have the RL circuit in Fig. (b)

2017

consent of McGraw-Hill Education

No reproduction

or distribution without the prior written

L τ

4 i(t)

= R Hence, 2 = = 0.5

= i(0)e-t τ = 4e-2t A

Solution 7.13

(a)

v(t) = i(t)R = 80e–1000t V = R5e–1000tx10–3 or R = 80,000/5 = 16 kΩ.

τ = 1 = 1ms 103 = 1 ms

But τ = L/R

3/103 = 16 H.

energy

in the

is 0.0005 0.0005 w = ∫ pdt = ∫ 0.4e 2000t dt = 0.4 e 2000t 0.0005 0 0 2000 0 = 200(1–e –1)x10–6 = 126.42 µJ.

ms (b)

= 1/10

= 16x10

(b) The

dissipated

resistor

(a) 16 kΩ, 16

126.42 µJ

Education RTh = (40 + 20)//(10 + 30) = 60x40 = 24kΩ 100 5x10 3 τ = L/R = = 0.2083µs 24x103

McGraw-Hill

Copyright © 2017 McGraw-HillEducation All rights reserved No reproductionor distribution without the prior written consent of McGraw-Hill Education R (a) (b) RTh R = 2 +10//40 =10Ω, = 40//160 + 48 = 40Ω, τ = L = 5/10 = 0.5s RTh τ = L = (20x10 3)/80 = 0.25ms Th Th (a) 10 Ω, 500 ms (b) 40 Ω, 250 µs

Solution 7.15

Solution 7.16

without the prior written consent of McGraw-Hill Education

R L1 2 L eq τ = R eq R1R 3 R 2 (R1 +R 3 ) +R1R 3 (a) L eq = L and R eq = R2 + 1 = + R 3 R1 + R 3 L(R +R ) τ = 1 3 R2 (R1 + R3 ) + R1R3 (b) where L L L = 1 2 and R R R R (R +R ) +R R = R + 1 2 = 3 1 2 1 2 eq + L L L (R + R ) eq 3 R1 + R2 R1 + R2 τ = 1 2 1 2 (L1 + L2 )(R3 (R1 + R2 )+ R1R2 )

reproduction

distribution

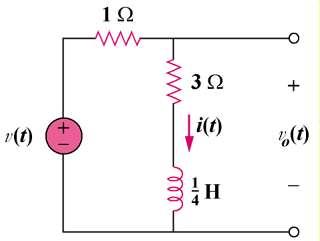
Consider the circuit of Fig. 7.97. Find v0(t) if i(0) = 15 A and v(t) = 0.

Solution

i(t) = i(0)e–t/τ where τ = L/Req = 2/4 = (½) s. Additionallyvo(t) = 3i(t) + 2di(t)/dt.

Thus, i(t) = [15e–2t]u(t) A and vo(t) = [45e–2t]u(t) – [(2)(2)15e–2t]u(t)

= [–15e–2t] V for all t ≥ 0.

Solution 7.17 2 H Figure 7.97 For Prob. 7.17.

Solution 7.18

If v(t) = 0, the circuit can be redrawn as shown below.

prior written consent of McGraw-Hill Education

All

No reproductionor distribution

rights reserved

without the

+ Req vo(t) i(t) 0.4 H 6 R eq = 2||3 = 5 , L τ = = R 2 5 1 × = 5 6 3 i(t) = i(0)e -t τ = 5e -3t v (t) = -L di = -2 (-3)5e -3t = 6 e -3t V o dt 5

Solution 7.19

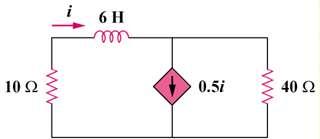
In the circuit of Fig. 7.99, find i(t) for t > 0 if i(0) = 5 A.

To find R th we replace the inductor by a 1-V voltage source as shown above

2017

without the prior written consent of McGraw-Hill Education

No reproduction

distribution

Solution i i1 i2 + 10  i1 i/2 i2 40 

Figure 7.99 For Prob. 7.19.

10i1 1 40i2  0 But i.e. i  i2  i 2 i1  2i2  i and i  i1 1 10i 1 20i  0  i  30 R th  1  30  i L   R th

find i(t) for t > 0 if i(0) = 5 A. 6   0.2 s 30 i(t)  5e–5tu(t) A

consent of McGraw-Hill Education Solution 7.19 In the circuit of Fig. 7.99,

The value of the energy remaining at 10 ms is given by: w10 = 0.03(30e–

)2 = 0.03(18.196)2 = 9.933 J

So, the fraction of the energy dissipated in the first 10 ms is given by: (27–9.933)/27 = 0.6321 or 63.21%.

Solution 7.20

(a) L 1    R 50  R  50L v  L di dt 90e -50t  L(30)(-50)e -50t R  50L  3 Ω  L  60 mH (b) L    R 1  20 ms 50 (c) w  1 Li2 (0)  1(0.06)(30)2  27 J 2 2

0.5

Solution 7.21

In the circuit in Fig. 7.101, find the value of R for which the steady-state energy stored in the inductor will be 2 J

7.21.

Solution

The circuit can be replaced by its Thevenin equivalent shown below.

Figure 7.101 For Prob.

Rth Vth + 2 H

80 + 40(60)

40 V 80 R th = 40||80+ R = 3

i(0) = i(∞) = Vth = R th + R 40 80 3+ R

2 = 2 or 40/(R+80/3) = 1.4142, thus, R+80/3 = 40/1.4142 or R = 28.285–26.667 = 1.618 Ω.

= 80

I =

w = (1/2)LI

= 0.5(2)[40/(R+80/3)]

Solution 7.23

Since the 2  resistor, 1/3 H inductor, and the (3+1)  resistor are in parallel, they always have the same voltage.

reproductionor distribution without the prior written consent of McGraw-Hill Education

-i  10  10  7.5  i(0)  -7.5 2 3 1

4 R th  2|| (3  1)  3 , L   R th 1 3 1   4 3 4 i(t)  i(0)e -t   -7.5e-4t , t  0 vL  v o  L di  -7.5(-4)(1/3)e-4t dt -4t v o  10e V , 1 t  0 -4t v x  3  1 vL  2.5e V, t  0

The Thevenin resistance R th at the inductor’s terminals is

the

(a) (b) v(t) = -5u(t) i(t) = -10[u(t) − u(t − 3)]+10[u(t − 3) − u(t − 5)] (c) = -10u(t) + 20u(t 3) 10u(t 5) x(t) = (t 1)[ u(t 1) u(t 2)]+ [ u(t 2) u(t 3)] + (4 t)[ u(t 3) u(t 4)] = (t −1)u(t −1) − (t − 2)u(t − 2) − (t − 3)u(t − 3) + (t − 4)u(t − 4) = r(t 1) r(t 2) r(t 3) + r(t 4) (d) y(t) = 2u(-t) 5[ u(t) u(t 1)] = 2u(-t) 5u(t) + 5u(t 1)

without

prior written consent of McGraw-Hill Education

Solution 7.25

Design a problem to help other students to better understand singularity functions.

Although there are many ways to work this problem, this is an example based on the same kind of problem asked in the third edition.

Problem Sketch each of the following waveforms.

(a) i(t) = [u(t–2)+u(t+2)] A

(b) v(t) = [r(t) – r(t–3) + 4u(t–5) – 8u(t–8)] V

Solution

The waveforms are sketched below.

(a) i(t) (A)

0 8 2 1

-2 -1 0 1 2 3 4 t (b) v(t) (V) 7 3 0 1 2 3 4 5 6 7 8 t –1

written

Education Solution 7.26 1 2 3 4 (a) v (t) = u(t +1) − u(t) + [ u(t −1) − u(t)] v1(t) = u(t + 1) 2u(t)+ u(t 1) (b) v (t) = (4 t)[ u(t 2) u(t 4)] v2 (t) = -(t 4)u(t 2) + (t 4)u(t 4) v2 (t) = 2u(t 2) r(t 2) + r(t 4) (c) v (t) = 2[ u(t 2) u(t 4)]+ 4[ u(t 4) u(t 6)] v3 (t) = 2u(t 2)+ 2u(t 4) 4u(t 6) (d) v (t) = -t[ u(t 1) u(t 2)] = -tu(t 1) + tu(t 2) v4 (t) = (-t +1−1)u(t −1) + (t − 2 + 2)u(t − 2) v4 (t) = -r(t 1) u(t 1)+ r(t 2)+ 2u(t 2)

without the prior

consent

McGraw-Hill

Solution 7.27

v(t)= [5u(t+1)+10u(t)–25u(t–1)+15u(t-2)] V

prior written consent of McGraw-Hill Education

All rights

No reproductionor distribution without

reserved

the

Solution 7.28

Sketch the waveform represented by i(t) = [r(t+1) – r(t) – 2u(t+1) +u(t–2) + r(t–3) – r(t–4)] A.

Solution i(t) is sketched below.

reproductionor distribution without the prior written consent of McGraw-Hill Education

i(t) 2 –1 0 1 2 3 4 t –2

Solution 7.29 (a) x(t) 3.679 0 1 t (b) y(t) 27.18 0 t (c) z(t) = cos4tδ (t 1) = cos4δ (t 1) = 0.6536δ (t 1),

1 0 t –0.653δ(t–1)

which is sketched below. z(t)

Copyright © 2017 McGraw-HillEducation All rights reserved No reproductionor distribution without the prior written consent of McGraw-Hill Education 2 2 (a) ∞ ∫ ∞ 4t δ(t −1) dt = 4t2 t=1 = 4 (b) ∞ ∫-∞ 4t cos(2πt)δ(t − 0.5) dt = 4t2 cos(2πt) t=0.5 = cos π = -1

Solution 7.30

Solution 7.31

© 2017 McGraw-HillEducation All rights reserved No reproductionor distribution without the prior written consent of McGraw-Hill Education ∫ ∫ (a) ∞ [e-4t2 δ(t 2)] dt = e-4t2 -∞ t=2 = e-16 = 112×10-9 (b) ∞ [5δ(t) + e-t δ(t) + cos2πtδ(t)] dt = (5+ e-t + cos(2πt)) -∞ t=0 = 5 +1+1= 7

Copyright © 2017 McGraw-HillEducation All rights reserved No reproductionor distribution without the prior written consent of McGraw-Hill Education 2 t t t (a) ∫u(λ)dλ = ∫1dλ = λ = t −1 1 1 1 4 1 4 2 (b) r(t −1)dt = 0dt + (t 1)dt = t t 4 = 4.5 ∫ ∫ ∫ 1 0 0 1 5 2 2 (c ) ∫(t 6) 1 δ (t − 2)dt = (t − 6) t=2 =16

Solution 7.32

Solution 7.33

The voltage across a 10-mH inductor is 45δ (t – 2) mV. Find the inductor current, assuming that the inductor is initially uncharged.

Solution

i(t) = 1 ∫t v(τ) dτ + i(0)

L 0 10-3 t i(t) = ∫ 45δ (τ 2) dτ + 0= 4.5u(t–2) A. 10×10-3 0

It should be noted that the integration of the impulse function, δ(t–t0), produces the unit step, u(t–t0) Whatever the multiplier (f(t)) of the impulse function at t = t0 ends up multiplying the unit step by the same amount (f(t0)) in this case f(2) = 4.5.

i(t) = 4.5u(t–2) A

or distribution

(a) (b) d [u(t 1) u(t + 1)] = δ (t 1)u(t + 1) + dt u(t 1)δ (t + 1) = δ (t 1)1+ 0δ (t + 1) = δ (t 1) d [r(t − 6) u(t − 2)] = u(t − 6)u(t − 2) + dt r(t 6)δ (t 2) = u(t 6)1+ 0δ (t 2) = u(t 6) (c) d [sin4t u(t 3)] = 4cos4t u(t 3) + sin4tδ (t 3) dt = 4cos4t u(t − 3) + sin4x3δ (t − 3) = 4cos4t u(t 3) 0.5366δ (t 3)

reproduction

without the prior written consent of McGraw-Hill Education

© 2017 McGraw-HillEducation All rights reserved No reproductionor distribution without the prior written consent of McGraw-Hill Education (a) (b) v = Ae 2t , v(t) = –e–2tu(t) V i = Ae3t / 2 , i(t) = 2e–1.5tu(t) A v(0) = A = 1 i(0) = A = 2

Solution 7.35 Copyright

Solution 7.36

(a) v(t) = A + Be-t , t > 0

A =1, v(0) = 0 =1+ B or B = -1

v(t) = 1 e-t V, t > 0

(b) v(t) = A + Bet 2 , t > 0

A = -3, v(0) = -6 = -3+ B or B = -3

v(t) = -3(1+ et 2 ) V, t > 0

Copyright © 2017 McGraw-HillEducation All rights reserved No reproductionor distribution without the prior written consent of McGraw-Hill Education  Let v = vh + vp, vp =10. 1 0 t / 4 vh  4 vh   vh  Ae v  10  Ae 0.25t v(0)  2  10  A v  10 8e 0.25t  A  8 (a)   4s (b) v()  10 V (c ) v 10 8e 0.25t u(t) V

Solution 7.37

Copyright © 2017 McGraw-HillEducation All rights reserved No reproductionor distribution without the prior written consent of McGraw-Hill Education h Let i = ip +ih  i h  3ih  0  i  Ae 3t u(t) Let i  ku(t),  i  0, 3ku(t)  2u(t)  k  2 p p 3 i  2 u(t) p 3 i  (Ae 3t  2 )u(t) 3 If i(0) =0, then A + 2/3 = 0, i.e. A=-2/3. Thus, i  2 (1 e 3t )u(t) 3

Solution 7.38