La “media” naranja
“Donde los datos encuentran su otra mitad”

“Donde los datos encuentran su otra mitad”
“Siamaslospromediosestaestumedia naranja”
¿CREES EN LAS MEDIAS NARANJAS? NOSOTROS SÍ… PERO LAS CALCULAMOS. BIENVENIDO A LA MEDIA NARANJA, LA REVISTA DONDE LOS DATOS SE MEZCLAN CON EL HUMOR, LA PROBABILIDAD COQUETEA CON LA ESTADÍSTICA, Y LAS GRÁFICAS TIENEN MÁS CURVAS QUE UNA TELENOVELA.
SI ALGUNA VEZ TE PREGUNTASTE QUÉ TIENEN EN COMÚN EL AZAR, LOS PROMEDIOS Y LOS CRUSHES IMPOSIBLES, ESTA ES TU LECTURA IDEAL. ¡NO TE LO PIERDAS!
INTRODUCCIÓN
ORGANIZACIÓN Y PRESENTACIÓN DEL CONJUNTO DE DATOS 1 2 3 4 5 6 7
8 9 10 11 13 12
MODELO MATEMATICO
FENÓMENOS PROBABILÍSTICOS
NATURALEZA Y OBJETIVOS DE LA ESTADISTICA
EL METODO ESTADISTICO Y LA FRECUENCIA RELATIVA
ESTADISTICA DESCRIPTIVA
ORDENACION Y TABLA DE FRECUENCIA
LA SUMATORIA Y SUS PROPIEDADES
CONSTRUCCION NUMEREICA DE LA TABLA DE FRECUENCIA
DISTRIBUCION DE FRECUENCIA RELATIVA ACUMULADA
MEDIDAS DESCRIPTIVAS PARA UN CONJUNTO DE DATOS
MEDIDAS DE CENTRALIZACION O TENDENCIA CENTRAL
MEDIDAS DE DISPERCION O ESPARCIMIENTO
VARIABLES
DEFINICION LA
DIFERENTES
UNIFORME
��
¿Qué tienen en común lanzar un dado, revisar el clima y predecir cuántos memes verás hoy?
¡Exacto! Todo eso tiene que ver con Probabilidad y Estadística.
Imagina que eres un detective... pero en lugar de resolver crímenes, resuelves misterios de datos: ¿cuál sabor de helado es el más popular?, ¿qué equipo tiene más chance de ganar?, o ¿cuál ruta es más rápida para llegar a casa?
La probabilidad es como tu bola de cristal científica: te dice qué tan posible es que algo ocurra (aunque a veces parezca que el universo juega a los dados).
Y la estadística es tu superpoder para entender el mundo a través de números: tomas datos, los ordenas, los analizas, y ¡zas! descubres patrones, tendencias y sorpresas escondidas.
Así que si te gusta resolver acertijos, tomar decisiones inteligentes o simplemente ganar más apuestas con tus amigos, estás a punto de entrar a un mundo donde los números hablan y predicen el futuro (más o menos). ��
Bienvenido al universo de la Probabilidad y la Estadística… donde el azar no es tan al azar como parece.
�� ¿Qué es la probabilidad?
La probabilidad es como el arte de predecir el futuro… pero con matemáticas.
Por ejemplo:
Si lanzas una moneda, ¿qué probabilidad hay de que salga águila?
→ 50% (¡a menos que la moneda esté cargada ��!)
¿Qué probabilidad hay de que llueva mañana?
→ El clima no lo adivinan: usan datos pasados, modelos matemáticos y... ¡estadística!
En resumen, la probabilidad nos dice qué tan posible es que algo ocurra. Se expresa como números entre 0 (imposible) y 1 (seguro), o en porcentajes.
�� ¿QUÉ ES UN MODELO MATEMÁTICO?
UN MODELO MATEMÁTICO ES UNA REPRESENTACIÓN DE LA VIDA REAL
USANDO MATEMÁTICAS PARA ENTENDER, EXPLICAR O PREDECIR ALGO.
ES COMO DECIR:
�� “¿QUÉ PASARÍA SI CONVIERTO ESTA SITUACIÓN REAL EN NÚMEROS, FÓRMULAS O GRÁFICAS?”
�� EJEMPLO SÚPER SIMPLE:
SITUACIÓN REAL:
CADA ENTRADA AL CINE CUESTA $5 Y COMPRAS 2 PALOMITAS A $3 CADA UNA.
MODELO MATEMÁTICO:
COSTO TOTAL=5X+3Y
DONDE:
X = NÚMERO DE ENTRADAS
Y = NÚMERO DE PALOMITAS
�� ¿PARA QUÉ SIRVE?
PARA PREDECIR LO QUE VA A PASAR
PARA ENTENDER CÓMO FUNCIONA ALGO
PARA TOMAR DECISIONES CON LÓGICA (NO CON SUPOSICIONES)
�� ¿PARA QUÉ SIRVE?
PARA PREDECIR LO QUE VA A PASAR
PARA ENTENDER CÓMO FUNCIONA ALGO
PARA TOMAR DECISIONES CON LÓGICA (NO CON SUPOSICIONES)
EN RESUMEN: ✅ ES UNA HERRAMIENTA MATEMÁTICA PARA REPRESENTAR LA REALIDAD ✅ USA FÓRMULAS, FUNCIONES, ECUACIONES O GRÁFICOS
✅ NOS AYUDA A PENSAR ANTES DE ACTUAR (¡COMO UN SUPERPODER LÓGICO! ��
)
1.2 3
LOS FENÓMENOS PROBABILÍSTICOS SON SITUACIONES O EVENTOS QUE
NO SABEMOS CON CERTEZA QUÉ VA A PASAR, PERO SÍ PODEMOS
PREDECIR LO QUE PODRÍA PASAR CON CIERTOS NÚMEROS LLAMADOS PROBABILIDADES.
DICHO DE OTRA FORMA:
SON COSAS DE LA VIDA QUE DEPENDEN DE LA SUERTE, EL AZAR O LA
INCERTIDUMBRE… COMO CUANDO ABRES UNA BOLSA DE PAPITAS Y
ESPERAS QUE TRAIGA MUCHAS, ¡PERO SOLO HAY AIRE! ��
EJEMPLOS
1. �� TIRAR UN DADO
¿QUÉ PASA? NO SABES QUÉ NÚMERO VA A
SALIR.
¿PROBABILIDAD? TODOS LOS NÚMEROS
DEL 1 AL 6 TIENEN LA MISMA (1 DE 6).
FENÓMENO PROBABILÍSTICO: ¡ADIVINAR EL NÚMERO ES TAN DIFÍCIL COMO
GANARTE LA LOTERÍA CON 6 AMIGOS!
3. �� SACAR CALCETINES DE UN CAJÓN A OSCURAS
TIENES 5 CALCETINES NEGROS Y 5 BLANCOS.
¿CUÁL SACARÁS? NO SABES, PERO PUEDES PREDECIRLO.
FENÓMENO PROBABILÍSTICO: SEGURO
SACAS UNO NEGRO Y UNO BLANCO...
PORQUE LA VIDA NO QUIERE QUE HAGAS JUEGO.
2. �� SACAR UN DULCE DE UNA BOLSA CON LOS OJOS CERRADOS
HAY 5 DE FRESA, 3 DE LIMÓN Y 2 DE MENTA.
NO SABES CUÁL SACARÁS, ¡PERO PUEDES
CALCULAR LAS PROBABILIDADES! FENÓMENO PROBABILÍSTICO: TUS PAPILAS GUSTATIVAS JUEGAN A LA RULETA RUSA. ��
4. �� QUE TU PERRO HAGA SUS NECESIDADES JUSTO DESPUÉS DE LIMPIAR
ESTO YA ES CASI UNA LEY UNIVERSAL. ��
NO SABES CUÁNDO LO HARÁ, PERO SABES QUE PASA MUY SEGUIDO. FENÓMENO PROBABILÍSTICO: ¡EL
PERRITO Y LA ESTADÍSTICA SON MEJORES AMIGOS!
LA ESTADÍSTICA ES COMO EL DETECTIVE MATEMÁTICO DE LA VIDA. ��
SE ENCARGA DE RECOLECTAR, ORGANIZAR, ANALIZAR Y PRESENTAR DATOS PARA AYUDARNOS A TOMAR DECISIONES, ENTENDER LO QUE PASA A NUESTRO ALREDEDOR Y NO VIVIR ADIVINANDO TODO EL TIEMPO.
ES COMO CUANDO QUIERES SABER CUÁL ES LA PIZZA FAVORITA DEL SALÓN, Y HACES UNA ENCUESTA... ¡ESA ES ESTADÍSTICA EN ACCIÓN!
OBJETIVOS
1. �� RECOLECTAR DATOS
OBJETIVO: OBTENER INFORMACIÓN DEL MUNDO REAL.
EJEMPLO: HACES UNA ENCUESTA A TUS AMIGOS PARA SABER SI LES GUSTA MÁS EL CHOCOLATE O LA VAINILLA. ����
(ESTE PASO ES COMO EL "MODO CHISMOSO" DE LA ESTADÍSTICA: ¡QUIERE SABERLO TODO!)
2. �� ORGANIZAR Y CLASIFICAR LOS DATOS
OBJETIVO: QUE LOS DATOS NO SEAN UN CAOS.
EJEMPLO: PONES LOS RESULTADOS EN UNA TABLA O EN UNA GRÁFICA
PARA VER CUÁNTOS ELIGIERON CADA SABOR.
(ESTE PASO ES COMO ORDENAR TU CUARTO: AL PRINCIPIO HAY UN DESASTRE, PERO LUEGO TODO SE ENTIENDE MEJOR.) ���� 1.3
EL METODO ESTADISTICO Y LA FRECUENCIA RELATIVA
�� ¿QUÉ ES EL MÉTODO ESTADÍSTICO?
ES EL PASO A PASO QUE SEGUIMOS CUANDO USAMOS LA ESTADÍSTICA
PARA ESTUDIAR UN PROBLEMA O ANALIZAR INFORMACIÓN.
ES COMO UNA RECETA DE COCINA PARA TRABAJAR CON DATOS. ���
�� PASOS DEL MÉTODO ESTADÍSTICO:
PLANTEAMIENTO DEL PROBLEMA
“¿QUÉ QUIERO SABER?”
EJEMPLO: ¿CUÁL ES EL SNACK FAVORITO DEL GRUPO?
RECOLECCIÓN DE DATOS
SALGO A ENCUESTAR COMO REPORTERO CHISMOSO.
EJEMPLO: PREGUNTO A 20 AMIGOS SI PREFIEREN PAPITAS, CHOCOLATE O GALLETAS.
ORGANIZACIÓN Y PRESENTACIÓN
ARMO MI TABLA Y QUIZÁS UNA GRÁFICA LINDA.
EJEMPLO: 10 PAPITAS, 6 CHOCOLATES, 4 GALLETAS.
ANÁLISIS DE LOS DATOS
¿QUÉ ME ESTÁN DICIENDO LOS NÚMEROS? ��
EJEMPLO: “¡LA MAYORÍA AMA LAS PAPITAS!”
CONCLUSIONES Y TOMA DE DECISIONES
¿QUÉ APRENDÍ Y QUÉ HARÉ CON ESTO?
EJEMPLO: LLEVO PAPITAS A LA PRÓXIMA REUNIÓN. ���� 1.4

"REFRESCA TU DÍA CON EL SABOR ÚNICO DE COCA-COLA."
ESTADISTICA DESCRIPTIVA
�� ¿QUÉ ES LA ESTADÍSTICA DESCRIPTIVA? ES LA PARTE DE LA ESTADÍSTICA QUE RECOLECTA, ORGANIZA, RESUME Y PRESENTA DATOS DE FORMA CLARA Y ORDENADA, SIN SACAR CONCLUSIONES GENERALES.
�� ES COMO CUANDO TOMAS UNA SELFIE GRUPAL Y SOLO DESCRIBES
QUIÉNES ESTÁN Y CÓMO SE VEN... ¡NO ESTÁS ADIVINANDO NADA, SOLO MOSTRANDO LO QUE HAY!
�� EN OTRAS PALABRAS: ESTADÍSTICA DESCRIPTIVA = “CONTAR LO QUE PASÓ CON LOS DATOS QUE YA TENGO.”
�� ¿QUÉ HACE? REÚNE DATOS
EJEMPLO: LAS EDADES DE TODOS EN TU SALÓN.
LOS ORGANIZA EN TABLAS, GRÁFICOS, LISTAS.
LOS DESCRIBE CON NÚMEROS COMO PROMEDIOS, PORCENTAJES, MEDIANAS, MODAS, ETC.
LOS PRESENTA DE MANERA VISUAL Y FÁCIL DE ENTENDER (GRÁFICAS, DIAGRAMAS, ETC.).
2.1 ORGANIZACION Y PRESENTACION DEL CONJUNTO DE DATOS
�� ¿QUÉ ES LA ORGANIZACIÓN Y PRESENTACIÓN DE DATOS?
ES EL PASO DEL MÉTODO ESTADÍSTICO DONDE PONEMOS EN ORDEN TODOS LOS DATOS QUE HEMOS RECOLECTADO, Y LUEGO LOS MOSTRAMOS DE FORMA CLARA, ORDENADA Y VISUAL PARA QUE SE ENTIENDAN FÁCILMENTE.
�� ES COMO CUANDO LIMPIAS TU CUARTO: TODO ESTABA REGADO (DATOS DESORDENADOS) Y TÚ LO DEJAS BONITO (DATOS ORGANIZADOS EN TABLAS O GRÁFICAS).
�� 1. ORGANIZACIÓN DE DATOS
SIGNIFICA AGRUPAR, CLASIFICAR Y ORDENAR LOS DATOS PARA QUE SEA MÁS FÁCIL ANALIZARLOS.
EJEMPLO: REUNISTE DATOS SOBRE LAS CALIFICACIONES DE 10 ALUMNOS: 7, 8, 9, 7, 6, 8, 10, 7, 9, 6
PUEDES ORGANIZARLOS:
�� EN ORDEN NUMÉRICO: 6, 6, 7, 7, 7, 8, 8, 9, 9, 10 �� EN UNA TABLA DE FRECUENCIA
�� ¿QUÉ ES LA ORDENACIÓN DE DATOS?
LA ORDENACIÓN ES SIMPLEMENTE PONER LOS DATOS EN ORDEN, GENERALMENTE DE MENOR A MAYOR (O A VECES DE MAYOR A MENOR), PARA QUE SEA MÁS FÁCIL ANALIZARLOS.
�� ES COMO CUANDO HACES FILA PARA ENTRAR AL CINE: PRIMERO LOS MÁS BAJITOS, LUEGO LOS MÁS ALTOS. ������
✅ EJEMPLO:
DATOS SIN ORDENAR:
7, 5, 9, 6, 8, 5, 10, 6, 7
DATOS ORDENADOS (DE MENOR A MAYOR):
5, 5, 6, 6, 7, 7, 8, 9, 10
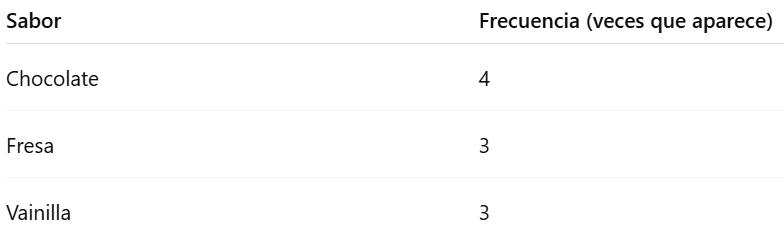
�� ¿QUÉ ES UNA TABLA DE FRECUENCIA?
UNA TABLA DE FRECUENCIA ES UNA FORMA DE ORGANIZAR LOS DATOS PARA SABER CUÁNTAS VECES SE REPITE CADA VALOR. ES MUY ÚTIL CUANDO HAY MUCHOS DATOS REPETIDOS.
�� ES COMO CONTAR CUÁNTOS AMIGOS PREFIEREN CADA SABOR DE HELADO, ¡Y ANOTARLO! 2.2 ORDENACION
➕ ¿QUÉ ES LA SUMATORIA?
LA SUMATORIA ES UN SÍMBOLO MATEMÁTICO (∑) QUE INDICA
QUE DEBES SUMAR VARIOS VALORES.
�� ES COMO DECIR: “SUMA TODOS ESTOS NÚMEROS UNO POR
UNO Y DAME EL TOTAL”.
✅ EJEMPLO:
SI TIENES LOS NÚMEROS:
2, 4, 6, 8
LA SUMATORIA SE ESCRIBE ASÍ:
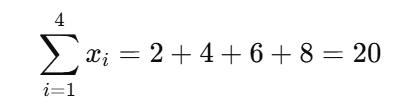
DONDE:
∑\SUM∑ ES EL SÍMBOLO DE SUMATORIA
I=1I = 1I=1 ES EL ÍNDICE INICIAL 444 ES EL NÚMERO TOTAL DE DATOS XIX_IXI ES EL VALOR DEL DATO NÚMERO I
�� PROPIEDADES DE LA SUMATORIA (¡LAS REGLAS DEL JUEGO!)
ESTAS REGLAS HACEN QUE TRABAJAR CON SUMATORIAS SEA MÁS FÁCIL Y ORDENADO. AQUÍ TE VA LA MÁS IMPORTANTE:
1. ✖ CONSTANTE MULTIPLICADA POR LA SUMATORIA SI MULTIPLICAS
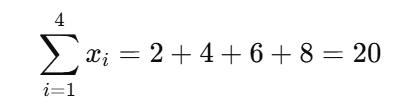
2.4
CONSTRUCCION NUMEREICA DE LA TABLA DE FRECUENCIA
�� ¿QUÉ ES LA CONSTRUCCIÓN NUMÉRICA DE LA TABLA DE FRECUENCIA?
LA CONSTRUCCIÓN NUMÉRICA DE LA TABLA DE FRECUENCIA ES EL PROCESO DE ORGANIZAR DATOS EN UNA TABLA PARA VER CUÁNTAS VECES SE REPITE CADA VALOR O GRUPO DE VALORES.
�� ES COMO HACER UN INVENTARIO DE DATOS: ¿CUÁNTOS 5 HAY? ¿CUÁNTOS 6? ¿CUÁL SE REPITE MÁS? ¿QUÉ TAN SEGUIDO APARECEN?
�� ¿QUÉ INCLUYE UNA TABLA DE FRECUENCIA? HAY VARIOS TIPOS DE FRECUENCIAS QUE PUEDES INCLUIR EN UNA TABLA:

DISTRIBUCION DE FRECUENCIA RELATIVA ACUMULADA
�� ¿QUÉ ES LA DISTRIBUCIÓN DE FRECUENCIA RELATIVA ACUMULADA?
��
(PERO EXPLICADO COMO SI FUERAS EN UNA MONTAÑA RUSA DE ESTADÍSTICAS)
IMAGINA QUE ESTÁS EN UN PARQUE DE DIVERSIONES Y HAY UNA
ATRACCIÓN LLAMADA:
�� "MONTAÑA DE DATOS" ��
TIENES VARIOS JUEGOS (QUE REPRESENTAN DIFERENTES VALORES O CATEGORÍAS) Y MUCHOS AMIGOS (QUE REPRESENTAN LOS DATOS) QUE VAN SUBIENDO A CADA JUEGO.
�� PASO 1: FRECUENCIA RELATIVA
PRIMERO CUENTAS QUÉ PORCENTAJE DE TUS AMIGOS SUBIÓ A CADA JUEGO.
ESO ES LA FRECUENCIA RELATIVA. POR EJEMPLO:
MONTAÑA RUSA: 20% DE LOS AMIGOS
CASA DEL TERROR: 30%
CARRUSEL: 10%
RUEDA DE LA FORTUNA: 40%
�� PASO 2: ¡VAMOS ACUMULANDO!
AHORA, IMAGINA QUE HACES UNA FILA Y EMPIEZAS A CONTAR CUÁNTOS
AMIGOS HAN SUBIDO EN TOTAL HASTA CIERTO PUNTO.
ESTO SE LLAMA FRECUENCIA RELATIVA ACUMULADA: VAS ACUMULANDO
LOS PORCENTAJES A MEDIDA QUE AVANZAS POR LOS JUEGOS.
MONTAÑA RUSA: 20% → ¡20% DEL TOTAL HASTA AQUÍ!
CASA DEL TERROR: 20% + 30% = 50%
CARRUSEL: 50% + 10% = 60%
RUEDA DE LA FORTUNA: 60% + 40% = 100% ��
¡LLEGASTE AL FINAL! TODOS TUS AMIGOS SE HAN SUBIDO A ALGO. ��
2.6
MEDIDAS DESCRIPTIVAS PARA UN CONJUNTO DE DATOS
�� ¿QUÉ SON LAS MEDIDAS DESCRIPTIVAS? (PIENSA EN ESTO COMO SI TUVIERAS QUE DESCRIBIR A TU GRUPO DE AMIGOS CON ESTADÍSTICAS ��)
LAS MEDIDAS DESCRIPTIVAS SON COMO LOS CHISMES MATEMÁTICOS SOBRE TUS DATOS. TE DICEN CÓMO SE COMPORTA EL GRUPO: SI SON TRANQUILOS, CAÓTICOS, PARECIDOS ENTRE SÍ O HAY ALGUIEN QUE SIEMPRE SE PASA DE RARO...
�� 1. MEDIDAS DE TENDENCIA CENTRAL (¿DÓNDE ESTÁ EL “CENTRO” DEL GRUPO?)
��MEDIA (PROMEDIO):
ES COMO DECIR:
“SI TODOS COMPARTIERAN TODO POR IGUAL, ¿CUÁNTO TENDRÍA CADA UNO?”
�� SE SUMA TODO Y SE DIVIDE ENTRE LA CANTIDAD DE DATOS.
�MEDIANA:
EL QUE ESTÁ EN EL MEDIO CUANDO TODOS SE ORDENAN.
“¡EL MÁS NEUTRAL DEL GRUPO!”
�� SI TIENES UNA FILA CON LOS DATOS ORDENADOS, LA MEDIANA ES EL DEL CENTRO.
��MODA: EL DATO MÁS POPULAR.
“¡EL QUE MÁS SE REPITE! ¡LA ESTRELLA DEL GRUPO!”
�� 2. MEDIDAS DE POSICIÓN (¿DÓNDE ESTÁ CADA UNO EN EL RANKING?)
��CUARTILES, PERCENTILES Y DECILES:
“¿QUIÉN ESTÁ EN EL TOP 25%? ¿QUIÉN ESTÁ EN EL 90% DE LOS DATOS?”
�� DIVIDEN LOS DATOS ORDENADOS EN PARTES IGUALES PARA VER EN QUÉ POSICIÓN ESTÁ CADA VALOR.
2.7
MEDIDAS DE CENTRALIZACION O TENDENCIA CENTRAL
��¿QUÉ SON LAS MEDIDAS DE TENDENCIA CENTRAL?
SON LAS QUE TE DICEN "DÓNDE SE CONCENTRA" LA INFORMACIÓN DE UN CONJUNTO DE DATOS.
ES COMO PREGUNTARSE:
�� "¿CUÁL ES EL VALOR TÍPICO O REPRESENTATIVO DEL GRUPO?"
IMAGINA QUE TIENES UN GRUPO DE PERSONAS COMIENDO TACOS ��. NO TODOS COMEN LO MISMO, PERO QUIERES SABER CUÁNTOS TACOS "EN PROMEDIO" COMIÓ CADA UNO, CUÁL FUE LA CANTIDAD MÁS COMÚN, Y QUIÉN QUEDÓ
EXACTAMENTE EN MEDIO DEL RANKING DE TRAGONES.
�� LAS 3 GRANDES ESTRELLAS DE LA TENDENCIA CENTRAL ��
1. �� MEDIA (PROMEDIO)
�� ¿QUÉ PASARÍA SI TODOS COMPARTIERAN LA COMIDA
EQUITATIVAMENTE?
�� FÓRMULA:
2. �� MEDIANA

¡PROMEDIO DE 4 TACOS POR PERSONA! ��
�� EL VALOR QUE ESTÁ JUSTO EN EL MEDIO CUANDO TODOS SE ORDENAN.
�� PASOS:
ORDENAS LOS DATOS.
SI HAY UN NÚMERO IMPAR DE DATOS, ES EL DEL CENTRO.
SI ES PAR, SACAS EL PROMEDIO DE LOS DOS DEL CENTRO.
�� EJEMPLO:
DATOS: 2, 3, 4, 4, 7
(YA ESTÁN ORDENADOS) → LA MEDIANA ES 4.
3. �� MODA
�� EL DATO QUE MÁS SE REPITE. ¡EL MÁS POPULAR!
�� EJEMPLO:
DATOS: 2, 3, 4, 4, 7
LA MODA ES 4 PORQUE APARECE DOS VECES (MÁS QUE CUALQUIER OTRO).
�� ¿PARA QUÉ SIRVEN?
MEDIA: MUY ÚTIL, PERO PUEDE SER ENGAÑOSA SI HAY EXTREMOS (COMO ALGUIEN QUE COMIÓ 30 TACOS ��).
MEDIANA: PERFECTA SI TIENES DATOS "RAROS" O EXTREMOS.
MODA: GENIAL PARA VER QUÉ VALOR ES MÁS COMÚN (POR EJEMPLO, LA TALLA DE ZAPATOS MÁS USADA EN UNA TIENDA ��).
2.8
MEDIDAS DE DISPERCION O ESPARCIMIENTO
�� ¿QUÉ SON LAS MEDIDAS DE DISPERSIÓN?
SON COMO LOS DETECTIVES DEL CAOS:
TE DICEN QUÉ TAN DESORDENADOS O DISPERSOS ESTÁN LOS DATOS EN UN CONJUNTO.
IMAGINA QUE ESTÁS EN UNA FIESTA CON TUS AMIGOS �� Y TODOS LLEVAN
REGALOS PARA UN INTERCAMBIO. SI TODOS LOS REGALOS VALEN MÁS O MENOS
LO MISMO, LA FIESTA ES TRANQUILA.
PERO SI UNO TRAE UNA PLAYSTATION Y OTRO TRAE UN LÁPIZ MORDIDO...
¡CAOS TOTAL! ��
�� ESO ES DISPERSIÓN.
�� PRINCIPALES MEDIDAS DE DISPERSIÓN (CON EJEMPLOS DIVERTIDOS)
1. �� RANGO
"¿CUÁNTA DIFERENCIA HAY ENTRE EL MÁS ALTO Y EL MÁS BAJO?"
�� EJEMPLO:
REGALOS DE VALOR: 10, 20, 25, 30, 100 → RANGO: 100 - 10 = 90 ����
2. �� VARIANZA
"¿QUÉ TANTO SE DESVÍAN LOS DATOS DEL PROMEDIO?"
(PERO LO HACE AL CUADRADO, PORQUE ES DRAMÁTICA ��) �� FÓRMULA (VERSIÓN SIMPLIFICADA PARA DATOS SIMPLES):
3. �� DESVIACIÓN ESTÁNDAR
"¿QUÉ TAN LEJOS ESTÁN LOS DATOS DEL PROMEDIO, EN UNIDADES NORMALES?"
�� ES LA RAÍZ CUADRADA DE LA VARIANZA.
Y SÍ, ES LA MÁS USADA PORQUE HABLA EN EL MISMO IDIOMA QUE LOS DATOS.
�� SI LA DESVIACIÓN ESTÁNDAR ES ALTA → LOS DATOS ESTÁN LOCOS Y DISPERSOS ��
SI ES BAJA → ESTÁN TRANQUILITOS Y BIEN PORTADOS ��
�� "MOMENTOS DE ORDENAR" (ANTES DE APLICAR FÓRMULAS)
ANTES DE SACAR CONCLUSIONES ESTADÍSTICAS, HAY QUE PONER
ORDEN EN EL CAOS DE LOS DATOS. ¡ES COMO LIMPIAR TU CUARTO
ANTES DE QUE LLEGUEN VISITAS! ����
��
1. RECOLECTAR LOS DATOS
PRIMERO NECESITAS TENER LOS DATOS. ES COMO TENER TODOS LOS
INGREDIENTES ANTES DE COCINAR. ��
EJEMPLO: CALIFICACIONES DE 5 AMIGOS → 7, 10, 6, 9, 8
��
2. ORDENAR LOS DATOS
AQUÍ ES DONDE LLEGAN LOS MOMENTOS DE ORDENAR:
DE MENOR A MAYOR: 6, 7, 8, 9, 10 (O DE MAYOR A MENOR SI LO PREFIERES, PERO NORMALMENTE ES DE MENOR A MAYOR)
ESTO ES CLAVE PARA:
ENCONTRAR LA MEDIANA
IDENTIFICAR LOS CUARTILES, PERCENTILES VER LA FORMA DE LA DISTRIBUCIÓN (¿HAY EXTREMOS? ¿ES SIMÉTRICA?)
�� 3. ORGANIZAR EN UNA TABLA DE FRECUENCIAS (OPCIONAL PERO ÚTIL)
2.10
MEDIDAS DE FORMA
�� ¿QUÉ SON LAS MEDIDAS DE FORMA?
LAS MEDIDAS DE FORMA SON COMO LOS ESTILISTAS DE LA ESTADÍSTICA:
SE ENCARGAN DE ANALIZAR LA FIGURA O EL “LOOK” DEL GRÁFICO DE DATOS, ES DECIR, CÓMO SE DISTRIBUYEN.
�� YA SABES CUÁNTO MIDE EL GRUPO (TENDENCIA CENTRAL), QUÉ TAN DIVERSO ES (DISPERSIÓN)…
�� AHORA TOCA VER LA FORMA DEL GRUPO: ¿ES SIMÉTRICO? ¿TIENE UNA JOROBA?
¿UNA COLA LARGA?
�� LAS 2 PRINCIPALES MEDIDAS DE FORMA:
1. �� ASIMETRÍA (SKEWNESS)
¿ESTÁ EL GRÁFICO INCLINADO HACIA UN LADO?
⚖ TIPOS DE ASIMETRÍA:
SIMÉTRICA (ASIMETRÍA = 0):
LA DISTRIBUCIÓN ES PAREJITA, COMO UNA MONTAÑA PERFECTA. ��
EJEMPLO TÍPICO: LA FAMOSA CAMPANA DE GAUSS.
ASIMETRÍA POSITIVA (DERECHA):
LA COLA LARGA ESTÁ A LA DERECHA ➡ (HAY VALORES MUY GRANDES QUE EMPUJAN LA MEDIA HACIA ARRIBA)
EJ: SUELDOS EN UNA EMPRESA CON UN JEFE MILLONARIO ��
ASIMETRÍA NEGATIVA (IZQUIERDA):
LA COLA LARGA ESTÁ A LA IZQUIERDA ⬅ (HAY VALORES MUY BAJITOS QUE BAJAN LA MEDIA)
EJ: CALIFICACIONES DE UN EXAMEN DIFÍCIL DONDE LA MAYORÍA SACÓ BAJAS ��
�� CURTOSIS = 0 (EN LA VERSIÓN ESTANDARIZADA)
LEPTOCÚRTICA (MÁS PICUDA):

"ATRÉVETE A MÁS. ELIGE PEPSI."
�� ¿QUÉ ES LA PROBABILIDAD?
LA PROBABILIDAD ES UNA RAMA DE LAS MATEMÁTICAS QUE ESTUDIA QUÉ TAN PROBABLE ES QUE OCURRA UN EVENTO.
EN PALABRAS SIMPLES:
PROBABILIDAD = EL ARTE DE PREDECIR LO INCIERTO.
SI LANZAS UN DADO, ¿CUÁNTAS OPCIONES TIENES?
SEIS: 1, 2, 3, 4, 5 Y 6.
CADA NÚMERO TIENE LA MISMA OPORTUNIDAD DE SALIR. ENTONCES, LA PROBABILIDAD DE SACAR UN 3 ES: 1/6
Ejemplo en la vida real
El clima ��
Juegos de azar ��
Deportes ⚽
Medicina ��
¿Dónde está la probabilidad?
"80% de probabilidad de lluvia"
¿Qué probabilidad hay de ganar en una máquina?
¿Cuáles son las probabilidades de que gane un equipo?
¿Qué probabilidad hay de que funcione un tratamiento?
Ciencia �� Experimentos con resultados aleatorios
�� DEFINICIÓN DE PROBABILIDAD
DEFINICIÓN FORMAL:
LA PROBABILIDAD ES UNA MEDIDA NUMÉRICA DE LA POSIBILIDAD DE QUE OCURRA
UN EVENTO DENTRO DE UN CONJUNTO DE RESULTADOS POSIBLES.
SU VALOR SIEMPRE ESTÁ ENTRE 0 Y 1, DONDE:
0 SIGNIFICA QUE EL EVENTO ES IMPOSIBLE.
1 SIGNIFICA QUE EL EVENTO ES SEGURO.
�� ¿CÓMO SE ESCRIBE MATEMÁTICAMENTE?
DONDE:

P(E) = PROBABILIDAD DE QUE OCURRA UN EVENTO E
CASOS FAVORABLES = LOS RESULTADOS QUE QUEREMOS
CASOS POSIBLES = TODOS LOS RESULTADOS QUE PUEDEN PASAR
EJEMPLO RICO:
IMAGINA UNA CAJA CON 5 PASTELES:
2 DE CHOCOLATE ��
2 DE VAINILLA ��
1 DE FRESA ��
SI SACAS UNO CON LOS OJOS CERRADOS, ¿CUÁL ES LA PROBABILIDAD DE QUE
SEA DE CHOCOLATE?
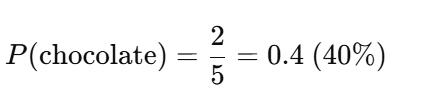
�� ¿QUÉ ES LA REGULARIDAD ESTADÍSTICA?
LA REGULARIDAD ESTADÍSTICA ES UN PRINCIPIO QUE DICE QUE, CUANDO REPETIMOS
UN EXPERIMENTO ALEATORIO MUCHAS VECES, LOS RESULTADOS TIENDEN A ESTABILIZARSE Y SEGUIR UN PATRÓN PREDECIBLE.
�� DEFINICIÓN MÁS FORMAL:
LA REGULARIDAD ESTADÍSTICA ES LA TENDENCIA DE LA FRECUENCIA RELATIVA DE UN EVENTO A ACERCARSE A SU PROBABILIDAD TEÓRICA A MEDIDA QUE EL NÚMERO DE REPETICIONES DEL EXPERIMENTO AUMENTA.
�� ¿QUÉ SIGNIFICA ESTO EN LA VIDA REAL?
�� EJEMPLO CLÁSICO: LANZAR UNA MONEDA
SUPÓN QUE LANZAS UNA MONEDA:
LA PROBABILIDAD TEÓRICA DE OBTENER CARA ES:
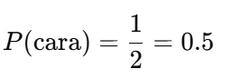
AHORA HAZ EL EXPERIMENTO:
SI LA LANZAS 5 VECES, PUEDE SALIR: CARA, CRUZ, CRUZ, CARA, CARA → 3 CARAS = 60%
PERO SI LA LANZAS 1,000 VECES, ES MÁS PROBABLE QUE LA FRECUENCIA DE CARAS SE ACERQUE AL 50%
�� ¡ESO ES REGULARIDAD ESTADÍSTICA! AUNQUE HAYA VARIACIÓN EN EL CORTO PLAZO, EN EL LARGO PLAZO TODO SE EQUILIBRA.
�� OTRO EJEMPLO DIVERTIDO: IMAGINA QUE ERES BUENÍSIMO LANZANDO TIROS LIBRES EN BÁSQUET Y TIENES 80% DE ACIERTOS.
SI HACES SOLO 5 TIROS, PODRÍAS METER 2 O 5, NO SE SABE.
PERO SI HACES 500 TIROS, ES MUY PROBABLE QUE METAS ALREDEDOR DE 400 (80%).
ESO ES LA REGULARIDAD ESTADÍSTICA ACTUANDO.
LOS POSTULADOS DE LA PROBABILIDAD SON COMO LAS REGLAS BÁSICAS QUE
PERMITEN TRABAJAR CON ESTA RAMA DE LAS MATEMÁTICAS. SON SIMPLES PERO PODEROSOS ��.
�� ¿QUÉ SON LOS POSTULADOS DE LA PROBABILIDAD? SON PRINCIPIOS FUNDAMENTALES (TAMBIÉN LLAMADOS AXIOMAS) EN LOS QUE SE
BASA TODA LA TEORÍA DE LA PROBABILIDAD. FUERON FORMULADOS POR ANDREY KOLMOGOROV EN 1933 (UN GENIO RUSO DE LAS MATES).
✅ LOS 3 POSTULADOS DE LA PROBABILIDAD:
�� POSTULADO 1: NO NEGATIVIDAD
LA PROBABILIDAD DE CUALQUIER EVENTO ES MAYOR O IGUAL A CERO.
�� ESTO SIGNIFICA QUE NO EXISTEN PROBABILIDADES NEGATIVAS.
EJEMPLO: NO PUEDES DECIR QUE LA PROBABILIDAD DE QUE LLUEVA ES -20%.
¡ESO NO TIENE SENTIDO! ��
�� POSTULADO 2: PROBABILIDAD TOTAL DE 1
LA PROBABILIDAD DEL ESPACIO MUESTRAL COMPLETO ES 1.
�� ESTO SIGNIFICA QUE ALGO SÍ O SÍ VA A PASAR DENTRO DEL CONJUNTO DE TODOS LOS RESULTADOS POSIBLES.
EJEMPLO: AL LANZAR UN DADO, SEGURO QUE SALDRÁ UN NÚMERO DEL 1 AL 6.
ENTONCES: 3.3
3.4
ESPACIOS MUESTRALES FINITOS
�� ¿QUÉ ES UN ESPACIO MUESTRAL?
EL ESPACIO MUESTRAL ES EL CONJUNTO DE TODOS LOS POSIBLES RESULTADOS DE UN EXPERIMENTO ALEATORIO.
SE REPRESENTA CON LA LETRA S (O A VECES CON LA LETRA GRIEGA Ω).
�� ¿QUÉ SON LOS ESPACIOS MUESTRALES FINITOS?
SON ESPACIOS MUESTRALES QUE TIENEN UN NÚMERO LIMITADO DE RESULTADOS POSIBLES.
ES DECIR: ¡SE PUEDEN CONTAR TODOS!
✅ DEFINICIÓN FORMAL:
UN ESPACIO MUESTRAL FINITO ES UN CONJUNTO S TAL QUE EL NÚMERO DE ELEMENTOS (RESULTADOS) ES UN NÚMERO FINITO (CONTABLE).
�� ¿Y CÓMO SE USA?
UNA VEZ QUE CONOCES EL ESPACIO MUESTRAL, PUEDES: CONTAR CUÁNTOS RESULTADOS FAVORABLES HAY USAR LA FÓRMULA DE PROBABILIDAD:

�� RESUMEN RÁPIDO:
✔ ESPACIO MUESTRAL FINITO = CONJUNTO DE TODOS LOS POSIBLES RESULTADOS, Y SÍ SE PUEDE CONTAR
✔ LO USAS PARA CALCULAR PROBABILIDADES
✔ MUY COMÚN EN JUEGOS, EXPERIMENTOS SIMPLES Y EJERCICIOS ESCOLARES
�� DEFINICIÓN DE ESPACIO MUESTRAL FINITO
EL ESPACIO MUESTRAL FINITO ES EL CONJUNTO DE TODOS LOS RESULTADOS
POSIBLES DE UN EXPERIMENTO ALEATORIO, Y CONTIENE UN NÚMERO LIMITADO (FINITO) DE ELEMENTOS.
SE REPRESENTA NORMALMENTE CON LA LETRA:
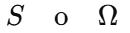
✅ EJEMPLO:
EXPERIMENTO: LANZAR UN DADO DE 6 CARAS ��
ESPACIO MUESTRAL:
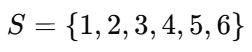
Característica
Espacio Muestral Finito
¿Qué es?
¿Cuántos resultados tiene?
¿Ejemplos?
Conjunto de todos los resultados posibles
Un número limitado, se pueden contar
Lanzar monedas, dados, sacar cartas, etc.
�� ¿QUÉ ES UN ESPACIO MUESTRAL EQUIPROBABLE?
UN ESPACIO MUESTRAL EQUIPROBABLE ES AQUEL EN EL QUE TODOS LOS RESULTADOS
POSIBLES TIENEN LA MISMA PROBABILIDAD DE OCURRIR.
ES DECIR:
NINGÚN RESULTADO ES MÁS PROBABLE QUE OTRO.
TODOS TIENEN IGUAL CHANCE.
�� ¿CÓMO SABER SI ES EQUIPROBABLE?
�� SI UN EXPERIMENTO TIENE N RESULTADOS POSIBLES, Y CADA UNO TIENE LA MISMA PROBABILIDAD, ENTONCES:
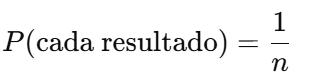
�� ¿Y CUÁNDO NO ES EQUIPROBABLE?
SI LOS RESULTADOS NO TIENEN LAS MISMAS CHANCES.
EJEMPLO: UNA MONEDA CARGADA QUE CAE MÁS VECES EN CRUZ → NO ES EQUIPROBABLE.
Término
Equiprobable
Fórmula
Ejemplos
Significado sencillo
Todos los resultados tienen igual probabilidad
P= 1/NUMERO DE RESULTADOS
Moneda justa, dado justo, ruleta balanceada
3.7
CALCULO DE PROBABILIDAD
�� ¿QUÉ ES EL CÁLCULO DE PROBABILIDAD?
EL CÁLCULO DE PROBABILIDAD ES UNA PARTE DE LAS MATEMÁTICAS QUE SE ENCARGA
DE ESTUDIAR EL AZAR, ES DECIR, QUÉ TAN POSIBLE ES QUE OCURRA UN EVENTO.
ES COMO UNA HERRAMIENTA MATEMÁTICA QUE NOS PERMITE RESPONDER PREGUNTAS
COMO:
¿QUÉ TAN PROBABLE ES GANAR UN SORTEO?
¿CUÁL ES LA POSIBILIDAD DE QUE LLUEVA MAÑANA?
¿QUÉ PROBABILIDAD HAY DE QUE UN EQUIPO GANE UN PARTIDO?
�� OBJETIVO DEL CÁLCULO DE PROBABILIDAD:
�� MEDIR LA INCERTIDUMBRE Y ASIGNAR UN VALOR NUMÉRICO (ENTRE 0
Y 1) A LA POSIBILIDAD DE QUE OCURRA UN EVENTO.
�� TIPOS DE PROBABILIDAD
PROBABILIDAD CLÁSICA (MATEMÁTICA):
SE USA CUANDO TODOS LOS RESULTADOS SON EQUIPROBABLES (TIENEN LA MISMA POSIBILIDAD).
EJEMPLO: DADO, RULETA JUSTA, MONEDA.
PROBABILIDAD FRECUENCIAL (EXPERIMENTAL):
SE BASA EN HACER EXPERIMENTOS REALES.
EJEMPLO: LANZAR UNA MONEDA 100 VECES Y VER CUÁNTAS VECES CAE CARA.
PROBABILIDAD SUBJETIVA:
SE BASA EN OPINIONES, EXPERIENCIAS O CREENCIAS.
EJEMPLO: “CREO QUE HAY UN 80% DE QUE GANE MI EQUIPO”.
3.8 TECNICA PARA LA NUMERACION DE PUNTOS MUESTRALES
�� ¿QUÉ ES LA NUMERACIÓN DE PUNTOS MUESTRALES?
ES UNA TÉCNICA QUE CONSISTE EN LISTAR TODOS LOS POSIBLES RESULTADOS (PUNTOS MUESTRALES) DE UN EXPERIMENTO ALEATORIO, DE MANERA ORDENADA Y SIN REPETIR.
ESTO ES CLAVE PARA NO OLVIDAR NINGÚN RESULTADO POSIBLE, ESPECIALMENTE CUANDO LOS ESPACIOS MUESTRALES SON COMBINACIONES, PRODUCTOS O ARREGLOS.
�� OBJETIVO: REPRESENTAR EL ESPACIO MUESTRAL COMPLETO
VISUALIZAR TODOS LOS CASOS POSIBLES
CONTAR FÁCILMENTE LOS CASOS PARA APLICAR LA FÓRMULA DE PROBABILIDAD
�� TÉCNICAS SEGÚN EL TIPO DE EXPERIMENTO:
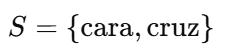
1. LISTAS O CONJUNTOS
CUANDO EL NÚMERO DE RESULTADOS ES PEQUEÑO.
EJEMPLO: LANZAR UNA MONEDA
2. TABLAS
CUANDO HAY COMBINACIONES SIMPLES, COMO LANZAR DOS DADOS.
EJEMPLO: LANZAR DOS DADOS
3. DIAGRAMAS DE ÁRBOL ��
CUANDO HAY MÁS DE UNA ETAPA (COMO SACAR BOLAS DE COLORES, TIRAR DOS MONEDAS, ETC.)
EJEMPLO: TIRAR 2 MONEDAS
RAMA 1: CARA O CRUZ
RAMA 2: CARA O CRUZ
3.9 EVENTOS INDEPENDIENTES
�� ¿QUÉ SON LOS EVENTOS INDEPENDIENTES?
DOS EVENTOS SON INDEPENDIENTES SI LA OCURRENCIA DE UNO NO AFECTA LA PROBABILIDAD DE QUE OCURRA EL OTRO.
�� EN PALABRAS FÁCILES:
�� LO QUE PASE EN UN EVENTO NO CAMBIA LO QUE PUEDE PASAR EN EL OTRO.
CADA EVENTO OCURRE POR SU CUENTA, SIN INFLUENCIAR AL OTRO.
✏ DEFINICIÓN MATEMÁTICA:
DOS EVENTOS A Y B SON INDEPENDIENTES SI:
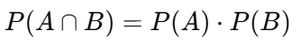
✅ EJEMPLOS SENCILLOS:
�� EJEMPLO 1: LANZAR DOS DADOS
EVENTO A: QUE EL PRIMER DADO SEA 3
EVENTO B: QUE EL SEGUNDO DADO SEA 6
➡ LO QUE SALGA EN UN DADO NO AFECTA AL OTRO → SON INDEPENDIENTES
�� ¿CÓMO SABER SI SON INDEPENDIENTES?
PREGÚNTATE:
➤ “¿LO QUE PASA EN A CAMBIA LA POSIBILIDAD DE B?”
SI NO ➝ SON INDEPENDIENTES
APLICA LA FÓRMULA:
➤ SI SE CUMPLE QUE
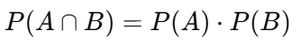
ENTONCES SON INDEPENDIENTES
�� ¿QUÉ ES UNA VARIABLE ALEATORIA?
UNA VARIABLE ALEATORIA ES UNA FUNCIÓN QUE ASIGNA UN VALOR NUMÉRICO A CADA RESULTADO POSIBLE DE UN EXPERIMENTO ALEATORIO.
�� EN PALABRAS SIMPLES:
�� ES UNA FORMA DE TRANSFORMAR RESULTADOS AL AZAR EN NÚMEROS QUE PODAMOS ANALIZAR.
✅ EJEMPLO SIMPLE:
�� EXPERIMENTO: LANZAR UN DADO
RESULTADOS POSIBLES: {1, 2, 3, 4, 5, 6}
DEFINIMOS LA VARIABLE ALEATORIA X COMO: “EL NÚMERO QUE APARECE EN EL DADO”
�� ¿PARA QUÉ SIRVE UNA VARIABLE ALEATORIA?
✅ PARA ESTUDIAR EL COMPORTAMIENTO DEL AZAR CON NÚMEROS
✅ PARA CALCULAR PROBABILIDADES, MEDIAS, VARIANZAS Y MÁS
✅ PARA HACER GRÁFICAS Y MODELOS ESTADÍSTICOS
Concepto
Variable aleatoria
¿Por qué "aleatoria"?
¿Qué hace?
¿Cómo se representa?
Descripción breve
Asocia un número a cada resultado aleatorio
Porque depende del azar del experimento
Transforma eventos en números para analizarlos
Con letras mayúsculas: X, Y, Z
VARIABLES DISCRETAS Y SUS DISTRIBUCIONES DE PROBABILIDAD
�� ¿QUÉ ES UNA VARIABLE ALEATORIA DISCRETA?
ES UNA VARIABLE ALEATORIA QUE SOLO PUEDE TOMAR VALORES NUMÉRICOS ESPECÍFICOS Y CONTABLES, GENERALMENTE ENTEROS (COMO 0, 1, 2...).
�� EN PALABRAS SIMPLES:
�� UNA VARIABLE DISCRETA ES AQUELLA QUE CUENTA COSAS: CUÁNTAS VECES ALGO OCURRE.
�� EJEMPLOS DE VARIABLES DISCRETAS:
Experimento
Lanzar un dado
Lanzar una moneda 3 veces
Encuestar personas
Contar llamadas en 1 hora
Variable discreta (X)
Resultado del dado (1 a 6)
Número de caras obtenidas (0 a 3)
Número de personas que dicen “sí”
Total de llamadas recibidas (0,1,2,…)
�� ¿QUÉ ES UNA DISTRIBUCIÓN DE PROBABILIDAD?
ES UNA TABLA O FUNCIÓN QUE INDICA LA PROBABILIDAD DE QUE UNA VARIABLE DISCRETA TOME CADA UNO DE SUS VALORES POSIBLES.
✅ EJEMPLO PRÁCTICO:
SUPÓN QUE LANZAS UN DADO, Y LA VARIABLE X ES EL NÚMERO QUE SALE.
DISTRIBUCIÓN DE PROBABILIDAD:

CUANDO EL CAMINO EXIGE LO MEJOR, KENWORTH RESPONDE CON POTENCIA, INNOVACIÓN Y CONFIABILIDAD. CADA UNO DE NUESTROS CAMIONES ESTÁ DISEÑADO PARA ENFRENTAR LOS DESAFÍOS MÁS DUROS DEL TRANSPORTE, CON TECNOLOGÍA DE PUNTA, RENDIMIENTO SUPERIOR Y LA RESISTENCIA QUE SOLO UNA MARCA LÍDER PUEDE OFRECER. CON MÁS DE 100 AÑOS EN MOVIMIENTO, KENWORTH NO SOLO FABRICA CAMIONES: CREA ALIADOS DE TRABAJO QUE ACOMPAÑAN A LOS VERDADEROS PROTAGONISTAS DE LA CARRETERA. KENWORTH. HECHO PARA LOS QUE NUNCA SE DETIENEN.
��
1. ¿QUÉ ES UNA VARIABLE ALEATORIA DISCRETA?
UNA VARIABLE ALEATORIA DISCRETA:
ES EL RESULTADO NUMÉRICO DE UN EXPERIMENTO ALEATORIO.
TOMA VALORES AISLADOS, ES DECIR, NO INFINITOS NI DECIMALES CONTINUOS, SINO
VALORES COMO 0, 1, 2, 3, ETC.
EJEMPLOS COMUNES:
NÚMERO DE HIJOS EN UNA FAMILIA
NÚMERO DE VECES QUE SALE CARA AL LANZAR UNA MONEDA 3 VECES
NÚMERO DE LLAMADAS QUE RECIBE UNA EMPRESA POR HORA
�� 2. ¿QUÉ ES UNA DISTRIBUCIÓN DE PROBABILIDAD?
UNA DISTRIBUCIÓN DE PROBABILIDAD DISCRETA:
ES LA FORMA DE ASIGNAR UNA PROBABILIDAD ESPECÍFICA A CADA VALOR POSIBLE
DE LA VARIABLE.
MUESTRA QUÉ TAN PROBABLE ES CADA RESULTADO DEL EXPERIMENTO.
LA SUMA TOTAL DE TODAS LAS PROBABILIDADES DEBE SER 1 (100%).
�� EJEMPLO ILUSTRADO:
EXPERIMENTO: LANZAR DOS MONEDAS
VARIABLE ALEATORIA (X): NÚMERO DE CARAS
RESULTADOS POSIBLES:
(CRUZ, CRUZ) → X = 0
(CARA, CRUZ) → X = 1
(CRUZ, CARA) → X = 1
(CARA, CARA) → X = 2
LA DISTRIBUCION DE PROBABILIDAD
�� ¿QUÉ ES UNA DISTRIBUCIÓN DE PROBABILIDAD?
UNA DISTRIBUCIÓN DE PROBABILIDAD ES UNA REGLA, TABLA O FÓRMULA QUE ASOCIA
CADA RESULTADO POSIBLE DE UN EXPERIMENTO ALEATORIO CON SU PROBABILIDAD DE OCURRENCIA.
✅ EN PALABRAS SENCILLAS: ES COMO UNA GUÍA QUE DICE QUÉ TAN PROBABLE ES CADA RESULTADO DE UN EXPERIMENTO AL AZAR.
�� TIPOS DE DISTRIBUCIONES DE PROBABILIDAD
Tipo
Discreta
Continua
¿Qué valores toma la variable? Ejemplo
Valores contables (0,1,2, )
Valores infinitos dentro de rangos
Lanzar un dado o una moneda
Peso, estatura, tiempo
�� REPRESENTACIONES COMUNES
TABLA DE VALORES
GRÁFICA DE BARRAS (PARA VARIABLES DISCRETAS)
FÓRMULAS O FUNCIONES MATEMÁTICAS
�� ¿PARA QUÉ SIRVE UNA DISTRIBUCIÓN DE PROBABILIDAD?
✅ SABER QUÉ RESULTADOS SON MÁS PROBABLES ✅ CALCULAR ESPERANZA (MEDIA), VARIANZA, DESVIACIÓN
✅ MODELAR FENÓMENOS ALEATORIOS REALES
✅ TOMAR DECISIONES CON BASE EN DATOS
4.3 DIFERENTES DISTRIBUCIONES DE PROBABILIDAD DISCRETA
�� 1. DISTRIBUCIÓN UNIFORME DISCRETA
ES CUANDO TODOS LOS RESULTADOS POSIBLES TIENEN LA MISMA PROBABILIDAD DE OCURRIR.
�� IMAGINA QUE LANZAS UN DADO JUSTO: CUALQUIER NÚMERO DEL 1 AL 6
TIENE LA MISMA CHANCE DE SALIR.
�� EJEMPLO: LANZAR UN DADO → CADA NÚMERO TIENE 1 ENTRE 6 DE PROBABILIDAD.
�� 2. DISTRIBUCIÓN BINOMIAL
SIRVE PARA CONTAR CUÁNTOS ÉXITOS HAY EN VARIOS INTENTOS DE UN MISMO EXPERIMENTO.
�� SI LANZAS UNA MONEDA 10 VECES, PUEDES USAR ESTA DISTRIBUCIÓN
PARA SABER CUÁNTAS VECES ES PROBABLE QUE SALGA CARA.
�� EJEMPLO: ¿CUÁNTAS CARAS SALEN AL LANZAR UNA MONEDA 10 VECES?
�� 3. DISTRIBUCIÓN DE BERNOULLI
ES UN CASO ESPECIAL DE LA BINOMIAL, PERO CON UN SOLO INTENTO.
�� SOLO HAY DOS RESULTADOS: ÉXITO O FRACASO (POR EJEMPLO, GANAR O PERDER).
�� EJEMPLO: ¿SALE CARA EN UN SOLO LANZAMIENTO DE MONEDA?
�� 4. DISTRIBUCIÓN GEOMÉTRICA
SIRVE PARA SABER CUÁNTOS INTENTOS NECESITAS HASTA QUE OCURRA EL PRIMER ÉXITO.
�� SI LANZAS UNA MONEDA VARIAS VECES, ESTA DISTRIBUCIÓN TE DICE CUÁNTAS VECES DEBES LANZARLA HASTA QUE SALGA CARA POR PRIMERA VEZ.
�� EJEMPLO: ¿CUÁNTAS VECES TENGO QUE LANZAR LA MONEDA HASTA QUE SALGA CARA?
4.4 UNIFORME DISCRETA
�� ¿QUÉ ES LA DISTRIBUCIÓN UNIFORME DISCRETA?
ES UNA DISTRIBUCIÓN EN LA QUE TODOS LOS RESULTADOS POSIBLES TIENEN LA MISMA PROBABILIDAD DE OCURRIR.
�� EN OTRAS PALABRAS:
TODOS LOS VALORES SON IGUAL DE PROBABLES.
��♂�� ¿CUÁNDO SE USA?
CUANDO TIENES UN EXPERIMENTO ALEATORIO DONDE NO HAY VENTAJA
PREFERENCIA POR NINGÚN RESULTADO.
�� EJEMPLOS CLAROS:
LANZAR UN DADO JUSTO
CUALQUIER NÚMERO DEL 1 AL 6 PUEDE SALIR CON LA MISMA PROBABILIDAD.
SACAR UNA CARTA AL AZAR DE UN MAZO COMPLETO
CUALQUIERA DE LAS 52 CARTAS TIENE LA MISMA OPORTUNIDAD.
ESCOGER UN NÚMERO AL AZAR DEL 1 AL 10
TODOS LOS NÚMEROS DEL 1 AL 10 SON IGUALMENTE PROBABLES.
�� CARACTERÍSTICAS CLAVE
LOS VALORES POSIBLES SON FINITOS Y CONTABLES (1, 2, 3, ...).
CADA VALOR TIENE LA MISMA PROBABILIDAD.
ES UNA DE LAS MÁS SIMPLES Y JUSTAS DISTRIBUCIONES.
�� ¿POR QUÉ ES IMPORTANTE?
PORQUE MUCHAS SITUACIONES REALES SIMULAN CONDICIONES DE IGUALDAD AL AZAR.
ESTA DISTRIBUCIÓN ES LA BASE PARA ENTENDER OTRAS MÁS COMPLEJAS.
�� EN RESUMEN RÁPIDO:
✅ TODOS LOS RESULTADOS POSIBLES TIENEN LA MISMA PROBABILIDAD
✅ SE USA EN JUEGOS, SORTEOS, RIFAS, DADOS, CARTAS
✅ ES UNA DISTRIBUCIÓN DISCRETA (VALORES CONTABLES)
✅ MUY ÚTIL
4.5 BINOMIAL
�� ¿QUÉ ES LA DISTRIBUCIÓN BINOMIAL?
ES UNA DISTRIBUCIÓN DISCRETA QUE MODELA LA CANTIDAD DE ÉXITOS QUE
SE PUEDEN OBTENER EN UN NÚMERO FIJO DE REPETICIONES DE UN EXPERIMENTO, CUANDO HAY SOLO DOS RESULTADOS POSIBLES: ÉXITO O FRACASO.
�� EXPLICADO SENCILLO:
IMAGINA QUE REPITES UN EXPERIMENTO MUCHAS VECES, COMO LANZAR UNA MONEDA. CADA VEZ PUEDE SALIR CARA (ÉXITO) O CRUZ (FRACASO).
LA DISTRIBUCIÓN BINOMIAL TE DICE CUÁN PROBABLE ES OBTENER CIERTO NÚMERO DE CARAS (O ÉXITOS) EN UN NÚMERO DETERMINADO DE LANZAMIENTOS.
✅ CONDICIONES PARA USARLA:
HAY UN NÚMERO FIJO DE ENSAYOS (POR EJEMPLO, 10 LANZAMIENTOS).
CADA ENSAYO TIENE SOLO DOS POSIBLES RESULTADOS (ÉXITO O FRACASO).
LA PROBABILIDAD DE ÉXITO ES CONSTANTE EN TODOS LOS ENSAYOS. TODOS LOS ENSAYOS SON INDEPENDIENTES (UNO NO AFECTA AL OTRO).
�� EJEMPLO RÁPIDO
EXPERIMENTO: LANZAR UNA MONEDA 5 VECES
PREGUNTA: ¿CUÁL ES LA PROBABILIDAD DE QUE SALGAN EXACTAMENTE 3 CARAS?
USAMOS BINOMIAL PORQUE:
HAY 5 ENSAYOS (LANZAMIENTOS)
SOLO HAY 2 RESULTADOS POSIBLES (CARA O CRUZ)
LA PROBABILIDAD DE CARA SIEMPRE ES 0.5
LOS LANZAMIENTOS SON INDEPENDIENTES
�� ¿QUÉ ES LA DISTRIBUCIÓN GEOMÉTRICA? ES UNA DISTRIBUCIÓN DE PROBABILIDAD DISCRETA QUE MODELA EL NÚMERO DE INTENTOS NECESARIOS PARA OBTENER EL PRIMER ÉXITO EN UNA SERIE DE ENSAYOS INDEPENDIENTES.
�� DICHO EN PALABRAS SIMPLES: IMAGÍNATE QUE REPITES UN EXPERIMENTO (COMO LANZAR UNA MONEDA) UNA Y OTRA VEZ HASTA QUE LOGRAS EL RESULTADO QUE QUIERES (POR EJEMPLO, QUE SALGA CARA). LA DISTRIBUCIÓN GEOMÉTRICA TE DICE CUÁNTOS INTENTOS TE VA A TOMAR EN PROMEDIO OBTENER ESE PRIMER ÉXITO.
�� CONDICIONES PARA USARLA CADA INTENTO TIENE DOS POSIBLES RESULTADOS: ÉXITO O FRACASO.
LA PROBABILIDAD DE ÉXITO ES CONSTANTE EN CADA INTENTO.
LOS INTENTOS SON INDEPENDIENTES ENTRE SÍ.
EL EXPERIMENTO SE REPITE HASTA QUE OCURRE EL PRIMER ÉXITO.
�� EJEMPLOS RÁPIDOS:
1. LANZAR UNA MONEDA
¿CUÁNTAS VECES DEBO LANZARLA HASTA QUE SALGA CARA POR PRIMERA VEZ?
2. UN EXAMEN DE OPCIÓN MÚLTIPLE
¿CUÁNTAS PREGUNTAS NECESITO RESPONDER HASTA QUE POR FIN ACIERTE UNA AL AZAR?
3. UN PRODUCTO DEFECTUOSO
¿CUÁNTOS PRODUCTOS DEBO REVISAR HASTA QUE ENCUENTRE EL PRIMERO DEFECTUOSO?
�� ¿QUÉ MIDE ESTA DISTRIBUCIÓN?
EL NÚMERO DE FRACASOS ANTES DEL PRIMER ÉXITO (O TAMBIÉN EL NÚMERO TOTAL DE INTENTOS HASTA EL ÉXITO, DEPENDIENDO DEL ENFOQUE).
BINOMIAL NEGATIVA
�� ¿QUÉ ES LA DISTRIBUCIÓN BINOMIAL NEGATIVA?
ES UNA DISTRIBUCIÓN DE PROBABILIDAD DISCRETA QUE MODELA CUÁNTOS INTENTOS NECESITAS PARA OBTENER UN NÚMERO FIJO DE ÉXITOS.
�� EN PALABRAS SIMPLES:
MIENTRAS LA DISTRIBUCIÓN GEOMÉTRICA TE DICE: �� “¿CUÁNTOS INTENTOS HASTA EL PRIMER ÉXITO?”
LA BINOMIAL NEGATIVA TE DICE:
“¿CUÁNTOS INTENTOS NECESITO HASTA OBTENER VARIOS ÉXITOS (POR
EJEMPLO, 3, 5, 10, ETC.)?”
✅ CONDICIONES PARA USARLA
CADA INTENTO TIENE SOLO DOS RESULTADOS: ÉXITO O FRACASO.
LOS INTENTOS SON INDEPENDIENTES ENTRE SÍ.
LA PROBABILIDAD DE ÉXITO ES CONSTANTE EN CADA INTENTO.
EL PROCESO TERMINA CUANDO ALCANZAS UN NÚMERO FIJO DE ÉXITOS.
�� EJEMPLOS RÁPIDOS
�� EJEMPLO 1: LANZAR UNA MONEDA
¿CUÁNTAS VECES TENGO QUE LANZAR UNA MONEDA HASTA QUE SALGAN 3 CARAS?
LA BINOMIAL NEGATIVA TE DICE CUÁNTOS LANZAMIENTOS NECESITARÁS (EN PROMEDIO O EXACTAMENTE) PARA OBTENER ESAS 3 CARAS.
�� EJEMPLO 2: ENCUESTAR PERSONAS
QUIERES ENCONTRAR 5 PERSONAS QUE DIGAN "SÍ" A UNA PREGUNTA.
¿CUÁNTAS PERSONAS NECESITAS ENTREVISTAR HASTA LOGRAR ESOS 5 "SÍ"?
�� ¿QUÉ ES LA DISTRIBUCIÓN HIPERGEOMÉTRICA?
ES UNA DISTRIBUCIÓN DE PROBABILIDAD DISCRETA QUE SE USA CUANDO SACAS
ELEMENTOS DE UN GRUPO SIN DEVOLVERLOS, Y QUIERES SABER CUÁNTOS ÉXITOS PUEDES OBTENER.
�� EN PALABRAS SENCILLAS:
ES COMO UNA RIFA O UNA LOTERÍA DONDE SACAS BOLETOS SIN REGRESARLOS AL MONTÓN.
A DIFERENCIA DE OTRAS DISTRIBUCIONES COMO LA BINOMIAL (DONDE CADA INTENTO ES INDEPENDIENTE), AQUÍ LOS INTENTOS SÍ AFECTAN A LOS DEMÁS, PORQUE UNA VEZ
QUE SACAS ALGO, NO LO DEVUELVES.
✅ CARACTERÍSTICAS CLAVE:
LA SELECCIÓN ES SIN REEMPLAZO
SE TOMA UNA MUESTRA DE UN GRUPO FINITO Y CONOCIDO
SE QUIERE SABER CUÁNTOS ELEMENTOS “BUENOS” O “EXITOSOS” HAY EN
LA MUESTRA
�� EJEMPLO ILUSTRATIVO: SUPONGAMOS QUE TIENES UNA CAJA CON 10 BOLAS: 4 ROJAS �� (ÉXITO) 6 AZULES �� (FRACASO) Y SACAS 3 BOLAS SIN DEVOLVERLAS.
�� LA DISTRIBUCIÓN HIPERGEOMÉTRICA TE AYUDA A CALCULAR LA PROBABILIDAD DE SACAR POR EJEMPLO, 2 ROJAS EN ESAS 3 EXTRACCIONES.
Distribución ¿Con reemplazo? ¿Independientes? ¿Tamaño del grupo cambia? Binomial
Sí
Sí
No (grupo no cambia)
Sí (grupo se reduce)
4.9 POISSON
�� ¿QUÉ ES LA DISTRIBUCIÓN DE POISSON?
ES UNA DISTRIBUCIÓN DISCRETA QUE MODELA EL NÚMERO DE VECES QUE OCURRE
UN EVENTO EN UN INTERVALO FIJO DE TIEMPO, ESPACIO O ÁREA, SI CONOCES EL PROMEDIO CON QUE OCURRE.
�� EXPLICADO FÁCIL:
IMAGINA QUE:
EN PROMEDIO, LLEGAN 3 CLIENTES POR MINUTO A UNA TIENDA.
QUIERES SABER: “¿CUÁL ES LA PROBABILIDAD DE QUE LLEGUEN EXACTAMENTE 5 CLIENTES EN UN MINUTO?”
LA DISTRIBUCIÓN DE POISSON TE AYUDA A CALCULAR ESO. ��
✅ CONDICIONES PARA USARLA
EL EVENTO PUEDE OCURRIR VARIAS VECES, PERO DE FORMA ALEATORIA.
SE CONOCE EL PROMEDIO DE OCURRENCIA (Λ).
LOS EVENTOS OCURREN DE FORMA INDEPENDIENTE.
NO SE PRESENTAN DOS EVENTOS AL MISMO TIEMPO EXACTO.
�� EJEMPLOS RÁPIDOS
1. TRÁFICO
EN PROMEDIO, PASAN 10 AUTOS POR UN CRUCE CADA HORA.
¿CUÁL ES LA PROBABILIDAD DE QUE PASEN 8 AUTOS EN UNA HORA?
2. MENSAJES
UNA APP RECIBE 4 MENSAJES POR MINUTO.
¿CUÁL ES LA PROBABILIDAD DE RECIBIR 6 MENSAJES EN UN MINUTO?
3. ERRORES DE IMPRESIÓN
UN LIBRO TIENE EN PROMEDIO 2 ERRORES POR PÁGINA.
¿CUÁL ES LA PROBABILIDAD DE QUE UNA PÁGINA TENGA 0 ERRORES?
Fundamentos de estadística.
2.ª ed. Alianza Editorial.
→ Más teórico, pero muy útil si quieres bases sólidas.
Larson, R., & Farber, B. (2014).
Probabilidad y estadística para ingeniería y ciencias.
9.ª ed. Cengage Learning.
→ Excelente para ejemplos prácticos, distribuciones y enfoque aplicado.
Triola, M. F. (2018).
Elementary Statistics: A Step by Step Approach.
10.ª ed. McGraw-Hill.
→ Muy visual, paso a paso, ideal para principiantes.
Peña, D. (2001).
Estadística.
13.ª ed. Pearson Educación.
→ Lenguaje claro y muchos ejemplos de vida real; ideal para estudiantes.
Montgomery, D. C., & Runger, G. C. (2014).
Walpole, R. E., Myers, R. H., Myers, S. L., & Ye, K. (2012).
Probabilidad y estadística para ingeniería y ciencias.
9.ª ed. Pearson Educación.
→ Uno de los libros más completos para entender teoría y aplicaciones estadísticas.
Devore, J. L. (2015).