First course in the finite element method 6th edition logan solutions manual 1 by kurtis.wells397

First Course in the Finite Element Method 6th

Edition by Logan

ISBN 1305635116

9781305635111

Download solution manual at:

https://testbankpack.com/p/solution-manual-for-first-course-inthe-finite-element-method-6th-edition-by-logan-isbn1305635116-9781305635111/

Chapter 6

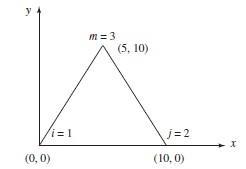
By Equation (6.2.18) Ni + Nj + Nm = 1 [(i + j + m) + (i + j + m) x + [i + j + m)y] (1) 2A By Equation (6.2.10) i + j + m = xj ym – yj xm + yi xm – xi ym + xi yj – yi xj = 2A (by Equation (6.2 9)) (2) i + j + m = yj – ym + ym – yi + yi – yj = 0 (3) i + j + m = xm – xj + xi – xm + xj – xi = 0 (4) By using (2)–(4) in (1), we obtain Ni + Nj + Nm = 1 identically 6.2

1 p = {d}T [B]T [D] [B] dV{d} – {d}T { f } 2 [B] = 1 2A [D] = E 1– v 2 , {d} =

6.1 For sketch of Ni see Figure 6.8. Others follow similarly By Equation (6.2.47)

317 © 2017 Cengage Learning All Rights Reserved May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part i j j m m i i i j m m d 0 0 0 0 E dV  1 – [ui vi uj vj um vm] { f } v i = 2 1 v dV ui – f1x v i C = 2C dV vi – f1y = 2C dV uj – f2x = 2C dV vj – f2y = 2C dV um – f3x = 2C dV vm – f3y i i i i v i j  = 2C v i i m i j m v j j v m m m m i i j m m m

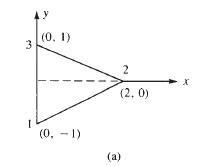
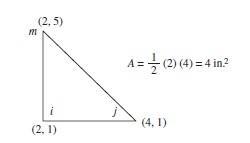
318 © 2017 Cengage Learning All Rights Reserved May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part i i j j m m  dV –From Equation (3.10.27) or Equation (6 2.48) = 0  = B T [D] [B] dV{d} – { f } = 0 v 6.3 (a) [k] = t A [B]T [D] [B] xi = 0, yi = –1, xj = 2, yj = 0, xm = 0, ym = 1 E = 10106 psi v = 0.25 t = 1in A = 1 2 b h = 1 (2)(2) = 2 in.2 2 i = yj – ym = 0 – 1 = – 1 j = ym – yi = 1 – (–1) = 2 m = yi – yj = – 1 – 0 = – 1 i = xm – xj = 0 – 2 = – 2 j = xi – xm = 0 – 0 = 0 m = xj – xi = 2 – 0 = 2 [B] = 1 2A

319 © 2017 Cengage Learning All Rights Reserved May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part 1 2 3 2 1.5 0.5 0.25 0 25 v Since it is plane stress [D] = E v (1 v v  1 0 2  0 2 1     10 106  2 0 0 1 0.25 0 So [B]T [D] =   0 25 1 0  4(0 9375)  0 0 2    1 0 2   0 0 0.375  0 2 1  1 0.25 0.75   0.5 2 0.375    2 0.5 0  10 106 =    0 0 0.75  4(0.9375)  –1 0.25 0.75     0.5 2 [k] = t A[B]T [D] [B] 0.375  1 0.25 0.75   0.5 2 0.375   10 106  2 0.5 0   [k] = (1in.)(2)   4(0.9375)  0 0 0.75   1 0.25 0.75     0.5 2 0.375 1 4 i j m

320 © 2017 Cengage Learning All Rights Reserved May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part 2 1 4 0 2 1 1 5 0 75 0 1 5 1 5 0 75 3.625 1 0.75 1.25 4.375 [k] = 1.333  106 (b) xi = 1.2, yi = 0, xj = 2 4, yj = 0, xm = 1.2, ym = 1

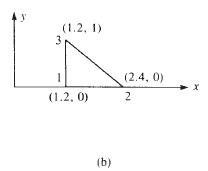
321 © 2017 Cengage Learning All Rights Reserved May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part 0 1.2 0 1 0.25 0.45 0.3 1.2 0 0.3 1.2 0 i = yj – ym = 0 – 1 = – 1 j = ym – yj = 1 – 0 = 1 m = yi – yj = 0 – 0 = 0 i = xm – xj = 1.2 – 2.4 = – 1.2 j = xi – xm = 1.2 – 1.2 = 0 m = xj – xi = 2.4 – 1.2 = 1 2 A = 1 2 (1.2) (1) = 0.6 in.2 So [B]T [D] = 10 106 (1.2)(0.9375) 8.33 106 = 0.9375 [k] = t A[B]T [D] [B] [k] = (1in.)(6in.2 )8.33106 2(0 6) (0 9375)

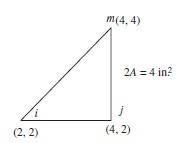
322 © 2017 Cengage Learning All Rights Reserved May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part 1 2 3 3 0 0 1 44 T 2 i j m [k] = 4 44 106 (c) E = 10  106  = 0.25 t = 1 Triangle coordinate definition x his defines an array variable i = x coordinate is the top y y coordinate is the bottom j = Area of triangle = 1 base  height m = A = 1 2 (jx – ix) (my – iy) A = 1 Develop stiffness matrix i = jy – my i = –1 i = mx – jx i = –2 j = my – iy j = 1 j = ix – mx j = 0 m = iy – jy m = 0 m = jx – ix m = 2 1 i [Bi] = i 2A 1 [Bj] = 2A i i 1 [Bm] = 2A Gradient matrix [B] = augment (Bi, Bj, Bm)

323 © 2017 Cengage Learning All Rights Reserved May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part 0 0.5 1 0 0 0 2 6 7 6 7 4 10 3 2 10 4 10 0 0 3 2 10 1 0 2) 0 0 0 j j u [B] = Plane stress Constitutive matrix [D] = E 1 1 067 107 2 67 106 0    [D] =  2 67 106 1 067 107 0   0 0 0.4 107    [k] = t A [B]T D] B] Constant-strain triangular element stiffness matrix 1 [k] = 3 6.4 In general we know that {} = E  1 (1 2A

For the first element we have

(a)

The principal stresses are given by the equations

and the plane that are acting upon is

324 © 2017 Cengage Learning All Rights Reserv copied or duplicated, or posted to a publicly accessible website, in part 1,2 2 2 2 2 x y 2 x y x y 2 y xy = xy 2 2 2 x y xy 1 0 25 0 0 25 1 0 0 0 0 375 1 0 2 10 106  1 0 25 0   1 0 2 0 1 1 0 = 0 25 1 0    0 2 0 0 0 2 (1 0 252 )   2(2)   0  0 0 0 375   2 1 0 2 2 1  0.0025    6400psi 0.0012     =  1600psi  0    0.0    0.0025  5000psi

1 1 2

p = 1 tan–1 2 2 1 = 6400 +1600  6400 1600 2 +   + ( 5000) 1 2  2  2 = 9546 psi  2   1 2 = 6400 +1600  6400 1600 2   + (–5000)2  2  2 = – 1545 psi  2   5000 p = 1 tan–1 = – 32.2° 2 ( 6400 – 1600 ) (b)

10 106 = (1 0.25)2  1 2(0.6)

For the second element we have

325 © 2017 Cengage Learning All Rights Reserved May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part 0 0.5 1 0 3  xy  2  x = 10667 psi   =  y = 2667 psi   = 8333 psi  1 = 10667 + 2667  10667 2667 2 +   + ( 8333) 1 2  2  2 1 = 15910 psi  2   1 2 = 10667 + 2667  10667 2667 2   + ( 8333)2  2  2 2 = – 2577 psi 1  2   8333 p = tan–1 2 (10667 2667 ) p = –32.2° (c) For third element we have [B] = [D] = 1 067 107  2 67 106 2.67 106 1 067 107 0   lb 0     in 2  0 0 0.4 107    u1 = 0.0 in. v1 = 0 0025 in. u2 = 0.0012 in. v2 = 0.0 in. u3 = 0.0 in. v3 = 0 0025 in. {d

= Displacement matrix Stress evaluation = [D] B] d}

}

326 © 2017 Cengage Learning All Rights Reserved May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part xy 2 x y 2 x y  6.4 103    lb = 1 6 103     in 2  5 103    Principal stresses 1 = 2 2 = 2 max = 0.955  104 lb in.2 = 1 min = – 1.546  103 lb in.2 =  Principal angle atan 2 xy p = x y 2 p = – 32.179 deg. 6.5 Von Mises stress for biaxial stress state (a) 1 = 9546 2 = – 1546 e = e = 1.041  104 psi (b) 1 = 15910 2 = –2577 e = e = 1.734  104 psi 6.6 (c) e = e = 1.041  104 lb in 2

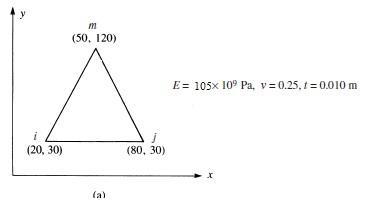
328 © 2017 Cengage Learning All Rights Reserved May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part 3 5 4 10 2 0 60 0 15 60 0 1350 1800 1350 1800 0 3600 i = yj – ym = 30 – 120 = – 90 i = xm – xi = 50 – 80 = – 30 j = ym – yi = 120 – 30 = 90 i = xi – xm = 20 – 50 = –30 m = yi – yj = 30 – 30 = 0 m = xj – xi = 80 – 20 = 60 2A = xi(yj – ym) + xj(ym – yi) + xm(yi – yj) = 20(– 90) + 80(90) + 50(0) = 5400 mm2 [B] = 1 5400 105 109  1 0 25 0  [D] = 0 25 1 0  = 1.12  1011 1 (0.25)2   0 0 0 375 [k] = t A [B]T [D] [B] [k] = (0.01) (1.12  1011) [B] [k] = 0.56  109 1 5.4 [k] = 1.037  105 (b) Similarly i = – 5 i = 0 j = 2.5 j = –5

329 © 2017 Cengage Learning All Rights Reserved May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part Symmetry 27 343 9 8 9 7 8 8 8 8 8 8 9 2.8 10 5.6 10 2.8 10 –5.6 10 0 1.12 10 90 0 m = 2.5 m = 5 [k] = 2.24  107 Now solve P6-6c for stiffness matrix t = 0.01 A = tA A = 5  10–5 2 [k] = t A [B]T [D] [B] [k] = 6.7 (a) By Equation (6.2.36) {} = [D] [B] {d} Using results of Problem 6.5 (a) 1 121011  1 0 25 0  = 0 25 1 0  540010 3   0 0 0.375  10–3 m mm  2.645 GPa  =  0 078GPa     0.1165GPa  

330 © 2017 Cengage Learning All Rights Reserved May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part p  0     0.003      +  + 2 1,2 = 2 645 ( 0 078)  2.645 0.078   + 0.11652 2 = – 1.86 1.29  2  1 = – 0.07 GPa 2 = – 2.65 GPa tan 2 = 2(0.1165) 1 2 645 + 0 078 = – 0.091 p = – 2.59° (b) From Problem 6.5 (b)  ’s and  ’s given 1 121011  1 0 25 0  = 0 25 1 0  2510 6     0 0 0 375   0.002   0.001     0   10–3 m mm 0.0005 = 21.0GPa  +   0.001   2 16.8GPa  1,2 = 0 21 0   21 +16 82 2  2  (c) = 10.5 19.8 1 = 30.3 GPa 2 = – 9.3 GPa tan 2p = 2(16 8) 0 21.0 p = – 29°

331 © 2017 Cengage Learning All Rights Reserved May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part P l a n e s t r e s s a l s o f i n d v o n M i s e s s t r e s s

332 © 2017 Cengage Learning All Rights Reserved May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part 1 0 2 0 0 2 i = – 10 mm i = – 5 mm j = 10 mm j = – 5 mm m = 0 m = 10 mm A = 2.5  10–5 m2 {} = [D] [B] {d} [D] = v E v 1 v v  (105109 N ) 1 0 25 0  2   [D] = m 0 25 1 0  1 (0 25)2    0 0 1 0.25   2  [D] = 112  109 N m 2 {d} = Determine the stresses in the element with nodal displacements listed u1 = 0.002 v1 = 0 001 u2 = 0 0005 v2 = 0 u3 = 0 003 v3 = 0 001 Here are the coordinates for the element x1 = 0 y1 = 0 x2 = 0.01 y2 = 0 x3 = 0.005 y3 = 0.01 E = 105  109 v = 0 25 E {d} = [D] = [D] = [D] 1– v 2

Note: use the left bracket after the sigma then the 0, or 1 or 2 for the values in the sigma matrix

333 © 2017 Cengage Learning All Rights Reserved May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part 1 1 2 2 2 3 –50 –100 –50 100 100 0 x y 2 2 x y 1.12 1011 2.8 1010 0    Equation (6.1.8) [D] =  2.8 1010 1.12 1011 0   0 0 4.2 1010    Equation (6.2.10) 1 = y2 – y3 1 = – 0.01 1 = x3 – x2 1 = – 5  10–3 2 = y3 – y1 2 = 0.01 2 = x1 – x3 2 = – 5  10–3 3 = y1 – y2 3 = 0 3 = x2 – x1 3 = 0.01 TA = x1 (y2 – y3) + x2 (y3 – y1) + x3 (y1 – y2) TA = 1  10–4 twice the area, Equation (6.2.9) Equation (6.2.32) combined [B] = 1 TA [B] = In-plane stresses { = [D] [B] {d} 10 10  –1.54 10   x = 0  x = 1.54 10   { =  1.4 109   y = 1  y = 4.2109  3.15 109   =   = 3.15109   xy 2 xy

Principal stresses 1 1 = 2 1 = 1.971  109 N m 2 1 sqrt = ave = 2

335 © 2017 Cengage Learning All Rights Reserved May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part 2 1 –2 ) 2 1 ( 2 = – 1.597  1010 N m 2 p = – 0.179 p = – 10.278° Principal angle 6.8 Von Mises stress (a) 1 = – 0.07 2 = – 2.65 e = e = 2.615 GPa (b) 1 = 30.3 2 = – 9.3 e = e = 35.87 GPa (c) 1 = 1.97 GPa 2 = – 15.95 GPa P6.8c von Mises stress, Equation (6.5.37a) 1 1 vm = 2 6.9 (a) vm = 1.705  1010 N m 2 Plane strain i = yj – ym = 1–5 = – 4 i = xm – xj = 2 – 4 = – 2 j = ym – yi = 5 – 1 = 4 j = xi – xm = 2 – 2 = 0 m = yi – yj = 1 – 1 = 0 m = xj – xi = 4 – 2 = 2 10106 = 0 75 0 25 0  0 25 0 75 0  (1+ 0 25)1 2(0 25)   0 0 0.25

336 © 2017 Cengage Learning All Rights Reserved May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part 0    5000  =  15000 psi  6000    +  2 1,2 = 5000 ( 15000) +  5000 ( 15000)  ( 6000)2 2  2  = –10000 ± 7813 1 = – 2187 psi 2 = –17810 psi 2( 6000) tan 2p = 5000 ( 15000) (b) p = – 25.1° i = 2 – 4 = – 2 i = 4 – 4 = 0 j = 4 – 2 = 2 j = 2 – 4 = – 2 m = 2 – 2 = 0 m = 4 – 2 = 2 = 16  106

337 © 2017 Cengage Learning All Rights Reserved May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part 3 2 2   p  5,000  =  15,000  psi  7000    1,2 = 5 = 000 = 15000   5 = 000 = ( 1 = 5000) 2 + ( 7000)2 2 2 1 = – 1398 psi 2 = –18600 psi tan 2 = 2( 7000) 5000 ( 15000) p = – 27.2°

Given displacements (in.) u1 = 0.001 v1 = 0.005 u2 = 0.001 v2 = 0.0025 u3 = 0 v3 = 0 {d} = Material definition E = 10  106 psi v = 25 Geometry description i = 0 – 2 (yj – ym) j = 2 – 0 (ym – yi) m = 0 – 0 (yi – yj) i = 0 – 2 (xm – xj) j = 0 – 0 (xi – xm) m = 2 – 0 (xj – xi) A = 1 2 A = 2

(c)

338 © 2017 Cengage Learning All Rights Reserved May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part i i j j m m 0 0 2 2 x y 2 x y   x y [B] = 1 2A Plane strain constitutive matrix [D] = v v E v v 1 v v v Stress matrix { = [D] B] {d}  1104   =   3 104    0 7 104   = 1104(psi)  = 3  104 (psi)  = 0 7  104 (psi) xy 1 = 2 1 = – 0.7793  104 psi 2 = 2 2 = – 3.221  104 psi p = 1 atan xy 2 x y

339 © 2017 Cengage Learning All Rights Reserved May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part 2 2 2 1 2 2 3 3 1 0 75 0 25 0     p p = – 0.305 (rad) 3 = 0 1 vm = 2 (d) vm = 2.91  104 (psi)  1 = – 4  1 = 0  2 = 2  2 = – 2  3 = 2  3 = 2 = 16  106  5.5 =  8.5 ksi  8.5 2  +  1,2 = 5.5 8.5  5.5 8.5   + ( 8.5)2 2  2  (e) 1 = 1.63 ksi 2 = – 15.6 ksi tan 2 = 2( 8 5) 5.5 + 8.5 p = – 40.0° 1 1 1

(f) Material properties

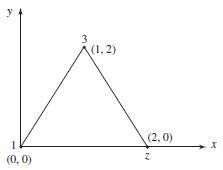
Nodal coordinates (coordinates defined CCW around element)

© 2017 Cengage Learning All Rights Reserved May not be scanned, copied or duplicated, o whole or in part   = 0.375 in.2  i = 1 – 3.25 = – 2.25  i = 2.25 – 3 = – 0.75  j = 3.25 – 3 = 0.25  j = 2 – 2.25 = – 0.25  m = 3 – 1 = 2  m = 3 – 2 = 1 {} = [D] [B] {d}  1 0.75  55.3  =  80.67 ksi  62    +  + 2 1,2 = 55 3 ( 80 67)  55 3 80 67   + ( 62)2 2  2  1 = – 4.73 ksi 2 = – 131.3 ksi   p = 1 1 2( 62)  tan  = – 39.2° 2 

55.3 + 80.67  E =



6 psi Modulus of elasticity.

v = 0.25 Poisson ratio

in. y1 =

in. x2 = 2 in. y2 = 0 in. x3 = 1 in. y3 = 2 in. 335

= 0

336 © 2017 Cengage Learning All Rights Reserved May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part 1 1 2 2 3 3 0 0.5 0 0 0 0 0 –0 25 0 0 5 1 in. 0.25 0.5 0.25 0.5 0.5 0 0 0 2 2 Nodal displacements u1 = 0.001 in. v1 = 0.005 in. u2 = 0.001 in. v2 = 0.0025 in u3 = 0 in. v3 = 0 in. Set-up displacement vector {d} = (u1 v1 u2 v2 u3 v3)T {d}T = (0.001 0.005 0.0001 0.0025 0 0) in. Area of triangular element ( 1  base  height) A = 1 (x – x ) (y – y ) 2 1 3 1 2 A = 2 in.2 Calculate gradient matrix, B, as given in text Equation (6.2.32) Elements of B given by text Equation (6 2.10)  1 = y2 – y3  2 = y3 – y1  3 = y1 – y2  1 = x3 – x2  2 = x1 – x3  3 = x2 – x1 [B] = 1 2A [B] = Calculate constitutive matrix for plane strain [D] = v v E v v 1 v v v 1.2 107 0.4 107 0    [D] =  0.4 107 1.2 107 0  psi  0 0 0.4 107   

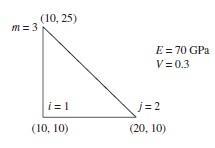
337 © 2017 Cengage Learning All Rights Reserved May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part 2 2 x   = [D] B] {d}  7500  =  22500 psi  7000    Principal stresses 1 = x y x y 2 xy 1 = – 0.474  104 psi 2 = x y x y 2 xy 2 = – 25.30  103 psi Angular location of principal stress plane atan 2 xy p = x y 2 p = – 21.513° 6.10 (a) i = – 15 i = – 10 j = 15 j = 0 m = 0 m = 10 2A = 150 mm2 = 150  10–6 m2 105106 = 0.7 0.3 0  0.3 0.7 0  (1+ 0 3)1 2(0 3)   0 0 0.2

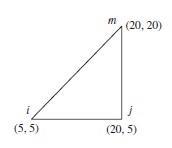
338 © 2017 Cengage Learning All Rights Reserved May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part 15 0 15 0 0 0 1 0 x 150  10–3  78.75 =  49.2  MPa    8.07    +  + 2 1,2 = 78 75 ( 49 2)  78.75 49.2   + ( 8.07)2 2  2  = – 63.98 ± 16.83 1 = – 47.15 MPa 2 = – 80.81 MPa (b) 2p = tan–1 2( 8.07) 78 75 ( 49 2) p = 14.32° = 28.64° 141.3 60.6 0  = 109  141.3 0  1   22510 6   40 35    10–3

339 © 2017 Cengage Learning All Rights Reserved May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part x 10 0      47.1  =  20.25 MPa  8.07     + 2 1,2 = 47 1 20 5  47 1 20 25   + (8 07)2 2  2  = – 33.66 ± 15 69 (c) 1 = – 17.97 MPa 2 = – 49.35 MPa tan 2p = 2(8.07) 47 1 + 20 25 p = – 15.5° =  150 0.7 0.3 0   0.3 0.7 0  1  1 30.4    200   0 0 0.2   10–3  41.4  =  29.25 MPa 6.06     + 2 1,2 = 41.4 29.25  41 4 29 25   + 6 062 2  2  1 = – 26.85 MPa 2 = – 43.95 MPa

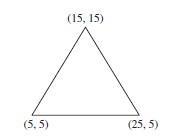
341 © 2017 Cengage Learning All Rights Reserved May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part 1 0 2 0 3 1 1 2 2 3 3 0 v) (1– 2 0 0 2 u1 x E = 105  109 v = 3 t = 1 y1 = 0 015 x1 = 0.005 y2 = 0 005 x2 = 0 015 y3 = 0 015 x3 = 0 025 1 = y2 – y3 2 = y3 – y1 3 = y1 – y2 1 = x3 – x2 2 = x1 – x3 3 = x2 – x1 (d) A = 1 2 p = – 22.5° [x1 (y2 – y3) + x2 (y3 – y1) + x3 (y1 – y2)] [B] = 1 2A [D] = E (1 v) [k] = t A [B]T [D] [B] u1 = 0 000005 v1 = 0.000002 u2 = 0 v2 = 0 u3 = 0 000005 v3 = 0 {d} = {} = [D] [B] {d} =  105 0 7 0 3 0   0 3 0 7 0  1  1.30 4    200   0 0 0.2

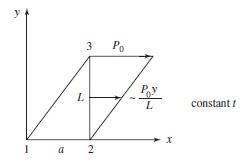
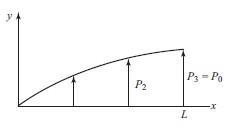
341 © 2017 Cengage Learning All Rights Reserved May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part 2 10 0 0 0 10 0 0 0 10 0 10 0 10 0 10 0 10 10 10 10 5 0 y 2 x x y 2   10–3  1.575 =  1.05  MPa    5.25    1 = 2 2 = –2  + 2 1,2 = 1.575 1.05  1 575 1 05   + ( 5 25)2 2  2  1 = –5.145 MPa 2 = – 5.67 MPa 1  2( 5 25)  p = tan–1   2  1 575 1 05  p = 38° 6.11 (a) Equation (6 3.7)    N1 P0 y  N1 0  L   0 N1   0    t L N 0  P0 y  N P y  L 2 0 {fs} =    2   L  dz dy = t   L  dy

342 © 2017 Cengage Learning All Rights Reserved May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part    0 0  0 N2  0 0  0   N3 0   N3 P0 y     L   0 N3 evaluated at x = a  0  y = y  

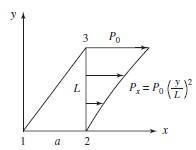
343 © 2017 Cengage Learning All Rights Reserved May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part 0 fs x 1 0 0 N y 0 y 0 P0 L 0 y y L s 3 By Equations (6.3 12) – (6.3 17) N1 = L a x 2A , N2 = Lx 2A , N3 = ay 2A {f } = t P0 , = aL 2 2 (b) By Equation (6.3 11) {fs} = t Now N1 = 0, N2 = Lx ay , N = ay 2A 2A {fs} = t Simplifying and integrating

343 © 2017 Cengage Learning All Rights Reserved May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part 0 2 2 2 p1 3 2 s f = P tL {f } = P0 t = 1 2 2 aL 6.12 or (a) P0 tL 2x 12 f3x = 0 4 Py(x) = ax2 + bx + c Given a + p1 = p2 aL2 + bL + p1 = p3 c = p1 Find (a, b, c) → ( p ) (1) a(p1, p2, p3) = 2 1 2 L2 b(p , p , p ) = (– 3p1 – p3 1 2 3 L c(p1, p2, p3) = p1 (2) (3)

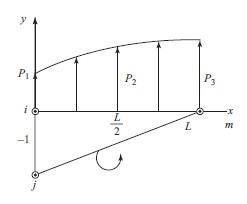
344 © 2017 Cengage Learning All Rights Reserved May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part b( p1, p2, p3)x c ( p1, p2, p3) L L 1 b( p1, p2, p3)x c ( p1, p2, p3) L L 1 2 s s Forces in y direction at nodes 1 and 3 are N1 = Ni 2 1 f 1y = , p3)x dx → 6 Lp1 3 L = x N3 = Nm 2 1 f 3 y = , p3)x dx → 6 Lp3 3 L = dx 0 (Special case) Want If p1 = 0 p3 = p0 p(x) = ax2 + bx + c p(x) = p0 = ax2 + bx + c  a = p0 = 2 (p0 – 2p2) using (1) L2 L2

(These answers match P6.11 for special case)

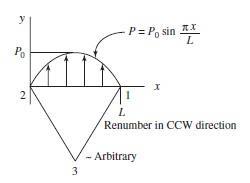
345 © 2017 Cengage Learning All Rights Reserved May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part T in Ni 0 N j 0 Nm 0 0 N 0 N 0 N i j m s s s N T 2 p0 –p0 = 4 p2 L2 L2 p0 L2 L2 = 4 p2 L2 Then p2 = p0 4 1 0 1 1 p0 p0L pL f = L p1 1 y 6 + Lp2 = L 3 3 = 4 12 → Like 6.11 b with fsx = 12 p0 p0 4 1 || 1 || 3 p0L f = 3 y 6 Lp3 + 3 Lp2 = Lp0 = 12 4  f3x in 6.11b (b)

{ f } = s s [Ts ] ds [Ts ] = Surface tractions = = N P L [Ns] = Shape function matrix evaluated along edge 1-2 = Let i = 1 j = 2 m = 3

346 © 2017 Cengage Learning All Rights Reserved May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part m N1(y = 0) = 1 ( i +  i x) 2A  i = xj ym – yj xm = 0(ym) – 0(xm) = 0  i = yj – ym = 0 – ym = – ym 1 N1(y = 0) = (0 – ym x) = 2A 2A 1 Nj = N2 = 2A ( j +  j x +  j y) N2(y = 0) = 1 ( i +  i x) 2A  j = yj xm – xj ym = 0(xm) – Lym = – Lym  j = ym – yi = ym – 0 = ym 1 y N2(y =0)= [– Lym + ymx]= m 2A 2A 1 [x – L] Nm = N3 = 2A 1 [m + mx + my] N3(y = 0) = [m + mx] 2A m = xi yj – yi xj = L(0) – 0(0) = 0 m = yi – yj = 0  Nm(y = 0) = 0 As expected { fs} = dz dx

347 © 2017 Cengage Learning All Rights Reserved May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part L 0 x L sin 0 x L x s L t y3P0 xL cos 2 cos 0 y3 0 ) t y3P0 n x y sin 2A 0 L 2A L t y L x L x sin dx L 2A 0 L L L 2  2 = t dx = t dx (A) 2nd term in (A) (ym = y3) udv = uv – vdu fs1y = t y P x L x x dx u = x du = dx 2A L x x dv = sin dx v = –cos L L L = 2A L = t y P xL x L x 2A L L = 2A fs1y = 2A t P L = 0 A = 2 4th term in (A) Ly3 fs2y = t dx = t y3 P 2A 0 DONE IN 2nd TERM = t y3P0 2A = t y3P0 L t y P L L [–1 + 1] 2A A

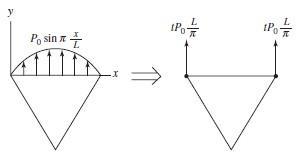
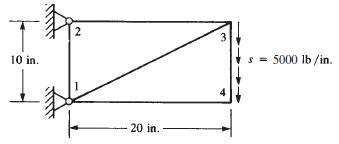
348 © 2017 Cengage Learning All Rights Reserved May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part f Symmetry 87   t y P L2 t y L2 P t L P fs2y = 3 0 = 3 0 = 0 2A 2 t P L  s = = t P L 6.13 Refer to Section 6.5 for [K] Since u1 = v1 = 0, u2 = v2 = 0  0   25,000  0  = 75000 0.91     25,000  Solving u3 = 2.50  10–3 in. v3 = – 1.376  10–2 in. u4 = – 3.04  10–3 in. v4 = – 1.466  10–2 in. Using element (1) By Equation (6.2.36), {} = [D] [B] {d}

349 © 2017 Cengage Learning All Rights Reserved May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part 6 106 0.3 1 0 0 0 0.35              {} = 30 (0 91)(200)  0   0     2.510 3      1.37610 2   0      0  4123  = 1,2 =  1237  psi  7938 = 4123 += 1237   = 4123 = 1237 2   + ( 7938)2 2  2  1 = 10748 psi 2 = – 5388 psi p = 1 tan–1  2 7938  2  4123 1237  p = – 40° Using element (2) {} = 30 0.91(200)  0   0     3.04 10 3   1.466 10 2   2.50 10 3      1.376 10 2    4123 =  1469  psi    2062 +  2 1,2 = 4123 1469   4123 1469  + ( 2062)2 2  2 