https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
Вибери номер параграфа


































































































































https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
1.
1) 12x = 0; - лінійне рівняння.
2) 4x + 2y = 9; - має дві змінні, тому не є рівнянням з
3) 7x = x2; - не лінійне, оскільки містить x2 (це квадратне рівняння).
4) 0x = 12; - суперечливе рівняння (немає розв’язків), але не лінійне, бо коефіцієнт біля x дорівнює 0.
5) 1 х – 7 = 0; - не лінійне, оскільки містить 1 х (дробова залежність).
6) 0x = 0. - тотожність (вірне для всіх x), але не є власне рівнянням.
2. Яке із чисел є коренем рівняння x2 – x = 2x + 4:
1) 0; 2) –1; 3) 1;
4) 2; 5) 4; 6) –3?
x2 – x = 2x + 4
x2 – x – 2x – 4 = 0
x2 3x – 4 = 0
(x 4)(x + 1) = 0
x – 4 = 0 ⇒ x = 4
x + 1 = 0 ⇒ x = 1
Тобто коренями є x = 4 і x = 1.
Відповідь: 2 і 5.
3. Яке із чисел є коренем рівняння x2 – 3x = x + 5:
1) 1; 2) 0; 3) –1;
4) 3; 5) 5; 6) –2?
x2 3x = x + 5
x2 3x – x – 5 = 0
x2 4x – 5 = 0
(x 5)(x + 1) = 0
x – 5 = 0 ⇒ x = 5
x + 1 = 0 ⇒ x = 1
Тобто коренями є x = 5 і x = 1.
Відповідь: 3 і 5.
4. Розв’яжіть рівняння: 1) 4х = -8
4х : 4 = -8 : 4
х = -2
3) 7 – (3х + 2) = 5 7 – 3х – 2 = 5 5 – 3х = 5 -3х = 0
х = 0
2) 9х – 13 = 3х + 5
9х – 3х = 5 + 13
6х = 18
х = 3 4) 1 8 х = 1 1 8 1 8 х = 9 8 х = 9
5) 8 – 2х = -(4х + 3) 8 – 2х = -4х – 3 -2х + 4х = -3 – 8 2х = -11
х = − 11 2 = −5 1 2
6) 3(х – 3) = 4х + 21
3х – 9 = 4х + 21
3х – 4х = 21 + 9 -х = 30
х = -30
1) -5х = -20
-5х : (-5) = -20 : (-5)
х = 4
2) 7х – 11 = 2х + 1
7х – 2х = 1 + 11
5х = 12
9x + 36 = 0
9х = -36
= -4
2x = 12 x = 6
3x = 3 ⋅ 6 = 18 (т.) Відповідь: 18
на 6
2x + 6 = 48
2x = 42
x = 21 (н.) Відповідь:
5x = 2(x + 9)
5x = 2x + 18
5x 2x = 18
3x = 18
x = 6 (км/год) –
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
3) 9 – (5х + 1) = 10
9 – 5х – 1 = 10 8 – 5х = 10 -5х = 10 – 8 -5х = 2
5) 7 – 3х = -(2х – 7)
7 – 3х = -2х + 7 -3х = -2х -3х + 2х = 0 -х = 0 х = 0
6) 9(х – 1) = 8х + 13
9х – 9 = 8х + 13
9х – 8х = 13 + 9 х = 22
+ 72 = 0
= -72
= -4
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
x + 8 кг, відповідно:
2(x + 8) = 3x
2x + 16 = 3x
16 = 3x 2x x = 16 (кг) – маса ящика зі сливами.
16 + 8 = 24 (кг) – маса ящика з яблуками.
Відповідь: 16 кг; 24 кг.
Розв’яжіть
+ 5y та
2х 5 3 = 5х+1 9
9(2х – 5) = 3(5х + 1)
18х – 45 = 15х + 3
18х – 15х = 3 + 45
3х = 48
х = 16 7(у + 3) – 9(у – 1) = 24 7у + 21 – 9у + 9 = 24
100х + 5у = 100 ⋅ 16 + 5 ⋅ 3 = 1600 + 15 = 1615 (рік
академія») 12. Розв’яжіть рівняння 2х 1 3 = 3+4х 7 і
7(2х – 1) = 3(3 + 4х) 14х – 7 = 9 + 12х 14х – 12х = 9 + 7
2х = 16
х = 8 7(у – 2) – 3(у + 5) = 11 7у – 14 – 3у – 15 = 11 4у – 29 = 11 4у = 11 + 29 4у = 40 у = 10
200х + 11у = 200 ⋅ 8 + 11 ⋅ 10 = 1600 + 110
13. Розв’яжіть рівняння: 1) ǀхǀ - 2 = 9
ǀхǀ = 9 + 2
ǀхǀ = 11
х = 11 або х = -11 3) ǀх - 2ǀ= 3 х – 2 = 3 або х – 2 = -3 х = 5 х = -1
2) 5 - ǀхǀ = 7 -ǀхǀ = 7 – 5
ǀхǀ = 2
= -2
2х – 1 = 0
2х = 1
хибне 4) ǀ2х - 1ǀ = 0
ǀ5х + 2ǀ = 3 5х + 2 = 3 або 5х + 2 = -3 х = 1 5 х = -1
х = 1 2 = 0,5 6) 1 3 ǀх - 2ǀ + 3 = 7
ǀх - 2ǀ + 9 = 21 ǀх - 2ǀ = 21 – 9
- 2ǀ = 12
– 2 = 12 або х – 2 = -12 х = 14 х = -10
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
5x + 12 = 52
5x = 40
x = 8 (см) – перша сторона.
3x = 3 ⋅ 8 = 24 (см) – друга сторона.
x + 12 = 8 + 12 = 20 (см) – третя сторона.
Відповідь: 8 см; 24 см; 20 см.
15. В одному
третьому. Скільки
x + 6
(x + 6) + x + 2(x + 6) = 66
(x + 6) + x + 2x + 12 = 66
4x + 18 = 66
4x = 48
x = 12 (кг) – другий мішок.
x + 6 = 12 + 6 = 18 (кг) – перший мішок.
2(x + 6) = 2(12 + 6) = 36 (кг) – третій мішок.
Відповідь: 18 кг; 12 кг; 36 кг.
16. За якого значення a рівняння x + a = 9 і 4x – a = 3x
1) x + a = 9 ⇒ x = 9 a
2) 4x – a = 3x ⇒ 4x 3x = a ⇒ x = a
Тепер прирівняємо вирази для x з обох рівнянь:
9 – a = a
9 = 2a
а = 9 2 = 4,5
Відповідь: а = 4,5.
17. За якого значення b рівняння x – b = 7 і 5x + b = 4x мають однакові корені?
1) x – b = 7 ⇒ x = b + 7
2) 5x + b = 4x ⇒ 5x 4x = b ⇒ x = b
Тепер прирівняємо вирази для x з
рівнянь: b + 7 = b
b + b = 7
2b = 7
b = 7 2 = 3,5
Відповідь: b = -3,5.
вирази
18. Подайте у вигляді степеня: 1) c3c5 = с3+5 = с8; 2) m9mm15 = m9+15 = m24; 3) p12 : p3 = р12-3 = р9; 4) (x9)7 = х9⋅7 = х63
19. Подайте у вигляді степеня: 1) p7p2 = p7+2 = p9; 2) tt2t3 = t2+3 = t5; 3) c15 : c5 = c15−5 = c10; 4) (a3)8 = a3⋅8 = a24
20. Виконайте множення: 1) p(x – 2) = p ⋅ x – p ⋅ 2 = px 2p
2) –c(m – 4) = c ⋅ m + c ⋅ 4 = cm + 4c
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
3) x(c – 3 – d) = x ⋅ c – x ⋅ 3 – x ⋅ d = xc 3x xd
21. Виконайте множення:
1) t(3 – c) = t ⋅ 3 – t ⋅ c = 3t tc
2) – x(p – 2) = x ⋅ p + x ⋅ 2 = xp + 2x
3) a(t – b – 9) = a ⋅ t – a ⋅ b – a ⋅ 9 = at – ab 9a
22. Знайдіть значення виразу:
1) (–3)4 = 34 = 3 ⋅ 3 ⋅ 3 ⋅ 3 = 81
2) (–6)3 = -63 = -(6 ⋅ 6 ⋅ 6) = -216
3) 0,1 ⋅ 103 = 10-1 ⋅ 103 = 102 = 100
4) (2,6 – 2,7)2 = (-0,1)2 = � 1 10�2 = 1 100 = 0,01
23. Знайдіть значення виразу:
1) (–2)4 = 24 = 2 ⋅ 2 ⋅ 2 ⋅ 2 = 16
2) (–5)3 = -53 = -(5 ⋅ 5 ⋅ 5) = -125
3) 0,2 ⋅ 53 = 5-1 ⋅ 53 = 52 = 25
4) (1,5 – 1,8)2 = (-0,3)2 = � 3 10�2 = 9 100 = 0,09
24. Перетворіть вираз на многочлен:
1) 4a2(3 – a) = 4a2 ⋅ 3 4a2 ⋅ a = 12a2 4a3
2) 7(x – 2) – 2(x – 7) = 7x – 14 2x + 14 = 5x
3) (x – 5)(x + 3) = x2 + 3x 5x – 15 = x2 2x 15
4) – 5c2(8 – c3 + c) = 5c2 ⋅ 8 + 5c2 ⋅ c3 5c2 ⋅ c = 40c2 + 5c5 5c3
5) 4(2x – 3) – (8x – 9) = 8x 12 8x + 9 = 3
6) (2b – a)(a + b) = 2b ⋅ a + 2b ⋅ b – a ⋅ a – a ⋅ b = 2ab + 2b2 a2 – ab = ab + 2b2 a2
25. Перетворіть на многочлен вираз:
1) 7b2(b – 3) = 7b2 ⋅ b 7b2 ⋅ 3 = 7b3 21b2
2) 4(b – 3) – 2(2b + 1) = 4b – 12 4b – 2 = 14
3) (m + 2)(m – 4) = m2 4m + 2m – 8 = m2 2m 8
4) –2x3(4 – x2 + x) = 2x3 ⋅ 4 + 2x3 ⋅ x2 2x3 ⋅ x = 8x3 + 2x5 2x4
5) 3(2c – 6) – (5c – 18) = 6c – 18 5c + 18 = c 6) (3x + y)(x – y) = 3x ⋅ x 3x ⋅ y + y ⋅ x – y ⋅ y = 3x2 3xy + xy y2 = 3x2 2xy y2
26. Подайте у вигляді многочлена:
1) (b – 6)2 = (b 6)(b 6) = b2 12b + 36
2) (7x + 2)2 = (7x + 2)(7x + 2) = 49x2 + 28x + 4
3) (4a – 1)2 – 16a2 = (16a2 8a + 1) 16a2 = 8a + 1
4) (p – 3)(p + 3) = p2 9
5) (7 + x)(x – 7) = 7x – 49 + x2 7x = x2 49 6) (2y – 3)(2y + 3) + 9 = 4y2 – 9 + 9 = 4y2
27. Подайте у вигляді многочлена:
1) (с + 5)2 = (c + 5)(c + 5) = c2 + 10c + 25
2) (8b – 3)2 = (8b 3)(8b 3) = 64b2 48b + 9
3) (4x + 3)2 – 9 = (16x2 + 24x + 9) – 9 = 16x2 + 24x
4) (c + 2)(c – 2) = c2 4
5) (m – 9)(9 + m) = (m 9)(m + 9) = m2 81
6) (5p – 2)(5p + 2) – 25p2 = (25p2 4) 25p2 = 4
28. Розкладіть на множники:
1) 4a + 12b = 4(a + 3b)
2) 15ac – 20a = 5a(3c 4)
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
3) a(c – x) + 9c – 9x = a(c x) + 9(c x) = (c x)(a + 9)
4) –7c2 – 21c5 = 7c2(1 + 3c3)
5) a3 + a7 – a5 = a3(1 + a4 a2) = a3(1 + a2(a2 1))
6) 5a + 5b – ay – yb = 5(a + b) y(a + b) = (a + b)(5 y)
29. Розкладіть на множники:
1) 9x – 18y = 9(x 2y)
2) 4 xm + 6m = 2m(2x + 3)
3) m(x – p) + 3x – 3p = m(x p) + 3(x p) = (x p)(m + 3)
4) –2x3 – 8x5 = 2x3(1 + 4x2)
5) b2 – b5 + b3 = b2(1 b3 + b) = b2(b b3 + 1)
6) 7 c + 7n – cx – xn = 7(c + n) x(c + n) = (c + n)(7 x)
30. Знайдіть
1) 256 : 27 ⋅ 8 = 256 ∙ 1 27 ∙ 8
256 = 28, отже: 28 : 27 ⋅ 8 = 28-7 ⋅ 8 = 2 ⋅ 8 = 16
3) 0,59 ⋅ 29 = �12�9
1) (x2 – 3x)(x + 1) – x2(x – 2) = 3x (x2 3x)(x + 1) = x2(x + 1) 3x(x + 1) = x3 + x2 3x2 3x =
(x3 2x2 3x) (x3 2x2) = x3 2x2 3x
+
=
–
2) (2a – 3)2 – (4a – 1) (a + 3) = 23a + 12 (2a 3)2 = (2a 3)(2a 3) = 4a2 12a + 9 (4a 1)(a + 3) = 4a(a + 3) 1(a + 3) = 4a2 + 12a – a – 3 = 4a2 + 11a – 3
(4a2 12a + 9) (4a2 + 11a 3) = 4a2 12a + 9 4a2 11a + 3= 23a + 12
33. Перетворіть на многочлен стандартного
1) m2(m + 3) – (m2 + 4m)(m – 1) = 4m m2(m + 3) = m3 + 3m2 (m2 + 4m)(m 1) = m2(m 1) + 4m(m 1) = m3 m2 + 4m2 4m = m3 + 3m2 4m (m3 + 3m2) (m3 + 3m2 4m) = m3 + 3m2 m3 3m2 + 4m = 4m 2) (9x – 1)(x + 3) – (3x – 2)2 = 38x 7 (9x 1)(x + 3) = 9x(x + 3) 1(x + 3) = 9x2 + 27x – x – 3 = 9x2 + 26x – 3 (3x 2)2 = (3x 2)(3x 2) = 9x2 6x 6x + 4 = 9x2 12x + 4 (9x2 + 26x 3) (9x2 12x + 4) = 9x2 + 26x – 3 9x2 + 12x – 4 = 38x – 7
(9x – 1)(4x + 2) – (6x – 7)(6x + 7)
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
(9x 1)(4x + 2) = 9x(4x + 2) 1(4x + 2) = 9x ⋅ 4x + 9x ⋅ 2 – 1 ⋅ 4x – 1 ⋅ 2 = 36x2 + 18x 4x – 2 = 36x2 + 14x – 2
(6x 7)(6x +7) = 6x(6x + 7) 7(6x + 7) = 6x ⋅ 6x + 6x ⋅ 7 – 7 ⋅ 6x – 7 ⋅ 7 = 36x2 + 42x 42x –49 = 36x2 – 49
(36x2 + 14x 2) (36x2 49)
36x2 + 14x – 2 36x2 + 49 = 14x + 47
14(−3) + 47 = 42 + 47 = 5
Відповідь:
= 16a2 – 9 (8a 7)(2a
= 16a2 22a + 7
(16a2 9) (16a2 22a + 7)
– 9
+ 22a
1) 6a3 – 2a2 – 12a = 2a(a 1)(3a + 2)
2) x5 – 3x3 – 2x2 + 6 = (x2 3)(x3 2)
3) –4x2 + 20x – 25 = (2x 5)2
4) 0,36p8 – c10x12 = 0,36 �р8 с10 х12 �
5) 64m3c9 + t30
вийде.
6) c2 + 2cd + d2 – 25 = (c + d 5)(c + d + 5)
37.
1) 8p4 – 4p5 + 12p = 4p(2p3 p4 + 3)
2) a5 – 2a2 – 3a3 + 6 = (a2 3)(a3 2)
3) –9m2 – 6m – 1
Не існує простого
4) 0,49m4 – t16p2 = 0,49(m4 t16p2)
5) 125a6 – b9 = (5a3)2 і b9 = (b4,5)2
6) a2 – 2ax + x2 – 36 = (a – x 6)(a – x + 6)
38. Розв’яжіть рівняння:
1) 4x2 – x = 0
х(4х – 1) = 0
х = 0 або 4х – 1 = 0
х = 0 х = 1 4
2) 25x2 + 10x + 1 = 0
(5х + 1)2 = 0
5х + 1 = 0
5х = -1
х = 1 5 = 0,2
3) (x – 1)2 – 4 = 0
(х – 1 – 2)(х – 1 + 2) = 0
(х – 3)(х + 1) = 0
х – 3 = 0 або х + 1 = 0
х = 3 х + 1 = 0
х = 3 х = -1
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
39. Розв’яжіть рівняння: 1) 2x2 + x = 0
х(2х + 1) = 0
х = 0 або 2х + 1 = 0
х = 0 х = − 1 2 = −0,5
40.
2) 36x2 – 12x + 1 = 0
(6х – 1)2 = 0
6х – 1 = 0
6х = 1 х = 1 6
12) + n є непарним числом. (2n 3)(5n 1) = 10n2 2n 15n + 3 = 10n2 17n + 3
2n(5n 12) = 10n2 24n (10n2 17n + 3) (10n2 24n) + n
10n2 17n + 3 10n2 + 24n + n (10n2 10n2) + (−17n + 24n + n) + 3 = 8n + 3 Для будь-якого натурального nnn вираз 8n + 3 є непарним
3) (x + 2)2 – 9 = 0
(х + 2 – 3)(х + 2 + 3) = 0
(х – 1)(х + 5) = 0
х – 1 = 0 або х + 5 = 0
х = 1 х = -5
. 41. Доведіть, що якщо m – натуральне число, то
(3m + 2)(4m – 1) – 2m(6m – 7) + m є парним числом. (3m + 2)(4m 1) = 12m2 3m + 8m – 2 = 12m2 + 5m – 2 2m(6m 7) = 12m2 14m (12m2 + 5m 2) (12m2 14m) + m 12m2 + 5m – 2 12m2 + 14m + m (12m2 12m2) + (5m + 14m + m) – 2 = 20m – 2 Для будь-якого натурального mmm
20m 2
42. Виконайте множення (m2 – 2m + 3)(m2 + m – 5). (m2 – 2m + 3)(m2 + m – 5) = m2 ⋅ (m2 + m – 5) – 2m ⋅ (m2 + m –
–
+
– 15 43. Відомо, що 2xy2 = 5. Знайдіть
1) xy2 = 2�������� 2 2 = 5 2 = 2,5
3) –4x2y4 = (2���� ���� 2 )2 = (5)2 = 25 4) 8x3y6 = (2���� ���� 2 )3 = (5)3 = 125
Відомо, що 5ab2 = 7.
125a3b6 = (5�������� 2 )3 = (7)3 = 343
1) m = 2p – 9;
2) 4x – 9 = 9
3) у = 2х х 3
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
4) 36 : 9 – 4 = 0; не є функцією
5) c = n2 – n3; функція
Незалежна змінна (аргумент): n
Залежна змінна: c
6) 2 x – 9 > 3; не є функцією
46. (Усно.) Чи є лінійною функція:
1) у = 2х2; Не є лінійною, оскільки містить x2,
2) y = 2x; Лінійна функція.
3) y = 2; Лінійна функція.
x.
4) у = 1 2х 3; Не є лінійною, оскільки змінна x знаходиться в знаменнику.
5) y = 2x – 3; Лінійна функція.
6) y = 2x2 – 3; Не є лінійною, оскільки містить x2.
47. Функцію задано формулою y = 3 – 2x. Знайдіть:
1) значення функції, якщо значення аргументу дорівнює –4; 1,5;
Якщо х = -4, то:
y = 3 2(−4) = 3 + 8 = 11
Якщо х = 1,5, то:
y = 3 2(1,5) = 3 – 3 = 0
2) значення аргументу, якщо значення функції дорівнює –7; 5.
Якщо у = -7, то:
7 = 3 2x
7 – 3 = 2x
10 = 2x
x = 5
Якщо у = 5, то:
5 = 3 2x
5 – 3 = 2x
2 = 2x
x = 1
48. Функцію задано формулою y = 4x – 5. Знайдіть:
1) значення функції, якщо значення аргументу дорівнює –1,5; 6;
Якщо х = -1,5, то: y = 4(−1,5) – 5 = 6 – 5 = 11
Якщо х = 6, то: y = 4(6) – 5 = 24 – 5 = 19
2) значення аргументу, якщо значення функції дорівнює –9; 1.
Якщо у = -9, то:
9 = 4x 5
9 + 5 = 4x
4 = 4x
x = 1
Якщо у = 1, то:
1 = 4x 5
1 + 5 = 4x
6 = 4x
x = 6 : 4 = 1,5
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
1) у = 3х – 6, усі числа
D(y) = (−∞; +∞)
3) у = 5
3х 6, усі числа, крім х = 2
D(y) = (−∞; 2) ∪ (2; +∞)
50. Знайдіть область визначення функції:
1) у = 2х + 4, усі числа
D(y) = (−∞; +∞)
3) у = 7 2х+4, усі числа, крім х = 2
2) у = 3х 6 5 , усі числа
D(y) = (−∞; +∞)
4) у = 7 х+6, усі числа, крім х = 6
D(y) = (−∞; 6) ∪ (−6; +∞)
2) у = 2х+4 7 , усі числа
D(y) = (−∞; +∞)
D(y) = (−∞; 2) ∪ (−2; +∞) 4) у = 9 х 4,
51. Не виконуючи побудови
1) у = 7х
0 = 7x x =
числа, крім х = 4
= (−∞; 4) ∪ (4; +∞)
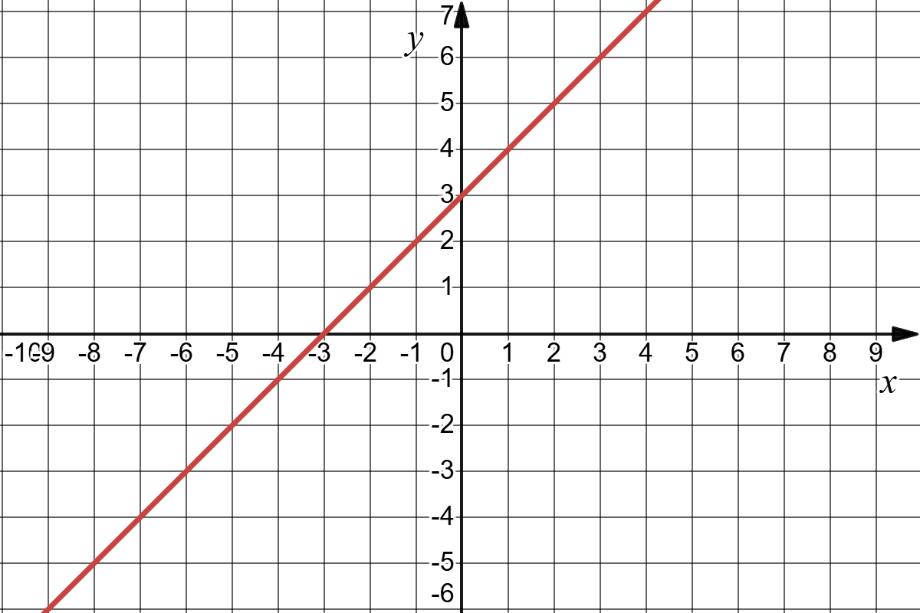

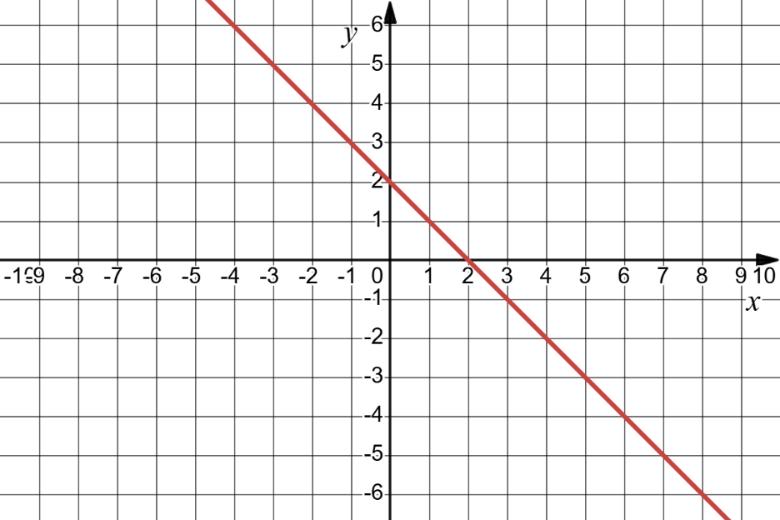
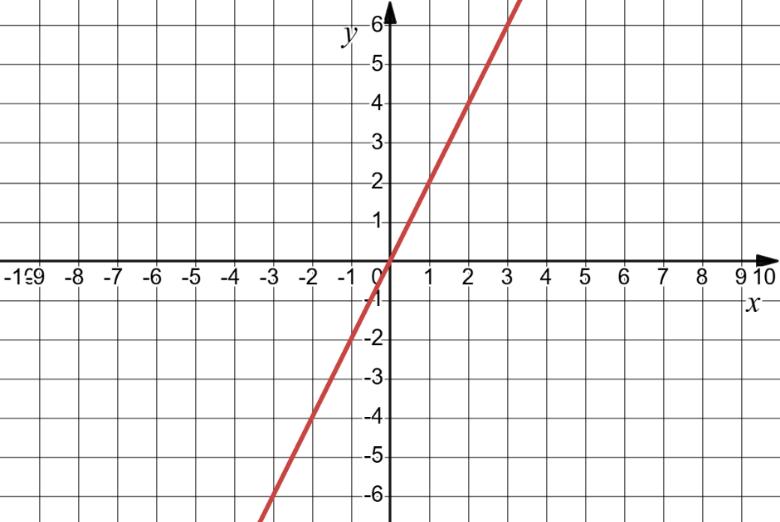
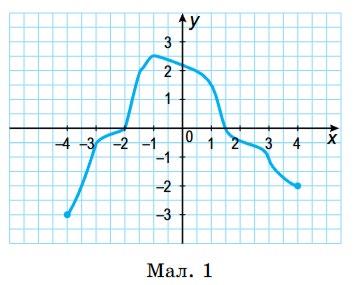
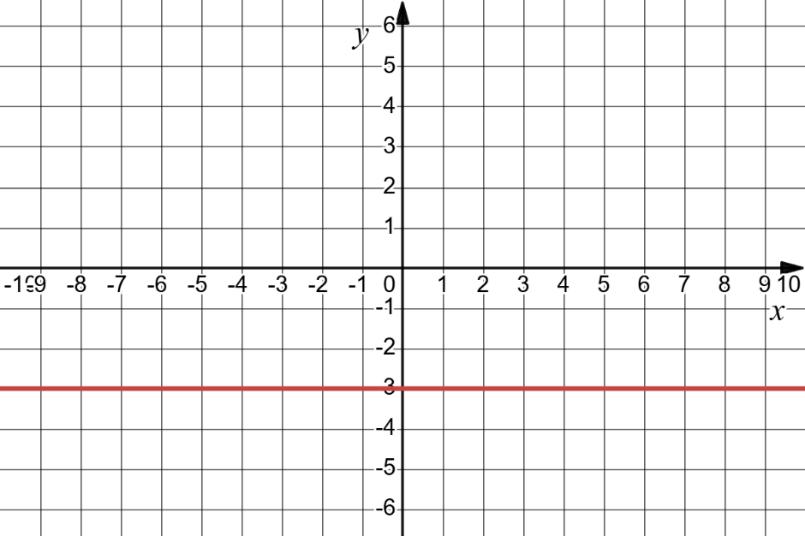
1) значення y, якщо x = –3,5; –1; 0,5;
Якщо x = –3,5, то y ≈ -2.
Якщо x = –1, то y ≈ 2,5.
Якщо x = 0,5, то y ≈ 2.
2) значення x, якщо y = –0,5; 2; 2,5;
Якщо y = –0,5, x ≈ -3 та x ≈ 2
Якщо y = 2, x ≈ -1,5 та x ≈ 1.
Якщо y = 2,5, x ≈ -1.
3) нулі функції; Нулі функції
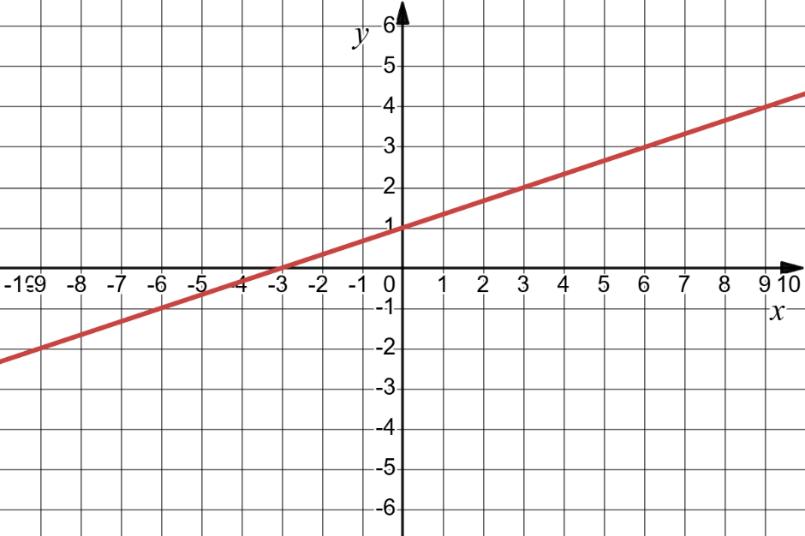

https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
-4 ≤ x < -3, -0,5 < x < 2.
інтервалах x ∈ (–4; –2) та x ∈ (1,5; -2).
56. На
знайдіть:

1) значення y, якщо x = –1; –0,5; 2,5; Якщо x = –1, y ≈ 0.
Якщо x = –0,5, y ≈ –1.
Якщо x = 2,5, y ≈ –2,5.
2) значення x, якщо y = –3; –2; 1; Коли y = –3, x ≈ 2.
Коли y = –2, x ≈ 3.
Коли y = 1, x ≈ –2 та x ≈ 4.
3) нулі функції; x ≈ –1, x ≈ 3,5.
4) значення аргументу, для яких
На інтервалах x ∈ (–3; –1) та x ∈ (3,5; 5).
5) значення аргументу, для яких функція
На інтервалах x ∈ (–1; 3,5).
57. Не виконуючи побудови, знайдіть
графіка функції:
1) y = 0,5x – 4
Щоб знайти точку
0 = 0,5x – 4
0,5x = 4
х = 4
0,5 = 8
Отже, точка перетину з
Щоб знайти
4 = 4
точка
2) y = 16 – x2
0 = 16 x2
x2 = 16
x = ±4
y = 16 (0)2 = 16 Отже, точка
x це (8, 0).
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
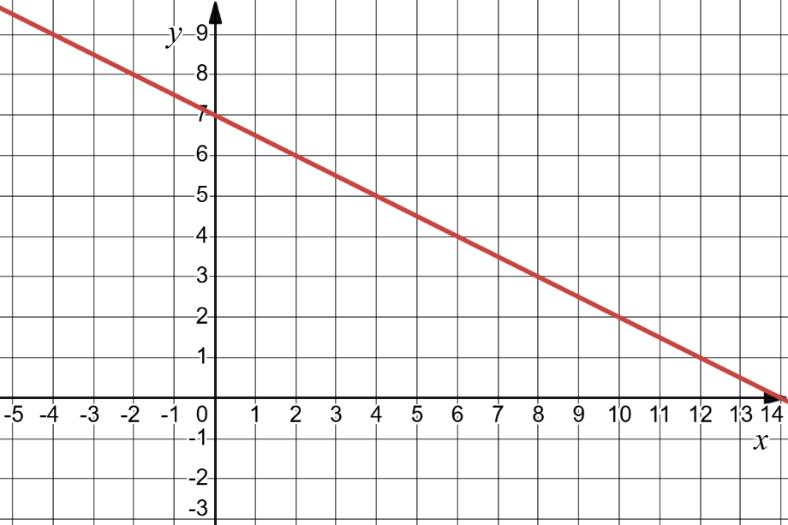
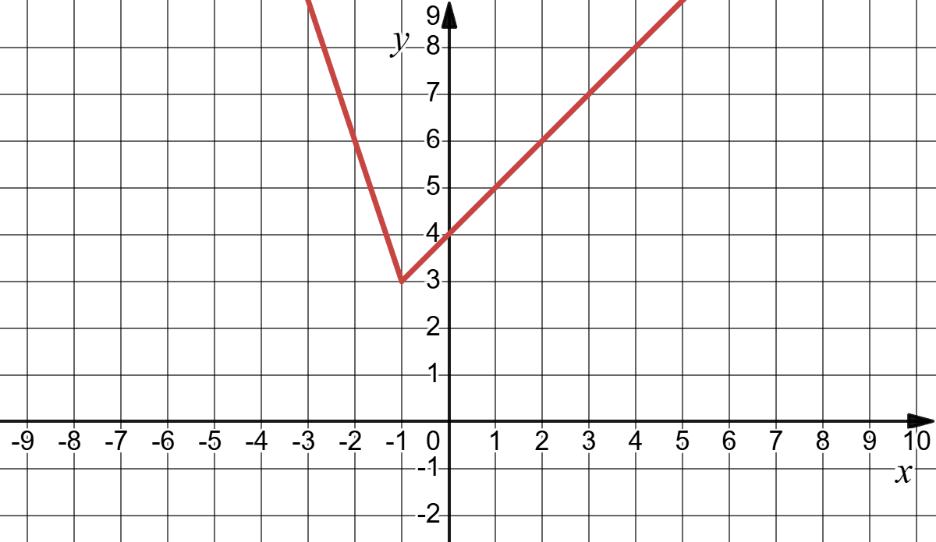
1) y = 3 – 2x
0 = 3 2x
2x = 3
х = 3 2
Отже, точка перетину з віссю x це (3 2, 0).
Щоб знайти точку
y = 3 2(0) = 3
Отже, точка
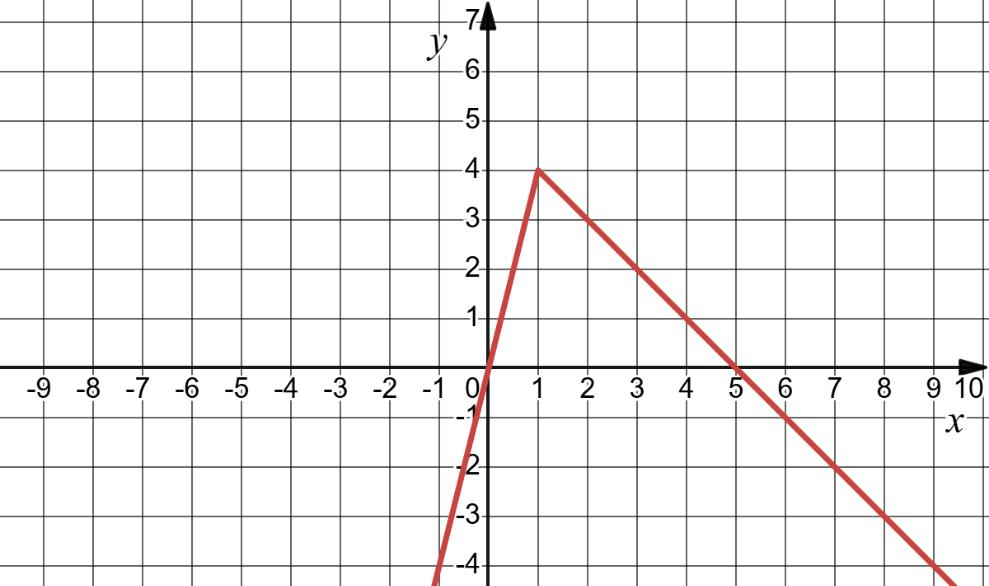
з віссю y це (0, 3). 2) y = x2 + 2x
Щоб знайти точку перетину
0 = x2 + 2x
x(x + 2) = 0
Отже, x = 0 або x = 2.
Точки перетину з віссю x це (0, 0) і (−2, 0).
Щоб знайти точку
y = (0)2 + 2(0) = 0
61. (Усно.)
1) (6; 1); - належить.
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
2) (8; –2); - не належить.
3) (1; –6); - не належить. 4) (3; 4); - належить.
62. (Усно.) Чи є розв’язком
1) (4; 3); - не є розв’язком 2) (3; 2); - є розв’язком 3) (4; 1); - не є розв’язком
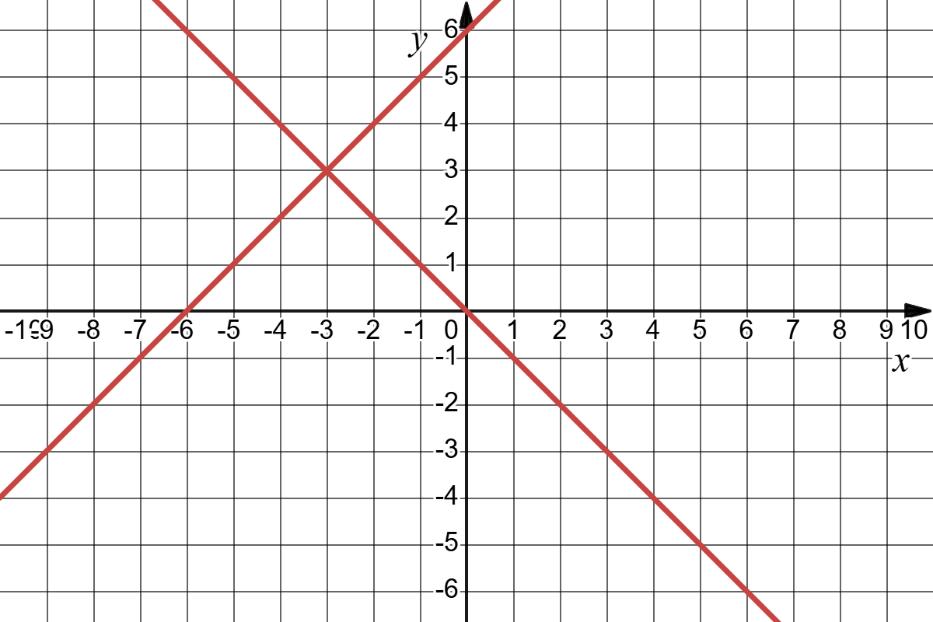
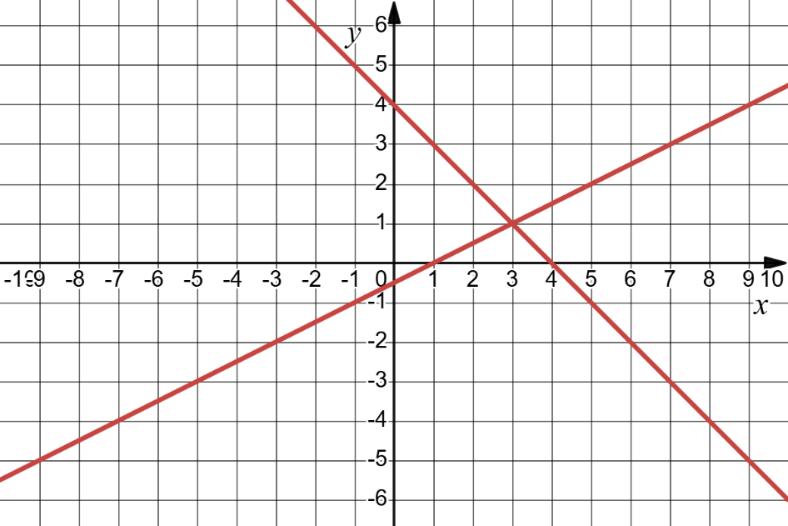
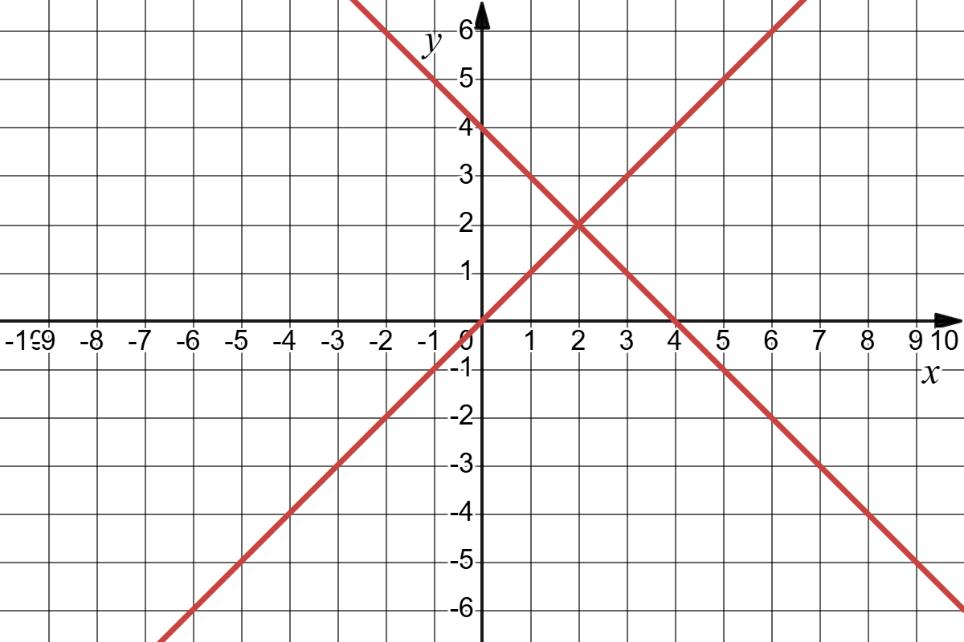
63. Побудуйте графік рівняння: 1) x – y = 4;


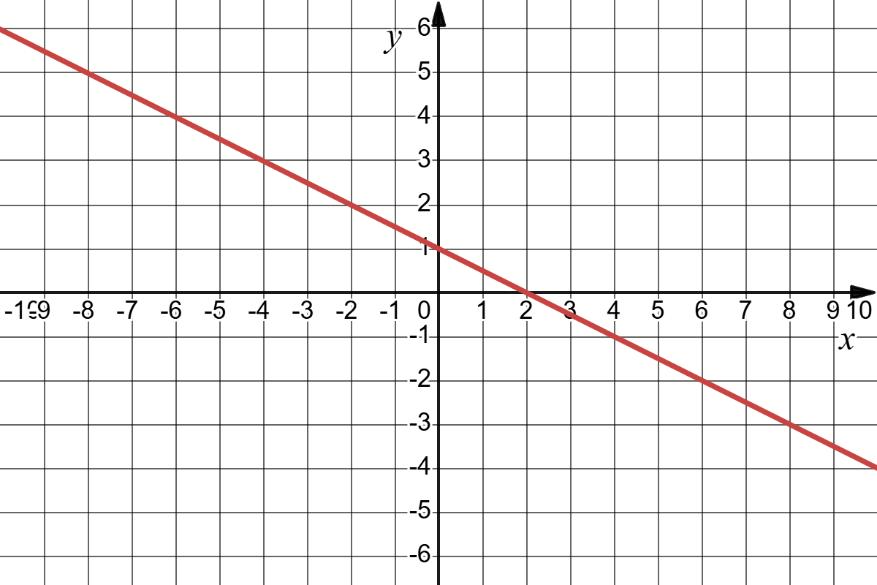
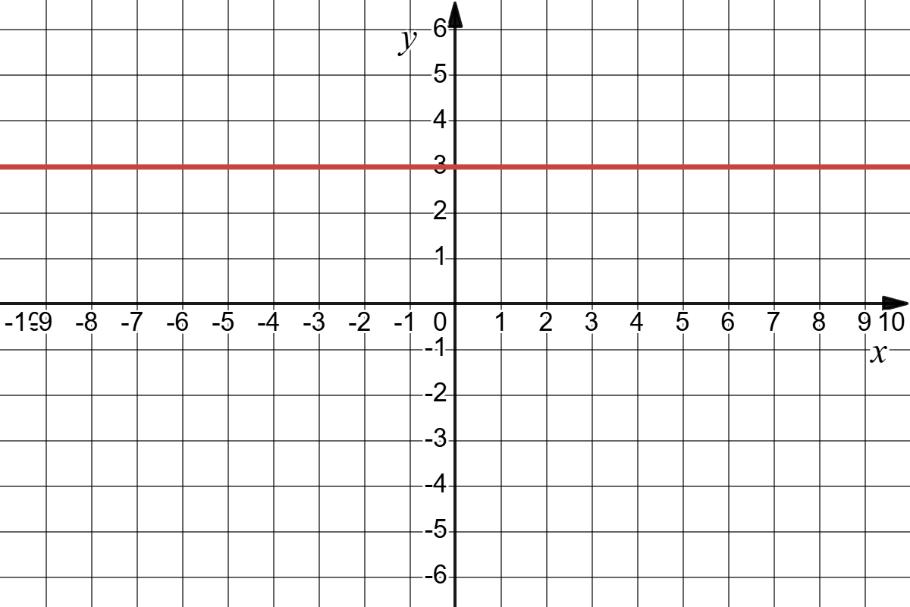
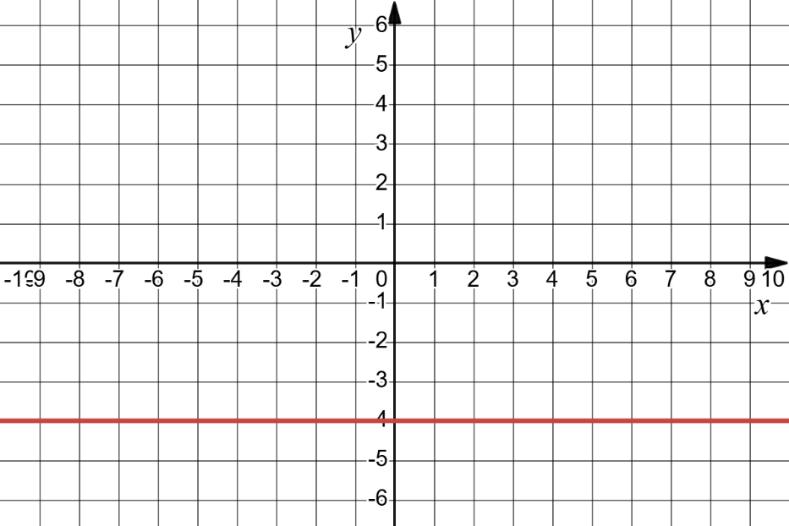
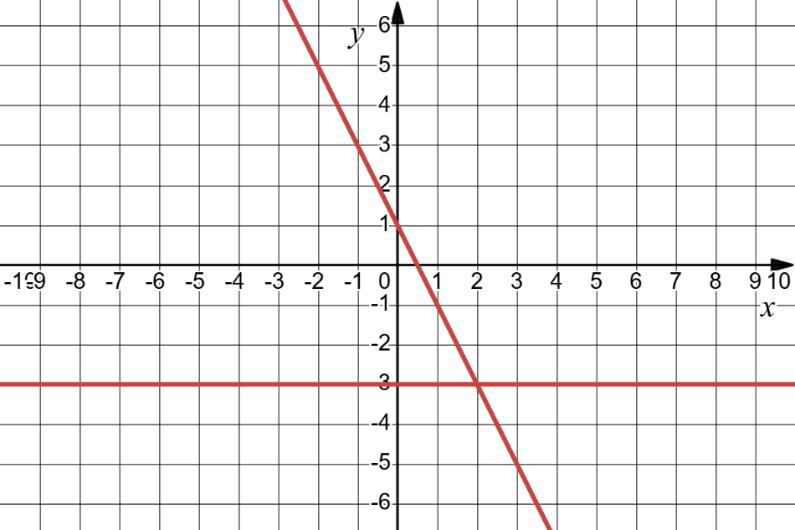
x + y = 3; 2) x – 0,5y = 2;
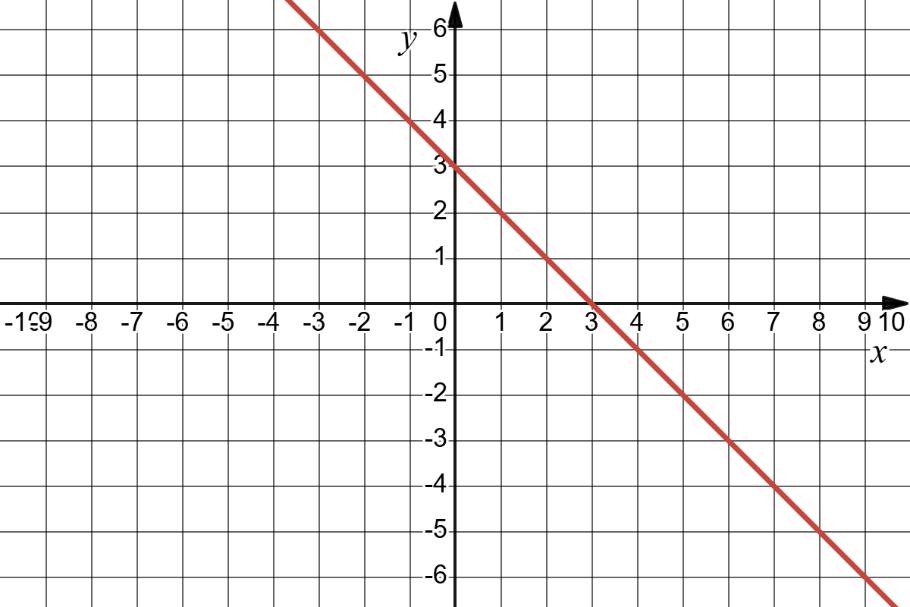

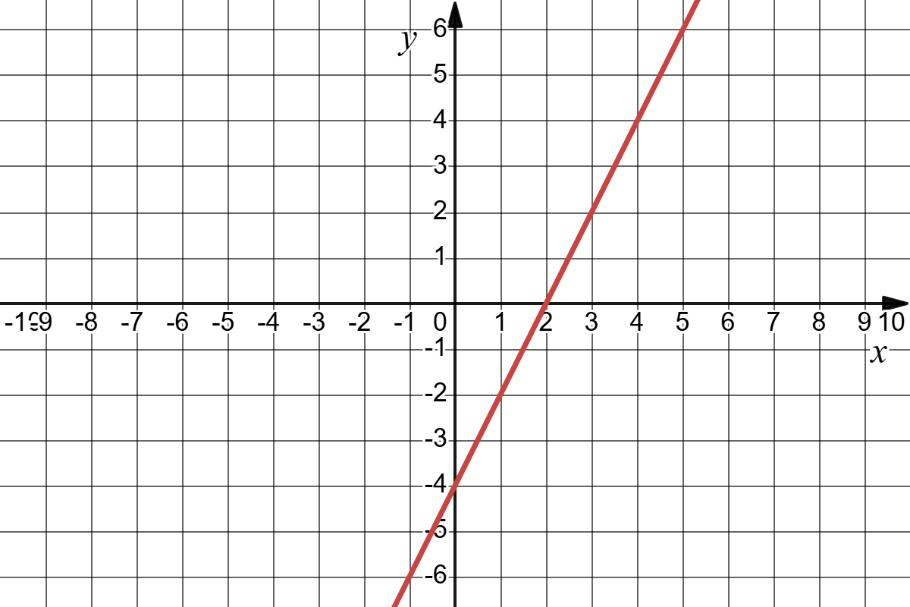
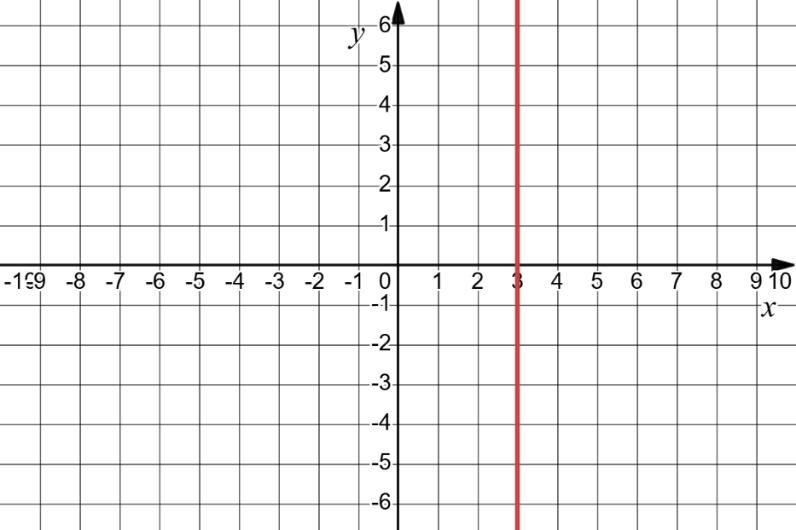



1) � 3���� = 12,
2���� + 3���� = 2;
х = 12 : 3 = 4
2(4) + 3y = 2
8 + 3y = 2
3y = 6 y = 2
Відповідь: (4; -2)
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
2) � ���� = ���� 2, 4���� 3���� = 5; 4(y 2) 3y = 5
4y – 8 3y = 5
y – 8 = 5 y = 3 x = 3 – 2 = 1
Відповідь: (1; 3)
68. Розв’яжіть способом підстановки систему рівнянь:
1) � 4���� = 8,
5���� + 2���� = 1;
у = (-8) : 4 = -2
5x + 2(−2) = 1
5x – 4 = 1
5x = 5
x = 1
Відповідь: (1; -2)
69. Розв’яжіть
1) � 3���� + ���� = 2, 2���� ���� = 3;
(3x + y) + (2x y) = 2 + 3
3x + 2x + y – y = 5
5x = 5
x = 1
3(1) + y = 2
3 + y = 2
y = 1
Відповідь: (1; -1)
2) � ���� = ���� + 3, 2���� 3���� = 8; 2x 3(x + 3) = 8
2x 3x – 9 = 8
x – 9 = 8
x = 1
x = 1
y = 1 + 3 = 2
Відповідь: (-1; 2)
2) � 2���� + 3���� = 1, 2���� 4���� = 13; (2x + 3y) (2x 4y) = 1 (−13) 2x + 3y 2x + 4y = 1 + 13 7y = 14 y = 2 2x + 3(2) = 1 2x + 6 = 1 2 x = 5
х = 5 2
Відповідь: ( 5 2; 2)
70. Розв’яжіть способом додавання систему рівнянь:
1) � ���� + 3���� = 1, −���� + 4���� = 6; (x + 3y) + (−x + 4y) = 1 + 6
x – x + 3y + 4y = 7
7y = 7
y = 1
x + 3(1) = 1
x + 3 = 1
x = 2
Відповідь: (-2; 1)
2) � 3���� 5���� = 11, 4���� 5���� = 13; (4x 5y) (3x 5y) = 13 11
4x 3x 5y + 5y = 2
x = 2
3(2) 5y = 11
6 5y = 11
5y = 5
у = 1
Відповідь: (2; 1)
3) � 3���� + ���� = 3, 4���� + 5���� = 7. y = 3 3x 4x + 5(3 3x) = 7 4x + 15 15x = 7 11x + 15 = 7 11x = 22 x = 2 y = 3 3(2) = 3 – 6 = 3
Відповідь: (2; -3)
3) � ���� 2���� = 5, 3���� + 5���� = 4.
x = 2y + 5
3(2y + 5) + 5y = 4
6y + 15 + 5y = 4
11y + 15 = 4
11y = 11 y = 1
x = 2(−1) + 5 = 2 + 5 = 3
Відповідь: (3; -1)
3) �4���� 3���� = 11, 5���� + 9���� = 1. 12x 9y = 33 (12x 9y) + (5x + 9y) = 33 + 1 12x + 5x 9y + 9y = 34
17x = 34
x = 2
4(2) 3y = 11
8 3y = 11 3y = 3 y = 1
Відповідь: (2; -1)
3) �4���� 3���� = 15, 8���� + 5���� = 19.
8x 6y = 30
(8x 6y) (8x + 5y) = 30 19
8x 8x 6y 5y = 11
11y = 11
y = 1
4x 3(−1) = 15
4x + 3 = 15
4x = 12
x = 3
Відповідь: (3; -1)
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
2���� + ���� = 40
���� + 2���� = 44
4x + 2y = 80
(4x + 2y) (x + 2y) = 80 44
4x – x + 2y 2y = 36
3x = 36 x = 12
2(12) + y = 40
24 + y = 40 y = 16 Відповідь:
3���� + ���� = 44 ���� + 3���� = 68
3(x + 3y) = 3(68)
3x + 9y = 204
(3x + 9y) (3x + y) = 204 44
3x 3x + 9y – y = 160
8y = 160
y = 20
3x + 20 = 44
3x = 24
x = 8
Відповідь:
рівняння:
1) 2x – 3y = 24;
2x 3(0) = 24
2x = 24
x = 12
Точка: (12; 0)
2(0) 3y = 24
3y = 24
y = 8
Точка: (0; -8)
2) 0 x + 5y = 15; 5y = 15 y = 3
Точка: (0; 3)
3) –4 x = 12. 4x = 12 x = 3
Точка: (-3; 0)
рівняння:
1) 4x + 5y = 40;
4x + 5(0) = 40
4x = 40
x = 10
Точка: (10; 0)
4(0) + 5y = 40
5y = 40
y = 8
Точка: (0; 8)
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
2) 2x + 0y = –16; 2x = 16 x = 8
Точка: (-8; 0)
75. Розв’яжіть систему рівнянь:
1) � 2���� + 3���� = 0, 4���� 5���� = 22;
4a + 6b = 0
(4a + 6b) (4a 5b) = 0 (−22)
4a 4a + 6b + 5b = 22
11b = 22
b = 2
2a + 3(2) = 0
2a + 6 = 0
2a = 6
a = 3
a = 3, b = 2
3) � 3���� + 5���� = 9, 4���� 3���� = 17.
9x + 15y = 27
20x 15y = 85
(9x + 15y) + (20x 15y) = 27 + (−85)
9x + 20x = 58
29x = 58
x = 2
3(−2) + 5y = 9
6 + 5y = 9
5y = 15
y = 3
x = 2, y = 3
3) 3y = 6. y = 2
Точка: (0; 2)
2) � 4���� 5���� = 1, 3���� + 10���� = 42; 8x 10y = 2
(8x 10y) + (3x + 10y) = 2 + 42
8x + 3x = 44 11x = 44
x = 4
4(4) 5y = 1 16 5y = 1 5y = 15
y = 3
x = 4, y = 3
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
1) � 2���� 3���� = 7,
5���� + 6���� = 4; 4m 6n = 14
15m + 18n = 12
(4m 6n) + (15m + 18n) = 14 + 12
4m + 15m = 26
19m = 26
m = 26 19
2 �26 19� − 3���� = 7 52 19 − 3���� = 7
3���� = 7 52 19
3���� = 133 19 52 19
3���� = 81 19 ���� = 27 19 m = 26 19; n = 27 19
3) � 4���� + 7���� = 5, 5���� − 3���� = 18.
12x + 21y = 15
35x 21y = 126
(12x + 21y) + (35x 21y) = 15 + 126
12x + 35x = 141
47x = 141
x = 3
4(3) + 7y = 5
12 + 7y = 5
7y = 7
y = 1
x = 3, y = 1
1) (vb + vt) ⋅ 2 + (vb vt) ⋅ 3 = 88
2vb + 2vt + 3vb 3vt = 88
(2vb + 3vb) + (2vt 3vt) = 88
5vb – vt = 88
2) (vb + vt) ⋅ 4 = (vb vt) ⋅ 5
4vb + 4vt = 5vb 5vt
4vb 5vb = 5vt 4vt
vb = 9vt
vb = 9vt
3) 5(9vt) – vt = 88
2) � 2���� 3���� = 6, 8���� + 5���� = 24; 10x 15y = 30
24x + 15y = 72 (10x 15y) + (24x + 15y) = 30 + 72 10x + 24x = 102 34x = 102 x = 3
2(3) 3y = 6 6 3y = 6 3y = 0 y = 0
x = 3, y = 0
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
45vt – vt = 88
44vt = 88
vt = 2км/год
4) vb = 9 ⋅ 2 = 18км/год
78. Складіть рівняння
���� = 5 11 2 ( 1) = 6 3 = 2
y – 11 = 2(x (−1))
y – 11 = 2(x + 1)
y – 11 = 2x 2
y = 2x + 9
79. Графік
���� = 23 2 4 ( 3) = 21 7
y – 2 = 3(x (−3))
y – 2 = 3(x + 3)
y – 2 = 3x + 9
y = 3x + 11
80. За
1) 4x + 3y = 195
1,1x + 0,8y = 53
2) 11x + 8y = 530
3) 8(4x + 3y) = 8(195) ⇒ 32x + 24y = 1560
3(11x + 8y) = 3(530) ⇒ 33x + 24y = 1590
(33x + 24y) (32x + 24y) = 1590 1560 x = 30
4) 4(30) + 3y = 195
120 + 3y = 195
3y = 195 120
3y = 75 y = 25 Відповідь:
1), 3), 4), 6), 7)
2), 5), 8) –
a3 − ab; ���� 17; 17 ���� ; t(t − 1) + ���� ���� ; 1 9 a 1 8 b; 7 ���� 2 + 1 − 5;
6)
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
4) x ≠ 0; x ≠ −2;
5) y ≠ 1; y ≠ −6;
6) будь-яке значення m.
1.9. За t
(у км/год).
v = 240 ���� , t (год).
Якщо t = 3 год, то v = 240 3 = 80 км/год;
якщо t = 4 год, то v = 240 4 = 60 км/год.
Відповідь: 80 км/год; 60 км/год.
1.10. Пенсіонерка
1.11.
1) −2; 2) 9; 3) 0,01; 4) −4,9?
1) ���� + 2
8 = 2; x + 2 = −16; x = −18;
2)
+ 2 8 = 9; x + 2 = 72; x = 70; 3)
+ 2 8 = 0,01; x + 2 = 0,08; x = −1,92; 4)
+ 2 8 = 4,9; x + 2 = −39,2; x = −41,2.
1.12. Для якого
1) −8; 2) 0,25?
1) ���� 1 10 = 8; m – 1 = −80; m = −79; 2) ���� 1 10 = 0,25; m – 1 = 2,5; m = 3,5.
1.13. Для якого значення x дорівнює
1) 4���� 8 ���� = 0; �4���� – 8 = 0, ���� ≠ 0; � ���� = 2, ���� ≠ 0; 2) (���� 1)(���� + 7) ���� + 5 = 0; � ���� – 1 = 0, ���� + 7 = 0, ���� + 5 ≠ 0; � ���� = 1, ���� = – 7, ���� ≠ – 5; 3) ���� (���� + 3) ���� 2 = 0; ����� + 3 = 0, ���� ≠ 0; ����� = – 3,
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
3) (���� + 2)(���� 3) ���� + 4 = 0; � ���� + 2 = 0, ���� – 3 = 0, ���� + 4 ≠ 0; � ���� = – 2, ���� = 3, ���� ≠ – 4;
4) ���� + 1 5���� + 5 = 0; � ���� + 1 = 0, 5���� + 5 ≠ 0; ����� = – 1, ���� ≠ – 1. Розв’язків немає.
Відповідь: 1) y = 0; y ≠ 7 5; 2) y = –1; y ≠ 0;
3) y = –2; y = 3; y ≠ –4; 4) розв’язків немає.
1.15. Знайдіть допустимі
1) ���� + 1 (���� 1)(2���� + 7); (a – 1)(2a + 7) ≠ 0; a – 1 ≠ 0 або 2a + 7 ≠ 0; 2a ≠ –7, a ≠ –3,5.
Відповідь: a – будь-яке, крім 1 і –3,5. 2) ���� + 2 ���� 2 7���� ; t2 – 7t ≠ 0; t(t – 7) ≠ 0; t ≠ 0 або t – 7 ≠ 0 t ≠ 7. Відповідь: t – будь-яке, крім 0 і 7.
3) ���� ����2 25; m2 – 25 ≠ 0;
(m – 5)(m + 5) ≠ 0; m – 5 ≠ 0 або m + 5 ≠ 0 m ≠ 5 m ≠ – 5.
Відповідь: m – будь-яке, крім 5 і –5. 4) 5 (���� 9)2 ; (x – 9)2 ≠ 0; x – 9 ≠ 0; x ≠ 9.
1.16. Знайдіть
1) ���� 7 (9 ����)(4���� + 10); (9 – p)(4p + 10); 9 – p ≠ 0 або 4p + 10 ≠ 0, p ≠ 9 4p ≠ –10 p ≠ –2,5
Відповідь: p – будь-яке, крім 9 і –2,5.
3) ���� 4 ���� 2 ; 4 – с2 ≠ 0; (2 – c)(2 + c) ≠ 0; 2 – c ≠ 0 або 2 + c ≠ 0; c ≠ 2 c ≠ –2.
Відповідь: c –
1)
-яке,
Відповідь: x – будь-яке, крім 9.
2) ���� + 2 5���� ����2 ; 5a – a2 ≠ 0; a(5 – a) ≠ 0; a ≠ 0 або 5 – a ≠ 0 a ≠ 5.
Відповідь: a – будь-яке, крім 0 і 5.
2 і –2. 4) ���� (���� + 1)2 ; (a + 1)2 ≠ 0; a + 1 ≠ 0; a ≠ –1.
Відповідь: a – будь-яке, крім –1.
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
2| ≠ 4, |���� – 2| ≠ – 4; � ���� ≠ 6, ���� ≠ – 2.
Відповідь: 1) a ≠ 2; a ≠ 3; 2) x ≠ ±1; 3) m ≠ 1; m ≠ 0; 4) k ≠ 6; k ≠ –2. 1.19. Знайдіть область визначення виразу:
1) x(x + 2) − 4x − 8 ≠ 0; x(x + 2) − 4(x + 2) ≠ 0; (x + 2)(x − 4) ≠ 0; � ���� + 2 ≠ 0, ���� − 4 ≠ 0; ����� ≠ 2, ���� ≠ 4; 2) 4 − |m| ≠ 0; |m| ≠ 4; m ≠ ±4; 3) 1 ���� + 1 ≠ 0; 1 + ���� ���� ≠ 0; �1 + ���� ≠ 0, ���� ≠ 0; ����� ≠ – 1, ���� ≠ 0; 4) |a + 2| − 3 ≠ 0; |a + 2| ≠ 3; � ���� + 2 ≠ 3, ���� + 2 ≠ 3; � ���� ≠ 1, ���� ≠ – 5; Відповідь: 1) x ≠ −2; x ≠ 4; 2) m ≠ ±4; 3) x ≠ −1; x ≠ 0; 4) a ≠ 1; a ≠ −5. 1.20. Визначте знак дробу:
1) Додатні, так як x > 0, то x7 > 0; y < 0, то y8 > 0; 2) m + 1 > 0, так як m > 0; n < 0, то n7 < 0, то знак дробу від’ємний; 3) p < 0, то |p − 1| > 0; якщо n > 0, то n19 > 0, знак дробу додатній; 4) якщо a < 0, то |a| + 1 > 0; якщо с < 0, то c8 > 0, знак дробу додатній.
Відповідь: 1) додатнє; 2) від’ємне;
1) 7 ����2 + 1, є додатним; 2) 4 ����2 2 є
недодатним.
1) Враховуючи, що a2 + 1 > 0 для будь-якого a, то значення
3) Враховуючи, що a2 + 7 >
1) (a2 + 2a − 7) − (a2 − 4a − 9) = a2 + 2a − 7 − a2 + 4a + 9 = 6a + 2; 2) 3x2y(2x − 3y + 7) = 6x3y − 9x2y2 + 21x2y;
3) (x2 − 2x)(x + 9) = x3 + 9x2 – 2x2 – 18x = x3 + 7x2 − 18x;
4) (x2 − 5)2 + 10x2 = x4 − 10x2 + 25 + 10x2 = x4 + 25.
1.23. Розв’яжіть рівняння:
4x(2x − 7) + 3x(5 − 2x) = 2x2 + 39;
8x2 − 28x + 15x − 6x2 = 2x2 + 39; 2x2 − 13x = 2x2 + 39; −13x = 39;
x = −3. Відповідь: −3.
Зведіть дріб: 1) 1 8 до знаменника 24; 2) 2 7 до знаменника 28; 3) 4 15 до знаменника 30; 4) 8 9 до знаменника 63.
1) m3m4 = m3 + 4 = m7; 2) pp7 = p1 + 7 = p8; 3) x9 : x3 = x9 − 3 = x6;
4) (a3)7 = a3 · 7 = a21;
5) b2 · (b3)4 = b2 · b12 = b2 + 12 = b14; 6) (c4)5 : c12 = c20 : c12 = c20 − 12 = c8 . 1.27.
1) 2a2b · a = 2a3b;
2) 2a2b · b3 = 2a2b4; 3) 2a2b · 2a3 = 4a5b;
4) 2a2b · 8a2b2 = 16a4b3 .
1.28. Розкладіть на множники многочлен:
1) ab – b2 = b(a − b);
2) m7 + m5 = m5(m2 + 1);
3) 8m2 − 4mn = 4m(2m − n);
4) 6a3b + 15a2b2 = 3a2b(2a − 5b);
5) x2 + 6x + 9 = (x + 3)2; 6) c2 − 10c + 25 = (c − 5)2; 7) x2 − 25 = x2 − 52 = (x − 5)(x + 5);
8) p4 − 49m2 = (p2)2 − (7m)2 = (p2 − 7m)(p2 + 7m);
9) a2 + ab + 7a + 7b = (a2 + ab) + (7a + 7b) =
рівняння:
10x + y = xy + (x + y);
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
10x + y = xy + x + y; 9x − xy = 0; x(9 − y) = 0; x = 0 не є розв’язком задачі; 9 − y = 0; y = 9.
Тобто x може бути будь-яке число.
Маємо: 19; 29; 39; 49; 59; 69; 79; 89; 99.
Відповідь: 9.
2.1. (Усно.) Скоротіть дріб:
2.2.
a2 – ab = a(a – b), то
= 5����
(���� ����) = 5���� ����2 �������� ;
Оскільки m2 + 2mn + n2 = (m + n)2 , то 4 ���� + ���� = 4(���� + ����) (���� + ����)(���� + ����) = 4(���� + ����) (���� + ����)2 = 4���� + 4���� ����2 + 2�������� + ����2 ;
3) Оскільки x2 – y2 = (x – y)(x + y), то 9 ���� ���� = 9(���� + ���� ) (���� ���� )(���� + ���� ) = 9(���� + ���� ) ���� 2 ���� 2 ;
2.24. Знайдіть область визначення
1) y = ���� 2 + 6���� 6���� + 36 .Спростимо вираз: ���� 2 + 6����
6���� + 36 = ����(���� + 6) 6(���� + 6) = ���� 6
Тобто маємо y = ���� 6 – пряма, x ≠ −6. Якщо x = 6, то y = 1.
Відповідь: (−6; −1).
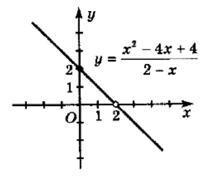
2) y = ���� 2 4���� + 4 2 ���� Спростимо вираз: ���� 2 4���� + 4
2 ���� = (���� 2)2 2 ���� = (2 ����)2 2 ���� = 2 x. Тобто маємо y = 2 – x, x ≠ 2. y = 2 – x x 2 0 y 0 2
Відповідь: (2; 0).


2.25. Знайдіть
1) y = ���� 2 5���� 25 5���� .
Спростимо вираз: ���� 2 5����
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
25 5���� = ���� (���� 5) 5(���� 5) = ���� 5 .
Тобто маємо y = ���� 5 , x ≠ 5.
Якщо x = 5, то y = −1.
Відповідь: (5; −1).
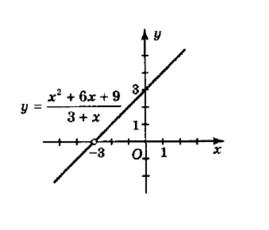
2) y = ���� 2 + 6���� + 9 3 + ����
Спростимо вираз: ���� 2 + 6���� + 9
3 + ���� = (���� + 3)2 ���� + 3 = x + 3.
Тобто маємо y = x + 3, x ≠ −3. y = x + 3 x 0 3 y 3 0
Відповідь: (−3; 0).
2.26. Обчисліть значення виразу:


1) 212 214 = 212 14 = 2 2 = 1 22 = 1 4 ; 2) 39 36 = 39 6 = 33 = 27;
3) 74 49 = 74 72 = 74 2 = 72 = 49; 4)
2.27. Розв’яжіть систему рівнянь:
.
1) ����� + 3���� = 2, | ∙ (– 3) 3���� 2���� = 17; � 3���� 9���� = 6, 3���� 2���� = 17; –11y = 11; y = –1, то маємо x – 3 = 2; x = 5; (5; −1).
2) � 3���� + 2���� = 2, 7���� 2���� = 22; 10���� = 20; ���� = 2, то маємо – 6 + 2y = 2; 2y = 8; y = 4; (−2; 4).
Відповідь: 1) (5; −1); 2) (−2; 4).
2.28. Спростіть вираз: 1) (2x + 3y)2 − (x + 7y)(4x − y) = 4x2 + 12xy + 9y2 − (4x2 − xy + 28xy − 7y2) = = 4x2 + 12xy + 9y2 − 4x2 + xy − 28xy + 7y2 = − 15xy + 16y²; 2) (m + 3)(m2 − 5) − m(m − 4)2 = m3 − 5
2.29. Обчисліть:
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
Нехай x – кількість міського населення, тоді x • (1 – 0,38375094) = = x • 0,61624906 – сільське населення.
1) x + x • 0,61624906 = 42 760 516
x • (1 + 0,61624906) = 42 760 516
x = 42 760 516 : 1,61624906
x ≈ 26 456 637 (ос.) – міського населення;
2) 42 760 516 – 26 456 637 = 16 303 879 (ос.) – сільського населення. Відповідь: міського населення – 26 456 637 осіб, сільського – 16 303 879 осіб.
2.31. Катер за течією
3.13.
3.22. Спростіть вираз:
3.23.
3.25.
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
1) 15a3b7 = 3ab5 · 5a2b2;
2) 15a3b7 = −5a2b7 · (−3a);
3) 15a3b7 = −b6 · (−15a3b);
4) 15a3b7 = 15ab · a2b6 . 3.27. 1)
7
1) Для того, щоб
2) Розглянемо суму (a1 – b1) + (a2 – b2) + (a3 – b3) + ... + (a7 – b7). Оскільки b1, b2, ..., b7 це числа a1, a2, ..., a7, які узято
нулю.
3) Припустимо, що всі числа a1 – b1, a2 – b2, ..., a7 – b7
припущення неправильне. 4)
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html

https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
Відповідь: Ні.
4.46. Скільки кілограмів солі міститься
5% від 60 = 0,05 · 60 = 3 (кг).
Відповідь: 3 кг солі.
4.47. З двох міст одночасно назустріч
між містами становить s км, швидкості велосипедисток
1)
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
2) 2660 : 900 : 1000 = 2394000 : 1000 = 2394 (м2)

1)
2)
x,
���� 2 16 |���� +1| 5;
1. |x + 1| – 5 = 0; |x + 1| = 5; x + 1 = –5 або x + 1 = 5;
x = –5 – 1 або x = 5 – 1;
x1 = –6, x2 = 4.
x будь-які, крім –6 і 4
2. ���� 2 16 |���� +1| 5 = 0; � ���� 2 16 = 0, |���� + 1| − 5 ≠ 0; �(���� 4)(���� + 4) = 0, ���� ≠ 6, ���� ≠ 4; ����� = 4 або ���� = 4, ���� ≠ 6, ���� ≠ 4.
Відповідь: 1) x будь-які, крім –6 і 4; 2)
Спростіть вираз 3(���� 2���� ) (���� 3)(���� 4) ���� 2 6���� (3 ���� )(4 ���� ) = 3(
3)(
4) = 3(���� 2���� ) (���� 2 6���� ) (���� 3)(���� 4) = 3���� 6���� ���� 2
3 ���� – 2 до знаменника:
1. Оскільки 7a – 14 = 7(a – 2), то 3 ���� 2 = 3 ⋅ 7 7(���� 2) = 21 7���� 14 . 2. Оскільки a2 – 2a = a(a – 2), то 3 ���� 2 = 3���� ���� (���� 2) = 3���� ���� 2 2���� . 3. Оскільки 16 – 8a = 8(2 – a) = –8(a – 2), то 3 ���� 2 = 3 ⋅ ( 8) 8(���� 2) = 24 16 8���� .
4. Оскільки a2 – 4 = (a – 2)(a + 2), то 3 ���� 2 = 3(���� + 2) (���� 2)(���� + 2) = 3���� + 6 ���� 2 4 .
13. Доведіть тотожність
22,5���� 2 2,5���� 2
7,5���� 2 − 2,5�������� = 2,5(9���� 2 ���� 2 ) 2,5(3����2 − �������� ) = (3���� ���� )(3���� + ���� ) ���� (3���� − ���� ) = 3���� + ���� ���� .
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
Міркуючи аналогічно, як у пункті 1. маємо n = 1; n = 2; n = 3; n = 6. ����. ����2 10���� +6
Маємо n = 1; 2; 4; 8; 16 для перевірки.
n = 1; 1 – 10 + 16 1 = 7 — натуральне число;
n = 2; 2 – 10 + 16 2 = 0 — не є натуральним числом;
n = 4; 4 – 10 + 16 4 = –2 — не є натуральним числом;
n = 8; 8 – 10 + 16 8 = 0 — не є натуральним числом;
n = 16; 16 – 10 + 16 16 = 7 — натуральне число.
Отже n = 1 або n = 16.
Відповідь: 1. 1; 2; 2. 1; 2; 3; 6; 3. 1; 16. 26. Побудуйте
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
a = –24; b = –6. 2. ���� ���� 3 + ���� ���� + 3 = 18 ���� 2 9 ;
(���� + 3) + ����(���� − 3) (���� 3)(���� + 3) = 18 ���� 2 9 ; �������� + 3���� + �������� − 3���� ���� 2 9 = 18 ���� 2 9 ; ���� (���� + ���� ) + 3(���� ���� ) ���� 2 9 = 18 ���� 2 9 ;
(���� + ���� ) + (3���� 3���� ) = 18; � ���� + ���� = 0| ∙ 3 3���� 3���� = 18; � 3���� + 3���� = 0, 3���� − 3���� = 18; 6���� = 18; ���� = 18: 6; ���� = 3; ���� = 3.
Відповідь: a = 3; b = –3. 37. Човен, власна
���� = 12, ���� = 45, то 2�������� ���� 2 9 = 2 ⋅ 45 ⋅ 12 (12 3)(12 + 3) = 2 ⋅ 45 ⋅ 12 9 ⋅ 15 = 8.
2�������� ���� 2 9 ; 8 год.
1. (Усно.)
Гострі:
1) ∠A = 32;
4) ∠D = 59° 30′;
7) ∠L = 89°;
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
3) ∠C = 150°; 6) ∠N = 120°; 8) ∠M = 113° 20′
2. Знайдіть кут, суміжний з кутом:
1) 25°; 180° – 25° = 155°
2) 90°; 180° – 90° = 90°
3) 116°. 180° – 116° = 64°
3. Знайдіть кут, суміжний з кутом:
1) 140°; 180° – 140° = 40°
2) 83°. 180° – 83° = 97°

2) ∠B = 90°;
5) ∠K = 180°;
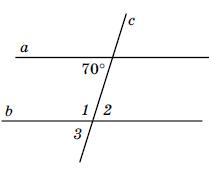
3. ∠3 = 70° (як відповідні кути);
∠1 = 180° – ∠3 = 180° – 70° = 110° (як суміжні);
∠2 = ∠3 = 70° (як вертикальні).
2 = 115° (як відповідні кути);
1 = 180° – ∠2 = 180° – 115° = 65° (як суміжні); ∠3 = ∠2 = 115° (як вертикальні).


+ KD = 28 мм + 40 мм = 68 мм
KD, якщо CD = 5 дм, CK = 2 дм 6 см.
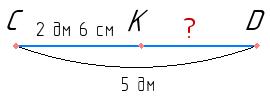
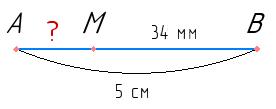
= CD 26 см = 24 см


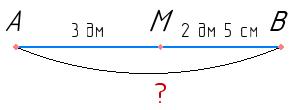

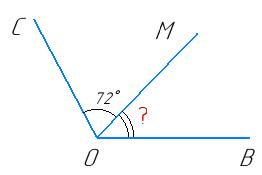

AOK = 42°,
KOD = 37°.

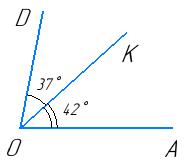
AOD = ∠AOK + ∠KOD = 42° + 37° = 79°

∠2 = 115° (як
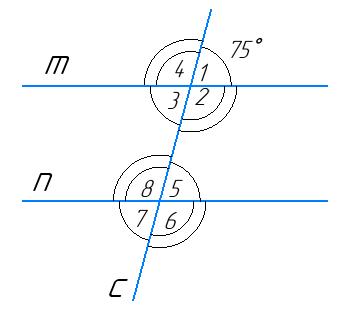
130°. Знайдіть інші сім кутів.
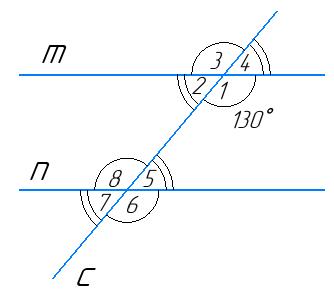
Дано: m∥n, с січна, ∠1 = 75°.
∠2 = 180° − 75° = 105° (як суміжні)
∠3 = ∠1 = 75° (як вертикальні кути)
∠4 = ∠2 = 105° (як вертикальні) ∠3 = ∠5 = 75° (як внутрішні різносторонні
при m∥n та січній с) ∠2 = ∠8 = 105° (як
при m∥n та січній с)
∠7 = ∠5 = 75° (як вертикальні кути)
∠6 = ∠8 = 36° (як вертикальні кути)
Дано: m∥n, с січна, ∠1 = 130°.
∠2 = 180° − 130° = 50° (як суміжні)
∠3 = ∠1 = 130° (як вертикальні кути)
∠4 = ∠2 = 50° (як вертикальні)
∠5 = ∠2 = 50° (як внутрішні різносторонні
при m∥n та січній с)
∠8 = ∠1 = 130° (як внутрішні різносторонні
при m∥n та січній с)
∠7 = ∠5 = 50° (як вертикальні кути)
∠6 = ∠8 = 130° (як вертикальні кути)
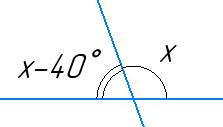
х + 0,8х = 180°
1,8х = 180°
х = 100°
3х = 180° х = 60°
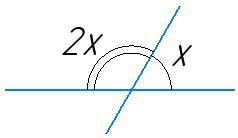
х + 2 7 х = 180°
9 7 х = 180°
9х = 180° ∙ 7
х = 20° ∙ 7
х = 140°

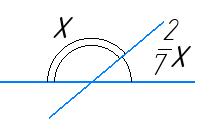
AK
AK : KB = 3 : 7
1) Нехай AK = х, тоді KB = 3х:
3х + х = 20
4х = 20
х = 5 (см) — літера В
3х = 3 ∙ 5 = 15 (см) — літера Я
2) Нехай AK = х, тоді KB = 2 3 х:
х + 2 3 х = 20
5 3 х = 20
х = 20 ∙ 3 : 5
х = 12 (см) — літера И
2 3 х = 2 3 ∙ 12 = 8 (см) — літера Н
3) Нехай AK = 3х, тоді KB = 7х:
3х + 7х = 20
10х = 20
х = 2
3х = 3
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
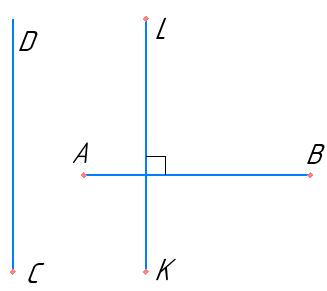
17. Прямі AB, MN і CD перетинаються в точці O, причому AB ⊥ MN (мал. 3).

18. Прямі MN, KL і AB

Знайдіть:
1) ∠DOB, якщо ∠CON = 70°;
∠MOD = ∠CON = 70° (як вертикальні)
∠MOB = 90° (оскільки AB ⊥ MN)
∠DOB = ∠MOB − ∠MOD = 90° − 70° = 20°
2) ∠AOC, якщо ∠DON = 105°.
∠MOC = ∠DON = 105° (як вертикальні)
∠MOA = 90° (оскільки AB ⊥ MN)
∠AOC = ∠MOC − ∠MOA = 105° − 90° = 15°
Знайдіть:
1) ∠KOB, якщо ∠NOA = 120°;
∠BOM = ∠NOA = 120° (як вертикальні)
∠KOM = 90° (оскільки MN ⊥ KL)
∠KOB = ∠BOM − ∠KOM = 120° − 90° = 30°
2) ∠KOA, якщо ∠BON = 40°.
∠AOM = ∠BON = 40° (як вертикальні)
∠KOM = 90° (оскільки MN ⊥ KL)
∠KOA = ∠AOM + ∠KOM = 40° + 90° = 130°

х + 3х = 180°
4х = 180°
х = 45° —
3х = 3 ∙ 45° = 135°
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html

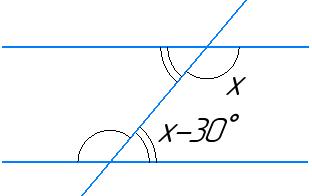

1) 60°, 60°, 61°;
2) 20°, 70°, 90°; 3) 10°, 100°, 70°; 4) 50°, 60°, 80°?
+ х − 30° = 180°
2х = 180° + 30°
2х = 210° х = 105°
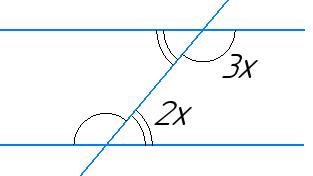
2х + 3х = 180°
5х = 180°
х = 36°
3х = 3 ∙ 36° = 108° —
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
1) 60° + 60° + 61° = 181° � Не існує
2) 20° + 70° + 90° = 180° � � Існує
3) 10° + 100° + 70° = 180° � � Існує
4) 50° + 60° + 80° = 190° � Не існує
23. (Усно.) Чи існує трикутник
1) 7 см, 2 см, 9 см;
2) 12 см, 10 см, 8 см;
3) 3 см, 4 см, 6 см; 4) 8 см, 8 см, 15 см?
Щоб з’ясувати, чи існує
трикутника: сума
1) 7 + 2 = 9 →
3) 3 + 4 = 7 > 6
3 + 6 = 9 > 4
4 + 6 = 10 > 3
2) 12 + 10 = 22 > 8
12 + 8 = 20 > 10
10 + 8 = 18 > 12
4) 8 + 8 = 16 > 15
8 + 15 = 23 > 8
8 + 15 = 23 > 8
= 5 + 7 + 7 = 19 (см)
Відповідь: 19 см.
25. Знайдіть периметр
Основа на 3 см менша, тобто: 10 – 3 = 7 (см)
У рівнобедреному трикутнику
P = 7 + 10 + 10 = 27 (см)
Відповідь: 27 см.
26. У трикутнику ABC відрізок BK – медіана, AK = 5 см. Знайдіть KC і AC.
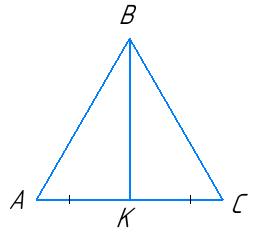
Оскільки BK медіана, то точка K середина відрізка AC:
AK = KC
А якщо AK = 5 см, то:
KC = 5 (см)
Тоді довжина AC:
AC = AK + KC = 5 + 5 = 10 (см)
Відповідь:
KC = 5 см; AC = 10 см.
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
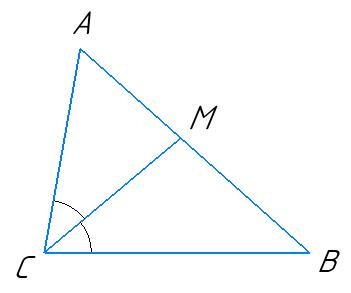
29.
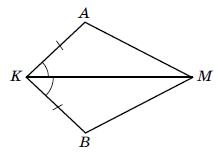
△AKM і △BKM:
1) AK = BK — за умовою 2) ∠AKM = ∠BKM — за умовою
3) KM — спільна сторона.
і
рівності трикутників): △AKM = △BKM.
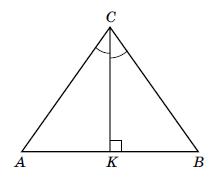
що △ACK = △BCK (мал. 6), якщо CK ⊥ AB і ∠ACK = ∠BCK. У трикутниках △ACK = △BCK:
1) ∠ACK = ∠BCK = 90° — за умовою
2) ∠ACK = ∠BCK — за умовою
3) CK — спільна сторона.
трикутників): △ACK = △BCK.
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html

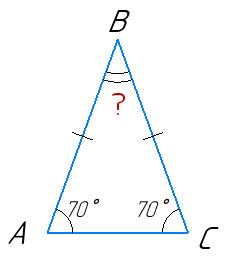
∠A + ∠B + ∠C = 180°
х + 100° + х = 180°
2х = 180° − 100°
2х = 80°
х = 40°
Відповідь: 40°. 32. Зовнішній

∠A + ∠B = ∠BCM
Підставляємо:
∠A + 60° = 110°
∠A = 110° − 60°
∠A = 50°
Відповідь: 50°. 33.
80°.
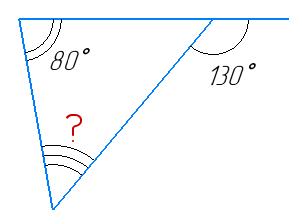
Внутрішній кут, суміжний до кута 130° (згідно властивості суміжних
180° − 130° = 50°
кут, не суміжний із зовнішнім, дорівнює 80°.
Знайдемо третій внутрішній кут. Сума внутрішніх кутів трикутника — 180°: Третій кут = 180° − 50° − 80° = 50°
Відповідь: 50°.
34. У прямокутному трикутнику ABC (∠C = 90°), ∠A = 60°. Знайдіть:
1) AC, якщо AB = 10 см; 2) AB, якщо AC = 4 см.
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
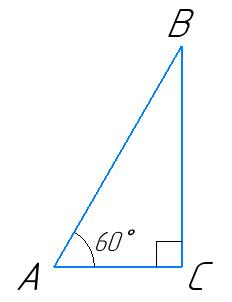
∠B = 90° ∠A = = 90° 60° = 30°;
AC = 1 2 AB.
1) AC = 1 2 AB = 1 2 ∙ 10 = 5 (см);
2) AB = 2AC = 2 ∙ 4 = 8 (см).
Відповідь: 1) 5 см; 2) 8 см. 35. У прямокутному трикутнику ABC (
1) AB, якщо BC = 8 дм; 2) BC, якщо AB = 18 см. Згідно

трикутника: Катет прямокутного трикутника, що лежить проти кута 30°, дорівнює
BC = 1 2 AB ⇒ AB = 2BC
1) AB = 2BC = 2 ∙ 8 = 16 (дм); 2) BC = 1 2 AB = 1 2 ∙ 18 = 9 (см).
Відповідь: 1) 16 дм; 2) 9 см.
Дві сторони трикутника: a = 2,7 см, b = 6,3 см.
Межі для третьої сторони c: |a b| < c < a + b
|6,3 2,7| < c < 6,3 + 2,7
3,6 < c < 9,0
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
Позначимо сторони трикутника так:
Нехай перша сторона (найменша) x;
Друга сторона 3x;
Третя сторона x + 10.
Периметр: x + 3x + (x + 10) = 45
Розв’яжемо рівняння:
x + 3x + x + 10 = 45
5x + 10 = 45
5x = 35
x = 7
Знаходимо сторони:
Перша сторона: x = 7 см
Друга: 3x = 21 см
Третя: x + 10 = 17 см
Відповідь: 7 см, 21 см, 17 см.
39. Одна
3 см
Периметр трикутника дорівнює 35 см.
Позначимо невідому сторону як x.
Тоді згідно з умовою:
Одна сторона x
Друга x + 3
Третя 2x
Периметр: x + (x + 3) + 2x = 35
Розв’яжемо рівняння: x + x + 3 + 2x = 35
4x + 3 = 35
4x = 32
x = 8
Знайдемо сторони:
Перша сторона: x = 8 см
Друга: x + 3 = 11 см
Третя: 2x = 16 см
Відповідь: 8 см, 11 см, 16 см.
40. На малюнку 7 AB = BD, AC = CD. Доведіть, що BC – бісектриса кута ABD.
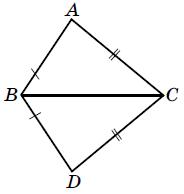
Розглянемо трикутники △ABC і △DBC:
BC спільна сторона;
AB = BD за умовою; AC = CD за умовою.
і C, якщо:
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
кута C
B удвічі більший за кут C
∠B : ∠C = 1 : 3
У всіх випадках маємо: ∠A = 60° Сума кутів трикутника:
∠A + ∠B + ∠C = 180° ⇒ ∠B + ∠C = 120°
1) Нехай ∠C = x, тоді ∠B = x 20
Підставимо в рівняння:
x + (x 20) = 120
2x 20 = 120
2x = 140 x = 70
Отже:
∠C = 70° літера О
∠B = 50° літера Л
2) Нехай ∠C = x, тоді ∠B = 2x
x + 2x = 120
3x = 120 x = 40
Отже:
∠C = 40° літера И
∠B = 80° літера Р
3) Нехай ∠B = x, тоді ∠C = 3x
x + 3x = 120
4x = 120
x = 30
Отже:
∠B = 30° літера П
∠C = 90° літера К
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
Другий кут x + 20
Третій кут 2x
Сума кутів трикутника:
x + (x + 20) + 2x = 180°
4x + 20 = 180°
4x = 160°
x = 40°
Обчислимо всі кути:
Перший: x = 40°
Другий: x + 20 = 60°
Третій: 2x = 80°
Відповідь: 40°, 60°, 80°.
43. Знайдіть гострі кути прямокутного
1) один із них на 26° більший за інший;
Оскільки трикутник прямокутний,
також дають 90°.
Нехай менший кут x, тоді більший x +
x + (x + 26) = 90°
2x + 26° = 90°; 2x = 64°
x = 32° менший кут
x + 26° = 32 + 26° = 58° більший кут
2) один із них становить 80 % від іншого. Нехай
x + 0,8x = 90°
1,8x = 90°
x = 50° більший кут 0,8x = 0,8 ∙ 50° = 40° менший кут 44. Знайдіть гострі кути
5x = 5
5x
2x
3x
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
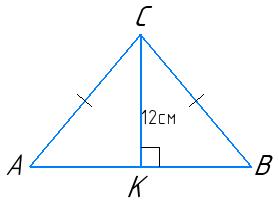
Периметр трикутника ACK:
AK + CK + AC = 30
AK + 12 + AC = 30
AK + AC = 18
У трикутнику ABC:
AB = 2 ∙ AK; AC = BC
Отже: P△ABC = AB + AC + BC = 2 ∙ AK + 2 ∙ AC
Підставимо з попереднього:
2 ∙ AK + 2 ∙ AC = 2(AK + AC) = 2 ∙ 18 = 36 см
Відповідь: 36 см.
трикутника ABM, якщо периметр трикутника ABC дорівнює 32 см і AM = 8 см.
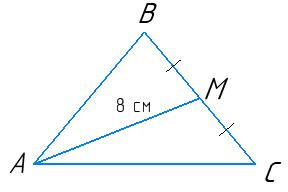
Розв’язок:
Позначимо AB = AC = x, а BC = y
Тоді периметр △ABC дорівнює:
x + x + y = 32
2x + y = 32
y = 32 2x
Знайдемо сторону BM
Оскільки M — середина BC, то:
BM = y 2 = 32−2x 2 = 16 − x
Периметр △ABM — це сума сторін:
Дано: △ABC — рівнобедрений, з основою BC ⇒
AB = AC (бо в рівнобедреному трикутнику
рівні) AM — медіана до основи BC ⇒
Точка M — середина відрізка BC, тобто:
BM = MC = BC 2
Периметр △ABC = 32 см
AM = 8 см
Потрібно
периметр трикутника ABM.
AB + BM + AM = x + (16 x) + 8 = 16 + 8 = 24 см.
Відповідь: 24 см.
47. Знайдіть кути рівнобедреного
1:
2x + y = 180° та y = x + 24°
Підставимо:
2x + (x + 24°) = 180°
3x = 156°
x = 52°
y = 52 + 24 = 76°
Випадок 2:
2x + y = 180 та x = y + 24
y = x - 24
Підставимо:
2x + (x - 24) = 180
3x = 204
x = 68
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
Кути: 52°, 52°, 76° y = 68 - 24 = 44
68°, 68°, 44°
Випадок 1: 52°, 52°, 76°;
Випадок 2: 68°, 68°, 44°.
48. Чи існує
на 3 см менша від третьої?
Позначимо сторони трикутника як:
a друга сторона; b = a + 4 перша сторона (на 4 см більша за другу);
c = b + 3 = a + 4 + 3 = a + 7 третя сторона (на 3 см більша за першу).
Периметр трикутника дорівнює 20 см, тобто:
a + b + c = 20
Підставляємо b і c через a:
a + (a + 4) + (a + 7) = 20
3a + 11 = 20
3a = 9
a = 3
Тоді:
b = 3 + 4 = 7
c = 3 + 7 = 10
Отже, сторони: 3 см, 7 см, 10 см
Перевірка існування трикутника
За нерівністю трикутника, сума
1. 3 + 7 = 10 �
2. 3 + 10 = 13 > 7 � �
3. 7 + 10 = 17 > 3 � �
Відповідь: не існує.
49. (Усно.) Знайдіть: 1) діаметр кола, якщо його радіус дорівнює
а) r = 6 см
d = 2 ∙ 6 = 12 см; б) r = 7 дм
d = 2 ∙ 7 = 14 дм.
2)
а) d = 4 дм
r = 4 2 = 2 дм;
б) d = 5 см
r = 5 2 = 2,5 см.
50. Знайдіть
1) 80°;
2) 200°.
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html

BAC
тоді:
BAC = ∠BOC : 2
1) Якщо центральний кут ∠BOC = 80°, то
∠BAC = 80° : 2 = 40°
2) Якщо центральний кут ∠BOC = 200°, то
∠BAC = 200° : 2 = 100°
Відповідь: 1. 40°; 2. 100° 51. Визначте градусну
1) 50°; 2) 110°. Нехай задано

BOC – центральний кут;
тоді: ∠BAC = ∠BOC : 2 ⇒ ∠BOC = 2 ∙ ∠BAC
1) Якщо вписаний кут ∠BAC = 50°, то
∠BOC = 2 ∙ 50° = 100°
2) Якщо вписаний кут ∠BAC = 110°, то
∠BOC = 2 ∙ 110° = 220°
Відповідь: 1. 100°; 2. 220° 52. На малюнку
O
1) кута O, якщо ∠C = 46°; 2)
D, якщо ∠O = 96°.
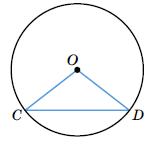
1) ∠C = ∠D = 46°, тоді
COD
OC = OD
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
∠O = 180° - (∠C + ∠D) = 180° - (46° + 46°) = 88°.
2) ∠C = ∠D = x, тоді
96° + x + x = 180°
2x = 84°
x = 42°
Відповідь: 1. ∠O = 88°; 2. ∠D = 42°.
53. На малюнку 8 точка O – центр кола. Знайдіть градусну міру:
1) кута C, якщо ∠O = 94°;
2) кута O, якщо ∠D = 44°.

1) Нехай ∠C = ∠D = x, тоді:
x + x + 94° = 180°
2x = 86°
Трикутник COD рівнобедрений, оскільки OC = OD (радіуси кола).
Загальна властивість: У рівнобедреному трикутнику кути при
також сума всіх трьох кутів дорівнює 180°: ∠C + ∠D +∠O = 180°
x = 43° 2) Оскільки ∠D = ∠C = 44°, то: 44° + 44° + ∠O = 180° ∠O = 180° - 88° = 92°
Відповідь: 1. ∠C = 43°; 2. ∠O = 92°.
54. На малюнку 9 точка O
1) ∠OBA, якщо ∠ABC = 62°; 2) ∠DBA, якщо ∠OBA = 30°.
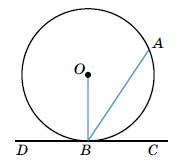
O
1) ∠ABC, якщо ∠OBA = 32°; 2) ∠OBA, якщо ∠DBA = 136°.
Радіус, проведений у точку
дотичної (згідно
кола), тому ∠OBC = ∠DBO = 90°.
1) ∠OBA = ∠OBC − ∠ABC = 90° − 62° = 28°;
2) ∠DBA = ∠DBO + ∠OBA = 90° + 30° = 120°.
Відповідь:
1. ∠OBA = 28°
2. ∠DBA = 120°
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html

56. Точки A і B
1)
d = R r = 8 - 5 = 3 см
2) зовнішній дотик. Коли
= R + r = 8 + 5 = 13 см
Відповідь:1. 3 см; 2. 13 см. 58. Радіуси
кола), тому
∠OBC = ∠DBO = 90°.
1) ∠ABC = ∠OBC – ∠OBA = 90° – 32° = 58°;
2) ∠OBA = ∠DBA – ∠DBO = 136° – 90° = 46°.
Відповідь:
1. ∠ABC = 58°
2. ∠OBA = 46°
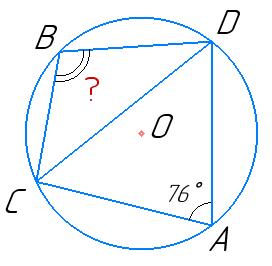
◡CBD = 2∠CAD = 2 ∙ 76 = 152°
Тоді, ◡CAD = 360° − ◡CBD = 360° − 152° = 208°
∠CBD = ◡
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
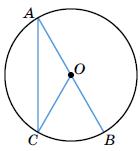
теореми
про вписаний кут):
∠CAB = ∠COB : 2 = 40° : 2 = 20°
Відповідь: ∠CAB = 20°.
60. На малюнку 10 точка O – центр кола, ∠ACO = 21°. Знайдіть ∠COB. OC = OB (як радіуси), тому △ACO рівнобедрений. Оскільки у рівнобедреного трикутника кути при основі рівні, то ∠ACO = ∠CAO = 21°.

61.
BMK, якщо
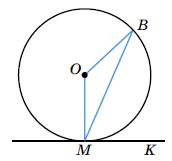
x + x + 130° = 180°
2x = 50°
x = 25°
∠BMK = 65°.
∠COB — центральний кут, що спирається на дугу CB, ∠CAB — вписаний кут, що також спирається на ту саму дугу CB. Центральний кут вдвічі більший за вписаний, якщо
кут): ∠COB = 2 ∙ ∠CAB = 2 ∙ 21° = 42°
Відповідь: ∠COB = 42°
BOM = 130°.
Трикутник OMB рівнобедрений, оскільки OM = OB (радіуси кола).
Загальна властивість: У рівнобедреному трикутнику
сума всіх трьох
дорівнює 180°: ∠MOB + ∠OBM +∠OMB = 180°
Нехай ∠OBM = ∠OMB = x, тоді:
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html

Загальна властивість:
кола), тому ∠OMK = 90°.
Тоді
∠OMB = ∠OMK − ∠BMK = 90° – 70° = 20°.
Трикутник OMB — рівнобедрений, оскільки OM = OB (радіуси кола).
У рівнобедреному трикутнику кути при основі рівні (∠OBM = ∠OMB), а також сума
трьох кутів дорівнює 180°:
∠MOB + ∠OBM +∠OMB = 180°
∠MOB + 20° + 20° = 180°
∠MOB = 140°
Відповідь: ∠MOB = 140°
63. Відстань між центрами
Знайдіть радіуси кіл, якщо вони мають:
1) внутрішній дотик;
Позначимо:
R — більший радіус
r — менший радіус
d — відстань між центрами радіусів тоді R = 5x, r = 3x
При внутрішньому дотику:
R - r = d
5x - 3x = 16
2x = 16
x = 8
Тоді:
R = 5x = 40 см, r = 3x = 24 см
2) зовнішній дотик.
При зовнішньому дотику:
R + r = d
5x + 3x = 16
8x = 16
x = 2
Тоді:
R = 5x = 10 см, r = 3x = 6 см
Відповідь: 1) 40 см, 24 см; 2) 10 см, 6 см.
64. Прямі AB і AC дотикаються
BC, якщо AB = 4 см, ∠OAC = 30°.
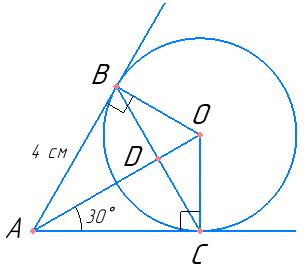
Відрізки дотичних, проведених
властивості відрізків дотичних, проведених з однієї точки): AB = AC = 4 см
Дотична до кола є перпендикулярною до радіуса, який проведений в точку
властивості дотичної до кола):
АВ⊥ОВ, АС⊥ОС, отже ΔВОA і ΔCОA – прямокутні.
Оскільки AB = AC (катети), АО – спільна сторона (гіпотенуза), то ΔВОA = ΔCОA (згідно
ознаки рівності прямокутних трикутників за катетом і гіпотенузою)
У рівних трикутників відповідні елементи рівні, тому ∠OAB = ∠OAC = 30°.
Розглянемо трикутник ABC. В ньому AD –
CDA та BDA – прямокутні, сторони AB і AC – гіпотенузи.
Катет, прямокутного трикутника, що
гіпотенузи (згідно
BD = AB : 2 = 4 : 2 = 2 см
CD = AC : 2 = 4 : 2 = 2 см
Тоді
BC = BD + CD = 2 + 2 = 4 см
Відповідь: 4 см. 65. Коло,
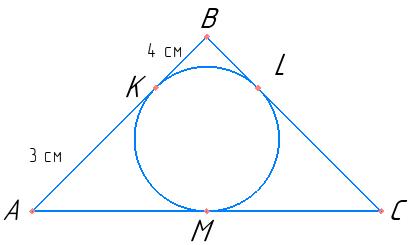
ΔABC – рівнобедрений (AB = BC), KB = 2 см, AK = 5 см.
BL = KB = 2 см, AM = AK = 5 см, CM = CL = 5 см.
PΔABC = AK + KB + BL + CL + CM + AM = = 5 см + 2 см + 2 см + 5 см + 5
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html

Нехай ΔABC – рівнобедрений (AB = BC), KB = 4 см, AK = 3 см. За властивістю дотичних,
BL = KB = 4 см, AM = AK = 3 см, CM = CL = 3 см.
PΔABC = AK + KB + BL + CL + CM + AM = = 3 см + 4 см + 4 см + 3 см + 3 см + 3 см = 20 см. Відповідь: 20 см.
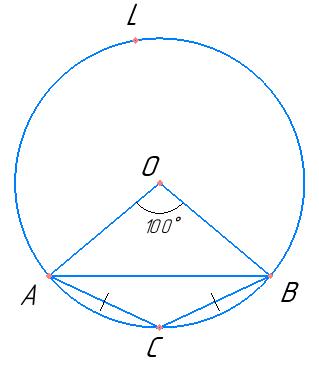
розв’язок ∠AOB – центральний кут; ∠ACB – вписаний кут;
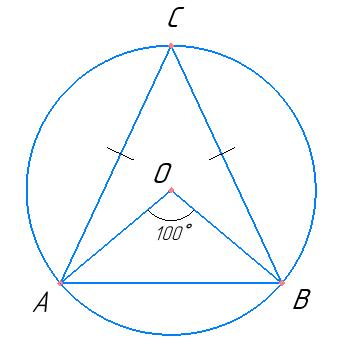
центрального кута (це
випливає із теореми про вписаний кут), тоді:
∠ACB = ∠AOB : 2 = 100° : 2 = 50°
Кути при основі рівнобедреного трикутника рівні:
∠CBA = ∠CAB = x Сума кутів трикутника рівна 180°:
∠ACB + ∠CBA + ∠CAB = 180°
50° + х + х = 180°
2х = 130°
х = 65°
Відповідь: 65°, 65°, 50°.
∠AOB – центральний кут;
∠ACB – вписаний кут;
◡ACB = ∠AOB = 100°
◡ALB = 360° − ◡ACB = = 360° − 100° = 260°
∠ACB = ◡ALB : 2 = 260° : 2 = 130°
рівні:
∠CBA = ∠CAB = (180° − ∠ACB) : 2 = = (180° − 130°) : 2 = 50° : 2 = 25°
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
5.4 Накресліть
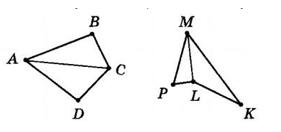
5.5 Чи
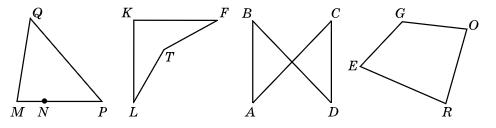
1. 70°, 90°, 100° і 120°;
2. 130°, 60°, 70° і 100°?
1. 70° + 90° + 100° + 120° = 380°
Відповідь: ні.
2. 130° + 60° + 70° + 100° = 360°.
Відповідь: так.
5.6 Чи можуть
1. 140°, 60°, 90° і 70°;
2. 120°, 110°, 80° і 60°?
1. 140° + 60° + 90° + 70° = 360°.
Відповідь: так.
2. 120° + 110° + 80° + 60° = 370°.
Відповідь: ні.
5.7 Знайдіть четвертий
1. 150°, 110° і 80°;
2. 80°, 60° і 30°.
Яким —
чи неопуклим
1. 360° − (150° + 110° + 80°) = 20°.
2. 360° − (80° + 60° + 30°) = 190°.
5.8 Знайдіть четвертий
1. 20°, 70° і 80°;
2.
1. 360° − (20° + 70° + 80°) = 190°.
2.
P = 34 + 25 + 40 + 70 = 169 (мм).
5.10
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
P = 80 + 70 + 63 + 52 = 265 (мм).
5.11
1. гострими; 2. прямими; 3. тупими?
1. Ні, оскільки
2. Так, бо 4 · 90° = 360°.
3. Ні,
5.12
невідомі кути чотирикутника. (360° − 120°) : 3 = 80°.
Відповідь: 80°; 80°; 80°.
5.13 Периметр чотирикутника дорівнює
невідомі сторони чотирикутника, якщо
рівні. (60 − 24) : 3 = 12 (см).
Відповідь: 12 см; 12 см; 12 см.
5.14 У чотирикутнику ABCD BC = CD і ∠ ACB = ∠ ACD. Доведіть, що ∠ B = ∠ D.

1. BC = CD (за умовою); ∠ACB = ∠ACD (за умовою). AC — спільна сторона трикутників ABC і ADC. Тому ΔABC = ΔADC (за першою ознакою).
2. Оскільки ΔABC = ΔADC, то ∠B = ∠D, що й треба було довести.
5.15 У чотирикутнику ABCD ∠ BAC = ∠ ACD, ∠ BCA = ∠ CAD. Доведіть, що AB = CD.
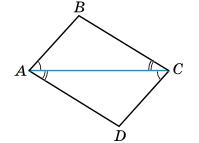
1. ∠BAC = ∠ACD; ∠BCA = ∠CAD (за умовою); AC спільна сторона трикутників ABC і CDA. Тому ΔABC = ΔCDA (за другою ознакою).
2. Оскільки ΔABC = ΔCDA, то AB = CD, що й треба було довести.
5.16 Знайдіть сторони чотирикутника, якщо
периметр чотирикутника дорівнює 65 см.
1. Нехай сторони чотирикутника дорівнюють 4x, 5x, 8x і 9x.
Тоді 4x + 5x + 8x + 9x = 65; 26x = 65;
x = 2,5.
2. Тоді сторони чотирикутника:
4 · 2,5 = 10 (см);
5 · 2,5 = 12,5 (см);
8 · 2,5 = 20 (см);
9 · 2,5 = 22,5 (см).
Відповідь: 10 см, 12,5 см, 20 см, 22,5 см.
5.17 Знайдіть
1. Нехай кути чотирикутника дорівнюють 4
Тоді 4x + 5x + 7x + 8x = 360°;
,
,
8
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
24x = 360°; x = 15°.
2. Тоді кути чотирикутника:
4 · 15° = 60°;
5 · 15° = 75°;
7 · 15° = 105°;
8 · 15° = 120°.
Відповідь: 60°, 75°, 105°, 120°.
5.18 Знайдіть невідомі кути
1. Нехай другий кут дорівнює 7x,
7���� + 5���� 2 = 6����.
2. Тоді 90° + 7x + 5x + 6x = 360°; 18x = 270°; x = 15°.
3. Отже, невідомі кути чотирикутника:
7 · 15° = 105°; 5 · 15° = 75°; 6 · 15° = 90°.
Відповідь: 105°, 75°, 90°. 5.19 Знайдіть
сторін 18 см,
третьої.
другого та третього.
1. Нехай друга сторона чотирикутника 7x (см), а третя 3x (см).
7���� 3���� 2 = 4���� 2 = 2���� (см).
2. За умовою 18 + 7x + 3x + 2x = 54; 12x = 36; x = 3 (см).
3. Отже, друга сторона чотирикутника дорівнює
7 · 3 = 21 (см),
третя 3 · 3 = 9 (см),
четверта 2 · 3 = 6 (см).
Відповідь: 21 см, 9 см, 6 см.
5.20 Доведіть, що в кожному чотирикутнику
1. Припустимо, що у чотирикутнику
2.
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
5.23
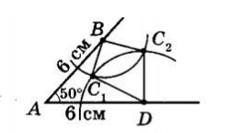
5.24
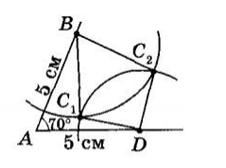
5.25
сторін. Доведіть, що:
розв’язки. AB = BC = 6 см; ∠B = 50°;
AD1 = AD2 = 4 см; CD1 = CD2 = 3 см.
два розв’язки.
AB = AD = 5 см; ∠A = 70°;
BC1 = BC2 = 4 см;
DC1 = DC2 = 3 см.
1. діагональ BD ділить навпіл і кут B,
D; 2.
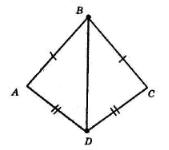
1. 2. AB = BC; AD = DC (за умовою), BD — спільна сторона трикутників ABD і CBD. Тому ΔABD = ΔCBD.
1. Оскільки ΔABD = ΔCBD, то ∠ABD = ∠CBD і ∠ADB = ∠CDB.
Отже, діагональ BD ділить навпіл як кут B, так і кут D.
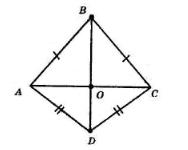
2. BO — бісектриса рівнобедреного трикутника,
до
BO є також і висотою. Отже, BO ⊥ AC, а тому BD ⊥ AC, тобто

З ΔABD: BD = PΔABD − (AB + AD).
З ΔBCD: BD = PΔBCD − (BC + CD).
BD + BD = PΔABD + PΔBCD − (AB + AD + BC + CD);
2BD = PΔABD + PΔBCD − PABCD; 2BD = 20 + 21 − 29; 2BD = 12;
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
BD = 6.

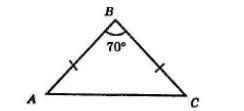
Задача має два розв’язки.
Випадок 1.
В ΔABC AB = BC, ∠B = 70°.
Кути при основі рівні, тоді
6 см.
Нехай ∠1 = 70°, тоді:
∠2 = 180° − 70° = 110° (властивість суміжних кутів);
∠3 = ∠1 = 70° (як вертикальні);
∠4 = ∠2 = 110° (як вертикальні);
∠5 = ∠2 = 110° (як відповідні) або
∠5 = ∠4 = 110° (як внутрішні різносторонні);
∠6 = ∠3 = 70° (як відповідні);
∠7 = ∠5 = 110° (як вертикальні);
∠8 = ∠6 = 70° (як відповідні).
Відповідь: Три кути по 70°; чотири по 110°.
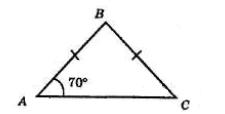
∠A = ∠C = (180° − ∠B) : 2 = (180° − 70°) : 2 = 55°.
Випадок 2.
В ΔABC AB = BC, ∠A = 70°.
∠C = ∠A = 70° як кути при основі.
∠B = 180° − (∠A + ∠C);
∠B = 180° − 2 · 70° = 40°.
Відповіді:
1. 55°, 55°, 70°; 2. 70°, 70°, 40°.
5.29

трикутника, що
маємо: CD = АВ : 2 = AD = BD. ∠A = 90° − ∠B = 30°. Тоді BC —
оскільки
меншого кута. За умовою CD + BC = 10 см.
У ΔBCD CD = BD, ∠B = 60°, тоді ΔBCD — рівносторонній, CD = BC = 10 см : 2 = 5 см.
AB = 2CD = 2 · 5 см = 10 см.
10 см. 5.30
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
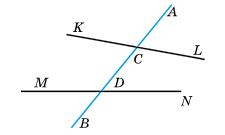
кути: ∠KCD і ∠MDC; ∠NDC і ∠DCL.
Внутрішні різносторонні кути: ∠KCD і ∠CDN; ∠DCL і ∠MDC.
Відповідні кути: ∠KCA і ∠MDC; ∠ACL і ∠CDN; ∠KCD і ∠MDB; ∠DCL і ∠BDN.
5.31 Яким є взаємне розміщення прямих a і b, якщо:
1. ∠2 + ∠4 = 180°;
2. ∠1 > ∠4;
3. ∠3 = 120°, ∠4 = 121°;
4. ∠2 = 60°, ∠4 = 119°;
5. ∠1 = ∠4 = 122°;
6. ∠3 = ∠4?
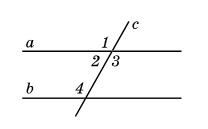
1, 5, 6 прямі a і b паралельні. 2, 3, 4 — прямі a і b перетинаються.
5.32 1. Доведіть, що △ABC = △CDA, якщо AB = CD і ∠BAC = ∠ACD.
2. Доведіть, що BC = AD і ∠BCA = ∠CAD.
3. Чи паралельні прямі BC і AD?
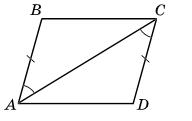
1. AB = CD; ∠BAC = ∠ACD (за умовою).
AC — спільна сторона трикутників ABC і CDA. Тому ΔABC = ΔCDA (за першою ознакою).
2. Оскільки ΔABC = ΔCDA, то BC = AD і ∠BCA = ∠CAD. 3. Оскільки ∠BCA = ∠CAD, і ці кути — внутрішні
1. 2 · (150 + 200) = 2 · 350 = 700 (м) —
2. (700 м · 4) : 16 = 2,8 км : 16 = 0,175 год = = 0,175 · 60 хв = 10,5
3. (700 м · 3) : 14 = 2,1 км : 14 = 0,15 год = = 0,15 · 60 хв = 9 хв —
4. 10 хв 30 с – 9 хв = 1 хв 30 с —
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
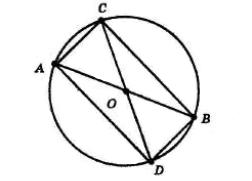
діаметром кола).




https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
180°.
рівні.
Якщо один кут дорівнює 110°, то сусідній: 180° − 110° = 70°.
Отже, кути будуть: 110°, 70°, 110°, 70°.
6.7 Знайдіть периметр паралелограма,
3 см більша за неї.
1. 12 + 3 = 15 (см) — друга сторона; 2. P = 2(12 + 15) = 54 (см).
Відповідь: 54 см.
6.8 Знайдіть периметр паралелограма,
удвічі менша.
1. 18 : 2 = 9 (см) — друга сторона; 2. P = 2(18 + 9) = 54 (см).
Відповідь: 54 см.
6.9 Розв'яжіть
1. ∠A + ∠C = 120° ⇒ 2∠A = 120° ⇒
∠A = 60°, ∠B = 120°.
2. ∠A = ∠B + 20° і ∠A + ∠B = 180° ⇒
∠B = 80°, ∠A = 100°.

3. ∠A = 1 3 ∠B, ∠A + ∠B = 180° ⇒
∠B = 135°, ∠A = 45°.
4. ∠A : ∠B = 3 : 2 ⇒ 5k = 180° ⇒ ∠A = 108°, ∠B = 72°.
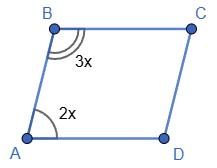
2.
3.
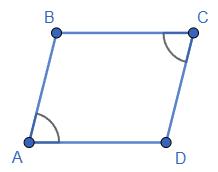
1. ∠B + ∠D = 200°; ∠B = ∠D = 200° 2 = 100°.
Тоді ∠A = ∠C = 180° − 100° = 80°.
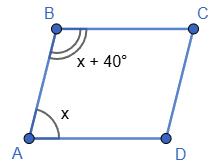
2. Нехай ∠A = x, тоді ∠B = x + 40°.
Маємо x + x + 40 = 180; 2x = 140; x = 70.
Отже, ∠A = ∠C = 70°; ∠B = ∠D = 70° + 40° = 110°.
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
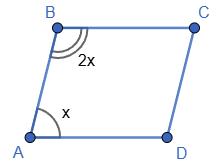
3. Нехай ∠A = x, тоді ∠B = 2x.
Маємо x + 2x = 180; 3x = 180; x = 60.
Отже, ∠A = ∠C = 60°;
∠B = ∠D = 60° · 2 = 120°.
4. Оскільки ∠A : ∠B = 4 : 5, то можна
позначити
∠A = 4x, ∠B = 5x.
Маємо 4x + 5x = 180;
9x = 180; x = 20.
Отже, ∠A = ∠C = 4 · 20° = 80°;
∠B = ∠D = 5 · 20° = 100°.
6.11 У
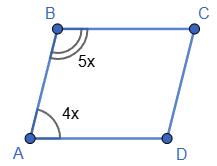
паралелограмі ABCD ∠ BAD = 80°, ∠ ACD = 50°. Знайдіть ∠ ACB і ∠ ABC.

6.12 У
1. ∠BCD = ∠BAD = 80°.
2. ∠ACB = ∠BCD − ∠ACD = 80° − 50° = 30°.
3. ∠ABC = 180° − ∠BAD = 180° − 80° = 100°.
Відповідь: ∠ACB = 30°; ∠ABC = 100°.
паралелограмі ABCD ∠ BAC = 35°, ∠ BCA = 40°.

1. ∠ABC = 180° − (35° + 40°) = 105°.
2. ∠CDA = ∠ABC = 105°.
3. ∠BAD = ∠BCD = 180° − 105° = 75°.
Відповідь: ∠BAD = ∠BCD = 75°; ∠ABC = ∠CDA = 115°.

https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
1. Нехай AB = x см, тоді BC = (x + 4) см.
Маємо 2(x + x + 4) = 40; 2x + 4 = 20; 2x = 16; x = 8 (см).
Отже, AB = CD = 8 (см); BC = AD = 8 + 4 = 12 (см).
Відповідь: 8 см; 10 см.
2. Оскільки AB : BC = 3 : 7, то можна
позначити AB = 3x, BC = 7x.
Маємо 2(3x + 7x) = 40; 10x = 20; x = 2 (см).
Отже, AB = CD = 3 · 2 = 6 (см); BC = AD = 7 · 2 = 14 (см).
Відповідь: 6 см; 14 см.

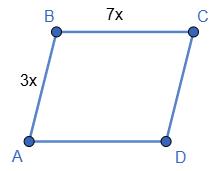
6.15 Периметр паралелограма дорівнює 36 дм. Знайдіть його сторони, якщо:
1. одна з них на 2 дм менша від другої;
2. одна з них у 5 разів більша за другу.
P = 2(a + b), де a і b — сторони паралелограма.
1. Менша сторона x дм, більша сторона
— (x + 2) дм.
P = 2(x + x + 2) = 4x + 4.
За умовою 4x + 4 = 36, 4x = 32, x = 8.
8 + 2 = 10 (дм).
Відповідь: 8 дм, 10 дм.
2. Менша сторона x дм, більша сторона
— 5x дм.
P = 2(x + 5x) = 12x. 12x = 36, x = 3.
3 · 5 = 15 (дм).
Відповідь: 3 дм, 15 дм.
6.16
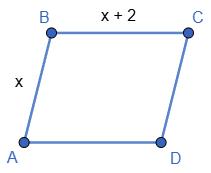
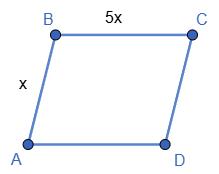
BD = 20см, AB = 15 см, а периметр трикутника AOB дорівнює 32 см.
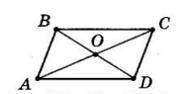
1. OB = BD 2 = 20 2 = 10 (см).
2. AO = PΔAOB − (AB + BO) = 32 − (15 + 10) = 7 (см).
3. AC = 2 · AO = 2 · 7 = 14 (см).
Відповідь: 14 см.
2.17 У чотирикутнику ABCD ∠ 1 = ∠ 2, ∠ 3 = ∠ 4. Доведіть, що ABCD —

https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
1. ∠BAD = ∠2 + ∠3; ∠BCD = ∠1 + ∠4. Але ∠1 = ∠2; ∠3 = ∠4, тому ∠BAD = ∠BCD.
2. ∠B = 180° − (∠1 + ∠3); ∠D = 180° − (∠2 + ∠4).
Оскільки ∠2 = ∠1, ∠3 = ∠4, то ∠B = ∠D.
3. Оскільки у чотирикутнику ABCD протилежні кути попарно рівні, то він є паралелограмом, що й треба було довести.
6.18 △ ABC = △ CDA. Доведіть, що ABCD — паралелограм.
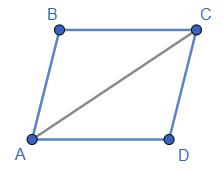
6.19
1. Оскільки ΔABC = ΔCDA, то AB = CD і BC = DA.
2. У чотирикутнику ABCD протилежні сторони попарно рівні, то він є паралелограмом, що й треба було довести.

96°, 84°.
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
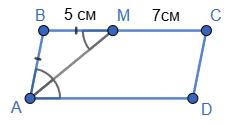
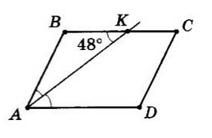
ΔABM рівнобедрений, оскільки ∠BMA = ∠MAD (як внутрішні різносторонні при AD || BC і січній AM), а
∠BAM = ∠MAD (за означенням бісектриси).
Отже, AB = BM = 5 см.
BC = BM + MC = 5 см + 7 см = 12 см.
PABCD = 2(AB + BC) = 2 · (5 + 12) = 2 · 17 = 34 (см).
Відповідь: 34 см.
6.23 У паралелограмі ABCD AB = 4 см, BC = 12 см. Бісектриса кута A перетинає сторону BC у точці P. Знайдіть BP і PC.
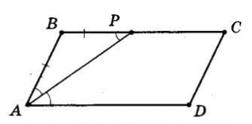
∠BPA = ∠PAD (як внутрішні різносторонні при AD || BC і січній AP);
∠BAP = ∠PAD (за означенням бісектриси).
Тоді ∠BAP = ∠BPA, тобто ΔABP — рівнобедрений, BP = AB = 4 см. BC = BP + PC, PC = BC − BP = 12 см − 4 см = 8 см.
Відповідь: 4 см, 8 см.
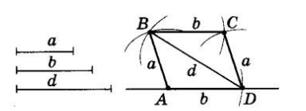
6.24 Побудуйте паралелограм за стороною і діагоналями. Припустимо, що ABCD шуканий паралелограм, O точка перетину його діагоналей.
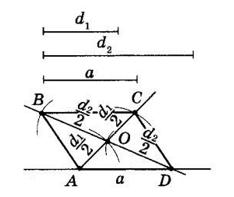
Тоді у нього AO = ����₁ 2 , DO = ����₂ 2 , AD = a. У ΔAOD
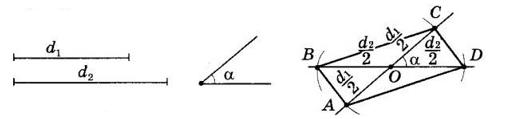
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
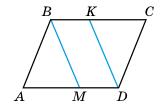
1. ABCD паралелограм, тому AB = CD, ∠ABM = ∠KDC.
2. ∠ABM = ∠KDC (за умовою). Тому ΔABM = ΔCDK (за
ознакою). Отже, AM = CK.
3. Оскільки AM = CK і AD = BC, то MD = BK.
4. MD = BK і MD || BK. Оскільки дві сторони чотирикутника BMDK паралельні й рівні, то за ознакою BMDK є паралелограмом, що й треба було довести.
6.27 На сторонах AD і BC паралелограма ABCD позначено точки M і K так, що AM = KC. Доведіть, що BMDK — паралелограм.

6.28 Доведіть, що
перпендикулярні.
1. ABCD паралелограм, тому AD = BC; AD || BC.
2. За умовою AM = KC.
3. BK = BC − KC; MD = AD − AM. Тому BK = MD.
4. BK || MD і BK = MD. Оскільки дві сторони чотирикутника BMDK паралельні й рівні, то за ознакою BMDK є паралелограмом, що й треба було довести.
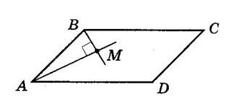
Якщо AM і BM бісектриси кутів A і B, то ∠BAM = 1 2 ∠A, ∠ABM = 1 2 ∠B. ABCD — паралелограм, тому ∠BAM + ∠ABM = 1 2 (∠A + ∠B) = 1 2 · 180° = 90°.
З ΔAMB ∠AMB = 180° − (∠BAM + ∠ABM) = 180° − 90° = 90°.
Таким чином, у будь−якому
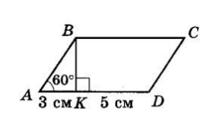
AB = 2AK = 2 · 3 см = 6 см
AD = AK + KD = 3 см + 5 см = 8 см.
BC = AD = 8 см.
BK ⊥ AD — висота.
З ΔABK (∠K = 90°)
∠ABK = 90° − ∠BAK = 90° − 60° = 30°.
PABCD = 2(AB + AD) = 2 · (6 + 8) = 28 (см). Відповідь: 28 см.
6.30 У паралелограмі
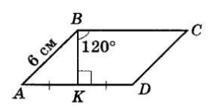
AK = 1 2
ABCD паралелограм, тоді ∠A + ∠B = 180°, ∠A = 180° − ∠B = 180° − 120° = 60°.
BK ⊥ AD — висота. З ΔABK ∠ABK = 90° − ∠A= 90° − 60° = 30°.
AB = 1 2 · 6 см = 3 см як
AD = 2AK = 2 · 3 см = 6 см за умовою.
PABCD = 2(AB + AD) = 2 · (6 + 6) = 24 (см).
Відповідь: 24 см.
30°.
LAK = 140°.
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
C
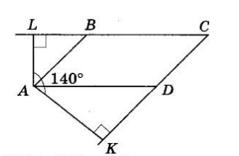
ABCD паралелограм. AL ⊥ BC, AK ⊥ CD його висоти.
Оскільки BC || AD, AB || CD, то AL ⊥ AD, AK ⊥ AB.
∠LAK = ∠LAD + ∠DAK,
∠DAK = ∠LAK − ∠LAD = 140° − 90° = 50°.
Аналогічно, ∠LAB = ∠LAK − ∠BAK = 140° − 90° = 50°.
∠BAD = ∠LAK – (∠LAB + ∠DAK) = 140° − (50° + 50°) = 40°.
∠C = ∠BAD = 40° як протилежні кути
Відповідь: 40°.
6.32 У паралелограмі ABCD з вершини тупого
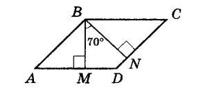
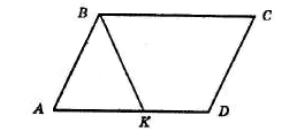
умовою
CBK і
паралельних прямих BC і AD і січній BK.
Тому ΔABK — рівнобедрений, AB = AK = x см.
Тоді KD = (x – 1) см, AD = (2x − 1) см.
Периметр паралелограма дорівнює (x + 2x – 1) · 2, що за умовою становить 40 см. (AB + BC) = 40 см. (x + 2x – 1) · 2 = 40; 3x – 1 = 20; 3x = 21; x = 7.
Отже, AB = AK = 7 см, AD = 7 + 7 – 1 = 13 (см). BC = AD = 13 см; CD = AB = 7 см.
Відповідь: 7 см, 13 см.
6.34 Бісектриса кута
BK : KC = 3 :
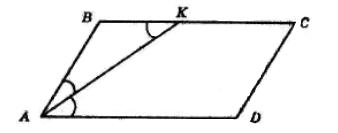
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
умовою 26x = 78, x = 3. AB = BK = 3 · 3 = 9 (см); BC = 10 · 3 = 30 (см).
Відповідь: 9 см, 30 см. 6.35 Два
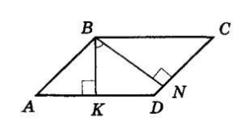
1. ABCD паралелограм. BK ⊥ AD, BN ⊥ CD
висоти, проведені з вершини тупого кута B. За умовою ∠A : ∠B = 5 : 7.
Нехай x — коефіцієнт пропорційності, тоді
∠A = ∠C = 5x,
∠B = ∠D = 7x
Сума сусідніх кутів паралелограма дорівнює 180°.
5x + 7x = 180;
12x = 180; x = 15.
Отже, ∠D = 7 · 15° = 105°.
Сума кутів чотирикутника KBND = 360°:
∠KBN + ∠BND + ∠NDK + ∠BKD = 360°;
∠KBN + 90° + 105° + 90° = 360°;
∠KBN = 360° − 285° = 75°.
Відповідь: 75°.

2. ABCD паралелограм. AM ⊥ BC, AN ⊥ CD висоти, проведені з вершини гострого кута A.
За умовою ∠A : ∠B = 5 : 7.
Нехай x — коефіцієнт пропорційності, тоді
∠A = ∠C = 5x,
∠B = ∠D = 7x
Сума сусідніх
5x + 7x = 180;
12x = 180; x = 15.
∠C = 5 · 15° = 75°.
∠A + ∠M + ∠C + ∠N = 360°;
∠A + 90° + 75° + 90° = 360°;
∠A + 255° = 360°;
∠A = 105°. Відповідь: 105°.
2x = 168; x = 84.
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
∠A = ∠C = 84°;
∠B = ∠D = 84° + 12° = 96°.

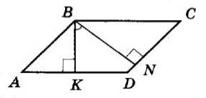
6.37
1. AM ⊥ BC, AN ⊥ CD висоти, проведені з вершини
гострого кута A.
Сума кутів чотирикутника AMCN дорівнює 360°:
∠A + ∠M + ∠C + ∠N = 360°;
∠A + 90° + 84° + 90° = 360°;
∠A + 264° = 360°;
∠A = 96°.
Відповідь: 96°.
2. BK ⊥ AD, BN ⊥ CD висоти, проведені з вершини
тупого кута B.
Сума кутів чотирикутника KBND дорівнює 360°:
∠KBN + ∠BND + ∠NDK + ∠BKD = 360°;
∠KBN + 90° + 96° + 90° = 360°;
∠KBN + 276° = 360°;
∠KBN = 84°.
Відповідь: 84°.
точці (ортоцентрі трикутника).
Доведення. 1. Нехай AH1, BH2, CH3 — висоти гострокутного трикутника ABC. Проведемо через
Одержимо трикутник A1B1C1. Чотирикутник
Тому BA1 = AC.
Аналогічно
одній точці. Доведення аналогічне до доведення п. 1.
1. Нехай AH1, BH2, CH3 — висоти
через вершини трикутника прямі, паралельні протилежним сторонам. Одержимо трикутник A1B1C1.Чотирикутник ABA1C — паралелограм (за побудовою).
Тому BA1 = AC. Аналогічно ACBC1 — паралелограм і C1B = AC. Отже, C1B = BA1, точка B — середина A1C1.
BH2 ⊥ AC і AC || A1C1, то BH2 ⊥ A1C₁.
BH2 належить серединному перпендикуляру
AH1 і
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
6.38
1. 20°;
2. 65°
1. 90° − 20° = 70°;
2. 90° − 65° = 25°.
6.39 Дві сторони
7,2 − 2,5 < c < 7,2 + 2,5; 4,7 < c < 9,7.
Отже, c = 9 см.
Відповідь: 9 см.
6.40 Зовнішній кут трикутника
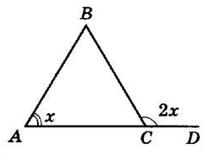
з ним. Доведіть, що трикутник є рівнобедреним. ∠BCD зовнішній кут трикутника ABC.
6.41
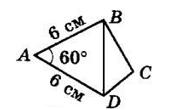
між рівними сторонами?
Нехай ∠A = x, тоді ∠BCD = 2x за умовою.
∠BCA = 180° − 2x (як суміжний з ∠BCD).
Сума кутів ΔABC дорівнює 180°:
∠B = 180° − (∠A + ∠BCA);
∠B = 180° − (x + (180° − 2x));
∠B = 180° − x − 180° + 2x = x
Отже, ∠B = ∠A, значить, ΔABC рівнобедрений.
сторонами 6 см, 6 см, 4 см
Припустимо, що ABCD шуканий чотирикутник,
BD — його діагональ.
AB = AD = 6 см, ∠A = 60°.
Тоді ΔABD — рівносторонній, BD = 6 см.
В ΔBCD: BC + CD = 4 см + 2 см = 6 см.
Маємо: BC + CD = BD, що суперечить нерівності трикутника. Відповідь: ні, не можна.
6.42 Знайдіть периметр і площу прямокутника, сторони якого
1. 5 см і 7 см;
2. 2 дм і 14 см.
1. a = 5 см, b = 7 см.
P = 2(5 + 7) = 24 см; S = 5 · 7 = 35 см2
6.43 1.
2. a = 2 дм = 20 см, b = 14 см.
P = 2(20 + 14) = 68 см; S = 20 · 14 = 280 см2
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
2) 0,1 м2 — 80 кг 1 м2 — ?
80 · 0,1 = 800 (кг) — важить 1 м2 зерна.
3) 12 · 8 · 2,5 = 12 · 20 = 240 (м2) — об'єм засіка.
4) 240 · 800 = 192 000 (кг) = 192 (т) — загальна вага зерна. 2.
192 · 6000 = 1 152 000 (грн)
2. Українська
3. Український письменник,
політичний діяч (1856-1916).
4. Відома спортсменка, рекордсменка
5.



https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html

8 см, діагональ BD = 12 см. Діагоналі прямокутника рівні, тому AC = BD = 12 см. Діагоналі точкою перетину діляться навпіл:
BO = CO = 1 2 BD = 6 см.
PΔABC = BD + 2BO = 8 + 2 · 6 = 20 (см).
Відповідь: 20 см.
7.7 O — точка перетину діагоналей прямокутника ABCD. AC = 12 см, периметр трикутника AOB дорівнює 16 см. Знайдіть сторону AB.

7.8 (Усно) Що
2.
У прямокутнику ABCD діагоналі рівні і точкою
діляться навпіл.
Тому BD = AC = 12 см, BO = AO = 12 : 2 = 6 см.
PΔAOB = AB + 2AO;
AB = PΔAOB − 2AO.
AB = 16 − 2 · 6 = 16 − 12 = 4 (см).
Відповідь: 4 см.
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
дорівнює 360° : 4 = 90°. ABCD
1. Нехай BC = x см, тоді AB = (x + 2) см.
P = (x + (x + 2)) · 2 = (2x + 2) · 2 = 4x + 4.
За умовою, 4x + 4 = 40; x + 1 = 10; x = 9.
Отже, BC = 9 см, AB = 9 + 2 = 11 см.
2. Нехай x коефіцієнт пропорційності.
Тоді AB = 2x, BC = 3x
P = (2x + 3x) · 2 = 10x.
За умовою, 10x = 40; x = 4.
AB = 2 · 4 = 8 см, BC = 3 · 4 = 12 см.
2. сторони відносяться як 4 : 1.
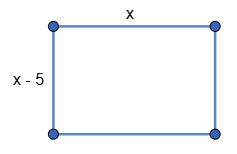
1. Нехай a = x см, тоді b = (x − 5) см. P = (a + b) · 2 = (x + x − 5) · 2 = (2x − 5) · 2 = 4x − 10.
За умовою 4x − 10 = 50; 4x = 60; x = 15.
a = 15 см, b = 15 − 5 = 10 (см).
Відповідь: 15 см, 10 см.

https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
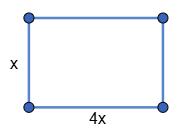
x коефіцієнт
Тоді a = 4x,
b = x.
P = (4x + x) · 2 = 10x.
За умовою 10x = 50;
x = 5.
a = 4 · 5 = 20 (см), b = 5 см.
Відповідь: 20 см, 5 см.
7.13 (Усно) На
кути. ∠1 = ∠5 = ∠4 = ∠8; ∠
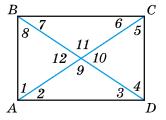
7.14 Знайдіть за малюнком:
1. ∠3, якщо ∠8 = 50°;
2. ∠2, якщо ∠10 = 41°.

7.15 Знайдіть за малюнком:
1. ∠5, якщо ∠2 = 40°; 2. ∠12, якщо ∠3 = 32°.

1. Якщо ∠8 = 50°, то ∠3 = 90° – 50° = 40°.
2. Якщо ∠10 = 41°, то ∠2 = 10 : 2 = 41° : 2 = 20,5°.
Відповідь: 1. 40°; 2. 20,5°.
1. Якщо ∠2 = 40°, то ∠5 = 90° – 40° = 50°.
2. Якщо ∠3 = 32°, то ∠12 = 2 · ∠3 = 2 · 32° = 64°.
1. 50°; 2. 64°. 7.16

https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
1.
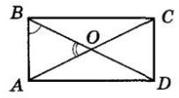
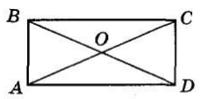
У прямокутнику ABCD AC і BD — діагоналі, O — точка їх перетину, AB < BC.
1. Нехай ∠AOB = x, тоді ∠ABO = x − 15°. ∠OAB = ∠ABO як кути при основі рівнобедреного ΔAOB (AO = BO як половини рівних діагоналей).
Сума кутів трикутника 180°.
x + x + 15 + x − 15 = 180;
3x – 30 = 180;
3x = 210; x = 70.
∠AOB = 70°;
∠ABO = 70° – 15° = 55°.
Відповідь: 55°.
2. Нехай ∠ABO = x, тоді ∠BOC = x + 50°.
∠AOB = 180° − (x + 50°) = 130° − x (як суміжні).
∠OAB = ∠ABO як кути при основі рівнобедреного ΔAOB (AO = BO як половини рівних
x + x + 130 − x = 180;
x + 130 = 180;
x = 50.
∠ABO = 50°.
Відповідь: 50°. 7.19
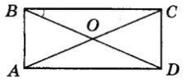
3x = 90; x = 30.
∠OBC = 30°.
Відповідь: 30°.
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
2. Нехай ∠CBO = x, тоді ∠AOB = x + 40°.
Тоді ∠BOC = 180° − ∠AOB = 180° − (x + 40°) = 180° − x − 40° = 140° − x
(∠AOB і ∠COB — суміжні).
∠BCO = ∠CBO як кути при основі рівнобедреного трикутника BOC (BO = CO як
половини рівних діагоналей).
x + x + 140 − x = 180; x = 180 – 140; x = 40.
∠CBO = 40°.
Відповідь: 40°.
7.20 У прямокутнику ABCD діагоналі перетинаються
CAB = 70°. Знайдіть ∠ DOE.
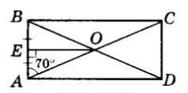
ABCD — прямокутник, O — точка перетину його діагоналей; BE = AE; ∠CAB = 70°.
У ΔAOB AO = BO як половини рівних діагоналей.
За умовою OE — медіана рівнобедреного ΔAOB.
Значить, OE ⊥ AB.
У ΔAOE ∠AOE = 90° − ∠OAE = 90° − 70° = 20°.
OE — бісектриса ∠AOB:
∠BOE = ∠AOE = 20°.
∠DOE = ∠DOB = ∠BOE (як суміжні).
∠DOE = 180° − 20° = 160°.
Відповідь: 160°.
7.21 У прямокутнику ABCD діагоналі
трикутника AOB, ∠ DOP = 130°. Знайдіть ∠ CAB.
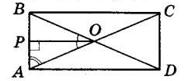
ABCD — прямокутник, O — точка перетину
OP —
ΔAOB; ∠DOP = 130°.
ΔAOB — рівнобедрений, AO = BO як
∠BOP = 180° − ∠DOP = 180° − 130° = 50° (як суміжні).
∠AOP = ∠BOP = 50° за умовою.
З ΔAOP (∠P = 90°) ∠OAP = 90° − 50° = 40°.
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
Отже, ∠CAB = 40°.
Відповідь: 40°.
7.22 У
BMDN — прямокутник.

ABCD — паралелограм, O — точка перетину його діагоналей.
OM = OB, ON = OD.
ΔBON = ΔMOD за двома сторонами і кутом між
∠BON = ∠MOD як вертикальні).
BO = OD за властивістю діагоналей паралелограма.
Тоді MO = BO = ON = OD і BDО = MN.
(BO = MO, DO = NO
Трикутники MOD і BON — рівнобедрені, їх кути при основі рівні.
З рівності трикутників випливає, що BN = MD, ∠BNO = ∠DMO, а ці кути є внутрішніми
різносторонніми при прямих BN і MD і січній MN.
Отже, BN || MD.
MBND — паралелограм (BN || MD, BN = MD).
Раніше довели, що BD = MN, тому MBND — прямокутник.
7.23 Точки B і D належать колу із центром O, AC — діаметр кола, AD = BC. Доведіть, що ABCD — прямокутник.
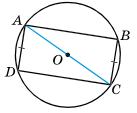
AC діаметр кола, тому ΔABC і ΔADC прямокутні. ΔABC = ΔCDA за катетом і гіпотенузою (AD = BC за умовою, AC — спільна гіпотенуза).
Звідси ∠CAD = ∠ACB.
Ці кути внутрішні різносторонні при прямих AD і BC і січній AC, тому AD || BC.
ABCD — паралелограм за ознакою (AD || BC, AD = BC).
ABCD — прямокутник за ознакою, як паралелограм, який має прямий кут. 7.24 Перпендикуляри, проведені з точки перетину діагоналей прямокутника до його сусідніх сторін, дорівнюють 4 см і 9 см. Визначте периметр прямокутника. ABCD прямокутник. NO ⊥ BC, MO ⊥ AB, тоді NO || AB, MO || BC за ознакою

MBNO —
У ΔAOB BO = AO, тоді висота OM є
AB = 2BM = 2 · 4 см = 8 см.
Аналогічно BC = 2BN = 2 · 9 см = 18 см.
PABCD = 2(AB + BC) = 2 · (8 + 18) = 2 · 26 = 52 (см).
Відповідь: 52 см.
7.25
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html

Тоді ∠BAK = ∠BKA,
ABCD прямокутник, AK — бісектриса кута A.
BK = KC.
∠BKA = ∠KAD як
AK.
у ΔABK AB = BK = 1 2 BC = 20 см : 2 = 10 см.
PABCD = 2(AB + BC) = 2 · (10 + 20) = 2 · 30 = 60 см.
Відповідь: 60 см.
7.26
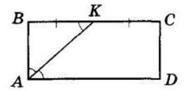
Тоді ∠BAK = ∠BKA,
у ΔABK AB = BK = 8 дм.
BC = 2BK = 16 дм.
ABCD прямокутник, AK — бісектриса кут а A. BK = KC.
∠BKA = ∠KAD як
різносторонні при BC || AD і січній AK.
PABCD = 2(AB + BC) = 2 · (8 + 16) = 2 · 24 = 48 (дм).
Відповідь: 48 дм.
7.27 На малюнку ABCD — прямокутник, BK ⊥ AC, ∠ ACD = 60°:
1. OK = a. Знайдіть: DB і AB; 2. AC = m Знайдіть: AK і CD.
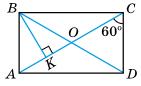
1. ∠BAC = ∠ACD = 60° як внутрішні різносторонні при AB || CD і січній BD.
ΔABO — рівнобедрений, AO = OB за властивістю діагоналей прямокутника.
Тоді ∠ABO = ∠OAB = 60° як кути при основі.
∠AOB = 180° − 2 · 60° = 60°.
ΔAOB — рівносторонній. Висота BK є медіаною.
AO = 2AK = 2a.
AB = AO = 2a;
BD = 2BO = 2 · 2a = 4a.
Відповідь: 4a і 2a.
2. В ΔACD (∠D = 90°) ∠CAD = 90° − 60° = 30°.
Тоді CD = 1 2 AC = 1 2 m як катет, протилежний куту 30°.
∠BAC = ∠ACD = 60° як внутрішні різносторонні
ΔABO — рівнобедрений (AO = BO
при основі.
Тоді ΔAOB — рівносторонній.
AB = BO = AO = ���� 2 .
BK — висота і медіана.
AB || CD і січній BD.
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
AK = 1 2 AO = 1 2 · ���� 2 = ���� 4 .
Відповідь: ���� 4 ; ���� 2 .
7.28 На малюнку ABCD — прямокутник, BK ⊥ AC, ∠ ACD = 60°, AB = b. Знайдіть BD і
OK.
∠BAC = ∠ACD = 60° як внутрішні різносторонні при AB || CD і січній BD.
ΔAOB — рівнобедрений (AO = BO за властивістю
при основі.
Тоді ΔAOB — рівносторонній.
AB = BO = AO = b. BD = 2BO = 2b за властивістю
В ΔAOB BK — висота і медіана.
OK = 1 2 AO = 1 2 b = ���� 2 .
Відповідь: 2b; ���� 2 .
7.29 У рівнобедреній

7x = 35; x = 5.
KN = 2 · 5 = 10 (см).
KL = 3 · 5 = 15 (см).
Тоді KL = 3x, KN = 2x. В ΔABC ∠B = ∠C = 45°.
Тоді ΔBKN і ΔMLC також
NK = BK = ML = LC = 2x.
і рівнобедрені;
BC = BK + KL + LC = 2x + 3x + 2x = 7x або 35 см за умовою.
P = 2(KN + KL) = 2 · (10 + 15) = 50 (см).
Відповідь: 50 см.
7.30 У рівнобедрений прямокутний

В ΔABC (∠A = 90°) AB = AC = 20 см, AKMN
ΔKBM і ΔMNC — прямокутні і рівнобедрені (KM = KB, MN = NC).
AK = MN, AN = KM так як AKMN – прямокутник. Отже, KA + KM = KA + KB = AN + NC = AN + NM = 20 см. PAKMN = 2 · 20 = 40 (см). Відповідь: 40 см. 7.31
якщо BK = 1 2 AB.
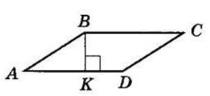
ABCD — паралелограм, BK ⊥ AD, BK = 1 2 AB.
В ΔABK (∠K = 90°) BK = 1 2 AB за умовою, тоді ∠A = 30°.
∠C = ∠A = 30° як протилежні.
∠B = 180° − ∠A = 180° − 30° = 150°;
7.32 1.
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
2 + x = 180;
3x = 360; x = 120.
120° : 2 = 60°.
Відповідь: 60°.
2. Нехай x — сума трьох кутів чотирикутника.
Тоді четвертий кут дорівнює ���� 3 .
3 + x = 360;
4x = 360 · 3; x = 270.
270° : 3 = 90°.
Відповідь: 90°.
7.33 Через точку P, що

7.34 Дано: AB = BC = CD = DA.
P
ABC. Проведемо промінь BP і
ньому PN = BP. Побудуємо NK || BC і NM || AB. BKNM — паралелограм. Його діагональ KM точкою P ділиться навпіл. Отже, KM — шукана пряма.
Довести: ∠ A = ∠ C, ∠ B = ∠ D. ΔABD = ΔCBD за трьома сторонами (AB = BC = CD = AD за умовою, BD — спільна сторона).
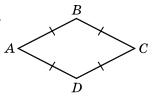
7.35
∠A = ∠C. Аналогічно ΔABC = ΔABC, ∠B = ∠D.
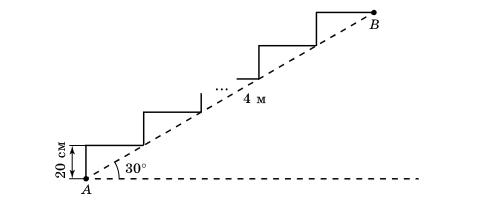
BC
BC:
20 см · x = 200 см
x = 200 : 20
x = 10 — сходинок.
Відповідь:
7.36



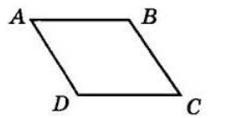
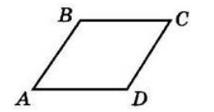
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
Відповідь: 65°.
8.8 Діагональ
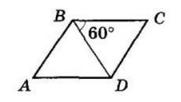
8.9 Діагональ
20° · 2 = 40°.
Відповідь: 40°.
8.10 У ромбі ABCD кут A дорівнює 36°. Знайдіть кути трикутника AOB, де O — точка
перетину діагоналей.
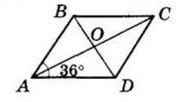
8.11 O —
ABCD ромб, ∠A = 36°, O — точка перетину діагоналей.
∠BAO = ∠DAO = 1 2 ∠A = 18°,
∠BOA = 90° за властивістю діагоналей ромба.
∠ABO = 90° − ∠BAO = 90° − 18° = 72°.
Відповідь: 18°, 90°, 72°.
BOC

8.12
P = 4 · 7
= 28 см.
ромба: 16 см : 2 = 8 см.
P = 4 · 8 см = 32 см.
Відповідь: 32 см.
8.14 ABCD — ромб, ∠ 2 = 66°.
∠BOC = 90°, ∠OBC = 1 2 ∠B = 1 2 · 118° = 59°.
∠BCO = 90° − ∠OBC = 90° − 59° = 31°.
Відповідь: 90°, 59°, 31°.
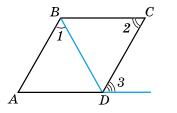
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
∠B = 180° − ∠2 = 180° − 66° = 114°.
∠1 = 1 2 ∠B = 1 2 · 114° = 57°.
Відповідь: 57°.
8.15 ABCD — ромб, ∠ 1 = 58°. Знайдіть ∠ 2 .

∠B = 2 · ∠1 = 2 · 58° = 116°.
∠2 = 180° − ∠B = 180° − 116° = 64°.
Відповідь: 64°.
8.16 ABCD — ромб, ∠ 1 = 55°.
Знайдіть ∠ 3 . ∠BDC = ∠1, оскільки ∠B = ∠D, ∠1 = 1 2 ∠B, ∠BDC = 1 2 ∠D.

Тоді ∠D = 2∠BDC = 2 · 55° = 110°.
∠3 = 180° − ∠D = 180° − 110° = 70° (суміжні кути).
Відповідь: 70°.
8.17 ABCD — ромб, ∠ 3 = 50°.
Знайдіть ∠ 1 .

∠D = 180° − ∠3 = 180° − 50° = 130° (суміжні кути).
∠B = ∠D як протилежні кути ромба.
∠1 = 1 2 ∠B = 1 2 · 130° = 65° за властивістю діагоналей ромба.
Відповідь: 65°.
8.18 У ромбі ABCD, AB = BD. Знайдіть
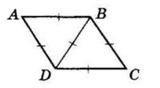
8.19 (Усно)
ABCD ромб, AB = BD за умовою.
Але AB = BC = CD = AD.
Тоді ΔABD — рівносторонній.
∠A = 60°.
∠B = 180° − ∠A = 180° − 60° = 120°.
∠C = ∠A = 60°.
∠D = ∠B = 120°.
Відповідь: 60°, 120°, 60°, 120°.

1.
протилежні, тому рівні.
∠A = ∠C = 80° : 2 = 40°.
Тоді ∠B = ∠D = 180° − 40° = 140°.
Відповідь: 40°, 140°, 40°, 140°.
2. Оскільки дані кути не рівні, то вони не протилежні, а сусідні; їх сума дорівнює 180°.
Нехай ∠A = x°, тоді ∠B = (x + 20)°.
x + x + 20 = 180;
2x = 160; x = 80.
∠A = ∠C = 80°, ∠B = ∠D = 80° + 20° = 100°.
Відповідь: 80°, 100°, 80°, 100°.
8.21 Знайдіть
1. сума
2.
другого.
1. Сума даних кутів не дорівнює 180°, отже, ці кути не
протилежні, тому рівні.
∠B = ∠D = 2 ∠105°. Тоді ∠A = ∠C = 180° − 105° = 75°.
Відповідь: 75°, 105°, 75°, 105°.
2. Оскільки кути не рівні, то вони не протилежні,
∠A = x°;
тоді ∠B = (x + 50)°;
x + x + 50 = 180;
2x = 130;
x = 65.
∠A = ∠C = 65°;
∠B = ∠D = 65° + 50° = 115°.
Відповідь: 65°, 115°, 65°, 115°.
8.22 (Усно) Чи правильне твердження:
1. якщо в чотирикутнику діагоналі перпендикулярні, то він є ромбом; 2. якщо в чотирикутнику
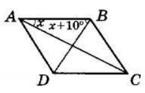
2
4x + 20 =
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
4x = 160; x = 40.
Отже, ∠A = ∠C = 2 · 40° = 80°; ∠B = ∠D = 2 · (40° + 10°) = 100°.
Відповідь: 80°, 100°, 80°, 100°.
8.24 Знайдіть
як 2 : 3.
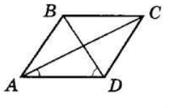
8.25 Побудуйте ромб: 1. за стороною і
2. за діагоналями.
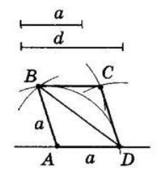
Нехай x коефіцієнт пропорційності, тоді ∠CAD = 2x, ∠BDA = 3x. ∠A = 2∠CAD = 4x; ∠D = 2∠BDA = 6x.
4x + 6x = 180;
10x = 180; x = 18.
∠A = ∠C = 4 · 18° = 72°;
∠B = ∠D = 6 · 18° = 108°.
Відповідь: 72°, 108°, 72°, 108°.
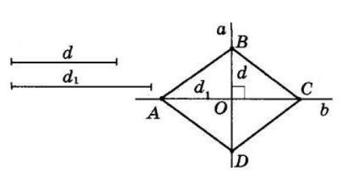
1. План побудови: 1. Побудувати трикутник ABD за трьома сторонами AB = AD = a, BD = d. Для цього провести пряму, вибрати
точку A. Побудувати коло радіуса a з центром A, воно перетне пряму в точці D. Побудувати коло радіуса d з центром D. B — точка перетину двох кіл. 2. Провести два кола з центрами B і D радіуса a. C — точка їх перетину.
3. ABCD — ромб. AB = BC = CD = AD = a, BD = d.
2. План побудови: 1. a ⊥ b.
2. OB = OD = 1 2 d1, OA = OC = 1 2 d2.
3. ABCD — ромб, BD = d1, AC = d2.
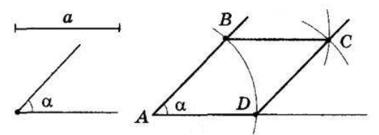
1. ∠A = α.
2. AB = a, AD = a.
3.
4.
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
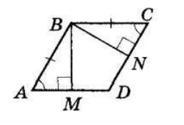
8.28
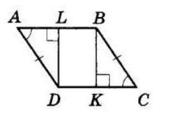
ABCD ромб, ∠B тупий, BM ⊥ AD, BN ⊥ CD.
△ABM = △CBN за
(AB = BC, ∠A = ∠C
⊥ AB,
∠A = ∠C за властивостями ромба). Звідси випливає, що DL = BK.

8.30 Висоти, проведені
Знайдіть кути ромба.
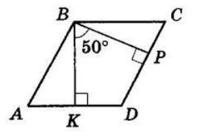
ABCD ромб, ∠A гострий кут.
AK ⊥ BC, AP ⊥ CD, ∠KAP = 110°.
BC || AD, AK ⊥ BC, тоді AK ⊥ AD.
∠KAP = ∠KAD + ∠DAP, ∠DAP = ∠KAP − ∠KAD = 110° − 90° = 20°.
Аналогічно, ∠KAB = 20°.
∠BAD = ∠KAP − (∠KAB + ∠DAP) = = 110° − (20° + 20°) = 70°.
∠C = ∠A = 70°, ∠B = ∠D = 180° − 70° = 110°.
Відповідь: 70°, 110°, 70°, 110°.
ABCD ромб, ∠B тупий. BK ⊥ AD, BP ⊥ CD. Сума кутів чотирикутника KBPD дорівнює 360°:
∠K + ∠KBP + ∠P + ∠D = 360°, ∠D = 360° − (∠K + ∠KBP + ∠P) = = 360° − (90° + 50° + 90°) = 360° − 230° = 130°. ∠B = ∠D = 130°, ∠A = ∠C = 180° − 130° = 50°.
50°, 130°, 50°, 130°. 8.31
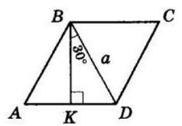
1. З △BКD ∠BDK = 90° − ∠KBD = 90° − 30° = 60°.
∠D = 2 · ∠KBD = 2 · 60° = 120° (
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
∠B = ∠D = 120°, ∠A = ∠C = 180° − ∠D = 180° − 120° = 60°.
Відповідь: 60°, 120°, 60°, 120°.
2. Рівнобедрений трикутник з
AB = AD = BD = a см, PABCD = 4a см.
Відповідь: 4a см.
8.32 У ромбі висота, проведена з вершини тупого кута, ділить сторону
Знайдіть:
1. кути ромба;
2. периметр ромба, якщо його менша діагональ дорівнює b см.
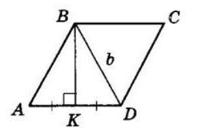
ABCD ромб, ∠B тупий, BD = b см
BK ⊥ AD, AK = KD.
У △ABD AB = AD за означенням ромба.
Але у △ABD висота BK за умовою є медіаною, отже, AB = BD.
Тоді △ABD рівносторонній.
∠A = ∠C = 60°. ∠B = ∠D = 180° − 60° = 120°.
AB = AD = BC = CD = b см.
PABCD = 4b см.
Відповідь: 1. 60°, 120°, 60°, 120°; 2. 4b см. 8.33
що AM =

розміщення точок M і N). 1 випадок
ABCD ромб, тому AB = BC = CD = AD.
AM = CN за умовою.
∠BAM = ∠DAM = ∠BCN = ∠DCN за властивістю ромба.
Тоді △AMB = △AMD = △CNB = △CND за двома сторонами і кутом між ними.
Звідси BM = BN = DN = DM.
∠BNC = ∠DNC = ∠BMA = ∠DMA, тоді ∠BNM = ∠DNM = ∠BMN = ∠DMN як суміжні з рівними кутами, а вони є внутрішніми різносторонніми при прямих BN і MD та BM і ND та січній MN.
Тоді BN || MD, BM || ND.
MBND паралелограм, у якого всі сторони рівні, тобто, ромб.
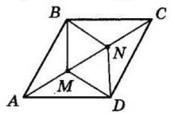
2 випадок
ABCD ромб, AC його діагональ, AM = CN.
△ABM = △CDN за двома сторонами і кутом між ними (AB = CD, AM = CN за умовою, ∠BAM = ∠DCN за властивістю діагоналей). З рівності трикутників BM = DN, ∠BMA = ∠DNC. Ці кути внутрішні різносторонні
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
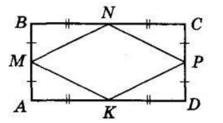
то MNPK ромб.
8.35 У рівносторонній трикутник ABC вписано
мають спільний кут A , а точка N лежить на стороні BC . Знайдіть периметр трикутника, якщо периметр ромба дорівнює 40 см. △ABC рівносторонній, AMNK ромб.

8.36 Сторони
∠A = ∠B = ∠C = 60°.
∠BMN = ∠A = 60°, ∠NKC = ∠A = 60° як відповідні.
Тоді △MBN і △KNC рівносторонні.
MN = BN = MB, KC = KN = NC.
PAMNK = 4AM, 4AM = 40 см, AM = 10 см.
PABC = AM + MB + NC + AK + KC = 6AM = 60 см.
Відповідь: 60 см.
як 5 : 2 .
15 см. Нехай x

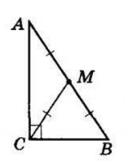
менша сторона дорівнює 2x см, а
більша 5x см.
За умовою: 5x − 2x = 15 3x = 15 x = 5
Периметр паралелограма: (2x + 5x) · 2 = 14x 14 · 5 = 70 (см).
Відповідь: 70 см.
2. Ні. 2p − p = p.
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
3. Ні. 2p − (p − 1) = 2p − p − 1 = p – 1. p + 1 > p − 1. Сторона
чотирикутнику ABCD бісектриса кута A перетинає бісектриси
прямим кутом. Визначте вид чотирикутника ABCD.
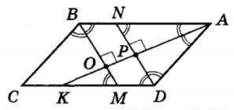
ABCD — чотирикутник. AK, BM і DN — бісектриси кутів A, B і D відповідно.
DN ⊥ AK, BM ⊥ AK за умовою.
Тоді BM || DN за ознакою (дві прямі, перпендикулярні третій, паралельні).
∆APN = ∆ADP за спільним катетом AP і гострим кутом (∠NAP = ∠DAP за умовою).
Звідси ∆ANP = ∆ADP.
∠ANP = ∠NDC — внутрішні різносторонні при прямих AB || CD і січній ND.
За ознакою AB || CD.
MBDN — паралелограм за означенням. ∠NBM = ∠NDM = ∠CBM, ∠NBM = ∠BMC як
внутрішні різносторонні. Тоді ∆MCB = ∆NAD за стороною і прилеглими
BC = AD, ∠A = ∠C, AB = CD.
ABCD — паралелограм.
Відповідь: паралелограм.
8.40 Знайдіть периметр
1. 5 см; 2. 2,1 дм; 3. 3 4 м; 4. 11 2 дм.
P = 4a, S = a2 .
1. P = 4 · 5 = 20 (см); S = 5 · 5 = 25 (см2).
3. P = 43 4 = 3 (м); S = (3 4)2 = 9 16 (м2).
2. P = 4 · 2,1 = 8,4 (дм); S = 2,12 = 4,41 (дм2).
4. P = 4 · 11 2 = 6 (дм); S = (11 2)2 = (3 2)2 = 9 4 = 21 4 (дм2).
1. 2 · (5 · 3) + 2 · (3,5 · 3) = 2 · 15 + 2 · 10,5 = 30 + 21 = 51 (м2) – площина стін
51 – 51 · 1 6 = 51 – 8,5 = 42,5 (м2) –
10 · 0,5 = 5 (м2) – площа рулону
42,5 : 5 = 8,5 = 9 – рулонів.
2. 9 · 180 = 1620 (грн) – вартість
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
1620 грн · 5% = 1620 · (100% − 5%) = 1620 · 95% = 1620 · 0,95 = 1539
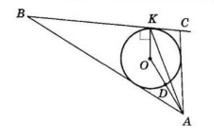
9.1
За нерівністю трикутника: OK < AK − OA ; OK < AK − OD − DA ; OK + OD < AK − DA ; d < AK − DA . Оскільки DA > O, то очевидно, що d < AK.
P = 4a , де a — сторона квадрата. a = P : 4; a = 24 см : 4 = 6 см.
6 см.
9.2 Сторона квадрата дорівнює
P = 4 · 5 дм = 20 дм.
9.3 (Усно
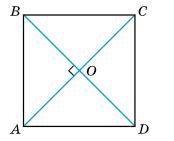
AB = BC = CD = AD ; OA = OB = OC = OD ; AC = BD . 9.4

AO = 3 см, AC = 2AO = 6 см,
BD = AC = 6 см,
AC + BD = 6 см + 6 см = 12 см. Відповідь: 12 см.
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html

9.7
P = 2 · 12 см = 24 см.
9.8 Сума
a = 15 : 3 = 5 дм, P = 4a = 4 · 5 = 20 дм.
9.9
1. Протилежні сторони
3.
ABCD квадрат,
AC + BD = 16 см,
AC = BD , тоді AC = 16 : 2 = 8 см.
AO = 1 2 AC = 8 : 2 = 4 см.
Відповідь: 4 см.
4. Діагоналі ділять кути навпіл. 9.10 (Усно) Які спільні властивості
1. Протилежні сторони
2.
3. Діагоналі
4. Точка
9.11
квадрата та його периметр.
P = 4a, за умовою 4a – a = 18 см,
3a = 18 см, a = 6 см.
P = 4a = 6 · 4 = 24 см.
9.12 Сусідні сторони прямокутника рівні. Доведіть, що він є квадратом.
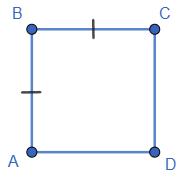
9.13 Один з
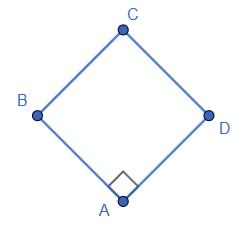
9.14 (Усно) Чи
ABCD прямокутник, AB = BC . Протилежні сторони прямокутника рівні.
Тоді AB = CD , BC = AD , а значить, AB = BC = CD = AD .
ABCD — квадрат.
ABCD ромб, ∠A = 90°.
Тоді ∠C = ∠A = 90° як протилежні; Оскільки, сума любих
∠B = 180° − ∠C = 180° − 90° = 90°;
∠D = ∠B = 90° як протилежні.
∠A = ∠B = ∠C = ∠D = 90°.
Отже, ABCD — квадрат.
рівна 180°, то:
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
1. Так; 2. Ні; 3. Ні; 4. Так; 5. Ні; 6. Так.
9.15 ABCD — квадрат, EF ⊥ BD. Знайдіть ∠ BFE . У ∆EBF, ∠ABD = ∠ FBD = 45° за властивістю діагоналі
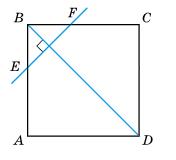
квадрата.
Висота є бісектрисою, тоді ∆EBF — рівнобедрений (EB = FB). ∠BFE = 45° (кут при основі рівнобедреного прямокутного трикутника).
Відповідь: ∠BFE = 45°.
9.16 ABCD — квадрат, ∠ BOC = 70°. Знайдіть ∠ OKA . У ∆AOK ∠AOK = ∠BOC = 70° як вертикальні, ∠OAK = 45° за
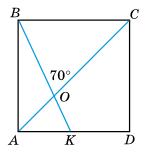
9.17 Побудуйте квадрат:
1. за його периметром; 2. за його діагоналлю.
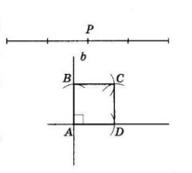
властивістю діагоналі.
∠OKA = 180° − (∠AOK + ∠OAK) = 180° − (70° + 45°) = 65°. Відповідь: 65°.
1. План побудови.
1. Побудувати дві взаємно перпендикулярні прямі, A
їх точка перетину.
2. Поділити даний відрізок p на 4 рівні частини.
3.
AD = 1 4 p
4. Провести кола радіуса 1 4 p з центрами

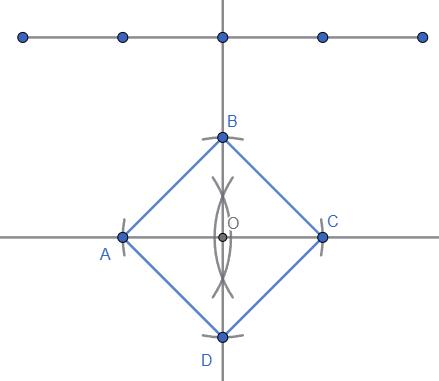
1.
2.
4.
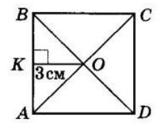
його діагоналей, OK ⊥ AB — відстань від точки O до сторони
AB, OK = 3 см. В ∆ABO OA = OB, OA ⊥ OB
властивістю діагоналей. OK –висота і медіана. ∆OBK ∠OBK = 45°, тоді ∠BOK = 45°, ∆OBK — рівнобедрений. BK = OK = 3 см. AB = 2BK = 2 · 3 = 6 см. PKB = 4 · 6 см = 24 см. Відповідь: 24 см.
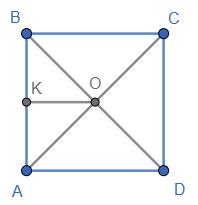
AK = KB = 1 2 AB = 4 см.
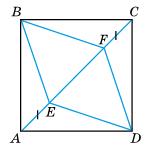
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
∆ABE = ∆CBF = ∆CDF = ∆ADE рівні
між ними (AB = BC = CD = AD, AE = CF за умовою, ∠BAE = ∠BCF = ∠DCF = ∠DAE за властивістю діагоналей).
Тоді BE = BF = DE = DF, EBFD паралелограм і ромб (протилежні сторони попарно рівні).
9.22 ABCD квадрат, AE = AF = CG = CH. Доведіть, що EFGH прямокутник. ∆AEF = ∆CHG за двома катетами (AE = AF = CG = CH за умовою).
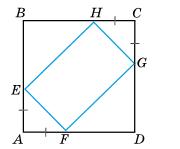
Тоді EF = HG. Оскільки сторони квадрата рівні, то EB = BH = GD = DF.
Тому ∆EBM = ∆GDF за двома катетами, звідки EH = FG. EFGH паралелограм (протилежні сторони попарно рівні).
∆EBH, ∆HCG, ∆EAF, ∆GDF є рівнобедреними прямокутними, їх гострі кути дорівнюють 45°.
∠EGH = 180° − (∠BHE + ∠CHG) = 180° − (45° + 45°) = 90°.
Отже, EFGH прямокутник за ознакою.
AB і AC , B і C точки
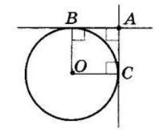
9.24 У
AC ⊥ AB за умовою, OB ⊥ AB, як радіус, проведений у точку
дотику, тоді AC || OB. Аналогічно
кола.
Тому ABOC ромб.
Кут A = 90° за умовою, отже, ABOC квадрат.
трикутник ABC (∠ C = 90°) вписано квадрат CMNK так, що прямий кут у
b см.
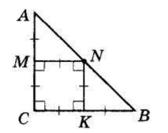
периметр квадрата. У ∆ABC кут C = 90°, CA = CB = b см, CMNK квадрат, вписаний у ∆ABC. ∆ABC прямокутний і рівнобедрений.
Тоді ∠CAB = ∠CBA = 45°. У ∆NKB ∠NKB = 90° як суміжний із прямим кутом, ∠NBK = 45°, тоді ∠BNK = 90° − 45° = 45°.
∆NKB прямокутний і рівнобедрений, NK = BK. MN = CK, як протилежні сторони квадрата.
Отже, катет дорівнює двом сторонам квадрата.
PCMNK = 2CB = 2b (см).
Відповідь: 2b см.
9.25 У рівнобедрений
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
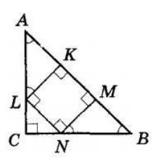
∆ABC прямокутний і рівнобедрений, тому ∠A = ∠B = 45°.
LK ⊥ AB за умовою, тоді в ∆ALK, ∠ALK = 45° і ∆ALK
рівнобедрений, тому LK = AK. Аналогічно в ∆NMB, NM = MB.
PLNMK = 12 см, тоді MK = 12 : 4 = 3 см. AB = AK + KM + MB = 3MK = 3 · 3 = 9 см. Відповідь: 9 см.
вершини трикутників, які не є
квадрата.
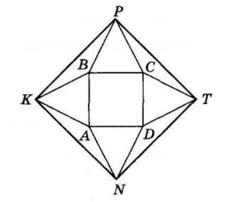
Розглянемо трикутники ABK, BCP, CDT, DAN.
Оскільки вони рівносторонні і
квадрата, то BK = BP = CP = CT = DT = DN = AN = AK і
всі кути цих трикутників дорівнюють 60°.
У квадрата ABCD ∠A = ∠B = ∠C = ∠D = 90°.
Тоді ∠KBP = ∠PCT = ∠TDN = ∠NAK = = 360° − (90° + 60° + 60°) = 150°.
∆AKP = ∆PCT = ∆TDN = ∆NAK за двома сторонами і
кутом між ними.
Тоді KP = PT = TN = NK і KPTN ромб.
∠KPT = ∠KPB + ∠BPC + ∠TCP, де ∠BPC = 60°, ∠KPB = ∠TPC (із рівності трикутників) і
∠KPB = ∠TPC = 180° − 150° 2 = 15°
Тоді ∠KPT = 15° + 60° + 15° = 90°.
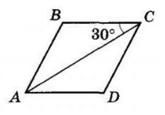
B = 180° −
A = 180° − 60° = 120°.
D = ∠B = 120° як протилежні.
60°, 120°, 60°, 120°. 9.28 У чотирикутнику
кутів чотирикутника дорівнює 360°.
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
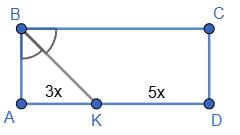
у точці K.
AK : KD = 3 : 5.
Тоді AK = 3x, KD = 5x.
∠AKB = ∠KBC як внутрішні різносторонні при BC || AD і січній BK. Тоді ∠BKA =
∠AKB, ∆ABK рівнобедрений, AB = AK = 3x.
CD = AB = 3x, AD = BC = 3x + 5x = 8x як протилежні сторони прямокутника.
PABCD = 2(AB + AD) = 2(3x + 8x) = 22x.
За умовою 22x = 110, x = 5.
Тоді AB = CD = 3 · 5 = 15 (см),
BC = AD = 5 · 8 = 40 (см).
Відповідь: 15 см; 40 см.
9.30. Виконайте множення:
9.31. Обчисліть:
1. 12 · (12 · 0,35) = 12 · 4,2 = 50,4 (м2) –
2. 3 · 2 · 1,7 = 6 · 1,7 = 10,2 (м2) – площа
3. 10,2 : 50,4 = 0,2024 – відношення площин.
Відповідь:
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
Відповідь: В. 145°
3. Знайдіть
A. 4 см Б. 6 см В. 9 см Г. 12 см
a = P : 4 = 36 : 4 = 9 (см).
Відповідь: В. 9 см.
4. Периметр прямокутника
Знайдіть довжину меншої сторони прямокутника: A. 5 см Б. 6 см В. 7 см Г. 8 см
1. Нехай AB = x см, тоді AD = x + 2 (см).
2. Тоді 2(x + x + 2) = 24; 2x + 2 = 12; 2x = 10; x = 5 (см).
Відповідь: A. 5 см.
5. ABCD — ромб, ∠ A = 50°. Знайдіть ∠ ABD :
A. 55° Б. 50° В. 75° Г. 65° 1. ∠ABC = 180° − ∠A = 180° − 50° = 130°. ����. ∠ABD = ∠ABC 2 =
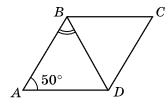
6. Укажіть правильне твердження: A.
Відношення
Г. 65°.
числам 2, 3, 5 і 8: A. 120° Б. 130° В. 150° Г. 160°
1. Позначимо кути 2x; 3x; 5x і 8x. Тоді 2x + 3x + 5x + 8x = 360°; 18x = 360°; x = 20°.
2. Найбільший кут чотирикутника 8 · 20° = 160°. Відповідь: Г. 160°.
8. Висоти,

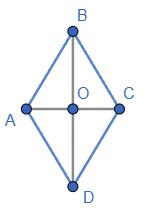
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
Нехай
ромб ABCD. ∠BAO − ∠ABO = 40°.
Знайти: ∠ABC — ?
Нехай ∠ABO = x°, тоді ∠BAO = x° + 40° і
x + x + 40 = 90.
2x + 40 = 90;
2x = 50; x = 25.
∠ABC = 2∠ABO = 2 ∙ 25° = 50
Відповідь: B. 50°.
що AK : KB = 1 : 3. Знайдіть AB, якщо периметр паралелограма дорівнює
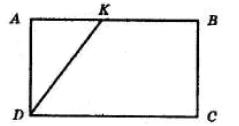
то DC || AB, DK — січна при прямих DC і AB. Отже, ∠AKD = ∠KDC як
і січній.
Тоді трикутник AKD — рівнобедрений з основою DK, оскільки ∠ADK = ∠KDC.
AK = AD = x см, KB = 3x см.
За умовою задачі 2(x + 4x) = 60,
тоді x + 4x = 30; 5x = 30; x = 6.
Отже, AD = 6 (см), AB = 4 · 6 = 24 (см).
Відповідь: Б. 24 см.
11. З вершини тупого кута A ромба ABCD проведено висоту AK . ∠ CAK = 30°, AC = 6 см. Знайдіть периметр ромба.
A. 18 см Б. 24 см В. 30 см Г. 36 см
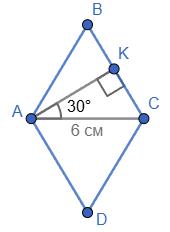
Нехай ABCD ромб, у якого AK ⊥ BC, тобто AK висота, ∠CAK = 30°, AC = 6 см.
Із трикутника ACK маємо: ∠ACK = 90° − ∠CAK = 90° − 30° = 60°.
Оскільки трикутник ACB — рівнобедрений, то ∠CAB = 60°. Тоді ∠B = 180° − 60° − 60° = 60°, отже, трикутник ACB є рівностороннім і за умовою AC = 6 см, то периметр ромба дорівнюватиме 4AB = 24 см. Відповідь: Б. 24 см.
AB = 12 см. A. 24 см Б. 20 см В. 12 см Г. 16 см
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html

Нехай ABC даний прямокутний трикутник, у якому
∠C = 90°, AC = CB, KNML — квадрат. AB = 12 см.
У трикутнику ABC ∠A = ∠B = 45°, оскільки цей трикутник рівнобедрений.
Отже, у трикутнику AKN, де ∠AKN = 90° (оскільки KNML — квадрат), теж ∠ANK = ∠KAN = 45°.
Таким чином, трикутник AKN — рівнобедрений, AK = KN.
Аналогічно в трикутнику LMB, де ∠MLB = 90°, ∠LMB = ∠B = 45° і LM = LB.
Оскільки AB = 12 см, то KL = 12 : 3 = 4 (см).
Отже, PKNML = 4KL = 16 см.
Відповідь: Г.
13. У прямокутнику ABCD діагоналі перетинаються
AOB
1. ∠ABO; 2. ∠AOB; 3. ∠OAD
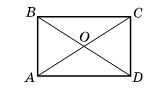
За умовою ∠ABO = ∠AOB – 18°: x = (180° – 2x) – 18° 3x = 162° x = 54°.
∠OAB = ∠ABO = x.
Тоді ∠AOB = 180° – 2x.
Отже, ∠AOB = 180° – 2 ∙ 54° = 72°.
У прямокутнику ∠BAD = 90°, тому
∠OAD = 90° – ∠OAB = 90° – 54° = 36°.
Відповідь: 1. ∠ABO = 54° → В; 2. ∠AOB = 72° → Г; 3. ∠OAD = 36° → А
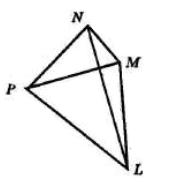
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
Відповідь: 100°, 80°, 100°, 80°.
3.
4. Периметр
за другу.
Нехай x см — менша сторона, тоді (x + 1) см — більша сторона.
Отримуємо рівняння: (x + x + 1) · 2 = 18;
x + x + 1 = 9;
2x + 1 = 9;
2x = 8;
x = 4,
тоді x + 1 = 5.
Оскільки протилежні сторони прямокутника рівні, то сторони
дорівнюють 4 см; 5 см; 4 см; 5 см.
Відповідь: 4 см; 5 см; 4 см; 5 см.
5. ABCD — ромб, ∠ ABD = 50°. Знайдіть кути ромба.
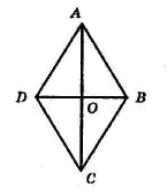
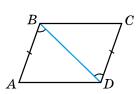
У ромбі ABCD ∠ABD = 50°, тоді
∠ABC = 2∠ABD = 2 · 50° = 100° — за властивістю
∠BAD = 180° − ∠ABC = 180° − 100° = 80°. Оскільки протилежні
рівні, то в ромбі ABCD
∠A = 80°, ∠B = 100°, ∠C = 80°, ∠D = 100°.
Відповідь: ∠A = 80°, ∠B = 100°, ∠C = 80°, ∠D = 100°.
∠ ABD = ∠ BDC, AB = DC. Доведіть, що ABCD — паралелограм. Оскільки ∠ABD = ∠CDB за умовою
ABCD — паралелограм.
7. Знайдіть кути чотирикутника, якщо вони пропорційні
Позначимо кути даного чотирикутника
Оскільки сума кутів чотирикутника дорівнює
то 2x + 3x + 4x + 6x =
Отримуємо: 15x = 360, x = 24.
Тоді: 2x° = 48°, 3x° = 72°, 4x° = 96°, 6x° = 144°.
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
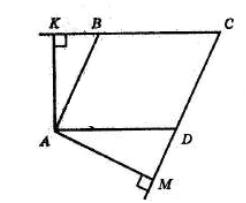
У ромбі ABCD AM ⊥ CD, AK ⊥ BC, ∠KAM = 120°.
чотирикутника MAKC, у якому
дорівнює 120°, знаходимо:
∠KCM = 360° − 2 · 90° − 120° = 60°.
Звідси за властивістю протилежних кутів ромба ∠BAD = ∠BCD = 60°.
За властивістю сусідніх кутів ромба маємо:
∠ABC = ∠ADC = 180° − 60° = 120°.
Отже, кути ромба: 120°; 60°; 120°; 60°.
Відповідь: 120°; 60°; 120°; 60°.
9. Бісектриса кута A паралелограма ABCD ділить сторону BC на відрізки BK і KC так, що BK : KC = 4 : 3. Знайдіть сторону паралелограма, якщо його периметр дорівнює 88 см.
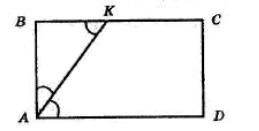
Нехай у паралелограмі ABCD AK бісектриса кута A паралелограма. Нехай BK = 4x см, KC = 3x см.
Оскільки ABCD — паралелограм, то BC || AD, AK — січна при прямих BC і AD. Отже, ∠AKB = ∠KAD як внутрішні різносторонні при паралельних прямих і січній.
Тоді трикутник AKB — рівнобедрений з основою AK, оскільки ∠BAK = ∠BKA.
BK = AB = 4x см, BC = 7x см.
Оскільки периметр паралелограма дорівнює 88 см, то маємо рівняння:
2(4x + 7x) = 88,
то маємо:
11x = 44, x = 4.
Отже, сторони паралелограма дорівнюють:
AB = CD = 16 см, AD = BC = 28 см.
Відповідь: 16 см, 28 см, 16 см, 28 см. 10. У рівнобедрений
KLMN

трикутнику ABC ∠C = ∠B = 45°, оскільки цей трикутник рівнобедрений.
Отже, у трикутнику BKN, де ∠BKN = 90° (оскільки KLMN — прямокутник), також ∠BNK = ∠KBN = 45°.
Таким чином, трикутник BKN — рівнобедрений, BK = KN.
Аналогічно в трикутнику LMC, де ∠MLC = 90°, ∠LMC = ∠C = 45°, і LM = LC.
Оскільки BC = 23 см, то KN = (23 − 2) : 3 = 7 см, KL = KN + 2 = 9 см.
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
Отже, PKLMN = 2(7 + 9) = 32 см.
32 см.
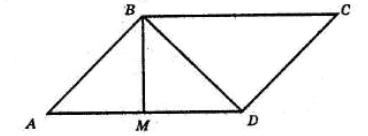
трикутник ABD рівнобедрений, то ∠ABD = 60°. Оскільки трикутник ABD є рівностороннім і за умовою PABCD = 40 см, то AB = 10 см, і тоді менша діагональ ромба дорівнюватиме 10 см.
Відповідь: 10 см.
Вправи для повторення теми 2
1. Накресліть чотирикутник AMCN. Запишіть вершини, сторони та
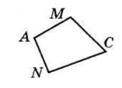
Вершини A, M, C, N; Сторони AM, MC, CN, AN; Кути AMC, MCN, CNA, NAM.
2. Чи можуть у чотирикутнику три кути бути прямими, а четвертий:
1. гострим; 2. тупим?
Сума кутів чотирикутника 360°. Сума трьох прямих
четвертий кут може бути тільки
Відповідь: 1. ні; 2. ні.
3. Два кути чотирикутника
BCDA, CDAB, DABC.
∠1 = x, ∠2 = x + 10°, ∠3 = x + 50°, ∠4 = 2x.
x + x + 10 + x + 50 + 2x = 360;
5x = 360 − 60;
5x = 300;
x = 60.
∠1 = 60°,
∠2 = 60° + 10° = 70°,
∠3 = 60° + 50° = 110°,
∠4 = 2 · 60° = 120°.
Відповідь: 60°, 70°, 110°, 120°.
6.
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
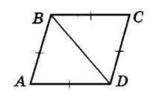
У ΔABD ∠A + ∠ABD + ∠ADB = 180°,
∠A + ∠CDB + ∠ADB = 180°,
∠A + ∠ADC = 180°.

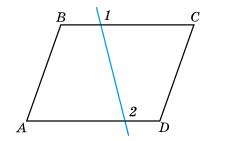
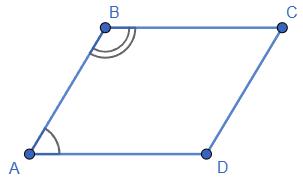
AD = BC,

односторонніми при прямих BC і AD і січній AB. Тоді за ознакою паралельності прямих BC || AD. ∠B + ∠C = 180° — сума внутрішніх односторонніх кутів при прямих AB і CD і січній BC. За ознакою паралельності прямі AB || CD. Отже, в чотирикутнику ABCD AB || CD і BC || AD, за означенням ABCD паралелограм.
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
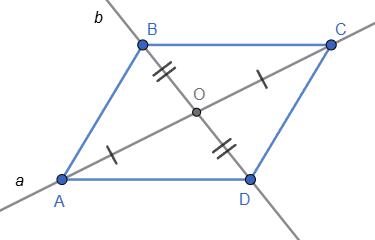
12. Дано паралелограм ABCD і трикутник ENM. Чи можливо, щоб одночасно
виконувались рівності ∠A = ∠E, ∠B = ∠N, ∠C = ∠M? Ні, неможливо. ∠E + ∠N + ∠M = 180°, тоді ∠A + ∠B +
C = 180° і ∠D = 360° − 180° = 180°. Але це неможливо, кут чотирикутника не може дорівнювати 180°.
13. У паралелограмі ABCD точка M — середина AD, N — середина BC. Доведіть, що відрізки AN і BM точкою
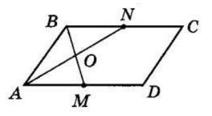
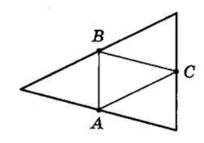
ABCD — паралелограм. BC = AD, BN = 1 2 BC, AM = 1 2 AD.
ABNM — паралелограм (сторони BN і AM рівні і паралельні).
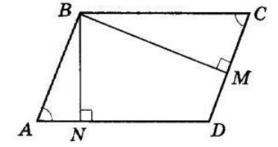
NBM +
BMD + ∠D + ∠BND = 360°;
NBM = 360° − (∠BMD + ∠D + ∠BND);
NBM = 360° − (90° + 180° − α + 90°) = = 360° − (360° − α) = α.
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
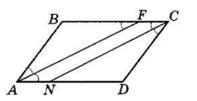
Нехай AF — бісектриса кута BAD, CN — бісектриса кута BCD.
Тоді ∠FAD = 1 2 ∠BAD, ∠BCN = 1 2 ∠BCD.
∠BAD = ∠BCD (за властивістю протилежних кутів паралелограма).
Отже, їх половини також рівні: ∠FAD = ∠BCN. BC || AD (за означенням паралелограма).
Значить, ∠FAD = ∠AFB (як внутрішні різносторонні кути при BC || AD і січній BC).
∠FAD = ∠BCN, ∠FAD = ∠AFB, тоді ∠BCN = ∠AFB.
А оскільки ці кути — відповідні при прямих AF і CN і січній BC, то AF || CN (за ознакою паралельності прямих).
Якщо всі сторони паралелограма рівні, бісектриси протилежних кутів лежать на одній прямій. В цьому випадку з того, що AB = BC випливає, що ΔABC — рівнобедрений з
основою AC, а значить, ∠BAC = ∠BCA (як при основі рівнобедреного
8 см і 20 см.
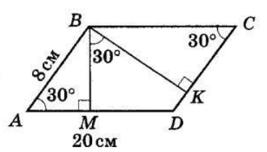
однієї з них.
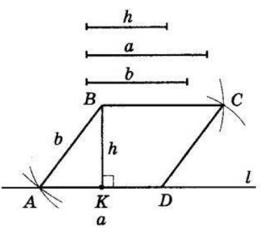
між висотами паралелограма, проведеними
вершини B, дорівнює куту A.
A =
C = ∠MBK.
ΔABM BM = 1 2 AB = 1 2 · 8 = 4 (см) (як катет, що
проти кута 30°). Аналогічно в ΔBKC BK = 1 2 BC = 1 2 · 20 = 10 (см).
Відповідь: 4 см, 10 см.
1. Провести довільну пряму l і позначити на ній довільну точку K.
2. Через точку K провести пряму, перпендикулярну прямій l і відкласти на ній відрізок KB = h.
3. З центра B провести коло радіуса b, воно перетне пряму l у точці A.
4. Від точки A на прямій l відкласти відрізок AD = a.
5. Побудувати коло з центром B радіуса a і точкою D радіуса c.
6. ABCD — шуканий паралелограм (BC = AD, AB = CD).
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html


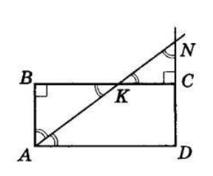
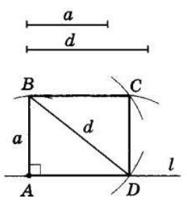
∠BKA = ∠KAD = 1 2 ∠A = 45° як
AD || BC і січній AK.
NKC = ∠BKA = 45° як вертикальні. У ΔKNC ∠KNC = 180° – (∠NKC + ∠NCK) = = 180° – (45° + 90°) = 45°. Відповідь: 45°.
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
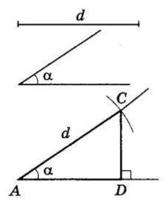

2. 1. Побудувати
A. 2.
AC = d
3.
4.
промінь з точки D і
ньому відрізок DB = d.
5. ABCD
3. 1. Розділити дану діагональ навпіл.
2. Побудувати ∠O = α.
3. На сторонах кута O та на їх продовженнях
4. ABCD — шуканий прямокутник.
23. Бісектриса кута A прямокутника ABCD
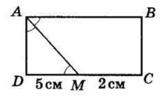
Тоді ∠AMD =
DAM,
△ADM AD = DM = 5 см.
DC = DM + MC = 5 + 2 = 7 (см).
PABCD = 2(AD + CD) = 2 · (5 + 7) = 24 (см).
Відповідь: 24 см. 24.
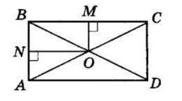
ABCD O точка
OM ⊥ BC, ON ⊥ AB —
AB = 20M, AD = 20N. Нехай OM = x см, тоді ON = (x + 2) см.
OM = 1 2 AB.
PABCD = 2(AB + AD) = 2(2x + 2(x + 2)) = 4x + 4x + 8 = 8x + 8; 8x + 8 = 56; 8x = 48; x = 6,
AB = 2 · 6 = 12 (см);
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
AD = 2 · (6 + 2) = 16 (см).
Відповідь: 12 см, 6 см.
25. Перпендикуляр, проведений
дорівнює a см.
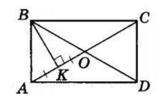
ABCD прямокутник, AC = a діагональ, BK ⊥ AC; AK : KC = 1 : 3. Нехай O — точка перетину діагоналей. AO = OC, тому AK = KO = 1 4 a см.
Отже, в △ABO висота BK є медіаною, тоді за ознакою рівнобедреного трикутника AB = BO. Але BO = AO,
тому AB = BO = OA, △ABO — рівносторонній.
∠ABK = 1 2 ∠ABO = 1 2 · 60° = 30°.
AB = 2AK = 2 · 1 4 a = ���� 2 (см) (катет проти кута 30°).
Відповідь: ���� 2 см.
26. Бісектриси кутів A і D прямокутника ABCD перетинають його
і K відповідно. BL = 7 см, LK = 2 см. Знайдіть периметр прямокутника ABCD. Скільки
випадків слід розглянути?
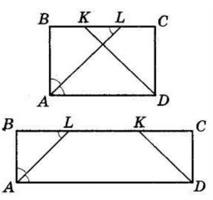
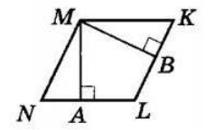
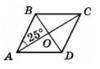
Можливі два випадки. ∠BLA = ∠LAD як внутрішні різносторонні при BC || AD і
січній AL.
За умовою ∠BAL = ∠LAD, тому ∠BAL = ∠BLA.
△ABL — рівнобедрений (за ознакою), AB = BL = 7 см.
Аналогічно, у △KCD KC = CD = 7 см.
1 випадок: BC = AD = BL + KC − KL = 7 + 7 − 2 = 12 (см).
PABCD = 2(AB + BC) = 2 · (7 + 12) = 38 (см).
2 випадок: BC = AD = BL + LK + KC = 7 + 7 + 2 = 16 (см).
PABCD = 2(AB + BC) = 2 · (7 + 16) = 46 (см). Відповідь: 38 см
46 см.
C = ∠A = 50°.
B = ∠D = 180° − ∠A = 180° − 50° =130°.
50°, 130°, 50°, 130°.
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html

— 180°. 2x + 3x = 180; 5x = 180; x = 36.
∠A = ∠C = 2 · 36° = 72°, ∠B = ∠D = 3 · 36° = 108°. Відповідь: 72°, 108°, 72°, 108°.
У ромбі ABCD з вершини гострого кута A проведено висоти AM і AN. Доведіть, що AM = AN.
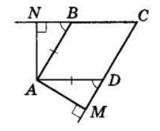
ABCD ромб; AN ⊥ BC, AM ⊥ CD висоти. △ABN = △ADM за гіпотенузою і гострим кутом (AB = AD як сторони ромба, ∠NBA = ∠MDA як кути, суміжні з рівними протилежними кутами B і D ромба). З рівності трикутників випливає, що AN = AM.
31. Діагоналі паралелограма
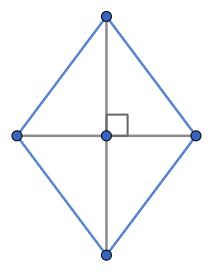
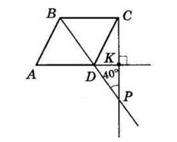
У △BCP ∠CBD = 90° − ∠P = 90° − 40° = 50°.
∠B = ∠D = 2 · 50° = 100°;
∠A = ∠C = 80°.
Відповідь: 100°, 80°. 33. Висота ромба
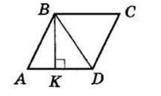
1. ABCD ромб, BK ⊥ AD, BK = 10 см висота.
PABCD = 80 см, тоді AB = BC = CD = AD = 80 : 4 = 20 (см).
30°.
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
Отже, ∠A = 30°, ∠C = ∠A = 30°.
∠B = ∠D = 180° − 30° = 150°.
Відповідь: 30°, 150°.
2. ∠BDK = 1 2 см ∠D = 1 2 см · 150° = 75°.
∠KBD = 180° − (∠BKD + ∠BDK) = 180° − (90° + 75°) = 15°.
Відповідь: 15°.
34. Побудуйте ромб за діагоналлю й висотою.

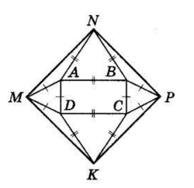

P = 4 · 3 = 12 (см).
1. Побудуємо прямі x і y. M точка їх перетину.
2. Побудуємо коло з центром M і радіусом h. A — Точка перетину кола з прямою y.
3. Побудуємо коло з центром A і радіусом d. C — Точка
перетину його з прямою x.
4. З'єднаємо точки A і C. Отримаємо діагональ AC, розділимо її навпіл. O — середина AC.
5. Проведемо пряму z ⊥ AC через точку O. B точка перетину кола з прямою z і прямої x.
6. Побудуємо коло з центром A радіусом AB. D —
7. З'єднаємо точки D і C. Отримаємо
△MAN = △PBN = △MDK = △PSK
(AM = BP = CP = DM = AD = BC, AN = BN = CK = DK = AB = CD; ∠MAN = ∠NBP = ∠PCK = ∠MDK = = 360° − (60° + 90° + 60°) = 150°).
MN = PN = KP = KM.
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html

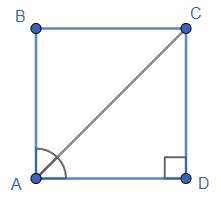
40.
AA1 = BB1 = CC1 = DD1.
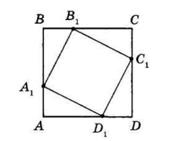
З рівності трикутників
A1B1C1D1.
△A1BB1 = △B1CC1 = △C1DD1 = △D1AA1, за двома катетами (AA1 = BB1 = CC1 = DD1, за умовою, A1B = B1C = C1D = D1A, як частини рівних сторін
відрізків).
Тоді A1B1 = B1C1 = C1D1 = A1D1. A1B1C1D ромб.
∠B1A1D1 = 180° − (∠D1A1A + ∠BA1B1);
∠A1B1C1 = 180° − (∠CB1C1 + ∠BB1A1);
∠B1C1D1 = 180° − (∠B1C1C + ∠DC1D1);
∠C1D1A1 = 180° − (∠C1D1D + ∠A1D1A).
∠BA1B1 = ∠CB1C1 = ∠DC1D1 = ∠A1D1A,
∠BB1A1 = ∠CC1B1 = ∠DD1C1 = ∠AA1D1.
Тоді ∠B1A1D1 = ∠A1B1C1 = ∠B1C1D1 = ∠C1D1A1
Ромб A1B1C1D1, у якого
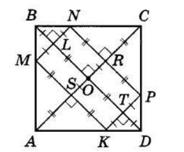
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
NR = RC = RP, PT = DT = KT.
KS = AS = MS.
PMPNK = 2(MN + NP) = 2 · AC = 2d (см).
Відповідь: 2d см.
ТЕМА 3.
10.28.
.
систему
1 8 (���� + ����) = 3, 1 3 (���� ����) = 5, ����� + ���� = 24, ���� ���� = 15.
2x = 39; x = 19,5.
Тоді y = 24 – 19,5; y = 4,5. ����. ����� 1 3 + ���� 1 2 = 2, | ⋅ 6, ���� 1 2 ���� 1 12 = 4 3 , | ⋅ 12 �2(���� ����) + 3(���� 1) = 12, 6(���� 1) (���� 1) = 16,
2���� − 2 + 3���� − 3 = 12, 6���� − 6 − ���� + 1 = 16, �2���� + 3���� = 17, ���� = 6���� − 21.
2x + 3(6x – 21) = 17; 2x + 18x – 63 = 17; 20x = 80; x = 4.
Тоді y = 6 · 4 – 21; y = 3.
Відповідь: 1. (19,5; 4,5); 2. (4;3).
10.29. Побудуйте
функції ���� = ���� 3 8 ���� 2 ���� 2 = (���� 2)(���� 2 + 2���� + 4) ���� 2 ���� 2 = ���� 2 + 2���� + 4 ���� 2 = 2���� + 4;
D(y) = {x – будь-яке, крім 2}.
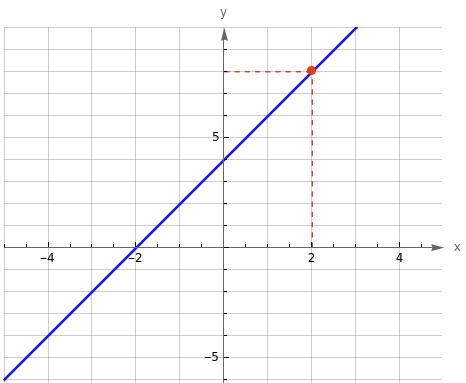
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
Початкове число: 2500 = 22 · 54 .
Час: 1 година = 60 хвилин → 60 дій (множення або ділення на 2 чи 5).
1) 10000 = 24 · 54
Потрібно додати 2 двійки (2 множення на 2). Інші 58 дій можна нейтралізувати (множення/ділення на 5, або парами ділення і множення на 2).
Отже, через 60 хвилин можна отримати 10 000.
2) 20000 = 25 · 54
Потрібно додати 3 двійки (3 множення на 2). Залишається 57 операцій, а це
число 20 000 не можна отримати.
Відповідь: 1) Так; 2) Ні
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
(2 ⋅ 4,2 − 1,6)(4,2 + 2 ⋅ 1,6) (4,2 2 ⋅ 1,6)(2 ⋅ 4,2 + 1,6) = 6,8 ⋅ 7,4 1 ⋅ 10 = 50,32 10 = 5,032.
Відповідь: 5,032.
11.18. Спростіть вираз
0,5���� 2
���� 3
11.19. Доведіть тотожність
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
1) 40000 · 1,1 = 44000 (грн)
3)
0,7���� + 15
���� + 15 = 0,8
Маємо 0,7x + 15 = 0,8x + 12;
0,1x = 3;
x = 30.
x + 15 = 30 + 15 = 45 Відповідь: 45
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
89 – 412 = (23)9 – (22)12 = 227 – 224 = 224(23 – 1) = 224(8 – 1) = 7 · 224 —
функції: ����. ���� = �2���� + 4, якщо ���� < 0, 4 ���� , якщо ���� ≥ 0.
функції y = 2x + 4 є пряма. x 0 –2 y 4 0
Графік функції y = 4 – x є пряма. x 0 4 y 4 0
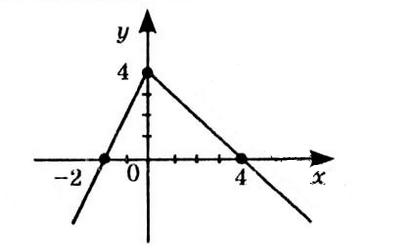
=
.
2���� + 5, якщо ���� < – 1, 3, якщо –1 ≤����≤ 4, ���� –1, якщо ���� > 4.
функції y = 2x + 5 є пряма. x –1 –2 y 3 1
функції y = x – 1 є пряма. x 4 5 y 3 4
Графік функції y = 3 є пряма, що
через точку (0; 3)

https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
����. (���� − 1)���� ���� + 2 = 0; �����(���� 1) = 0, ���� + 2 ≠ 0; ����� = 0 або ���� = 1, ���� ≠ 2.
Відповідь: 0; 1.
����. ���� 2 2���� 8 = 0; ���� 2 2���� = 0; ���� (���� 2) = 0;
���� = 0 або ���� 2 = 0; ����1 = 0, ����2 = 2.
Відповідь: 0; 2.
����. (���� + 2)���� ����2 4 = 0; �(���� + 2)���� = 0, ����2 4 ≠ 0;
���� = 0 або ���� = 2, (���� 2)(���� + 2) ≠ 0; ����� = 0 або ���� = 2, ���� ≠ 2, ���� ≠ 2
Відповідь: 0.
����. ���� ���� 2 + ���� = 0; � ���� = 0, ���� 2 + ���� ≠ 0;
���� = 0, ���� (���� + 1) ≠ 0; � ���� = 0, ���� ≠ 0, ���� ≠ 1.
Відповідь: рівняння розв’язків не має.
12.37. Розв’яжіть рівняння:
1. 2(x − 3) = 4(x + 7) − 11; 2x − 6 = 4x + 28 − 11; 2x − 4x = 28 – 11 + 6; −2x = 23; ���� = 23 2 = 11 1 2 = 11,5;
2. 5(x − 2) − 7(x + 1) = 9(x − 8); 5x − 10 − 7x − 7 = 9x − 72; 5x − 7x − 9x = −72 + 7 + 10; −11x = −55; x = −55 : (−11); x = 5.
12.38. Розв’яжіть рівняння,
����. 2���� 4 7 = 3���� + 1 9 | · 63; 9(2x − 4) = 7(3x + 1); 18x − 36 = 21x + 7; 18x − 21x = 7 + 36; 3x = 43;
Відповідь: 14 1 3
����. 2���� − 11 5 = 3���� + 17 10 | · 10;
2(2x − 11) = 3x + 17;
4x − 22 = 3x + 17; 4x − 3x = 17 + 22; x = 39.
Відповідь: 39.
12.39.
1), 3) Ні; 2), 4) Так.
13.3.
1), 4) Так; 2), 3) Ні.
13.4.
13.8.
. 5 ���� 2 = 3 ���� + 4 ; �5(���� + 4) = 3(���� 2), ���� ≠ 2, ���� ≠ 4;
5���� + 20 = 3���� 6,
5(x – 12) = x;
5x – 60 = x;
4x = 60; x = 60 : 4; x = 15.
То маємо 15 − 12 15 = 3 15
Відповідь: 3 15 .
13.16.
13.17.
3.
13.18. Розв’яжіть рівняння:
2x2 + x + 8x + 4 = 2x2 + 16x – x –
9x + 4 = 15x – 8; –6x = 12; x = –12 : (–6); x = 2;
Відповідь: 2.
3.
x – 5 = 40; 5x =
Відповідь: 9.
Розв’яжіть
+ 5; 5x =
=
. ���� + 1 3���� + 1 ���� 3���� 1 = 0; (���� + 1)(3���� 1) ���� (3���� + 1) (3���� + 1)(3���� 1) = 0; 3���� 2 + 3���� ���� 1 3���� 2 ���� (3���� + 1)(3���� 1) = 0; ���� − 1 (3���� + 1)(3���� 1) = 0; ⎩ ⎪ ⎨ ⎪ ⎧���� 1 = 0, ���� ≠ 1 3 , ���� ≠ 1 3 ; ⎩ ⎪ ⎨ ⎪ ⎧���� = 1, ���� ≠ 1 3 , ���� ≠ 1 3 .
Відповідь: 1. ����. 1 6���� − 1 2���� = 1 6 ; 1 3 6���� = 1 6 ; 2 6���� = 1 6 ; �6���� = 12, ���� ≠ 0; ����� = 2, ���� ≠ 0;
Відповідь: –2 ����. 3 + 1 1 ���� = ���� ���� 1 ; 3(1 ���� ) 1 ���� = ���� ���� 1 ;
3 3���� + 1 1 ���� ���� ���� 1 ; 4 3���� 1 ���� + ���� 1 ���� = 0;
3���� + ���� 1 ���� = 0; 4 2���� 1 ���� = 0; �4 2���� = 0, 1 − ���� ≠ 0; �2���� = 4, ���� ≠ 1; � ���� = 2, ���� ≠ 1.
Відповідь: 2.
����. 1 4���� + 4 1 ���� + 1 = 3 8 ; 1 4(���� + 1) 1 ���� + 1 = 3 8 ; 1 4
4(���� + 1) = 3 8 ; 3 4(���� + 1) = 3 8 ; �12(���� + 1) = 24, ���� ≠ −1; �12���� + 12 = 24, ���� ≠ 1.
12x = −24 − 12; 12x = −36; x = −3.
Відповідь: 3.
13.20. Чи є рівносильними рівняння
2���� + 6 ���� + 1 + 3���� 7 ���� 2 = 5; (���� 2)(2���� + 6) + (���� + 1)(3���� 7) (���� + 1)(���� 2) = 5 1 ;
2���� 2 + 6���� 4���� 12 + 3���� 2 7���� + 3���� 7 (���� + 1)(���� 2) = 5 1 ;
5���� 2 2���� 19
(���� + 1)(���� − 2) = 5 1 ; �
5���� 2 2���� 19 = 5(���� + 1)(���� 2), ���� ≠ 2, ���� ≠ 1;
5x2 – 2x – 19 = 5(x2 – x – 2); 5x2 – 2x – 19 = 5x2 – 5x – 10; 5x2 – 2x – 5x2 + 5x = – 10 + 19; 3x = 9; x = 3.
���� 2
���� + 2 + ���� + 2 ���� 2 = 8 ���� 2 4 ; ���� 2 ���� + 2 + ���� + 2 ���� 2 8 (���� 2)(���� + 2) = 0;
(���� 2)2 + (���� + 2)2 8 (���� 2)(���� + 2) = 0;
���� 2 4���� + 4 + ���� 2 + 4���� + 4 8 (���� 2)(���� + 2) = 0;
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
Нехай ���� 5
���� 5 + 14 ���� − 1 = ���� ���� − 5 ; ���� + 9 ���� − 1 = ���� ���� − 5 ;
(���� 1) = (���� 5)(���� + 9), ���� ≠ 1, ����
5;
x2 – x = x2 + 9x – 5x – 45;
x2 – x – x2 – 9x + 5x = – 45; –5x = –45; x = 9;
x – 5 = 9 – 5 = 4.
Відповідь: 4 9 .
13.23. Знаменник
Нехай ���� ���� + 3
дріб, тоді ���� + 8
+ 8) = (���� + 2)(���� + 3),
≠ 0,
≠ −2;
x2 + 8x = x2 + 3x + 2x + 6; x2 + 8x – x2 – 3x – 2x = 6; 3x = 6; x + 3 = 2 + 3 = 5.
Відповідь: 2 5 .
13.24. Знайдіть корені рівняння: ����. ���� 2 2 ���� 2 + 2���� = ���� 1 ���� + ���� + 3 ���� + 2 ; ���� 2 2 ���� (���� + 2) = (���� 1)(���� + 2) ���� 2 + 3���� ���� (���� + 2) ;
2 − 2 = ���� 2 + 2���� − ���� − 2 + ���� 2 + 3���� ,
≠ 0,
≠ 2;
2 + 4���� = 0,
≠ 0,
≠ 2; ����� (���� + 4) = 0, ���� ≠ 0, ���� ≠ 2; ���� = −4.
Відповідь: –4. ���� ���� 2 + 1 ���� 2 1 = ���� ���� + 1 + 2 ���� 1 ;
���� 2 + 1 (���� − 1)(���� + 1) = ���� (���� 1) + 2(���� + 1) ���� (���� + 2) ;
2 + 1 = ���� 2 ���� + 2���� + 2,
Відповідь:
13.25. Розв’яжіть рівняння:
1;
Відповідь: –4
. ���� 2 + 8 ���� 2 − 4 = ���� ���� + 2 + 3 ���� − 2 ; ���� 2 + 8 (���� 2)(���� + 2) = ���� (���� 2) + 3(���� + 2) (���� + 2)(���� 2) ;
2 + 8 = ���� 2 2���� + 3���� + 6, ���� ≠ −2, ���� ≠ 2; �����
0,
Відповідь: –1.
розв’язків.
13.28. Для яких значень a рівняння не
− 2���� ���� (���� 8) = 0; ����� 2���� = 0, ���� ≠ 0, ���� ≠ 8; ����� = 2����, ���� ≠ 0, ���� ≠ 8.
2a = 0 або 2a = 8; a = 0 або a = 4.
Відповідь: a = 0, a = 4. ����. ���� ���� + 1 ���� 2 3���� = 0; ���� ���� + 1 ���� (���� 3) = 0; ����� ���� + 1 = 0, ���� (���� 3) ≠ 0; ����� = ���� − 1, ���� ≠ 0, ���� ≠ 3; a – 1 = 0 або a – 1 = 3; a = 1 або a = 4.
Відповідь: a = 1, a = 4.
13.29. Для яких значень a рівняння
(���� ���� )(���� 2���� 1) ���� 3 = 0.
рівняння
x – a = 0
x − 2a − 1 = 0. Тобто x = a або x = 2a + 1.
= 3
2a + 1 = 3, тобто a = 1.
Відповідь: a = 3; a = 1.
13.30. Спростіть
10���� ���� + 2 ���� 8 3���� + 6 ·
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html

2) Яка найбільша
Відповідь: А
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
–2;
Відповідь: 8;
. 4���� 2 1 ���� + 1 = 4���� ; �4���� 2 1 = 4���� (���� + 1), ���� + 1 ≠ 0;
4���� 2 1 = 4���� 2 + 4���� , ���� ≠ 1; �4���� 2 4���� 2 4���� = 1, ���� ≠ 1;
Відповідь: 1 4
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
1 2 ?
5 + ���� 12 + ���� = 1 2 ; �12 + ���� = 2(5 + ���� ), 12 + ���� ≠ 0; �12 + ���� = 10 + 2���� , ���� ≠ 12; ����� 2���� = 10 12, ���� ≠ 12;
���� = 2, ���� ≠ 12; ����� = 2, ���� ≠ 12.
Відповідь: ���� = 2.
32. Розв’яжіть рівняння: ����. 2���� 1 3���� + 1 2���� + 1 3���� − 5 = 0; (2���� 1)(3���� 5) (2���� + 1)(3���� + 1) (3���� + 1)(3���� 5) = 0; 6����² − 10���� − 3���� + 5 − 6����² − 2���� − 3���� − 1 (3���� + 1)(3���� 5) = 0; 18���� + 4 (3���� + 1)(3���� 5) = 0;
18���� + 4 = 0, ���� ≠ − 1 3 , ���� ≠ 5 3 , ⎩ ⎪ ⎨ ⎪ ⎧ 18���� = 4, ���� ≠ 1 3 , ���� ≠ 1 2 3 , ���� = 4 18 = 2 9 .
2 = 0; �4���� 6 = 0, ���� 2 ≠ 0; �4���� = 6, ���� ≠ 2;
= 6 4 = 3 2 = 1,5, ���� ≠ 2.
Відповідь: 1,5.
. 8 3���� − 3 + 2 + ���� ���� − 1 = 5 2 − 2���� 5 18 ; 8 3(���� 1) + 2 + ���� ���� 1 5 2(1 ���� ) + 5 18 = 0; 8 3(���� 1) + 2 + ���� ���� 1 + 5 2(���� 1) + 5 18 = 0;
48 + 18(2 + ���� ) + 45 + 5(���� 1) 18(���� 1) = 0;
48 + 36 + 18���� + 45 + 5���� 5 18(���� − 1) = 0;
23���� + 124 18(���� 1) = 0; �23���� + 124 = 0, ���� 1 ≠ 0; �23���� = 124, ���� ≠ 1;
= 124 23 = 5 9 23, ���� ≠ 1; ���� = 5 9 23 . Відповідь: 5 9 23 .
(
1)(���� + 1) ���� ���� + 1 ���� ���� 1 = 0; 2���� ���� (���� 1) ���� (���� + 1) (���� − 1)(���� + 1) = 0; 2���� 2����² (���� 1)(���� + 1) = 0; �2���� (1 ���� ) = 0, ���� ≠ 1, ���� ≠ 1, ����� = 0 або ���� = 1, ���� ≠ 1,
0.
80x 160 = 64x + 128; 80x 64x = 128 + 160; 16x = 128; x = 288 : 16; x = 18.
Відповідь: 18 км / год. 34. Розв’яжіть рівняння:
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html


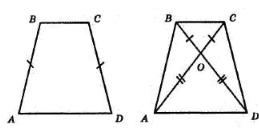
14.6
1.
− 30° = 150°
2. 180° − 110° = 70°
Відповідь: 150°, 70°. 14.7
100° + 50° = 150° ≠ 180°, то
Тоді інші кути дорівнюють:
1. 180° − 100° = 80°
2. 180° − 50° = 130°
Відповідь: 80°, 130°.
14.8
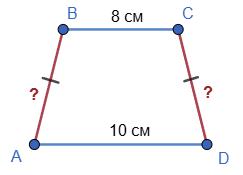

2 = 5 (см).
= 7 + 5 + 2 · 3 = 18 (см).
3. тупі?

1.
2.
3.
14.11
2.

2.
2.
1. 2 : 3 : 4 : 1;
2. 2 : 3 : 5 : 2?
Сума
трапеції дорівнює 360°.
1. 2x + 3x + 4x + x = 360; 10x = 360; x = 36.
∠1 = 2 · 36° = 72°;
∠2 = 3 · 36° = 108°;
∠3 = 4 · 36° = 144°;
∠4 = 36°.
∠1 + ∠2 = 72° + 108° = 180°;
∠3 + ∠4 = 144° + 36° = 180°.
Відповідь: так.
2. 2x + 3x + 5x + 2x = 360; 12x = 360; x = 30.
∠1 = 2 · 30° = 60°;
∠2 = 3 · 30° = 90°;
∠3 = 5 · 30° = 150°;
∠4 = 2 · 30° = 60.
Відповідь:
180°.
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
1. 3 : 1 : 2 : 2;
2. 3 : 1 : 2 : 4?
1. 3x + x + 2x + 2x = 360; 8x = 360; x = 45.
∠1 = 3 · 45° = 135°;
∠2 = 45°;
∠3 = ∠4 = 2 · 45° = 90°.
∠1 + ∠2 = 135° + 45° = 180°;
∠3 + ∠4 = 2 · 90° = 180°
Відповідь: так.
14.16

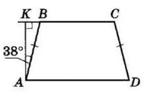
2. 3x + x + 2x + 4x = 360; 10x = 360; x = 36.
∠1 = 3 · 36° = 108°;
∠2 = 36°;
∠3 = 2 · 36° = 72°;
∠4 = 4 · 36° = 144°.
Відповідь: ні, оскільки сума
В ∆АВК ∠КВА = 90° − ∠ВАК = 90° − 42° = 48°.
∠АВС = 180° − ∠КВА = 180° − 48° = 132° як суміжні.
∠ВАD = ∠КВА = 48° як внутрішні різносторонні
= ∠АВС = 132°; ∠D = ∠BAD = 48° як кути при основі.
48°, 132°, 132°, 48°. 14.18
рівнобічної
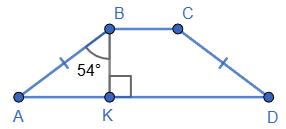
14.19
= 90° − 54° = 36°.
D = ∠A = 36°
B = ∠C = 180° − ∠A = 180° − 36° = 144°.
36°, 144°, 144°, 36°.
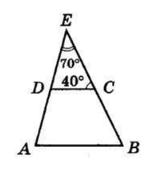
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
В ∆DEC ∠EDC = 180° − (∠DEC + ∠ECD) = 180° − (70° + 40°) = 70°.
∠A = ∠EDC = 70°,
∠B = ∠ECD = 40° як відповідні при DC || AB і січних AD і BC.
∠CDA = 180° − ∠A = 180° − 70° = 110°,
∠BCD = 180° − ∠B = 180° − 40° = 140° як прилеглі до бічної
сторони.
Відповідь: 70°, 110°, 140°, 40°.
14.20 У трапеції ABCD BC менша основа. На відрізку AD взято точку E так, що BE || CD ; ∠ ABE = 60°, ∠ BEA = 40°. Знайдіть кути трапеції.
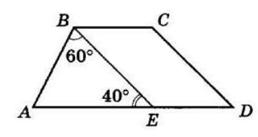
14.21 У
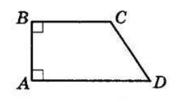
14.22
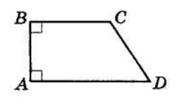
14.23 У рівнобічній
В ∆АВЕ ∠А = 180° − (∠АВЕ + ∠ВЕА) = = 180° − (60° + 40°) = 80°. ∠АВС = 180° − ∠А = 180° − 80° = 100°. ∠CDA = ∠BEA = 40° як відповідні при BE || CD і січній AD. ∠BCD = 180° − ∠D = 180° − 40° = 140°. Відповідь: 80°, 100°, 140°, 40°.
В трапеції ABCD ∠A = ∠B = 90°, ∠C = 2∠D.
∠D = x, тоді ∠C = 2x
x + 2x = 180; 3x = 180; x = 60.
Отже, ∠D = 60°, ∠C = 2 · 60° = 120°.
Відповідь: 90°, 90°, 120°, 60°.
В трапеції ABCD ∠A = ∠B = 90°.
∠D = x, тоді ∠C = x + 40°.
x + x + 40 = 180; 2x = 140; x = 70.
Отже, ∠D = 70°, ∠C = 70° + 40° = 110°.
Відповідь: 90°, 90°, 110°, 70°.

ABCD трапеція, AB = CD, BK ⊥ AD
В ∆АВК AB = 2BK, тоді BK катет, що лежить проти кута 30°, тобто ∠A = 30°, тоді
∠D = ∠A = 30° як кути при основі.
∠B = ∠C = 180° − 30° = 150°.
Відповідь: 30°, 150°, 150°, 30°.
14.24 У трапеції ABCD ∠ A + ∠ C = 180°. Визначте вид трапеції.
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
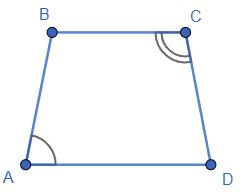
по 16 см. Знайдіть меншу основу.

14.26
ABCD трапеція, ∠A = ∠B = 90°, ∠D = 60°,
AD = CD = 16 см. Проведемо діагональ AC. ΔACD рівнобедрений, ∠D = 60°, тоді
∠CAD = ∠DCA = 60°, ΔACD рівносторонній,
AC = AD = CD = 16 см.
В ΔABC ∠BAC = ∠A − ∠CAD = 90° − 60° = 30°.
BC = 1 2 AC = 1 2 · 16 см = 8 см як катет
Відповідь: 8 см.
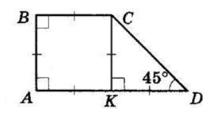
14.27

14.28
кута 30°.
ABCD трапеція, ∠A = ∠B = 90°, ∠D = 45°,
BC = AB = 18 см. Проведемо CK ⊥ AD.
ABCK квадрат (всі
рівні).
Звідси CK = AB = AK = 18 см.
ΔCKD прямокутний рівнобедрений, оскільки
кут дорівнює 45°. Отже, KD = CK = 18 см.
AD = AK + KD = 18 см + 18 см = 36 см.
Відповідь: 36 см.
ΔABD рівнобедрений (AD = BD за умовою).
∠DAB = ∠DBA = (180° − ∠BDA) : 2 = = (180° − 40°) : 2 = 140° : 2 = 70°.
∠CDA = ∠DAB = 70° як кути при основі.
∠BDC = ∠CDA = 70° − 40° = 30°.
∠CBD = ∠BDA = 40° як внутрішні різносторонні
січній BD.
В ΔBCD ∠C = ∠ABC = ∠ABD + ∠CBD = 70° + 40° = 110°.
Відповідь: 70°, 110°, 110°, 70°.

трапеція, AB = BC = CD,
∠BCA = 20°.
ΔABC
BCA = 20°.
∠CAD = ∠BCA = 20° як
BC || AD і січній AC.
∠BAD = ∠BAC + ∠CAD = 20° + 20° = 40°.
BAC =
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html

14.30


рівнобічна. Доведіть це.
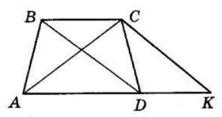
Отже, AD = 9 см, BC = 5 см. Відповідь: 9 см, 5 см.
Проведемо CK || BD. BCKD паралелограм (CK || BD, BC || AK).
ΔACK рівнобедрений, оскільки AC = BD = CK,
∠CAD = ∠CDA.
CK || BD, ∠BDA = ∠CKD, тоді ∠CAD = ∠CKD.
ΔABD = ΔDCA (AC = BD, BD спільна сторона, ∠CAD = ∠CKD), тоді AB = CD, тобто ABCD рівнобічна
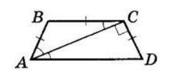
BCA
AC. Тоді ∠BAC = ∠CAD, ∠CDA = ∠BAD = 2∠CAD.
14.34 У
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
Нехай ∠CAD = x, тоді ∠CDA = 2x.
З ΔACD x + 2x = 90;
3x = 90; x = 30.
Тоді ∠BAD = ∠CDA = 2 · 30° = 60°.
∠ABC = ∠BCD = 180 – 60 = 120
Відповідь: 60°, 120°.
рівнобічній трапеції ABCD AD більша основа. AD = CD, ∠ BAC = 18°. Знайдіть кути трапеції.

У ΔACD ∠CAD = ∠ACD (AD = CD за умовою).
∠BCA = ∠CAD як внутрішні різносторонні
AC.
Тоді ∠BCA = ∠CAD = ∠ACD.
Нехай ∠CAD = x, тоді ∠BAD = x + 18°,
∠ABC = ∠BCD = 2x.
x + 18 + 2x = 180;
3x = 162;
x = 54;
∠A = ∠D = 54° + 18° = 72°,
∠B = ∠C = 54° + 54° = 108°.
Відповідь: 72°, 108°.
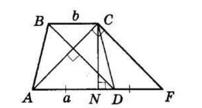
CF || BD, і продовжимо
пряму AD до перетину з CF. Чотирикутник BCFD паралелограм (BC || DF як основи, BD || CF за побудовою).
Значить, CF = BD, DF = BC, і AF = AD + BC. ΔACF прямокутний (оскільки пряма перпендикулярна одній
прямих, то вона перпендикулярна і другій).
Оскільки в рівнобічній трапеції діагоналі
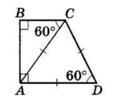
AD = AC = CD.
ΔABC ∠BAC = 90° − ∠BCA = 90 − 60° = 30°, тоді BC = 1 2 AC як
30°. Отже, AD : BC = 2 : 1.
2 : 1.
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
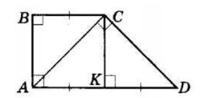
ABCD трапеція, ∠A = ∠B = 90°, AC ⊥ CD, ∠BCD = 3∠CDA.
Нехай ∠CDA = x, тоді ∠BCD = 3x x + 3x = 180; 4x = 180; x = 45.
Отже, ∠CDA = 45°.
У ΔACD ∠ACD = 90°, тоді ∠CAD = ∠CDA = 45°, ΔACD рівнобедрений.
Проведемо CK ⊥ AD. CK висота і медіана, AK = KD.
ABCK прямокутник, тому BC = AK.
Отже, AD : BC = 2 : 1.
Відповідь: 2 : 1.
14.38 Побудуйте трапецію за
сторонами c і d. Нехай трапеція ABCD має основи AD = a, BC = b і бічні сторони AB = c, CD = d. Проведемо відрізок CE || AB. В ΔCDE CD = d, CE = c, DE = a − b. Будуємо ΔCDE за трьома сторонами c, d, a − b Продовжуємо відрізок DE на AE = b, отримуємо
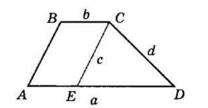
AD і відкладаємо CB = b. ABCD шуканa трапеція. 14.39 Кут
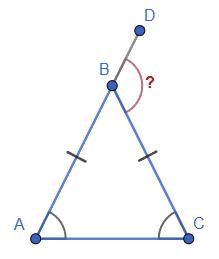
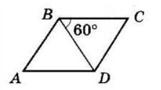
У ромбі ABCD BD = 5 см, ∠ABC = ∠ADC = 120°.
∠ABD = ∠CBD = ∠ADB = ∠CDB = 60° (
ΔABD = ΔBCD рівносторонній, AB = BC = CD = AD = BD = 5 см.
PABCD = 4 · 5 см = 20 см. Відповідь: 20 см.
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
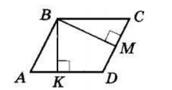
ABCD паралелограм, BK ⊥ AD, BM ⊥ CD.
ΔABK = ΔCBM за катетом і гострим кутом (BK = BM за умовою, ∠A = ∠C як протилежні). З рівності трикутників AB = BC. Отже, ABCD ромб, як паралелограм, у якого
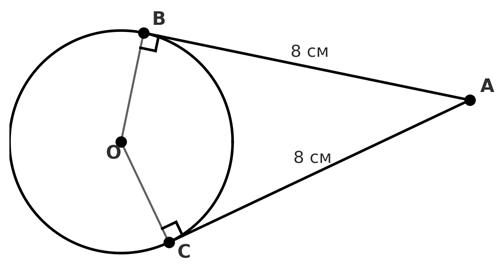
2.
1. 2 · (5,2 + 3,8)
2. 17,2 · 50 = 860 (грн) – ціна покупки.
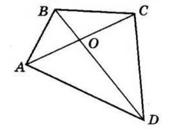
OA + OB + OC + OD ≥ AC + BD, при цьому OA + OB + OC + OD = AC + BD тоді
AC і BD, тобто є точкою
діагоналей чотирикутника
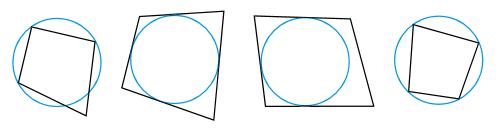
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
15.2 Чи
1. ∠ A = 30°; ∠ C = 150°;
2. ∠ B = 90°; ∠ D = 80°?
1. Навколо чотирикутника ABCD можна
180°. За умовою ∠A + ∠C = 30° + 150° = 180°. Оскільки сума кутів чотирикутника
Отже, навколо чотирикутника ABCD можна
Відповідь: так.
2. ∠B + ∠D = 90° + 80° = 170° ≠ 180°.
Відповідь: ні.
15.3
1. ∠ M = 20°; ∠ K = 150°;
2. ∠ N = 90°; ∠ L = 90°?
1. ∠M + ∠K = 20° + 150° = 170° ≠ 180°.
Відповідь: ні.
2. ∠N + ∠L = 90° + 90° = 180°.
Відповідь: так.
15.4 Чи
як:
1. 5 : 3 : 4 : 7;
2. 3 : 2 : 4 : 5?
Щоб у чотирикутник
рівними.
1. 5x, 3x, 4x, 7x сторони чотирикутника.
5x + 4x = 9x;
3x + 7x = 10x;
9x ≠ 10x.
Отже, у цей чотирикутник
2. 3x, 2x, 4x, 5x сторони чотирикутника.
3x + 4x = 2x + 5x = 7x
Так, у цей чотирикутник можна вписати коло.
15.5 Чи може бути описаним чотирикутник,
1. 7 : 3 : 2 : 6;
2. 5 : 4 : 3 : 6?
Пояснення:
1. 7x, 3x, 2x, 6x сторони
7x + 2x = 3x + 6x = 9x
2. 5x, 4x, 3x, 6x
5x + 3x = 8x
4x + 6x = 10x
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
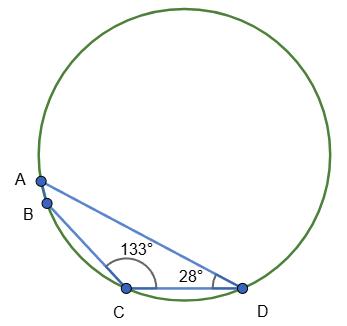

15.8 У
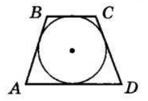
AB + CD = BC + AD.
∠A + ∠C = 180°,
∠A + 133° = 180°,
∠A = 180° − 133°,
∠A = 47°.
∠B + ∠D = 180°,
∠B + 28° = 180°,
∠B = 180° − 28°,
∠B = 152°.
Відповідь: 47°, 152°.
∠A + ∠C = 180°,
139° + ∠C = 180°,
∠C = 180° − 139°,
∠C = 41°.
∠B + ∠D = 180°, 48° + ∠D = 180°,
∠D = 180° − 48°,
∠D = 132°.
Відповідь: 41°, 132°.
Тоді AB + CD = 1 2 PABCD, 2AB = 1 2 · 16 см.
2AB = 8 см;
AB = 4 см.
Відповідь: 4 см.
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
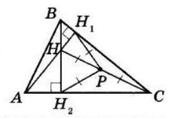
HH1CH2.
15.11 Точка M лежить на стороні AB гострокутного трикутника ABC. MP і MK перпендикуляри до сторін AC і BC відповідно. Доведіть, що навколо чотирикутника MPCK можна описати коло, діаметром якого буде відрізок CM. В ∆ABC M ∈ AB, MP ⊥ AC, MK ⊥ BC. Проведемо MC і
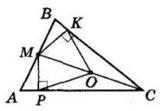
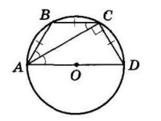
позначимо точку O середину MC. В ∆МКС середина гіпотенузи O центр
AB = BC = CD за умовою. Проведемо
AC.
∠BCA = ∠CAD як
AC.
В ΔABC ∠BAC = ∠BCA як кути при основі рівнобедреного ΔABC. ∠ACD = 90°, бо
спирається на діаметр AD.
Нехай ∠BAC = ∠CAD = ∠BCA = x.
Сума протилежних
x + x + x + 90 = 180;
3x = 90; x = 30.
Отже, ∠CAD = 30°.
Тоді в ΔACD (∠C = 90°) CD = 1 2 AD = 1 2 · 2R = R як
PABCD = R + R + R + 2R = 5R.
Відповідь: 5R.
15.13 AB
AIB = a (a > 90°).
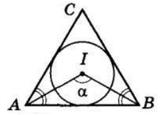
ΔABC AC = BC, I
AIB = α. ΔAIB
ΔABC). ∠IAB = ∠IBA = 180° α 2 ; ∠A = ∠B = 2 ∠IAB = 2 180° α 2 = 180° − α; ∠C = 180° − 2(180° − α) = 180° − 2 · 180° + 2α = 2α − 180°.
180° − α, 180° − α, 2α − 180°.
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
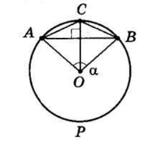

I випадок.
∠AOB = ᴗACB = α, тоді
∠CAB = ∠CBA = 180° (180° α 2 ) 2 =
∠AOB = ᴗAPB = α.
∠ACB = 1 2 ᴗAPB = α
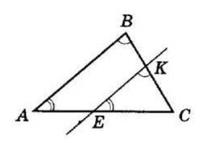
1.
2.
3. 4800 : 100 = 48 (мішків)
точок.
R
1. Проведемо коло радіуса
4.
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
§ 16. Теорема Фалеса
16.1 (Усно) На малюнку A1B1 || A2B2 || A3B3, A1A2 = 4 см, A2A3 = 4 см, B1B2 = 7 см. Знайдіть B2B3.
B2B3 = B1B2 = 7 см.
16.2 На малюнку A1B1 || A2B2 || A3B3, B1B2 = B2B3, A2A3 = 5 см. Знайдіть A1A2

A1A2 = A2A3 = 5 см.
16.3 На малюнку M1N1 || M2N2, OM1 = M1M2, ON1 = 6см. Знайдіть ON2.

N1N2 = ON1 = 6 см. ON2 = ON1 + N1N2 = 6 см + 6 см = 12 см.
16.4 На малюнку M1N1 || M2N2, ON1 = 7 см, N1N2 = 7 см, OM1 = 4 см. Знайдіть OM2.

M1M2 = OM1 = 4 см. OM2 = OM1 + M1M2 = 4 см + 4 см = 8 см.
16.5 Поділіть даний відрізок на 5 рівних частин.
AB даний відрізок.
1. З точки A проведіть довільний промінь AK.
2. На промені AK від точки A
A1K1 = K1K2 = K2K3 = K3K4 = K4K5.
3. Через точки K5 і B проведіть пряму.
4. Через точки K1, K2, K3, K4
K5B.
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html

16.8 Поділіть
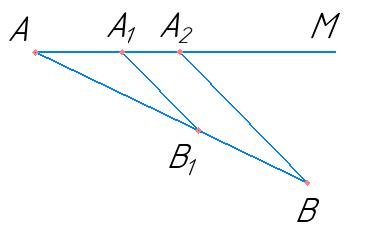
+ циркуль):
1. Дано відрізок AB.
Проведи з точки A довільний промінь AP.
2. Циркулем відклади на промені 7 рівних відрізків AP1 = P1P2 = … = P6P7.
3. З’єднай P7 з B.
4. Через P1, P2, …, P6 проведи прямі, паралельні P7B, до перетину з AB у точках A1, …, A6.
2 : 5.
промінь AM. Відкладемо на промені AM відрізки AA1 = 2a, A1A2 = 5a, де a деякий одиничний відрізок. Проводимо відрізок A2B. Через точку A1 проведемо пряму, паралельну до відрізка A2B. B1 точка її перетину з відрізком AB.
Маємо:
AB1 = 2c, B1B = 5c (за теоремою Фалеса). Отже, відрізок AB поділено на 2 частини, відношення яких дорівнює 2 : 5.
3 : 2.
Проводимо довільний промінь AM.
Відкладемо на промені AM відрізки AA1 = 3a, A1A2 = 2a, де a деякий одиничний відрізок. Проводимо відрізок A2B. Через точку A1 проведемо пряму, паралельну до відрізка A2B.
B1 точка її перетину з відрізком AB.
Маємо:
AB1 = 3c, B1B = 2c (за теоремою Фалеса).
Отже, відрізок AB поділено на 2 частини, відношення яких дорівнює 3 : 2.
16.9 На малюнку A1A2 = A2A3, A1B1 || A2B2 || A3B3. A1A2 : B1B2 = 3 : 5, B2B3 – A2A3 = 8 см. Знайдіть A1A2, A2A3, B1B2, B2B3. За умовою A1A2 : B1B2 = 3 : 5. Оскільки за теоремою Фалеса A₁A₂ A₂A₃ = B₁B₂ B₂B₃ , то A₂A₃ B₂B₃ = 3 5 .
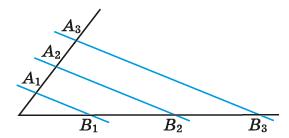
За умовою B2B3 – A2A3 = 8 см.
Нехай A2A3 = x см, тоді B2B3 = (x + 8) см.
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
A₁A₂
B₁B₂ = A₂A₃ B₂B₃ ; 3
5 = ���� ���� + 8; 5x = 3x + 24; 2x = 24; x = 12.
Отже, A1A2 = A2A3 = 12 (см); B1B2 = B2B3 = 12 + 8 = 20 (см).
Відповідь: 12 см, 20 см.
16.10 На малюнку ON1 = N1N2, M1N1 || M2N2, ON1 : OM1 = 7 : 4, N1N2 + M1M2 = 33 см.
Знайдіть ON2 і OM2.
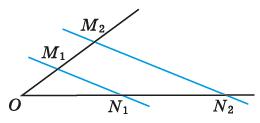
За умовою ON1 : OM1 = 7 : 4, тоді N1N2 : M1M2 = 7 : 4.
Нехай N1N2 = x см, тоді M1M2 = (33 – x) см. ���� 33 – ���� = 7 4; 4x = 7(33 − x); 4x = 231 − 7x; 11x = 231, x = 21.
Отже, ON1 = N1N2 = 21 см; OM1 = M1M2 = 33 − 21 = 12 (см).
Тоді ON2 = 2 · 21 = 42см; OM2 = 2 · 12 = 24 (см).
Відповідь: 42 см, 24 см. 16.11 M і N точки

Доведіть,
AL = LK = KC.
(MB || ND, MB = ND як половини рівних сторін). Тоді BN || MD.
Розглянемо кут BAC.
За теоремою Фалеса AM : MB = AL : LK.
Оскільки AM = MB, то AL = LK.
Аналогічно CN : ND = CK : LK, звідки CK = LK.
Отже, AL = LK = CK.
16.12 Точки E, F і G ділять медіану
(AE = EF = FG = GD).
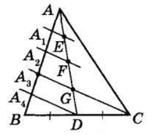
= A3A4 = A4B.
= A1A2 = A2A3
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
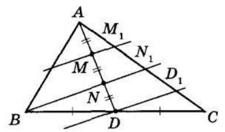
N
ACB
CD1 = N1D1 Отже, AM1 = M1N1 = N1D1 = D1C, звідки AN1 = N1C, тобто N1 середина AC, BN1 містить медіану трикутника.
16.14 Точка K середина медіани AD трикутника ABC. Відрізок BK перетинає сторону AC у точці M. Знайдіть AM : MC.
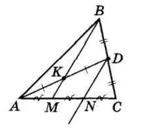
За умовою D середина BC, K середина AD.
Проведемо DN || BK. Паралельні прямі BM і DN перетинають
сторону трикутника DAC. AK = KD, значить, AM = MN.
Паралельні прямі BM і DN перетинають сторону кута BCA.
За умовою BD = DC, значить, MN = NC.
Отже, AM = MN = NC. Тоді AM : MC = 1 : 2. 16.15
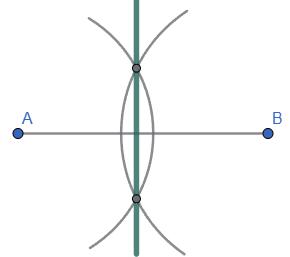
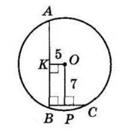
1.
кола до хорди AB; OP ⊥ BC = 7 см
кути прямі); OP = KB = 7 см, OK = PB = 5 см. За властивістю хорди, перпендикуляр до радіуса, K
AB, P
BC. Отже, AB = 2KB = 2 ⋅ 7 = 14 (см), BC = 2BP = 2 ⋅ 5 = 10 (см).
Відповідь: 14 см, 10 см.

4. Якщо на AP як на
2.
∠PAB + ∠APB + ∠BPC + ∠PCB + ∠CBA = 360°(1).
3. Але ∠APB = ∠ACB + 60°; ∠BPC = ∠BAC + 60°. Підставляючи це в рівність (1) та враховуючи те, що
∠ACB + ∠BAC + ∠CBA = 180°, маємо 180° + ∠PAB + ∠PCB + 60° + 60° = 360°; а, отже, ∠PAB + ∠PCB = 60°.
то точки Pb і P���� лежатимуть на ньому (оскільки ∠APbP = ∠APcP = 90°). Тому ∠APbP���� = ∠PAPc (як
що спираються на ту саму дугу).
5. Аналогічно ∠PPbPa = ∠PCPa, бо точки Pb і Pa лежатимуть на колі діаметра PC.
6. Маємо ∠PaPbPc = ∠PPbP���� + ∠PPbPa + ∠PAB + ∠PCB = 60°.
7. Аналогічно доводимо, що ∠PbPaPc = 60° і ∠PaPcPb = 60°. Отже, ΔPaPbP����

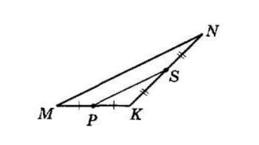
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
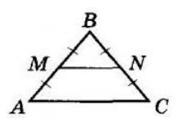
17.4 KL середня лінія трикутника ABC.
1. AB = 16 см. Знайдіть KL; 2. KL = 5 дм. Знайдіть AB.

1. KL = 1 2 AB = 1 2 ⋅ 16 см = 8 см;
2. KL = 1 2 AB, AB = 2KL = 2 ⋅ 5 дм = 10 дм.
17.5 KL середня лінія трикутника ABC.
1. AB = 18 см. Знайдіть KL; 2. KL = 3 дм. Знайдіть AB.

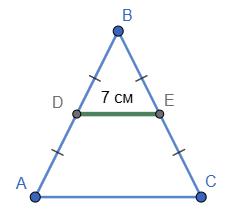
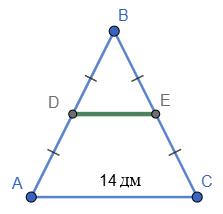
1. KL = 1 2 AB = 1 2 ⋅ 18 см = 9 см;
2. KL = 1 2 AB, AB = 2KL = 2 ⋅ 3 дм = 6 дм.
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
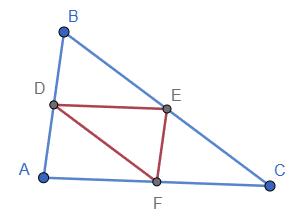
17.9
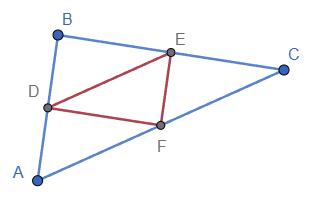
17.10

1. Рівнобедрений;
2. рівносторонній.
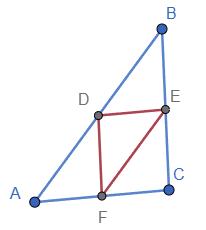
7 ⋅ 2 = 14 (см);
8 ⋅ 2 = 16 (см);
10 ⋅ 2 = 20 (см).
P = 14 + 16 + 20 = 50 (см).
Відповідь: 50 см.
12 : 2 = 6 (дм);
16 : 2 = 8 (дм); 18 : 2 = 9 (дм);
P = 6 + 8 + 9 = 23 (дм).
Відповідь: 23 дм.
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html

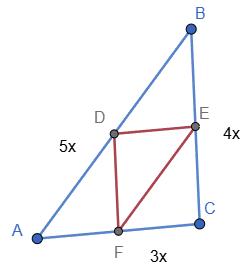
4 · 10 = 40 (см); 3 · 10 = 30 (см); 5 · 10 = 50 (см). Відповідь: 40 см, 30 см, 50 см.

P = 8x + 18x + 14x = 40
40x = 80; x = 2.
8 · 2 = 16 (см);
18 · 2 = 36 (см); 14 · 2 = 28 (см).
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
випадків слід розглянути?
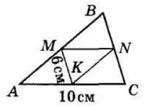
Нехай в ΔABC AC = 10 см, M середина AB, N середина BC, K середина AC. MN не
6 см, бо MN = 1 2 AC = 1 2 · 10 = 5 (см). Нехай MK = 6 см. Можливі два
випадки:
1. Сторона AB у 1,5 рази більша за BC.
BC = 2MK = 2 · 6 = 12 (см).
AB = 1,5 · BC = 18 (см).
Відповідь: 12 см і 18 см.
2. Сторона BC у 1,5 рази більша за AB.
BC = 2MK = 2 · 6 = 12 (см).
AB = BC : 1,5 = 12 : 1,5 = 8 (см).
Відповідь: 12 см, 8 см.
17.17 E, F, G, H − середини сторін AB, BC, CD і DA опуклого чотирикутника ABCD.
Знайдіть периметр чотирикутника EFGH, якщо AC = 16 см, BD = 10 см. Проведемо діагоналі AC і BD чотирикутника EFGH.
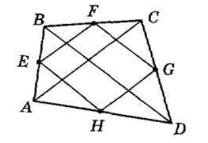
У ΔABC EF середня лінія, EF || AC, EF = 1 2 AC.
У ΔACD HG середня лінія, HG || AC, HG = 1 2 AC.
Отже, EF = HG = 1 2 AC = 1 2 · 16 см = 8 см.
Аналогічно FG середня лінія ΔBCD, EH середня лінія ΔABD, FG || BD, FG = 1 2 BD; EH || BD, EH = 1 2 BD.
FG = EH = 1 2 · 10 см = 5 см.
PEFGH = 2 · (8 + 5) = 26 (см).
Відповідь: 26 см.
17.18 Діагональ прямокутника дорівнює 10 см. Знайдіть
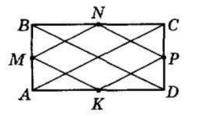
якого є середини сторін цього прямокутника. AC і BD діагоналі прямокутника ABCD; точки M, N, P, і K середини його сторін. MN середня лінія ΔABC, MN = 1 2 AC = 1 2 · 10 см = 5 см. KP середня лінія ΔACD, KP = 1 2 AC = 1 2 · 10 см = 5 см.
MN || AC, KP || AC, тому MN || KP за ознакою паралельних прямих.
NP середня лінія ΔBCD, NP = 1 2 BD = 1 2 · 10 см = 5 см (діагоналі прямокутника рівні).
MK середня лінія ΔABD, MK = 1 2 BD = 1 2 · 10 см = 5 см.
NP || BD, MK || BD, тоді NP || MK. Отже, MNPК паралелограм за означенням.
NP = MK = KP = MN = 5 см, тому MNPК ромб.
PMNPK = 4 · 5 = 20 см.
Відповідь: 20 см.
17.19 O −
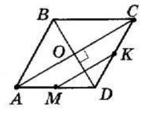
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
що MK ⊥ OD.
В ромбі ABCD BD ⊥ AC як діагоналі. MK середня лінія трикутника ACD. Тоді MK || AC, а значить, MK ⊥ BD і MK ⊥ OD (пряма, перпендикулярна одній з двох паралельних прямих, перпендикулярна і другій).
17.20 AK − медіана рівнобедреного трикутника ABC з основою BC. Точки P і F − середини сторін AB і AC відповідно. Доведіть, що PF ⊥ AK. У ΔABC AB = AC, AK медіана, а значить, і висота, проведена до основи: AK ⊥ BC. PF середня лінія
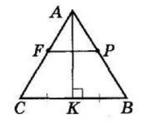
умовою, тоді PF || BC. Якщо AK ⊥ BC, то AK ⊥ PF.
середини сторін даних трикутників.
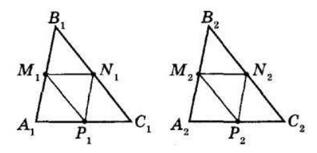
За умовою ΔA1B1C1 = ΔA2B2C2, тому їх відповідні сторони рівні: A1B1 = A2B2, B1C1 = B2C2, A1C1 = A2C2.
Точки M1, N1, P1 і M2, N2, P2 середини відповідних сторін трикутників. M1N1
середня лінія.
M1N1 = 1 2 A1C1; M2N2 середня лінія. M2N2 = 1 2 A2C2.
Але A1C1 = A2C2 за умовою, тоді M1N1 = M2N2.
Аналогічно M1P1 = M2P2, N1P1 = N2P2.
Отже, ΔM1N1P1 = ΔM2N2P2 за трьома сторонами.
17.22 Точка M −
трикутника ABC (
C = 90°).
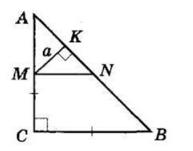
ΔABC ∠C = 90°, AC = BC, M
AMK AK = MK = a.
AC, MK ⊥ AB,
ΔAMN AM = 1 2 AC, MN = 1 2 BC, тому AM = MN.
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
AB = 20

У ΔABC ∠C = 90°, AC = BC, K середина BC, KD ⊥ AB відстань від точки K
гіпотенузи.
У ΔABC ∠A = ∠B = 45°, ΔKDB рівнобедрений, KD = DB. Проведемо KP || AC.
За теоремою Фалеса P середина AB, тобто KP середня
KP = 1 2 AC.
Оскільки AC = BC, то KP = 1 2 BC = KP.
ΔBKP рівнобедрений, ∠PKB = 90° (AC ⊥ BC, KP || AC).
В рівнобедреному ΔBKP KD висота, а значить, медіана.
Точка D середина гіпотенузи, тоді KD = PD = BD =
Відповідь: 5 см.
17.24 Доведіть, що середини сторін ромба
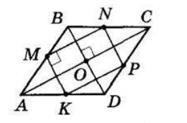
прямокутника. ABCD ромб, O точка перетину діагоналей.
Точки M, N, P і K середини сторін.
У ΔABC MN середня лінія, MN || AC, MN = 1 2 AC.
У ΔACD KP середня лінія, KP || AC, KP = 1 2 AC.
Оскільки MN || AC і KP || AC, то MN || KP. KP = MN = 1 2 AC.
Чотирикутник MNPK паралелограм за означенням. AC ⊥ BD за властивістю діагоналей ромба. MN || AC, тоді MN ⊥ BD. У ΔABD MK середня лінія, MK || BD, тоді MN ⊥ MK. MNPK прямокутник (як паралелограм, у якого один з кутів прямий).
17.25 У рівнобедреному трикутнику ABC (AB = AC) M − точка перетину медіан.
що AM = 8 см. Знайдіть відстань
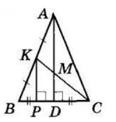
У ΔABC AB = AC, M точка
⊥
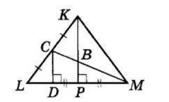
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
CD ⊥ LM, значить, CD || KP. За теоремою
D середина LP.
CD середня лінія ΔKLP, CD = 1 2 KP, звідки KP = 2 · CD = 2 · 9 = 18 см.
KB : BP = 2 : 1, Отже, KB = 18 : 3 · 2 = 12 (см).
Відповідь: 12 см.
17.27 У трикутнику ABC ∠ A = 40°, ∠ B = 80°, O центр описаного кола. Знайдіть
∠AOB, ∠ BOC, ∠ COA.
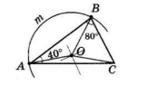
У ΔABC ∠C = 180° − (∠A + ∠B) = 180° − (40° + 80°) = 60°.
∠C вписаний, ∠C = 1 2 ᴗAmB,
ᴗAmB = 2∠C = 2 · 60° = 120°.
∠AOB центральний, він спирається на ту саму дугу.
∠AOB = ᴗAmB = 120°.
Аналогічно, ∠BOC = 2∠A = 2 · 40° = 80°;
∠AOC = 2∠B = 2 · 80° = 160°.
Відповідь: 120°, 80°, 160°.
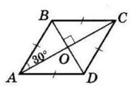
ABCD ромб, AC і BD його діагоналі, BD = 7 см.
∠BAC = 30°. Діагоналі
тому
AB = AD = BD = 7 см.
PABCD = 4 · 7 = 28 (см).
Відповідь: 28 см. 17.29
1. бічну сторону трапеції;
2. периметр трапеції;
3. чи можна в трапецію вписати коло. ABCD трапеція, AB = CD, AD = a, BC = b (a > b). ∠BAD = ∠CDA = 60°. Проведемо BK ⊥ AD висоту трапеції. У ΔCKD
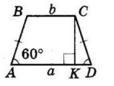
1. CD = 2KD = 2���� ���� 2 = a
2. PABCD = 2AB + BC + AD = 2(a – b) + b +
1. 100 · 12 · 10 = 1200 · 10 = 12000 (м3)
2. 12000 · 50 = 600000 (м3) – 50
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
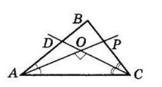

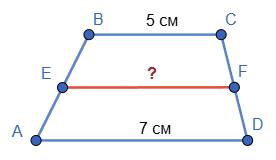
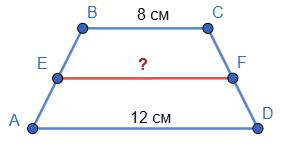
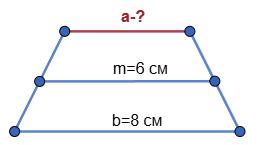
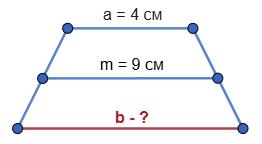
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
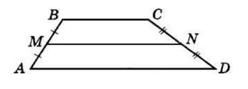
BC = 8 см, AD = 2 · BC = 2 · 8 = 16 (см). MN = BC + AD 2 = 8 + 16 2 = 24 2 = 12 (см).


C
ередня лінія трапеції:
MN = (�������� + ��������) : 2 = 30 см.
1. AB = x см, CD = (x − 8) см.
MN = ���� + (���� 8) 2 = ���� 4.
x − 4 = 30;
x = 34.
AB = 34 см, CD = 34 − 8 = 26 (см).
2. AB = x см, CD = 4x см.
MN = ���� + 4���� 2 = 2,5���� .
2,5x = 30;
x = 12.
AB = 12 см, CD = 4 · 12 = 48 (см).
3. Нехай CD = 2x, AB = 3x.
MN = 2���� + 3���� 2 = 5���� 2 = 2,5����.
2,5x = 30;
x = 12.
CD = 2 · 12 = 24 (см), AB = 3 · 12 = 36 (см).
Відповідь:
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
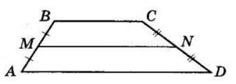
1. BC = x см, AD = (x + 2) см;
MN = ���� + ���� + 2 2 = x + 1;
x + 1 = 16; x = 15.
BC = 15 (см), AD = 15 + 2 = 17 (см).
Відповідь: 15 см, 17 см.
2. BC = x см, AD = 3x см.
MN = ���� + 3���� 2 = 2���� .
2x = 16;
x = 8.
BC = 8 (см), AD = 3 · 8 = 24 (см).
Відповідь: 8 см, 24 см.
3. BC = 3x, AD = 5x.
MN = 3���� + 5���� 2 = 8���� 2 = 4x;
4x = 16; x = 4.
BC = 3 · 4 = 12 (см), AD = 5 · 4 = 20 (см).
Відповідь: 12 см, 20 см.
18.9 K – точка перетину діагоналей BD трапеції
що BK = KD.
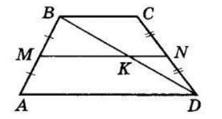
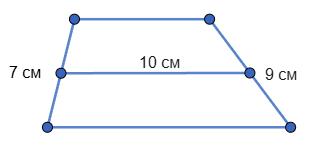
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
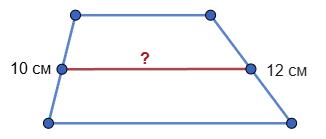
18.12 Чи може середня лінія трапеції:
1. дорівнювати одній з основ;
2. бути меншою від меншої основи;
3. бути більшою за більшу основу;
4. бути рівною меншій
52 − (10 + 12) = 30 (см) сума основ трапеції.
30 : 2 = 15 (см) середня лінія (півсума основ).
Відповідь: 15 см.
і b основи трапеції a > b, m середня лінія. m = ���� + ���� 2 .
Перевіримо задані умови.
Відповідь: ні.
Відповідь: ні. ����. ���� + ���� 2 > ���� ;
a + b > 2a; b > a.
Відповідь: ні. ����. ���� + ���� 2 = ���� 2 ;
a + b = a; b = 0.
Відповідь: ні.
18.13 EF – середня лінія трапеції ABCD, яка перетинає діагональ BD у точці N. EN = 5 см, N'F = 3 см. Знайдіть основи трапеції.
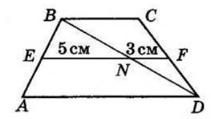
EF середня лінія трапеції ABCD, EF || AD, EF || BC.
В ΔABD E середина AB, EN || AD, за теоремою
N середина BD, EN середня лінія ΔABD.
EN = 1 2 AD, AD = 2EN = 2 · 5 = 10 (см).
В ΔBCD FN середня лінія.
FN = 1 2 BC, BC = 2FN = 2 · 3 = 6 (см).
Відповідь: 10 см, 6 см.
18.14 MN – середня лінія трапеції ABCD, яка
MK і KN, якщо
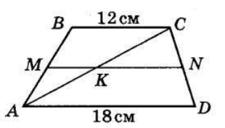
MN середня
AC у точці K.
18 см і 12 см.
трапеції, MN || AD, MN || BC. У ΔABC M середина AB, MK || AD, тоді K середина
AC, MK середня лінія ΔABC.
MK = 1 2 BC = 1 2 · 12 = 6 (см).
KN середня лінія ΔACD, KN = 1 2 AD = 1 2 · 18 = 9 (см).
Відповідь: 6 см, 9 см.
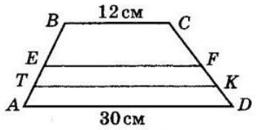
2 =
2 = 21 (см).
умовою T середина AE. TK || AD за умовою. Оскільки AD || EF, то TK || EF. Тоді за теоремою Фалеса K середина DF, TK середня лінія трапеції AEKD (EF || AD). TK = EF + AD 2 = 21 + 30 2 = 51 2 = 25,5 (см).
Відповідь: 21 см, 25,5 см.
18.16 У трапеції ABCD M
M і N
AB, N – середина MB.
прямі, паралельні BC, які перетинають CD у точках K і L
MK = 12 см, NL = 8 см. Знайдіть основи трапеції.
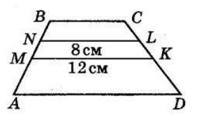
ABCD трапеція, BC || AD. MK || BC, значить, MK || AD. Отже, MBCK трапеція. N середина AB, NL || BC, значить, NL || MK. За теоремою Фалеса NL середня лінія трапеції MBCK.
NL = BC + MK 2 ; 8 = BC + 12 2 ; BC + 12 = 16; BC = 4 см.
Аналогічно, MK середня лінія трапеції ABCD.
MK = AD + BC 2 ; 12 = AD + 4 2 ; AD + 4 = 24; AD = 20.
Отже, BC = 4 см, AD = 20 см.
Відповідь: 4 см, 20 см. 18.17 У
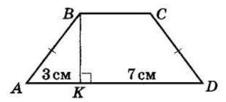
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
18.18
основи AD. AK = 4 см, BC = 6 см.
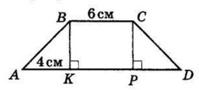
ABCD трапеція, BK ⊥ AD висота, AK = 4 см, BC = 6 см.
Проведемо CP ⊥ AD. Чотирикутник KBCP прямокутник (BC || KP, BK || CP, ∠BKP = 90°). KP = BC = 6 см, PD = AK = 4 см (з рівності трикутників ABK і DCP за гіпотенузою і гострим кутом).
AD = AK + KP + PD = 4 + 6 + 4 = 14 (см).
Середня лінія трапеції дорівнює:
BC + AD 2 = 6 + 14 2 = 20 2 = 10 (см).
Відповідь: 10 см.
18.19
7 см, а
l.

AA1 ⊥ l, BB1 ⊥ l, MM1 ⊥ l відстані
AA1 || MM1 || BB1, чотирикутник A1ABB1 трапеція. Точка M1 середина AB.
теоремою
M1 середина A1B1, MM1 середня
трапеції A1ABB1.
MM1 = AA₁ + BB₁ 2 ;
2MM1 = AA1 + BB1; BB1 = 2MM1 − AA1 = 2 · 5 − 7 = 10 − 7 = 3 (см). Відповідь: 3 см.
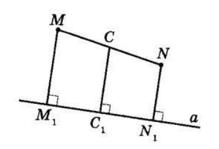
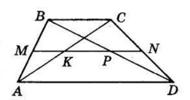
= MM₁ + NN₁ 2 = 10 + 16 2 = 13 (см).
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
PN = 1 2 BC = 1 2 · 6 см = 3 см.
MN = 1 2 (BC + AD) = 1 2 (6 + 14) = 10 (см).
KP = MN – (MK + PN) = 10 – (3 + 3) = 4 (см).
Відповідь: 3 см, 4 см, 3 см.
18.22 Діагоналі ділять середню лінію
см. Знайдіть основи трапеції.

ABCD трапеція (AD || BC), MN середня
BD діагоналі.
AC і
Точки K і P точки перетину діагоналей і середньої
MK = PN = 7 см, KP = 8 см. У ΔABC M середина AB, MK || BC (як частина середньої лінії), тоді за теоремою Фалеса K середина AC.
Отже, MK середня лінія ΔABC: MK = 1 2 BC, BC = 2MK = 2 · 7 = 14 (см).
MN = MK + KP + PN = 7 + 8 + 7 = 22 (см).
MN = AD + BC 2 ;
2MN = AD + BC; AD = 2MN − BC;
AD = 2 · 22 − 14 = 44 − 14 = 30 (см).
Відповідь: 14 см, 30 см. 18.23 У трапеції ABCD (AD || BC) ∠ A = 90°, ∠ C = 135°, AB = 6 см. Знайдіть середню
лінію трапеції, якщо її діагональ
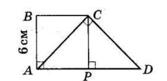
бічної сторони.
ABCD трапеція (AD || BC), ∠A = 90°, ∠C = 135°, AB = 6 см, AC ⊥ CD.
∠BCD = ∠BCA + ∠ACD,
∠BCA = ∠BCD − ∠ACD = 135° − 90° = 45°.
У ΔABC ∠B = 90°, оскільки ∠A = 90°, a BC || AD, ∠BCA = 45°, тоді ∠BAC = 45°.
ΔABC рівнобедрений (кут при основі рівні).
BC = AB = 6 см. Проведемо CP ⊥ AD.
У ΔACD ∠D = 180° − ∠BCD = 180° − 135° = 45°.
∠ACD = 90°, тоді ∠CAD = 45°. ΔACD рівнобедрений, AC = CD.
Висота CP є медіаною, AP = PD. Але AP = BC,
тому AD = 2BC = 2 · 6 = 12 (см).
Середня лінія: AD + BC 2 = 12 + 6 2 = 9 (см).
Відповідь: 9 см.
18.24
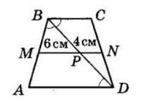
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
MP = 1 2 AD як середня лінія ΔABD.
AD = 2MP = 2 · 6 = 12 (см).
Аналогічно, в ΔBCD BC = 2PN = 2 · 4 = 8 (см).
∠CBD = ∠BDA як внутрішні різносторонні при BC || AD і січній BD.
Але ∠CBD = ∠ABD за умовою, тоді ∠ABD = ∠BDA, ΔABD рівнобедрений, AB = AD = 12 см.
PABCD = AD + 2AB + BC = 12 + 2 · 12 + 8 = 44 (см).
Відповідь: 44 см.
18.25 Діагональ рівнобічної трапеції ділить її
лінію – на відрізки 3 см і 7 см. Знайдіть периметр трапеції. ABCD трапеція, AD || BC, AB = CD, MN середня лінія трапеції.
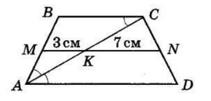
AC діагональ, AC бісектриса кута A.
MK = 3 см, KN = 7 см.
У ΔABC M середина AB. MK || BC як частина середньої лінії трапеції.
Тоді K середина AC за теоремою Фалеса, а MK середня лінія ΔABC, MK = 1 2 BC.
Звідки BC = 2MK = 2 · 3 = 6 (см).
Аналогічно, KN середня лінія ΔACD.
KN = 1 2 AD, AD = 2KD = 2 · 7 = 14 (см).
∠BCA = ∠CAD як внутрішні різносторонні при BC || AD і січній AC.
Але ∠CAD = ∠BAC за умовою, тоді ∠BCA = ∠BAC і ΔABC рівнобедрений, AB = BC = 6 см.
PABCD = AB + BC + CD + AD = 6 + 6 + 6 + 14 = 32 (см).
Відповідь: 32 см.
18.26 Знайдіть кути M і N чотирикутника MNKL, вписаного в коло, якщо ∠K = 37°, ∠L = 119°. У вписаного в коло чотирикутника сума протилежних кутів дорівнює 180°.
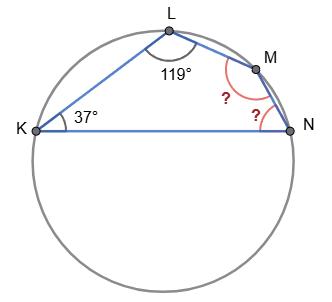
18.27 Коло вписано в рівнобічну
∠M = 180° − ∠K = 180° − 37° = 143°. ∠N = 180° − ∠L = 180° − 119° = 61°. Відповідь: 143°, 61°.
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
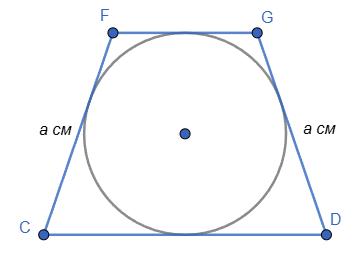
a + a = 2a (см). Pтр = 2a + 2a = 4a (см).
4a см. 1
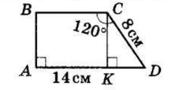
основу трапеції.
В трапеції ABCD ∠A = ∠B = 90°, ∠C = 120°.
AD = 14 см, CD = 8 см (найбільша бічна сторона, бо похила
більша за перпендикуляр).
Проводимо CK ⊥ AD. ΔBCK прямокутник (BC || AK, AB || CK, ∠A = 90°).
∠DCK = ∠BCD − ∠BCK = 120° − 90° = 30°.
Тоді у ΔCKD KD = 1 2 CD = 1 2 · 8 = 4 (см) (за властивістю катета, що лежить проти кута 30°).
У прямокутнику ABCD AK = BC = AD − KD = 14 − 4 = 10 (см).
Відповідь: 10 см.
18.29. Знайдіть значення степеня:
1. (–2)3 = –8;
2. 142 = 196;
3. (–1)11 = –1;
4. 05 = 0;
5. (0,3)3 = 0,027; 6. (–0,8)2 = 0,64; ����. �− 2 7�2 = 4 49 ; ����. � 1 5�3 = 1 125.
18.30. Обчисліть:
1. 25 – 32 = 32 – 9 = 23;
2. (–1)9 + (–1)8 = –1 + 1 = 0;
����. 42 · � 3 4�2 = 16 · 9 16 = 9;
����. 53 ∶ �5 6� 2 = 125 · 36 25 = 180.
18.31. Подайте у вигляді степеня з:
1) основою 2 числа 2, 4, 8, 16, 32, 128, 512; 2) основою 3 числа 81, 243;
1. 2 = 21; 4 = 22; 8 = 23; 16 = 24; 32 = 25; 128 = 27; 512 = 29 .
2. 81 = 34; 243 = 35
3. 5 = 51; 25 = 52; 625 = 54 .
4. 100 = 102; 10000 = 104.
18.32. Ширина
2.
1 га = 10000 м2, 6 км/год = 6000 м/год
1. S = 6000 · 2 = 12000 (м2) – площа
3. 150 · 1,2 = 180 (кг) – витрачає насіння за 1 год; m (кг) = 180 · t (
4. 270 : 180 = 1,5 год = 1 год 30 хв –
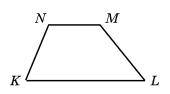
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
Якщо середня лінія = 6 см, то сторона:
a = 6 ∙ 2 = 12 (см).
Відповідь: В. 12 см.
3. На малюнку M1N1 || M2N2, ON1 = N1N2, OM2 = 16 см. Знайдіть M1M2.
А. 4 см
Б. 8 см
В. 6 см
Г. Знайти неможливо
M1M2 = 1 2 OM2 = 1 2 · 16 = 8 (см).
Відповідь: Б. 8 (см).
4. Чотирикутник ABCD вписано в коло.
цього чотирикутника.
А. ∠ C = 80°, ∠ D = 160°
Б. ∠ C = 150°, ∠ D = 80°
В. ∠ C = 20°, ∠ D = 100°
Г. ∠ C = 160°, ∠ D = 80°
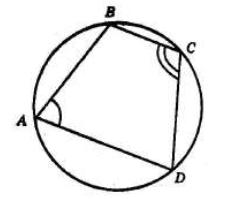
А. 11 см
Б. 12 см
В. 14 см
∠C =
A =
Г. 16 см У трикутнику ABC AB = 4 см, BC = 10 см, AC = 10 см.
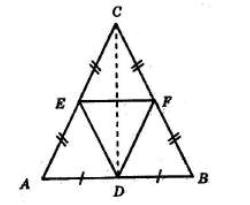
DF, DE, FE.
трикутника маємо: DF = 1 2 AC = 1 2 · 10 = 5 (см), DE = 1 2 BC = 1 2 · 10 = 5 (см), FE = 1 2 AB = 1 2 · 4 = 2 (см).
Тоді PDFE = DF + FE + DE = 5 + 2 + 5 = 12 (см). Відповідь: Б. 12 см.
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
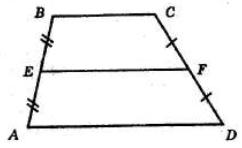
Нехай BC = 2x см, тоді AD = 3x см і за теоремою
EF = BC + AD 2 ; звідси 20 = 2���� + 3���� 2 ,
або 5x = 40; x = 8.
Отже, BC = 2x см = 16 (см).
Відповідь: А. 16 см. 7. У рівнобічній
A. 110
Б. 95
B. 105
Г. 115
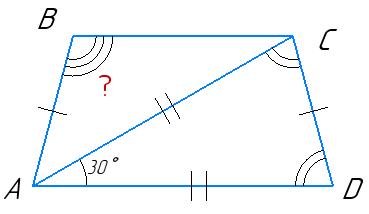
Сума
трапеції):
∠BCD + ∠CBA = 180° ⇒
Нехай ABCD рівнобічна трапеція, AD більша основа, BC менша, AB = CD
сторони.
Діагональ AC = AD, ∠CAD = 30°. У △ACD, AC = AD. Це означає, що △ACD рівнобедрений
CD, а його
рівні (∠ACD = ∠ADC).
Сума кутів △ACD = 180°: 30° + 2x = 180° x = 75°.
∠ABC = ∠BCD = 180° − 75° = 105° .
Відповідь: B. 105°.
8. Коло вписано в рівнобічну трапецію, бічна сторона якої дорівнює 10 см. Знайдіть
периметр трапеції.
А. 50 см
Б. 20 см
В. 30 см
Г. 40 см
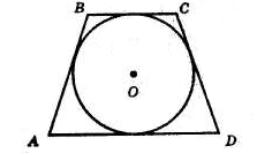
В. 27 см
Г. 30 см
ABCD трапеція, описана навколо кола,
AB = CD = 10 см, тоді AB + CD = 20 см.
Оскільки
рівнобедрену трапецію
ABCD, то AB + CD = BC + AD, тоді
PABCD = 20 + 20 = 40 (см).
Відповідь: Г. 40 см.
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
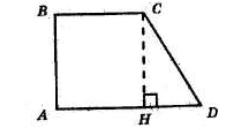
Нехай ABCD прямокутна трапеція, AD || BC, AB ⊥ AD. ∠CDA = 60°, BC = 18 см, CD = 18 см (за умовою задачі). Проведемо CH || AD.
Оскільки ∠CDA = 60°, то ∠HCD = 90° − 60° = 30°.
Отже, у трапеції ABCD HD = 1 2 CD = 1 2 · 18 = 9 (см)
Тоді AD = BC + HD = 18 + 9 = 27 (см).
Відповідь: B. 27 см.
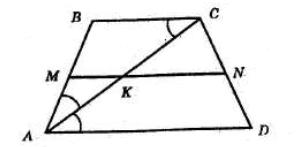
ABCD рівнобічна трапеція, AD || BC, MN середня
трапеції ABCD, MK = 4 см, KN = 5 см.
∠BAC = ∠DAC за умовою задачі, тоді:
∠CAD = ∠BCA, як різносторонні кути при
паралельних прямих AD і BC та січній AC.
Оскільки ∠BAC = ∠DAC і ∠CAD = ∠BCA, то
∠BAC = ∠BCA, отже, трикутник ABC рівнобедрений.
З рівнобедреного трикутника ABC за теоремою про середню лінію
AB = BC = 2MK = 2 · 4 = 8 см.
За теоремою про середню
AD = 2KN = 2 · 5 = 10 (см).
Тоді PABCD = 3BC + AD = 24 + 10 = 34 (см).
Відповідь: Б. 34 см.
11. Точка N середина медіани AD трикутника ABC. BN перетинає AC у точці F.
Знайдіть AF, якщо AC = 18 см.
А. 6 см
Б. 9 см
В. 3 см
Г. 2 см
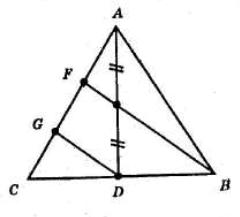
Через точку D проведемо прямі DG паралельні
BF.
Оскільки BD = DC і DG || BF, то CG = GF (за теоремою Фалеса).
Оскільки DN = NA і DG || NF, то GF = FA (за теоремою Фалеса).
Оскільки CG = GF і GF = FA, то AF = 18 : 3 = 6 (см).
Відповідь: А. 6 см.
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
18 см
9 см
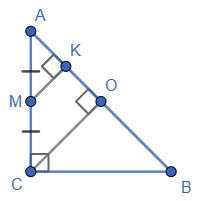
Нехай ABC даний прямокутний трикутник, у якому ∠C = 90°, AC = CB, AM = MC, MK ⊥ AB, CO ⊥ AB, AB = 36 (см).
У трикутнику ABC ∠A = ∠B = 45°, оскільки цей трикутник рівнобедрений.
CO висота, медіана трикутника ABC, CO = AO.
MK середня лінія трикутника ACO, тоді CO = 1 2 AB = 1 2 · 36 = 18 (см).
MK = 1 2 CO = 1 2 · 18 = 9 (см).
Відповідь: Г. 9 см. 13. MN середня

середині.
MK
трапеції: MN = �������� +�������� 2 = 8; AB + DC = 16.
За умовою AB = 10, отже DC = 16 – 10 = 6 см. У трикутнику ABD: точка M середина AD, пряма MN
точка K.
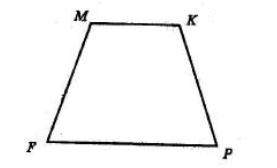
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
Тоді сторона:
a = 4 ∙ 2 = 8 см.
Периметр: P = 3a = 3 ∙ 8 = 24 см.
Відповідь: 24 см.
3. На малюнку A1B1 || A2B2, OB1 = B1B2, OA1 = 2 см. Знайдіть OA2. OA2 = 2OA1 = 2 · 2 = 4 (см).
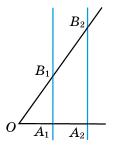
Відповідь: 4 см.
4. Знайдіть кути A і B чотирикутника ABCD, вписаного в
якщо ∠C = 140°, ∠D = 70°.
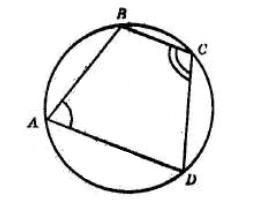
чотирикутник ABCD є
∠A = 180° − ∠C = 180° − 140° = 40°
∠B = 180° − ∠D = 180° − 70° = 110°

трикутнику ABC AB = 10 см, BC = 12 см, AC = 16 см
Проведено середні лінії DF, DE, FE.
маємо: DF = 1 2 BC = 1 2 · 12 = 6 (см), DE = 1 2 AC = 1 2 · 16 = 8 (см), FE = 1 2 AB = 1 2 · 10 = 5 (см).
PDFE = DF + FE + DE = 8 + 5 + 6 = 19 (см).
19 см.
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html

Нехай BC = x см, тоді AD = (x + 4) см і
середню
EF = BC + AD 2 ;
звідси: 8 = ���� + ���� + 4 2 ;
або x + 2 = 8; x = 6.
Отже, BC = 6 (см), AD = (x + 4) см = 10 (см).
Відповідь: 6 см і 10 см.

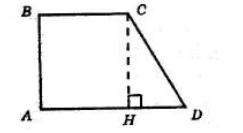
ABCD
AB = CD, PABCD = 20 см.
ABCD,
то AB + CD = BC + AD = 20 : 2 = 10 (см).
Тоді AB = CD = 10 : 2 = 5 (см). Відповідь: 5 см.
Нехай ABCD
AD || BC, AB ⊥ AD.
трапеція,
∠CDA = 60°, AD = 12 см, CD = 12 см за умовою
Проведемо CH ⊥ AD.
Оскільки ∠CDA = 60°, то ∠HCD = 90° − 60° = 30°.
Отже, у трапеції ABCD: HD = 1 2 CD = 1 2 · 12 = 6 (см) за властивістю
30°.
Тоді BC = AD − HD = 12 − 6 = 6 (см).
Відповідь: 6 см.
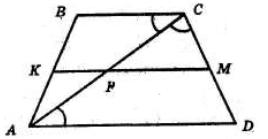
AD = DC = 2PM = 18 см.
BC = 2KP = 2 · 7 = 14 (см).
Нехай ABCD рівнобічна трапеція, AD || BC, MK середня лінія трапеції ABCD, KP = 7 см, PM = 9 см. ∠BCA = ∠DCA за умовою задачі, тоді: ∠CAD = ∠BCA як різносторонні кути при
паралельних прямих AD і BC та січній AC. Оскільки ∠BCA = ∠DCA і ∠CAD = ∠BCA, то ∠DAC = ∠DCA, отже,
PABCD = BC + 3AD = 14 + 54 = 68 (см).
68 см.
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
K, L, M
= LM = MD). AM
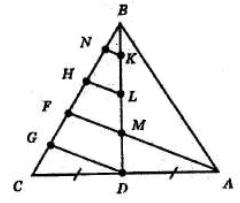
Через точки K, L, D проведемо прямі KN, LH, DG, паралельні прямій AM.
Оскільки AD = DC і DG || AM, то CG = GF (за теоремою Фалеса).
Оскільки DM = ML = LK = KB і AM || LH || DG || NK, то GF = FH = HN = NB (за теоремою Фалеса).
Оскільки CG = GF і GF = FH = HN = NB, то
CF : FB = 2 : 3.
Відповідь: 2 : 3.
11. Точка D середина катета BC рівнобедреного прямокутного трикутника ABC (∠C = 90°). Відстань від точки D до гіпотенузи трикутника на 15 см менша від гіпотенузи. Знайдіть гіпотенузу трикутника.
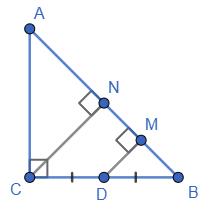
Нехай ABC даний прямокутний трикутник, у якому ∠C = 90°, AC = CB, DB = DC. DM ⊥ AB, CN ⊥ AB, DM + 15 = AB.
У трикутнику ABC ∠A = ∠B = 45°, оскільки цей трикутник рівнобедрений. CN висота, медіана трикутника ABC, CN = AN. MD середня лінія трикутника BCN, тоді
CN = 1 2 AB, MD = 1 2 CN = 1 4 AB.
Отже, 1 4 AB + 15 = AB;
AB + 15 · 4 = 4AB;
3AB = 60;
AB = 20 (см).
Відповідь: 20 см.
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
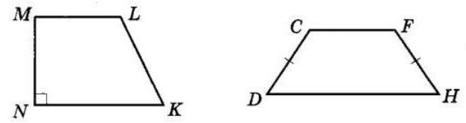
NMLK:
2
основі. P = 8 + 5 + 2 · 5 = 23 (см).
Відповідь: 23 см.
3.
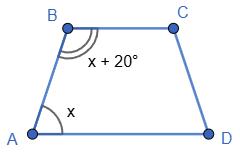

x + x + 20 = 180;
2x = 160;
x = 80°.
∠A = 80°,
∠B = 80° + 20° = 100°.
Відповідь: 80°, 100°.
У трапеції ABCD ∠A = ∠B = 90°. Проведемо CK ⊥ AD. ABCK прямокутник, CK = AB.
За умовою CD = 2AB = 2CK. Тоді в △CKD гіпотенуза CD вдвічі більша
означає, що кут D = 30°. ∠BCD = 180° − ∠D = 180° − 30° = 150°.
90°, 90°, 150°, 30°.
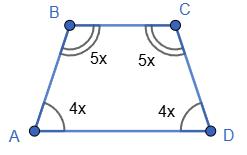
Нехай ∠A = 4x,
∠B = 5x, 4x + 5x = 180°; 9x = 180°; x = 20.
Отже, ∠A = 4 · 20° = 80°, ∠B = 5 · 20° = 100°.
Відповідь: 80°, 100°, 100°, 80°.
180°.
катет CK.
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
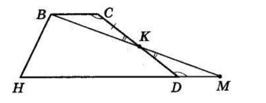
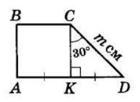

BC || AM і січній CD;
CK = KD за умовою;
∠BKC = ∠DKM як
трапеції ABCD BC || AD, AB = CD.
BCA = ∠CAD як внутрішні різносторонні
BC || AD і січній AC. Але за умовою ∠BCA = ∠ACD, тому ∠CAD = ∠ACD, AC основа рівнобедреного △ACD, CD = AD = 10 см.
PABCD = AD + BC + 2CD = 10 + 6 + 2 · 10 = 36 (см).
Відповідь: 36 см.
9. ABCD прямокутна трапеція, ∠D = ∠C = 90°, AD більша основа, ∠BDC = 45°, ∠ABD = 90°, AD = 10 см. Знайдіть BC і CD.
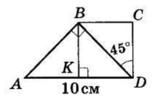
Проведемо BK ⊥ AD.
У △ABD ∠ADB = ∠ADC − ∠BDC = 90° − 45° = 45°.
Тоді ∠BAD = 45° і у △ABD AB = BD.
Висота BK є медіаною, проведеною
B: BK = AK = KD = 1 2 AD = 1 2 · 10 = 5 (см).
CD = BK = 5 см (як відрізки двох перпендикулярів, що містяться
паралельними прямими).
△BCD є рівнобедреним (він
BC = CD = 5 см.
Відповідь: BC = 5 см, CD = 5 см. 10.
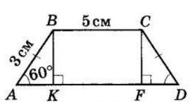
AK = FD = 1 2 AB = 1,5 см
KBCF прямокутник (BK || CF, BK = CF, ∠BKF = 90°).
KF = BC = 5 см.
PABCD = AB + BC + CD + AD = = 3 + 5 + 3 + (1,5 + 5 + 1,5) = 19 (см). Відповідь: 19 см.
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
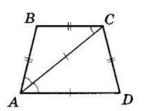
У △ABC AB = BC, тому ∠BAC = ∠BCA.
∠BCA = ∠CAD як внутрішні різносторонні
AC.
∠CDA = BAD за умовою.
Нехай ∠BCA = x, тоді ∠BAD = 2x.
У △ACD AC = AD за умовою, тоді ∠ACD = ∠ADC = 2x,
∠BCD = ∠BCA + ∠ACD = x + 2x = 3x.
∠BCD + ∠ADC = 180°.
Маємо рівняння: 3x + 2x = 180°; 5x = 180°; x = 36°.
∠A = 2 · 36° = 72°,
∠B = 3 · 36° = 108°.
∠C = ∠B = 108°,
∠D = ∠A = 72°.
Відповідь: 72°, 108°, 108°, 72°.
12. Побудуйте
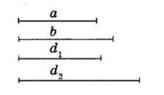
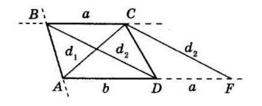
Припустимо, що трапецію побудовано.
Проведемо через
перетину з основою AD через F. Тоді у △ACF нам відомі всі сторони: AC = d1, CF = d2, AF = b + a Побудуємо цей трикутник
План побудови:
1. Будуємо пряму, відкладаємо на ній відрізки AB = b в DF = a.
2. Провести коло з центром A радіуса d1.
3. Провести коло з центром F радіуса d2.
4. Точка перетину кіл C.
5. Провести коло з центром D радіуса d2
6. Провести коло з центром

BC = AE, CE = AB.
P△CED = CE + CD + ED = AB + CD + AD − BC = = AB + CD + AD + BC − 2BC = PABCD − 2BC = = 56 – 2 · 10 = 36 (см).
36 см.
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
1. AB = 5 см, BC = 3 см, CD = 4 см, DA = 6 см;
2. AB = 3 дм, BC = 7 дм, CD = 8 дм, DA = 10 дм?
Коло можна
рівні.
1. AB + CD = 5 + 4 = 9 (см); BC + DA = 3 + 6 = 9 (см);
AB + CD = BC + DA.
Відповідь: так.
2. AB + CD = 8 + 3 = 11 (дм); BC + DA = 7 + 10 = 17 (дм);
AB + CD ≠ BC + DA.
Відповідь: ні.
15. Чи можна описати коло навколо чотирикутника,
відносяться як:
1. 2 : 7 : 10 : 5;
2. 3 : 5 : 8 : 4?
1. 2x + 10x = 12x; 7x + 5x = 12x.
Суми пар протилежних кутів рівні.
Відповідь: так.
2. 3x + 8x = 11x; 5x + 4x = 9x; 11x ≠ 9x.
Суми пар
16. ABCD – чотирикутник, описаний навколо кола, AB = 3 см, BC = 9 см, CD = 10 см.
Знайдіть AD.
AB + CD = 3 + 10 = 13 (см).
Значить, BC + AD = 13 (см).
AD = 13 см − BC = 13 см − 9 см = 4 (см).
Відповідь: 4 см.
17. У чотирикутнику ABCD ∠ABC = 100°, ∠ADC = 80°, ∠BDC = 30°. Знайдіть ∠BAC.

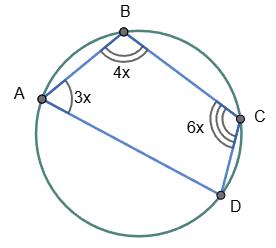
1. Оскільки ∠ABC + ∠ADC = 10° + 80° = 180°, то чотирикутник ABCD є вписаним у коло. 2. Оскільки кути ∠BAC і ∠BDC є кутами,
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
∠A = 3 · 20° = 60°,
∠B = 4 · 20° = 80°,
∠C = 6 · 20° = 120°,
∠D = 5 · 20° = 100°.
Відповідь: 60°, 80°, 120°, 100°.
19. Чотирикутник ABCD
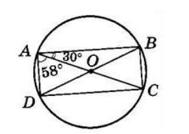
Знайдіть ∠AOD, якщо ∠BAC = 30°, ∠CAD = 58°. ∠ABC = 90° як вписаний, що спирається на діаметр AC.
Тоді в ΔABC ∠ACB = 90° − ∠BAC = 90° − 30° = 60°.
∠DBC = ∠CAD = 58° як вписані, що спираються
дугу. З ΔBOC ∠BOC = 180° − (∠OBC + ∠OCB) = = 180° − (58° + 60°) = 62°.
Відповідь: 62°.
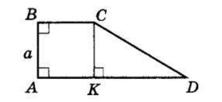
∠D = x, ∠C = 5x.
Тоді x + 5x = 180, 6x = 180, x = 30.
Отже, ∠D = 30°.
Проведемо CK ⊥ AD. CK = AB = a см як відстані
З ΔKCD CK = 1 2 CD,
CD = 2CK = 2a.
Оскільки трапеція
BC + AD = AB + CD = a + 2a = 3a
PABCD = 2 · 3a = 6a (см).
Відповідь: 6a см.
21. На малюнку прямі A1B1, A2B2 і A3B3
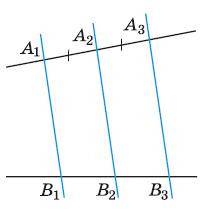
B1B2 = B2B3; A1A3 = B1B3.
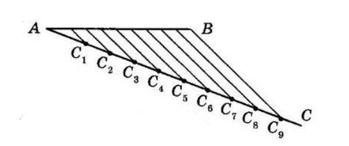
До § 16
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
4. Відрізок C9B.
5.
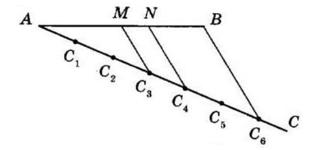
K
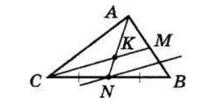
1. AB даний відрізок.
2. Промінь AC.
3. На промені AC відкладають 6 рівних
(3 + 1 + 2 = 6):
AC1 = C1C2 = C2C3 = C3C4 = C4C5 = C5C6.
4. Відрізок C6B.
5. Через точки C3, C4 провести C3M || C6B, C4N || C6B.
Оскільки AC3 : C3C4 : C4C6 = 3 : 1 : 2, то за теоремою Фалеса AM : MN : NB = 3 : 1 : 2.
NP || CM.
NAB AK : KN = 2 : 1
BP : PM = 1 : 1. Отже, AM = 2MP, але MP = PB, тому AM = MB. 25.
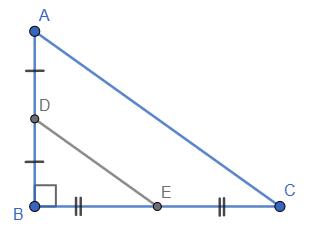
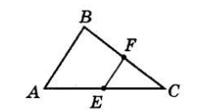
BC ), CE = 3 см, CF = 5 см, EF = 7
CE = 1 2 AC, AC = 2CE = 2 · 3 = 6 (см).
CF = 1 2 BC, BC = 2CF = 2 · 5 = 10 (см).
EF = 1 2 AB, AB = 2EF = 2 · 7 = 14 (см).
PΔABC = AB + BC + AC = 14 + 10 + 6 = 24 (см).
Відповідь: 24 см.
PΔ = 3 · 4 = 12 (см).
Відповідь: 12 см.
29. Бічна сторона
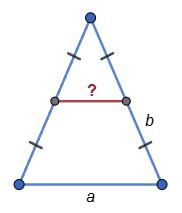
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
Нехай a основа, b бічна сторона. PΔ = a + 2b, a = PΔ − 2b, a = 20 − 2 · 7 = 6 (см).
Середня лінія, кінці якої належать бічним сторонам, паралельна основі і дорівнює її половині: 6 см : 2 = 3 (см).
Відповідь: 3 см.
30. Точки D, E, F, відповідно середини сторін AB, BC і CA трикутника ABC. Доведіть, що чотирикутник DEFA паралелограм. DE середня лінія ΔABC за означенням, тому DE || AC. EF середня лінія ΔABC, EF || AB.
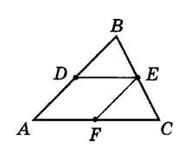
Отже, у чотирикутнику ADEF DE || AF, EF || AD. Тоді ADEF паралелограм.
31. Сторона трикутника дорівнює 12 см. Знайдіть
одна з його середніх ліній дорівнює 5 см, а периметр трикутника, утвореного
середніми лініями, дорівнює 18 см.
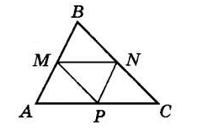
Нехай MNP трикутник, утворений середніми
трикутника ABC.
Нехай AC = 12 см. MN || AC, MN = 1 2 AC = 1 2 · 12 = 6 (см).
Нехай MP = 5 см. MP || BC, MP = 1 2 BC, BC = 2MP = 2 · 5 = 10 (см).
PΔMNP = MN + MP + NP, NP = PΔMNP − (MN + MP) = 18 − (6 + 5) = 7 (см).
NP || AB,
NP = 1 2 AB,
AB = 2NP = 2 · 7 = 14 (см).
Відповідь: 10 см, 14 см. 32.
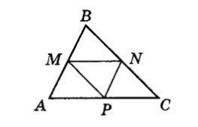
Нехай PAMNP = 22 см, PBNPM = 24 см, PCPMN = 26 см.
PAMNP = 2AM + 2AP = AB + AC, PBNPM = 2BN + 2BM = BC + AB, PCPMN = 2CN + 2CP = BC + AC.
+ AC = 22,
AB + BC = 24, AC + BC = 26; �
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
AB = 22 AC , 22 AC + BC = 24, AC + BC = 26; �
AB = 22 AC , AC + BC = 2, AC + BC = 26;
= 22 AC , 2BC = 28, AC + BC = 26; �AB = 22 AC , BC = 14, AC + 14 = 26; � AB = 10, BC = 14, AC = 12.
Отже, AB = 10 см, BC = 14 см, AC = 12 см.
PΔABC = 10 + 14 + 12 = 36 (см).
MN = 1 2 AC = 1 2 · 12 = 6 (см),
NP = 1 2 AB = 1 2 · 10 = 5 (см),
MP = 1 2 BC = 1 2 · 14 = 7 (см).
PΔMNP = 6 + 5 + 7 = 18 (см).
Відповідь: 36 см, 18 см.
33. Побудуйте
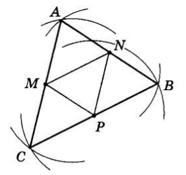
трикутник.
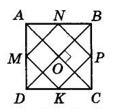
ABCD квадрат, M, N, P, K середини
сторін. AC = BD = d діагоналі квадрата.
У ΔABC NP середня лінія, NP || AC, NP = 1 2 AC = ���� 2 . У ΔADC MK середня лінія, MK || AC, MK = 1 2 AC = ���� 2 . Дві протилежні сторони чотирикутника MNPK
MNPK паралелограм.
Аналогічно, MN || BD, MN = 1 2 BD = ���� 2 . KP || BD, KP = 1 2 BD = ���� 2 . Отже, MNPK ромб.
MN ⊥ MK (MN || BD, MK || AC, BD ⊥ AC), тоді MNPK квадрат.
PMNPK = 4���� 2 = 2d (см). Відповідь: квадрат. До § 18

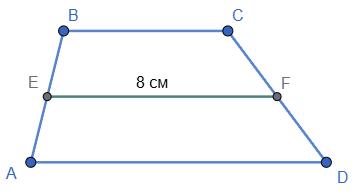
сума основ: 8 см · 2 = 16 см.
Pтр = 16 + 17 = 33 (см).
Відповідь: 33 см. 37.

38.
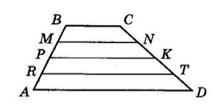
2, ���� + ���� = 28.
2a = 30, a = 15, 15 − b = 1, b = 13.
Відповідь: 13 см, 15 см.
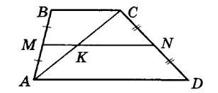
MN = 18 см
Нехай MK = x см, тоді KN = 2x см.
x + 2x = 18;
3x = 18;
x = 6.
Отже, MK = 6 см, KN = 2 · 6 = 12 (см).
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
MN
середина AC.
BC = 2MK = 2 · 6 = 12 (см).
KN середня лінія ΔACD, AD = 2KN = 2 · 12 = 24 (см).
Відповідь: 12 см, 24 см. 40. Середня
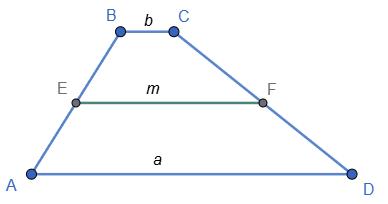
основи трапеції, a > b, m її середня лінія. За умовою: m = 3b, a − b = −12. За властивістю середньої
Отже
Відповідь: 6 см, 30 см. 41. Середня
дорівнюють 2 : 3 : 2.
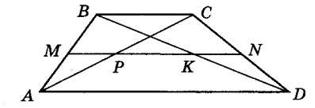
відношення яких
трапеції. MN середня лінія трапеції ABCD, AC і BD її діагоналі.
MP : PK : KN = 2 : 3 : 2.
Нехай MP = 2x, PK = 3x, KN = 2x.
У ΔABC M середина AB, MP || BC (MP частина MN, MN || BC).
Тоді за теоремою Фалеса, P середина AC, MP середня лінія ΔABC, MP = 1 2 BC, BC = 2MP = 2 · 2x = 4x.
В ΔACD PN середня лінія, PN = PK + KN = 3x + 2x = 5x. PN = 1 2 AD, AD = 2PN = 2 · 5x = 10x.
AD : BC = 10x : 4x = 5 : 2.
Відповідь: 5 : 2. 42.

https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
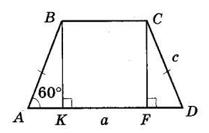
Проведемо BK ⊥ AD, CF ⊥ AD висоти трапеції. У ΔABK ∠ABK = 90° − ∠BAK = 90° − 60° = 30°.
Тоді AK = 1 2 AB = ���� 2 (як катет, що лежить проти кута 30°).
BK || CF (BK ⊥ AD, CF ⊥ AD) BK = CF за гіпотенузою і гострим кутом (AB = CD, ∠A = ∠D за умовою).
Тоді KBCF паралелограм. BC = KF = AD − (AK + FD) = a − 2���� 2 = a – c
Середня
19.1. (Усно.) Чи правильна рівність: 1), 4) Так; 2), 3) Ні.
19.2. Замініть
����. 2a 3 = 2 a3 ;
����. 3mb 1 = 3m b ;
����. a2 b 3 c = a2 c b 3 ;
����. a 3 b 7 = 1 a3 b 7 .
19.13. Подайте
����. 4b 5 = 4 b 5 ; ����. 7a 1 p
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
���� + 2 = ���� 2, 2(���� 2) = ���� + 2; � ���� = ���� 4, 2(���� 4) 4 = ���� + 2.
2y - 8 - 4 = y + 2; y = 14.
Тоді x = 10.
19.30. Подайте у вигляді степеня:
1. a5a3 = a8;
2. b7 : b3 = b4;
3. (c5)4 = c20;
4. m7m = m8;
5. t10 : t = t9;
6. (p7)2 = p14 .
19.31. Піднесіть до степеня одночлен:
1. (mn2)7 = m7n14;
2. (-2p3)2 = 4p6;
3. (-5cm2)3= -125c3m6;
4. (-a2c3)10 = a20c30 .
19.32. Спростіть вираз:
1. (5m2n)3 · (0,2m3n)2 = 125m6n3 · 0,04m6n2 = 5m12n5;
2. (-0,1p7c3)4 · (10pc2)3 = -0,0001p28c12 · 1000p3c6 = 0,1p31c18 .
19.33. Рейтингова
48 - 32 = 16;
Б = 8 · (3 + 2) + 4 · 4 - 0,01 · 3600 = 40 + 16 - 36 = 56 - 16 = 40;
В = 8 · (4 + 3) + 4 · 1 - 0,01 · 3800 = 56 + 4 - 38 = 60 - 38 = 22; Г = 8 · (4 + 2) + 4 · 3 - 0,01 · 4200 = 48 + 12 - 42 = 60 - 42 = 18.
1) 367,92 : 72 = 5,11; 2) 867,96 : 72 = 12,005 (умові
20.1. (Усно.)
2. a7 · a-9 = a-2;
4. c8 : c -5 = c13;
6. m : m8 = m-7;
7. (a7)-1 = a-7 .
20.2. Подайте у
1. a5 · a-2 = a5+(-2) = a3;
2. a-7 · a6 = a-7+6 = a-1;
3. a9 · a-9 = a9+(-9) = a0 = 1;
4. a-4 · a-3 = a-4+(-3) = a-7 .
20.3. Подайте у вигляді степеня добуток:
1. b7 · b-3 = b7+(-3) = b4;
2. b-6 · b3 = b-6+3 = b-3;
3. b-5 · b-7 = b-5+(-7) = b-12;
4. b-8 · b8 = b-8+8 = b0 = 1.
20.4. Подайте у
1. m3 : m-2 = m3-(-2) = m5;
2. m5 : m6 = m5-6 = m-1;
3. m-3 : m-3 = m-3-(-3) = m-3+3 = m0 = 1;
4. m-1 : m-8 = m-1-(-8) = m-1+8 = m7 .
20.5. Подайте у вигляді степеня частку:
1. c5 : c-1 = c5-(-1) = c6;
2. c2 : c8 = c2-8 = c-6;
3. c-2 : c-3 = c-2-(-3) = c-2+3 = c1 = c;
4. c-4 : c-4 = c-4-(-4) = c-4+4 = c0 = 1.
20.6. Піднесіть степінь до степеня:
1. (x-4)-2 = x8;
2. (x-1)17 = x-17;
3. (x0)-5 = x0 = 1;
4. (x7)-4 = x-28 .
20.7. Піднесіть степінь
1. (n-2)-7 = n14;
2. (n15)-1 = n -15;
3. (n-8)0 = n0 = 1;
4. (n5)-3 = n -15 .
20.8.
a-10
1. a-10 = a-3 · a-7;
2. a-10 = a7 · a-17;
3. a-10 = a-1 · a-9;
4. a-10 = a12 · a-22
20.9. Подайте
0.12.
1. a7 : a3 · a 12 = a4 · a 12 = a 8;
2. (a5) 3 · a12 = a 15 · a12 = a 3;
3. (a 8)3 : a4 = a 24 : a4 = a 28;
4. a0 · (a 3)4 · a5 = 1 · a 12 · a5 = a 7;
5. a 3 · a0 : a5 : a = a 3 : a5 : a = a 8 : a = a 9;
6. (a3) 2 · (a 1) 6 = a 6 · a6 = a0 = 1.
20.13. Подайте у
1. b3 : b7 · b2 = b 4 · b2 = b 2;
2. (b 2)4 · b10 = b 8 · b10 = b2;
3. (b3) 2 : b3 = b 6 : b3 = b 9; 4. b7 · (b 2)3 · b0 = b7 · b 6 · 1 = b1 = b;
5. b0 · b 4 : b3 : b = b 7 : b = b 8;
6. (b 4) 1 · (b2) 2 = b4 · b 4 = b0 = 1.
20.14. Спростіть вираз: 1. 4a 8b7 · 5a10b 3 = 20a2b4; 2. 10m 6n4 · 0,4m6n 9 = 4m0n 5 = 4n 5
1. 10m3n 2 2m 5n4 = 20m 2n2; 2. 0,02a 8b3 · 100a8b 7 = 2a0b 4 = 2b 4; ����. 1 8 ���� 3 ����
1. (xy) 2 = x 2 · y 2; 2. (ab 2) 3
20.18.
1. 64m 3 = (4m
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
3x = 72 x = 24.
Відповідь: огірки 24 грн/кг, помідори 32
20.35. Доведіть,
на 8.
Нехай 2n + 1 і 2n + 3
(2n + 3)2 - (2n +
8(n + 1) кратне 8.
20.36. Виконайте дії:
1. 2,7 · 103 = 2,7 · 1000 = 2700; 2. 1,32 · 105 = 1,32 · 100 000 = 132 000;
3. 4,7 · 10-3 = 4,7 · 0,001 = 0,0047;
4. 3,42 · 10-4 = 3,42 · 0,0001 = 0,000342.
20.37. У магазині
1. 4500 + 1200 + 800 = 4500 + 2000 = 6500 (грн)
2. 4500 + 800 = 5300 (грн)
3. 1200 · (100% − 10%) = 1200 · 90% = 1200 · 0,9 = 1080 (грн) вартість
4. 5300 + 1080 = 6380 (грн)
5. 6500 − 6380 = 120 (грн) заощадить.
Відповідь: Юлі потрібно
заплатить 6380 грн, а заощадить 120 грн.
20.38. (Олімпіада Нью-Йорка, 1977 р.) Розв’яжіть рівняння 2x + 1 = y2 в натуральних числах1 .
2 ���� + 1 = ���� 2
Оскільки 2 ���� парне число, то 2 ���� + 1, а
Звідки y непарне число.
2 ���� = ���� 2 1; 2 ���� = (���� 1)(���� + 1).
Оскільки y непарне число, то (
тому
2 ���� = 2n ⋅ (2���� + 2); ���� ∈ 1; 2; 3; …
2 ���� = 2n ⋅ 2(���� + 1); 2 ���� = 4����(���� + 1), де n(���� + 1) два
2 ���� , де x натуральне число, є
x штук
число.
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
1), 4), 5), 7) Ні; 2), 3), 6), 8) Так.
21.2. Які із чисел
1), 2), 7)
21.3. Назвіть
1) 5; 2) −17; 3) 1; 4) 0.
21.4. Яким є порядок
1) 5; 2) 12; 3) 0; 4) −1.
21.5. Запишіть у стандартному
1. 200 000 = 2 · 105;
2. 5800 = 5,8 · 103;
3. 20 500 = 2,05 ·104;
4. 739 = 7,39 · 102;
5. 107,5 = 1,075 · 102;
6. 37,04 = 3,704 ·10;
7. 2700,5 = 2,7005 · 103;
8. 300,8 = 3,008 · 102;
9. 0,37 = 3,7 · 10−1;
10. 0,0029 = 2,9 · 10−3;
11. 0,000007 = 7 · 10−6;
12. 0,010203 = 1,0203 · 10−2.
21.6. Подайте у стандартному
1. 50 000 = 5 · 104;
2. 470 000 = 4,7 ·105;
3. 5 030 000 = 5,03· 106;
4. 975 = 9,75 · 102;
5. 32,5 = 3,25 · 10;
6. 409,1 = 4,091 · 102;
7. 12 900,5 = 1,29005 · 104;
8. 87,08 = 8,708 · 10;
9. 0,43 = 4,3 · 10−1;
10. 0,00017 = 1,7 · 10−4;
11. 0,00004 = 4 · 10−5;
12. 0,90807 = 9,0807 · 10−1.
21.7.
1.
16 370 = 1,637 ∙ 104
2. Батурин 3 066 = 3,066 ∙ 103
3.
200 131 = 2,00131 ∙ 105 4.
1 065 008 = 1,065008 ∙ 106 5.
6.
7.
8.
56 242 = 5,6242 ∙ 104
284 236 = 2,84236 ∙ 105
9 515 = 9,515 ∙ 103
1 470 092 = 1,470092 ∙ 106
1. 27 · 105 = 2,7 · 10 · 105 = 2,7 · 106;
2. 427 · 10−3 = 4,27 · 102 · 10−3 = 4,27 · 10−1;
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
3. 0,00027 · 105 = 2,7 · 10−4 · 105 = 2,7 · 10;
4. 0,0037 · 10−4 = 3,7 · 10−3 · 10−4 = 3,7 · 10−7.
21.9. Запишіть у стандартному
1. 58 · 10−8 = 5,8 · 10 · 10−8 = 5,8 · 10−7;
2. 237,2 · 107 = 2,372 · 102 · 107 = 2,372 · 109;
3. 0,2 · 10−4 = 2 · 10−1 · 10−4 = 2 · 10−5;
4. 0,0017 · 105 = 1,7 · 10−3 · 105 = 1,7 · 102 .
21.10.
1. 6,037 · 105 км2 = 603 700 км2;
2. 2,8 · 10−7 мм = 0,00000028 мм;
3. 2,888 · 106 осіб = 2 888 000 осіб;
4. 1,7 · 10−3 кг = 0,0017 кг.
21.11.
1. 137 152 ≈ 137 200 = 1,372 · 105;
2. 12 311 ≈ 12 300 = 1,23 · 104;
3. 2197,2 ≈ 2200 = 2,2 · 103;
4. 1000,35 ≈ 1000 = 1 · 103 .
21.12. Запишіть у
1. 2,735 · 104 = 27 350;
2. 3,7 · 10−3 = 0,0037;
3. 3,17 · 107 = 31 700 000;
4. 1,2 · 10−5 = 0,000012.
21.13.
1. (1,7 · 103) · (3 · 10 8) = (1,7 · 3) · (103 · 10 8) = 5,1 · 10 5;
2. (2,5 · 10−5) · (6 · 10−2) = 15 · 10−7 = 1,5 · 10 · 10−7 = 1,5 · 10−6.
21.14.
1. (1,2 · 10−8) · (4 · 105) = (1,2 · 4) · (10−8 · 105) = 4,8 · 10−3;
2. (1,5 · 107) · (8 ·103) = 12 · 1010 = 1,2 · 10 · 1010 = 1,2 · 1011 . 2
1. (4,2 · 107) : (2,1 · 103) = 2 · 104;
2. (1,4 · 105) : (2,8 · 10−2) = 0,5 · 107 = 5 · 10−1 · 107 = 5 · 106
21.16.
1. (7,2 · 105) : (2,4 · 102) = 3 · 103;
2. (1,7 · 10−3) : (8,5 · 10−7) = 0,2 · 104 = 2 · 10−1 · 104 = 2 · 103.
21.17. Порівняйте числа:
1. 1,7 · 105 < 2,8 · 105;
2. 1,3 · 10−4 > 1,29 · 10−4.
21.18. Порівняйте числа:
1. 2,8 · 10−3 < 3,7 · 10−3;
2. 1,42 · 105 < 1,5 · 105.
21.19.
1. 2,7 · 103 + 3,2 · 103 = 103(2,7 + 3,2) = 5,9 · 103;
2. 4,7 · 10−15 3,2 · 10−15 = 10−15(4,7 3,2) = 1,5 · 10−15.
21.20. Виконайте
1. 4,7 · 10−8 + 5,1 · 10−8 = 10−8(4,7 + 5,1) = 9,8 · 10−8;
2. 2,9 · 107 1,8 · 107 = 107(2,9 1,8) = 1,1 · 107 .
21.21. Порівняйте
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
1. 2,9 · 108 < 1,8 · 109;
2. 1,12 · 10−7 > 1,12 · 10−8.
21.22. Порівняйте числа:
1. 1,7 · 105 > 1,7 · 104;
2. 1,8 · 10−6 > 8,9 · 10−7
21.23. Виконайте дії та
1. 2,7 · 104 + 3,2 · 105 = 2,7 · 10−1 · 105 + 3,2 · 105 = 105(0,27 + 3,2) = 3,47 · 105;
2. 1,42 · 10−1 2,8 · 10−2 = 1,42 · 10−1 2,8 · 10−1 · 10−1 = 10−1(1,42 0,28) = 1,14 · 10−1.
21.24.
1. 2,7 · 10−5 + 1,7 · 10−4 = 2,7 · 10−4 · 10−1 + 1,7
21.27. Виразіть:
1. 8,3 · 106 т = 8,3 · 106 · 106 г = 8,3 · 1012 г;
2. 3,72 · 10−3 г = 3,72 · 10−3 · 10−6 т = 3,72 · 10−9 т;
3. 4,9 · 10−5 км = 4,9 · 10−5 · 105 см = 4,9 см;
4. 4,97 · 107 см = 4,97 · 107 · 10−2 м = 4,97 · 105 м.
21.28. Подайте:
1. 3,87 · 105 см = 3,87 · 105 · 10−5 км = 3,87 км;
2. 4,92 · 10−2 км = 4,92 · 10−2 · 103 м = 49,2 м;
3. 3,7 · 10−3 кг = 3,7 · 10−3 · 10−2 ц = 3,7 · 10−5 ц;
4. 1,8 · 109 т = 1,8 · 109 · 103 кг = 1,8 · 1012 кг.
21.29. У ставку живуть
1. 30 · 24 = 720 (год) −
2. 720 : 3 = 240 (разів) −
2240 ≈ 1,77 · 1072 (бактерій) −
через місяць утвориться 1,77 · 1072 бактерій.
21.30. Порядок числа
. 1. D(y) = {x – будь-які, крім −4}; 2. x 3
y −5 −2 −1 −0,5 −0,2 0 1 7 0,25 1 3 0,4 y( 3) = 3 2 3 + 4 = 5 1 = 5; y( 2) = 2 2 −2 + 4 = 4 2 = 2; y( 1) = 1 2 1 + 4 = 3 3 = 1; y(0) = 0 2 0 + 4 = 2 4 = 1 2 = 0,5; y(1) = 1 2 1 + 4 = 1 5 = 0,2; ����(2) = 2 2 2 + 4 = 0 6 = 0; ����(3) = 3 2 3 + 4 = 1 7 ; ����(4) = 3 2 3 + 4 = 2 8 = 1 4 = 0,25; ����(5) = 5 2 5 + 4 = 3 9 = 1 3 ; ����(6) = 6 2 6 + 4 = 4 10 = 0,4.
21.35.
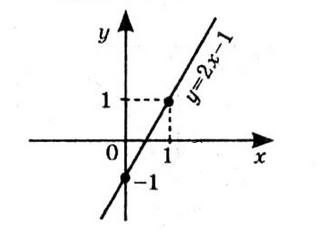
2. y = 5x;
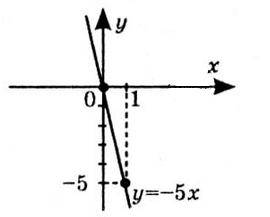
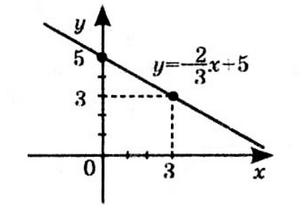
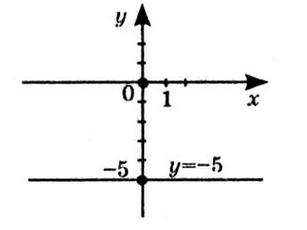
5. y = 4;

6. y = 0,3x + 2; x 0 10 y 2
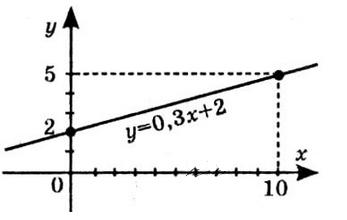
21.36. Чи
y = x2 – x
1. A (1; 1); 1 ≠ 12 – 1; 1 ≠ 0. Отже, точка A
функції y = x2 – x
належить; 2. B (−1; 2); 2 = (−1)2 – (−1); 2 = 1 + 1; 2 = 2.
функції y = x2 – x;
3. C (0; 0); 0 = 02 – 0; 0 = 0.
4. D (5; 30); 30 ≠ 52 – 5; 30 ≠ 20. Отже, точка D
21.37. 1)
1.
функції y = x
y = x2 – x;
4) 12 · 30 = 360 (л) – за місяць. Відповідь:
2. 360 : 100 = 3,6 (діб) – вистачило
3. Відповідь:
більші за суму своїх цифр.
Нехай x сотні, y
скласти рівняння:100x + 10y + z
За умовою, сума цифр цього числа 12 ⋅ (x + y + z),
12 ⋅ (x + y + z) = 100x + 10y + z
12x + 12y + 12z = 100x + 10y + z
100x − 12x + 12z – z = 12y – 10y
88x − 11z = 2y
Оскільки 88 і 11 діляться на 11, то і 2y теж має
Але 2 не ділиться на 11, отже, y = 0.
Отримуємо:
88x − 11z = 0 | : 11
8x – z = 0 x = 1, y = 0, z = 8.
Перевірка:
108 : (1 + 8) = 108 : 9 = 12
Відповідь: це число 108.
22.1. (
22.2.
22.4.
x = –2, то y = 20 –2 = 10;
якщо x = 5, то ���� = 20 5 = 4;
якщо x = –10, то ���� = 20 –10 = 2;
якщо x = 1, то ���� = 20 1 = 20.
22.5.
Якщо x = –3, то ���� = 12 –3 = 4;
якщо x = 4, то ���� = 12 4 = 3;
на 11.
22.6.
( 8) = 8 8 = 1;
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
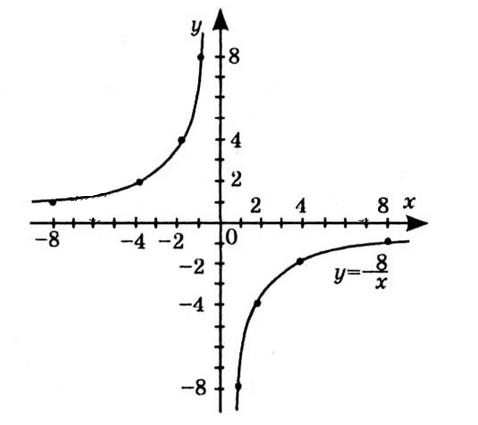
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
����( 12) = 12 12 = 1;
����( 6) = 12 6 = 2;
����( 4) = 12 4 = 3;
����( 3) = 12 3 = 4;
����( 2) = 12 2 = 6;
����( 1) = 12 1 = 12;
����(1) = 12 1 = 12;
����(2) = 12 2 = 6;
����(3) = 12 3 = 4;
����(4) = 12 4 = 3;
����(6) = 12 6 = 2; ����(12) = 12 12 = 1. x 12 6 4 3
y 1 2
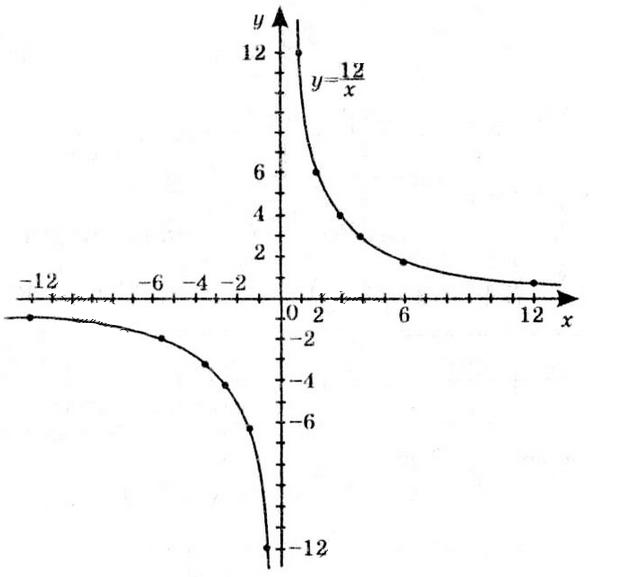
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
1. A (4; 32); 32 = 128 4 ; 32 = 32.
2. B (−8; 16) 16 = 128 8 .
3. C (−2; −64); 64 = 128 2 ; 64 = 64.
точку C;
4. D (0; −128); Оскільки
1. A (−6; 27); 27 = − 162 6 ; 27 = 27.
2. B (9; 18) 18 ≠ 162
3. C (0; 162);
2
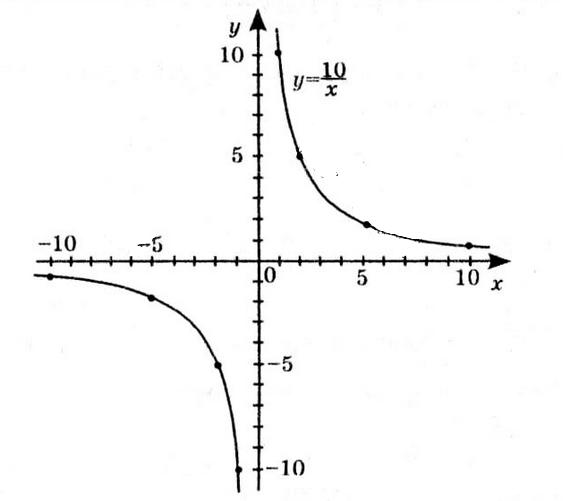
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
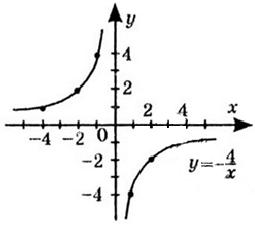
22.16. Графік
y = ���� ���� ; ���� 4 = 12; k = 12 · ( 4) = 48.
Отже, ���� = 48 ���� . Відповідь: ���� = 48 ���� .
22.17.
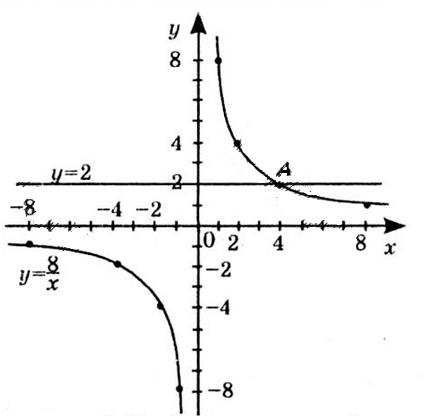
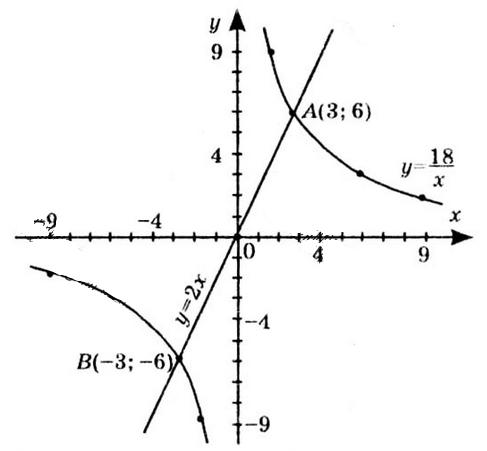
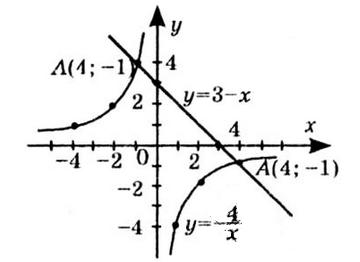
Точки A (4; 1) та B ( 1; 4) точки
x1 = 1, x2 = 4. Відповідь: 1; 4. 22.20.
A (2; 3)


Точки A (2; 2) і B ( 2; −2)
2.
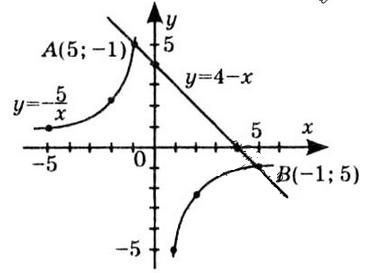
Точки A (5; 1) та B ( 1; 5)
x1 = 5, x2 = 1.
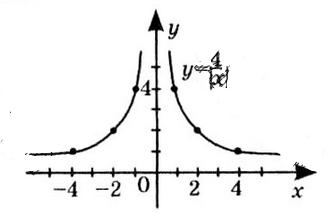
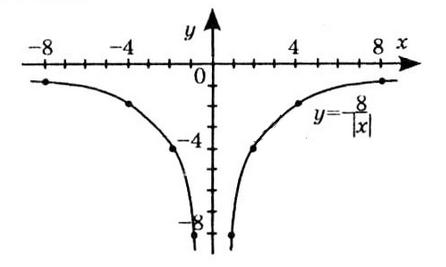
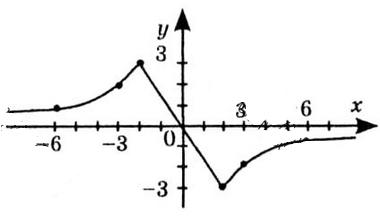
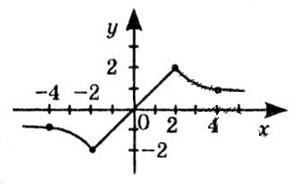
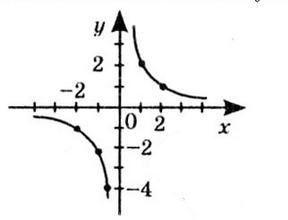
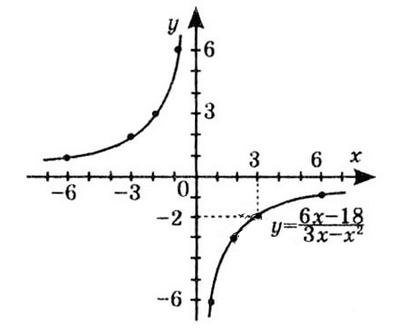
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
1) 4 · 520 = 2080 (грн)
2) 520 · (100% − 25%) = 520 · 75% = 520 · 0,75 = 390 (грн)
3) 390 · 2 = 780 (грн)
4) 780 · 20 = 15600 (грн)
5) 15600 + 2080 = 17680 (грн)
22.29.
(x2 – x
y( 6) = 9 6 = 1,5.
В
Відповідь: Г
Відповідь: В
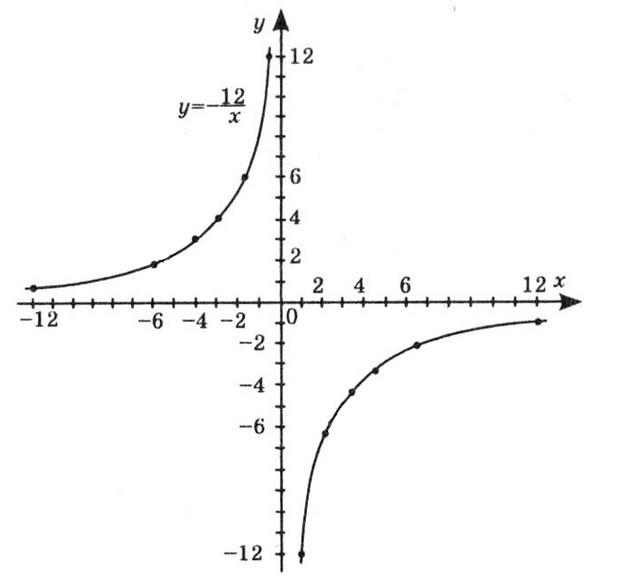
((1 + (1 2 1 ) 1 ) 1 ) 3 = 27.
) 1 2 1 = 1 1 2 = 2 2 1 2 = 1 2 ; б) �12� 1 = 2; в) 1 + 2 = 3;
) 3 1 = 1 3 ;
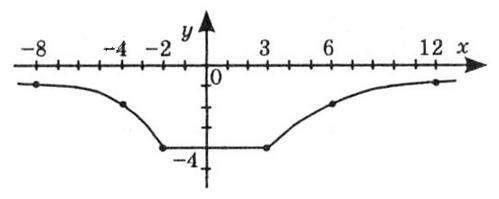
3.
1. 130 000 = 1,3 · 105;
2. 783,5 = 7,835 · 102;
3. 0,0012 = 1,2 · 10–3;
4. 0,001002003 = 1,002003 · 10–3. 23.
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
1. 1 год = 3600 с = 3,6 · 103 с;
2. 1 доба = 24 · 3600 с = 86 400 с = 8,64 · 104 с;
3. 1 місяць (30 днів) = 8,64 · 104 · 30 = 259,2 · 104 = 2,592 · 102 · 104 = 2,592 · 106 (с);
4. 1 рік (365 днів) = 86,4 · 104 · 365 = 3,1536 · 103 · 104 = 3,1536 · 107 (с);
5. 1 сторіччя = (75 · 365 · 8,64 · 104 + 25 · 366 · 8,64 · 104) с = 315 576 · 104 с = = 3,15576 · 109 (с). До § 22
4. Функція y = 4 ����
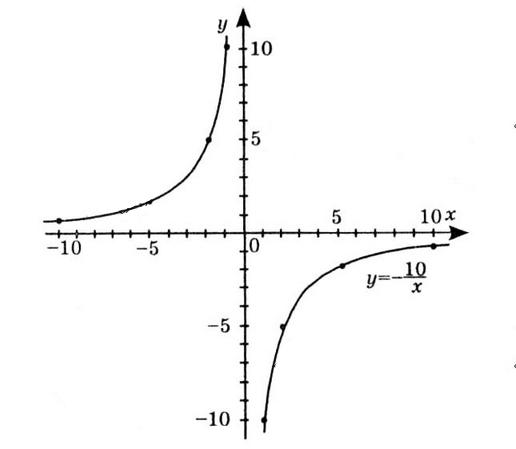
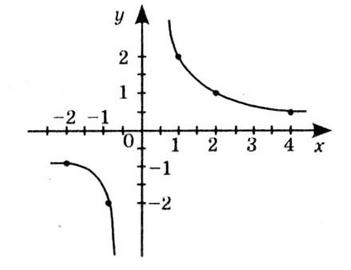
����. C(2; 6); 12 2 = 6; 6 = 6.
точка C

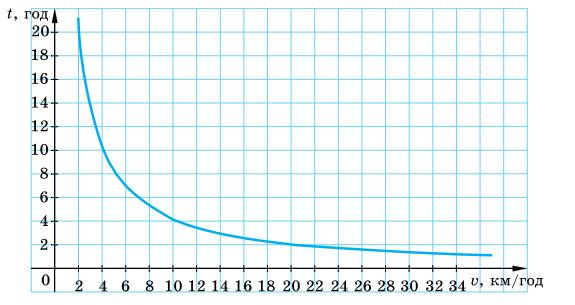
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
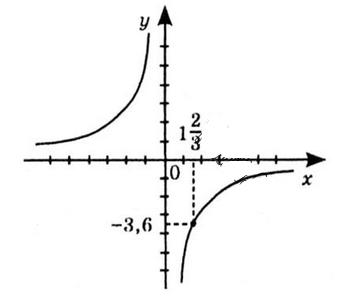
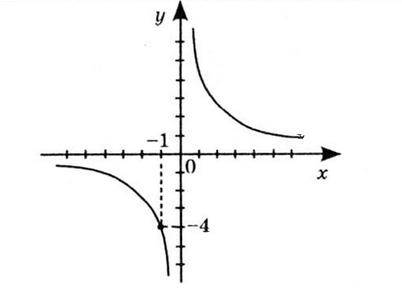


23.3 На
AB ∥ CD, OB = 2, BD = 3, OA = 1. Знайдіть AC.

AC = OB BD ; AC = OA · BD OB = 1 · 3 2 = 1,5.

AC CE = BD DF ;
AC = CE · BD DF = 3 · 4 2 = 6 (см).
AE = AC + CE = 6 + 3 = 9 (см).
Відповідь: 9 см.
23.6 Паралельні прямі AB, CD і EF перетинають сторони кута з вершиною O. OA = 3 см, AC = 4 см, BD = 5 см, DF = 2 см. Знайдіть CE і OB.

OA
AC = OB BD ;
= OA ·
= 3 · 5 4 = 15 4 = 3 3 4 (см).
AC CE = BD DF ; CE = AC · DF BD = 4 · 2 5 = 8 5 = 1 3 5 (см).
Відповідь: 33 4 см, 13 5 см.
23.7 Паралельні прямі AB, CD і EF перетинають сторони кута з вершиною O. OB = 5, BD = 7, AC = 4, CE = 3. Знайдіть OA і DF.

OA AC = OB BD ; OA = AC · OB BD = 4 · 5 7 = 20 7 = 2 6 7 (см)
AC CE = BD DF ; DF = CE · BD AC = 3 · 7 4 = 21 4 = 5 1 4 (см).
Відповідь: 26 7 см, 51 4 см.
23.8 Дано
a, b, c. Побудуйте
x = ab ���� .


6 = ���� 15 ���� ;
2(15 − x) = 3x;
30 − 2x = 3x;
5x = 30; x = 6.
OB = 6; BD = 15 − 6 = 9.
Відповідь: 6; 9.
23.11 На малюнку AB ∥ CD, OB = 5, BD = 7. Знайдіть відрізки OA і AC, якщо AC − OA = 1.

Нехай OA = x, тоді AC = x + 1. За узагальненою теоремою Фалеса: OA
OB = AC BD ; ���� 5 = ���� + 1 7 ;
7x = 5(x + 1);
7x = 5x + 5; 2x = 5; x = 2,5.
OA = 2,5; Ac = 2,5 + 1 = 3,5.
Відповідь: 2,5; 3,5.
23.12 На стороні AB трикутника ABC позначено
CM
Відрізок CM перетинає медіану AP в точці K.
PN || CM. Розглянемо кут ABC. BP : BC = 1 : 1.
за узагальненою теоремою
AM : MB = 1 : 3,
AM : MN = 1 : 1,5.
M так, що AM : MB = 1 : 3. У
AP трикутника ABC?
BN : NM = 1 : 1, тобто N
BAC. AM : MN = AK : KP, AK : KP = 1 : 1,5
AK : KP = 2 : 3.
2 : 3. 23.13 AD
K точка перетину відрізків AD і BM.
Проведемо DN || BM. Кут DAC:
AK : KD = AM : MN,
AM : MN = 5 : 3.
Кут BCA: CD : DB = 1 : 1, CN : NM = 1 : 1.
Тоді N середина MC.
AM : MC = 5 : (3 + 3);
AM : MC = 5 : 6.
Відповідь: 5 : 6.
23.14 Діагональ чотирикутника
PΔABC = 12 см, PΔACD = 14 см, AC = 5 см.
PΔABC = AB + BC + AC, AB + BC = PΔABC − AC = 12 − 5 = 7 (см).
PΔACD = AD + CD + AC, AD + CD = PΔACD − AC = 14 − 5 = 9 (см).
PABCD = AB + BC + AD + CD = 7 + 9 = 16 (см). Відповідь:16 см.
сторони. Проведемо CK ⊥ AD. За умовою ΔACD рівнобедрений, AC = CD.
Тоді CK висота і медіана: AK = KD.
ΔBCK прямокутник, BC = AK.
Нехай BC = x, тоді AD = 2AK = 2x Середня лінія: BC + AD 2 = ���� + 2���� 2 = 3���� 2 .
У ΔCKD ∠DCK = 120° − 90° = 30°,
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
тоді KD = 1 2 CD (катет
CD = 2KD = 2x.
Відношення середньої
3����
2 : 2���� = 3���� ∶ 4���� = 3 ∶ 4.
Відповідь: 3 : 4.
23.16 ΔABC = ΔMKL. Заповніть
1. ∠A = ∠M,
2. ∠B = ∠K,
3. ∠C = ∠L,
4. MK = AB,
5. ML = AC,
6. KL = BC.
23.17 Сторони
= a + b + c.
P2 = 2a + 2b + 2c = 2(a + b + c) = 2P
Відповідь:
Так.
2. ΔABC = ΔA1B1C1? Ні. Сторони
1 м2 = 40
– 20 м
1. S = a · b = 30 · 20 = 600 м2
трикутників:
1. ∠A = ∠M,
2. ∠B = ∠N,
3. ∠C = ∠K.
24.2 Дано: ΔABC ∼ ΔKLM, AB KL = 3.
Згідно подібності трикутників, якщо AB KL = 3, то:
���� AC KM = 3;
����. BC LM = 3.
24.3 Дано: ΔMLF ∼ ΔPNK. Складіть
властивості,
=
= ML PN . 24.4 Дано: ΔMNL ∼ ΔABC, ∠M = 50°, ∠B = 70°.
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
∠D = ∠A = 40°;
∠C = ∠F = 90°;
∠B = ∠E = 180° − (40° + 90°) = 50°.
24.6 Дано: ΔABC ∼ ΔA1B1C1, AB = 8 см, A1B1 = 2 см. Знайдіть:
Згідно властивості подібних трикутників:
AB
A₁B₁ = 8 2 = 4 1 . ����. A₁C₁ AC = A₁B₁ AB = 1 4 ; ����. B₁C₁ BC = A₁B₁ AB = 1 4 .
24.7 Дано: ΔABC ∼ ΔA1B1C1, AB = 10, BC = 8, CA = 6, A1B1 = 5. Знайдіть: B1C1 і C1A1.
Якщо ΔABC ~ ΔA1B1C1, тоді
A₁B₁ AB = B₁C₁ BC = A₁C₁ AC = 5 10 = 1 2 .
B₁C₁
BC = 1 2 ; B₁C₁ 8 = 1 2 ;
B₁C₁ = 8 · 1 2 = 4.
C₁A₁ CA = 1 2 ; C₁A₁ 6 = 1 2 ;
C₁A₁ = 6 · 1 2 = 3.
Відповідь: 4 : 3.
24.8 Дано: ΔKLM ∼ ΔK1L1M1, KL = 12, KM = 9, LM = 21, K1L1 = 4. Знайдіть: K1M1, L1M1.
Якщо ΔKLM ~ ΔK1L1M1, тоді:
K₁L₁
KL = 4 12 = 1 3 .
K₁M₁
KM = 1 3 ; K₁M₁ 9 = 1 3 ;
K₁M₁ = 9 · 1 3 = 3.
L₁M₁
LM = 1 3 ; L₁M₁ 21 = 1 3 ;
L₁M₁ = 21 · 1 3 = 7.
Відповідь: 3; 7.
24.9
AB : BC : AC = 7 : 8 : 9, то і A1B1 : B1C1 : A1C1 = 7 : 8 : 9 (згідно
Позначимо A1B1 = 7x, B1C1 = 8x, A1C1 = 9x.
1. За умовою A1B1 = 21 см.
7x = 21, x = 3.
Отже, B1C1 = 8 · 3 = 24 (см),
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
A1C1 = 9 · 3 = 27 (см).
Відповідь: 24 см, 27 см.
2. За умовою A1C1 − B1C1 = 5 см, 9x − 8x = 5, x = 5.
A1B1 = 7 · 5 = 35 (см);
B1C1 = 8 · 5 = 40 (см);
A1C1 = 9 · 5 = 45 (см).
Відповідь: 35 см, 40 см, 45 см.
3. За умовою A1B1 + B1C1 + A1C1 = 48 см.
7x + 8x + 9x = 48, 24x = 48, x = 2.
A1B1 = 7 · 2 = 14 (см);
B1C1 = 8 · 2 = 16 (см);
A1C1 = 9 · 2 = 18 (см).
Відповідь: 14 см, 16 см, 18 см.
14 см 24 см 35 см 27 см 21 см 16 см 40 см 18 см
В Я З О В
Марина Сергіївна В’язовська.
24.10 Сторони трикутника відносяться як 5 : 6 : 9.
йому трикутника у випадках, якщо його:
Нехай ΔABC ~ ΔA1B1C1.
Оскільки за умовою AB : BC : CA = 5 : 6 : 9,
то і A1B1 : B1C1 : C1A1 = 5 : 6 : 9.
Позначимо A1B1 = 5x, B1C1 = 6x, A1C1 = 9x.
1. За умовою C1A1 = 18 см, 9x = 18, x = 2.
A1B1 = 5 · 2 = 10 (см); B1C1 = 6 · 2 = 12 (см).
Відповідь: 10 см, 12 см. 2. За умовою B1C1 − A1B1 = 3 см, 6x − 5x = 3, x = 3.
A1B1 = 5 · 3 = 15 (см); B1C1 = 6 · 3 = 18 (см); C1A1 = 9 · 3 = 27 (см).
Відповідь: 15 см, 18 см, 27 см.
3. За умовою A1B1 + B1C1 + C1A1 = 100 см. 5x + 6x + 9x = 100, 20x = 100, x = 5.
A1B1 = 5 · 5 = 25 (см); B1C1 = 6 · 5 = 30 (см); C1A1 = 9 · 5 = 45 (см).
Відповідь: 25 см, 30 см, 45 см. 24.11 Доведіть, що
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
трикутнику ΔABC ∠A = ∠B = ∠C = 60°, AB = BC = AC, тому AB : BC : AC = 1 : 1 : 1.
У рівносторонньому ΔA1B1C1 ∠A1 = ∠B1 = ∠C1 = 60°, A1B1 = B1C1 = A1C1, тобто A1B1 : B1C1 : A1C1 = 1 : 1 : 1. Отже, ΔABC ~ ΔA1B1C1
A1B1 : B1C1 : A1C1 = AB : BC : AC. 24.12
дорівнює 20 см. Знайдіть
відносяться як 2 : 3 : 4.
Відомо, що відношення периметрів
сторін.
Нехай ΔABC ~ ΔA1B1C1.
Оскільки за умовою AB : BC : AC = 2 : 3 : 4,
то і A1B1 : B1C1 : A1C1 = 2 : 3 : 4.
Позначимо AB = 2x, BC = 3x, AC = 4x P∆ABC
P∆A₁B₁C₁ = AC A₁C₁ = 2 3 ,
тоді 4���� A₁C₁ = 2 3 ;
A₁C₁ = 4���� · 3 2 = 6����
За умовою AC + A1C1 = 20 см; 4x + 6x = 20;
10x = 20; x = 2.
AB = 2 · 2 = 4 (см);
BC = 3 · 2 = 6 (см);
AC = 4 · 2 = 8 (см).
AB
A₁B₁ = 2 3 ; 4 A₁B₁ = 2 3 ;
A₁B₁ = 4 · 3 2 = 6 (см);
BC
B₁C₁ = 2 3 ; 6 B₁C₁ = 2 3 ;
B₁C₁ = 6 · 3 2 = 9 (см)
A1C1 = 6 · 2 = 12 (см).
Відповідь: 4 см, 6 см, 8 см і 6 см, 9 см, 12 см. 24.13 Периметри
як 3 : 4 : 5.
ΔABC ~ ΔA1B1C1.
за умовою AB : BC : CA = 3 : 4 : 5,
і A1B1 : B1C1 : C1A1 = 3 : 4 : 5. Позначимо AB = 3x, BC = 4x, AC = 5x.
P∆ABC
P∆A₁B₁C₁ = AB A₁B₁ = 4 3 ;
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
A₁B₁ = 3���� · 3 4 = 2,25���� .
BC
B₁C₁ = 4 3 ;
B₁C₁ = 4���� · 3 4 = 3���� .
AC
A₁C₁ = 4 3 ;
A₁C₁ = 5���� · 3 4 = 3,75���� .
За умовою AB + A1B1 = 21 см; 3x + 2,25x = 21; 5,25x = 21; x = 4.
AB = 3 · 4 = 12 (см);
BC = 4 · 4 = 16 (см);
AC = 5 · 4 = 20 (см).
A1B1 = 2,25 · 4 = 9 (см);
B1C1 = 3 · 4 = 12 (см),
A1C1 = 3,75 · 4 = 15 (см).
Відповідь: 12 см, 16 см, 20 см і 9 см, 12 см, 15 см. 24.14 У паралелограмі ABCD діагоналі перетинаються в точці O.
рівних трикутників, що при цьому утворилися.
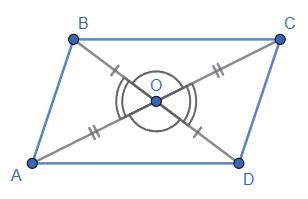
ΔBOC = ΔDOA за
BOC = ∠DOA як вертикальні).
Аналогічно, ΔABD = ΔCDB.
ΔABD = ΔCDB, ΔABC = ΔCDA
AB = CD, BC = AD як протилежні сторони).
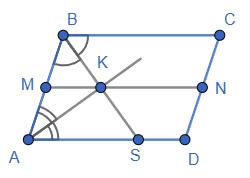
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html

кг/м3 .
Довжина – 4,5 м
Ширина – 20 см
Висота – 55 см
Щільність – 520 кг/м3
1 робітник – 70 кг
1. 4,5 · 0,2 · 0,55 = 0,495 м3 – об'єм балки;
2. 520 · 0,495 = 257,4 (кг) – вага балки;
3. 257,4 : 70 ≈ 3,68 = 4 – робітника.
Відповідь: потрібно 4 робітника, щоб
24.18 Точки K і L належать
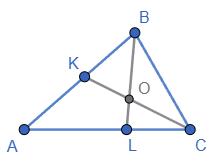
KO = OC, BO = OL, ∠KOB = ∠
ΔKOB = ΔCOL
BKO = ∠LCO,
KC. Тоді AB || AC, що суперечить умові.
25.
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
яких умов ΔABC ∼ ΔMNK:
2. Дві сторони, що утворюють рівні кути, пропорційні, і кут між ними рівний (ознака подібності за двома сторонами і кутом між ними).
4. Біля рівних кутів прилеглі сторони пропорційні.
25.4 Доведіть, що ΔABC ∼ ΔA1B1C1, якщо:
����. AB A₁B₁ = 2 4 = 1 2 ; BC
B₁C₁ = 3 6 = 1 2 ; AC
A₁C₁
. ΔABC ~ ΔA1B1C1 за третьою ознакою.
2. ∠A = ∠A1 = 20°, AB A₁B₁ = 3 9 = 1 3 ; AC
A₁C₁ = 5 15 = 1 3 ; AB
A₁B₁ = AC A₁C₁
ΔABC ~ ΔA1B1C1 за другою ознакою.
3. ∠C = 180° – (∠A + ∠B) = 180° – (30° + 40°) = 110°.
∠A1 = 180° – (∠B1 + ∠C1) = 180° – (40° + 110°) = 30°.
∠A = ∠A1, ∠B = ∠B1.
ΔABC ~ ΔA1B1C1 за першою ознакою. 25.5 Доведіть, що ΔMNK ∼ ΔM1N1K1, якщо:
1. ∠M = ∠M1; MN M₁N₁ = 5 10 = 1 2 ; MK
M₁K₁ = 6 12 = 1 2 .
ΔMNK ~ ΔM1N1K1 за двома сторонами і кутом між ними.
2. ∠M1 = 180° – (∠N1 + ∠K1) = 180° – (40° + 50°) = 90°.
∠M = ∠M1 = 90°;
∠N = ∠N1 = 50°.
ΔMNK ~ ΔM1N1K1 за двома рівними кутами.
����. MN M₁N₁ = 3 6 = 1 2 ;
N₁K₁ = 4 8 = 1 2 ; MK
M₁K₁ = 5 10 = 1 2
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
ΔMNK ~ ΔM1N1K1 за трьома сторонами.
25.6 Прямі AB і CD перетинаються в точці O, AC ∥ BD. Доведіть, що ΔAOC ∼ ΔBOD.

ΔAOC ~ ΔBOD за двома кутами:
∠AOC = ∠BOD як вертикальні;
∠ACO = ∠BDO як внутрішні різносторонні при паралельних прямих
CD.
25.7 Прямі MN і KL перетинаються в точці O, ∠MLO = ∠NKO. Доведіть, що ΔMOL ∼ ΔNOK.
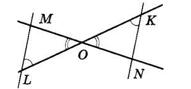
ΔMOL ~ ΔNOK за двома кутами:
∠MLO = ∠NKO за умовою,
∠MOL = ∠KON як вертикальні.
25.8 На сторонах

A спільний; AB AP = 3 1 , CA AL = 3 1 1 за умовою. 25.9
= 2 3KL, KB = 2 3 KN. Доведіть, що ΔKAB ∼ ΔKLN.
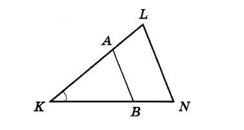
ΔKAB ~ ΔKLN за двома сторонами і кутом
K спільний; KL : AK = KL : 2 3 KL = 3 : 2;
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
KN : KB = KN : 2 3 KN = 3 : 2.
25.10 Чи
трикутники ABC і A1B1C1, якщо:
1. AB : BC : CA = 3 : 4 : 6; A1B1 : B1C1 : C1A1 = 6 : 8 : 11.
AB : BC : CA ≠ A1B1 : B1C1 : C1A1
Відповідь: ні.
2. ∠A1 = x, ∠B1 = 2x, ∠C1 = 3x.
x + 2x + 3x = 180;
6x = 180; x = 30.
∠A1 = 30°;
∠B1 = 2 ⋅ 30° = 60°;
∠C1 = 3 ⋅ 30° = 90°.
∠A = ∠A1 = 30°,
∠B = ∠B1 = 60°.
ΔABC ~ ΔA1B1C1 за двома кутами.
Відповідь: так.
25.11
1. A1B1 : B1C1 : C1A1 = 4 : 3 : 7.
AB : BC : CA = 4 : 3 : 7.
ΔABC ~ ΔA1B1C1 за трьома сторонами.
Відповідь: так.
2. ∠A = 2x, ∠B = 3x, ∠C = 4x.
Тоді: 2x + 3x + 4x = 180°;
9x = 180° x = 20°.
Отже:
∠A = 2 ⋅ 20° = 40°;
∠B = 3 ⋅ 20° = 60°;
∠C = 4 ⋅ 20° = 80°.
Трикутники не подібні.
Відповідь: ні.
25.12
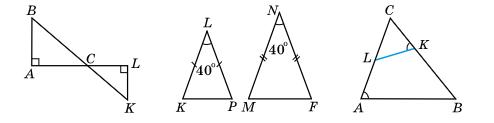
1. Мал. 1. ∠BAL = ∠LAB = 90°;
∠BCA = ∠KCL (як вертикальні).
Тому ΔBAC ~ ΔKCL (за двома кутами).
2. Мал. 2. KL = LP і NM = NF, тому
KL
NM = LP NF .
Також маємо ∠L = ∠N = 40°;
ΔKLP ~ ΔMNF (за двома сторонами і
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
3. Мал. 3. ∠CKL = ∠A;
∠C спільний кут для ΔABC і ΔKLC.
Тому ΔABC ~ ΔKLC (за двома кутами).
25.13

∠BLK = ∠BCA, ∠B спільний.
ΔABC ~ ΔKBL за двома кутами.
На мал. 2 ∠PMT = 180° − 110° = 70°.
∠PMT = ∠HKN, PM : MT = HK : KN.
ΔPMT ~ ΔHKN за двома сторонами і
На мал. 3 ∠ABC = ∠FTC, ∠C спільний.
ΔABC ~ ΔFTC за двома кутами.
25.14 O – точка перетину
ΔCOD.
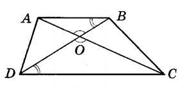
∠AOB = ∠COD як вертикальні;
∠ABD = ∠BDC як внутрішні різносторонні
ΔAOB ~ ΔCOD за двома кутами.
25.15 O – точка перетину діагоналей трапеції
см, OD = 4 см. Знайдіть OB.
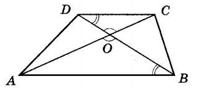
∠DOC = ∠AOB як
∠CDO = ∠OBA
ΔCOD ~ ΔAOB
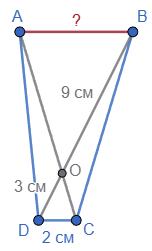
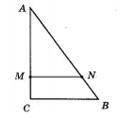
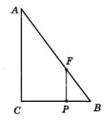
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
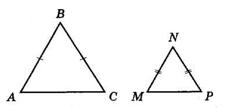
∠A = ∠M за умовою. Оскільки ∠C = ∠A,
∠P = ∠M за властивістю рівнобедреного трикутника, то ∠P = ∠C.
ΔABC ~ ΔMNP за двома кутами.
MN : MP = 5 : 2,
тому AB : AC = 5 : 2.
Позначимо AB = 5x, AC = 2x.
Тоді 5x + 5x + 2x = 36; 12x = 36, x = 3.
AB = 5 · 3 = 15 (см);
AC = 2 · 3 = 6 (см).
Відповідь: 15 см, 15 см, 6 см. 25.20 Дано
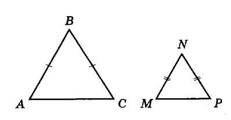
ΔABC = ΔMNP, AB BC = 1, MN NP = 1,
отже ΔABC ~ ΔMNP
MP MN = 1 2 , AC AB = 1 2 .
Нехай AC = x,
тоді AB = BC = 2x. x + 2x = 30; 3x = 30; x = 10.
AC = 10 см, AB = BC = 2 · 10 = 20 (см). Відповідь: 10 см, 20 см, 20 см. 25.21

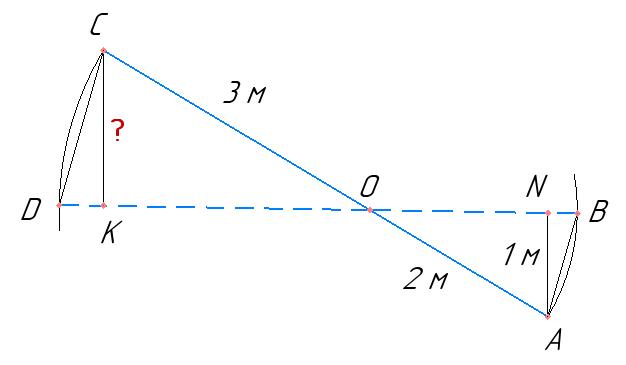
Нехай вісь обертання точка O. До повороту кінці плеч розташовані в точках A (коротке) і C (довге), після у B і D відповідно. Позначимо підйом короткого AN = 1 м та опускання довгого CK = ?.
1. Трикутники AOB і COD рівнобедрені (OA = OB = 2, OC = OD = 3) і мають рівні кути при вершинах (∠AOB = ∠COD) (це вертикальні кути). Отже, вони подібні, тому �������� �������� = �������� �������� = 3 2 .
2. Прямі, на яких лежать основи цих рівнобедрених трикутників, паралельні: AB ∥ CD (бо кути при вершині O рівні, а сторони OA і OC, OB і OD лежать на одних прямих).
3. Розглянемо прямокутні трикутники ∆ANB і ∆CDK.
Маємо ∠ANB = ∠CDK = 90°, а також ∠NBA = ∠KDC як внутрішні різносторонні
січній BD і паралельних AB ∥ CD. Отже, ∆ANB ~ ∆CDK і �������� �������� = �������� �������� . 4. Тоді �������� = �������� ⋅ �������� �������� = 1 ⋅ 3 2 = 1,5 м.

https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
2. ∠NMA = ∠CMB (як вертикальні).
3. Тому ΔNAM ~ ΔCBM (за двома кутами).
4. ∠NDC = ∠NAM (відповідні, утворені при перетині паралельних прямих AB і CD січною ND).
5. ∠N спільний для ΔNAM і ΔNDC.
6. ΔNAM ~ ΔNDC (за двома кутами).
7. Тоді ΔCBM ~ ΔNDC (за двома кутами).
Малюнок 2.
1. ∠KBC = ∠KAL; ∠K спільний для ΔKBC; ΔKAL.
2. ΔKBC ~ ΔKAL (за двома кутами).
3. ∠CDL = ∠KAL; ∠L спільний для ΔCDL і ΔKAL; ΔCDL ~ ΔKAL (за двома кутами).
4. Тому ΔCDL ~ ΔKBC.
Малюнок 3.
1. Використовуючи перші дві задачі, ΔAPL ~ ΔBPF ~ ΔDKL.
2. ∠FKC = ∠DKL (як вертикальні);
∠CFK = ∠FLD (внутрішні різносторонні).
Тому ΔDKL ~ ΔCKF.
25.23 На малюнку ABCD – трапеція, ∠ABC = ∠ACD. Знайдіть
малюнку і доведіть, що CA2 = BC · AD.
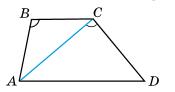
∠BCA = ∠CAD як внутрішні різносторонні
∠ABC = ∠ACD за умовою.
Тоді ΔABC ~ ΔACD за двома кутами.
подібних
BC
CA = CA AD ,
звідки CA · CA = BC · AD, CA2 = BC · AD.
25.24
2a + 3a + 4a = 180, 9a = 180, a = 20.
∠1 = 2 · 20° = 40°;
∠2 = 3 · 20° = 60°;
∠3 = 4 · 20° = 80°.
x + x + 20° + x − 20° = 180°
3x = 180°, x = 60°.
∠1 = 60°,
∠2 = 60° + 20° = 80°,
∠3 = 60° − 20° = 40°.
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
Тоді a + 3a + 2a = 180°, 6a = 180°, тобто a = 30°.
∠1 = 30°;
∠2 = 3 · 30° = 90°;
∠3 = 2 · 30° = 60°.
У другого трикутника
x,
2x. x + 2x = 90; 3x = 90; x = 30.
Отже, два інших кути 30° і 60°.
У даних трикутниках всі кути рівні, значить, трикутники подібні.
Відповідь: так.
25.26 У паралелограмі ABCD точки E, F, M і N належать відповідно сторонам AB, BC, CD і DA. EB BF = DM DN . Доведіть, що ∠BFE = ∠DNM.
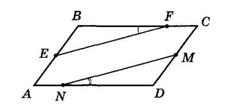
ΔEBF ~ ΔDMN за двома сторонами і кутом між ними:
∠B = ∠D як протилежні за умовою паралелограма.
EB BF = DM DN за умовою.
подібності трикутників ΔBFE ~ ΔDNM.
25.27 Відрізки AB і CD перетинаються
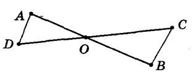
AOD ~ ΔBOC
AOD = ∠COB як вертикальні, AO OB = DO OC ).
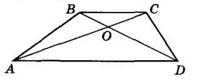
точці O, AO OB = DO OC . Доведіть, що ∠BCO = ∠ADO.
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
За умовою AD + BC 2 = 22 см,
AD + BC = 44 см.
Нехай AD = x см,
тоді BC = (44 − x) см.
З подібності трикутників: DO
OB = DA CB .
7 4 = ���� 44 ���� ; 4x = 308 − 7x; 11x = 308; x = 28.
Отже, AD = 28 (см), BC = 44 − 28 = 16 (см).
Відповідь: 16 см і 28 см.
25.29 O – точка
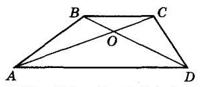
ΔBOC ~ ΔDOA за двома кутами (∠BOC = ∠DOA як вертикальні, ∠CBO = ∠ODA як внутрішні різносторонні
AD || BC і січній DB).
Нехай BO = x см, тоді OD = (x + 3) см.
З подібності трикутників
BO OD = BC AD . ���� ���� + 3 = 5 11 ; 11x = 5x + 15; 6x = 15; x = 2,5 см.
BO = 2,5 см, OD = 2,5 + 3 = 5,5 (см).
Відповідь: 2,5 см, 5,5 см. 25.30 У трикутнику ABC AB = 9 см, BC = 12 см, AC = 18 см. На стороні AC відкладено
відрізок CK = 6 см, на стороні BC – відрізок CP = 4 см.
1. Чи подібні трикутники ABC і KPC? 2. Чи паралельні прямі AB і KP? 3.
PK.

= 6 18 = 1 3 ;
= 4 12 = 1 3 .
1. ΔCKP ~ ΔCAB

ΔMNC ~ ΔABC (лема).
AB MN = AC MC.

ΔAKL ~ ΔABC (лема).
AB AK = BC KL .
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
Нехай AK = x см,
тоді AB = AK + KB = (x + 6) см.
���� + 6
���� = 12 9 ;
9(x + 6) = 12x;
9x + 54 = 12x;
3x = 54; x = 18.
AB = 18 + 6 = 24 (см).
Відповідь: 24 см.
25.33 Знайдіть відстань від подорожнього
дерева A
іншому березі, якщо BN = 30 м, CD = 20 м, BC = 5 м. На
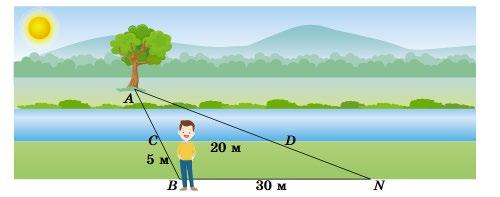
ΔACD подібний ΔABN
BN).
Із подібності трикутників
AB
AC = BN CD
За умовою:
BN = 30 м, CD = 20 м,
тому AB AC = BN CD = 30 20 = 1,5;
тобто AB = 1,5AC.
На малюнку видно, що з іншого боку: AB = AC + BC = AC + 5.
Прирівнюючи отриманий рівності, отримаємо: 1,5AC = AC + 5 ⇒ 1,5AC − AC = 5 ⇒ 0,5AC = 5 ⇒ AC = 10 (м),
тоді AB = 1,5 · 10 = 15 (м).
Відповідь: відстань від подорожнього
25.34
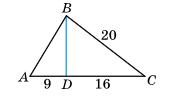
ΔABC ~ ΔBDC
AC
CB = 9 + 16 20 = 25 20 = 5 4 ;
CB
CD = 20 16 = 5 4 .
25.35
15
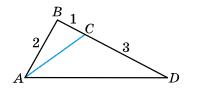

випадки.
����. MN MP = 4 7 .
Тоді і AB AC = 4 7 .
Нехай AB = BC = 4x, AC = 7x
AB + BC + AC = 90 см; 4x + 4x + 7x = 90; 15x = 90; x = 6.
AB = BC = 4 · 6 = 24 (см), AC = 7 · 6 = 42 (см).
Відповідь: 24 см, 24 см, 42 см.
����. MN MP = 4 7 .
Тоді і AC AB = 4 7
Нехай AB = BC = 7x, AC = 4x.
AB + BC + AC = 90 см.
7x + 7x + 4x = 90; 18x = 90; x = 5.
AB = BC = 7 · 5 = 35 (см), AC = 4 · 5 = 20 (см).
Відповідь: 35 см, 35 см, 20 см. 25.37
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html

За наслідком з теореми про ознаки подібності трикутників ΔABC ~ ΔMNP.
Розглянемо два випадки.
1. MN : MP = 5 : 8, тоді AB : AC = 5 : 8.
AB = BC = 5x, AC = 8x
За умовою 5x + 5x + 8x = 126; 18x = 126; x = 7.
AB = BC = 5 · 7 = 35 (см); AC = 8 · 7 = 56 (см).
Відповідь: 35 см, 35 см, 56 см.
2. MN : MP = 5 : 8, тоді AC : AB = 5 : 8.
AB = BC = 8x, AC = 5x
За умовою 8x + 8x + 5x = 126, 21x = 126, x = 6.
AB = BC = 8 · 6 = 48 (см).
AC = 5 · 6 = 30 (см).
Відповідь: 48 см, 48 см, 30 см.
25.38 ΔABC ∼ ΔA1B1C1, CD і C1D1 –
трикутників. Доведіть, що ΔADC ∼ ΔA1D1C1.
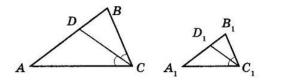
ΔABC ~ ΔA1B1C1, тоді ∠C = ∠C1. 1 2 ∠C = 1 2 ∠C1.
∠ACD = ∠A1C1D1, ∠A = ∠A1.
ΔADC ~ ΔA1D1C1 за двома кутами. 25.39 ΔABC ∼ ΔA1B1C1, AM і A1M1 –
трикутників. Доведіть, що ΔAMC ∼ ΔA1M1C1.
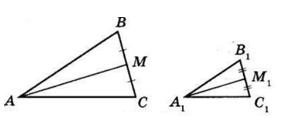
ΔABC ~ ΔA1B1C1, тоді ∠C = ∠C1.
AC A₁C₁ = BC B₁C₁ = 1 2 BC 1 2 B₁C₁ = MC M₁C₁ .
ΔAMC ~ ΔA1M1C1 за двома
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
25.40 На
AB = 6 см.

ΔBAF ~ ΔBCA за двома кутами (∠B спільний, ∠BAF = ∠BCA за умовою).
BF
BC = AB AC ;
BC = AB · AB BF ;
BC = 6 · 6 4 = 9 (см).
Відповідь: 9 см.
KC, якщо AB = 2 см, AK = 1 см.

ΔABC ~ ΔAKB за двома кутами (∠A спільний, ∠ABK = ∠C за умовою).
AB
AK = AC AB ;
AC = AB² AK ; AC = 2² 1 = 4 (см).
KC = AC − AK = 4 − 1 = 3 (см).
Відповідь: 3 см.
25.42 У прямокутний трикутник ABC
квадрат AKLM, K ∈ AB, L ∈ BC, M ∈ AC. Знайдіть сторону квадрата.
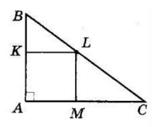
AB = a, AC = b.
Нехай AK = KL = LM = AM = x.
У ΔBKL: ∠BLK = 90° − ∠B.
У ΔABC: ∠C = 90° − ∠B. Отже, ∠BLK = ∠C, тоді
~ ΔLMC.
BK
KL = LM MC ;
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
���� ;
(a − x)(b − x) = x2;
ab − ax − bx + x2 = x2;
ab = ac + bx;
ab = (a + b)x;
���� = �������� ���� + ����
Відповідь: �������� ���� + ���� см.
25.43 Периметр паралелограма дорівнює 24 см,
як 5 : 3. Знайдіть сторони паралелограма.

У паралелограмі ABCD, BK ⊥ AD, BP ⊥ CD.
BP : BK = 5 : 3.
За умовою 2(AB + BC) = 24.
AB + BC = 12.
Нехай AB = x см, тоді BC = (12 − x) см.
ΔABK ~ ΔCBP (∠A = ∠P).
AB
BC = BK BP ; ����
12 ���� = 3 5 ;
5x = 36 − 3x;
8x = 36;
x = 4,5.
AB = 4,5 см;
BC = 12 − 4,5 = 7,5 (см).
Відповідь: 4,5 см, 7,5 см. 25.44 Периметр паралелограма дорівнює 30 см,
сторони паралелограма.
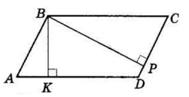
У паралелограмі ABCD BK ⊥ AD, BP ⊥ CD висоти.
BK = 4 см, BP = 8 см.
ΔABK ~ ΔCBP за
Тоді AB BK = BC BP .
За умовою 2(AB + BC) = 30 см.
AB + BC = 15 см.
Якщо AB = x см, то BC = (15 − x) см.
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
4 = 15 ���� 8 ;
8x = 60 − 4x;
12x = 60; x = 5.
AB = 5 (см),
BC = 15 − 5 = 10 (см).
Відповідь: 5 см, 10 см.
25.45 У трикутник ABC вписано ромб AKFP так, що кут A в ньому спільний, P ∈ AB, F ∈
BC, K ∈ AC. Знайдіть сторону ромба, якщо CK = 4 см, PB = 9 см.
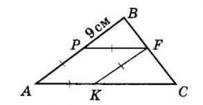
ΔPBF ~ ΔKFC за двома кутами (∠BPF = ∠A, ∠FKC = ∠A як відповідні, тоді ∠BPF = ∠FKC; ∠BFP = ∠C, як відповідні).
PB
PF = KF KC ;
PF · KF = PB · KC; PF2 = 9 · 4; PF = 6 (см).
Відповідь: 6 см.
25.46 У рівнобедрений трикутник, основа якого
6 см, а бічна сторона – 10 см, вписано коло.
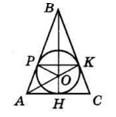
Нехай P і K точки дотику вписаного
ΔAPO = ΔAHO за катетом і
Тоді AP = AH = 1 2 AC = 1 2 6 = 3 (см).
BP = AB − AP = 10 − 3 = 7 (см). Оскільки PB = PK, то ΔPBK ~ ΔABC за
PK
AC = BP AB;
PK = AC · BP AB = 6 · 7 10 = 4,2 (см).
Відповідь: 4,2 см.
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
25.47

Середня лінія трикутника дорівнює половині сторони, якій вона паралельна.
три середні лінії рівні, то всі сторони трикутника також рівні,
60°. 25.48 У рівнобічній трапеції ABCD (AD ∥ BC) E – середина AD, F – середина BC, K –середина AB. Доведіть, що KE = KF.
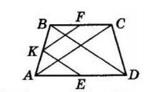
AB, F середина BC за умовою.
Отже, KF середня лінія ΔABC, KF = 1 2 AC.
Аналогічно, KE середня лінія ΔABD, KE = 1 2 BD. Оскільки в рівнобічній
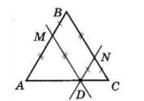
Аналогічно, ∠DNC = ∠B як відповідні при паралельних прямих DN і AB і січній BC.
Отже, ΔAMD = ΔDNC.
Паралельні сторонам прямі MD і DN витинають
ΔABC трикутники AMD і DNC, подібні йому.
Тоді ΔAMD ~ ΔDNC за кути при вершині.
AM = MD, DN = NC.
PMBND = MB + BN + ND + MD = MB + AM + BN + NC = AB + BC = 2a (см).
Відповідь: 2a см.
25.50
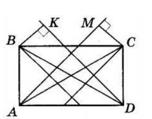
прямокутних трикутників AMC і DKB (
випливає, що MC = KB. Довжини цих
протилежних кутів прямокутника ABCD, тобто
прямокутника. Отже, сторони утвореного прямокутника рівні, тоді це квадрат. 25
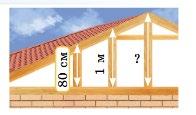
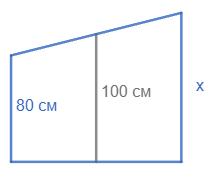
80 см,
• більша основа шуканий стовп: x,
• середній стовп
лінії трапеції відомо:
Середня лінія = сума основ
100 = 80 + ���� 2 .
Звідси:
x = 200 − 80 = 120 см = 1
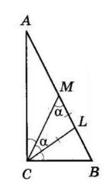
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
Отже, у ∆CML CL = ML.
Тоді ∠CML = ∠MCL = α.
∠CLB = 2α як зовнішній.
У ∆CAL ∠ACL = 45°, ∠A = ∠ACM = 45° − α.
У ∆ABC ∠B = 90° − ∠A = 90° − (45° − α) = 45° + α.
У ∆CLB ∠LCB + ∠CLB + ∠B = 180°; 45° + 2α + 45° + α = 180°; 3α = 90°; α = 30°.
Тоді ∠A = 45° − 30° = 15°.
Відповідь: так, 15°.
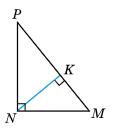
1. MK
2.

1. NK2 = PK · KM; 2. NM2 = PK · KM; 3. PK · PM = NP2; 4. PK · KM = NK2 .
1. k2 = 2 · 8 = 16; 16 = 42; k = 4 см
2. k2 = 27 · 3 = 81; 81 = 92; k = 9
. 26.5
1. k2 = 16 · 1 = 16; 16 = 42; k = 4 дм.
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
2. k2 = 4 · 9 = 36; 36 = 62; k = 6 см.
26.6
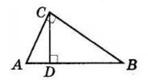
CD2 = AD · DB; CD2 = 9 · 25; CD2 = 225;
CD = 15 см. (152 = 225)
26.7
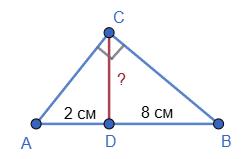
CD2 = AB · BD;
CD2 = 2 · 8;
CD2 = 16;
CD = 4 см. (4² = 16)
26.8

AC2 = AB · AD;
AC2 = 16 · 4;
AC2 = 64;
AC = 8 см.
26.9
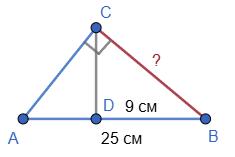
BC2 = AB · BD;
BC2 = 25 · 9;
BC2 = 225; BC = 15 см.
26.10

BC2 = AB · BD; 182 = AB · 9; 324 = AB · 9; AB = 324 : 9; AB = 36 см.
26.11
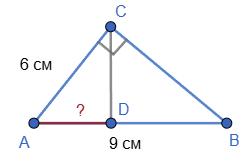
AC2 = AB · AD; 62 = 9 · AD; 36 = 9 · AD; AD = 36 : 9; AD = 4 см.
26.12
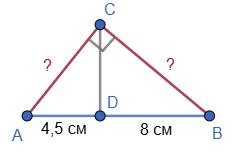
Нехай AD = 4,5 см, BD = 8 см.
AB = AD + DB = 8 + 4,5 = 12,5 (см).
AC2 = AB · AD;
AC2 = 12,5 · 4,5;
AC2 = 56,25; AC = 7,5 (см).
BC2 = AB · BD;
BC2 = 12,5 · 8;
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
BC2 = 100;
BC = 10 (см).
Відповідь: 7,5 см, 10 см. 26.13
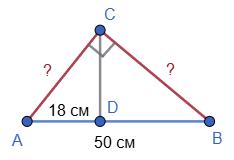
AB = 50 см,
AD = 18 см,
тоді BD = AB – AD = 50 – 18 = 32 см.
AC2 = AB · AD;
AC2 = 50 · 18;
AC2 = 900;
AC = 30 (см).
BC2 = AB · BD;
BC2 = 50 · 32;
BC2 = 1600; BC = 40 (см).
Відповідь: 30 см, 40 см.
26.14

У ΔABC AB = BC, K середина AC, KD ⊥ BC.
CD = 1 см, BD = 8 см.
KC2 = BC · CD; KC2 = (CD + BD) · CD; KC2 = 9 · 1; KC2 = 9; KC = 3 см.
AC = 2KC = 6 см; BC = 9 см.
PΔABC = AC + 2BC = 6 + 2 · 9 = 24 (см).
24 см.
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html

У ΔABC AB = BC, K середина AC, KD ⊥ BC.
BD = 6 см, DC = 2 см.
BC = BD + DC = 6 + 2 = 8 (см).
KC2 = BC · DC;
KC2 = 8 · 2;
KC2 = 16;
KC = 4 см.
AC = 2KC = 2 · 4 = 8 см.
PΔABC = AC + 2BC = 8 + 2 · 8 = 24 (см).
Відповідь: 24 см.
26.16
24 см.
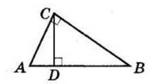
Нехай AD = 9x, BD = 16x.
CD2 = AD · BD;
242 = (9x)2 · (16x)2; 576 = 144x2;
x2 = 576 : 144;
x2 = 4;
x = 2 (x > 0).
AD = 9 · 2 = 18 (см);
BD = 16 · 2 = 32 (см);
AB = 18 + 32 = 50 (см).
AC2 = AD · AB;
AC2 = 18 · 50;
AC2 = 900;
AC = 30 см.
BC2 = AB · BD;
BC2 = 50 · 32;
BC2 = 1600;
BC = 40 см.
Відповідь: 30 см, 40 см.

У ΔABC (∠C = 90°) CD ⊥ AB, BD = 16 см.
AD : CD = 3 : 4. Нехай AD = 3x см, CD = 4x см.
CD2 = AD · BD; (4x)2 = 3x · 16; 16x2 = 48x; x = 3 (x > 0, x ≠ 0).
CD = 4 · 3 = 12 (см).
Відповідь: 12 см.
26.18 Коло, вписане в
Знайдіть радіус кола.
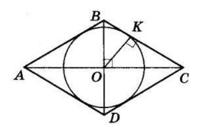
OK ⊥ BC як радіус, проведений
∠BOC = 90° за властивістю
Тоді OK2 = BK · KC,
OK2 = 1 · 4;
OK = 2 см.
Відповідь: 2 см.
26.19 Знайдіть висоту рівнобічної трапеції,
перпендикулярна до бічної
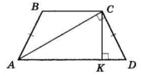
У трапеції ABCD AD || BC, AD = 10 см, BC = 8 см; AC ⊥ CD, CK ⊥ AD висота, тоді:
KD = AD – BC 2 = 10 – 8 2 = 1 (см),
AK = AD – KD = 10 – 1 = 9 (см).
CK2 = AK ⋅ KD;
CK2 = 9 ⋅ 1;
CK2 = 9;
CK = 3 (см).
Відповідь: 3 см.
26.20
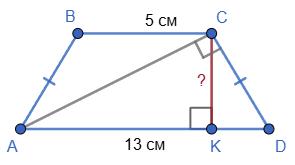
У трапеції ABCD, де AD || BC, AB = CD, AD = 13 см, BC = 5 см, AC ⊥ CD, CK ⊥ AD
висота, тоді:
KD = AD – BC 2 = 13 – 5 2 = 8 2 = 4 (см),
AK = AD – KD = 13 – 4 = 9 (см).
CK2 = AK ⋅ KD;
CK2 = 9 ⋅ 4;
CK2 = 36;
CK = 6 (см)
Відповідь: 6 см.
26.21
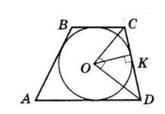
Центр вписаного
∠OCK = 1 2 ∠C;
∠ODK = 1 2 ∠D;
∠OCK + ∠ODK= 1 2 ∠C + 1 2 ∠D =
Тоді ΔCOD прямокутний, ∠COD = 90°.
OK ⊥ CD радіус, проведений у точку
OK2 = CK ⋅ KD;
OK2 = 4 ⋅ 9;
OK2 = 36;
OK = 6 см.
Висота трапеції
h = 2OK = 2 ⋅ 6 = 12 (см).
Відповідь: 12 см.
26.22 Коло,

https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
OP ⊥ AB, OK ⊥ CD радіуси, проведені в точки дотику.
BP = 2 см, AP = 8 см, CK = 4 см.
∠OBA = 1 2 ∠B;
∠OAB = 1 2 ∠A;
∠OBA + ∠OAB= 1 2 ∠B + 1 2 ∠A = 1 2 (∠B + ∠A) = 1 2 ⋅ 180° = 90°.
ΔAOB прямокутний (∠AOB = 90°.).
OP2 = AP ⋅ PB;
OP2 = 2 ⋅ 8;
OP2 = 16;
OP = 4 см.
OK = OP як радіуси.
OK2 = CK ⋅ KD; 42 = 4 ⋅ KD;
KD = 16 : 4; KD = 4 см.
AB = AP + PB = 2 + 8 = 10 (см),
CD = CK + KD = 4 + 4 = 8 (см).
Оскільки в трапецію
Тоді:
PABCD = 2(AB + CD) = 2(10 + 8) = 36 (см).
Відповідь: 36 см.
26.23 Бісектриса
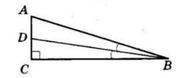
У ΔABC (∠C = 90°), BD бісектриса;
∠CBD=18°.
Тоді:
∠B = 2∠CBD = 2 ⋅ 18° = 36°.
∠A = 90° − ∠B = 90° − 36° = 54°.
Відповідь: 36°, 54°.
26.24 Про трикутники ABC і KLM відомо, що
Чи подібні ці трикутники?
Так. Трикутники подібні за двома кутами.
У ΔABC ∠C = 180° − (∠A + ∠B),
∠A = 180° (∠B + ∠C).
У ΔKLM ∠M = 18° − (∠K + ∠L),
∠K = 180° − (∠L + ∠M).
За умовою:
∠A + ∠B = ∠K + ∠L, тоді ∠C = ∠M;
∠B + ∠C = ∠L + ∠M, тоді ∠A = ∠K.
26.25
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html

ABCD трапеція, AD || BC, AB = CD; O точка перетину діагоналей ∠BAC = ∠CAD.
Позначимо для зручності ∠BAC = ∠CAD = α.
Тоді:
∠A = 2α.
∠B = 180° − ∠A = 180° − 2α.
∠BCA = ∠CAD = α, як внутрішні різносторонні
AC.
У ΔCBO ∠CBO = ∠BCO = α, кути при основі рівнобедреного трикутника.
∠BOC = 180° − (∠CBO + ∠BCO) = 180° − 2α. Отже, ∠ABC=∠BOC.
кг – 1 а
– S
1. 40 · 20 = 800 м2 = 8 (а) –
2. 40 · 8 = 320 (кг) – потрібно картоплі. Відповідь: знадобиться 320 кг картоплі.
26.27 (Олімпіада Нью-Йорка, 1976 р.) Висоти гострокутного трикутника ABC
перетинаються в точці O, а на відрізках OB і OC
= ∠AC1B = 90°. Доведіть, що AB1 = AC1.

У ΔAB1C, AB1 2 = AN ⋅ AC.
У ΔAC1B, C1A2 = AK ⋅ AB.
ΔABN ~ ΔACK за двома кутами (∠A спільний, ∠CKA = ∠BNA = 90°).
Тоді: AC AB = AK AN ,
звідки AC ⋅ AN = AB ⋅ AK.
Отже, AB12 = AC12,
а оскільки AB1 > 0 і AC1 > 0, то AB1 = AC1.
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
27.1 BP –
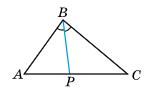
Пропорціями є лише: ����. BC
AB = CP AP ; ����. AP CP = BA BC ; ����. AB AP = BC PC .
27.2 BP – бісектриса трикутника ABC. AP : PC = 1 : 2, AB = 3 см. Знайдіть BC.

AP : PC = 1 : 2, тоді AB : BC = 1 : 2, 3 : BC =1 : 2, BC = 3 ⋅ 2 = 6 (см).
Відповідь: 6 см.
27.3 BP – бісектриса трикутника ABC. AB : BC = 1 : 2, AP = 5 см. Знайдіть PC.

AB : BC = 1 : 2, тоді AP : PC = 1 : 2, 5 : PC = 1 : 2, PC = 5 ⋅ 2 = 10 (см).
Відповідь: 10 см.
27.4 BD – бісектриса трикутника ABC, AD = 3 см, DC = 9 см. Знайдіть
�������� �������� .
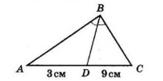
AB BC = AD DC = 3 9 = 1 3
Відповідь: 1 3 .
27.5 MA – бісектриса трикутника MNL, ML = 4 см, MN = 16 см. Знайдіть
�������� �������� .
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
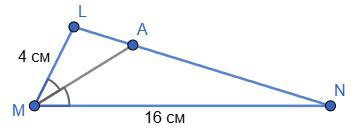
Згідно властивості бісектриси трикутника: LA AN = ML MN = 4 16 = 1 4 .
Відповідь: 1 4 .
27.6 MD – бісектриса трикутника KMP, KM = 8 см, MP = 6 см. Менший з відрізків,
бісектриса MD ділить сторону KP, дорівнює 3 см. Знайдіть KP.
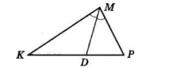
KM : MP = KD : DP.
Оскільки MP < KM, то DP < KD, тоді маємо: 8 : 6 = KD : 3;
KD = 8 ⋅ 3 6 = 24 6 = 4 (см).
KP = KD + DP = 4 + 3 = 7 (см).
Відповідь: 7 см.
27.7 У трикутнику ABC AB = 6 см, BC = 12 см. Більший з відрізків,
BK ділить сторону AC, дорівнює 6 см. Знайдіть AC.
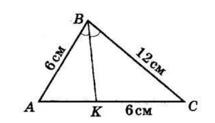
Оскільки BC > AB, то KC > AK, тоді KC = 6 см.
AB
AK = BC KC ;
AK = AB ⋅ KC
BC ; AK = 6 ⋅ 6 12 = 3 (см).
AC = AK + KC = 3 + 6 = 9 (см).
Відповідь: 9 см.
27.8 AL – бісектриса трикутника ABC, AB = 15 см, AC = 12 см, BC = 18 см. Знайдіть BL і
LC.
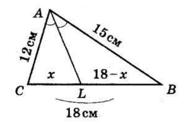
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
Нехай CL = x, тоді BL = (18 – x) см.
AC CL = AB BL ; 12
���� = 15 18 – ���� ; 216 – 12x = 15x;
27x = 216; x = 8.
Отже, CL = 8 см, BL = 18 – 8 = 10 (см).
Відповідь: 8 см, 10 см.
27.9 Бісектриса трикутника

BL бісектриса ΔABC. Відомо: AB = 8 см, BC = 6 см.
Оскільки AB > BC, то AL > LC.
Нехай LC = x см, тоді: AL = (x + 1) см.
AB AL = BC LC ; 8 ���� + 1 = 6 ���� ;
8x = 6x + 6;
2x = 6; x = 3.
Отже, LC = 3 см, AL = 3 + 1 = 4 (см).
PΔABC = AB + BC + AC = 8 + 6 + (3 + 4) = 21 (см).
Відповідь: 21 см.
27.10 Основа рівнобедреного трикутника дорівнює 18
трикутника.

У ΔABC AB = BC, AD бісектриса
AC = 18 см, DC = 12 см.
Нехай BD = x см, тоді AB = (x + 12) см.
За властивістю бісектриси
AB
BD = AC CD ; ���� + 12 ���� = 18 12 ;
A.
12x + 144 = 18x; 18x − 12x = 144; 6x = 144, x = 24.
Отже, BD = 24 см, AB = BC = 24 + 12 = 36 (см).
PΔABC = 2AB + AC = 2 ⋅ 36 + 18 = 90 (см).
Відповідь: 90 см.
27.11 У рівнобедреному трикутнику
бісектриса
трикутника.

У ΔABC AB = BC, AD бісектриса.
DC : BD = 2 : 5.
Нехай AC = x см, тоді AB = (x + 9) см за умовою.
AB
AC = BD DC ;
���� + 9 ���� = 5 2 ;
5x = 2x + 18;
3x = 18, x = 6.
AC = 6 см, AB = 6 + 9 = 15 (см).
PΔABC = 2AB + AC = 2 ⋅ 15 + 6 = 36 (см).
Відповідь: 36 см.
27.12
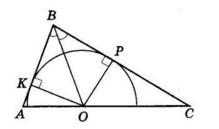
���� = 21 24 − ���� ;
15(24 − x) = 21x,
360 − 15x = 21x,
36x = 360, x = 10.
Отже, AO = 10 (см), CO = 24 − 10 = 14 (см).
Відповідь: 10 см, 14 см.
27.13 У трикутник ABC вписано ромб CKLM так, що кут C у них спільний, K ∈ AC, L ∈ AB, M ∈ BC. Знайдіть довжини відрізків AL і LB, якщо AC = 18 см, BC = 12 см, AB = 20 см.
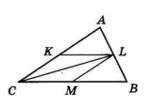
Діагональ CL ромба, вписаного в ΔABC, є бісектрисою кута C.
Тоді AC : AL = BC : LB.
AB = 20 см,
нехай AL = x см, тоді BL = (20 − x) см.
Таким чином, 18
���� = 12 20 ���� ; 360 18x = 12x; 30x = 360, x = 12.
Отже, AL = 12 см, LB = 20 − 12 = 8 (см).
Відповідь: 12 см, 8 см.
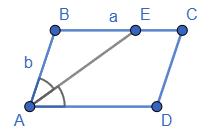
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html

Нехай діагональ AC трапеції ABCD є бісектрисою кута A:
∠BAC=∠CAD.
∠BCA=∠CAD як
би куту C.
Але це неможливо, оскільки протилежні кути трапеції не рівні. Отже, бісектриса кута A не може бути бісектрисою кута C.
Відповідь: ні.
27.16 У трикутнику ABC проведено висоту CH, причому CH2 = AH · BH і точка H
належить стороні AB. Доведіть, що трикутник ABC – прямокутний (∠C = 90°).

За умовою: CH2 = AH ⋅ BH,
звідки AH CH = CH BH .
Тоді ΔCHB ~ ΔAHC за двома сторонами і кутом
У подібних трикутниках відповідні кути рівні:
∠HAC = ∠HCB,
∠HCA = ∠HBC.
Але у ΔAHC (∠AHC = 90°)
∠HAC+∠HCA=90°.
Отже, ∠C = ∠HCA + ∠HBC = 90°.
Отже, ΔABC прямокутний (∠C=90°).
27.17
1. 4,5 ⋅ 3,5 ⋅ 2,8 = 44,1 (м2) −
2. 2 ⋅ 0,9 = 1,8 (м2) – площа дверей;
3. 2,2 ⋅ 1,8 = 3,96 (м2) – площа вікна;
4. 44,1 − 1,8 − 3,96 = 38,34 (м2) –
5. 6 : 5 = 1,2 (м.) – витрачає на 1 м2;
6. 38,34 ⋅ 1,2 = 46 (м.) – потрібно
(∠CHB = ∠CHA = 90°).
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
∠A + ∠B = 180°.
1. Нехай ∠B = x, тоді ∠A = x + 20.
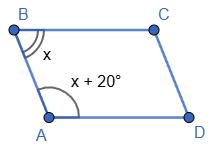
x + x + 20 = 180;
2x = 160; x = 80.
∠B = 80°, (Р)
∠A = 80° + 20° = 100°. (Л)
2. Нехай ∠A = x, тоді ∠B = 3x.

x + 3x = 180; 4x = 180; x = 45.
∠A = 45°, (К)
∠B = 3 ⋅ 45° = 135°. (В)
3. Нехай ∠A = 7x, тоді ∠B = 5x.
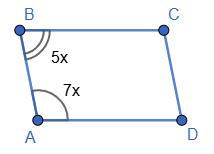
7x + 5x = 180; 12x = 180; x = 15.
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
∠A = 7 ⋅ 15° = 105°, (Ь)
∠B = 5 ⋅ 15° = 75°. (О) 45°
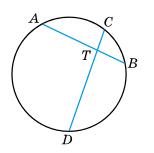
Правильними є лише:
2. AT ⋅ TB = CT ⋅ TP.
4. CT ⋅ DT = AT ⋅ BT.
28.2 TA
та M і N.
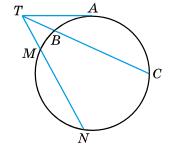
Правильними є лише:
1. TA2 = TB · BC;
2. TA2 = TM · TN.
28.3 Хорди AB і CD
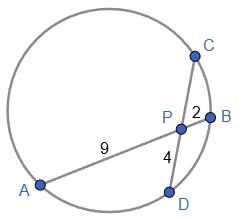
CP = 9 ⋅ 2 4 = 4,5 (см).
Відповідь: 4,5 см.
28.4 Хорди MN і KL
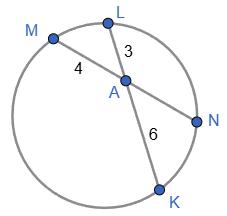
MA ⋅ AN = KA ⋅ AL,
AN = KA ⋅ AL MA ; AN = 6 ⋅ 3 4 = 4,5 (см).
Відповідь: 4,5 см.
28.5 SA
перетинає коло в точках B і C, SA = 6 см, SB = 4 см. Знайдіть SC і BC.
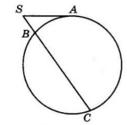
SA2 = SB ⋅ SC;
SC = SA2 : SB.
SC = 62 : 4 = 36 : 4 = 9 (см).
BC = SC – SB = 9 – 4 = 5 (см).
Відповідь: 9 см, 5 см.
28.6 MP – відрізок
P
M, перетинає коло в точках B і C. MP = 4 см, MC = 8 см. Знайдіть MB і BC.

MP2 = MB ⋅ MC;
MB = MP2 : MC;
MB = 42 : 8 = 16 : 8 = 2 (см).
BC = MC – MB = 8 – 2 = 6 (см).
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
Відповідь: 2 см, 6 см. 28.7
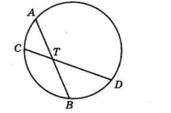
AB = AT + TB,
TB = AB – AT = 16 – 2 = 14 (см).
AT ⋅ TB = CT ⋅ TD; TD = AT ⋅ TB CT ; TD = 2 ⋅ 14 1 = 28 (см)
CD = CT + TD = 1 + 28 = 29 (см).
Відповідь: 29 см.
28.8 Хорда CD завдовжки
хорди MN.

CD = CA + AD,
AD = CD – CA = 13 – 4 = 9 (см).
CA ⋅ AD = MA ⋅ AN, AN = CA ⋅ AD MA = 4 ⋅ 9 2 = 18 (см).
MN = MA + AN = 2 + 18 = 20 (см).
Відповідь: 20 см.
28.9 Січна,
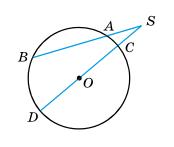
звідки SD = SA ⋅ SB SC .
SD = 4 ⋅ 16 2 = 32 (см).
R = 1 2 CD = 1 2 (SD SC) = 1 2 (32 2) = 15 (см).
Відповідь: 15 см. 28.10

SA ⋅ SB = SC ⋅ SD.
Звідки:
SD = SA ⋅ SB SC
SD = 4 ⋅ 9 3 = 12 (см).
CD = SD – SC = 12 – 3 = 9 (см).
Відповідь: 9 см. 28.11 Для
AB = 1 м, AB1 = 6 м.
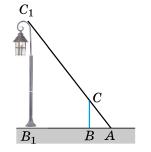
ΔABC ~ ΔAB1C1 як
C₁B₁ CB = AB₁ AB ;
C₁B₁ = CB ⋅ AB₁ AB = 1,5 ⋅ 6 1 = 9 (м).
Відповідь: 9 м.
28.12
AB = 2,5 м.
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html

ΔABC ~ ΔAB1C1 (∠AB1C1 = ∠ABC = 90°, ∠A спільний).
Тоді:
C₁B₁ CB = AB₁ AB ; CB = C₁B₁ ⋅ AB AB₁ = 8 ⋅ 2,5 10 = 2 (м).
Відповідь: 2 м. 28.13
AC, якщо AB = 30
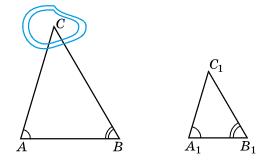
A₁B₁ = 30 ⋅ 0,07 0,05 = 42 (м).
Відповідь: 42 м. 28.14 Хорди кола AB і CD перетинаються
E. AE : BE = 1 : 3, CD = 20 см, DE = 5 см. Знайдіть AB.
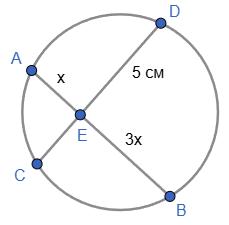
AE ⋅ BE = CE ⋅ DE. За умовою: AE : BE = 1 : 3.
Нехай AE = x, BE = 3x, тоді: x ⋅ 3x = (20−5) ⋅ 5; 3x2 = 75; x2 = 25; x = 5.
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
Отже, AE = 5 см, BE = 3 ⋅ 5 = 15 (см).
AB = AE + BE = 5 + 15 = 20 (см).
Відповідь: 20 см.
28.15
MB, CM = 16 см, DM : MC = 1 : 4. Знайдіть AB.
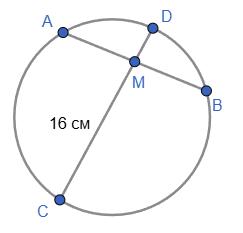
За умовою CM = 16 см, DM : MC = 1 : 4.
DM : 16 = 1 : 4,
DM = 16 4 = 4 (см).
AM = MB,
тому: AM ⋅ MB = CM ⋅ MD; AM2 = 16 ⋅ 4;
AM2 = 64; AM = 8 см.
AB = 2AM =16 (см).
Відповідь: 16 см.
28.16 На малюнку AB – дотична
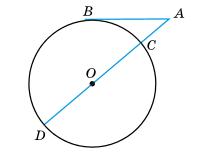
AB2 = AO2 − OC2; 32 = 52 OC2; OC2 = 25 – 9; OC2 = 16; OC = 4 см; CD = 2OC = 2 ⋅ 4 = 8 (см).
Відповідь: 8 см.
28.17
AB

AB2 = AO2 OC2; 82 = 102 OC2; OC2 = 100 – 64; OC2 = 36; OC = 6 (см).
Відповідь: 6 см.
28.18
M. AM = 2 см, CM = 4 см.
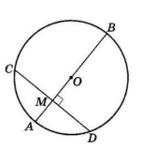
1.
2. DM = CM = 4 см.
3. За властивістю хорд AM ⋅ MB = CM ⋅ MD;
2 ⋅ MB = 4 ⋅ 4; MB = 8 (см).
4. Радіус кола ���� = AB 2 = 2 + 8 2 = 5 (см)
Відповідь: 5 см. 28.19 Діаметр
PB = 12 см, NP = 18 см.
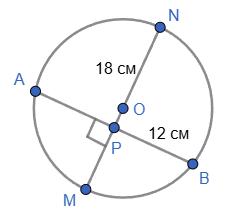
AP ⋅ PB = MP ⋅ PN.
Оскільки MN ⊥ AB, то P середина AB, AP = PB = 12 см.
12 ⋅ 12 = MP ⋅ 18;
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
144 = MP ⋅ 18; MP = 144 : 18; MP = 8 см.
MN = MP + PN = 8 + 18 = 26 (см).
Відповідь: 26 см.
28.20 Перпендикуляр, проведений
відношенні 5 : 8, починаючи

Продовжимо радіус AO до діаметра AK, а перпендикуляр BC до хорди BD.
Оскільки AK ⊥ BD, то BC = CD = 24 см.
За умовою AC : OC = 8 : 5.
Тоді AC = 8x, OC = 5x, OK = AO = 8x + 5x = 13x KC ⋅ AC = BC ⋅ CD; 8x ⋅ 18x = 242; 144x2 = 576; x2 = 4; x = 2.
AO = KO = 13 ⋅ 2 = 26 (см).
Відповідь: 26 см.
28.21 Знайдіть бісектрису AL трикутника ABC, якщо AC = 15 см, AB = 12 см, BC = 18 см.
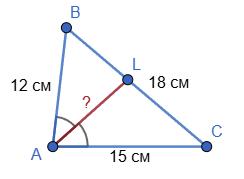
Скористаємось формулою, доведеною в задачі 1 § 17: AL2 = AB ⋅ AC – BL ⋅ CL.
Нехай CL = x см, тоді BL = (18 − x) см.
За властивістю бісектриси: AC CL = AB BL ; 15 ���� = 12 18 ���� ; 15 (18 − x) = 12x 270 − 15x = 12x;
27x = 270; x = 10.
Отже, CL = 10 см, BL = 18 − 10 = 8 (см).
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
AL2 = 12 ⋅ 15 – 8 ⋅ 10 = 180 – 80 = 100; AL = 10 (см).
Відповідь: 10 см.
28.22
третього кута.

План побудови:
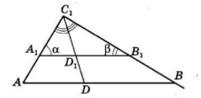
1. Побудуємо довільний ΔA1B1C1, подібний
задані кути α і β.
2. Побудуємо бісектрису C1D1. На ній відкладемо
3. Проведемо через точку D пряму, паралельну A1B1, до перетину з A1C1 та C1B1.
4. ΔABC1 шуканий.
28
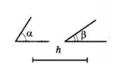
План побудови:
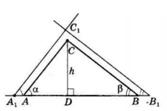
1. Побудуємо довільний ΔA1B1C1, подібний
задані кути α і β.
2. З довільної точки D відрізка A1B1
відрізок DC = h.
3. Через точку C провести прямі, паралельні A1C1 і B1C1. 4.
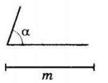
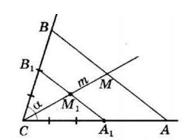
A1B1
і
28.25
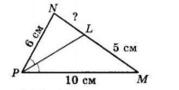
Позначимо їх 3x, 4x, 6x.
Тоді 3x + 4x + 6x = 52; 13x = 52; x = 4.
Сторони трикутника:
3 ⋅ 4 = 12 (см),
4 ⋅ 4 = 16 (см),
6 ⋅ 4 = 24 (см).
Відповідь: 12 см, 16 см, 24 см. 28.27 Основи рівнобічної
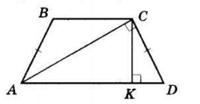
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
– 1,2 м
куб – ? м2 0,2 кг – 1 м2 ? кг – 2 ⋅ S
3. 17,28 ⋅ 0,2 = 3,456 (кг) –
4. 3,456 ≈ 1 кг + 2,5 кг = потрібні
1. Потрібно пофарбувати 17,28 м2 .
2. потрібно придбати 3,5 кг фарби – 1 кг + 2,5 кг банки. 28.29
CM = BC. Чи може кут ABM бути:
1. гострим; 2. прямим?
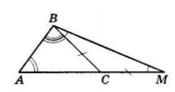
Оскільки за умовою у ΔABC сторона AC найбільша, то і ∠B найбільший.
Отже, ∠B − ∠A > 0.
Таким чином, ∠ABM не може
90° + ∠B ∠A 2 .
Відповідь: 1. ні; 2. ні. Домашня самостійна робота 6
1. Дано: AB ∥ CD, OA = 3 см; OB = 4 см; BD = 12 см. Знайдіть AC.

OB = AC BD ; 3
;
4 ⋅ AC = 3 ⋅ 12; 4AC = 36; AC = 9 (см)
Відповідь: Б. 9 см
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
2. ΔABC ∼ ΔDEF; AB : DE = 2 : 3. Знайдіть відношення EF : BC.
ΔABC ∼ ΔDEF, тому AB DE = BC EF ; BC
EF = 2 3 ; EF BC = 3 2
Відповідь: Г. 3 : 2
3. За яких з наведених умов ΔABC ∼ ΔA1B1C1?
Трикутники подібні за умови В.
Відповідь: В. ∠B = ∠B1, ∠C = 47°, ∠C1 = 47°.
4. CL – бісектриса трикутника ABC. AC = 6 см, BC = 9 см. Більший з відрізків, на які
бісектриса CL ділить сторону AB, дорівнює 3 см. Знайдіть AB.

����. AС BC = AL LB .
2. Оскільки AC < BC, то AL < LB.
За умовою AL = 3 (см).
����. Маємо 6 9 = 3 LB ; 6LB = 27; LB = 4,5 (см).
4. Тоді AB = 3 + 4,5 = 7,5 (см).
Відповідь: A. 7,5 см.
5. Катет прямокутного трикутника дорівнює 12 см, а його проекція на
– 8 см. Знайдіть гіпотенузу трикутника.
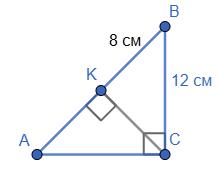
1. В ∆ABC : ∠C = 90°; BC = 12 см; CK висота трикутника; KB = 8 см.
2. За властивістю катета маємо BC2 = AB · KB; 122 = 8 · AB; AB = 18 (см).
Відповідь: Б. 18 см.
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
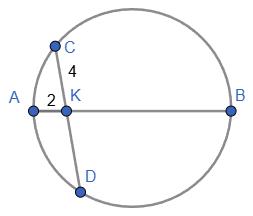
AK ∙ KB = CK ∙ KD
KB = AB – AK = 12 – 2 = 10 см.
KD = AK ∙ KB CK = 2 ∙ 10 4 = ���� см.
CD = CK + KD = 4 + 5 = 9 см. Відповідь: A. 9 см.
7.
1. Оскільки сторони трикутника відносяться як 3 : 4 : 5, то
трикутника відносяться, як 3 : 4 : 5.
2. Позначимо ці сторони як 3x см, 4x см і 5x см.
Маємо 4x + 5x = 72; 9x = 72; x = 8 (см).
3. Найменша сторона дорівнює 3 ⋅ 8 = 24 (см).
Відповідь: Г. 24 см.
8. ABCD – трапеція, AB і CD – її
AO = 8 см, OC = 6 см. Знайдіть AB.
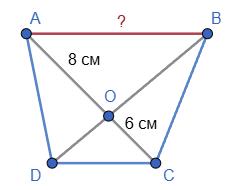
1. Позначимо DC = x см, тоді AB = x + 4 (см).
2. ∠AOB = ∠COD як вертикальні;
∠ABD = ∠BDC як
AOB ~ ΔCOD за двома кутами, тоді AO CO = AB CD ; 8 6 = ���� + 4 ���� ;
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
8x = 6x + 24; 2x = 24; x = 12 (см).
3. Тоді AB = 12 + 4 = 16 (см).
Відповідь: Б. 16 см.
9. Пряма KL паралельна стороні BC трикутника ABC, K ∈ AB, L ∈ AC. BC = 9 см, KL = 6 см, KB = 4 см. Знайдіть довжину сторони AB.
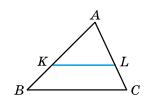
1. KL || BC, тому ∠AKL = ∠ABC (відповідні кути).
2. ∆AKL ~ ∆ABC (за двома кутами), тому AK
AB = KL BC .
3. Позначимо AK = x см, тоді ���� ���� + 4 = 6 9 ; 9x = 6x + 24; 3x = 24; x = 8 (см).
4. Тому AB = 8 + 4 = 12 (см).
Відповідь: А. 12 см.
10. Периметр паралелограма дорівнює 30 см,
сторону паралелограма.
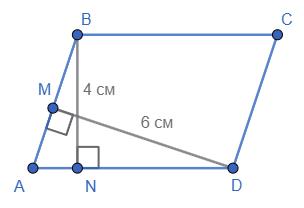
1. PABCD = 30 см; 2(AB + AD) = 30; AB + AD = 15.
2. Позначимо AB = x см, тоді AD = 15 – x (см).
3. ∆ABM ~ ∆ADN (за двома кутами).
Тоді AB AD = BM DN . ����. ���� 15 – ���� = 4 6 ; 6x = 60 – 4x; 10x = 60; x = 6 (см).
5. Отже, AB = 6 см, AD = 15 – 6 = 9 (см).
Відповідь: Б. 9 см.
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
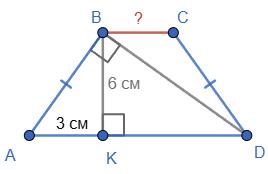
1. Оскільки ∠ABD = 90°, то
BK2 = AK · KD; 62 = 3 · KD; KD = 12 (см).
2. MD = AK = 3 см.
3. BC = KM = KD – MD = 12 – 3 = 9 (см).
Відповідь: Б. 9 см.
12.
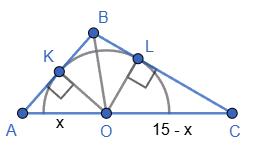
1. ∆OKB ~ ∆OLB (за катетом і гіпотенузою), тому ∠KBO = ∠LBO.
2. BO бісектриса ∆ABC.
3. Позначимо AO = x см, тоді OC = 15 – x см.
4. За властивістю бісектриси AB AO = BC OC; 8 ���� = 12 15 – ���� ; 120 – 8x = 12x; 20x = 120; x = 6 (см).
5. Отже, AO = 6 см; OC = 15 – 6 = 9 см.
Відповідь: A. 6 см і 9 см.
13. У △ ABC: ∠C = 90∘ , CK – висота трикутника, KB = 9 см, AK ∶ CK = 4 ∶ 3
(A– Γ).

���� 2 = �������� ⋅ ��������,
���� 2 = �������� ⋅ �������� ,
���� 2 = �������� ⋅ �������� .
умови �������� : �������� = 4: 3 ⇒ �������� = 4 3 �������� .
���� ���� 2 = �������� ⋅ �������� = 4 3 �������� ⋅ 9 ⇒ �������� = 12 см, �������� = 4 3 ⋅ 12 = 16 см, �������� = �������� + �������� = 16 + 9 = 25 см
Далі
���� 2 = �������� ⋅ �������� = 16 ⋅ 25 = 400 ⇒ �������� = 20 см,
���� 2 = �������� ⋅ �������� = 9 ⋅ 25 = 225 ⇒ �������� = 15 см.
Відповідь: 1 Г, 2 А, 3 В.
для
знань до §§ 23–28
1. ΔABC ∼ ΔLMN, AB LM = 3. Знайдіть відношення AC LN .
∆ABC ~ ∆LMN; AB
LM = AC LN ; AC LN = 3.
Відповідь: AC LN = 3.
2. Доведіть, що ΔABC ∼ ΔA1B1C1, якщо AB = 3 см, BC = 4 см, AC = 5 см, A1B1 = 6 см, B1C1 = 8 см, A1C1 = 10 см.
Оскільки 3 6 = 4 8 = 5 10 , то AB A₁B₁ = BC B₁C₁ = AC A₁C₁ .
Тому ∆ABC ~ ∆A1B1C1 (за трьома сторонами).
3. Дано: KL ∥ MN, OL = 3 см, LN = 6 см, OK = 2 см. Знайдіть KM.
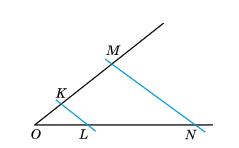
OK PL = KM LN ;
3 = KM 6 ;
3 · KM = 12; KM = 4 (см).
4. Знайдіть катет
см, а гіпотенуза – 25 см.

1. ∆ABC прямокутний; AB гіпотенуза; CD висота трикутника; BD = 4 см; AB = 25 см.
2. За властивістю маємо: BC2 = AB · BD; BC2 = 25 · 4 = 100, тому BC = 10 (см).
Відповідь: 10 см.
5. AL – бісектриса трикутника ABC, AB = 8 см, AC = 10 см. Менший
бісектриса AL
сторону BC,
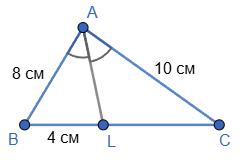
1. За властивістю бісектриси AB AC = BL LC .
2. Оскільки AB < AC, то BL < LC.
За умовою BL = 4 (см).
����. 8 10 = 4 LC ;
8 · LC = 40; LC = 5 (см).
4. Тоді BC = 4 + 5 = 9 (см).
Відповідь: 9 см.
BC.
6. Хорда CD завдовжки 9 см перетинає хорду �������� у точці M, CM = 3 см, AM = 9 см.
хорди AB.
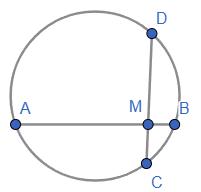
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
AM ∙ MB = DM ∙ MC
DM = DC – MC = 9 – 3 = 6 см �������� = �������� ∙ �������� �������� = 6 ∙ 3 9 = 2 см
AB = AM + MB = 9 + 2 = 11 см.
11 см.
7. Сторони
1. Оскільки сторони трикутника відносяться як 5 : 6 : 7, то сторони
трикутника відносяться так само.
2. Позначимо ці сторони 5x см; 6x см і 7x см.
За умовою: 5x + 7x = 24; 12x = 24; x = 2 см.
3. Сторони трикутника дорівнюють:
5 · 2 = 10 (см)
6 · 2 = 12 (см)
7 · 2 = 14 (см)
Відповідь: 10 см, 12 см, 14 см.
8. O – точка перетину діагоналей трапеції ABCD (AB ∥ CD), AO = 6 см, OC = 4 см.
Знайдіть основи трапеції, якщо їх
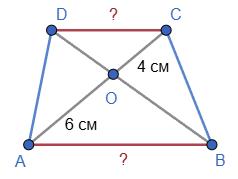
1. Позначимо AB = x (см), тоді CD = 20 – x (см).
2. За задачею №13.1, маємо ∆AOB ~ ∆COD,
тоді AO CO = AB CD ;
6 4 = ���� 15 – ���� ; 120 – 6x = 4x; 120 = 10x; x = 12 (см).
Отже, AB = 12 (см), CD = 20 – 12 = 8 (см).
Відповідь: 12 см; 8 см.
9.

20 см.
BK
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
AD = 10 см; BC = 6 см.
����. AK = AD – BC 2 = 10 – 6 2 = 4 2 = 2 (см).
3. Тоді KD = 10 – 2 = 8 (см).
4. Оскільки ∠ABD = 90° (за умовою), то BK
проведена до гіпотенузи.
За властивістю висоти маємо:
BK2 = AK · KD; BK2 = 2 · 8 = 16;
Тому BK = 4 см.
Відповідь: 4 см.
10. У двох рівнобедрених трикутниках
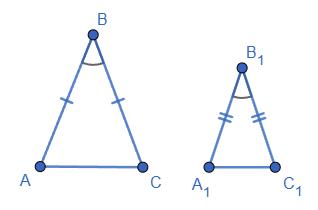
1. Нехай у ∆ABC : AB = BC, а у ∆A1B1C1 : A1B1 = B1C1, крім
і кутом між ними).
2. P∆ABC = 56 см.
Сторони трикутника A1B1C1 відносяться як 2 : 3.
Оскільки ∆ABC ~ ∆A1B1C1, то й сторони трикутника ABC відносяться, як 2 : 3.
3. Необхідно розглянути два випадки.
І випадок.
AB : AC = 2 : 3.
Тоді позначимо AB = BC = 2x (см), AC = 3x (см).
Маємо 2x + 2x + 3x = 56; 7x = 56;
x = 8 (см).
Тоді AB = BC = 2 · 8 = 16 (см),
AC = 3 · 8 = 24 (см).
ІІ випадок.
AC : BC = 2 : 3.
Тоді позначимо AC = 2x (см), AB = BC = 3x (см).
Маємо 2x + 3x + 3x = 56; 8x = 56;
x = 7 (см).
Тоді AC = 2 · 7 = 14 (см)
AB = BC = 3 · 7 = 21 (см).
Відповідь: 16 см; 16 см; 24 см або 14 см; 21 см; 21 см.
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
AK = 4
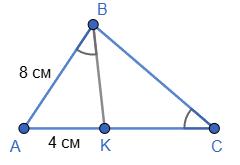
1. ∆ABC ~ ∆AKB (за двома кутами). ����. Тому AB AC = AK AB ; 8 AC = 4 8 ;
4 · AC = 64; AC = 16 (см).
3. Тоді KC = 16 – 4 = 12 (см).
Відповідь: 12 см.
1. На малюнку MN ∥ KL.
1. OM : ON = 2 : 3. Знайдіть MK : NL.
2. OL : ON = 7 : 5. Знайдіть OK : OM.

1. MK : NL = 2 : 3; 2. OK : OM = 7 : 5.
2. Паралельні
ON = MK.
MN

умовою ON = MK, тоді: OM ON = ON NL , ON2 = OM ⋅ NL;
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
ON2 = 4 ⋅ 9; ON2 = 36; ON = 6(ON > 0).
Відповідь: 6.
3.

OA = a Проведемо пряму AB.
OB BD = OA AC ;
малюнку AE : EC = 2 : 1, BD : DC = 3 : 2. Знайдіть BK : KE.
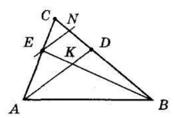
Проведемо пряму EN || AD.
AE : EC = 2 : 1 за умовою, тоді за узагальненою
DN : NC = 2 : 1.
BD : DC = 3 : 2;
BD : DN = 3 : (22 3) = 9 : 4.
Тоді: BK : KE = 9 : 4.
Відповідь: 9 : 4.
5. ΔABC ∼ ΔKLM. Заповніть
���� AB AC = KL KM ; ����. BC AC = LM KM .
§ 24
6. ΔABC ∼ ΔA1B1C1, AB = 8 см, BC = 6 см, A1B1 = 12 см, A1C1 = 18 см. Знайдіть
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
ΔABC ~ ΔA1B1C1.
A₁B₁
AB = 12 8 = 3 2 .
B₁C₁
BC = 3 2 ; B₁C₁ 6 = 3 2 ;
B₁C₁ = 6 ⋅ 3 2 = 9 (см).
A₁C₁
AC = 3 2 ; 18
AC = 3 2 ;
AC = 18 ⋅ 2 3 = 12 (см). Відповідь: 9 см, 12 см. 7. Сторони трикутника
якщо:
середня
Нехай ΔABC ~ ΔA1B1C1.
Оскільки за умовою AB : BC : CA = 2 : 5 : 6,
то і A1B1 : B1C1 : C1A1 = 2 : 5 : 6.
Позначимо A1B1 = 2x,
B1C1 = 5x,
C1A1 = 6x
1. За умовою B1C1 = 20 см;
5x = 20, x = 4.
A1B1 = 2 ⋅ 4 = 8 (см), C1A1 = 6 ⋅ 4 = 24 (см).
PΔA₁B₁C₁ = 8 + 24 + 20 = 52 (см).
Відповідь: 52 см.
2. За умовою A1B1 + C1A1 = 40 см.
2x + 6x = 40,
8x = 40, x = 5.
A1B1 = 2 ⋅ 5 = 10 (см),
B1C1 = 5 ⋅ 5 = 25 (см),
C1A1 = 6 ⋅ 5 = 30 (см).
PΔA₁B₁C₁ = 10 + 25 + 30 = 65 (см).
Відповідь: 65 см.
8. У трикутнику
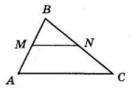
У
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
ΔABC M середина AB, N середина BC.
Тоді MN середня лінія, MN = 1 2 AC.
У трикутниках ABC і MBN
∠B спільний,
∠BMN = ∠BAC,
∠BNM = ∠BCA як відповідні (MN||AC).
MB = 1 2AB,
NB = 1 2BC,
MN = 1 2 AC.
Отже, ΔABC ~ ΔMBN
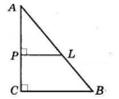

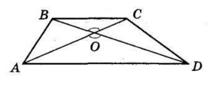
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
OD = CO OA = 2 3 за умовою.
Тоді BC AD = 2 3 , звідки
AD = 3BC 2 = 3 ⋅ 8 2 = 12 (см).
Відповідь: 12 см.
13.
K1. Знайдіть LM, якщо L1M1 = 4 см. ΔKLM ~ ΔK1L1M1 за
K = ∠K1, KL KL₁ = KM
10 см.
14. ABCD – трапеція, AD ∥ BC, ∠BAC = ∠ADC.
2. Доведіть,
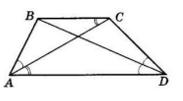

https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html

ΔABC ~ ΔBKC за двома кутами (∠C спільний, ∠BKC = ∠ABC за умовою).
Значить, BC AC = KC BC ;
BC2 = AC ⋅ KC;
BC2 = (16 + 9) ⋅ 9;
BC2 = 25 ⋅ 9;
BC = 15 (см).
Відповідь: 15 см.
17. У трикутнику ABC через
що MN · NK = BM · CK.
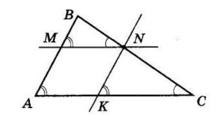
∠BNM = ∠BCA як відповідні
∠BMN = ∠A як відповідні (MN || AC, AB січна),
∠A = ∠NKC як відповідні (NK || AB, AC січна),
тоді ∠BMN = ∠NKC.
ΔMBN ~ ΔKNC за двома кутами.
Звідки MN KC = BM NK , MN ⋅ NK = BM ⋅ KC.
18. ΔABC ∼ ΔA1B1C1, точки I і I1
Доведіть, що ΔAIB ∼ ΔA1I1B1.
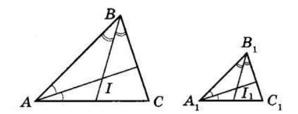
1. Оскільки ΔABC ~ ΔA1B1C1,
то ∠CAB = ∠C1A1B1 і ∠CBA = ∠C1B1A1.
2. ∠IAB = ∠I1A1B1 (як половини рівних кутів); ∠IBA = ∠I1B1A1 (аналогічно).
3. ΔAIB ~ ΔA1I1B1 (за двома кутами). Що й треба було довести.
19. У трикутник ABC вписано
K
AC, N
B, якщо AC = 24 см.
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
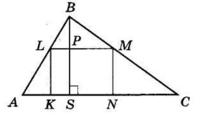
LM || KN, отже, LM || AC.
Пряма LM, паралельна стороні AC, відтинає від ΔABC подібний йому ΔLBM.
Проведемо BS ⊥ AC висоту ΔABC, тоді BP висота ΔLBM.
LPSK прямокутник, PS = LK = 10 см.
Нехай BS = x см, тоді BP = (x − 10) см.
Отже, ΔABC ~ ΔLBM, тоді AC
LM = BS BP ; 24 16 = ���� ���� 10 ;
24x – 240 = 16x;
24x − 16x = 240; 8x = 240; x = 30.
Отже, BS = 30 (см).
Відповідь: 30 см.
20. BD і AE –
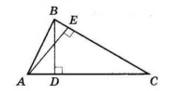
ΔAEC ~ ΔBDC
звідки DC
EC = BC AC , DC
AC = EC ⋅ BC.
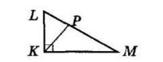
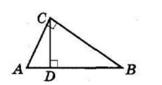
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
AC2 = AD ⋅ AB;
AC2 = 1 ⋅ (1 + 8);
AC2 = 9;
AC = 3 (см).
Відповідь: 3 см.
23.

У ΔABC (∠C = 90°) CD ⊥ AB;
CD = 24 см, AD = 18 см.
CD2 = AD ⋅ DB; 242 = 18 ⋅ DB; 576 = 18 ⋅ DB; DB = 576 : 18; DB = 32 см.
AB = AD + DB = 18 + 32 = 50 (см).
AC2 = AD ⋅ AB = 18 ⋅ 50 = 900; AC = 30 см.
BC2 = DB ⋅ AB = 32 ⋅ 50 = 1600; AC = 40 см.
Відповідь: 32 см, 30 см, 40 см.
24. BM – бісектриса рівнобедреного трикутника ABC (AB = BC). З точки M до
проведено
KC = 9 см, MK = 12 см.
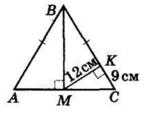
У ΔABC AB = BC.
BM бісектриса, проведена до основи, значить, BM висота.
MK ⊥ BC, тоді:
MK2 = BK ⋅ KC; 122 = BK ⋅ 9, звідки BK =144 : 9 = 16 (см).
BC = BK + KC = 16 + 9 = 25 (см).
BM2 = BK ⋅ BC;
BM2 = 16 ⋅ 25; BM2 = 400;
BM = 20 см.
MC2 = KC ⋅ BC; MC2 = 9 ⋅ 25; MC2 = 225;
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
MC = 15 см.
AC = 2MC = 2 ⋅ 15 = 30 (см).
PΔABC = AC + 2BC = 30 + 2 ⋅ 25 = 30 + 50 = 80 (см).
Відповідь: 20 см, 80 см.
25. Перпендикуляр, проведений з
відрізки, довжини яких відносяться як 9 : 16. Знайдіть
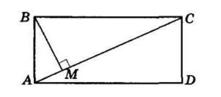
BM висота, опущена на
AM : MC = 9 : 16,
BM = 12 см.
Нехай AM = 9x, MC=16x
BM2 = AM ⋅ MC; 122 = 9x ⋅ 16x; 144 = 144x2 , x2=1, x=1.
Отже AM = 9 см, MC = 16 см.
AC = AM + MC = 9 + 16 = 25 см.
AB2 = MC ⋅ AC.
AB2 = 9 ⋅ 25 = 225;
AB = 15 см.
BC2 = MC ⋅ AC;
BC2 = 16 ⋅ 25 = 400;
BC = 20 см.
PΔABC = 2(AB + BC) = 2 ⋅ (15 + 20) = 2 ⋅ 35 = 70 (см).
Відповідь: 70 см.
26.
Знайдіть діагоналі ромба.
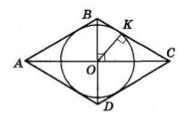
ABCD ромб, центр вписаного кола O точка перетину діагоналей ромба.
AC ⊥ BD,
BO = 12BD, CO = 12AC (за властивістю діагоналей ромба).
OK ⊥ BC радіус, проведений в точку дотику.
BK = 3,6 см, KC = 6,4 см
BC = BK + KC = 3,6 + 6,4 = 10 (см).
OB2 = BK ⋅ BC;
OB2 = 3,6 ⋅ 10 = 36;
OB = 6 см.
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
BD = 2OB = 2 ⋅ 6 = 12 (см)
OC2 = KC ⋅ BC
OC2 = 6,4 ⋅ 10 = 64, OC = 8 см.
AC = 2 ⋅ OC = 2 ⋅ 8 = 16 (см).
Відповідь: 8 см, 16 см. 27. У рівнобічній трапеції
дорівнює 6 см,

ABCD трапеція, AD || BC, AC ⊥ BC.
CK ⊥ AD висота, CK = 9 см.
Середня
трапеції
AD + BC 2 . AK = AD + BC 2 . Тоді AK
AK = 9 см.
CK2 = AK ⋅ KD,
KD = CK² AK = 36 9 = 4 (см).
AD = AK + KD = 9 + 4 = 13 (см).
AD + BC 2 = 9; 13 + BC = 18; BC = 5 (см).
Відповідь: 13 см, 5 см.
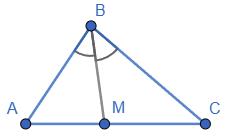
AM MC = AB BC = 1 3 .
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
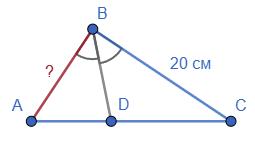
Згідно властивості бісектриси трикутника:
AB
BC = AD DC ; AB 20 = 3 5 ;
AB = 20 ⋅ 3 5 = 12 (см).
Відповідь: 12 см.
30.
ділить

Нехай AB = x см, тоді BC = (x + 9).
За властивістю бісектриси: AB AK = BC KC ; ���� 4 = ���� + 9 10 ; 10x = 4x + 36; 6x = 36; x = 6.
Отже, AB = 6 см, BC = 6 + 9 = 15 (см).
PABCD = 2(AB + BC) = 2 ⋅ (6 + 15) = 42 (см).
Відповідь: 42 см.
31. Периметр прямокутника 60 см. Бісектриса, що виходить з вершини кута
прямокутника, ділить його діагональ на відрізки, що відносяться як 7 : 8. Знайдіть
сторони прямокутника.
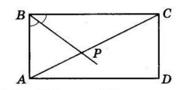
ABCD прямокутник.
PABCD = 60 см,
тоді AB + BC = 1 2PABCD = 1 2 ⋅ 60 = 30 (см).
Нехай AB = x см,
то BC = (30 − x).
AC діагональ, BP бісектриса кута B.
AP : PC = 7 : 8.
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
AB AP = BC PC ; ����
7 = 30 ���� 8 ;
8x = 7(30 − x);
8x = 210 − 7x; 15x = 210; x = 14.
Отже, AB = 14 см, BC = 30 – 14 = 16 (см).
Відповідь: 14 см, 16 см.
32. Точка D належить стороні AB трикутника ABC. Порівняйте кути ACD і BCD, якщо AC = 6 см, BC = 8 см, AD = 3 см, DB = 7 см.

Якби відрізок CD був бісектрисою кута C, то
би рівність AC BC = AD BD .
Нехай AD = x см, тоді BD = (3 + 7 – x) = (10 – x) см.
6
8 = ���� 10 – ���� ; 60 – 6x = 8x; 14x = 60; ���� = 4 2 7 . Отже,
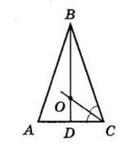
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
Отже, DC = 9 см, AC = 2 ⋅ 9 = 18 (см).
BC = AB = 4 ⋅ 9 = 36 (см).
Відповідь: 18 см, 36 см, 36 см.
34. S – точка перетину хорд AB і CD. AS = 4, SB = 1. Якому числу
CS · DS?
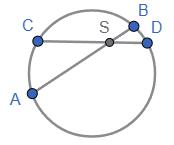
CS ⋅ DS = AS ⋅ SB = 4 ⋅ 1 = 4.
35.
A і B, а січна b – у точках C і D. Відомо, що MA · MB = 28, MC = 4. Знайдіть MD і CD.
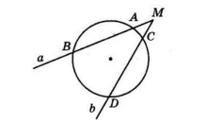
MA ⋅ MB = MC ⋅ MD; 28 = 4 ⋅ MD;
MD = 28 : 4 = 7.
CD = MD – MC = 7 – 4 = 3.
Відповідь: 7, 3.
36. З точки A до
і PK, якщо AM = 8 см, AP = 16 см.
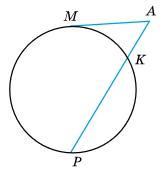
AM2 = AK ⋅ AP, звідки AK = AM2 : AP; AK = 82 : 16 = 64 : 16 = 4 (см). PK = AP – AK = 16 – 4 = 12 (см).
Відповідь: 12 см.
37. З точки A до
AM = 10 см, AP : AK = 4 : 1. Знайдіть AK, AP і KP.

AM2 = AK ⋅ AP,
За умовою AP : AK = 4 : 1,
тоді AK = x, AP = 4x
102 = x ⋅ 4x;
100 = 4x2 , x2 = 25, x = 5.
Отже, AK = 5 (см), AP = 4 ⋅ 5 = 20 (см).
KP = AP – AK = 20 – 5 = 15 (см).
Відповідь: 5 см, 20 см, 15 см.
38. Продовження медіани AM рівнобедреного трикутника ABC (AB = AC) перетинає
коло, описане навколо трикутника, у точці P. AM = 6 см, BC = 8 см. Знайдіть AP.

У ΔACP, ∠C = 90° як вписаний кут, що спирається на діаметр.
У ΔABC (AB = AC) AM медіана, а значить, і висота.
Отже, AM ⊥ CB.
З ΔACP, за властивістю висоти, опущеної
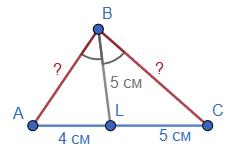
https://shkola.in.ua/3272-hdz-matematyka-8-klas-ister.html
AB BC = AL LC = 4 5.
Нехай AB = 4x, BC = 5x.
52 = 4x ⋅ 5x = 4 ⋅ 5; 25 = 20x2 – 20; 45 = 20x2 .
���� 2 = 45 20 ; ���� 2 = 9 4 ; ���� = 3 2 ; ���� = 1,5
AB = 4 ⋅ 1,5 = 6 (см), BC = 5 ⋅ 1,5 = 7,5 (см).
Відповідь: 6 см, 7,5 см.
40. Побудуйте трикутник ABC за даним кутом A,
AL.
План побудови

1. Побудувати кут A.
2. На сторонах кута A відкласти відрізки AC1 і AB1 так, що AC1 : AB1 = 4 : 3.
одній стороні кута відкласти 4 рівних відрізки (AC1), на другій 3 таких же відрізки (AB1).
3. Поділити кут A навпіл і провести бісектрису AL.
4. На промені AL відкласти відрізок AL = l.
5. Через точку L провести пряму BC, паралельну B1C1.
6. ΔABC шуканий.
