h-8-al-ta

https://shkola.in.ua/3296-hdz-alhebra-8-klas-tarasenkova.html

косила!

( 0,7)3 = 0,343 – А ( 6)30 =630 – А −77 = −823543 – П

( 0,3)8 = 6561 108 – О

1,64 =6,5536 – И

( 1,6)2 =2,56 – Ч

0,36 =0,000729 – Т

02024 =0 – Л 12023 =1 – И

( 0,7)5 = 0,16807 – В 54 = 625 – Н

-823543(П); -0,343(А); -0,16807(В); 0(Л); 6561 108 (О); 0,000729(Т); 1(И); 2,56 (Ч); 6,5536(И); 625(Н); 630 (А).

https://shkola.in.ua/3296-hdz-alhebra-8-klas-tarasenkova.html

1) 2; 2) 2; 3) 2; 4) 3 6.

10) �� 2 4�� +4 16�� 2 = 15�� 2 4�� +4= (15�� 2 +4�� 4) = = −(15�� 2 + 10�� − 6�� − 4)= −(5��(3�� +2) − 2(3

11) �� 3 + 125 =(�� +5)(�� 2 5�� + 25)

12) 27�� 3 8=(3�� 2)(9�� 2 +6�� +4)

7. Доведіть тотожність:

1) 10a – (3a – 9b) = 7a + 9b

10a 3a + 9b = 7a + 9b

Ліва частина

2) (0,5c + d) – 2(0,5d – 0,3c) = 1,1c

0,5c + d – 2 ⋅ 0,5d + 2 ⋅ 0,3c

0,5c + d – d + 0,6c = 1,1c

Ліва частина

3) 9m + 1 = 4(m + n) – 5(n – m) + (n + 1)

9m + 1 = 4m + 4n 5n + 5m + n + 1

9m + 1 = 9m + 1

Ліва

4) 10a – 2(3a – 2b) = (2a + b) – (-2a – 3b)

10a 6a + 4b = 2a + b + 2a + 3b

4a + 4b = 4a + 4b

Ліва

https://shkola.in.ua/3296-hdz-alhebra-8-klas-tarasenkova.html

1) а = 15 см; 2) а = 30,1 см.

P = 2 ⋅ (a + (a 3)) = 2 ⋅ (2a 3) = 4a – 6

Формула площі:

S = a ⋅ (a 3) = a2 3a

Якщо а = 15 см, то: P = 4(15) – 6 = 60 – 6 = 54 см

S=152 – 3 ⋅ 15 = 225 – 45 = 180 см2

Якщо a = 30,1 см, то: P = 4(30,1) – 6 = 120,4 – 6 = 114,4 см S = (30,1)2 – 3 ⋅ 30,1 = 906,01 90,3 = 815,71 см2

https://shkola.in.ua/3296-hdz-alhebra-8-klas-tarasenkova.html

20x + y + z = 112 Число

y = z + 4

Підставимо y = z + 4 у

20x + z + 4 + z = 112

20x + 2z = 112 – 4

20x + 2z = 108

10x + z = 54

Підберемо можливі

Якщо х = 5, то:

10x + z = 54 ⇒ z = 54 – 10х = 54 – 50 = 4, тоді

y = z + 4 = 4 + 4 = 8

Отже:

- перше число: 10 ⋅ 5 + 8 = 58

- друге число: 10 ⋅ 5 + 4 = 54

Перевірка:

- сума: 58 + 54 = 112

Відповідь:58; 54.

12.

10x + y = (x + y) + 18

10x + y – x – y = 18

9x = 18 x = 2

Число

2 y = 2 – 2 = 0

10(2) + 0 = 20

Відповідь: 20

(0; 2); (2; 0); (–3; 5,5); (–5;

1) x = –4, y = 3; x = 6, y = –2. x = –1, y = 5; x = 7, y = 0. x = 1, y = 2.

2) y = –3, x = –5; x = 5.

3) y > 0, x = –2; x = 0; x = 8.

4) y < 0, x = –5; x = 3; x = 5. (0; 2) – ні; (2; 0) – так; (–3; 5,5) – так; (–5; –3) – так.

https://shkola.in.ua/3296-hdz-alhebra-8-klas-tarasenkova.html

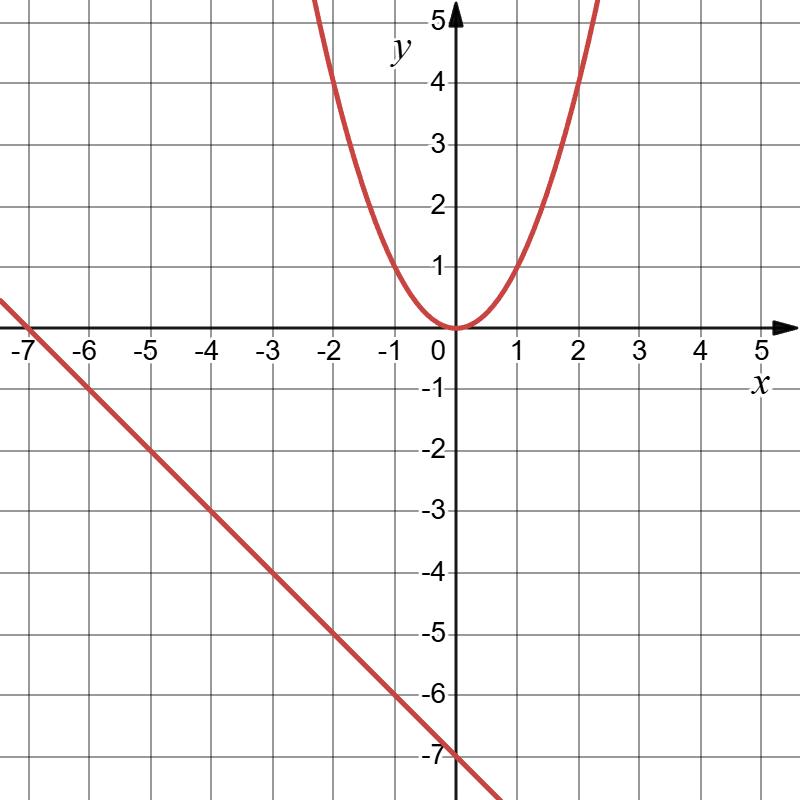
у = х2 – 6х + 9 точка: 1) А(3; 0); 2) В (–3; 18); 3) С(4; 1); 4) D (1,5; 2,25).

y = x2 – 6x + 9. Чи належить

функції точка: 1) В(3; 0): 0 = 32 – 6 ⋅ 3 + 9; 0 = 9 – 18 + 9; 0 = 0. Так.

2) В(–3; 18): 18 = (–3)2 – 6 ⋅ (–3) + 9; 18 = 9 + 18 + 9; 18 ≠ 36. Ні. 3) С(4; 1): 1 = 42 – 6 ⋅ 4 + 9; 1 = 16 – 24 + 9; 1 = 1. Так. 4) D(1,5; 2,25): 2,25 = 1,52 – 6 ⋅ 1,5 + 9; 2,25 = 2,25 – 9 + 9; 2,25 = 2,25. Так.

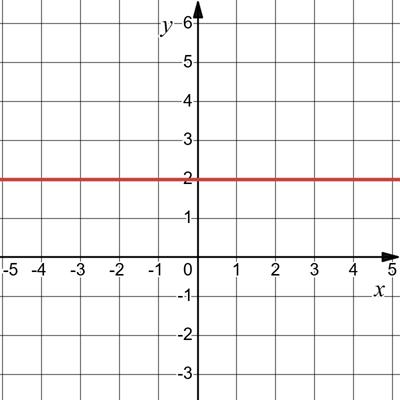
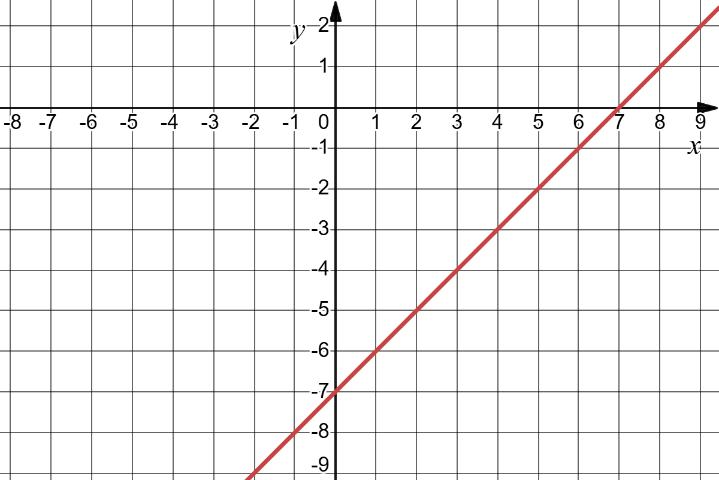
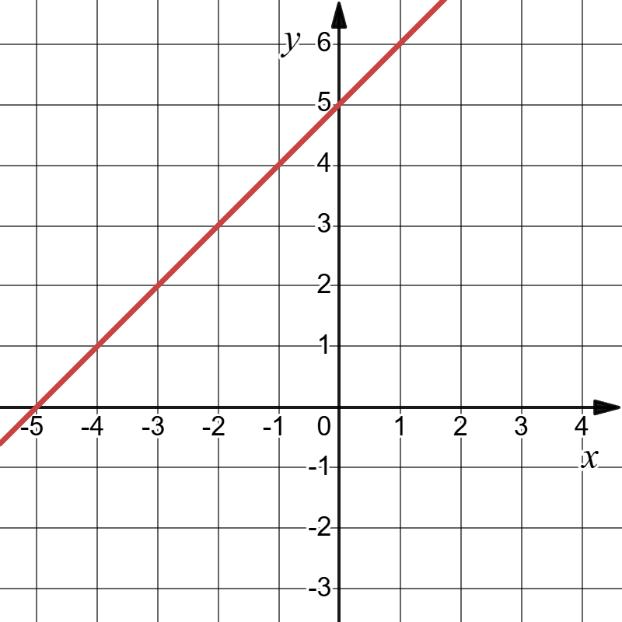
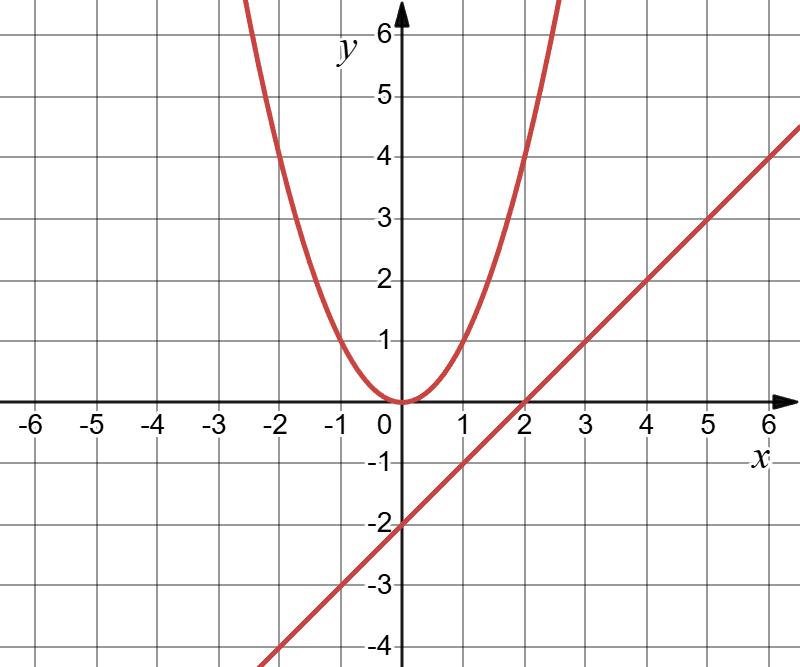
17. Побудуйте графік функції: 1) у = -3; 2) у = х + 3; х 0 1 у 3 4

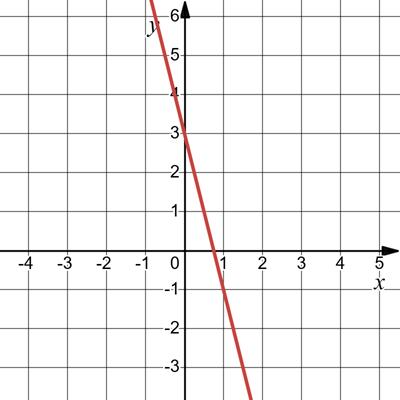
3) у = -2х + 4; х 0 1

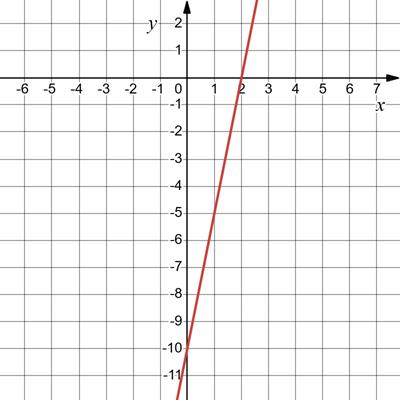
4 2 4) у = 0,5х; х 0 2

https://shkola.in.ua/3296-hdz-alhebra-8-klas-tarasenkova.html

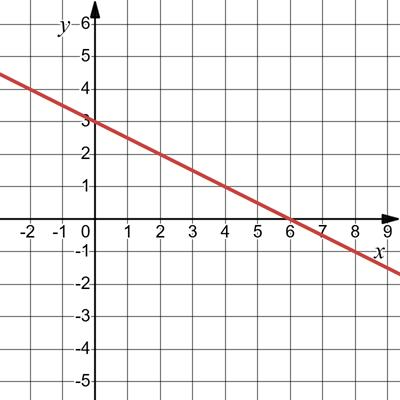
y = 1 2 x – 4. З віссю Ох: y = 0; 0 = 1 2 x – 4; x = 8. (8; 0) З віссю Оу: х = 0 y = 1 2 ⋅ 0 – 4 = –4. (0; –4).

х 0 2

у -4 -3

Пряма відтинає

8 од. В 4 од. Відповідь: (0; –4), (8; 0); прямокутний трикутник.

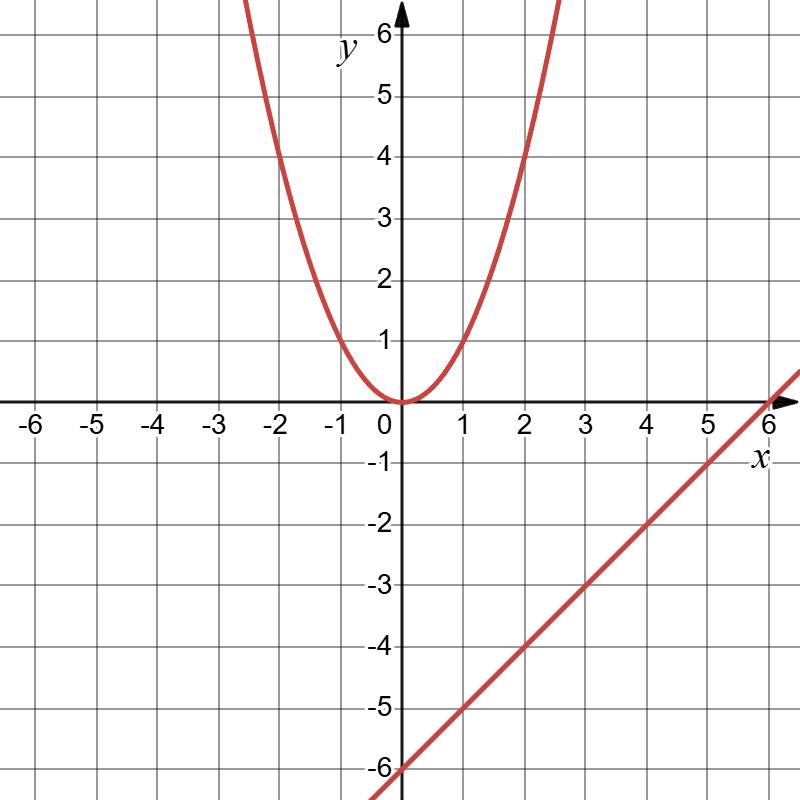
y = –0,5x + 3 З віссю Ох: y = 0; 0 = –0,5x + 3; 0,5x = 3; x = 6. (6; 0)

З віссю Оу: x = 0. y = –0,5 ⋅ 0 + 3 = 3. (0; 3).

х 0 4

у 3 1 Пряма

6 од. і 3 од.

Відповідь: (0; 3), (6; 0); прямокутний трикутник.

1) a = –1, b = –2. (–1; –2): –2 = k ⋅ (–1); k = 2.

2) a = –0,2, b = 1. (–0,2; 1): 1 = k ⋅ (–0,2); k = –5.

3) a = 3, b = 0,6. (3; 0,6) : 0,6 = k ⋅ 3; k = 0,2.

=

(–1) –

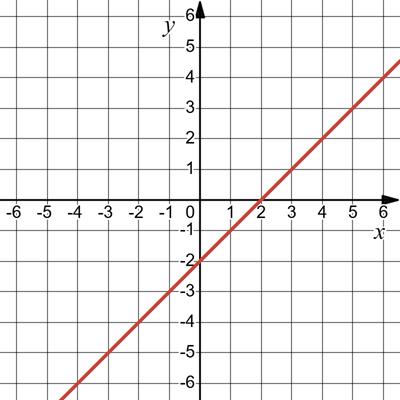
https://shkola.in.ua/3296-hdz-alhebra-8-klas-tarasenkova.html

24. Графік функції y =

a і b.

–7 = a ⋅ (–1) + b;

–2 = a ⋅ 0 + b; b = –2; –a – 2 = –7; a + 2 = 7; a = 5.

Відповідь: a = 5, b = –2.

+ b

25. Знайдіть корінь рівняння:

1) 7x – 3x – 3 = 10 – 4x; –3x + 4x = 10 – 7 + 3; x = 6.

y – будь–яке число.

3) –1,2х + 5 = 3(–0,4х + 1); –1,2х + 5 = –1,2х + 3;

0х = –2;

коренів немає

26. Чи є рівносильними рівняння.

1) 9x – 1 = 8x + 7 і 9x – 8x = 1 + 7.

9x – 8x = 7 + 1; x = 8.

x = 8

2) 5 – 5a = –5a + 5 і 0a = 0.

0a = 0; a – будь–яке число.

a – будь–яке число.

3) 2(x + 1) = 3(2 – x) і 2x + 3x = 4

2x + 2 = 6 – 3x; 5x = 4;

2x + 3x = 6 – 2; x = 0,8.

5x = 4; x = 0,8.

Відповідь: 1) так; 2) так; 3) так.

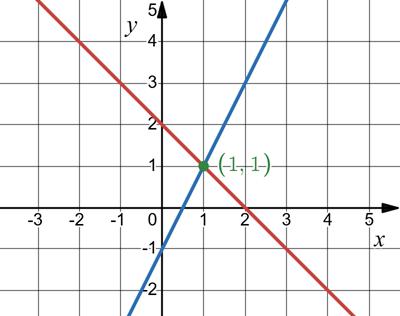
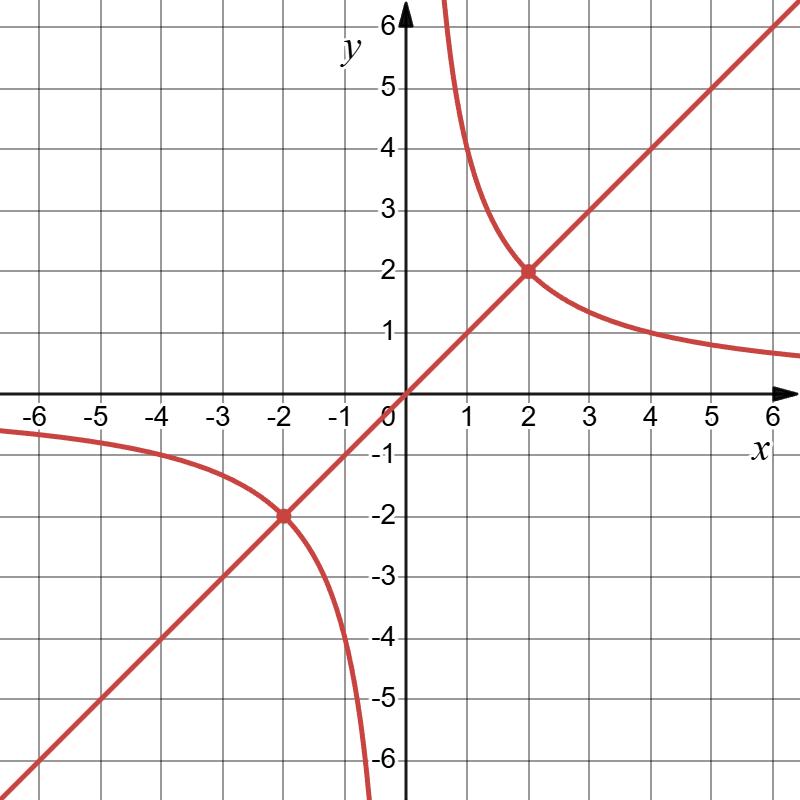
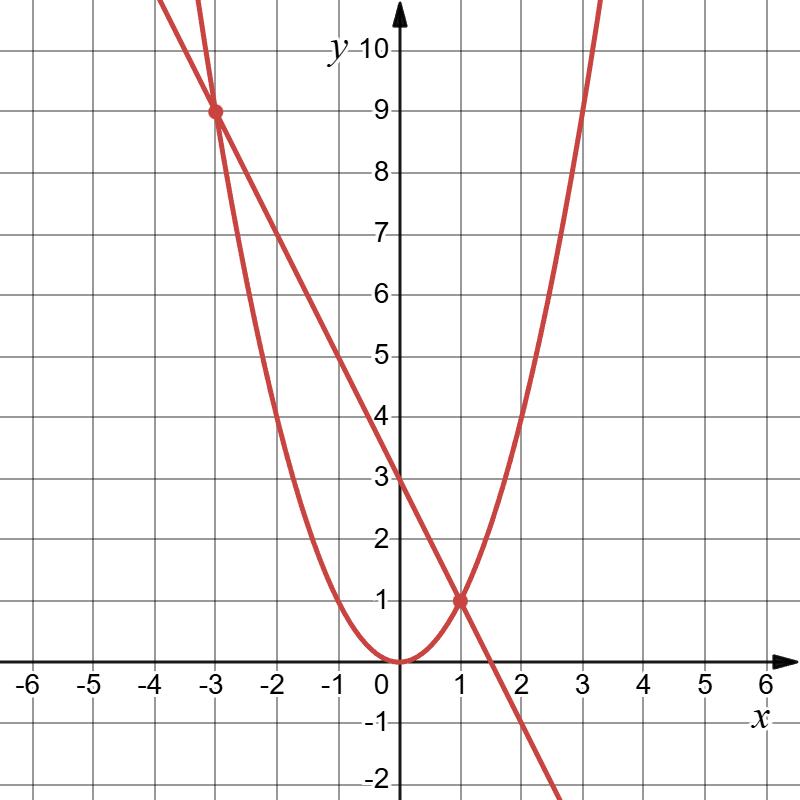
27. Розв’яжіть графічно систему рівнянь:

1) � х + у = 2;

2х −у =1;

х + у = 2;

у = 2 – х.

х 0 1

у 2 1

2х – у = 1;

у = 2х – 1.

х 0 1

у -1 1

Відповідь: (1; 1).

2) 5 + 12y – 7y = 5(y + 1); 5 + 5y = 5y + 5; 0y = 0.

4) 1,5y – 4 = 5 + 0,9y; 1,5y – 0,9y = 5 + 4; 0,6y = 9; y = 15.

https://shkola.in.ua/3296-hdz-alhebra-8-klas-tarasenkova.html

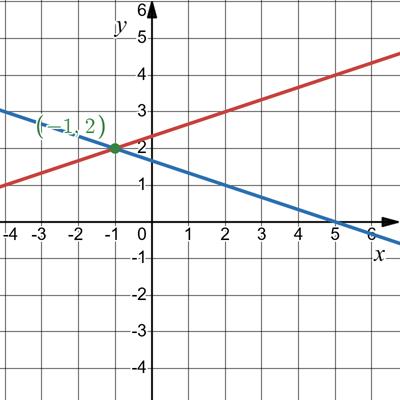
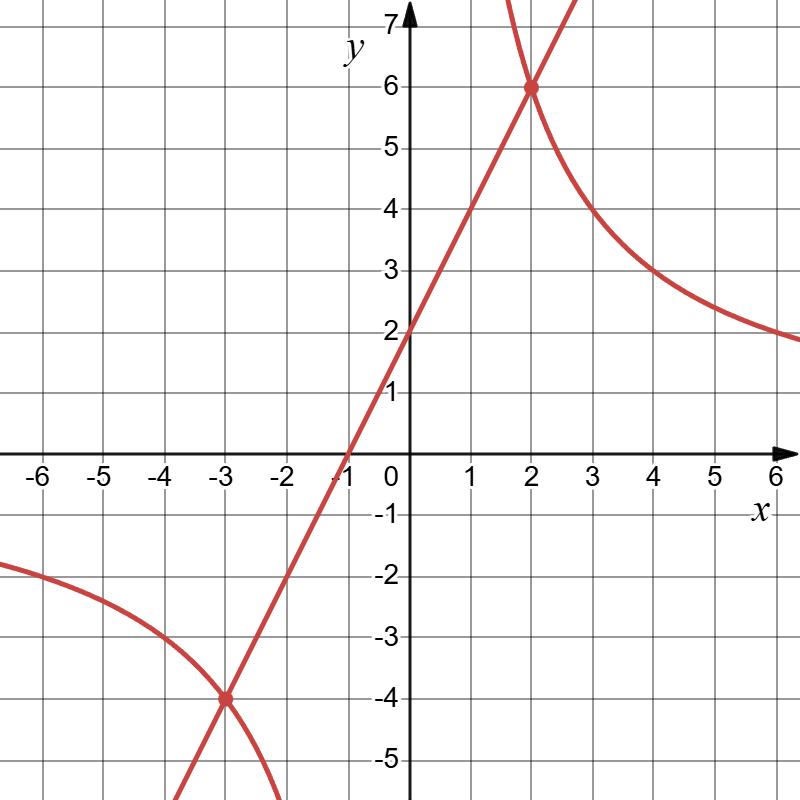
2) �х 3у = 7; х + 3у =5;

х – 3у = -7; 3у = х + 7;

у = 1 3 х + 7 3;

х -1 2

у 2 3

х + 3у = 5;

3у = 5 – х; у = 5 3 1 3 х;

х -1 -4

у 2 3

Відповідь: (-1; 2).

3) � 2х у = 5; −х +0,5у = 2,5; 2х – у = 5; у = 2х – 5. -х + 0,5у = -2,5; 0,5у = х – 2,5; у = 2х – 5.

х 1 2

у -3 -1

Відповідь: безліч розв’язків.

4) �−х + 2у + 4 = 0; 2х 4у +3=1; -х + 2у + 4 = 0; 2у = х – 4; 2у = 1 2 х− 2

х 0 2

у -2 -1

2х – 4у + 3 = 1; -4у = -2х – 3 + 1; -4у = -2х – 2;

у = 1 2 х + 1 2

х 1 3

у 1 2

Відповідь: немає розв’язку.

https://shkola.in.ua/3296-hdz-alhebra-8-klas-tarasenkova.html

1) �5х − у = 9;

х + 3у =5; + �15х 3у = 27;

х + 3у =5;

16х = 32;

х = 2;

2 + 3у = 5;

3у = 5 – 2;

3у = 3; у = 1.

Відповідь: (2; 1).

3) � 2х у = 5; −х +0,5у = −2,5ǀ ⋅ (−2); �2х −у =5;

2х −у =5;

Відповідь: безліч розв’язків.

500x + 250 ⋅ 4x = 15000;

500x + 1000x = 15000;

1500x = 15000; x = 10;

10 пакетів по 500 г; 4 ⋅ 10 = 40 (п.) – по 250

2) �3х + 5у = 7; 7х 6у = 19;

�18х + 30у = 42;

35х 30у = 95;

53х = 53; х = 1;

3 ⋅ 1 + 5у = -7; 5у = -7 – 3; 5у = -10; у = -2.

Відповідь: (1; -2).

4) � х + 2у + 4 = 0ǀ ⋅ ( 2);

2х 4у +3=1; � 2х 4у =0;

2х 4у = 2;

Відповідь: немає розв’язків.

– 10 л;

https://shkola.in.ua/3296-hdz-alhebra-8-klas-tarasenkova.html

– по 0,5 л і 0,75 л – ? б.

2 ⋅ 0,75 + 17 ⋅ 0,5 = 10;

4 ⋅ 0,75 + 14 ⋅ 0,5 = 10;

6 ⋅ 0,75 + 11 ⋅ 0,5 = 10;

8 ⋅ 0,75 + 8 ⋅ 0,5 = 10;

10 ⋅ 0,75 + 5 ⋅ 0,5 = 10;

12 ⋅ 0,75 + 2 ⋅ 0,5 = 10;

20 ⋅ 0,5 = 10.

80% = 0,8%; 60% = 0,6. Нехай х тис. грн. –

(х + 50) тис. грн. –

Складаємо рівняння:

0,8(х + 50) – 0,6х = 130; 0,8х + 40 – 0,6х = 130; 0,2х = 90; х = 450.

450 тис. грн – на ІІ склад.

Відповідь: 500 тис. грн; 450 тис. грн. 33.

становлять 1,5 року. Скільки

1,5 : 0,3 = 5 (р.)

Нехай

Складаємо рівняння: х+х+5

2 = 22,5;

2х + 5 = 45;

2х = 45 – 5;

2х = 40;

х = 20;

20 років – І спортсмену; 20 + 5 = 25 (р.)

https://shkola.in.ua/3296-hdz-alhebra-8-klas-tarasenkova.html

3х + у = 50; 1,5х 0,5у = 20| ⋅ 2; �3x + y = 50; 3x y = 40; 6x = 90; x = 15;

3 ⋅ 15 + y = 50; y = 50 – 45 = 5;

Vвл. = 15 км/год;

Vтеч. = 5 км/год.

Відповідь: 15 км/год; 5 км/год.

35. За 3 год

течії річки.

Vвл. – х км/год;

Vтеч. – у км/год.

Складаємо систему рівнянь:

3(x + y) + 1(x y) = 82; 1(x + y) + 2(x + y) = 54; �3x + 3y + x y = 82; x + y + 2x 2y = 54;

4x + 2y = 82; 3x y = 54| ⋅ 2; � 4x + 2y = 82; 6x 2y = 108; 10x = 190; x = 19.

4 ⋅ 19 + 2y = 82; 2y = 82 – 76; 2y = 6; y = 3;

Vвл. = 19 км/год; Vтеч. = 3 км/год.

Відповідь: 19 км/год; 3 км/год. 36.

бортів басейну прокладено доріжку

Довжина – ?, на 5 м > Ширина – ?

Доріжка – 94 пл. розміром 1м2 х 1м2

1) 94 – 4 = 90 (пл.)

2) 90 : 2 = 45 (пл.)

Нехай х м – ширина басейну, тоді

х + х + 5 = 45;

2х = 40;

х = 20;

20 м – ширина

20 + 5 = 25 (м)

25 ⋅ 20 = 500 (м2)

https://shkola.in.ua/3296-hdz-alhebra-8-klas-tarasenkova.html

1)

2) 14 : 0,56 = 25 (д.);

2.

25 ⋅ 0,36 = 9 (д.);

3. Яке відсоткове відношення

дітей, які правильно розв’язали її?

1) 25 ⋅ 0,08 = 2 (д.) – не змогли розв’язати

2) 2 14 ⋅ 100% = 14,3%.

Відповідь: 1) 25 д.; 2) 9 д.; 3) 14,3%.

38. За

решту 13,5 км.

1. Скільки кілометрів

1)

2) 13,5 : 0,27 = 50 (км);

2. Скільки

50 ⋅ 0,37 = 18,5 (км);

3.

37% – 27% = 10%.

Відповідь: 1) 50 км; 2) 18,5 км; 3) на 10%.

39.

40% = 0,4; 25% = 0,25.

Нехай потрібно

Складаємо рівняння:

(0,5 + х) ⋅ 0,25 = 0,5 ⋅ 0,4;

0,125 + 0,25х = 0,2; 0,25х = 0,2 – 0,125; 0,25х = 0,075; х = 0,3.

Відповідь: 0,3 л. води.

40. Скільки

10 % –й розчин? 35% = 0,35; 10% = 0,1.

https://shkola.in.ua/3296-hdz-alhebra-8-klas-tarasenkova.html

акторів: 160 см, 161 см, 163 см, 166 см, 156 см, 164 см, 160 см, 164 см, 164 см, 166 см.

Складіть

драматичного гуртка.

160 см, 161 см, 163 см, 166 см, 156 см, 164 см, 160 см, 164 см, 164 см, 166 см.

156 160 161 163

162,4 см.

1; 2; 0; 1; 3; 5; 4; 0; 5; 3; 1; 2; 2; 6; 3; 1; 5; 4; 2; 0. Упорядкуйте

1; 2; 0; 1; 3; 5; 4; 0; 5; 3; 1; 2; 2; 6; 3; 1; 5; 4; 2; 0. 0; 0; 0; 1; 1; 1; 2; 2; 2; 2; 3; 3; 3; 4; 4; 5; 5; 5; 6.

Відповідь: 2,5.

три уроки — українська

3 уроки – українська мова, фізкультура

3 ⋅ 2 ⋅ 1 = 6 (в.)

Відповідь: 6. 44. Скільки трицифрових чисел можна скласти

1) усі цифри числа – різні.

3 ⋅ 2 ⋅ 1 = 6 (сп.)

2) цифри

3 ⋅ 3 ⋅ 3 = 27 (сп.)

Відповідь: 1) 6 сп.; 2) 27 сп. 45. Олексій, Микита

https://shkola.in.ua/3296-hdz-alhebra-8-klas-tarasenkova.html

TikTok?

YouTybe – 23 млн; Facebook – 15,6 млн; Instagram – 13,2 млн; TikTok – 12 млн.

1) 13,2 млн – 12 млн = 1,2 млн

2) (1,2 млн)/(12 млн) ⋅ 100% = 10%. Відповідь: 10%.

2х−6 – так. 5) (х – 3) : (х + 3) – ні; 6) (х2 – 3) : (х – 3) –

Визначте ОДЗ

1) 2х+1 х−2 ; ОДЗ: х – 2 ≠ 0; х ≠ 2. 2) 3с−1 3−с ; ОДЗ: 3 – с ≠ 0; с ≠ 3.

3) 5�� +2 5�� −5;

: (b2 + 1); ОДЗ: b2 + 1 ≠ 0; b – будь–яке число.

6) (с + 4)(4 – с); ОДЗ: с – будь–яке число. 59.

1) 2х−3

https://shkola.in.ua/3296-hdz-alhebra-8-klas-tarasenkova.html

1) (1 – 2) : (1 + 2) = -1 + 3 =1 3;

2) (2 – 0,5) : (2 + 0,5) = 1,5 : 2,5 =

https://shkola.in.ua/3296-hdz-alhebra-8-klas-tarasenkova.html

с = 0. ОДЗ: а ≠ 0, с ≠ 0. 2) 3�� 4��2 ; 4ab2 = 0; ab2 = 0. a = 0 або b2 = 0; b = 0. ОДЗ: а = ≠ 0; b ≠ 0.

3) (3х + у) : 4ху3; 4ху3 = 0; ху3 = 0. х = 0 або у3 = 0; у = 0; ОДЗ: х ≠ 0, у ≠ 0.

5) 2х2у : ((3 – х)(у – 4)); (3 – х)(у – 4) = 0; 3 – х = 0 або у – 4 = 0; х = 3; у = 4. ОДЗ: х ≠ 3; у ≠ 4.

7) 5��

2(��−5)2 (1−�� );

2(b – 5)2(1 – c) = 0; (b – 5)2(1 – c) = 0;

(b – 5)2 = 0 або 1 – с = 0; b – 5 = 0; c = 1; b = 5.

ОДЗ: b ≠ 5; c ≠ 1.

9) 5��

6(4��−1)(1−4�� ); 6(4b – 1)(1 – 4c) = 0; (4b – 1)(1 – 4c) = 0;

4b – 1 = 0 або 1 – 4с = 0; 4b = 1; 4c = 1; b = 1 4; c = 1 4 .

ОДЗ: b ≠ 1 4; c ≠ 1 4 .

1) 2а+1

4−а2 ;

4 – а2 = 0; (2 – а)(2 + а) = 0; 2 – а = 0 або 2 + а = 0; а = 2; а = -2.

ОДЗ: а ≠ 2; а ≠ -2.

4) 2ас 2(а−1)(с+1); 2(а – 1)(с + 1) = 0; (а – 1)(с + 1) = 0; а – 1 = 0 або с + 1 = 0; а = 1; с = -1. ОДЗ: а ≠ 1, с ≠ -1.

6) 3ас (а+1)2 с3 =0; (а + 1)2с3 = 0; (а + 1)2 = 0 або с3 = 0; а + 1 = 0; с = 0.

а = -1. ОДЗ: а ≠ -1; с ≠ 0.

8) 7ас 3(2−а)2 (с+2; 3(2 – а)2(с + 2) = 0; (2 – а)2(с + 2) = 0; (2 – а)2 = 0 або с + 2 = 0; 2 – а = 0; с = -2. а = 2.

ОДЗ: а ≠ 2, с ≠ -2.

10) 2cd : ((3d – 4)(5 – 3c)); (3d – 4)(5 – 3c) = 0; 3d – 4 = 0 або 5 – 3с = 0; 3d = 4; 3c = 5; d = 4 3; c = 12 3 $

ОДЗ: d ≠ 4 3; с ≠ 12 3

2) 3�� 2 9−��2 ; 9 – b2 = 0; (3 – b)(3 + b) = 0; 3 – b = 0 або 3 + b = 0; b = 3; b = -3.

ОДЗ: b ≠ 3, b ≠ =3.

https://shkola.in.ua/3296-hdz-alhebra-8-klas-tarasenkova.html

3) 3ху : (х2 – 16);

х2 – 16 = 0;

(х – 4)(х + 4) = 0;

х – 4 = 0

або х + 4 = 0;

х = 4; х = -4.

ОДЗ: х ≠ 4, х ≠ -4.

5) 3��

4(��2 −6��+9);

4(b2 – 6b + 9) = 0;

b2 – 6b + 9 = 0;

(b – 3)2 = 0;

b – 3 = 0; b = 3.

ОДЗ: b ≠ 3.

4) 2а а2 −2а+1;

а2 – 2а + 1 = 0;

(а – 1)2 = 0;

а – 1 = 0; а = 1.

ОДЗ: а ≠ 1.

6) (5 – х2) : (25 + 10х2 + х4)

25 + 10х2 + х4 = 0;

(5 + х2)2 = 0;

5 + х2 = 0;

х2 = -5; немає коренів.

ОДЗ: х – будь-яке число. 70. Визначте ОДЗ кожної змінної виразу.

1) 2�� 3��

7�� ;

7bc = 0;

bc = 0;

b = 0 або с = 0.

ОДЗ: b ≠ 0, с ≠ 0.

3) 6ху

(3х−8)(2х+6); (3х – 8)(2х + 6) = 0;

3х – 8 = 0 або 2х + 6 = 0;

3х = 8; 2х = -6;

х = 8 3; х = -3. х = 22

2) 3ab : ((2 – a)b)2; ((2 – a)b)2 = 0 (2 – a)b = 0

2 – a = 0 або b = 0

ОДЗ: а ≠ 2, b ≠ 0.

4) 3y(y² – 8y + 16); y² – 8y + 16 = 0; (y – 4)² = 0; y – 4 = 0; y = 4. ОДЗ: у ≠ 4.

1)

х = 50 км/год; 2) х з = 60 км/год; 3) х = 80 км/год; 4) х

U = x км/год;

S = (2x + 40) км; t = 2х+40

3) якщо х = 80 км/год, то

4) якщо х =

км/год, то

https://shkola.in.ua/3296-hdz-alhebra-8-klas-tarasenkova.html

1)

; |n| + 10 = 0; |n| = –10; немає коренів.

ОДЗ: n – будь–яке число.

2) 3+��

3−ǀ��ǀ; 3 – |n| = 0; |n| = 3; n = –3 або n = 3.

ОДЗ: n ≠ –3, n ≠ 3.

3) 4 : (2|n| – 1); 2|n| – 1 = 0; 2|n| = 1; |n| = 0,5; n = –0,5 або n = 0,5.

ОДЗ: n ≠ –0,5, n ≠ 0,5.

4) 4+ǀ��ǀ

ǀ��−1ǀ−1; |n – 1| – 1 = 0; |n – 1| = 1; n – 1 = –1 або n – 1 = 1; n = –1 + 1; n = 1 + 1; n = 0. n = 2.

ОДЗ: n ≠ 0; n ≠ 2.

5) 2+ǀ��ǀ

ǀ��+3ǀ−3; |n + 3| – 3 = 0; |n + 3| = 3;

https://shkola.in.ua/3296-hdz-alhebra-8-klas-tarasenkova.html

n + 3 = –3 або n + 3 = 3; n = –3 – 3; n = 3 – 3; n = –6; n = 0.

ОДЗ: n ≠ –6; n ≠ 0.

6) (3 – |n + 1|) : (7 – 2|n – 1|); 7 – 2|n – 1| = 0; –2|n – 1| = –7; |n – 1| = 3,5;

n – 1 = –3,5 або n – 1 = 3,5; n = –3,5 + 1 n = 3,5 + 1; n = –2,5 n = 4,5.

ОДЗ: n ≠ –2,5; n ≠ 4,5.

82.

2) (-2a – 6b) : 5c + 1 = -2(a + 3b) : 5c + 1 = -2 ⋅

1. Довжина – а

https://shkola.in.ua/3296-hdz-alhebra-8-klas-tarasenkova.html

3) у = х2 +10х+25 х+5 = (х+5)2 х+5 = х +5.

х + 5 ≠ 0

110. Розв’яжіть рівняння.

1) х2 −25

х+5 =0; �(х− 5)(х +5) =0; х +5 ≠ 0; �х =5 або х = 5; х≠ 5. Відповідь: 5.

2) х2 −121 −121+х2 =1; х2 −121 х2 −121 =1; ОДЗ: х2 – 121 ≠ 0; (х – 11)(х + 11) ≠ 0; х – 11 ≠ 0 або х + 11 ≠ 0;

-11.

3) 6х−1

3−18х = 1 3; 6х−1

3(6х−1) = 1 3 ǀ∙ ( 3) ;

6х−1

https://shkola.in.ua/3296-hdz-alhebra-8-klas-tarasenkova.html

6х−1 =1. ОДЗ: 6х – 1 ≠ 0; 6х ≠ 1; х ≠ 1 6 .

Відповідь:

111. Скоротіть дріб.

х2 −3х+2

1)

х2 −5х+6 = (х−2)(х−1) (х−2)(х−3) = х−1 х−3; х2 – 3х + 2 = 0; х2 – 5х + 6 = 0;

=2; ��2 =1;

2) 3х2 +12х+9

=2; ��2 =3.

3х4 +15х2 +18 = 3(х2 +4х+3) 3(х4 +5х2 +6) = х2 +4х+3 х4 +5х2 +6;

3) х8 +х4 +1

х4 +х2 +1 = х4 −х2 +1; -х8 + х4 + 1 |х4 + х2 + 1 х8 + х6 + х4 |х4 – х2 + 1 -х6 + 1 -х6 – х4 – х2 -х4 + х2 + 1 х4 + х2 + 1 0

112. Побудуйте графік функції.

у

х2 ǀхǀ

у = � х, х >0; −х, х <0; ОДЗ: х ≠ 0; у = х; х 1 2 у 1 2 у = -х х -2 -1 у 2 1

https://shkola.in.ua/3296-hdz-alhebra-8-klas-tarasenkova.html

2) у = 4−х2

2+ǀхǀ; х ≥ 0; у = 4−х2

2+х = (2−х)(2+х) 2+х =2 −х

х < 0; у = 4−х2

2−х = (2−х)(2+х) 2−х =2+ х;

у = �

2 −х, х≥ 0; 2+ х, х <0; у = 2 – х;

х 0 1

у 2 1 у = 2 + х; х -2 -1 у 0 1

3) у = х2 −6х+9 ǀ3−хǀ ;

ОДЗ: 3 – х ≠ 0; х ≠ 3.

х > 3; у = х2 −6х+9 (3−х) = (х−3)2 х−3 = х− 3;

х < 3; у = х2 −6х+9 3−х = (х−3)2 3−х =3 −х;

у = х – 3; х > 0; 3 – х; х < 3;

у = х – 3;

х 4 5

у 1 2

у = 3 – х. х 0 1 у 3 2

https://shkola.in.ua/3296-hdz-alhebra-8-klas-tarasenkova.html

1) х = 100 см; 2) х = 150 см; 3) х = 200 см. І – (х – 10) ⋅ (х – 20) см2

– (х – 10) ⋅ (х – 30) см2 .

(х−10)(х−20) (х−10)(х−30) = х−20 х−30;

1) якщо х = 10 см, то

2) якщо х = 150 см, то 150−20 150−30 = 130 120 = 13 12 = 1 1 12 (р.);

3) якщо х = 200 см, то 200−20 200−30 = 180 170 = 18 17 = 1 17 (р.).

Відповідь: 1) 1 1 7 р.; 2) 1 1 12 р.; 3) 1 1 17 р. § 3. Зведення раціональних

114. Чи правильно, що

https://shkola.in.ua/3296-hdz-alhebra-8-klas-tarasenkova.html

1) P = 4a; 2) P = 3a; 3) P = 32a; 4) P =

1) P = 8b; 2) P = 9b; 3) P = 36b; 4) P = 52b.

https://shkola.in.ua/3296-hdz-alhebra-8-klas-tarasenkova.html

4) (�� + 2)(5�� 1) = 0 �� +2= 0 або 5��− 1=0

= 2; 5�� =1

= 2; �� = 1 5

7) �� 2 4 = 0 (��− 2)(�� +2) =0

�� 2 6�� = 0

+1= 0 або ��− 4=0

(�� +5) =0

=0; �� =6 6) �� 2 + 5�� = 0

=2; �� = 2 8) 50 2�� 2 = 0 2�� 2 = 50

238. Розв’яжіть рівняння. 1) �� (6 2�� ) = 0

= 0 або 6 2�� =0 2�� = 6

=3;

3) (5 �� )(�� 4) =

2 = 25

=0; �� = 5

4) (�� +1)3

241. Розв’яжіть рівняння.

1) 2�� +1 =0

�� - будь-яке число, крім − 1. 2�� =0

=0 2) �� 3 2�� =0

4) �� + 3 ��− 3 =0

�� - будь-яке число,

крім 3.

�� +3=0

�� = 3

- будь-яке число,

3=0

=3

2 =0

3) �� 2 �� +2 =0 �� - будь-яке число, крім − 2. ��− 2=0 �� =2

=0 6) �� 2 1 3�� =0

- будь-яке число,

2 1=0

��− 1)(�� +1) =0

= 1 або �� = 1 7) 3�� 3 �� +3 =0 �� - будь-яке число, крім 3. 3�� 3 =0 �� = 0 8) �� 5 5�� =0

242. Розв’яжіть рівняння.

1) �� 2 + �� =0

�� 2 + �� = �� (�� +1)

- будь-яке число,

=5

�� - будь-яке число, крім 0 і 1. �� =0 розв’язків немає 2) ��

немає 3) 5�� 3 �� 3 +5�� 2 =0 �� 3 +5�� 2 = �� 2 (�� +5) �� - будь-яке число,

1) 2 ⋅ �� +1 =0 �� - будь-яке число, крім 1. 2 ⋅�� =0

=0

3) �� 2 −�� =0

2 −�� = �� (��− 1)

- будь-яке число, крім 0 і 1. �� =0

розв’язків немає 4) �� + 3 �� 2 +3�� =0

- будь-яке число, крім 0 і 3.

+3=0 �� = 3 розв’язків немає 244. Розв’яжіть рівняння.

1) �� 1 �� 2 1 =0 �� 2 1= (��− 1)(�� +1) �� - будь-яке число, крім 1 і 1.

1=0

=1

немає

4) 3�� − 6 �� 2 4 =0

�� 2 4= (��− 2)(�� +2)

�� - будь-яке число, крім 2 і 2.

3��− 6=0

- будь-яке число, крім 2 і 2. �� +2=0

= 2 розв’язків немає

�� =2 розв’язків немає 5) �� 2 1 ��− 1 =0

7) �� 2 16 ��− 4 =0 �� - будь-яке число,

4.

2 16 =0

��− 4)(�� +4) =0

=4 або �� = 4

= 4

3=0

- будь-яке число, крім 1.

�� 2 1=0

(��− 1)(�� +1) =0 �� =1 або �� = 1

�� = 1

�� 2 16 3�� + 12 =0

=4 або �� = 4

= 4

2) �� 2 − 9 4�� + 12 =0

�� + 12 =4(�� +3)

(��− 3)(�� +3) =0 �� =3 або �� = 3

= 3

3) 2�� + 2 �� 2 1 =0 �� 2 1= (��− 1)(�� +1) �� - будь-яке число, крім 1 і 1. 2�� +2=0

= 1

немає

6) �� 2 4 ��− 2 =0

�� - будь-яке число, крім 2. �� 2 4=0

(��− 2)(�� +2) =0

�� =2 або �� = 2 �� = 2

https://shkola.in.ua/3296-hdz-alhebra-8-klas-tarasenkova.html

1) �� 1

�� 3 1 =0

�� - будь-яке число, крім 1.

��− 1=0

�� =1

розв’язків немає

4) 2�� + 2 �� 3 +1 =0

�� - будь-яке число,

крім − 1.

2�� +2=0

�� = 1

розв’язків немає

https://shkola.in.ua/3296-hdz-alhebra-8-klas-tarasenkova.html

2) �� + 2 �� 3 +8 =0

�� - будь-яке число, крім 2.

�� +2=0

�� = 2

розв’язків немає

5) �� 3 9�� 15 5�� =0

3) �� 2 4 3�� +6 =0

�� - будь-яке число, крім 2.

�� 2 4=0

(��− 2)(�� +2) =0

�� =2 або �� = 2

�� =2

�� - будь-яке число, крім 3. �� 3 9�� =0 �� (��− 3)(�� +3) =0 �� =0; �� =3; �� = 3 �� =0; �� = 3 6) 3�� 3 12�� 4 2�� =0

- будь-яке число, крім 2. 3�� 3 12�� =0 3�� (��− 2)(�� +2) =0

https://shkola.in.ua/3296-hdz-alhebra-8-klas-tarasenkova.html

3) �� 4+ �� 4 + �� − 4 = 64 16 −�� 2 �� (��− 4) − (4+ �� )2 �� 2 16 = −64 �� 2 16

12��− 16 �� 2 16 = 64 �� 2 16 �� - будь-яке число, крім 4 і 4 12��− 16 = 64

12�� = 48

= 4 (не підходить)

немає

3��− 5�� 2

5

яке число,

300 = 30��

�� = 10 км/год

�� + 30 = 40 км/год

Відповідь: 10 км/год; 40 км/год.

257. Знаменник

5 ⋅ 3

3+3 ⋅ 11 = 8 36 = 2 9 Відповідь: 2 9 . 261.

3 Рівняння

https://shkola.in.ua/3296-hdz-alhebra-8-klas-tarasenkova.html

∈ (−3, −2, −1,0,1).

Правильна: 2) (4−3 )5 =4−15 .

Перевірка: (4−3 )5 =4−3⋅5 =4−15 .

Правильна: 4) (4−2 )−5 =410 .

Перевірка: (4−2 )−5 =4−2⋅(−5) =410 .

Відповідь: 2), 4).

https://shkola.in.ua/3296-hdz-alhebra-8-klas-tarasenkova.html

17) 2300,02 ⋅ 10−1 =2,30002 ⋅ 102 ; 18) 118,8 ⋅ 1010 =1,188 ⋅ 1012 ; 19) 0,32 ⋅ 102 =3,2 ⋅ 101 ; 20) 0,00051 ⋅ 103 =5,1 ⋅ 10−1 ; 21) 5072 ⋅ 106 =5,072 ⋅ 109 ; 22) 0,0074 ⋅ 10−2 =7,4 ⋅ 10−5 ; 23) 0,003 ⋅ 1010 =3 ⋅ 107 ; 24) 0,00008 ⋅ 103 =8 ⋅ 10−2 . 343. Запишіть у стандартному

число: 1) 37 =3,7 ⋅ 101 ; 2) 19 =1,9 ⋅ 101 ; 3) 207 =2,07 ⋅ 102 ; 4) 0,02 =2 ⋅ 10−2 ; 5) 0,38 =3,8 ⋅ 10−1 ; 6) 13,005 =1,3005 ⋅ 101 ; 7) 0,065 =6,5 ⋅ 10−2 ; 8) 0,000075 =7,5 ⋅ 10−5 ; 9) 91 ⋅ 103 =9,1 ⋅ 104 ; 10) 482 ⋅ 10−5 =4,82 ⋅ 10−3

https://shkola.in.ua/3296-hdz-alhebra-8-klas-tarasenkova.html

1) 5 ⋅ 10−7 і 1,2 ⋅ 10−7 ;

5>1,2 ⇒ 5 ⋅ 10−7 >1,2 ⋅ 10−7 ;

сума: (5+1,2) ⋅ 10−7 =6,2 ⋅ 10−7 ;

різниця: (5 1,2) ⋅ 10−7 =3,8 ⋅ 10−7 ;

добуток: 5 ⋅ 1,2 ⋅ 10−7−7 =6 ⋅ 10−14 .

2) 3,1 ⋅ 104 і 3 ⋅ 104 ; 3,1>3 ⇒ 3,1 ⋅ 104 >3 ⋅ 104 ;

сума: (3,1+3) ⋅ 104 =6,1 ⋅ 104 ;

різниця: (3,1 3) ⋅ 104 =0,1 ⋅ 104 =1 ⋅ 103 ;

добуток: 3,1 ⋅ 3 ⋅ 104+4 =9,3 ⋅ 108 .

як степінь з основою 0,1: 1) 0,01 = (0,1)2 ;

2) 1= (0,1)0 ;

3) 10 = (0,1)−1 ; 4) 100 = (0,1)−2 ; 5) 1000 = (0,1)−3 ; 6) 10 000 = (0,1)−4 .

5) (4,5)−20 = (4,5−�� )5 ; (4,5−�� )5 = (4,5)−5�� ; 20 = 5�� , �� =4. 352. Знайдіть x, якщо: 1) ��

3) 3−36 = (3−�� )9 ; 3−36 =3−9�� ⇒ −

1) 6⋅ 10−8 і 1,2 ⋅ 10−9 ; 6 ⋅ 10−8 >1,2 ⋅ 10−9 ;

6,12 ⋅ 10−8 ; добуток:

3) 0,63 ⋅ 10−11 і 2,1 ⋅ 10−10 ; 6,3 ⋅ 10−12 <2,1 ⋅ 10−10 ;

https://shkola.in.ua/3296-hdz-alhebra-8-klas-tarasenkova.html

1)

2)

3)

4)

5)

7)

https://shkola.in.ua/3296-hdz-alhebra-8-klas-tarasenkova.html

2)

1)

https://shkola.in.ua/3296-hdz-alhebra-8-klas-tarasenkova.html

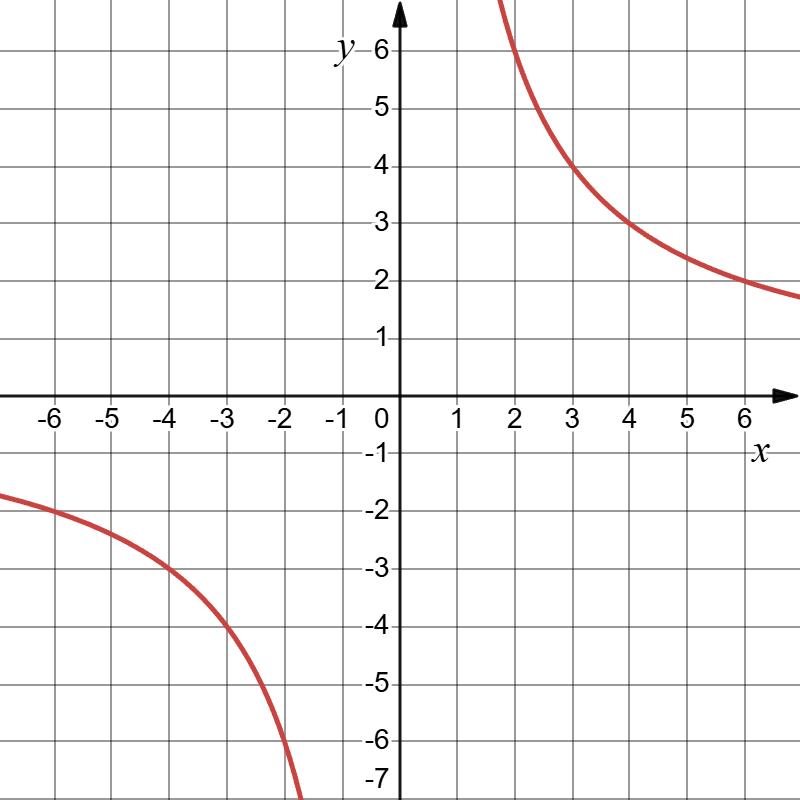
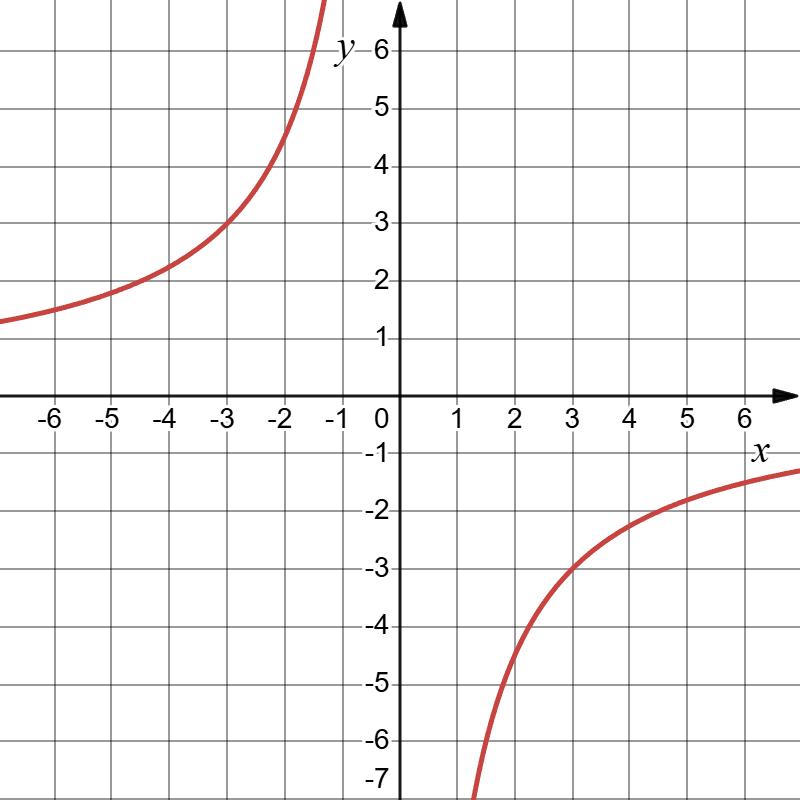
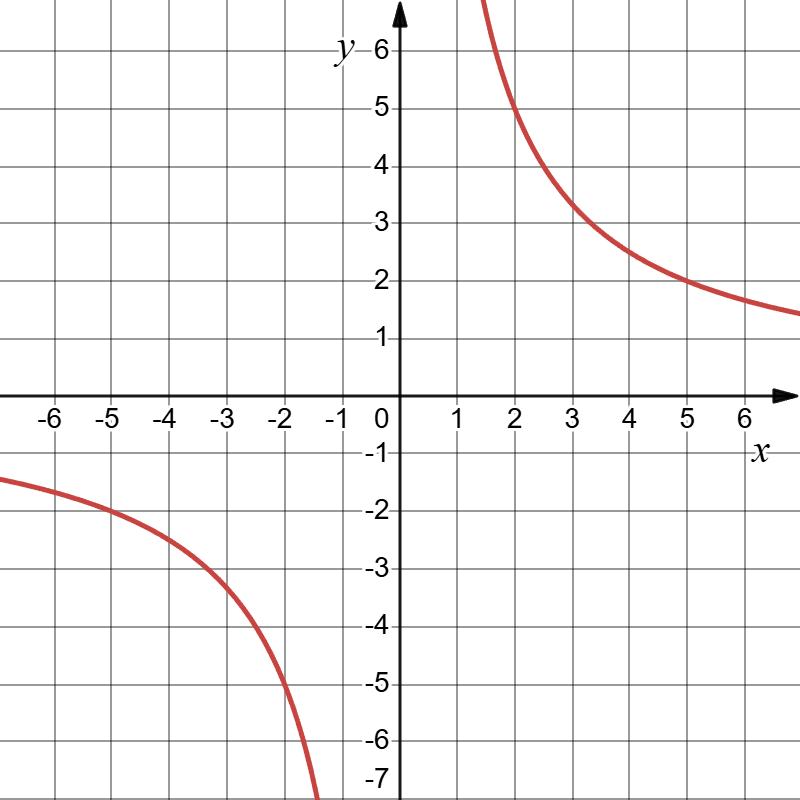
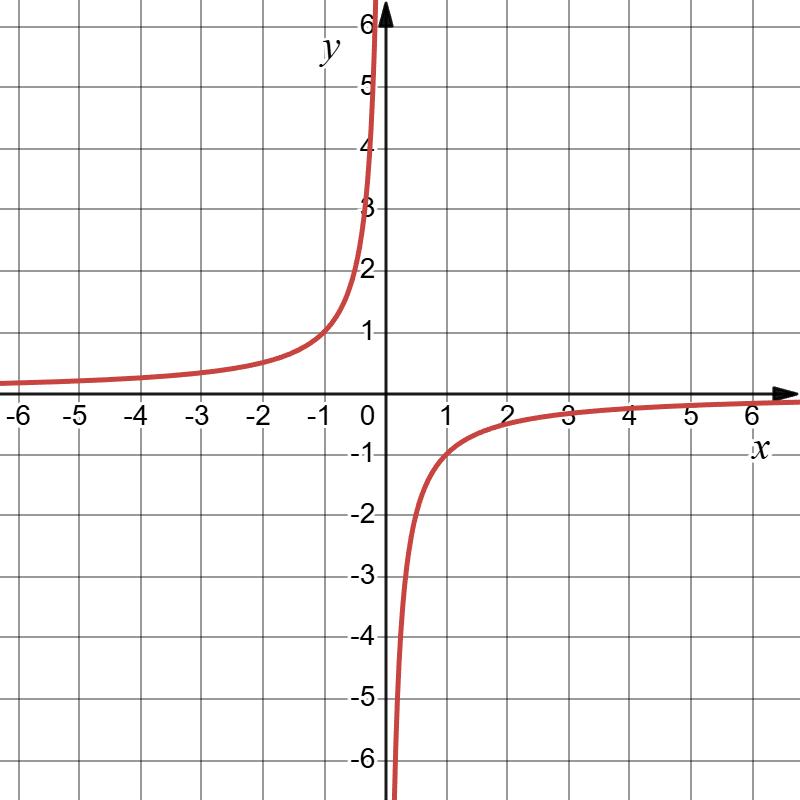
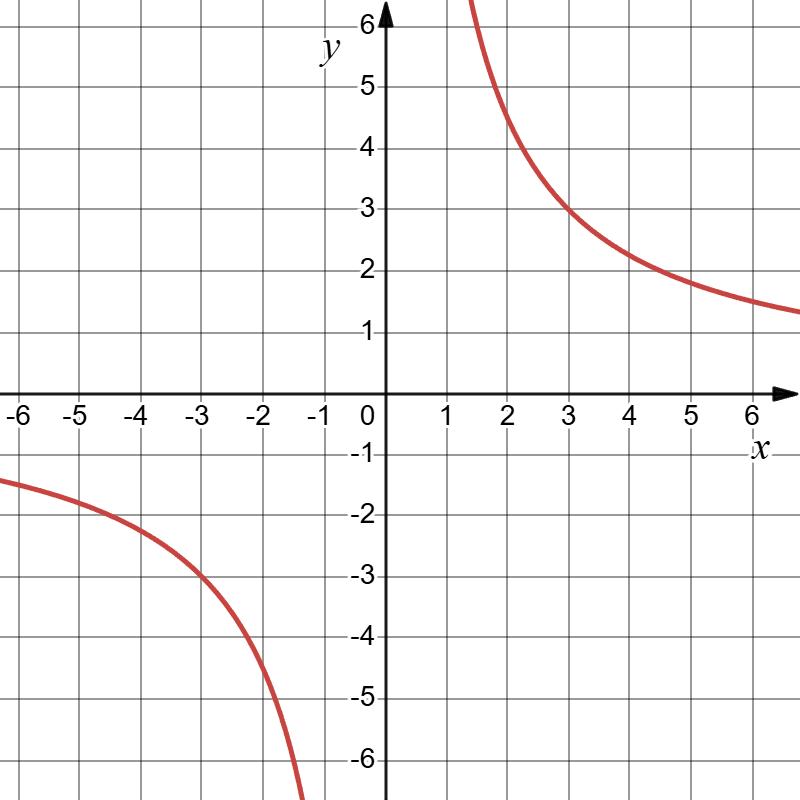
Мал. 15 — гіпербола,

https://shkola.in.ua/3296-hdz-alhebra-8-klas-tarasenkova.html

9) ��(8;0,5) 0,5= 4 8 ;0,5= 1 2 ;0,5=0,5 → Правильно.

429. Чи

1) ��(1; −10) −10 = 10 1 ; −10 = 10 →

2) �� (2;5) 5= 10 2 ; 5=5 → Належить.

3) �� (0;0) 0= 10 0 Ділення

4) �� ( 1; 10) 10 = 10 −1 ; 10 = 10 → Належить.

5) �� (10;1) 1= 10 10 ;1=1 → Належить.

6) �� (−10; −10) −10 = 10 −10; −10 = −1 → Не належить.

�� =

Точки: (1; 9); ( 3;3); (9; 1).

3) �� = 18 ��

Точки: (1; 18); (2;9); ( 3; 6)

4) �� = 20 ��

Точки: (1; 20); ( 2; 10); (4; 5).

5) �� = 25 ��

Точки: (1; 25); (5;5); (−5; −5).

6) �� = 25 ��

Точки: (1; −25); (−5;5); (25; −1).

7) �� = 10 ��

Точки: (1; 10); (2; 5); ( 5;2).

8) �� = 14 ��

Точки: (1; 14); (2; 7); ( 7;2).

1) �� = 15 ��

Точки: (1; 15); (3;5); ( 5; 3).

2) �� = 30 ��

Точки: (1; 30); (3; 10); ( 6;5)

434. Знайдіть

1) ��(1; 10) 10 = �� 1 ; �� = 10

2) �� (2;8)

8= �� 2 ;�� =8 ⋅ 2; �� = 16

3) �� ( 9; 3)

3= �� −9; �� =( 3) ⋅ ( 9) ; �� = 27

4) �� ( 2;1)

1= �� −2; �� =1 ⋅ ( 2); �� = 2

https://shkola.in.ua/3296-hdz-alhebra-8-klas-tarasenkova.html

1) ��(0,5; 10)

https://shkola.in.ua/3296-hdz-alhebra-8-klas-tarasenkova.html

�� = ��⋅��; �� =0,5 ⋅ ( 10); �� = 5.

2) �� (0,1; 100) �� = ��⋅��; �� =0,1 ⋅ 100; �� = 10.

3) �� ( 6;0,05)

4) �� (1,5;0,02)

= ��⋅��; �� =1,5 ⋅ 0,02; �� =0,03.

5) �� 2 5 ; 15�

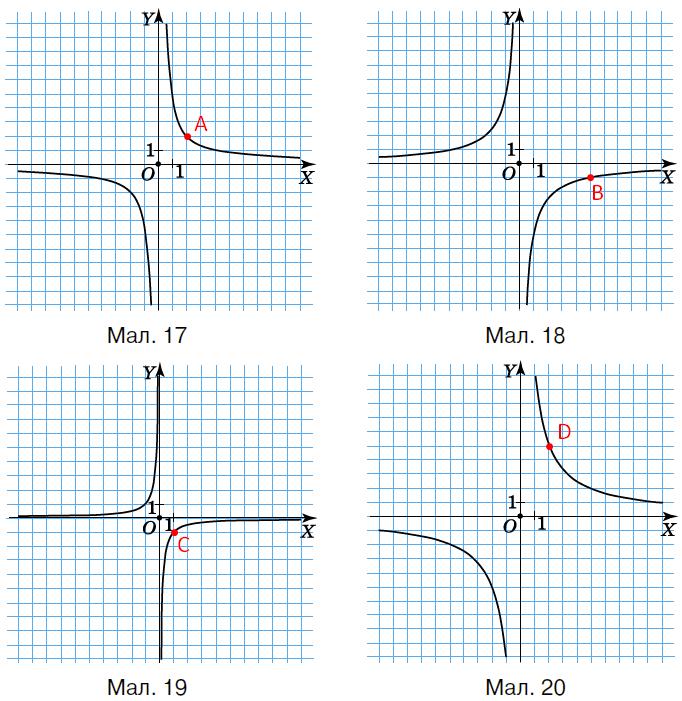
https://shkola.in.ua/3296-hdz-alhebra-8-klas-tarasenkova.html

Мал. 17. Точка ��(2;2)

�� = ��⋅��; �� =2 ⋅ 2; �� =4.

Мал. 18. Точка �� (1; 5)

�� = ��⋅��; �� =1 ⋅ ( 5); �� = 5.

Мал. 19. Точка �� (1; 1)

�� = ��⋅��; �� =1 ⋅ (−1); �� = −1.

Мал. 20. Точка �� (2;5) �� = ��⋅��; �� =2 ⋅ 5; �� = 10.

449. На

7)

https://shkola.in.ua/3296-hdz-alhebra-8-klas-tarasenkova.html

(3,5)> �� (4)

4) �� = 5 і �� = 3; 5< 3. Оскільки

https://shkola.in.ua/3296-hdz-alhebra-8-klas-tarasenkova.html

(

��( 10)> ��( 1)

�� = −5

��( 5)= 1 −5 = 1 5

�� =5

(5)= 1 5 . ��( 5)> ��(5)

https://shkola.in.ua/3296-hdz-alhebra-8-klas-tarasenkova.html

�� = 12

��( 12)= 1 −12 = 1 12 .

(5)= 1 5 .

( 12)> ��(5)

https://shkola.in.ua/3296-hdz-alhebra-8-klas-tarasenkova.html

1 2 3 6

https://shkola.in.ua/3296-hdz-alhebra-8-klas-tarasenkova.html

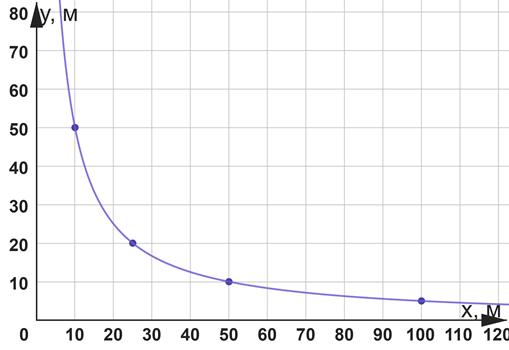
= 500 м2 ; Довжина — �� м;

1) Якщо �� = 50 м, то �� = 500: 50 = 10 (м)

Якщо �� = 25 м, то �� = 500: 25 = 20 (м)

2) Якщо �� = 10 м, то �� = 500: 10 = 50 (м)

Якщо �� = 20 м, то �� = 500: 20 = 25 (м)

x 10 25 50 100 y 50 20 10 5

https://shkola.in.ua/3296-hdz-alhebra-8-klas-tarasenkova.html

Якщо �� =0: �� =02 =0 Якщо �� =6: �� =62 = 36 Якщо �� =8: �� =82 = 64

точку:

(4;2); 2) ��( 2;4); 3) �� (4; 16); 4) �� (0;4); 5) �� (10; 100); 6) �� ( 8; 16); 7) �� (0;0); 8) �� ( 1;1)?

1) ��(4;2) �� = �� 2 ;2=42 ;2= 16 →

2) �� ( 2;4) �� = �� 2 ;4=( 2)2 ;4=4 → Правильно

Графік проходить через точку �� .

3) �� (4; 16) �� = �� 2 ; 16 =42 ; 16 = 16 →

Графік проходить через точку �� .

https://shkola.in.ua/3296-hdz-alhebra-8-klas-tarasenkova.html

4) �� (4;8) �� = �� 2 ;8=42 ;8= 16 → Неправильно Графік не проходить через точку �� .

474. Які з точок ��(3;9) , �� ( 3; 9) , �� (9; 3) , �� (9;3) , �� ( 5; 25) , �� (5; 10) , �� (7; 49) , �� (6; 36) належать графіку функції �� = �� 2 ?

��(3;9) �� = �� 2 ;9=32 ;9=9 → Належить

�� ( 3; 9) �� = �� 2 ; 9=( 3)2 ; 9=9 → Не належить �� (9; 3) �� = �� 2 ; 3=92 ; 3= 81 → Не належить �� (9;3) �� = �� 2 ;3=92 ;3= 81 → Не належить �� ( 5; 25) �� = �� 2 ; 25 =( 5)2 ; 25 = 25 → Належить ��(5; 10) �� = �� 2 ; 10 =52 ; 10 = 25 → Не

�� (7; 49) �� = �� 2 ; 49 =72 ; 49 = 49 → Належить

(6; −36) �� = �� 2 ; −36 =62 ; −36 = 36 →

(8; 64); 4) �� ( 2;6); 6) ��( 10; 10)?

��(1; 10)

https://shkola.in.ua/3296-hdz-alhebra-8-klas-tarasenkova.html

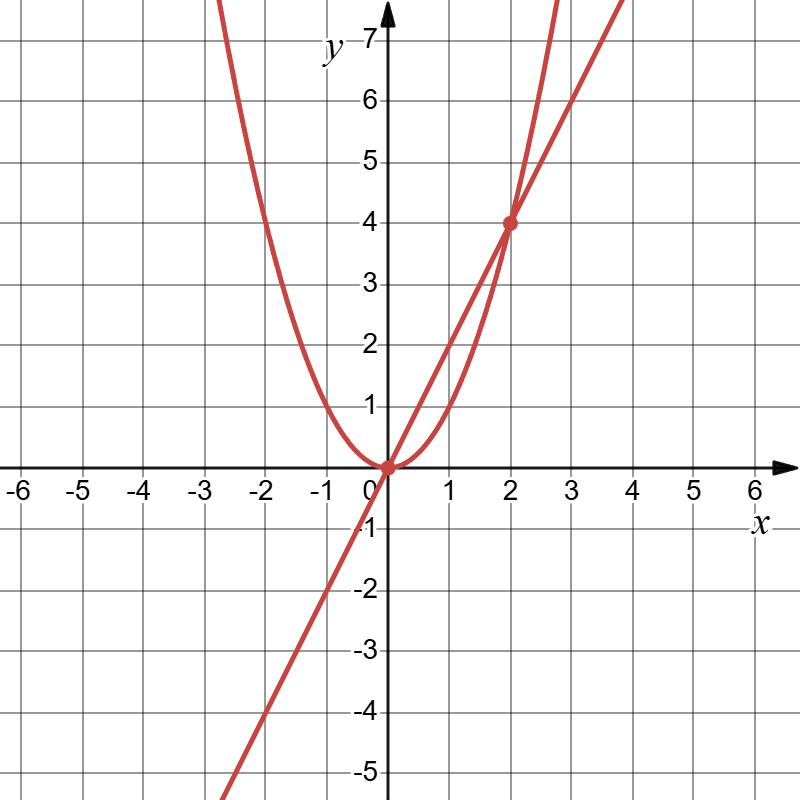
4) �� = �� 2 i �� =3�� x 0 1 y 0 3

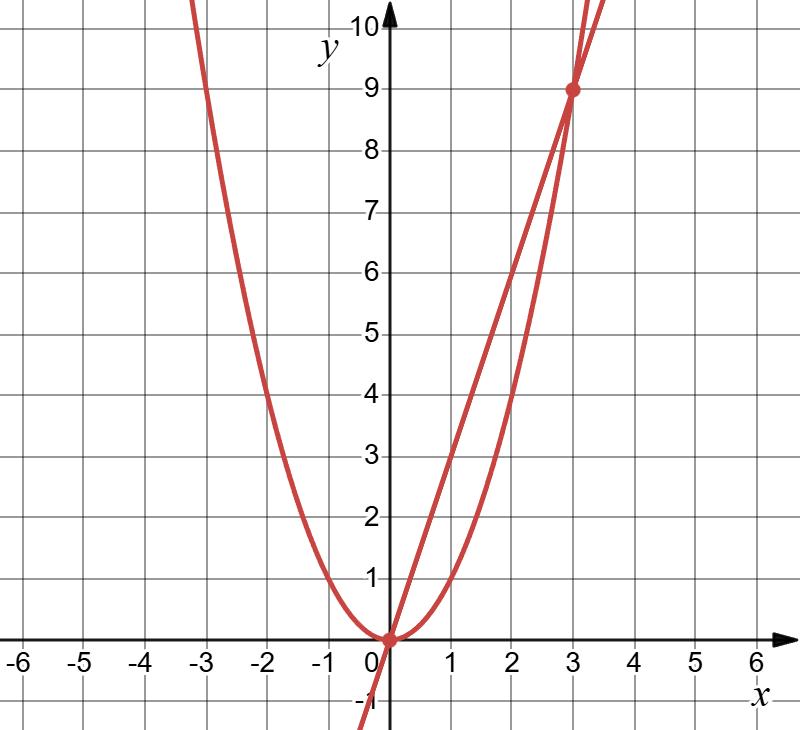
Точки перетину: (0;0) i (3;9)

482. Розв’яжіть

1) �� =4�� ; �� = �� 2 ; �� =4�� . x 0 1 y 0 4

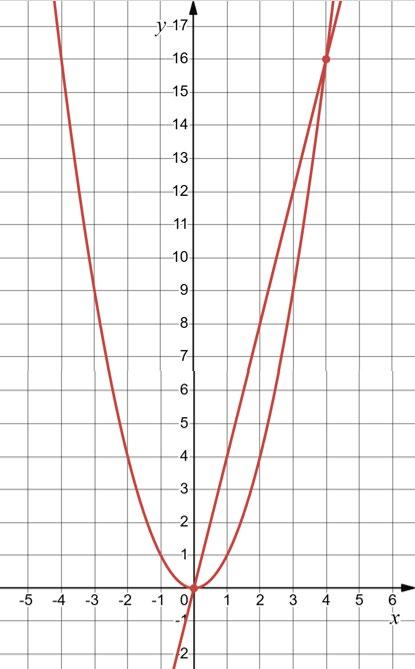
(0; 0) i (4; 16).

Відповідь: не має розв'язків.

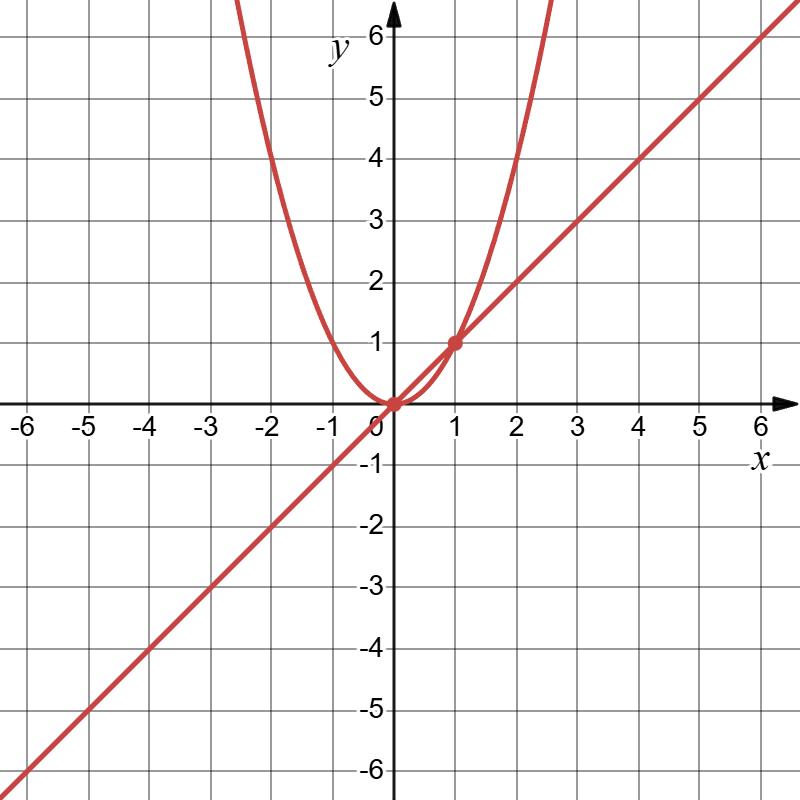
485. Розв’яжіть графічно рівняння: 1) �� 2 =1 �� = �� 2 і �� =1.

1 і 1.

https://shkola.in.ua/3296-hdz-alhebra-8-klas-tarasenkova.html

2,7>2; отже, (2,7)2 >22 ⇒ y(2,7)>y(2)

4) �� =0,7 і �� =1,2.

Обидва аргументи >0

0,7<1,2; отже, (0,7)2 <(1,2)2 ⇒ y(0,7)<y(1,2)

5) �� = 4 і �� = 2.

<0

4< 2; отже, ( 4)2 >( 2)2 ⇒ y( 4)>y( 2)

6) �� = 3 і �� = 6. Обидва

<0.

3> −6;

(−3)2 <(−6)2 ⇒ y(−3)<y(−6) 7) �� = −2,4 і �� = −2.

2,4< 2; отже, ( 2,4)2 >( 2)2 ⇒ y( 2,4)>y( 2)

8) �� = 10 і �� = 8.

Обидва

<0.

10 < 8; отже, ( 10)2 >( 8)2 ⇒ y( 10)>y( 8) 489. Порівняйте значення функції

1) �� =9 і �� = 15.

>0.

9< 15; отже, 92 < 152 ⇒ y(9)<y(15) 2) �� = 32 і �� = 64.

https://shkola.in.ua/3296-hdz-alhebra-8-klas-tarasenkova.html

4) �� = 2�� 3 +6�� 2 2��+6 = �� 2 (2��+6) 2��+6 = �� 2 ; 2�� +6=0; 2�� = 6; �� = 3.

1) �� = �0, якщо ��≤ 0, �� 2 , якщо �� >0;

https://shkola.in.ua/3296-hdz-alhebra-8-klas-tarasenkova.html

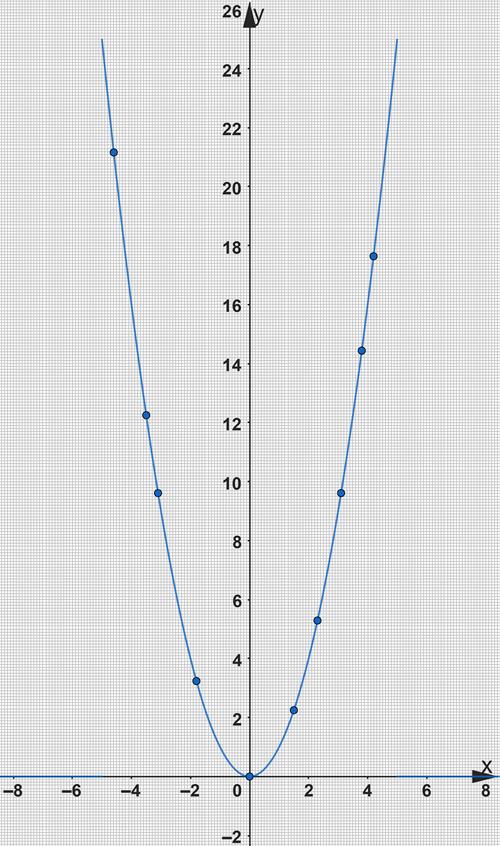
21,1 -4 16

≈12,25 -3,1 ≈9,6 -3 9 -2 4 -1,8 ≈3,2 -1 1 0 0 1 1 1,5 ≈2,25 2 4 2,3 ≈5,3 3 9 3,1 ≈9,6 3,8 ≈14,4 4 16 4,2 ≈17,6 5 25

https://shkola.in.ua/3296-hdz-alhebra-8-klas-tarasenkova.html

4) 0 є квадратним

02 =0.

Правильно, бо квадрат числа 0 дорівнює 0.

499. Чи правильно, що:

1) 2 є арифметичним

2 — від'ємне.

Отже, 2 не може бути арифметичним квадратним

2) 2 є арифметичним квадратним

2 —

22 =4.

Отже, 2 є

3) 5 є

6) √��

Підкореневий вираз: �� .

1) √4 = 2

√4 — це

2 ≠−2

2) √9 =3

3 — невід'ємне число.

32 =9.

Правильно.

3) √36 =6

6 — невід'ємне число.

62 = 36. Правильно.

4) √64 = 8

√64 =8

8 ≠−8 Неправильно.

1) √3 < √5

2) √7 < √2

https://shkola.in.ua/3296-hdz-alhebra-8-klas-tarasenkova.html

Отже, √7 < √2 — неправильно.

3) √6 < √5

Порівнюємо підкореневі вирази: 6 і 5.

Оскільки 6>5, то √6 > √5.

Отже, √6 < √5 — неправильно.

4) √10 > √11

Порівнюємо підкореневі вирази: 10 і 11.

Оскільки 10 < 11, то √10 < √11.

Отже, √10 > √11 — неправильно.

503. Чи правильно, що для �� >0:

1) √�� <0

Оскільки �� >0, то √�� — додатне число,

<0 — неправильно.

2) √�� =0

Це можливо,

https://shkola.in.ua/3296-hdz-alhebra-8-klas-tarasenkova.html

2) Значення виразу √�� 3

Правильно.

3)

4) Значення виразу √�� 3 існує, якщо ��

Корінь

2)

Неправильно.

3) (√�� )2 = ��

Правильно.

4) √�� = �� 2

Правильно

Неправильно.

507.

https://shkola.in.ua/3296-hdz-alhebra-8-klas-tarasenkova.html

Неправильно.

4) √�� = �� 2

1) 16

42 = 16

( 4)2 = 16

https://shkola.in.ua/3296-hdz-alhebra-8-klas-tarasenkova.html

Корені: 4 і 4. 2) 25 52 = 25 ( 5)2 = 25

Корені: 5 і 5.

5) 169

132 = 169 ( 13)2 = 169

Корені: 13 і 13. 6) 196 142 = 196 ( 14)2 = 196

9) 0,16

0,42 =0,16 ( 0,4)2 =0,16

3) 49 72 = 49 ( 7)2 = 49

Корені: 7 і 7. 4) 121 112 = 121 ( 11)2 = 121 Корені: 11 і 11.

Корені: 14 і 14. 7) 256 162 = 256 ( 16)2 = 256

Корені: 0,4 і 0,4. 10) 0,25

0,52 =0,25 ( 0,5)2 =0,25

Корені: 16 і 16. 8) 400 202 = 400 ( 20)2 = 400 Корені: 20 і 20.

Корені: 0,5 і 0,5. 11) 0,49

0,72 =0,49 ( 0,7)2 =0,49

Корені: 0,7 і 0,7. 12) 1,21 1,12 =1,21 ( 1,1)2 =1,21 Корені: 1,1 і 1,1.

13) 1,69

1,32 =1,69 ( 1,3)2 =1,69

Корені: 1,3 і 1,3. 14) 1,96 1,42 =1,96 ( 1,4)2 =1,96

1,4 і 1,4. 15) 2,56 1,62 =2,56 ( 1,6)2 =2,56

1,6 і 1,6. 16) 0,04 0,22 =0,04 ( 0,2)2 =0,04 Корені: 0,2 і

1)

2) √5 Підкореневий вираз: 5. 5>0. Має

3) √0 Підкореневий

4)

2

5) √52

Підкореневий

6) � 3+ √3

https://shkola.in.ua/3296-hdz-alhebra-8-klas-tarasenkova.html

Оскільки √3 <3, то √3 3<0

Не має змісту.

7) 5 √−4

У знаменнику корінь √ 4

Підкореневий вираз: 4 4<0

Не має змісту (знаменник містить

8) 1 √6

У знаменнику корінь √6.

Підкореневий вираз: 6.

6>0, тому √6 має зміст і √6 ≠ 0

515. Чи є правильним твердження:

1) якщо 22 =4, то √4 =2

4 =2, бо 2 —

і 22 =4. Правильно.

2) якщо ( 2)2 =4, то √4 = 2 Арифметичний корінь не може

3) якщо (−5)2 = 25, то √25 =5

25 =5, бо 5 — невід'ємне і 52 = 25. Той факт,

516.

https://shkola.in.ua/3296-hdz-alhebra-8-klas-tarasenkova.html

10) √62 <8. 11) 6< √39. 12) √12 <4. 524. Порівняйте числа: 1) √6 <0

2) 0< √0,01. 3) −5< √26. 4) √35 > √37. 5) √74 <9. 6) 6< √38. 7) 6> √33. 8) √101 > 10. 9) √101 < √99

Чи є правильною рівність: 1) (√8)2 = 16 За тотожністю, (√8)2 =8. 8 ≠ 16.

Неправильно.

2) (√5)2 =5 За тотожністю, (√5)2 =5 Правильно.

3) (√10)2 = 10 За тотожністю, (√10)2 = 10. 10 ≠−10. Неправильно. 4) (√9)2 =3

обчислюємо корінь: √9 =3.

(√9)2 =32 =9.

за тотожністю: (√9)2 =9. 9 ≠ 3. Неправильно.

526. Обчисліть:

таблицею: 862 = 7396)

1000 =0,086.

8) √0,0000729 = � 729 10000000 .

Або:

таблицею: 272 = 729)

⋅ 0,001 =0,027 9) �0,005625 = � 5625 1000000 = √5625 √1000000.

таблицею: 752 = 5625)

1000 =0,075.

4) 3√2 і √18

5√2 >7. 6) 2√3 і

5√2 >7.

2) 4√5 і 9

4 < √6 < √9, тобто 2< √6 <3 Для √6: 3< √6 < 2.

Відповідь: -3 і -2.

3) √5

4 < √5 < √9, тобто 2< √5 <3.

2 і 3.

4) √10

Спочатку

5) √14 Оскільки 32 =9 і 42 = 16, то 9< 14 < 16.

4<7<9.

2< √7 <3 Для √7: 3< √7 < 2.

Відповідь: -3 і -2.

3) √15

32 =9 і 42 = 16.

9< 15 < 16.

9 < √15 < √16, тобто 3< √15 <4.

3 і 4. 4) √23

42 = 16 і 52 = 25. 16 < 23 < 25. √16 < √23 < √25, тобто 4< √23 <5 Відповідь: 4 і 5. 5) 3√6

.

< 54 < 64, тобто 7<3√6 <8.

3√

2 і 3.

8) 5√0,1 Вносимо

https://shkola.in.ua/3296-hdz-alhebra-8-klas-tarasenkova.html

(√2)2 +2√2√3 +(√3)2 +(√2)2 2√2√3 +(√3)2 = =2+2√6 +3+2 2√6 +3 =(2+3+2+3)+(2√6 − 2√6)= 10 +0= 10.

1,2 =

10 = √30 5 =0,2√30 0,2√30 + √3 0,2√30 = √3. 8) 2 5+2√6 + 2 5−2√6

2(5−2√6)+2(5+2√6) (5+2√6)(5−2√6) = 10−4√6+10+4√6 52 (2√6)2 20 25−24 = 20. 9) √5+1 √15 − 1 √3 √5+1 √15 1⋅√5 √3 √5 = √5+1−√5 √15

1 8+2√7 + 1 8−2√7 8−2√7+8+2√7 (8+2√7)(8−2√7) = 16 82 (2√7)2 16

1) √24 √3 2√2−1

√3⋅2√2 √3⋅1 2√2−1 = √3(2√2−1) 2√2−1 = √3.

√8+√6

2)

√3+2

√4⋅2+√6

√2+3√3 + 5 √2−3√3

5(√2−3√3)+5(√2+3√3) (√2+3√3)(√2−3√3)

https://shkola.in.ua/3296-hdz-alhebra-8-klas-tarasenkova.html

2) Чи правильно, що

Множина планет Сонячної системи: {Меркурій, Венера,Земля

3)

https://shkola.in.ua/3296-hdz-alhebra-8-klas-tarasenkova.html

583.

Припустимо, що до моєї родини входять: Мама, Тато, Я, Сестра та Бабуся.

Множина �� (члени родини): �� ={Мама, Тато, Я, Сестра, Бабуся}

Приклади підмножин множини ��:

Множина жінок у родині (підмножина �� ): �� ={Мама, Сестра, Бабуся} ��⊂��

Множина дорослих членів родини (підмножина �� , якщо мені 13 років, а сестрі 10): �� ={Мама, Тато, Бабуся} ��⊂��

Множина дітей у родині (підмножина �� ): �� ={

1)

2) �� ={2;4;6}

Множина �� ={3; 30}

Перевіряємо

1) �� ={10; 20; 30}

Кількість

0 елементів: ∅

1 елемент: {10},{20},{30}

2 елементи: {10; 20},{10; 30},{20; 30}

3 елементи: {10; 20; 30}

Усі підмножини: ∅,{10},{20},{30},{10; 20},{10; 30},{20; 30},{10; 20; 30}

2) �� ={100; 1000; 10000}

Кількість елементів: �� =3

∅

1 елемент: {100},{1000},{10000}

2 елементи: {100; 1000},{100; 10000},{1000; 10000}

3 елементи: {100; 1000; 10000}

Усі підмножини: ∅,{100},{1000},{10000},{100; 1000},{100; 10000},{1000; 10000},{100; 1000; 10000}

3) �� ={−2; −1;0;1;2}

Кількість елементів: �� =5. Кількість підмножин: 25 = 32. Підмножини, що містять:

https://shkola.in.ua/3296-hdz-alhebra-8-klas-tarasenkova.html

0

1

∅

елемент: { 2},{ 1},{0},{1},{2}

2 елементи: { 2; 1},{ 2;0},{ 2;1},{ 2;2},{ 1;0},{ 1;1},{ 1;2},{0;1},{0;2},{1;2}

3

елементи: 2; 1;0, 2; 1;1, 2; 1;2, 2;0;1, 2;0;2, 2;1;2, 1;0;1, { 1;0;2},{ 1;1;2},{0;1;2}

4 елементи: {−2; −1;0;1},{−2; −1;0;2},{−2; −1;1;2},{−2;0;1;2},{−1;0;1;2}

5 елементів: {−2; −1;0;1;2}

Усі підмножини: ∅, 2, 1,0,1,2, 2; 1, 2;0, 2;1, 2;2, 1;0, −1;1, −1;2,0;1,0;2,1;2, −2; −1;0, −2; −1;1, −2; −1;2, 2;0;1, 2;0;2, 2;1;2, 1;0;1, 1;0;2, 1;1;2,0;1;2, { 2; 1;0;1},{ 2; 1;0;2},{ 2; 1;1;2},{ 2;0;1;2},{ 1;0;1;2},{ 2; 1;0;1;2}

4) �� ={▫;•;⋄}

Кількість елементів: �� =3. Кількість підмножин: 23 =8. Підмножини, що містять:

0

1

елементів: ∅

елемент: {▫},{•},{⋄}

2 елементи: {▫;•},{▫;⋄},{•;⋄}

3

підмножини: ∅,{▫},{•},{⋄

https://shkola.in.ua/3296-hdz-alhebra-8-klas-tarasenkova.html

6) 34

7) 100,1

8) 99

9) 9,010101

10) 0,445566445566

1)

2) 2,2222 …

Повторюється

3) 1,554444 …

4) 0,4235235235

2,(8)=2,888888

2) 19,(3)

3) 1,3(25)

https://shkola.in.ua/3296-hdz-alhebra-8-klas-tarasenkova.html

4) 5,9(87)

Число, записане як 5,9(87), має передперіод 9

5,9(87)=5,987878787 …

5) 21,88(9)

Число, записане як 21,88(9), має передперіод 88

21,88(9)= 21,88999999 …

6) 4,5(0)

Число, записане як 4,5(0), має

4,5(0)=4,500000 …

7) 21,(0)

Число,

21,(0)= 21,000000 …

8) 5,101(12)

Число,

5,101(12)=5,10112121212 …

590. Запишіть

1) 3,(4)

Число,

3,(4)=3,444444 …

2) 5,5(12)

Число,

5,5(12)=5,512121212

3) 7,54(0)

Число,

4) 6,(0) Число,

1) 1 2 =0,5=0,5(0) Період

2) 3 8 =0,375 =0,375(0)

Період дробу: 0.

3) 5 6 =0,8333 …=0,8(3)

Період дробу: 3.

4) 1 13 =0,076923076923 …=0,(076923)

Період дробу: 076923

5) 5 11 = 0,454545 …= 0,(45)

Період дробу: 45.

6) −1 2 7 = − 1⋅7+2 7 = − 9 7 = −1,285714285714 …= −1,(285714)

Період дробу: 285714.

1) 1 3 =0,3333 …=0,(3)

Період дробу: 3.

2) 2 5 =0,4000 …=0,4(0)

Період дробу: 0. 3) 7 9 =0,7777

4) − 2 7 —

https://shkola.in.ua/3296-hdz-alhebra-8-klas-tarasenkova.html

5) 11 — раціональне число;

Число 11 є цілим, отже, його

правильно.

6) 5 — ціле число;

Число 5 належить множині цілих чисел (ℤ).

7) 2,4444 … — ірраціональне число;

Число 2,4444 …=2,(4) є нескінченним

раціональне, а не ірраціональне. Ні, неправильно.

8) 1,55555 … — дійсне число;

Число 1,55555 …=1,(5) є раціональним,

чисел (ℝ). Так, правильно.

9) √7 — раціональне число;

10) �� — ціле число;

594.

https://shkola.in.ua/3296-hdz-alhebra-8-klas-tarasenkova.html

3) √5 — раціональне число; √5 є

4) 1 5 — ірраціональне число? Число 1 5 = 0,2

, неправильно.

595. Чи є правильним твердження:

1) 5 ∈ℕ (натуральні числа);

5 є натуральним числом. Так, правильно.

2) 5 ∈ℤ (цілі числа);

5 є цілим числом. Так, правильно.

3) 5 ∈ℚ (раціональні числа);

5= 5 1, отже, воно раціональне. Так, правильно.

4) 5 ∈�� (ірраціональні числа);

5 є раціональним числом, отже, не є ірраціональним. Ні, неправильно.

5) 5 ∈ℝ (дійсні числа);

5 є раціональним числом, отже, воно дійсне. Так, правильно.

6) −5 ∈ℕ (натуральні числа);

включає лише додатні цілі числа. Ні, неправильно.

7) 5 ∈ℤ (цілі числа);

5 є цілим від'ємним числом. Так, правильно. 8) 5 ∈ℚ (раціональні числа);

5= −5 1 , отже, воно раціональне.

https://shkola.in.ua/3296-hdz-alhebra-8-klas-tarasenkova.html

5 =0,2 не є цілим числом. Ні, неправильно.

13) 1 5 ∈ℚ (раціональні числа); 1 5 є звичайним дробом. Так, правильно.

14) 1 5 ∈�� (ірраціональні числа); 1 5 є раціональним числом, отже, не є ірраціональним. Ні, неправильно.

15) 1 5 ∈ℝ (дійсні числа);

Так, правильно.

16) √5 ∈ℕ (натуральні числа);

√5 ≈ 2,236 , це не ціле число. Ні,

17) √5 ∈ℤ (цілі числа);

√5 не є цілим числом. Ні, неправильно.

18) √5 ∈ℚ (раціональні числа);

√5 — це нескінченний неперіодичний десятковий

отже, не є раціональним. Ні, неправильно.

19) √5 ∈�� (ірраціональні числа);

√5 є нескінченним неперіодичним

20) √5 ∈ℝ (дійсні

https://shkola.in.ua/3296-hdz-alhebra-8-klas-tarasenkova.html

(ℝ). Так, правильно.

6) √16 ∈ℕ

Обчислимо: √16 = 4. Число 4 є

чисел (ℕ). Ні, неправильно.

597. Серед чисел −0,(4),1, − 9 3 ,0, − 1 2 ,4, − 3 5 ,1,0333 …,9, √6, −√6 оберіть числа:

Натуральні (ℕ): Це додатні цілі числа. 1,4,9

Цілі (ℤ): Це натуральні числа, число 0 та від'ємні цілі числа.

1, 9 3 →−3,0,4,9

Тобто: 3,0,1,4,9

Раціональні (ℚ): Це числа, які

скінченні

0,(4),1, 9 3 →−3,0, 1 2 ,4, 3 5 ,1,0333 …,9

Тобто: 0,(4),1, 3,0, 0,5,4, 0,6,1,0(3),9

Ірраціональні (��): Це числа, які

−3,(9) →−4,0, √25 → 5, −5,22

5, 4,0,2,5,22

12 6 , 3,(9),0, √25,7,8888 …, 5, 1 3 , 22

Тобто: 2, 4,0,5,7,(8), 5, 0,(3),22

https://shkola.in.ua/3296-hdz-alhebra-8-klas-tarasenkova.html

( �� ): Це

√2, √8, √17 2

Дійсні (ℝ): Це всі раціональні та ірраціональні числа разом.

12 6 , 3,(9),0, √25,7,8888 …, 5, √2, 1 3 , √8, 22, √17 2

Тобто: 2, 4,0,5,7,(8), 5, √2, 0,(3), √8, 22, √17 2 599. Наведіть приклад числа, яке:

1) Приклад числа, яке є дійсним, але не є раціональним:

Число, яке є дійсним, але не раціональним, має бути ірраціональним.

Приклад: √3 (Інші приклади: �� , √10, �� )

2) Приклад числа, яке є раціональним, але не є цілим:

Число, яке є раціональним, але не цілим,

скінченний чи нескінченний періодичний

числа, яке є від'ємним ірраціональним:

яке є

602. Порівняйте числа:

1) 4,105 <5,01

2) 3,056 >3,05555

3,056 >3,0(5)

3) 5,1412 <5,141414

5,1412 <5,(14)

4) 3,056 <3,06666 …

3,056 <3,0(6)

5) 9,(9)=9+0,(9)=9+1= 10.

10 =9,(9)

6) 4,34444 …<4,43333 …

4,3(4)<4,4(3)

7) 0,0(5)<1,00(5)

8) 3,056 >3,05555

3,056 >3,0(5)

603. Порівняйте числа:

1) 15 < 15,(1)

2) 5,342 >5,333 …

5,342 >5,(3)

3) 0,165000 …<0,165555 …

0,165 <0,16(5)

4) 2,999 …>2,(10)

604. Чи

https://shkola.in.ua/3296-hdz-alhebra-8-klas-tarasenkova.html

1) �� ={1; √2;3}; 1 ∉��⇒��⊄��

2) �� ={√3}; ��⊂��

3) �� ={��∣��− раціональне число}; ℚ⊄��

4) �� ={��∣��− дійсне число}; ℝ⊄��

606. Чи є правильним твердження:

1) ℕ⊂�� — Ні, неправильно.

2) ��⊂ℚ — Ні, неправильно.

3) ℚ⊂ℤ — Ні, неправильно.

4) ℚ⊂ℝ — Так, правильно.

5) ℝ⊂�� — Ні, неправильно.

6) ℚ⊂�� — Ні, неправильно.

607. Дано множини: �� ={ 5; 4; 3; 2; 1;0} , �� ={0;1;2;3;4;5} , �� ={ 4; 2;4} , �� ={0}. Запишіть множину:

1) Множина �� , для якої ��⊂�� і ��⊂�� .

4;

2} 2) Множина �� , для якої ��⊂�� і ��⊂�� .

={ 5; 4; 3; 2; 1;0;1;2;3;4;5}

={ 5; 4; 3; 2; 1;0;1;2;3;4;5} 608. Порівняйте числа:

4) 0,(6) і 3 5

0,(6)= 6 9

https://shkola.in.ua/3296-hdz-alhebra-8-klas-tarasenkova.html

613.

4) Множина �� (порожня множина):

614. На парті лежать

множини предметів на парті. �� ={щоденник,підручник,зошит,ручка}.

Підмножини: {щоденник},{підручник},{зошит},{ручка},

щоденник,підручник},{щоденник,зошит},{

1)

https://shkola.in.ua/3296-hdz-alhebra-8-klas-tarasenkova.html

1

1) �� = 10. ( 10)+8= 10 +8= 18 >0. Так.

2) �� = 6. ( 6)+8=6+8= 14 >0. Так.

3) �� = 1,2. ( 1,2)+8=1,2+8=9,2>0. Так.

4) �� =0. −0+8=8>0. Так.

5) �� =1. 1+8=7>0. Так.

6) �� =8. 8+8=0. Ні.

7) �� = 10. 10 +8= 2<0. Ні.

8) �� = 20. 20 +8= 12 <0. Ні.

624.

1 √��+3

1) �� = 5. �� +3= 5+3= 2<0. Ні.

2) �� = 3. �� +3= 3+3=0. Ні.

3) �� =0. �� +3=0+3=3>0. Так.

4) �� =3. �� +3=3+3=6>0. Так.

5) �� = 10. �� +3= 10 +3= 13 >0. Так.

6) ��

https://shkola.in.ua/3296-hdz-alhebra-8-klas-tarasenkova.html

√��

4) √��− 2 9=0; √��− 2 =9;

2=92 ;

2= 81; �� = 81 +2;

= 83 5) √��− 12 =7; ��− 12 =72 ;

7) √�� +3 +4=0;

+3 = 4;

8) 3√�� + 9 = 0;

√�� = 9;

= 9:3;

= −3;

2 ; �� = 9

√�� + 21 = −3;

9) −2√�� + 9 + 6 = 0; 2√�� + 15 =0; 2√�� = 15;

√�� = 15;

= 15:2;

=7,5;

=7,52 ;

= 56,25

1) √�� =5;

=52 ;

= 25

https://shkola.in.ua/3296-hdz-alhebra-8-klas-tarasenkova.html

2) √�� − 4=0; √�� =4;

=42 ;

= 16

4) √��− 1 2=0;

1 =2;

1=22 ;

1=4;

=4+1;

=5 5) √�� + 30 = 30;

3) 2√�� +7 =8; √�� +7 =8:2;

+7 =4;

+7=42 ;

+7= 16;

= 16 7;

=9

https://shkola.in.ua/3296-hdz-alhebra-8-klas-tarasenkova.html

10 =0;

�� = 10

4) (�� + 12)2 36 =0;

(�� + 12)2 = 36;

�� + 12 = √36 або �� + 12 = √36;

�� + 12 =6 або �� + 12 = 6;

�� =6 − 12 або �� = −6 − 12;

�� = 6 або �� = 18

5) (�� +9)2 81 =0; (�� +9)2 = 81;

�� +9= √81 або �� +9= √81;

�� +9=9 або �� +9= 9;

�� =9 9 або �� = 9 9;

�� =0 або �� = 18

6) (��− 9)2 − 3=0; (��− 9)2 =3;

��− 9= √3 або ��− 9= √3;

�� =9+ √3 або �� =9 √3

7) (�� +5)2 5=0; (�� +5)2 =5;

�� +5= √5 або �� +5= √5;

�� = 5+ √5 або �� = 5 √5

8) (��− 10)2 + 320 =0; (��− 10)2 = −320

коренів немає

9) (�� +8)2 +8=0;

(�� +8)2 = 8

коренів немає

10) (��− 10)2 10 =0.

(��− 10)2 = 10; (��− 10)2 = −10

https://shkola.in.ua/3296-hdz-alhebra-8-klas-tarasenkova.html

666. Розв'яжіть рівняння:

1) (�� +2)2 =4;

�� +2= √4 або �� +2= √4;

�� +2=2 або �� +2= 2;

�� =2 2 або �� = 2 2;

�� =0 або �� = 4

2) (��− 9)2 = 100;

��− 9= √100 або ��− 9= √100;

��− 9= 10 або ��− 9= 10;

�� = 10 +9 або �� = 10 +9;

�� = 19 або �� = 1

3) (��− 25)2 =0;

��− 25 =0;

�� = 25

4) (�� +4)2 3=0; (�� +4)2 =3;

�� +4= √3 або �� +4= √3;

�� = 4+ √3 або �� = 4 √3

5) (��− 7)2 11 =0; (��− 7)2 = 11;

��− 7= √11 або ��− 7= √11;

�� =7+ √11 або �� =7 √11

6) (�� +7)2 + 49 =0.

(�� +7)2 = −49;

немає 667. Розв'яжіть рівняння: 1) (2�� +1)(�� +1) 3�� =4�� 2 ;

2�� 2 +2�� + �� +1 − 3�� =4�� 2 ;

2�� 2 +3�� +1 3��− 4�� 2 =0;

2�� 2 +1=0;

668. Розв'яжіть рівняння:

1) (3�� +1)(��− 3)+8�� =2�� 2 ; 3�� 2 9�� + ��− 3+8��− 2�� 2 =0; 3�� 2 2�� 2 9�� + �� +8��− 3=0;

2) (�� +2)(��− 2) 3�� 2 =0; �� 2 − 4 − 3�� 2 =0; 2�� 2 4=0; 2�� 2 =4;

2 = 4 −2 ;

3) (2�� +1)(�� +3)= �� (�� +7); 2�� 2 +6�� + �� +3= �� 2 +7�� ; 2�� 2 +7�� +3 −�� 2 7�� =0;

https://shkola.in.ua/3296-hdz-alhebra-8-klas-tarasenkova.html

5) √�� +3 5√�� +3 +4=0; (1 5)√�� +3 = 4;

4√�� +3 = 4;

√�� +3 = −4 −4 ;

√�� +3 =1;

�� +3=12 ;

�� +3=1; �� =1 3; �� = −2

670. Розв'яжіть рівняння:

1) 3√�� +2√�� = 10;

6) √�� +1 +3√�� +1 =8. (1+3)√�� +1 =8; 4√�� +1 =8; √�� +1 =8:4; √�� +1 =2;

�� +1=22 ; �� +1=4; �� =4 1; �� =3

5√�� = 10; √�� = 10:5; √�� =2; �� =22 ; �� =4 2) √�� 3√�� =6; (1 3)√�� =6; 2√�� =6; √�� =6:(−2); √�� = 3; коренів немає

3) √16�� √25�� =0;

4√�� 5√�� =0; (4 5)√�� =0; √�� =0;

√�� =0;

�� =02 ; �� =0 4) √�� +5 7√�� +5 + 12 =0 (1 7)√�� +5 = 12; 6√�� +5 = 12; √�� +5 = −12 −6 ; √�� +5 =2; �� +5=22 ; �� +5=4; �� =4 5; �� = 1

Turn static files into dynamic content formats.

Create a flipbook