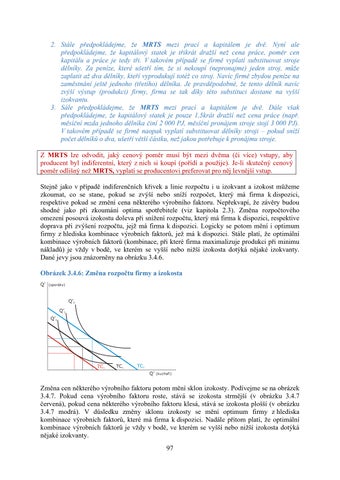
2. Stále předpokládejme, že MRTS mezi prací a kapitálem je dvě. Nyní ale předpokládejme, že kapitálový statek je třikrát dražší než cena práce, poměr cen kapitálu a práce je tedy tři. V takovém případě se firmě vyplatí substituovat stroje dělníky. Za peníze, které ušetří tím, že si nekoupí (nepronajme) jeden stroj, může zaplatit až dva dělníky, kteří vyprodukují totéž co stroj. Navíc firmě zbydou peníze na zaměstnání ještě jednoho (třetího) dělníka. Je pravděpodobné, že tento dělník navíc zvýší výstup (produkci) firmy, firma se tak díky této substituci dostane na vyšší izokvantu. 3. Sále předpokládejme, že MRTS mezi prací a kapitálem je dvě. Dále však předpokládejme, že kapitálový statek je pouze 1,5krát dražší než cena práce (např. měsíční mzda jednoho dělníka činí 2 000 PJ, měsíční pronájem stroje stojí 3 000 PJ). V takovém případě se firmě naopak vyplatí substituovat dělníky stroji – pokud sníží počet dělníků o dva, ušetří větší částku, než jakou potřebuje k pronájmu stroje. Z MRTS lze odvodit, jaký cenový poměr musí být mezi dvěma (či více) vstupy, aby producent byl indiferentní, který z nich si koupí (pořídí a použije). Je-li skutečný cenový poměr odlišný než MRTS, vyplatí se producentovi preferovat pro něj levnější vstup. Stejně jako v případě indiferenčních křivek a linie rozpočtu i u izokvant a izokost můžeme zkoumat, co se stane, pokud se zvýší nebo sníží rozpočet, který má firma k dispozici, respektive pokud se změní cena některého výrobního faktoru. Nepřekvapí, že závěry budou shodné jako při zkoumání optima spotřebitele (viz kapitola 2.3). Změna rozpočtového omezení posouvá izokostu doleva při snížení rozpočtu, který má firma k dispozici, respektive doprava při zvýšení rozpočtu, jejž má firma k dispozici. Logicky se potom mění i optimum firmy z hlediska kombinace výrobních faktorů, jež má k dispozici. Stále platí, že optimální kombinace výrobních faktorů (kombinace, při které firma maximalizuje produkci při minimu nákladů) je vždy v bodě, ve kterém se vyšší nebo nižší izokosta dotýká nějaké izokvanty. Dané jevy jsou znázorněny na obrázku 3.4.6. Obrázek 3.4.6: Změna rozpočtu firmy a izokosta
Změna cen některého výrobního faktoru potom mění sklon izokosty. Podívejme se na obrázek 3.4.7. Pokud cena výrobního faktoru roste, stává se izokosta strmější (v obrázku 3.4.7 červená), pokud cena některého výrobního faktoru klesá, stává se izokosta plošší (v obrázku 3.4.7 modrá). V důsledku změny sklonu izokosty se mění optimum firmy z hlediska kombinace výrobních faktorů, které má firma k dispozici. Nadále přitom platí, že optimální kombinace výrobních faktorů je vždy v bodě, ve kterém se vyšší nebo nižší izokosta dotýká nějaké izokvanty. 97
Obrázek 3.4.7: Změna ceny jednoho vstupu a změna sklonu isokvanty
V levé části obrázku vidíme změnu ceny vstupu Q1. Výchozím stavem je izokosta TC1. V případě, že dojde ke zlevnění vstupu Q1, posune se izokosta vpravo do nové pozice TC2. V opačném případě, tedy když cena vstupu Q1 vzroste, posune se izokosta vlevo do nové pozice TC 3. Protože se cena vstupu Q2 nemění, maximální množství tohoto vstupu, které si firma může pořídit, zůstává vždy stejné. Izokosta tudíž mění při změně ceny vstupu Q1svůj sklon – při růstu ceny je strmější, při poklesu ceny plošší. V pravé části obrázku jsou znázorněny linie rozpočtu při změně ceny vstupu Q2. Výchozím stavem je opět izokosta TC1. V případě, že dojde ke zlevnění vstupu Q2, posune se izokosta nahoru do nové pozice TC2. V opačném případě, tedy když cena vstupu Q´2 vzroste, posune se izokosta dolů do nové pozice TC 3. Maximální množství vstupu Q1, které si firma může pořídit, zůstává vždy stejné, cena vstupu Q1 se nemění. Protože se cena vstupu Q1 nemění, maximální množství tohoto vstupu, které si firma může pořídit, zůstává vždy stejné. Izokosta tudíž mění při změně ceny vstupu Q2 svůj sklon – při růstu ceny je strmější, při poklesu ceny plošší. Při zvýšení svého rozpočtu si firma může dovolit koupit více jednotek všech vstupů, při poklesu příjmů opačně. Graficky lze změnu příjmů vyjádřit posunem izokosty – při růstu příjmů severovýchodně, při poklesu jihozápadně. Mění-li se cena určitého vstupu, může si firma tohoto vstupu koupit více (při poklesu ceny) nebo méně (při růstu ceny). Graficky se změna ceny jednoho vstupu projeví tak, že izokosta mění svůj sklon, při poklesu ceny vstupu je plošší, při růstu ceny strmější. Zdůrazněme na závěr této kapitoly, že v dalším textu budeme předpokládat, že firma usiluje o minimalizaci nákladů. Jednotlivá množství produkce se snaží produkovat s takovou kombinací vstupů, která je pro produkci každého množství nejlevnější. 3.5
Náklady v krátkém a dlouhém období
Jak explicitní, tak implicitní náklady můžeme dělit z řady hledisek. Jedno z nejpodstatnějších je hledisko času, kdy rozlišujeme náklady v krátkém období a v dlouhém období. Krátké období je obecně takové období, pro které platí, že množství některých výrobních faktorů je fixní – nelze je zejména zvýšit a zpravidla ani snížit. V krátkém období můžeme tedy zvýšit produkci jedině tím, že zvýšíme množství pouze jednoho vstupu nebo velmi malého množství vstupů, nemůžeme však zvyšovat množství všech vstupů. 27 Skutečnost, že množství 27
Speciálním příkladem krátkého období je tzv. velmi krátké období, kdy vůbec nelze změnit žádný vstup, a tudíž nelze změnit ani výši produkce (výstupů).
98
některých výrobních faktorů nelze v daném čase zvýšit, případně ani snížit, plyne z objektivní povahy. Např. v případě kapitálových statků (kupř. budov a strojů) trvá nějaký čas, než jsou pořízeny (např. budovy postaveny, stroje nakoupeny). Rovněž tak v případě kapitálových statků není úplně jednoduché se jich zbavit (např. budovu či stroj prodat, vypovědět nájemní smlouvu apod.). V krátkém období může být fixním faktorem i práce – legálně nelze třeba zaměstnance propustit, najít nového (dodatečného) zaměstnance rovněž obvykle trvá nějaký čas. Příklad 3.5-1 Postavit novou automobilku a pořídit do ní stroje atd. nějakou dobu trvá. Po nějakou dobu se nelze těchto budov a strojů ani zbavit, respektive je využít k jiným účelům. Množství určitých vstupů je v krátkém období fixní. Pokud náš pohled poněkud rozšíříme, tak zjistíme, že v krátkém období mohou být fixní i ceny. Firmám se nemusí vyplatit ceny toho, co produkují, měnit – změna pro ně může být příliš nákladná, respektive změny by znesnadňovaly kalkulaci firem z hlediska jejich nákladů, příjmů a zisků. Proto je snaha změnu cen v krátkém období omezovat. Podívejme se na příklad. Příklad 3.5-2 Fixnost cen vstupů a cen výstupů v krátkém období: 1. Firma odebírá určitý vstup za 100 PJ. Pokud by se cena vstupu dramaticky měnila (např. rostla), mohly by se měnit i náklady firmy (např. růst), takže by firma neměla jistotu, zdali dosáhne zisku. Je proto možné, že firma uzavře se svým dodavatelem smlouvu, že po určitý čas se cena, za kterou vstup odebírá, nebude měnit. Případné porušení smlouvy je sankcionováno, takže se dodavateli nevyplatí ceny měnit. 2. Firma prodává určitý statek za 500 PJ. Pokud by firma cenu statku dramaticky měnila, nevěděla by, jak se bude měnit poptávané množství, a tím i celkový příjem firmy. Firma by potom nemusela dosáhnout dostatečného příjmu, aby její zisk byl kladný. Změna cen by přitom mohla poškodit i odběratele firmy. Je proto možné, že firma se svými odběrateli (nebo alespoň s některými z nich) uzavře smlouvu, která stanoví, že jim po určitý čas bude statek dodávat za pevnou cenu. Případné porušení smlouvy je sankcionováno, takže se firmě nevyplatí ceny měnit. Skutečnost, že ceny jsou v krátkém období fixní, vyjadřuje ekonomická teorie pojmem náklady jídelníčku (anglicky menu cost) – pojem vychází z dřívější praxe, kdy pro restaurace bylo nákladné často měnit ceny jídel, protože to znamenalo přepisovat jídelní lístek. V dnešní době (době počítačů a tiskáren) si pod pojmem náklady jídelníčku lze představit náklady na cenovky, tisk nových katalogů apod. Z hlediska fixnosti cen firem uveďme ještě následující: to, co firmy produkují, jsou jednak finální statky, dále kapitálové statky a nejrůznější meziprodukty (např. mouka k pečení chleba). Nemění-li se ceny finálních statků, jsou strnulé ceny výstupů, nemění-li se ceny kapitálových statků a meziproduktů, nemění se ceny vstupů. Pokud většina firem nemění v krátkém období ceny vstupů ani ceny výstupů, nedochází ani ke změně cen na agregátní úrovni. Cenová hladina (souhrn cen na agregátní úrovni) je potom fixní. V dlouhém období zde uvedené fixnosti mizí: 1. Jednak mizí fixnost výrobních faktorů – v dlouhém období bude možno získat dodatečné jednotky výrobního faktoru, případně se zbavit nepotřebných jednotek výrobního faktoru (např. ukončit pronájem nemovitosti, vyřadit stroj). Na základě 99
Ukázka elektronické knihy