Kapitola A: Systémová metodologie matikou a teorií složitosti. Zajímá se o možnosti „aritmetizace logiky“, tj. vyjádření některých logických pojmů, postupů a tvrzení v řeči přirozených čísel a s důsledky této aritmetiky. Jedním z nich jsou například slavné Gödelovy věty o neúplnosti teorie množin. Přinášejí pohledy na podstatu a filozofii matematiky, neboť z ní vyplývá, že sebelepší axiomatika teorie množin bude vždy obsahovat nerozhodnutelná tvrzení (množinu všech matematických pravd nelze popsat žádnou soustavou axiomů) a že pokud teorie, kterou chceme používat k popisu všech matematických pravd, je bezesporná, nelze tuto bezespornost dokázat. ■■ Teorie důkazu – zabývá se vytvářením a zkoumáním různých formálních deduktivních systémů jakožto základů pro pojem formálního důkazu.
E. Matematická logika
Je to formální logika „pěstovaná“ jako matematická disciplína. Abstraktní znaky z formální logiky se v matematické logice převádí na matematické symboly (proto též i symbolová logika) a veličiny. Předmět poznání se zužuje na matematické věty, zabývá se výstavbou matematických teorií, teorií algoritmů, používá se v teorii elektrických obvodů apod. Formální logika je předpokladem vytváření matematických teorií a tím i výpočtového modelování, které z nich vychází.
F. Fuzzy logika
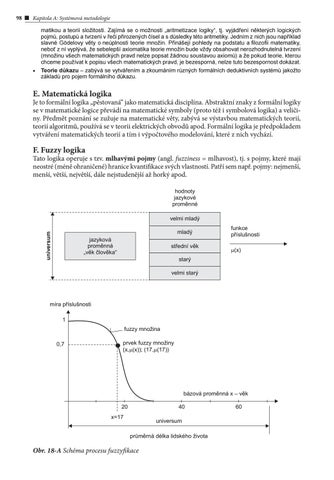
Tato logika operuje s tzv. mlhavými pojmy (angl. fuzziness = mlhavost), tj. s pojmy, které mají neostré (méně ohraničené) hranice kvantifikace svých vlastností. Patří sem např. pojmy: nejmenší, menší, větší, největší, dále nejstudenější až horký apod. hodnoty jazykové proměnné velmi mladý mladý
universum
98
jazyková proměnná „věk člověka“
střední věk
funkce příslušnosti (x)
starý velmi starý
míra příslušnosti 1 fuzzy množina 0,7
prvek fuzzy množiny (x, (x)); (17, (17))
bázová proměnná x – věk 20
40
x=17
60
universum průměrná délka lidského života
Obr. 18-A Schéma procesu fuzzyfikace
Ukázka elektronické knihy, UID: KOS185087