Santrauka
√ 1. Ko reikia, kad suprastumėte funkcijas
√ 1.1. Kam naudojamos funkcijos?
√ 1.2. Kas yra funkcijos?
√ 1.3. Sąsaja tarp funkcijų ir lygčių
√ 1.4. Kas yra funkcijos apibrėžimo ir reikšmių sritys?
√ 2. Kaip rasti tiesinių funkcijų išraiškas?
√ 2.1. Tiesinių funkcijų sankirtos
√ 2.2. Kaip manipuliuoti tiesines funkcijas?
√ 2.3. Skirtingi būdai užrašyti tiesinę funkciją
√ 2.4. Atstumas koordinačių plokštumoje
√ 2.5. Mišrių uždavinių įtvirtinimas
√ 3. Kas yra kvadratinės funkcijos?
√ 3.1. Kvadratinių funkcijų sąsajos su kvadratinėmis lygtimis
√ 3.2. Parabolės viršūnė ir simetrijos ašis
√ 3.3. Kvadratinės funkcijos apibrėžimo ir reikšmių sritys
√ 3.4 Skirtingos kvadratinės funkcijos formos
√ 3.5. Kaip nustatyti kvadratinės funkcijos išraišką?
√ 3.6. Mišrūs skyriaus įtvirtinimo uždaviniai
√ Sprendimai ir atsakymai
Kas yra funkcija?
1.2. Kas yra funkcijos?
Funkcija yra taisyklė, kuri vienam arba keliems apibrėžimo srities aibės elementams (x-ams) priskiria vienintelį elementą kitoje, funkcijos reikšmių, aibėje (kuri, beje, gali sutapti su pirmąja).

1.0 pav. Kaip veikia funkcija
Paprastais žodžiais tariant, funkcija matematikoje yra kaip mašina (1.0 pav.), kuri priima kažkokią įvestį x (angl.input), ką nors su ta įvestimi padaro ir pateikia išvestį y (angl.output). Funkcija yra procesas tarp input ir output –vieno kintamojo priklausomybė nuo kito.
Dažniausiai funkciją išreiškiame raidėmis f(x) (skaitoma f nuo x). Kaip f (visa funkcijos reikšmė) priklauso nuo x (skaičiaus, kurį įrašome į x vietą)? Pavyzdžiui, jei funkcija yra užrašoma kaip f(x) = 2x ir į x vietą įrašome skaičių 1, tai f(1) = 2, arba kitais žodžiais, kai x = 1, funkcija lygi 2. Funkcijos išreiškiamos koordinačių plokštumoje.
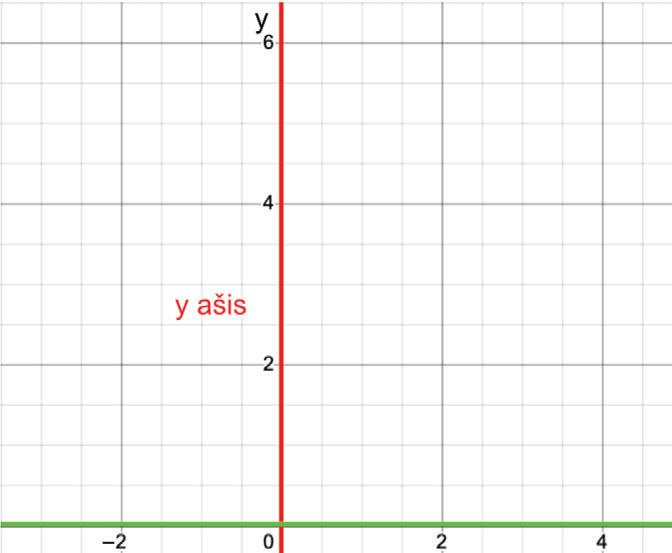
x ašis yra horizontali, o y ašis –vertikali. Taigi, x ašis vadinama abscise, o y ašis – ordinate.

1.1 pav. Koordinačių plokštuma






1.3. Sąsaja tarp funkcijų ir lygčių
Reiškinys, arba simbolių kombinacija, sudaryta pagal matematikoje priimtas taisykles. Reiškiniai gali būti sudaryti iš skaičių, kintamųjų dydžių ir matematinių veiksmų, t. y. dalybos, atimties, sudėties ir daugybos. Kitaip sakant, funkcijos yra būdas perteikti reiškinį koordinačių plokštumoje ir pavaizduoti visas reikšmes, kurias reiškinys gali įgyti su skirtingomis kintamųjų reikšmėmis.
f(x) = 2x + 3.
Jei norėtume sužinoti, kokias reikšmes šis reiškinys gali įgyti, galėtume įrašyti skaičius vietoj x:
2(1) + 3 = 5; 2(1,6) + 3 = 6,2; 2(348) + 3 = 699.
Šį reiškinį taip pat galime pavaizduoti funkcija, kuri pademonstruotų visas įmanomas reiškinio reikšmes vertikalioje y ašyje.
2. Kaip rasti tiesinių funkcijų išraiškas?
22. Užrašykite tiesinių funkcijų išraiškas:







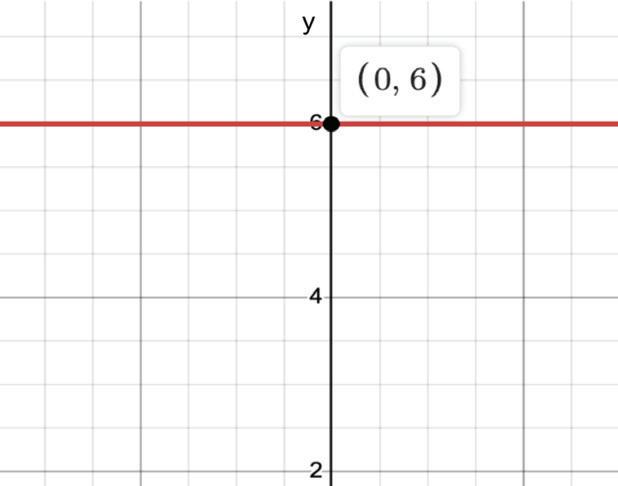

23.Žinome, kad tiesinė funkcija kerta y ašį taške (0, 5) ir eina per tašką (−3, 0). Užrašykite funkcijos išraišką.
24. Žinome, kad tiesinės funkcijos krypties koeficientas yra −3 ir funkcija eina per tašką (−4, 6). Raskite funkcijos b narį.
25. Žinome, kad tiesinė funkcija eina per taškus (3, 7) ir (10, 49). Užrašykite funkcijos išraišką.



3.8 pav. Kvadratinė funkcija





3.9 pav. Kvadratinė funkcija 4 pav. Kvadratinė funkcija a > 0 a < 0 a > 0
Kodėl kvadratinė funkcija taip atrodo?
Kvadratinė funkcija yra (arba )formos, nes bet kuris realusis skaičius pakeltas antruoju laipsniu negali būti neigiamas. Skaičių kėlimas kvadratu priverčia funkcijos ašis atsiverti į tą pačią kryptį. Nesvarbu, ar x vietoje pasirinksime 3 ar −3, gausime tokią pačią y reikšmę. Kvadratinė funkcija yra formos, nes kvadratas panaikina neigiamas reikšmes.
Visos kvadratinės funkcijos turi viršūnę, kuri yra žemiausias arba aukščiausias funkcijos taškas (jei funkcija atsiveria žemyn, tas taškas bus lygus didžiausiai galimai funkcijos reikšmei, o jei funkcija atsiveria aukštyn, viršūnė bus lygi žemiausiai jos reikšmei). Kvadratinės funkcijos atsiveria aukštyn, kai a narys yra teigiamas, nes skaičius ax 2, pakeltas kvadratu, didėja eksponentiškai (įrašydami vis didesnes ir didesnes x reikšmes, gauname neproporcingai didesnes y reikšmes), o skaičius ±bx, padaugintas iš kito skaičiaus, negali keistis eksponentiškai (nes santykis tarp y ir x išlieka b). Dėl to didėjant x reikšmei, anksčiau ar vėliau galimai neigiamos narių bx ir c reikšmės tampa neapsakomai mažos, palyginti su ax 2 Kvadratinės funkcijos atsiveria žemyn, kai a narys yra neigiamas, nes bet koks skaičius −ax 2, pakeltas antruoju laipsniu ir padaugintas iš neigiamo skaičiaus, bus neigiamas ir mažės eksponentiškai. Kai funkcijos argumentas didėja, ax 2 reikšmė didėja labai greitai, palyginti su b ir c nariais (b narys auga pastoviu tempu, o c narys nesikeičia), dėl to funkcija įgyja mažesnes ir mažesnes reikšmes.
Viršūnės x koordinatė taip pat yra simetrijos ašis. Tiek iš kairės, tiek iš dešinės pusės nuo simetrijos ašies kvadratinė funkcija atrodo vienodai.
3.5. Kaip nustatyti kvadratinės funkcijos išraišką?
Kaip nustatyti parabolės išraišką?
Yra daug skirtingų būdų nustatyti parabolės išraišką, tačiau bene lengviausias – perrašyti parabolę į viršūnės formą. Perrašę parabolę į viršūnės formą, galėsime ją užrašyti ir visomis kitomis formomis. Viršūnės forma parodo pačius svarbiausius parabolės bruožus:
± a(x − h)2+ k.
Nors tai gali atrodyti kaip didelis kiekis informacijos, viskas yra gana paprasta. Funkcijos išraiškos paieškos procesą galima išskirstyti į tokius pagrindinius žingsnius:
1. Raskite parabolės viršūnę.
2. Užrašykite funkciją tokia forma f(x) = ±a(x − h)2+ k. (Jei nežinote a nario reikšmės, jums reikia sužinoti dar vieną tašką, per kurį funkcija eina, ir palyginti jį su funkcijos išraiška. Išsprendę lygtį, sužinosite a nario reikšmę.)
3. Jei užduotyje prašoma, galite pertvarkyti funkciją į standartinę: atskliausti skliaustus, padauginti a su skaičiais už skliaustų ir sutraukti panašius narius.
Kiti parabolės išraiškos nustatymo metodai (ką daryti, kai nežinote parabolės viršūnės?)
• Jei žinosite abi x koordinates, kuriose funkcija lygi nuliui (kerta x ašį), ir žinosite a nario reikšmę, galite pasinaudoti sprendinių forma f(x) = a(x − x1)(x − x2) ir sužinoti visą funkcijos išraišką. Jei užduotyje prašoma pateikti funkciją kita forma, galite pertvarkyti sprendinių formą į standartinę arba net viršūnės formą. Nepamirškite, kad parabolės viršūnę galima rasti pritaikius formulę X v = ───. X1 + X2 2
• Nors tai naudosite labai retai, bet vis tiek reikia mokėti rasti parabolės išraišką taikant trigubą lygčių sistemą. Jums bus duoti 3 taškai, per kuriuos eina parabolė. Galite sudaryti trigubą lygčių sistemą, įrašę skirtingas x ir y reikšmes į kiekvieną. Taip pat galite sudaryti lygčių sistemą, kur viena iš lygčių būtų = x. Šioje lygtyje viršūnės x koordinatę turite lyginti su jos formule, kad 2a rastumėte b ir a reikšmes. Kaip spręsti trijų lygčių sistemą, ieškant parabolės išraiškos, pateiktas 3.9 uždavinio pavyzdyje. b 2a
g) p(x) = (x − 1)(x − 5);
h) q(x) = (x + 2)2;
i) r(x) = (x − 4)2;
e) s(x) = (x − 5)2;
k) t(x) = (x + 2)(x + 3);
l) u(x) = (x + 3)(x + 6).
3. Žinome, kad kai funkcija užrašyta formule f(x) = a(x − h)2+ k, h = xv, o k = yv.
f(x) = 2(x − 2)2+ 0 = 2(x 2− 4x + 4) = 2x 2− 8x + 8. >
Palyginę f(x) su nuliu sužinome, kad funkcijos sprendiniai x1 ir x2 yra x1 = x 2 = 2;
f(x) = 2(x − 2)(x − 2) = 2(x − 2)2. >
4. Šį uždavinį galėtume išspręsti keliais būdais (pavyzdžiui, atskleisti ir sutraukti panašiuosius narius ir pritaikyti formulę xv = − ), bet bene paprasčiausias yra pritaikyti viršūnės formulę xv = = = 4, nes žinome, kad b 2a x1 + x2 2 3 + 5 2
2(x − 3)(x − 5) = a(x − x1)(x − x2).
f(4) = (4 − 3)(4 − 5) = −1 = yv . >
Funkcijos viršūnės koordinatės yra (4, −1). >
5. Kadangi funkcija f(x) = 2x 2− 4x + 8 yra pateikta standartine forma, patogiausia būtų tiesiog pritaikyti viršūnės formulę xv = − ─ . b 2a xv = − ─ = − ─ = 1 > b 2a −4 2(2) yv = 2(1) − 4(1) + 8 = 6. >
Funkcijos viršūnės koordinatės yra (1, 6). >
6. Žinodami, kad funkcijos viršūnė yra (1, 0), galime pritaikyti formulę xv = − ─ ir rasti a reikšmę: b 2a
− ─ = 1; > −10 2a a = 5. >
Tada funkcija viršūnės formule: f(x) = 5(x − 1)2+ 0 = 5(x − 1)2. >
