International Journal of Molecular Sciences Article
DNASequenceandStructureunderthePrismofGroupTheory andAlgebraicSurfaces
MichelPlanat 1,*,† ,MarceloM.Amaral 2,† ,FangFang 2 ,DavidChester 2 ,RaymondAschheim 2 andKleeIrwin 2
1 InstitutFEMTO-STCNRSUMR6174,UniversitédeBourgogne-Franche-Comté,F-25044Besançon,France
2 QuantumGravityResearch,LosAngeles,CA90290,USA
* Correspondence:michel.planat@femto-st.fr
†Theseauthorscontributedequallytothiswork.
Citation: Planat,M.;Amaral,M.M.; Fang,F.;Chester,D.;Aschheim,R.; Irwin,K.DNASequenceand StructureunderthePrismofGroup TheoryandAlgebraicSurfaces. Int.J. Mol.Sci. 2022, 23,13290. https://doi.org/ 10.3390/ijms232113290
AcademicEditors:GiuseppeZanotti andZhongzhouChen
Received:16September2022 Accepted:26October2022 Published:31October2022
Publisher’sNote: MDPIstaysneutral withregardtojurisdictionalclaimsin publishedmapsandinstitutionalaffiliations.
Abstract: TakingaDNAsequence,awordwithletters/basesA,T,GandC,astherelationbetween thegeneratorsofaninfinitegroup π,onecandiscriminatebetweentwoimportantfamilies:(i) thecardinalitystructureforconjugacyclassesofsubgroupsof π isthatofafreegroupononeto fourbases,andtheDNAword,viewedasasubstitutionsequence,isaperiodic;(ii)thecardinality structureforconjugacyclassesofsubgroupsof π isnotthatofafreegroup,thesequenceisgenerally notaperiodicandtopologicalpropertiesof π havetobedetermineddifferently.Thetwocasesrelyon DNAconformationssuchasA-DNA,B-DNA,Z-DNA,G-quadruplexes,etc.Wefoundafewsalient results:Z-DNA,wheninvolvedintranscription,replicationandregulationinahealthysituation, implies(i).Thesequenceoftelomericrepeatscomprisingthreedistinctbasesmostofthetimesatisfies (i).Fortwo-basesequencesinthefreecase(i)ornon-freecase(ii),thetopologyof π maybefoundin termsofthe SL(2, C) charactervarietyof π andtheattachedalgebraicsurfaces.Thelinkingoftwo unknottedcurves—theHopflink—mayoccurinthetopologyof π incasesofbiologicalimportance, intelomeres,G-quadruplexes,hairpinsandjunctions,afeaturethatwealreadyfoundinthecontext ofmodelsoftopologicalquantumcomputing.Forthree-andfour-basesequences,otherknotting configurationsarenoticedandabuildingblockofthetopologyisthefour-puncturedsphere.Our methodshavethepotentialtodiscriminatebetweenpotentialdiseasesassociatedtothesequences.

Keywords: DNAconformations;transcriptionfactors;telomeres;infinitegroups;freegroups; algebraicsurfaces;aperiodicity;charactervarieties
1.Introduction
Copyright: ©2022bytheauthors. LicenseeMDPI,Basel,Switzerland. Thisarticleisanopenaccessarticle distributedunderthetermsand conditionsoftheCreativeCommons Attribution(CCBY)license(https:// creativecommons.org/licenses/by/ 4.0/).

Grouptheoryandalgebraicgeometryservethedeciphermentof‘thebookoflife’[1], abookmadeofalanguageemployingfourletters/nucleotides:A(adenine),T(thymine), G(guanine)andC(cytosine),asdescribedinthiswork.Therearefinitegroups,groups madeofafinitenumberofgeneratorsandafinitenumberofelementsthatmaybeusedto mapthecodonstoaminoacids,ascarriedoutinourpapers[2,3].Suchanapproachtoward thegeneticcodeismadepossiblebyidentifyingtheirreduciblecharactersofthegroupto theaminoacids.Themultipletsofcodonsattachedtoaselectedaminoacidcorrespond totheirreduciblecharactershavingthecorrespondingdimensionoftherepresentation (Table3in[2],Table4in[3]).Avirtueoftheapproachisthattheusedirreduciblecharacters arealsoseenasquantumstatescarryingcompletequantuminformation.
FormodelingDNAinitsvariousconformationstakenintranscriptionfactors,telomeresandotherbuildingblocksofmolecularbiology,weneedinfinitegroupsdefinedfrom amotif.AsequenceoftheDNAnucleotidesservesasthegeneratorofthegroup[4].Inthis context,ithasbeenfoundthatagroupthatisnotfreeisoftenthewitnessofapotential disease.Wecoinedtheterm‘syntacticalfreedom’forrecognizingthisproperty,withinspirationfromanearlierwork[5].Wealsoshowedthatsuchfreegroupshavethedistinctive
propertyofgeneratinganaperiodicsubstitutionrule,providingaconnectionbetween (group)syntacticalfreedomandirrationalnumbers(Section4in[4]).Foraninfinitegroup, therepresentationcannotbebasedoncharactersbutontheso-calledcharactervariety. ThistopicleadstoarelationshipbetweenDNA,algebraictopologyandalgebraicgeometry. Toolsalreadyproposedfortopologicalquantumcomputing[6]arealsousedinthecontext ofDNAconformations.
InSection 2,webrieflyaccountforthemanytypesoftopologiesthatDNAcanshow, intermsofdoublestrandsormorestrands.Then,werecallthemathematicalconcepts employedinourpaperwithsomeredundancywithearlierwork[4,6].
InSection 3,weexplaintheconceptofan SL(2, C) charactervarietyassociatedto aninfinitegroupwithtwoorthreegenerators.TheformercasecorrespondstoDNA motifshavingonlytwodistinctnucleotides.Insuchacase,thevarietyoftencontains theCayleycubicassociatedtotheHopflink,thenondisjointunionoftwocirclesinthe three-dimensionalspace.Inthelatercase,thevarietycontainstheFricke–Kleinseventh variablepolynomialthatischaracteristicofthetopologyofthethree-dimensionalsphere withfourpointsremoved.
InSection 4,weapplythesemathematicalmethodstotranscriptionfactors,telomeric sequencesandaspecificDNAdecamersequence,wherealmostallofitsconformations havebeencrystallized.
2.MaterialsandMethods
MathematicalcalculationsperformedinthispaperareonthesoftwareMagma[7](for groups)oronSagesoftware[8](forcharactervarieties).
2.1.DNAConformations
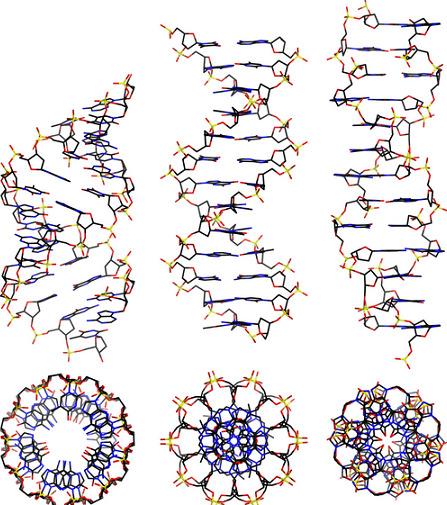
DNAisalongpolymermadefromachainofthenucleotidesA,T,CorG.DNAexists inmanypossibleconformations,whichincludeadouble-strandedhelixofA-DNA,B-DNA andZ-DNA,althoughonlyB-DNAandZ-DNAhavebeendirectlyobservedinfunctional organisms[9,10].TheB-DNAformismostcommonundertheconditionsfoundincells, butZ-DNAisoftenpreferredwhenDNAbindstoaprotein.Aviewofadoublehelix intheA-,B-andZ-DNAformsisgiveninFigure 1 OtherDNAconformationsalsoexist, suchasasingle-strandedhairpinusedmostlyinmacromolecularsynthesisandrepair, atriple-strandedH-DNAfoundinpeptides,aG-quadruplexstructurefoundintelomeres andaHollidayjunction.
Figure1. Fromlefttoright,thestructuresofA-,B-andZ-DNA.Theviewofthedoublehelixfrom above(orbelow)showsdistinctsymmetries, 11-foldfortheA-DNA, 10-foldfortheB-DNAand 6-foldfortheZ-DNA[9,10].
2.2.FinitelyGeneratedGroups,FreeGroupsandTheirConjugacyClasses,andAperiodicity ofSequences
Thefreegroup Fr on r generators(ofrank r)consistsofalldistinctwordsthatcanbe builtfrom r letterswheretwowordsaredifferentunlesstheirequalityfollowsfromthe groupaxioms.Thenumberofconjugacyclassesof Fr ofagivenindex d isknownandisa goodsignatureoftheisomorphism,orthecloseness,ofagroup π to Fr.Inthefollowing, thecardinalitystructureofconjugacyclassesofindex d in Fr iscalledthecardinality sequence(cardseq)of Fr,andweneedthecasesfrom r = 1 to 3 tocorrespondtothenumber ofdistinctbasesinaDNAsequence.Thecardseqof Fr isinTable 1 forthethreesequences ofinterestinthecontextofDNA[11].
Table1. Numberofconjugacyclassesofsubgroupsofindex d infreegroupofrank r = 1 to 3 [11]. Thelastcolumnistheindexofthesequenceintheon-lineencyclopediaofintegersequences[12].
rCardSeqSequenceCode
1 [1,1,1,1,1,1,1,1,1, ] A000012
2 [1,3,7,26,97,624,4163,34470,314493, ] A057005 3 [1,7,41,604,13753,504243,24824785,1598346352, ··· ] A057006
Next,givenafinitelygeneratedgroup fp witharelation(rel)givenbythesequence motif,weareinterestedinthecardseqofitsconjugacyclasses.Often,theDNAmotifin thesequenceunderinvestigationisclosetothatofafreegroup Fr,with r + 1 beingthe numberofdistinctbasesinvolvedinthemotif.However,thefinitelygeneratedgroup f p = x1, x2|rel(x1, x2) ,or f p = x1, x2, x3|rel(x1, x2, x3) or f p = x1, x2, x3, x4|rel(x1, x2, x3, x4) (wherethe xi aretakeninthefourbasesA,T,GandC,andrelisthemotif),maynotbethe freegroup F1 = x1, x2|x1 x2 ,or F2 = x1, x2, x3|x1 x2 x3 or F3 = x1, x2, x3, x4|x1 x2 x3 x4 Theclosenessof f p to Fr canbecheckedbyitssignatureinthefiniterangeofindicesofthe cardseq.
2.2.1.Groups f p ClosetoFreeGroupsandAperiodicityofSequences
Accordingtoreference[5],aperiodicitycorrelatestothesyntacticalfreedomofordering rules.Thisstatementwascheckedintherealmoftranscriptionfactors(Section4in[4]). Letusintroducetheconceptofageneralsubstitutionruleinthecontextoffreegroups. Ageneralsubstitutionrule ρ onafinitealphabet Ar on r lettersisanendomorphismofthe correspondingfreegroup Fr (Definition4.1in[13]).Theendomorphismpropertymeans thetworelations ρ(uv)= ρ(u)ρ(v) and ρ(u 1)= ρ 1(u),forany u, v ∈ Fr.
Aspecialroleisplayedbythesubgroup Aut(Fr ) ofautomorphismsof Fr.Weintroduce themap α : Fr → Zr from Fr totheAbeliangroup Zr inordertoinvestigatethesubstitution rule ρ withthetoolsofmatrixalgebra.
Themap α inducesahomomorphism M :End(Fr ) → Mat(r, Z).Under M, Aut(Fr ) mapstothegenerallineargroupofmatriceswithintegerentries GL(r, Z).Given ρ,thereis auniquemapping M(ρ) thatmakesthemapdiagramcommutative[13](p.68).Thesubstitutionmatrix M(ρ) of ρ maybespecifiedbyitselementsatrow i andcolumn j asfollows: (M(ρ))i,j = card(ρai (aj ))
Thisapproachwasappliedtobindingmotifsoftranscriptionfactors[4].Thebindingmotifrelinthefinitelypresentedgroup fp = A, T, G, C|rel(A,T,G,C) issplitinto appropriatesegmentssothat rel = relArelT relGrelC withthesubstitutionrules A → relA, T → relT , G → relG, C → relC Weareinterestedinthesequenceoffinitelygeneratedgroups f (l) p = A, T, G, C|rel(rel(rel (A, T, G, C))) (withrelapplied l times)
whosecardseqisthesameateachstep l andequaltothecardseqofthefreegroup Fr (in thefiniterangeofindicesthatitispossibletocheckwiththecomputer).
Undertheseconditions,(group)syntacticalfreedomcorrelatestotheaperiodicity ofsequences.
2.2.2.AperiodicityofSubstitutions
Thereisnodefinitiveclassificationofaperiodicorder,theintermediatebetween crystallineorderandstrongdisorder,butinthecontextofsubstitutionrules,somecriteria canbefound.First,weneedafewdefinitions.
Anon-negativematrix M ∈ Mat(d, R) isonewhoseentriesarenon-negativenumbers. Apositivematrix M (denoted M > 0)hasatleastonepositiveentry.Astrictlypositive matrix(denoted M >> 0)hasallpositiveentries.Anirreduciblematrix M =(Mij )1≤i,j≤d isoneforwhichthereexistsanon-negativeinteger k with (Mk )ij > 0 foreachpair (i, j) Aprimitivematrix M isonesuchthat Mk isastrictlypositivematrixforsome k
APerron–Frobenius(PFforshort)eigenvector v ofanirreduciblenon-negativematrix istheonlyonewhoseentriesarepositive: v > 0.Thecorrespondingeigenvalueiscalled thePFeigenvalue.
Wewillusethefollowingcriterion(Corollary4.3in[13]).Aprimitivesubstitution rule ρ ofsubstitutionmatrix M(ρ) withanirrationalPF-eigenvalueisaperiodic.
Awell-studiedprimitivesubstitutionruleistheFibonaccirule ρ = ρF : a → ab, b → a ofsubstitutionmatrix MF = 11 10 andPF-eigenvalueequaltothegoldenratio
λPF = φ =(√5 + 1)/2 (Example4.6in[13]).Asexpected,theirrationalityof λ correspondstotheaperiodicityoftheFibonaccisequence.
ThesequenceofFibonacciwordsisasfollows:
a, b, ab, aba, abaab, abaababa, abaababaabaab, ThewordshavelengthsequaltotheFibonaccinumbers1,1,2,3,5,8,13,21, Allfinitelygeneratedgroups f (l) p whoserelations rel(a, b)= ab, aba, abaab, abaababa, haveacardseqwhoseelementsare 1s,asforthecardseqofthefreegroup F1.TheFibonacci sequenceisourfirstexamplewheregroupsyntacticalfreedomcorrelatestoaperiodicity.
2.2.3.AFour-LetterSequencefortheTranscriptionFactoroftheFosGene
Letusnowapplythemethodtoatranscriptionfactorofimportance.Thetranscription factorofgeneFoshasselectedmotif rel = TGAGTCA [14].Forthiscase,thefour-letter generatedgrouphasacardseqsimilartothefreegroup F3 giveninTable 1 Wesplitrelintofoursegmentssothat rel = relArelT relGrelC withthesubstitution maps A
haveacardseqwhoseelementsare
1,7,41,604,13753,504243, , whichisthecardseqofthefreegroup F3.FortheFostranscriptionfactor,groupsyntactical freedomcorrelatestoaperiodicityasexpected.
FurtherexamplesareobtainedinthecontextofDNAsequencesfortranscription factors(Section4in[4])andbelow,inrelationtoDNAconformationsandtelomeres.
3.Discussion
Inthefollowing,wemakeuseof SL(2, C) representationsoftheinfinitegroups π arisingfromspecificDNAsequences.Thecharactervarietyhasmanyinterpretations inmathematicsandphysics.Forinstance,inmathematics,thevarietyisthespaceof representationsofhyperbolicstructuresofthree-manifolds M withfundamentalgroup π(M),andthevarietyofthecharactersof SL(2, C) representationsof π(M) isreflected inthealgebraicgeometryofthecharactervariety[15,16].Inphysics,thegroup SL(2, C) expressesthesymmetriesoffundamentalphysicallaws.ItisalsoknownastheLorentz group;moreprecisely,thedoublecoveroftherestrictedLorenzgroupis SL(2, C),whichis thespingroup.
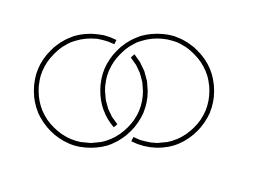
Figure2. (Left):theHopflink.(Right):thelink L = A ∪ B isattachedtotheplane R2 inthe half-space R3 + .Itisnotsplittable.Thiscanbeprovedbycheckingthatthefundamentalgroup π = π2(L) isnotfree[17]andp.90in[18].Onegets π2 = x, y, z|(x, (y, z))= z ,where(.,.) meansthegrouptheoreticalcommutator.Thecardinalitysequenceofccofsubgroupsof π2 is [1,3,10,51,164,1365,9422,81594,721305, ] (Figure3in[4]).
3.1.SL(2, C) CharacterVarietiesandAlgebraicSurfaces
Recently,wefoundthattherepresentationtheoryoffinitegroupswiththeircharacter tableallowsustoderiveanapproachofthegeneticcode[3].
Forinfinitegroups π suchasthosedefinedbyDNAsequences,itisusefultodescribe therepresentationsof π intheLorentzgroup SL(2, C),thegroupof (2 × 2) matriceswith complexentriesanddeterminant 1.Suchagroupexpressesthefundamentalsymmetryof allknownphysicallaws,apartfromgravitation.
Representationsof π in SL(2, C) arehomomorphisms ρ : π → SL(2, C) withcharacter κρ (g)= tr(ρ(g)), g ∈ π.Thesetofcharactersallowsustodefineanalgebraicsetbytaking thequotientofthesetofrepresentations ρ bythegroup SL2(C),whichactsbyconjugation onrepresentations[15,19].
Fortwo-generatorgroups,thecharactervarietymaybedecomposedintotheproduct ofsurfaces,whichrevealsthetopologyof M.Werecentlyfoundaconnectionbetweensome groupswhosetopologyisbasedontheHopflinkandamodeloftopologicalquantum computing[6].TheHopflinkunderliesmanyDNAsequenceswhosegroupstructureis (orisnot)thatofthefreegroup F1.Theclassificationoftheinvolvedalgebraicsurfacesin
thevarietyisperformedusingspecifictoolsavailableinMagma[7];see(Section2.1in[6]) fordetails.
Forthree-generatorgroups,wefindthattheFricke–Kleinquarticispartofthecharactervariety.
3.2.TheHopflink
TakingthelinkingoftwounknottedcurvesasinFigure 2 (Left),theobtainedlinkis calledtheHopflink H =L2a1,whoseknotgroupisdefinedasthefundamentalgroupof theknotcomplementinthethree-sphere S3
Π1(S3 \ L2a1)= a, b|[a, b] = Z2,(1)
where [a, b]= abAB (with A = a 1 , B = b 1)isthegrouptheoreticalcommutator. Thereareinterestingpropertiesoftheknotgroup Π1 oftheHopflink.
Figure3. Left:athree-dimensionalpictureofthe SL2(C) charactervariety ΣH fortheHopflink complement H.Right:amodifiedcharactervarietyofdefiningequation f H (x, y, z) withsimilarsingularities.
First,thenumberofcoveringsofdegree d of Π1 (whichisalsothenumberofconjugacy classesofindex d)ispreciselythesumofdivisorfunction σ(d) [20].
Second,aninvarianceof Π1 underarepetitiveactionofthegoldenratiosubstitution (theFibonaccimap) ρ : a → ab, b → a orunderthesilverratiosubstitution ρ : a → aba, b → a exists.ThetermsgoldenandsilverrefertothePerron–Frobeniuseigenvalueofthe substitutionmatrix(Examples4.5and4.6in[13]).SuchanobservationlinkstheHopflink, thegroup Π1 ofthe2-torusandaperiodicsubstitutions.
UsingSagesoftware[8]developedfromRef.[19],the SL2(C) charactervarietyisthe polynomialcorrespondingtotheso-calledCayleycubic f H (x, y, z)= xyz x2 y2 z2 + 4.(2)

Asexpected,thethree-dimensionalsurface Σ : f H (x, y, z)= 0 isthetraceofthe commutatorandisknowntocorrespondtothereduciblerepresentations(Theorem3.4.1 in[21]).ApictureisgiveninFigure 3 (left).
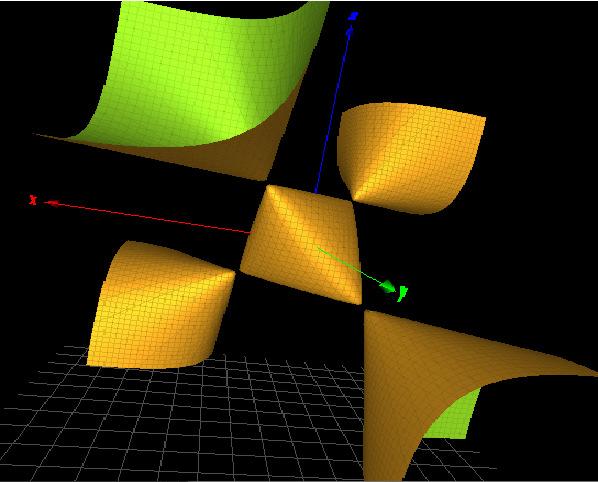
Intheperspectiveofalgebraicgeometry,weclassifythehomogenizationofequation f H asarationalsurfaceofdegree3delPezzotype.Itdisplaysfoursimplesingularities.
3.3.BeyondtheHopfLink
Asshownin[6],theHopflinkistheirreduciblecomponentofmanycharactervarietiesrelevanttoamodeloftopologicalquantumcomputing.InthecontextofDNA groupsinvestigatedinthenextsection,wealsofindanothersurfacewithsimilarsimple singularitiesasshowninFigure 3 (right).Thedefiningpolynomialis
f H (x, y, z)= z4 2xyz (+z3)+ 2x2 + 2y2 3z2( 4z) 4.(3)
Thehomogenizationofequation f H (x, y, z) allowsustoclassifyitasaconicbundlein thefamilyof K3 surfaces.
FortheDNAsequence,whosegroup πH containsthecomponent f H (x, y, z),werefer tothethirdsubsectionoftheResultssectionbelowandthefirsttableinthissubsection. Therelevanttripletnnn=CGGofthedodecamericsequence d(CCnnnN6 N7 N8GG) leadsto aDNAconformationwiththelabel1ZEYinthePDBbank.
TheDNAdodecamersequenced(CCCCCGCGGGGG)isalsofoundinthePDBbank withlabel 2D47,correspondingtoacompleteturnofA-DNA.Thecharactervarietyforthe groupdefinedbythissequencecontainsthepolynomial f H andapolynomialsimilarto f H withoutthethird-orderterm z3 andthefirst-orderterm 4z,butinthesamefamily.
3.4.TheFricke–KleinSeventhVariablePolynomial
TheCayleycubicisasubsetofthecharactervarietyforthefour-puncturedthreedimensionalsphere S2 4 (thesphereminusfourpoints).Itsfundamentalgroup Π1 isisomorphictothefreegroup F3 ofrank 3, Π1(S2 4)= α, β, γ, δ|αβγδ ,wherethefourhomotopy classes α, β, γ, δ correspondtoloopsaroundthepunctures. The SL(2, C) charactervarietyfor Π1(S2 4) satisfiesaquarticequationintermsofthe Fricke–Kleinseventhvariablepolynomial[21](p.65)and[22]: f (x, θ)= xyz + x2 + y2 + z2 θ1 x θ2 x θ3z + θ4,(4) with θ1 = uv + wk, θ2 = uw + vk, θ3 = uk + vw, θk = uvwk + u2 + v2 + w2 4.
4.Results
Inthissection,weapplythe SL(2, C) representationtheorytospecificnon-canonical DNAsequenceshavingregulatoryfunctionsingeneexpression(thetranscriptionfactors), replication(thetelomeres)andDNAconformations.
4.1.GroupStructureandTopologyofTranscriptionFactors
Inatranscriptionfactor,amotif-specificDNAbindingfactorcontrolstherateofthe transcriptionofagenefromDNAtomessengerRNAbybindingaproteintotheDNA motif.Inreference[4],wefoundacorrelationbetweenmotifswhosesubgroupstructure isthatofafreegroupandthelackofapotentialdiseasewhilethegeneisactivatedin transcription,thepropertyof‘syntacticalfreedom’.
InTable 2,thisideaisillustratedbyrestrictingtoafewtranscriptionfactorswhose motifcomprisestwobases.Thecardseqofthemotifiseitherthefreegroup F1,closeto F1 orawayfromafreegroupwhenthecardseqisthatofthemodulargroup H3,ofthe Baumslag–Solitargroup BS( 1,1) orthatofgroups π1 and π1.Comparedtotheresults providedin[4],thereistheadditionalfourthcolumnthatsignalswhentheGroebnerbase fortheidealringofthe SL(2, C) charactervarietycontainstheCayleycubic,theunique componentinthecaseoftheHopflink[6],adegree 3 delPezzosurface(denotedHL),or not.Anadditionalfifthcolumnisfilledtocheckthepresenceofasurfaceoftype K3.Only thelastrowofthetableforthetranscriptionfactorofgeneEHFdoesnotshowthisproperty.
Table2. Groupstructureofmotifsforafewtwo-lettertranscriptionfactors.Thecardseqforthemodulargroup H3 is [1,1,2,3,2,8,7,10,18,28, ].TheBaumslag–Solitargroup BS( 1,1) isthefundamentalgroupoftheKleinbottle.Thecardseqfor BS( 1,1) is [1,3,2,5,2,7,2,8,3,8,2,13,2,9,4, ] Thecardseqfor π1 is [1,4,1,2,4,2,1,7,2,2,4,2,2,8,1,2,7,2,3, ];for π1,itis [1,1,1,2,1,3,3,1,2,2,1,1,9,2,14,2,1, ··· ].ThesymbolHLmeansthattheCayleycubicis partoftheGroebnerbasefortheidealringofthecorresponding SL(2, C) charactervariety. Forthree-lettertranscriptionfactors,theidealringofthecorresponding SL(2, C) charactervariety containstheFricke–Kleinseventhvariablepolynomial 4,whichisafeatureofthefour-punctured spheretopology.Thegroupstructureofthree-lettertranscriptionfactorsnotleadingtofreegroupsis shownin(Table5in[4]).
GeneMotifCardSeqLinkTypeLiterature
DBXTTTATTA F1 HL K3 [23],MA0174.1
SPT15TATATATAT....,MA0386.1 PHOX2ATAATTTAATTA ≈F1 ...,MA0713.1
FOXATGTTTGTTT F1 ..[24,25]
FOXGTTTGTTTTT...[24]
NKX6-2TAATTAA H3 no K3 [23],[MA0675.1,MA0675.2]
FOXGTGTTTG BS( 1,1) no K3 [23,26],MA1865.1 HoxA1,HoxA2TAATTA π1 no K3 [23],[MA1495.1,MA0900.1] POU6F1,Vax.,[MAO628.1,MA0722.1] RUNX1TGTGGT.no..,MA0511.1 RUNX1TGTGGTT π1 no K3 [23],MA0002.2 EHFCCTTCCTC.HL.,MA0598.1
TheCharacterVarietyfortheTranscriptionFactoroftheDBXGene
Weexplicitlyshowthe SL(2, C) charactervarietyforthetranscriptionfactorofthe DBXgene.
fDBX (x, y, z)= f H (x, y, z)(yz2 y2 xz y + 2)(xy2 z3 yz x + 3z) (5) (y3 z2 3y + 2)(y2z xy yz + x z)(z4 x2y + xz 4z2 + y + 2)
Thefactorsin(5)arethreedegree 3 delPezzosurfaces(includingtheCayleycubic f H ), tworationalruledsurfacesanda K3 surfacebirationallyequivalenttotheprojectiveplane, respectively.Thelatterfactoralsobelongstothecharactervarietyofgroup Π1(S4 \ E6), where S4 isthefour-sphereand E6 isthesingularfiber IV∗ inKodaira’sclassificationof minimalellipticsurfaces(Figure4bin[6]).
Itisimportanttomentionthat,forthree-lettertranscriptionfactors,theidealringof thecorresponding SL(2, C) charactervarietycontainstheFricke–Kleinseventhvariable polynomial(4),whichisafeatureofthefour-puncturedspheretopology.
Table 3 providesashortaccountofthefunctionorpotentialdysfunctionofthegenes underconsideration.Asmentionedbefore,mostofthetime,suchadysfunctioniscorrelatedtoacardseqawayfromthatofthefreegroup F1
Inviewofourresults,itisinterestingtocorrelatethepresenceoftheHopflinkHLin thecharactervarietywiththepossibleremodelingofB-DNAintoZ-DNAoranotherDNA conformation.Toourknowledge,generalinformationaboutthissubjectisstilllacking. Fromabiologicalpointofview,itisknownthatsomeoftheZ-DNA-formingconditionsthat arerelevantinvivoarethepresenceofDNAsupercoiling,Z-DNA-bindingproteins[27] andbasemodifications.Whentranscriptionoccurs,themovementofRNApolymeraseII alongtheDNAstrandgeneratespositivesupercoilinginfrontof,andnegativesupercoiling behind,thepolymerase[28].
Table3. Ashortaccountofthefunctionordysfunction(throughmutationsorisoforms)ofgenes associatedwithtranscriptionfactorsandsectionsinTable 2
GeneTypeFunctionDysfunction
DBXdrosophilasegmentation
SPT15TATA-boxgeneexpression,regulation bindingproteininSaccharomycescerevisiae
PHOX2Ahomeodomaindifferentiation,maintenancefibrosis ofnoradrenergicphenotypeofextraocularmuscles FOXproteinsforkheadboxgrowth,differentiation,
FOXA2.insulinsecretiondiabete longevity
NKX6-2homeoboxcentralnervoussystem,pancreasspasticataxia
FOXGforkheadboxnotochord(neuraltube)chordoma
HoxA1homeoboxembryonicdevtoffaceandhearautism HoxA2..cleftpalate
Pou6F1.neuroendocrinesystemclearcelladenocarcinoma
Vax.forebraindevelopmentcraniofacialmalform.
RunX1Runt-relatedcelldifferentiation,painneuronsmyeloidleukemia
EHFhomeoboxepithelialexpressioncarcinogenesis,asthma
PerhapsthelackofHLinthecharactervarietyfortranscriptionfactorsofgenesin Table 2 meansthattheZ-DNA-formingconditionisnotrealized.
4.2.GroupStructureandTopologyofDNATelomericSequences
TerminalstructuresofchromosomesaremadeofshorthighlyrepetitiveG-richsequenceswithproteinsknownastelomeres.Theyhaveaprotectiveroleagainsttheshorteningofchromosomesthroughsuccessivedivisions.Mostorganismsuseatelomere-specific DNApolymerasecalledtelomerasethatextendsthe3’endoftheG-richstrandofthe telomere[29].Telomereshorteningisassociatedwithaging,mortalityandaging-related diseasessuchascancer.
AlistofresultsobtainedbyusingourgrouptheoreticalapproachisinTable 4.For two-letter telomeresequences,the SL(2, C) charactervarietycontainstheCayleycubic, thecharacteristicoftheHopflinkHL,onlyinthefirstrow.InadditiontotheCayley cubic,onefindssurfacesofageneraltype.Inthenexttworows,theCayleycubicisnot found.Therearedegree 3 delPezzosurfacesinthefactorsofthecharactervarietybutnot generalsurfaces.
AsfortheHopflink,thesequenceisfoundtobeaperiodicwiththePerron–Frobenius eigenvalue λPF equaltothegoldenratio.Forthree-lettertelomeresequences,thecardseq isthatofthefreegroupof F2,exceptforthelastrow,wheretheidentifiedgroupis π2;see Figure 2 (right)forthedefinitionofsuchagroup.Intheformersevencases,theDNA topologyisknowntobeaG-quadruplexstructure[30–36].Wecouldidentifyanaperiodic structureofthetelomeresequencewiththePerron–Frobeniuseigenvalue λPF asshownin column5.Inthelattercase,thetopologyisofthebaskettype[36]andnoaperiodicityof thetelomeresequencecouldbefound.
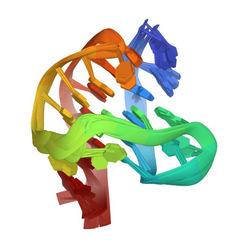
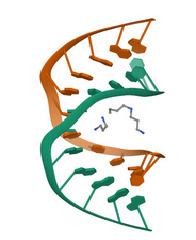
Figure 4,takenfromtheproteindatabank(PDB2HY9),illustratestheG-quadruplex structureofthetelomeresequenceinvertebrates.
Table4. Groupanalysisofthetelomeresequencefoundinsomeeukaryotes.Thefirstcolumnis forthetelomererepeat,thesecondcolumnistheorganismunderinvestigation,thethirdcolumnis forthePDBcode,thefourthcolumnisforthecardseqofthegroup π orthatofthecorresponding groupthatisidentified,thefifthcolumnisforthePerron–Frobeniuseigenvaluewhenthesequence isfoundtobeaperiodic,thesixthcolumnidentifiesthepresenceoftheHopflink(intwo-base sequences)ortheDNAconformation(inthree-basesequences)andtheseventhcolumnisarelevant reference.ThenotationG-quadrisfortheG-quadruplex;seeFigure 4.Thecardseqfor π1 is [1,3,2,16,16,69,118,719,1877,8949 ].TheHeckegroup H4 isdefinedin(Table2in[4]).
SeqOrganismPDBCardSeq λPF Link/DNAConfRef
G4T4G4Oxytricha1D59 π1 (√5 + 1)/2HL[37] TG4Tuniversal244D_1 H4 .no[38]
T2G4Tetrahymena230D H4 .no[29]
T2AG3Vertebrates2HY9 F2 2.5468G-quadr.[30] TAG3Giardia2KOW F2 2.2055G-quadr[31]
T2AG2Bombysmoriunknown F2 noG-quadr[32] T4AG3Greenalgaeunknown F2 3.07959unknown[33] G2T2AGHumanunknown F2 2.5468G-quadr[34] TAG3T2AG3Human2HRI F2 3.3923G-quadr[35] G3T2AG3T2AG3THumanunknown F2 4.3186G-quadr[36] (GGGTTA)3G3THumanunknown π2 nobasket[36]
Figure4. HumantelomereDNAquadruplexstructureinK+solutionhybrid-1form,PDB2HY9[30].
4.3.GroupStructureandTopologyoftheDNADecamerSequenced(CCnnnN6 N7 N8GG) [10]
AchallengingquestionofstructuralbiologyistodetermineifandhowaDNA(or RNA)sequencedefinesthethree-dimensionalconformation,aswellasthesecondaryand tertiarystructureofproteins.Intheprevioustwosubsections,wetackledtheproblem withregardtotranscriptionfactorsandtelomericsequences,respectively.Intheformer case,werestrictedtotheDNApartofthetranscriptionsincetheDNAmotifisalmost exactlyknownfromX-raytechniqueswhilethesecondarystructureofthebindingprotein stronglydependsonthemodelemployedandthechoicemadetorecognizethesections ofthesecondarystructures(e.g.,alphahelices,betasheetsandcoils)[39].Inthelatter case,inmanyorganisms,natureinventedtelomerasefortakingcareofthereplication withoutdamagingthesequencesatthe 3-endstoomuch,whilekeepingthecatalyzing actionofDNApolymerase.Again,thereisaloopcomplexintelomerasecomprising telomere-bindingproteins,withsecondarystructuresnotbeinganalyzedsofarwithour grouptheoreticalapproach.
Inthissection,wealsostudyDNAconformationsandtheirrelationshiptoalgebraic topologyinaspecificDNAdecamersequenceinvestigatedinreference[10]byastandard crystallizationtechniquefollowedbyX-raydiffractiondiscrimination.Inthesequence d(CCnnnN6 N7 N8GG),thefactors N6, N7 and N8 aretakeninthetwonucleotidesGand C,andnnnisspecifiedinordertomaintaintheself-complementarityofthesequence. Thisinverserepeatedmotifistheminimummotifusedtodistinguishbetweenthedoublestrandformsof B-and A-DNA,whileexcludingthe Z-DNAforms.Athirdconformation isallowedandcalledthefour-strandedHollidayjunction J.Wereferto(Table1in[10])for themainresults.
Onourside,thecardseqofeachsequencewasdeterminedandthe SL(2, C) character varietywasobtained.OurresultsaresummarizedinthefourTables 5–8
Table5. Groupanalysisofthesequence d(CCnnnN6 N7 N8 GG),where N6, N7 and N8 aretakenin thetwonucleotides G and C and nnn isspecifiedinordertomaintaintheself-complementarity ofthesequence[10].Thefirstcolumnisfortheselectedtriplet N6 N7 N8,thesecondcolumnisfor thecodeintheproteindatabank,thethirdcolumnisfortheDNAconformationwhenknown(see Table1in[10]),thefourthcolumnisforthecardinalitystructureofsubgroupsof π andthefifth columncheckstheoccurrenceofasurfacecorrespondingtotheHopflinkinthefactorizationofthe SL(2, C) of π.ThesymbolsA,BandJareforA-DNA,B-DNAandafour-strandedHollidayjunction; lowercaseisusedwhentheconformationisnotconfirmedin[10].
TripletPDBConformationCardSeq(π)Knot CCC1ZF1A [1,1,1,1,7,1,1,2,9,6, ] HL CCC1ZF2JidemHL CCG1ZEXAidemHL CGG1ZEYA [1,1,1,2,6,3,1,4,2,6, ] HLlike CGCnoneunknown [1,1,2,1,6,3,2,1,3,6, ] no GGG1ZF9A [1,1,1,1,10,25,25,9,2,1798, ] no GCCnoneb/J [1,1,1,1,6,1,2,1,1,6, ] HL GCGnoneunknown [1,1,2,2,7,5,1,4,5,9, ] no GGCnoneB/a [1,1,1,1,6,11,9,5,2,208, ] no (cardseqofHeckegroup H5)
Table6. Groupanalysisofthesequence d(CCnnnN6 N7 N8 GG),where N6, N7 and N8 aretaken inthetwonucleotidesA,T[10].Groups π3 and π3 areasin(Table5in[4]).Thecardseqfor π3 is [1,7,50,867,15906,570528, ];for π3 ,itis [1,7,50,739,15234,548439, ];for π(4) 3 ,itis [1,7,59,1258,24787, ].Groups π3 and π3 maybesimplifiedtoagroupwhosecardseqisthatof π2,thefundamentalgroupofthelink L = A ∪ B describedinFigure 3 (right).
5, N6, N7 and N8 aretakeninthetwonucleotides G and C,formingeight tripletsandtheassociatedtwo-letterdecamersequences.Notethatthetriplet CCC producestwodistinctDNAconformations A and J.ThecharactervarietyoftheHopflinkHL (theCayleycubic)ispresentinthefactorsoftheidealringofthe SL(2, C) charactervariety infivecasesovertheninepossibilities,whereonecase(withtriplet CGG andcode1ZEYin theproteindatabank)showsanalgebraicsurfacesimilartotheCayleycubic(withfour
simplesingularities)asdefinedinEquation(3)andasshowninFigure 3 (right).Wedonot observeaclearcorrelationbetweenthetypeofDNAconformationandtheunderlyingHL topology,butthepresenceofHLinthevarietyseemstoexcludetheB-DNAconformation. Inaddition,thecharactervarietyalwayscontainsasurfaceoftype K3 initsfactors.
Table7. Groupanalysisofthesequence d(CCnnnN6 N7 N8 GG) [10],where N6, N7 and N8 aretaken inthetwonucleotidesA,G(left)andA,C(right).Groups π3 and π3 areasin(Table5in[4]).Thecard seqfor π(3) 3 is [1,7,41,668,14969, ]and,for π(5) 3 ,itis [1,7,41,604,28153, ].
TripletPDBConformation π
TripletPDBConformation π
AGA1ZEWB F3 ACAnoneunknown π(3) 3 → π2
AGGnoneunknown π(5) 3 ACCnoneJ F3 GGA1ZFAA F3 CCAnoneunknown F3 AAGnoneunknown F3 AAC1ZF0B π3 ” → π2
TGTnoneunknown F3 TCTnoneb π(3) 3 → π2 TGG1ZF6A F3 TCCnoneunknown F3 GGT1ZF8A F3 CCTnoneb F3 TTGnoneunknown π3 TTCnoneB π3 ” → π2
Table8. Groupanalysisofthesequence d(CCnnnN6 N7 N8 GG) [10],where N6, N7 and N8 are takeninthethreenucleotidesA,G,C(left)andA,T,C(right).Thecardseqfor π(6) 3 is [1,7,59,874,20371,748320 ··· ]
TripletPDBConformation π TripletPDBConformation π
AGC1ZFMB F3 ATC1ZFC/1ZF3B/J π(6) 3
ACGnoneunknown F3 ACTnoneB π(3) 3 → π2 GCA1ZFEB F3 TCAnoneunknown π(3) 3 → π2 GAC1ZF7B F3 TACnoneunknown π(6) 3 CAGnoneunknown F3 CATnoneunknown F3 CGAnoneunknown F3 CTAnoneunknown F3
InTable 6, N6, N7 and N8 aretakeninthetwonucleotides A and T,formingeight triplets.TheDNAconformation(whenknown)isoftype B.Thecardseqthatweobtain isgroups π3, π3 or π(4) 3 asdescribedinthecaptionofTable 5.Insixcasesovertheeight possibilities,thegroupsencapsulatethetopologyoftherank 2 group π2,whoseassociated linkisshowninFigure 2 (right).Asalreadymentioned,the SL(2, C) charactervariety containstheFricke–Kleinseventhvariablepolynomial 4 InTable 7, N6, N7 and N8 aretakeninthetwonucleotides A, G (leftpart)and A, C (rightpart).Thistime,eitherthecardseqofthegroup π isthatofthefreegroup F3, ofrank 3 (10casesoverthe 16 possibilities),ornot.Inthelattercase,thegroupencapsulates thetopologyof π2 onlyattherightsideofthetable.SimilarconclusionsholdinTable 8 when N6, N7 and N8 aretakeninthetwonucleotides A, G, C (leftpart)and A, T, C (right part).
Tosummarizethissection,noclearcorrelationisobservedbetweentheDNAconformationsoftheconsidereddecamerandourgroupanalysis.Longersequencesmaybe neededtoobtainsuchacorrelation.Forinstance,thetwo-letterDNAdodecamersequence d(CCCCCGCGGGGG) (PDB2D47)correspondingtoacompleteturnofA-DNA—see Figure 5 (right)—featuresthepolynomial f H (forHL)andafourth-orderpolynomialsimilarto f H withfoursimplesingularities,asannouncedattheendofSection 3
Figure5. (Left)Thefour-strandHollidayjunction J:PDB 1ZF2,(Right)AcompleteturnofADNA:PDB 2D47.ItisassociatedtoDNAdodecamersequence d(CCCCCGCGGGGG) with SL(2, C) containingthefactor f H = xyz x2 y2 z2 + 4 (theCayleycubic)andthefactor f H = z4 2xyz + 2x2 + 2y2 3z2 4.

5.Conclusions
Inthepresentpaper,followingearlierworkaboutthegeneticcode[2,3]andabout theroleoftranscriptionfactorsingenetics[4],wemadeuseofgrouptheoryappliedto appropriateDNAmotifsandwecomputedthecorrespondingvarietyof SL(2, C) representations.TheDNAmotifsunderconsiderationmaybecanonicalstructures,suchas (double-stranded)B-DNA,ornon-canonicalDNAstructures[40],suchas(single-stranded) telomeres,(double-stranded)A-DNA,Z-DNAorcruciforms,(triple-stranded)H-DNA, (four-stranded)i-motifsorG-quadruplexes,etc.Oneobjectiveoftheapproachistoestablish acorrespondencebetweenthealgebraicgeometryandtopologyofthe SL(2, C) character varietyandthetypesofcanonicalornon-canonicalDNA-forms.Forexample,fortwo-letter transcriptionfactors,onecancorrelatethepresenceoftheCayleycubicand/ora K3 surface inthevarietywithDNAsupercoilingintheremodelingofB-DNAtoZ-DNA.Forthree-or four-letterDNAstructures,ourworkneedstobedevelopedinordertoputthefeatures ofthevarietyandpotentialdiseasesincorrespondence.Inaseparateworkdevotedto topologicalquantumcomputing,thetopologyofthefour-puncturedsphereandtherelatedFrickesurfaces(generalizingtheCayleycubic)arerelevant[41].Inaddition,Fricke surfacesmaybeputinparallelwithdifferentialequationsofthePainlevéVItype.Itwill beimportanttocomparethesemodelswithotherqualitativemodelsbasedonnon-linear differentialequations[42,43].Inthenearfuture,weintendtoapplythesemathematical toolstothecontextofDNAstructures.
AuthorContributions: Conceptualization,M.P.,F.F.andK.I.;methodology,M.P.,D.C.andR.A.;software,M.P.;validation,R.A.,F.F.,D.C.andM.M.A.;formalanalysis,M.P.andM.M.A.;investigation, M.P.,D.C.,F.F.andM.M.A.;writing—originaldraftpreparation,M.P.;writing—reviewandediting, M.P.;visualization,F.F.andR.A.;supervision,M.P.andK.I.;projectadministration,K.I.;funding acquisition,K.I.Allauthorshavereadandagreedtothepublishedversionofthemanuscript.
Funding: FundingwasobtainedfromQuantumGravityResearchinLosAngeles,CA,USA.
InstitutionalReviewBoardStatement: Notapplicable.
InformedConsentStatement: Notapplicable.
DataAvailabilityStatement: Thedatasetsusedand/oranalyzedduringthecurrentstudyare availablefromthecorrespondingauthoronreasonablerequest.
ConflictsofInterest: Theauthorsdeclarenoconflictofinterest.
References
1. Nerlich,B.;Dingwall,R.;Clarke,D.D.Thebookoflife:HowthecompletionoftheHumanGenomeProjectwasrevealedtothe public. HealthInterdiscip.J.Soc.StudyHealthIlln.Med. 2002, 6,445–469.
2. Planat,M.;Aschheim,R.;Amaral,M.M.;Fang,F.;Irwin,K.CompletequantuminformationintheDNAgeneticcode. Symmetry 2020, 12,1993.
3. Planat,M.;Chester,D.;Aschheim,R.;Amaral,M.M.;Fang,F.;Irwin,K.FinitegroupsfortheKummersurface:Thegeneticcode andquantumgravity. QuantumRep. 2021, 3,68–79.
4. Planat,M.;Amaral,M.M.;FangF.;Chester,D.;Aschheim,R.;Irwin,K.GrouptheoryofsyntacticalfreedominDNAtranscription andgenomedecoding. Curr.IssuesMol.Biol. 2022, 44,1417–1433.
5. Irwin,K.Thecode-theoreticaxiom;thethirdontology,Rep.Adv.Phys.Sci. 2019, 3,1950002.
6. Planat,M.;Amaral,M.M.;FangF.;Chester,D.;Aschheim,R.;IrwinK.Charactervarietiesandalgebraicsurfacesforthetopology ofquantumcomputing. Symmetry 2022, 14,915.
7. Bosma,W.;Cannon,J.J.;Fieker,C.;Steel,A.(Eds). HandbookofMagmaFunctions,Australia,Edition2.23;UniversityofSydney: Sydney,Australia,2017;5914p.
8. PythonCodetoComputeCharacterVarieties.Availableonline: http://math.gmu.edu/~slawton3/Main.sagews (accessedon 1May2021).
9. DNA.Availableonline: https://en.wikipedia.org/wiki/DNA (accessedon1January2022).
10. Hays,F.A.;Teegarden,A.;JonesZ.J.R.;Harms,M.;Raup,D.;Watson,J.;Cavaliere,E.,Ho,P.S.Howsequencedefinesstructure: AcrystallographicmapofDNAstructureandconformation. Proc.Natl.Acad.Sci.USA 2005, 20,7157–7162.
11. Kwak,J.H.;Nedela,R.Graphsandtheircoverings. Lect.NotesSer. 2007, 17,118.
12. TheOn-LineEncyclopediaofIntegerSequences.Availableonline: https://oeis.org/book.html (accessedon1June2022).
13. BaakeM.,GrimmU. AperiodicOrder,Vol.I:AMathematicalInvitation;CambridgeUniversityPress:Cambridge,UK,2013.
14. Glover,J.N.;Harrison,S.C.CrystalstructureoftheheterodimericbZIPtranscriptionfactorc-Fos-c-JunboundtoDNA. Nature 1995, 373,257–261.
15. Culler,M.;ShalenP.B.Varietiesofgrouprepresentationsandsplittingof3-manifolds. Ann.Math. 1983, 117,109–146.
16. Cooper,D.;Culler,M.;Gillet,H.;Long,D.D.;Shalen,P.B.Planecurvesassociatedtocharactervarietiesof 3-manifolds. Invent.Math. 1994, 118,47–84.
17. ZeemanE.C.Linkingspheres. Abh.Math.Sem.Univ.Hambg. 1960, 24,149–153.
18. RolfsenD. KnotsandLinks;AMSChelseaPublishing:Providence,RI,USA,2000.
19. Ashley,C.;BurelleJ.P.;Lawton,S.Rank1charactervarietiesoffinitelypresentedgroups. Geom.Dedicata 2018, 192,1–19.
20. Liskovets,V.;Mednykh,A.Onthenumberofconnectedanddisconnectedcoveringsoveramanifold. ArsMath.Contemp. 2009, 2, 181–189.
21. Goldman,W.M.TracecoordinatesonFrickespacesofsomesimplehyperbolicsurfaces.In HandbookofTeichmüllerTheory; EuropeanMathematicalSociety:Zurich,Switzerland,2009;Volume13,pp.611–684.
22. Cantat,S.;Loray,F.Holomorphicdynamics,PainlevéVIequationandcharactervarieties. arXiv 2007,arXiv:0711.1579v2.
23. Sandelin,A.;Alkema,W.;Engström,P.;Wasserman,W.W.;Lenhard,B.JASPAR:Anopen-accessdatabaseforeukaryotic transcriptionfactorbindingprofiles. NucleicAcidsRes. 2004, 32,D91–D94.Availableonline: https://jaspar.genereg.net/ (accessed on1January2022).
24. LambertS.A.;JolmaA.;CampitelliL.F.;DasP.K.;YinY.;AlbuM.;ChenX.;TalpaleJ.;HughesT.R.;WeirauchM.T.Thehuman transcriptionfactors. Cell 2018, 172,650–665.Availableonline: http://www.edgar-wingender.de/huTF$_$classification.html (accessedon1January2022).
25. Lantz,K.A.;Vatamaniuk,M.Z.;Brestelli,J.E.;Friedman,J.R.;Matschinsky,F.M.;Kaestner,K.H.Foxa2regulatesmultiplepathways ofinsulinsecretion. J.Clin.Investig. 2004, 114,512–520.
26. José-Edwards,D.S;Oda-Ishii,I.;KuglerJ.E.,Passamaneck,Y.J.;Katikala,L.;Nibu,Y.;DiGregorio,A.Brachyury,Foxa2andthe cis-RegulatoryOriginsoftheNotochord. PLoSGenet. 2015, 11,e1005730.https://doi.org/10.1371/journal.pgen.1005730.
27. Ray,B.K.;Dhar,S.;Shakya,Ray,A.Z-DNA-formingsilencerinthefirstexonregulateshumanADAM-12geneexpression. Proc.Natl.Acad.Sci.USA 2011, 108,103–106.
28. Ravichandran,S.;Subramani,V.K.;Kil,K.K.Z-DNAinthegenome:Fromstructuretodisease. Biophys.Rev. 2019, 11,383–387.
29. Nugent,C.I;Lundblad,V.Thetelomerasereversetranscriptase:Componentsandregulation. GeneDev. 1998, 12,1073–1085.
30. Dai,J.;Punchihewa,C.;Ambrus,A.;ChenD.;JonesR.A.;Yang,D.StructureoftheintramolecularhumantelomericG-quadruplex inpotassiumsolution:Anoveladeninetripleformation. Nucl.AcidsRes. 2007, 35,2440–2450.
31. Hu,L.;Lim,K.W.;Bouazuz,S.;Phan,A.T.GiardiaTelomericSequenced(TAGGG)4FormsTwoIntramolecularG-Quadruplexes inK+Solution:EffectofLoopLengthandSequenceontheFoldingTopology. J.Am.Chem.Soc. 2009, 131,16824–16831.
32. Kettani,A.;Bouazziz,S.;Wang,W.;Jones,R.A.;Patel,D.J.BombyxmorisinglerepeattelomericDNAsequenceformsa G-quadruplexcappedbybasetriads. Nat.Struc.Biol. 1997, 4,383–389.
33. Fulne˘cková,J.;Hasíková,T.;FajkusJ.;Luke˘sová,A.;Eliá˘s,M.Sýkorová,E.DynamicEvolutionofTelomericSequencesinthe GreenAlgalOrderChlamydomonadales. GenomeBiol.Evol. 2012, 4,248–264.
34. Gavory,G.;Farrow,M.;Balasubramanian,S.MinimumlengthrequirementofthealignmentdomainofhumantelomeraseRNA tosustaincatalyticactivityinvitro. Nucl.AcidsRes. 2002, 30,4470–4480.
Int.J.Mol.Sci. 2022, 23,13290
35. Parkinson,G.N.;Ghosh,R.;Neidle,S.Structuralbasisforbindingofporphyrintohumantelomeres. Biochemistry 2007, 46, 2390–2397.
36. Zhang,N.;Phan,A.T.;Patel,D.J.(3+1)assemblyofthreehumantelomericrepeatsintoanasymmetricdimericG-Quadruplex. J.Am.Chem.Soc. 2005, 127,17277–17285.
37. Kang,C.;Zhang,X.;Ratliff,R.;Moyzis,R.;Rich,A.Crystalstructureoffour-strandedOxytrichatelomericDNA. Nature 1992, 356, 126–131.
38. Laughlan,G.;Murchie,A.I.H.;NormanD.H.;Moore,M.H.;Moody,P.C.E.;LilleyD.M.J.;Luisi,B.TheHigh-ResolutionCrystal StructureofaParallel-StrandedGuanineTetraplex. Science 1994, 265,520–524.
39. M.Planat,R.Aschheim,M.M.Amaral,F.FangandK.Irwin.Quantuminformationintheproteincodes, 3-manifoldsandthe Kummersurface. Symmetry 2021, 13,39.
40. Bansal,A.;Kaushik,S.;Kukreti,S.Non-canonicalDNAstructures:Diversityanddiseaseassociation. Front.Genet. 2022, 13, 959258.https://doi.org/10.3389/fgene.2022.959258.
41. Planat,M.;Chester,D.;Amaral,M.;IrwinK.Fricketopologicalqubits. Preprints 2022 .https://doi.org/10.20944/preprints202210.0125.v1.
42. Matsutani,S.;Previato,E.Analgebro-geometricmodelforthshapeofsupercoliedDNA. Phys.DNonlinearPhenom. 2022, 430,133073.
43. Rand,D.A.,Raju,A.;Saez,M.;Siggia,E.D.Geometryofgeneregulatorydynamics. Proc.Natl.Acad.Sci.USA 2021, 118, e2109729118.https://doi.org/10.1073/pnas.2109729118.
