Procesos Estocásticos
M O D E L O D E C O L A S
ELEMENTOS DE UN MODELO DE COLAS
Los elementos principales que hay que conocer para entender un modelo de colas son el cliente y el servidor. El cliente es aquel que, en busca de un servicio, llega a una instalación partiendo de una fuente, y es atendido por el servidor. Una vez en la instalación, el cliente puede ser atendido de inmediato o esperar formado en una cola, en caso que la instalación esté en uso en ese momento. Una vez la instalación queda libre, el siguiente en cola es atendido por el servidor, y se repite este proceso hasta que la cola esté vacía.
MODELO DE COLAS GENERAL DE POISSON
El modelo de colas general en función de una suposición Poisson, es decir, siguiendo una distribución exponencial, se basa en el estado estable de las colas en el sistema, el cual se alcanza cuando dicho sistema ha estado en funcionamiento por un tiempo lo suficientemente largo y ha alcanzando un nivel de funcionamiento constante. En este sentido, el modelo general asume que la tasa de entrada y salida del sistema dependen de la cantidad de personas que se encuentren en la cola, ya que es habitual una tendencia de acelerar el proceso cuando hay demasiados clientes en espera (por ejemplo, una caseta de cobro en una carretera durante la hora pico).
MODELOS DE UN SOLO SERVIDOR
Este tipo de modelos consideran una situación donde la afluencia de los clientes desde la fuente es infinita, y dichos clientes son atendidos por un único servidor en la instalación. Los modelos de un sólo servidor se dividen en dos:
(M/M/1):(GD/∞/∞). Los clientes entran a la instalación siguiendo una distribución exponencial, y no se limita la cantidad de clientes que pueda haber en el sistema (puede ser infinita).
(M/M/1):(GD/N/∞).Los clientes entran a la instalación siguiendo una distribución exponencial, y la cantidad de clientes que pueda haber en el sistema es limitada conforme al valor de N (no se permite la entrada a nuevos clientes si el sistema ya alberga N clientes).
Víctor Parra
MODELOS DE VARIOS SERVIDORES
Tipo de sistema que tiene una sola cola de espera y varios servidores que atienden a los clientes que llegan. Este modelo se usa para analizar y optimizar la eficiencia y productividad de los sistemas de atención al cliente y procesos de producción Algunos s , Para estudiar este modelo, se usan herramientas matemáticas como la teoría de colas, que se basa en supuestos como que las llegadas de los clientes son aleatorias y siguen una distribución de Poisson, que los tiempos de servicio son independientes y siguen una distribución exponencial, que la disciplina de la cola es primero en llegar, primero en salir (FIFO), y que la capacidad de la cola es infinita.
Con estas suposiciones, se pueden calcular las características de operación del sistema, como la probabilidad de que haya clientes en la cola, el número promedio de clientes en el sistema, el tiempo promedio de espera en la cola, el tiempo promedio de permanencia en el sistema, la utilización de los servidores, etc.
Estas características de operación permiten evaluar el desempeño del sistema y tomar decisiones sobre el número óptimo de servidores, la tasa de servicio, el costo de espera, el costo de operación, etc. Así, se puede mejorar la satisfacción de los clientes, reducir los tiempos de espera, aumentar la productividad, y maximizar los beneficios.
Tipo de sistema de colas que tiene una fuente finita de clientes, que son las máquinas que se descomponen y requieren reparación. El sistema tiene una sola cola de espera y R servidores o mecánicos que atienden a las máquinas descompuestas a una tasa µ. El número total de máquinas en el taller es K, y la tasa de descomposturas por máquina es λ. Este modelo se usa para analizar y optimizar el funcionamiento y el mantenimiento de un taller con máquinas automáticas
Modelo de aprendizaje automático que se utiliza para predecir la confiabilidad de las máquinas. Se basa en un conjunto de datos de características de máquinas, como la antigüedad, el historial de mantenimiento y las condiciones de funcionamiento. El modelo utiliza estas características para aprender la relación entre ellas y la confiabilidad de la máquina.
SISTEMA (M/G/1):(GD/
Este sistema en la teoría de colas, representa un sistema con un solo servidor, donde las llegadas siguen una distribución de Poisson y los tiempos de servicio siguen una distribución general. La disciplina de servicio es general, donde los clientes se agrupan en lotes y parten del sistema juntos después de su servicio. El sistema tiene un número infinito de servidores para cada lote, lo que da a lugar que no haya espera para el servicio dentro de un lote.
Kevin Gil
C.I.:30.381.542
FÓRMULA P-K
Para la realización de estos sistemas como es el (M/G/1): (GD/∞/∞) se suele utilizar la formula PollaczekKhintchine (P-K) para calcular la longitud media de la cola (L) en un sistema de colas en estado estable la formula seria:
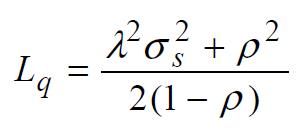
La fórmula P-K es una herramienta valiosa para analizar el rendimiento de sistemas de colas con un solo servidor y una distribución general de tiempos de servicio, pero tenga esta solo se debe utilizado en el caso de que sea un sistema en estado estable, es decir, cuando el promedio de clientes que llegan al sistema es igual al promedio de clientes que lo abandonan.
