Chapter 2 Graphs and Functions
5.
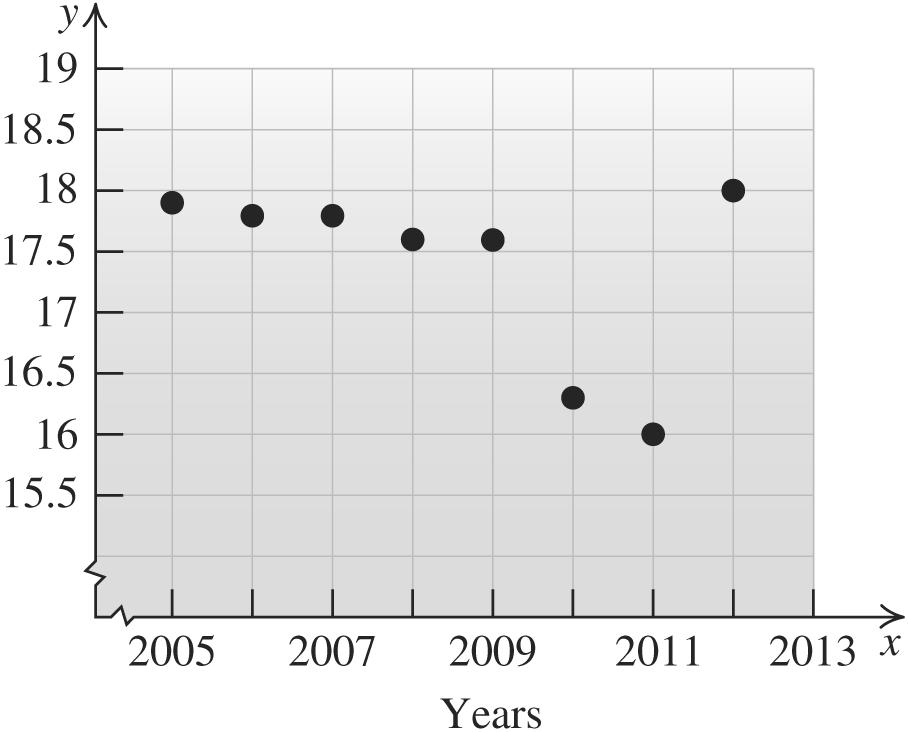
Weareaskedtofindthedistancebetweenthe points A(60,0)and B(0,60).
6.
2.1 Basic Concepts and Skills
1. Apointwithanegativefirstcoordinateanda positivesecondcoordinateliesinthesecond quadrant.
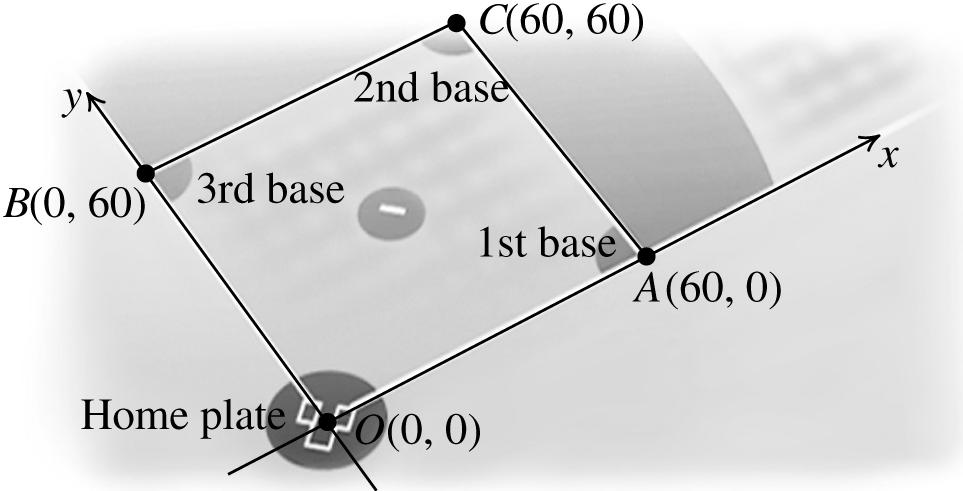
2. Anypointonthe x-axishassecondcoordinate 0
3. Thedistancebetweenthepoints ( ) 11 , Pxy and ( ) 22 , Qxy isgivenbytheformula
()() 22 2121 ,.dPQxxyy =−+−
4. Thecoordinatesofthemidpoint M(x, y)ofthe linesegmentjoining ( ) 11 , Pxy and ( ) 22 , Qxy aregivenby
1212 ,,. 22 xxyy
5. True
6. False.Thepoint(7,−4)is4unitstotheright and6unitsbelowthepoint(3,2).
Copyright©2015PearsonEducationInc.
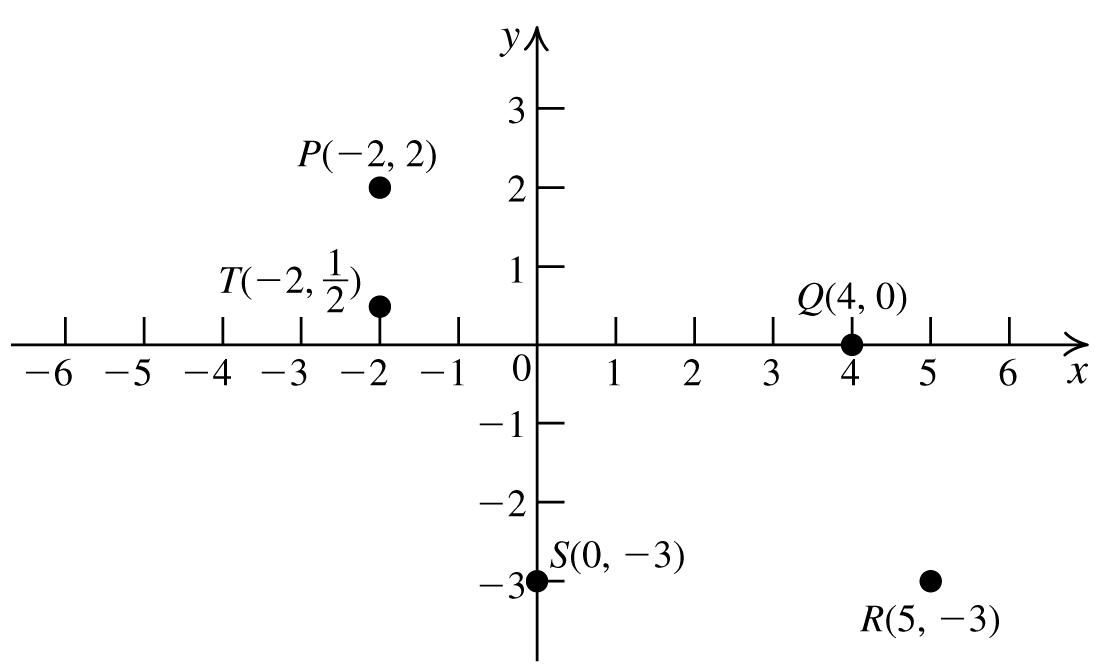
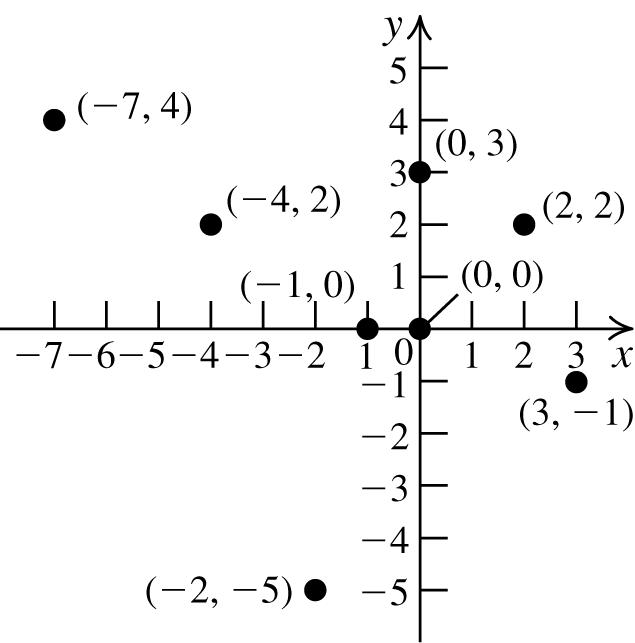
7.
(2,2):Q1;(3,−1):Q4;(−1,0): x-axis (−2,−5):Q3;(0,0):origin;(−7,4):Q2 (0,3): y-axis;(−4,2):Q2
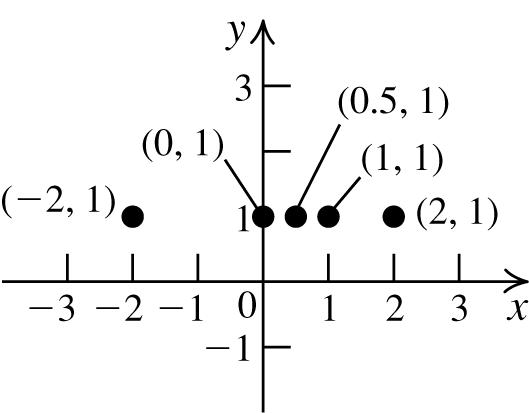
8. a. Answerswillvary.Sampleanswer: (2,0),(1,0),(0,0),(1,0),(2,0) The y-coordinateis0.
b.
Thesetofallpointsoftheform(x,1)is ahorizontallinethatintersectsthe y-axis at1.
9. a. Ifthe x -coordinateofapointis0,thepoint liesonthe y-axis.
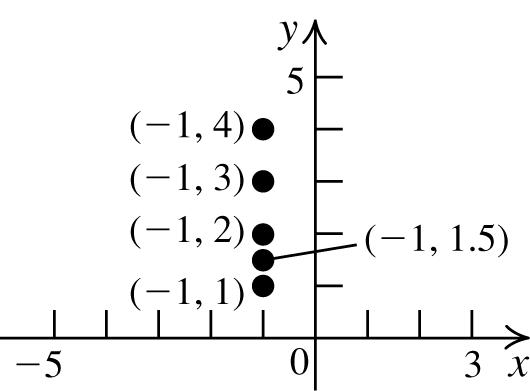
b.
Thesetofallpointsoftheform(–1, y)isa verticallinethatintersectsthe x-axisat–1.
10. a. Averticallinethatintersectsthe x-axis at–3.
b. Ahorizontallinethatintersectsthe y -axis at4.
11. a. 0 y > b. 0 y <
c. 0 x < d. 0 x >
12. a. QuadrantIII b. QuadrantI
c. QuadrantIV d. QuadrantII
InExercises13−22,usethedistanceformula, ()() 22 2121 dxxyy =−+− andthemidpoint
formula,1212 (,),22 xxyy xy ++ ⎛ ⎞ = ⎜
13. a. 222 (22)(51)44 d =−+−==
b. () 2215 ,2,3 22 M ++ ⎛⎞ ==
14. a. 222 (23)(55)(5)5 d =−−+−=−=
b. () 3(2)55,0.5,5 22 M +−+ ⎛⎞ == ⎜⎟
15. a. 22 22 (2(1))(3(5)) 3213 d =−−+−−− =+=
b. () 125(3),0.5,4 22 M −+−+− ⎛⎞ ==−
16. a. 22 22 (7(4))(91) (3)(10)109 d =−−−+−− =−+−=
b. () 4(7)1(9),5.5,4 22 M −+−+− ⎛⎞ ==−−
17. a. 22 22 (3(1))(6.51.5) 4(8)8045 d =−−+−− =+−==
b. () 131.5(6.5),1,2.5 22 M −++− ⎛⎞ ==−
18. a. 22 22
d =−+−− =+−===
(10.5)(10.5) 510 (0.5)(1.5)2.522
b. () 0.510.5(1),0.75,0.25 22 M ++− ⎛⎞ ==− ⎜⎟ ⎝⎠
19. a. () 222 22(54)11 d =−+−==
b. () 2245 ,2,4.5 22 M ⎛⎞ ++ == ⎜⎟
=+−−+− ==
20. a. 22 2 (()())() (2)2 dvwvwtt ww
Copyright©2015PearsonEducationInc.
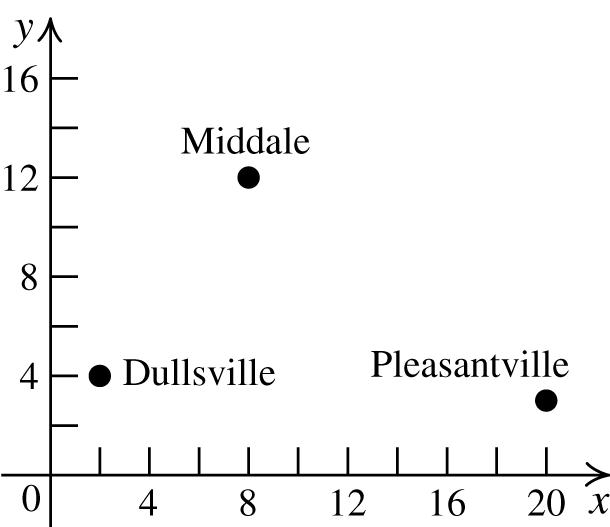
32. First,findthemidpoint M of PQ ( ) () 816412 ,4,4 22 M ⎛+−⎞ −+ ==− ⎜⎟
Nowfindthemidpoint R of PM. ( ) () 8444 ,2,0 22 R ⎛+−⎞ −+ ==− ⎜⎟
Finally,findthemidpoint S of MQ. ( ) () 416412 ,10,8 22 S ⎛−+−⎞ + ==−
Thus,thethreepointsare(−2,0),(4,−4),and (10,−8).
22 22
22 22 22
Copyright©2015PearsonEducationInc.
Allthesidesareequal,sothequadrilateralis eitherasquareorarhombus.Nowfindthe lengthofthediagonals:
dPR dQS
()()2222
(5)02(2)(03)
()()
(,)14711(12)172
(,)22(1)43172
()() 22 22
=−+−−= =−−+−−=
Thediagonalsareequal,sothequadrilateralis asquare.
42. Firstfindthelengthsofthesides:
Thecoordinatesof R are 8 ,0 7
dRS dSP
()()
(,)9811(10)2
(,)8912(11)2 dPQ dQR
=−+−−−= =−+−−−=
()() 22 22
46. P =(7,–4), Q =(8,3), R =(0, y)(R isonthe y-axis,sothe x -coordinateis0).
(,)7811(12)2
(,)8710(11)2
dPR dQS
=−+−−−= =−+−−−=
()() ()() 22 22
Allthesidesareequal,sothequadrilateralis eitherasquareorarhombus.Nowfindthe lengthofthediagonals.
()() 22 22 (,)07(4) (,)(08)(3) dPRy dQRy =−+−− =−+−
()() 22 22 07(4) (08)(3) y y
−+−− =−+−
(,)8812(10)2
(,)7911(11)2
()() ()() 22 22
=−+−−−= =−+−−−=
Thediagonalsareequal,sothequadrilateralis asquare. 43. ()() 22
yy yyyy yy +−−=+− +++=+−+ +=−+ = =
Thecoordinatesof R are 4 0, 7
⎛⎞ ⎜⎟ ⎝⎠ .
47.
48.
45. P =(–5,2), Q =(2,3), R =(x,0)(R isonthe x-axis,sothe y -coordinateis0).
()() 22 22 (,)(5)02 (,)(2)(03) dPRx dQRx =−−+− =−+−
()
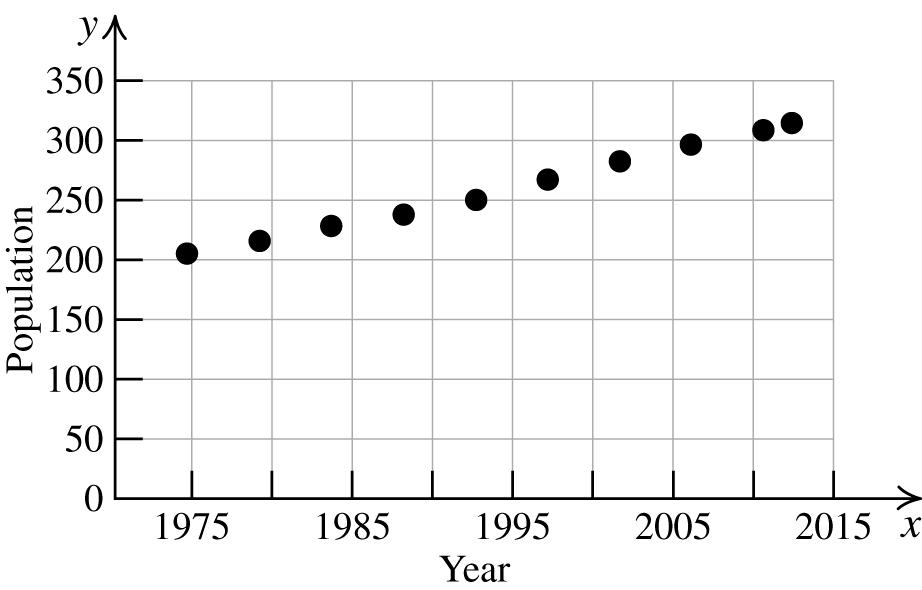
20002012282314 , 22 2006,298
M ++ ⎛ ⎞ = ⎝ ⎠ = Themidpointofthesegmentgivesagood approximationtotheactualvalue,about300 million.
Copyright©2015PearsonEducationInc.
53. 16,92914,61215,770.5 2 M + ==
Therewereabout15,771murdersin2009.
54. 2009isthemidpointoftheinitialrange,so 2009 228320 274 2 M + == .
2008isthemidpointoftherange [2007,2009],so2008 228274 251 2 M + ==
2010isthemidpointoftherange [2009,2011],so2010 274320 297 2 M + == .
So,in2008,$251billionwasspent;in2009, $274billionwasspent,and$297wasspentin 2010.
55. 2008isthemidpointoftheinitialrange,so
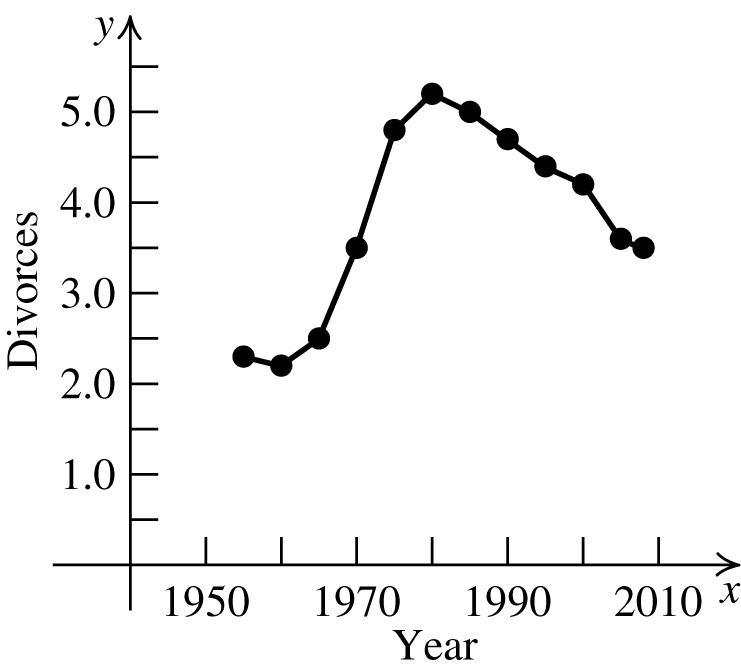
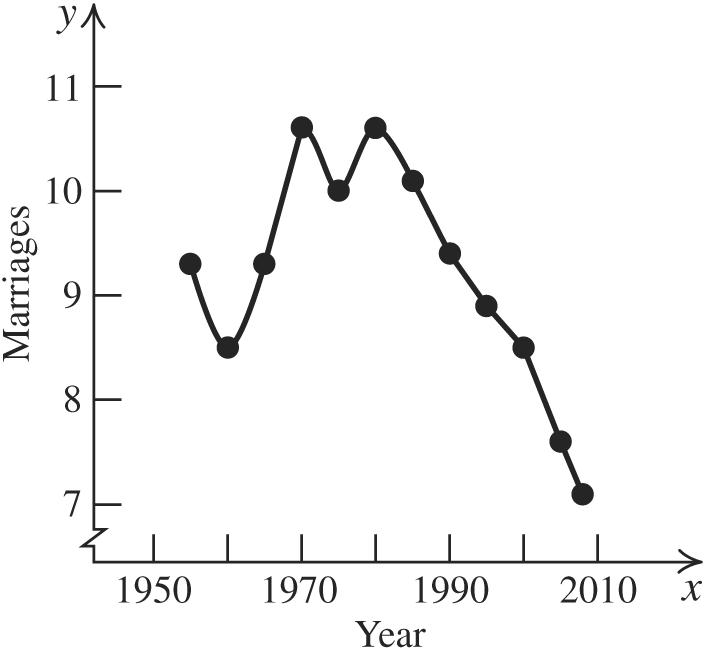
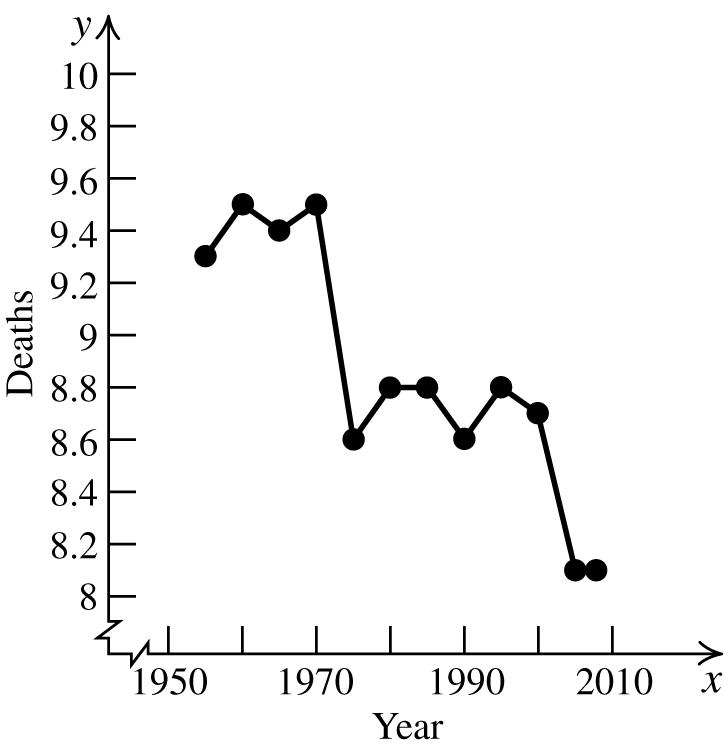
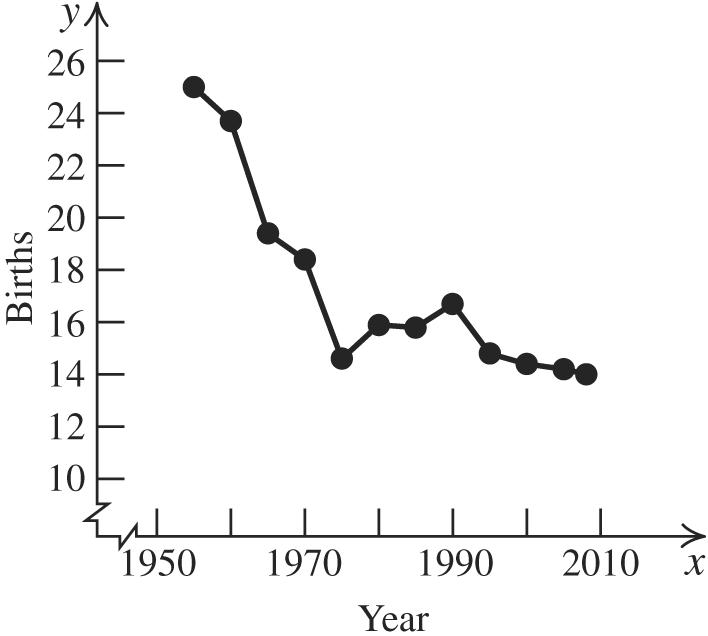
2008 548925 736.5 2 M + ==
2006isthemidpointoftherange [2004,2008],so
2006 548736.5 642.25 2 M + ==
2005isthemidpointoftherange [2004,2006],so
2005 548642.25 595.125 2 M + == .
2007isthemidpointoftherange [2006,2008],so
2007 642.25736.5 689.375 2 M + ==
Usesimilarreasoningtofindtheamountsfor 2009,2010,and2011.Defensespendingwas asfollows:
YearAmountspent
2004$548billion
2005$595.125billion
2006$642.25billion
2007$689.375billion
2008$736.5billion
2009$783.625billion
2010$830.75billion
2011$877.875billion
2012$925billion
56. Denotethediagonalconnectingtheendpoints oftheedges a and b by d.Then a, b,and d formarighttriangle.BythePythagorean theorem,222 abd += .Theedge c andthe diagonals d and h alsoformarighttriangle,so 222 cdh += .Substituting2 d fromthefirst equation,weobtain2222 abch ++=
Copyright©2015PearsonEducationInc.
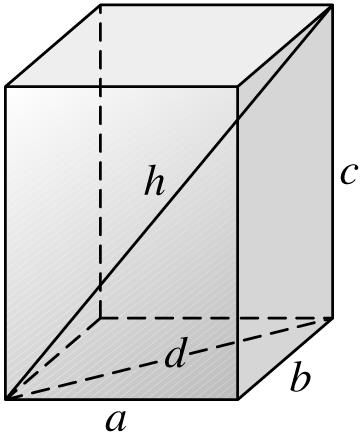
60. a. If AB isoneofthediagonals,then DC isthe otherdiagonal,andbothdiagonalshavethe samemidpoint.Themidpointof AB is
⎜⎟ ⎝⎠
.Themidpointof
⎛⎞
⎜⎟ ⎝⎠
dDM dMP
(,)(800200)(1200400) 1000
=−+− = =−+−
b. 22 22
(,)(2000800)(3001200) 1500
Thedistancetraveledbythepilot =1000+1500=2500miles.
Sowehave 3 3.54 2 x x + =⇒= and 8 3.5 2 y + =⇒ 1 y =−
Thecoordinatesof D are(4,–1).
b. If AC isoneofthediagonals,then DB isthe otherdiagonal,andbothdiagonalshavethe samemidpoint.Themidpointof AC is
c. 22 (,)(2000200)(300400)
dDP =−+−
58. First,findtheinitiallengthoftheropeusing thePythagoreantheorem:
22 241026 c =+=
⎛⎞
=
.Themidpointof
⎜⎟ ⎝⎠
Sowehave 5 2.50 2 x x + =⇒= and 4 5.5 2 y + =⇒ 7 y =
Thecoordinatesof D are(0,7).
tx ttx ttx ttx −=+ −+=+ −+= −+=
22 22 2 (263)10 6761569100 5761569 5761569
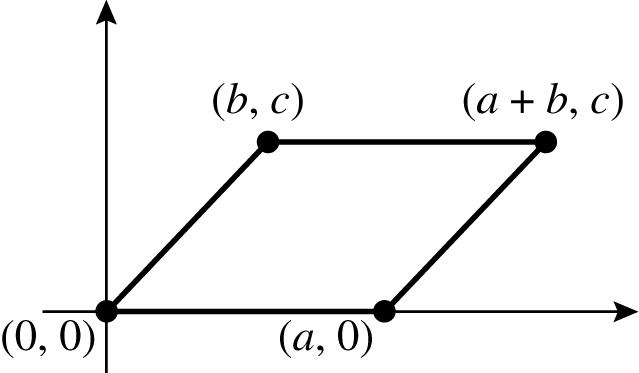
59. Themidpointofthediagonalconnecting(0,0) and(a + b, c)is,. 22 abc + ⎛⎞ ⎜⎟ ⎝⎠ Themidpointof thediagonalconnecting(a,0)and(b, c)is also,. 22 abc + ⎛⎞ ⎜⎟ ⎝⎠ Becausethemidpointsof thetwodiagonalsarethesame,thediagonals bisecteachother.
c. If BC isoneofthediagonals,then DA isthe otherdiagonal,andbothdiagonalshavethe samemidpoint.Themidpointof BC is
⎜⎟ ⎝⎠
.Themidpointof DA is 23 (4,6),. 22 xy++ ⎛ ⎞ = ⎜ ⎟ ⎝ ⎠ Sowehave 2 46 2 x x + =⇒= and 3 69 2 y y + =⇒= Thecoordinatesof D are(6,9).
61. Themidpointofthediagonalconnecting(0,0) and(x, y)is,22 xy ⎛ ⎞ ⎜ ⎟ ⎝ ⎠ .Themidpointofthe diagonalconnecting(a,0)and(b, c)is ,.22 abc + ⎛ ⎞ ⎜ ⎟ ⎝ ⎠ Becausethediagonalsbisecteach other,themidpointscoincide.So
22 xab + =⇒ xab =+ ,and 22 yc yc=⇒= Therefore,thequadrilateralisaparallelogram.
Copyright©2015PearsonEducationInc.
62. a. Themidpointofthediagonalconnecting (1,2)and(5,8)is () 1528 ,3,5. 22 ++ ⎛⎞ = ⎜⎟ ⎝⎠
Themidpointofthediagonalconnecting (–2,6)and(8,4)is
2864 ,(3,5).22 −++ ⎛⎞ = ⎜⎟ ⎝⎠ Becausethe midpointsarethesame,thefigureisa parallelogram.
b. Themidpointofthediagonalconnecting (3,2)and(x, y)is 32 ,.22 xy++ ⎛ ⎞ ⎜ ⎟ ⎝ ⎠ The midpointofthediagonalconnecting(6,3) and(6,5)is(6,4).So 3 69 2 x x + =⇒= and 2 46 2 y y + =⇒=
63. Let P(0,0), Q(a,0), R(a + b, c),and S(b, c)be theverticesoftheparallelogram. PQ = RS = 22 (0)(00). aa −+−= QR = PS =
() 2222 ()(0). abacbc +−+−=+
Thesumofthesquaresofthelengthsofthe sides=2222(). abc ++
22
(,)(). dPRabc =++
() 22 (,)(0). dQSabc =−+−
Thesumofthesquaresofthelengthsofthe diagonalsis ( ) ( ) 2222()() abcabc +++−+=
222222 22 aabbcaabbc ++++−++= 222222 2222(). abcabc ++=++
ab dRMb abab ab dPM abab
22 2222 22 2222
65. Let P(0,0), Q(a,0),and R(0, a)bethe verticesofthetriangle.
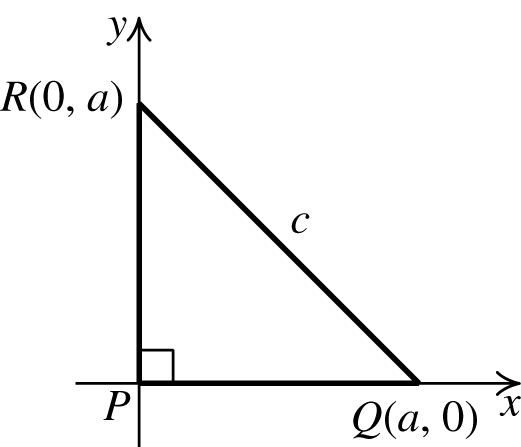
=−+−⎛⎞⎛⎞
(,)022 222
ab dQMa abab =−+−⎛⎞⎛⎞ ⎜⎟⎜⎟ ⎝⎠⎝⎠ + ⎛⎞⎛⎞ =−+= ⎜⎟⎜⎟ ⎝⎠⎝⎠ =−+−⎛⎞⎛⎞ ⎜⎟⎜⎟ ⎝⎠⎝⎠ + ⎛⎞⎛⎞ =−+−= ⎜⎟⎜⎟ ⎝⎠⎝⎠
caacaca acc
=+⇒=⇒=⇒ ==
UsingthePythagoreantheorem,wehave 2222222 12 22
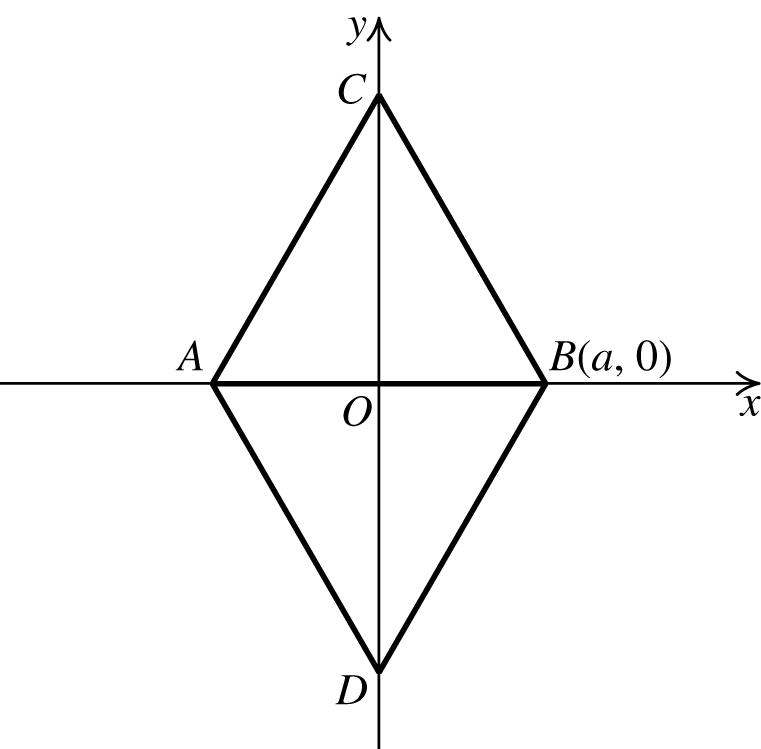
66. Since ABC isanequilateraltriangleand O is themidpointof AB,thenthecoordinatesof A are(−a,0).
AB = AC = AB =2a.Usingtriangle BOC and thePythagoreantheorem,wehave ()2 22222 22222 2 433 BCOBOCaaOC aaOCaOCOCa =+⇒=+⇒ =+⇒=⇒= Thus,thecoordinatesof C are ( ) 0,3a and thecoordinatesof D are ( ) 0,3. a
Copyright©2015PearsonEducationInc.
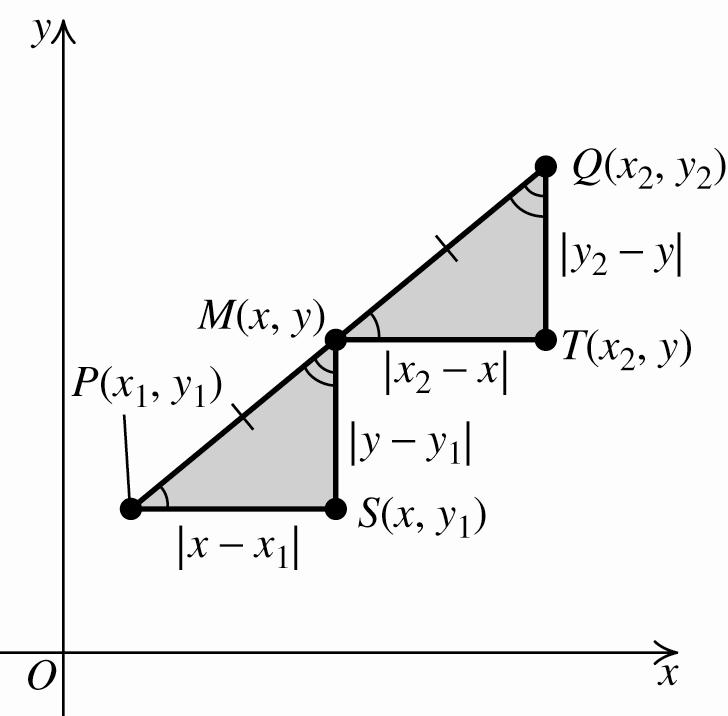
Toshowthat M isthemidpointoftheline segment PQ,weneedtoshowthatthe distancebetween M and Q isthesameasthe distancebetween M and P andthatthis distanceishalfthedistancefrom P to Q (continuedonnextpage)
2.1 Critical Thinking/Discussion/Writing
69. a. y-axis
b. x-axis
70. a. Theunionofthe x-and y-axes
b. Theplanewithoutthe x-and y-axes
71. a. QuadrantsIandIII
b. QuadrantsIIandIV
72. a. Theorigin
b. Theplanewithouttheorigin
73. a. Righthalf-plane
b. Upperhalf-plane
74. Let(x, y)bethepoint. Thepointliesinif
QuadrantI x >0and y >0
QuadrantII x <0and y >0
QuadrantIII x <0and y <0
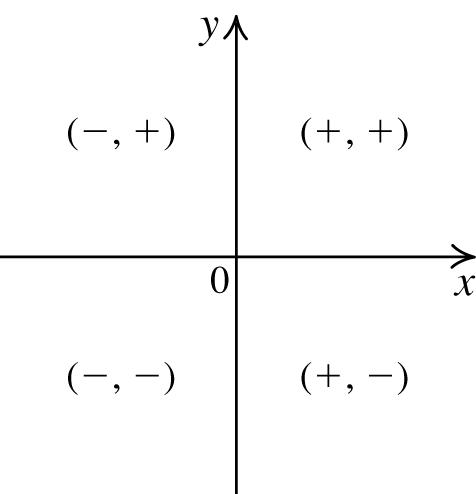
QuadrantIV x >0and y <0
2.1 Maintaining Skills
75. a. 22 22111121 224442 xy ⎛⎞⎛⎞ +=+=+==
b. 22 2222221 2244 xy
b.
Section 2.2 Graphs of Equations
2.2 Practice Problems
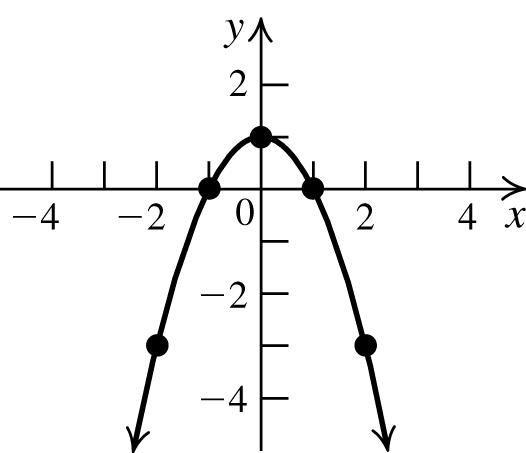
1. 21 yx=−+
x y = −x 2 + 1 (x, y)
−2 y =(−2)2+1(−2,−3)
−1 y =(−1)2+1(−1,0)
0 y =(0)2+1(0,1)
1 y =(1)2+1(1,0)
2 y =(2)2+1(2,−3)
2. Tofindthe x-intercept,let y =0,andsolvethe equationfor x: 2 0232 xx =+−⇒
()() 1 0212or2 2 xxxx =−+⇒==− .To findthe y-intercept,let x =0,andsolvethe equationfor y:
()() 2 203022.yy =+−⇒=−
The x-interceptsare 1 2 and−2;the y-intercept is−2.
3. Totestforsymmetryaboutthe y-axis,replace x with–x todetermineif(–x, y)satisfiesthe equation.
() 222211xyxy −−=⇒−= ,whichisthe sameastheoriginalequation.Sothegraphis symmetricaboutthe y-axis.
4. x-axis: () 3 223 , xyxy =−⇒=− whichisnot thesameastheoriginalequation,sothe equationisnotsymmetricwithrespecttothe x-axis.
y-axis: () 2323 , xyxy −=⇒= whichisthe sameastheoriginalequation,sotheequation issymmetricwithrespecttothe y-axis.
origin: ()()2323 , xyxy −=−⇒=− whichis notthesameastheoriginalequation,sothe equationisnotsymmetricwithrespecttothe origin.
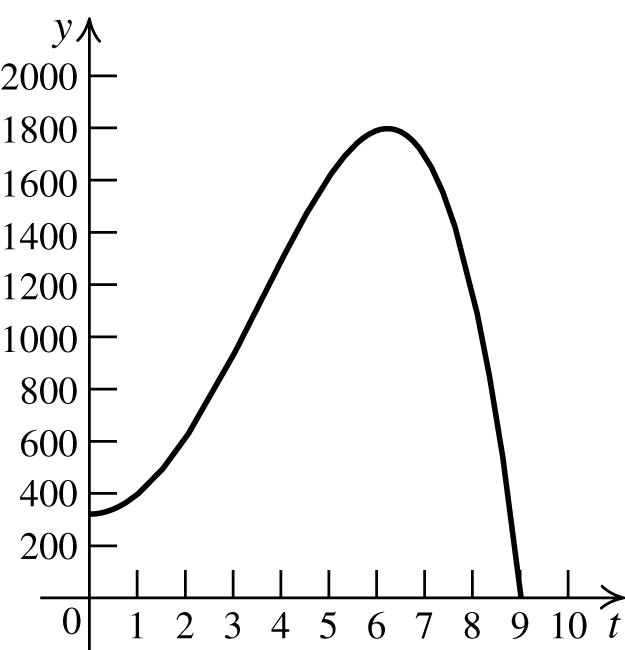
5. 4277324ytt=−++
a. First,findtheintercepts.If t =0,then y =324,sothe y-interceptis(0,324). If y =0,thenwehave
So,the
Next,checkforsymmetry.
t-axis:4277324ytt −=−++ isnotthe sameastheoriginalequation,sothe equationisnotsymmetricwithrespectto the t-axis.
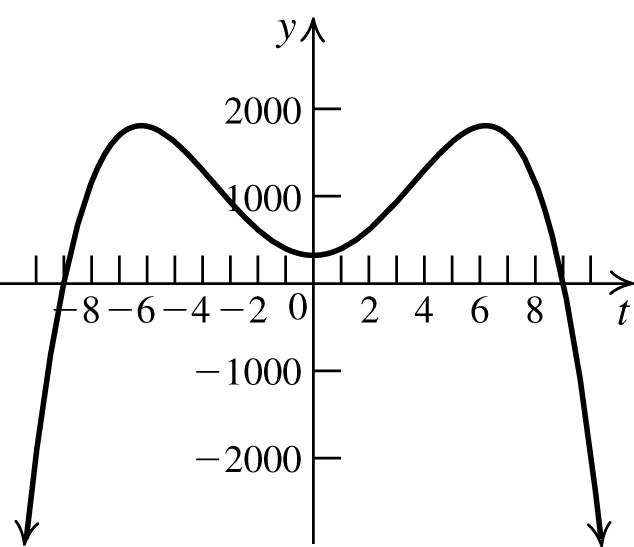
y-axis: ()() 4277324ytt =−−+−+⇒ 4277324,ytt=−++ whichisthesameas theoriginalequation.Sothegraphis symmetricwithrespecttothe y-axis.
origin: ()() 4277324ytt −=−−+−+⇒ 4277324,ytt −=−++ whichisnotthe sameastheoriginalequation.Sothegraph isnotsymmetricwithrespecttotheorigin. Now,makeatableofvalues.Sincethe graphissymmetricwithrespecttothe y-axis,if(t, y)isonthegraph,thensois (−t, y).However,thegraphpertainingto thephysicalaspectsoftheproblemconsists onlyofthosevaluesfor t ≥ 0.
t y = −t4 + 77t2 + 324 (t, y)
0324(0,324)
1400(1,400)
2616(2,616)
3936(3,936)
41300(4,1300)
51624(5,1624)
61800(6,1800)
71696(7,1696)
81156(8,1156)
90(9,0)
(continuedonnextpage)
Copyright©2015PearsonEducationInc.
c. Thepopulationbecomesextinctafter9 years.
6. Thestandardformoftheequationofacircle is222 ()() xhykr −+−= (h, k)=(3,−6)and r =10 Theequationofthecircleis 22 (3)(6)100. xy−++=
7. ()()()() 22 2136,2,1,6 xyhkr −++=⇒=−= Thisistheequationofacirclewithcenter (2,−1)andradius6.
2.2 Basic Concepts and Skills
1. Thegraphofanequationintwovariables, suchas x and y,isthesetofallorderedpairs (a, b)thatsatisfytheequation
2. If(–2,4)isapointonagraphthatis symmetricwithrespecttothe y-axis,thenthe point(2,4)isalsoonthegraph.
3. If(0,−5)isapointofagraph,then−5isa y- interceptofthegraph.
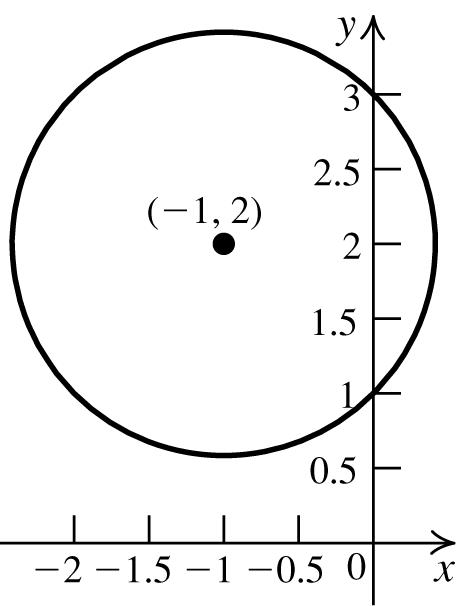
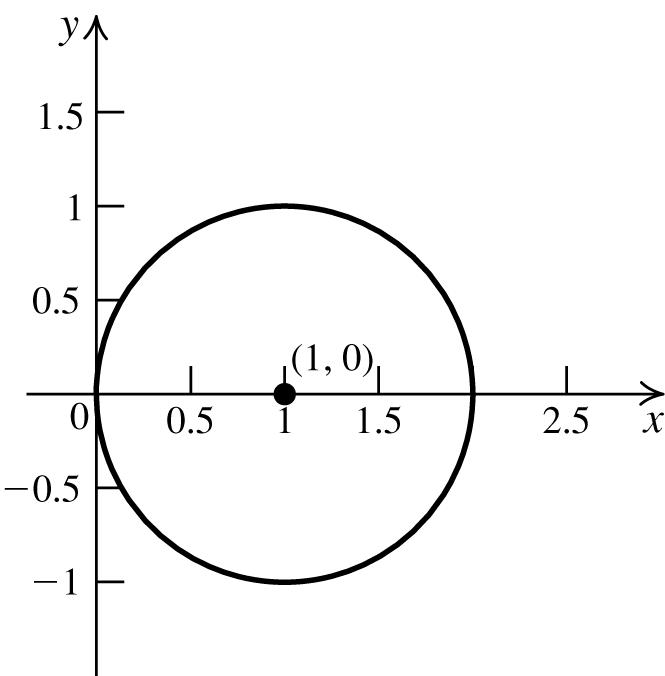
4. Anequationinstandardformofacirclewith center(1,0)andradius2is () 22 14xy−+= .
5. False.Theequationofacirclehasbothan 2 x -termanda2 y -term.Thegivenequation doesnothavea2 y -term.
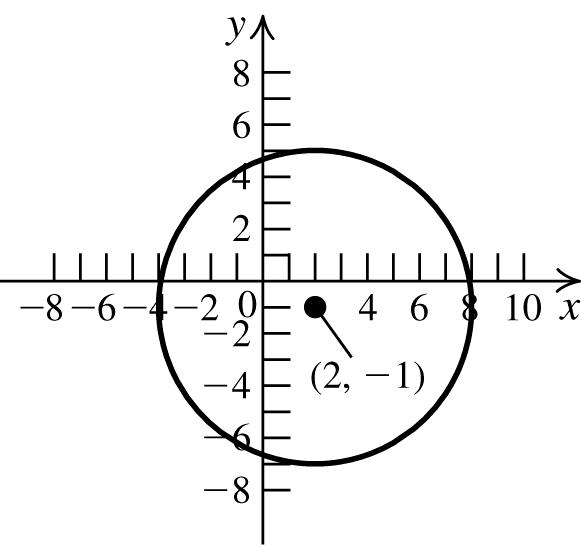
6. False.Thegraphbelowisanexampleofa graphthatissymmetricaboutthe x-axis,but doesnothavean x-intercept.
8. 2246120 xyxy++−−=⇒
224612xxyy++−= Nowcompletethesquare:
2244691249xxyy+++−+=++⇒
()() 22 2325xy++−= Thisisacirclewithcenter(−2,3)and radius5.
Inexercises7−14,todetermineifapointliesonthe graphoftheequation,substitutethepoint’s coordinatesintotheequationtoseeiftheresulting statementistrue.
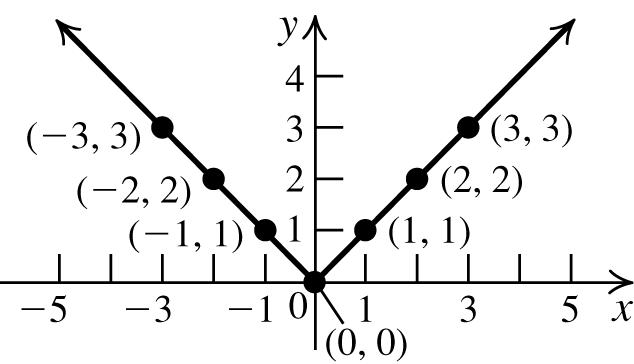
7. onthegraph:(–3,–4),(1,0),(4,3);notonthe graph:(2,3)
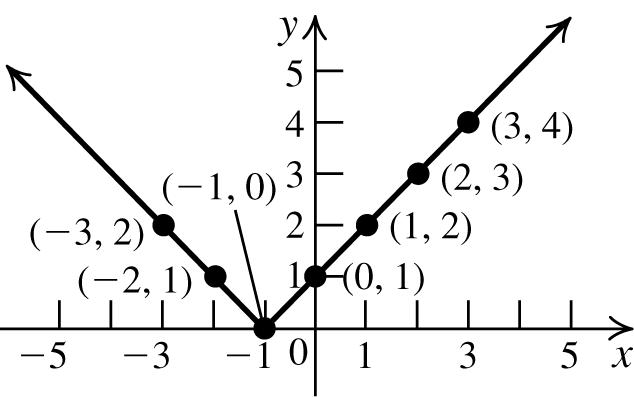
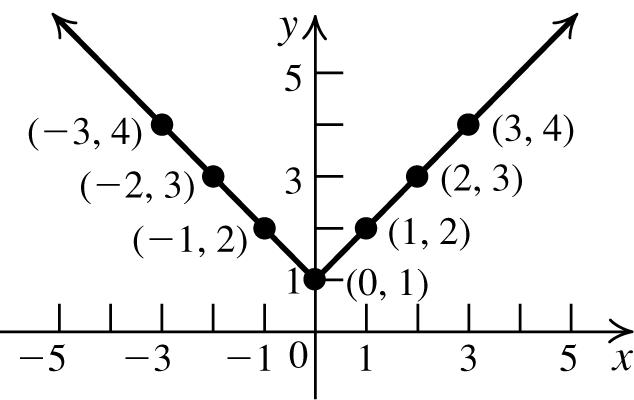
8. onthegraph:(–1,1),(1,4), 5 ,0 3 ⎛⎞
;noton thegraph:(0,2)
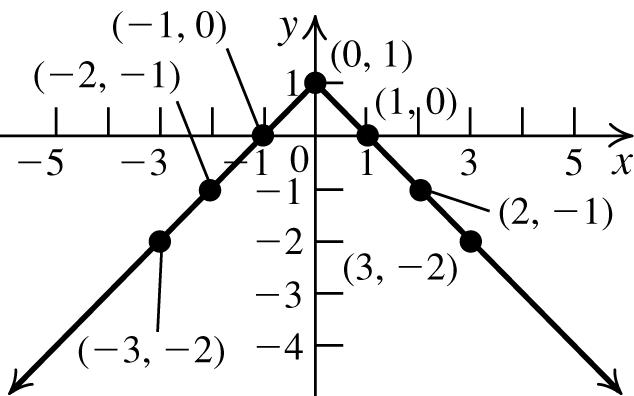
9. onthegraph:(3,2),(0,1),(8,3);notonthe graph:(8,–3)
10. onthegraph:(1,1), 1 2, 2 ⎛⎞ ⎜⎟ ⎝⎠ ;notonthegraph: (0,0), 1 3, 3
11. onthegraph:(1,0), ( ) ( ) 2,3,2,3;noton thegraph:(0,–1)
12. Eachpointisonthegraph.
13. a. x-intercepts:–3,3;no y-intercepts
Copyright©2015PearsonEducationInc.
b. Symmetricaboutthe x -axis, y -axis,and origin.
14. a. No x-intercepts; y-intercepts:–2,2
b. Symmetricaboutthe x -axis, y -axis,and origin.
15. a. x-intercepts:−3,3; y-intercepts:–2,2
b. Symmetricaboutthe x -axis, y -axis,and origin.
16. a. x-intercepts:−3,3; y-intercepts:–3,3
b. Symmetricaboutthe x -axis, y -axis,and origin.
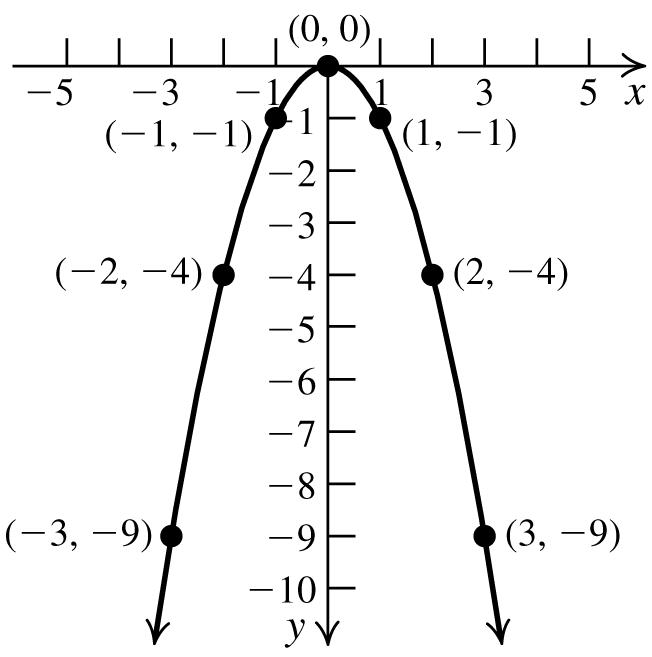
17. a. x-intercept:0; y-intercept:0
b. Symmetricaboutthe x -axis.
18. a. x-intercepts:,0,; ππ y-intercept:0
b. Symmetricabouttheorigin.
19. a. x-intercepts:−3,3; y-interceps:2
b. Symmetricaboutthe y -axis.
20. a. x-intercepts: 33 ,,,;2222 ππππ y-intercept:2
b. Symmetricaboutthe y -axis.
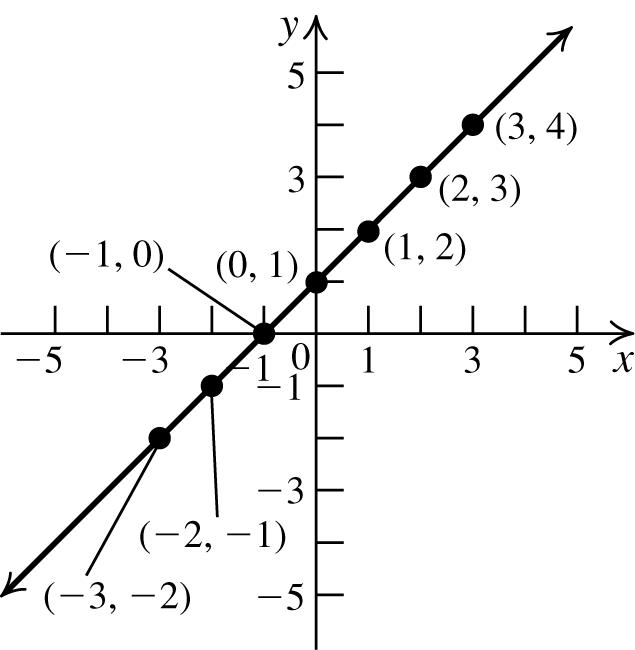
21. a. No x-intercept; y -intercept:1
b. Nosymmetries
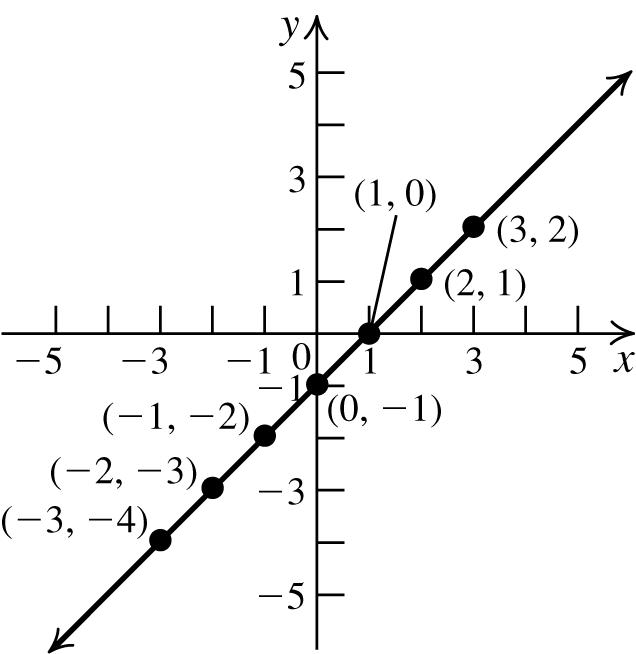
22. a. x-intercept:1;no y-intercepts
b. Nosymmetries
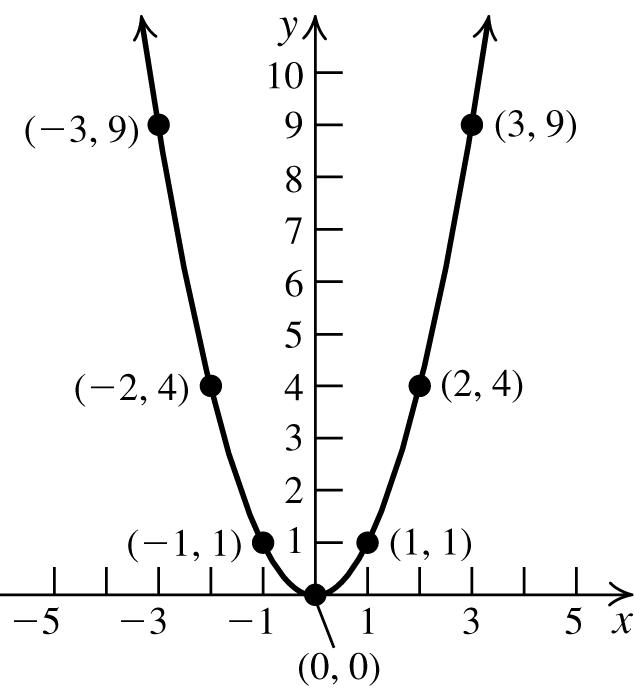
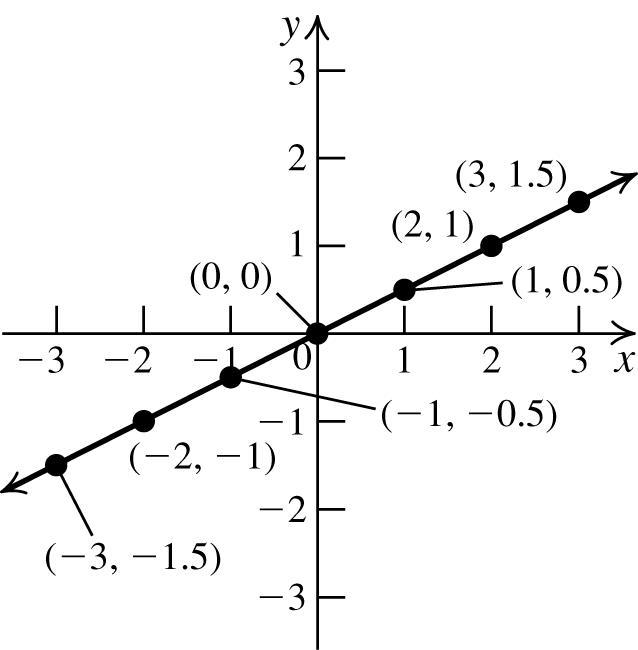
23. a. x-intercepts:0,3; y-intercept:0
b. Symmetricaboutthe x -axis.
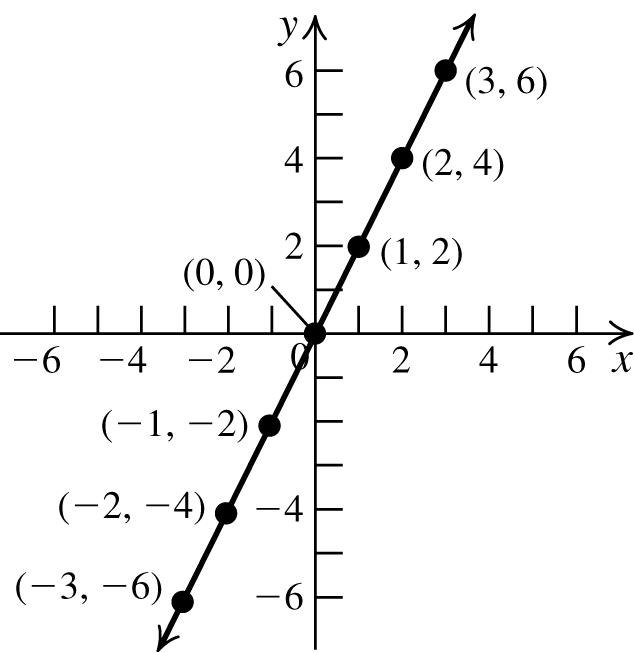
24. a. x-intercept:0; y-intercept:0
b. Symmetricaboutthe x -axis, y -axis,and origin.
Copyright©2015PearsonEducationInc.

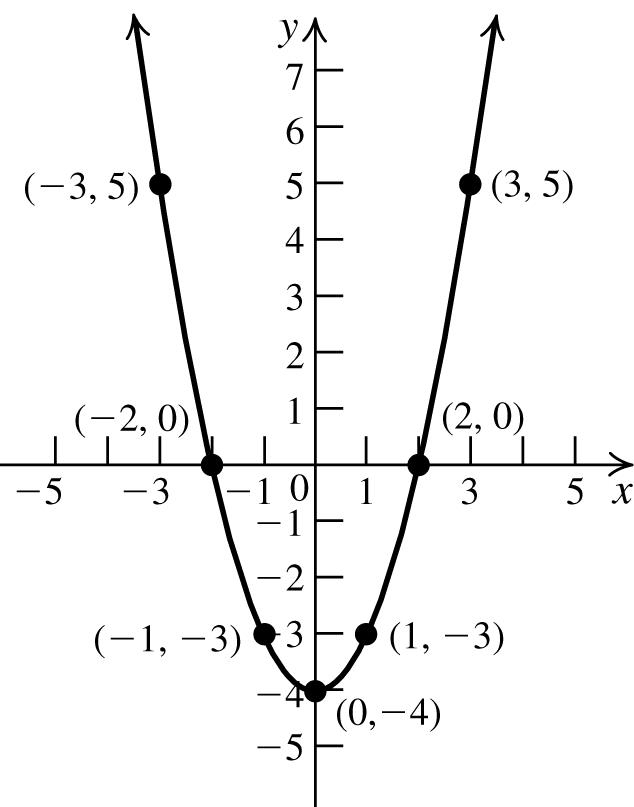


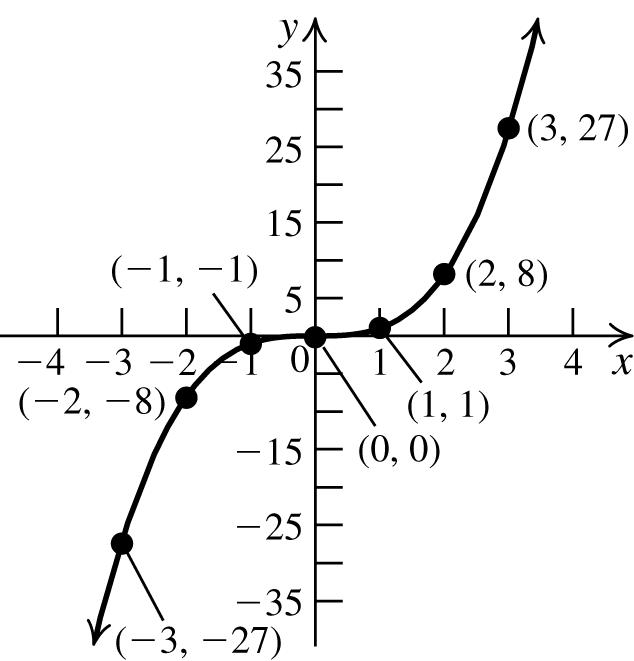
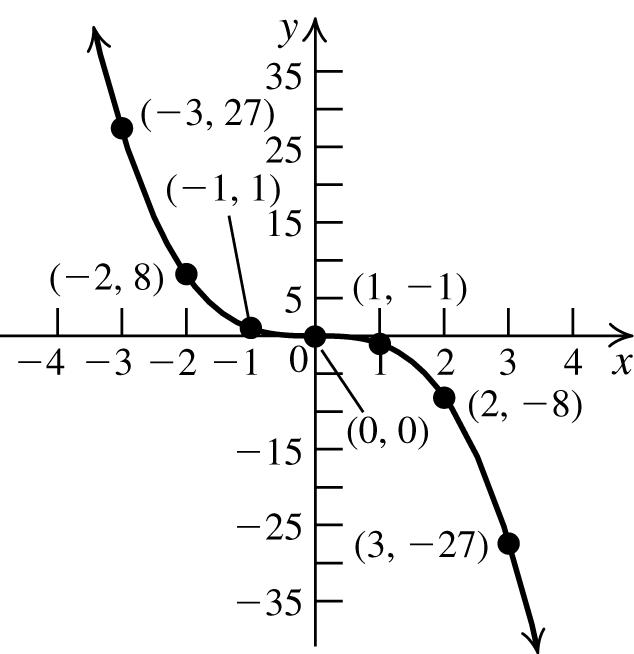
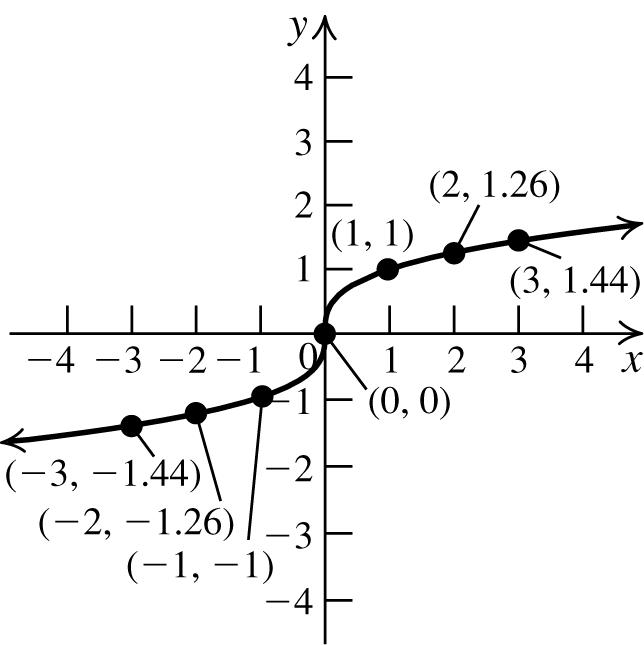

47. Tofindthe x -intercept,let y =0,andsolvethe equationfor x:34(0)124. xx +=⇒= To findthe y-intercept,let x =0,andsolvethe equationfor y:3(0)4123. yy +=⇒= The x-interceptis4;the y -interceptis3.
48. Tofindthe x -intercept,let y =0,andsolvethe equationfor x: 0 15. 53 x x +=⇒= Tofindthe y-intercept,let x =0,andsolvetheequation for y: 0 13. 53 y y +=⇒=
The x-interceptis5;the y -interceptis3.
49. Tofindthe x -intercept,let y =0,andsolvethe equationfor x: 2 0684or xxx =−+⇒=
2. x = Tofindthe y -intercept,let x =0,and solvetheequationfor y: 2 06(0)8 y =−+⇒
8. y = The x-interceptsare2and4;the y-interceptis8.
50. Tofindthe x -intercept,let y =0,andsolvethe equationfor x: 2 05(0)66.xx =−+⇒=
Tofindthe y -intercept,let x =0,andsolvethe equationfor y: 2 0562or yyy =−+⇒=
3. y = The x-interceptis6;the y -intercepts are2and3.
51. Tofindthe x -intercept,let y =0,andsolvethe equationfor x: 22042.xx+=⇒=±
Tofindthe y -intercept,let x =0,andsolvethe equationfor y: 22 042. yy +=⇒=±
The x-interceptsare–2and2;the y-intercepts are–2and2.
52. Tofindthe x -intercept,let y =0,andsolvethe equationfor x: 2 093. xx =−⇒=±
Tofindthe y -intercept,let x =0,andsolvethe equationfor y: 2 903.yy=−⇒= The x-interceptsare–3and3;the y-intercept is3.
53. Tofindthe x -intercept,let y =0,andsolvethe equationfor x: 2 011. xx =−⇒=±
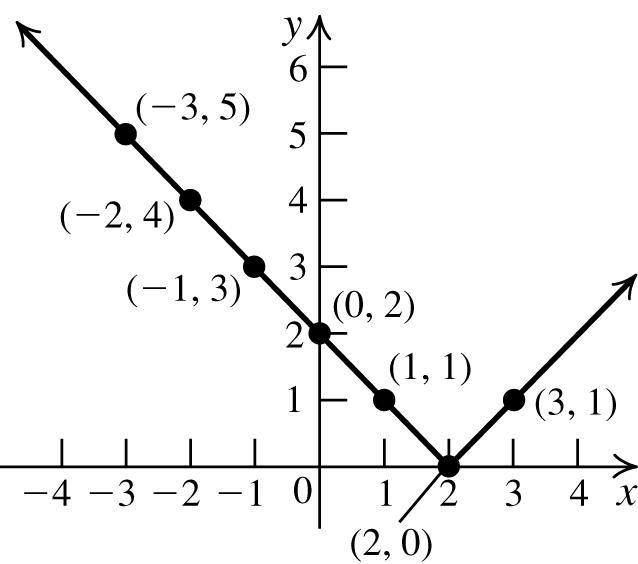
Tofindthe y -intercept,let x =0,andsolvethe equationfor y: 2 01 y =−⇒ nosolution. The x-interceptsare–1and1;thereisno y-intercept.
54. Tofindthe x -intercept,let y =0,andsolvethe equationfor x:(0)1 x =⇒ nosolution.
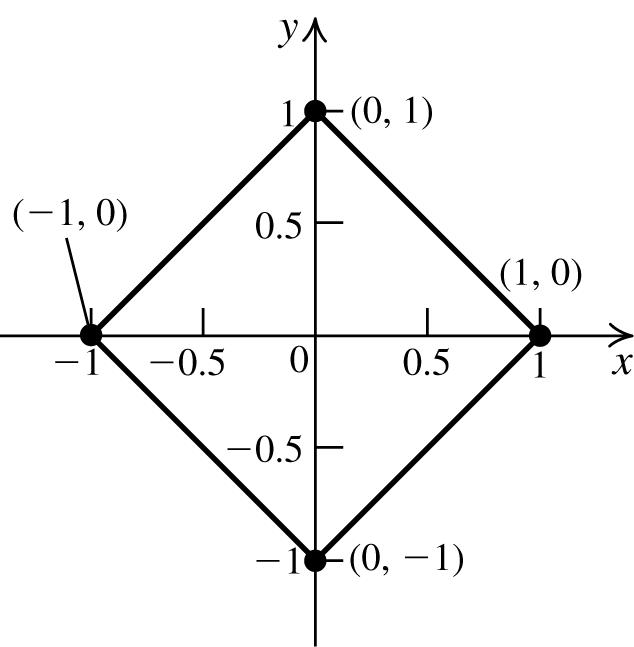
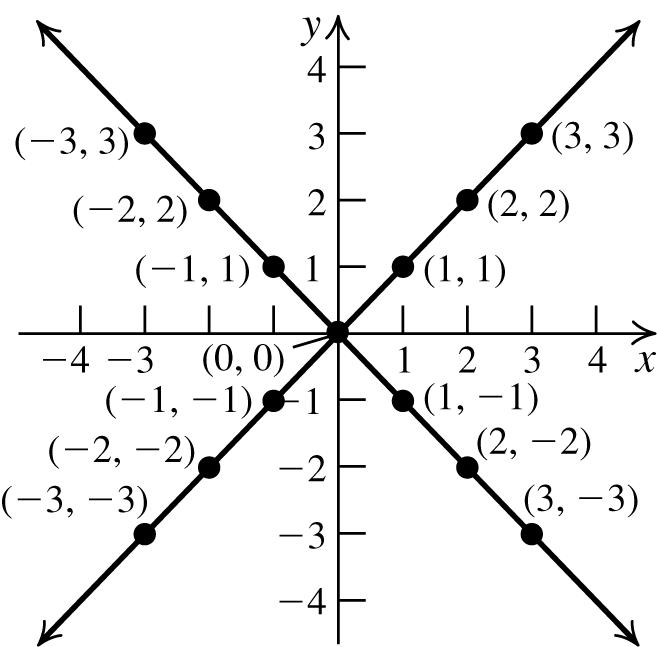
Tofindthe y -intercept,let x =0,andsolvethe equationfor y:(0)1 y =⇒ nosolution. Thereisno x-intercept;thereisno y-intercept.
55. Tofindthe x -intercept,let y =0,andsolvethe equationfor x: 2 01 xx =++⇒
()() () 2 1141113 212, x −±− −±− == which arenotrealsolutions.Therefore,thereareno x-intercepts.Tofindthe y-intercept,let x =0, andsolvetheequationfor y:
2 0011. y =++=
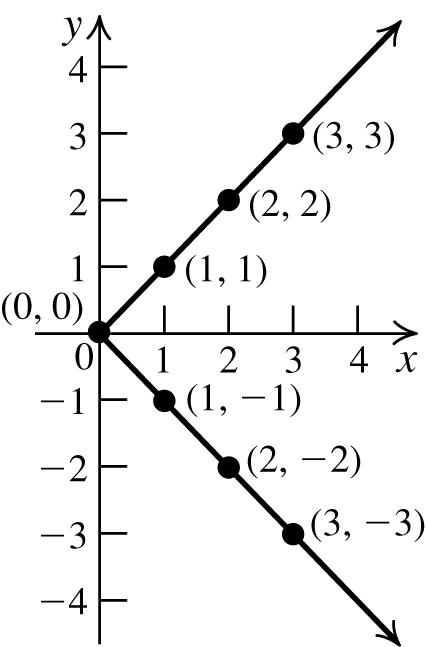
Thereareno x-intercepts;the y-interceptis1.
Copyright©2015PearsonEducationInc.
56. Tofindthe x -intercept,let y =0,andsolvethe equationfor x:
() 333300111.xxxx ++=⇒=⇒= Tofind the y-intercept,let x =0,andsolvethe equationfor y:
() 333 030111. yyyy ++=⇒=⇒= The x-interceptis1;the y -interceptis1. Inexercises57–66,totestforsymmetrywithrespect tothe x-axis,replace y with–y todetermineif(x,–y) satisfiestheequation.Totestforsymmetrywith respecttothe y-axis,replace x with–x todetermineif (–x, y)satisfiestheequation.Totestforsymmetry withrespecttotheorigin,replace x with–x and y with–y todetermineif(–x,–y)satisfiestheequation.
57. 21 yx −=+ isnotthesameastheoriginal equation,sotheequationisnotsymmetric withrespecttothe x -axis.
2 ()1yx=−+⇒ 21 yx=+ ,sotheequationis symmetricwithrespecttothe y-axis.
2 ()1yx −=−+⇒ 21 yx −=+ ,isnotthe sameastheoriginalequation,sotheequation isnotsymmetricwithrespecttotheorigin.
58. 22 ()11xyxy =−+⇒=+ , sotheequationis symmetricwithrespecttothe x-axis.
21 xy −=+ isnotthesameastheoriginal equation,sotheequationisnotsymmetric withrespecttothe y -axis.
2 ()1xy −=−+⇒ 21 xy −=+ isnotthesame astheoriginalequation,sotheequationisnot symmetricwithrespecttotheorigin.
59. 3 yxx−=+ isnotthesameastheoriginal equation,sotheequationisnotsymmetric withrespecttothe x -axis.
()3 yxx=−−⇒ 3 yxx=−−⇒
3 ()yxx =−+ isnotthesameastheoriginal equation,sotheequationisnotsymmetric withrespecttothe y -axis.
()33 yxxyxx −=−−⇒−=−−⇒
33 (), yxxyxx −=−+⇒=+ sotheequation issymmetricwithrespecttotheorigin.
60. 23 yxx−=− isnotthesameastheoriginal equation,sotheequationisnotsymmetric withrespecttothe x -axis.
3 2()() yxx=−−−⇒ 23 yxx=−+⇒
3 2() yxx =−− isnotthesameastheoriginal equation,sotheequationisnotsymmetric withrespecttothe y -axis.
332()()2 yxxyxx −=−−−⇒−=−+⇒
332()2 yxxyxx −=−−⇒=− ,sothe equationissymmetricwithrespecttothe origin.
61. 4252 yxx−=+ isnotthesameasthe originalequation,sotheequationisnot symmetricwithrespecttothe x-axis.
425()2() yxx =−+−⇒ 4252 yxx =+ ,so theequationissymmetricwithrespecttothe y-axis.
442 5()2()52 yxxyxx −=−+−⇒−=+ is notthesameastheoriginalequation,sothe equationisnotsymmetricwithrespecttothe origin.
62. 64232 yxxx −=−++ isnotthesameasthe originalequation,sotheequationisnot symmetricwithrespecttothe x-axis.
642 3()2()() yxxx =−−+−+−⇒
64232 yxxx =−++ ,sotheequationis symmetricwithrespecttothe y-axis.
642 3()2()() yxxx −=−−+−+−⇒
64232 yxxx −=−++ isnotthesameasthe originalequation,sotheequationisnot symmetricwithrespecttotheorigin.
63. 5332 yxx−=−+ isnotthesameasthe originalequation,sotheequationisnot symmetricwithrespecttothe x-axis.
53 3()2() yxx =−−+−⇒ 5332 yxx =− is notthesameastheoriginalequation,sothe equationisnotsymmetricwithrespecttothe y-axis.
5353 3()2()32 yxxyxx −=−−+−⇒−=−⇒
5353 (32)32 yxxyxx −=−−+⇒=−+ ,so theequationissymmetricwithrespecttothe origin.
Copyright©2015PearsonEducationInc.
64. 22 yxx−=− isnotthesameastheoriginal equation,sotheequationisnotsymmetric withrespecttothe x -axis.
2()2 yxx=−−−⇒ 22 yxx =− ,sothe equationissymmetricwithrespecttothe y-axis.
2()2 yxx −=−−−⇒ 22 yxx−=− isnot thesameastheoriginalequation,sothe equationisnotsymmetricwithrespecttothe origin.
65. 2222 ()2()121 xyxyxyxy −+−=⇒−= is notthesameastheoriginalequation,sothe equationisnotsymmetricwithrespecttothe x-axis.
2222 ()2()121 xyxyxyxy −+−=⇒−= is notthesameastheoriginalequation,sothe equationisnotsymmetricwithrespecttothe y-axis.
22 ()()2()()1 xyxy −−+−−=⇒
2221xyxy+= ,sotheequationissymmetric withrespecttotheorigin.
66. 2222()1616xyxy+−=⇒+= ,sothe equationissymmetricwithrespecttothe x-axis.
2222 ()1616 xyxy −+=⇒+= ,sothe equationissymmetricwithrespecttothe y-axis.
2222 ()()1616 xyxy −+−=⇒+= ,sothe equationissymmetricwithrespecttothe origin.
Forexercises67–80,usethestandardformofthe equationofacircle,222 ()() xhykr −+−= .
67. Center(2,3);radius=6
68. Center(–1,3);radius=4

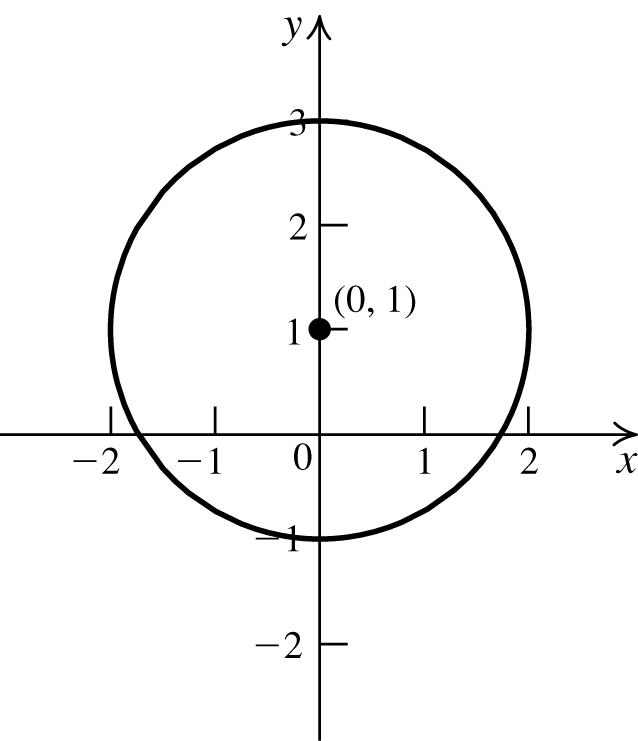
69. Center(–2,–3);radius=11
70. Center 13 , 22 ⎛⎞ ⎜⎟ ⎝⎠ ;radius= 3 2
71. 22(1)4xy+−=
72. 22 (1)1 xy−+=
73. 22 (1)(2)2 xy++−=
74. 22 (2)(3)7 xy+++=
75. Findtheradiusbyusingthedistanceformula: 22 (13)(5(4))97 d =−−+−−= .
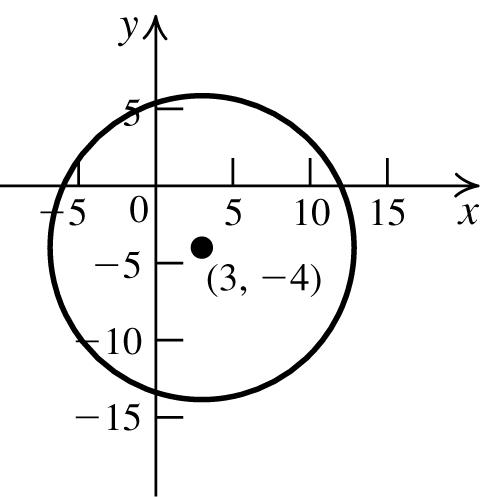
Theequationofthecircleis 22 (3)(4)97. xy−++=
Copyright©2015PearsonEducationInc.
76. Findtheradiusbyusingthedistanceformula:
22 (12)(15)255 d =−−+−== .The equationofthecircleis

22 (1)(1)25. xy++−=
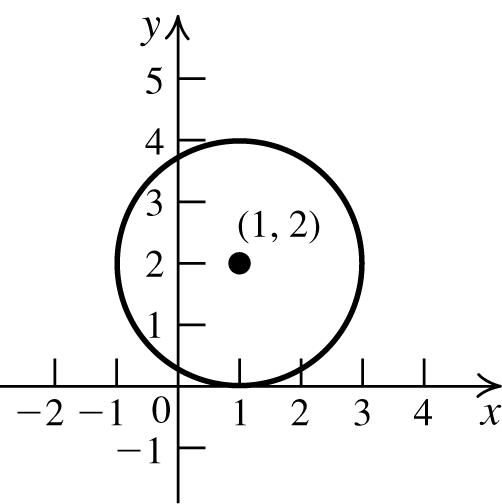
77. Thecircletouchesthe x-axis,sotheradius is2.Theequationofthecircleis 22 (1)(2)4. xy−+−=
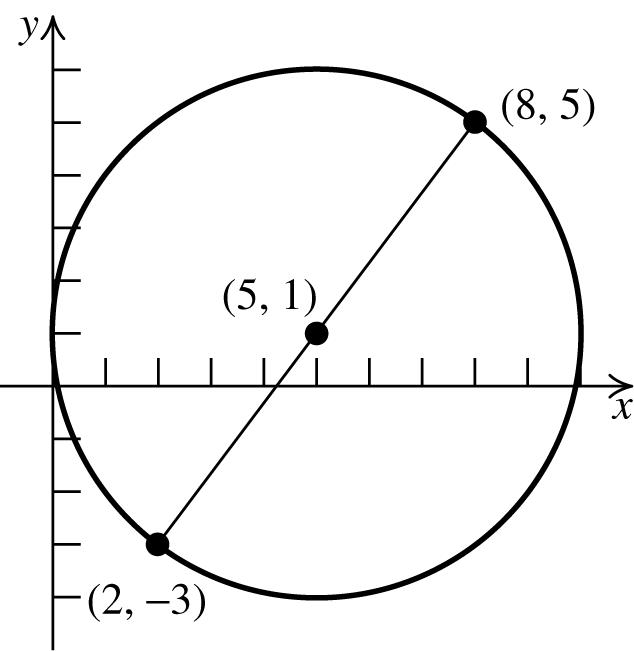
80. Findthecenterbyfindingthemidpointofthe diameter: () 2835,5,122 C +−+
Findthelengthoftheradiusbyfindingthe lengthofthediameteranddividingthatby2. 22 (28)(35)10010 d =−+−−==
Thus,thelengthoftheradiusis5,andthe equationofthecircleis 22 (5)(1)25. xy−+−=
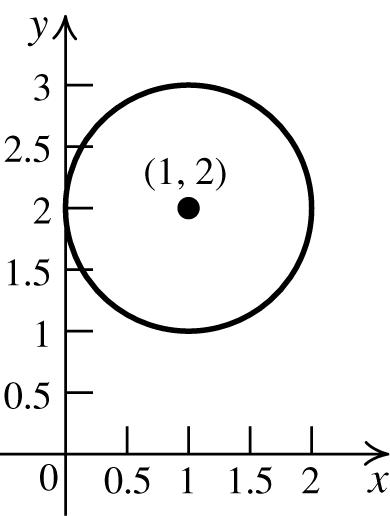
78. Thecircletouchesthe y-axis,sotheradius is1.Theequationofthecircleis 22 (1)(2)1 xy−+−= .
81. a. 222240 xyxy+−−−=⇒
22224xxyy−+−=
Nowcompletethesquare:
222121411xxyy−++−+=++⇒
22 (1)(1)6 xy−+−= .Thisisacirclewith center(1,1)andradius6.

b. Tofindthe x-intercepts,let y =0andsolve for x:
79. Findthediameterbyusingthedistance formula:
22 (37)(64)104226 d =−−+−== Sotheradiusis26.Usethemidpoint formulatofindthecenter:
() 7(3)46,2,5 22 M +−+ ⎛⎞ == ⎜⎟
.Theequation ofthecircleis22(2)(5)26 xy−+−=
()
() 222 2 (1)(01)6116 151515 xx xxx −+−=⇒−+=⇒ −=⇒−=±⇒=±
Thus,the x-interceptsare ( ) 15,0 + and ( ) 15,0.
Tofindthe y-intercepts,let x =0andsolve for y:
()
() 222 2 (01)(1)6116 151515 yy yyy −+−=⇒+−=⇒ −=⇒−=±⇒=±
Thus,the y-interceptsare ( ) 0,15 + and ( ) 0,15.
Copyright©2015PearsonEducationInc.
82. a. 2242150 xyxy+−−−=⇒
224215xxyy−+−=
Nowcompletethesquare:
2244211541xxyy−++−+=++⇒
22 (2)(1)20. xy−+−= Thisisacircle withcenter(2,1)andradius25.
b. Tofindthe x-intercepts,let y =0andsolve
for x: 22 (2)(01)20 x −+−=⇒
()() 22 2120219 219219 xx xx −+=⇒−=⇒ −=±⇒=±
Thus,the x-interceptsare ( ) 219,0 + and ( ) 219,0.
Tofindthe y-intercepts,let x =0andsolve
for y: 22 (02)(1)20 y −+−=⇒
() 22 4(1)20116 143,5 yy yy +−=⇒−=⇒ −=±⇒=−
Thus,the y-interceptsare(0,−3)and(0,5).
83. a. 22 2240 xyy++=⇒
22 2(2)0 xyy++=⇒ 2220.xyy++=
Nowcompletethesquare: 22222101(1)1.xyyxy +++=+⇒++=
Thisisacirclewithcenter(0,–1)and radius1.
b. Tofindthe x-intercepts,let y =0andsolve
for x: 222(01)100xxx ++=⇒=⇒=
Thus,the x-interceptis(0,0).
Tofindthe y-intercepts,let x =0andsolve
for y:
22 0(1)1110,2 yyy ++=⇒+=±⇒=−
Thus,the y-interceptsare(0,0)and(0,−2).
84. a. 22 3360 xyx++=⇒
22 3(2)0 xyx++=⇒ 2220.xxy++=
Nowcompletethesquare:
2222 2101(1)1.xxyxy +++=+⇒++=
Thisisacirclewithcenter(–1,0)and radius1.
b. Tofindthe x-intercepts,let y =0andsolve for x: 22 (1)01110,2 xxx ++=⇒+=±⇒=− Thus,the x-interceptsare(0,0)and(−2,0). Tofindthe y-intercepts,let x =0andsolve for y: 222 (01)100 yyy ++=⇒=⇒= Thus,the y-interceptis(0,0).
85. a. 222200.xyxxxy+−=⇒−+= Nowcompletethesquare:
2211 0 44xxy−++=+⇒ 2 2 11 . 24xy
Thisisacirclewith center 1 ,0 2 ⎛ ⎞
andradius 1 2
b. Tofindthe x-intercepts,let y =0andsolve for x: 2 2 1111 0 2422 xx ⎛⎞−+=⇒−=±⇒
0,1. x = Thus,the x-interceptsare(0,0) and(1,0).Tofindthe y-intercepts,let x =0 andsolvefor y: 2 22 1111 0 2444 yy
200.yy=⇒= Thus,the y-interceptis(0,0).
86. a. 2222101.xyxy++=⇒+=− The radiuscannotbenegative,sothereisno graph.
b. Therearenointercepts.
2.2 Applying the Concepts
87. Thedistancefrom P(x, y)tothe x-axisis x whilethedistancefrom P tothe y-axisis. y
Sotheequationofthegraphis xy =
88. Thedistancefrom P(x, y)to(1,2)is 22 (1)(2) xy−+− whilethedistancefrom P to(3,–4)is22 (3)(4) xy−++
Sotheequationofthegraphis
2222 (1)(2)(3)(4) xyxy −+−=−++⇒ 2222 (1)(2)(3)(4) xyxy −+−=−++⇒
Copyright©2015PearsonEducationInc.
College Algebra 3rd Edition Ratti Solutions Manual
Full Download: http://testbanktip.com/download/college-algebra-3rd-edition-ratti-solutions-manual/
(continued)
222144xxyy−++−+=
2269816xxyy−++++⇒
2456825 xyxy −−+=−++⇒
15 42012. 33xyyx −=⇒=−
89. Thedistancefrom P(x, y)to(2,0)is (2)22 xy −+ whilethedistancefrom P to the y-axisis x .Sotheequationofthegraph is 22222 2222 22
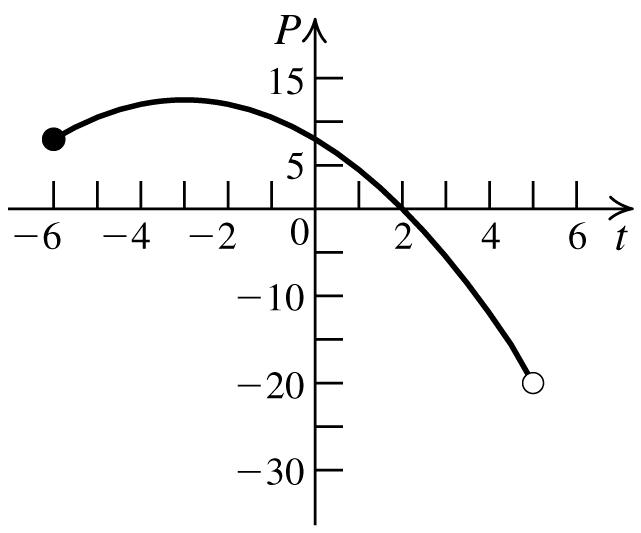
d. Tofindthe t-intercept,set P =0andsolve for t: 2 00.538 tt =−−+⇒ 2 3(3)4(0.5)(8)325 2(0.5)1
t ±−−− ± == =−
2or8
The t-interceptsrepresentthemonthswith noprofitandnoloss.Inthiscase, t =−8 makesnosenseintermsoftheproblem,so wedisregardthissolution. t =2represents Sept2012.
(2)(2) 4444 4 1 44
xyxxyx xxyxyx yy x
−+=⇒−+=⇒ −++=⇒=−⇒ + =+=
90. 2004isthemidpointoftheinitialrange,so 2004 136234 185. 2 M + == 2002isthemidpointoftherange
e. Tofindthe P -intercept,set t =0andsolve to P: 2 0.5(0)3(0)88.PP =−−+⇒= The P-interceptrepresentstheprofitinJuly 2012.
92. a.
So,in2002,$160.5billionwasspent,in2004, $185billionwasspentandin2006,$209.50 wasspent.
91. a. SinceJuly2012isrepresentedby t =0, March2012isrepresentedby t =–4.Sothe monthlyprofitforMarchisdeterminedby 2 0.5(4)3(4)8$12 P =−−−−+= million.
b. SinceJuly2012isrepresentedby t =0, October2012isrepresentedby t =3.Sothe monthlyprofitforOctoberisdeterminedby 2 0.5(3)3(3)8$5.5 P =−−+=− million. Thisisaloss.
c.
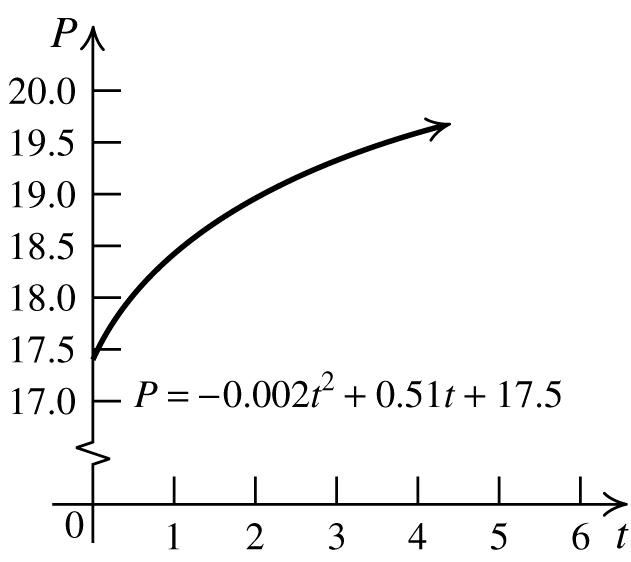
b. Tofindthe P -intercept,set t =0andsolve to P: 2 0.002(0)0.51(0)17.5 P =−++⇒
17.5. P = The P-interceptrepresentsthe numberoffemalecollegestudentsin2005.
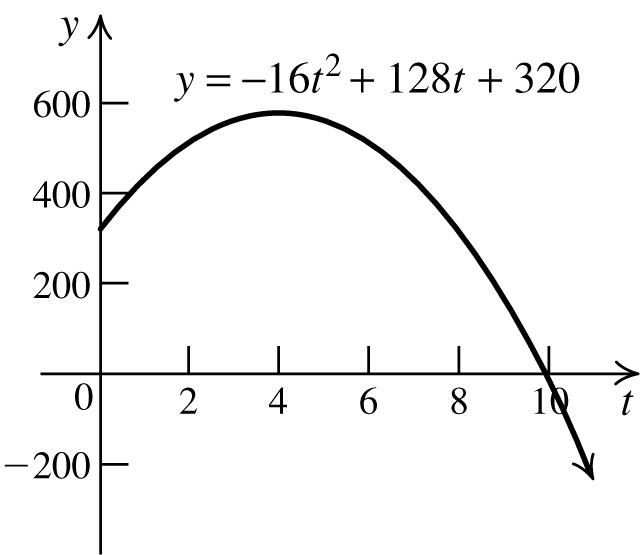
93. a. t Height=216128320 tt −++
0320feet
1432feet
2512feet
3560feet
4576feet
5560feet
6512feet
b.
c. 010 t ≤≤
Copyright©2015PearsonEducationInc.
