SAS Journal of Mathematics Vol.1

Singapore American School

Journal of Mathematics Vol.1

Matrices, Pixels, and RGB

Exploring Recursive Sequences with Eigenvalues and Eigenvectors

An Introduction to Combinatorial Partitions

Calculating Implied Volatility using the Black-Scholes Model

Countably and Uncountably Infinite Sets

Introduction to Chaos Theory Investigating the Theoretical and Practical Applications of Fractals

Singular Value Decomposition and a Recommendation Algorithm

Natural Eigenvectors in High Number Systems

Evaluating Epidemiological Solutions through S-I-R Modeling

EDITOR’S LETTER

Welcome to our groundbreaking project that brings together math enthusiasts to dive into the depths of diverse mathematical concepts and applications! This mini-mathematical journal that showcases the passion and expertise of our math club members. We want to provide an opportunity for everyone in the school community to engage with the exciting and fascinating world of math.

Through this journal, readers will discover innovative and insightful research articles that delve into a wide range of mathematical topics. We aim to make these complex ideas accessible to all, without sacrificing academic rigor.

We invite you to join us on this exciting journey as we pave the way for a vibrant and stimulating mathematics-focused community at our school!

Gyulim Jessica Kang, Frank Xie Editors-in-Chief

55

43

Singular Value Decomposition and a Recommendation Algorithm

Frank Xie

49

Natural Eigenvectors in High Number Systems

Gaurav Goel Evaluating Epidemiological Solutions through S-I-R Modeling

Gaurav Goel

64 Finding an Alternate Model to Malthusian Population Growth Model

Irene Choi, Morgan Ahn, Vyjayanti Vasudevan

69 Application of Eigenvectors and Eigenvalues: SVD Decomposition in Latent Semantic Analysis

Gyulim Jessica Kang

77 Creating a Machine Learning Pipeline to Perform Topological Data Analysis

Gyulim Jessica Kang

82 Evaluating Affirmative Action in School Choice: Comparing Mechanisms with Minority Reserves

Gyulim Jessica Kang

Matrices, Pixels, and RGB

Written by Hyeonseo Kwon

Matrices,Pixels,andRGB(ATLAProject)

HyeonseoKwon

kwon49627@sas.edu.sg

TeacherReviewers: Mr.Zitur,Mr.Craig

Abstract

FromInstagramtoTiktok,socialmediahasgrowntobean intrinsicpartofmodernsocietytoday.Outofmany,oneof itsmostprominentfeaturesthatcaughtmyattentionwasthe differenttypesoffacefiltersinstalledincamerasofsocial mediaapps.Withsocialmedia,thereisnolimittohowyou wantyourphotostolook.Ithoughtthiswasparticularlyinteresting.UsingtheconceptsofmatrixmanipulationofRGB excelpixels,Idecidedtogoastepfurtherandexploretheapplicationofmatrixcalculationsincreatingfacefilters.

Keywords:matrices,RGB,Gaussianblur

1PixelProject

Let’sbreakdownthebasicprinciplesofhowthepixels ofimagesworkinExcel.Whendigitalphotosareturnedinto excelspreadsheets,eachpixelisdividedintothreeRGBvalues:Theamountofred,green,andbluestoredinthepixel. Therefore,performingmatrixmultiplicationtoeachpixel’s setofRGBvaluesallowsustomanipulatethevaluesinthe photosandchangehowtheyappearonthescreen.

thiscalculationisdoingisscalingdowntheRGBmatrix oftheoriginalimagetoacertainlevel(forexample,0.5), scalingdowntheRGBmatrixofthefiltertoanumberthat isthescalefactoroftheRGBmatrixoftheoriginalimage subtractedfrom1(whichinthiscasewouldbe0.5),and addingthetwomatricestogethertocreateanewmatrixthat istheresultofthematrixcalculation.Toputthisintothe perspectiveofnumbercalculations,let’ssayoneofthepixel valuesoftheoriginalimagehasanRGBmatrixof[206,192, 175],andoneofthepixelvaluesofthefilterhasanRGB matrixof[189,131,120].

Figure1:Overlayingavintagefilteronanimage

Here,Iwasabletocreateacolorfilterbybreaking theimageaboveintopixelsandmultiplyingtheportionof thevaluesofthisimagebytheportionofthevaluesofthe originalimage.Theformulausedtoperformthiscalculation was DA1$A$228+(1-$A$228)HA1,where DA1 wasthe locationofthefirstpixeloftheoriginalimageand HA1 was thelocationofthefirstpixelofthe“filter.”Essentially,what

Iwantedtousetheseconceptstocreatefiltersthat somewhatimitatetheactualfiltersthatcanbeseeninsocial mediaapps.

2Extension1

IfirstconvertedtwophotosintoRGBpixelsand pastedthemontoExcel.

Idecidedtosettheopacityto50%asit madethemostsense.Then,Iusedtheformula

Figure2: A, B ,and 0 5 A +0 5 B

A1*$A$611+(1-$A$611)*HA1 (thecolumnand rownumberchangesforeachpixel)whichsetstheopacity ofthephotosto50%andcombinethemtogethertocreate asingleimage.Thisprocessallowedmetogeneratean averagefacebetweentheyoungerandolderversionof AudreyHepburn.Iwasaimingtoimitatethefiltersthattake yourbabyfaceandcreateahypotheticalversionofyour olderself.

Thisisbecausethecolorsgetbrighterapproachwhite astheRGBvaluesgetcloserto255.Forexample,ifapixel intheoriginalimagehadtheRGBvaluesof[100100100], andamatrixof[303030]wasadded,theresultwouldbe [130130130]pixelwouldachieveagreaterRGBvaluethus alightercolor.Here,matrix A representstheRGBvalues oftheoriginalimage,andmatrix B representsthe“filter”. Iusedtheinverseoftheidentitymatrixtocreateamirroringfilter.Thismatrixallowsthevaluesinthematrixtobe mirroredliketheexamplebelow.Here,youcanseethatmultiplyingtheinverseoftheidentitymatrixflipsthelocation of ac and bd.

3Investigation2/Extension2(Coding)

Formysecondextension,IwantedtocreateafilterwithcodingthatimitatesthePhotoshopfilterslikeface brighteningormirroringeffects.Toachievethis,Iusedbasic matrixcalculationprincipleslikematrixadditionandmultiplyingtheinverseofanidentitymatrix.Forthebrightening effect,Iusedthefollowingformula:

Ithoughtitwasparticularlyinterestinganddecidedto employthismethodtotrymirroringimagesaswellusing thesameprinciple.

1 # Whitening skin

2 img=cv2.imread("face.jpg",cv2. IMREAD_COLOR)

3 mag=img.shape

4

5 whiten=np.zeros((mag[0],mag[1],3))

6 7 whiten[:,:,0]=np.ones([mag[0],mag [1]])*30

8 whiten[:,:,1]=np.ones([mag[0],mag [1]])*30

9 whiten[:,:,2]=np.ones([mag[0],mag [1]])*30

10

11

cv2.imwrite(’whiten.jpg’,whiten)

12 whiten=cv2.imread("whiten jpg",cv2. IMREAD_COLOR) 13 14 applied=cv2.add(img,whiten) 15 cv2.imshow(’original’,img) 16 17 cv2.imshow(’applied’,applied)

1 (6720,4480,3)

Theprintedvaluefromthesecondbox(6720,4480, 3)showsthesizeofthematrixofthephotos.Thismeans thattheoriginalphotohadthreematriceswiththesizeof 6720 × 4480,eachmatrixbeingeitherthered,green,or

Figure3:2imagesofAudreyHepburn

Figure4:BlendedimageofAudreyHepburn

bluecomponentofthepixels.Withthisoriginalmatrix, A, thefiltermatrix, B,wouldalsobe6720 × 4480withthe samevalue(inthiscase,it’s30)inallentries.Thissnippetof codeallowstheimagetogainhigherRGBvaluesfollowing thematrixadditionrule.Thus,the B matrixhastobeadded toallthreematricesof A,andthethreematricesaltogether showthefinalimage.

Thesecondstepwastocreateamirroringfilterthatreversestheimage.InUnit1,whiledoingthecartoonproject, thematrixthatallowedtheplotstobereflectedagainstthe y -axiswasthefollowingmatrix.

C = 10 01

However,becausewearedealingwithRGBvaluesin thisproject,thismatrixcannotbeused(colorintensitycan notbenegative).Thereforethealternativematrixthatcould beusedherewastheinverseoftheidentitymatrix.

1 # getting mirror image

2

3 img_flig_lr=cv2.flip(img,1)

4 cv2.imshow(’flip’,img_flip_lr)

5

6 #display image for 20 seconds

7 cv2.waitKey(20000)

8 cv2.destroyAllWindows()

Thiscodesnippetfollowsthesameprincipleasthe matrixcalculationwiththeinverseoftheidentitymatrix, which,asshownabove,resultsinaflippedimage.Thiscode printsthefollowingmirroredimage.

ThethirdthingIdecidedtoaddwasablurringfilter thatintentionallyblursthephoto.ThisisoftenusedtoPhotoshoppeople’sskinandremoveanyblemishesorpimples. TheformulausedherewastheGaussianblur.

TheGaussianfilterformulacalculatestheweighted averageofthecurrentpixelandneighboringpixelvalues toreplacethecurrentpixelvalue.Theclosertothecurrentpixel,thegreatertheweight,andthefarther,thesmaller theweight.Whenthisformulaisusedinimages,itreduces noiseandsmoothenstheimage.However,theborderofthe imageisalsoblurred.Inordertopreservetheborders,the originalformulaismodified:

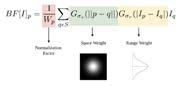
1 blur=cv2.bilateralFilter(applied ,50,75,75)

2 # bilateralFilter(src, dst1, 5, 250, 10) ;

3 blur2=cv2.cvtColor(blur,cv2. COLOR_BGR2RGB)

4 plt.subplot(121),plt.imshow(img2),plt. title(’Original’)

5 plt.xtics([]),plt.yticks([])

6 plt.subplot(122),plt.imshow(blur2),plt. title(’Blurred’)

7 plt.xticks([]),plt.yticks([])

8 plt.show()

Figure5:Original(L)Afteraddingfilter(R)

Figure6:OriginalImage

9

10 cv2.imshow("before",applied)

11 cv2.imshow("after",blur)

12 cv2.waitKey(3000)

13 cv2.destroyAllWindows()

ThiscodesnippetemploystheGaussianblurformula andblursthephoto.The(50,75,75)inthefirstlineofthe coderepresentthediameter,sigmaColor,andsigmaSpace, respectively.Thelargerthediameteris,theblurrierthephoto getsduetothefactthatlargerdiameterscoverlargerareas.

ZiturLinearAlgebra-1.7.6PixelPictures.(2023). Retrieved31January2023,from https://sites.google.com/a/sas.edu.sg/zitur-linearalgebra/home/unit-1/1-2-5-pixel-into-pictures?authuser=0

31January2023,from https://parklanda.tistory.com/15761458

4Summary

Overall,Ireallyenjoyedthefreedomofchoosingthe topicandtinkeringwithdifferenttypesofcomputersoftware.Comingupwithanideawasdefinitelychallengingat first,butIwaseventuallyabletogenerateoriginalideasthat reallyhelpedmepropeltheprojectforward.Althoughmy extensionswerenotperfect,Igenuinelyenjoyedtheprocessandwassatisfiedwithmyproduct.Tosummarize,this projectusesthebasicprinciplesofmatrixcalculationand appliestheminabroadercontextfromtheperspectiveof images.Themainthemeofthisprojectwasfacefilters,and Iaimedtoimitatepopularfiltersonsocialmediaorcamera appsonmyownusingExcelandJupyternotebook.Itwasa veryinterestingexperiencebeingabletomergevisualswith mathtogetherandunderstandhowthereisalwayssomesort ofmathbeneatheverything.

References

ApplicationsofLinearAlgebrainImageFilters[PartI]Operations.(2020).Retrieved31January2023,from https://medium.com/swlh/applications-of-linear-algebra-inimage-filters-part-i-operations-aeb64f236845 opencv-python.(2022).Retrieved31January2023,from https://pypi.org/project/opencv-python/ Python—BilateralFiltering-GeeksforGeeks.(2019). Retrieved31January2023,from https://www.geeksforgeeks.org/python-bilateral-filtering/ Rosebrock,A.(2021).OpenCVLoadImage(cv2.imread)PyImageSearch.Retrieved31January2023,from https://pyimagesearch.com/2021/01/20/opencv-load-imagecv2-imread/

Figure7:Original(L)Aftertheblurfilter(R)

아름다움의 정상, 오드리 햅번의 생애 .(2013).Retrieved

Exploring Recursive Sequences with Eigenvalues and Eigenvectors

Written by Akshay Agarwal

ExploringRecursiveSequenceswithEigenvaluesandEigenvectors

AkshayAgarwal agarwal45366@sas.edu.sg

TeacherReviewer:

Mr.Son

Abstract

Abstract

Recursivesequencesarewell-knownandwell-studied.Generally,whenlearningabouttheminearliermathclassessuch asPrecalculusandAlgebra,theonlywaytheywerecomputed were...recursively.Forinstance,thefibonaccisequencetends tobecalculatedbymanuallyaddingtheterms 0+1=1+1= 2+1=3...However,representingrecursivesequencesinthis mannerhidesalotoftheintricaciesandbeautyinrecursive sequences...especiallythefibonaccisequence.Afterexploringthefibonaccisequence,wegoontogenerateourown spiralswithcomplexeigenvaluesandcalculatethetransformationsthatformthespiral.

Keywords: Fibonaccisequence,eigenvalues,eigenvectors, complexnumbers,transformations,matrices

1TheFibonacciSequence

TheFibonaccisequenceisawell-knownsequence, whichconsistsof:

youlistenoughnumbers,theratiooftwoconsecutiveterms inthesequencegetscloserandcloserto

Figure2:CurvefitthroughtheFibonacciSequencepoints ϕ,thegoldenratio!

Thus,findingandsolvingthecharacteristicpolynomialyields: (1 λ) ·−λ 1= λ2 λ 1=0

Bythequadraticformula, λ = 1+√( 1)2 +4 1 2 = 1+√5 2 = ϕ

WhichISthegoldenratio!

FibonacciSequenceisn’tUnique?

Aswe’vealreadyfoundtheeigenvaluesofthefibonaccimatrix,itnaturallyfollowstofindtheeigenvectors

Reducingthematrix:

Astheeigenvalueisalso ϕ,thatmeansthatitshould beaneigenvectorforanystartingvalue,asthey-coordinate willeventuallybecome ϕ timesthex-coordinate.Let’stest this:

2RecursiveSequenceswithComplex Eigenvalues

GeneratingtheRecursiveSequence

Ascalculatingtheeigenvalue, λ,fora 2x2 matrixrequiresusingthequadraticformula,ifthecharacteristicpolynomialofthematrix’sdiscriminantisnegative, λ willbe complex.

Ihadtofindamatrixwithcomplexeigenvaluesthat stillfunctionedasaseries,whichmeantthatmymatrix A hadtobeintheform: ab 10 aswhenmultiplying an an 1 = ab 10 an 1 an 2 , thebottomvalueoftheresultantmatrixwillbe an 1 ,which createstheidealsequence.

Next,thematrixneedstohavecomplexeigenvalues, thecharacteristicpolynomialofthematrix a λb 1 λ

is λ2 + λa b =0

Thediscriminantofthispolynomialis a2 +4b,where a2 +4b< 0 needstobesatisfied.Ichoseasimplesolution where a =2,b = 2,suchthat a2 +4b =22 +4( 2)=

Thus,thematrixIcreatedforthisextensionis A = 2 2 10 .

Thismeansthatmyrecursivesequenceisdefinedas

Whengraphingthissequence,aninterestingrelationshipisdiscovered:

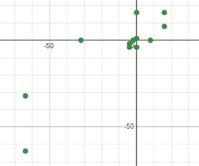
Figure3:Complexeigenvaluebasedrecursivesequence graphedonthe x-y plane.

Asopposedtoaregularspiral,thisspiralseemstobe tilted,asifit’srotatedaboutanellipse.Aderivationofthe transformationsthatleadstothisisthepremiseofmyextension.

DerivingtheTransformations

Inordertocomputethetransformations,theeigenvaluesandeigenvectorswouldlikelybenecessary,sothey shouldbecalculatedfirst.

Fortheeigenvalues,simplysolvethecharacteristic polynomialwederivedearlierof λ2 2λ +2=0,where λ = 2±√ 4 2 =1 ± i

Astheeigenvaluesareconjugates,theeigenvectors willlikelybetoo...let’scomputetheeigenvectorwhen λ = 1+ i.Theresultingmatrixtorowreduceisthen: 1 i 20 1 1 i 0 ∼ 1 1 i 0 000 ,somy

eigenvectoris 1+ i 1

Now,asissimilartoseparatingthebasisofasolutionset,wecanseparatetherealandimaginarypartsofthe eigenvectortoformamatrixwhosecolumnsrepresentthe eigenvector:

P = 11 10 ,asthefirstcolumnaretherealcomponentsandthesecondaretheimaginarycomponents.

Now,usingdiagonalization,wecantriviallyfindthe transformationmatrixwith P 1 A P = 11 11 ,by matrixmultiplication.

Now,inthespiralwesawearlier,it’sintuitivethatthe transformationstakingplaceforeachiterationisarotation andscalar(that’showthespiralshapeforms).Thiscanalso beverifiedbylookingattheformofourtransformationmatrix.

Thegenericformofascalarmatrixis r 0 0 r ,while

thegenericformofarotationmatrixis cos(θ ) sin(θ ) sin(θ )cos(θ )

Multiplyingthesematricesyields:

r cos(θ ) r sin(θ )

r sin(θ ) r cos(θ ) ,whichisinthesameformas thetransformationmatrixwegotasthetop-leftandbottomrighttermarethesame,whilethetop-rightandbottom-left termarenegativeinversesofeachother.

Thescalarshouldsimplybethemagnitudeofthe eigenvalue, λ = i + i,whichgives √12 +12 = √2

Wethenget, 11 11 = √2cos(θ ) √2sin(θ ) √2sin(θ ) √2cos(θ ) As cos(θ )= 1 √2 , θ = π 4 , whichmeansthatthespiralshownscalesthepointsby √2 androtatesthemby 45 degrees.

WhatIcoulddeduceaboutthereasoningforthetilt isthatthetransformationmatrixwegotwillsimplygraph thestraightspiral,butbecauseweseparatedtheeigenvector intotherealandimaginarycomponents,multiplyingbymatrix A transformsitinthebasisoftherealandimaginary components 1 1 and 1 0 ,respectively.

Therefore,foranysequencewithcomplexeigenvalues,thespiraltransformationscanbederivedinthismethod.

3Conclusion

Here,weinitiallyinvestigatedfibonaccisequencesto seehoweigenvaluesandeigenvectorscanrevealnewinsightsaboutthem.Then,weextendedthatknowledgeto tryingtounderstandhowrecursivesequenceswithcomplex eigenvalueswork;eventuallyformingspiralsandcomputing thetransformationswhichdefinethem.Thisisreallyjust thebrinkofthesurfacewhenitcomestoexploringcomplexeigenvaluesandeigenvectors,astheonlypatternswe deducedarethoseofthetransformations,whereasonecan alsoinvestigatethelimits,theslope,andseveralothercharacteristicsofanyspiral.Agoodsupplementmayalsobeexploringifthespiralsdifferwhenthestartingmatrixdoesn’t definearecursivesequence.

References

Aron.(n.d.).reference—p5.js.P5js.org.RetrievedApril6, 2023,fromhttps://p5js.org/reference/group-IO FibonacciNumbers,T.(n.d.).Fibonaccinumbersfrom eigenvectorsandeigenvalues.RetrievedApril6,2023,from

https://www.d.umn.edu/mhampton/m3280f12/FibonacciNumbers.pdf Ph.D,A.C.(2021,August18).TheLinearAlgebraViewof theFibonacciSequence.Medium. https://medium.com/@andrew.chamberlain/the-linearalgebra-view-of-the-fibonacci-sequence-4e81f78935a3

An Introduction to Combinatorial Partitions

Written by Akshay Agarwal

SAS23

AnIntroductiontoCombinatorialPartitions

AkshayAgarwal

agarwal45366@sas.edu.sg

TeacherReviewer: Ms.Poluan

Abstract

Thispaperpresentsanintroductiontoamajorpartofmoderndaycombinatoricsandnumbertheory:partitions.Thedefinitionofapartitionofanypositiveinteger n issimplyinvestigatingthewaysonecanwrite n asasumof positive integers.MathematicianssuchasRamanujanhavebeendelving intopartitionsforhundredsofyears,findingidentitiesand formulaeregardingthetypeofpartition,howthey’reconstructed,andhowthey’remodeled,whichforthosewhoare well-accustomedtocalculus,isagreatsupplementtothispaper.Butthispaperwillbefocusingonthecombinatorialside ofpartitions,whichiscountingthembasedonanumberof restrictions.Thecontentinthispaperisinterestingfroma puremathview(withafew,newlyderivedformulae),butalso servesasanexpositorypieceforthosewhoarecompetingin mathcompetitions.

Keywords: StarsandBars,combinations,one-to-onecorrespondence,recursive

1AnIntroductiontoPartitions

Incolloquialterms,apartitionofanumber n canbe thoughtofasanactionofputting n ballsintoboxes,such thatifyouhave 5 ballsandput 1 inonebox, 2 inanother box,and 1 inathirdbox,thepartitionwillbe 1+2+1 Thus,wecanthinkaboutpartitionsinfourdifferentcategories,listedbelow:

1. Ballsareidenticalandboxesaredistinguishable.

2. Ballsareidenticalandboxesareidentical.

3. Ballsaredistinguishableandboxesareidentical.

4. Ballsaredistinguishableandboxesaredistinguishable.

Noticehowincase 1 wheretheboxesaredistinguishable, 1+2+1 willbeconsideredadifferentcasefrom 2+1+1,whereasitwouldbeconsideredasonepossibility incase 2.Thispaperwillprimarilybecoveringthefirsttwo cases,wherethefirsttool,StarsandBars,willaddresscase 1,andthesecond,recursivetool,willaddresscase2.

2StarsandBars

Forsomecontext,asampleproblemwhichissolved bystarsandbarsispresented:

Example1.0.1 Dr.Evil’s5thgradeclasshas6students. Dr.Evilhas6identicalcandiestogivetothe6students.

However,asDr.Evilisevil,hedoesn’tnecessarilywantto give1toeachstudent.Howmanywaysarethereforhimto givethesecandiestothestudents?

Whenreadingthisproblem,it’seasytonoticetwo things.First,thisfollowsourguidelineofidenticalballsand distinguishableboxes.Inthiscase,thecandiesareidentical, andevidently,thestudentsaredistinguishable.

Secondly,ifweweretophysicallycountthembylistingthemallout,itwould (a) beextremelytime-consuming and (b) beextremelyeasytomiscount;thisiswhereStars andBarscomesin.

StarsandBarsasaPicture

Tostartgettinganideaofhowtousestarsandbars, let’sutilizeexample1.0.1.Letusimagineeachofthe identicalcandiestobecircles/ballsasshownbelow.

[color=black!60,fill=white!5,verythick](-1,0)circle(0.25); [color=black!60,fill=white!5,verythick](-1,0)circle(0.25); [color=black!60,fill=white!5,verythick](-1,0)circle(0.25); [color=black!60,fill=white!5,verythick](-1,0)circle (0.25); [color=black!60,fill=white!5,very thick](-1,0)circle(0.25); [color=black!60, fill=white!5,verythick](-1,0)circle(0.25);

Letusimagineputtinglinesorbarsinbetweengaps ofthecirclestoseehowmanycandieseverystudentgets.A smallexampleisdemonstratedbelow.

[color=black!60,fill=white!5,verythick](-1,0)circle(0.25);[black,thick](-1,0.5)–(-1,-0.5); [color=black!60,fill=white!5,verythick](-1,0)circle(0.25);[black,thick](-1,0.5)–(-1,-0.5); [color=black!60,fill=white!5,verythick](-1,0)circle(0.25);[black,thick](-1,0.5)–(-1,-0.5); [color=black!60,fill=white!5,verythick](-1,0)circle(0.25);[black,thick](-1,0.5)–(-1,-0.5); [color=black!60,fill=white!5,verythick](-1,0)circle(0.25); [black,thick](-1,0.5)–(-1,-0.5);[color=black!60, fill=white!5,verythick](-1,0)circle(0.25);

[color=black!60,fill=white!5,verythick](-1,0)circle (0.25);

Intheconfigurationabove,wehavedividedthecandiesintosixpartitionsusingfivelines.Eachpartitionhas sizeone,meaningeverystudenthasonecandy.Now,letus

lookatanotherconfigurationandbasesomeconclusionson that.

[color=black!60,fill=white!5,verythick](-1,0)circle(0.25); [black,thick](-1,0.5)–(-1,-0.5);[black,thick](-0.75,0.5) –(-0.75,-0.5);[color=black!60,fill=white!5,very thick](-1,0)circle(0.25);

[color=black!60,fill=white!5,verythick](-1,0) circle(0.25);[black,thick](-1,0.5)–(-1,-0.5);[black, thick](-0.75,0.5)–(-0.75,-0.5);[color=black!60, fill=white!5,verythick](-1,0)circle(0.25);

[color=black!60,fill=white!5,verythick](-1,0) circle(0.25);[black,thick](-1,0.5)–(-1,-0.5); [color=black!60,fill=white!5,verythick](-1,0)circle(0.25); [color=black!60,fill=white!5,verythick](-1,0)circle (0.25);

Intheconfigurationshownabove,weagainhavedividedthecandiesintosixpartitionsusingfivelines.Yet, thepartitionsizesarevarying,meaningthateachstudent getsavariedamountofcandies.Thenumberofcandiesare 1, 0, 2, 0, 2, 1 perstudentfromlefttoright.

Thesetwoconfigurationsinformusofseveralthings. Firstofall,wecannowbesurethattheballsareidentical, andthattheboxesaredistinguishable.Theballsareidenticalbecausewearepartitioningthe interchangeable balls. Inaddition,withthesticks,wecanrepeatedlychangethe candydistribution(toaccountforallthevariouscases).For example,inthesecondconfigurationshown,thedistribution ofcandiesis1-0-2-0-2-1,yetthedistributioncouldalsobe 2-0-1-2-1-0.Here,weseethattheindividualnumberscan beidentical,yettheorderisdifferent.Therefore,theboxes havetobedistinctiveforustousethistechnique.

Addingtoabove,puttingthebarsindifferentgapsbetweentheballswillyielduseverypossiblearrangement, thusensuringwewon’tbeover-countingorunder-counting. Now,therewillbetwosolutionspresentedtoexample1.0.1. Theinitialsolutionwillbea“bogus”solution,whichisan incorrectsolution,butitwillindicateacommonmistake. Thesecondsolutionwillaccuratelyutilizethestrategywe developedabove.

Example1.0.1:Dr.Evil’s5thgradeclasshas6students. Dr.Evilhas6identicalcandiestogivetothe6students. However,asDr.Evilisevil,hedoesn’tnecessarilywantto give1toeachstudent.Howmanywaysarethereforhimto givethesecandiestothestudents?

Solution1(Bogus): Wecannowtrytouseournewdiscoveriestothisproblem.Let’sdrawall6balls,representingthe 6candies.

[color=black!60,fill=white!5,verythick](-1,0)circle(0.25); [color=black!60,fill=white!5,verythick](-1,0)circle(0.25); [color=black!60,fill=white!5,verythick](-1,0)circle(0.25); [color=black!60,fill=white!5,verythick](-1,0)circle (0.25); [color=black!60,fill=white!5,very thick](-1,0)circle(0.25); [color=black!60, fill=white!5,verythick](-1,0)circle(0.25);

Now,letusmarkallthegapsinwhichwecaninsert thelinesaswedidabove.Notethatanypersoncanhave0 candies,whichiswhywehavetocountthegaptotheleft

oftheleftmostballandthegaptotherightoftherightmost ball.

[black,thick](-1.25,-0.25)–(-0.75,-0.25); [color=black!60,fill=white!5,verythick](-1,0)circle (0.25);[black,thick](-1.25,-0.25)–(-0.75,-0.25); [color=black!60,fill=white!5,verythick](-1,0)circle (0.25);[black,thick](-1.25,-0.25)–(-0.75,-0.25); [color=black!60,fill=white!5,verythick](-1,0)circle (0.25);[black,thick](-1.25,-0.25)–(-0.75,-0.25); [color=black!60,fill=white!5,verythick](-1,0)circle (0.25);[black,thick](-1.25,-0.25)–(-0.75,-0.25); [color=black!60,fill=white!5,verythick](-1,0)circle (0.25);[black,thick](-1.25,-0.25)–(-0.75,-0.25); [color=black!60,fill=white!5,verythick](-1,0)circle (0.25);[black,thick](-1.25,-0.25)–(-0.75,-0.25); Intherepresentationabove,wecanseethatwemarked 7gapsforustoputthelines.Also,aswepreviouslysaw,we need5linestosplittherowofcandiesinto6differentparts. Therefore,wehavetochoose5outof7gapstoputthelines. Theansweristhen 7 5 = 21 .

So,whyisthissolutionincorrect?Wecanlookatthe 2ndconfigurationwemadeonpage5.There,weputtwo linesonthesamegaptoallow anyone toget0candies.Inthe gapsweidentifiedinsolution1,onlythefirstandlaststudent couldget0candies,meaningweseverelyundercounted. However,addingintheextragapsisnotveryeasy. Everygapbetweentheballscouldhaveupto5(allofthe lines)linesinsideofit.Asweinitiallyhadsevenslots,we wouldnowhave 7 5=35 slots.Wenowfaceanannoying, yettrueconundrum.Ifwehavefivegapsbutonlyputone line,it’sidenticalifthelineisonthe1stgap,the2ndgap, the3rdgap,the4thgap,orthe5thgap.

Thediagrambelowshowsanexampleofthisbeing true.Assumethegapsareinbetweentwoballs.

[color=black!60,fill=white!5,verythick](-1,0)circle(0.25); [black,thick](-1.25,-0.25)–(-0.75,-0.25);[black,thick](1,0.25)–(-1,-0.75);[black,thick](-1.25,-0.25) –(-0.75,-0.25); [black,thick](-1.25,-0.25)–(-0.75,-0.25); [black,thick](-1.25,-0.25)–(0.75,-0.25);[black,thick](-1.25,-0.25)–(-0.75,0.25);[color=black!60,fill=white!5,verythick](-1,0) circle(0.25);

Puttingjustonelineinthefirstslotlikethatisequivalenttoputtingjustonelineonanothergap,asshownbelow. [color=black!60,fill=white!5,verythick](-1,0)circle(0.25); [black,thick](-1.25,-0.25)–(-0.75,-0.25); [black,thick](-1.25,-0.25)–(-0.75,0.25);[black,thick](-1.25,-0.25)–(-0.75,-0.25); [black,thick](-1.25,-0.25)–(-0.75,-0.25);[black,thick](1,0.25)–(-1,-0.75);[black,thick](-1.25,-0.25) –(-0.75,-0.25);[color=black!60,fill=white!5,very thick](-1,0)circle(0.25);

Therefore,usingitlikethiswillseverelyovercount thenumberofcases.Sohowdowemakesurewedon’t undercountlikewedidinsolution1,butalsonotover countlikewe’redoinghere.Instead,wecouldlookatthe linesalittlebitdifferently.Insteadofputtinglines,let’sput

filledcircles,asshownbelow.

[color=black!60,fill=white!5,verythick](-1,0)circle(0.25); [color=black!60,fill=white!5,verythick](-1,0)circle(0.25); [color=black!60,fill=white!5,verythick](-1,0)circle(0.25); [color=black!60,fill=white!5,verythick](-1,0)circle(0.25); [color=black!60,fill=white!5,verythick](-1,0)circle(0.25); [color=black!60,fill=white!5,verythick](-1,0)circle(0.25); [color=black!60,fill=white!5,verythick](-1,0)circle (0.25);[color=black!60!,fill=black!60,verythick](1,0)circle(0.25);[color=black!60!,fill=black!60, verythick](-1,0)circle(0.25);[color=black!60!, fill=black!60,verythick](-1,0)circle(0.25); [color=black!60!,fill=black!60,verythick](-1,0)circle(0.25);[color=black!60!,fill=black!60,very thick](-1,0)circle(0.25);

Let’strytosimulateoneoftheconfigurationsusing thispicture.

[color=black!60!,fill=black!60,verythick](-1,0)circle(0.25);[color=black!60,fill=white!5,verythick](1,0)circle(0.25);[color=black!60,fill=white!5, verythick](-1,0)circle(0.25);[color=black!60, fill=white!5,verythick](-1,0)circle(0.25); [color=black!60!,fill=black!60,verythick](-1,0)circle(0.25);[color=black!60,fill=white!5,verythick](1,0)circle(0.25);[color=black!60,fill=white!5, verythick](-1,0)circle(0.25);[color=black!60!, fill=black!60,verythick](-1,0)circle(0.25);

[color=black!60,fill=white!5,verythick](-1,0) circle(0.25);[color=black!60!,fill=black!60,verythick](1,0)circle(0.25);[color=black!60,fill=white!5,very thick](-1,0)circle(0.25);

[color=black!60!,fill=black!60,verythick](-1,0)circle(0.25);

Inthisconfiguration,thefilledinmarkersseparated thecandiesinto0-3-2-0-1-0.Therefore,withthismethod, wewillbeabletocounteverything,including0’s.Sowe nowknowthecorrectsolution2.

Solution2: Letusfirstdrawoutourfilledcirclesand regularcircles.

[color=black!60,fill=white!5,verythick](-1,0)circle(0.25); [color=black!60,fill=white!5,verythick](-1,0)circle(0.25); [color=black!60,fill=white!5,verythick](-1,0)circle(0.25); [color=black!60,fill=white!5,verythick](-1,0)circle(0.25); [color=black!60,fill=white!5,verythick](-1,0)circle(0.25); [color=black!60,fill=white!5,verythick](-1,0)circle(0.25); [color=black!60,fill=white!5,verythick](-1,0)circle (0.25);[color=black!60!,fill=black!60,verythick](1,0)circle(0.25);[color=black!60!,fill=black!60, verythick](-1,0)circle(0.25);[color=black!60!, fill=black!60,verythick](-1,0)circle(0.25); [color=black!60!,fill=black!60,verythick](-1,0)circle(0.25);[color=black!60!,fill=black!60,very thick](-1,0)circle(0.25);

Aswesawabove,wejustneedtofindthenumberof wayswecanarrangethefilledcircles.Asthereare11total positionsand5filledcircles,thetotalnumberofwaysis 11 5

=462 .And462isindeedthecorrectanswer.

DerivingtheFormulas

Nowthatwehaveadecentunderstandingofwhatstars andbarsisandhowtovisualizeit,letustrytousethese techniquestogeneralizeaformula.

Wearegoingtoderivetwoformulaspertainingtostars andbars.Thefirstdirectlyfollowsfromexample1.0.1.Ifwe consider n tobethenumberofcandiesand r tobethenumberofstudentsDr.Evilhastodistributethemto,wehadto arrange r 1 filledballs(asittakes r 1 barstomake r partitions),inagroupof n + r 1 balls,leadingtotheformula:

Theorem1.2.2 Ifweneedtosplit n identicalitemsto k distinguishablegroups,whereeachgroupcanhave0ormore items,thetotalnumberofwaystodistributeitis n+k 1 k 1 Followingfromthat,whatifwemodifiedtheinitial questionslightly,suchthatnow,eachstudentmustreceive atleast 1 candy.

Example1.2.1 Dr.Evilhastodistribute6identicalcandies to3students,suchthateachstudenthasatleastonecandy. Howmanywaysaretheretodothis?

Itmaybeintuitivethatnow,wedon’thavetoworry aboutmultiplesticksoverlappingona 0 spot,meaningwe justhavetoarrange r 1 barsin n 1 spots,simplyleading totheformula:

Theorem1.2.1 Ifwehavetosplit n identicalitemsinto k distinguishablegroups,whereeverygrouphasatleastone item,thenumberofwaystodosois n 1 k 1

Thisisessentiallywhatstarsandbarsis.Inthenext section,we’lllookattheconceptofpartitionsrecursively, whichsometimesoverlapswithstarsandbarsproblems.

3PartitionsRecursively

Thissectionwillbetargetingcase2,wherewe’re dealingwithidenticalballsandidenticalboxes.Aswecan nolongerusetheStarsandBarsmethod,arecursiveconcept willbepresented.Asusual,webeginwithaproblem:

Example1.3.1 Howmanywayscan3positivenumberssumto10iftheorderoftheaddendsdoesn’tmatter? Byorderoftheaddendsdoesn’tmatter,itmeans 3+3+4 isthesameas 4+3+3. We’llstartbydrawingourexampleintheproblem 4+3+3 intoadiagram.

[color=black!60,fill=white!5,verythick](-1,0)circle(0.2); [color=black!60,fill=white!5,verythick](-1,0)circle(0.2); [color=black!60,fill=white!5,verythick](-1,0)circle (0.2);[color=black!60,fill=white!5,verythick](-1,0) circle(0.2);[color=black!60,fill=white!5,verythick](-3.1,0.5)circle(0.2);[color=black!60,fill=white!5,very thick](-3.1,-0.5)circle(0.2);[color=black!60, fill=white!5,verythick](-3.1,-0.5)circle(0.2); [color=black!60,fill=white!5,verythick](-4.5,-1)circle (0.2);[color=black!60,fill=white!5,verythick](-4.5,-

1)circle(0.2);[color=black!60,fill=white!5,very thick](-4.5,-1)circle(0.2);

Thinkingaboutthisdiagramrecursivelymeanstoreducethediagramtoasimpleronewhichwealsohavecontrolover.Here,thislookslikecreatinga one-to-onecorrespondence,atermwhichmeanstomakeachangetothe scenario,whilekeepingtheanswerconstant.

We’lldrawalinethroughthediagram,whichsignals removingthecirclesthelineintersects.

[color=black!60,fill=white!5,verythick](-1,0)circle(0.2); [color=black!60,fill=white!5,verythick](-1,0)circle (0.2);[color=black!60,fill=white!5,verythick](-1,0) circle(0.2);[color=black!60,fill=white!5,very thick](-1,0)circle(0.2);[color=black!60,fill=white!5,very thick](-3.1,-0.5)circle(0.2);[color=black!60, fill=white!5,verythick](-3.1,-0.5)circle(0.2); [color=black!60,fill=white!5,verythick](-3.1,-0.5) circle(0.2);[color=black!60,fill=white!5,verythick](4.5,-1)circle(0.2);[color=black!60,fill=white!5, verythick](-4.5,-1)circle(0.2);[color=black!60, fill=white!5,verythick](-4.5,-1)circle(0.2);[black,very thick](-5.9,-1)–(-5.9,0);

Let’sthinkaboutwhatwecandowiththis.Ifwefind thenumberofwaysthreenumbers x1 + x2 + x3 =10,andif welet x′ i = xi +1,thenthenumberofsolutionsto x′ 1 + x′ 2 + x′ 3 =7,isthesameasthenumberofsolutionstotheprior equation.Thisisbecauseeverysolutionto x′ 1 + x′ 2 + x′ 3 =7 isjustasolutionto x1 + x2 + x3 =10 ifyouadd1toeach oftheaddends.

Sowe’vereducedthenumber 10 toamuchsimpler numberwithoutchangingtheactualscenario.

Ifwelet p(n,k )= thenumberofways k positive numberscansumto n,weunfortunatelycannotgeneralize theabovetosay p(n,k )= p(n k,k )...thiscanbeseenby drawingtheYoungDiagramwithadifferentconfiguration.

Thistime,letusdrawtheYoungDiagramwithadifferentconfigurationthatsumsto10.Specifically, 6+3+1 [color=black!60,fill=white!5,verythick](-1,0)circle(0.2); [color=black!60,fill=white!5,verythick](-1,0)circle(0.2); [color=black!60,fill=white!5,verythick](-1,0)circle(0.2); [color=black!60,fill=white!5,verythick](-1,0)circle(0.2); [color=black!60,fill=white!5,verythick](-1,0)circle(0.2); [color=black!60,fill=white!5,verythick](-1,0)circle(0.2); [color=black!60,fill=white!5,verythick](-4.5,-0.5)circle (0.2);[color=black!60,fill=white!5,verythick](-4.5,0.5)circle(0.2);[color=black!60,fill=white!5,very thick](-4.5,-0.5)circle(0.2);[color=black!60,fill=white!5, verythick](-5.9,-1)circle(0.2);

Now,youmaynoticethatifweweretodrawaline totrytodothe1to1correspondenceagain, k wouldbe reducedasthesmallestnumberis 1.Thisisshowninthediagrambelow. [color=black!60,fill=white!5,verythick](-1,0)circle(0.2); [color=black!60,fill=white!5,verythick](-1,0)circle(0.2); [color=black!60,fill=white!5,verythick](-1,0)circle(0.2); [color=black!60,fill=white!5,verythick](-1,0)circle(0.2); [color=black!60,fill=white!5,verythick](-1,0)circle(0.2); [color=black!60,fill=white!5,verythick](-1,0)circle(0.2); [color=black!60,fill=white!5,verythick](-4.5,-0.5)circle (0.2);[color=black!60,fill=white!5,verythick](-4.5,-

0.5)circle(0.2);[color=black!60,fill=white!5,very thick](-4.5,-0.5)circle(0.2);[color=black!60,fill=white!5, verythick](-5.9,-1)circle(0.2);[black,verythick](-5.9,-1) –(-5.9,0);

Therefore,wewewouldn’tbeabletosubtractanother 3 from n asthatguaranteesthateachpartitionisatleast 2 Therefore,wecantryandcoverthecaseswhereapartition is 1 inaseparatecase.

Letustryremovingthatlone1inthebottomleft corner.[color=black!60,fill=white!5,verythick](-1,0)circle(0.2); [color=black!60,fill=white!5,verythick](-1,0)circle(0.2); [color=black!60,fill=white!5,verythick](-1,0)circle(0.2); [color=black!60,fill=white!5,verythick](-1,0)circle(0.2); [color=black!60,fill=white!5,verythick](-1,0)circle(0.2); [color=black!60,fill=white!5,verythick](-1,0)circle(0.2); [color=black!60,fill=white!5,verythick](-4.5,-0.5)circle (0.2);[color=black!60,fill=white!5,verythick](-4.5,0.5)circle(0.2);[color=black!60,fill=white!5,very thick](-4.5,-0.5)circle(0.2);

Now,wehaveasituationwherewehavetwonumbers sumto9.Asthisisthecasewhereatleastoneofthenumbersis1,wecanjustputa1asthethirdnumber.Therefore, thisderivationworks!

Puttingitinthe p(n,k ) notationweusedbefore,we getthiscaseis p(n 1,k 1) aswe’relosingonegroupand onenumber.Wecanputthistogetherwithour p(n k,k ), todevelopourfirstformula.

Theorem1.3.1 Given p(n,k ) isthenumberofways k positivenumberscansumupto n,wheretheorderdoesn’tmatter, p(n,k )= p(n k,k )+ p(n 1,k 1)

Usingthis,let’ssolveexample1.3.1.

Solution2: Inthisproblem,wewanttofind p(10, 3).Using whatwelearnedpreviously, p(10, 3)= p(7, 3)+ p(9, 2)= p(4, 3)+ p(6, 2)+ p(9, 2) p(4, 3)=1,astheonlywayis 1+1+2 p(6, 2)=3,astheonlywaysare 5+1, 4+2,and 3+3 p(9, 2)=4,astheonlywaysare 8+1, 7+2, 6+3, 5+4.Summingthesevaluesup,weget 4+3+1= 8 . Butnow,whatifwechangeonewordintheproblem statement?

Example1.3.2 Howmanywayscan3positive distinct numberssumto10iftheorderoftheaddendsdoesn’tmatter?Byorderoftheaddendsdoesn’tmatter,itmeans 3+5+2 isthesameas 5+3+2

Ourinitialformulaunfortunatelyaccountsforall cases,notjustdistinctcases,meaningwe’llhavetoderive somethingelse.Asshouldbeexpectedbynow,let’sstart outbydrawingtheYoungDiagramfor 5+3+2.

[color=black!60,fill=white!5,verythick](-1,0)circle(0.2); [color=black!60,fill=white!5,verythick](-1,0)circle(0.2); [color=black!60,fill=white!5,verythick](-1,0)circle(0.2); [color=black!60,fill=white!5,verythick](-1,0)circle(0.2); [color=black!60,fill=white!5,verythick](-1,0)circle(0.2); [color=black!60,fill=white!5,verythick](-3.8,-0.5)circle (0.2);[color=black!60,fill=white!5,verythick](-3.8,0.5)circle(0.2);[color=black!60,fill=white!5,very thick](-3.8,-0.5)circle(0.2);[color=black!60,fill=white!5, verythick](-5.2,-1)circle(0.2);[color=black!60, fill=white!5,verythick](-5.2,-1)circle(0.2);

Onceagain,wecanmakea1to1correspondence.Ifeverynumberisdistinctandifwesubtract onefromeachofthenumbers,thenthey’llstaydistinct. Therefore,wecandrawalinethroughthefirstcolumn likewedidwhenwewerederivingthe p(n,k ) formula. [color=black!60,fill=white!5,verythick](-1,0)circle(0.2); [color=black!60,fill=white!5,verythick](-1,0)circle(0.2); [color=black!60,fill=white!5,verythick](-1,0)circle(0.2); [color=black!60,fill=white!5,verythick](-1,0)circle(0.2); [color=black!60,fill=white!5,verythick](-1,0)circle(0.2); [color=black!60,fill=white!5,verythick](-3.8,-0.5)circle (0.2);[color=black!60,fill=white!5,verythick](-3.8,0.5)circle(0.2);[color=black!60,fill=white!5,very thick](-3.8,-0.5)circle(0.2);[color=black!60,fill=white!5, verythick](-5.2,-1)circle(0.2);[color=black!60, fill=white!5,verythick](-5.2,-1)circle(0.2); [black,verythick](-5.9,-1)–(-5.9,0);

Letussay q (n,k )= thenumberofways k distinct numberscansumton.Withwhatwedidabove,wethink q (n,k )= q (n k,k ),asthereare k fewerballs.Wecan nowstartansweringtheexample!

Asyou’reprobablysuspecting,wehavetoaccountfor thecasewhereoneofthenumbersis1.Asexpected,wewill drawourYoungDiagramagain,thistimewith 6+3+1 [color=black!60,fill=white!5,verythick](-1,0)circle(0.2); [color=black!60,fill=white!5,verythick](-1,0)circle(0.2); [color=black!60,fill=white!5,verythick](-1,0)circle(0.2); [color=black!60,fill=white!5,verythick](-1,0)circle(0.2); [color=black!60,fill=white!5,verythick](-1,0)circle(0.2); [color=black!60,fill=white!5,verythick](-1,0)circle(0.2); [color=black!60,fill=white!5,verythick](-4.5,-0.5)circle (0.2);[color=black!60,fill=white!5,verythick](-4.5,0.5)circle(0.2);[color=black!60,fill=white!5,very thick](-4.5,-0.5)circle(0.2);[color=black!60,fill=white!5, verythick](-5.9,-1)circle(0.2);

Ourfirstinstinctwouldbetodowhatwedidwith p(n,k ) andremovethatsingularballinthebottomleftcorner.Let’stakeitoutfromourdiagram.

[color=black!60,fill=white!5,verythick](-1,0)circle(0.2); [color=black!60,fill=white!5,verythick](-1,0)circle(0.2); [color=black!60,fill=white!5,verythick](-1,0)circle(0.2); [color=black!60,fill=white!5,verythick](-1,0)circle(0.2); [color=black!60,fill=white!5,verythick](-1,0)circle(0.2); [color=black!60,fill=white!5,verythick](-1,0)circle(0.2); [color=black!60,fill=white!5,verythick](-4.5,-0.5)circle (0.2);[color=black!60,fill=white!5,verythick](-4.5,0.5)circle(0.2);[color=black!60,fill=white!5,very thick](-4.5,-0.5)circle(0.2);

Althoughitseemslikewecandoour1to1correspondencewiththiscaseinthismanner,weareactuallyover counting.Thatisbecauseinanyofthetworemainingrows, therecanbeoneball.Then,whenweaddathirdgroupof oneball,we’llhavetwogroupsofoneball,whichmeansthat they aren’tdistinct.Therefore,wehavetothinkofsomethingelsetodo.

Tocomeupwithacorrespondencethatactuallysatisfiesthecasewithonegrouphavinga1,wecantrytoremove theentirecolumnjustlikewedidwiththe1stcase. [color=black!60,fill=white!5,verythick](-1,0)circle(0.2);

[color=black!60,fill=white!5,verythick](-1,0)circle(0.2); [color=black!60,fill=white!5,verythick](-1,0)circle(0.2); [color=black!60,fill=white!5,verythick](-1,0)circle(0.2); [color=black!60,fill=white!5,verythick](-1,0)circle(0.2); [color=black!60,fill=white!5,verythick](-1,0)circle(0.2); [color=black!60,fill=white!5,verythick](-4.5,-0.5)circle (0.2);[color=black!60,fill=white!5,verythick](-4.5,0.5)circle(0.2);[color=black!60,fill=white!5,very thick](-4.5,-0.5)circle(0.2);[color=black!60,fill=white!5, verythick](-5.9,-1)circle(0.2);[black,verythick](-5.9,-1) –(-5.9,0);

Thisactuallyworks!Becausewearegoingtoadd1to eachofthefirsttworows,neitherofthemcouldbe1.So, wearesurethey’redistinct!Usingour q (n,k ) notation,this yieldsus q (n k,k 1) aswearelosingonegroupwhen wetakeoutonecolumn,andwehave k lessballs.

Wecanaddthistoourinitial q (n k,k ) toobtainour secondformula!

Theorem1.3.2 If q (n,k ) isthenumberofways k distinct positivenumberssumto n, q (n,k )= q (n k,k )+ q (n k,k 1)

Withthisinmind,thesolutiontotheexampleisrudimentary:

SolutiontoExample1.3.2: Weneedtofind q (10, 3).Usingtheformulawederivedearlier, q (10, 3)= q (10 3, 3)+ q (10 3, 3 1)= q (7, 3)+ q (7, 2)= q (4, 3)+ q (4, 2)+ q (7, 2) q (4, 3) isobviously 0 q (4, 2)=1,astheonlyconfigurationthatworkare 3+1 q (7, 2)=3,astheconfigurationsthatworkare 6+1, 5+2,and 4+3.Summingthese valuesup, 0+1+3= 4

Asexpected,wewillbederivingourfinalformulausingaproblemaswell.

Example1.3.3 Howmanywaysaretherefortwoormore positiveintegerstosumto10,suchthattheordermatters? (forexample, 6+3+1 isdifferentfrom 1+3+6). Letusfirstdraw10balls,eachrepresentingone,ina row.

[color=black!60,fill=white!5,verythick](-1,0)circle (0.2);[color=black!60,fill=white!5,verythick](1,0)circle(0.2);[color=black!60,fill=white!5, verythick](-1,0)circle(0.2);[color=black!60, fill=white!5,verythick](-1,0)circle(0.2); [color=black!60,fill=white!5,verythick](-1,0)circle(0.2); [color=black!60,fill=white!5,verythick](-1,0)circle(0.2); [color=black!60,fill=white!5,verythick](-1,0)circle(0.2); [color=black!60,fill=white!5,verythick](-1,0)circle(0.2); [color=black!60,fill=white!5,verythick](-1,0)circle(0.2); [color=black!60,fill=white!5,verythick](-1,0)circle(0.2); Iwillbeusingtwodifferentsymbolstorepresentdifferentthings: + toseparatetheaddendsand ∗ tocombine theballswithinanaddend.

Thediagrambelowsimulateshowwe’reinterpreting thesymbols.

[color=black!60,fill=white!5,verythick](-1,0)circle (0.2);

+ [color=black!60,fill=white!5,verythick](-1,0) circle(0.2);

∗ [color=black!60,fill=white!5,verythick](-1,0) circle(0.2);

Thesimulationaboveshows 1+2,asthe ∗ combines 1and1.

Theexampleaboveperhapsgivesyouanideaofwhat wecandotosolvethisproblem.Betweenanytwoballs,we caneitherputa + or ∗,whichmeansthereare2choices foreverygap.Asthereare 10 1=9 gaps,wehave 29 possibilities.However,wecannotcombineallofthemasthe questionasksforatleasttwopositiveintegers.Therefore, ouransweris 29 1= 511 .Thisisthesolutiontoexample 1.3.3!

Hopefully,youwillbeabletogeneralizethisto n numberstoobtainourthirdandfinalformula.

Theorem1.3.3 Ifwewanttofindthenumberofwaystwo ormorepositivenumberssumto n,wheretheordermatters, thenumberofwaysis 2n 1 1.

4Conclusion

Thispaperisanintroductiontotheworldofpartitions andaimstoprovidethefundamentalknowledgenecessary forfurtherexploration.Theconceptsandformulaspresented herearederivedusingrudimentarylogicandmathematics. Therefore,youareencouragedtoextendthepresentedconceptstotryderivingmoreformulasonyourown,especially forthelasttwotypesofpartitions.

References

N/A.

References

N/A

04 Calculating Implied Volatility using the Black-Scholes Model

Written by Benjamin Cheong

CalculatingImpliedVolatilityusingtheBlack-ScholesModel(ATLAProject)

BenjaminCheong cheong43465@sas.edu.sg

TeacherReviewers: Mr.Zitur,Mr.Craig

Abstract

OptionstradersoftenusetheBlack-Scholesmodelorsome extensionofittoestimatethevalueofoptions.TheBlackScholesmodelemploysdifferentmathematicalconceptsincludingpartialdifferentialequations,stochasticcalculus,and probabilitytheorytoestimatethevalueofaEuropeancalloption.Despiteitslimitations,theBlack-Scholesmodelremains largelyunrivaledintermsofmathematicalmodelsestimating thevalueofoptions.

Inthispaper,IwillexplaintheintuitionbehindtheBlackScholesformula.Inmyextension,Iwillanalyzethevolatility oftheSPDRS&P500ETFTrust(SPY),anETFthatclosely representstheUSequitymarket.IplantocalculatethehistoricalvolatilityofSPYandcompareitwiththeimpliedvolatilityofSPYatdifferentexerciseprices.Finally,Iwillhighlight afewlimitationsofthemodelthatmayhaveaffectedmycalculationsrelatingtotheimpliedvolatilityofSPYshares.

Keywords: Black-Scholesmodel,partialdifferentialequations,stockmarket,totalderivative,volatility

1TheBlack-ScholesModel

1.1HistoryandBackground

Developedin1973byFischerBlack,MyronScholes,and RobertC.Merton,theBlack-Scholesmodelwascreatedto calculatethevalueofaEuropeancalloption.Thecreation ofthemodelledtoasignificantincreaseinoptionstradingvolumeandearnedScholesandMertontheNobelPrize inEconomics.TounderstandtheBlack-Scholesmodel,it isfirstimportanttounderstandwhatEuropeanoptionsare. Optionsarefinancialderivativesthatallowsomeonetobuy orsellsharesatapredeterminedpriceonaspecificdate. EuropeanoptionsdifferfromAmericanoptionsintheway thattradersofEuropeanoptionsareonlyallowedtoexercisetheiroptionsontheoptionexpirydatewhiletradersof Americanoptionscanexercisetheiroptionsanytimebefore theexpirydate,thereforesimplifyingthemathematicsrequiredtoestimateavalueforEuropeancalloptions.Hereis anexampleofaEuropeancalloptiontoprovidethereader withabetterunderstandingofit:

Let’ssayBobbuysaEuropeancalloptionfromDanfor $10.Thecalloptionstatesthatintwodays,Bobhasthe optiontobuyoneNestlesharefromDanfor$200.Twodays later,oneNestlesharenowcosts$300.Bobexerciseshis

option,buysoneNestlesharefromDanfor$200,andsells thatsharefor$300,makinga$90profitsincehehadtopay Dan$10inthebeginning.

TheBlack-Scholesmodel,ifemployedcorrectly,helpsa traderaccuratelyvalueoptions,enablingthetradertospot arbitrageopportunitiesinthemarkettogenerateprofit.

1.2TheModel

TheBlack-ScholesModelcanbebrokendownasfollows:

C =calloptionvalue

S =sharepriceofunderlyingstock

K =exerciseprice

r =risk-freeinterestrate

N (d) =cumulativedistributionfunctionfornormaldistribution

t =timetoexpirationofoption

σ =volatility/standarddeviationoflognormalfunction

Inlayman’sterms,acalloptionisvaluedbydeducting theshareprice(S )bythediscountedpresentvalue(e rt ) oftheexerciseprice(K ),bothofwhichareweightedby aprobabilityfactor N (d1 ) and N (d2 ) respectively.Wecan illustratethismoreclearlyatcalloptionmaturitywhenthe valueofthecalloptionisessentiallythesharepriceminus theexerciseprice.

N (d1 ) and N (d2 ) aremoredifficulttounderstandbutintuitively N (d1 ) istherisk-adjustedprobabilitythattheoptionwillnotexpirein-the-moneywhile N (d2 ) istheriskadjustedprobabilitythattheoptionwillexpirein-the-money.

1.3PresentValueAdjustmenttoCallOption Price

Weneedtodiscounttheexercisepricetocalculatethe presentvalueoftheexerciseprice.Sincetheoptionexercise isatafuturedate,weneedtotakeintoaccountthevalueof

theoptionnowversusthevalueatthetimeofexpiration.We canusetheformulaforcontinuouscompoundinginterest, e rt ,where r istherisk-freeinterestrateand t isthetimeto maturitytodiscountthecalloptionexerciseprice.

NPVofcalloptionprice= Ke rt

1.4HighlightsofMathematicalDerivation

ThemathematicalderivationoftheBlack-Scholesmodel isverycomplex,combiningdifferentbranchesofcalculus includingpartialdifferentialequations,stochasticcalculus, martingales,andIt ˆ o’slemma.Wewillexaminesomeofthe conceptsusedinthederivationoftheBlack-Scholesmodel below.

TheBlack-ScholesmodelassumesthatsharepricesfollowageometricBrownianmotionwithmeangrowthrate µ, volatility σ and W isaWienerprocessorBrownianmotion. Brownianmotionisarandomprocessandiswidelyusedto modelpercentagechangesinshareprices.

dS S = µdt + σdW

WeapplyabranchofcalculuscalledIt ˆ o’slemmatocalculatethepayoffofanoption V asfollows:

risk-adjustedprobabilitythattheoptionwillnotbeexercised.Itisalsotheoptiondeltaorthesensitivityoftheoptionpricetochangesinthesharepriceoftheunderlying stock.

Greatervolatilitymeansthatthecalloptionhasgreater value.Greatervolatilityincreasesthevalueof d1 asthe volatilityinthenumeratorissquaredoverthevolatilityin thedenominator.Thisleadstoahigherprobabilityproduced bythenormaldistributionfunctionandthereforeagreater calloptionvalue.Greatervolatilitydecreasesthevalueof d2 asthevolatilityinthenumeratorissquaredandnegative overthevolatilityinthedenominator.Alower d2 leadstoa lowerprobabilityproducedbythenormaldistributionfunctionandacorrespondinghighercalloptionvalue.

Greatertimetoexpirationmeansthatthecalloptionhas greatervalue.Greatertimetoexpirationaffect d1 and d2 similarly.However,asthevariable t increases,thefunction e t tendstowardszero,decreasingthenegativecomponent oftheequation,thereforeleadingtoagreatercalloption value.

Ahighersharepriceovertheexercisepricewillleadto ahighercalloptionvalue.Similarly,ahigherrisk-freerate willresultinahighercalloptionvalue.

2ComparingHistoricalCalculatedVolatility toImpliedVolatility

*Notethat ∂f/∂x representsthepartialderivativeof f with respectto x.

Byusingaconceptcalleddelta-hedgeportfolio,weeffectivelyshortoneoptionandlongshares.Thisallowsus toeffectivelyremove dW fromtheequation,thusneutralizingtheeffectoftheBrownianmotion.Astheportfoliois nowfully-hedged,theappropriatereturnistherisk-freerate ofinterest r .ThisallowsustoarriveattheBlack-Scholes partialdifferentialequation.

Iwantedtoinvestigatehowsimilarthehistoricalcalculatedvolatilitywastotheimpliedvolatilityofcalloptions atdifferentexercisepricesoftheSPYETFinthemonthof September2022usingtheBlack-Scholesmodel.

2.1CalculationofHistoricalVolatility

Theequationtocalculatehistorical/annualizedvolatility is:

ln( px px 1 )) × √d 1

HV=historicalvolatility

SD=standarddistributionmodel

d =numberofdaysinthedataset

P (d) =sharepriceonthatday d

N (d) isthecumulativedistributionfunction(0%to 100%)whichisusedtocalculateprobabilitiesunderanormaldistributionfunction. N (d2 ) canbethoughtofasariskadjustedprobabilitythatthefuturestockpricewillbeabove theexercisepriceatexpiration. N (d1 ) isthoughtofasthe

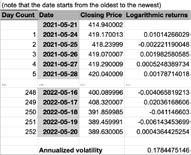
IamcalculatingthehistoricalvolatilityoftheS&P500 ETFindex(SPY),ahighlyliquidanddeeply-tradedETF,usingtheclosingpricesofthetradingdaysofthelastyear-todate.Therewere252tradingdaysfromtheyear-to-dateof 21May2022.Historicalvolatilityisconsideredasthestandarddeviationofthesumofthelogarithmicreturns.First,I usedtheequation ln(px /px 1 ) todeterminethelogarithmic returnsforeverydayexcludingthefirstdayasthereareno valuesfor px 1 .Next,IenteredtheresultintotheSTDEV() standarddeviationfunctioninGoogleSheetstocalculatethe standarddeviationofallthelogarithmicreturns.Finally,I multipliedthehistoricalvolatilitybythesquarerootofthe numberoftradingdaysinmydataset,sincevolatilityisthe squarerootofthevariance,tocalculateannualizedvolatility.Myresultofannualizedvolatilitywas0.1784475146or around17.8448%.

*NotethatIonlyincludedthefirsttendaysofmydataset

2.2CalculationofImpliedVolatilityusing Black-ScholesModel

UsingtheBlack-Scholesmodelandthemarketcalloption valueonYahooFinance,Iestimatedthevariablesoftime toexpirationofoptionandrisk-freeinterestratetoreverse engineertheimpliedvolatilitiesforthemonthofSeptember 2022.

IestimatedthetimetoexpirationoftheoptionbyusingtheNETWORKDAYS()functioninGoogleSheetsthat computedthenumberoftradingdaysbetweentoday’sdate, 21May2022,andthedatethattheoptionswouldexpire, 30September2022.Idividedthattimebythetotalnumber oftradingdaysinayear(253days)tocalculatethetimeto expirationinpercentageform.

Iestimatedtherisk-freeinterestrateforSeptember2022. Idividedthenumberoftradingdayscalculatedaboveby30 days,roughlythenumberofdaysinamonth,tocalculatethe numberofmonthsuntiltheoptionwouldexpire,obtaining theresultof4.4months.Iestimatedtherisk-freeinterest ratebyinterpolatingthe3-monthand6-monthUStreasury interestratesfromtheUSFederalReservewebsiteof1.03% and1.51%respectivelytocalculatetheUStreasuryinterest ratein4.4monthswhentheEuropeancalloptionswould expire.

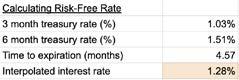
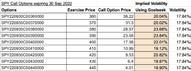
Thedetailedspreadsheetcontainingmycalculationsisinthe GoogleSheetlinkbelow: https://docs.google.com/spreadsheets/d/1 8CwUfFklZNCd 6nyynn6iTug1TH0T3ISeTITq8oZuRI/edit#gid=0

Withallmyvaluescomputedorgiven,Idownloadedand usedtheGoalSeekfunctiononGoogleSheetswhichissimilartothe.solve()functionontheTI-Nspirecalculator.Ienteredthevaluesandbegancomputingtheimpliedvolatilities—thatis,thevolatilitiesrequiredtoobtainthestated calloptionvalues.NotethatIhadtorepeatedlychangethe exercisepriceasmyresearchwaswithregardstothetrends ofvolatilityduetoexerciseprice.

2.3Observations&Analysisof“Trendsof VolatilityduetoExercisePrice”Graph Thereareseveralsignificanttakeawaysfromthe“trends ofvolatilityduetoexerciseprice”graph.

Theimpliedvolatilitystaysabovetheannualizedvolatilityforallthelistedexerciseprices.Impliedvolatilityis baseduponpresentvolatilitywhileannualizedvolatilityis baseduponthevolatilityofthepastyear-to-date.Therefore, thisobservationcanbeexplainedbythehighvolatilityof theAmericanmarketforthelastthreemonthsaftertheRussianinvasionofUkraineinFebruary.Thelowerannualized volatilityisanaverageofasignificantlylargerdatasetand thereforeislessaffectedbytherecenttrend.Inaddition,the impliedvolatilityatdifferentexercisepricesdoesnotfollowacleartrendthroughout,thoughitseemstobelargely decreasingafteritsinitialmaximumataroundthe$390exerciseprice.

Differentexercisepriceschangethevolatility.Basedon furtherresearchfromInvestopedia,thereisaconceptcalled volatilityskewwherein-the-moneyoptionshavehigherimpliedvolatilityvsout-of-the-moneycalloptions.Although mygraphlooksalittleskewed,Isuspectthatthedeviation isfromthecurrentmarketvolatility.

3Limitations

3.1AmericanvsEuropeanOptions

Onelimitationtomycalculationsoftheimpliedvolatility oftheSPYindexisthattheS&P500ETFindex(SPY)isan Americanoption,notaEuropeanoption.Thisissignificant becausethemathematicsbehindtheBlack-Scholesmodelis gearedtowardsthemorestraightforwardEuropeanoption.

WhileEuropeanoptionscanonlybeexercisedonthedayof expiry,Americanoptionscanbeexercisedonanydaybeforetheoptionexpires.IresearchedAmericanoptionpricingmodelsandfoundthattheBjerksund-Stenslandmodel isamodeloftenusedtopriceAmericanoptions,butfound thatthemathistoocomplexforthisdiscussion.

3.2Fat-tails

AnotherlimitationisthattheBlack-Scholesmodelhasa significantflawthatmayhaveimpactedourestimation.The Black-Scholesmodelassumesthatthedistributionoftheoptionvalueislognormal,butthisisnotnecessarilytrue.The modelfailstotakeintoaccountthepossibilityoffattails orkurtosisandBlackSwans,asuddenlargelyunforeseen changeinmarketconditionssuchasthe2007financialcrisis,meaningthatasuddenchangeinhowtheoptionprices aredistributedcanhaveadrasticimpactontheaccuracyof theoptionpricing.Thisisextremelysignificantasitcould causetheuseroftheBlack-Scholesmodeltohighlyundervalueorovervaluecertainoptions,causingtheusersignificantfinancialloss.

3.3HistoricalVolatilityvsCurrentVolatility

AnotherlimitationisthattheannualizedvolatilitythatI calculatedisevidentlynotagoodpredictorofthecurrent impliedvolatilityaccordingtomygraph.Thereasonbehind thedifferencebetweentheannualizedandimpliedvolatility canbeattributedtothehighlyvolatilemarketconditionsthat havebeencausedbytherecentFederalReserveinterestrate hikesandtheuncertaintyovertheRussia-Ukrainewar.Since theimpliedvolatility,whichisbasedonthelastfewmonths, isgreaterthantheannualizedvolatility,whichisbasedon thelastyear-to-date,itisevidentthatannualizedvolatility cannotberelieduponintheincreasingly-volatilemarketof today.

4Conclusion

Inconclusion,throughmyresearch,Ifoundthatthe Black-Scholesmodelisprimarilycomprisedofapresent valueadjustmentequationtakingintoaccounttheprobabilities d1 and d2 ,theprobabilitythattheoptionwillnotexpirein-the-moneyandtheprobabilitythattheoptionwillexpirein-the-moneyrespectively,plottedoveranormaldistribution graph N (d).Throughmyextensioninvestigatingtherelationshipbetweenannualizedvolatilityandimpliedvolatility oftheSPYETFoverthemonthofSeptember2022,Ifound thattheimpliedvolatilitywassignificantlygreaterthanthe annualizedvolatilitywhichcanbeattributedtothegreater volatilityinthepastfewmonthsduetotheuncertaintysurroundingreal-worldevents.Annualizedvolatilitymaynot beagoodpredictorofcurrentandfuturevolatility.

Throughmyresearchoffinancialderivatives,Inoticed thatitishighlydifficulttoderiveequationsthatadequately representtheuncertaintyinfinancialmarkets.Itisevident thateventheBlack-Scholesmodel,whichwonitscreators theNobelPrizeinEconomics,hasseveralsignificantlimitations.Forexample,themodelreliesonanassumption thatoptionpriceisrepresentedbylognormaldistribution

andthereforedoesnotaccountfortheoptionpricefollowingothertypesofdistributionmodelslikefat-tailorkurtosis distribution.

References

”DerivingtheBlack-ScholesEquation”(QuantStart,n.d.). Retrievedfrom

https://www.quantstart.com/articles/Deriving-the-BlackScholes-Equation/.

Hayes,A.(2022,April3).”WhatIstheBlack-Scholes Model?”Investopedia.

https://www.investopedia.com/terms/b/blackscholes.asp. Hayes,A.(2022,February8).”Volatility.”Investopedia. https://www.investopedia.com/terms/v/volatility.asp#tochow-to-calculate-volatility.

”HowtoCalculateHistoricalVolatilityinExcel” (Macroption,n.d.).Retrievedfrom https://www.macroption.com/historical-volatility-excel/. ”Ito’sLemma”(QuantStart,n.d.).Retrievedfrom https://www.quantstart.com/articles/Itos-Lemma/.

Louis(2019,October29).”TheBlackScholesModel Explained”TradeOptionsWithMe.

https://tradeoptionswithme.com/black-scholes-explained/. Nibley,B.(2021,June21).”TheBlack-ScholesModel, Explained.”SoFi.https://www.sofi.com/learn/content/whatis-the-black-scholes-model/.

”ResourceCenter”(U.S.DepartmentoftheTreasury,n.d.). Retrievedfromhttps://home.treasury.gov/resourcecenter/data-chart-center/interestrates/TextView?type=daily treasury yield curve&#38;field tdr date value month=202205.

Turner,E.(2010).”TheBlack-ScholesModeland Extensions.”UniversityofChicago. http://www.math.uchicago.edu/may/VIGRE/VIGRE2010/REUPapers/Turner.pdf. Veisdal,J.(2021,December1).”TheBlack-Scholes Formula,Explained.”Cantor’sParadise. https://www.cantorsparadise.com/the-black-scholesformula-explained-9e05b7865d8a.

Countably and Uncountably Infinite Sets

Written by Benjamin Cheong

CountablyandUncountablyInfiniteSets

BenjaminCheong

cheong43465@sas.edu.sg

Abstract

Bornin1845,GermanmathematicianGeorgCantorwasa pioneerindevelopingsettheory—inspecific,infinitesettheory.Infinitesettheoryisabranchofmathematicsthatfocuses onstudyingthebehaviorofinfinitecollectionsofnumbers. Inthispaper,wewillestablishthatinfinityisaconceptand examinetheconclusionsCantordrewregardinginfinitesets, relatingtocountabilityandcardinality.Pleasenotethatthis paperwillnotbedescribingproofsinamathematicallyrigorousmanner,butwillratherbeexplaininginamoreeasy-tounderstandmanner.’

Keywords: settheory,infinity,Cantor’sdiagonalizationargument,cardinality,bijective,Cantor’stheorem

1InfinityisaConcept

Infinityonlyexistsasaconceptandhasfundamental flawswhenappliedasanumber.Whenwelaterdelve intoinfinitesets,itisimportanttoregardthatinfinityasa conceptaswell.First,let’sproveinfinitycan’tbeanumber.

1.Thecircumferenceof

Figure2:Twotangentsemicircleswithradius 1 2 linedup

Foursemi-circleswithradius 1 4 ?Thetotalcircumference

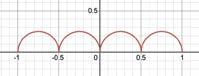
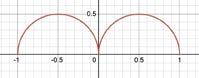
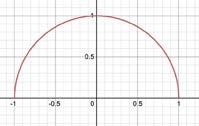
1 4

Eightsemi-circleswithradius 1 8 ?Sixteensemi-circles withradius 1 16 ?Asthenumberofsemi-circlesincreases,the totalcircumferenceremainsthesameat π .Yet,aninfinite numberofsemi-circleseachwithaninfinitelysmallradius wouldresemblealineinstead.Alinewhichis 2 unitslong.

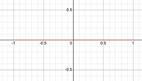
Copyright©2023,AssociationfortheAdvancementofArtificial Intelligence(www.aaai.org).Allrightsreserved.

Therefore,wheninfinityisusedasanumber, π isequiv-

Figure1:Asinglesemicriclegraphedonthe x-y plane

Figure3:Foursemicircleswithradius

Figure4:An 2 unitlonglineonthe x y plane

alentto 2.Since π cannotbeequivalentto 2,thereforeit followsthatinfinitycannotbeusedasanumber.Thelimit asthenumberofsemi-circlesapproachesinfinitydoesapproach 2,but,aswelearnincalculus,thelimitcanoftenbe differentfromtheactualanswer.

2.2CountabilityofIntegerSet

Doestheintegersetcorrespondone-to-onetothenatural set?Let’ssee.

Integers 0 1 -1 2

NaturalNumbers 1 2 3 4

Yes,itdoes!Tocorrespondeveryintegertoanaturalnumber,wehavetostartwithzeroandthengotothepositiveand negativeofeachfollowinginteger.Byworkingtobothpositiveandnegativeinfinity,wecancorrespondeverynatural numbertoexactlyonenumberintheintegerset.

2.3CountabilityofthePositiveRational NumbersSet

Doesthepositiverationalnumbersetcorrespondone-toonetothenaturalset?Let’ssee. RationalNumber

Forexample,intheabovegraph, f (x)= x2 ,for x =1, and f (x)=3 for x =1.Therefore, limx→1 f (x)=1, while f (1)=3.Therefore,thelimitisdifferentfrom theactualanswerwhenthegraphhasajumporpoint discontinuity.

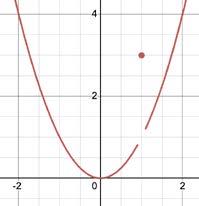
2CountablyandUncountablyInfiniteSets

Todeterminewhetheraninfinitesetiscountableoruncountable,wecanusebijection,amethoddevelopedby Cantor.Abijectionisaone-to-onecorrespondence.Ifthe infinitesetcancorrespondone-to-onetothenaturalset,the infinitesetiscountable.Ifitcannotcorrespondone-to-one tothenaturalset,theinfinitesetisuncountable.Pleasenote thatthenaturalsetofnumbersis {1,2,3,4,5,6,7,... }. Wewilllatershowthatanysubsetofacountablyinfinite set,suchasthenaturalset,andanuncountablyinfiniteset isalsocountablyinfiniteanduncountablyinfinite,respectively.Here,wewillassessthecountabilityofafewinfinite setsandexplainourreasoning.

2.1CountabilityofEvenIntegerSet

Doestheevenintegersetcorrespondone-to-onetothe naturalset?Let’ssee.

EvenIntegers 2 4 6 8

NaturalNumbers 1 2 3 4

Yes,itdoes!Everynaturalnumbercorrespondstoexactly onenumberintheevenintegerset.

Figure6:Allrationalnumbersasfractions

Yes,itdoes!Sinceallrationalnumberscanberepresented asafraction,wecancorrespondeverynumberinthepositiverationalnumbersettoanumberinthenaturalsetby employingadiagonalapproachshownabove.Theblueand pinknumbersrepresentthedenominatorandnumeratorof thenumberrespectively.Allrepeatednumbers(e.g 1 1 , 2 2 , 3

) areskipped.Nootherapproachwouldworkaswecannot gotoinfinityandcomeback(e.g1, 1 2 , 1 3 , 1 4 ,2, 2 3 , 2 5 ,... ). Pleasealsonotethatbyprovingthecountabilityofthepositiverationalnumbersset,wecaneasilyprovethecountabilityoftherationalnumberssetasawholebyaddingzeroin frontandaddinganegativenumberaftereachpositivenumber—similartowhatwedidfortheintegernumberset.All subsetsofcountablyinfinitesetsmustbecountablyinfinite themselvesbecausetheyareeitherfiniteoraremadeupof allthenumbersinanalreadyprovensetandthereforeshare thesamecharacteristics.

2.4CountabilityofRealNumberSet

Doestherealnumbersetcorrespondone-to-onetothe naturalset?Let’sthinkaboutit.

Figure5:Agraphof f (x)= x2 ,for x =3

No,itdoesn’t.Thereisnowaytoestablishone-to-one correspondencebetweentherealnumbersetandthenatural set.Althoughitmayinitiallyseemliketheinfinitybetween arealnumbersetfrom [0, 1] shouldbethesameinfinityin apositiveintegerset,thisconclusionfailstoconsiderinfinitelyrepeatingnumberslike 1 3 .Thenumber 1 3 inthereal numbersetisnotrepresentedinthepositiveintegersetasit requiresinfinitedecimalsthatdonotexistinintegers.

Aclearerproofthattherealnumbersetisuncountablecan beshownbyCantor’sdiagonalargument.Cantor’sdiagonalargumentprovesthatarealnumbersetfrom [0, 1] is uncountable,thereforeprovingthatallrealnumbersetsare uncountable.Usingproofbycontradiction,firstassumethat theinfiniterealnumbersetiscountable.

therealnumbersareindeeduncountable.

Pleasenotethatthechangefrom0to1iscompletelyarbitrary.Aslongasyouaresomehowchangingeachofthe red-highlightednumbers,youcanproveCantor’sdiagonal argument.

2.5CountabilityofIrrationalNumberSet

Doestheirrationalnumbersetcorrespondone-to-oneto thenaturalset?Let’ssee.

No,itdoesn’t.Sincetheirrationalnumbersetisinfinite, wecanprovethatitisuncountableusingthesamelogicbehindCantor’sdiagonalizationargument.Pleasenotethatwe cannotstatethattheirrationalnumbersetisuncountablebecauseitisasubsetoftherealnumberset.Otherwise,we wouldbeabletostateafinite,definitelycountablesetwould beuncountable.Instead,wecanstatethattherealnumberset isuncountablebecausetheirrationalnumbersetisaswell. Foruncountablesets,thesubsetdeterminestheoverallset’s countability,nottheotherwayaround.

3CardinalityofInfiniteSets

Thecardinalityisthesizeofaset.Here,wewillbedeterminingthecardinalityoftheinfinitesetspreviouslydiscussed.

3.1CardinalityDefinitions

Definition1:AhasthesamecardinalityasBifthereisa bijectivefunctionbetweenthetwo.

Definition2:AhascardinalitylessthanBifthereis aninjectivefunctionfromAtoBbutnobijectivefunction. Notethatinjectivefunctionsareone-to-onefunctionswhere BmayhavemorepointsthatarenotmappedbyA.

Pleasealsonotethatabijectivefunctionisafunction thatisbothinjectiveandsurjective.Surjectivefunctionsare one-to-onefunctionswhereAmayhavemorepointsthat arenotmappedbyB.

Sinceweassumetheinfiniterealnumbersetiscountable,allrealnumbersshouldexistwithintheinfinitereal numberset.Thepictureaboveisaninfinitelistofinfinite digits.Lookatthered-highlightednumbersandthenlook attheblue-highlightednumbersatthebottom.Iftheredhighlightednumberis1,theblue-highlightednumberinits columnbecomes0.Ifthered-highlightednumberis0,the blue-highlightednumberinitscolumnbecomes1.Thebluehighlightednumbersatthebottomaredifferentfromany numberintheinfinitelist.Theyaredifferentfromthenumberinthefirstrowbythenumberinthefirstcolumn,differentfromthenumberinthesecondrowbythenumberinthe secondcolumn,differentfromthenumberinthethirdrow bythenumberinthethirdcolumn,andsoon.Therefore,the blue-highlightednumbersatthebottomaredifferentfrom allthenumbersintheinfinitelistandyetshouldexistasa numberintheinfinitelist.Suchacontradictionprovesthat

Definition1-CardinalityofCountablyInfiniteSets: Twosetshavethesamecardinalityifthereisabijection betweenthetwo.Sincecountablyinfinitesetsmusthavea bijectionorone-to-onecorrespondencetothenaturalsetto becountable,itfollowsthatallcountablyinfinitesetshave thesamecardinalityasthenaturalsetandeachother.

Definition2-CardinalityofUncountablyInfinite Sets: Thecardinalityofuncountablyinfinitesetsismuch moreinteresting.Countablyinfinitesetshavecardinality lessthanuncountablyinfinitesets.Thereisaninjective functionfromthenaturalsettotherealnumbersetbecause thenaturalsetisasubsetintherealnumberset.Thereal numbersethasintegers,ofwhichthepositivebelongto thenaturalset,anddecimals.Thereisnobijectivefunction fromonetotheothersetbecausethenaturalsetiscountable andtherealnumbersetisuncountable.

4Conclusion

Inconclusion,thispaperhasprovidedaclearintroduction tocountablyanduncountablyinfinitesets.Webeganbyex-

Figure7:DiagramshowingCantor’sdiagonalargument

plainingwhyinfinityonlyexistsasaconceptandnotanumber.Next,weexplainedhowonemightdeterminewhether infinitesetsarecountableoruncountableusingbijection,a methoddevisedbyGeorgCantor.Finally,weexaminedthe cardinalityofcountablyanduncountablyinfinitesets.

References

N/A.

Introduction to Chaos Theory: History Examples, Applications

Written by Sunghan Billy Park

IntroductiontoChaosTheory:HistoryExamples,Applications

Sunghan(Billy)Park

park44253@sas.edu.sg

TeacherReviewer: Ms.Poluan

Abstract

Chaostheoryisabranchofmathematicsthatdealswiththe studyofdynamicsystemsandtheirseeminglyrandombehavior.Inthisresearchpaper,weaimtoprovideacomprehensive overviewofchaostheory,coveringitskeyconceptsandexamples,aswellasitsapplicationsinvariousfields.Webeginbydiscussingthehistoryanddevelopmentofchaostheory,includingthepioneeringworkoffiguressuchasHenri Poincar ´ eandEdwardLorenz.Wethendelveintosomeexamplesofchaostheory,suchasthedoublependulumand Newton’sthree-bodyproblem.Finally,weexploresomeof thereal-worldapplicationsofchaostheory,includingitsuse inpredictingweatherpatternsandunderstandingbiological systems.Overall,thisresearchpaperaimstoprovideacomprehensiveandaccessibleintroductiontochaostheoryfor studentsandresearchersinterestedinthisfascinatingandimportantfield.

Keywords: Butterflyeffect,Doublependulum,Newton’s three-bodyproblem

1IntroductionandHistory

Chaostheoryisdefinedasthebranchofmathematicsthat dealswithcomplexsystemswhosebehaviorishighlysensitivetoslightchangesininitialconditions,sothatsmall alterationscangiverisetostrikinglygreatconsequences. ChaostheoryhasitsrootsintheworkofHenriPoincar ´ e, aFrenchmathematicianwhostudiedthestabilityofthesolarsysteminthelate19thcentury.PonderinguponNewton’sthree-bodyproblem,Poincar ´ ediscoveredthattheorbitsofcelestialbodieswerenotaspredictableaspreviously thought,andthatsmallvariationsininitialconditionscould leadtosignificantdifferencesinthelong-termbehaviorof thesystem.

However,itwasnotuntilthe1960sthatchaostheorywas fullydevelopedandrecognizedasadistinctfieldofmathematics.Thedevelopmentofchaostheorycanbeattributed toEdwardLorenz,amathematicianandmeteorologistatthe MassachusettsInstituteofTechnology.Lorenzwasstudyingthebehaviorofweatherpatternsusingcomputersimulations,whenin1961heinadvertentlydiscoveredaninterestingphenomenon.Hewasrunningsimulationsoftwelve weathervariablesusingacomputermodel,buttosavetime, hestartedhalfwaythroughaprevioussimulation.Tohissurprise,hefoundthattheresultswerecompletelydifferent.He

thenrealizedthatthenumbersheusedthistimeweretruncatedtothreedecimalplaces,whiletheprevioussimulation usedsix.Thissmall,seeminglyinsignificantdifferencewas amplified,resultinginacompletelydifferentoutcome.This phenomenon,coinedthe“butterflyeffect”byLorenz(based onthemetaphorthatabutterflyflappingitswingsinBrazil couldcauseatornadoinTexas),becamethecornerstoneof chaostheory.

2Examples

2.1TheDoublePendulum

Oneofthemostnotableexamplesofchaostheoryin actionisthedoublependulum.Thenameisratherselfexplanatory;itisessentiallytwopendulumsconnectedto eachotherwhichcanbespunalonganaxis.Thedoublependulumisquiteunique,solelybecauseofitshighsensitivity toinitialconditions—acommontrendwithinchaostheory.

Asseenabove,droppingthependulumfrom100.00degrees,100.01degrees,and99.9degreeswouldlooksimilar atfirst,buttheirpathswoulddivergedrasticallyovertime.In additiontothis,theslightdifferencesofairpressure,gravity,temperature,andotherminisculedifferenceswouldalso haveanimpact;infact,itissaidthedoublependulumisso sensitivethatthegravitationalattractionofanearbyhuman couldaffectitscourse.

2.2Newton’sThree-BodyProblem

Anotherwell-knownexampleofNewton’sthree-body probleminorbitalmechanics.Thediscoveryofthishypotheticalproblemdatesbackto1687,wherenamesakeas-

Figure2.1.1:Asimulationofthreedoublependulumsdroppingatthesametime,withslightlydifferentinitialconditions.(Source:WikimediaCommons)

tronomerIssacNewtonquestionedwhetherlong-termstabilityispossible—particularlythesystemcomprisingthe Earth,theSun,andtheMoon—inhisbook PrincipiaMathematica.

Theproblemconsistsofthreecelestialobjectsmoving aroundeachother,andthegoalistofindaclosed-formsolutiontopredictthecourseofthesethreeobjects.However, thesmallestdiscrepancies,suchasaslightdifferenceofdistance,canleadtochaosandrandomness.Interestingly,there areafewspecial-casesolutionstothethree-bodyproblem, suchasthefigure-eightsolution(wherethethreebodiesorbiteachotherinafigure-eight)ortheelasticsolution(where thethreebodiesorbiteachotherelastically).

Finally,amoretheoreticalbutinterestingexampleof chaostheoryliesintherealmofapopularconceptfantasized forcenturies:timetravel.Theoretically,ifonewereableto travelbackintimeandmakeasmallalteration,itcouldresultinsignificantchangesinthefuture.Forinstance,imaginegoingbackintimeandstrikingupaconversationwith apasserby.Thispersonwasontheirwaytoadineracross thestreet,andthisshortconversationcausesadelayoften seconds.Becauseofthisdelay,asthepersoniscrossingthe street,heishitbyacarthatwouldhavemissedhimifit wasn’tforthedelaycausedbytheconversation.Thisperson turnsouttobeRobertOppenheimer,themanwhowould latergoontocreatetheatomicbombduringWorldWarII. Asaresult,theUnitedStatesfallsbehindwhiletheAxisdevelopstheirownatomicbombanddefeatstheAllies.Inthis example,aseeminglyinsignificantconversationhasdrasticallychangedthecourseofhistory.However,onedoesnot havetoworryaboutthisastimetravelisnotareality...yet.

3Applications

Theapplicationsofchaostheoryarenotlimitedtorather mundanescenariosofpendulumsorbutterflies;rather,these applicationsarefar-reachingandplayapartinmeteorology, biology,socialscience,andevenbusiness.

AsmentionedbeforewithLorenz,chaostheoryisalso usedinpredictingweatherconditions,whereobservations thatareself-similarinregionshelpreducetheuncertainty posedbytheinitialweatherconditions,therebyreducing errors.Thisiswhywecanpredicttheweathermanydays inadvancewithconfidence—ahugeimprovementfrombefore.

Inbiology,chaostheoryhasplayedapartinpopulation dynamics,whichinvolvesunderstandinghowpopulationsof organismschangeovertime.Thiscanincludefactorssuchas birthanddeathrates,migration,andotherinfluences.Chaos theoryhasbeenusedtomodelthedynamicsofpopulations ofanimals,plants,andotherorganisms,andhashelpedto explainhowsmallchangesininitialconditionscanleadto largechangesinpopulationsizeovertime.Infact,chaos theoryhasevenbeenappliedbybiologiststounderstandand explainthespreadoftheCOVID-19virus.

Chaostheoryhasevenbeenappliedtoconceptsinthe socialsciencesrangingfrompoliticstopsychology.Specifically,forpolitics,chaostheoryhasbeenusedtostudythe factorsthatcontributetopoliticalinstability,suchaseconomiccrises,socialunrest,andchangesinleadership.Researchershaveusedchaoticmodelstoidentifytheconditionsthataremostlikelytoleadtoregimechangeandto predictthelikelihoodofsuchchangesoccurringindifferent countries.Forpsychology,ithasbeenusedtostudythefactorsthatinfluencedecision-makinginsocialgroups,suchas theroleofleadershipandgroupdynamics.Forexample,researchershaveusedchaoticmodelstostudyhowgroupsize andcompositioncanimpactdecision-makingandtoidentify theconditionsthataremostlikelytoleadtogroupconsensus.Chaostheoryhasalsobeenappliedinmentalhealth: itisusedtostudythedynamicsofmentalhealthdisorders, suchasdepressionandbipolardisorder.Researchershave usedchaoticmodelstodeveloppredictionsaboutthelikelihoodofrelapseinpatientsandtoidentifythefactorsthat contributetotheemergenceofthesedisorders.

Finally,intermsofbusinessandthestockmarket,chaos theorycanexplaintoinvestorswhyhealthyfinancialmarketscansuffercrashesandshocks.Byusingchaoticdynamics,investorscananalyzethemovementsofpricesandidentifypatternsthatmaynotbeimmediatelyapparent.

4Conclusion

Inconclusion,chaostheoryisafascinatingandcomplex fieldofstudythathasrevolutionizedourunderstandingof theworldaroundus.FirstdiscoveredbymeteorologistEdwardLorenz,itdealswiththebehaviorofdynamicsystems thatarehighlysensitivetoinitialconditions,oftenreferred toasthebutterflyeffect.Someexamplesofchaostheory includethedoublependulum,Newton’sthree-bodyproblem,andeventimetravel,whilethereal-worldapplications ofchaostheoryincludepredictingweatherpatterns,under-

Figure2.2.1:Asubfigure

Figure2.2.2:Asubfigure

standingbiologicalsystems,andmodelingstockmarkets.

Overall,chaostheoryoffersanewperspectiveonunderstandingcomplexsystemsandphenomenathatwerepreviouslythoughttobeunpredictable.Ithastransformedour understandingoftheworldaroundusandcontinuestobea valuabletoolinavariousfields.

References

Butterflies,Tornadoes,andTimeTravel.AmericanPhysical Society.(2004).RetrievedJanuary8,2023,from https://www.aps.org/publications/apsnews/200406/butterflyeffect.cfm

Halton,C.(2023,January2). Chaostheorydefinition. Investopedia.RetrievedJanuary8,2023,from https://www.investopedia.com/terms/c/chaostheory.asp:

standingbiologicalsystems,andmodelingstockmarkets. Overall,chaostheoryoffersanewperspectiveonunderstandingcomplexsystemsandphenomenathatwerepreviouslythoughttobeunpredictable.Ithastransformedour understandingoftheworldaroundusandcontinuestobea valuabletoolinavariousfields.

:text=Chaos%20Theory%20in%20the%20Stock%20Ma rket,-Chaos%20theory%20isamp;text=Proponents%20o f%20chaos%20theory%20believe,true%20health%20of %20the%20market.

Mangiarottietal.(2020).Chaostheoryappliedtothe outbreakofCOVID-19:anancillaryapproachtodecision makinginpandemiccontext. EpidemiologyandInfection, 148.https://doi.org/10.1017/s0950268820000990

References

Butterflies,Tornadoes,andTimeTravel.AmericanPhysical Society.(2004).RetrievedJanuary8,2023,from https://www.aps.org/publications/apsnews/200406/butterflyeffect.cfm

Oestreicher,C.(2022). Ahistoryofchaostheory.Taylor& Francis.RetrievedJanuary8,2023,from doi.org/10.31887/DCNS.2007.9.3/coestreicher WikimediaFoundation.(2022,December31). Three-body problem.Wikipedia.RetrievedJanuary8,2023,from https://en.wikipedia.org/wiki/Three-body problem WikimediaFoundation.(2022,November14). Double pendulum.Wikipedia.RetrievedJanuary8,2023,from https://en.wikipedia.org/wiki/Double pendulum

Halton,C.(2023,January2). Chaostheorydefinition Investopedia.RetrievedJanuary8,2023,from https://www.investopedia.com/terms/c/chaostheory.asp: :text=Chaos%20Theory%20in%20the%20Stock%20Ma rket,-Chaos%20theory%20isamp;text=Proponents%20o f%20chaos%20theory%20believe,true%20health%20of %20the%20market.

Mangiarottietal.(2020).Chaostheoryappliedtothe outbreakofCOVID-19:anancillaryapproachtodecision makinginpandemiccontext. EpidemiologyandInfection, 148.https://doi.org/10.1017/s0950268820000990 Oestreicher,C.(2022). Ahistoryofchaostheory.Taylor& Francis.RetrievedJanuary8,2023,from doi.org/10.31887/DCNS.2007.9.3/coestreicher WikimediaFoundation.(2022,December31). Three-body problem.Wikipedia.RetrievedJanuary8,2023,from https://en.wikipedia.org/wiki/Three-body problem WikimediaFoundation.(2022,November14). Double pendulum.Wikipedia.RetrievedJanuary8,2023,from https://en.wikipedia.org/wiki/Double pendulum

07 Investigating the Theoretical and Practical Applications of Fractals

Written by Doy yun, Munira Takalkar

InvestigatingtheTheoreticalandPracticalApplicationsofFractals

DoyYunMuniraTakalkar

yun45629@sas.edu.sg,takalkar42662@sas.edu.sg

TeacherReviewer: Ms.Poluan

Abstract

Abstract

Fractalsarefascinatinggeometricalfiguresthatappearintricateandcomplex,butareactuallymadeupofsmallrepeatingpatterns.Theycanbefoundinvariousnaturalandmanmadestructures,suchassnowflakes,coastlines,andAfrican designs.Thispaperexploresthedifferentdimensionsthatdistinguishfractals,highlightssomenotablemathematicalexamples,andshowcasesthepracticalapplicationsoffractals inourworld.Bycompilingvariousarticlesontheusesof fractals,itisevidentthattheyhaveenormouspotentialfor improvingourunderstandingofpatternsandprovidingmore efficientwaysofstudyingthem.Fractalsareavastandexcitingfieldthatisyettobefullyexplored,andtheirapplications areendless.Bydelvingintotheworldoffractals,wecangain anewappreciationforthebeautyandcomplexityofournaturalworld,andperhapsevendiscovernewwaysofsolving practicalproblems.

Keywords: fractals,Hausdorffdimension,Minkowski–Bouliganddimension,Mandelbrotset,Newton’sfractal

1Introduction

1.1BackgroundandPurposeofResearch

Thispaperinvestigatesboththetheoreticalandpractical applicationsoffractals,providinganaccessibleunderstandingofseeminglyabstractandinfiniteconcepts.Conceptualizedbythefatheroffractalgeometry,BenoitMandelbrot, withtheintentionofmodelingnature,fractalsareutilized toreflectamyriadofnaturalandchaoticprocesses,ranging fromgalaxyformationtocancergrowthatacellularlevel.

Tomodelthesenaturalphenomena,theideaoffractalsas self-similargeometricfiguresemerged,signifyingthateach componentregardlessofmagnitudehasthesamestatisticalpropertiesasthewhole.Suchfiguresprovideabasisto modelthecomplexity,yetregularity,ofcertainformsofvariety.Fractalgeometrycapturesthejaggednatureoffigures, andasonezoomsintoafractal,itappearstosmoothout.As partsofthispaperdelveintoabstractandtheoreticalideas, itisessentiallytokeeptheinitialintentoffractalsinmind: tomodelreality.Thus,theneedlessidealizationofperfectly self-similarfigurescontradictsfractalgeometryjustasmuch asthediametricoppositionofperfectlysmoothfigures.

2FractalDimension

Oneofthekeycharacteristicsofafractalisitspossessionofafractaldimensionexceedingitsintegertopologicaldimension(Albertovich&Aleksandrovna).Integerdimensionscanbeobservedwithtwo-dimensionalandthreedimensionalfigures;however,whilefractionaldimensions alignwithsimilarconcepts,theydifferfromstandarddimensionspresentinEuclideangeometry(Ross).

2.1HausdorffDimension

Fractalsfoundinmathematicscanbeexpressedinboth algebraicandgeometricmanners.Themostcommonmathematicaldefinition,andthedefiningfactorofafractal,isthe presenceofself-similarityinapattern(Ross).Self-similarity isnottheonlyclassificationofafractal,however.Selfsimilarfractalsarerepeatedinternally,meaningthatwhen thepatternisenlarged,thesameimageiscreatedatasmaller scale.Essentially,suchfiguresaremadeupofsmallerversionsofthemselves(Bishop).

Thescaleofthisrepetition,calledfractaldimension,falls alongthesamescaleastraditionaldimensionswithinEuclideanspace(Albertovich&Aleksandrovna).Ingeometry,alineisconsideredone-dimensional,asquareistwodimensional,andacubeisthree-dimensional.Wheneachof theseisseparatedtoproduceself-similarobjects,thescaleat whichthelength,area,orvolume–whichcanbereferredto asmagnitude–decreasesis 1 2 , 1 4 ,and 1 8 ,respectively,while thescalefactorofasidelengthremains 1 2 .Thedimensionof thesegeometricalfigurescanthereforebethoughtofasany givenpowerrequiredtoraisethescalefactorofasidelength suchthatitisequaltothescaledmagnitude.Settingthemagnitudeat M andscalefactorat s,therelationcanbedefined as M = sD ,with D definedasthefigure’sHausdorffdimension(Albertovich&Aleksandrovna).Given M and s, D can easilybefoundthroughtheequation D =log s M = log M log s

ReturningtotheinitialexamplesusingstandardgeometricalfigurespresentinEuclideanspace,intheline’scase, whenscaledbyafactorof 1 2 ,themagnitudebecomes 1 2 of theoriginal,resultinginadimensionof1,as 1 2 =( 1 2 )1 Lookingatthesquare,whenthelengthisscaledbythesame factorof 1 2 ,themagnitudeis 1 4 oftheinitialfigure’s,resultinginadimensionof2,as 1 4 =( 1 2 )2 .Thisrelationremains constantacrossfiguresofvaryingdimensions(Ross).

Thisevolveddefinitionofdimensioncanbeextendedto fractalfigures.TakingtheSierpinskitriangleforinstance, thescaleofself-similarityis 1 3 oftheoriginalsize,meaningthatwhenasidelengthisscaledby 1 2 ,themagnitude isscaledby 1 3 ,formingtheequation 1 3 =( 1 2 )D ,where D equalsapproximately1.585(Bishop).Inlayman’sterms, theHausdorffdimensionofafigureisessentiallyameasure ofirregularity,withanincreaseddimensionindicatingincreasedroughness.Asthefractalincreasesincomplexity, thedimensionheightens.

3CorrelationDimension

Beneficialtothemeasuringofroughnessinadatasetis anunderstandingoftheset’sdensity,accomplishedthrough thecalculationofitscorrelationdimension,wherebyballs ofradius ε areplacedcenteredatapoint x ofapointcloud and Nx (ε) representsthenumberofpointswithintheball (Ross).Theradiusisthenvaried,with Nx (ε) ∝ εd ,and theaveragevalueof Nx (ε) isfoundovervariouspointsto find C (ε),whichisalsoproportionalto εd .Toestimate d graphically,thegraphof ln(C ) and ln(ε) isplotted,andthe slopeofthecurveistakenasthedimension(Bishop).This excludestheleftmostandrightmostsidesofthecurve,as theseflattenduetobeingtoosmalltoreachotherpointsand engulfingtheentireset,respectively.

fractaldimensionofaset S inametricspace (X,d) (Albertovich&Aleksandrovna).Thisdimensionisinmanycases equivalenttoafigure’sHausdorffdimension,thoughincertainsetstheMinkowskidimensionexceedstheHausdorff dimension,suchasinthesetofrationalpointsbetween[0,1], wheretheyare1and0,respectively.However,itconsistently differsfromafigure’scorrelationdimension,asitdoesnot takeintoaccountthedensityofaset(Bishop).

Inordertocomputethisdimensionalvalue,boxesofside lengtharecreatedalongtheset,with N (ε) representingthe totalboxesthatcomeincontactwiththedata.Givenacurve oflength L,itcanbefoundthat N (ε) ∝ L ε (ross).Continuing,givenaplaneofarea A, N (ε) ∝ A ε2 ,andgivenathreedimensionaldatasetofvolume V , N (ε) ∝ V ε3 .Itcanthereforebeconcludedthat N (ε) ∝ 1 εd .Inordertoachievethe mostaccuratedimension, ε mustbereduced,producingthe equation d =limε→0 lnN (ε) ln( 1 ε ) (ifthelimitexists).However, thisdefinitionbeginstodeterioratewhenfiguressuchasthe Sierpinskitrianglecomeintoplay,consideringtheconsensusonitsareaismurkyatbest(Ross).Insuchinstances, log N (ε) isplottedagainst log 1 ε ,withitsslopetakenasthe dimension.

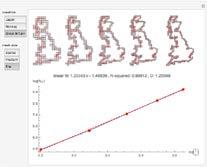
3.2CoastlineApplications

Growntobecomealmostsynonymouswithfractaldimensions,thecoastlineparadoxpresentsthequestionof howtocalculateinformationregardingacoastline,consideringitdoesnothaveaclearlydefinedlength,resultingfromridgesandinconsistenciesthatonlycompoundas thefieldofviewnarrows(Bishop).Coastlinelengthsvary greatly,therefore,basedonthescaleofmeasurement,eventuallyapproachinginfinity.Takingintoaccountacoastline’s shape–neithertrulyself-similar,noraprimitiveshape–the Minkowski–Bouliganddimensionisthemosteffectivedimensiontodetermineacoastline’sfractaldimension.

(Arshadetal.,2021)

3.1Minkowski–BouligandDimension

Whilecomputingafigure’sfractaldimensionusingHausdorffdimensionmaybedirectregardingsimpleorself-similarshapes,asEuclideanobjectsbecome morecomplex,itbecomesmoreeffectualtofindtheir Minkowski–Bouliganddimension,asubsetoffractaldimension.Minkowski–Bouliganddimension,additionallyknown asbox-countingdimension,isamannerofdeterminingthe

Throughtheslopeofthelineofbestfit,itisapparentthat thecoastlineofBritain’sfractaldimensionisapproximately

Figure1:Asamplecurvedproducedbygraphing ln(C ) against ln(ε)

Figure2:AnestimationofthecoastlineofBritain’sfractal dimension(Mahieu,2014)

1.25,actingasaquantitativeindexofthecomplexityofthe region’scoastline,comparabletoothers.

4MathematicalExamplesofFractals

Fractalsarewhatareknowntobenever-endingpatterns, beinginfinitelycomplexandjagged.Thoughself-similarity isn’tnecessarilyarequisiteforfractals,duetotheiterative natureoffractalcreation,self-similarityinmathematicalexamplesiswidespread.

4.1DragonCurve

Dragoncurvesaredefinedasanymemberofafamilyof self-similarfractals,approximatedbyarecursivesystemof alternatingdirections,resultinginafractalresemblingthe shapeofthemythicalcreature.FirstinvestigatedbyNASA physicistsJohnHeighway,BruceBanks,andWilliamHarter,theHeighwaydragoncurveisarguablythemostprominentdragoncurve(Albertovich&Aleksandrovna.Starting fromasingleline,thecurveisconstructedbyaniterative processofthelinesplittingintotwoperpendicularsmaller linesandforminganisoscelestrianglewiththeoriginalline. Witheachiteration,thedirectionofthesplitalternatedbetweenrightandleft,creatingthecurve.Anothermethodin constructingthisshapeistopickapivotpoint,eitheronthe farleftorright,copytheoriginalfigure,androtateit90degrees,alternatingrightandleft.Afterundergoingjustseveraliterations,thedragoncurveisformed.Asthisparticular fractalrequiresarecursivesequenceofconstantcopyingand pasting,itisconsideredtobeaself-similarshape,withfractaldimension,orthedimensionalvalueforself-similarity, beingaround1.5236.

Davinchi.Thefractaldimensionofthisfractalisthegolden ratio,or1.618033.Asseenbythecomparison,thefractal dimensionofthegoldendragonfractalismoresimilarto thatoftheHeighwaydragonthantheTerdragon,thus,the shapeofthegoldendragonisalsomorealiketotheHeighwaydragon.However,insteadofutilizingaperfectlyperpendicularbisectingiterativesequence,theconstructionof thegoldendragonreliespredominantlyonthesidelengths ofthetwolinesegments(Albertovich&Aleksandrovna). Theratiobetweenthetwosidelengthsis r ,with r being definedas (1/Φ)( 1/Φ).Witheachiteration,thesidessplit intoevenmoreintricatesegments,alternatingrightandleft, maintainingthesameratio.Theresultantdragonfigureisa beautifulcurveofintricatedetail.

Thoughthedragoncurvesthemselvesdonothavemuch useinthedevelopmentofourknowledgeinanyfield,it demonstratestheideaofhowasimplecode,undermany iterations,canbecomecomplexandlarge.

4.2JuliaSet

DiscoveredbytherenownedFrenchmathematician,GastonJulia,theJuliasetisoneofthemostcrucialexamples ofamathematicalfractalwhenitcomestothefieldofcomplexdynamics(Bishop).TheJuliaset,alongwiththeFatouset,arecomplementarysetsdefinedbyuniquefunctions,withasetpointandconstanttoproduceafractal. FatousetsandJuliasetsaresimilarintheiriterationprocesses;however,theFatousetconsistsofnumericalvalues thatbehavesimilarlyevenwhenundergoingmultipleiterations,whereastheJuliasetconsistsofnumericalvaluesthat behavechaoticallywhenchanged,evenintheslightestquantity.Juliasetscanbecreatedusingavarietyofformulas, thoughthemostwidelyknownisthequadraticfunctiondefinedby w = z 2 + C .Themostsignificantfactorineach set’sdifferencearetheinitialvaluesof Z and C ,astheiterationprocessremainsconstant(Albertovich&Aleksandrovna).Boththevaluesof Z and C arecomplexnumbers, consistingofarealandimaginarypart,thusresultinginthe set’spositiononthecomplexplaneasopposedtothestandardCartesianplane.

Severallesser-knownversionsofthedragoncurveare alsopresent,suchasthetwindragon,terdragon,andgolden dragon.Thetwindragon,simplyput,istwoHeighwaydragonsplacedbacktoback,withoneofthedragonsrotated180 degrees.Theterdragonisamoreelaborateversionofthe Heighwaydragon;asopposedtobisectingtheinitiallineto form90-degreeangles,theterdragontrisectsandforms120degreeangles,resemblingasidewaysZ.Thedimensionfor self-similarityislessthanthatoftheHeighwaydragon,approximatelyat1.26186(Ross).

TheGoldenDragonfractalisonethatiscloselyrelated tothatoftheGoldenRatio,firstdiscoveredbyLeonardo

Thoughthevalueof Z consistentlyrepresentsthepoint ofinterest,andthevalueofCrepresentsasaconstant,the multitudeofcombinationsofthesevaluesallowsforaninfinitenumberofJuliasets.IneachJuliaset,the“fate”ofeach complexnumber Z isevaluated(Bishop).Inotherwords, whether,asitisintegrated,thenumberconvergesordiverges.Theresultantisamyriadofdifferentshapes,each visuallyrepresentedbyblackareasandvariedcolors.The blackregionsindicatepointswherethenumbersconverge orstaybetweenaboundedregionastheyundergoiterations. Thecoloredregions,ontheotherhand,representthecomplexnumbersof Z thatdiverge,withthechromaticityindicatingthespeedatwhichthenumbertendstowardinfinity (Ross).

4.3TheMandelbrotSet

StemmingfromtherevelationofJuliasets,theMandelbrotsetwascreatedbyBenoitMandelbrot,utilizingthe

Figure3:Amodelonhowiterationscreatethedragoncurve (Mahieu,2014)

samequadraticfunction, w = z 2 + C .Asopposedtothe Juliasets,however,theMandelbrotsetonlyhasasingular variabilityfactor, C ,andalwayssetstheinitialvalueof Z tozero(ross).Duetothis,theresultantisasingularimage, whichcanbeinterpretedasavisualrepresentationofallthe quadraticfunctionedJuliasets.

ItwasdiscoveredthatforanyJuliaset,thepoint(0,0) onthecomplexplanedeterminesthefateoftheset,ifthe pointisconnected,orshadedblack,thentheentiresetis connected;however,ifthepointisdisconnected,orcolored, thentheentiresetisinfinitelydisconnected(Albertovich& Aleksandrovna).Duetothis,bycompilingtheoriginsof eachJuliasetattheoriginpoint,theresultantimageofthe Mandelbrotsetvisuallyrepresentsthebehaviorofallthe complex C valuesintheJuliaset,eachpointrepresentinga uniqueJuliaset(Bishop).IfaJuliasetwithapairofspecific valuesfortheirvariablesdoesn’tdivergetoinfinitywheniterated,thecorrespondingpointisshadedblack.Conversely, if,underiteration,theJuliasetescapestoinfinity,thepoint iscolored,withthedifferenthuesrepresentingtherateat whichthecomplex C -valuesdivergetoinfinity.

simplyutilizingelementaryrules.

4.4NewtonFractals

Newtonfractalsarefractalsthathavebeenmadeusingthe generalizedformofNewton’siteration.Contrarytobelief, IsaacNewtonwasnotthecreatorofthisparticularfractalseries,andonthecontrary,wasn’tawareofitsexistence.Newton’siterationisundoubtedlyaconceptthatiswell-knownin thecalculuscommunity,usingderivativestoobtainaclose approximationoftheroot(s)ofafunction.Theiteration, alsoknownastheNewton-Raphsonmethod,isusuallyinthe generalformof x(n +1)= x(n) [f (x)/f ′ (x)],utilizing tangentlinesslopesasawaytoapproximate(Albertovich& Aleksandrovna).Pickingastartingpointclosetothatofthe approximationvalueleadstoalmostasuddenconvergence totheroot(s);however,whenthestartingapproximationis inaccurateandhasahigherrorbound,aninterestingphenomenonoccurs.Inthecontextofcalculus,theinitialapproximatevalueistypicallypickedwithintherealmsofreal numbers,butforNewton’sfractals,thisboundisexpanded toimaginarynumbers,andmainlyemployscomplexnumbers.

Newton’sFractalsareaspecialcaseofJuliasets,withintricatedetailsarisingfromsimplefunctionsduetotherepetitionofinteractivesequences.TheoutcomeofNewton’s fractalsishighlydependentonthestartingpointandcandiffergreatlyfromoneanother,despitethestartingpointyieldingsuchaminusculechange(Bishop).SimilartotheMandelbrotset,Newton’sfractalsaresetinthecomplexplane andcanberepresentedasamapofallthepossiblestarting valuesoftheapproximation.Undergoingmultipleiterations, whicheverrootvalueeachpointendsupwithisthecolorthat isassigned,andwhenthepointisplacedbackintoitsoriginalposition,Newton’sfractalisformed(Ross).Thefractal shapecanchangedramaticallybasedontheinitialfunction conditions,andthenumberofiterationsundergonecanenlargethedetailswithineachfractal.

TheoutlineoftheMandelbrotsetconsistsofamaincardioidshape,andasmallercircularshapewithconverging blackregionsoneitherside.Thesetwofiguresarewithin thex-valueboundariesof-2and0.25,ofwhichthereare C -valuestowhichtheJuliasetisconnected.Thecardioid shaperepresentsthevaluesofanattractivefixingpointof theJuliasets,ofwhicharebetweentheboundsof-0.75to 0.25(Ross).Thecircularshaperepresentsthevaluesofbehavinginadifferentmannerandissituatedwithin-1.25and -0.75.Theothervaluesareunabletoescapetowardinfinity,despiteconstantiterations;however,theydonotfallinto eithercriterionofbehavior.

TheMandelbrotsetitselfposesseveralinterestingphenomenons,includingmanyoftheJuliasetsthemselvesbeingembeddedintothemappingoftheMandelbrotset.InfinitelymanyJuliasetsofavarietyofshapesandsizescan befoundwithinallareasoftheMandelbrotset.Furthermore,asignificantlyscaled-downfigureoftheMandelbrot setcanbefoundcenteredaroundeachoftherespectiveJulia sets(Bishop).Takingtheroleofoneofthemorecelebrated mathematicalfractals,theMandelbrotsetisanexcellentexampleoftheideaofacomplexstructurebeingproduced

4.5TheFibonacciSequence

Anadditionalmathematicalexampleofafractalisthe Fibonaccisequence,thelessrenownedcounterpartofthe goldenratio.Thisparticularfractal,however,isunlikethat ofthepreviouslyexploredfractalsinthispaperandcan beclassifiedasanarithmeticfractalratherthanageometricfractal.NamedafterLeonardodaVinci’spenname, Fibonacci,theFibonacciSequenceisauniquepatternof whichisdefinedbytherecursiverulesof xn = xn 1 + xn 2

.Setting x0 at0and x1 at1allowsforthesequenceto emergeasthefollowing:0,1,1,2,3,5,8,13,21,34....

Thegoldenratioemergesfromthesenumbers;asthesequencecontinuesontoinfinity,theratiobetween xn and xn 1 becomescloserandclosertowhatwenowdefineas thegoldenratio,orabout1.618.Usingthisratio,DaVinci wasabletofigureoutthenthtermoftheFibonaccisequences,proventobe xn =(Φn (1 Φ)n )/√5.Within hisexploration,however,DaVincifoundthatsquaringthe numberswithintheFibonaccisequenceallowedforaperfectlyfittedarrangementofsquares,which,whenconnected,

Figure4:TheMandelbrotSet(TheMandelbrotSet,n.d.)

becameaperfectspiral,translatingintothebasicofdivine proportions–thegoldenspiral.

5ApplicationofFractals

Thoughfractalswereinitiallyamoretheoreticaldiscovery,theyhavesincebeenfoundapplicableinvariousaspects ofourlives,inbothnaturalandindustrialsettings.With theirinitialfindings,fractalshavebeenproventruetobean incrediblyvaluabletoolinsynthesizingandanalyzingpatterns,evenwhenitisn’tblatantlyobvious.Usingthistool hasallowedforvariousadvancementsinthefieldofbiology,computerscience,andmedicine,andwillcontinueto assistinmakinggroundbreakingdiscoveries.

5.1FractalsinNature

Fractals,despitetheirbasisbeingmathematical,are presenteverywhereinnature.Fromthephysicalshapeof naturalfigures,totheformationoftheirgrowingpatterns, fractalsarehighlyprevalentinanalyzingnature’spatterns.

TheFibonaccisequence,duetoitsrecursiveruleofhavingthesumofthetwoprevioustermsbethenext,has thevaluablecharacteristicofspaceefficiency—atoolthat greatlyassistsineffectivelyutilizingthespaceprovided(Albertovich&Aleksandrovna).Consequently,treebranches, lightning,waterfalls,andevenorganisms’reproductionpatternsmimicthesequenceofFibonacci,allowingforexpansionwithefficientusageofspace.Furthermore,onaccount ofthegoldenratiobeingaprinciplelawpertainingtonatural figures,thegoldenspiralcanbefoundtranslatedintonature, suchasintheshapesofseashellsorthegalaxyitself.

TheJuliasetsembeddedintotheMandelbrotsetarealso seeninvariousnaturalreferences.Duetoitsflexibilityinits manipulationofshapeandsize,Juliasetsofdiverseformationscanbeappliedtosimilarorganismstobettertailorthe exactdetailsofeachone(Bishop).Theshapeofoctopustentacles,ferns,andwavesareallinaccordancewithabranch ofJuliasets,whetherthatbetheentiretyoftheJuliaset,or justaportion.

Inordertoachievethefigureofanoctopustentacleora wave,theentireJuliasetwouldhavetobeused.However, incontrast,onlyasmallportionoftheJuliasetwouldbe usedinmimickingtheshapeofafern.Theabilityfornature tobedescribedwithasingularfractalopensupanarrayof possibilitiesintheirapplication.

Asfractalsarehighlyrelevantinnature,itis,inturn, highlyrelevantinmodelingitwiththeassistanceofmoderntechnology.Asaforementioned,fractalsoftentimesresembletheshapeofanaturalfigure,withtheirsystemicbut notperfectlysymmetricalfigure.Asnaturebeingimperfect hasbeenanestablishedfact,havingafigurethatcanembed flawsintoitsdesignishighlyusefulinthefieldofcomputerscience(Bishop).Theiterativenatureoffractalsleadingtomorecomplexfiguresallowsforcodetobewrittenin amuchshorteramountoftime,whilstsimultaneouslycreatingamoreuniqueandaccuraterepresentationofnature asaresult.ThoughtheMandelbrotsetitselfisn’tfoundin naturalapplications,aspectsofithavebeenappliedinremodelingnature,coastlines,low-flyingterrainnavigation, areameasurements,andevencityplanning(Ross).Theassistanceoffractalshaslikewiseledtoanimprovementin thefieldofCGI,enablinggraphicdesignerstocreatemore realisticanimationsandmodels.

5.2FractalsinMedicine

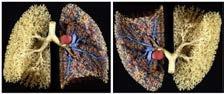
Beyondseeminglyabstractanddisconnectedapplications,however,breakthroughsinthefieldofmedicineusing fractalshaveveritableimplicationsonhumanlifeandwellbeing.FromtheuseoffractalsinECGanalysistodetermine bloodvesselhealth,tothefractal-likenatureofthelungs, similartothatofatree,whosefunctionsbothconstituterespiration(Albertovich&Aleksandrovna).Surfaceareaisdirectlyproportionaltotheefficiencyofgasexchange,aprocessbywhichoxygenandcarbondioxidemovebydiffusionacrossasurface,andfractalbranchingisaneffectual methodtomaximizesurfaceareawhileconcurrentlyminimizingspace.

Fractalpatternsadditionallyhavethepotentialtoquantifytheprecisestageofdeteriorationoftheretinaduringthe clinicaldiagnosisofdiabeticretinopathy,acomplicationof diabetesthatdamagestheretinaandaffects80percentof allpatientswithdiabetesforovertenyears(Albertovich& Aleksandrovna).Thisquantificationofdeteriorationopens pathwaystoevaluatetheprogressoftreatmentovertimeand

Figure5:AFractalResemblinganOctopusTentacle(Patterns-IndustryIoTConsortium,2023)

Figure6:Acomparisonofthestructureofhumanlungsand atree.(Kelshiker,2021)

determineareferencevaluetoactasanindicatorofpathologicalcases,developinganon-invasivemethodofearly detectionofretinalvasculardiseases.Diabeticretinopathy changesthestructureofbloodvessels,impactingthefractaldimensionoftheretina(Albertovich&Aleksandrovna). ApparentinFigure4,whensubjectedtofractalanalysis, pathologicalcaseshavealowerMinkowski-Bouliganddimension,ascomparedtoanormaleye,aidinginthediagnosisofsuchadisease.

6Conclusion

Thefieldoffractalgeometryisavastarenathathasextensivepotentialinitsapplicationsindiversedisciplines.Itwill unquestionablycontributetoamultitudeofmedicinaland technologicaladvances,facilitatingtherapidrevolutionizationoftheworld.

References

Albertovich,T.D.&Aleksandrovna,R.I.(2017,July26). TheFractalAnalysisoftheImagesandSignalsinMedical Diagnostics.IntechOpen.

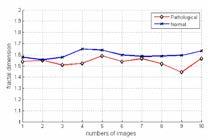
https://www.intechopen.com/chapters/55028

Arshad,M.H.,Kassas,M.,Hussein,A.E.,Abido,M.A. (2021,January4). ASimpleTechniqueforStudyingChaos UsingJerkEquationwithDiscreteTimeSineMap ResearchGate.

https://www.researchgate.net/publication/348243264 A Simple Technique for Studying Chaos Using Jerk Equation with Discrete Time Sine Map

Bishop,C.,Peres,Y.(2016).FractalsinProbabilityand Analysis(CambridgeStudiesinAdvancedMathematics). Cambridge:CambridgeUniversityPress.

doi:10.1017/9781316460238

Kelshiker,A.(2021,March16). HowMathCouldSave Lives–DartmouthUndergraduateJournalofScience https://sites.dartmouth.edu/dujs/2021/03/16/ow-mathcould-save-lives/ Mahieu,E.(2014,January). WolframDemonstrations

Project

https://demonstrations.wolfram.com/BoxCountingTheDimensionOf Coastlines/ Patterns-IndustryIoTConsortium.(2023,April4). IndustryIoTConsortium.

https://www.iiconsortium.org/patterns/ Ross,S.(2022).FractalDimension-Box-Counting CorrelationDimension[Video].https://www.youtube.com/ watch?v=IfP4wAC4HtA&ab channel=RossDynamicsLab TheMandelbrotSet.(n.d.).

http://www.math.utah.edu/alfeld/math/mandelbrot/mandelbrot.html

Uahabi,K.L.,M.Atounti.(2015). Applicationsoffractals inmedicine.AnnalsoftheUniversityofCraiovaMathematicsandComputerScienceSeries; https://www.semanticscholar.org/paper/Applications-offractals-in-medicine-UahabiAtounti/ab3a0a5bde175e501896ffab1ac8319d111bc8bf

Figure7:Acomparisonofthefractaldimensionofblood vesselswithinnormaleyesagainstthatofpatientswithdiabeticretinopathy.(Uahabi&Atounti,2015)

08

Singular Value Decomposition and a Recommendation Algorithm

Written by Frank Xie SingularValueDecompositionandaRecommendationAlgorithm(ATLAProject)

FrankXie

xie48478@sas.edu.sg

TeacherReviewer: Mr.Zitur

Abstract

GiventhedependenceofmostinternetusersonGoogle, Amazon,orothersearchandrecommendationengines,itis importanttorecallthebasisofmanyoftheseengines.This paperwillreconstructarudimentaryrecommendationalgorithmandpresentapotentialuseforitintheformofabook recommenderusingdatafromKaggle.Themaintoolusedin thealgorithmissingularvaluedecomposition,orSVD,and codewasexecutedinPython.

Keywords:recommendationalgorithm,SingularValueDecomposition(SVD),eigenvalues,diagonalization,Kaggle

Thesquarerootsofeach λn correspondto

,σ whichareindescendingorder.These

singularvaluesof A,andrepresentthelengthsofthevectors Av 1 , Av 2 ,..., Av n ,amongotherthings.Thesevaluesare keytocreatingaSVD.

SingularValueDecompositionandaRecommendationAlgorithm(ATLAProject)

FrankXie xie48478@sas.edu.sg

SingularValueDecompositionandaRecommendationAlgorithm(ATLAProject)

TeacherReviewer: Mr.Zitur

FrankXie

xie48478@sas.edu.sg

Abstract

TeacherReviewer: Mr.Zitur

Thesquarerootsofeach λn correspondto σ1 ,σ2 ,...,σn whichareindescendingorder.These σn = √λn arethe singularvaluesof A,andrepresentthelengthsofthevectors Av 1 , Av 2 ,..., Av n ,amongotherthings.Thesevaluesare keytocreatingaSVD.

Abstract

GiventhedependenceofmostinternetusersonGoogle, Amazon,orothersearchandrecommendationengines,itis importanttorecallthebasisofmanyoftheseengines.This paperwillreconstructarudimentaryrecommendationalgorithmandpresentapotentialuseforitintheformofabook recommenderusingdatafromKaggle.Themaintoolusedin thealgorithmissingularvaluedecomposition,orSVD,and codewasexecutedinPython.

Keywords:recommendationalgorithm,SingularValueDecomposition(SVD),eigenvalues,diagonalization,Kaggle

GiventhedependenceofmostinternetusersonGoogle, Amazon,orothersearchandrecommendationengines,itis importanttorecallthebasisofmanyoftheseengines.This paperwillreconstructarudimentaryrecommendationalgorithmandpresentapotentialuseforitintheformofabook recommenderusingdatafromKaggle.Themaintoolusedin thealgorithmissingularvaluedecomposition,orSVD,and codewasexecutedinPython.

TheSVDcanbestatedas A = UΣV T ,forany m × n matrix A withrank r ,and Σ adiagonalmatrixoftheform

Thesquarerootsofeach λn correspondto σ1 ,σ2 ,...,σn whichareindescendingorder.These σn = √λn arethe singularvaluesof A,andrepresentthelengthsofthevectors Av 1 , Av 2 ,..., Av n ,amongotherthings.Thesevaluesare keytocreatingaSVD.

TheSVDcanbestatedas A = UΣV T ,forany m × n matrix A withrank r ,and Σ adiagonalmatrixoftheform

1Introduction

Keywords:recommendationalgorithm,SingularValueDecomposition(SVD),eigenvalues,diagonalization,Kaggle

1Introduction

Asthedigitalworldgrowsincreasinglycompetitive, manyonlinecompanieshaveracedtomaketheirproducts andservicesmoreaddictive,personal,andattractivethan ever.Astheycatertomorepeople,however,itbecomesnext toimpossibletousehumantimetocustomiseoradjustto asignificantdegree-instead,algorithmsareused.Among themostfamous(orinfamous)aretheYouTubealgorithm, Spotify’srecommendations,andAmazon’s”Customerswho boughtthisitemalsobought...”Onemethodusedtomake thesealgorithmsissingularvaluedecomposition,orSVD.

Singularvaluedecompositionisanextremelyusefultechniqueinmanyareasofscience,mathematics,anddataanalysis,andisanextendedversionofeigendecomposition,also knownasdiagonalisation.Thereasonthatitismorepowerfulthandiagonalisationisbecauseitcanfactorallmatrices,whilediagonalisationcanonlybeperformedoncertain (non-defective)matrices.

Asthedigitalworldgrowsincreasinglycompetitive, manyonlinecompanieshaveracedtomaketheirproducts andservicesmoreaddictive,personal,andattractivethan ever.Astheycatertomorepeople,however,itbecomesnext toimpossibletousehumantimetocustomiseoradjustto asignificantdegree-instead,algorithmsareused.Among themostfamous(orinfamous)aretheYouTubealgorithm, Spotify’srecommendations,andAmazon’s”Customerswho boughtthisitemalsobought...”Onemethodusedtomake thesealgorithmsissingularvaluedecomposition,orSVD.

Singularvaluedecompositionisanextremelyusefultechniqueinmanyareasofscience,mathematics,anddataanalysis,andisanextendedversionofeigendecomposition,also knownasdiagonalisation.Thereasonthatitismorepowerfulthandiagonalisationisbecauseitcanfactorallmatrices,whilediagonalisationcanonlybeperformedoncertain (non-defective)matrices.

BeforecreatingaSVD,theconceptofsingularvaluesof an m × n matrix A shouldbeconsideredfirst.Theseare theeigenvaluesof AT A,whichmustnecessarilybe n × n, andtheremustexistanorthonormalbasisfor Rn consisting oftheeigenvectorsof AT A, v1 , v2 ,..., vn withassociated nonnegativeeigenvalues λ1 ,λ2 ,...,λn .Withsomerenumbering,itisalwayspossibletoassumethattheeigenvalues canbearrangedindescendingordersuchthat

BeforecreatingaSVD,theconceptofsingularvaluesof an m × n matrix A shouldbeconsideredfirst.Theseare theeigenvaluesof AT A,whichmustnecessarilybe n × n, andtheremustexistanorthonormalbasisfor Rn consisting oftheeigenvectorsof AT A, v1 , v2 ,..., vn withassociated nonnegativeeigenvalues λ1 ,λ2 ,...,λn .Withsomerenumbering,itisalwayspossibletoassumethattheeigenvalues canbearrangedindescendingordersuchthat

if σr istheleastnonzerosingularvalueof A;andwhere U and V areorthogonalmatrices.

2ConstructionofanSVD

if σr istheleastnonzerosingularvalueof A;andwhere U and V areorthogonalmatrices.

Theconstructionofasingularvaluedecompositioncan besplitinto3steps(”LinearAlgebraanditsApplications”). Thisexamplewillshowthedecompositionof

2ConstructionofanSVD

Theconstructionofasingularvaluedecompositioncan besplitinto3steps(”LinearAlgebraanditsApplications”). Thisexamplewillshowthedecompositionof

Step1. Findanorthogonaldiagonalisationof AT A.This isoftendifficultwithlargermatrices(duetothedifficultyin findingtheireigenvalues),butforsmallermatricesisdoable. First,findtheeigenvaluesof AT A,whichinthiscaseare25, 9,and0.Then,since AT A issymmetrictheeigenvectors mustbeorthogonal,sosimplycomputingthemisenough. Wefindtheeigenvectorsasunitvectors

322 23 2

Step1. Findanorthogonaldiagonalisationof AT A.This isoftendifficultwithlargermatrices(duetothedifficultyin findingtheireigenvalues),butforsmallermatricesisdoable. First,findtheeigenvaluesof AT A,whichinthiscaseare25, 9,and0.Then,since AT A issymmetrictheeigenvectors mustbeorthogonal,sosimplycomputingthemisenough. Wefindtheeigenvectorsasunitvectors

Then,findingavectororthogonaltobothvectors(i.e.notingthattheirdotproductwillequal0)yieldsthefinaleigenvector

wouldotherwiseberoughlylinear—notgreatfor,say,48 milliondatapoints.Thisimplementationwillbedonein python.

Thealgorithmisinroughlythreestages:preprocessing thedata,performingsingularvaluedecomposition,andinterpretingtheoutput.Theimportedlibrariesare

1 import numpyasnp

2 import pandasaspd

3 from scipy.linalg import svd

4 import matplotlib.pyplotasplt

5 from mpl_toolkits.mplot3d import Axes3D

6 import os

Step2. Setup Σ and V V issimply [v1 v2 v3 ],fortheir correspondingeigenvaluesindecreasingorder.Inthefinal SVD,thetranspose, V T isused,whichequals

whichareusedtoprocessandvisualisethedata.Anextremelyrigorouslycollectedsetofdataonfoodpreferences isusedasanexampledataset(whereA=Apple,B=Banana,C=Curry,D=Durian, ´ E= ´ Eclair,andF=Fries; scoresrangefrom0to10.Yes,Ireallyaskedpeoplethis. Yes,theywereconfused.):

ABCD ´ EF

AM 41010637

BU 6701033

JL 710105310

JZ 674367

HC 471382

HY 3610576

RY 5407610

Then,usingthesingularvalues(simplythesquareroots ofthenonzeroeigenvaluesinorder)5and3,

RP 690416

JK 550378

SB 2810497

ZK 511011010

WH 684340

AL 001001010

Notethe0columnpaddingoutthematrixintoa 2 × 3 matrix.

Step3.Construct U.Finally,usingtheformula

3.1PreprocessingtheData

Thisstepeitherrandomlygeneratesortakesa.csvfile andoutputsamatrixthatisusersbyitemsinsize.Thisis necessaryforthenextsteps,asthedatathatisgiveninthe mainmethod(seevisualisingthedata)isunpackedintoalist andneedstobeamatrix.

1 def randmatrix(users,items): # creates random matrix that is users x items

Then,thesingularvaluedecompositionofthematrixis

2 data=[]

3 for i in range(users):

4 user=[np.random.randint(11)/10 for in range(items)]

5 data.append(user)

6 mat=pd.DataFrame(data)

7 mat.index=["User " + str(i) for i in range(users)]

Thisprocesscanbecleverlymodifiedtoincreasecomputationspeedforcomputers,butthismethodwillsufficefor mosthumanrequirements.

3RecommendationAlgorithm

Thecodeusedherewillbeintentionallyreductive,asprogrammingafullimplementationofallthestepsinvolvedin SVDisunnecessarilycomplex.Forlargeralgorithms,some clevermathandprogrammingisrequiredtoreducetheprocessingpowerrequired,astheincreaseinprocessingpower

8 mat.columns=["Item " + str(i) for i in range(items)]

9 return mat 10

11

12 def matrix(users,values): # creates predefined matrix (values) that is users x items 13 data=[]

14 for i in range(users):

15 user=[values[6*i+k] for k in range(6)]

18 mat.index=["User " + str(i+1) for i in range(users)]

19 mat.columns=["Item " + str(i+1) for i in range(6)]

20 return mat

3.2ProcessingtheData

ThisstepsimplyperformsSVDonthematrix A thatis outputtedfromthepreviousstep,returningthesmallestpossible U, Σ,and V T .Whileitispossibletoprogramthisdecompositionmyself,thelibraryprovidedasignificantlyless computationallyintensivealgorithm.Usually,SVDisfairly difficultforacomputertoprocess.Thisalgorithmalsoreducesthedimensionalityof U and V inordertokeepthe matricesaseasytovisualiseaspossible.Thecolumnsthat arekept(k)correspondtothehighestsingularvalues.

1 def do_svd(mat,k=0,option=False): # performs singular value decomposition on matrix mat and returns sigma, u, and vt

2 u,sigma,vt=svd(mat)

3 u=pd.DataFrame(u[:,:k])

4 vt=pd.DataFrame(vt[:k,:])

5 if option:

6 return sigma

7 else:

8 return u,vt

3.3InterpretingtheOutput

Theoutputisprocessedhere.Thismethodtakesinanitem and V T ,returningthemost’recommended’itembasedon thepreferencesofeveryoneinthedataset.Thisiscomputed bydottingeachcolumnof V T withtheitem,andfindingthe itemtheleastdistance(which,bySVD,mustbethemost similar).

1 def recommend(item,vt,output_num=1): # recommendation using dot product distance

2 global rec

3 rec=[]

4 for item in range(len(vt.columns)):

5 if item!=item:

6 rec.append([item,np.dot(vt[ item],vt[item])])

7 final_rec=[i[0] for i in sorted( rec,key=lambda x:x[1],reverse=True) ]

8 return final_rec[:output_num]

3.4VisualisingtheData

Finally,thedataisvisualised.Themethoddefinedabove simplyplotsthedatausingmatplotlib,andthemainmethod usestheabovefunctionstoextractdatafromthe.csvand createabasicinterface.

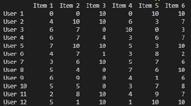
1 def plot_data(mat,data_type,camera= None): # plots data using matplotlib

2 fig=plt.figure()

3 ax=fig.add_subplot(111,projection =’3d’)

4 if camera!=None:

5 ax.view_init(elev=camera[0], azim=camera[1])

6 for index,row in mat.iterrows():

7 ax.scatter(row[0],row[1],row [2],alpha=0.8)

8 ax.text(row[0],row[1],row[2],’ {0} {1}’.format(data_type,index), size=10)

9 plt.show()

10

11 //skip// 12

13

14 if __name__== "__main__":

15 filename=os.getcwd()+"\\Downloads \\"+"likesdata txt"

16 a=matrix(12, list(np.array([*[[int (i) for i in line.split(",")] for line in open(filename, "r").readlines ()]]).reshape((-1)))) # this works

17 #a = randmatrix(20, 10)

Theoutputoftheprogramlookslikethis:

Figure2:Theuppernumberisuser-inputted;thealgorithm returnsthatifauserlikedcurry(2)thattheywouldmost likelyalsolikebananas(1)andfries(5)

Ineededbookrecommendations,butinteractingwith peopleiscringe.SoIusedmyalgorithmtocuremybook ennui.

Figure1:Printoutofthedatatable

4Extension:CuringEnnui

4.1HowtoCureEnnuiwithMath

Havinggonethroughthelegworkofcreatingthealgorithm,myextensionismostlyinrefiningandapplyingthealgorithmtosomethingthatwillhelpmepersonally,andpotentiallyothers,withmotivation.Thefirst partoftheextensionisinfindingthedata,forwhichI turnedtothescourgeofBigData-Kaggle.Asmuch asIhatethemoderninvasionofprivacythattheinternethasprovided,Alphabet’sbenevolenceinprovidingthisdataisveryhelpful.ThedatasetIimported wasBookRatings:https://www.kaggle.com/arashnic/bookrecommendation-dataset?select=Ratings.csv

4.2Preprocessing

Thebookdatasetwasverylarge(340,556uniqueusers, eachratingalargenumberofbooks),soefficiencywasmore importantinanalysingthedataset.Thefirsttaskwastogenerateamatrix,withsizeusersxbooks,whichwasdoneusingthefollowingcode:

1 import os

2 import pandas

3 import numpyasnp

4 5 df=pandas.read_csv(os.getcwd()+"\\"+" Ratings.csv")

6 7 books=df["ISBN"].unique()

8 books=books[:5000]

9

10 df_small=df.loc[df["ISBN"].isin(books) ]

11 users=df_small["User-ID"].unique()

12

13 df=df_small.copy()

14

15 matrix=pandas.DataFrame(data=np.zeros( dtype=np.uint8,shape=(len(users),len( books))),index=users,columns=books)

16 for _,row in df.iterrows():

17 matrix.at[row["User-ID"],row["ISBN" ]]=row["Book-Rating"]

18

19 matrix.to_csv(os.getcwd()+"\\"+"matrix csv")

20 print(matrix)

whichIranseparatelyfromthemaincode,asthisremovesthenecessityofgeneratingthewholematrixevery timethisalgorithmisrun.

Thispreprocessingstepalsoservedtochooseasampling ofthebooks-thefirst5000uniquebooksbytheirISBN, whichwasrandomised.Thiswastoreduceprocessingtime, astheoriginalalgorithmIappliedtookextremelylongto run,andwouldhavegeneratedafilethatcontainedupwards of400GBofdata.

4.3Output

Theoutputofthealgorithmissimilartoearlier.Thematrixlookslikethis:

Mostusersfellalongaparticularline,butafewwereoutliers(theyratedalotofbooks!),andthemostpopularbooks alsobecameoutliers:

Figure3:Agraphiscreatedthatshowsthepropinquity(similarity)ofeachuser-user7(RY)isverysimilartouser9 (JK),astheyareclosetoeachother

Figure4:Outputmatrix

Figure5:Graphofusers

Notethattheplots,forreadability’ssake,donotploteverysingleuseroritem.Themostinterestingpartofthealgorithm,forme,wasgettingthebookrecommendation,which wasasfollows:

2023,fromhttps://towardsdatascience.com/understandingsingular-value-decomposition-and-its-application-in-datascience-388a54be95d SingularValueDecomposition(SVD)tutorial.(2023). Retrieved25January2023,from https://web.mit.edu/be.400/www/SVD/Singular Value Decomposition.htm

Lay,Lay,Mcdonald(2015)LinearAlgebraandIts Applications.Pearson.

160correspondedtoTheCatcherintheRye,and173and 9toTheCatcherintheRye-Barron’sBookNotesand TheAdventuresofHuckleberryFinn,respectively.Conveniently,Ihaven’treadTheAdventuresofHuckleberryFinn before,soImayverywellreaditnow.Notethatthealgorithmisfairlyefficient;evenrunningwith16824500datapoints(33649 × 5000),itonlytakes10minutesorsotorun, afteranupdatetothewaythedataispacked(asamatrix .csv,ratherthanaplainlist).

5Summary

Thisalgorithmhasbeenshownnowtobeusefulenough inprovidingrecommendations.Thelargestbottlenecksin performancecomefromthegenerationofthematrixand thematrixcomputationsneeded.Otherimplementations ofthisalgorithm,orfutureusesofthisimplementation, shouldprobablyspendsometimedesigningamore friendlyGUIandoptimisingperformance.Otherdatasets availableonlinearealsousablewiththisalgorithm: https://www.kaggle.com/shadey/spotify-2010-2019/data, forexample,whichisaSpotifymusicpreferencedataset.

References

DeepDiveintoNetflix’sRecommenderSystem.(2021). Retrieved25January2023,from https://towardsdatascience.com/deep-dive-into-netflixsrecommender-system-341806ae3b48

UnderstandingSingularValueDecompositionandits ApplicationinDataScience.(2022).Retrieved25January

Figure6:Graphofbooks

09 Natural Eigenvectors in Higher Number Systems

Written by Gaurav Goel

NaturalEigenvectorsinHigherNumberSystems

GauravGoel

goel47628@sas.edu.sg

TeacherReviewer: Mr.Craig

Abstract

Abstract

Linearalgebraisgenerallyintroducedthroughworkingwith therealnumbersystemindifferentdimensions(R, R2 , R3 , andsoon).However,thereareavarietyofalternativenumber systemsthatarefields,whichembracemultidimensionalityin amuchmoreaccessibleandnaturalmanner.

Inthispaper,Iaimtoinvestigateafewofthesenumbersystems,interpretthemthroughlinearalgebra,anddiscovera highernumbersystemwhichembraceseigenvaluesinanaturalway.Essentially,Iwillextendonmyunderstandingof linearalgebraandeigenvectorstointerpretthebehaviourof differentnumbersystems.

Keywords: eigenvalues,CliffordAlgebra,multidimensionality,numbersystems

1ExplorationofDifferentNumberSystems

Thereareavarietyofdifferentnumbersystemsthatwe caninvestigate.Theseincludetherationalnumbers(Q), complexnumbers(C),quarternions(H),finitefields(Zn ), andmanymore.However,theaimhereisnottoinvestigateanarbitrarynumbersystem.Rather,wewanttoinvestigatenumbersystemsthatnaturallyincorporateelements andpropertiesoflinearalgebra.Thismeansthatwewantto findnumbersystemsthatnaturallycombinescalarandvectorproperties.Infact,aftersomeresearching,thereisindeed aclassofnumbersystemswhichdojustthis:CliffordAlgebras.

ACliffordAlgebra,denotedCla,b (R),isaclassofalgebraswhereanygeneralelement q = a + ⃗ v ,where a isthe scalarpartand ⃗ v isthevectorpart.Addingtwoelements simplymakesuseofscalarandvectoraddition,butmultiplyingtwoelementsgivesusaninterestingcombinationof scalarmultiples,dotproducts,andcrossproducts.

Moregenerallyspeaking,if ⃗ e1 , ⃗ e2 , ⃗ e3 ,... areorthogonal unitvectors,aCliffordAlgebraelementcanbedefinedas:

And,sinceCliffordAlgebrasalreadydefineadditionand multiplicationbetweenelementsforus,wecandirectlytake thesedefinitionstolinearalgebra,byusingvectoradditionandmatrixmultiplication.Thisgivesusanumbersystemframeworkthatnaturallyincorporatesvectorandmatrix properties.

NowthatwehaveabasicunderstandingofhowlinearalgebracanbeappliedtounderstandCliffordAlgebras,we seektounderstandhoweigenvectorscanbeappliedtothese algebras.Inparticular,justaseigenvectorsseektounderstandhowmatrixmultiplicationandscalarmultiplicationact equivalentlyonavector,intheseCliffordAlgebras,wewant todiscoverwhetherornotelement-wisemultiplicationand scalarmultiplicationactequivalentlyonelements. WemaybeginbyselectingafewbasicCliffordAlgebras andanalyzingwhetherornotthisispossible.

2ComplexNumbers

ThemostintuitiveCliffordAlgebratobeginwithis Cl1,0 (R),orthecomplexnumbersystem(C).Thisisbecauseeach z ∈ C canbewrittenintwocomponents(a + bi). Inordertodiscoverwhetherornoteigenvectorscanbeappliedtocomplexnumbers,wehavetotaketwosteps.First, weapplylinearalgebratocomplexnumbers.Second,we searchforeigenvectorsinthislinearalgebrarepresentation ofcomplexnumbers.

2.1ApplyingLinearAlgebratoComplex Numbers

Applyinglinearalgebratocomplexnumberstakesthree steps.First,weneedtorepresenteachcomplexnumberasa vectorinlinearalgebra.Second,weneedtodefineaddition inthisalgebra.Third,weneedtodefinemultiplicationin thisalgebra.

Inthiscase,thecolumnvectorrepresentingourelement q is:

First,itisnottoohardtorepresenteachcomplexnumber asavectorinlinearalgebra.Tomap C → R2 ,foreach z ∈ C,where z = a + bi (for a,b ∈ R),wehave:

Thisisjustnormalvectoraddition.

Thisisclearlynotnormalvectormultiplication.Instead, wecangive

Ingeneral,for

Thischecksout,soournewdefinitionofmultiplication holds.

2.2EigenvectorsintheComplexNumbers

Inordertofindeigenvectorsinthecomplexnumbers,we ask:isitpossibletofindasetofcomplexnumbers S such

Thiscanbeverifiedinafewsteps. First,supposeweknow

Sincethedeterminantoftheleft-handmatrixmustbe equalto 0,bytheeigenvectorcharacteristicequation,weget:

(λ1 a0 λ2 )2 +(λ1 b0 )2 =0

However,thisisonlysatisfiedifboth λ1 a0 λ2 =0 and λ1 b0 =0.If λ1 b0 =0,either λ1 =0 or b0 =0,bothof whicharetrivialsolutions.

2.3SummaryforComplexNumbers

Unfortunately,thesetrivialsolutionssuggesttousthat thereexistnosucheigenvectorsandeigenvaluesinthecomplexnumbers.Intuitivelythough,thisshouldmakesense. Whenmultiplyingbyacomplexnumber,theresult,forany othercomplexnumber,isarotationandadilation.Thisrotationsetsitofftheaxiswewouldideallywantittobeon. Thus,wemustlooktodifferentnumbersystemsforoursolution.

3Split-ComplexNumbers

Afterrecognizingthatthepreviousissueliedwithinthe sumofsquaresinthefinalcharacteristicequation,wemay approachadifferentCliffordAlgebratoovercomethisissue,namelythesplit-complexnumbersystem(Cl0,1 (R)), or R ⊗ R.Thisnumbersystemworksverysimilartothe complexnumbers,exceptthat i2 =1 instead.Inorderto discoverwhetherornoteigenvectorscanbeappliedtosplitcomplexnumbers,wetakethesametwostepsaslasttime. First,weapplylinearalgebratothisnumbersystem.Second, wesearchforeigenvectorsinthislinearalgebrarepresentationofsplit-complexnumbers.

3.1ApplyingLinearAlgebratoSplit-Complex Numbers

Onceagain,applyinglinearalgebratosplit-complex numberstakesthreesteps.First,weneedtorepresenteach z ∈ Cl0,1 (R) asavectorinlinearalgebra.Second,weneed todefineadditioninthisalgebra.Third,weneedtodefine multiplicationinthisalgebra.

First,justasbefore,itisnottoohardtorepresenteach z ∈ Cl0,1 (R) asavectorinlinearalgebra.TomapCl0,1 (R) → R2 ,foreach z ∈ Cl0,1 (R),where z = a + bi (for a,b ∈ R), wehave:

z = a b

Then,foraddition,given z1 = a1 + b1 i and z2 = a2 + b2 i, weknowthat z1 + z2 =(a1 + a2 )+(b1 + b2 )i.So,wehave:

This,onceagain,isjustnormalvectoraddition.

Finally,formultiplication,given z1 = a1 + b1 i and z2 = a2 + b2 i,weknowthat z1 z2 =(a1 a2 + b1 b2 )+(a1 b2 + a2 b1 )i.Notethedifferenceherefromlasttime.So,wehave:

Thisisclearlynotnormalvectormultiplication.Instead, wecangive z2 amultiplicationmatrix,say Az2 ,suchthat z1 z2 inthesplit-complexnumbersequals Az2 z1 inlinear algebra.

Ingeneral,for z = a + bi,say:

is:

Thischecksout,soournewdefinitionofmultiplication holds.

3.2EigenvectorsintheSplit-ComplexNumbers

Inordertofindeigenvectorsinthesplit-complexnumbers,weask:isitpossibletofindaset S ⊂ Cl0,1 (R) such thatforall z

(for λ

Thiscanbeverifiedinafewsteps.

First,supposeweknow z0 = a0 + b0 i ∈ S Then, z = a + bi ∈ S ifandonlyif z = λ1 z0 and

Breakingthisintotwoparts,onthetopwehave:

equalto 0,bytheeigenvectorcharacteristicequation,weget:

3.3SummaryforSplit-ComplexNumbers

Unfortunately,thesetrivialsolutionsalsosuggesttous thatthereexistnosucheigenvectorsandeigenvaluesinthe split-complexnumbersystem.Whilethereisnointuitiveexplanationhere,wemuststilllooktodifferentnumbersystemsforoursolution.

4Cl1,1 (R)

ItseemssofarthatthereisnoCliffordAlgebrawhichincorporateslinearalgebraandeigenvectorsinanaturalway. However,beforegeneralizingourconclusionstothewider classofCliffordAlgebras,itisworthconsideringanalgebrawithalargercolumnmatrix.Inparticular,wewillconsidertheCliffordAlgebraCl1,1 (R).Thisnumbersystem canalmostbeconsideredasacombinationofcomplexand split-complexnumbers.Basically,inthissystem,wehave twobasisvectors i and j ,suchthat i2 = 1 and j 2 =1 Thismeansthateach z ∈ Cl1,1 (R) canbeexpressedas z = a + bi + cj + dij .Inordertodiscoverwhetherornot eigenvectorscanbeappliedtoCl1,1 (R),wetakethesame twostepsaslasttime.First,weapplylinearalgebratothis numbersystem.Second,wesearchforeigenvectorsinthis linearalgebrarepresentationofCl1,1 (R)

4.1ApplyingLinearAlgebratoCl1,1 (R)

Onceagain,applyinglinearalgebratoCl1,1 (R) takes threesteps.First,weneedtorepresenteach z ∈ Cl1,1 (R) asavectorinlinearalgebra.Second,weneedtodefineadditioninthisalgebra.Third,weneedtodefinemultiplication inthisalgebra.

First,justasbefore,itisnottoohardtorepresenteach z ∈ Cl1,1 (R) asavectorinlinearalgebra.TomapCl1,1 (R) → R2 ,foreach z ∈ Cl1,1 (R),where z = a + bi + cj + dij (for a,b,c,d ∈ R),wehave:

This,onceagain,isjustnormalvectoraddition. Finally,formultiplication,given

Thisisclearlynotnormalvectormultiplication.Instead, wecangive z2 amultiplicationmatrix,say A( z2 ),suchthat

2 inthesplit-complexnumbersequals A( z2 ) · z1 in linearalgebra.

Ingeneral,for z = a + bi + cj + dij ,say:

Then,wehavethat

Thischecksout,soournewdefinitionofmultiplication holds.

4.2EigenvectorsintheCl1,1 (R)

InordertofindeigenvectorsinCl1,1 (R),weask:isitpossibletofindaset S ⊂ Cl1,1 (R) suchthatforall z1 ,z2 ∈ S , z2 = λ1 z1 and z1 z2 = λ2 z1 (for λ1 ,λ2 ∈ R)?

Thiscanbeverifiedinafewsteps.

First,supposeweknow z0 = a0 + b0 i + c0 j + do ij ∈ S

Then, z = a + bi + cj + dij ∈ S ifandonlyif z = λ1 z0 and z0 z = λ2 z0 .

So,since z = λ1 z0 :

Sincethedeterminantoftheleft-handmatrixmustbe equalto 0,bytheeigenvectorcharacteristicequation,we getaverycomplicatedequation.Aftersimplifyingandcancelling,weareleftwith:

Giventhatthisequationissocomplex,itisextremelyhard totreatitsimilarlytoourpreviouscharacteristicequations, whichonlyhadtwoterms.Rather,herewecansearchfor nontrivialsolutionsthatsatisfythisequation.

Forinstance,consider:

Aswecansee,forthesevalues,if λ =1,thecalculations checkout.

Aftersignificantlymoretrialanderror,weseethatour potentialnontrivialvaluesof z0 and z ,forarbitrary λ1 ,λ2 ∈ R arelimitedto:

Unfortunately,althoughthisisquitepromising,since

and z arenotscalarmultiples,thesespecificelementsdonot fulfilouroriginalexpectations.However,theseelementsdo haveaname:pseudoscalars,whichwewilltakealookatin ouroverallconclusion.

5Conclusion

Wehaveinvestigatedavarietyofnumbersystemsthat embracedlinearalgebrainamorenaturalmanner,bylookingatnumbersystemswhichnaturallyhadcolumnmatrices andvectorparts.Whilethegoalwastofindalineargroup ofnumbers,throughtheseinvestigations,wemayconclude thatnosuchgroupexists.

10 Evaluating Epidemiological Solutions through S-I-R Modeling

Written by Gaurav Goel

EvaluatingEpidemiologicalSolutionsthroughS-I-RModeling

GauravGoel

goel47628@sas.edu.sg

TeacherReviewer: Mr.Craig

Abstract

Abstract

Throughpreviousinvestigation,Ihaveformedtheopinion thateventhoughlinearalgebraisaneattooltoconceptualizeoperationsinhighermath,theimportanceoflinearalgebratrulyliesinitsreal-worldcomputationalapplication.As aresult,forthisproject,Iexploredatopicwithreal-world implications.

Inthispaper,IaimtoreanalyzethederivationoftheSIR modelthroughdifferentialequationsandlinearalgebra,and thenmyextensionwillbetoadapttheSIRmodeltomeasure theimpactsofepidemiologicalsolutionssuchasvaccination andlockdownthroughthedeathssustainedunderdifferent scenarios.

Keywords:SIRModel,pandemic,differentialequations,epidemiology,computationalmodelling

1ExplorationoftheBasicSIRModel

ThebasicSIRmodelconsistsofthreecompartments:Susceptible,Infected,andRecovered.Theflowofpeopleinand

therecoveryrate,ortheproportionofinfectedindividuals thatrecoveroveraperiodoftime.

Withthisinformation,wecansaythat:

• theinstantaneousbirthrateis µN

• thedeathratesoutofeachcompartmentare µS , µI µR respectively

• therecoveryrateis γI

• theinfectionrateis βSI

Atthispoint,ourdefinitionsraisethequestion:Whatis β ?Thisvariableisslightlymorecomplicatedthantherest.

Inessence, β = kp,where k isthenumberofinteractions apersonmakeswithacertainpopulationand p istheproportionthattheaverageinteractionbetweenasusceptible individualandaninfectedindividualspreadstheinfection.

Giventhediagram,wecancreateasetofdifferential equationstomodelthisidea.

TeacherReviewer: Mr.Craig

Abstract

Throughpreviousinvestigation,Ihaveformedtheopinion thateventhoughlinearalgebraisaneattooltoconceptualizeoperationsinhighermath,theimportanceoflinearalgebratrulyliesinitsreal-worldcomputationalapplication.As aresult,forthisproject,Iexploredatopicwithreal-world implications.

therecoveryrate,ortheproportionofinfectedindividuals thatrecoveroveraperiodoftime.

Withthisinformation,wecansaythat:

• theinstantaneousbirthrateis µN

EvaluatingEpidemiologicalSolutionsthroughS-I-RModeling

• thedeathratesoutofeachcompartmentare µS , µI ,and µR respectively

• therecoveryrateis γI

Inthispaper,IaimtoreanalyzethederivationoftheSIR modelthroughdifferentialequationsandlinearalgebra,and thenmyextensionwillbetoadapttheSIRmodeltomeasure theimpactsofepidemiologicalsolutionssuchasvaccination andlockdownthroughthedeathssustainedunderdifferent scenarios.

GauravGoel

• theinfectionrateis βSI

goel47628@sas.edu.sg

TeacherReviewer: Mr.Craig

Keywords:SIRModel,pandemic,differentialequations,epidemiology,computationalmodelling

1ExplorationoftheBasicSIRModel

Abstract

ThebasicSIRmodelconsistsofthreecompartments:Susceptible,Infected,andRecovered.Theflowofpeopleinand outofthesethreecompartmentscanbesummarizedbythe diagramIhavedrawnbelow:

Throughpreviousinvestigation,Ihaveformedtheopinion thateventhoughlinearalgebraisaneattooltoconceptualizeoperationsinhighermath,theimportanceoflinearalgebratrulyliesinitsreal-worldcomputationalapplication.As aresult,forthisproject,Iexploredatopicwithreal-world

1ExplorationoftheBasicSIRModel

Atthispoint,ourdefinitionsraisethequestion:Whatis β ?Thisvariableisslightlymorecomplicatedthantherest. Inessence, β = kp,where k isthenumberofinteractions apersonmakeswithacertainpopulationand p istheproportionthattheaverageinteractionbetweenasusceptible individualandaninfectedindividualspreadstheinfection. Giventhediagram,wecancreateasetofdifferential equationstomodelthisidea.

therecoveryrate,ortheproportionofinfectedindividuals thatrecoveroveraperiodoftime.

Withthisinformation,wecansaythat:

dS

• theinstantaneousbirthrateis µN

dt = birth death infection = µN µS βSI

• thedeathratesoutofeachcompartmentare µS , µI ,and µR respectively

dI

dt = infection death recovery = βSI µI γI

• therecoveryrateis γI

dR

• theinfectionrateis βSI

dt = recovery death = γI µR

Fromhere,thereisalotofadditionaltheoreticalanalysis wecoulddo.

Forinstance,wecouldderivethebasicreproductionrate (theaveragenumberofindividualsthateachinfectedindividualinfects).Inparticular,wecanaskourselves:When areinfectionsgrowing?Weseethatinfectionsaregrowing when dI dt > 0.Thisgivesus:

Atthispoint,ourdefinitionsraisethequestion:Whatis β ?Thisvariableisslightlymorecomplicatedthantherest. Inessence, β = kp,where k isthenumberofinteractions apersonmakeswithacertainpopulationand p istheproportionthattheaverageinteractionbetweenasusceptible individualandaninfectedindividualspreadstheinfection. Giventhediagram,wecancreateasetofdifferential equationstomodelthisidea.

βSI µI γI> 0

Let’sdefinesomevariablesandthenexaminewhateach rateis.

ThebasicSIRmodelconsistsofthreecompartments:Susceptible,Infected,andRecovered.Theflowofpeopleinand outofthesethreecompartmentscanbesummarizedbythe diagramIhavedrawnbelow:

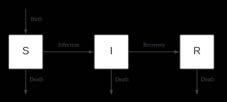
First, S , I ,and R arethenumberofpeopleineachofthe respectivecompartments.Furthermore, S + I + R = N , whichisthetotalpopulationweareobserving.Next,we needtodefineabirth/deathrate.Wewillconsiderthese equal,andusethevariable µ tosignifytheproportionofpeoplethatdieoveraperiodoftime.Last,weuse γ torepresent

dS

Figure1:SIRmodel

Let’sdefinesomevariablesandthenexaminewhateach rateis.

First, S , I ,and R arethenumberofpeopleineachofthe respectivecompartments.Furthermore, S + I + R = N , whichisthetotalpopulationweareobserving.Next,we needtodefineabirth/deathrate.Wewillconsiderthese equal,andusethevariable µ tosignifytheproportionofpeoplethatdieoveraperiodoftime.Last,weuse γ torepresent

dI

βSI>µI + γI

dt = birth death infection = µN µS βSI

βSI

µI + γI > 1

dt = infection death recovery = βSI µI γI

dR

βS µ + γ > 1

dt = recovery death = γI µR

Infact,thisvalue, βS µ+γ ,isthebasicreproductionrate,or R0 .Conceptually,thiscanbeexplainedbytheideathatthe

Fromhere,thereisalotofadditionaltheoreticalanalysis wecoulddo.

Forinstance,wecouldderivethebasicreproductionrate (theaveragenumberofindividualsthateachinfectedindividualinfects).Inparticular,wecanaskourselves:When areinfectionsgrowing?Weseethatinfectionsaregrowing when dI dt > 0.Thisgivesus:

βSI µI γI> 0

βSI>µI + γI

βSI

µI + γI > 1

βS

µ + γ > 1

Infact,thisvalue, βS µ+γ ,isthebasicreproductionrate,or R0 .Conceptually,thiscanbeexplainedbytheideathatthe

Figure1:SIRmodel

rateofinfectionisgrowingifeachinfectedpersonisinfectingmorethanoneotherindividual,justasweseeinour equation.

Wecouldalsoanalyzepotentialequilibriumstates.Inparticular,wereachanequilibriumstatewhen dI dt =0.This givesus:

βSI µI γI =0 (βS µ γ )I =0

Thisimpliesoneoftwothings,First,when I =0,there arenoinfections,whichisknownasthedisease-freeequilibrium,Second,whenwehave βS µ γ ,wherethere arestillinfections,wehavewhatisknownasanendemic equilibrium.

However,thesesameconclusionscanbederivedfromobservingalinearalgebraicmodeloftheSIRmodel.

2ApplyingLinearAlgebratotheSIRModel

InordertoapplylinearalgebratotheSIRmodel,wemust firstdiscretizeourdifferentialequations.Inorderwords, ratherthantakinginstantaneousrates,wemaylookatthe changeintheSIRvaluesoverasmall,macroscopicperiod oftime,perhapsaweek.Then,wegetnewequations,identicalbefore,butusingmacroscopicratherthaninfinitesimal increments:

Wemustmakeonechangehere.Inparticular,weseethat wecannothavethe βS terminsideourmatrix,as S will continuetochange.Thus,whilethismayincreaseerrorin ourfinalmodel,simplyforthesakeofourcalculations,we willapproximate S to N .Thisgivesusthefinaltransition matrixof:

γI

Considertheinitialstatewithapopulationof N =1000 and I0 =2 infectedpeople.Letusapproximatevaluesfor therestoftheparameters(notethatthesevaluesareexaggeratedforthesakeofthesimulation).Aproportionofapproximately µ =0 01 peoplearebornanddieeachweek.A proportionof γ =0 08 peoplewillrecovereachweek.And, wecanassign k =0.005 and p =0.05,givingusavalueof β =0.0025. Wenowgetaninitialmatrixof:

t = recovery death = γI µR

Here,oneapproachwouldbetofindtheJacobianmatrix ofthecolumnvectorofthesedifferentialequations,andthen buildthenextgenerationmatrixofthesedifferentialequations.However,aswewillseelater,thatdoesnotserveour purposeoflookingattheoverallmodelasawhole,andthus, wewantasimplerlinearalgebraicmodel.

ThesimplermodelistocreatebasicMarkovChainmatrix,giventheinformationweknowaboutthechangesinthe respectivevalues.

Inparticular,ifwethinkofeachvalueasitsprevious valueplustheincrementalchange(e.g. Sn+1 = Sn +∆Sn ), thenwegettheequationsbelow.

Sn+1 = Sn +(µN µS βSI )∆t

In+1 = In +(βSI µI γI )∆t

Rn+1 = Rn +(γI µR)∆t

Oneeditwemustmakeistorewritethe S equationwithouttheconstant,givingus:

Sn+1 = Sn +(µI + µR βSI )∆t

Ifweconsidereachratetobeamacroscopicraterather thananinfinitesimalone,the ∆t termvanishes.Thus,when representedasamatrix,weobtainthetransitionmatrix:

Wegetatransitionmatrixof:

1 2 490 01 03 410 00 080 99

Aftersimulatingthisdiseasespread,wegettheseresults (roundedtothenearestnaturalnumbers):

yrs/wksSIR

0/099820

0.5/268639047

1/52244278479

1.5/7821198691

2/10429848655

2.5/13037641582

3/15641453533

3.5/18239974527

4/20836184554

Figure2:SIRmodelincludinginfectiousdeath

Furthermore,ournewdifferentialequationsareasfollows:

dS

dt = birth death infection = µN µS βSI

dI

6/31236568567

6.5/33836571564

dt = infection death infectiousdeath recovery = βSI µI αI γI

dR

dt = recovery death = γI µR

dD

dt = infectiousdeath = αI

Throughthemethodweusedbefore,wecantakethese differentialequationsintolinearalgebraonceagain.Our transitionmatrixis:

Aswecansee,thediseasespreadtoaround 65% ofthe population,andreachedasteadystaterightaroundthesixth year.

Now,let’susethisunderstandingtodevelopmoresophisticatedmodels.

3TheInfectiousDeathSIRModel

Thefirstthingwewillattempttodoisintroducetheidea ofdeathbyinfection.Inthisway,wecanquantifyexactly howlargethemortalityimpactoftheinfectionactuallywas. Usingthis,wecancompareresultsacrossdifferenttreatmentsandsolutions.

Weintroducethisideabyaddinganextracompartment, D ,fordeathbyinfection.

Wecannowdefineafewmorevariables.

Wewillcalltheproportionofinfectedindividualswho diefromthedisease(notfromnaturalcauses) α.Thismeans thattherateofflowfrom I to D is αI .

Thisisdepictedinthediagrambelow:

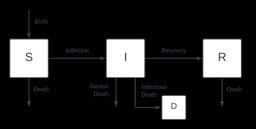
Usingthesamevalueswehadlasttime,butnowincluding that α =0 015,wegainanewsimulation. Ourinitialmatrixisonceagain:

However,ourtransitionmatrixisnow:

0/0998200

0.5/2689165367

1/5232823236477

1.5/7823877550135

2/10430928509154

2.5/13038918432162

3/15645018364169

3.5/18248224317177

4/20847736299199

6/31239133322241

6.5/33840328303266

Wecanseehowtheseresultsdifferedslightlyfromlast time.Withtheincorporationoftheinfectiousdeathscompartment,weseeadecreaseinthenumberofinfectiouspeopleandrecoveredpeopleleftover(probablybecausealotof themdied).

Wewillusethissimulationasacontroltomeasureagainst thesolutionswepropose.

4TheLockdownSIRModel

Thefirstsolutionwecanlookatisputtingcitizensinto lockdown.Whateffectdoesthissolutionhave,andhow shoulditimpactourmodel.Well,inessence,lockdowndoes nothelpwithanything,exceptforthefactthatitdecreases thenumberofinterpersonalinteractionsinacountry.Inparticular,thismeansthat k willdecrease.Saythatthenew valueof k is kl ,forsomelockdownfactor l .Then,forour newvalueof β , klp = βl Ourdiagramisasfollows:

Onceagain,wecreateatransitionMarkovMatrixfor thesedifferentialequations:

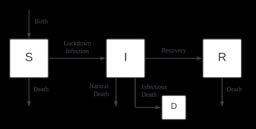
0/0998200

0.5/26985672

1/5295018266

1.5/78869417317

2/1047456315537

2.5/1306406123762

3/1565954327883

3.5/1825962827997

4/20861620258106

Intermsofourequations,thereareafewimplications.

First,weusethevariable ρ torepresenttheproportion ofindividualswhogetvaccinatedatbirth.Thisgivesusa rateof µ(1 ρ)N babiesbeingbornintothesusceptible compartmentand µρN babiesbeingbornintotherecovered compartment.

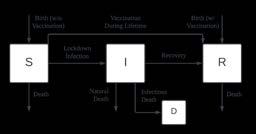
Second,weusethevariable ν torepresenttheproportionofsusceptibleindividualswhochoosetogetvaccinated duringtheirlifetime.Thisgivesusarateof νS individuals flowingfromthesusceptiblecompartmenttotherecovered compartment.

Giventhesechanges,hereareournewdifferentialequations:

dS

dt = birth(w/outvaccine) death vaccination infection

dI

= µ(1 ρ)N µS νS βSI

dt = infection death infectiousdeath recovery

= βSI µI αI γI

6/31270511157127

6.5/33871512142131

dR

dt = birth(wvaccine) + vaccination + recovery death

= µρN + νS + γI µR

Aswecansee,evenbyjustlimitinginteractionsbetween peopleby 40%,lockdownisasolutionthatcanliterally halvethenumberofpotentialdeaths.

5TheVaccinationSIRModel

Thenextsolutionwecanlookatisimplementingvaccination.Thiscanbeimplementedbothatbirthandduring people’slifetimes,sowewillassumebothhappen.Inparticular,thishastwoimplications.One,someindividualsare borndirectlyintotherecoveredcompartmentasaresultof beingvaccinatedfrombirth.Two,individualswhogetvaccinatedduringtheirlifetimesskipovertheinfectedstageand godirectlyfromsusceptibletorecovered.

Thiscanbeseeninthisdiagram:

dD

dt = infectiousdeath = αI

OurtransitionalMarkovMatrixis:

Let’schoosevaluesfor ρ and ν .Atbirth,thevaccination ratecanbe ρ =0.009.Duringalifetime,thevaccination ratecanbe ν =0.01.

Thesevaccinationstatisticsgiveusresultsof:

0/0998200

0.5/26744372375

1/5242210947336

1.5/782906462371

2/1043002764088

2.5/1303381461696

3/1563739591100

3.5/1824007572103

4/2084207561106

dS

dt = birth(w/outvaccine) death vaccination infection

=

dI

dt = infection death infectiousdeath recovery

dR

= βlSI µI αI γI

dt = birth(wvaccine) + vaccination + recovery death

= µρN + νS + γI µR

6/31244511564119

6.5/33844313572123

Aswecanseeonceagain,theselevelsofvaccination provetobeextremelyeffectiveincurbingthenumberof deaths.Evenifonly 0 9% ofthepopulationgetsvaccinated eachweek,whichmeansaround 750 outof 1000 peopleover thecourseof 2 5 years,wecanseemassivebenefitsinterms ofreducingthenumberofdeathssustained.

dD

dt = infectiousdeath = αI

OurtransitionalMarkovMatrix:

Finally,ourresultsare:

6CombiningtheTwoSolutions

6 Combining the Two Solutions

Finally,wecancombinethetwosolutions,asinthediagrambelow: Ourdifferentialequations:

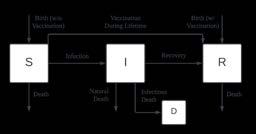
4/20855305728

6/31257706078

6.5/33858406158

Here,thecombinationofthetwosolutionsprovestobefar moreeffectivethanwecouldevenimagine!Thisisbecause theybothpreventthespreadofthediseaseindifferentways. Vaccinationincreasesthenumberofindividualsintherecoveredcompartment,whilelockdowndecreasesthelikelihoodasusceptibleindividualwilltransitionintotheinfected compartment.Thismodelprovestobequitevolatile,asthe rateofinfectionisdirectlydependentonthenumberofinfectionspresent.Thus,bycontainingthenumberofinfected individualswellfromthebeginning,weseemassivebenefits inthelong-run.

7Conclusion

Toconclude,wefirstsawthatwecanadapttheSIRmodel inavarietyofwaystomimiccertaineventsandphenomena, andwewereabletodevelopavarietyofmorecomplexmodelsinordertoanalyzepotentialsolutionstothespreadof aninfectionordisease.Furthermore,wecanseethatusing methodsoflockdownandvaccinationtocontainthespread ofdiseaseare,infact,extremelyeffective,especiallywhen usedintandem.

Ithinkperhapsthemostimportantpartofthisprojectis thewaythatitcanbetranslatedintoreal-worldapplications, duringpandemicsandepidemicssuchas,say,COVID-19. BecauseoftheadaptabilityoftheSIRmodel,wecanmodel theeffectofsolutionsrangingfarbeyondjustvaccination andlockdown.Thismeansthatthismodelcanbeanexcellentpredictorforworldcrisessuchasthesediseases,andit amazesmejusthowmuchlinearalgebraandmathcanbe appliedtomakeanimpact.

SourcesUsed

HerearetherangeofsourcesIusedinordertounderstand thistopic:

PurdueUniversity(DifferentialEquationsandLinearAlgebra)

MathematicalAssociationofAmerica(TheSIRModelfor SpreadofDisease)

AndrewBrouwer(UnderstandingtheBasicReproduction NumberthroughLinearAlgebra)

Wikipedia(FundamentalMatrix-LinearDifferentialEquations)

duringpandemicsandepidemicssuchas,say,COVID-19. BecauseoftheadaptabilityoftheSIRmodel,wecanmodel theeffectofsolutionsrangingfarbeyondjustvaccination andlockdown.Thismeansthatthismodelcanbeanexcellentpredictorforworldcrisessuchasthesediseases,andit amazesmejusthowmuchlinearalgebraandmathcanbe appliedtomakeanimpact.

May 2023

SourcesUsed

HerearetherangeofsourcesIusedinordertounderstand thistopic:

PurdueUniversity(DifferentialEquationsandLinearAlgebra)

MathematicalAssociationofAmerica(TheSIRModelfor SpreadofDisease)

AndrewBrouwer(UnderstandingtheBasicReproduction NumberthroughLinearAlgebra)

Wikipedia(FundamentalMatrix-LinearDifferentialEquations)

7

11 Finding an Alternate Model to Malthusian Population Growth Model

Written by Vyjayanti Vasudevan, Irene Choi, Morgan Ahn

FindinganAlternateModeltoMalthusianPopulationGrowthModel

VyjayantiVasudevanIreneChoiMorganAhn

vasudevan773999@sas.edu.sg,choi790186@sas.edu.sg,ahn787838@sas.edu.sg

TeacherReviewer: Mr.Son

Abstract

Abstract

TheMalthusianPopulationGrowthModelhasbeenusedfor decadestopredicttheoutcomeofanation’slivingstandards. However,manycriticizethismodel,statingthatitoverlooks themajortechnologicaladvancementtoday.Inthispaper,we willprovideanintroductiontotheMalthusianGrowthModel, itsprosandcons,aswellasanexaminationofalternatefactorsthatshouldbeconsideredwhenmakingpredictionsregardingpopulationgrowthmovingforward.

Keywords: MalthusianCheckpoints,populationgrowth model,lineargrowth,analysis,predictions

1Introduction

FirstobservedbyThomasRobertMalthusinthefirst editionofhis1798paper,theMalthusiangrowthmodelis onethathasbeentrustedtodemonstratepopulationstagnationforcenturies.Malthus’spublication‘AnEssayon thePrincipleofPopulation’suggestedthatfoodproduction growsarithmeticallywhilepopulationnumbersgrowexponentially,statingthat‘MalthusianCheckpoints’arenecessaryinordertomaintainequilibriumbetweenpopulation growthandfoodproduction.MalthusianCheckpoints,asdefinedbyMalthus’s1798publication,categorizemeansof populationregulationintotwo:one,positivechecks,defined aschecksthatpromotepopulationregulationthroughreducinglifeexpectancy,andtwo,preventativechecks,definedas checksthatlowerthefertilityratesofapopulation.

ThispaperaimstoexaminetheMalthusianGrowthModel andproposeanalternativewaytoillustratepopulationmanagement,accountingforotherfactorsinfluencingpopulation growthorstagnation.OnecommoncritiqueoftheMalthusianPopulationGrowthModelisthatitdoesnotaccount formodernsustainedeconomicgrowthinthepost-Industrial Revolutionera.

2GeometricandLinearGrowth

Thecombinedequation, F (0)+ r2 t = P (0)e(r1 t) (given theconditions P0 = P (0) and F0 = F (0) mustbesatisfied),isdesignedsothatitscyclicalpatternappropriately managespopulationsize.‘r1 ’representsthegrowthrateof thepopulationdensity;‘t’representsthedurationoftime; P (0) representstheinitialpopulationdensity(incounts); ‘ r2 ’representstheproportionofgrowthinfoodproduction;

F (0) representstheinitialamountoffoodproduction.We modelthisusinglogarithmicandlineargrowth,whichthe followingequationsdisplay: P (t)= P (0)e(r1 t) andF (t)= F (0)+ r2 t

Thesignificanceofthedisparitiesinpopulationgrowth versusthatofconsumergoodsisthateventhroughoutthe sametimeperiod,thepopulationwillbecomelargeenough suchthattheresourcesavailablecannotmaintainit.Malthus arguedthatthe“MalthusianCatastrophe”wouldoccurduringtheintersectionofavailableresourcesandthepopulation,statingthatthiswaswherefurtherpopulationgrowth wouldonlyresultintheoverexploitationoftheeconomy.

3KeyTerminology

3.1Neo-Malthusianism

Neo-Malthusianismisamovementthatembodiedthe panicoftheBritishpeoplefollowingtheBlackDeathin England.ManyusedMalthus’sinitialhypothesistoadvocateinfavoroftheirownpolicies.ThemainpurposeofNeoMalthusianismistopromotepopulationplanning;however, moremodernversionsofNeo-Malthusianismalsodiscuss theuseofmoderncontraceptives,strayingfromMalthus’s initialcommendationofabstinence.Suchideologiesthat povertywouldonlybeworsenedthroughcharitabilityand theincreaseinthereproductionofthelowerclasswerealso usedtoimplementlawsthatdecreasedimmigrationquotas.

3.2PreventativeChecks

Preventativechecksincludepopulationmanagementprior tothe“MalthusianCatastrophe,”whereresourcesavailable areunabletosatisfypopulationdemand.Malthuspromoted abstinenceuntilmarriageandlawsthatpunishedparents whohadchildrentheycouldnotprovidefor(ie.schooling, food,andshelter).

3.3PositiveChecks

PositivechecksoccurduringtheMalthusiancrisis,or whennationshavealreadyreachedexcessiveeconomic strain,rangingfromfaminestodroughtsanddeathlywars whichlimitthelifespanofcitizens.Malthus’sargument wasthatasnationsreachresourcescarcity,thequalityof theirhealthcareandotheressentialservicesdecline.Thisin-

natelylowersthelifeexpectancyofapopulation,resulting inpopulationdecline.

4MalthusianModelApplicationintheReal World

TheMalthusianpopulationgrowthmodelisbasedonthe ideathatpopulationgrowthwilloutstripfoodproduction, leadingtoapopulationcrash.Themodelarguesthatpopulationgrowthwillincreaseatageometricrate(i.e.2,4,8, 16,etc.)whilefoodproductionwillonlyincreaseatanarithmeticrate(i.e.2,4,6,8,etc.).Thiswilleventuallyleadtoa populationcrashduetostarvationanddisease.TheMalthusianmodelcanbeappliedtootherreal-worldcontexts,includingpopulationstudies,economicanalysis,andenvironmentalresearch.

OneofthemostcommonapplicationsoftheMalthusian modelisstudyingpopulationgrowthindevelopingcountries.Themodelcanbeusedtoanalyzethepotentialconsequencesofhighpopulationgrowthratesinthesecountries, suchasfoodinsecurity,poverty,andenvironmentaldegradation.Forexample,researchershaveusedtheMalthusian modeltostudypopulationgrowthinsub-SaharanAfrica, wherepopulationgrowthrateshavebeenamongthehighestintheworldandfoodproductionhasstruggledtokeep pace.

TheMalthusianmodelisalsorelevantineconomicanalysis,whichcanbeusedtounderstandtherelationshipbetweenpopulationgrowthandeconomicdevelopment.For example,someeconomistshaveusedthemodeltostudy howpopulationgrowthaffectseconomicgrowthandthedistributionofwealth.

Inaddition,theMalthusianmodelhasbeenappliedinenvironmentalresearch,particularlyinthestudyofresource depletion.Themodelcanbeusedtounderstandhowpopulationgrowthcanstrainwater,land,andenergyavailability, contributingtoenvironmentalproblemssuchasdeforestationandpollution.

What’smore,Malthusbasedhistheoryonobservationsof populationgrowthinhistime,particularlyinEurope,where populationgrowthhadbeenincreasingrapidly.TheMalthusianmodelwasmodeledoffofhistoricaleventsmarkedby overpopulation,foodscarcity,andahighdeathrate.The BlackDeath,whichravagedEuropeinthe14thcentury,and TheGreatFamineinIrelandduringthe19thcenturyareexamplesofsuchevents.

Insummary,theMalthusianPopulationGrowthModel highlightsthepotentialconsequencesofuncheckedpopulationgrowth,anditisstillarelevanttopicintoday’sworld. Ithasdiverseapplicationsinreal-worldcontexts,suchas populationstudies,economicanalysis,andenvironmental research.

5DrawbacksoftheMalthusianPopulation GrowthModelbasedonHistorical Evidence

TheMalthusianpopulationgrowthmodelhasbeenused toexplainpopulationgrowthanditspotentialconsequences

invariousreal-worldsituations.However,themodel’spredictionshavenotalwayscometopass,andtherehavebeen instanceswherethemodelhasnotbeenabletopredictpopulationgrowthaccurately.

OneexampleofasituationwheretheMalthusianmodel hasbeenusedtoexplainpopulationgrowthisinsubSaharanAfrica.Inmanycountriesinthisregion,population growthhasoutpacedfoodproduction,leadingtoconcerns aboutfoodsecurity.ThisisconsistentwiththeMalthusian model’spredictionthatpopulationgrowthwilloutstripfood production,leadingtoapopulationcrash.

AnotherexampleofasituationwheretheMalthusian modelhasbeenusedtoexplainpopulationgrowthisin thehistoryofEurope.Somehistorianshavearguedthatthe Malthusianmodelcanhelpexplainthepopulationcrashes duringtheBlackDeathinthe14thcentury,andtheGreat FamineinIrelandinthe19thcentury.Thesehistoricalevents fitwellwiththeMalthusianmodel’spredictionsofpopulationcrashesduetostarvationanddisease.However,there arealsoexamplesofsituationswheretheMalthusianmodel cannotpredictpopulationgrowthaccurately.Oneexample isindevelopedcountriessuchasJapanandEurope,where populationgrowthhasslowedorevendecreasedinrecent years.ThisisinconsistentwiththeMalthusianmodel’spredictionthatpopulationgrowthwillcontinuetoincrease. Anotherexampleistheglobalpopulationgrowthinrecent decades,wheretheavailabilityofbirthcontrolandother familyplanninghasplayedacrucialroleincurbingpopulationgrowth.Thishasledtosomecountriesexperiencingbelow-replacementfertilityrates,whichisalsoinconsistentwiththeMalthusianmodel’spredictionofpopulation growth.

TheMalthusianPopulationGrowthModelhasbeenused toexplainpopulationgrowthanditspotentialconsequences invariousreal-worldsituations.Still,itisnotaone-size-fitsallmodel,andthereareexampleswherethemodel’spredictionshaveyettocometopass.Themodel’sprediction thatpopulationgrowthwilloutstripfoodproduction,leadingtoapopulationcrash,hasbeenseeninsomedeveloping countriesandhistoricalevents.Also,itdoesnotconsiderthe availabilityofbirthcontrolandotherformsoffamilyplanning.Themodelalsodoesnotconsiderthetechnological advancementinfoodproduction,whichhasallowedfora higherfoodsupply.

6AlternateModels

AlthoughtheMalthusiantheoryofpopulationsuggests amethodtoanalyzetherelationshipbetweenpopulation growthandfoodsupplies,itstillhassomelimitationsin itsapplications.Oneofthemaincriticismsisthatthetheorydoesnotreflectthetechnologicaladvancementsofcurrentsociety.SincethetheoryrootsinearlyEurope,where thefoodsupplywasunstable,itassumesfoodavailabilitytobethemostimportantfactorinpopulationgrowth. Malthusfailedtopredictthetechnologicaldevelopmentthat decreasedfoodinsecurity,reducingthecorrelationbetween foodavailabilityandpopulationgrowth.Todealwiththe problemsthatarisefromtheMalthusiantheory,twomain theoriesofthepopulationweredeveloped.

Oneofthetwotheoriesiscalledtheoptimumtheoryof population.Theoptimumpopulationisthestateinwhich giventheresourcesavailable,producesmaximumreturnsof incomeperhead.

Asshownbythegraph,whenthepopulationreaches point M ,thepercapitaincomeismaximized.Thus,accordingtotheoptimumtheoryofpopulation,societywill favorpopulationincreaseordecreasebasedonthepercapita income;thus,whenthesocietyisunderpopulatedthesocietywillshifttoincreaseitspopulationandviceversa. Point M changeswiththechangeofanyofthefollowing factors:naturalresources,productiontechniques,stockof capital,habitsofthepeople,theratiooftheworkingpopulation,workinghoursoflabor,andmodesofbusinessorganizations.Tonumericallymeasurehowmuchthecurrent populationdeviatesfromtheoptimumpopulation,inother words,Maladjustment,Daltonsuggestedthefollowingformula: M = A O O ,when M standsformaladjustment, A fortheactualpopulation,and O fortheoptimumpopulation.When M ispositive,thecountrycanbeassumed tobeoverpopulatedandwhen M isnegative,thecountry isunderstoodasunderpopulated.However,duetothecurrentinabilitytopreciselymeasuretheoptimumpopulation, theequationisonlyusedforacademicpurposes.Theoptimumtheoryofpopulationhassomesuperioritiesoverthe Malthusiantheorem.Forexample,whileMalthussuggestsa directlyproportionalrelationshipbetweenfoodsupplyand populationgrowth,Canaan,oneofthefoundersoftheoptimumtheoryofpopulationgrowth,relatedtheproblemof thepopulationtoboththeindustrialandagriculturaloutputofthecountry.Moreover,sincetheoptimumtheoryof populationgrowthtakesimprovementsinknowledgeand otheradvancementsintoaccountwhiledecidingtheoptimumpopulationforthecountry,theoptimumtheoryofpopulationgrowthisknowntobemorepracticalandapplicable inreallife.Yet,therearestilllimitationstothetheory.Since theoptimumpopulation (O ) isyetimpossibletocalculate, themathematicalmodelofpopulationgrowthstillremains vague.Althoughitmaybeoneofthenewtheoriesforpopulationgrowthwithstrongtheoreticalevidence,itstillhas somelimitationstobeingpracticallyapplied.

Theothertheoryexplainingpopulationgrowthisthetheoryofdemographictransition.Thetheoryofdemographic transitionisbasedonobservedpopulationchangesincountries.Accordingtothetheory,althoughtheexactnumbers maydifferbasedonhowpeopledistinguishphases,there areabout5differentstagesofpopulationchange:highsta-

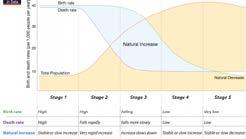
Figure2:(Source:Top3TheoriesofPopulation,Kwatiah)

tionarystage,earlyexpandingphase,lateexpandingphase, lowstationarystage,anddecliningphase.Duringthehigh stationarystage,alsoknownasthepre-transitionstage,both thebirthrateandthemortalityrateremainhigh.Asthe stagerepresentstheperiodbeforetheindustrialrevolution, parentswhoneededmorefamilymemberstosupportthe worktendedtohavemorechildren,whilethehighmortality rateduetopoorhealthserviceskeptthepopulationgrowth lowandstable.Next,duringtheearlyexpandingphase,also knownasthepopulationexplosionstage,thebirthratekeeps onincreasingwhilethedeathratedecreases.Duetoanincreasedsupplyoffoodandimprovementinsanitaryconditions,deathratesstartedtosignificantlyfallwhilebirthrates werestillkepthighduetoaneedformoreworkforcesin thefamily.ThisstageisoftenshowninLeastDeveloped Countries(LDCs).Duringthelateexpandingstage,both thebirthrateandthedeathratestarttodecrease.Aseconomicconditionsgotbetterandtheoveralleducationlevel startedtoincrease,peoplestartedtofavorlessonhavinga childandstartedspendingmoretimeonthemselves.However,thereisstillagapbetweenthedeathrateandthebirth rateduringthethirdstage.Mostofthedevelopingcountries areinthethirdphase.Thelowstationarystageiswhenthe birthratesanddeathratesofcountriesareapproximatelythe same.Duringthisstage,thepopulationsteadilyrises.Most ofthedevelopedcountriesareinthisstage.Duringthedecliningphase,mortalityratesstarttoexceedthebirthrates ofcountries.Duetopeople’swillingnesstohaveasmaller familywithfewerchildren,theelderlypopulationincreases whiletheyoungerpopulationdecreases.Theinformationis alsoshownbelow.

7AnalysisofDifferentModels

Asthispopulationgrowththeoryisbasedonreal-lifeevidence,itdoesnothaveaclearmathematicalformulatofollow.However,becauseitreflectshowsocietyhaschanged overtime,itisoneofthemostwell-acceptedtheoriesofpopulationgrowth.Insituationswheremathematicalcalculationsarerequiredandexactnumbersareasked,theMalthusiantheorymaybethebesttheorytofollow.However,to seetherealchangeinpopulationovertimeinregardtobirth anddeathrates,thedemographictransitionmightbethebest

Figure1:(Source:Top3TheoriesofPopulation,Kwatiah)

theorytorelyon.

8Conclusion:TheFutureofMalthusian

Theorem

theorytorelyon.

8Conclusion:TheFutureofMalthusian Theorem

Withourever-evolvingworld,wemayneverseeapop-

RobertMalthushimselfreferencedtheMalthusiancheck-

Withourever-evolvingworld,wemayneverseeapopulationgrowthmodelthatperfectlyreflectsreality;however,thefoundingprinciplesofallproposedtheorieslink twomainconceptstogether—supplyanddemand.Thomas RobertMalthushimselfreferencedtheMalthusiancheckpointasoccurringwhentheeconomicstrainontheeconomy,causedbyscarcity,willleadtostarvationandwar. Manybelievehismodelstillappliesinthecurrentday,usingJapanasanexampleofanationwithmoreresourcesthan peoplethatdemandit.However,wehavealsoseenitfailundermanycircumstances.WhetheritbeinChinawithmassiveunemploymentratesdespitehavingmoreresourcesthan necessarytomaintainitspopulation.Unevenlydistributed wealthandunpredictabilityinthedevelopmentofnations gocompletelyunaccountedforbytheMalthusiantheorem. Asaresult,multiplecriticismsofthemodelhavebeenmade inthecurrentday.Ratherthandiscardthemodelasawhole, scientistsandpoliticiansshouldcometogetherinthefuture inordertoenhancethecapabilitiesofnations’inpopulation management.

References

peoplethatdemandit.However,wehavealsoseenitfailundermanycircumstances.WhetheritbeinChinawithmassiveunemploymentratesdespitehavingmoreresourcesthan necessarytomaintainitspopulation.Unevenlydistributed wealthandunpredictabilityinthedevelopmentofnations gocompletelyunaccountedforbytheMalthusiantheorem. Asaresult,multiplecriticismsofthemodelhavebeenmade inthecurrentday.Ratherthandiscardthemodelasawhole, scientistsandpoliticiansshouldcometogetherinthefuture inordertoenhancethecapabilitiesofnations’inpopulation management.

References

HowPopulationsGrow:TheExponentialandLogistic Equations—LearnScienceatScitable.(2023).Retrieved 29January2023,from

HowPopulationsGrow:TheExponentialandLogistic Equations—LearnScienceatScitable.(2023).Retrieved 29January2023,from https://www.nature.com/scitable/knowledge/library/howpopulations-grow-the-exponential-and-logistic-13240157/ Sachs,J.(2008).AreMalthus’sPredicted1798Food ShortagesComingTrue?(Extendedversion).Retrieved29 January2023,from https://www.scientificamerican.com/article/are-malthuspredicted-1798-food-shortages/ ThomasMalthus.(2023).Retrieved29January2023,from https://ucmp.berkeley.edu/history/malthus.html

ThomasMalthus—Biography,Theory,Overpopulation, Poverty,Facts.(2022).Retrieved29January2023,from https://www.britannica.com/biography/Thomas-Malthus Top3TheoriesofPopulation(WithDiagram).(2016). Retrieved29January2023,from https://www.economicsdiscussion.net/theory-ofpopulation/top-3-theories-of-population-withdiagram/18461

https://www.nature.com/scitable/knowledge/library/howpopulations-grow-the-exponential-and-logistic-13240157/ Sachs,J.(2008).AreMalthus’sPredicted1798Food ShortagesComingTrue?(Extendedversion).Retrieved29 January2023,from

https://www.scientificamerican.com/article/are-malthuspredicted-1798-food-shortages/ ThomasMalthus.(2023).Retrieved29January2023,from https://ucmp.berkeley.edu/history/malthus.html

WhoIsThomasMalthus?.(2023).Retrieved29January 2023,from https://www.investopedia.com/terms/t/thomas-malthus.asp

ThomasMalthus—Biography,Theory,Overpopulation, Poverty,Facts.(2022).Retrieved29January2023,from https://www.britannica.com/biography/Thomas-Malthus Top3TheoriesofPopulation(WithDiagram).(2016). Retrieved29January2023,from https://www.economicsdiscussion.net/theory-ofpopulation/top-3-theories-of-population-withdiagram/18461

WhoIsThomasMalthus?.(2023).Retrieved29January 2023,from https://www.investopedia.com/terms/t/thomas-malthus.asp

12 Investigating Applications of Linear Algebra Concepts in Natural Language Processing

Written by Gyulim Jessica Kang

InvestigatingApplicationsofLinearAlgebraConceptsinNaturalLanguage Processing(ATLAProject)

GyulimKang

kang782455@sas.edu.sg

TeacherReviewer: Mr.Zitur

Abstract

Abstract

DuetotherapiddevelopmentoftheInternetthroughoutthe 21stcentury,researchersnowhaveanabundanceofinformationattheirfingertips.Thisoverflowofinformationhas producedmanypositiveconsequences—suchasprovidingresearcherswithmoredatatoanalyse,ensuringincreasedaccuracy—butalsopresentsseveralcriticalchallenges,especially inthefieldofnaturallanguageprocessing(NLP).Thisbranch ofartificialintelligencecentersaroundthestructureoflanguage,constructingrulestoestablishintelligentsystemswith theabilitytoextractmeaningfromspeechandtext.Acrucial NLPtechniquewidelyusedtodayislatentsemanticanalysis (LSA),whichdissectstherelationshipsbetweentermswithin asetofdocumentstoproducecommontopics.LSAestablishesthesetopicsfirstbyanalysingwordfrequenciesacross differentdocuments,thenbyperformingsingularvaluedecomposition(SVD).SVDisacrucialstepinLSAthatperformsdimensionalityreductionupontheoriginalmatrixthat depictsthefrequencyofeachwordineachdocumentwithin thecorpus.ThefoundationofSVDlieswithinconceptsin linearalgebra—thestudyofthepropertiesofvectorspaces andmatrices—suchasmatrixfactorization,eigenvalues,and eigenvectors.Linearalgebraformsthebasisofcountlessareasofcomputersciencesuchasmachinelearning,imageprocessing,naturallanguageprocessing,andmore.Thisstudy aimstoinvestigatetheapplicationsofspecificlinearalgebra conceptswithinLSAandtheirlimitations.Finally,thestudy seekstoextendtheseapplicationstogainmoreinsightinto theperformanceofLSAinbroader,real-lifecontextssuchas withininformationretrievalthroughsearchengines.

Keywords: NaturalLanguageProcessing(NLP),Latent SemanticAnalysis(LSA),SingularValueDecomposition (SVD),eigenvalues,eigenvectors

1Introduction

1.1BackgroundandPurposeofResearch

Thepurposeofthispaperistoexploretheimplementationsoflinearalgebraconceptswithinlatentsemanticanalysisindifferentsettingsandanalyzetheirlimitations.The growingprevalenceoftheInternethasproducedarichand accessiblesourceofdataforresearchinunprecedenteddegrees.Asaresult,researchersinthefieldofnaturallanguage processing(NLP)areoftenabletocompilealargecollection ofdocuments—sometimeshundredsofthousands—when investigatingtheirresearchquestions.However,itisoften

thecasethatresearchersarenotabletoindividuallyunderstandandanalyzeeachdocumentduetothemassivesample size.Thischallengehasledtothedevelopmentofkeymachinelearningtechniquessuchastopicmodelingthatare abletoextracttopicsfromasetofdocumentsandclassify documentsintoclustersbasedonthesetopics.

Figure1:Abasicvisualrepresentationoftopicmodeling processes

Theunderlyingprinciplesofmanytopicmodelingtechniquessuchaslatentsemanticanalysisarerootedinlinear algebra.Thispaperwillexaminethestep-by-stepprocess oflatentsemanticanalysis,analyzetheextentoftheuseof certainlinearalgebraconcepts,andfinally,assessthelimitationsoflatentsemanticanalysis.Thispaperassumesa familiaritywithbasiclinearalgebra.

2ExplanationofLatentSemanticAnalysis Process

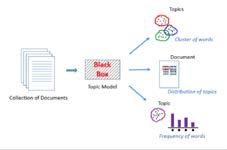
2.1BasicPrinciples

Latentsemanticanalysisislargelyfoundedupontwofundamentalprinciples.Thefirstisthatthemeaningofsentences,documents,andindividualwordsiscalculatedmathematically.The“meaning”ofawordisdefinedasitsaverage frequencyacrossallofthedocumentsitoccursin,andthe meaningofsentencesanddocumentsisdefinedthesumof the“meanings”ofallofthewordstheycontain.Thesecond

principlestatesthatwithinLSA,associationsbetweendifferentwordsandsentencesaredescribedimplicitly(Foltz, 1996).Thismeansthatlatentsemanticanalysiscannotidentifyspecifictopicsbutisabletoorganizedocumentsinto clusterscontainingthemostrelevancetoaspecifictopic.

Overall,theTF-IDFscoreplacesweightsonwordsbased ontheirrarity,ensuringthatmoresignificanceisplaced uponthewordsthatoccurfrequentlywithinadocument butinfrequentlyacrossthecorpus,ortheentiresetofdocuments.AhighTF-IDFscoreisachievedifthetermappears frequentlyinaspecificdocumentbutlessfrequentlyacross thewholecollectionofdocuments.

2.3SingularValueDecomposition

ThenextstepofLSAinvolvesreducingthedimensions oftheterm-documentfrequencymatrix.Thisisanimportantstepoftheprocessbecauselarge,complexdatasets oftencontainhigherdimensionsthataremoredifficultfor thecomputertoprocessandinterpret(“Singularvaluedecomposition”,2017).SVDisaprocessthatcanoptimizethe amountofinformationpreservedwithinthematrixwhile stillloweringthedimensiontoenablefasterandmoreaccurateanalysis.Thedecompositioncanbeexpressedinthe form A = UΣV T ,where U and V areorthogonalmatrices and Σ isadiagonalmatrix.

2.2InitialSteps

ThefirststepwhenperformingLSAistoconstructatermdocumentfrequencymatrix.Therowsarerepresentedby eachuniqueword,andthecolumnsarerepresentedbyeach documentwithinthecorpus.Theentryattheintersection ofrowiandcolumnjwillberepresentedbythetermfrequencyvalueofwordiwithindocumentj.Thisfrequency canbecalculatedinmultipleways,butthepreferredmethod istouseTermFrequency-InverseDocumentFrequency.

wi,j = tfi,j × log ( N dfi )

Theequationabovedescribesthemethodusedinlatent semanticanalysistocalculatetheTermFrequency-Inverse DocumentFrequency(TF-IDF)score,whichistheproducttwostatistics:termfrequencyandinversedocumentfrequency. tfi,j representstermfrequency(TF)and log ( N dfi ) representsinversedocumentfrequency(IDF). tfi,j denotes therawnumberofoccurrencesofword i indocument j , dfi denotesthenumberofdocumentscontainingword i, and N denotesthetotalnumberofdocumentswithinthe dataset.Sincethetermfrequencycountsonlythenumber ofoccurrencesofawordwithineachdocument,theinverse documentfrequencywasincorporatedtooffsettheincorrectemphasisthatmaybeplacedoncommonwordssuchas “a,”“an,”“the,”“she,”and“they”withoutgivingsufficient weighttomoremeaningfulwords.Thisisbecausehigher frequencydoesnotalwayswarranthighersignificance(Kaur &Kaur,2021).

Theinversedocumentfrequencyisobtainedbytakingthe logarithmoftheresultwhendividingthetotalnumberof documentsbythenumberofdocumentscontainingtheterm. Itisimportanttonotethatthisquotient (Ndfi ) willalways begreaterthanorequalto1;asaresult,theIDFandTF-IDF scorewillapproach0asthetermappearsinmoredocuments andthequotientapproaches1.

Figure3:ArepresentationoftheprocessofSVDleadingup todimensionalityreduction

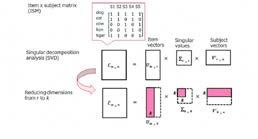
U and V representrotationsand Σ representsadilation ineachcoordinatedirection.RotationsanddilationsareexamplesoflineartransformationsandareutilizedinSVDto reconfigurethedimensionsoftheoriginalterm-document frequencymatrix.Bythedefinitionofanorthogonalmatrix, UT = U 1 (theinverseof U)and V T = V 1 .SVD isacrucialstepwithintheprocessoftopicmodellingbecauselarge,complexdatasetsoftencontainhigherdimensions,makingthemsparse;theyarealsonoisy,meaningthat theycontainmanylow-frequencywords.Thesecharacteristicsmakeitmoredifficultforthecomputertoprocessandinterpretthedocumentstoproduceacommonsetoftopicsand documentclusters.SVDoptimizesthepreservationofvaluableinformationwhilereducingdimensionsforfaster,more accurateanalysis(Kherwa&Bansal,2017).Weareableto findmatrix U byfindingthediagonalizationsof AT A:

Figure2:Adiagramdepictingthetransitionbetweenascatteredcollectionofdocumentstoorganizeddocumentclusters.

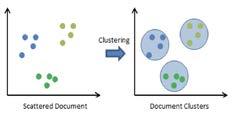
First,theeigenvaluesmustbederivedusingthefollowing equation: det(A λI)=0.Afterfindingthecorresponding eigenvectors,theymustbeorganizedindescendingorder. Thecolumnsof U willbetheeigenvectorsof A.Theeigenvectorsmustalsobenormalized,meaningthateachtermin thevectorshouldbedividedbythevector’smagnitudeto scaleittoaneigenvectorthathasaunitlengthof1.Next,we canfind Σ :thediagonalentriesareequivalenttothepositivesquarerootoftheeigenvaluesorganizedindescending order.

Finally, V canbefoundusingthefollowingequation:

0 65520174 0 75545396

0 755453960 65520174

Thediagonalentriesof Σ willbeequivalenttothesquare rootsofthetwopositiveeigenvalues(whichwere5(3+)and 5(3-))indescendingorder:

5.398345640 00 92620968

Finally,wefind V usingthefactthat V = A 1 UΣ, then normalize:

0 923880 382683

0 382683 0 92388

Nowthatwehaveallthreematrices—U, V ,and Σ—we willbeabletoconstructourSVDfactorization(UΣV T )of matrix A:

0 65520174

0 75545396

0 755453960 65520174

5 398345640 00 92620968

Thevectorsof V mustalsobenormalized.

Thefirststepwouldbetofindthediagonalizationsof AAT and AT A tofindmatrices U and V ,respectively.

0.923880.382683 0.382683 0.92388

3ApplicationofLSA 3.1Walkthrough

Toapplytheseconceptsinareal-life,adatasetonKaggle waschosenthatcontainedinformationaboutvariousnews articlesacrossarangeofmediaoutlets—includingtheNew YorkTimes,CNN,andmore—fromtheyears2016to2017. ThefeaturesofthedatasetincludedtheID,title,publication, author,date,year,month,URL,andfulltextofeacharticle.

Thecharacteristicpolynomialof AAT isthefollowing:

Usingthequadraticformula,wecandeducethatthe eigenvaluesof AAT are5(3+22)and5(3-22).Thecorrespondingeigenvectorsarethefollowing: 1+5√2 7 1 5√2 7

Arrangingtheeigenvaluesindescendingorder,wearrive atthefollowingmatrixfor U (thisisbeforenormalizing):

1+5√2 1 5√2 77

Afternormalizing,wegetthefollowingfinalmatrixfor U:

Figure4:Publicationsrepresentedwithindataset Fortheanalysis,themainfocuswasonthe“title”and “content”columns,asthesewerethecolumnsthatcontained informationmostrelevanttothetopicscoveredwithinthe article.Beforeconstructingthewordfrequencymatrix,the datasetwaspre-processedtoremoveextraneousinformation suchaspunctuation,numbers,orarticles(eg.‘a’)thatdonot contributemeaningtothearticle’scontentandriskhindering accuracyofanalysis.

1 stop_words= set(stopwords.words(’ english’))

2 newHeadlines=[]

3

4 for x in headlines:

5 x=x.lower()

6 x=x.replace(" " , "")

7 x=x.replace(" " , "")

8 for character in string.punctuation:

9 x=x.replace(character, ’’)

10 x=x.replace("the new york times", ’’)

11 x= ’’.join(c for c in x if not c. isdigit())

12 x=x.strip()

13 newHeadlines.append(x)

Afterward,thenextstepwastoconstructthetermfrequencymatrixandperformtheSVDfactorization,respectively.Thiswasachievedbyusingthebuilt-infunctionsof theScikitLearnlibrary,aPythonlibrarythatcontainsmany usefulmachinelearningtoolssuchasdimensionalityreduction,regression,andmore.

1 tfidfvectorizer=TfidfVectorizer( analyzer=’word’,stop_words= ’english’ )

2 tfidf_wm=tfidfvectorizer.fit_transform (df[’New Headlines’])

3 tfidfvectorizer1=TfidfVectorizer( analyzer=’word’,stop_words= ’english’ )

4 tfidf_wm1=tfidfvectorizer1. fit_transform(df[’New Content’])

5 svd=TruncatedSVD(n_components=100)

6 lsa=svd.fit_transform(tfidf_wm)

Afterconstructingtheterm-documentmatrices,wecan observethefeatures—theuniquewordsthatcomprisethe rowsofthematrices.Thefeaturescanbederivedusingthe codebelow.

Figure6:Constructingtheterm-documentfrequencymatrix containingtheTF-IDFscoresforeachtermwithintheTitle andContentcolumns

1 dictionary=tfidfvectorizer. get_feature_names()

2 print(dictionary)

3.2Results

Afterward,documentclusterswereidentifiedbyimplementingadditionalcode.Beforeobservingtheclusters,the silhouettescoresoftheclusterswerereviewedtoconfirm howeffectivelythedocumentclusterswerecreated.Viewing thesilhouettescoresenablesustoassesstheperformanceof theLSAmodelonthedatasetanddeterminewhetherspecificconditions(suchasthoseinpre-processing)mustbe adjustedtoobtainthedesireddegreeofaccuracy.

1 s_list=[]

2

3 for clus in tqdm(range(2,21)):

4

5 km=KMeans(n_clusters=clus,n_init =50,max_iter=1000) # Instantiate KMeans clustering

6

7 km.fit(lsa) # Run KMeans clustering

8

9 s=silhouette_score(lsa,km.labels_ ) 10

11

s_list.append(s)

12 plt.plot(range(2,21),s_list)

13 plt.show()

Thisplotshowsthatmostofthesilhouettescoresare onthehigherendofthescale,suggestingthatmostofthe

Figure5:DatasetrepresentationwithinJupyternotebook

Figure7:Silhouettescoreplot

clustersarelinearlyseparableorthereislittletomoderate amountofoverlapsamongthem.Toverifythisresult,aTdistributedStochasticNeighborEmbedding(TSNE)scatterplotwascreated.ATSNEscatterplotenablesustoview higher-dimensionaldatainalowdimensionalspace—in thiscase,two-dimensionalsincetheplotcontainstwo axes—whilepreservingtheoverallstructure.Thismeans thatsimilarpointsthatareclosetoeachotherinthehigherdimensionalspacewillalsobeclosetogetherintheTSNE scatterplot.

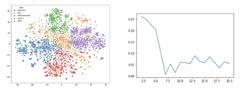
datasetandverifytheaccuracyofthevisualizationscreated above(Appendix).

4Extension

4.1Walkthrough

Inordertoextendthisapplicationandinvestigateacommonreal-lifeuseofLSA—informationretrievalthrough searchengines—asearchenginewascreatedbasedonthe samedataset.LSAisanidealtechniquetoutilizeforcreatingsearchenginesasitdoesnotrelyonkeywordsearches, meaningthatonlyresultscontainingtheliteralkeywordsinputtedintothesearchenginewillappear,butratheronsemanticsearches.Thisallowsthesearchenginetoreturnrelevantresultswithoutnecessarilycontainingtheexactwords inputted.

Usingtheterm-documentmatrixforthe‘content’columnthatwascreatedpreviouslyintheApplicationsection, awordcloudwasconstructedtoobservethewordsthatoccurredthemostoften.

Althoughmostoftheclustersarerepresentedwiththe colorpink,makingthedistinctionsbetweenclustersabit difficulttodiscern,itcanbeseenthatmostoftheclusters areorganizedinanorderlymannerofcircularshapesrather thanbeingspreadout.Figure9,whichdepictsLSAperformeduponaverysmallsetofdocuments(thereforedirect topicassignmentwaspossible),illustratesthisdifference;it canbeobservedthatwhilethedocumentspertainingtothe green,purple,blue,andredtopicsareclusteredinarelativelyorderlyway,thedocumentspertainingtotheorange topicareveryspreadout.Thisexplainsthereasonwhythe majorityofthesilhouettescoresforthisdatasetareonthe lowerendofthescale.

Tobegincreatingthesearchengine,afunctioncalled search resultswasconstructed.Thisfunctioninvolvedusing theterm-documentmatricescontainingeachterm’sTF-IDF scoreforeachdocumenttocompilealistofthearticlesthat containedwordswiththehighestsimilaritytothosewithin thesearchquery.

ThePythonlibraryprimarilyusedforthisextension wasGensim,whichcontainsnumerousfunctionsfordocumentindexing,topicmodeling,andsimilarityretrievalwith largecorpora.TheMatrixSimilarityfunctionseenbelow calculatesthesimilarityofeachfeature—termsanddocuments—withinthecorpusagainsttheotherandstoresthis informationinanindexmatrix;wewillusethismatrixlater tocomparethesimilaritiesofthewordswithinoursearch querytothesefeatures.

1 from gensim.similarities import MatrixSimilarity

3.3LimitationsofLSA

AkeylimitationofLSAisthatitdoesnotdeterminespecifictopicsfromasetofdocumentsasitisanunsupervised algorithm.Asaresult,itismainlyutilizedtoclustersimilar documentstogether.Additionaltopicmodelingtechniques thatarenewertothefieldofNLPsuchasBERTopicleveragesTF-IDFtocreateeasilyinterpretabletopicsandkeywordswithineachtopicdescription.TheBERTopictechniquewasutilizedtoconductamorein-depthanalysisofthe

2 articleIndex=MatrixSimilarity(lsa1, num_features=lsa1.num_terms)

Afterwritingthecodethatwouldanalysethetermswithin thesearchqueryandfetchthemostrelevantarticles(by identifyingthetermswithintheTF-IDFterm-documentmatrixthenusingtheresultstoinvestigatethesimilaritiesof thetermstoothertermsanddocumentsthroughtheindex matrix),thesearchengineprintedthelistofthefivemost relevantarticlesalongwiththepercentageofrelevanceusingthesimilarityvaluefromtheindexmatrix.

Figure8:TSNEscatterplot

Figure9:SampleTSNEplotwithlowsilhouettescore

Figure10:WordCloud

4.2Results

Thefollowingfiguredepictsasamplequeryanditssearch resultsfromthesearchengine.Althoughsomeofthearticles didnotexplicitlycontainthewordswithinthequeries,these articlesstillcameupasresultsbecausetheycontainedthe wordsmostsimilartothewordsinthequery.

References

Carlsson,Gunnar.”Topologyanddata.”Bulletinofthe AmericanMathematicalSociety46.2(2009):255-308. Garin,A.,&Tauzin,G.(2019,December).Atopological” reading”lesson:ClassificationofMNISTusingTDA.In 201918thIEEEInternationalConferenceOnMachine LearningAndApplications(ICMLA)(pp.1551-1556). IEEE.

Koplik,G.(2022,June16).Persistenthomology:A Non-MathyIntroductionwithExamples.Medium. RetrievedJuly5,2022,from https://towardsdatascience.com/persistent-homology-withexamples-1974d4b9c3d0

Uponafurtherinvestigationintotheseresultsbyreading thearticlecontent,itwasobservedthatallofthearticles weresufficientlyrelevanttotheinputtedsearchqueries.To furthertesttheperformanceofthesearchengine,however, itmaybebeneficialtoinputlonger,morecomplexphrases (eg.“impactofcontroversialartongalleriesnationwide”, “statisticsofhatecrimes”,etc.)toobservewhethertheresultsarerelevantnotonlytothespecificwordswithinthe querybuttheoverallmeaningofthequery.

5.1Summary

5Conclusion

Insummary,eigenvaluesandeigenvectorshavenumerous applicationswithinthefieldofNaturalLanguageProcessingthatformthebasisofLSA,aprominenttopicmodelling technique.SingularValueDecompositionisakeyprocess baseduponlinearalgebraconceptsthatisutilizedwithin LSAtoperformdimensionality.LSAhasseveralimportant advantagesanddisadvantages.Byanalysingareducedrepresentationoftheoriginalterm-documentfrequencymatrix (throughSVD)thatpreservesthecorrelationoftermsbetweendocuments,LSAisabletoensuretheaccuracyofits analysistosomeextent.However,somedisadvantagesare thatLSAisnotabletoexplicitlydescribetopicswithinthe corpusandthatitsaccuracycandiminishovertimeasthe sizeofthecorpusincreases.SomelimitationsofthisinvestigationarethatadditionalapplicationsoflinearalgebraconceptsintopicmodellingsuchasNon-negativeMatrixFactorization(NMF)werenotcoveredindetail.Theevaluation ofthesearchengineresultscouldalsohavebeenmorecomprehensivebyinvestigatingthesearchengine’sperformance basedonmorediverse(eg.inlength,complexity,andtopic) searchqueries.Thefieldoftextualanalysisisever-evolving, andtherearenumerouscomplexandinnovativemethodsregardingtheautomationofthisanalysisthatcanbeexplored.

Infuturestudies,IwouldliketodivefurtherintoNMFand experimentwithusingdifferentsearchqueriesonsearchenginescreatedusingLSAtoovercomethelimitationswithin theinvestigationofthecurrentstudy.

Otter,Nina,etal.”Aroadmapforthecomputationof persistenthomology.”EPJDataScience6(2017):1-38. Talebi,S.(2022,June17).PersistentHomology.Medium. RetrievedJuly6,2022,from https://medium.datadriveninvestor.com/persistenthomology-f22789d753c4

Tauzin,Guillaume,etal.”giotto-tda::ATopologicalData AnalysisToolkitforMachineLearningandData Exploration.”J.Mach.Learn.Res.22(2021):39-1. Zomorodian,Afra,andGunnarCarlsson.”Computing persistenthomology.”Discrete&ComputationalGeometry 33.2(2005):249-274.

6Appendix

FigureA1:Plotrepresentingsimilaritiesbetweentopics Itcanbeobservedthattheclustersoftopicsare well-organized,whichalignswiththehighsilhouettescores thatwearrivedatpreviouslyusingLSA.Thebarchart belowshowsthemostcommontopicsandtheirkeywords.

Figure11:Searchengineperformance

FigureA2:Commontopicsbarchart Forexample,wecaninferthatTopic0isrelatedto healthcare,Topic2isrelatedtopoliceand/orpolice violence,Topic3isrelatedtofirearmsandfirearm-related policies,andsoon.

13 Creating a Machine Learning Pipeline To Perform Topological Data Analysis

Written by Gyulim Jessica Kang

CreatingaMachineLearningPipelineToPerformTopologicalDataAnalysis

GyulimKang

kang782455@sas.edu.sg

TeacherReviewer: Mr.Son

Abstract

Abstract

Inappliedmathematics,topologicaldataanalysis(TDA)utilizesconceptsfromtopologytoextractqualitativefeatures fromdatasuchasitsshape.TDAhasavarietyofapproaches toextractstructurefromunstructureddata,orpointclouds, anditiswell-suitedforhigh-dimensionalandnoisydatasets. Pointcloudsareafinitesetofpointswithinthedata,and persistenthomologyisusedtorepresentthedataasasimplicialcomplex:acomplexofsimplexes,ortrianglesgeneralizedinmultidimensionalspaces.ThefirststepofTDA involvesrepeatedlyusingfiltrationonthepointcloudtoarriveatafilteredcomplex.Second,thekeytopologicalfeaturesofthefilteredcomplex—thenumberofconnectedcomponentsandholes—areanalyzedthroughpersistenthomology.Finally,thetimelineofthebirthanddeathoftopological featuresthroughouttheprocessoffiltrationisdisplayedina persistentdiagram.Thecomputationofpersistenthomology isafast-evolvingareawithnumerousintriguingchallenges; newalgorithmsandsoftwareimplementationsinthefieldare beingupdatedandreleasedrapidly.Premisedontheideathat theshapeofdatasetscontainsrelevantinformation,TDArepresentsapromisingbridgebetweentopologyanddatascience thatwarrantsfurtherexploration.

Keywords: TopologicalDataAnalysis(TDA),pointcloud, simplicialcomplex,Vietoris-Ripscomplex,persistenthomology,persistencediagram,filtration,vectorizationmethods

1Introduction

1.1BackgroundandPurposeofResearch

Thispaperexplorestopologicaldataanalysis,anon-therisedatasciencetool,anditsapplicationsinmachinelearning.ThegrowingprevalenceoftheInternethasproduced arichandaccessiblesourceofdataforresearchtounprecedenteddegrees.Theapplicationofpersistenthomologyindatascienceprovidesarobusttheoreticalfoundation foramathematicallyrigorousanalysisofshapewithindata (Carlsson,2009).Theshapeofthedatacanbeinterpreted inseveralformsdependingonthetypeofdata.Forexample,let’ssaywehavedataconsistingofafinitenumberof pointsscatteredinthecoordinatespace;younaturallystart thinkingabouthowthesepointsareroughlyshapedorclustered.Thisissimilartohowwelookupatthestarsinthe nightskyandseeconstellationsintheshapesofpolarbears

orscorpions.Thatisbecauseitisoneofourhumantendenciestoextractfamiliar,meaningfulshapesfromseemingly randomandscattereddata.Hereisanotherexample:ifyou havehandwrittenimagedata,youcanenvisioncharacteristicssuchashowmanyholesthereareinthenumbers.TDA aimstoencodethepersistenthomologyofadatasetinanaccessiblevisualrepresentationcalledthepersistentdiagram. Theprinciplesoftopologicaldataanalysisarerootedinpersistenthomologyandthepremisethattheshapeofadataset containsrelevantinformation.Thispaperwillexaminethe frameworkofTDA,provideexamplesofTDAresultson variousdatasets,andanalyzeitsapplicationsinmachine learningalongwithitslimitations.

2KeyDefinitions

2.1PointClouds

Let’ssayourdataisgivenasafinitesetofpointsinEuclideanspaceRd.Wecallthissetofpointsapointcloud. Forexample,asetcontainingeachreflectionofalaserpulse fromalidarformsa3-dimensionalpointcloudwith(x,y, z)coordinates.Asetofpointsmightappeartoberandomly scatteredonthesurface,buttheremightbesomehiddengeometric,ortopologicalpatterns.Ultimately,TDAuseshomologytoanswermeaningfulquestionssuchas‘Howcan weidentifygeometricfeaturesfromdata?’and‘Howdowe knowthatthesegeometricfeaturesaresignificant?’

2.2SimplicialComplex

Asimplexisthegeneralizationofatriangle,thefundamentalshapeofgeometry,inmultidimensionalspaces.For example,a0-simplexisapoint,a1-simplexaline,a2simplexatriangle,a3-simplexatetrahedron,andsoon(Koplik,2022).WithinTDA,wecanusepersistenthomology

Figure1:Geo-referencedpointcloudofRedRocks,Colorado

totranslatedataintoacollectionoftriangles:asimplicial complex.Theformaldefinitionofasimplicialcomplexisas follows,satisfyingthetwoconditionsbelow:Everyfaceof asimplexfromKisalsoinK.Thenon-emptyintersection ofanytwosimplices ϵ1 , ϵ2 inKisafaceofboth ϵ1 and ϵ2 WhenperformingTDA,weusethefollowingstepsto transformthedatasetintoasimplicialcomplex.First,we plotourdatainanN-dimensionalspace,withadimension foreachuniquevariable.Second,wechoosearadius ϵ and drawanN-dimensionalballofradius ϵ aroundeachdata pointinthepointcloud.Third,iftwoballsoverlapweconnectthecorrespondingpointswithaline,ora1-simplex. Ifthreeballsoverlap,wefillintheareabetweenthemto formatriangle,ora2-simplex.Thiscontinuesinthesame patternforsubsequentintersectionsandsimplices.Through thesimplicialcomplex,wecanderivethehomologygroup, composedofconnectedcomponents,holes,andcavities. H0 commonlyrepresentsthegroupofconnectedcomponents, H1 thegroupofholes,and H2 thegroupofcavities.A naturalquestionarises:Howarewesupposedtoknowthe bestradiusattheoutset?Thisiswherepersistenthomology comesin.

2.3Vietoris-RipsComplex

TheVietoris-RipsComplexisawayofformingatopologicalspacefromdistancesinasetofpoints(Garin&Tauzin, 2019).Inotherwords,wecreateasimplicialcomplexthat canbedefinedfromanydistance δ byformingasimplex foreveryfinitesetofpointsinthedatathathasadiameter atmost δ .Formally,weconstructaVietoris-Ripscomplex throughthefollowingprocess:

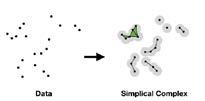
1.Drawacirclearoundeachpointwitharadiusof ϵ.

2.If ϵ isgreaterthanthedistancebetweenpointsiandjin thepointcloud,inotherwords,iftheintersectionoftwo circlesincludesboththeircenters,weconnectthetwo centerpointswithalinesegment.

3.Ifthreepointsformatriangle,wefillintheareatocreate a2-simplex.

Below,wewillcreateaplotofourowntoanalyzethrough TDA.First,weuseNumpyarraytogenerate8random pointsforourpointcloud.

Lookingatthischart,wecanthinkaboutwhatgeometricintuitionwecangainfromthecollectionofpoints.For example,itmayappearthatthefourdotsclusteredatthe topleftoftheplotaregoingtoformasquare.Inthisway,

humansstrivetoextractfamiliargeometricshapesfromrandomcollectionsbyconnectingpointsthatareclosetoeach other.Theapproximationoftopologicalspacefromthepoint cloudwiththissimpleideaiscalledtheVietoris-RipsComplex.

Thescreenshotsaboveshowcasethetransformationofthe simplicialcomplexastheepsilonvaluegetslarger:overlap increases,andmoreconnectedcomponents(H0 )andholes (H1 )arebirthedinthecomplex.Itcanbeobservedfromthe diagramsthattrianglesandedgesappear,merge,anddisappearwiththechangeofepsilon.Additionally,thetotalnumberofcomponentsdecreasesovertime;if ϵ issufficiently large,therewillonlybeoneunitedconnectedcomponent remaininginthesimplex.Insummary,thenumberofcomponentsandholescanbeimportantindicatorsofkeygeo-

Figure2:(Talebi,2022)

Figure3:EvolvingComplex

Figure4:Randomlygeneratedeightpointplot

Figure5:TransformationoftheVietorisRipsComplex

metricfeatures,andwecanobtainthembycomputingthe homologyofthecomplex.

Byvisualizingthecomplexes,weareabletogaingeometricintuition.However,itisdifficulttodeterminewhichepsilonvaluebestrepresentstheshapeofdatamerelythrough observation.Foreveryepsilon,wemustbeabletosummarizehowthenumberofcomponentsandholesarebeingchanged.Persistenthomology,analgebraicmethodfor computingtopologicalfeaturesinaspace,allowsustodo this(Otteretal.,2017).Itistheconceptofmeasuringwhich featuresarebornanddiefromthecomplexastheepsilon value,orradius,changes.Persistenthomologyistheprimary methodusedinTDAtostudyqualitativefeaturesofdata thatpersistacrossmultiplescales.Ithasmanyadvantages aswell;itisrobusttoperturbationsofinputdata,independentofdimensionsandcoordinates,andprovidesacompact representationofthequalitativefeaturesoftheinput.

3TDAFramework

3.1Filtration

TheinitialstepofTDAistorepeatedlyusefiltrationtoarriveatafilteredcomplex.Filtrationisdefinedastheprocess ofadjustingtheparameterofepsilon,ortheradius,toassess changesinthedataset.Filtrationhasnumerousapplications inreallife,includingheightfiltrationonimages.Performing heightfiltrationallowsustoconductimagesegmentation. Forexample,inthepictureofwoodcellsbelow,wecanuse heightfiltrationtoextracttheconnectedcomponents(inthis case,individualcells)fromtheimage.Althoughimperfect, thisalgorithmhasahighlevelofaccuracy;thisisimpressive consideringonlyafewparameters,suchastheblurparameter,needtobeadjusted.

3.2PersistenceDiagram

Apersistentdiagramrepresentsthebirthanddeathof connectedcomponentsandholesofaVietoris-Ripscomplexthroughoutthechangeofepsilon.Inordertoconstruct thediagram,persistenthomologytrackswhentwoballsof radiusepsilon,eachcenteredaroundapointonthepoint cloud,intersect.Apointisaddedtothediagramwhenthe ballinoneconnectedcomponentfirstintersectsaballof anotherconnectedcomponent,becausethemergingoftwo connectedcomponentssignifiesthedeathofoneofthem. Thefinalremainingsimplexdiesatinfinity.Apointlocated nearthediagonalmeansthatthisfeaturediedalmostimmediatelyafteritwasborn.Inotherwords,thismeansthat thefurtherthefeatureislocatedabovethediagonal,the greateritspersistence.Highpersistencefeaturesaregenerallythoughttobestatisticallysignificant,whilelowerpersistencefeaturesmorerepresentativeofstatisticalnoise.

ComparingTwoPersistentDiagrams(bottleneck/Wassersteindistance)Whencomparingthepersistentdiagramsof twopointclouds,weareabletoutilizemetricssuchasthe Wassersteindistance.TheWassersteindistanceisadistance functionbetweenprobabilitydistributionsonaparticular metricspaceM.Thismetriccomparestheprobabilitydistributionsoftwodifferentvariables,whereonevariableis derivedfromtheotherbyrandomordeterministicperturbations.

Now,wewilltryexperimentingwithusingTDAandpersistencediagramstodiscriminatebetweentwopointclouds extractedfromdistributionsthatlooksimilartothenaked eyebutare,inreality,completelydifferent.

Thefirstpointcloudconsistsof200pointsextractedfrom aGaussiannormaldistribution.Therefore,statistically,the geometricinformationofthispointcloudwillbesimilarto thegeometricinformationthatanormaldistributionsurface wouldhave.

Thesecondpointcloudconsistsof200pointsscatteredby

Figure6:OriginalWoodCellImage

Figure7:Blurredimagewith1dimensionofcolor

Figure8:ConnectedComponents

Figure9:FirstPointCloud

Figure10:SecondPointCloud

firstrandomlyselecting200anglesandapplyingconstant noisetotwoadjacentcircles.Althoughthesepointclouds werecreateddifferently,it’sdifficulttodistinguishbetween thetwopointcloudstodeterminewhichwascreatedthrough whichdistribution.Nowwewillseeifwecanobserveadistinctpatternwithintheirrespectivepersistentdiagrams.One differencethatcanbeobservedisthatinthesecondpersistentdiagram,unlikethefirst,thepersistenceoftheH1group isespeciallystrong.

Regardingtheapplicationofpersistentdiagramsinmachinelearning,however,persistentdiagramsaren’tsuitable foruseasinputvectorsbecausethenumberofpointsconstitutingthediagramwilldifferdependingontheimage.In otherwords,eachdatasetwillberepresentedasavectorofa differentdimension.Asaresult,itisnecessarytotransform thepersistentdiagramintoavectorofsomefixeddimension byusingvectorizationmethodssuchasHeatKernel.

4SampleApplicationinMachineLearning

VectorizationMethods(HeatKernel)Onevectorization methodoftenusedinTDAisHeatKernel.Givenapersistencediagrammadeupofthetriples[b,d,q]representing birth-death-dimension,subdiagramscorrespondingtovarioushomologydimensionsaretakenintoaccountindividuallyandseenassumsofDiracdeltas.Then,arectangular gridoflocationsuniformlysampledfromsuitableranges ofthefilteringparameterisusedtoperformtheconvolutionusingaGaussiankernel.Thereflectedpicturesofthe subdiagramsaroundthediagonalareprocessedinthesame way,andthedifferencebetweentheoutputsofthetwoconvolutionsiscomputed.A(multi-channel)rasterpicturecan becomparedtotheoutcome.MachineLearningPipeline MNIST:Binarization → Filtration → PersistentDiagram Thispipelineusesamixofvariousfiltering,distancemetrics(eg.Wasserstein,bottleneck),andvectorizationmethods includingHeatKernel.Thispipelinecanbeusedtoperform

efficientmachinelearningandTDAanalysisonthetraining data.What’snoteworthyisthatwhenweusethispipeline, we’renolongerusinganyinformationfromtheimagepixels themselves.Instead,we’reonlyusingthetopologicalfeaturesoftheimagedataseenfrommultipleperspectives.

5Conclusion

Inconclusion,persistenthomologyhasmanyapplications indatascience.Persistenthomologyistheprimarymethod usedinTDAtostudyqualitativefeaturesofdatathatpersistacrossmultiplescales.Ithasalotofadvantagestoo;it’s robusttoperturbationsofinputdata,independentofdimensionsandcoordinates,andprovidesacompactrepresentationofthequalitativefeaturesoftheinput.Forfuturework,I wouldliketodivedeeperintothemathematicalbackground ofpersistenthomologyalongwiththevariousapplications ofTDAinreallife.

References

Carlsson,Gunnar.”Topologyanddata.”Bulletinofthe AmericanMathematicalSociety46.2(2009):255-308. Garin,A.,Tauzin,G.(2019,December).Atopological” reading”lesson:ClassificationofMNISTusingTDA.In 201918thIEEEInternationalConferenceOnMachine LearningAndApplications(ICMLA)(pp.1551-1556). IEEE.

Koplik,G.(2022,June16).Persistenthomology:A Non-MathyIntroductionwithExamples.Medium. RetrievedJuly5,2022,from https://towardsdatascience.com/persistent-homology-withexamples-1974d4b9c3d0

Otter,Nina,etal.”Aroadmapforthecomputationof persistenthomology.”EPJDataScience6(2017):1-38. Talebi,S.(2022,June17).PersistentHomology.Medium. RetrievedJuly6,2022,from https://medium.datadriveninvestor.com/persistenthomology-f22789d753c4

Tauzin,Guillaume,etal.”giotto-tda::ATopologicalData AnalysisToolkitforMachineLearningandData Exploration.”J.Mach.Learn.Res.22(2021):39-1. Zomorodian,Afra,andGunnarCarlsson.”Computing persistenthomology.”DiscreteComputationalGeometry 33.2(2005):249-274.

Figure11:Persistentdiagramoffirstpointcloud

Figure12:Persistentdiagramofsecondpointcloud

Evaluating Affirmative Action in School Choice: Comparing Mechanisms with Minority Reserves

Written by Gyulim Jessica Kang

EvaluatingAffirmativeActioninSchoolChoice:ComparingMechanismswith MinorityReserves

GyulimKang

kang782455@sas.edu.sg

TeacherReviewer: Mr.Son

Abstract

Intheeconomictheoryoftwo-sidedmany-to-onematching,a particularproblemofinterestisthemechanismofschoolassignment.Eversincethedeferredacceptancealgorithmwas firstproposedbyGaleandShapley(1962),therehasbeen muchresearchaboutmechanismsthatoptimallymatchstudentstoschoolsinreal-worldsituations.PathakandSönmez(2013)triedtoincorporatetruncatedpreferencesintothe existingmatchingframework,whereasHafalir,Yenmezand Yildirim(2013)consideredreservesforminoritystudents.In thispaper,weexploretherelativelyundevelopedareaoftruncatedpreferencesinschoolmatchingwithminorityreserves. Specifically,wepresentanovelframeworkformechanism analysiswithminorityreservesandcomparemechanismsby theirstability,Paretooptimality,andvulnerabilitytomanipulation.OurresultsshowthattheoldChicagomechanismis atleastasmanipulableasanyotherstablemechanismandis strictlymoremanipulablethantheserial-dictatorshipmechanism.

Keywords: Gale-Shapleyalgorithm,marketdesign,mechanismdesign,schoolchoice,truncatedpreferences

1Introduction

Givenasetofmenandwomenwhosepreferencesarein theoppositegender,howshouldweformpairssuchthatno agenthastheincentivetorematch?ThisquestionwasoriginallyproposedandansweredbyGaleandShapleyin1962; sincethen,thesolutionstothevariantsofthequestionhave beenappliedtoschoolchoice,medicalresidencymatching, andtheassignmentofcadetstomilitarybranches.Galeand Shapleytriedtofindaone-to-onestablematching(asetof pairingsinwhich(1)allmenandwomenfindtheirpartners acceptableand(2)noman/womanpairpreferseachotherto theirassignedpartners).Byaprocesscalledthedeferredacceptancealgorithm,GaleandShapleyprovedthatastable matchingexistsforanyfinitesetofmenandwomenandtheir preferences.Thealgorithmisdescribedasfollows:

1)Eachmanproposestohismostpreferredwoman.Each womanselectshermostpreferredmanoutofthosewho proposedtoherandputshimonherwaitinglist;therest arerejected.

2)Eachmanthatwasrejectedproposestohisnextpreferredwoman.Eachwomanselectshermostpreferred

manamongthosethatproposedtoher,includingtheman onthewaitinglist.

3)RepeatStep2untilnomenwhoareavailabletopropose areleft.

GaleandShapleyprovedthatthematchingobtainedatthe terminationofthealgorithmisstable.Forexample,consider thefollowingsituationwith5menand4women:

����5 wouldratherstaysinglethanbematchedwith

.Assumethatthepreferencesofthewomenareasfollows:

Ifweapplythedeferredacceptancealgorithmtothisspecificexample,

,whoonlyholds

proposeto ����4 ,whoonlyholds ����2 .Thisyieldsa tentativematching

Inaddition,eachmanweaklyprefershismatchunderthe deferredacceptancealgorithmcomparedtoanyotherwoman thathecouldhavebeenmatchedtoinanotherstablematching.AdditionalpropertiesofthedeferredacceptancealgorithmincludeParetooptimality,whichdescribestheexistenceofamatchingwherethereisnoothermatchingthat makessomeagentsbetteroffwithoutmakinganyoneworse off,andmanipulability,whichisequivalenttoanagent’sabilitytoprofitfromamechanismbymisrepresentinghispreferences.

1.1IntroductiontoSchoolChoiceContext

Aninterestingapplicationofthedeferredacceptancealgorithmisthatmanyofitsconsequencescanbeextendedto many-to-onematchings;examplesincludesituationswhere anagentononesideismatchedtomorethanoneagenton theotherside,suchastheinternshipassignmentproblemor collegeadmissionproblem.

Applicationsofmatchingsinschoolchoicehavebeen madetomimicreal-lifescenarios.Ehlers,Hafalir,Yenmez, andYildirimstudiedcontrolledchoiceoverpublicschools; Benabbou,Chakraborty,Ho,Sliwinski,andZickinvestigatedtheimpactofdiversityconstraintsonpublichousing allocation.PathakandSönmezcomparedvariousmechanismsbytheirsusceptibilitytomanipulation.

Thispaperisstructuredasfollows.InSection2,wewill comparemultiplematchingalgorithmsthatareknownto recordtruncatedpreferencesunderdiversitysituations.More specifically,wewillbediscussingfactorsincludingstableness,manipulability,andParetooptimalityforeachmechanism.

2GeneralFramework

Wefirststartwithsometraditionaldefinitionsoftenused inthemarketdesigntheoryofschoolchoice.

1.afinitesetofstudents ���� = ����1 ,...,�������� ;

2.afinitesetofschools ���� = ����1 ,...,�������� ;

3.acapacityvectorq=(��������1 ,...,������������ ),where �������� isthecapacity ofschool ���� ∈ ���� orthenumberofseatsin ���� ∈ ���� ;

4.astudents’preferenceprofile �������� =(��������1 ,...,������������ ),where �������� isthestrictpreferencerelationofstudent ���� ∈ ���� over ���� .Inotherwords, ���� �������� ���� ′ meansthatstudent ���� strictly prefersschool ���� toschool ���� ′ ;

5.aschools’priorityprofile ≻���� =(≻����1 ,...,≻�������� ),where ≻���� is thestrictpriorityrankingofschool ���� ∈ ���� over ����; ���� ≻���� ����′ meansthatstudent ���� hashigherprioritythanstudent ����′ to beenrolledatschool ���� ;

6.atypespace ���� = ����1 ,...,�������� ;

7.atypefunction ���� : ���� ←→ ���� ,where ���� (����) isthetypeofstudent ����;

8.foreachschool ���� ,thetypespecificconstraintvector ���� ���� ���� = (���� ����0 ���� ,...,���� �������� ���� ) suchthat ���� ���� ���� ⩽ �������� forall ���� ∈ ����

3SchoolChoiceApplications

Toincorporatediversityquotasintoschoolchoicemechanisms,westartwithsomedefinitions.

1.Foreachschool �������� , ����0 (�������� ) oftheseatsaredeterminedby thestudents’compositescores,while �������� (�������� ) oftheseats aresetasideforstudentsineachofthe ���� types,withcompositescoredeterminingrelativepriorityamongstudents intype ����.Therefore, Σ���� �������� (�������� )= ���� (�������� ).

2.Thematchingalgorithmtreatseachselectiveenrollment highschoolas ���� +1 hypotheticalschools:Theset �������� of seatsateachschoolbispartitionedintosubsets �������� = ����0���� ∪ ����1���� ∪ ∪ ������������ .Theseatsin ����0���� are“openseats,” forwhichstudents’prioritiesaredeterminedentirelyby compositescores.Seatsin ������������ are“reserved”forstudents oftypei—theygivetypeistudentspriorityoverother students,andusecompositescorestorankstudentswithin typei.

3. Thematchingalgorithmmustconvertstudents’true preferences �������� intostrictpreferencesoverthefullset ofhypotheticalschools.

Thelastdefinitionisofparticularinterest,sinceweare givenfullautonomyoverhowwewillsetthepreferenceof hypotheticalschoolsoveroneanother.Toelaborate,takestudent ���� oftype ����.Willheprefertobeplacedintheset ����0���� or ������������ forschool ����?Obviously,heisineligibleforaplacein ������������ where ���� ≠ ���� and ���� ≠ 0,sothatpreferenceistrivial—just place ������������ suchthata �������� ������������ .Thepreferencebetween ����0���� and ������������ ismuchlessobvious;tosolvethisdilemma,weapplythe Gale-Shapleyalgorithmforeachcase.

Assumewehavestudents ����1 ,����2 ,����3 ,����4 andschool ���� with preference ����1 ≻����2 ≻����3 ≻����4 .Students ����1 and ����4 are intype1andstudents ����2 and ����3 areintype2. ���� hasa quotaof3andmusttakeinatleastonestudentfromeach type.Inotherwords, |����0���� | = |����1���� | = |����2���� | =1.Ifwe assume ����0���� �������� ������������ foreachstudent ���� oftype ����,theGaleShapleyalgorithmyields, (����0 ����1 ����2

����1 ����2 ����4 ) whichisunstablewithablockingpairof (����3 ,���� ).Ontheotherhand,if ������������ �������� ����0���� ,theGale-Shapleyalgorithmyieldsastablematching of (����0 ����1 ����2

����3 ����1 ����2 )

Accordingtothisobservation,itonlyseemsrightthatwe adapttheassumptionof ������������ �������� ����0���� .Underthisdefinition,we getthefollowingresult: Theorem 3.1. ThematchingobtainedfromtheGale-Shapley algorithmwithminorityreservesisstable.

3. ����2 proposesto ����2 ,whorejects ����5 andholds ����2 .The tentativematchingisthusrevisedto

4. ����5 proposesto ����4 ,whorejects ����5 andholds ����4 ,which stopstheprocedureandresultsin

Proof)Assumethereexistsaschool ���� andastudent ���� intype ���� suchthat ������������ ���� (����).Atsomepointaappliedto �������� andS0 andwasrejected.Everystudentin ����0 isrankedhigherthan student ����.Additionally,everystudentin �������� isrankedhigher thananystudentoftype ���� in ����0 .Therefore, (������ ���� ) cannotform ablockingpairandthematchingisstable. ■

WenowwonderwhetherthequalitiesoftheoriginalGaleShapleyalgorithmwilltransfertothisframework.

Theorem 3.2. ThematchingobtainedfromtheGale-Shapley algorithmwithminorityreservesisPareto-efficientforstudents(student-optimal)outofallstablematchings.

Proof)BecausetheGale-Shapleyalgorithmisstudentefficient,thismatchingisoptimalforstudentsoutofallstablematchings.However,wemustalsoobservewhetherthe matchingisParetoefficientforallmatchings.Considerthe followingexample:

intheGale-Shapleyalgorithm.Sinceall ���� ∈ ���� ′ haverejectedacceptablestudentsfrom ����′ , ���� hadsomestudent ���� onthewaitlistwhenitreceiveditslastapplication.Then, (������ ���� ) isthedesiredblockingpairbecause ���� isnotin ����′ becauseifso,afterhavingbeenrejectedby ���� ,hewouldhave appliedagaintoanothermemberof ���� ′ ,contradictingthe factthat ���� receivedthelastapplication.Butaprefers ���� to hisschoolunder �������������������� andsinceheisnobetteroffunder ���� ,heprefers ���� to ���� (����).Ontheotherhand, ���� wasthelast studenttoberejectedby ���� so ���� musthaverejectedanother studentunder ���� beforeitrejected ����.Hence ���� prefers ���� to thelaststudentin ���� (���� ).

FromClaim1,wegetacontradiction. ■

NowthatwehavediscussedthefeaturesoftheGaleShapleyalgorithm,wecomparetheperformanceoftheGaleShapleyandChicagomechanisms.Forthis,weneedtoexaminethebehavioroftheChicagomechanismunderthe sameminority-reservesconditionsastheGale-Shapleyalgorithm.

Theorem 3.4. ThematchingobtainedfromtheChicagoalgorithmwithminorityreservesisnotstable.

Proof)ItissufficienttoprovethattheChicagoalgorithm withoutminorityreservesisnotstable.Considerasetofstudents

suchthat

IfweapplytheGale-Shapleyalgorithmwherethestudentappliestotheschool,wegetastablematching

.However,theParetooptimalmatchingforstudentsis

,sotheGale-Shapleyalgorithmisnot Pareto-efficientoutofallmechanisms. ■

TheGale-Shapleyalgorithmisstudent-optimaloutofall stablemechanismsbutmaynotbeParetoefficientforthestudents.Anothercharacteristicwemustobserveisthestrategyproofness(non-manipulability)oftheGale-Shapleymechanism.

Theorem 3.3. ThematchingobtainedfromtheGale-Shapley algorithmwithminorityreservesisstrategy-proof. Proof)Assumeotherwise.Then,therewillbeastudentschoolmatchingthatastudentcouldmisreporthispreferences.

Claim1:Themechanismthatyieldsthestudent-optimal stablematching(intermsofstatedpreferences)makesita dominantstrategyforeachstudenttostatehistruepreferences.

Proof.Considerforcontradictionthatsomenonempty subset ����′ ofstudentsmisreporttheirpreferencesandare strictlybetteroffundersomematching ���� ,whichisstable for ����′ .Thiswouldimplythat ���� (����) ≻���� �������������������� (����) forevery ���� ∈ ����′

1. ���� (����′ ) ≠ �������������������� (����′ ).Choose ���� ∈ ���� (����′ )∖�������������������� (����′ ),for example ���� = ���� (����′ ).Then, ����′ prefers ���� to �������������������� (����′ ),so���� prefers �������������������� (���� )= ���� to ����′ .But ���� isnotin ����′ since ���� is notin ���� (����′ ),so ���� prefers ���� to ���� (����).Thus (������ ���� ) blocks ���� .

2. ���� (����′ )= �������������������� (����′ )= ���� ′ .Let ���� bethelastschoolin ���� ′ toreceiveanapplicationfromanacceptablestudentof ����′

ThentheresultingmatchingfromtheChicagoalgorithm withoutminorityreservesis ( ����1 ����2

1 ����2 ) ,whichisnotstable since(����2 �� ����3 ) isablockingpair. ■

Theorem 3.5. ThematchingobtainedfromtheChicagoalgorithmwithminorityreservesisnotPareto-efficientoutof allstablematchings.

Proof)Assumethatthereisamatching ���� suchthatall studentsarebetteroff.Thenthereisastudent ����1 suchthat ���� (����1 )����( ����1 )�������� (����1 ).Letusdefine ����1 = �������� (����1 ) and ����2 = ���� (����1 ).Since ���� strictlydominates �������� ,weknowthat ���� (����2 ) ≻( ����2 )�������� (����2 ),meaningthatthereexistsastudent ����2 suchthat ranked ����2 prefers ����2 ,andeither ����2 ranked ����2 higherthan ����1 ranked ����2 or ����1 and ����2 ranked ���� 2inthesameranking,but ����2 prefers ����2 .Denote ����(�������� �� �������� ) astheranking �������� gaveto �������� , andinductivelydefine ����( ���� +1)= ���� (�������� ) and ����( ���� +1)= �������� (���� (�������� )).Then

����(����( ���� +1)�� ����( ���� +1))= ����(�������� (���� (�������� ))�� ���� (�������� )))

⩽ ����(�������� �� ���� (�������� )) <����(�������� �� �������� ) ,andbythemethodofinfinitedecent,wefindthatthereisa contradiction. ■

Theorem 3.6. ThematchingobtainedfromtheChicagoalgorithmwithminorityreservesisnotstrategy-proof.

Proof)Wecontinuewiththeexampleofstudentsand schoolsgivenin3.4:

rankorderlist,shecanmanipulate ������������ ���� byrankingstudent ����’sassignmentashertopchoiceagaincontradicting ������������ ���� isnotmanipulableforproblem ���� .

2.Letstudent ���� bethehighestscoringstudentinwhoranked lowerthanthenext Σ���� ���� 0 ���� students.Sincestudent ���� hasa completerankorderlist,shecanmanipulate ������������ ���� by rankingstudent ����’sassignmentashertopchoiceagain contradicting ������������ ���� isnotmanipulableforproblem ���� .

Claim3.InproblemP,thematchingobtainedthrough ������������ ���� (���� ) istheuniqueweaklystablematching.

TheChicagomechanismisneitherstablenorstrategyproofwhenevaluatedinthecontextofminorityreserves withinaschoolchoicesystem.However,itisPareto-optimal. WhenboththeChicagoandGale-Shapleymechanismsare subjectedtotruncatedpreferences,theyarefoundtobeneitherstablenorPareto-optimal,andbotharemanipulable. Therefore,thequestionarisesastowhichmechanismismore manipulablethantheother.Whileitispossiblethatneither mechanismismoremanipulable,ifitcanbedemonstrated thattheGale-Shapleyalgorithmproducesamorefavorable matchingthantheChicagoalgorithmundertruncatedpreferences,itcanbeconcludedthattheGale-Shapleyalgorithmis objectivelysuperiortotheChicagoalgorithminthiscontext.

Theorem 3.7. Supposeeachstudenthasacompleterankorderingand ������ 1.TheoldChicagoPublicSchoolsmechanismwithminorityreserves ������������ ���� ������������ isatleastasmanipulableasanyweaklystablemechanism.

Proof)First,fixaproblem ���� andlet Φ beanarbitrary mechanismthatisweaklystable.Supposethat ������������ ���� isnot manipulableforproblem ����

Claim1:Anystudentassignedunder ������������ ���� ������������ (���� ) receives hertopchoiceschool.

Proof.Theremustbeastudentthatisassignedtoaschool shehasnotrankedfirst.Ifnot,sinceeachstudenthasacompleterankorderlist, |�������� | �� �������� foralltypes ���� and ������ 1, theremustbeastudent ���� thatisassignedtoaschoolshehas notrankedfirst.Considerthehighestcompositescorestudent ���� whoisunassignedandisinthesametypeasstudent ���� Student ���� canrankschool ���� firstandwillbeassignedaseat thereinthefirstroundof ������������ ���� mechanisminsteadofsome studentwhohasnotrankedschool ���� first.Thatcontradicts ������������ ���� isnotmanipulableforproblem ����

Claim2:Thesetofstudentswhoareassignedaseatunder ������������ ���� (���� ) isequaltothesetoftop ���� ���� ���� ���� compositescore studentsintypetandthenext ���� ���� 0 ���� studentswhoarenot assignedaseat.

Proof.Ifnot,thereisaschoolseatassignedtoastudenty whodoesnothaveatop ���� ���� ���� ���� scoreintype ���� ortoastudent ���� whorankedlowerthanthenext ���� ���� 0 ���� students.

1.Letstudent ���� bethehighestscoringtop ���� ���� ���� ���� studentin type ���� whoisnotassigned.Sincestudent ���� hasacomplete

Proof.Letusdefinetheterm“topstudents”asthetop Σ���� ���� ���� ���� compositescorestudentsintype ���� andthenext Σ���� ���� 0 ���� studentswhoarenotassignedaseat.ByClaims1and2, itispossibletoassignthetopstudentsaseatattheirtop choiceschoolunder ���� and ������������ ���� (���� ) picksthatmatching. Let ���� ≠ ������������ ���� (���� ).Thatmeansunder ���� thereexistsatop student ���� whoisnotassignedtohertopchoice ����.Pickthe highestcompositescoresuchstudent ����.

Sinceallhigherscorestudentsareassignedtotheirtop choices,eitherthereisavacantseatathertopchoice ���� orit admittedastudentwithlowercompositescore.Itistrivial thatthepair (����,����) stronglyblocksmatching ���� intheformer case,andinthelatter,thereisalwaysastudentrankedlower than ���� whoisnotinthequotaofhistype.Hence ������������ ���� (���� ) istheuniqueweaklystablematchingunder ���� .Wearenow readytocompletetheproof.ByClaim3, Φ(���� )= ������������ ���� (���� ) andhencemechanism Φ assignsalltopstudentsaseatat theirtopchoices.Noneofthetopstudentshasanincentiveto manipulate Φ sinceeachreceiveshertopchoice.Moreover, nootherstudentcanmanipulate Φ becauseregardlessoftheir statedpreferences, Φ(���� )= ������������ ���� (���� ) remainstheunique weaklystablematchingandhence ���� picksthesamematching forthemanipulatedeconomy.Hence,anyotherweaklystable mechanismisalsonotmanipulableunderP. ■ Proposition3.8 Supposethereareatleast ���� schoolsandlet ������ 1.ThetruncatedoldChicagomechanismforminorities (������������ ���� ������������ )ismoremanipulablethanthetruncatedGaleShapleymechanism (�������� ���� ������������ ) forminorities.

Proof)Ifwelookataproblemwiththreeschoolsandthree studentswhosepreferencesaretruncatedasthefollowing:

TheGale-Shapleymechanismyieldsthefollowingmatching:

,whichisstrategy-proof.However,theChicagomechanism resultsin

,whichismanipulablesince ����3 canfalselyreporthispreferencesas ���� (����3 )= ����3 ,����2 andbebetteroffbybeing matchedwith ����3 .Therefore, ������������ ���� ������������ ismoremanipulable than �������� ���� ������������ ■

Hence,wecanconcludethatinaminority-reservecontext, whenpreferencesaretruncated,theChicagomechanismis moremanipulablethantheGale-Shapleymechanism. Conjecture3.9. Wecanfindcounterexamplesintheproof aboveregardlessofthenumberofschoolsandstudents,numberoftypes,andquotaforeachschool.

Explanation)Todothis,wefirstdefine ����(����,���� ) asthequotaof type ���� forschool ���� (���� startsat 1, ���� startsat 0).Forexample, ����1,5 isthequotaoftype5studentsforschool1.Also,define Σ���� ��������,���� by �������� (> |�������� | for ���� ⩽ 1),whichisthenumberofstudentsin school ����.Wearecuriouswhetherwecanalwaysfindaset ofpreferencesforany ���� and ��������,���� .Thisproblemisyettobe solved.

4Conclusion

Thefocusofourresearchwastocomparetheperformance oftwodifferentmechanisms,theGale-Shapleyalgorithm andtheChicagomechanism,inaschoolchoicecontext.We evaluatedwhetherthesemechanismspossessedthepropertiesofstability,Pareto-efficiency,andmanipulability,and comparedtheirperformancewhenpreferencesaretruncated.

Ourfindingsindicatedthatwhenpreferencesaretruncated,theChicagomechanismismoremanipulablethanthe Gale-Shapleyalgorithm.Thishasimportantimplicationsfor understandingthestrengthsandweaknessesofeachmechanisminpracticalapplications.

Furthermore,thisstudycontributestotheexistingbody ofresearchbyfillingagapintheliterature.Weconstructed aframeworkthatenablesresearcherstoassesstheperformanceofmatchingmechanismsinminorityreserves.Overall,thisresearchprovidesvaluableinsightsintotherealworldapplicationsofmatchingmechanismsandunderscores theneedforcarefulconsiderationofspecificcharacteristics whenselectinganappropriatemechanism.

References

Abdulkadiroğlu,A.,Sönmez,T.(2003).Schoolchoice:A mechanismdesignapproach.Americaneconomicreview, 93(3),729-747.

Benabbou,N.,Chakraborty,M.,Ho,X.V.,Sliwinski,J., Zick,Y.(2018,July).Diversityconstraintsinpublic housingallocation.In17thInternationalConferenceon AutonomousAgentsandMultiAgentSystems(AAMAS 2018).

Ehlers,L.,Hafalir,I.E.,Yenmez,M.B.,Yildirim,M.A. (2014).Schoolchoicewithcontrolledchoiceconstraints: Hardboundsversussoftbounds.JournalofEconomic theory,153,648-683.

Gale,D.,Shapley,L.S.(1962).Collegeadmissionsandthe stabilityofmarriage.TheAmericanMathematical Monthly,69(1),9-15.

Pathak,P.A.,Sönmez,T.(2013).Schooladmissions reforminChicagoandEngland:Comparingmechanisms

bytheirvulnerabilitytomanipulation.AmericanEconomic Review,103(1),80-106.

Roth,A.E.,Sotomayor,M.(1992).Two-sidedmatching. Handbookofgametheorywitheconomicapplications,1, 485-541.

Sönmez,T.,Switzer,T.B.(2013).Matchingwith (branch-of-choice)contractsattheUnitedStatesMilitary Academy.Econometrica,81(2),451-488.

CONTRIBUTORS

First, we would like to express our deepest gratitude to the following contributors for helping create Singapore American School’s very first pure and applied mathematics journal:

TEACHER REVIEWERS

Mr. Saylar Craig, Mathematics Department

Mr. Jason Son, Mathematics Department

Ms. Darlene Poluan, Mathematics Department

Mr. Tim Zitur, Mathematics Department from Singapore American School

Contact kang782455@sas.edu.sg

40 Woodlands Street 41, Singapore 738547

Singapore American School

Welcome to the launch of the SAS Mathematics Journal, the school’s first-ever publication dedicated to showcasing the diverse and fascinating world of math!

This journal was brought to life through the hard work of our teacher reviewers and talented team of editors who share a passion for helping people understand and appreciate the power and beauty of math. With this journal, we aim to engage and inspire readers of all ages and levels of mathematical knowledge; whether you’re a seasoned mathematician or just starting to explore this intricate field, there’s something for everyone.

We’re excited to embark on this journey, and we look forward to your feedback and ideas for future issues. Happy reading!

STUDENT AUTHORS

Editors-in-Chief

Gyulim Jessica Kang (11th grade, class of 2024)

Frank Xie (11th grade, class of 2024)

Editors

Gaurav Goel (12th grade, class of 2023)

Morgan Ahn (11th grade, class of 2024)

Irene Choi (11th grade, class of 2024)

Hyeonseo Kwon (11th grade, class of 2024)

Akshay Agarwal (10th grade, class of 2025)

Benjamin Cheong (11th grade, class of 2024)

Sunghan Billy Park (10th grade, class of 2025)

Application of Eigenvectors and Eigenvalues: SVD Decomposition in Latent Semantic Analysis

Finding an Alternate Model to Malthusian Population Growth Model

Evaluating Affirmative Action in School Choice

Contact: kang782455@sas.edu.sg

40 Woodlands Street 41, Singapore 738547

Creating a Machine Learning Pipeline to Perform Topological Data Analysis

2023