Elementary Algebra 4th Edition by Carson Jordan
ISBN 032191600X 9780321916006
Download solution manual at:
https://testbankpack.com/p/solution-manual-for-elementary-algebra-4thedition-by-carson-jordan-isbn-032191600x-9780321916006/
Download full test bank at :
https://testbankpack.com/p/test-bank-for-elementary-algebra-4th-edition-bycarson-jordan-isbn-032191600x-9780321916006/
MULTIPLE CHOICE Choose the one alternative that best completes the statement or answers the question List all natural number factors of the given number.
1
1) 30 A) 1, 2, 3, 5, 6, 10, 20, 30 B) 5, 6, 10, 30 C) 1, 2, 3, 5, 6, 10, 15, 30 D) 1, 5, 6, 30 1) 2) 28 A) 1, 2, 4, 7, 8, 14, 28 B) 1, 2, 7, 14, 28 C) 2, 7, 14, 28 D) 1, 2, 4, 7, 14, 28 2) 3) 36 A) 1, 2, 4, 6, 12, 18, 36 B) 1, 2, 3, 4, 6, 9, 12, 18, 36 C) 1, 2, 3, 4, 5, 6, 9, 10, 12, 18, 36 D) 2, 4, 6, 12, 18, 36 3) 4) 45 A) 1, 3, 5, 9, 15, 30, 45 B) 1, 3, 5, 9, 15, 45 C) 1, 2, 3, 5, 9, 15, 30, 45 D) 1, 3, 5, 15, 45 4) 5) 56 A) 1, 2, 3, 4, 7, 8, 14, 18, 28, 56 B) 1, 2, 4, 7, 8, 14, 28, 56 C) 1, 2, 4, 7, 8, 14, 18, 28, 56 D) 2, 4, 7, 8, 14, 28 5) 6) 63 A) 3, 5, 7, 9, 11, 21, 63 B) 1, 3, 5, 7, 9, 11, 21, 63 C) 1, 2, 3, 7, 9, 21, 36, 63 D) 1, 3, 7, 9, 21, 63 6)
2 7) 66 A) 1, 3, 11, 22, 33, 66 B) 1, 2, 3, 4, 11, 16, 22, 33, 66 C) 1, 2, 3, 6, 11, 22, 33, 66 D) 1, 2, 3, 9, 11, 22, 33, 66 7) 8) 70 A) 1, 3, 5, 7, 9, 15, 20, 35, 70 B) 1, 2, 3, 5, 7, 9, 15, 35, 70 C) 1, 2, 5, 7, 35, 70 D) 1, 2, 5, 7, 10, 14, 35, 70 8) 9) 72 A) 1, 2, 3, 4, 6, 8, 9, 12, 24, 36, 72 B) 1, 2, 3, 4, 6, 9, 12, 14, 18, 24, 36, 72 C) 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72 D) 1, 2, 3, 4, 5, 6, 7, 8, 9, 12, 18, 24, 36, 72 9) 10) 84 A) 1, 2, 3, 4, 5, 6, 7, 8, 9, 12, 14, 21, 28, 42, 84 B) 1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 84 C) 1, 2, 3, 4, 7, 14, 21, 28, 42, 84 D) 1, 2, 3, 4, 6, 7, 12, 14, 21, 42, 84 10) Find the GCF. 11) 12, 16 A) 1 B) 12 C) 4 D) 2 11) 12) 60, 72 A) 2 B) 1 C) 6 D) 12 12)
3 13) 60, 19 A) 10 B) 19 C) 6 D) 1 13) 14) 280, 200 A) 8 B) 5 C) 40 D) 20 14) 15) 152, 304 A) 152 B) 8 C) 19 D) 76 15) 16) 38, 95 A) 18 B) 190 C) 19 D) 10 16) 17) 39, 52, 91 A) 1 B) 13 C) 39 D) 6 17) 18) 54, 72, 126 A) 9 B) 36 C) 18 D) 2 18) 19) 108, 378, 486 A) 18 B) 2 C) 54 D) 50 19) 20) 12, 18, 27 20) A) 6 B) 3 C) 12 D) 1 21) 4x, 6 A) 4 B) 2x C) 2 D) 12x 21) 22) 15m3, 135m8 A) 2025m5 B) 15m5 C) 135m3 D) 15m3 22) 23) 40x4, 20x9 A) 10x5 B) 20x4 C) 40x4 D) 30x4 23) 24) s3t6, s2t8 A) s2t6 B) s3t6 C) s2t2 D) s5t8 24) 25) -m6n8, -mn7 A) -mn7 B) n7 C) -m6n7 D) m6n8 25) 26) 64a8b4, 40a6b8 A) 8a8b8 B) 8a6b4 C) 320a8b8 D) 4a2b4 26) 27) 4x5y8, 16y2z4 27)
4 A) 4y2 B)
C) 2y2 D) 4xyz
x5y2
5 28) p3q3r, p6q2r5 A) p3q2r B) p3q2r5 C) p3q2 D) p3q1r4 28) Factor out the GCF. 29) 9z - 27 A) 9(z + 3) B) 9(z - 3) C) 9(z - 27) D) 3(z9) 29) 30) 7x + 21 A) 7 B) 7(x + 3) C) 7(x + 21) D) 3(x + 7) 30) 31) xz-xy A) xz(-xy) B) x(z + y) C) x D) x(zy) 31) 32) 5x2 + 20x A) 5x(x + 4) B) x(5x + 20) C) 5x2(x + 4) D) 5x(x + 20) 32) 33) 13x4 + 13x A) 13x(x3) B) 13(x5 + 1) C) 13(x4 + x) D) 13x(x3 + 1) 33) 34) t11 - 9t6 A) t6(t5 + 9) B) t6(t5 - 9) C) t5(t6 - 9) D) t(t109t5) 34) 35) 2s6 + 8s3 A) 6(s3 + 4s) B) s3(2s3 + 8) C) 2(s6 + 4s3) D) 2s3(s3 + 4) 35) 36) m4n4 - m3n6 A) mn(16 - 18) B) m3n4(m - n2) C) m4n4(1 - mn2) D) m4n6(mn2) 36) 37) 6s4t2 + 2s2t3 A) s2t2(6s + 2t) B) 2s4t3(3s2 + t) C) 2s2t2(3s2 + t) D) 2s2t(3s + t) 37) 38) 3x2y4 + 18x2y3 A) 3x2y3(y + 6) B) x2y3(3y + 6) C) 3x3y2(y + 6) D) y + 6 38) 39) 3t2 - 15t - 15
6 A) 3t(t2 - 5t - 5) B) 3(t2 - 5t - 5) C) 3(t2 - 15t - 15) D) 3(t2 - 12t12) 39) 40) 16wx - 8wy - 12wz A) 4w(4x - 2y - 3z) B) 4w(4x - 8wy12wz) C) 4(4wx - 2wy - 3wz) D) 16w(x - 8y12z) 40) 41) 6m7 + 8m4 - 8m2 A) no common factor B) m2(6m5 + 8m28) C) 2m2(3m5 + 4m2 - 4) D) 2(3m7 + 4m44m2) 41)
42) 80m7 - 160m4 - 64m2
A) m2(80m5 - 160m2 - 64)
B) no common factor
D) 16m2(5m5 - 10m24)
C) 16(5m7 - 10m4 - 4m2)
43) 64x9y9 + 32x5y7 + 16x3y5
A) 16(4x9y9 + 2x5y7 + 1x3y5)
B) no common factor
43)
C) 16x3(4x6y9 + 2x2y7 + 1y5)
D) 16x3y5(4x6y4 + 2x2y2 + 1)
44) 24x8y8 - 72x3y6 + 56x5y3
A) 8(3x8y8 - 9x3y6 + 7x5y3)
B) 8x3y3(3x5y5 - 9y3 +
44)
7x2) C) no common factor
D) 8x3(3x5y8 - 9y6 + 7x2y3)
45) 6x12 - 12x9 + 18x6 - 24x3
A) 6(x9 - 2x6 + 3x3 - 4)
B) 6x3(x9 - 2x6 + 3x3 -
D) 6x3(x4 - 2x3 + 3x2 - 4)
4) C) x3(x9 - 2x6 + 3x3 - 4)
46) x10y6 - x10y5 + x8y3 - x7y3
A) x7y3(x3y3 - x3y2 + x - 1)
B) x7y3(x3y3 - x2y2 + x -
D) x6y3(x3y3 + x3y2 + x +
1) C) x7y3(x2y3 - x2y2 + xy - 1)
n7 - 31nw7 + 5n3w8 - 11n7w7
Factor by factoring out the negative of the GCF
7
42)
45)
46) 47)
A) n2(n6
n6w6) B) nw7(n6 - 31 + 5n2w1
n6) C) n(n6
D) nw(n6
31w6 + 5n2w7
n6w6) 47)
1)
- 31w6 + 5n2w7 - 11
- 11
- 31w7 + 5n2w8 - 11n6w7)
-
11
48)
A)
B)
8(z
C) -10(z
D)
10(z
80) 48) 49) -10x - 30 A) -10 B) -10(x + 30) C) -3(x + 10) D) -10(x + 3) 49) 50) -5x2 - 20x A) -x(5x + 20) B) -5x2(x + 4) C) -5x(x + 4) D) -5x(x + 20) 50) 51) -20x3 - 20x A) -20x(x2) B) -20x(x2 + 1) C) -20(x3 + x) D) -20(x4 + 1) 51)
-10z + 80
-10(z + 8)
-
- 10)
- 8)
-
-
8 52) -3t2 + 12t + 6 A) -3t(t2 + 4t + 2) B) -3(t2 - 9t - 3) C) -3(t2 - 4t - 2) D) -3(t2 - 12t6) 52) 53) -8x3 - 16x2 + 12x A) -4(2x3 + 4x2 - 3x) B) -4x(2x2 + 4x3) C) -8x(x2 + 2x - 3) D) -4x(2x2 - 4x + 3) 53)
9 54) -21s6t2 - 7s4t3 A) -7s2t(3s + t) B) -7s4t2(3s2 + t) C) -s4t2(21s + 7t) D) -7s6t3(3s2 + t) 54) 55) -12wx + 12wy + 20wz A) -4w(3x - 3y - 5z) B) -4(3wx - 3wy - 5wz) C) -12w(x - 12y - 20z) D) -4w(3x - 12wy20wz) 55) 56) -8x12 + 16x9
24x6 + 32x3 A) -x3(x9 - 2x6 + 3x3 - 4) B) -8x3(x4 - 2x3 + 3x24) C) -8(x9 - 2x6 + 3x3 - 4) D) -8x3(x9 - 2x6 + 3x3 - 4) 56) 57) -x9y7 + x9y6 - x7y4 + x6y4 A) -x6y4(x3y3 - x3y2 + x - 1) B) -x5y4(x3y3 + x3y2 + x + 1) C) -x6y4(x2y3
x2y2 + xy - 1) D) -x6y4(x3y3 - x2y2 + x - 1) 57) Factor out the polynomial GCF. 58) s(u + v) + t(u + v) 58) A) (s + u)(t + v) B) (s + t)(uv) C) (s + t)(u + v) D) st(u + v) 59) x(y + 9) - z(y + 9) A) xz(y + 9) B) (x + y)(-z + 9) C) (x - z)(9y) D) (x - z)(y + 9) 59) 60) r(s - 10) + 4(s - 10) A) (r - 4)(s + 10) B) 4r(s - 10) C) (r + 4)(s - 10) D) r(s - 10) + 4 60) 61) j(k - 1) - 10(k - 1) A) (j - 10)(k1) B) (j - 10)(k + 1) C) (j + 10)(k - 1) D) -10j (k - 1) 61) 62) t(2 - m) + s(2m) A) t(2 - m) + s B) (t + s)(2 - m) 62) C) no common factor D) (t - s)(2 - m) 63) 3x(5x - 6) + 4(5x6) A) (15x - 4)(x + 6) B) (3x + 4)(5x - 6) C) (15x + 4)(x - 6) D) (3x - 4)(5x + 6) 63) 64) 3m(5 - m) + 5n(5m) A) (3m - 5n)(5m) B) (3m + 5n)(5 - m) 64) C) no common factor D) m(3 + 5n)(5 - 1) Factor by grouping. 65) r3 + r2 + 6r + 6 A) (r2 + 6)(r + 6) B) (r2 + 1)(r + 6) C) (r2 + 6)(r + 1) D) (r2 + 6)(r6) 65)
-
-
10 66) s2 + 8s + 3s + 24 A) (s + 8)(s - 3) B) s(s + 35) C) (s + 8)(s + 3) D) (s - 8)(s3) 66)
4x2 - 4x2y - 16x + 16xy A) 4x(y - 1)(x + 4)
9p3 - 9p2q + p3q - p2q2 A) p2(p + q)(9 - q)
11 67) x3 + 8x2 + 7x + 56 A) (x + 8)(x2 - 7) B) (x - 8)(x3 + 7) C) (x + 8)(x2 + 7) D) (x + 8x)(x2 + 7) 67) 68) uv - 7u + 5v - 35 A) 5u(v - 7) B) (v + 7)(u - 5) C) (v - 7)(u + 5) D) (v - 7)(u5) 68) 69) 36r2 + 27ry - 4xr - 3xy 69) A) (4r + 3y)(9x - r) B) (4r + 3y)(9r - x) C) (3r + 4y)(9r - x) D) (4r + 3y)(x - 9r) 70) 45 - 5t - 9s + ts A) (9 + t)(5 + s) B) (9 - t)(5 - s) C) (9 - t)(5 + s) D) (9 + t)(5 - s) 70) 71) pq - 10p + q - 10 A) p(q - 10) + 1 B) (p - 1)(q - 10) C) (p + 1)(q - 10) D) p(q - 10) 71) 72) 12wx - 3wy - 4xz + yz A) (3wz)(4x - y) B) (3w - z)(4x - y) 72) C) (3w + z)(4x + y) D) (3 - z)(4wx - y) 73) x3 + 8x2 - 3x - 24 A) (x2 + 8)(x - 3) B) (x - 8)(x2 - 3) C) (x + 8)(x2 - 3) D) (x + 8)(x3 - 3x) 73) 74) 2x3 - 18x2 - 3x
27 A) (x - 9)(2x2 - 3) B) (x + 9)(2x2 - 3) 74) C) (x
9)(x2 + 3) D) (x + 27)(x2 - 18x - 3) Factor
75) 3x2
27y A) (x + y)(x + 9) B) 3(x + y)(x + 9) C) 9(x + y)(x + 3) D) 3(y + x)(y + 9) 75) 76)
76)
D)
77)
B)
4) C) 4x(1
D)
77) 78)
B)
D)
q) 78)
+
-
completely.
+ 3xy + 27x +
16m2n + 64m2 - 4mn16m A) (4m - 1)(n + 4) B) 4m(4m + 1)(n - 4)
C) 4m(4m - 1)(n + 4)
m(4m - 1)(n - 4)
4(1 + y)(x +
- y)(x - 4)
(1 - y)(x - 4)
(p - q)(9 + q) C) p2(p - q)(9 + q)
p(p2 - pq)(9 +
Write an expression for the area of the shaded region; then factor completely.
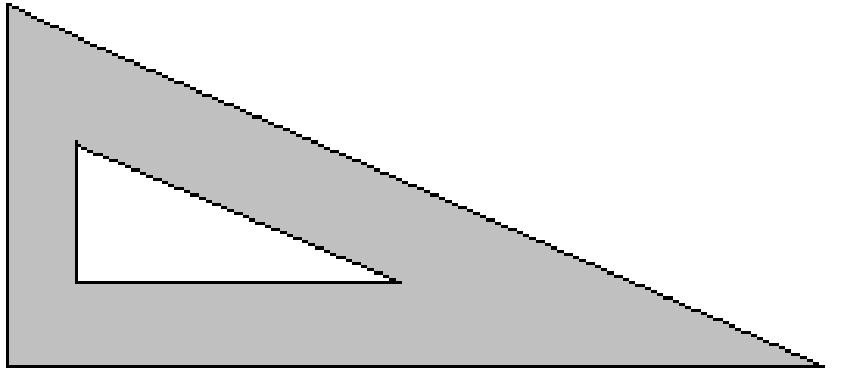
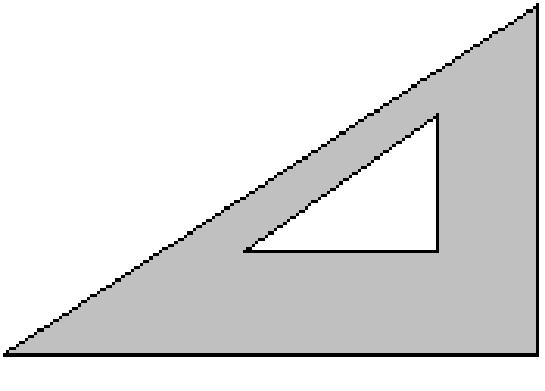
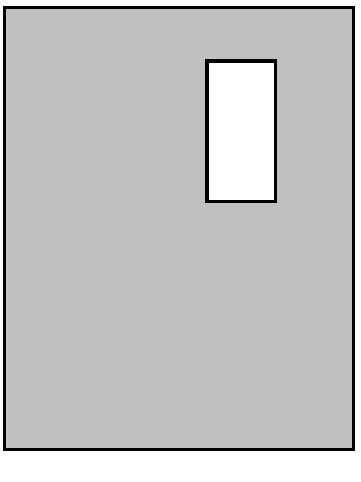
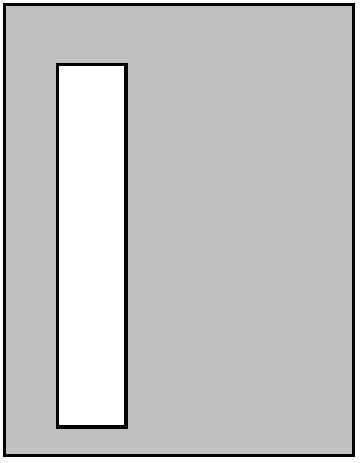
12
79) x 5x 6x x + 4 A) x(x2 + 24) B) x(24x + 1) C) x(x + 24) D) x2(1 + 24x) 79) 80) 80) 12x x 18x x + 2 A) 6x(x + 6) B) 3x(x + 6) C) 3x(x + 12) D) 6x(x + 12) 81) 81) h h + 4 8h 10h A) h(h - 4) B) 20h(h + 1) C) h(10h + 1) D) h(h + 20) 82) 82) h + 16 h 12h 28h A) h(8h + 28) B) 8h(h + 4) C) 28(h2 + 8) D) 8h(h + 28)
Solve the problem.
83) A rectangular photograph measures 25 inches by 40 inches. The photographer wishes to frame the photograph with a frame x inches wide, as shown Write an expression in factored form for the area of the frame in terms of x.
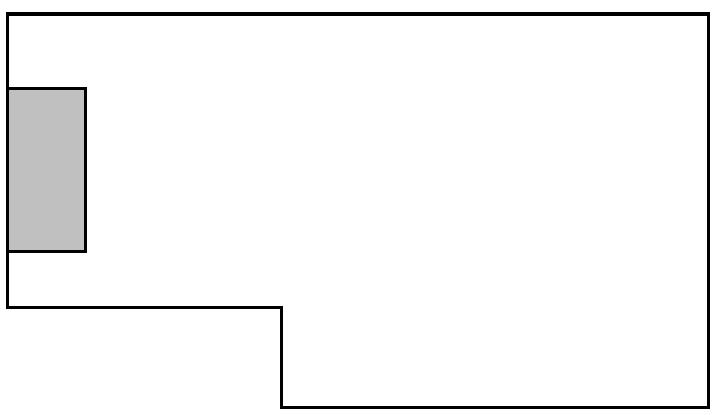
84) A homeowner is measuring a room in order to purchase new carpet. The diagram shows the floor plan of the room with the landing. Write an expression in factored form of the area of the room excluding the landing, which is 2 feet by 4 feet. 9x + 2 6x + 4
85)

13
A) 4x(x - 65) B) 2x(2x + 65) C) 2(2x2 + 65x + 1000) D) 2(x + 20)(2x + 25)
83)
x 5x A) 5x(10x + 23) B) 2x(25x + 23) C) 2x(29x + 24) D) 59x2 + 48x
84)
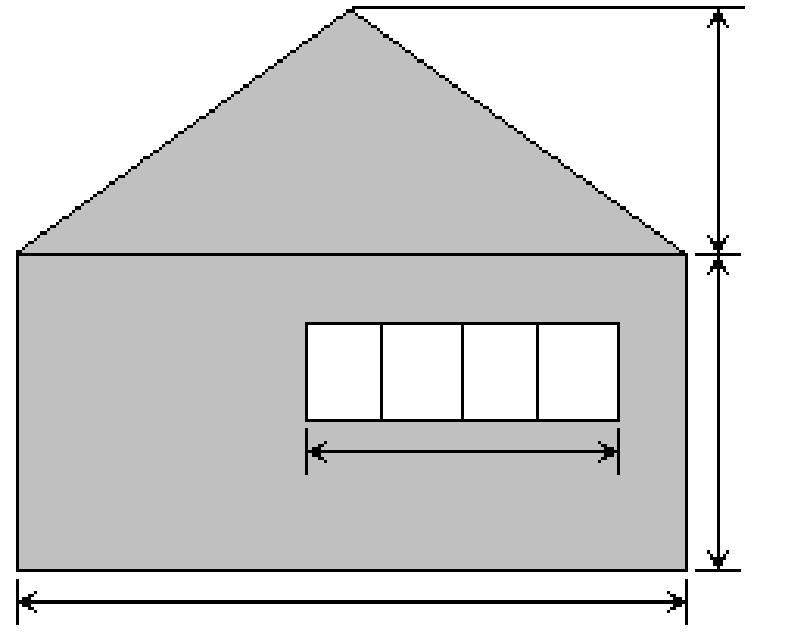
85) Write an expression in factored form for the area of the side of the house shown excluding the window 4x x 6x 2x
14 10x + 3 A) 6x(13x + 8) B) 6x(13x + 4) C) 6x(11x + 4) D) 6x(11x + 8)
Complete the factoring.
Factor. If the polynomial is prime, so state.
15
86) x2 + 13x + 40 = (x + 5)( ) A) x - 18 B) x + 35 C) x2 + 8 D) x + 8 86) 87) x2 + 3x - 28 = (x + 7)( ) A) x - 4 B) 4 - x C) -x - 4 D) x + 4 87) 88) x2 - 6x + 9 = (x - 3)( ) A) 3 - x B) x + 3 C) x - 3 D) x2 + 3 88) 89) x2 - 3x - 54 = (x - 9)( ) A) x - 6 B) x + 6 C) 9 - x D) x2 + 9 89)
90) s2 + 8s + 16 A) (s + 16)(s + 8) B) (s + 16)(s - 1) C) (s + 4)(s + 4) D) (s - 4)(s4) 90) 91) u2 - 10u + 24 A) (u + 6)(u - 4) B) (u - 6)(u + 4) C) (u - 6)(u - 4) D) (u + 6)(u + 4) 91) 92) x2 - x - 56 A) (x + 7)(x - 8) B) (x + 8)(x - 7) C) prime D) (x + 1)(x56) 92) 93) x2 + 6x - 72 A) (x + 12)(x - 6) B) prime C) (x - 12)(x + 6) D) (x - 12)(x + 1) 93) 94) x2 - 6x - 16 A) (x - 2)(x + 1) B) (x + 2)(x - 8) C) (x - 2)(x + 8) D) prime 94) 95) r2 + 5r - 14 A) prime B) (r - 14)(r + 5) C) (r - 7)(r + 2) D) (r + 7)(r2) 95) 96) t2 - 18t + 80 A) (t + 8)(t + 10) B) (t - 8)(t - 10) C) prime D) (t - 40)(t2) 96) 97) x2 - x - 54 A) (x + 6)(x - 9) B) prime C) (x - 54)(x + 1) D) (x - 6)(x + 9) 97)
Factor the trinomial containing two variables. If the polynomial is prime, so state.
16 98) x2 + 83x + 84 A) prime B) (x + 12)(x - 7) C) (x + 84)(x - 1) D) (x - 12)(x + 7) 98)
99) x2 + 3xy - 18y2 A) (x + 6y)(x - 3y) B) (x - 6y)(x + y) C) (x - 6y)(x + 3y) D) (x - y)(x + 3y) 99)
10 100) u2 - 4uv - 21v2 A) (u - v)(u + 7v) B) (u - 3v)(u + 7v) C) (u - 3v)(u + v) D) (u + 3v)(u7v) 100) 101) u2 - 2uv - 48v2 A) (u - 6v)(u + v) B) (u - 6v)(u + 8v) C) (u + 6v)(u - 8v) D) (u - v)(u + 8v) 101) 102) x2 + 2xy - 195y2 A) (x - 15y)(x + 13y) B) (x - 15y)(x + y) C) (x + 15y)(x - 13y) D) (x - y)(x + 13y) 102) 103) x2 + 2xy - 15y2 A) (x + 5y)(x - 3y) B) (x - 5y)(x + y) C) (x - 5y)(x + 3y) D) (x - y)(x + 3y) 103) 104) u2 - 2uv - 35v2 A) (u + 5v)(u - 7v) B) (u - 5v)(u + 7v) C) (u - v)(u + 7v) D) (u - 5v)(u + v) 104) 105) x2 - 2xy - 35y2 A) (x - 7y)(x + y) B) (x - 7y)(x + 5y) C) (x - y)(x + 5y) D) (x + 7y)(x5y) 105) Factor completely 106) 2x2 - 2x - 12 A) 2(x - 2)(x + 3) B) 2(x + 2)(x - 3) C) Prime D) (2x + 4)(x3) 106) 107) 4x2 - 12xy - 16y2 A) Prime B) (4x - 4y)(x + 4y) C) 4(x + y)(x - 4y) D) 4(x - y)(x + 4y) 107) 108) 4x2 - 20x + 24 A) 4(x - 2)(x - 3) B) (4x - 8)(x - 3) C) 4(x - 6)(x + 1) D) (x - 2)(4x12) 108) 109) 3x3 + 9x2y - 30xy2 A) 3x(x - 2y)(x + 5y) B) (x - 2y)(3x2 + 15xy) C) 3x(x + 2y)(x - 5y) D) (3x2 + 6xy)(x - 5y) 109) 110) 2x3 + 4x2 - 30x A) (x - 3)(2x2 + 10) B) (2x2 + 6x)(x - 5) C) 2x(x - 3)(x + 5) D) 2x(x + 3)(x5) 110) 111) x3 - x2 - 56x
11 A) (x2 + 1)(x - 56) B) x(x + 8)(x - 7) C) Prime D) x(x + 7)(x8) 111) 112) x3y + 17x2y2 + 72xy3 A) xy(x + 8y)(x + 9y) B) y(x + 8y)(xy + 9y2) C) xy(x2 + 17x + 72y2) D) x(xy + 8y2)(x + 9y) 112) 113) 3a3 + 6a2 - 45a A) 3a(a - 5)(a - 3) B) 3a(a + 5)(a + 3) C) 3a(a - 5)(a + 3) D) 3a(a + 5)(a3) 113)
Find all natural number values of b that make the trinomial factorable.
Solve the problem.
119) The expression h2 + 6h + 8 describes the area of the bottom of the box shown, where h represents its height The unknown expression for the length is the sum of h and an integer, and the expression for the width is the sum of h and a different integer. Find the expressions for the length and width.
119) h length? width?
A) length: (h + 8); width: (h - 1)
B) length: (h - 4); width: (h -
D) length: (h + 8); width: (h + 6)
2) C) length: (h + 4); width: (h + 2)
120) The expression w2 + 3w - 108 describes the area of the top of the eraser shown, where w represents the width of the base of the eraser. The unknown expression for the length of the top of
120) length? width?

12
114) x2 + bx + 35 A) 12 B) 36 C) 12, 35 D) 12, 36 114) 115) x2 + bx + 28 A) 11, 16, 29 B) 1, 14, 28 C) 16, 29 D) 11, 16 115) 116) x2 + bx - 91 A) 20, 92 B) 6, 90 C) 6 D) 90 116) 117) x2 + 9x + b A) 8, 14, 18 B) 8, 14 C) 5, 6, 7, 8 D) 8, 14, 18, 20 117) 118) x2 - 10x + b A) 5, 6, 7, 8, 9 B) 9, 16, 21 C) 9, 16, 21, 24 D) 9, 16, 21, 24, 25 118)
the eraser is the sum of w and an integer. The expression for the width of the top of the eraser is the difference of w and an integer. Find the expressions for the length and width of the top of the eraser. w
A) length: (w - 12); width: (x + 1)
B) length: (w + 9); width: (w12)
C) length: (w + 12); width: (x - 9)
D) length: (w + 3); width: (w - 9)
13
121) The expression w2 - 13w + 42 describes the viewing area in the framed mirror shown, where w represents the width of the frame. The unknown expression for the length of the viewing area is the difference of w and an integer. The expression for the width of the viewing area is the difference of w and a different integer. Find expressions for the length and width of the viewing area in the frame
121) width? w
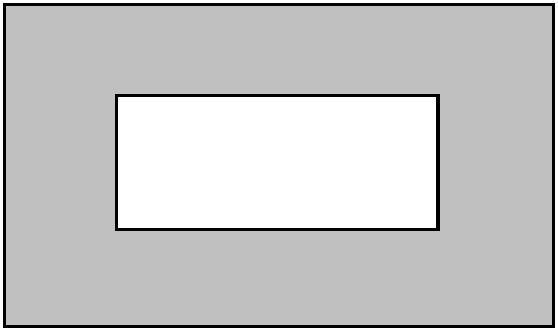
length?
B) length: (w - 6); width: (w7) C) length: (w - 7 ); width: (w - 6)
A) length: (w - 6); width: (w - 42)
D) length: (w - 42); width: (w - 1)
122) The expression πr2 - 10πr + 25π describes the area occupied by the circular top of the step stool shown, where r represents the radius of the circle which makes up the part on which a person would step The expression that describes the radius of the circular top is the difference of r and an integer. Find the expression that describes the circular top radius?

14
A) r - 5 B) r - 36 C) r - 6 D) r - 25 122) Complete the factorization. 123) 12x2 + 19x + 5 = (3x + )(4x + ) A) 6, 4 B) 1, 5 C) 5, 1 D) 4, 6 123) 124) 12x2 - 19x + 5 = (3x - )(4x - ) A) 6, 4 B) 4, 6 C) 1, 5 D) 5, 1 124) 125) 6y2 - 29y + 20 = ( - 5)( - 4) 125) A) y, 6y B) 6y, y C) 3y, 2y D) 6y, 2y 126) 8n2 - 34n - 9 = ( + 1)( - 9) 126) A) 2n, 4n B) 8n, n C) 4n, 2n D) n, 8n 127) 2m2 - 11m + 5 = ( - 1)(m - ) A) 5m, 2 B) 2m, 1 C) m, 5 D) 2m, 5 127)
Factor completely. If prime, so indicate.
15
128) 9x2 + 12x + 4 A) (3x + 2)(3x + 2) B) prime C) (9x + 2)(x + 2) D) (3x - 2)(3x2) 128)
16 129) B) (9y + 4)(y + 2) C) (3y - 4)(3y - 2) D) prime 131) B) (2z + 3)(5z - 2) C) prime D) (2z - 3)(5z + 2) 132) B) (m + 6)(5m + 2) C) (m + 6)(4m + 2) D) (m - 6)(5m - 2) 129) 9y2 + 18y + 8 A) (3y + 4)(3y + 2) 130) 20z2 + 7z - 6 A) (4z + 3)(5z - 2) B) prime C) (4z - 3)(5z + 2) D) (20z + 3)(z2) 130) 131) 10z2 - 11z - 6 A) (10z - 3)(z + 2) 132) 5m2 + 32m + 12 A) (m + 2)(5m + 6) 133) 81x2 - 126x + 49 133) A) prime B) (81x - 7)(x - 7) C) (9x + 7)2 D) (9x - 7)2 134) 4x2 - 9x + 4 A) prime B) (4x - 1)(x - 4) C) (2x - 4)(2x - 1) D) (4x - 4)(x - 1) 134) 135) 12x2 - 17xt + 6t2 A) (4x + 3t)(3x + 2t) B) prime C) (4x - 3t)(3x - 2t) D) (12x - 3t)(x2t) 135) 136) 6x2 + 11xt + 3t2 136) A) prime B) (3x + t)(2x + 3t) C) (3x - t)(2x - 3t) D) (6x + t)(x + 3t) 137) -30a2 - 32a - 8 A) (-6a - 4)(5a + 2) B) -2(3a + 2)(5a + 2) C) (3a + 2)(-10a - 4) D) -2(3a - 2)(5a2) 137) 138) -75x3 - 55x2 + 60x A) x(3x + 4)(-25x + 15) B) x(-15x - 20)(5x3) C) -5x(3x + 4)(5x - 3) D) -5(3x2 + 4)(5x - 3) 138) 139) 6x2 - 26x - 20 A) 2(3x - 2)(x + 5) B) (3x + 2)(2x - 10) C) 2(3x + 2)(x - 5) D) (6x + 4)(x5) 139) 140) 14x2 - 49x - 28 A) (2x - 1)(7x + 28) B) (14x - 7)(x + 4) C) 7(2x - 1)(x + 4) D) 7(2x + 1)(x - 4) 140)
17 A) prime B) x(6x - 1)(x + 4) C) (6x2 - 1)(x + 4) D) x(6x + 1)(x4) 141) 4y2 + 18y - 10 A) 2(2y - 1)(y + 5) B) (2y - 1)(2y + 10) C) (4y - 2)(y + 5) D) 2(2y + 1)(y - 5) 141) 142) 6x3 + 23x24x 142)
Find all natural numbers that can replace b and make the expression factorable.
Solve the problem.
Given the area of the figure, factor to find possible expressions for the length and the width.

151) Given the area of the figure, factor to find possible expressions for the length and the width.

18 143)
x
12 A) prime B) -2(3x + 2)(2x3) C) (-6x + 4)(2x + 3) D) -2(3x - 2)(2x + 3) 143)
60x2
xy
5y2 A) prime B) (15x + 5y)(4x + y) C) 5(3x + y)(4x + y) D) 5(3x - y)(4xy) 144) 145) 12x2y2 + 5xy2
25y2 A) y2(4x - 5)(3x + 5) B) (4x - 5y)(3x + 5y) C) y2(x - 5)(12x + 5) D) (3x - 5y)(4x + 5y) 145)
-12x2 - 10
+
144)
+ 35
+
-
146) 5x2 + bx + 5 A) 10 or 26 B) 26 C) 10 or 25 D) 10 146) 147) 5x2 + bx + 10 A) 15 B) 15 or 51 C) 15, 27, or 51 D) 15 or 27 147) 148) 3x2 + bx - 7 A) 10 or 22 B) 4 C) 20 D) 4 or 20 148) 149) 8x2 + bx - 5 A) 3 or 6 B) 9, 18, 27, or 36 C) 3, 6, 18, or 39 D) 6, 18, or 39 149)
A) (6x + 3)(x + 4) B) (6x +
)(x
6) C) (2x - 3)(3x - 4) D) (2x + 3)(3x + 4) 150)
150)
3
-
A ) ( 4 y3
19 )(4y - 3) B) (4y + 3)(4y + 3) C) (16y + 3)(y + 16) D) (16y + 3)(y + 3) 151)
152) Given the area of the figure, factor to find possible expressions for the length and the width.
152)
A) (10x + 3)(x + 4) B) (10x + 3)(x + 3)
C) (2x - 3)(5x - 4) D) (2x + 3)(5x + 4)



153) Two adjacent parking lots are for sale The area of the larger parking lot is described as 9w2 - 6w - 8 square feet, where w is the width of the smaller parking lot. Factor to find possible expressions for the dimensions of the larger parking lot.
153)
B) (3w + 2)(3w4) C) (9w + 2)(w - 4)
A) (3w - 4)(9w + 2)
D) (3w - 2)(3w + 4)
154) A sifter used at an archaeological dig has an area of 8h2 - 31h - 45 square inches, where h represents the height of the lip of the sifter. Factor to find possible expressions for the width and length of the sifter.
154) h ?
A) (9h + 8)(h - 5) B) (8h + 9)(h - 5) C) (8h + 1)(h - 45) D) (8h - 5)(h + 9)
SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question. Provide an appropriate response.
155) What steps would you take to factor x2 + 16x + 64 ?
155)
20
156) What steps would you take to factor x2 + 8x + 16 ?
157) Use the FOIL method to show that (8x + 16)(x - 8) is 8x2 - 48x - 128. If you were asked to completely factor 8x2 - 48x - 128, why would it be incorrect to give (8x + 16)(x - 8) as your answer?
157)
158) Explain the error in the following: x2 + 2x - 15 = (x - 5)(x + 3) 158)
159) Assuming you have factored out the largest common factor at the outset, why can you 159) reject a possible factor such as (2x + 2) or (3x - 6) when you are factoring a trinomial?
160) Explain the error in the following: 25x2 + 10x - 4 = (5x + 2)2
MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Factor the trinomial that is a perfect square. If it is not a perfect square, respond "not a perfect square." 161) x2 + 12x + 36
- 6)2
+ 6)(x - 6)
x2 - 8x + 64
not a perfect square
- 8) D) (x +
a perfect square
)2
163) b2 - 14b + 49 A) (b + 7)(b - 7) B) (b + 7)2 C) (b - 7)2 D) not a perfect square
164) m2 + 16m + 64
A) (m + 8)(m - 8) B) not a perfect square C) (m - 8)2 D) (m + 8)2
165) x2 + 18xy + 81y2
164)
A) (x + 9y)2
C) (x - 9y)2 B) (x + 9y)(x - 9y)
166) 25x2 - 30x + 9 A) (5x - 3)(5x + 3)
D) not a perfect square
(5x + 3)2
C) not a perfect square D) (5x - 3)2
21
156)
160)
A) (x
B)
C)
D) (x
161) 162)
A)
B) (x
8)2 C) (x + 8)(x
8
not
(x
+ 6)2
-
162)
163)
165)
166)
B)
22 167) 49x2 - 112xy + 64y2
(7x - 8)2
not a perfect square 167)
(7x - 8y)(7x + 8y)
(7x + 8)2
A)
B)
C)
D)
Factor the binomial that is a difference of squares. If
23 168) b2 -
+ 289 A) (b
17)(b - 17) B) not a perfect square C) (b + 17)2 D) (b - 17)2 168)
169) y2 - 49 A) (y + 7)(y - 7) B) prime C) (y - 7)2 D) (y + 7)2 169) 170) y2 - u2 A) prime B) (y - u)(y + u) C) (y2 - u)(y2 + u) D) (y - u)(yu) 170) 171) 25x2 - 49 A) (5x - 7)2 B) prime C) (5x + 7)(5x - 7) D) (5x + 7)2 171) 172) 49y4 - 64 A) (7y2 + 8)(7y2 - 8) B) (7y2 + 8)2 C) (7y2 - 8)2 D) prime 172) 173) 81k2 - 121m2 A) (9k + 11m)(9k - 11m) B) prime C) (9k - 11m)2 D) (9k + 11m)2 173) 174) 25s2 - 81t4 A) (5s + 9t2)(5s - 9t2) B) (5s9t2)2 C) prime D) (5s + 9t2)2 174) Factor. 175) x3 - 343 A) Prime B) (x - 7)3 C) (x - 7)(x2 + 7x + 49) D) (x + 7)(x2 - 7x + 49) 175) 176) y3 - 27 A) (y + 3)(y2 - 3y - 9) B) (y - 3)(y2 - 9) C) (y - 3)(y2 + 3y + 9) D) (y - 3)(y2 + 3y9) 176) 177) 343p3 - 1
17b
+
prime, so state.
24 A) (7p - 1)(49p2 + 1) B) (7p - 1)(49p2 + 7p + 1) C) (7p - 1)3 D) Prime 177) 178) 8r3 - 27 A) (2r - 3)(4r2 - 6r - 9) B) (2r + 3)(4r2 + 6r + 9) C) (2r - 3)(4r2 - 9) D) (2r - 3)(4r2 + 6r + 9) 178)
179) 343y3 - 216
A) (7y - 6)3
179)
B) Prime
D) (7y - 6)(49y2 + 36)
C) (7y - 6)(49y2 + 42y + 36)
180) 729y3 - 343
A) (729y - 7)(y2 + 63y + 49)
B) (9y - 7)(81y2 + 49)
180)
C) (9y + 7)(81y2 - 63y + 49)
D) (9y - 7)(81y2 + 63y + 49)
181) 64a3 - 125b3
A) (4a - 5b)(16a2 + 20ab + 25b2)
B) (4a - 5b)(16a2 + 25b2)
181)
C) (4a + 5b2)(16a2 - 20ab + 25b2)
D) (64a - 5b)(a2 + 20ab + 25b2)
182) d3 + 64
182)
B) (d + 4)(d2 - 4d + 16) C) (d + 4)(d2 + 16)
A) (d + 4)(d2 + 4d + 16)
D) (d + 4)(d2 - 4d - 16)
183) t3 + 1000
B) (t + 10)(t2 + 100) C) (t + 10)(t2 - 10t + 100)
A) (t - 10)(t2 + 10t + 100)
(t1000)(t2 - 1)
184) 729p3 + 1 A) (9p - 1)(81p2 + 9p + 1)
(9p + 1)(81p2 - 9p +
+ 1)(p2 - 9p + 1)
185) 216k3 + m3
184)
185)
B) (6k + m)(36k2 - 6kmm2) C) (6k + m)(36k2 + m2)
A) (6k + m)(36k2 + 6km + m2)
D) (6k + m)(36k2 - 6km + m2)
186) 343s3 + 64t3
186)
B) (7s + 4t)(49s2 + 28st + 16t2) C) (7s - 4t)(49s2 - 28st + 16t2)
A) (7s + 4t)(49s2 - 28st + 16t2)
D) (12s + 4t)(49s2 + 16t2)
187) 125c3 + 216
187)
B) (125c + 6)(c2 - 30c + 36) C) (5c + 6)(25c2 + 36)
A) (5c - 6)(25c2 + 30c + 36)
D) (5c + 6)(25c2 - 30c + 36)
25
D)
183)
1
D)
B)
) C) (9p + 1)(81p2 + 1)
(729p
188) 125x9 + 216y6
A) (5x3 + 6y2)(25x6 + 30x3y2 + 36y4)
B) (5x3 - 6y2)( 5x3 + 6y2)
188)
C) (5x3 + 6y2)(25x6 - 30x3y2 + 36y4)
D) (5x3 - 6y2)(25x2 + 30x3y2 + 36y4b2)
Factor. If prime, so state.
189) 256x2 - 36
A) 4(8x + 3)2
C) (8x - 3)(32x + 12)
B) (32x - 12)(8x +
3) D) 4(8x - 3)(8x +
3)
189)
26
27 190) 63x2 - 343y2 A) (21x + 49y)(3x - 7y) B) 7(3x - 7y)2 C) (3x + 7y)(21x - 49y) D) 7(3x + 7y)(3x7y) 190) 191) 25x - 49x3 191) A) x(5 - 7x)(57x) C) prime B) x(5 + 7x)(57x) D) x(5 + 7x)2 192) 98a4 - 18b2 A) 2(7a2 - 3b)2 B) prime 192) C) 2(7a2 + 3b)(7a2 - 3b) D) 2(7a2 + 3b)2 193) 98a4b - 72b3 A) prime B) 2b(7a + 6b)2 193) C) 2b(7a2 + 6b)(7a2 - 6b) D) 2b(7a - 6b)2 194) 50 - 2x4y4 A) 2(25 + x2y2)(25 - x2y2) B) 2(5 + x2y2)(5 - x2y2) 194) C) prime D) 2(5 + xy2)(5 - xy2) 195) 2u3 + 128 A) (u + 4)(u2 - 4u + 16) B) 2(u - 4)(u2 + 4u + 16) 195) C) 2(u + 4)(u2 - 4u + 16) D) (u - 4)(u2 + 4u - 16) 196) x5 + 125x2 A) x3(x - 5)(x2 + 5x + 25) B) x2(x + 5)(x2 - 5x + 25) 196) C) x2(x - 5)(x2 + 5x - 25) D) (x + 5)(x2 - 5x + 25) 197) 2m4 - 16m A) (m - 2)(m2 + 2m + 4) B) 2m(m + 2)(m2 - 2m + 4) 197) C) 2m(m - 2)(m2 + 2m + 4) D) 2(m + 2)(m2 - 2m + 4) 198) 2c4 - 16cd3 A) 2(c + 2)(c2 - 2c + 4) B) 2c(c - 2d)(c2 + 2cd + 4d2) 198) C) c(c + 2d)(c2 - 2cd + 4d) D) 2c(c + 2d)(c2 - 2cd + 4d2) 199) 64xy4 + 125x4y A) (4y - 5y)(16y2 + 20xy + 25x2) B) xy(4y - 5x)(16y2 + 20xy + 25x2) 199) C) x(4y + 5y)(16y2 - 20xy + 25x2) D) xy(4y - 5y)(4y2 + 20xy + 5x2) Factor completely. 200) (r + s)2 - 64 A ) (
28 r + s)2 - 8 2 B) (r + s - 8)(r + s + 8) C) (r + s + 8)2 D) (r + s - 8)2 200)
Find a natural number b that makes the expression a perfect square trinomial
Provide an appropriate response.
Write a polynomial for the area of the shaded region; then factor completely

20 201) 49(x + 3)2 - 64y2 A) 7(x + 3) - 8y 7(x + 3) + 8y B) 7(x + 3)2 - 8y 7(x + 3)2 + 8y C) 7(x + 3) - 7y 7(x + 3) - 8y D) (x + 3) - 8y (x + 3) + 8y 201) 202) (s + 7)3 - 8 A) (s2 + 5)(s2 + 16) B) (s + 5)(s2 + 16s + 67) C) (s + 5)(s2 - 9s + 53) D) (s - 5)(s2 - 16s + 67) 202) 203) (s + 3)3 - 27 A) s(s2 + 9s + 27) B) s(s + 3)(s9) C) (s - 3)(s2 - 9s + 27) D) s(s2 - 9s + 27) 203) 204) 8 - (m + 5n)3 A) [4 - (m + 5n)][(2 + 2(m + 5n) + (m + 5n)2] B) [2 - (m + 5n)][(4 + 2(m + 5n) + (m + 5n)2] C) [2 - (m + 5n)][(4 - 2(m + 5n) + (m + 5n)2] D) [2 - (m + 5n)][(4 + (m + 5n)2] 204)
205) 4x2 + bx + 9 A) 72 B) 6 C) 12 D) 36 205) 206) 49x2 - bx + 16 A) 56 B) 784 C) 28 D) 1568 206) 207) x2 + 16x + b 207) A) 8 B) 256 C) 16 D) 64 208) x2 - 18x + b A) 18 B) 81 C) 324 D) 9 208) 209) 49x2 + 28x + b A) 196 B) 4 C) 2 D) 14 209) 210) 49x2 - 70x + b A) 5 B) 25 C) 1225 D) 35 210)
211)
211) 2 125 x
21 10x A) 2(x - 5)(x + 5) B) 10(x - 5)(x + 5) C) 5(x - 2)(x + 2) D) 10(x - 2)(x + 2)

22 212)
10x 18 212) 4 5x A) (4x + 5)(6x
5) B) (36x
25)2 C) (6x
5)(6x
5) D) (6x + 5)2 213)
213) 3x 2 1 4 x 9x A) (2x + 3)2 B) (2x - 3)(9x2 + 6x + 4) C) (3x - 2)(9x2 + 6x + 4) D) (3x - 2)2 214)
214) r 5 6r A) 6πr3 B) 6πr(x - 5)(x + 5) C) 150πr D) 6πr(x + 25) Factor
215) 64x2 + 49 A ) (
Write a polynomial for the area of the shaded region; then factor completely.
-
+
+
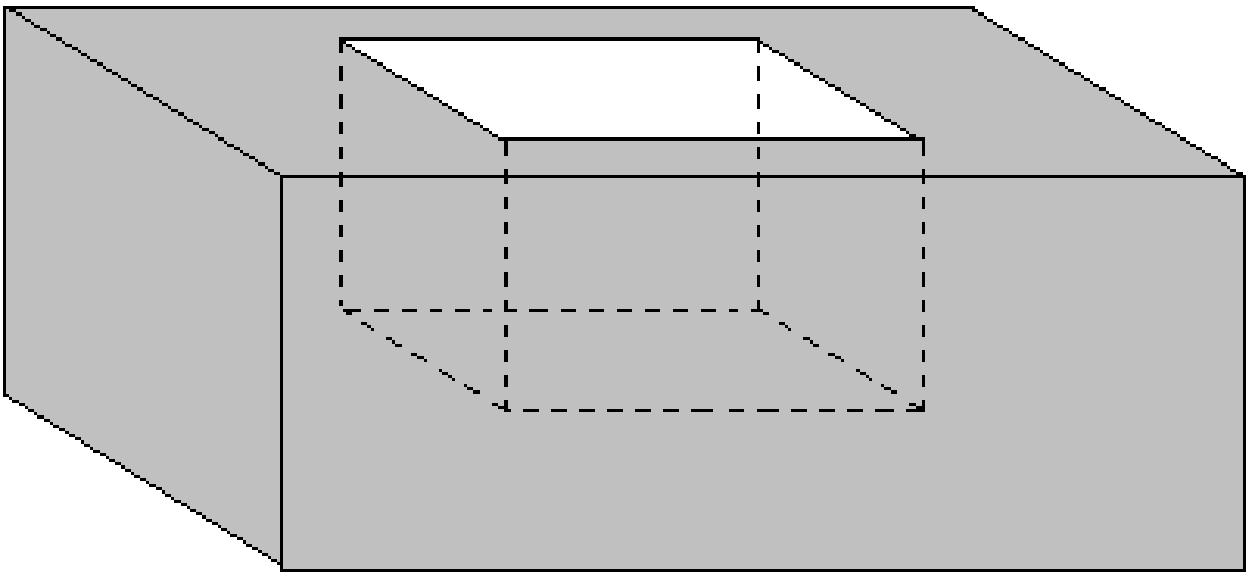
-
Write a polynomial for the volume of the region between the small box and the large box.
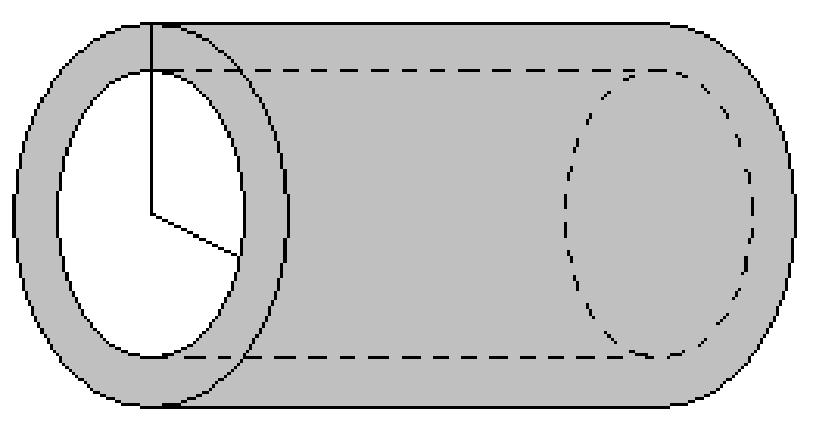
Write a polynomial for the volume of the region between the small cylinder and the large cylinder.
completely. If prime, so state.
23 8x + 7)(8x - 7) B) prime C) (8x - 7)2 D) (8x + 7)2 215)
24 216) w2 + s2 A) (w + s)(w + s) B) prime C) 1 w + 1 s 1 w1 s D) (w - s)(w + s) 216) 2 2 2 2 217) y4 - r4 A) (y + r)2(y - r)2 B) (y2 + r2)(y - r)(y + r) C) (y2 + r2)(y2 - r2) D) (y2 + r2)(y - r)(y - r) 217) 218) 32x2 - 8 A) 8(2x - 1)2 B) (16x + 8)(2x - 1) C) 8(2x + 1)(2x - 1) D) (2x + 1)(16x8) 218) 219) 98a4b - 8b3 A) 2b(7a - 2b)2 B) prime C) 2b(7a2 + 2b)(7a2 - 2b) D) 2b(7a + 2b)2 219) 220) x4 - 625 A) prime B) (x2 - 25)(x + 5)(x5) C) (x2 + 25)(x + 5)(x - 5) D) (x + 5)2(x - 5)2 220) 221) 250k3m - 16m4 A) (10km - 4m2)(25k2 + 4m2) B) 2m(5k + 2m2)(25k2 - 10km + 4km2) C) 2m(5k - 2m)(25k2 + 10km + 4m2) D) 2m(125k - 2m)(k2 + 10km + 4m2) 221) 222) 27s3 + 1 A) (3s - 1)(9s2 + 3s + 1) B) (3s + 1)(9s2 + 1) C) (27s + 1)(s2 - 3s + 1) D) (3s + 1)(9s2 - 3s + 1) 222) 223) 81 - 25y2 A) (9 + 5y)2 B) (81 + 25y)(8125y) C) (9 - 5y)2 D) (9 + 5y)(95y) 223) 224) m3 - 9m4 A) m4(m - 9) B) m2(1 + 3m)(13m) C) m3(1 - 9m) D) m3(9m) 224) 225) x2 + 17x + 18 A) (x + 6)(x - 3) B) prime C) (x + 18)(x - 1) D) (x - 6)(x + 3) 225)
25 226) x2 - 5xy - 14y2 A) (x - y)(x + 2y) B) (x + 7y)(x - 2y) C) (x - 7y)(x + 2y) D) (x - 7y)(x + y) 226)
234) An object is dropped from a height of 100 feet The expression 100 - 16t2 gives the height of the falling object after t seconds. Factor 100 - 16t2.
235) The voltage in a circuit is the product of two factors, the resistance in the circuit and the current If the voltage in a circuit is described by the expression 18ir + 21i - 30r - 35, find the expressions for the current and resistance. (The expression for the current will contain i and the expression for resistance will contain r.)
3i - 5, resistance: 6r - 7
6r + 7
current: 3i + 5, resistance: 6r + 7
26 227)
A) prime B) 3x(x + 2y)(x5y) C) (3x2 + 6xy)(x - 5y) D) 3x(x - 2y)(x + 5y) 227) 228) 25x2 + 10x + 1 A) (5x + 1)(5x - 1) B) (5x + 1)2 C) prime D) (5x1)2 228) 229) 6x2 - 60x + 150 A) 6(x + 5)2 B) prime C) 6(x - 5)2 D) (6x60)2 229) 230) 20x2 - 15x + 12x - 9 A) (20x - 3)(x + 3) B) (20x + 3)(x - 3) C) (5x + 3)(4x - 3) D) (5x - 3)(4x + 3) 230) 231) 40m9 + 12m7 - 12m3 A) 4m3(10m6 + 3m4 - 3) B) No common factor C) m3(40m6 + 12m4 - 12) D) 4(10m9 + 3m73m3) 231) 232) x3 - x2 - 81x + 81 A) (x - 1)(x2 - 81) B) (x - 1)(x - 9)2 C) (x - 1)(x2 + 81) D) (x - 1)(x + 9)(x9) 232) 233) 7x2 + 7xy + y2 A) 7(x + y)2 B) (7x + y)(x - y) C) (7x + y)(x + y) D) prime 233) Solve.
3x3 + 9x2y - 30xy2
A) 4(5 + 2t)(5 - 2t) B) 8(5 + 2t)(5 - 2t) C) 16(5 + t)(5 - t) D) 2(5 + 4t)(54t) 234)
A)
B)
C) current: 3i
resistance:
D) current:
resistance:
35 235)
current:
- 5,
18i + 1,
r -
SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question. Provide an appropriate response.
236) Is it always necessary to remove any GCF first when factoring? Why or why not?
237) After factoring out any greatest common factor, what should you consider when deciding how to factor a polynomial?
238) Recall that A = s2 is the formula for the area of a square. If the area of a square is represented by 4x2 - 28x + 49, how can the length of each side be represented?
236)
237)
238)
27
MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. 239) If the area of a rectangle is given by 64n2 - 25, find expressions for the length and width of the rectangle
SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question. 240) The formula for the volume of a rectangular solid is V = LWH. Let the following trinomial represent the volume of a rectangular solid Find monomials and/or binomials that could represent the length, width, and height
MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
using the zero-factor theorem.
28 244) B) 1, -11 C) -1, -11 D) 11, 0 245) C) 2, 0 D) 2, -10
A) n + 5, n - 5 B) 8n + 5, 8n + 5 C) 64n + 5, 64n - 5 D) 8n + 5, 8n5 239)
V = 4x3 + 12x2 - 40x 240)
Solve
241) (x - 8)(x + 3) = 0 241) A) 8, -8, 3, -3 B) 8, -3 C) 8, 3 D) -8, 3 242) (8y + 13)(6y + 17) = 0 242) 8 6 13 17 13 17 A)5 ,17 B)8 ,6 C) 8 , 6 D) 5, 11 243) x(6x + 30) = 0 A) 0,1 5 B) 0, -5 C) 0, 5 D) 0, 1 5 243) 244) b(b + 11) = 0 A) -11, 0 245) (5y - 10)2(y + 10) = 0 A) -2, 10 B) 1 , -10 2 Solve 246) n2 - 9 = 0 246) A) -3, 3 B) 0, 3 C) 3 D) -3 247) x2 + 9x - 36 = 0 A) 12, 3 B) 12, -3 C) -12, 3 D) -12, 1 247) 248) 5x2 - 30x + 40 = 0 A) -2, -4 B) 0, 2, 4 C) 2, 4 D) 5, 2, 4 248)
29 249) 15y2 + 26y + 8 = 0 249) 4 2 A) 3 ,5 4 2 B) 3 , 5 4 1 C)15 ,4 4 2 D)3 ,5




















