Excerpts from (From recent issues)
The Energy Advocate A monthly newsletter promoting energy and technology P.O. Box 7609, Pueblo West, CO 81007 Copyright © The Energy Advocate
Input, Output, and Results At the risk of seeming too professorial, I will be discussing spectra, because there has been some nonsense floating around the Internet. Sunlight heats the earth, and infrared going out cools it, but understanding the balance requires knowing a few details. It is all too easy to draw an arrow to represent radiation and pretend to understand it. In this essay, we will discuss the complications: blackbody radiation and some variants, line spectra, band spectra, absorption spectra and emission spectra, to name a few.
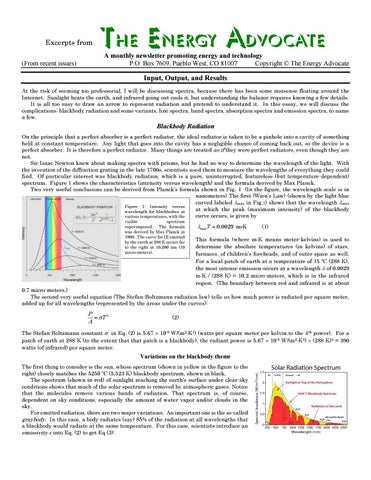
Blackbody Radiation On the principle that a perfect absorber is a perfect radiator, the ideal radiator is taken to be a pinhole into a cavity of something held at constant temperature. Any light that goes into the cavity has a negligible chance of coming back out, so the device is a perfect absorber. It is therefore a perfect radiator. Many things are treated as if they were perfect radiators, even though they are not. Sir Isaac Newton knew about making spectra with prisms, but he had no way to determine the wavelength of the light. With the invention of the diffraction grating in the late 1700s, scientists used them to measure the wavelengths of everything they could find. Of particular interest was blackbody radiation, which is a pure, uninterrupted, featureless (but temperature-dependent) spectrum. Figure 1 shows the characteristics (intensity versus wavelength) and the formula derived by Max Planck. Two very useful conclusions can be derived from Planck’s formula shown in Fig. 1 (In the figure, the wavelength scale is in nanometers) The first (Wien’s Law) (shown by the light blue curved labeled max in Fig.1) shows that the wavelength max Figure 1: Intensity versus at which the peak (maximum intensity) of the blackbody wavelength for blackbodies at curve occurs, is given by various temperatures, with the visible spectrum superimposed. The formula was derived by Max Planck in 1900. The curve for IR emitted by the earth at 288 K occurs far to the right at 10,200 nm (10 micro-meters).
maxT = 0.0029 m K
(1)
This formula (where mK means meter-kelvins) is used to determine the absolute temperatures (in kelvins) of stars, furnaces, of children’s foreheads, and of outer space as well. For a local patch of earth at a temperature of 15 ºC (288 K), the most intense emission occurs at a wavelength of 0.0029 mK / (288 K) = 10.2 micro-meters, which is in the infrared region. (The boundary between red and infrared is at about
0.7 micro-meters.) The second very useful equation (The Stefan-Boltzmann radiation law) tells us how much power is radiated per square meter, added up for all wavelengths (represented by the areas under the curves):
P = T 4 A
(2)
The Stefan-Boltzmann constant in Eq. (2) is 5.67 10-8 W/(m2K4) (watts per square meter per kelvin to the 4 th power). For a patch of earth at 288 K (to the extent that that patch is a blackbody), the radiant power is 5.67 10-8 W/(m2K4) (288 K)4 = 390 watts (of infrared) per square meter.
Variations on the blackbody theme The first thing to consider is the sun, whose spectrum (shown in yellow in the figure to the right) closely matches the 5250 ºC (5,523 K) blackbody spectrum, shown in black. The spectrum (shown in red) of sunlight reaching the earth’s surface under clear-sky conditions shows that much of the solar spectrum is removed by atmospheric gases. Notice that the molecules remove various bands of radiation. That spectrum is, of course, dependent on sky conditions, especially the amount of water vapor and/or clouds in the sky. For emitted radiation, there are two major variations. An important one is the so-called graybody. In this case, a body radiates (say) 85% of the radiation at all wavelengths that a blackbody would radiate at the same temperature. For this case, scientists introduce an emissivity into Eq. (2) to get Eq (3):