Design of fluid thermal systems si edition 4th edition janna solutions manual 1 by jodi.dillon505

Design of Fluid Thermal Systems SI Edition 4th Edition Janna

Full download at: Solution Manual: https://testbankpack.com/p/solution-manual-for-design-of-fluid-thermal-systems-si-edition-4thedition-by-janna-isbn-1305076079-9781305076075/

Chapter 4 OptimizationProblems

1. Find two positive numbers whose sum is 100, and whose product is as large as possible.

2. Find two positive numbers whose product is 100, and whose sum is as small as possible.

3. An open rectangular box has a square base, x by x. Find the height h of the box if its volume is 50 cm3 , and the material needed to construct it is a minimum.

4-1

4-1 100 dS 100 x dx = 1 x2

Solution: x + y = 100 xy = Product = P y = 100 x P = x(100 x) = 100x x2 dP dx = 100 2x = 0 x = 50 and y = 50

100 Solution: x + y = Sum = S xy = 100 y = x 2 S = x + = 0 x = 100 x = ±10 x = 10 y = 10 (Reject the negative value.)

Solution: Volume = x2h = 5 × 10 5 m3 Work in cm for

than

is the square cm of surface area = M = x2 + 4(hx) 5 × 10 5 2 h = x2 M = x + 4x 5 × 10 5 2 x2 = x + 2 × 10 4 x d M dx = 2x = 2 × 10 4 x2 = 0 x3 = 1 × 10 4 x = 0.0464 m h = 0.0232 m

this problemrather

m. Material

4. A window is shown in Figure P4.4. Find the value of r such that the perimeter of the window is 3 m, and the area of the window is as large as possible.

4-2

πr 2 A = 2 + 2rh P = πr + 2h + 2r = 3 m 3 2h = 3 πr 2r h = 2 πr 2 r r π r 2 3 A = 2 + 2r 2 d A π r 2 r π r 2 2 = 2 + 3r πr 2r2 h dr = πr + 3 2πr 4r = 0 3 r(π 2π 4) = 3 r = 4 π r = 0 42 m FIGURE P4.4

5. A rectangular area used to enclose machinery is to be fenced off using 300 m of material. What are the dimensions of such a rectangular enclosure if the area is maximized?

6. A large soup can is designed to hold 8.28 ×10 4 m3 of soup. The can diameter is r, and its height is h. Find the values of r and h, such that the amount of metal needed is as small as possible.

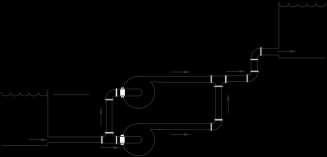
7. Figure P4.7 shows a pump and tank at A and a tank at B. It is desired to install a pipeline from A to B in the shortest possible distance. The pipeline is to be buried, and it will have to cross a roadway whose width is w. However, the roadway is used extensively by forklifts and other material handling equipment. So, to minimize the disruption involved, it is necessary for the pipeline to cross the roadway at a right angle, and the pipeline will therefore take the path indicated in the figure. Determine the minimum pipeline length from A to B; that is, determine the value of x that minimizes the distance between A and B [Hint: express the length equation in terms of c (= b a w) rather than b.]

Solution: Area = A = LW Perimeter = P = 2L + 2W = 300 m 2L = 300 2W L = 150 W A = (150 W)W = 150W W2 dA dW = 150 2W = 0 W = 75 m L = 75 m

Solution: Volume = πr 2h = 8 28 × 10 4 m3 = 828cm3 = V 828 Material needed = M = π(2r)h + 2πr 2 h = πr 2 828 2 1656 2 d M 1656 M = π(2r) πr 2 + 2πr = r + 2πr dr = r2 + 4πr = 0 1656 = 4πr 3 r = 5 08 cm h = 10 18 cm

Solution: a + w + c = b = a constant L = (a2 + x2)1/2 + w + [(d x)2 + c2]1/2 d L 1 2 2 1/2 1 2 2 1/2 dx = 2(a + x ) (2x) + 0 + 2[(d x) + c ] 2(d x)( 1) = 0 x (d x ) 0 (a2 + x2)1/2 [(d x)2 + c2]1/2 = x or (a2 + x2)1/2 (d x ) = [(d x)2 + c2]1/2 Squaring x 2 (a2 + x2) (d x )2 = [(d x)2 + c2] 2 2 2 2

c 2015 Cengage Learning All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 4-4 Inverting (a + x ) x2 = a2 [(d x ) + c ] (d x)2 c2 Simplify x2 + 1 = 1 + (d x)2

Note: Had we used the negative value in the square root step, the solution would be x =

would be negative, which has no physical meaning.

possible that c could be greater than a, and the denominator would be negative. In this

8. Aproduction facilityproducesmetalfasteners,andrealizesaprofit of$800permachinepermonthfor 10 machines. Each machine requires cooling water to keep it running effectively Management wishes to install more machinery, but the cooling water available cannot keep up with unlimited demand, and adding more machines would cause them all to run more slowly Each additional machine reduces profit by $25 per month. Thus with 10 machines, the profit is $8000 (= 800 × 10) For 11 machines, the profit is $8525 [= (800 25) × 11], Likewise for 12 machines, the profit is $9000 [= (800 2(25))×12]. Determinetheoptimumnumberofmachinesthatshouldbeinstalledto maximizeprofit.

Solution: N = number of machines P = profit = [800 (N 10)(25))N ]

9. The strength S of a rectangular beam is proportional to its width x and the square of its depth y, so that S = kxy2 where k is a positive constant. The beam is to be cut from a circular log whose

not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 4-5

not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 4-5 d B x w a b d N + a2 or x2 c2 = (d x)2 Square root a2(d x)2 = c2x2 a(d x) = ± cx Use the + Simplify ad ax = cx ad = x(a + c) a d Solve x = a c a d

× c 2015 Cengage

May

× c 2015 Cengage Learning

May

It is c

case x 0.75 m y A

FIGURE P4.7 FIGURE P4.8

d P P =

N = 1050N 25N2 = 1050 50N = 0

[800 25

+ 250]

N = 21 machines

diameter is 0 75 m. What are the dimensions of the strongest beam that can be cut from such a log?

(See Figure P4.9.)

Solution: S = kxy2 x2 + y2 = 0 75 x2 + y2 = 0 5625 m2

10. Figure P4.10 shows a rectangular open channel conveying a liquid. We wish to find a relationship among the variables that will yield a hydraulically optimum cross section, which is one that provides maximum conveyance or volume carrying capacity for a given flowarea.

Manning equation for flowrate in an open channel is

where A is the cross-sectionalarea, P is the perimeter, S is the channel slope, and n is a friction term. The flowrate Q can be maximized if the perimeter is minimized. The flowarea is given by A = bz. The perimeter is given by P = 2z + b.

Solve the area equation for b and substitute into the equation for perimeter. Differentiate the resulting equation for perimeter with respect to z and set the result equal to zero. Show that for a hydraulically optimum cross section

11. Figure P4.2 shows a trapezoidal open channel conveying a liquid. We wish to find a relationship among the variables that will yield a hydraulically optimum cross section, which is one that provides maximum conveyance or volume carrying capacity for a given flowarea.

The Manning equation for flowrate in an open channel is

× c 2015 Cengage Learning All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 4-7 × c 2015 Cengage Learning All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 4-7 2 x = 0 5625 y2 S = ky2 0 5625 y2 = ky2 (0 5625 y2)1/2 dS 2 1 2 1/2 2 1/2 dy = ky (0.5625 y ) 2 ( 2y) + k(0.5625 y ) (2y) = 0 1 y2 (0.5625 y2) 1/2 + (0 5625 y2)1/2 = 0 y 2 2 = 0 5625 y2 3 y 2 2 2 = 0 5625 y = 0 375 y = 0 612 m x = 0 433 m

The

Q = AV = ARh 2/3S1/2 n = A5/3S1/2 P2/3n

b z = 2 z z 1 b α b m

FIGURE P4.10 FIGURE P4.11

= ARh 2/3S1/2

= A5/3S1/2

/3n

where A is the cross sectional area, P is the perimeter, S is the channel slope, and n is a friction term.

4-8

The flowrate Q can be maximized if the perimeter is minimized. The flowarea is given by A = bz + z2 cot α. The perimeter is given by

Solve the area equation for b and substitute into the equation for perimeter. Differentiate the resulting equation for

Show that for a hydraulicallyoptimum cross section

12. The figureshows a heat exchanger that consists of a shell of inside diameter ID, and length L Inside the shell are a number of tubes. One fluidflowsthrough the tubes, and another in the shell outside the tubes. Calculations on such an exchanger yield results about the surface area required to exchange heat between the two fluids;specifically,how many tubes and how large a shell are needed to transfer the required heat.

The cost of the shell of inside diameter D and length L (both in ft) is given by

Typically, to obtain the preceding equation, we would need data on heat exchanger costs, and derive the cost equation by using curve fitting techniques. This method is not difficult, but gathering and obtaining the necessarydata could be cumbersome.

4-9

4-9 = = 2√ = + 2 = + √ 3 = =

2z P = b + sin α z 1 α b m

2 √ 3 FIGURE P4.2 A z2 cot α A b = 3 z 2z d P A 2 b z P z z cot α + sin α dz = z2 cot α + sin α = 0 z2 = A sin α 2 cos α dz 2z dα = A 1 (2 cos α) cos α sin α(sin α) (2 cos α)2 = 0 reduces to 2cos α 1 = 0 cos α = 2 α = 60◦ Substituting into z2 = A sin α 2 cos α A = √ 3 z2 A z 3 with A bz z cot α bz 3 z2 Setting both area equations equal, z 2√ 3 = bz + √ giving 2 √ 3 b z 3

= $1,800D2 5L (i)

One problem with such exchangers is that the tube and shell surfaces will become fouled. They will have deposits of minerals or other substances on the surfaces that retard the flow of heat. The heat exchanger will of necessity have to be cleaned annually. The cost of cleaning is an annual cost, but the manufacturer will clean the exchanger for an initial one time fee given by:

Cf = $350DL (ii)

× c 2015 Cengage Learning All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 4-10 × c 2015 Cengage Learning All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 4-10

The firstcost of the heat exchanger tubing that will be contained within the exchanger is given by

Ct = $2,000 (iii)

Thus, the firstcost of the exchanger is given by the sum of Equation i, ii and iii:

C = 1,800D2 5L + 350DL + 2,000

This cost equation is to be minimized in this problem.

Now tube spacing within a shell and tube heat exchanger is dictated by safety concerns as well as performance requirements. The more tubes we can fit into the exchanger, the greater the surface area, and correspondingly, the greater the heat transfer rate. However, the tubes must fit together into a leakproof configuration without weakening the structure of the heat exchanger itself. Ordinarily, we would have an idea of the required tube surface area, and hence tube diameter, that must be used for the heat transfer requirements. From such calculations, suppose it is known that a total tube length of 150 m must be used. That is, the shell area × tube length per area should equal 150 m. Thus

(At L m3)(200 tubes/m2) = 150 m

In terms of shell diameter, the preceding equation (our constraint) becomes

πD2

4 L(200) = 150

Determinethe diameter D and length L ofthe heat exchangershell for minimumfirst cost conditions.

× c 2015 Cengage Learning All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 4-11 × c 2015 Cengage Learning All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 4-11 D2 L ID

Solution: Solve the constraint equation for L = 0 75(4)/πD2 = 0 955/D2 Substitute into the cost equation: 0 955 C = 1,800D2 5L + 350DL + 2,000 = 1,800D2 5 + 350D 0 955 D2 + 2,000 C = 1718 9D0 5 + 334 25 D dC + 2,000 Take d D = 0 d C 0 5 334 25 0 5 334 25 d D = 0 = 0 5(1718 9)D − D2 859 5D = D2

× c 2015 Cengage Learning All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 4-12 × c 2015 Cengage Learning All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 4-12 D1 5 = 0.388 9 D = 0.533 m

13. Shown in Figure P4.4 are two pumps connected in parallel that move water from one tank up to another The total volume flow rate to be delivered is a known quantity, Q = 0 01 m3/s. To deliver this flowrate, calculations indicate that the pressure rise to be provided by each pump is given by:

Δ p1 = C1Q1 2 and Δ p2 = C2Q2 2 (i) where Δp is in Pa, and the flowrates are in m3/s for lines 1 and 2, respectively The two pump/motor combinations are nearly identical. The efficiencyof both pumps is η = 0 75. Determine an equation for the volume flowrates required to minimize the total power by completing the following steps:

a. The power delivered by either pump is given by

Assuming no changes in kinetic or in potential energies, verify that the power equation reduces to dW dt = ΔpQ

Accounting for the pump efficiency,we have dWa dt = ΔpQ η

Substituting for the pressures, show that the total power is given by:

dWa dt = total

C1Q1 3 η + C2Q2 3 η

which is our objective function.

The total flow Q was given so

Q2 = Q Q1

h 2 Q1 Q Q2 Q 1

FIGURE

∂W p V 2 p V 2 ∂t = ρAV ρ + 2 + gz out ρ + 2 + gz in

P4.4

which is the constraint. Substitute the constraint equation into the total power equation. Differentiate the resulting equation, and set the result equal to zero. Show that Q1 is given by:

× c 2015 Cengage Learning All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 4-14 × c 2015 Cengage Learning All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 4-14

C2 Q ± C2 2 Q 2 + (C1 C2 )C2 Q 2 Q1 = (C1 C2)

b. If C1 = 2.5 × 1010 and C2 = 3.4 × 1010 , calculate the flowrates required for minimum power. Show that for minimum power,

Q1 = 0.005 4 m3/s and Q2 = 0.004 6 m3/s

c. Show that the minimum power is 9 6 kW.

14. The inlet to a wind tunnel is in the shape of a converging duct, as shown in the figure. The duct is configured such that the x axis is coincident with the axial direction. The area of the duct at any location is given by

A = 3 5 2 5x/3 (in m2) (i)

It is desired to locate the place where flowstraighteners will be placed. The cost of the straighteners is proportional to the flowarea and is given by

C = C1 An

where A is area, C1 is a constant, and n is another constant. The annual cost of the straighteners is found by multiplying the preceding equation by an amortization rate a:

CS = aC1 An

The pressure drop across the straighteners is given by

where K is the minor loss associated with the straighteners.

a. Express velocity in terms of flowrate and area, and pressure drop in terms of Δh(= Δpgc/ρg) Show that

2 Δh = 2A2g

The pumping cost associated with this loss is

KQ2

CP = C2Δh = C2 2A2g

where C2 is a constant. Verify that the total cost is given by

KQ2

CT = aC1 An + C2 2A2g

b Differentiate this expression with respect to area A, and solve for the optimized area Aopt

c. Substitute Equation i for area and solve for x

d. For the following conditions, determine a numerical value for x:

Q = 30 m3/s a = 0 5/yr C1 = $200/(m2)n C2 = $20 80/m

K = 0 75 n = 1 1

K ρV 2

Δp =

15. The inlet in an open channel that feeds a pump is in the shape of a converging duct as shown in the figure. The duct is configured such that the x axis is coincident with the axial direction. The area of the duct at any location is given by

4-16

c = 3 m r A x

Solution: Δpgc ρV 2 gc V 2 Q 2 Q 2 Δh = ρg = K 2g ρg = K 2g V = A V = A2 Q 2 1 KQ2 n KQ2 Δh = K A2 2g CP = C2Δh = C2 2A2g CT = aC1 A + C2 2A2g dCT d A = anC1 An−1 2C2 KQ2 2A3g = 0 anC1 An−1 = 2C2 KQ2 2A3g A3+n−1 = C2KQ2 anC1g 1 C2 KQ2 n+2 A C1 ang 1 C2 KQ2 n+2 2 5x 1 C2 KQ2 n+2 A = 3 5 2 5x/3 = C1 ang 3 = 3 5 C1 ang 1 C2 KQ2 n+2 20.80 0 75(30)2 1 3 1 x = 4.2 1.2 C1 ang = 4.2 1.2 200 0 5(1 1)(9 81) x = 1 45 m

flow straighteners

× c 2015 Cengage Learning All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 4-17 × c 2015 Cengage Learning All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 4-17 A = 2 79 3 35x/2 + x 2/2 (in m2) (i)

where x varies from 0 to 1 83 m. It is desired to locate the place where flow straighteners will be placed. The cost of the straighteners is proportional to the flowarea and is given by

C = C1 An

where A is area, C1 is a constant, and n is another constant. The annual cost of the straighteners is found by multiplying the preceding equation by an amortization rate a:

CS = aC1 An

The pressure drop across the straighteners is given by

where K is the minor loss associated with the straighteners. If we express velocity in terms of flow rate and area, and pressure drop in terms of Δh(= Δp/ρg), we obtain

The pumping cost associated with this loss is

where C2 is a constant.

a. Verify that the total cost is given by KQ2

CT = aC1 An + C2 2A2g

b Differentiate this expression with respect to area A and solve for the optimized area Aopt

c. Substitute Equation i for area and solve for x.

d. For the following conditions, determine a numerical value for x:

Q = 10 76m3/s a = 0 2/yr C1 = 1441/(m2)n C2 = $1969/m

K = 0 10 n = 1 8

× c 2015 Cengage Learning All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 4-18 × c 2015 Cengage Learning All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 4-18 1.83 m flow straighteners r A x

ρV 2 Δp = K 2

KQ2 Δh

2A2g

KQ2 CP = C2Δh

C2 2A2g

+ 1 = 2 Solution: Δp ρV 2 gc V 2 Q 2 Q 2 Δh = ρg = K 2 ρg = K 2g V = A V = A2 Q 2 1 KQ2 n KQ2 Δh = K A2 2g CP = C2Δh = C2 2A2g CT = aC1 A + C2 2A2g dCT d A = anC1 An−1 2C2 KQ2 2A3g = 0 anC1 An−1 = 2C2 KQ2 2A3g A3+n−1 = C2KQ2 anC1g 1 C2 KQ2 n+2 A C1 ang 3 35 x 2 1 C2 KQ2 n+2 2 1 C2 KQ2 n+2 A = 2 79 2 x 2 = C1 ang x 3 35x + 5 58 = 2 C1 ang x2 3.35x + 3 35 2 2 1 C2 KQ2 n+2 = 2 C ang 5.58 + 3 35 2 2 3 35 2 ⎡ C 1 ⎤ KQ2 n+2 x 2 = ⎣2 C1 ang 2 774⎦ 3 35 ⎡ 1 C2 KQ2 n+2 ⎤1/2 x = 2 ± ⎣2 C1 ang 2.774⎦ 3 35 ⎡ 1969 0 1(10 76)2 1 3 8 ⎤1/2 x = 2 ± ⎣2 1441 0 2(1 8)(9 81) 2 774⎦ = 1 675 ± 0 44 x = 2 115 m or 1 235 m. We select 1.235 m

duct

1 83 m in

because the

is only

length. Thus

x = 1 235 m

16. Thedevelopment regardingoptimumeconomicdiameterwasformulated usingpipecostsexpressedas

C = C1 Dn

Suppose instead that we use a parabolic curve fit:

C = Bo + B1 D + B2 D2

Following the development in the text, formulate an equation for the pipe costs; differentiate it and set it equal to zero. Show that the condition for minimum cost is given by

× c 2015 Cengage Learning All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 4-20 × c 2015 Cengage Learning All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 4-20

Economic Diameter

17. Using the information in Table 4.2, verify that Equation 4.10 is dimensionallyconsistent.

Solution:

Inproblemsof this type, the unit “ year”becomesfundamental,and maybe treated just like F, L, M, T

, actually $/yr; we use yr instead of T(time), and yr will not cancel with T expressed in yr seconds, or hours, etc.

T = PT + O P = + + o + 1 + 2 + η or 40 f m ˙ 3 C2 t 1/6 Dopt = Solution: (a + b)(1 + F)(2B2 Dopt + B1)ηπ2ρ2 C = Bo + B1D + B2D2 CP F = (1 + F)(Bo + B1 D + B2 D2) C LC C (a b)(1 F)(B B D B D2)L mC2 t ΔHg + 8 fLm3 C2 t dCT η 8 fLm3 C2 t π2ρ2 D5 η d D = (a + b)(1 + F)(B1 + 2B2D)L 5 π2ρ2 D6 η = 0 40 fLm ˙ 3 C2 t (a + b)(1 + F)(B1 + 2B2D)L = π2ρ2 D6 where D = Dopt ; L cancels Dopt 6 = 40 f m3 C2 t (a + b)(1 + F)(B1 + 2B2Dopt )π2ρ2η 40 f m3 C2 t 1/6 Dopt = (a + b)(1 + F)(B1 + 2B2Dopt )π2ρ2η

(a + b)(1 + F)C1 DnL = (1/yr + 1/yr)(1 + dimensionless) MU Ln)L = MU (checks) Ln+1 ( yr mC2 t (H H ) g M MU T L F T2 (L) MU(checks) η 2 1 gc = T F·L yr T2 M·L = yr 8 fLm ˙ 3 C2 t M M M MU T L

18. Beginning with Equation 4.10, derive Equation 4.12.

Solution: Easy but length derivation.

× c

Cengage Learning All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 4-22 = T T T F L yr π2ρ2 D5gc η = M M 5 M L MU (checks) yr L3 L3 L F T2

2015

19. Verify that Equation 4.12 is dimensionallyconsistent.

It is.

Dopt = L (Dimensionally OK)

20. Verify that the derivation of Equation 4.14 is correct, beginning with Equation 4.12.

Solution: Easy Derivation.

21. Verify that Equation 4.14 is dimensionallycorrect.

Dimensions cancel; dimensionlessresult.

22. Showninthe accompanying chartaredataonthecostofPVCplasticpipeobtainedfromtheclassified section of a newspaper:

Nominal Diameter (schedule 40) in Inches Cost per m (clearance prices) 2 $1 84 3 $4 43 4 $5 12

a. Construct a graph of the data on linear paper

4-23

4-23 1 ⎣ ⎦

⎡ M M M MU T 1 ⎤ n+5 Dopt = ⎢ T T T F·L yr ⎥ = [Ln+5] n+5 ⎢ 1 1 MU M M M·L ⎥ yr + yr Ln+1 L3 L3 F T2

Solution:

Solution: F T2 M L F T2 M L F T2 M L F T2 M L M M L2 T T F T L2 F T n L2 F T 2n L2 F T n L2 F·T· 2n 1/6 4n M L F T 1 MU M M F L yr Tn Fn Tn Mn·Ln · yr Ln+1 L3 L3 MU T

6 $13 10 8 $26 12

b. Construct a graph of the data on log-log paper.

c. Determine the parameters of the following equation:

C p = C1 Dn

where C p has dimensions of MU/L, C1 has dimensions of MU/Ln+1 evaluated numerically for 12-nominal pipe, and D has dimensions of L

Cengage Learning All Rights

be scanned, copied

duplicated, or posted to a publicly accessible website, in whole or in part. 4-15

All Rights

copied

duplicated, or posted to a publicly accessible website, in whole or in part.

× c 2015

Reserved. May not

× c 2015 Cengage Learning

Reserved. May not be scanned,

4-15

Cost/ft = 0 1248D1 9402 (in which 0.1248 corresponds to the cost of 1 nominal)

Cost/ft = 15 49D1 9402 (in which 15.49 corresponds to the cost of 12 nominal)

23. Repeat Problem22 for the following data, which are of PVC high-pressureplastic pipe:

Nominal Diameter Cost per meter (schedule 40) in Inches (clearance prices)

Solution:

The nominaldiameter data is to be changed to m, which is the fundmentalunit for length in SI. When this is done, the following equation and graphs result:

Cost/foo t ($/ft) Cost/m ($/m) Cost/m ($/m) Cost/foo t ($/ft) Solution: 9 8 7 6 5 4 3 2 1 0 0 2 4 6 8 10 Nominal diameter in inches 10 1 0.1 1 10 100 Nominal diameter in inches

4 $9.92/m 8 $26.12/m 10 $39.24/ m 12 $52.36/m

Cost/m = 306 09D1 51 60 50 40 30 20 10 0 0 0.2 0.4 Nominal diameter in m 100 10 1 0.1 1 Nominal diameter in m

24. A galvanized steel pipeline conveys ethyl alcohol at a rate of 0.04m3/s. Determine the optimum economic pipe size for the installation given that:

We begin by obtaining properties from the appropriate tables:

Substituting into the optimum economic diameter equation:

The Reynolds number of the flowis given by:

Assume a randomly selected friction factor; f = 0.030, and substitute into Equation i:

Rights

be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 4-15

Reserved.

be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 4-15

× c 2015 Cengage Learning All

Reserved. May not

× c 2015 Cengage Learning All Rights

May not

C2 = $0.05/kwh n = 1.2 C1 = $1100/mn+1 a = 1/10 = 0 10 t = 6000 hr/yr b = 0.01 F = 6 75 η = 0 75

ethyl alcohol ρ = 787 kg/m3 μ = 1 095 × 10 3N s/m2 [Table B.1] galvanized steel ε = 0 000152 m [Table 3.1]

the volume

Q = 40 01/s = 0 0400m3/s, the mass flowrate is m ˙ = ρ Q = 0.787(1 000)(0.0400) = 31.48 kg/s

1 40 f m ˙ 3 C2 t n+5 0 1613 Dopt = n(a + b)(1 + F)C1ηπ2ρ2 = 0.2150 f (i)

Solution:

With

flowrate given as

ρVD 4ρ Q 4m ˙ Re = μ = πDμ = πDμ Re(D) = 3 66 × 104

Dopt = 0.2150(0.030)0 1613 = 0.122 Then Re = 3 66 × 104/0 122 = 3 00 × 105 ⎫ ⎪ ⎬ f = 0.022 (S-J Eq) ε 0.000152 D = 0.122 = 0 00125 Substituting into Equation (i), Dopt = 0 2150(0 022)0 1613 = 0 116 m Then Re = 3 66 × 104/0 116 = 3 16 × 105 ⎫ ⎪ ⎬ f ≈ 0 022 (S-J Eq) ε 0.000152 D = 0 116 = 0 00131 which equals

our assumed value. So

× c 2015 Cengage Learning All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 4-16 × c 2015 Cengage Learning All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 4-16 Dopt = 0 116 m (close enough)

25. A commercialsteel pipeline conveysethylene glycol at a rate of 0.015 m3/s. Determine the optimum economic pipe size for the installation given that:

We begin by obtaining properties from the appropriate tables:

The Reynolds number of the flowis given by:

duplicated,

accessible website, in whole or in part. 4-17

copied

duplicated, or

to a publicly accessible website, in whole or in part. 4-17

or posted

a publicly

posted

C2 = $0.04/kwh n = 1.2 C1 = $1050/mn+1 a = 1/7 = 0 14 t = 7000 hr/yr b = 0.01 F = 6 5 η = 0 75 Solution:

ethylene glycol ρ = 1100 kg/m3 μ = 16 2 × 10 3 N s/m2 [Table B.1] commercial steel ε = 0 000046 m [Table 3.1]

the volume

Q = 0.0150 m3/s, the mass

m = ρ Q = 1 1(1000)(0 0150) = 16 50 kg/s Substituting into

1 40 f m3 C2 t n+5 0 1613 Dopt = n(a + b)(1 + F)C1ηπ2ρ2 = 0 1341 f (i)

With

flowrate given as

flowrate is

the optimum economic diameter equation:

ρVD 4ρ Q 4m Re = μ = πDμ = πDμ Re(D) = 1.30 × 103 Assume a randomly selected friction

f = 0.030, and

into Equation i: Dopt = 0 1341(0 030)0 1613 = 0 076 Then Re = 1 30 × 103/0 076 = 1 70 × 104 ⎫ ⎪ ⎬ f = 0 028 (S-J Eq) ε 0 000046 D = 0 076 = 0.00060 Substituting into Equation (i), Dopt = 0 1341(0 028)0 1613 = 0 075 m Then Re = 1.30 × 103/0.075 = 1.72 × 104 ⎫ ⎪ ⎬ f ≈ 0 028 (S-J Eq) ε 0 000046 D = 0 075 = 0 00061 which equals our assumed value. So

factor;

substitute

26. A commercial steel pipeline conveys kerosene at a rate of 1.893 × 10 4m3/s. Determine the optimum economic pipe size for the installation given that:

Solution: We begin by obtaining properties from the appropriate tables:

The Reynolds number of the flowis given by:

Substituting, we get

Start by assuming a randomly selected friction factor, f = 0 030, and substituting:

Again, substituting into Equation (i),

website,

4-17

accessible website, in whole

in part.

⎪

C2 = $0 01/kwh n = 1 4 C1 = $1990/mn+1 a = 1/7 = 0 14 t = 7800 hr/yr b = 0 01 F = 6 5 η = 0 8

Kerosene ρ = 823 kg/m3 μ = 1 64 × 10 3 N s/m2 [Table B.1] commercial steel ε = 0 014 mm [Table 3.1]

volume flowrate is

as Q = 1 893 × 10 4m3/s. The mass flowrate is calculated as m ˙ = ρ Q = 823 × 1.893 × 10 4 = 0.156 kg

1 40 f m3 C2 t n+5 0 1563 Dopt = n(a + b)(1 + F)C1ηπ2ρ2 = 0 0126 f (i)

in whole or

part.

4-17

The

given

Substituting into the equation for optimum diameter gives:

ρVD 4ρ Q 4m ˙ Re = μ = πDμ = πDμ

Re = 121/D

Dopt = 0.0126

030)0 1563 = 0

00728 m Then Re = 121/0 00728 = 1 66 × 104 ⎫ ⎪ ⎬ f = 0.031 (S-J Eq) ε 0 014 D = 7.28 = 0 0019

(0.

Dopt = 0 0126(0 031)0 1563

0 00728 m Then Re = 121/0 00728 = 1 66 × 104 ⎫ ⎬ ε D = 0 00192 ⎪ ⎭ f ≈ 0.031 (S-J Eq)

which equals our assumed value. So

Dopt = 0 00728 m = 7 28 mm (close enough)

4-18

27. A PVC pipeline conveys heptane at a rate of 0.1 m3/s. Determine the optimum economic pipe size for the installation given that:

We begin by obtaining properties from the appropriate tables:

With the volume flowrate given as Q

the mass flowrate is

the optimum economic diameter equation:

The Reynolds number of the flowis given by:

which equals our assumed value. So

scanned, copied

duplicated, or

to a publicly accessible website, in whole or in part. 4-19

copied or duplicated, or

to a publicly accessible website, in whole or in part. 4-19 ⎪ ⎪

posted

C2 = $0 05/kwh n = 1 2 C1 = $1300/mn+1 a = 1/10 = 0 10 t = 4000 hr/yr b = 0.01 F = 6 75 η = 0 75 Solution:

heptane ρ = 681 kg/m3 μ = 0 376 × 10 3N s/m2 [Table B.1] PVC ε = 0 [Table 3.1]

= 0 1000 m3/s,

m ˙ = ρ Q = 681(0 1000) = 68 10 kg/s

into

1 40 f m ˙ 3 C2 t n+5 0 1613 Dopt = n(a + b)(1 + F)C1ηπ2ρ2 = 0.2983 f (i)

Substituting

ρVD 4ρ Q 4m Re = μ = πDμ = πDμ Re(D) = 2 31 × 105

0 030,

Dopt = 0 2983(0 030)0 1613 = 0 169 Then Re = 2.31 × 105/0.169 = 1.36 × 106 ⎫ ⎬ ε D = 0 ⎪ ⎭ f = 0 011 (S-J Eq) Substituting into Equation (i), Dopt = 0 2983(0 011)0 1613 = 0 144 m Then Re = 2.31 × 105/0.144 = 1.60 × 106 ⎫ ⎬ ε D = 0 ⎪ ⎭ f ≈ 0 011 (S-J Eq)

Assume a randomly selected friction factor; f =

and substitute into Equation i:

opt = 0 144 m (close enough)

28. A drawn tubing pipeline conveys linseed oil at a rate of 0.0010 m3/s. Determine the optimum economic pipe size for the installation given that:

Solution: We begin by obtaining properties from the appropriate tables:

The

number of the flowis given by:

At this low value of the Reynolds number, we start by assuming laminar flow

Substituting into Equation i, we get

As a check on the laminar flowassumption, we calculate 36 36

= 1013.7 (laminar OK)

.7 = 0 0631

4-21

in part.

part.

4-21

2 = $0 04/kwh C1 = $700/mn+1 t = 7000 hr/yr F = 6 75 n = 1 2 a = 1/10 = 0 10 b = 0 01 η = 0 75

linseed oil ρ = 930 kg/m3 μ = 33 1 × 10 −3 N·s/m2 [Table B.1] drawn tubing ε = 0 000002 m [Table 3.1]

Q = 0 0010 m3/s,

mass

m ˙ = ρ Q = 0.93(1 000)(0.0010) = 0.93 kg/s

1 40 f m ˙ 3 C2 t n+5 0 1613 Dopt = n(a + b)(1 + F)C1ηπ2ρ2 = 0 0551 f (i)

ρVD 4ρ Q 4m ˙ Re = μ = πDμ = πDμ = 36/D

With the volume flowrate is given as

the

flowrate is calculated as

Substituting into the equation for optimum diameter gives:

Reynolds

64 f = Re = 64D 36

789D

Dopt = 0.0551 f 0 1613 = 0.0551(1.789Dopt)0 1613 = 0.061Dopt 0 1613 Solving yields Dopt(1 0 1613

061 or Dopt = 0 0353

= 1

) = 0.

m = 35 3 mm

0353

64 64 f = Re = 1013

= 0

× c 2015 Cengage Learning All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 4-22 × c 2015 Cengage Learning All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 4-22 and Dopt = 0 0551 f 0 1613 = 0 0551(0 0631)0 1613 Dopt = 0 0353 m = 35 3 mm

29. A commercial steel pipeline conveys methyl alcohol at a rate of 240.0 1/s. Determine the optimum economic pipe size for the installation given that:

We begin by obtaining properties from the appropriate tables:

The Reynolds number of the flowis given by:

be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 4-23

not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 4-23

× c 2015 Cengage

May not

× c 2015 Cengage Learning

May

C2 = $0.05/kwh n = 1 C1 = $700/mn+1 a = 1/10 = 0 10 t = 750 hr/yr b = 0.01 F = 6 75 η = 0 65 Solution:

methyl alcohol ρ = 789 kg/m3 μ = 0 56 × 10 3 N·s/m2 [Table B.1] commercial steel ε = 0.000046 m [Table 3.1]

the volume flowrate

as Q = 240 0 l/s = 0 2400 m3/s, the mass flowrate is m ˙ = ρ Q = 0 789(1 000)(0 2400) = 189 36 kg/s Substituting into

1 40 f m ˙ 3 C2 t n+5 0 1667 Dopt = n(a + b)(1 + F)C1ηπ2ρ2 = 0.4028 f (i)

With

given

the optimum economic diameter equation:

ρVD 4ρ Q 4m ˙ Re = μ = πDμ = πDμ Re(D) = 4 31 × 105 Assume

Dopt = 0 4028(0 030)0 1667 = 0 225 Then Re = 4 31 × 105/0 225 = 1 92 × 106 ⎫ ⎪ ⎬ f = 0.014 (S-J Eq) ε 0.000046 D = 0 225 = 0 00020 Substituting into Equation (i), Dopt = 0.4028(0.014)0 1667 = 0.199 m Then Re = 4 31 × 105/0 199 = 2 17 × 106 ⎫ ⎪ ⎬ f ≈ 0 015 (S-J Eq) ε 0.000046 D = 0 199 = 0 00023

a randomly selected friction factor; f = 0 030, and substitute into Equation i:

which equals our assumed value. So

Dopt = 0 199 m (close enough)

4-24

30. Octane flowsat a rate of 3.15 × 10 4m3/s through a pipeline made of drawn tubing. Determine the optimum economic pipe size for the installation given that:

We begin by obtaining properties from the appropriate tables:

The Reynolds number of the flowis given by:

Start by assuming a randomly selected friction factor, f = 0 030, and substituting:

not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 4-25 ⎪

× c 2015

× c 2015 Cengage Learning

May

C2 = $0 05 s/kwh n = 12 C1 = $750/mn+1 a = 1/5 = 0.20 t = 4000 hr/yr b = 0 01 F = 6 75 η = 0 75 Solution:

Octane ρ = 701 kg/m3 μ = 5 12 × 10 4 Pa·s [Table B.1] drawn tubing ε = 0 00152 mm [Table 3.1] The volume flowrate is given as Q = 3.15 × 10 4 m3/s. The mass flowrate is calculated as m ˙ = ρ Q = 701 × 3.15 × 10 4 = 0.221 kg/s Substituting into the equation for optimum diameter gives: 1 40 f m ˙ 3 C2 t n+5 0 1613 Dopt = n(a + b)(1 + F)C1ηπ2ρ2 = 0 0182 f (i)

ρVD 4ρ Q 4m ˙ Re = μ = πDμ = πDμ

Re = 550/D

Dopt = 0 0182(0 030)0 1613 = 0 01034 m Then Re = 550/0.01034 = 5.32 × 104 ⎫ ⎪ ⎬ f = 0 021 (S-J Eq) ε 0 00152 D = 10 34 = 0 00015 Again,

Dopt = 0 0182(0 021)0 1613 = 9 754 × 10 3 m Then Re = 550/9.754 × 10 3 = 5.63 × 104 ⎫ ⎬ ε D = 0 00015 ⎪ ⎭

Substituting, we get

substituting into Equation (i),

Cengage

not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 4-26

not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 4-26 f ≈ 0 021 (S-J Eq) which equals our assumed value. So Dopt = 9 75 × 10 3 m = 9 75 mm (close enough)

× c 2015

Learning

May

× c 2015

May

31. A drawn tubing pipeline conveys propane at a rate of 0.15

3/s. Determine the optimum economic pipe size for the installation given that:

We begin by obtaining properties from the appropriate tables:

or duplicated, or

to a publicly accessible website, in whole or in part. 4-27

duplicated, or

to a publicly accessible website, in whole or in part. 4-27

posted

C2 = $0 05/kwh n = 1 2 C1 = $850/mn+1 a = 1/6 = 0 17 t = 5000 hr/yr b = 0 01 F = 6 75 η = 0 65 Solution:

propane ρ = 495 kg/m3 μ = 0 11 × 10 3 N·s/m2 [Table B.1] drawn tubing ε = 0 000002 m [Table 3.1] With the volume flowrate given as Q = 150.0 l/s = 0.1500 m3/s, the mass flowrate is m = ρ Q = 0 495(1 000)(0 1500) = 74 25 kg/s Substituting into the optimum

diameter equation: 1 40 f m ˙ 3 C2 t n+5 0 1613 Dopt = n(a + b)(1 + F)C1ηπ2ρ2 = 0 3629 f (i)

Reynolds

ρVD 4ρ Q 4m ˙ Re = μ = πDμ = πDμ Re(D) = 8 59 × 105 Assume a randomly selected friction factor; f = 0 030, and substitute into Equation i: Dopt = 0 3629(0 030)0 1613 = 0 206 Then Re = 8.59 × 105/0.206 = 4.17 × 106 ⎫ ⎪ ⎬ f = 0.010 (S-J Eq) ε 0 000002 D = 0 206 = 0 00001 Substituting into Equation (i), Dopt = 0.3629(0.010)0 1613 = 0.172 m Then Re = 8 59 × 105/0 172 = 5 00 × 106 ⎫ ⎪ ⎬ f ≈ 0 010 (S-J Eq) ε 0 000002 D = 0 172 = 0 00001 which equals our assumed value. So

economic

The

number of the flowis given by:

× c 2015 Cengage Learning All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 4-28 × c 2015 Cengage Learning All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 4-28 Dopt = 0 171 m (close enough)

32. A galvanized steel pipeline conveys propylene glycol at a rate of 0.1 m3/s. Determine the optimum economic pipe size for the installation given that:

Solution: We begin by obtaining properties from the appropriate tables:

given as

Substituting into the optimum economic diameter equation:

The Reynolds number of the flowis given by:

be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 4-29

c 2015 Cengage

May not

× c 2015

C2 = $0.05/kwh n = 1.2 C1 = $1000/mn+1 a = 1/10 = 0 10 t = 4000 hr/yr b = 0.01 F = 6 75 η = 0 75

propylene glycol ρ = 968 kg/m3 μ = 42 × 10 3N·s/m2 [Table B.1] galvanized steel ε = 0.000152 m [Table 3.1]

= 100 0 l/s = 0 1000 m3/s,

mass

m = ρ Q = 0 968(1 000)(0 1000) = 96 80 kg/s

With the volume flowrate

the

flowrate is

1 40 f m ˙ 3 C2 t n+5 0 1613 Dopt = n(a + b)(1 + F)C1ηπ2ρ2 = 0 3294 f (i)

ρVD 4ρ Q 4m ˙ Re = μ = πDμ = πDμ Re(D) = 2 93 × 103

Dopt = 0.3294(0.030)0 1613 = 0.187 Then Re = 2 93 × 103/0 187 = 1 57 × 104 ⎫ ⎪ ⎬ f = 0 029 (S-J Eq) ε 0 000152 D = 0 187 = 0.00081 Substituting into Equation (i), Dopt = 0 3294(0 029)0 1613 = 0 186 m Then Re = 2.93 × 103/0.186 = 1.58 × 104 ⎫ ⎪ ⎬ f ≈ 0 029 (S-J Eq) ε 0 000152 D = 0.186 = 0 00082

Assume a randomly selected friction factor; f = 0.030, and substitute into Equation i:

which equals our assumed value. So

Dopt = 0 186 m (close enough)

4-30

33. A galvanized steel pipeline conveys castor oil at a rate of 0.0120 m3/s. Determine the optimum economic pipe size for the installation given that: C

We begin by obtaining properties from the appropriate tables:

With

Substituting into the equation for optimum diameter gives:

is calculated as

The Reynolds number of the flowis given by:

At this low value of the Reynolds number, we start by assuming laminar flow.

Substituting into Equation i, we get

As a check on the laminar flowassumption, we calculate 23 23

157 = 144 0 (laminar OK)

website,

4-31

in whole or in part.

$850

n+1 t =

hr/yr F = 6 75 n = 1 4 a

= $0.05/kwh

5000

= 1/7 = 0.14 b = 0.01

= 0.60

Solution:

castor oil ρ = 960 kg/m3 μ = 650 × 10 3N

/m2 [Table B.1] galvanized steel ε = 0 000152 m [Table 3.1]

ρ Q

the volume flowrate given as Q = 0 0120 m3/s, the mass flowrate

= 0 96(1 000)(0 0120) = 11 52 kg/

1 40 f m3 C2 t n+5 0 1563 Dopt = n(a + b)(1 + F)C1ηπ2ρ2 = 0 1778 f (i)

ρVD 4ρ Q 4m Re = μ = πDμ = πDμ = 23/D

64 f = Re

= 64D 23 = 2 836D

Dopt 0 1563

Dopt

or Dopt

opt = 0 1778 f 0 1563 = 0 1778(2 836Dopt)0 1563 = 0 209

Solving yields

(1 0 1563) = 0 209

= 0 157 m = 15 7 cm

f = Re

Re =

= 0

= 144 0 = 0 4443

× c 2015 Cengage Learning All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 4-32 × c 2015 Cengage Learning All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 4-32 and Dopt = 0 1778 f 0 1563 = 0 1778(0 4443)0 1563 Dopt = 0 1567 m