Introductory algebra for college students 6th edition blitzer solutions manual

6.1 Check Points

1. a. 32 22 1836 1535 xxx xx

 

TheGCFis23. x

b. 22 422 32

  

204(5) 1243 40410

xx xxx xxx

TheGCFis24. x



xyxyx xyxyxy xyxy  

TheGCFis2xy

2. 222 6186636(3) xxx

3. 23222 253555575(57) xxxxxxx 



4. 5433233 32 151227353439 3(549) xxxxxxxx xxx





5. 3222 2 8142242721 2(471) xyxyxyxyxyxyxxy xyxyx



6. 453452332222 23322 162420444(6)45 4(465) abababababababab ababab  

7. a. GCFGCF 22 (1)7(1)(1)(7) xxxxx 

b. GCFGCF (4)7(4)(4)(7) xyyyx  

8. 3232



2 2

xxxxxx xxx xx

5210(5)(210) (5)2(5) (5)(2)





9. 3515(3)5(3) (3)(5) xyxyxyy yx  

270Copyright©2013PearsonEducation,Inc.

6.1 Concept and Vocabulary Check

1. factoring

2. greatestcommonfactor;smallest/least

3. false

4. false

6.1 Exercise Set

2. TheGCFof5and15x is5.

4. TheGCFof2 20 x and15 x is5. x

6. TheGCFof4 3 x and3 6 x is33. x

8. TheGCFof5 10 y , 2 20, y and5 y is5. y

10. TheGCFof23 ,3 xyxy ,and2 6 x is2 x

12. TheLCDof5463 18,6, xyxy and45 12 xy is436. xy

14. 9991 xx

16. 5551 yy

18. 1030103 xx

20. 3224843 xx

22. 266 xxxx

24. 22 2015543 yy

26.  322 615325 xxxx 

28.  2 11301130 yyyy

30.

46421015523 yyyy

32.

34.

22 1539353 yyyy 

Copyright©2013PearsonEducation,Inc.271

36. 43222 32282164 xxxxxx 

38. 53223 2613391323 yyyyyy 

40.  232642232 xxxxxx 

42. 2 1225 x cannotbefactoredbecausethetwoterms havenocommonfactorotherthan1.

44.    232 2

70.

72.

462223 223

 

xyxyxyxyxy xyxy

46. 2322271845xyxyxy 

 

939295 9325

xyxyxyyxyx xyxyyx

   2 2

48.  3232 2 181224 6324 xyxyxy xyxyx 

50. 22 15205(34) xx 

52. 43222 18963(632) xxxxxx 

54. 232 9123(34) abababab 

56. 32322 2432168(342) xyxyxyxyxyx 

58.  7107710xxxxx 

60.  38338xxxxx 

62.  9119911xyyyx 

64.   771 71 xxyxyxxyxy xyx  

84.

 

66.   52121521121 2151 xxxxxx xx

68.  2 97272 xxx

86.

2 2 972172 7291

xxx xx

 

272Copyright©2013PearsonEducation,Inc.

88.

90.

92.

94

96. Theareaofthesquareis2 4416. xxx  Thearea ofeachcircleis2 x  .Theareaofbothcirclesis

2 2. x  Sotheshadedareaistheareaofthesquare minustheareaofthetwocircles,whichis

 222 16228. xxx

98. a. Usetheformula,2 7216, xx fortheheightof thedebrisabovetheground.Substitute4for. x

227216724164

288161628825632

Therefore,theheightofthedebrisafter4 secondsis32feet.

b.  2 7216892 xxxx 

c. Substitute4for x inthefactoredpolynomial.

84924329832132

Youdogetthesameanswerasinpart(a)but thisdoesnotproveyourfactorizationiscorrect.

100. Usetheformulafortheareaofa rectangle, A lw .Substitute4714xx for A and7 x for w

Thelength, l,is  32 x units.

102. – 106. Answerswillvary.

108. doesnotmakesense;Explanationswillvary. Sampleexplanation:Youcanalwayscheckyour factoringbymultiplying.

110. makessense

112. true

114. true

116. Answerswillvary.Oneexampleis 432 48216 yyyy 

118. Thegraphsdonotcoincide.

FactorouttheGCFfromtheleftside.

 3632. xx  Changetheexpressiononthe rightsideto  32. x 

120. Thegraphsdonotcoincide.

Factorbygrouping.   222212 21 xxxxxx xx  

Changetheexpressionontherightsideto  21.xx

121.  2 2 71010770 1770 xxxxx xx

 



Graphbothequationsonthesameaxes.

24: xy x-intercept:−2; y-intercept:4



 

Thelinesintersectas 3,2.

Thesolutionsetis 3,2.

123. First,findtheslope  523 1 473 m 

Writethepoint-slopeequationusing 111and,7,2.mxy



yymxx yx yx

Note:If 4,5isusedas  11xy ,thepoint-slope equationwillbe 514 54 yx yx

     

Thisalsoleadstotheslope-interceptequation 9. yx

124. 248and246 

125. (3)(2)6and(3)(2)5 

126. (5)(7)35and(5)72 

6.2 Check Points

1. 256xx

Factorsof66,16,12,32,3 SumofFactors7755

Thefactorsof6whosesumis5,are2and3. Thus,256(2)(3). xxxx 

Check:

2 2 (2)(3)326 56 xxxxx xx

 

2. 268xx

Factorsof88,18,12,42,4 SumofFactors9966

Thefactorsof8whosesumis–6,are–2and–4. Thus,268(2)(4). xxxx 

Check:

2 2 (2)(4)428 68 xxxxx xx

 

3. 2310xx

11 217 217

  

Factorsof1010,110,15,25,2 SumofFactors9933

 

Nowrewritethisequationinslope-interceptform. 27 9 yx yx  

Thefactorsof–10whosesumis3,are5and–2. Thus,2310(5)(2). xxxx 

Check: 2 2 (5)(2)2510 310 xxxxx xx

 

274Copyright©2013PearsonEducation,Inc.

4. Thefactorsof–27whosesumis–6,are–9and3. Thus,2627(9)(3). yyyy 

5. Nofactorpairof–7hasasumof1. Thus,27 xx isprime.

6. Thefactorsof3whosesumis–4,are–3and–1. Thus,2243(3)(). xxyyxyxy 

7. Firstfactoroutthecommonfactorof2. x 322 26562(628) xxxxxx 

Continuebyfactoringthetrinomial. 322 26562(628) 2(4)(7) xxxxxx xxx  

8. Firstfactoroutthecommonfactorof2. 22 210282(514) yyyy 

Continuebyfactoringthetrinomial. 22 210282(514) 2(2)(7) yyyy yy  

6.2 Concept and Vocabulary Check

1. 20;12

2. completely

3. +10

4. 6

5. +5

6. 7

7. 2y

6.2 Exercise Set

2. 298xx

Factorsof88,18,1

SumofFactors99

Thefactorsof8whosesumis9are8and1. Thus,  29881. xxxx 

Check:  2 2 81188 98 xxxxx xx

 

4.   291472 2714;279 xxxx  

6.   21312112 11212;11213 xxxx 

8.   2134058 5840;5813 xxxx 

10.   281644 4416;448 xxxx 



12.   28771 717;718 yyyy 



14.   232874 7428;743 xxxx  

16.   252483 8324;835 yyyy 



18.   24551 515;514 xxxx 



20.   25661 516;615 xxxx 



22. 245xx isprimebecausethereisnopairof integerswhoseproductis5andwhosesumis4.

24.   2102173 7321;7310 yyyy 



Copyright©2013PearsonEducation,Inc.275

26. 2410xx isprimebecausethereisnopairof integerswhoseproductis−10andwhosesumis4.

21264164 16464;16412 wwww  

28.  

30. 





22272184 18472;18422 yyyy 

32. 

 21516161 16116;16115 rrrr 



34. 2155yy isprimebecausethereisnopairof integerswhoseproductis5andwhosesumis−15.

36. 



226824 248;246 xxyyxyxy  

38. 



2291427 2714;279 xxyyxyxy  

223065 6530;651 xxyyxyxy 

40.  

42.  

221880108 10880;10818 aabbabab 



44. 2 32136 xx

FirstfactorouttheGCF,3.Thenfactorthe remainingtrinomial.

22 321363712 334



xxxx xx

 



46. 

22 331836 332 yyyy yy

 



48. 

xxxx xx

 



22 210482524 283

50. 

 rrrrrr rrr



  54.   322 31518356 332

xxxxxx xxx

  56.   322 39543318 363

rrrrrr rrr

  58.  

43222 2

yyyyyy yyy

12351235 57

  60.  

43222 2

xxxxxx xxx

2212022120 1210

  62.  

43222 2

wwwwww www

  64.   22 201001202056 2032 xyxyyyxx yxx

35413531845 3315

  66.   322322 2323 3 xyxyxyxyxxyy xyxyxy

 

22 16809616(56) 16(6)(1) tttt tt   70. 22 336333(1211) 3(11)(1) xxxx xx   72. 22445(445) (9)(5) xxxx xx   74. 322 36243(28) 3(4)(2) xxxxxx xxx   76.  

68. 23028 21514 214

22222 222 2

xyxyzxz xyyzz xyzyz

  

276Copyright©2013PearsonEducation,Inc.

2 2

 

 

abxabxab abxx abxx





1336 1336 94

78. 

98. Inorderfor24xxb  tobefactorable, b mustbe anintegerwithtwopositivefactorswhosesumis4. Theonlysuchpairsare3and1,or2and2.





 2 2 3143 2244 xxxx xxxx



80. 



 20.50.060.60.1 0.60.10.06;0.60.10.5 xxxx 

82. 22111 3933 111112 ; 339333

xxxx   

   

84. a.

22 1632481623

b. Substitute3for t intheoriginalpolynomial:

22 16324816332348

1699648

144144

Substitute3for t inthefactoredpolynomial:

1631163331

Theanswersarethesame. Thisanswermeansthatafter3secondsyouhit thewater.

86. – 88. Answerswillvary.

90. doesnotmakesense;Explanationswillvary. Sampleexplanation:Thereareaninfinitenumberof suchpairs.

92. makessense

94. false;Changestomakethestatementtruewillvary. Asamplechangeis:Sometrinomialshavetwo identicalfactors.Forexample 269(3)(3). xxxx 

96. false;Changestomakethestatementtruewillvary. Asamplechangeis:24 x  isprime.

Therefore,thepossiblevaluesof b are3and4.

100. 22099 nn xx

Noticethat  22 nn xx 

xxxx xx

2220992099 911

nnnn nn

102.

Theboxhasthefollowingdimensions:

height=. x

Therefore,thevolumeis

whichisequivalenttothefactorizationabove.

104. Thegraphsdonotcoincide.

Changethepolynomialontherightto

Copyright©2013PearsonEducation,Inc.277

106. Thegraphsdonotcoincide.  

Step 1 2 5148(5)() xxxx 



xxxx xx 

Changethepolynomialontherightto  231. xx

 

107.  4235 4835 85 13

Thesolutionsetis{13}.

108. Graph6530 xy withasolidline.Sincethetest point(0,0)makestheinequalitytrue,shadethehalfplanethatcontainsthetestpoint.

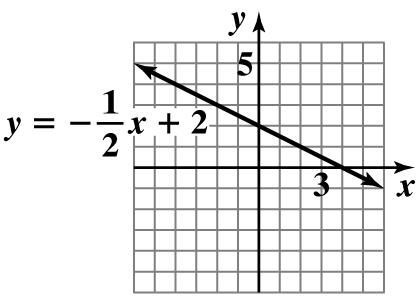
109 1 2 2 yx

The y-interceptis2.Findanadditionalpointby usingtheslope.Fromthe y-intercept,movedown oneunitandtotheright2units. Drawthelinethroughthesepoints.



110.  2 2 2322436 26 xxxxx xx 

111.

 2 2

9154 xxxxx xx

112. 2 822052(41)5(41) (41)(25) xxxxxx xx 

Step 2 Thenumber8haspairsoffactorsthatare eitherbothpositiveorbothnegative.Becausethe middleterm,14 x ,isnegative,bothfactorsmust benegative.

Step 3

PossibleFactorsofSumofOutsideand 5148InsideProducts (54)(2)10414 (52)(4)20222 (51)(8)4041 (58)(1)5813 xxxxx xxxxx

Check:

2 requiredmiddleterm

xxxxx xxxxx

xx    

2 2 (54)(2)51048 5148 xxxxx xx

 

Step 1 FindtwoFirsttermswhoseproductis26. x

2 6197(6)() xxxx 

2 6197(3)(2) xxxx 

Step 2 Thelastterm,–7,haspossiblefactorizations of1(7)and1(7).

Step 3

2 PossibleFactorsofSumofOutsideand 6197InsideProducts (61)(7)4241 (67)(1)67 (61)(7)4241 (67)(1)67 (31)(27)21219 (37)(21)31411 (31)(27)







xx xxxxx xxxxx xxxxx xxxxx xxxxx xxxxx xx   



 requiredmiddleterm 21219 (37)(21)31411 xxx xxxxx



Check: 2 2 (31)(27)62127 6197 xxxxx xx





Thus,26197(31)(27) xxxx  .

278Copyright©2013PearsonEducation,Inc.

3. Factor22 3134 xxyy  bytrialanderror.

Step 1 FindtwoFirsttermswhoseproductis22. x 22 3134(3)() xxyyxx 

Step 2 Thelastterm,24, y haspairsoffactorsthat areeitherbothpositiveorbothnegative.Because themiddleterm,13, xy isnegative,bothfactors mustbenegative.Thusthelasttermhaspossible factorizationsof2(2)or(4). yyyy

Step 3 22 requiredmiddleterm

6.3 Concept and Vocabulary Check

1. greatestcommonfactor

2. 3

3. 4

4. 2x 3

5. 3x+4

6. 2 xy

xxyy xyxyxyxyxy xyxyxyxyxy xyxyxyxyxy   

Check:

 



22 22 (3)(4)3124 3134 xyxyxxyxyy xxyy



Thus,223134(3)(4) xxyyxyxy 

4. Factor2310 xx bygrouping. 3and10,so3(10)30.acac 

Thefactorsof–30whosesumis–1are5and–6.

22 31035610

xxxxx xxx xx

  

(35)2(35) (35)(2)

5. Factor28103 xx bygrouping.  8and3,so8324.acac 

Thefactorsof24whosesumis–10are–6and–4. 22 81038463



xxxxx xxx xx





4(21)3(21) (21)(43)

6. FirstfactorouttheGCF. 43222 5136(5136) yyyyyy 

Thenfactortheresultingtrinomial. 43222 2 5136(5136) (53)(2) yyyyyy yyy

 

6.3 Exercise Set

2. Factor2352 xx bytrialanderror.

Step 1  2 3523 xxxx 

Step 2 Thenumber2haspairsoffactorsthatare eitherbothpositiveorbothnegative.Becausethe middleterm,5 x ,ispositive,bothfactorsmustbe positive.Theonlypositivefactorizationis 12.

Step 3

2 PossibleFactorsofSumofOutsideand 352InsideProducts



321325



31267

xx xxxxx xxxxx

Check:

  

 2 2 3213322 352 xxxxx xx

 

Thus,  2 352321. xxxx 

4. Factor2273 xx bytrialanderror. Theonlypossibilityforthefirsttermsis  2 22. xxx 

Becausethemiddletermispositiveandthelast termisalsopositive,theonlypossiblefactorization of3is 13.

2 PossibleFactorsofSumofOutsideand 273InsideProducts 21367 231235



 



xx xxxxx xxxxx



Thus,  2 273213 xxxx 

Copyright©2013PearsonEducation,Inc.279

6. Factor221935 xx bygrouping.  2and35,so23570.acac 

Thefactorsof70whosesumis19are14and5.



22 21935214535 2757 725

18. Factor232528 xx bygrouping. 3and28,so84.acac 

Thefactorsof−84whosesumis−25are3and−28.

xxxxx xxx xx









8. Factor25176 yy bytrialanderror.Thefirst termsmustbe5and. yy Becausethemiddletermis negative,thefactorsof6mustbe−3and−2or 1and6.



20. Factor261712 ww bygrouping. 6and12,so72.acac 

Thefactorsof72whosesumis−17are−8and−9.





5325136





yyyy yyyy yyyy yyyy



5235176



2 2 2 2

5165316 5615116



Thus,  2 5176523 yyyy 

10. Factor234 yy bygrouping. 3and4,so12.acac 

Thefactorsof12whosesumis1are4and3.



22 343434 34134 341

yyyyy yyy yy





 

12. Factor23145 xx bygrouping. 3and5,so15.acac 

Thefactorsof15whosesumis14are15and1.

22 31453155 3515 531

22. Factor27436 xx bygrouping. 7and6,so42.acac 

Thefactorsof42whosesumis43are42and1.

24. Factor232216 xx bytrialanderror. 

Becausethecorrectfactorizationhasbeenfound, thereisnoneedtotryadditionalpossibilities. Thus,  2 32216328 xxxx  .

xxxxx xxx xx

  





14. Factor23107 xx bytrialanderror. 

 2 2 3173227 3713107 xxxx xxxx

 

Thus,  2 3107371 xxxx  .

16. Factor2583 yy bytrialanderror.Thesignsof bothfactorsmustbenegative.



 2 2 5135163 531583 yyyy yyyy

 

Thus,  2 583531. yyyy 

26. Factor26724 yy bytrialanderror.Tryvarious combinationsuntilthecorrectoneisobtained.











342661024 342661024 38236724 38236724



2 2 2 2





yyyy yyyy yyyy yyyx

Thus,  2 67243823 yyyy  .

28. Factor2932 xx bygrouping. 9and2,so18.acac  Therearenofactorsof18whosesumis3. Therefore,2932 xx isprime.

280Copyright©2013PearsonEducation,Inc.

30. 2 9124 zz

Usetrialanderroruntilthecorrectfactorizationis obtained.Thesignsinbothfactorsmustbepositive.







2 2 34319154 32329124 zzzz zzzz



Thus,  2 91243232 zzzz 

32. Factor215132 yy bygrouping. 15and2,so30.acac 

Thefactorsof−30whosesumis13are15and−2.

22 15132151522

40. 2 954 yy

Usetrialanderroruntilthecorrectfactorizationis obtained.Thesignmustbenegativeinonefactor andpositiveintheother.





 

yyyyy yyy yy





34. 2 351 xx







15121 1152

Usetrialanderror.Thesignsinbothfactorsmust benegative.



2 311341 xxxx 

Therearenootherpossiblecombinationstotry, so 2 351 xx isprime.

36. 2 164615 yy

Usetrialanderror.Thesignsofbothfactorsmust benegative.Tryvariouscombinationsuntiltheone withthecorrectmiddletermisfound.



41415166415



852383415



832584615



Thus,  2 1646158325. yyyy 

38. Factor28225 xx bygrouping. 8and5,so40acac 

Thefactorsof40whosesumis−22are−2and−20.



xxxxx xxx xx





241541 4125



3134994 3431994 9149354 941954



2 2 2 2

yyyy yyyy yyyy yyyy





Thus,  2 954941. yyyy 

42. Factor215196 xx bygrouping. 15and6,so90.acac 

Thefactorsof90whosesumis−19are−10and−9.



22 15196151096 532332 3253

xxxxx xxx xx



 

44.  22 343 xxyyxyxy 

46. Factor22 3116 xxyy  bytrialanderror.

  22 22 363196 3233116 xyxyxxyy xyxyxxyy

 

Thus,  22 3116323 xxyyxyxy  .

48. Factor22 352xxyy  bygrouping. 3and2,so6.acac 

Thefactorsof6whosesumis5are1and6.

2222 352362 323 32

xxyyxxyxyy xxyyxy xyxy

  

 

50. Factor22 675xxyy bygrouping. 6and5,so30.acac 

Theonlyfactorsof30whosesumis7are 10and3.

2222 67561035 23535 352

xxyyxxyxyy xxyyxy xyxy

  

 

Copyright©2013PearsonEducation,Inc.281

52. Factor22 153110 xxyy  bytrialanderroruntil thecorrectfactorizationisobtained.Thesignmust benegativeinbothfactors.Tryvarious combinationsuntiltheonewiththecorrectmiddle termisfound.







5310155310 5235153110 xyxyxxyy xyxyxxyy

22 22



Thus,  22 1531105235. xxyyxyxy 

54. Factor22 252 aabb  bygrouping. 2and2,so4.acac 

Theonlyfactorsof4whosesumis5are1and4.



22 36612662 62132 yyyy

22 1616124443 42321 yyyy yy 

2222 252242 222 22

aabbaababb aabbab abab









56. Factor22 314 aabb bytrialanderror.Thesign mustbepositiveinonefactorandnegativeinthe other.Tryvariouscombinationsuntiltheonewith thecorrectmiddletermisfound.







22 22 372314 372314

ababaabb ababaabb



Thus,  22 314372 aabbabab 

58. Factor22 12712 xxyy  bygrouping. 12and12,so144.acac 

Theonlyfactorsof144whosesumis7are16 and9.

2222 127121216912





xxyyxxyxyy xxyyxy xyxy

60. 2 41810 xx



434334 3443

 

FirstfactorouttheGCF,2.Thenfactortheresulting trinomialbytrialanderrororgrouping. 

22 418102295 2215

xxxx xx

 



62. 2 123321 xx

FirstfactorouttheGCF,3.Thenfactortheresulting trinomialbytrialanderrororgrouping.

xxxx

xx

  322 31483148 324 xxxxxx xxx   70.   322 64102325 2351 xxxxxx xxx   72.   322 101222561 2511 yyyyyy yyy   74.   322 80806020443 202123 zzzzzz zzz   76.   43222 2 2410421252 24132 xxxxxx xxx   78.   54332 3 1521521 5131 xxxxxx xxx   80.   2222 414102275 225 xxyyxxyy xyxy   82.   2222 24327389 389 xxyyxxyy xyxy   84.   22 62602330 23103 xyxyyyxx yxx   86.   22322 12341426177 2372 ababbbaabb babab  

282Copyright©2013PearsonEducation,Inc.



88. 2444 42 4

101412 2(576) 2(53)(2)

xyxyy yxx yxx

90. 

92. a.  2 352312 xxxx 

104. doesnotmakesense;Explanationswillvary. Sampleexplanation:Thepolynomialcanbe factoredfurtherbecause 256(2)(3). xxxx 

106. false;Changestomakethestatementtruewillvary. Asamplechangeis:Thefactorizationof 2 12133 xx is(43)(31). xx

108. false;Changestomakethestatementtruewillvary. Asamplechangeis:2321 xx isprime.

110. 2 23 xbx

2 32 32

2 2 253 22136

0 xx xxxx xx xx xx

96.  2 231211. xxxx 

98. – 100. Answerswillvary.

102. makessense

    2 2 2 2 231253 213273 231253 213273 xxxx xxxx xxxx xxxx    

Thepossiblemiddletermsare 5,7,5and7, xxxx so 2 23 xbx canbe factoredif b is5,7,−5,or−7.

112. 2 274 nn xx

Since2 nnnnn xxxx  

,thefirsttermsofthe factorswillbe2 n x and. n x Usetrialanderroror groupingtoobtainthecorrectfactorization.

2 274(21)(4) nnnn xxxx

113. 4105 710 xy xy

 

Multiplythesecondequationby–4andthenaddthe equations.

 

4105 42840 29145 29145 2929 5

Back-substitutetofind x 710 7(5)10 3510 25    

xy x x x

Copyright©2013PearsonEducation,Inc.283