Engineering electromagnetics and waves 2nd edition inan solutions manual by jewell.woods198

Engineering Electromagnetics and Waves 2nd Edition Inan Solutions Manual Visit to Download in Full: https://testbankdeal.com/download/engineering-electromagn etics-and-waves-2nd-edition-inan-solutions-manual/

SolutionstoAddendumC CylindricalWaveguides

C.1Frequencyrangeofthedominantmode.

ThisworkisprotectedbyUnitedStatescopyrightlaws andisprovidedsolelyfortheuseofinstructorsinteaching theircoursesandassessingstudentlearning. Dissemination orsaleofanypartofthiswork(includingontheWorldWideWeb) willdestroytheintegrityoftheworkandisnotpermitted.

(a)ThecutoﬀfrequencyofthedominantTE10 modeinanair-ﬁlledhollowWR-10rectangular waveguidewith a = 0 254cmand b = 0 127cmisgivenby

(b)Since a = 2b,thenexthigher-ordermodesareTE11,TE20,andTM11.Thecutoﬀfrequencyof thesethreemodesis

(c)Therefore,thefrequencybandoverwhichonlythedominantTE10 modecanpropagateis fc20 fc10 ≃ 59 1GHz.

C.2AMwavesthroughatunnel?

Theminimumtunneldimension amin neededforthedominantTE10 modetopropagateat1MHz canbecalculatedas

As longas a > amin = 150m,TE10 willpropagateregardlessofthevalueoftheotherdimension b.Inpractice,sincethereisnotunnelwhichhassuchalargedimension,AMtransmissionthrough atunnelisnotfeasible.

fc10 = c 2π π a ≃ 3 × 1010 2(0 254) ≃ 59.1GHz

fc20 = 2fc10 ≃

11 =

118GHz

fc10 ≃ 3 × 108 2amin = 106 → amin =

150m!

© 2015 Pearson Education, Inc., Hoboken, NJ. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the publisher. Engineering Electromagnetics and Waves 2nd Edition Inan Solutions Manual Visit TestBankDeal.com to get complete for all chapters

AddendumC/ CylindricalWaveguides

C.3Propagationexperimentinaroadtunnel.

(a)Fortherectangularrailwaytunnelunderconsideration(a = 17mand b = 4.9m),thecutoﬀ frequenciesoftheTE10 andTE01 modesaregivenby

(b)Using (C.17),thelowest-ordermodesthatdonotpropagateatthe100MHzFMfrequencyare TE92 andTM92 sincethecutoﬀfrequencyofthesetwomodesisgivenby

C.4Radio-wavepropagationinrailwaytunnels.

Fortunnel1(a = 8mand b = 4m),thetotalnumberofpropagatingmodesat100MHzis26. ThesemodesareTE10,TE01,(TEandTM)02,(TEandTM)11,(TEandTM)12,(TEandTM)20, (TEandTM)21,(TEandTM)22,(TEandTM)30,(TEandTM)31,(TEandTM)32,(TEandTM)40, (TEandTM)41,and(TEandTM)50.Fortunnel2(a = 6mand b = 4m),thetotalnumberof propagatingmodesat100MHzis18.Unliketunnel1,(TEandTM)32,(TEandTM)40,(TEand TM)41,and(TEandTM)50 modesdonotpropagate.

C.5Rectangularwaveguidemodes.

(a)FortheWR-137rectangularairwaveguide(a = 3 484cm, b = 1 58cm),thecutoﬀfrequencies ofthefourlowest-ordermodesTE10,TE20 (andTM20),TE01,andTE11 (andTM11)arerespectively calculatedfrom(C.17)as f

(b)ForthedominantTE10 mode,thephasevelocity vp andtheguidewavelength λ atthetwoend frequencies(i.e.,5.85GHzand8.20GHz)ofthespeciﬁedfrequencyrangecanbecalculatedusing (C.20)and(C.21)as

fc10 = c 2a ≃ 3 × 108 2(17) ≃ 8.82MHz fc01 = c 2b ≃ 3 × 108 2(4.9) ≃ 30 6MHz

fc92 ≃ 3 × 108 2π √( 2π 4.9)2 + (9π 17 )2 ≃ 100 3MHz

c10 ≃ 4.31GHz, fc20 ≃ 8.61GHz fc01 ≃ 9.49GHz,and fc11 ≃ 10.4 GHz.

vp10|f=5 85GHz ≃ 3 × 108 √1 (4 31 5.85)2 ≃ 4.43 × 108 m-s 1 vp10|f=8 20GHz ≃ 3 × 108 √1 (4 31 8 20)2 ≃ 3 52 × 108 m-s 1 λ10 f=5.85GHz ≃ 3 × 108/(5.85 × 109) √1 (4 31 5 85)2 ≃ 7 57cm λ10 f=8 20GHz ≃ 3 × 108/(8.20 × 109) √1 (4 31 8 20)2 ≃ 4 30cm

C.6Dominantmode inarectangularwaveguide.

(a)ThecutoﬀfrequencyofthedominantTE10 modeintheWR-137rectangularairwaveguide (a = 3 484cm, b = 1 58cm)canbecalculatedfrom(C.17)as

(b)Repeatingthesamecalculationsasinpart(a)at7GHz,wehave

C.7Waveguidewavelength.

(a)Using(C.21),theguidewavelengthofthedominantTE10 modepropagatinginarectangular airwaveguidewith a = 2b = 7 214cmcanbewrittenas

used.Notethattheexpression foundfor λ10 aboveisonlyvalidfor f >∼ 2 08GHz(i.e.,propagatingcase).Thisexpression(i.e., λ10)isplottedasafunctionoffrequency f asshowninFigureC.1.

(b)Ifthesamewaveguideisﬁlledwithwater(assume ϵr ≃ 81),then, fc10 ≃ 2 08/√81 ≃ 0 231 GHz.Therefore, theguidewavelengthforthiscaseisgivenby

fc10 = c 2a ≃ 3 × 1010 2(3.484) ≃ 4 31GHz

value,thepropagationconstant γ10 andwaveimpedance ZTE10 at3.5GHzcanbefound

γ10 =¯ α10 = β√(fc10 f )2 1 ≃ 2π(3.5 × 109) 3 × 108 √(4.31 3.5 )2 1 ≃ 52 5np-m 1 ZTE10 = ηair √1 (fc10/f)2 ≃ 377 √1 (4.31/3.5)2 ≃ j526.3Ω NotethatthedominantTE10 modeisnotpropagatingat3.5GHzasexpectedsincefc10 ≃ 4 31GHz > f = 3 5GHz.

Usingthis

using(C.16)and(C.28)as

γ10 = jβ√1 (fc10 f )2 ≃ j 2π(7 × 109) 3 × 108 √1 (4 31 7 )2 ≃ j115 6rad-m 1 ZTE10 ≃ 377 √1 (4.31/7)2 ≃ 478Ω Notethat thedominantTE

modeisapropagatingmodeat7GHzsince ∼ 4 31GHz < 7GHz.

λ10 = c/f √1 (fc10/f)2 ≃ 30 √[f(GHz)]2 (2 08)2 cm where c ≃ 3 × 1010 cm-s 1 and fc10 = c/(2a) ≃ 2.08GHzare

λ10 ≃ 30/√81 √[f(GHz)]2 (0.231)2 cm

whichisvalidfor f >∼ 0 231GHz.ThisexpressionisplottedinFigureC.1asafunctionofthe frequency f

(c)ForthepropagatingTE20 modeintheairwaveguideofpart(a),the λ20 expressionisthesameas the λ10 expressionexcept2.08shouldbereplacedby4.16(i.e., fc20 = 2fc10).Thisexpressionisvalid for f >∼ 4.16GHzandisplottedasafunctionof f inFigureC.1.ForthepropagatingTE20 mode inthewater-ﬁlledwaveguideofpart(b), λ20 expressionisthesameasthe λ10 expressionfound inpart(b)exceptthat0.231shouldbereplacedby0.462.Thisexpressionisvalidfor f >∼ 0 462 GHzandisplottedinFigureC.1.

C.8Rectangularwaveguidemodes.

(a)FortheWR-42rectangularairwaveguide(a = 1 067cm, b = 0 432cm),thecutoﬀfrequencies oftheTE10,TE01,TE11,TE

NotethatallthesemodesexcepttheTE02 modearepropagatingat40GHz.Thepropagation constantsandthewaveimpedancesofthesemodescanbecalculatedusing(C.18)and(C.19)as

12 AddendumC/ CylindricalWaveguides 2 4 6 8 5 10 15 20 25 f (GHz) λ (cm) TE10 TE20 0.2 0.4 0.6 0.8 5 10 15 20 25 λ (cm) f (GHz) TE10 Air-filled waveguide Water-filled waveguide

FigureC.1 FigureforProblemC.7. Rightpanel: λ10 and λ20 versusfforair-ﬁlledwaveguide.Leftpanel: λ10 versus f forwater-ﬁlledwaveguide(i.e., ϵr ≃ 81).

20,andTE02 modesaregivenby fc10 ≃ 3 × 1010 2(1.067) ≃ 14 06GHz < 40GHz fc01 ≃ 3 × 1010 2(0.432) ≃ 34 72GHz < 40GHz fc11 ≃ 3 × 1010 2 √(1.067) 2 +(0.432) 2 ≃ 37.46GHz < 40GHz fc20 ≃ 3 × 1010 (1.607) ≃ 28 12GHz < 40GHz fc02 ≃ 3 × 1010 (0.432) ≃ 69 44GHz > 40GHz

γ10 ≃ j 2π(4 × 1010) 3 × 108 √1 (14 06 40 )2 ≃ j784 3rad-m 1

(b)For theTE10 mode,wehavefrom(C.20)and(C.21)

13 ZTE10 ≃ 377 √1 (14 06 40 )2 ≃ 402.7Ω γ01 ≃ j 2π(4 × 1010) 3 × 108 √1 (34.72 40 )2 ≃ j415 9rad-m 1 ZTE01 ≃ 377 √1 (34 72 40 )2 ≃ 759 4Ω γ11 ≃ j 2π(4 × 1010) 3 × 108 √1 (37 46 40 )2 ≃ j293.8rad-m 1 ZTE11 ≃ 377 √1 (37 46 40 )2 ≃ 1075Ω γ20 ≃ j 2π(4 × 1010) 3 × 108 √1 (28.1 40 )2 ≃ j595 9rad-m 1 ZTE20 ≃ 377 √1 (28 1 40 )2 ≃ 530Ω γ02 ≃ 2π(4 × 1010) 3 × 108 √(69 44 40 )2 1 ≃ 1189np-m 1 ZTE02 ≃ 377 √1 (69 44 40 )2 ≃ j265.65Ω

vp10 ≃ 3 × 108 √1 (14 06 40 )2 ≃ 3.20 × 108 m-s 1 λ10 ≃ 3×1010 4×1010 √1 (14 06 40 )2 ≃ 0.801cm Similarly,fortheTE01 mode,wehave vp01 ≃ 3 × 108 √1 (34 72 40 )2 ≃ 6.04 × 108 m-s 1 λ01 ≃ 3×1010 4×1010 √1 (34 72 40 )2 ≃ 1.51cm Ina similarfashion,fortheTE11 mode,weobtain vp11 ≃ 8.56 × 108 m-s 1 , λ11 ≃ 2.14cm,and fortheTE20 mode,weobtain vp20 ≃ 4.22 × 108 m-s 1,and λ11 ≃ 1.054cmrespectively. ThisworkisprotectedbyUnitedStatescopyrightlaws andisprovidedsolelyfortheuseofinstructorsinteaching theircoursesandassessingstudentlearning. Dissemination orsaleofanypartofthiswork(includingontheWorldWideWeb) willdestroytheintegrityoftheworkandisnotpermitted. © 2015 Pearson Education, Inc., Hoboken, NJ. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the publisher.

AddendumC/ CylindricalWaveguides

C.9Dielectric-ﬁlledwaveguide.

(a)FortheWR-22rectangularwaveguide(a = 0 569cm, b = 0 284cm)ﬁlledwithadielectric materialhaving ϵr,thephaseshiftexperiencedbythedominantpropagatingTE10 modeovera lengthof1cmat13.2GHzcanbewrittenas

But, from(C.18),wehave

30√

/(2 × 0 569) inGHz.Substituting,wehave

fromwhich solving,weﬁnd

(b)Notethat fc10 ≃ 8 78GHz.Since a ≃ 2b,thenexthighermodeisTE20 (orTE11)whichhasa cutoﬀfrequency fc20 ≃ 17 6GHz > 13 2GHz.Therefore,nomodeotherthanTE10 propagatesat 13.2GHz.

(c)Ifthedielectricﬁllingisreplacedwithair,then, fc10 ≃ 3 × 1010/(2 × 0.569) ≃ 26.4GHz > 13.2GHz.Therefore,inthiscase,nopropagationoccursdowntheguide.

C.10Rectangularwaveguidemodes.

(a)FortheWR-1500airwaveguide(a = 2b = 38.1cm),thecutoﬀwavelengthofthedominant TE10 modecanbefoundfrom(C.19)as λc10 = 2a = 76.2cm.

(b)Thephasevelocity,guidewavelength,andthewaveimpedanceforthedominantTE10 modeat λair = 0 8λc10 canbecalculatedfrom(C.20),(C.21)and(C.28)as

(c)At λair = 40 cm,onlythedominantTE10 modepropagatessincethenexthighermodeTE20 (orTE11)has λc20 = λc10/2 = 38.1cm < 40cm.

(d)At λair = 30cm,thepropagatingmodesareTE10,TE20 andTM20 (λc20 = 38.1cm),TE01 (λc01 = 38.1cm),andTE11 andTM11 (λ

.1cm).

β10l = 354 6◦ × π 180◦ → β10 ≃ 618 9rad-m 1

β10 ≃ 2π(13 2 × 109 (3 × 108/√ϵr) √1 (fc10(GHz)/13 2)2 ≃ 618 9 where fc10

β10 ≃ 276.5√ϵr√1 3.99/ϵr ≃ 618.9

ϵr

ϵr ≃

vp ≃ 3 × 108 √1 (0.8)2 ≃ 5 × 108 m-s 1 λ10 ≃ 0 8 × 76 2 √1 (0 8)2 ≃ 101 6cm ≃ 1 02 m ZTE10 ≃ 377 √1 (0 8)2 ≃ 628.3Ω

2ab/√a2

b2 ≃ 34

11 =

C.11Polyethylene-ﬁlledwaveguide.

(a)FortheWR-1500polyethylene-ﬁlledwaveguide(a = 2b = 38 1cm),thecutoﬀwavelengthof thedominantTE10 modecanbefoundfrom(C.19)as λc10 = 2a = 76 2cm.

(b)Thephasevelocity,guidewavelength,andthewaveimpedanceforthedominantTE10 modeat λair = 0 8λc10 canbecalculatedfrom(C.20),(C.21)and(C.28)as

(c)At

(d)At λair = 30cm,thepropagatingmodesareTE10,TE

C.12Unknownrectangularwaveguidemode.

(

c20 = 38 1cm),TE01 (λc01 = 38 1cm),andTE11 andTM11 (λc11 = 2ab/

34 1cm).

(a)Sincethe y componentoftheelectricﬁeldphasorisorientedintheguidingdirectionofthe rectangularwaveguide,thismodecanneitherbeTEMorTEmn,therefore,itmustbeaTMmn mode. Usingthewaveguidedimensions a = 4cm(inthe z direction)and b = 2cm(inthe x direction) andcomparingthe Ey expressiongivenintheproblemwiththe Ez expressiongivenby(C.15),we have

Therefore,this isaTM11 mode.Itisanevanescentwavebecauseoftheattenuationterm e 41πy .

(b)Using(C.16),theoperatingfrequencycanbeevaluatedfromtheattenuationconstant α11 as

(c)Notethatthecutoﬀfrequenciesofthetwolower-orderTE10 andTE01 modesare

vp ≃ 3 × 108/√2.25 √1 (0 8)2 ≃ 3 33 × 108 m-s 1 λ10 ≃ 0.8 × 76.2 √1 (0.8)2 ≃ 101 6cm ≃ 1 02 m ZTE10 ≃ 377/√2 25 √1 (0 8)2 ≃ 418 9Ω

modepropagatessincethenexthighermodeTE20

< 40cm.

λair = 40 cm,onlythedominantTE10

(orTE11)has λc20 = λc10/2 = 38.1cm

≃

20 andTM20

√a2

mπ 0 04 = 25π → m = 1 nπ 0.02 = 50π → n = 1

γ11 =¯ α11 = β√(fc11 f )2 1 ≃ 2πf(GHz) 0 3 √[ 8 39 f(GHz) ]2 1 ≃ 41π np-m 1 → (8 39)2 [f(GHz)]2 = (0 3 × 41 2 )2 → f ≃ 5 70GHz wherewereplaced β = 2πf/c, c ≃ 3 × 108 m-s 1,and fc11 = 0.5c√a 2 + b 2 ≃ 8.39GHz.

fc10 = c

(2a) ≃ 3.75GHz <∼ 5.7GHzand fc01 = c/(2b) ≃ 7.5GHz >∼ 5.7GHz.Therefore,onlyTE10 mode propagatesat ∼ 5.7GHz.

AddendumC/ CylindricalWaveguides

C.13Alargewaveguidefordeephyperthermia.

(a)Forthelargewaveguide(a = 6m, b = 30cm)designedtobeusedfordeephyperthermia,since a >> b,thecutofffrequencyofthelower-ordermodesisdeterminedbythelargerdimension a. Assumingthewaveguidetobeair-filled,thecutofffrequenciesofthefivelowest-orderTEm0 are givenby

(where vp = c ≃ 3 × 108 m-s 1)yielding fcTE10 = 25MHz, fcTE20 = 50 MHz, fcTE30 = 75MHz, fcTE40 = 100MHz,and fcTE50 = 125MHzrespectively.Notethatthecutoﬀfrequenciesofthe TMm0 modeswith m = 2, 3, 4, 5areexactlythesameasthecutoﬀfrequenciesoftheirTEm0 mode counterpartswith m = 2, 3, 4, 5.

(b)Ifthewaveguideisfilledwithwater(assume ϵr ≃ 81),then vp = c/√ϵr = c/9.Therefore, The cutofffrequenciesforthewater-filledwaveguideare1/9timesthecutofffrequenciesoftheairfilledwaveguideyieldingthecutofffrequenciesforthefivelowest-orderTEm0 modesas fcTE10 ≃ 2.78MHz, fcTE20 ≃ 5.56MHz, fcTE30 ≃ 8.33MHz, fcTE40 ≃ 11.1MHz,and fcTE50 ≃ 13.9MHz respectively.

(c)Forthewater-filledwaveguidewithnewdimensions a = 70cmand b = 30cm,thecutoff frequenciesofthefivelowest-orderTEmn modesarefoundtobe f

,TM30,andTM11 modeshaveexactlythesamecutoﬀfrequenciesastheirTEmn counterparts.

C.14Squarewaveguidemodes.

(a)Forthesquareairwaveguide(a = b = 3cm)at8GHz,thecutoﬀfrequenciesofallthe propagatingTEmn andTMmn modesat8GHzaregivenby

where vp = c ≃ 3 × 108 m-s 1 is used.Notethatallofthesevaluescutoﬀfrequencyvaluesare < 8GHzandthereforethesemodes(i.e.,TE10,TE01,TE11,andTM11)aretheonlypropagating modesat8GHz.

(b)Ifthesamesquarewaveguideisﬁlledwithpolystyrene(ϵr ≃ 2.56),then,werecalculatethe cutoﬀfrequenciesofthepropagatingmodesas

waveguideat8GHz.

fcm0 = mvp 2a

cTE10 ≃ 3 × 108/[2(0 7)(√81)] ≃ 23 8MHz, fcTE20 = 2fcTE10 ≃ 47 6MHz, fcTE30 ≃ 71 4MHz, fcTE01 ≃ 3×108/[2(0 3)(√81)] ≃ 55 6 MHz,and fcTE11 ≃ 3 × 108√(0 7) 2 +(0 3) 2/ (2√81) ≃ 60 4MHzrespectively.Notethatthe TM

fcTE10 =fcTE01 = vp 2a ≃ 5GHz fcTE11 =fcTM11 = vp a√2 ≃ 7.07GHz

fc10 = fc01 = c/(2a√ϵr) ≃ 3.13GHz, fc11 = c/(a√2ϵr) ≃ 4.42GHz, fc20 = fc02 = 2fc10 ≃ 6.25GHz, fc21 = fc12 =[c/(2√ϵr)]√(2/3)2 +(1/3)2 ≃ 6 99GHz,and fc22 =[c/(2√ϵr)]√(2/3)2 +(2/3)2 ≃ 8 84GHzrespectively.Notethatthenext highermode(TE30 orTE03)hasacutoﬀfrequencywhichis fc30 = 3fc10 ≃ 9.38GHz > 8GHzand sothisisnotapropagatingmode.Therefore,TE10,TE01,TE11.TM11,TE20,TM20,TE02,TM02, TE21,TM21,TE12,andTM

12 aretheonlypropagatingmodesonthepolystyrene-ﬁlledsquare

C.15SAR calibrationusingarectangularwaveguide.

(a)Forthespeciallydesignednonstandardair-ﬁlledwaveguidewithdimensions a = 19cmand

b = 14cm,theonlymodethatisexcitedat900MHzisthedominantTE10 modewhichhasa cutoﬀfrequency fc10 ≃ 3 × 1010/[2(19)] ≃ 789.5MHz < 900MHz.

(b)ThecutoﬀfrequencyofthenexthighermodewhichistheTE01 modeisgivenby fc01 ≃ 3 × 1010/[2(14)] ≃ 1 07GHz,so,thefrequencyrangeoverwhichonlythedominantmodecan propagatecanbefoundas fc01 fc10 ≃ 282MHz.

(c)IftheTE01 modedoesnotexist,then,thecutoﬀfrequencyofthenexthighermodewhichisthe TE11 mode(andtheTM11 mode)iscalculatedas

Therefore,thefrequencyrangeinwhichonlythedominantmodepropagates(ignoringtheexistence oftheweakTE01 mode)isgivenby

C.16Millimeter-waverectangularwaveguide.

(a)FortheW-bandrectangularairwaveguidewithdimensions a = 2 54mmand b = 0 7mm,the cutoﬀfrequenciesofthethreelowest-ordermodesaregivenby

(b)ThefrequencyrangeoverwhichonlythedominantTE

C.17TE10 modeinarectangularwaveguide.

fc11 = c 2√a 2 + b 2 ≃ 3 × 1010 2 √(19) 2 +(14) 2 ≃ 1.33GHz

fc11 fc10 ≃ 541MHz.

fcTE10 = c 2a ≃ 3 × 1011 mm-s 1 2(2.54mm) ≃ 59.1GHz fcTE20 = fcTM20 = 2fcTE10 ≃ 118GHz fcTE30 = fcTM30 = 3fcTE10 ≃ 177GHz

modecanpropagateisgivenby fcTE20 fcTE10 ≃ 59 1GHz

(a)Using(C.25),wehave π rad a ≃ 29rad-m 1 → a ≃ 0 1083m = 10 83cm andsince a = 2b isgiven, b = a/2 ≃ 5.4165cm.Theoperatingfrequencycanbefoundfrom β10 ≃ 42 3rad-m 1 valueas (β)2(2π c )2 (f2 f2 c10) ≃ (42 3)2 wheresubstituting thevalueofthecutoﬀfrequency fc10 = c/(2a) ≃ 3×1010/(2×10.83) ≃ 1.385 GHzyields f ≃ 2.449GHz.

AddendumC/ CylindricalWaveguides

(b)Note thatthetime-averagepowercarriedbythedominantTE10 modealongtherectangular waveguideisgivenby

0.1083m,and b ≃ 0.054165malongwiththevalueof C intheaboveexpression,weﬁnd Pav ≃ 964 4W.

C.18Dominantmodeinarectangularwaveguidedesign.

(a)Thethreedesigncriteriafortherectangularwaveguideunderconsiderationare

1 25fc10 ≤ 15GHz

1 25 × 18 5GHz ≤ fcnexthigher and Pav ofthedominantTE10 modeistobemaximized.Assuming a = 2b andusing fc10 = c/(2a) where c ≃ 3 × 1010 cm-s 1,theﬁrstdesigncriteriayields amin = 1.25cm.Next,using fcnexthigher = fc20 = 2fc10 = c/a,theseconddesigncriteriayields amax ≃ 1.2973cm.Therefore, thelongertransversedimension a mustlieintherange1.25 ≤ a ≤∼ 1.2973cm.However,since thethirddesigncriteriaistomaximizepowertransfer,wechoosethelargestpossiblevalueof a = amax ≃ 1.2973cm.Forthisvalueof a,thecutoﬀfrequencyofthedominantTE10 modecan becalculatedas fc10 ≃ 3 × 1010/(2 × 1 2973) ≃ 11 56GHz.

(b)ThecutoﬀfrequencyofthenexthigherTE20 (orTE01)modeis fc20 = 2fc10 ≃ 23 13GHz > 22GHz.

(c)Using(C.30)at15GHz,thetime-averagepowercarriedbythedominantTE10 modewithpeak electricﬁeldvalue E0 = 1.5 × 106 V-m 1 canbecalculatedas

C.19Rectangularwaveguidedesign.

(a)Usingthecutoﬀfrequencyofthedominantmode,wehave

TomaximizethefrequencyrangeoverwhichnoothermodebutthedominantTE10 modecan propagate,wechoose

(b)ThenexthighermodesareTE01 andTE20 (andTM20).Forthesemodes,thecutoﬀfrequency is5.16GHz.

2 where C

Hx givenby C ≃ 26A-m 1 . Substituting β10 ≃ 42

3rad-m 1 , ω = 2π(2.449 × 109) rad-s 1 , µ0 = 4π × 10 7 H-m 1 , a

β10ωµ0C2 2 ( a

)

istheamplitude oftheaxialmagneticﬁeldcomponent

≃

Pav ≃ (1 5 × 106)2 377 (1 297 × 10 2)(0 64865 × 10 2) 4 √1 [ (3 × 1010/(15 × 109) 2(1 2973) ]2 ≃ 80kW

fc10 = c 2a = 2.58GHz → a ≃ 5.814 cm

b = 0.5a ≃ 2.907cmsothat fc01 = fc20 = 2fc10 = 5.16GHz.

(c)Using(C.25), thepeakelectricﬁeldvalueintheairwaveguidewith a ≃ 5 814cmat4GHz canbewrittenas

fromwhich wecansolveforthemaximumpeakvalue C oftheaxialcomponentofthemagnetic ﬁeldcorrespondingtothebreakdownstrengthofairwithasafetyfactorof2atsealevelas

2 57kA-m 1.Substitutingthisvalue,themaximumtime-averagepowercarryingcapacityofthe waveguidecanbecalculatedas

C.20 Maximumﬁeldinarectangularwaveguide.

(a)FortheWR-650rectangularairwaveguide(a = 2b = 16 51cm),thecutoﬀfrequencyofthe dominantTE10 modeisgivenby

Therefore, sincethenexthigherTE20 mode(ortheTE01 mode)hasacutoﬀfrequencyof fc20 = 2fc10 ≃ 1 82GHz > 1 1GHz,onlythedominantTE10 modepropagatesontheWR-650waveguide at1.1GHz.FortheWR-975rectangularairwaveguide(a = 2b = 24 765cm),thecutoﬀfrequency ofthedominantTE10 modeisgivenby

Therefore, sincethenexthigherTE20 mode(ortheTE01 mode)hasacutoﬀfrequencyof fc20 = 2fc10 ≃ 1 21GHz > 1 1GHz,similartothecaseofWR-650waveguide,onlythedominantTE10 modepropagatesontheWR-975waveguideat1.1GHz.

(b)FortheWR-650waveguide,thepeakelectricﬁeldcorrespondingtothepeakpowerof2GW canbecalculatedfrom

|Ey|max = 2πfµ0aC π = 2(4 × 109)(4π × 10 7)(0.05814)C = 1.5 × 106

C ≃

Pavmax ≃ (64.02)(2π × 4 × 109)(4π × 10 7)(2, 566)2(0.05814)3(0.02907) 4π2 ≃ 1 927MW where β10 ≃ 2π(4 × 109) 3 × 108 √1 (2.58 4 )2 ≃ 64 02rad-m 1

isused.

fc10 = c 2a ≃ 3 × 1010 2(16.51) ≃ 9 085 × 108 Hz = 908 5MHz

fc10 = c 2a ≃ 3 × 1010 2(24.765) ≃ 6 057 × 108 Hz = 605 7MHz

Ppeak ≃ E2 0 377 (16.51 × 10 2)(8.255 × 10 2) 2 √1 ( 27.27 2 × 16.51)2 ≃ 2 × 109 as E0 ≃ 14MV-m 1 whereweused λ = c/f ≃ 3 × 1010/(1 1 × 109) ≃ 27 27cm.Similarly,for theWR-975waveguide,wehave Ppeak ≃ E2 0 377 (24.765 × 10 2)(12.383 × 10 2) 2 √1 ( 27.27 2 × 24.765)2 ≃ 2 × 109 yielding E0 ≃ 7.675MV-m 1

Dissemination

AddendumC/ CylindricalWaveguides

(c)WR-975 waveguideshouldbechosenforhigherpowercapacitysinceithasawidercrosssectionalareaandasaresultcanhandlemorepowerthantheWR-650waveguidebeforedielectric breakdownoccurs.

C.21Powercapacityofarectangularwaveguide.

(a)FortheWR-284rectangularairwaveguide(a = 7 214cm, b = 3 404cm),thecutoﬀfrequency ofthedominantTE10 modeisgivenby fc10 = c/(2a) ≃ 2 079GHz.>From(C.25),themaximum allowablepeakelectricﬁeldcanbewrittenas

Substituting f = 2 45GHz, a = 7 214cm,and µ0 = 4π × 10 7 H-m 1,wecansolveforthe allowablepeakvalueoftheaxialmagneticﬁeldcomponentas C ≃ 3, 377A-m 1.Thephase constant β10 correspondingtothedominantTE10 modecanbefoundfrom(C.25)as

Usingthe valuesof C and β10,wecancalculatethemaximumtime-averagepowerthatcanbe carriedbythedominantTE10 modealongtheWR-284rectangularairwaveguideas

(b)Repeatingthesamecalculationsinpart(a)fortheWR-430rectangularairwaveguide(

parts(a)and(b),onecanconcludethatthemaximumpowercapacityoftheWR-430waveguideis about4timeshigherthanthemaximumpowercapacityoftheWR-284waveguide.

C.22TE11 modeinarectangularwaveguide.

(a)Comparingthegiven Hz expressionforTE11 with(C.23),thewaveguidedimensioncanbe foundas

Theoperating frequencycanbeobtainedusingthephaseconstantgivenby(C.18)as

|Ey|max = 2πfµ0aC π = 1 5 × 106 V-m 1

β10 = 2πf c √1 (fc10 f )2 ≃ 2π(2 45 × 109 3 × 108 √1 (2 079 2 45 )2 ≃ 27.14rad-m 1

Pavmax = (27.14)(2π × 2.45 × 109)(4π × 10 7)(3, 377)2(7.214 × 10 2)3(3.404 × 10 2) 4π ≃ 1.938MW

10.922cm, b = 5.461cm),weﬁnd fc10 ≃ 1.37GHz, C ≃ 2.23 × 103 A-m 1 , β10 ≃ 42.49 rad-m 1,and Pavmax ≃ 7.37MW.Therefore,comparingthemaximumpowervaluesobtainedin

50π = mπ a = π a → a = 1 50 = 2cmand 100π = nπ b = π b → b = 1 100 = 1cm

β11 = 2πf c √1 (fc11 f )2 = 2π c √f2 f2 c11 = 100π → f = √(cβ11 2π )2 + f2 c11 = √(3 × 108 × 100π 2π )2 +(16 7 × 109)2 ≃ 22 5GHz wherethevalueofthecutoﬀfrequency fc11 iscalculatedfrom(C.17)as fc11 = c 2√ 1 a2 + 1 b2 ≃ 3 × 1010 2 √ 1 22 + 1 12 ≃ 16 77GHz

(b)Usingtheﬁeldcomponentsgivenin(C.23),thetime-averagePoyntingvectorfortheTE11 mode canbewrittenas

(c)TheothernonzerocomponentsoftheTE

(d)Usingthebreakdownvalueoftheelectricﬁeld,wecancalculatethenewvalueof C as

The maximumtime-averagepowercorrespondingtothisnewvalueof C isfoundtobe

kW.

C.23NoTM01 orTM10 modesinarectangularwaveguide.

Tohaveoneoftheindiceszeromeansthatthefieldquantitydoesnotvaryinthecorresponding directionacrossthecrosssectionoftheguide.ForaTMmode,themagneticfieldlinesareby definitionentirelytransverse,andbothcomponents(*x and *y)mustbenonzerosincethemagnetic fieldlinesmustalwayscloseonthemselves.However,eachcomponentmustthenvaryinitsown direction(i.e., *x mustvaryin x and *y mustvaryin y)inordertonotbeperpendiculartothe wallsasrequiredbytheboundarycondition.Thus,neither m nor n canbezero.

Sav = 1 2 5e{E × H∗} = ˆ z 1 2 [ExH∗ y EyH∗ x] = ˆ z 1 2 ωµβ11C2 h4 11 [( π b )2 cos2 ( πx a ) sin2 ( πy b ) + ( π a ) sin2 ( πx a ) cos2 ( πy b )] where h1 = π√a 2 + b 2.Thetotal time-averagepowercarriedbytheTE11modecanbefound byintegrating Sav overthecross-sectionalareaofthewaveguideas Pav = ∫ b 0 ∫ a 0 Sav · (ˆ zdxdy)= ωµβ11C2 2h2 11 ab 4 Usingthegivenparametervalues, Pav = 10kW, β11 = 100π rad-m 1 , ω ≃ 2π(22.5 × 109) rad-s 1,and h11 = π√(0.02) 1 +(0.01) 2,wecansolvefor C as 104 ≃ 2π(22.5 × 109)(4π × 10 7)(100π)C2(0.02)(0.01) 8(351 2)2 → C ≃ 940A-m 1

11 modecanbewrittenfrom(C.23)as Hx ≃ j376sin(50πx) cos(100πy) e j100πz A-m 1 Hy ≃ j752cos(50πx) sin(100πy) e j100πz A-m 1 Ex ≃ j4 25 × 105 cos(50πx) sin(100πy) e j100πz V-m 1 Ey ≃−j2 13 × 105 sin(50πx) cos(100πy) e j100πz V-m 1

ωµ h2 11 C π b = 2π(22.56 × 109)(4π 7) (351 2)2 C π 0 01 = EBR = 1.5 × 106 → C ≃ 3, 316A-m 1

Pav ≃ 124

AddendumC/ CylindricalWaveguides

C.24No TEMwaveinasingle-conductorwaveguide.

HavingaTEMmodewouldmeanthatthereisneitheran %z or *z component.However,since themagneticﬁeldlinesmustalwayscloseonthemselves, *x and *y mustbothbenonzero,and theirclosedloopsmustthengenerate(through(7.21c))displacementcurrent(i.e., ∂

)inthe z direction,contradictingouroriginalpremiseofno %z component.

C.25Powercapacityofarectangularwaveguide.

(a)Usingthetime-averagepowerexpressionofthedominantTE10 modeas

/∂

wherethe cutoﬀfrequencyofthedominantmodeisreplacedby

wesolvefortheamplitude C oftheaxialmagneticﬁeldcomponenttobe

(b) Sincepowerisproportionaltothesquareofthepeakvalueoftheelectricﬁeld,themaximum time-averagepowercarryingcapacityoftheTE10 modeunderthe |Ey|max = 1500kV-m 1 criteria canbecalculatedfrombasicratioas

C.26Cutoﬀ frequencyforacircularwaveguide.

11 modeina7cmdiametercircularairwaveguideisgiven by

∼2.51GHz.Therefore,nowavescanbetransmittedalongthiswaveguidebelow ∼ 2 51GHz.

C.27TE11 modeinacircularwaveguide.

(a)UsingthecutoﬀfrequencyofthedominantTE11 modeas

weﬁnd thesmallestdiameterofthecircularairwaveguidethatwillallowthepropagationofthe dominantmodeat40MHztobe2amin ≃ 4.396m.

Pav = β102πfµ0C2 2 ( a π )2 ab 2 = 100kW where a = 2.591 cm, b = 1.295cm, µ0 = 4π × 10 7 H-m 1 , f = 9GHz,and β10 = β√1 (fc10 f )2 ≃ 2π(9 × 109) 3 × 108 √1 (5 79 9 )2 ≃ 144.3rad-m 1

fc10 = c/(2a) ≃ 5 79GHz,

C ≃ 1, 307A-m 1 .

|Ey|max = 2πfµ0aC π ≃ 2π(9 × 109)(4π × 10 7)(0 02591)(1, 307) π ≃ 766kV-m 1

Therefore,using(C.25),thepeakvalueoftheelectricﬁeldinthewaveguidecanbecalculatedas

Pavmax ≃ (105)(1500)2 (766)2 ≃ 3.83 × 105 W = 383kW

ThecutoﬀfrequencyofthedominantTE

fc11 ≃ 1 8412c 2πa ≃ 1 8412 × 3 × 1010 2π(3 5) ≃ 2.51 × 109 Hz

fc11max ≃ 1.8412c 2πamin = 40 × 106 Hz

(b)Repeating part(a)for40GHzyields2amin ≃ 4 396mm.Inotherwords,whenthefrequency increasesbyafactorof1000,thediameterofthewaveguideisreducedbyafactorof1000forthe samemodeoperationtohold.

C.28Square-to-circularwaveguide.

(a)Forthesquareairwaveguidewithdimensions a = b = 2.4cm,thecutoﬀfrequencyofthe dominantTE10 andTE01 modesisgivenby

Therefore, onlythedominantTE10 andTE01 modescanpropagateat7GHz.

(b)Conservingtheperimeter,wehave2πa = 4 × 2 4cmfromwhichweﬁndtheradius a ofthe circularairwaveguideas a ≃ 1 528cm.Usingthisvalue,thecutoﬀfrequencyofthedominant TE11 modeisgivenby

The cutoﬀfrequencyofthenexthigherTM01 modecanbecalculatedas

Therefore,onlythedominantTE11 modepropagatesat7GHz.

C.29Southworth'sexperiments.

(a)Foranair-ﬁlledwaveguide,theminimumdiameter dmin requiredtoallowanypropagationat

air = 1mcanbecalculatedfromthecutoﬀwavelengthofthelowest-orderTE11 modeas

Similarly,forawater-ﬁlledwaveguide(ϵr ≃ 81),wehave

(b)Repeatingpart(a)foranair-ﬁlledwaveguideat λair = 15cm,weﬁnd dmin ≃ 8 79cm.

(c)Using2a = 12 7cmand λair = 15cm,thecutoﬀwavelengthisgivenby

) ≤ 2 660.Therefore,usingTablesC.2andC.3,onlyTE11 andTM01 modes propagateat

resultingin (

fc10 = fc01 = c 2a ≃ 3 × 1010 2 × 2.4 = 6 25 × 109 Hz = 6 25GHz

fc11 ≃ 1.8412c 2πa ≃ 1.8412 × 3 × 1010 9.6 ≃ 5 75 × 109 Hz = 5 75GHz < 7GHz

fc01 ≃ 2.4049c 9.6 ≃ 7 515 × 109 Hz = 7 515GHz > 7GHz

λcTE11 ≃ πdmin 1 8412 = λair = 1m → dmin ≃ 58.6 cm

λcTE11 ≃ πdmin 1 8412 = λwater = λair √ϵr ≃ 1 9 m → dmin ≃ 6.51cm

λcnl

2πa (snl or tnl) = (12.7cm)π (snl or tnl) ≥ λair = 15cm

tnl

λair = 15cm.

AddendumC/ CylindricalWaveguides

C.30Barrow'sexperiments.

Fora λair = 50cmsignalsource, f = c/λair ≃ 600MHz.ProfessorBarrowusedahollow cylindricalwaveguidewithradius a = 2.25cm.Thecutoﬀfrequencyofthelowest-orderTE11 modeforthiswaveguideisgivenby

Therefore,theexperimentwasunsuccessfulbecausenopropagationmodeexistsonthiswaveguide at600MHz.

(b) λair = 40cm → f ≃ 750MHz.Using a = 22 85cm,thecutoﬀfrequencyofthelowest-order TE11 modeinthisguideisgivenby

Therefore,TE11 modepropagatesat750MHzandasaresult,theexperimentinthiscasewas successful.DidProfessorBarrowobserveanyotherpropagatingmodesinthisexperiment?

C.31TheChannelTunnel.

(a)EquatingthecutoﬀfrequencyofamodetothehighestAMfrequency,wehave

Therefore,AM radiowavesdonotpropagatealongthe7.6mdiametertunnel.

(b)Using108MHzandfollowingasimilarapproachasinpart(a),weﬁnd (snl or (tnl) ≃ 8.595. Therefore,usingasourcesuchasBeattie(seefootnote22inChapter5),themaximumnumberof propagatingmodesat108MHzFMfrequencyisfoundtobe21.

(c)Followingasimilarapproachasinpart(a),again,wefindoutthatAMdoesnotpropagate. Using108MHz,wefind (snl or (tnl) ≃ 5 429andasaresult,maximumof9differentmodescan propagate.

C.32Unknowncircularwaveguidemode.

(a)Comparingthe Hϕ expressionwith(C.48)and(C.50),weconcludethatthismodeisaTMnl modeandthat n = 0.Toﬁndthevalueof l ,weuse

Comparingwith therootsprovidedinTableC.2,thismodeisidentiﬁedastheTM02 mode.This isapropagatingmode,asisevidentfromthe ej48πz term.

(b)Using(C.46),wecanwrite

fcTE11 ≃ 1 8412c 2πa ≃ 1 8412(3 × 1010) 2π(2 25) ≃ 3.91 × 109 Hz = 3.91GHz > 600MHz

fcTE11 ≃ 1.8412(3 × 1010) 2π(22.85) ≃ 3 85 × 108 Hz = 385MHz > 750MHz

fcnl = (snl or tnl)c 2πa = 1 605 × 106 Hz → (snl or tnl) ≃ 0 128!

tnl a = tnl 0.04 ≃ 138 → t nl ≃ 5 520

βTM02 ≃ (2πf)2 c2 (138)2 ≃ (48π)2 → f ≃ c 2π √(48π)2 +(138)2 ≃ 9 760GHz

(c)From(C.48), wehave

Therefore,the othernonzeroﬁeldcomponentsofthisTM02 modecanbewrittenas

(d)Fromthecutoﬀfrequencyexpressionwehave

UsingTablesC.2andC.3,thetotalnumberofpropagatingmodespossibleat ∼9.760GHzisfound tobe18(i.e.,7TMnl and11TEnl)modes.

C.33Unknowncircularwaveguidemode.

(a)ToﬁndtheunknownTEnl modepropagatinginthecircularairwaveguidewith a = 3.5cm,we use(C.50)whichyields n = 3and snl/(0.035m)= 120 → s3l ≃ 4.200andfromTableC.3,we

l = 1.Therefore,thisistheTE31 mode.Itisapropagatingmodebecauseofthe e j116 9z terminthe Hz phasorexpression.

(b)Theoperationfrequencycanbecalculatedfromthephaseconstantexpressiongivenby

(c)Toﬁndthehighest-orderpropagatingmodeat ∼ 8GHz,wehave

Therefore,the highest-orderpropagatingmodeat ∼ 8GHzistheTM02 mode.

(d)FortheTM02 modepropagatinginthe z direction,

5201fromTable C.2,the

jωϵ a tnl C0 ≃ C1 → C0 ≃ j254 3C1

Ez ≃ j254 3C1 J0(138r) ej48πz Er = 277.9C1 J′ 0(138r) ej48πz

fcnl = (tnl or snl) c 2πa ≤∼ 9.760GHz → (tnl or snl) ≤∼ 8.176

ﬁndthat

β2 31 ≃ (2π)2f2 (3 × 108)2 [1 (5.73 × 109)2 f2 ] ≃ (116 9)2 wherewe

fc31 = 4 201c/(2πa) ≃ 5 73GHz.Solvingtheoperatingfrequency

used

fromthe aboveequation,weﬁnd f ≃ 8 00GHz.

fcnl = (snl or tnl)c 2πa ≃ 8 × 109 → (snl or tnl) ≃ 5 864

Ez phasorexpressioncanbewrittenas Ez ≃ C2J0 (5 5201 0.035 r) e jβ02z ≃ C2J0(158r)e j18πz where β02 = 2πf c √1 (fc02/f )2 ≃ 2π(8 × 109 3 × 108 √1 (7 53/8)2 ≃ 18π and fc02 ≃ 5 5201c π(0 07) ≃ 7.53GHz areused.

Hz = 0.Using t02 ≃ 5

willdestroytheintegrityoftheworkandisnotpermitted. © 2015 Pearson Education, Inc., Hoboken, NJ. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the publisher.

Dissemination orsaleofanypartofthiswork(includingontheWorldWideWeb)

C.34Smallestcircularwaveguidedimension.

(a)FromTableC.2,thecutoﬀfrequencyoftheTM 21modeinacircularair-ﬁlledwaveguideis givenby

(b)ThecutoﬀfrequencyoftheTM12

C.35Circularwaveguidemodes.

(a)SincetheWC-80(a = 1.012cm)circularairwaveguide(i.e., vp = c ≃ 3 × 108 m-s 1)is operatedat16GHz,thecutoﬀfrequenciesofallthepropagatingmodesmustsatisfytheinequality

≃ 3 054),weﬁndthatthe onlymodesthatwillpropagateinthiswaveguideat16GHzareTE11,TM01 andTE21 respectively.

(b)Thecutoﬀfrequenciesofthepropagatingmodesaregivenby

Usingthese values,thephasevelocity,guidewavelength,andthewaveimpedanceofthesepropagatingmodesat16GHzcanbecalculatedas

AddendumC/ CylindricalWaveguides

fcTM21 ≃ 5.135c 2πa ≃ 5.136 × 3 × 1010 πd =

fromwhichthesmallestdiameter dmin canbeobtainedas dmin = 2amin ≃ 0 510cm

25GHz

fcTM21 ≃ 7.016c 2πa = 25GHz

≃ 0

modeisgivenby

fromwhich

min = 2

min

373cm.

fcTEorTM = (snl or tnl)c 2πa < 16GHz → (snl or tnl) <∼ 3.391

t01 ≃ 2 405, s11 ≃ 1 841and s21

Therefore,usingTablesC.2andC.3(

fcTE11 ≃ 1 8412c 2πa ≃ 8 69GHz fcTM01 ≃ 2.4048c 2πa ≃ 11.35GHz fcTE21 ≃ 3 054c 2πa ≃ 14 4GHz

vp11 = vp √1 (fc11/f)2 ≃ c √1 (8 69/16)2 ≃ 1 19c v01 ≃ 1.42c, v21 ≃ 2.30c, λ11 = vp/f √1 (fc11/f)2 ≃ 3 × 108/(16 × 109) √1 (8 69/16)2 ≃ 0 0223m = 2 23cm λ01 ≃ 2.66cm, λ21 ≃ 4.31cm, ZTE11 = ηair √1 (fc11/f)2 ≃ 377 √1 (8.69/16)2 ≃ 1 19(377Ω) ≃ 449Ω ThisworkisprotectedbyUnitedStatescopyrightlaws

Dissemination orsaleofanypartofthiswork(includingontheWorldWideWeb) willdestroytheintegrityoftheworkandisnotpermitted. © 2015 Pearson Education, Inc., Hoboken, NJ. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the publisher.

C.36Low-lossTE01 modeinacircularwaveguide.

(a)Foranair-ﬁlledcircularwaveguidewithradius a = 5cm,thecutoﬀfrequencyofthelow-loss TE01 modeisgivenby

(b)If thesamecircularwaveguideisﬁlledwithwater(assume ϵr ≃ 81),then,thenewcutoﬀ

01 modeis

C.37Low-lossTE01 modeinahighlyovermodedwaveguide.

(a)Usingthe Eϕ expressionin(C.50)alongwiththeroot s01 ≃ 3 8317fromTableC.3,wecan calculatethediameter d oftheair-ﬁlledwaveguideas

(b)Usingthecutoﬀfrequencyexpression

footnote21inAddendumC),thetotalnumberofpropagatingmodesinthiswaveguideoperating at ∼ 108GHzisfoundtobe339!

27 ZTE21 ≃ 867Ω,and ZTM01 = ηair√1 (fc11/f)2 respectively

fcTE01 = s01c 2πa ≃ 3 832(3 × 1010) 2π(5) ≃ 3 66 × 109 Hz = 3 66GHz

frequencyoftheTE

fcTE01 ≃ 3 832(3 × 1010) 2π(5)√81 ≃ 4.07 × 108 Hz = 407MHz

s01 a ≃ 3.8317 a ≃ 238 → d = 2a ≃ 3 22cm Usingthe phaseconstantexpressiongivenby β01 = 2πf c √1 (fc01/f)2 ≃ 716π → (716π)2 ≃ (2π c )2 [f2 f2 c01] where fc01 = s01c/(2πa) ≃ 11 36GHzand c ≃ 3 × 1010 cm-s 1 , wecancalculatetheoperating frequencytobe f ≃

108GHz.

fcnl = (snl or tnl)c 2πa ≃

108 × 109 Hz fromwhich weﬁnd (snl or tnl)max ≃ 36 42.Therefore,usingareferencesuchasBeattie(see

AddendumC/ CylindricalWaveguides

C.38Ahighlyovermodedcircularwaveguide.

(a)Theradiiofthetwocircularwaveguidesare a1 = 3 175cmand a2 = 1 39cm.Assumingairﬁlledwaveguide,thecutoﬀfrequenciesofthepropagatingmodesinthe6.35cmdiameterguide mustsatisfytheinequality

Therefore,usingareferencesuchasBeattie(seefootnote21inAddendumC),thetotalnumberof modespropagatinginthe6.35cmdiameterairwaveguideat60GHzisfoundtobe409.

(b)Repeatingpart(a)forthe2.78cmdiameterwaveguide,wehave

Therefore,usingBeattie,thetotalnumberofpropagatingmodesinthe2.78cmdiameterairwaveguideat60GHzis80.

C.39TE11 toTM11 modeconverter.

(a)Fortheinputairwaveguidewithradius a1 ≃ 1 19cm,thecutoﬀfrequencyofanypropagating modeat9.94GHzmustsatisfy

yielding (snl or tnl) <∼ 2 477.Therefore, usingthevaluesof snl and tnl providedinTablesC.2and C.3,theonlymodesthatcanpropagateontheinnerwaveguideat9.94GHzareTE11 andTM01 respectively.

(b)Repeatingpart(a)fortheoutputairwaveguidewithradius a2 ≃ 2 06cm,weﬁnd (snl or tnl) <∼ 4.289

fromwhichwedeterminethepropagatingmodesontheouterwaveguideat9.94GHzasTE11, TM01,TE21,TM11,TE01,andTE31 respectively.

C.40Circularwaveguidemodes.

(a)UsingTablesC.2andC.3,thecutoﬀfrequenciesofthedominantTE11 modeandthenexthigher TM01 modeona1cminnerdiametercircularairwaveguidearegivenby

Therefore, thefrequencyrangeoverwhichonlythedominantTE11 modecanpropagatecanbe foundas fcTM01 fcTE11 ≃ 5.383GHz.

fcnl = (snl or tnl)c 2πa1 < 60GHz → (snl or tnl)max <∼ 39 90

fcnl = (snl or tnl)c 2πa2 < 60GHz → (snl or tnl)max <∼ 17 46

fcnl = (snl or tnl)c 2πa1 <

× 109

fcTE11 = s11c 2πa ≃ (1.8412)(3 × 1010) π(1) ≃ 17 58GHz fcTM01 = t01c 2πa ≃ (2.4049)(3 × 1010) π(1) ≃ 22.97GHz

(b)Thecutoﬀ frequencyoftheTE01 andTE31 modeare

Therefore, excludingthepossibilityoftheTM01 andTE21 modes,thefrequencyrangeoverwhich onlytheTE11 andTE01 (andTM11)modescanpropagatecanbefoundas

C.41Circularwaveguidedesign.

(a)Usingtheﬁrstdesigncriteria,wehave

1 isused.Usingtheseconddesigncriteria,wehave

Therefore,thewaveguideradiusmustlieintherange ∼ 1.717 ≤ a ≤∼ 2.599cm.But,sincethe thirddesigncriteriaistomaximizethepowerdeliveringcapabilityofthewaveguide,wechoose

2 599cm.

(b)Thethreepossiblemodesthatcanpropagateat6.4GHzareTE11,TM01,andTE21,sincethe cutoﬀfrequenciesofthesethreemodesare

(c)Similartopart(b),thepossiblepropagatingmodesat9.6GHzcanbefoundasTE11,TM01,

.44GHz).

fcTE01 = s01c 2πa ≃ (3 832)(3 × 1010) π(1) ≃ 36.59GHz fcTE31 = s31c 2πa ≃ (4.201)(3 × 1010) π(1) ≃ 40 12GHz

fcTE31 fcTE01 ≃ 3.52GHz.

fcTE11 ≃ 1.8412c 2πa ≤ 0 8(6 4GHz) → amin ≃ 1 717cm where c ≃

cm-s

fcTE01 ≃ 3 832c 2πa ≥ 1.1(6.4GHz) → amax ≃ 2.599cm

3 × 1010

a = amax

≃

fcTE11 ≃ 1 8412c 2π(2 599) ≃ 3.38GHz fcTM01 ≃ 2 4049c 2π(2.599) ≃ 4 42GHz fcTE21 ≃ 3 0542c 2π(2.599) ≃ 5 61GHz

01 andTM11,bothofwhichhavethesamecutoﬀfrequenciesgiven

fcTE01 = fcTM11 ≃ 3.832c 2π(2.599) ≃ 7 04GHz > 6 4 GHz andtherefore,thesetwomodesdonotpropagateat6.4GHz.

ThenexthighermodesareTE

TE21,TE01,TM11,TE31 (with fcTE31 ≃ 7.72GHz),andTM21 (with fc

≃

TM21

AddendumC/ CylindricalWaveguides

C.42Circular waveguidemodes.

(a)FortheWC-109circularpolystyrene-ﬁlledwaveguidewithdiameter2a = 2.779cm,themodes thatcanpropagateat10GHzcanbeareTE11,TM01,TE

11,andTE31 whichhavecutoﬀ frequenciesgivenby

Note thatthenexthighermode(inthiscaseTM21)doesnotpropagatesinceitscutoﬀfrequencyis ∼ 11.03GHz >∼ 10GHz.

(b)Thephasevelocity,theguidewavelength,andthewaveimpedanceofthedominantTE11 mode at10GHzcanbecalculatedas

C.43Acircularwaveguideusedformicrowavetelecommunications.

At4GHz,thecutoﬀfrequenciesofallpropagatingmodesontheWC--281circularairwaveguide (d = 2a ≃ 7.14cm)mustsatisfy

UsingTablesC.2andC.3,weﬁndthatonlyTE11andTM01 modescanpropagateat4GHz.

At6GHz,weﬁnd (tnl or snl) <∼ 4 486,whichmeansthatonlysixmodes(TE11,TM01,TE21, TE01,TM11,andTE31)canpropagate.

At8GHz,weﬁnd (tnl or snl) <∼ 5.982,whichmeansthatonlytenmodes(TE11,TM01,TE21, TE01,TM11,TE31,TM21,TE41,TE12 andTM02)canpropagate.

01,TM

fcTE11 ≃ 1 8412(3 × 1010) π(2 779)√2 56 ≃ 3.954GHz fcTM01 ≃ 2.4049(3 × 1010) π(2 779)√2 56 ≃ 5 165GHz fcTE21 ≃ 3.0542(3 × 1010) π(2 779)√2 56 ≃ 6 559GHz fcTE01 = fcTM11 ≃ 3 832(3 × 1010) π(2.779)√2.56 ≃ 8 23GHz fcTE31 ≃ 4 201(3 × 1010) π(2.779)√2.56 ≃ 9.022GHz

,TE

vp11 ≃ (3 × 108 m-s 1)/√2.56 √1 (3.954/10)2 ≃ 2.04 × 108 m-s 1 λ11 ≃ (3cm)/√2.56 √1 (3.954/10)2 ≃ 2.04cm ZTE11 ≃ (377Ω)/√2 56 √1 (3 954/10)2 ≃ 256 5Ω

(tnl or snl) π(7 14) < 4GHz → (tnl or snl) <∼ 2.991

At11 GHz,weﬁnd (tnl or snl) <∼ 8 225,whichmeansthatonly18modes(uptotheTE32 mode) canpropagate.

C.44OrthogonallypolarizedTE11 modes.

(a)Wehave

(b)NextlowestcutoﬀforTMmodesisTM01,with

5GHz,whileforTEmodesisTE21,with fc ≃ 6 3GHz.Thus,theTE11 modeat4.43GHzisindeeddominant.

(c)From(C.8)wehave

s11 a = 80 → a = s11 80 = 1.841 80 = 2 3cm β11 = 47 =]ω 2 µϵ (s11/a)2] → f = c 2π [(47)2 +(80)2]1/2 ≃ 4 43GHz

c ≃

Htr = Hr + Hϕ = γ γ2 + ω2µϵ ∇trHz (C.6a) Etr = Er + Eϕ = jωµ γ Htr × ˆ z (C.6b) where β =[ω2µϵ (snl/a)2]1/2,and γ = jβ.Since ˆ ϕ ϕ ϕ × ˆ z = ˆ r,wehavefromtheabove Hϕ = β ωµ Er = β ωµ C1 r J1(80r)[sin ϕ + cos ϕ]e j47z =(1.34 × 10 3) C1 r J1(80r)[sin ϕ + cos ϕ]e j47z

γ 2 + ω 2 µϵ = (snl a )2 ∇tr = ˆ r ∂ ∂r + ˆ ϕ ϕ ϕ 1 r ∂ ∂ϕ andintegrating(C.8a):

z = (snl/a)2 jβ ∫ Hϕrdϕ = j (snl/a)2 ωµ C1J1(80r) e j47z ∫ [sin ϕ + cos ϕ]dϕ = j (snl/a)2 ωµ C1J1(80r) e j47z[cos ϕ sin ϕ]= j(0.183)C1 J1(80r) e j47z[cos ϕ sin ϕ] andfrom(C.6a)wehave Hr = jβ (s nl/a)2 ∂Hz ∂r = βωµ C1 J′ 1(80r) e j47z(80)[cos ϕ sin ϕ] = 0.107C1 J′ 1(80r) e j47z[cos ϕ sin ϕ] whereasfrom(C.6a)wehave Eϕ = jωµ jβ = 80C1 J′ 1(80r)e j47z[cos ϕ sin ϕ]

The

componentcanbe foundbynotingthat

ThisworkisprotectedbyUnitedStatescopyrightlaws andisprovidedsolelyfortheuseofinstructorsinteaching theircoursesandassessingstudentlearning.

AddendumC/ CylindricalWaveguides

(d)Theformachoiceofsinesandcosinesintherectangularcaseareduetotheboundaryconditions, whileinthecircularcasetheyareduetoanarbitraryselectionoftheoriginof ϕ

C.45Circularwaveguide-to-microstriptransition.

Thecutoﬀfrequencyofallthepropagatingmodesonthe2.1cmdiametercircularairwaveguide mustsatisfy

UsingTables C.2andC.3,weﬁndthatonlytheTE11 modecanpropagateinthiswaveguide,for thefrequencyrangespeciﬁed.

C.46Circularversusrectangularwaveguides.

Weseparatelyconsiderparallel-plate,rectangular,andcircularwaveguides.Forparallel-plate, examinationofFigure10.11indicatesthatpossiblelowlossmodesareTEMandTE1.ForTEM, wehave fc = 0,and αcTEM = Rs/(ηa).Fromthegivensheetsizewecanchoose

andselect avalueof a smallenoughsothatfringingﬁeldscanbenegligible,e.g.,

0.315cm.Theattenuationconstantisthen

ForTE1, wehave

sincewemusthave a ≤ 0.315cmtominimizefringingﬁelds,itappearsthatanyparallel-plate guidewecanmakefromthegivenmaterialwouldnotbesuitableforpropagatingtheTE1 mode. Forrectangularwaveguide,weseefromFigureC.8thatthebestmodetoconsideristheTE10 mode.

(tnl or snl)c 2πa < 10.66GHz → (tnl or snl) < π(2 1)(10 66 × 109) 3 × 1010 ≃ 2.344

b = 6 3 2 = 3.

a ≤ b

αcTEM = 1 0.315 × 10 2 317 46 Rs ηa = 317 46 Rs ηa

15cm,

fc1 = c (2a) ≤ 25GHz → a ≥ c 2.25 × 109 = 0 6cm

fc10 = c 2a ≤ 25GHz → a ≥ 0 6cm Also a ≥ b and a + b = 6 3 2 = 3.15cm → a ≥ 3 15 2 = 1.5757cm and a < 3 15 cmwhereas b = 3 15 a cm Theattenuationconstantis αcTE10 = Rs [1 +(2b/a)(fc10/f)2] ηb√1 (fc10/f)2 = Rs η 1 +[(6.3 2a)/a][c/(2πf)]2 (3.15 a) × 10 2√1 [c/(2πf)]2 ≃ 372 91 Rs η for f = 25GHz, and a = b = 1.575cm.

Wehave

Forcircular waveguide,wenotefromFigureC.13thatpossiblemodesareTE11 andTE01.We considertheseseparately:

for f = 25GHz and a = 1cm.

Comparisonof the αc valuesforthethreediﬀerentwaveguidesindicatesthatcircularwaveguide isthebestfromthepointofviewofminimizingattenuationduetoconductivelosses.

C.47Attenuationinacoaxialline.

Theexpressionfortheattenuationconstantforacoaxiallineis

where Rs = √ωµ0/(2σ) istheonlyfrequencydependentterm,foranonmagneticconductorsuch ascopper,andassumingthat η = √µ/ϵ isnotfrequencydependent,whichforanair-filledlineis simply ηair = √µ0/ϵ0.We aretoldthatthelineismadeof`thick'walls,whichat300MHzmust definitelybemuchlargerthantheskindepth (δ ≃ 3 82 µmforcopperat300MHz).Thus,thewall thicknessdoesnotexplicitlyappearintheexpressionfor αc,anddoublingitdoesnotsignificantly changetheattenuationconstant.

(a)At600MHz,thevalueof Rs ishigherbyafactorof √2,thuswehave αc ≃ 0.003√2 ≃ 0.0042np-m 1 .

(b) Asmentionedabove,doublingthethicknessofthecopperwallshasnosigniﬁcanteﬀect.When theconductorradiiare2a and2b,wehave

TE01 : fcTE01 = s01 2πa√µϵ = 3.832c 2πa ≤ 25GHz → a ≥ 3.8232c 2π(25 × 109) = 0 73cm Also2πa ≤ 6 3cm → a ≤ 1 00cm αcTE01 = Rs η 1 a [1 (fcTE01 f )2]1/2 [(fcTE01 f )2 + 1 (3.832)2 1] ≃ 89 34 Rs η

TE11 : fcTE01 = s11 2πa√µϵ = 1.841c 2πa ≤ 25GHz → a ≥ 3.8232c 2π(25 × 109) = 0 35cm Also2πa ≤ 6 3cm → a ≤ 1 00cm αcTE11 = Rs η 1 a [1 (fcTE11 f )2]1/2 [(fcTE11 f )2 + 1 (1.841)2 1] ≃ 57 91 Rs η

αc = Rs 2η ln(b/a) [1 a + 1 b] = 0.003np-m 1 at300 MHz

αc = Rs 2η ln[2b/(2a)] [ 1 2a + 1 2b] = 1 2 { Rs 2η ln(b/a) [1 a + 1 b]} αc at300MHz = 0.0015np-m 1

(c)Theattenuation rateduetodielectriclossesfortheTEMmodeinacoaxiallineﬁlledwith nonmagneticmaterialisgivenby(C.57),namely

(d)At600MHz, αd istwiceaslarge,sinceitisproportionaltofrequency.Thuswehave

C.48Optimumcoaxiallines.

Thereisatypointhestatementofthisproblem.Asshouldbeobviousfromthewording,the conditionforminimum αc foragivenouterconductorradius b is b = 3 6a,ratherthan

(a)Theexpressionfor αc forTEMmodeinacoaxiallineisgivenby(C.56),namely

AddendumC/ CylindricalWaveguides

αd ≃ ωϵ′′√µ0 2√ϵ′ where ϵ′′ = ϵ′ tan δc.Usingthe valuesgivenfor300MHzweﬁnd αd ≃ (2π)(300 × 106)(2ϵ0)[(15/π) × 10 4] 2√2ϵ0 ≃ 6 36 × 105√ϵ0 ≃ 1 89np-m 1 sothat thetotalattenuationrateis αtotal = αc + αd = 0.003 + 1.89 ≃ 1.90np-m 1

Itthusappearsthatthedielectriclossesareclearlydominant.

αtotal = 0 0042 +(2)(1 89)=

78np-m 1

a = 3 6b

αc = Rs 2η ln(b/a) [1 a + 1 b] Fora givenvalueof b,wecandiﬀerentiate αc withrespectto a andequatetozero ∂αc ∂a = Rs 2η        [1 a + 1 b] a[ln(b/a)]2 1 a2 ln(b/a)        = 0 whichreduces to a [1 a + 1 b] = ln(b/a) → 1 + 1 b/a = ln(b/a) → ζ = e 1+ζ 1 → ζ = b a ≃ 3.591

Z0 ≃ 60ln b a ≃ 60ln 3.6a a ≃ 76 7Ω

(b)Thecharacteristicimpedanceisgivenby(C.58)

Dissemination

(c)Theanswerisno.Ifwestartwithaﬁxedvalueoftheinnerconductorradius a,thenthelarger thevalueof b thebetter,sincetheaveragepowertransmitted(Pav)goesupproportionaltothe cross-sectionalareawhilethewalllosses(Ploss)aredeterminedbytheperimeter,thus αc,which isdeterminedbytheratioof Ploss to Pav canbemadearbitrarilysmallbychoosinganarbitrarily largevalueof b.

C.49Powercapacityofacoaxialline.

OuranswermustbebasedontheexpressionsfromSectionC.2.2fortheelectricandmagnetic ﬁeldsandtheaveragepowertransmittedforacoaxialline.Wehave

ﬁeldandsurfacecurrentconditionsdictatethefollowing:

Thus,itappears thatthesurfacecurrentcriteriaistheonethatlimitsthemaximumpowerhandling capacity.For H0 = 5wehave

C.50Higher-ordermodesonacoaxialline.

(a)Fortheair-ﬁlledcoaxiallinewith

nonzerocutoﬀfrequencyistheTE11 modewithcutoﬀfrequencyapproximatelygivenby(C.59) as

Thus,TE11 mode canpropagateonthecoaxiallineonlyatfrequenciesabove1.941GHz.

(b)Repeatingpart(a)forthesamecoaxiallineﬁlledwithNorylEN265material(ϵ′ r ≃ 2.65),we

(c)Based onthecutoﬀfrequencycalculatedinpart(b),itisclearthattheTEMapproximationis notvalidforfrequenciesabove ∼1.2GHz,sincethehigher-ordermodessuchastheTE11 canalso propagateonthelineandcancontributetotheresultsobtainedinthemeasurements.

H = ˆ ϕ ϕ ϕ H0 r e jβz ; E = ˆ r H0η r e jβz ; Pav = πηH2 0 ln (b a)

Js = ˆ n × H,sothat |Js| = |H|.Wenotethatboththeelectricﬁeldand

|Js|≤ 10A-mm 1 → H0 0.5 × 10 3 ≤ 10 × 103 → H0 ≤ 5 |E|≤ 10kV-mm 1 → H0(377) 0 5 × 10 3 ≤ 10 × 106 → H0 ≤ 13.26

Thesurfacecurrentdensity

thesurfacecurrentdensityaremaximumatthelowestradius,i.e.,at r =

.Thus,weonlyneedto payattentiontotheirvaluesat r =

.Forthegivenvalueof a = 0.5mm,themaximumelectric

Pav = πηH2 0 ln (b a) = π(377)(5) ln (2.5 0.5) = 9 53kW

a ≃ 1.49cmand b ≃ 3.

fc11 ≃ c π(a + b) ≃ 3 × 1010 π(1.49 + 3.429) ≃ 1 941GHz

429cm,themodewiththelowest

ﬁnd fc11 ≃ 3 × 1010/√2 65 π(1.49 + 3.429) ≃ 1

193GHz

C.51Group velocityfortheTE10 mode.

TheﬁeldexpressionsfortheTE10 modeinarectangularwaveguideare:

Following ananalysissimilartothatinSection10.3.3,wecanconsideraunitlength(1m)of waveguide.Thetimeaverageenergystoredinavolume

36 AddendumC/

CylindricalWaveguides

Ho z = Ccos

πx a ) Ho x = jβaC π sin ( πx a ) Eo y = jωµaC π sin ( πx a ) Eo x = Ho y = 0 β10 = √ω2µϵ ( π a )2 = [(2π λ )2 ( π a )2]1/2

(

V =(a)(b)(1)

Wstr = 1 4 ∫ a 0 ∫ b 0 ∫ 1 0 [ϵE · E∗ + µH · H∗]dzdydx = µω2µϵab 4(π/a)2 Thetimeaveragepowertransmittedcanbefoundas Pav = ∫ b 0 ∫ a 0 1 2 5e{E × H∗}dxdy = ωµβ10ab a(π/a)2 sothat thevelocityofenergytravelisgivenby ven = Sav W = ωβ10 ω2µϵ = v2 p vp = 1 √µϵ √1 (fc10 f )2 → ven = vg Thuswe seethatthegroupvelocityisindeedthevelocityofenergytransportfortheTE10 mode. ThisworkisprotectedbyUnitedStatescopyrightlaws

theircoursesandassessingstudentlearning.

,includingbothelectricand magneticparts,is

andisprovidedsolelyfortheuseofinstructorsinteaching

Dissemination orsaleofanypartofthiswork(includingontheWorldWideWeb)

TransientResponseofTransmissionLines

2.1Lumpedordistributedcircuitelement?

ThisworkisprotectedbyUnitedStatescopyrightlaws andisprovidedsolelyfortheuseof instructorsinteachingtheircoursesandassessingstudentlearning. Dissemination orsaleofanypartofthiswork(includingontheWorldWideWeb) willdestroytheintegrityoftheworkandisnotpermitted.

2.2Lumped-ordistributed-circuitelement?

(a)Using(2.9), Z0 = √ L C = √ 4 × 10 9 H-cm 1 1 6 × 10 12 F-cm 1 = 50Ω Using(2.7), vp = 1 √LC = 1 √(4 × 10 9 H-cm 1)(1 6 × 10 12 F-cm 1) = 1 25 × 1010 cm-s 1 = 12.5cm-(ns) 1 Hencetheone-waytimedelay td isgivenby td = l vp = 5cm 12.5cm-(ns) 1 = 0 4ns (b)Theratiobetweenthestepsourcerise-timeandtheone-waytimedelayis tr td = 0.1ns 0 4ns = 0 25 < 2 5 From(1.1),itisnotappropriatetomodelthetransmissionlineinthiscircuitasalumpedelement.

2 Chapter2/TransientResponseofTransmissionLines (a)Using(2.7) and(2.9),wehave vp = 1 √LC = 2c 3 ≃ 2×108 m-s 1 Z0 = √ L C = 50Ω Multiplyingthe abovetwoequationsyields vpZ0 = 1 C ≃ (2×108 m-s 1)(50Ω) → C ≃ 10 10 F-m 1 = 1pF-(cm) 1 Dividingtheabovetwoequationsintooneanotherresultsin vp Z0 = 1 L ≃ 2×108 m-s 1 50Ω → L ≃ 2 5 × 10 7 H-m 1 = 2 5nH-(cm) 1 (b) td = l 2c/3 ≃ 1m 2×108 m-s 1 ≃ 5ns (c) λ = 2c/3 f ≃ 2×108 m-s 1 109 Hz = 0 2m Using(1.6), wehave l = 1m > 0 01λ = 0 002m Therefore,thistransmissionlineshouldnotbetreatedasalumpedelement. 2.3Open-circuitedline. Sincewehaveanidealunitstepsource, Rs = 0.Asaresult,thesource-endreflectioncoefficient is Γs = Rs Z0 Rs + Z0 = 0 Z0 0 + Z0 = 1 Atthe loadend(opencircuit,i.e., RL = ∞),thereflectioncoefficientis ΓL = RL Z0 RL + Z0 = ∞− Z0 ∞ + Z0 =+1 © 2015 Pearson Education, Inc., Hoboken, NJ. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the publisher.

ThisworkisprotectedbyUnitedStatescopyrightlaws andisprovidedsolelyfortheuseof instructorsinteachingtheircoursesandassessingstudentlearning. Dissemination orsaleofanypartofthiswork(includingontheWorldWideWeb) willdestroytheintegrityoftheworkandisnotpermitted.

At t = 0,anincidentvoltageofamplitude

9+ 1 = Z0 Rs + Z0 V0 = 50 0 + 50 (1V) = 1V

islaunchedatthesourceendoftheline.Usingthesevalues,wehavethebouncediagramshown. Theloadendvoltage 9L(t) shownissketchedinFigure2.1usingthebouncediagram.

2.4Stepandpulseexcitationofalosslessline.

(a)Wefirstcalculatethereflectioncoefficientsatthesourceandload,andtheamplitudeofthe 9+ 1 voltagewavethatislaunchedat t = 0+:

Usingthese values,wecansketchthebouncediagraminFigure2.2a.Thesuccessive 9 and 9+ stepamplitudesarecalculatedusingtheloadandsourcereﬂectioncoeﬃcients.Forexample, 91 and 9+ 2 arefoundfrom 9+ 1 as:

Thebouncediagramcanbeusedtosketchtheload-andsource-endvoltages,asshownin Figure2.2b.

3 0 (V)

Figure2.1 FigureforProblem2.3

Γs = Rs Z0 Rs + Z0 = 10 90 10 + 90 = 0 8 ΓL = RL Z0 RL + Z0 = 630 90 630 + 90 = 0.75 9+ 1 = V0Z0 Rs + Z0 = (10)(90) 10 + 90 = 9V

91 =ΓL9+ 1 =(0.75)(9)= 6.75V 9+ 2 =Γs91 =( 0.8)(6.75)= 5.4V

(b)Wecanderivethesketchesfor 9s and 9L fromthesketchesinpart(a)bydelayingtheplotsby 0.3nsandsubtractingtheresult.TheresultingsketchesareshowninFigure2.3.

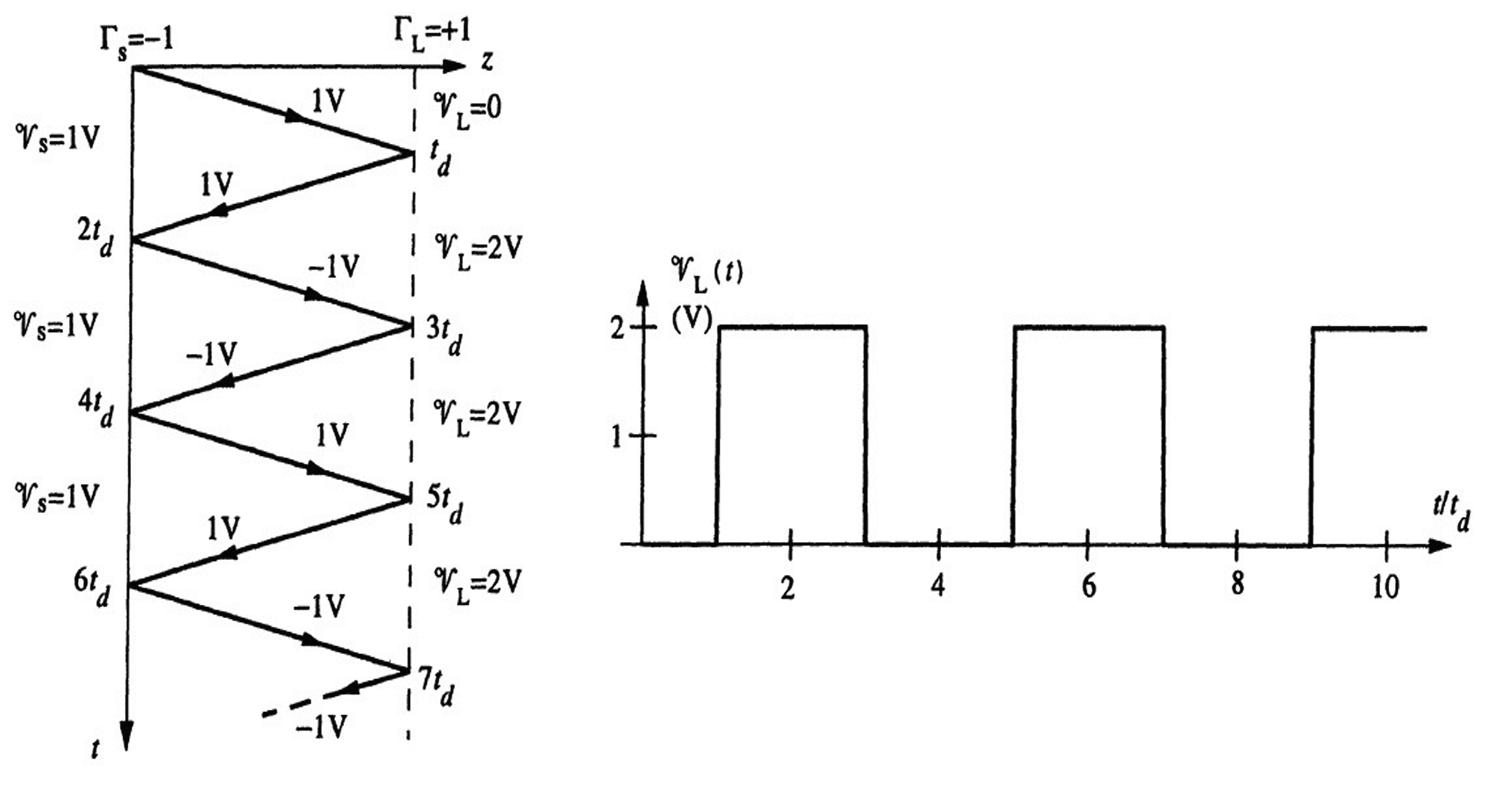
2.5Resistiveloads.

Since Rs = 0, Γs = 1.

(a)For RL = 25Ω,wehave

islaunchedatthesourceendoftheline.Usingthesevalues,thebouncediagramandtheload voltage 9L(t) versus t areasshowninFigure2.4.

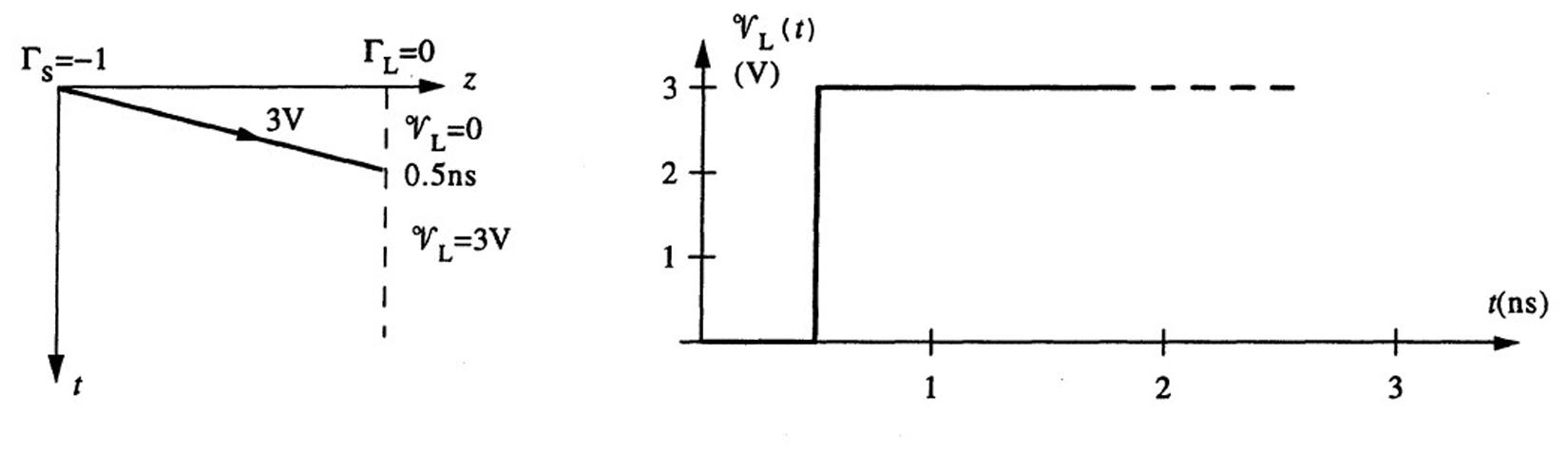
(b)For RL = 50Ω, ΓL = 0.Thebouncediagramandthesketchoftheloadvoltageforthiscase areasshowninFigure2.5.

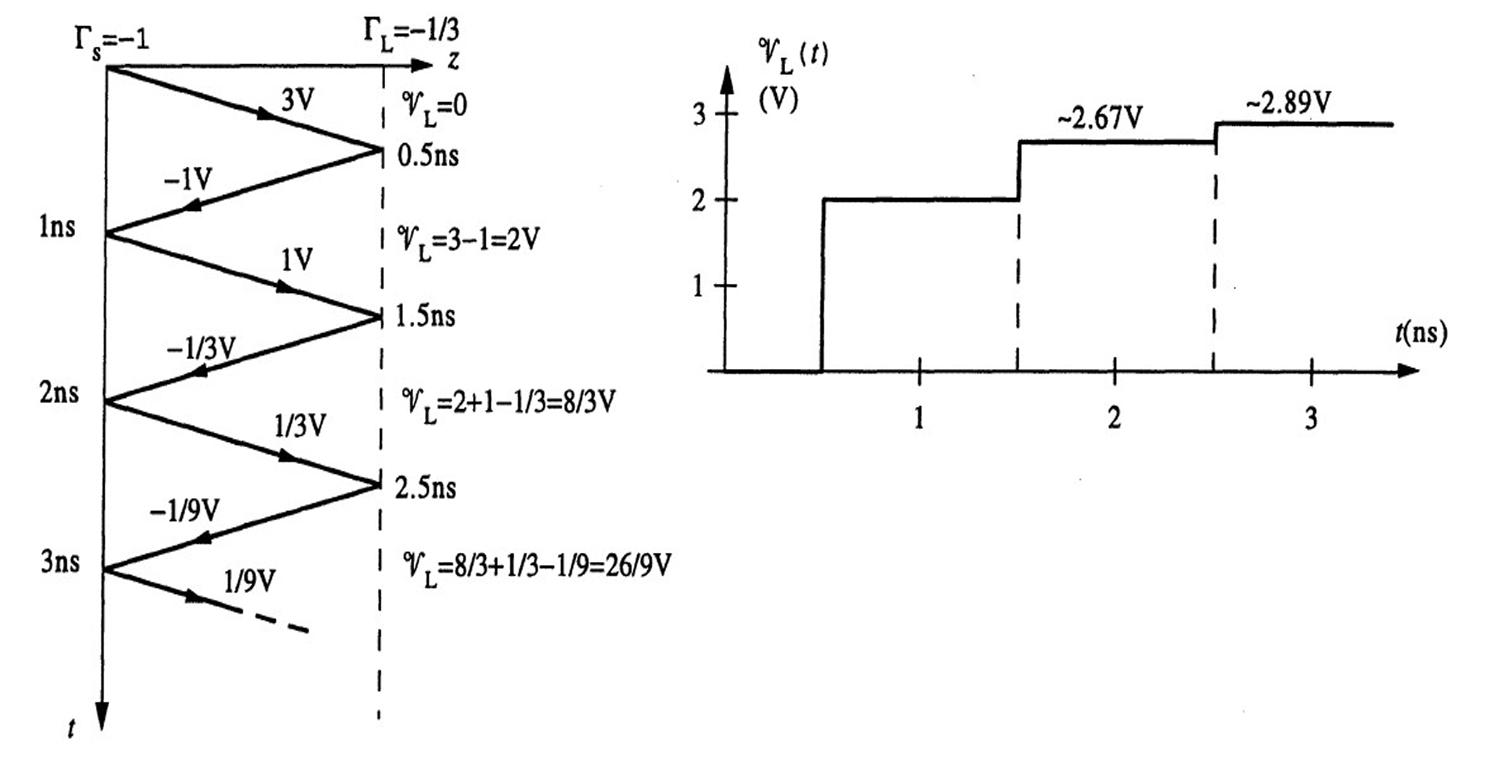
(c)For RL = 100Ω,theloadreﬂectioncoeﬃcientis

ΓL = 100 50 100 + 50 =+ 1 3

Again, thebouncediagramand 9L(t) versus t areasshowninFigure2.6.

4 Chapter2/TransientResponseofTransmissionLines 0 0 0 1.8 3.65.4 7.29.0 0 1.83.65.47.29.0 9 10.35 9.54 15.75 6.3 11.97 t (ns) t (ns) s(t) (V) L(t) (V) (b) (a) Γs= 0.8 0 3.6 91 = 9 V ΓL= 0.75 + 91 = 6.75 V 92 = −5.4 V + 92 = −4.05 V 93 = 3.24 V + 93 = 2.43 V 7.2 1.8 5.4 9.0 9L = 0 9L = 15.75 V 9L = 6.3 V 9L = 11.97 V 9s = 9 V 9s = 10.35 V 9s = 9.54 V t (ns)

Figure2.2 FigureforProblem2.4(a). (a)Bouncediagram.(b) 9

s and 9

versustime

ΓL = RL Z0 RL + Z0 = 25 50 25 + 50 = 1 3 At t

9+ 1 = Z0 RL + Z0 V0 = 50 0 + 50 (3V)= 3 V

= 0,an incidentvoltageofamplitudegivenby

ThisworkisprotectedbyUnitedStatescopyrightlaws andisprovidedsolelyfortheuseof instructorsinteachingtheircoursesandassessingstudentlearning. Dissemination orsaleofanypartofthiswork(includingontheWorldWideWeb) willdestroytheintegrityoftheworkandisnotpermitted.

5 0 1.8 3.65.4 7.2 9.0 1.8 3.6 5.4 7.29.0 9 1.35 -0.81 15.75 5.67 -9.45 0 t (ns) t (ns) s(t) (V) L(t) (V)

Figure2.3 FigureforProblem2.4(b). 9s and 9L versustime t. Figure2.4 FigureforProblem2.5a. RL = 25 Ω Figure2.5

FigureforProblem2.5b. RL = 50 Ω

2.6Ringing. Using(2.7)and(2.9),wehave

Theone-waytimedelaycanbefoundas

Theincident voltagewavelaunchedatthesource-endat t = 0canbefoundusingthevoltage dividerprincipleas

Theload-end andsource-endreﬂectioncoeﬃcientscanbefoundusing(2.12)and(2.14):

Next, wedrawabouncediagramupto t = 10ns,showninFigure2.7a.Usingtheload-end voltagevaluesonthebouncediagram,wecansketchtheload-endvoltage 9L(t) versustime,as showninFigure2.7b.

6 Chapter2/TransientResponseofTransmissionLines

Figure2.6 FigureforProblem2.5c. RL = 100 Ω

vp = 1 √LC = 1 √0 5×10 6 H-m 1 × 0 2×10 9 F-m 1 = 108 m-s 1 Z0 = √ L C = √0 5×10 6 H-m 1 0 2×10 9 F-m 1 = 50Ω

td = l vp = 15cm 1010 cm-s 1 = 1 5ns

9+ 1 = V0Z0 Rs + Z0 = (50)(3.6) 10 + 50 = 3V

ΓL = RL Z0 RL + Z0 RL→∞ =+1 Γs = Rs Z0 Rs + Z0 = 10 50 10 + 50 = 2 3

2.7Dischargingofachargedline.

At t = 0 (i.e.,immediatelybeforetheswitchopenswhensteady-stateconditionsareineﬀect), thesourceendcurrent )s isgivenby )

theswitchopens),thesourceendcurrentissuddenlyforcedtogotozero,i.e., )s(0+)= 0.Wecan representthischangein )s asanewdisturbancelaunchedfromthesourceendofthelinestarting at t = 0.Theamplitudeofthisnewcurrentwaveanditsaccompanyingvoltagewavearegiven respectivelyby )+ 1 = )s(0+) )

willnotaﬀectthevalueoftheloadendvoltageuntil

t < td, 9L(t)= 3V, regardlessofthevalueof RL.UsingthereﬂectioncoeﬃcientvaluescalculatedinProblem2.5, wedrawthebouncediagramandsketch 9L(t) asafunctionof t foreachvalueof RL,asshownin Figures2.8,2.9,and2.10.

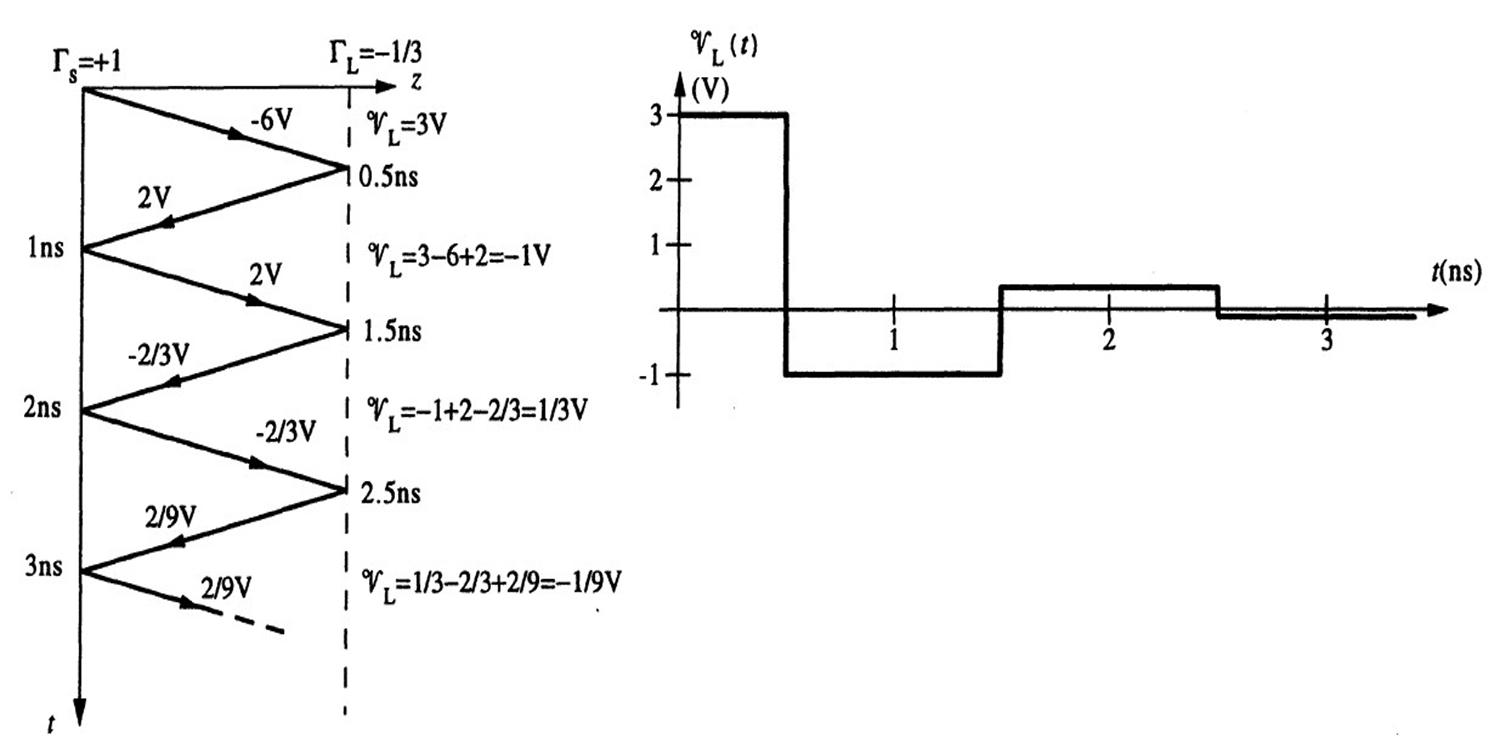
2.8Twostepvoltagesources.

Thereﬂectioncoeﬃcientsatsource1andsource2endsare,respectively,

7 (b) (a) Γs= − 2/3 0 3.0 91 = 3 V ΓL= +1 + 91 = 3 V 92 = −2 V + 92 = −2 V 93 = (4/3) V + 93 = (4/3) V 6.0 1.5 4.5 7.5 9.0 9L = 0 9L = 3 + 3 = 6 V 9L = 6 − 2 − 2 = 2 V 6 4.67 2 3.6 1.50 0 4.5 7.59.0 t (ns) t (ns) L(t) (V) 94 = −(8/9) V + 9L = 2 + 4/3 + 4/3 = ∼4.67 V

Figure2.7 FigureforProblem2.6. (a)Bouncediagram.(b) 9L versustime t

s(0 )= V0/RL = 3/RL.At t = 0+ (i.e.,immediatelyafter

0 )= 3/RL and 9+ 1 = Z0)+ 1 = 3Z0/RL.Thisdisturbance

0 5ns.So,for

t = td =

Γ1 = Rs1 Z0 Rs1 + Z0 = Z0 3 Z0 Z0 3 + Z0 = 0 5 Γ2 = Rs2 Z0 Rs2 + Z0 = Z0 Z0 Z0 + Z0 = 0 At t = 0 ,the systemisatasteadystate,andso © 2015 Pearson Education, Inc., Hoboken, NJ. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the publisher.

8 Chapter2/TransientResponseofTransmissionLines

Γs= +1 ΓL = 0 1 3 V 3 2 1 0.5 ns 2 3 t (ns) L(t) (V) L=3 V L=0 t (ns)

Figure2.8 FigureforProblem2.7a. Bouncediagramand 9L(t) versus t for RL = 25 Ω.

Γs= +1 ΓL = +1/3 1 3 2 1 0.5 ns 1.5 ns −1.5 V −0.5 V −0.5 V −0.5/3 V −0.5/3 V −0.5/9 V 2.5 ns 1 V 1/3 V 1/9 V 2.0 ns 3.0 ns 1.0 ns 2 3 t (ns) L(t) (V) L=3 V L=1 V L=1/3 V L=1/9 V t (ns)

Figure2.9 FigureforProblem2.7b. Bouncediagramand 9L(t) versus t for RL = 50 Ω.

100 Ω © 2015 Pearson Education, Inc., Hoboken, NJ. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the publisher.

Figure2.10 FigureforProblem2.7c. Bouncediagramand 9L(t) versus t for RL =

9 91(0 )= 92(0 ) = Rs2 Rs1 + Rs2 V0 = Z0 Z0 3 + Z0 V0 = 0.75V0 At t = 0, V0u( t) turnsoffand2V0u(t) turnson.Asaresult,wehavethebouncediagramshown inFigure2.11a.Notethat 9+ 1A isavoltagewavelaunchedduetosource V0u( t) turningoffat t = 0.Similarly, 91A isavoltagewavelauncheddueto2V0u(t) turningonat t = 0. Calculatingthevoltagewaveamplitudes,wehave 9+ 1A = Z0 Rs1 + Z0 V0 = 0.75V0 91A = Z0 Rs2 + Z0 (2V0)= V0 9+ 2A =Γ191A = ( 0 5)(V0)= 0 5V0 Usingthesevalues,wehave 91(t)=          0 75V0, t < 0 0, 0 < t < td 0.5V0, t > td and 92(t)=                0.75V0, t < 0 1 75V0, 0 < t < td V0, td < t < 2td 0.5V0, t > 2td ThevoltagesketchesareshowninFigure2.11b. 2.9Pulseexcitation. Theone-waytimedelayandthereflectioncoefficientsattheendsofthelineare td = l/vp = (10cm)/(20cm-ns 1)= 0 5ns, Γs = Rs Z0 Rs + Z0 = 25 75 25 + 75 = 0.5 ΓL = RL Z0 RL + Z0 = 0 75 0 + 75 = 1 respectively.At t = 0,anincidentvoltageislaunchedatthesourceendofthelinegivenby 9+ 1 = 75 25 + 75 (1V) = 0 75V © 2015 Pearson Education, Inc., Hoboken, NJ. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the publisher.

andisprovidedsolelyfortheuseof instructorsinteachingtheircoursesandassessingstudentlearning. Dissemination orsaleofanypartofthiswork(includingontheWorldWideWeb) willdestroytheintegrityoftheworkandisnotpermitted.

ThisworkisprotectedbyUnitedStatescopyrightlaws

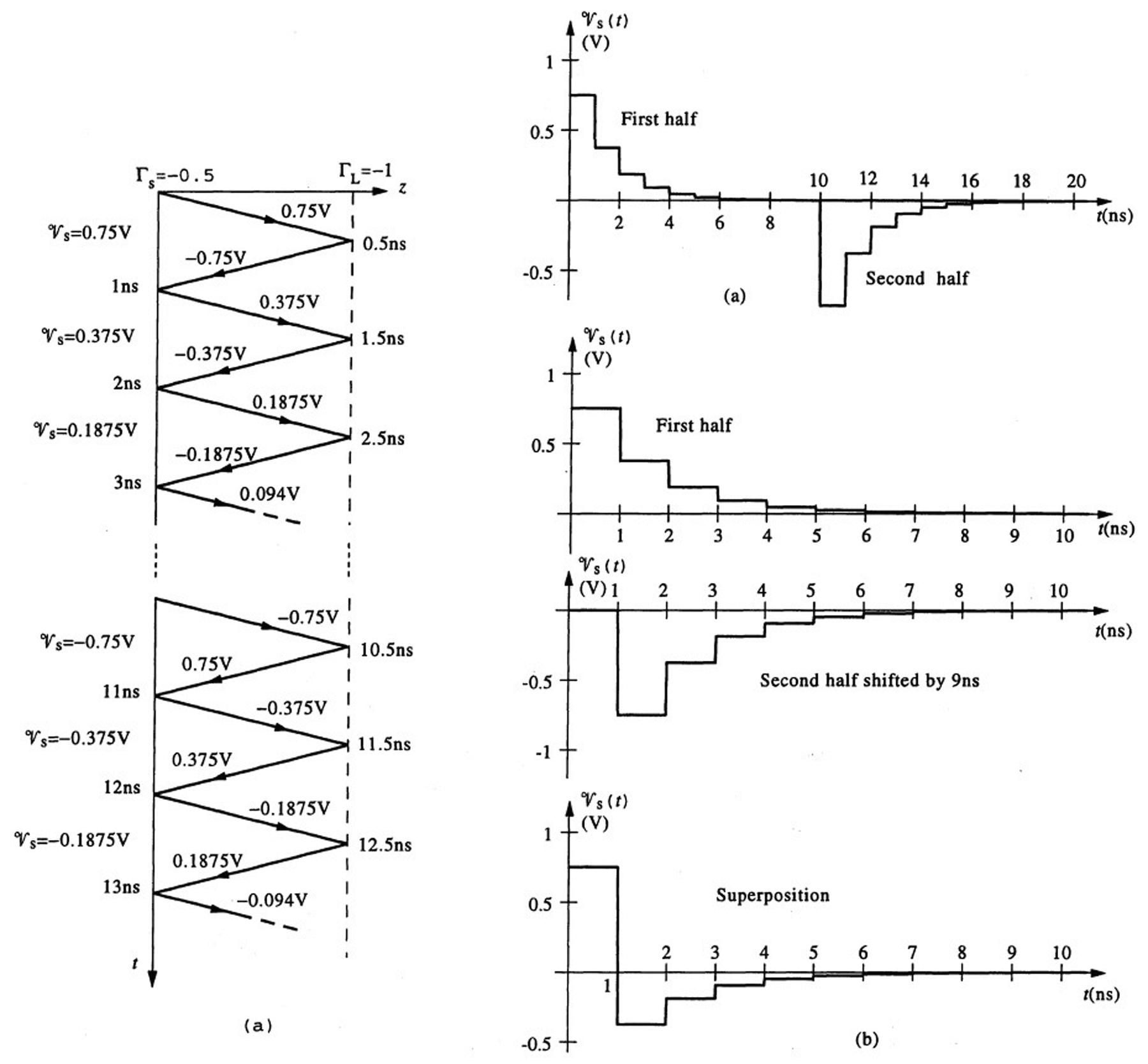
(a)Theinputvoltagehasapulsewidthof tw = 10ns,thatistheinputvoltageturnsoﬀat t = tw = 10ns.Werepresentthischangeintheinputvoltageasanewincidentvoltageofamplitude 9+∗ 1 = 9+ 1 = 0.75Vlaunchedatthesourceendofthelineat tw = 10ns.Thebouncediagram andthevariationofthesourcevoltage 9s(t) versus t areasshowninFigure2.12a.

(b)Forthecaseof tw = 1ns,thesourceendvoltage 9s(t) caneasilybeobtainedbyshiftingthe second-halfofthe 9s(t) sketchedinpart(a)by9nstotheleftandaddingitwiththeﬁrsthalf.The ﬁnalplotfor 9s(t) versus t isasshowninFigure2.12b.

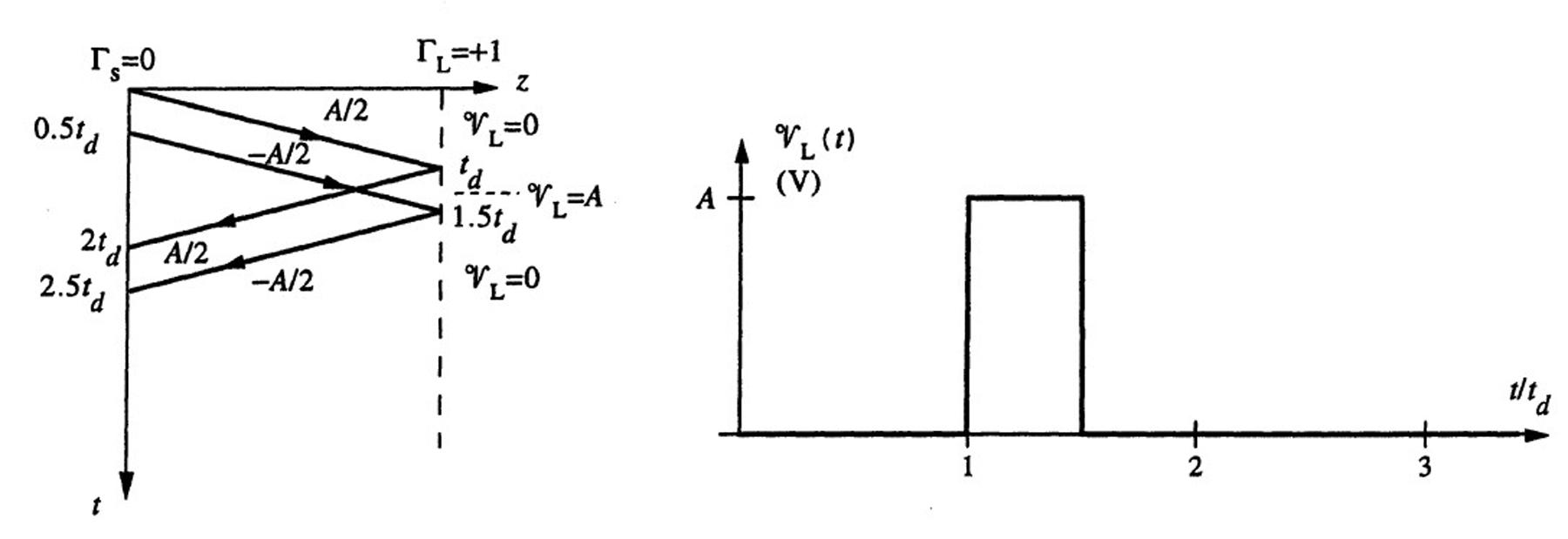
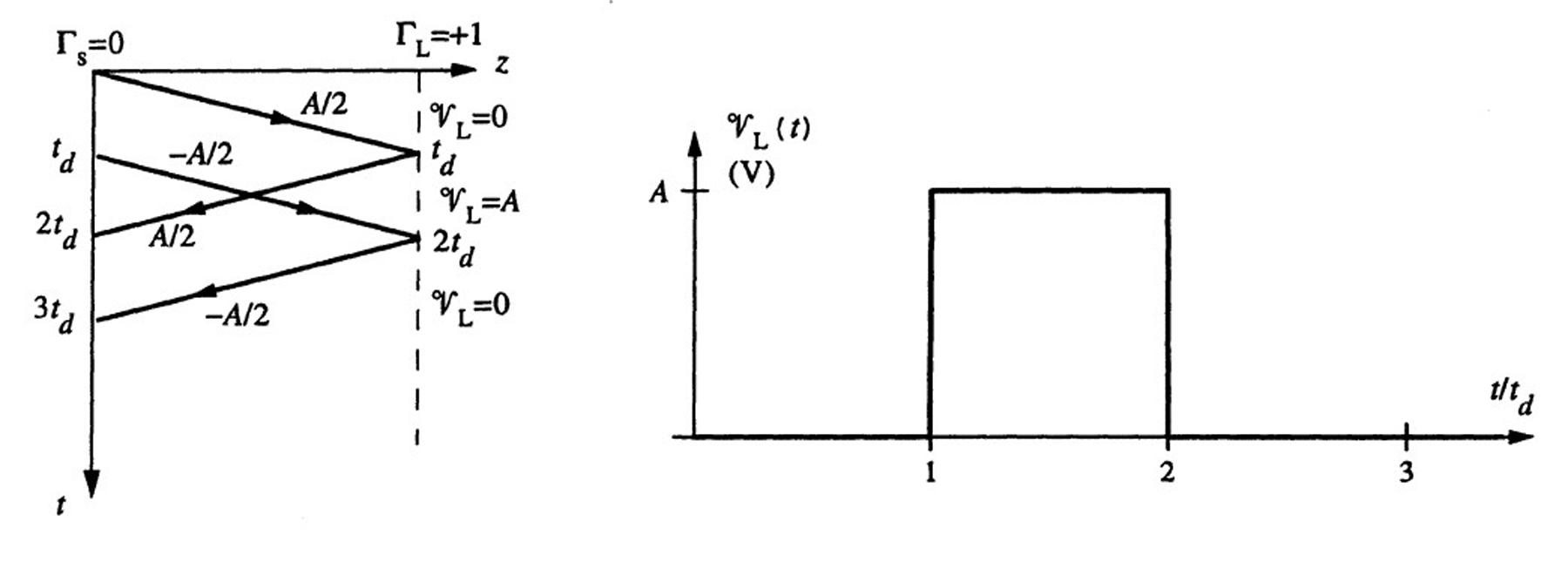
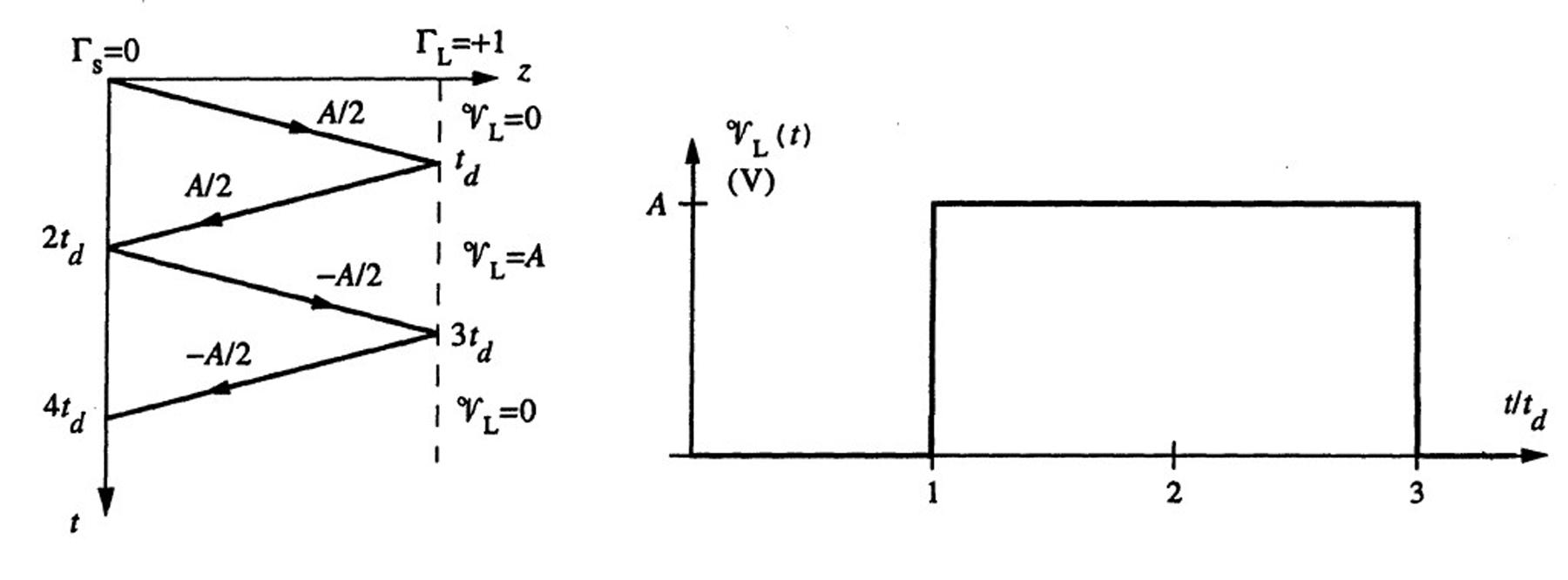
2.10Pulseexcitation.

Thereﬂectioncoeﬃcientsatthetwoendsofthelineare(using(2.12)and(2.14))

At t = 0,an incidentvoltageofamplitude

10 Chapter2/TransientResponseofTransmissionLines (b) (a) Γ1= − 0.5 91A Γ2 = 0 + 91A td 92A + td 2td 0.75 0.5 0.75 0 1 2 1.75 1.0 0.5 0 1 2 t / td t / td 1(t) /V0 2(t) /V0

Figure2.11 FigureforProblem2.8. (a)Bouncediagram.(b) 91 and 92 versustime t

Γs = Rs Z0 Rs + Z0 = Z0 Z0 Z0 + Z0 = 0 ΓL = RL Z0 RL + Z0 = 100Z0 Z0 100Z0 + Z0 ≃ +1

9+ 1 = Z0 Rs + Z0 A = Z0 Z0 + Z0 A = A 2 islaunched atthesourceendoftheline.Whentheinputpulseturnsoﬀat t = tw

berepresentedasanewvoltagedisturbance 9+∗ 1 = 9+ 1 = A 2 launchedat thesourceendofthelineat t = tw.Onebyone,thenewvoltagecancelsoutthe existingvoltagedisturbances 9+ 1 , 91 , 9+ 2 , 92 ,etc.alongtheline.Thebouncediagramandthe

,thischangecan

loadvoltage 9L(t) versustareprovidedinFigures2.13,2.14,and2.15.foreachcasecorresponding toadiﬀerentinputpulselengths.

ThisworkisprotectedbyUnitedStatescopyrightlaws andisprovidedsolelyfortheuseof instructorsinteachingtheircoursesandassessingstudentlearning. Dissemination orsaleofanypartofthiswork(includingontheWorldWideWeb) willdestroytheintegrityoftheworkandisnotpermitted.

Figure2.12 FigureforProblem2.9. (a)Bouncediagramand 9s(t) versus t.(b) 9s(t) versus t,obtainedviasuperposition.

ThisworkisprotectedbyUnitedStatescopyrightlaws andisprovidedsolelyfortheuseof instructorsinteachingtheircoursesandassessingstudentlearning. Dissemination orsaleofanypartofthiswork(includingontheWorldWideWeb) willdestroytheintegrityoftheworkandisnotpermitted.

12 Chapter2/TransientResponseofTransmissionLines

Figure2.13 FigureforProblem2.10a. (a)Bouncediagramand 9L(t) versus t for tω = 2td,where td istheone-waytimedelayalongtheline. Figure2.14 FigureforProblem2.10b. (a)Bouncediagramand 9L(t) versustfortω = td.

Figure2.15 FigureforProblem2.10c. (a)Bouncediagramand 9L(t) versus t.for tω =

d/2.

2.11Observerontheline.

(a)Usingthesketchof 9ctr versus t provided,theinitialvoltagelaunchedonthelineisgivenby

(b)Superimposingthedirectandreﬂectedpulses,thevoltage 9ctr(t) isasdrawninFigure2.16.

2.12Cascadedtransmissionlines.

Thereﬂectioncoeﬃcientsare

and ΓL = +1(since RL = ∞)respectively.Thebouncediagramandthesketchesofvoltages 9s(t) and 9L(t) areasshowninFigure2.17.

2.13Time-domainreﬂectometry(TDR).

Theinitialvoltage 9+ 1 launchedfromthesourceendofthelineisgivenby

Thesourceendvoltage 9s(t) changesfrom0 5Vto0 375Vwhenthevoltagewavereflected fromthejunctionpointbetweenthetwolinesreachesthesourceendoftheline,i.e.,attime 2td1 = 1nsor td1 = 0.5ns.Thelengthofthefirstline l1 canthenbefoundas l1 = vptd1 = (20cm-(ns) 1)(0.5ns)= 10cm.Thevoltage 91 reflectedfromthejunctionpointcanbeexpressedintermsof 9+ 1 as

13 9ctr (V) t/td 0.3 0.5 0.8 0.5 1 1.5 2 2.5 3 3.5 Figure2.16

FigureforProblem2.11.

9+ 1 = Z0 Rs + Z0 V0 = Z0 100 + Z0 (1V) = 0 5V → Z0 = 100 Ω Thereﬂectedvoltageisgivenby 91 =ΓL9+ 1 = RL Z0 RL + Z0 9+ 1 = RL 100 RL + 100 (0.5V) = 0.3V

RL = 400Ω

Solvingfor

,wehave

Γs

Rs = 50Ω), Γ12 = Γ21 = Z02 Z01 Z02 + Z01 = 75 50 75 + 50 =+0.2

= 0(since

9+ 1 = Z01 Rs + Z01 V0 = Z01 50 + Z01 (1V)= 0.5V → Z01 = Rs = 50 Ω

Figure2.18

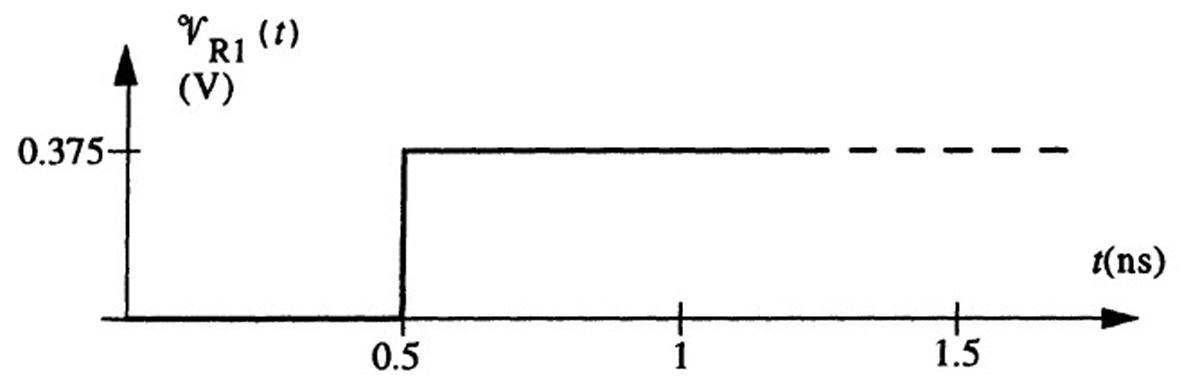
91 = (R1 || Z02) Z01 (R1 || Z02)+ Z01 9+ 1 where R1 || Z02 = R1Z02 R1 + Z02

Whenthereflected voltage 91 reachesthesourceendoftheline,noreflectiontakesplacessince Γs = 0.Thus,wehave 9+ 1 + 91 = 0.375V → 91 = 0.125V.Usingthisvalueintheabove expressionwith 9+ 1 = 0.5Vand Z01 = 50Ω,wefind R1 || Z02 = 30Ω.Since Z02 = 75Ω,wehave R1 = 50Ω.Thevoltage 9R1(t) versus t isplottedasshowninFigure2.18.

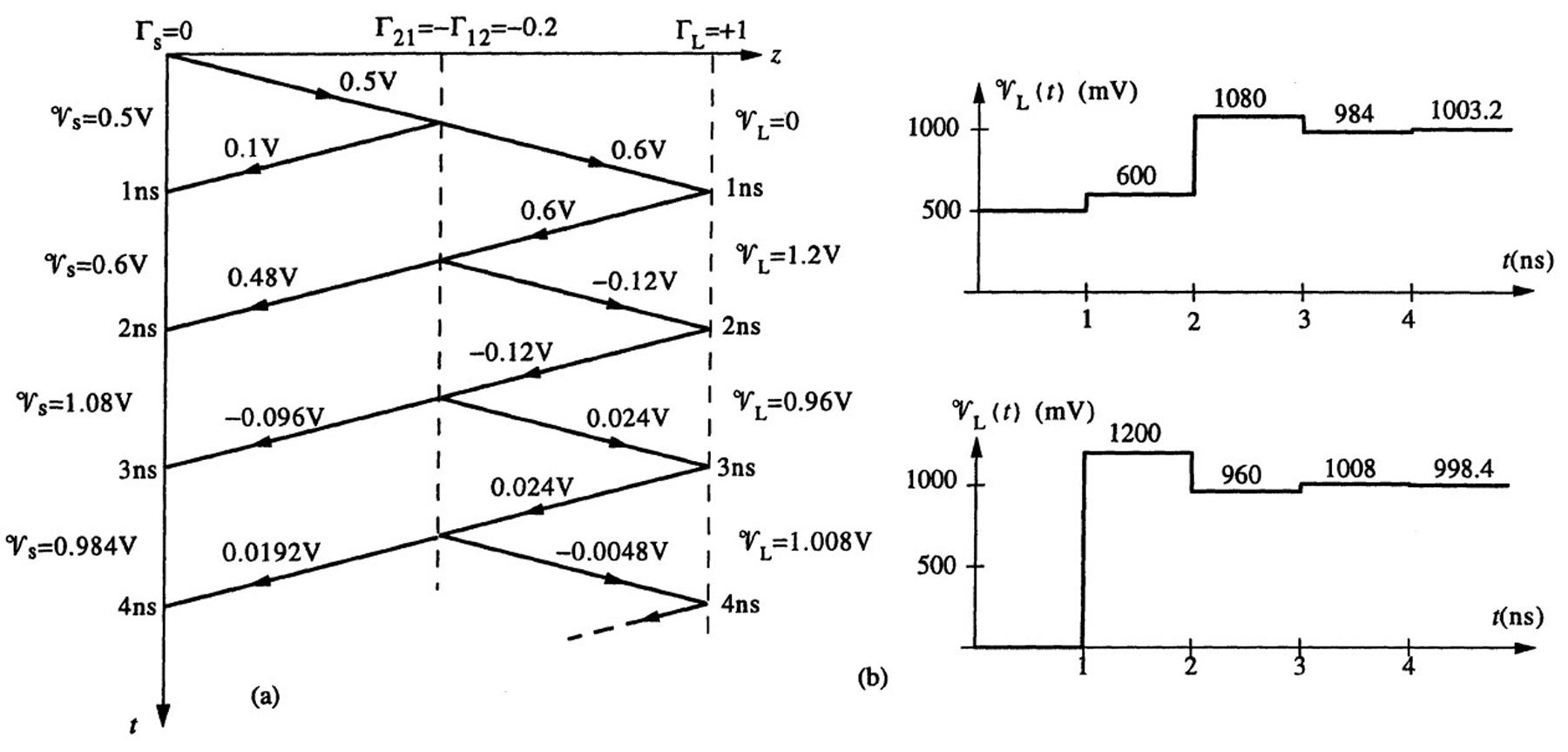
2.14Time-domainreﬂectometry(TDR).

(a)Theinitialvoltagelaunchedatthesourceendofthetransmissionlinesystemisgivenby 9+ 1 = Z01 Rs + Z01 V0 = Z01 100 + Z01 (3V)= 1 5V → Z01 = Rs = 100 Ω

Theone-waytimedelayofthetwotransmissionlinescanbefoundas td1 = 3ns/2 = 1.5nsand td2 =(7.5ns 3ns)/2 = 2.25ns.Since Γs = 0,thesourceendvoltage 9s at t = 2t+ d1 canbe

14 Chapter2/TransientResponseofTransmissionLines

Figure2.17 FigureforProblem2.12. (a)Bouncediagramforthecascadedlines.(b) 9s and 9 versus FigureforProblem2.13. 9R1 versus t.

writtenas © 2015 Pearson Education, Inc., Hoboken, NJ. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the publisher.

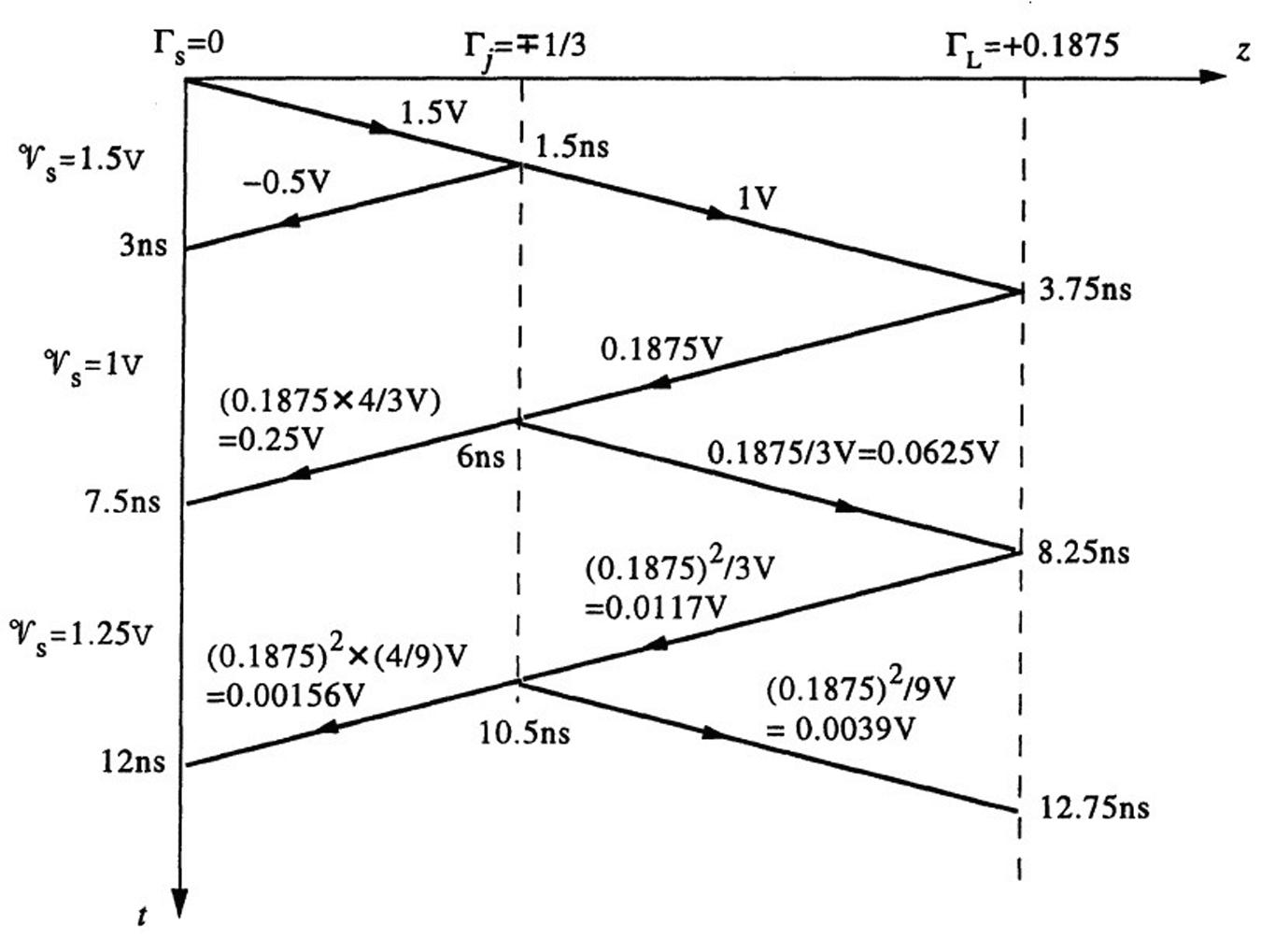
2.15Time-domainreﬂectometry(TDR).

15 =0.0156V

9s(2t+ d1)= 9+ 1 (1 +Γ12)=(1.5V)(1 +Γ12)= 1V → Γ12 = 1 3 where Γ12 = Z02 Z01 Z02 + Z01 = Z02 100 Z02 + 100 → Z02 = 50 Ω At t = 7.5+ ns, thesourceendvoltage 9s isgivenby 9s(t = 7.5+)= 9+ 1 (1 +Γ12)[1 +ΓL(1 +Γ21)]= 1.25V where Γ21 = Γ12 = Z01 Z02 Z01 + Z02 =+ 1 3 and ΓL = RL Z02 RL + Z02 Substituting 9+ 1 = 1.5V, Z01 = 100Ω and Z02 = 50Ω,weﬁnd ΓL = RL 50 RL + 50 = 0.1875 → RL ≃ 73.1 Ω

bouncediagramshownwenotethatthesourceendvoltage 9s changesagainat t = 12 ns,increasingbyanamountofabout ∼ 15.6mV.

Figure2.19 FigureforProblem2.14. Bouncediagram.

(b)Fromthe

willdestroytheintegrityoftheworkandisnotpermitted.

orsaleofanypartofthiswork(includingontheWorldWideWeb)