Contemporary Business Mathematics
Canadian 10th Edition by Hummelbrunner
Halliday Coombs ISBN 0133052311
9780133052312
Download solution manual at:
https://testbankpack.com/p/solution-manual-for-contemporarybusiness-mathematics-canadian-10th-edition-by-hummelbrunnerhalliday-coombs-isbn-0133052311-9780133052312/
Download full test bank at :
https://testbankpack.com/p/test-bank-for-contemporary-businessmathematics-canadian-10th-edition-by-hummelbrunner-hallidaycoombs-isbn-0133052311-9780133052312/
Chapter 4 Linear Systems
Copyright © 2015 Pearson Canada Inc.
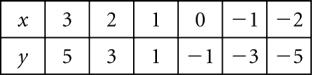
Exercise 4.1 A. 1. x + y = 9 x y = 7 (1)+(2) → In(1) Check: 2x = 16 x = 8 8+ y = 9 y = 1 (x, y) = ( 8, 1) (1) (2) In(1) LS= 8 1= 9 = RS In(2) LS=−8−(−1) =−7 = RS 2. x +5y = 0 x +2y = 6 (1) (2) (1)−(2)→ In(2)
Copyright © 2015 Pearson Canada Inc. Check: 3y =−6 y = 2 x 4 = 6 x =10 (x, y) = (10, 2) In(1) LS=10+5( 2) = 0 = RS In(2) LS=10+2( 2) = 6 = RS 3. 5x +2y = 74 7x 2y = 46 (1) (2) (1)+(2)→ 12x =120 x =10 In(1) 5(10)+2y = 74 2y = 24 y =12 (x, y) = (10,12) Check: In(1) LS= 5(10)+2(12) = 50+24 = 74 = RS In(2) LS= 7(10) 2(12) = 70 24 = 46 = RS
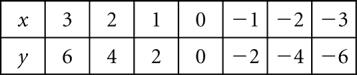
Copyright © 2015 Pearson Canada Inc. 128 CHAPTER 4 4. 2x +9y = 13 2x 3y = 23 (1) (2)→ 12y = 36 y =−3 (1) (2) In(1) 2x +9( 3) = 13 2x 27 = 13 2x =14 x = 7 (x, y) = (7, 3) Check: In(1) LS= 2(7)+9( 3) =14 27 = 13= RS In(2) LS= 2(7)−3(−3) =14+9 = 23= RS 5. y =3x +12 (1) x = y (2) Rearrange 3x y = 12 (3) x + y = 0 (4) (3)+(4)→ In(2) Check: 4x = 12 x = 3 3= y y = 3 (x, y) = (−3,3) In(1) LS = 3 RS = 3( 3)+12 = 9+12 = 3 In(2) LS = 3 RS = 3 6. 3x =10 2y 5y =3x 38 Rearrange (1) (2) 3x +2y =10 3x +5y = 38 (3) (4)
Copyright © 2015 Pearson Canada Inc. CHAPTER 4 129 (3)+(4)→ 7y = 28 y = 4 In(1) 3x =10 2( 4) 3x =18 x = 6 (x, y) = (6, 4) Check: In(1) LS = 3(6) =18 RS =10−2(−4) =10+8 =18 In(2) LS = 5( 4) = 20 RS = 3(6) 38 =18 38 = 20 B. 1. 4x + y = 13 x 5y = 19 To eliminate y (1) (2) (1)×5→ (3)+(2)→ 20x +5y = 65 x 5y = 19 21x = 84 x = 4 (3) (2) In(1) 4( 4)+ y = 13 16+ y = 13 y = 3 (x, y) = (−4,3) Check: In(1) LS= 4( 4)+3= 16+3= 13= RS In(2) LS= 4 5(3) = 4 15= 19 = RS 2. 6x +3y = 24 2x +9y = 8 To eliminate x (1) (2) (2)×3→ 6x + 27y = 24 (3) (1)×( 1) → 6x 3y = 24 (4)
Copyright © 2015 Pearson Canada Inc. 130 CHAPTER 4 (3)+(4)→ 24y = 48 y = 2 In(1) 6x +3( 2) = 24 6x 6 = 24 6x = 30 x = 5 (x, y) = (5, 2) Check: In(1) LS= 6(5)+3( 2) =30 6 = 24 = RS In(2) LS= 2(5)+9( 2) =10 18 = 8= RS 3. 7x 5y = 22 4x +3y =5 To eliminate y (1)×3→ (2)×5→ (3)+(4)→ In (2) Check: 21x 15y = 66 20x +15y = 25 41x = 41 x = 1 4+3y = 5 3y = 9 y = 3 (x, y) = ( 1,3) (1) (2) (3) (4) In(1) LS= 7(−1)−5(3) =−7−15 =−22 = RS In(2) LS= 4( 1)+3(3) = 4+9 =5 = RS 4. 8x +9y =129 6x +7y =99 To eliminate x (1)×3→ 24x +27y = 387 (1) (2) (3) (2)×( 4)→ 24x 28y = 396 (3)+(4)→ y = 9 y = 9 In (2) 6x +7(9) = 99 6x +63= 99 6x = 36 x = 6 (x, y) = (6,9) (4)
Copyright © 2015 Pearson Canada Inc. CHAPTER 4 131 Check: In(1) LS= 8(6)+9(9) = 48+81=129 RS=129 In(2) LS= 6(6)+7(9) = 36+63= 99 RS= 99 5. 12y =5x =16 6x +10y 54= 0 Rearrange 5x +12y =16 6x +10y = 54 To eliminate x (3)×6→ 30x +72y = 96 (1) (2) (3) (4) (5) (4)×5→ (5)+(6)→ In (1) Check: 30x +50y = 270 122y = 366 y = 3 12(3) = 5x +16 36 16 = 5x 5x = 20 x = 4 (x, y) = (4,3) (6) In(1) LS=12(3) = 36 RS= 5(4)+16 = 20+16 = 36 In(2) LS= 6(4)+10(3) 54 = 24+30 54 = 0 RS= 0 6. 3x −8y +44 = 0 7x =12y 56 Rearrange 3x −8y =−44 7x 12y = 56 To eliminate y (3)×3→ 9x 24y = 132 (1) (2) (3) (4) (5) (4)×( 2)→ 14x +24y =112 (6)
Copyright © 2015 Pearson Canada Inc. 132 CHAPTER 4 (5)+(6)→ 5x = 20 x = 4 In (1) 3(4) 8y +44 = 0 12 8y +44 = 0 8y = 56 y = 7 (x, y) = (4,7) Check: In(1) LS = 3(4) 8(7)+44 =12 56+44 = 0 RS= 0 In(2) LS = 7(4) = 28 RS =12(7) 56 = 84 56 = 28 C. 1. 0.4x +1.5y =16.8 1.1x 0.9y = 6.0 To eliminate decimals (1) (2) (1)×10→ (2)×10→ To eliminate y (3)×3→ (4)×5→ 4x +15y =168 11x 9y = 60 12x +45y = 504 55x 45y = 300 (3) (4) Add: 67x = 804 x =12 In(3) 4(12)+15y =168 48+15y =168 15y =120 y = 8 (x, y) = (12,8) 2. 6.5
=
(1)
(2)
decimals
(3)
(4)
3
(4)×( 7)→ 35x 63y = 1484
x +3.5y
128
2.5x +4.5y =106
To eliminate
(1)×9 → 13x +7y = 256
(2)×2→ 5x +9y = 212
To eliminate y (3)×
→ 117x +63y = 2304
Copyright © 2015 Pearson Canada Inc. CHAPTER 4 133 Add: 82x = 820 x =10 In(4) 5(10)+9y = 212 50+9y = 212 9y =162 y =18 (x, y) = (10,18)
2.4
(1)
0.6
(2)
eliminate decimals
5
12
8y =38 (3)
×5→ 19x +3y = 36 (4) To eliminate y (3)×3→ 36x +24y =114 (4)×( 8)→ 152x 24y = 288 Add: 116x = 174 x =1.5 In(3) 12(1.5)+8y = 38 18+8y = 38 8y = 20 y = 2.5 (x, y) = (1.5,2.5) 4. 2.25x +0.75y = 2.25 (1) 1.25x +1.75y = 2.05 (2)
eliminate decimals
3.
x +1.6y = 7.60
3.8x +
y = 7.20
To
(1)×
→
x +
(2)
To
(3)
(1)×100→ 225x +75y = 225
(4)
(2)×1005→125x +175y = 205
To simplify
(5)
(3)÷75→ 3x + y = 3
(6)
(4)÷(5) → 25x +35y = 41
To eliminate y
(5)×35→ 105x +35y =105
(6)×( 1) → 25x 35y = 41
Add: 80x = 64 x = 0.8
In(5) 3(0.8)+ y = 3
2.4+ y = 3 y = 0.6
(x, y) = (0.8,0.6)
5. 3x 2y = 13
4 3 6
4x + 3y = 123
5 4 10
To eliminate fractions
(1)×12→ 9x 8y = 26
(2)×20→16x +15y = 246
To eliminate y
(3)×15→135x 120y = 390
(4)×8→ 128x +120y =1968
Add: 263x =1578
x = 6
In(3) 9(6) 8y = 26 54 8y = 26 8y = 80 y =10
(x, y) = (6,10)
6. 9x + 5y = 47
5 4 10
2x + 3y = 5
9 8 36
To eliminate fractions
(1)×20→ 36x +25y =94
(2)×72→16x +27y =10
To eliminate x
(3)×4→ 144x +100y =376
(4)×( 9) → 144x 243y = 90
134 CHAPTER 4
Copyright © 2015 Pearson Canada Inc.
(1) (2)
(3)
(4) (1) (2) (3) (4)
Add: 143y = 286 y = 2
In(3) 36x 50 = 94 36x =144 x = 4 (x, y) = (4, 2)
7. x + 2y = 7
3 5 15
3x 7y = 1 2 3
(1)
(2)
(3)
(4)
To eliminate y
(4)×3→ 35x +42y = 49 27x 42y = 18
Add: 62x =31 x = 1 2
12
9 y
(x, y)
To eliminate fractions
3 4
,
2 4
(1)×84→ 21x +36y = 8
(1) (2) (3) (4)
Copyright © 2015 Pearson Canada Inc. CHAPTER 4 135
To eliminate fractions
(1)×15→ 5x +6y = 7
(2)×60→ 9x 14y = 6
(3)×7 →
1
3
In(3) 5 1 +6y = 7 2 5 +6y = 7 2 5+12y =14
y =
=
=
8. x + 3y = 2 4 7 21 2x + 3y = 7 3 2 36
(2)×36 → 24x +54y = 7

Copyright © 2015 Pearson Canada Inc. 136 CHAPTER 4 To eliminate y (3)
→
x +108y = 24
48x 108y =14 Add: 15x = 10 2 x = 3 In(3) 21 2 +36y = 8 3 14+36y = 8 36y = 6 y = 1 6 (x, y) = 2 , 1 3 6 Exercise 4.2 A. 1. A(−4,−3) B(0, 4) C(3, 4) D(2,0) E(4,3) F(0,3) G( 4,4) H( 5,0) 2. (a)
×3
63
(4)×( 2)→


Copyright © 2015 Pearson Canada Inc. ; CHAPTER 4 137 (b) 3. (a) (b) (c) (d) 4. (a) 4x +5y =11 5y = 4x +11 y = −4x + 11 5 5 Slope, 4 m = y-intercept, b = 11 5 5 (b) 2y 5x =10 2y =5x +10 y = 5x + 10 2 2 Slope, m = 5 ; 2 y-intercept, b =5 (c) 1 1 y = 2x 2 1 y = 2x 1 2 y = 4x +2 Slope, m = 4; y-intercept, b = 2
(d)
(e)
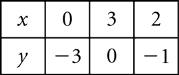
Slope, m = 0;(line to x-axis); y-intercept, b = 2
Copyright © 2015 Pearson Canada Inc. x + = 138 CHAPTER 4
3y +6 = 0 3y = 6 y = 2
) 0.15
= 0 15x +30y 12 = 0 30y = 15x +12 y = 15x + 12 30 30 1 2 y =− 2 5 Slope, m 1 ; y-intercept, b = 2 (g) 2 5 2 1 x = 0 2 2 = 1 x 2 x = 4
2x y =3 2x − y =9 y = 2x +9 y = 2x 9 Slope, m = 2; y-intercept, b = 9 (f
x +0.3y 0.12
2)(y
1) xy = 2 xy 2y + x 2 xy = 2 −2y =−x +4 y = x 2 2
-intercept,
Slope is undefined no y-intercept (h) (x
+
Slope, m = 1 ; 2 y
b = 2

Copyright © 2015 Pearson Canada Inc. CHAPTER 4 139 B 1 2. x 0 4 2 y 2 0 1 3. 4. x 0 4 4 y 0 2 2

Copyright © 2015 Pearson Canada Inc. 140 CHAPTER 4 5. 6. x 0 3 +6 y 2 0 2
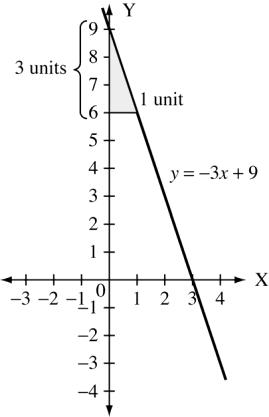
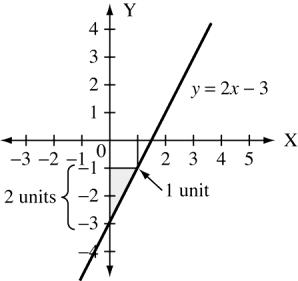
8. 9. For y = 2x 3 slope, m = 2 y-intercept, b =−3
7.
10. For y = 3x +9 slope, m = 3 y-intercept, b =9
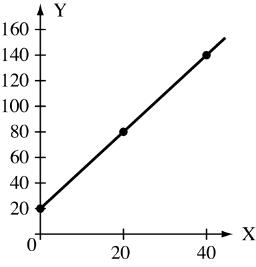
C. 1. For y =3x +20 x 0 20 40
20 80 140 or m =3 b = 20
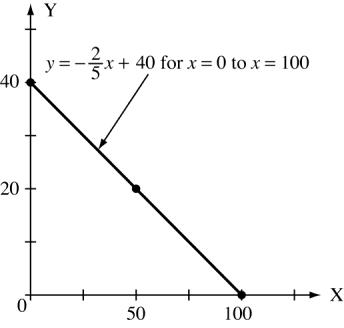
2. For y 2 x +40 5
0 50 100
Copyright © 2015 Pearson Canada Inc.
CHAPTER 4 141
= =
y
2 5
x
y 40 20 0 or m
b = 40
Copyright © 2015 Pearson Canada Inc. = 142 CHAPTER 4
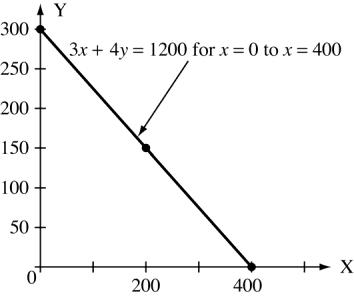
For 3x +4y =1200 x 0 200 400 y 300 150 0 or m 3 4 b =300
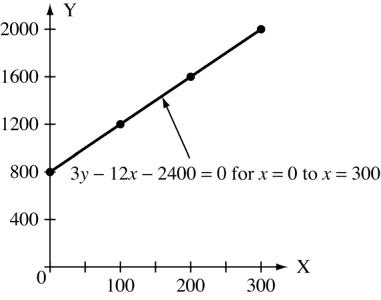
For 3y 12x 2400 = 0 x 0 100 200 300 y 800 1200 1600 2000 or m = 4 b =800
3.
4.

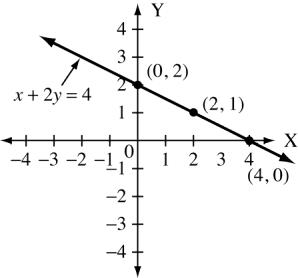
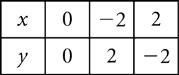
Copyright © 2015 Pearson Canada Inc. CHAPTER 4 143 Exercise 4.3 A. 1. 2. 3. x = 2y 1 x 3 1 5 y 2 0 2 y = 4 3x x 0 2 1 4 2 1 4. 2x +3y =10 x 5 2 1 y 0 2 4 3x 4y = 2 x 6 2 2 y 5 2 1
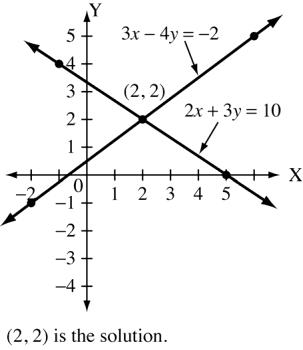
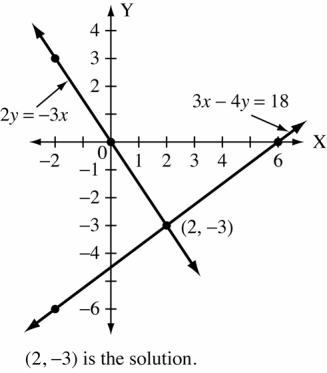
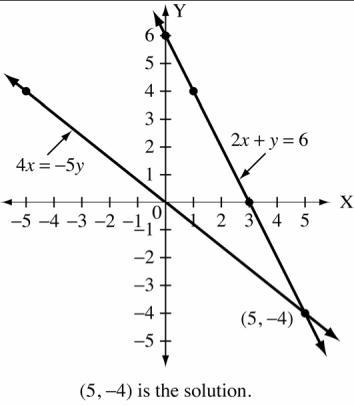
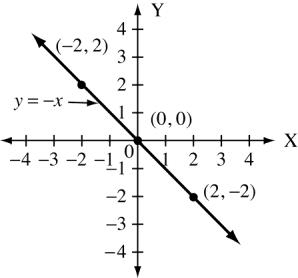
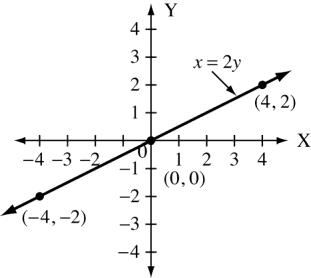
Copyright © 2015 Pearson Canada Inc. 144 CHAPTER 4 5. 3x 4y =18 x 6 2 2 y 0 3 6 2y = 3x x 0 2 2 y 0 3 3 6. 4x =−5y x 0 5 5 y 0 4 4 2x + y = 6 x 0 3 1 y 6 0 4
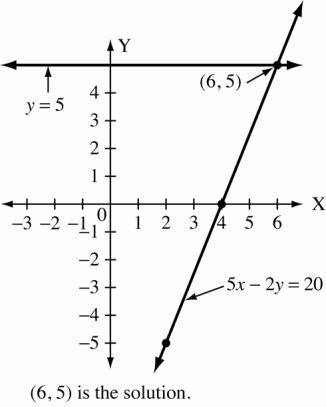
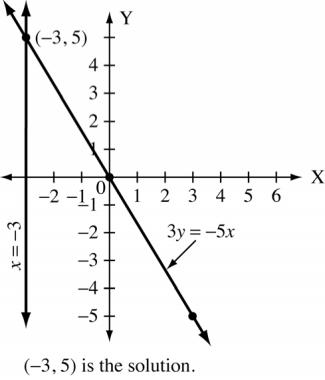
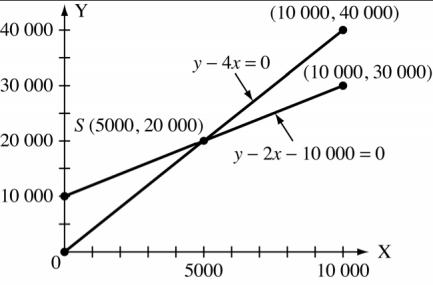
Copyright © 2015 Pearson Canada Inc. CHAPTER 4 145 7. 5x 2y = 20 x 4 2 6 y 0 5 5 8. 3y =−5x x 0 3 3 y 0 5 5 B. 1. For y 4x = 0 x 0 5000 10 000 y 0 20 000 40 000 For y 2x 10000 = 0 x 0 5000 10 000 y 10 000 20 000 30 000
Copyright © 2015 Pearson Canada Inc. 146 CHAPTER 4
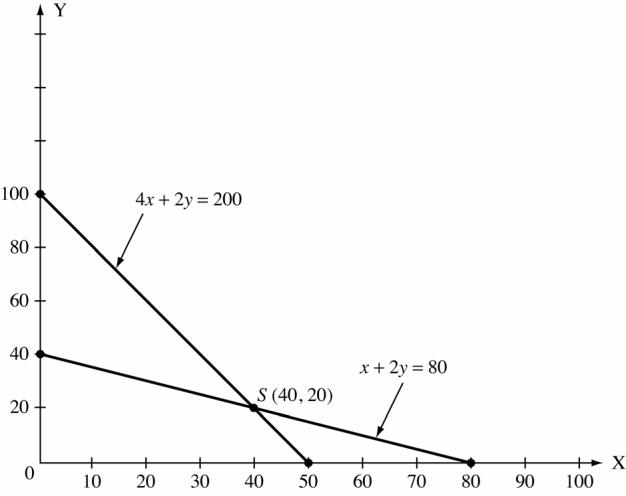
For 4x +2y = 200 x 0 20 40 50 y 100 60 20 0 For x +2y =80 x 0 40 80 y 40 20 0
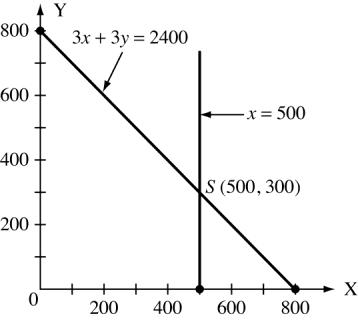
For 3x +3y = 2400 x 0 400 800 y 800 400 0
2.
3.
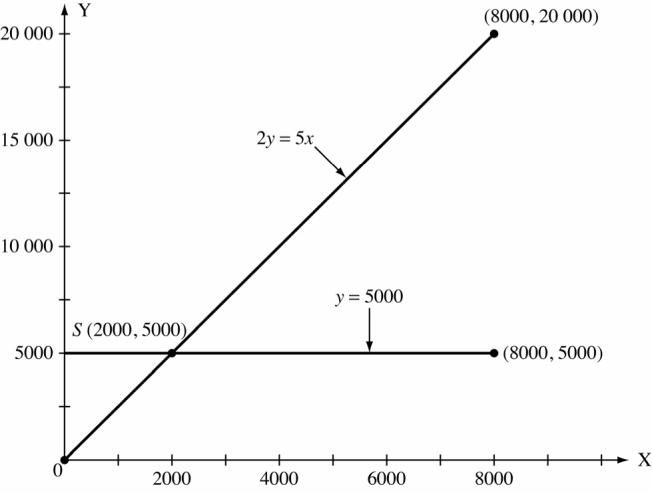
Copyright © 2015 Pearson Canada Inc. CHAPTER 4 147 4. For 2y = 5x x 0 4000 8000 y 0 10 000 20 000
Business Math News Box
SOLUTIONS:
1. Let x represent Mega Brands’ 2011 revenues
111.5% x = 420.3 million
x = 420.3 / 1.115 = 376.9
Mega Brands’ 2011 revenue was $377.0 million.
2. ($4 million – $234 000) / $234 000 = 16.094017 = 1609.4%
3. 118% × $108 million = $127.4 million
Mega Brands’ fourth quarter net sales for 2012 was $127.4 million.
4. 2012 annual sales: $420.3 million
Growth rate in sales revenue in 2012: 11.5%
Assuming an 11.5% growth in sales in 2013 and 2014: $420.3(1.115)(1.115) = $522.5 million
Yes, Mega Brands is on track to meet (exceed) its goal of delivering $500 million in annual sales by 2014.
Copyright © 2015 Pearson Canada Inc. 148 CHAPTER 4
Exercise 4.4
A. 1. Let the number of units of Product A be x and the number of units of Product B be y
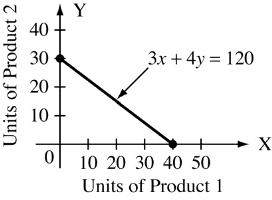
2. Let the number of units of Product 1 be x and the number of units of Product 2 be y.

3. Let the number of tax returns be x and the total cost be $y.
4. Let monthly sales be $x and the total salary be $y.
B. 1. Let x represent the number of employees at the larger location, y, the number of employees at the smaller location.
∴ x + y = 24
2x =3y +3
(1) (2)
(1)×3→
From(2) → 3x +3y = 72 2x 3y =3
Add: 5x = 75 x = 15
=9
Copyright © 2015 Pearson Canada Inc. CHAPTER 4 149
y
The number of employees is 15 at the larger location, and 9 at the smaller one.
Sum =15+9 = 24
2×15 =30 = (3×9)+3
2. Let x represent the number of orders for the 1st special, y those for the 2nd special.
There are 12 orders for the 1st special, 18 for the 2nd special
3. Let the number of jars of Brand X be x and the number of jars of the No-Name brand be y
Sales were 90 jars of Brand X and 50 jars of No-Name brand.
Copyright © 2015 Pearson Canada Inc. 150 CHAPTER 4
Check:
7x 4y
3 x + 2 y = 21 4 3 (2)×12→ (1)×2→ 9x +8y = 252 14x 8y = 24 (1) (2) Add: 23x = 276 x =12 In(1) 84 4y =12 4y = 72 y =18
=12
Check: 7×12 4×18 = 84 72 =12 3 2 ×12+ ×18 = 9+12 = 21 4 3
x + y =140 2.25x +1.75y = 290 (1) (2) (2)×4 → (1)×7 → 9x +7y =1160 7x +7y = 980 Subtract: 2x =180 x =90 y =50
Check
Totalsold
140 Value: 90
50×1.75
87.50
:
= 90+50 =
×2.25 = $202.50
=
= $290.00
4. Let Nancy’s sales be $x and Andrea’s sales be $y.
x + y =940
(2)
x =3y 140 (1)
(1)×3→
From (2)→ 3x +3y = 2820 x 3y = 140
4x = 2680 x = 670 y = 270
Nancy's sales were $670; Andrea's sales were $270.
Total = 670+270 =$940
3×270 140 =810 140 =$670
5. Let Kaya’s investment be $x, and Fred’s investment be $y.
∴x + y =55000 y = 2 x +2500 3
(2)×3→ 2x +3y = 7500
(1)×2→ 2x +2y =110 000
Add: 5y =117 500
y = 23 500
x = 31500
(1) (2)
Kaya's investment is $31 500 and Fred's investment is $23 500.
Check:
Total = 31500+23 500 = $55 000
2 ×31 500+2500 = 21 000+2500 = $23 500
3
6. Let the number of chairs produced by the first shift be x and the number of chairs produced by the second shift be y.
∴x + y = 2320
y = 4 x 60 3
(2)×3→ 4x +3y = 180
(1)×4→ 4x +4y = 9280
Add: 7y = 9100
y = 1300
x =1020
(1)
(2)
Copyright
Canada Inc. CHAPTER 4 151
© 2015 Pearson
The first shift produced 1020 chairs and the second shift 1300 chairs.
Copyright © 2015 Pearson Canada Inc.
Check: Total =1020+1300 = 2320
4 ×1020 60 =1360 60 =1300 3
7. Let the number of Type A lights be x and the number of Type B lights be y.
∴ x + y = 60 40x +50y = 2580 (1)
(2)÷10→ 4x +5y = 258
(1)×( 4)→ 4x 4y = 240
Add: y =18 x = 42
The number of Type A is 42, and the number of Type B is 18.
Check:
Total = 42+18 = 60
Value: 42×40 = $1680 18×50 = 900 $2580
8. Let the number of units of Product A be x and the number of units of Product B be y
∴ x + y = 60
4x +3y = 200 (1)×4→
The number of units of Product A is 20, and of Product B is 40.
Check:
Total number = 20+40 = 60
Number of hours:
ProductA:20×4 = 80
ProductB:40×3= 120
Totalhours = 200
Copyright © 2015 Pearson Canada Inc. 152 CHAPTER 4
(2)
4
4x
3y
y = 40 x = 20 (1) (2)
Subtract: 4x +
y = 240
+
= 200
9. Let the number of quarters be x and the number of loonies be y. ∴
x +100y =8575
Substitute (2) x = 3 (72)+1=54+1=55 4
Marysia has 55 quarters and 72 loonies.
Value:
55×0.25 =$13.75
72×1.00 = 72.00 $85.75
10. Let the number of $12-tickets be x and the number of $15-tickets be y.
The club bought 30 $12-tickets and 21 $15-tickets.
Check:
Value =30(12)+21(15) = 360+315=$675
Copyright © 2015 Pearson Canada Inc. CHAPTER 4 153
x = 3 y +1 4 (1) (2) (1)÷25 → (2)×4 → (3)×4 → x +4y = 343 4x = 3y +4 4x +16y =1372 (3) (4) (5) Rearrange (4) 4x 3y = 4 (6)
→ 19y =1368 y = 72
25
(5) (6)
12
15
y = 4 x 3 5 Substitute (2) in (1). 12x +15 4 x 3 = 675 (1) (2) 5 12x +12x 45= 675 24x = 720 x =30
y
x +
y = 675
Substitute in (2). y = 4 (30) 3 5
= 21
Review Exercise
1. (a) For 7x +3y = 6
3y =−7x +6 y = 7x +2 3
Slope, m 7 ; y-intercept, 3 b = 2
(b) For 10y =5x y = 5x 10 y = 1 x 2
Slope, m = 1 ; y-intercept, 2 b = 0
(c) For 2y 3x = 4 2 2y 3x =8 2y =3x +8 y = 3 x +4 2
Slope, m = 3 ; y-intercept, 2 b = 4
(d) For 1.8x +0.3y 3= 0 18x +3y 30 = 0
3y = 18x +30 y = 6x +10
Slope, m = 6; y-intercept, b =10
(e) For 1 x = 2 3 x = 6 Line is parallel to the y-axis.
Slope, m is undefined. There is no y-intercept.
Canada Inc.
Copyright © 2015 Pearson
=− 154 CHAPTER 4
(f) For 11x 33y =99 33y = 11x +99 y = 11x + 99 33 y = 1 x 3 3
33
Slope, m = 1 ;3 y-intercept, b = 3
(g) For xy (x +4)(y 1) =8 xy xy 4y + x +4 =8 4y = x +4 y = 1 x 1 4
Slope, m = 1 ; y-intercept, 4
(h) For 2.5y −12.5 = 0 25y 125 = 0 y =5
b = 1
Line is parallel to the x-axis; slope, m = 0; y-intercept, b =5
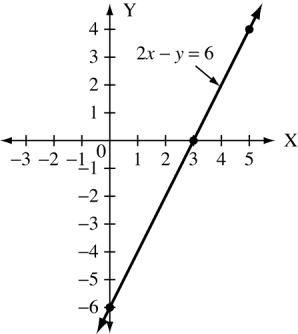
2. (a) 2x y = 6 x 3 0 5 y 0 6 4
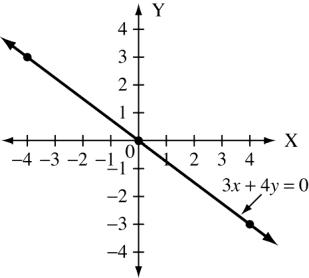
(b) 3x +4y = 0 x 0 4 4 y 0 3 3
Copyright © 2015 Pearson Canada Inc. CHAPTER 4 155
Copyright © 2015 Pearson Canada Inc. 156 CHAPTER 4
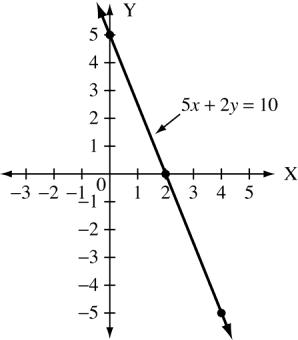
5x +2y =10 x 0 2 4 y 5 0 −5
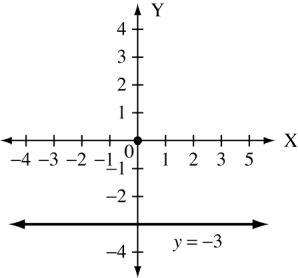
y = 3
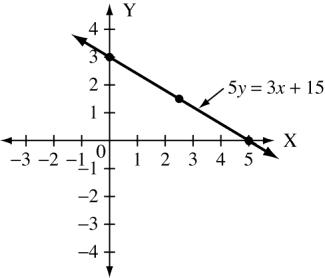
5y = 3x +15 x 0 5 2.5 y 3 0 1.5
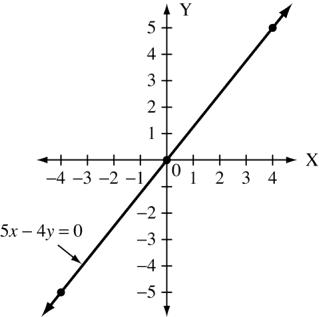
) 5x 4y = 0 x 0 4 4 y 0 5 5
(c)
(d)
(e)
(f
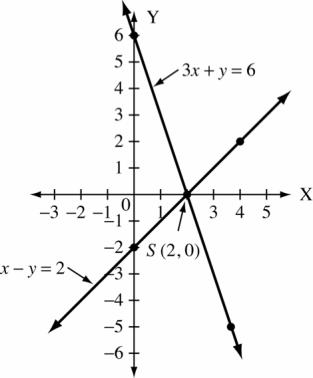
Copyright © 2015 Pearson Canada Inc. CHAPTER 4 157 (g) x = 2 (h) 3y = 4x 12 x −3 0 −6 y 0 4 4 3. (a) 3x + y = 6 and x y = 2 x 0 2 4 y 6 0 6 x 0 2 4 y 2 0 2
158 CHAPTER 4
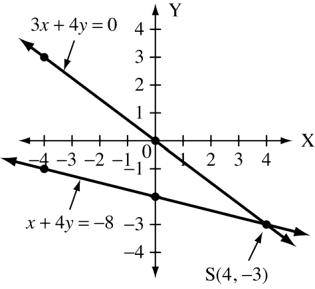
(b) x +4y = 8 and 3x +4y = 0
x 0 4 4
y 2 3 1
x 0 4 4 y 0 3 3
(c) 5x = 3y and y = 5
x 0 3 3 y 0 5 5
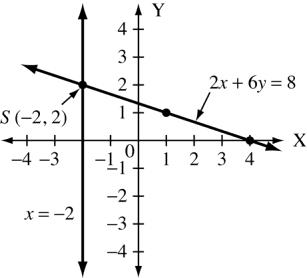
(d) 2x +6y =8 and x = 2
x 4 2 1 y 0 2 1
(e) y =3x 2 and y =3
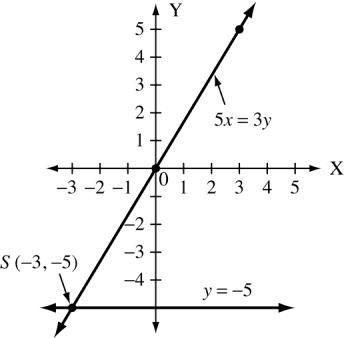
x 0 5/3 1 y 2 3 5
Copyright © 2015 Pearson Canada Inc.
(h) y =−2 and 5x +3y =15 x 3 0 4.2 y 0 5 2
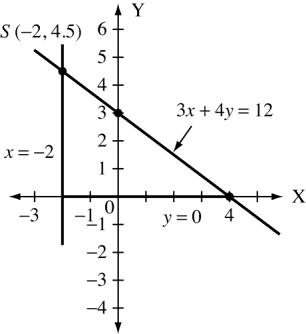


Copyright © 2015 Pearson Canada Inc. CHAPTER 4 159
x 0
y 0 8 4
(f ) y = 2x and x = 4
4 2
(g) x = 2 and 3x +4y =12 x 0 2 4 y 3 4.5 0

Copyright © 2015 Pearson Canada Inc. 160 CHAPTER 4 4. (a) 3x +2y = 1 5x +3y = 2 To eliminate y (1)×3→ 9x +6y = 3 (1) (2) (2)×(−2)→ −10x −6y = 4 Add: x =1 x = 1 In(1) 3( 1)+ 2y = 1 2y = 2 y =1 (x, y) = (−1,1) (b) 4x 5y = 25 3x +2y =13 To eliminate y (1) (2) (1)×2→ (2)×5→ 8x 10y = 50 15x +10y = 65 (c) Add: 23x =115 x = 5 In(2) 15+2y =13 2y = 2 y = 1 (x, y) = (5, 1) y = 10x 3y = 29 x Rearrange (1) (2) 10x + y = 0 x +3y = 29 (3) (4)
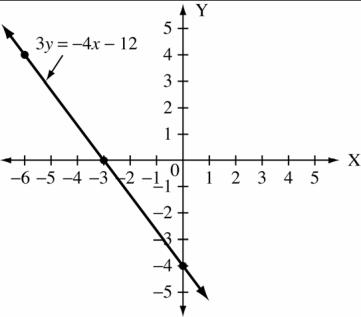
(d) 2y =3x +17 3x =11 5y
(e) 2x 3y =13 3x 2y =12
(2)
From(1)→ 2x 3y = 11
(2)×3→ 9x +3y = 39
Add: 7x = 28 x = 4
Copyright © 2015 Pearson Canada Inc. CHAPTER 4 161
30x +3y = 0 x +3y = 29
29x = 29 x = 1 In
Rearrange y = 10( 1) y =10 (x, y) = ( 1,10) (1) (2)
5
y = 4 In (2) 3x =11 20 3x = 9 x = 3 (x, y) = ( 3,4)
To eliminate y (3)×3→
Subtract:
(1)
3x +2y =17 3x +
y =11 Add: 7y = 28
(1) (2)
To eliminate y
(3)×2→ 4x 6y = 26
x = 2 In
3
y
3 (
(2,
×(3)→ 9x +6y = 36 Add: 5x = 10
(1) 2(2) 3y =13
y =9
=
x, y) =
3)
(1) (2)
(f) 2x =3y 11 y =13+3x
Copyright © 2015 Pearson Canada Inc. 162 CHAPTER 4 In (2) (g) 2a 3b 14 = 0 a + b 2 = 0 y =13+3( 4) y =13 12 y =1 (x, y) = ( 4,1) (1) (2) Rearrangeandmultiply(2)×2 2a 3b =14 2a +2b = 4 (h) Subtract: In (2) a + c = 10 8a +4c = 0 (1)×4→ Subtract: 5b =10 b = 2 a 2 2 = 0 a = 4 (a,b) = (4, 2) 4a +4c = 40 8a +4c = 0 4a = 40 a =10 (1) (2) In (1) 10+ c = 10 c = 20 (a,c) = (10, 20) (i) 3b 3c = 15 2b +4c =14 (1) (2) (1)×2→ 6b 6c = 30 (2)×3→ 6b +12c = 42 Add: 6c =12 c = 2 In (1) 3b 6 = 15 3b = 9 b = 3 (b,c) = (−3,2) (j) 48a 32b =128 16a +48b =32 (1) (2) (1)÷16→ (2)÷16→ 3a 2b =8 a +3b = 2 (3) (4)
Copyright © 2015 Pearson Canada Inc. CHAPTER 4 163 (4)×3→ (3)→ 3a +9b = 6 3a 2b = 8 Subtract: 11b = 2 b = −2 11 In (4) a +3 2 = 2 11 a = 2 6 11 (a,b) = 2 6 , 2 11 11 (k) 0.5m +0.3n =54 0.3m +0.7n = 74 (1) (2) (1)×10→ 5m +3n = 540 (2)×10→ 3m +7n = 740 (3)×3→ 15m +9n =1620 (4)×5→ 15m +35n = 3700 (3) (4) Subtract: 26n = 2080 n = 80 In (3) 5m +240=540 5m =300 m = 60 (m,n) = (60,80) (l) 3 m + 5 n = 3 4 8 4 5 n + 2 m = 7 6 3 9 To eliminate fractions (1)×8→ 6m +5n = 6 (2)×18→ 15n +12m =14 (3)×2→ 12m +10n =12 (4)→ 12m +15n =14 Subtract: 5n = 2 n = 2 5 (1) (2) (3) (4)
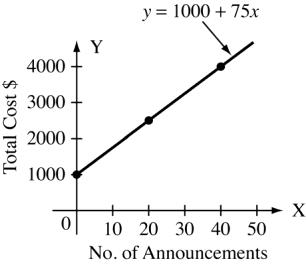
5. (a) Let the number of announcements be x and the total cost be $y.
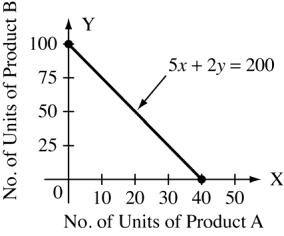
(b) Let the number of units of Product A be x and the number of units of Product B be y.
6. (a) Let x represent the number of sports tires sold, y the number of all-season tires sold.
(b) Let the number of $2.50-tickets be x and that of $3.50-tickets be y.
Copyright © 2015 Pearson Canada Inc. 3 5 164 CHAPTER 4 In (3) 6m +5 2 = 6 5 6m = 4 m = 2 3 (m,n) = 2 , 2
6x +5
(1) 3 x 2 y = 0 4 3 (2) (1)×12→ 9x – 8y = 0 (3) To eliminate y (3)×5→ 45x – 40y = 0 (1)×8→ 48x + 40y = 744 Add: 93x = 744 In (3) x =8 9(8) 8y = 0 8y = 72 y =9 8 sports tires were sold, 9 all-season tires were sold.
y =93
x + y =
(1) 2.5x +3.5
(2)
450
y =1300
The number of $2.50-tickets is 275 and the number of $3.50-tickets is 175.
(c) Let the price of a jacket be $x and that of a pair of pants be $y.
+2y =175
=3y Substitute (2) in (1)
y +2y =175
y =175 y =35 x =105
The price of the jacket is $105.
(d) Let the cost of a case of white bordeaux be $x and that of a case of red bordeaux be $y. 3x +5y = 438
Self-Test
Copyright © 2015 Pearson Canada Inc. CHAPTER 4 165
eliminate x (1)×2→ (2)×5→ 5x 7y = 2600 5x +5y = 2250
To
y =
x =
Subtract: 2 y = 350
175
275
x
x
3
5
(1) (2)
y
2
6
3x +5(2x 6) = 438 3x +10x 30 = 438 13x = 468 x =36 y = 2(36) 6 = 66 (1) (2)
=
x
Substitute (2) in (1)
A case of white bordeaux is $36; and a case of red bordeaux is $66.
(a)
y 11 = 3 Slope,
0; y-intercept, b
1.
For4y +11= y
m =
= 11 3
166
CHAPTER
Slope, m = 6; y-intercept, b = 9
(c) For x +3y = 0
3y = x y
Slope, m
1 = 3 1 ; y-intercept, b = 0 = 3
(d) For 6y 18= 0 6y =18 y = 3
Line is parallel to the x-axis; slope, m = 0; y-intercept, b = 3
(e) For 13 1 x = 0 2 26 x = 0 x = 26
Line is parallel to the y-axis; slope, m isundefined ; there is no y-intercept
(f ) For ax + by = c
by =−ax + c
Slope, m
a c y = b b a ; y-intercept, b = c = b b
2. (a) y = x 2 x 0 2 2 y 2 0 4 x y = 4 x 0 4 2 y 4 0 2
Copyright
Inc.
© 2015 Pearson Canada 4
x x +
(b) For 2 x 1 y =1 3 9 6x y =9 y = 6x 9
(b)
(b)
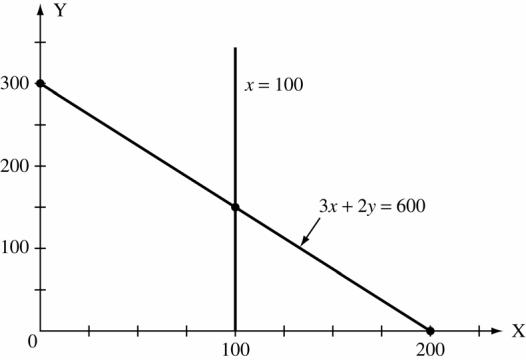
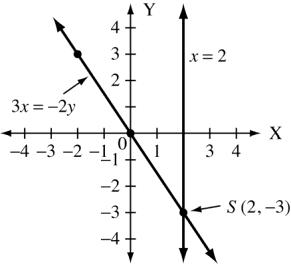
Copyright © 2015 Pearson Canada Inc. CHAPTER 4 167
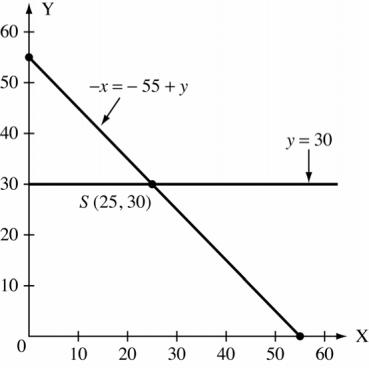
3x = 2y and x = 2 x 0 2 2 y 0 3 3 3. (a) For − x =−55+ y x 0 25 55 y 55 30 0
For 3x +2y = 600 x 0 100 200 y 300 150 0
4. (a) 6x +5y =9
4x 3y = 25
To eliminate y
(1)×3→ 18x +5y = 27
(2)×5→ 20x 15y =125
(b) 12 – 7x = 4y
6 – 2y = 3x
Rearrange 12 = 7x +4y
6 =3x +2y
To eliminate y
(1)×2→ 12 = 6x +4y 12 = 7x +4y
Subtract: 0 = x
Copyright © 2015 Pearson Canada Inc. 168 CHAPTER 4
(1)
(2)
5
y
3 (x, y)
(4, 3)
Add: 38x =152 x = 4 In (1) 24+5y =9
y =−15
=
=
(1)
(2)
(3) (4)
(x
0,3)
0.7
(1)
(2) (1)
10
2a +3b = 0 (2)
10
7a 2b = 2500 (1) (2) (3) (4) (3)
2→
4a
6b
0 21a
6b
a
In (3)
b
b
200 (a,b
)
4 b − 3 c =− 17 3 5 3 5 b + 4 c = 5 6 9 9 (1) (2)
In (1) 12 = 4y y =3
, y) =(
(c) 0.2a +0.3b = 0
a −0.2b = 250 To eliminate b from
and
×
→
×
→
×
(4)×3→
+
=
−
= 7500 Add: 25a = 7500
=300
600+3
= 0
=
) =(300, 200
(d)
(1)×15→ 20b 9c = 85 (3)
(2)×18→ 15b +8c =10 (4)
(3)×3→ 60b −27c =−255
(4)×4→ 60b +32c = 40
Subtract: 59c = 295
5. Let the amount invested at 4% be $x, and the amount invested at 6% be $y.
+ y =12000
The amount of interest earned at 4% is $0.04x; the amount of interest earned at 6% is $0.06y 0.04x +0.06y =560
To eliminate x from (1) and (2)
×100→
×4→ 4x +6y = 56 000 4x +4y = 48 000
Subtract: 2y = 8000
= 4000
(1) x +4000 =12 000
= 8000
Theamountinvestedat 4% is $8000; the amount invested at 6% is $4000.
6. Let Eyad’s share of the profit be $x, and Rahia’s share of the profit be $y.
+ y =12 700
x = 2 y +2200 5
To eliminate fractions
×5→ 5x = 2y +11 000
To eliminate y from (1) and (3) Rearrange(3)→
Copyright © 2015 Pearson Canada Inc. CHAPTER 4 169
In (4) c
b
(
c)
=5 15b +40 =10 15b = 30
= 2
b,
=( 2,5)
x
(1)
(2)
(1)
(2)
y
In
x
x
(1) (2) (2)
(3)
(1)
2
Add:
x =
×2→ 5x 2y =11 000
x +2y = 25 400
7x = 36 400
5200





























































