Solution Manual for College Physics 10th Edition by Young
ISBN 0321902785 9780321902788
Full download link at: Solution manual: https://testbankpack.com/p/solution-manual-for-college-physics-10thedition-by-young-isbn-0321902785-9780321902788/
Test bank: https://testbankpack.com/p/test-bank-for-college-physics-10th-edition-by-youngisbn-0321902785-9780321902788/
MOMENTUM
Answers to Multiple-Choice Problems
Solutions to Problems
8.1. Set Up: Use coordinates where +x the third object C is to the right. In (a) to (c) denote the two objects as A and B. In (d) call
8.2. Set Up: The signs of the velocity components indicate their directions. Call the objects A and B. Solve:
*8.3. Set Up: The signs of the velocity components indicate their directions.
Reflect: A has no x-component of momentum so Px is the same in (b) and (c). C has no y-component of momentum so Py in (c) is the sum of Py in (a) and (b).
8.4. Set Up: υ = 68 mph = 30.4 m/s, and 2646 lb = 1200.2 kg.
Solve: (a) p = mυ = (1200.2 kg)(30.4 m/s)
(b) Momentum is proportional to the speed, so the speed required to have half the momentum is
1/2 =υ 2 =(30 4 m/s) 2 =15 m/s.
(c) Kinetic energy is proportional to the speed squared. The speed υ′ required to have half the kinetic energy is
Reflect: In part (c), the two signs mean that the car can be traveling in the positive or negative direction. We retained the positive square root because speed normally has no direction associated with it, so it is positive.
*8.5. Set Up: 145 g = 0.145 kg; 57 g = 0 057 kg
=
Reflect: K depends on υ 2 and p depends on υ so a smaller increase in υ is required for the lighter ball to have the same kinetic energy
8.6. Set Up: p = mυ and direction.
and K = 1 mυ2 Recall that momentum is a vector and so is defined by both its magnitude 2
Solve: (a) The magnitude of the momenta is the same but, because the two carts are moving in different directions, the direction of their momenta are different. Therefore, the momenta of the carts are not the same
(b) The magnitude of the momentum of cart A is pA = mAυA =(5 kg)(2 m/s)=10 kg m/s. The magnitude of the momentum of cart B is is the same.
Copyright 2016 Pearson
Copyright 2016 Pearson
(c) The kinetic energy of cart A is K
kinetic energy of cart
K = m υ = (2 kg)(5 m/s)2 = 25J. Thus, the kinetic energy of the two carts is not the same
B 2 B B 2
Reflect: Although both K and υ are linear in mass, K depends on υ 2 and p depends on υ. Thus, kinetic energy and momentum scale the same in mass, but not in velocity.
8.7. Set Up: p = mυ From Problem 8.6, p = 2mK
Solve: (a) p = mc
p = 2mcKc . pd = 2mdKd . Kd = Kc and md = 3mc so pd = 2(3mc)Kc = 3p p p 3p υ
Reflect: In (b), υc = and υd = d = = c When the mass is increased the speed must be decreased to mc keep the same kinetic energy md 3mc 3
8.8. Set Up: Consider the system consisting of the two skaters. mA = (625 N)/(9 80 m/s2) = 638 kg
mB = (725 N)/(9 80 m/s2) = 74 0 kg Assume the heavier skater (B) travels to the right and take this to be the +x direction.
Pi, x = Pf, x The skaters are initially at rest so Pi, x = 0 mB (υB,f )x (74 0 kg)(1 50 m/s) (
A,f )x = = A 63 8 kg = 1 74 m/s
50
*8.9. Set Up: mE = 5.98 ×1024 kg. Consider the person and the earth to be an isolated system Use coordinates where + y is upward, in the direction the person jumps.
mperson υ = υ
75
© Copyright 2016 Pearson Education, Inc. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the publisher.
© Copyright 2016 Pearson Education, Inc. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the publisher.
Copyright 2016
Copyright 2016
(d) Ki = 1 (0.150 kg)(1.20 m/s)2 = 0.108 J. 2
K = 1 (0 150 kg + 0 250 kg)(0 450 m/s)2 = 0 0405 J f 2
Kf < Ki; kinetic energy is not conserved. Kinetic energy cannot be conserved in a collision where the objects stick together.
8.11. Set Up: Let +x be in the direction the ball is traveling initially. mA = 0.400 kg (ball). mB = 70.0 kg (you).
Solve: (a) Pi, x = Pf, x gives (0 400 kg)(10 0 m/s) = (0 400 kg + 70 0 kg)υf and υf = 0.0568 m/s.
(b) Pi, x = Pf, x gives (0 400 kg)(10 0 m/s) = (0 400 kg)( 8 00 m/s)
Reflect: The total momentum of the system is conserved but the total kinetic energy decreases 8.13. Set Up: Apply conservation of momentum and conservation of energy Let +x system is released, block A moves to the left and block B moves to the right.
*8.14. Set Up: Each component of momentum is conserved. Let +x be to the east and +y be north. Label the stalled car “A” and the other car “B.” The final x component of car A’s momentum is pA,f,x = mAυA,f,x = mAυA,f cos30°=(750 kg)(4 m/s)cos30°= 2598 kg m/s, and the final y component of car A’s momentum is pA,f, y = mAυA,f,y = mAυA,f sin30°=(750 kg)(4 m/s)sin30°=1500 kg m/s. The initial momentum of car B is pB,i = mBυB,i,x =(1000 kg)(10 m/s)=10,000 kg m/s.
Solve: (a) Conservation of the x component of momentum gives 0+ mBυB,i,x = mAυA,f,x + mBυB,f,x Conservation of the y component of momentum gives 0+ 0 = mAυA,f,y + mBυB,f,y We also know that υ 2 =υ 2 +υ 2 This gives three equations with three unknowns: υB,f,y , υB,f,x , and υB,f Solving for υB,f gives B,f B,f,x B,f,y υB,f =
© Copyright 2016 Pearson Education, Inc. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the publisher.
© Copyright 2016 Pearson Education, Inc. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the publisher.
Thus, the direction of car B’s final velocity is
Thus, car B’s final velocity is 7.6 m/s at 11° south of east.
(b) Before the collision the total kinetic energy is
After the collision, the total kinetic energy is
The ratio γ of the final kinetic energy to the initial kinetic energy is γ = 34,519 J = 0 69 50,000 J
Reflect: Each component of momentum is separately conserved. The kinetic energy of the system decreases because the collision is not elastic (some energy is converted in deforming the steel, sound, heat, etc.).
8.15. Set Up: Let +x be the direction you are moving. Before you catch it, the flour sack has no momentum along the x axis. The total mass of you and your skateboard is 60 kg. You, the skateboard, and the flour sack are all moving with the same velocity, after the catch.
Solve: (a) In the absence of ahorizontalforce, we know that Pi, x = Pf, x Thus, we have (60 kg)(4 5 m/s) = (625 kg)υf, x
Solvingforthefinal velocitywe obtain υf, x = 4 3 m/s
(b) To bring the flour sack up to your speed, you must exert a horizontal force on it. Consequently, it exerts an equal and opposite force on you, which slows you down.
(c) Since you exert a vertical force on the flour sack, your horizontal speed does not change and remains at 4.3 m/s Since the flour sack is only accelerated in the vertical direction, its horizontal velocity-component remains at 4 3 m/s as well. Reflect: Unless you or the flour sack are deflected by an outside force, you will need to be ready to catch the flour sack as it returns to your arms!
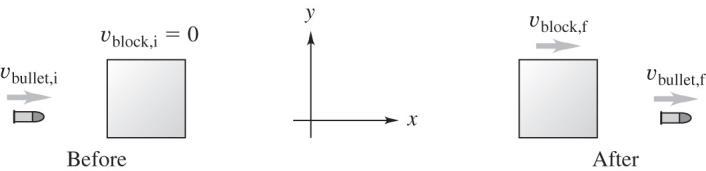
8.16. Set Up: Use coordinates where +x is in the direction of motion of the bullet. The figure below gives before and after sketches for the system of bullet and block.
Solve: There is no external force in the x direction, so Pi, x = Pf, x. This gives
© Copyright 2016 Pearson Education, Inc. All rights reserved. This material is protected
© Copyright 2016 Pearson Education, Inc. All rights reserved. This material is
Reflect: The momentum lost by the bullet equals the momentum gained by the block.
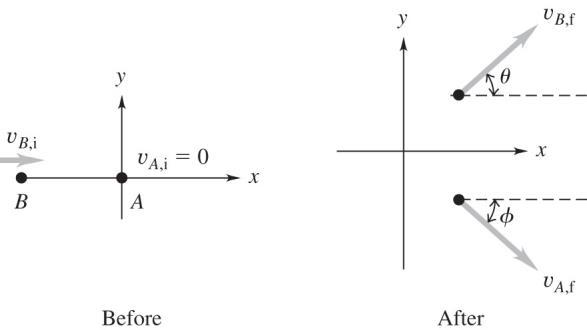
Set Up: Before and after diagrams are sketched in the figure below.
*8.18. Set Up: Use coordinates where +x is to the right and + y is upward. Apply conservation of momentum to solve the first part of the problem and conservation of energy for the second part of the problem
Solve: Collision: There is no external horizontal force during the collision so Pi, x = Pf, x This gives (5.00 kg)(12.0 m/s) = (10.0 kg)υf and υf = 6.00 m/s.
Motion after the collision: Because the valley is covered in frictionless ice, the blocks lose no energy when sliding up the hill, so they have the same kinetic energy when the slide back down the hill. This means that they have the same speed when they reach the valley floor again as they did initially. Their speed is therefore 6.00 m/s.
8.19. Set Up: The collision occurs over a short-time interval and the block moves very little during the collision, so the spring force during the collision can be neglected. Use coordinates where +x is to the right.
Solve: Collision: There is no external horizontal force during the collision and (3 00 kg)(8 00 m/s) = (15 0 kg)υblock,f (3 00 kg)(2 00 m/s) and υblock,f = 2 00 m/s Pi, x = Pf, x This gives
© Copyright 2016 Pearson Education, Inc. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the publisher.
© Copyright 2016 Pearson Education, Inc. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material
be reproduced, in any form or by any means, without permission in writing from the
Motion after the collision: When the spring has been compressed the maximum amount, all the initial kinetic energy of the block has been converted into potential energy 1 kd 2 that is stored in the compressed spring. Conservation of 2 energy gives 1 (15.0 kg)(2.00 m/s)2 = 1 (500.0 kg)d 2 and d = 0.346 m.
© Copyright 2016 Pearson Education, Inc. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the publisher.
© Copyright 2016 Pearson Education, Inc. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the publisher.
*8.20. Set Up: Let x be the direction of motion. Let each boxcar have mass m
says
25.0% of the original kinetic energy is dissipated. Kinetic energy is converted to other forms by work done by the forces during the collision.
8.21. Set Up: Let +x be to the right.
The final velocity is 1.60 m/s, to the left.
ΔK = Kf Ki = 1.47 J. Work done by nonconservative forces during the collision converts mechanical energy to other forms of energy such as heat, sound, etc.
8.22. Set Up: Let the initial direction of the block’s motion be the positive x direction. Use conservation of momentum to calculate the initial speed of the two blocks just after the collision. Then use conservation of energy to calculate how high up the incline the two blocks slide. The distance L that the blocks slide up the incline is related to the height h above the table by h = Lsinθ.
Solve: Using conservation of momentum, the speed of the two blocks just after the collision is mυi = 2mυf so
, where υ = 5 m/s. Using conservation of energy, the height h above the table that the blocks reach is f
i i
Thus the distance L that the blocks travel up the incline is
8.23. Set Up: The forces the two players exert on each other during the collision are much larger than the horizontal forces exerted by the slippery ground and it is a good approximation to assume momentum conservation. Each component of momentum is separately conserved. Let +x be east and +y be north. After the collision the two players have velocity v2 Let the linebacker be object A and the halfback be object B, so vA1x = 0,
and v
for
and
.
© Copyright 2016 Pearson Education, Inc. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the publisher.
© Copyright 2016 Pearson Education, Inc. All rights reserved. This material is protected under all copyright laws as they currently exist. No
The players move with a speed of 5.9 m/s and in a direction 58° north of east. Reflect: Each component of momentum is separately conserved.
*8.24. Set Up: Apply conservation of momentum to the collision and the work-energy equation to the motion after the collision. Let +x be the direction the bullet was traveling before the collision.
Solve: Motion after the collision: Wother + Ui + Ki = Kf + Uf There is no change in height so Ui = Uf The block stops so Kf = 0 n = mg, 1 fk = μkmg and Wother = W f = μkmgs Let υ be the speed of the block immediately 1 after the collision, so Ki = m
Therefore,
Collision: mbulletvbullet, i = mυ, where m =1 20 kg + 5 00 ×10 3 kg =1 205 kg
υbullet,i (1.205 kg)(0.950 m/s) 2 = = 2.3×10 m/s 5 00 ×10 3 kg
Reflect: Our analysis neglects the friction force exerted by the surface on the block during the collision, since we assume momentum is conserved in the collision. The collision forces between the bullet and block are much larger than the friction force, so this approximation is justified.
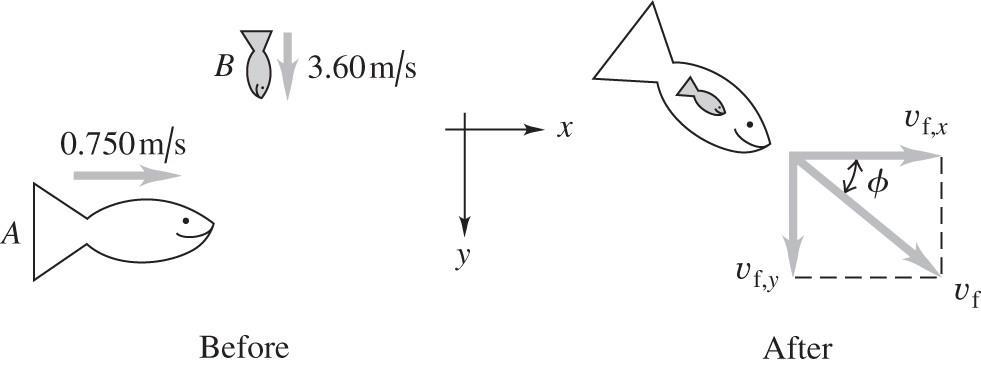
8.25. Set Up: Use coordinates where +x is east and +y is south. Let the big fish be A and the small fish be B. The system of the two fish before and after the collision is sketched in the figure below.
Solve: There are no external forces on the fish so Pi, x = Pf, x and Pi, y = Pf, y
Pi, x = Pf, x gives (11 5 kg)(0 750 m/s) = (12 75 kg)υf, x so υf, x = 0 676 m/s
Pi, y = Pf, y
gives (1 25 kg)(3 60 m/s) = (12 75 kg)υf, y 0 676 m/s
© Copyright 2016 Pearson Education, Inc. All rights reserved. This material is protected
so υf,y = 0 353 m/s
© Copyright 2016 Pearson Education, Inc. All rights reserved. This material is protected
0 763 m/s in a direction 27.6° south of east.
Reflect: Momentum is a vector and we must treat each component separately
© Copyright 2016 Pearson Education, Inc. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the publisher.
© Copyright 2016 Pearson Education, Inc. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material
in any form or by any means, without
8.26. Set Up: The system before and after the collision is sketched in the figure below. Use the coordinates shown. The collision forces are large so gravity can be neglected during the collision.
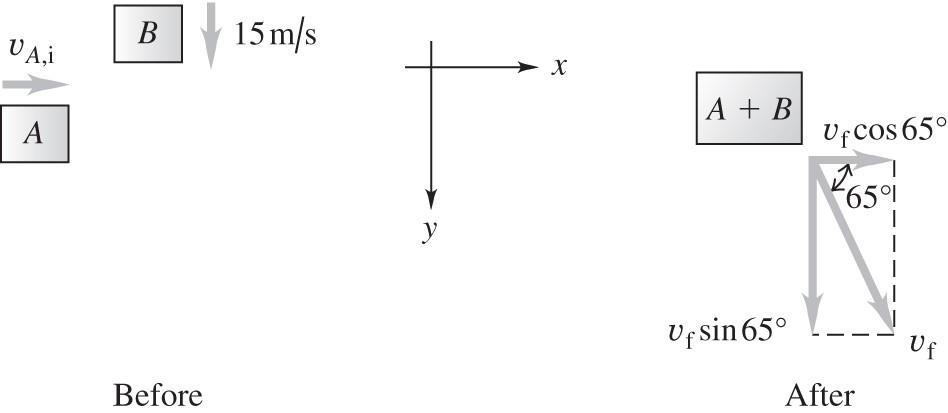
Solve: There is no external force on the system so Pi, x = Pf, x and Pi, y = Pf, y Pi, x = Pf, x gives (1 5 kg)(9 0 m/s)
= (1 5 kg)υraven,f cosφ and υraven,f cosφ = 9 0 m/s Pi, y = Pf, y gives (0 600 kg)(20 0 m/s) = (0 600 kg)( 5 0 m/s)
+(1 5 kg)υraven,f sinφ and υraven,f sinφ= 10 0 m/s Combining these two equations gives tanφ = 10 0 m/s 9 0 m/s and φ = 48°
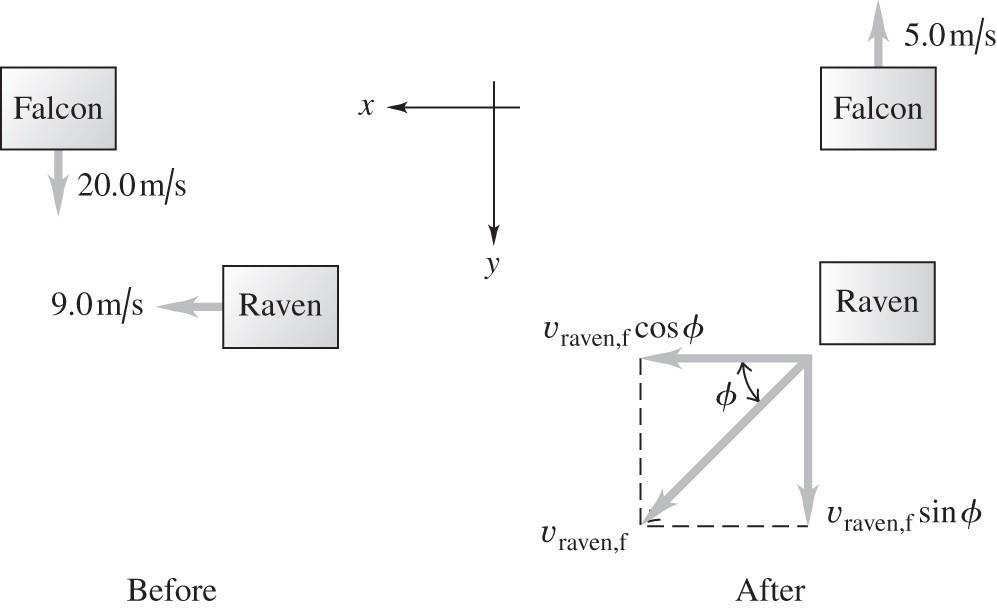
*8.27. Set Up: Use coordinates where +x is east and +y is south. The system of two cars before and after the collision is sketched in the figure below. Neglect friction from the road during the collision. The enmeshed cars have mass 2000 kg +1500 kg = 3500 kg
Solve: There are no external horizontal forces during the collision, so Pi, x = Pf, x and Pi, y = Pf, y
(a) Pi, x = Pf, x gives (1500 kg)(15 m/s) = (3500 kg)υf sin65° and υf = 7 1 m/s
(b) Pi, y = Pf, y gives (2000 kg)υA,i = (3500 kg)υf cos65° And then with υf = 7 1 m/s, υA,i = 5 2 m/s
Reflect: Momentum is a vector and we must treat each component separately.
© Copyright 2016 Pearson Education, Inc. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the publisher.
© Copyright 2016 Pearson Education, Inc. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the publisher.
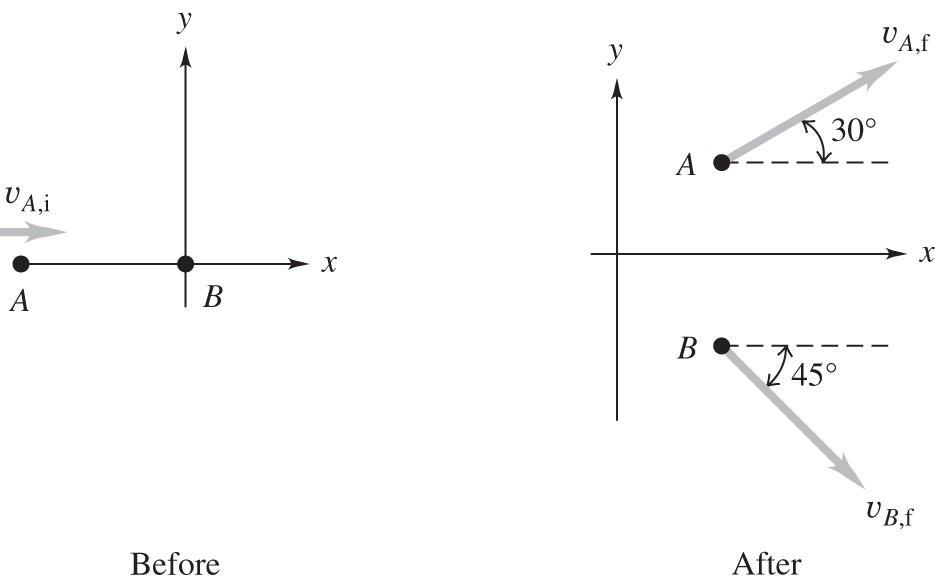
8.28. Set Up: The before and after diagrams are given in the figure below and the choice of coordinates is indicated. Each puck has mass m
19.6% of the original kinetic energy is dissipated during the collision.
*8.29. Set Up: For an elastic collision with B initially stationary, the final velocities are
The 0.300-kg glider moves to the right at 0.27 m/s and the 0.150-kg glider moves to the right at 1.1 m/s.
© Copyright 2016 Pearson Education, Inc. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the publisher.
© Copyright 2016 Pearson Education, Inc. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material
in any form or by any means, without permission in writing
Reflect: The relative velocity after the collision has magnitude 107 m/s 027 m/s = 0 80 m/s,
the same as before the collision The initial kinetic energy of the system is K A,i = (0.300 kg)(0.80 m/s)2 = 0.096 J. The final kinetic 2 energy is K A,f + KB,f = 0 097 J, the same as the initial kinetic energy, apart from a slight difference due to rounding
8.30. Set Up: Take the original direction of the penny (object A) as the positive direction. Since this is a onedimensional elastic collision, with the nickel (object B) initially stationary, we can use Eqs. (8.11) and (8.12). The
velocities are given by
Reflect: Since the equations we used involved a ratio of masses, there was no need to convert the masses into kilograms.
8.31. Set Up: Let +x be to the right. All velocities are x components but we will not write the x subscript. Use conservation of momentum and the relative velocity addition equation
8.32. Set Up: When the spring is compressed the maximum amount the two blocks aren’t moving relative to each other and have the same velocity υ relative to the surface. Apply conservation of momentum to find υ and conservation of energy to find the energy stored in the spring. Since the collision is elastic, Eqs. (8.11) and (8.12) give the final velocity of each block after the collision. Let +x be the direction of the initial motion of A.
Solve: (a) Momentum conservation gives (2.00 kg) (2.00 m/s) = (12.0 kg)υ and υ = 0.333 m/s. Both blocks are moving at 0.333 m/s, in the direction of the initial motion of block A Conservation of energy says the initial kinetic energy of A equals the total kinetic energy at maximum compression plus the potential energy Ub
stored in the bumpers: (2 00 kg)(2 00 m/s)2 = Ub +
2(12.0 kg)(0.333 m/s)2 and Ub = 3.33 J.
© Copyright 2016 Pearson Education, Inc. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the publisher.
© Copyright 2016 Pearson Education, Inc. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the publisher.
Reflect: When the spring is compressed the maximum amount the system must still be moving in order to conserve momentum
© Copyright 2016 Pearson Education, Inc. All rights reserved. This material is protected under all copyright laws as they currently exist.
Copyright 2016 Pearson Education, Inc. All rights reserved. This material is protected under all copyright laws as they currently exist. No
8.33. Set Up: Label the 2-kg block “A” and the other block “B ” Let the +x direction be the direction in which block A initially moves Apply conservation of momentum and conservation of energy to find the final speed and the mass of block B.
Solve: (a) Conservation of momentum gives mA
A,i = mA
A,f + MυB,f Conservation of energy gives
. Solving these equations for the mass M of block B gives
(b) The speed of block B after the collision is υB,f =υA,f +υA,i = 3m/s+10 m/s = 7 m/s. *8.34. Set Up: Assume the ball is initially moving to the right, and let this be the +x its final velocity is zero. direction. The ball stops, so
Solve: (a) J x = mυf, x mυi, x = 0 (0 145 kg)(36 0 m/s) = 522 kg m/s.The magnitude of the impulse applied to the ball is 5.22 kg m/s.
J 5.22 kg ⋅m/s
(b) J x = Fx Δt so Fx = x = = 2 6×102 N
Δt 20 ×10 3 s
Reflect: The signs of J x and Fx show that both these quantities are to the left.
8.35. Set Up: Let +x be to the right.
Solve: (a) Fx Δt = Pf, x Pi, x P
x = Pi, x + Fx Δt = (2.50 kg)(8.00 m/s) + (5.00 N)(5.00 s) = 45.0 kg ⋅m/s
Pf, x = mυf, x so υf, x 45.0 kg ⋅m/s = =18.0 m/s. The block is moving to the right at 18.0 m/s. 2 50 kg
(b) Pf, x = Pi, x + Fx Δt = (2.50 kg)(8.00 m/s) + ( 7.00 N)(5.00 s) = 15.0 kg ⋅m/s.
υf, x = 150 kg m/s = 6 00 m/s 2 50 kg
The block is moving to the left at 600 m/s
*8.36. Set Up: (a) Take the +x the ball is zero. direction to be along the final direction of motion of the ball. The initial speed of
(b) Take the +x direction to be in the direction the ball is traveling before it is hit by the opponent.
Solve: (a) J x = mυf, x mυi, x = (57 ×10 3 kg)(70 m/s 0) = 40 kg ⋅m/s
J 4.0kg ⋅m/s
F = = =1.3×102 N
x Δt 30 0 ×10 3 s
© Copyright 2016 Pearson Education, Inc. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the publisher.
© Copyright 2016 Pearson Education, Inc. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the publisher.
Reflect: The signs of J x and Fx show their direction. 130 N = 29 lb This very attainable force has a large effect on the light ball. 130 N is about 250 times the weight of the ball.
© Copyright 2016 Pearson Education, Inc. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the publisher.
© Copyright 2016 Pearson Education, Inc. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the publisher.
8.37. Set Up: Take + y to be upward. Use the motion of the ball after it leaves the racket to find its speed just after it is hit. After it leaves the racket ay = g At the maximum height υ y = 0. Solve: υ 2 =υ 2 + 2a (y y ) gives
8.38. Set Up: The impulse is the area under the Fx the left, so Fx is positive. versus t curve between ti and tf Let the +x direction be to
The
(ii)
of the ball is 80 m/s, to the left.
The final velocity of the ball is 50 m/s, to the left.
Reflect: In both (i) and (ii) of part (b) the change in velocity is the same, 80 m/s
8.39. Set Up: Choose the positive x axis in the direction of motion. We know that the impulse applied to the wagon will be equal to the wagon’s change in momentum: J x =Δpx The total mass of your sister and her wagon is 33 5 kg.
Solve:
(b) Since J x = Fxt, we have
Reflect: The force calculated in part (b) is the net force acting on the wagon which is the force that you must apply, assuming that no other forces act on the wagon.
*8.40. Set Up: Use Eq. (8.15) for impulse: J = pf pi The average force is given by Fav = J Δt To convert from N to lb, use 1 N = 0.2248 lb.
Solve: The initial momentum of the bullet is zero. Therefore, the magnitude of the impulse imparted by the exploding gunpowder is J = pf = mυf =(8.5×10 3 kg)(900 m/s)= 7.7 kg m/s.
(b) The magnitude of the average force exerted on the bullet is F J (7.65 kg⋅m/s) 0.2248lb 2 = = = 8.6×10 lb.
© Copyright 2016 Pearson Education, Inc. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the publisher.
© Copyright 2016 Pearson Education, Inc. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the publisher.
*8.41. Set Up: From the appendix we have mE = 5 97 ×1024 kg, mM = 7.35×1022 kg, and the distance between
the earth and the moon is 3 84 ×108 m Represent the earth and the moon as point masses located at their respective centers. Use coordinates with the origin at the center of the earth and with the moon on the +x xE = 0 and xM = 3 84 ×108 m axis; thus,
© Copyright 2016 Pearson Education, Inc. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the publisher.
© Copyright 2016 Pearson Education, Inc. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the publisher.
The center of mass is 4 67 ×106 m from the center of the earth along the line that connects the center of the earth to that of the moon.
Reflect: Since the radius of the earth is 6 38×106 m, the center of mass of the earth-moon system is roughly 1700 km below the earth’s surface.
8.42. Set Up: Since the beam is uniform, all its mass can be considered to be at its center. The mass of the beam is mb = 9 00 kg Let mA = 8 00 kg and mC = 7 50 kg For each choice of origin let the +x axis lie along the beam.
The center of mass is 1.29 m from the left-hand end of the beam
The center of mass is 1.71 m from the right-hand end of the beam and therefore 1.29 m from the left-hand end. (c) We get the same result for either choice of coordinates.
*8.44. Set Up: Label the 2-kg stone “A” and the 1-kg stone “B.” Use Eq. (8.18) to find the x and y coordinates of the center of mass. Let the origin of the coordinate system be at the right-hand base of the building, with +x pointing to the right and +y pointing up The position of each stone may be found by using the equations of kinematics. The
1 vertical position is given by yA (t)= yB(t)=
where yi = 50 m. The x position of the 2-kg stone is xA (t)= 0 and the x position of the 1-kg stone is xB(t)=υB,i,xt, where υi,x =10 m/s
Solve: The coordinates of the center of mass of the two-stone system are
© Copyright 2016 Pearson Education, Inc. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material
© Copyright 2016 Pearson Education, Inc. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material
be reproduced, in any form or by any means, without permission in writing from the publisher.
(a) For t = 0, the center-of-mass coordinates are (0 m, 50 m).
(b) For t = 2 s, the center-of-mass coordinates are (7 m, 3×101 m)
(c) They hit the ground when t = 50 m = 3.19s, 4.9 kg m/s2 so the x coordinate is xc m =(3.33m/s)(3.19 s)=11m
The y coordinate is zero, since both stones are on the ground. The center-of-mass coordinates are thus (11 m, 0 m).
8.45. Set Up: The leg in each position is sketched in Figure (a) and (b) below. Use the coordinates shown. The mass of each part of the leg may be taken as concentrated at the center of that part.

The center of mass of the leg is 40.4 cm in the direction that the leg is extended.
The center of mass is a vertical distance of 8.72 cm in the direction that the leg is bent and 31.7 cm in the direction that the leg is extended.
*8.46. Set Up: mA =1200 kg, mB =1800 kg. M = mA + mB = 3000 kg. Let +x be to the right and let the origin be at the center of mass of the station wagon.
The center of mass is between the two cars, 24.0 m to the right of the station wagon and 16.0 m behind the lead car.
© Copyright 2016 Pearson Education, Inc. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the publisher.
© Copyright 2016 Pearson Education, Inc. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the publisher.
8.47. Set Up: Let +x be to the right, with the origin at the initial position of the left-hand end of the canoe.
mA = 45 0 kg, mB = 60 0 kg
The center of mass of the canoe is at its center.
Solve: There is no net horizontal external force so υcm is constant Initially, υcm = 0, move. Initially, so the center of mass doesn’t After she walks,
AxA, i + mBxB,i =
A + mB xcm,i = xcm,f gives mAxA,i + mBxB,i = mAxA,f + mBxB,f She walks to a point 1 00 m from the right-hand end of the canoe, so she is 1.50 m to the right of the center of mass of the canoe and xA,f = xB,f +1.50 m
(45 0 kg)(1 00 m) + (60 0 kg)(2 50 m) = (45 0 kg)(xB,f +1 50 m) + (60 0 kg)xB,f
(105 0 kg)xB,f =127 5 kg m and xB,f =1 21 m to the left. xB,f xB,i =1 21 m 2 50 m = 1 29 m The canoe moves 1.29 m
*8.48. Set Up: Use Eq. (8.25).
t = (1600 m/s) 1 00 s = +80 0 N
(b) The absence of atmosphere would not prevent the rocket from operating. The rocket could be steered by ejecting the gas in a direction with a component perpendicular to the rocket’s velocity and braked by ejecting it in a direction parallel (as opposed to antiparallel) to the rocket’s velocity
8.49. Set Up: Use Eq. (8.26). Solve for Δm, with Δt =1 00 s
8.50. Set Up: Use Eq. (8.26). m = Solve for
© Copyright 2016 Pearson Education, Inc. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the publisher.
© Copyright 2016 Pearson Education, Inc. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the publisher.
Reflect: The acceleration is proportional to the speed of the exhaust gas and to the rate at which mass is ejected.
*8.51. Set Up: Use Eq. (8.24): ma = υ Δm ex Δt Assume that Δm is constant over the 5.0-s interval and that m Δt Δm doesn’t change much during that interval. The thrust is F = υex Δt . Take m to have the constant value
110 kg + 70 kg =180 kg. Note that the rate of change in mass, Δm , Δt is negative since the mass of the MMU decreases as gas is ejected.
© Copyright 2016 Pearson Education, Inc. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the publisher.
© Copyright 2016 Pearson Education, Inc. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the publisher.
Reflect: The mass change in the 5.0 s is a very small fraction of the total mass m, so it is accurate to take m to be constant.
8.52. Set Up: Let +x be the direction the balls travel. P
This is the average force on the paintballs. The average recoil force is 0.150 N, in the opposite direction. Reflect: We can only calculate the average recoil force since we do not have detailed information about the how the paintballs are fired.
*8.53. Set Up: Momentum is conserved in the explosion. At the highest point the velocity of the boulder is zero. Since one fragment moves horizontally the other fragment also moves horizontally Use projectile motion to relate the initial horizontal velocity of each fragment to its horizontal displacement. Use coordinates where +x is north. Since both fragments start at the same height with zero vertical component of velocity, the time in the air, t, is the same for both. Call the fragments A and B, with A being the one that lands to the north. Therefore, we have mB =
Apply
motion after the collision: x x = v t Since t is the same, (
south of the point of explosion. Reflect: The fragment that has three times the mass travels one-third as far.
8.54. Set Up: Place the origin of the coordinate system at the top of the building from where the stone is thrown Let the +y direction be down, and the +x direction be the direction in which the stone is thrown. Use the equations of kinematics to calculate the stone’s velocity when it hits the ground. The y component of the velocity is given by υ
= 2gh where h = 40 m is the height of the building. The x component of the velocity is given by
Solve: (b) The instant the stone is thrown, it has zero velocity in the y direction, so its y component of momentum is zero. Its x component of momentum is
(b) When the stone hits the ground, the y component of its momentum is
Thus, its momentum is
The x component of its momentum is the same as in part (a) because no force acts in the x direction on the stone (ignoring air resistance). Thus, its momentum is (8kg m/s,1×101 kg m/s) The magnitude of the impulse imparted
Copyright 2016
© Copyright 2016 Pearson Education, Inc. All rights reserved. This material is protected
Thus, the magnitude of the impulse
8.55. Set Up: Let +x be the initial direction of motion of the bullet and let + y be the direction of the final motion of the bullet. mA = 250 ×10 3 kg the figure below (bullet); mB = 0100 kg (stone) The before and after diagrams are sketched in
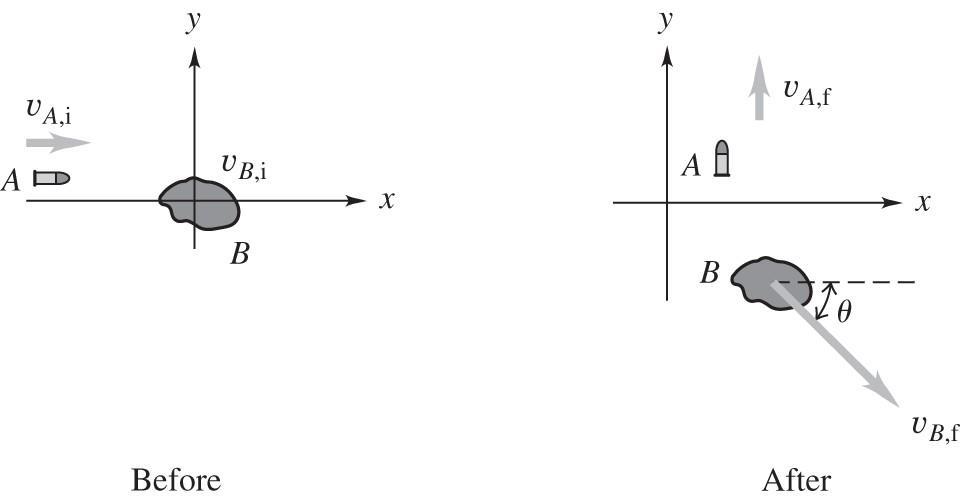
The stone rebounds at 146 m/s in a direction of 31 0° from the initial direction of motion of the bullet.
i = (2.50 ×10 3 kg)(500 m/s)2 = 312 J and
Kf < Ki and the collision is inelastic.
Reflect: Each component of momentum is separately conserved. Kinetic energy is a scalar, not a vector, and we never consider its “components.”
8.56. Set Up: Let + y be downward Use the heights to find υi, y just after it strikes the slab and υf, y , the velocity of the ball just before and Solve: (a)
© Copyright 2016 Pearson Education, Inc. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the publisher.
© Copyright 2016 Pearson Education, Inc. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the publisher.
(b) F = J y = y Δt 0.474 kg ⋅m/s 2.00 ×10 3 s = 237 N The average force on the ball is 237 N, upward.
(c) The kinetic energy before impact is equal to the initial potential energy, so Ki = mghi Likewise, the kinetic energy just after impact is equal to the final potential energy, so Kf = hghf The energy lost in the impact is thus
(d) If the impact had been perfectly elastic, the initial kinetic energy just after the impact would have been the same as just before the impact. In this case, by conservation of energy, the ball would have risen to its original height of 2.00 m.
*8.57. Set Up: Apply conservation of momentum to the collision between the two people. Apply conservation of energy to the motion of the stuntman before the collision and to the entwined people after the collision. For the motion of the stuntman, we have y1 y2 = 5 0 m Let υS be the magnitude of his horizontal velocity just before the collision. Let υ be the speed of the entwined people just after the collision. Let d be the distance they slide along the floor.
Reflect: Mechanical energy is dissipated in the inelastic collision, so the kinetic energy just after the collision is less than the initial potential energy of the stuntman.
8.58. Set Up: Use coordinates with +x in the direction the ball is traveling initially. mb = 57 ×10 3 kg and
= 61 kg (υb,i)x = 72 m/s, (υb,f )x = 45 m/s, and (υp,i)x = 0. The player is treated as a particle, with all her mass concentrated at her center of mass.
Solve: (a) Pi, x = Pf, x gives(57 ×10 3 kg)(72 m/s) = (57 ×10 3 kg)( 45 m/s) + (61 kg)(υp,f )x and (υp,f )x = 0 11 m/s
(b) Apply the impulse-momentum relation to the ball: J x = Fx Δt and J x = mb(υp,f )x mb(υp,i)x
m [(υ ) (υ ) ] 3
F = b b,f x b,i x = (57 ×10 kg)( 45 m/s 72 m/s) = 220 N x Δt 30.0 ×10 3 s
The racket exerts a force of 220 N on the ball. Apply the impulse-momentum relation to the player: mp[(υp,f )x (υp,i)x ] (61 kg)(0 11 m/s 0)
© Copyright 2016 Pearson Education, Inc. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the publisher.
Copyright 2016 Pearson
The ball exerts a force on 220 N on the racket. These two forces form an action-reaction pair and Newton’s third law requires that they have the same magnitude.
*8.59. Set Up: Apply conservation of energy to the motion before and after the collision and to the collision itself. Apply conservation of momentum to the collision. Label the mass m “A” and the mass 3m “B.” Let υA,i be the speed of the mass released at the rim just before it strikes mass B.
Solve: (a) Conservation of energy applied to mass A as it slides down the bowl gives 1 mυ2 = mgR, so
υA,i = 2gR Conservation of momentum applied to the collision gives mυA,i = mυA,f +3mυB,f . Conservation of energy applied to the collision gives
= m
3
+ m
. Solving these equations for
gives
υ = gR so the velocity of mass A is gR to the left. The velocity of mass B is υ = gR to the right.
(b) Applying conservation of energy to mass A gives mgh = 1 mυ2 so h = R . Applying conservation of energy 2 A,f A 4 to mass B gives 3mgh = 3 mυ2 so h = R . Thus, both masses will rise to a height of R/4.
B,f B 4
Reflect: No mechanical energy is lost in the collision, so the final gravitational potential energy is the same as the initial gravitational potential energy: U = mg R +3mg R = mgR. f 4 4
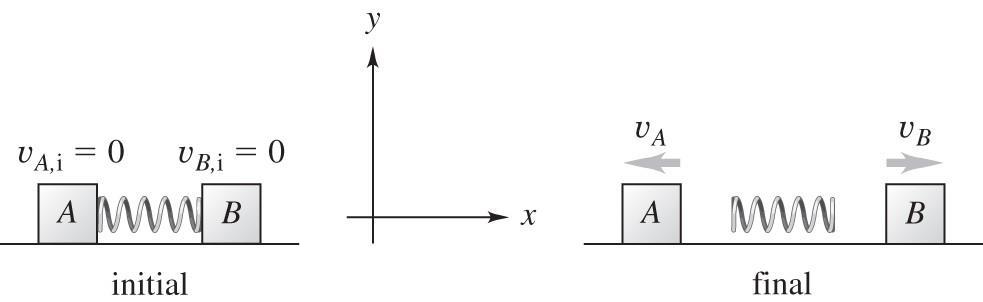
8.60. Set Up: Let the system be the two masses and the spring. The system is sketched in the figure below, in its initial and final situations. Use coordinates where +x is to the right. Call the masses A and B
Reflect: If the objects have different masses they will end up with different speeds. The lighter one will have the greater speed, since they end up with equal magnitudes of momentum
8.61. Set Up: Let +x be to the right. Apply conservation of momentum to the collision and conservation of energy to the motion after the collision. The total mass is m = mbullet + mblock =1 00 kg The spring has force constant
© Copyright 2016 Pearson Education, Inc. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the publisher.
© Copyright 2016 Pearson Education, Inc. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the publisher.
Let υ be the velocity of the block just after impact.
Solve: (a) Conservation of energy for the motion after the collision gives
(b) Conservation of momentum applied to the collision gives
© Copyright 2016 Pearson Education, Inc. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the publisher.
© Copyright 2016 Pearson Education, Inc. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material may be reproduced, in any form or by any means, without
8.62. Set Up: Let +x be to the right. Apply conservation of momentum to the collision and conservation of energy to the motion of the block after the collision. Let the bullet be A and the block be B Let υ be the velocity of the block just after the collision.
Solve: Motion of block after the collision: Ki =
Reflect: We assume the block moves very little during the time it takes the bullet to pass through it.
*8.63. Set Up: The center of mass of each piece of length L is at its center.
Solve: (a) From symmetry, the center of mass is on the vertical axis, a distance (L/2)cos(α/2) below the apex.
(b) The center of mass is on the vertical axis of symmetry, a distance 2(L / 2)/3= L/3 horizontal segment. above the center of the
(c) Using the wire frame as a coordinate system, the coordinates of the center of mass are equal and each is equal to (L/2)/2 = L/4 The center of mass is along the bisector of the angle, a distance L/ 8 from the corner.
(d) By symmetry, the center of mass is at the center of the equilateral triangle, a distance (L/2)tan60°= L/ 12 above the center of the horizontal segment.
8.64. Set Up: The horizontal component of the momentum of the sand plus railroad system is conserved. As the sand leaks out it retains its horizontal velocity of 15.0 m/s.
Solve: The horizontal component of the momentum of the sand doesn’t change when it leaks out so the speed of the railroad car doesn’t change; it remains 15.0 m/s. This result is similar to that of Problem8.15 (c). In contrast, in Problem
8.15 (a) the flour sack is falling vertically and initially has no horizontal component of momentum Its momentum changes when you catch it. Therefore, in order to conserve the total horizontal momentum you and your skateboard must slow down.
Reflect: The horizontal momentum of the sand does change when it strikes the ground, due to the force that is external to the system of sand plus railroad car.
8.65. Set Up: Apply conservation of momentum to the collision and conservation of energy to the motion after the collision. Let +x be to the right.
Solve: Collision: Pi, x = Pf, x gives (4.20 ×10 3 kg)υ = (4.20 ×10 3 kg + 2.50 kg)υ′
Motion after the collision: The kinetic energy of the block immediately after the collision is converted entirely to gravitational potential energy at the maximum angle of swing. The figure below shows that the maximum height h the block swings up is given by h = (0.750 m)(1 cos34.7°) = 0.133 m.
© Copyright 2016 Pearson Education, Inc. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the publisher.
© Copyright 2016 Pearson Education, Inc. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the publisher.
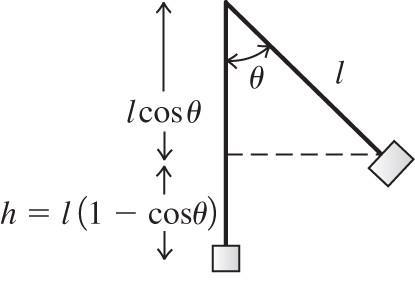
Then the conservation of momentum equation gives
Reflect: The original speed of the bullet is nearly three times the speed of sound in air. Kinetic energy is not conserved in the collision. Our analysis assumes that the block moves very little during the collision, while the bullet is coming to rest relative to the block. This is a good approximation since the velocity the block gets in the collision is much less than the initial velocity of the bullet.
*8.66. Set Up: Apply conservation of energy to the collision and to the motion after the collision. The height to which the steel ball must rise is h
8.67. Set Up: Eqs. (8.11), (8.12), and (8.13) give the outcome of the elastic collision. The blue puck is object A and the red puck is object B Let +x be the direction of the initial motion of
B,i = 0.
Solve:
gives
Reflect: We can verify that our results give K1 = K2 and P1x = P2x , as required in an elastic collision.
8.68. Set Up: For an elastic collision with object B initially at rest,
A is the alpha particle and B is the gold nucleus. υ =1 25 ×107 m/s
© Copyright 2016 Pearson Education, Inc. All rights reserved. This material is protected
© Copyright 2016 Pearson Education, Inc. All rights reserved. This material is protected
Reflect: In an elastic collision of a light object with a stationary heavy object, the light object bounces back with its speed only slightly reduced.
8.69. Set Up: Take + y to be upward. Let A be the lower piece and B be the upper piece, so mA = mB /4. (a) Apply conservation of momentum to the explosion. (b) After the explosion the upper piece is in free fall with ay = g At its maximum height υy = 0.
*8.70. Set Up: Apply conservation of momentum Take +x to be to the right. For (a) the collision is elastic. Let A be the cart that is initially moving to the right. For (b) the two carts stick together and the combined object has final speed υf
Reflect: Collision (b) is totally inelastic. All the initial kinetic energy is converted to other forms. Any collision in which the objects stick together must be inelastic.
8.71. Set Up: Call the fragments A and B, with mA = 2 0 kg and mB = 5 0 kg After the explosion fragment A moves in the +x direction with speed υA and fragment B moves in the x direction with speed υB
Solve: Pi, x = Pf, x gives 0 = m
Reflect: In an explosion the lighter fragment receives the most of the liberated energy
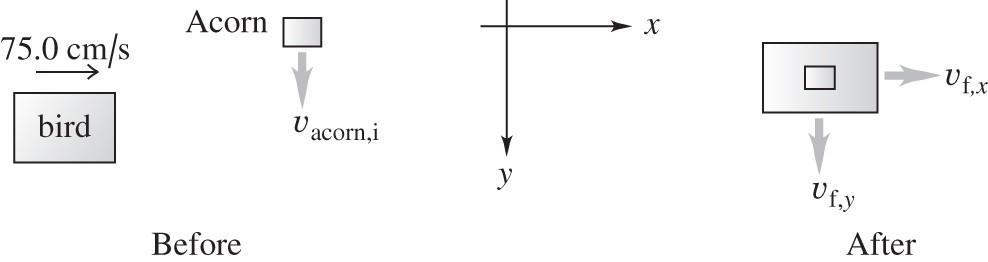
8.72. Set Up: Use constant acceleration equations for the free fall to find the speed of the acorn just before it collides with the bird. The system of the bird and acorn is sketched in the figure below, before and after the collision. Use the coordinates shown. Assume that gravity can be neglected during the collision.
Copyright 2016 Pearson
© Copyright 2016 Pearson Education, Inc. All rights reserved. This material is protected
All