Algebra and trigonometry 10th edition sullivan solutions manual by jannet.hudson213

Algebra and Trigonometry 10th Edition Sullivan Solutions Manual Visit to Download in Full: https://testbankdeal.com/download/algebra-and-trigonometr y-10th-edition-sullivan-solutions-manual/

Chapter 2 Graphs

Section 2.1

1. 0

2. () 5388 −−==

3. 22 34255 +==

4. 222 11601213600372161 +=+==

Since the sum of the squares of two of the sides of the triangle equals the square of the third side, the triangle is a right triangle.

5. 1 2 bh

6. true

7. x-coordinate or abscissa; y-coordinate or ordinate

8. quadrants

9. midpoint

10. False; the distance between two points is never negative.

11. False; points that lie in Quadrant IV will have a positive x-coordinate and a negative y-coordinate. The point () 1,4 lies in Quadrant II.

12. True; 1212 , 22 x xyy M ++  = 

13. b

14. a

15. (a) Quadrant II

(b) x-axis

(d) Quadrant I

(e) y-axis

(f) Quadrant IV

16. (a) Quadrant I

(b) Quadrant III

(d) Quadrant I

(e) y-axis

(f) x-axis

17. The points will be on a vertical line that is two units to the right of the y-axis.



Algebra and Trigonometry 10th Edition Sullivan Solutions Manual Visit TestBankDeal.com to get complete for all chapters

Chapter2: Graphs

18. The points will be on a horizontal line that is three units above the x-axis.

19. 22 12 22

dPP =−+− =+=+=

(,)(20)(10) 21415

20. 22 12 22

dPP =−−+− =−+=+=

(,)(20)(10) (2)1415

dPP

12 22

(,)2(1)(21) 319110

() () ()

(,)(53)44 2846468217 dPP =−+−−

dPP =−−+−−

(,)6(4)2(3) 10510025 12555 =+=+ ==

28. ()() 22 12 22

=−+−

dPPab abab

=−+−=+

()()

(,)(0)(0)

()() 22 dPPaa aa

aaaa

31. (2,5),(1,3),(1,0)ABC =−==−

(2)(3)4913

dPP =−−+− =+−=+= 26. ()() 22 12 22

(,)6(3)(02) 9(2)81485

12 22

dPP =−+−− =+=+= 27. () 2 2 12 22

131326 131326 2626 dABdBCdAC += += += =

dPP =−+−−

(,)(64)4(3) 2744953

=+=+=

148

=−+=+= 22.

2 2

=+=+= 23.

2 2

21. 22 12 22 2 2

(,)(21)(21) (3)19110 =+=+==

dPP =−−+− 2 2

() 2 2

=−−+−

24. () ()() ()

(,)2140 34916255

dPP =−−+− =+=+== 25. () 2

(,)422(3) 2542529

29. 22 12 2222

(,)(0)(0)

30. 22 12 22 222 =−+− =+==

=−+−

() () () 2 2 22 2 2 22 2 2 22 (,)1(2)(35) 3(2)9413 (,)11(03)

(,)1(2)(05) 1(5)12526 dAB dBC dAC =−−+− =+−=+= =−−+− =−+−=+= =−−−+− =+−=+=

[][][]

Verifying that ∆ ABC is a right triangle by the Pythagorean Theorem:

()()()

222 222 (,)(,)(,)

The area of a triangle is 1 2 A bh =⋅ . In this problem,

Verifying that ∆ ABC is a right triangle by the Pythagorean Theorem:

Verifying that

ABC is a right triangle by the Pythagorean Theorem:

Distance and Midpoint Formulas 149 Copyright © 2016 Pearson Education, Inc. [][] 1 (,)(,) 2 11131313 22 13 square units 2 A dABdBC=⋅ ⋅ =⋅=⋅ ⋅ = 32. (2,5),(12,3),(10,11)ABC =−==− () () () 2 2 22 2 2 22 2 2 22 (,)12(2)(35) 14(2) 1964200 102 (,)1012(113) (2)(14) 4196200 102 (,)10(2)(115) 12(16) 144256400 20 dAB dBC dAC =−−+− =+− =+= = =−+−− =−+− =+= = =−−+−− =+− =+= =

Section2.1: The

[][][] ()()() 222 22

(,)(,)(,) 10210220 200200400 400400 dABdBCdAC += += += = The area of a triangle is

2 A bh = . In

problem, [][] 1 (,)(,) 2 1 102102 2 1 1002100 square units 2 AdABdBC =⋅⋅ =⋅⋅ =⋅⋅=

(5,3),(6,0),(5,5)

=−== () () () 2 2 22 2 2 22 2 2 22 (,)6(5)(03) 11(3)1219 130 (,)56(50) (1)5125 26 (,)5(5)(53) 1021004 104 226 dAB dBC dAC =−−+− =+−=+ = =−+− =−+=+ = =−−+− =+=+ = =

∆

this

33.

ABC

[][][] ()()() 222 222 (,)(,)(,) 10426130 10426130 130130 dACdBCdAB

+= += = The area of a triangle is

A bh

1 2

= . In this

Verifying that ∆ ABC is a right triangle by the Pythagorean Theorem:

Chapter2: Graphs 150 Copyright © 2016 Pearson Education, Inc. problem, [][] 1 (,)(,) 2 1 10426 2 1 22626 2 1 226 2 26 square units A dACdBC=⋅⋅ =⋅⋅ =⋅⋅ =⋅⋅ = 34. (6,3),(3,5),(1,5)ABC =−=−=− () () () 2 2 22 2 2 22 2 2 22 (,)3(6)(53) 9(8)8164 145 (,)13(5(5)) (4)1016100 116229 (,)1(6)(53) 52254 29 dAB dBC dAC =−−+−− =+−=+ = =−−+−− =−+=+ == =−−−+− =+=+ =

[][][] ()()()

29229145 29429145 29116145 145145

+= +⋅= += =

222 222 (,)(,)(,)

dACdBCdAB +=

triangle

problem, [][] 1 (,)(,) 2 1 29229 2 1 229 2 29 square units A dACdBC=⋅⋅ =⋅⋅ =⋅⋅ =

() ()() () 2 2 22 22 22 2 2 22 (,)(04)3(3) (4)0160 16 4 (,)402(3) 451625 41 (,)(44)2(3) 05025 25 5 dAB dBC dAC =−+−−− =−+=+ = = =−+−− =+=+ = =−+−− =+=+ = =

The area of a

is 1 2 A bh = . In this

35. (4,3),(0,3),(4,2)ABC =−=−=

[][][] () 222 2 22 (,)(,)(,) 4541 162541 4141 dABdACdBC

+= += =

The area of a triangle is 1 2 A bh = . In this

Verifying that ∆ ABC is a right triangle by the

Section2.1: The Distance and Midpoint Formulas

The area of a triangle is 1 2 A bh = . In this problem,

37. The coordinates of the midpoint are:

22 44 35 , 22 80 , 22

38. The coordinates of the midpoint are:

39. The coordinates of the midpoint are: (,),1212 22

40. The coordinates of the midpoint are:

, 22

Pearson Education, Inc. problem, [][] 1 (,)(,) 2 1 45 2 10 square units A dABdAC=⋅⋅ =⋅⋅ = 36. (4,3),(4,1),(2,1)ABC =−== () ()() () 2 2 22 22 22 2 2 22 (,)(44)1(3) 04 016 16 4 (,)2411 (2)040 4 2 (,)(24)1(3) (2)4416 20 25 dAB dBC dAC =−+−− =+ =+ = = =−+− =−+=+ = = =−+−− =−+=+ = =

2016

Pythagorean Theorem: [][][] () 222 2 22 (,)(,)(,) 4225 16420 2020 dABdBCdAC += += += =

[][] 1 (,)(,) 2 1 42 2 4 square units A dABdBC=⋅⋅ =⋅⋅ =

(4,0)

  +−+  =    =   =

(,),1212

x xyy xy ++  =

() (,),1212

2204

=   −++  =    =   =

, 22 04 , 22 0,2

xyy xy ++ 

3620

3 ,1 2 x

  −++  =  

=    =  

, 22

xyy xy ++  =



2432

x xyy xy

 =   +−+  =    =    =− 

(,),1212 22

Chapter2: Graphs

41. The coordinates of the midpoint are:

42. The coordinates of the midpoint are:

Thus the coordinates will have an y value of 11213−−=− and 11211−+= . So the points are () 3,11 and () 3,13

b. Consider points of the form () 3, y that are a distance of 13 units from the point () 2,1 .

43. The coordinates of the midpoint are:

44. The coordinates of the midpoint are:

Thus, the points () 3,11 and () 3,13 are a distance of 13 units from the point () 2,1

48. a. If we use a right triangle to solve the problem, we know the hypotenuse is 17 units in length. One of the legs of the triangle will be 2+6=8. Thus the other leg will be:

45. The x coordinate would be 235 += and the y coordinate would be 523 −= . Thus the new point would be

46. The new x coordinate would be 123−−=− and the new y coordinate would be 6410 += . Thus the new point would be () 3,10

47. a. If we use a right triangle to solve the problem, we know the hypotenuse is 13 units in length. One of the legs of the triangle will be 2+3=5. Thus the other leg will be:

Thus the coordinates will have an x value of 11514 −=− and 11516 += . So the points are () 14,6 and () 16,6

152

(,),1212

4631

(5,1) x

 =   +−+  =    =   =−

, 22 2 10 , 22

xyy xy ++

(,),1212

22 1 1, 2 x xyy xy ++  =   −+−+  =    =    =−− 

32 , 22

(,),1212 22 00

22 x xyy xy ab ab ++  =   ++  =    =  

(,),1212 22 00

22 , 22 x xyy xy aa aa ++  =   ++  =    =  

()

5,3

222 2 2 513 25169 144 12 b b b b += += = =

()() ()() ()() 22 2121 22 22 2 2 3(2)1 51 2512 226 dxxyy y y yy yy =−+− =−−+−− =+−− =+++ =++ () ()() 2 2 22 2 2 13226 13226 169226 02143 01113 yy yy yy yy yy =++ =++ =++ =+− =−+ 110 11 y y −= = or 130 13 y y += =−

222 2 2 817 64289 225 15 b b b b += += = =

b. Consider points of the form () ,6 x that are a distance of 17 units from the point () 1,2 .

Section2.1: The Distance and Midpoint Formulas

433 x =+ or 433 x =−

Thus, the points () 433,0 + and () 433,0 are on the x-axis and a distance of 6 units from the point () 4,3

50. Points on the y-axis have an x-coordinate of 0. Thus, we consider points of the form () 0, y that are a distance of 6 units from the point () 4,3 .

Thus, the points () 14,6 and () 16,6 are a distance of 13 units from the point () 1,2

49. Points on the x-axis have a y-coordinate of 0. Thus, we consider points of the form () ,0x that are a distance of 6 units from the point () 4,3

325 y =−+ or 325 y =−−

Thus, the points () 0,325 −+ and () 0,325 are on the y-axis and a distance of 6 units from the point () 4,3

51. a. To shift 3 units left and 4 units down, we subtract 3 from the x-coordinate and subtract 4 from the y-coordinate.

()() 23,541,1 −−=−

b. To shift left 2 units and up 8 units, we subtract 2 from the x-coordinate and add 8 to the y-coordinate.

()() 22,580,13 −+=

153

Inc.

()() ()() () () 22 2121 2 2 2 2 2 2 126 218 2164 265 dxxyy x xx xx xx =−+− =−+−− =−++ =−++ =−+ () ()() 2 2 22 2 2 17265 17265 289265 02224 01416 xx xx xx xx xx =−+ =−+ =−+ =−− =+− 140 14 x x += =− or 160 16 x x −= =

()() ()() () 22 2121 22 2 2 2 2 430 1683 1689 825 dxxyy x xx xx xx =−+− =−+−− =−++− =−++ =−+ () 2 2 22 2 2 2 6825 6825 36825 0811 (8)(8)4(1)(11) 2(1) 864448108 22 863 433 2 xx xx xx xx x =−+ =−+ =−+ =−− −−±−−− = ±+± == ± ==±

()() ()()

2121

y yy yy yy =−+− =−+−− =+++ =+++ =++ () 2 2 22 2 2 2 6625

2 yy yy yy yy y =++ =++ =++ =+− −±−− = −±+−± == −± ==−±

22 22 2 2 403 496 1696 625 dxxyy

6625 36625 0611 (6)(6)4(1)(11) 2(1) 63644680

645 325

Chapter2: Graphs

52. Let the coordinates of point B be () ,x y . Using the midpoint formula, we can write

154

()

  This

1 2 2 14 5 x x x −+ = −+= = 8 3 2 86 2 y y y + = += =− Point B has coordinates () 5,2 .

Mxy

==   . () 111,(3,6) Pxy==− and

xy =− , so 12 2 2 2 2 3 1 2 23 1 x x x x x x + = −+ −= −=−+ = and 12 2 2 2 2 6 4 2 86 2 yy y y y y + = + = =+ = Thus, 2 (1,2) P =



()

12 1 1 1 2 7 5 2 107 3 x x x x x x + = + = =+ = and 12 1 1 1 2 (2) 4 2 8(2) 6 yy y y y y + = +− −= −=+− −= Thus, 1 (3,6) P =− 55. The midpoint of AB is: () 0600 , 22 3,0 D ++  =   = The midpoint of AC is: () 0404 , 22 2,2 E ++  =   = The midpoint of BC is: () 6404 , 22 5,2 F ++  =   = () 2 2 22 (,)04(34) (4)(1)16117 dCD =−+− =−+−=+= () 2 2 22 (,)26(20) (4)2164 2025 dBE =−+− =−+=+ == 22 22 (,)(20)(50) 25425 29 dAF =−+− =+=+ = 56. Let 12(0,0),(0,4),(,) PPPxy === () () () 22 12 22 1 22 22 22 2 22 22 ,(00)(40) 164 ,(0)(0) 4 16 ,(0)(4) (4)4 (4)16 dPP dPPxy xy xy dPPxy xy xy =−+− == =−+− =+= →+= =−+− =+−= →+−= Therefore, () 2 2 22 4 816 816 2 yy yyy y y =− =−+ = = which gives 22 2 216 12 23 x x x += = =± Two triangles are possible. The third vertex is ()() 23,2 or 23,2 .

Let () 1 0,0 P = , () 2 0, Ps = , () 3 ,0 Ps = , and () 4 , Pss = .

18 2,3, 22 x y −++  =

leads to two equations we can solve.

53. () 1212 ,,22 x xyy

++ 

(,)(1,4)

54. () 1212 ,,22 x xyy Mxy ++  == 

222,(7,2)Pxy==− and (,)(5,4) xy =− , so

57.

The points 1P and 4P are endpoints of one diagonal and the points 2P and 3P are the endpoints of the other diagonal.

1,4 00 ,, 2222 s sss M ++  == 

2,3 00 ,, 2222 s sss M ++  == 

The midpoints of the diagonals are the same. Therefore, the diagonals of a square intersect at their midpoints.

58. Let () 1 0,0 P = , () 2 ,0Pa = , and

. To show that these vertices form an equilateral triangle, we need to show that the distance between any pair of points is the same constant value.

Since all three distances have the same constant value, the triangle is an equilateral triangle. Now find the midpoints:

Since the sides are the same length, the triangle is equilateral.

155 Copyright

Pearson Education, Inc. y x (0, )s (0, 0) (, 0) s (, )ss

Section2.1: The Distance and Midpoint Formulas

3 3

22 aa P  =   

()()() ()() 22 122121 22 2 , 000 dPPxxyy aaa =−+− =−+−== ()()() 22 232121 2 2 222 2 , 3 0 22 34 444 dPPxxyy aa a aaa aa =−+−   =−+−     =+=== ()()() 22 132121 2 2 222 2 , 3 00 22 34 444 dPPxxyy aa aaa aa =−+−   =−+−     =+===

12 23 13 4 5 6 000 ,,0 222 3 33 0 , 22 , 44 22 3 00 3 22 ,, 2244 PP PP PP aa PM aa aa a PM aa aa PM ++  ===     ++  ===        ++    ===       () 2 2 45 2 2 22 33 ,0 424 3 44 3 16162 aaa dPP aa a aa   =−+−       =+      =+= () 2 2 46 2 2 22 3 ,0 424 3 44 3 16162 aaa dPP aa a aa   =−+−       =−+      =+= () 2 2 56 2 2 2 333 , 4444 0 2 42 aaaa dPP a a a   =−+−      =+   ==

Chapter2: Graphs

(,)(42)(11) dPP =−−−+−− =+− = = 22 13 22

dPP =−−+−− =−+− =+ = =

(,)4(4)(31) (,)(42)(31) (6)(4) 3616 52 213

triangle

triangle.

7(2) 494 53 dPP =−−+− =+− =+ = () 2 2 23 22 (,)46(52) (2)(7) 449 53 dPP =−+−− =−+− =+ = () 2 2 13 22 (,)4(1)(54) 5(9) 2581 106 dPP =−−+−− =+− =+ =

Since ()() 1223 ,, dPPdPP = , the triangle is isosceles.

Therefore, the triangle is an isosceles right triangle.

=−−+−− =+=+= = () 2 2 23 22 (,)30(27) 3(5)925 34 dPP =−+− =+−=+ = ()()

217

(,)3(2)2(1)

Since 2313 (,)(,) dPPdPP = , the triangle is isosceles.

Since [][][] 22 2 132312 (,)(,)(,) dPPdPPdPP += , the triangle is also a right triangle. Therefore, the triangle is an isosceles right triangle.

dPP dPP =−−+− =+=+ = = ()() 22 13 22

(,)4762 (3)4916 25 5

(6)0 36 6 dPP =−−+− =−+ = = () 2 2 23 22

59. 22 12 22 0(4) 16 4

Since [][][] 22 2 122313 (,)(,)(,) dPPdPPdPP += , the

is a right

60. () 2 2 12

(,)6(1)(24)

Since [][][] 22 2 122313 (,)(,)(,) dPPdPPdPP += , the triangle is a right triangle.

61. ()() 22 12 22 53259 34

(,)0(2)7(1) 2846468 dPP =−−+−− =+=+ =

dPP

22 13

1214125 55

62. ()() 22 12 22 =−−+− =−+− =+= = () 2 2 23 22

(,)4702 (11)(2) (,)4(4)(60) 866436 100 10

dPP =−+− =−+=+ = =

Since [][][] 22 2 132312 (,)(,)(,) dPPdPPdPP += , the triangle is a right triangle.

63. Using the Pythagorean Theorem: 222

9090 81008100 16200

16200902127.28 feet

Section2.1: The Distance and Midpoint Formulas

66. a. First: (60, 0), Second: (60, 60) Third: (0, 60)

64. Using the Pythagorean Theorem: 222

6060 360036007200

720060284.85 feet

b. Using the distance formula: 22

(18060)(2060)

120(40)16000

4010126.49 feet

c. Using the distance formula: 22

(2200)(22060)

22016074000

20185272.03 feet

65. a. First: (90, 0), Second: (90, 90), Third: (0, 90)

(31090)(1590)

b. Using the distance formula: 22 22

220(75)54025

52161232.43 feet

c. Using the distance formula: 22 22

(3000)(30090)

300210134100

30149366.20 feet

miles dtt

(30)(40) 9001600 =+ =+ = = d 40t

2500

157

Pearson Education, Inc.

2016

d d d d += += = ==≈ 90 90 90 90 d

d dd d += +=→= ==≈ 60 60 60 60 d

(0,0) (0,90) (90,0) (90,90) X Y

d =−+− =+−= =≈

d =−+− =+= =≈

(0,0) (0,60) (60,0) (60,60) x y

d =−+− =+−= =≈

d =−+− =+= =≈

67. The Focus heading east moves a distance 30t after t hours. The truck heading south moves a distance 40t after t hours. Their distance apart after t hours is: 22 22 2 tt t t

30t

68. 15 miles5280 ft1 hr 22 ft/sec 1 hr1 mile3600 sec

⋅⋅= () 2 2 2 10022 10000484 feet dt t =+

69. a. The shortest side is between 1 (2.6,1.5) P = and 2 (2.7,1.7) P = . The estimate for the desired intersection point is:

pair () 2013,23624 . The midpoint is

(2.651.4)(1.61.3)

(1.25)(0.3) 1.56250.09 1.6525

1212 ,,22 20072013345466 , 22 4020811 , 22 2010,405.5 xxyy

71. For 2003 we have the ordered pair

() 2003,18660 and for 2013 we have the ordered

() ()

200320131866023624 year, $,22

++ = = =

401642284 , 22 2008,21142

Using the midpoint, we estimate the poverty level in 2008 to be $21,142. This is lower than the actual value.

72. Answers will vary.

250

25 5 2 x x x −= = =

5 |

or (4)0

7116(1) 7116 1311 iiii i i i +−=−+−

515212187 7151225 510 2 xxx xxx xx x x −+≥−− −+≥−−

Chapter2: Graphs 158

100 22t d

() 1212

2222

2.65,1.6 xxyy++++  =      =   =

2.62.71.51.7 ,,

5.33.2 , 22

1.285

b. Using the distance formula: 22 22 d =−+− =+ =+ = ≈

units

() ()

xy ++ = ++ = = =

70. Let 1 (2007,345) P = and 2 (2013,466) P = . The midpoint is:

The estimate for 2010 is $405.5 billion. The estimate net sales of Wal-Mart Stores, Inc. in 2010 is $0.5 billion off from the reported value of $405 billion.

73. To find the domain, we know the denominator cannot be zero.

{}

≠

So the domain is all real numbers not equal to 5 2 or

(35)0

xx xx −−= +−= +=−= =−=

74. 2 37200 (35)(4)0

or 4

xx xx

So the solution set is: 5 ,4 3

=−−− =−+ =−

75.

(73)(12i)71436

−≥− −≥− ≤

76. 5(3)26(23)7

Section2.2: Graphs of Equations in Two Variables; Intercepts; Symmetry

Section 2.2

+−=−

x x x x +=− +=− =−

The solution set is {} 6

22 309 99 =+ = 22 039 018 =+ ≠ 22 0(3)9 018 =−+ ≠

2. 2 2 90 9 93

x x x

−= =

=±=±

3. intercepts

4. 0 y =

5. y-axis

6. 4

7. () 3,4

8. True

9. False; the y-coordinate of a point at which the graph crosses or touches the x-axis is always 0. The x-coordinate of such a point is an x-intercept.

2 yx=+

(0, 1) and (–1,

d 12.

(0,

(1, –1)

159

1. () () 2317 236 33 6

The solution set is {} 3,3 .

4 y xx=− 4 000 00 =− = 4 111 10 =− ≠ 4 4(2)2 4162 =− ≠− The point (0, 0) is on the graph of the equation. 14. 3 2 y xx=− 3 0020 00 =− = 3 1121 11 =− ≠− 3 1121 11 −=− −=−

10. False; a graph can be symmetric with respect to both coordinate axes (in such cases it will also be symmetric with respect to the origin). For example: 22 1 xy+= 11.

13.

points

The

and

are on the graph of the equation.

point (0, 3) is on the graph of

equation.

3 1 y x =+ 3 211 82 =+ ≠ 3 101 11 =+ = 3 011 00 =−+ =

15. 22 9 yx=+

The

the

16.

points

0) are

equation.

22 4 xy+= 22 024 44 += = 22 (2)24 84 −+= ≠ ()() 22 224 44 += = () (0,2) and 2,2 are on the

equation.

2244xy+= 22 0414 44 +⋅= = 22 2404 44 +⋅= = () 2 2 1 2 244 54 += ≠

points (0, 1) and (2, 0) are

equation.

The

on the graph of the

17.

graph of the

18.

The

on the graph of the

x-intercept: y-intercept: 02 2 x x =+ −= 02 2 y y =+ = The intercepts are () 2,0 and () 0,2

19.

intercept:

-intercept: 06 6 x x =− = 06 6 y y =− =−

20. 6 yx=−

The intercepts are () 6,0 and () 0,6

23. 2 1 yx=−

x-intercepts: y-intercept: 2 2

x x x

21. 28yx=+

x-intercept: y-intercept: 028 28 4

x x x

=+ =− =−

() 208 8 y y

=+ =

The intercepts are () 4,0 and () 0,8

22. 39yx=−

x-intercept: y-intercept: 039 39 3

x x x

=− = =

() 309 9 y y

=− =−

The intercepts are () 3,0 and () 0,9

=− = =±

01 1 1

01 1 y y

=− =−

The intercepts are () 1,0 , () 1,0 , and () 0,1

24. 2 9 yx=−

x-intercepts: y-intercept: 2

y y

=− =−

The intercepts are () 3,0 , () 3,0 , and () 0,9

25. 2 4 yx=−+

x-intercepts: y-intercepts:

() 2 04

Chapter2: Graphs 160

2 09 9 3 x x x =− = =± 2 09 9

4 2 x x x =−+ = =±

y =−+ =

Section2.2: Graphs of Equations in Two Variables; Intercepts; Symmetry

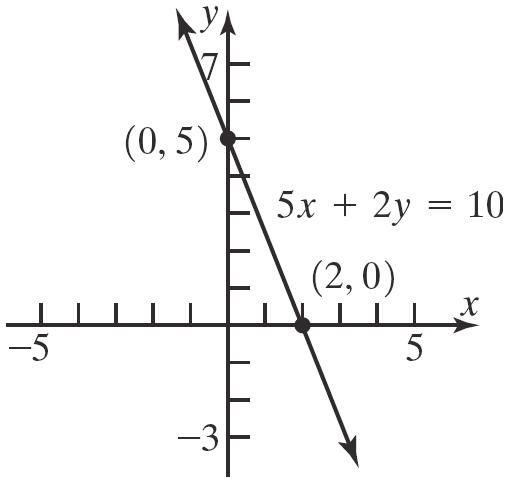
The intercepts are () 2,0 , () 2,0 , and () 0,4

28. 5210 xy+=

x-intercepts: y-intercept:

26. 2 1 yx=−+ x-intercepts: y-intercept:

29. 2 9436 xy+= x-

27. 236 xy+= x-intercepts: y-intercept:

The intercepts are () 3,0 and () 0,2 .

30. 2 44 xy+= x-

161

Education, Inc.

2 2 01 1 1 x x x =−+ = =± () 2 01 1 y y =−+ =

intercepts

The

are () 1,0 , () 1,0 , and () 0,1

()

x x

2306

3 x

+= = = () 2036 36 2 y y y += =

()

510 2

x x

210 5

52010

+= =

() 50210

y y

+= =

The intercepts are () 2,0 and () 0,5

() 2 2 2 94036 936 4 2 x x x x += = = =± () 2 90436 436 9 y y y += = =

intercepts: y-intercept:

The intercepts are () 2,0 , () 2,0 , and () 0,9 .

2 2 2 404 44 1 1 x x x x += = = =± () 2 404 4 y y += =

intercepts: y-intercept:

34. 35. 5 5 y 5 5 (a) = (5, 2) (b) = (5, 2) (c) = (5, 2) (5,−2) 36.

Chapter2: Graphs

31. 32. 33.

37. 38.

41. a. Intercepts: () 1,0 and () 1,0

b. Symmetric with respect to the x-axis, y-axis, and the origin.

42. a. Intercepts: () 0,1

b. Not symmetric to the x-axis, the y-axis, nor the origin

43. a. Intercepts: () 2 0 , π , () 0,1 , and () 2 ,0 π

b. Symmetric with respect to the y-axis.

44. a. Intercepts: () 2,0 , () 0,3 , and () 2,0

b. Symmetric with respect to the y-axis.

45. a. Intercepts: () 0,0

b. Symmetric with respect to the x-axis.

46. a. Intercepts: ()2,0, ()0,2, ()0,2, and () 2,0

b. Symmetric with respect to the x-axis, y-axis, and the origin.

47. a. Intercepts: () 2,0 , () 0,0 , and () 2,0

b. Symmetric with respect to the origin.

48. a. Intercepts: () 4,0 , () 0,0 , and () 4,0

b. Symmetric with respect to the origin.

49. a. x-intercept: [] 2,1 , y-intercept 0

b. Not symmetric to x-axis, y-axis, or origin.

50. a. x-intercept: [] 1,2 , y-intercept 0

b. Not symmetric to x-axis, y-axis, or origin.

51. a. Intercepts: none

b. Symmetric with respect to the origin.

52. a. Intercepts: none

b. Symmetric with respect to the x-axis.

Section2.2: Graphs of Equations in Two Variables; Intercepts; Symmetry

39. 40.

53. 54. 55. 56.

Chapter2: Graphs

57. 2 4 yx=+

x-intercepts: y-intercepts:

2 04 4 x x =+ −=

y y y

Test y-axis symmetry: Let x x =−

33 different yxx =−=−

=+ = =±

2 2 04 4 2

The intercepts are () 4,0 , () 0,2 and () 0,2 .

Test x-axis symmetry: Let yy =−

() 2 2 4 4 same yx yx −=+ =+

Test y-axis symmetry: Let x x =−

2 4 yx=−+ different

Test origin symmetry: Let x x =− and yy =−

() 2 2 4 4 different yx yx −=−+ =−+

Therefore, the graph will have x-axis symmetry.

58. 2 9 yx=+

x-intercepts: y-intercepts:

Test origin symmetry: Let x x =− and yy =−

−=−=− =

3 same y xx yx

Therefore, the graph will have origin symmetry.

60. 5 y x =

x-intercepts: y-intercepts:

3 0

= =

0 x x

5 00 y ==

The only intercept is () 0,0

Test x-axis symmetry: Let yy =−

5 different yx−=

Test y-axis symmetry: Let x x =−

55 different yxx =−=−

Test origin symmetry: Let x x =− and yy =−

x x x

=−+ =−+ =

2 (0)9 09 9

y y y

=+ = =±

2 2 09 9 3

The intercepts are () 9,0 , () 0,3 and () 0,3 .

Test x-axis symmetry: Let yy =−

() 2 2 9 9 same yx yx −=+ =+

Test y-axis symmetry: Let x x =−

2 9 yx=−+ different

Test origin symmetry: Let x x =− and yy =−

() 2 2 9 9 different yx yx −=−+ =−+

Therefore, the graph will have x-axis symmetry.

59. 3 y x =

x-intercepts: y-intercepts:

3 0 0 x x

= =

3 00 y ==

The only intercept is () 0,0 .

Test x-axis symmetry: Let yy =−

3 different yx−=

−=−=− =

55 5 same y xx yx

Therefore, the graph will have origin symmetry.

61. 2 90 xy+−=

x-intercepts: y-intercepts:

x x x

−= = =±

2 90 9

2 090 9 y y +−= =

The intercepts are () 3,0 , () 3,0 , and () 0,9

Test x-axis symmetry: Let yy =−

2 90 different xy−−=

Test y-axis symmetry: Let x x =−

() 2

−+−= +−=

90 90 same xy xy

Test origin symmetry: Let x x =− and yy =−

() 2

−−−= −−=

2 90 90 different xy xy

Therefore, the graph will have y-axis symmetry.

164

Section2.2: Graphs of Equations in Two Variables; Intercepts; Symmetry

62. 2 40 xy−−=

x-intercepts: y-intercept:

64. 22 44 xy+=

The intercepts are () 2,0 , () 2,0 , and () 0,4

Test x-axis symmetry: Let yy =−

() 2 2 40 40 different xy xy

−−−= +−=

Test y-axis symmetry: Let x x =−

() 2 2 40 40 same xy xy

−−−= −−=

Test origin symmetry: Let x x =− and yy =−

()() 2 2 40 40 different xy xy

−−−−= +−=

Therefore, the graph will have y-axis symmetry.

63. 22 9436 xy+= x-intercepts: y-intercepts:

x x x x

+= = = =±

Test x-axis symmetry: Let yy =−

() 2 2 22 9436 9436 same xy xy +−= +=

Test y-axis symmetry: Let x x =−

() 2 2 22 9436 9436 same xy xy −+= +=

Test origin symmetry: Let x x =− and yy =−

()() 22 22 9436 9436 same xy xy −+−= +=

Therefore, the graph will have x-axis, y-axis, and origin symmetry.

404

2 4 2

y y y += = =±

() 2 2 22

+−= +=

44 44 same xy xy

Test y-axis symmetry: Let x x =−

() 2 2 22

−+= +=

44 44 same xy xy

Test origin symmetry: Let x x =− and yy =−

()()22 22

−+−= +=

44 44 same xy xy

Therefore, the graph will have x-axis, y-axis, and origin symmetry.

65. 3 27 yx=−

3 3

27 3 x x x

=−

3 27 different yx −=−

Test y-axis symmetry: Let x x =−

()3 3

=−− =−−

27 different yx yx

Test origin symmetry: Let x x =− and yy =−

()3

−=−− =+

27 27 different yx yx

Therefore, the graph has none of the indicated symmetries.

165

Pearson Education, Inc.

2016

2 2

4 2 x x x −−= = =± 2

4 4

y y

−= =−

040

−−=

() 2 2 2 2 94036 936 4 2 x x x x += = = =± () 2 2 2 2 90436 436 9 3 y y y y += = = =±

2,0,

0,3, and

The intercepts are () 2,0 , ()

()

() 0,3 .

x-intercepts: y-intercepts: 22

2 () 2 2 2

404 44 1 1

The intercepts are () 1,0 , () 1,0 , () 0,2 , and () 0,2 .

Test x-axis symmetry: Let yy =−

= = 3

=−

x-intercepts: y-intercepts:

027

=−

The intercepts are () 3,0 and () 0,27

Test x-axis symmetry: Let yy =−

Chapter2: Graphs

66. 4 1 yx=−

x-intercepts: y-intercepts:

x x x

Test x-axis symmetry: Let yy =−

2 4 different yx −=+

4 4

=− = =±

01 1 1

4 01 1 y y

=− =−

The intercepts are () 1,0 , () 1,0 , and () 0,1

Test x-axis symmetry: Let yy =−

4 1 different yx −=−

Test y-axis symmetry: Let x x =− () 4 4

Test y-axis symmetry: Let x x =−

() 2

=−+ =+

4 4 same yx yx

Test origin symmetry: Let x x =− and yy =−

() 2 2

−=−+ −=+

4 4 different yx yx

Therefore, the graph will have y-axis symmetry.

=−− =−

1 1 same yx yx

69. 2 3 9 x y x = +

x-intercepts: y-intercepts:

−=−− −=−

Test origin symmetry: Let x x =− and yy =− () 4 4

1 1 different yx yx

Therefore, the graph will have y-axis symmetry.

67. 2 34yxx=−−

=−−

xx xx x x

()() 2 =−

=−+ ==− () 2 0304 4 y y =−−

Test x-axis symmetry: Let yy =−

2 34 different yxx −=−−

Test y-axis symmetry: Let x x =− ()() 2

2 3 0 9 30 0

= + = =

x x x x

() 2 30 0 0 9 09 y === +

The only intercept is () 0,0 .

Test x-axis symmetry: Let yy =−

2 3 different 9 x y x −= +

Test y-axis symmetry: Let x x =− () () 2

2 3 9 3 different 9 x y x x y x = −+ =− +

=−−−− =+−

34 34 different yxx yxx

Test origin symmetry: Let x x =− and yy =− ()() 2

−=−−−− −=+−

() () 2

34 34 different yxx yxx

Therefore, the graph has none of the indicated symmetries.

68. 2 4 yx=+

x x

=−

x-intercepts: y-intercepts: 2 2 04 4 no real solution

The only intercept is () 0,4

166

Inc.

x-intercepts: y-intercepts:

034 041 4 or 1

The intercepts are () 4,0 , () 1,0 , and () 0,4

2 04 4 y y =+ =

2 2

Test origin symmetry: Let x x =− and yy =−

3 9

same 9 x y x x y x x y x −= −+ −=− + = +

Therefore, the graph has origin symmetry.

Section2.2: Graphs of Equations in Two Variables; Intercepts; Symmetry

Test y-axis symmetry: Let x x =−

Therefore, the graph has origin symmetry. 71.

−= −= =

The only intercept is () 0,0

x y x x y x x y x

9 9 same 9

Therefore, the graph has origin symmetry.

72. 4 5 1 2 x y x + =

x-intercepts: y-intercepts: 4 5 4

x x x

1 0 2 1

+ = =−

no real solution

y + ==

() 4 5 011 0 20 undefined

There are no intercepts for the graph of this equation.

Test x-axis symmetry: Let yy =−

4 5 1 different 2 x y x + −=

Test y-axis symmetry: Let x x =−

x y x x y x

−+ = + =

1 2 1 different 2

() () 4 5 4 5

Test origin symmetry: Let x x =− and yy =− ()

Therefore, the graph has origin symmetry.

Pearson Education, Inc.

2 x y x =

2 2 2 4 0 2 40 4 2 x x x x x = −= = =± () 2

200 undefined y ==

2 x y x −=

() () 2 2

2 x y x x y x = =−

symmetry:

() () 2 2 2 4 2 4 2 4 same 2 x y x x y x x y x −= −= =

167 Copyright

2016

70. 2 4

x-intercepts: y-intercepts:

044

The intercepts are () 2,0 and () 2,0 Test x-axis symmetry: Let yy =− 2 4 different

Test

axis symmetry: Let x x =−

4 different

Test origin

Let x x =− and yy =−

3 2 9

y x = x-intercepts:

3 2 3 0 9 0 0 x x x x = −= = 3 2 00 0 9 09 y ===

y-intercepts:

Test x-axis symmetry:

yy =− 3 2 3 2 9 different 9 x y x x y x −= =

Let

() ()

3 2 3 2 9 different 9 x y x x y x = =

() ()

Test origin symmetry: Let x x =− and yy =−

3 2

4 5 4 5 4 5 1 2 1 2 1 same 2

x y x x y x

−=

()

x y x

−+

77. If the point () ,4 a is on the graph of 2 3 y xx=+ , then we have

78. If the point () ,5 a is on the graph of 2 6 y xx=+ , then we have

79. For a graph with origin symmetry, if the point () , ab is on the graph, then so is the point () , ab . Since the point () 1,2 is on the graph of an equation with origin symmetry, the point () 1,2 must also be on the graph.

80. For a graph with y-axis symmetry, if the point () , ab is on the graph, then so is the point () , ab . Since 6 is an x-intercept in this case, the point () 6,0 is on the graph of the equation. Due to the y-axis symmetry, the point () 6,0 must also be on the graph. Therefore, 6 is another xintercept.

81. For a graph with origin symmetry, if the point () , ab is on the graph, then so is the point () , ab . Since 4 is an x-intercept in this case, the point () 4,0 is on the graph of the equation. Due to the origin symmetry, the point () 4,0 must also be on the graph. Therefore, 4 is another x-intercept.

82. For a graph with x-axis symmetry, if the point () , ab is on the graph, then so is the point () , ab . Since 2 is a y-intercept in this case, the

Chapter2:

()()

2 2 43 034 041 aa aa aa =+ =+− =+− 40 4 a a += =− or 10 1 a a −= = Thus, 4 a =− or 1 a = .

()()

=++

2 2 56 065 051 aa aa aa −=+ =++

50 5 a a += =− or 10 1 a a += =− Thus, 5 a =− or 1 a =−

Section2.2: Graphs of Equations in Two Variables; Intercepts; Symmetry

point () 0,2 is on the graph of the equation. Due to the x-axis symmetry, the point () 0,2 must also be on the graph. Therefore, 2 is another yintercept.

83. a. () 2 2222 x yxxy+−=+

x-intercepts:

Test origin symmetry: Let x x =− and yy =−

2 2222

−+−−−=−+− ++=+

xyxxy xyxxy

2 2222 different

Thus, the graph will have x-axis symmetry.

84. a. 2 16120225 yx=−

x-intercepts: () 2 2 2

The intercepts are ()0,0, ()2,0, ()0,1, and () 0,1

b. Test x-axis symmetry: Let yy =−

xyxxy xyxxy

2222 2 2222 same

+−−=+− +−=+

Test y-axis symmetry: Let x x =−

−+−−=−+ ++=+

xyxxy xyxxy

2 2222 different

85. a.

y y y

=− =− =−

161200225 16225 225 16 no real solution

y-intercepts: () 2 160120225 0120225 120225 22515 1208

x x x x

=− =− −=− ==

The only intercept is 15 ,0 8 

b. Test x-axis symmetry: Let yy =−

() 2 2

−=− =−

16120225 16120225 same yx yx

Test y-axis symmetry: Let x x =−

() 2 2

=−− =−−

16120225 16120225 different yx yx

Test origin symmetry: Let x x =− and yy =−

()() 2 2

−=−− =−−

16120225 16120225 different yx yx

Thus, the graph will have x-axis symmetry.

169

() ()() () () 2 2222 2 22 4322 43 3 00 2 20 20 xxx xxx xxxx xx xx +−=+ −= −+= −= −= 3 0or20 02 xx xx =−= ==

intercepts: () ()() () () 2 2222 2 22 42 42 22 000 0 10 yy yy yy yy yy +−=+ = = −= −= 22 2 0or10 0 1 1 yy y y y =−= == =±

() ()() ()

()() ()() ()

2 2222

()()()

()





b. Since 2 x x = for all x , the graphs of 2 and y xyx== are the same.

c. For () 2 yx = , the domain of the variable x is 0 x ≥ ; for yx = , the domain of the variable x is all real numbers. Thus, () 2 only for 0. xxx=≥

d. For 2 yx = , the range of the variable y is 0 y ≥ ; for yx = , the range of the variable y is all real numbers. Also, 2 x x = only if 0 x ≥ . Otherwise, 2 x x =−

86. Answers will vary. A complete graph presents enough of the graph to the viewer so they can “see” the rest of the graph as an obvious continuation of what is shown.

87. Answers will vary. One example: y x

88. Answers will vary

89. Answers will vary

90. Answers will vary.

Case 1: Graph has x-axis and y-axis symmetry, show origin symmetry.

(from -axis symmetry) xyxy x →−

()() , on graph, on graph

−→−−

()() () , on graph, on graph from -axis symmetry xyxy y

Since the point () , x y is also on the graph, the graph has origin symmetry.

Case 2: Graph has x-axis and origin symmetry, show y-axis symmetry.

→−

()() () , on graph, on graph from -axis symmetry xyxy x

()() () , on graph, on graph from origin symmetry xyxy −→−

Since the point () , x y is also on the graph, the graph has y-axis symmetry.

Case 3: Graph has y-axis and origin symmetry, show x-axis symmetry.

→−

()() () , on graph, on graph from -axis symmetry xyxy y

()() () , on graph, on graph from origin symmetry xyxy −→−

Since the point () , x y is also on the graph, the graph has x-axis symmetry.

91. Answers may vary. The graph must contain the points () 2,5 , () 1,3 , and () 0,2 . For the graph to be symmetric about the y-axis, the graph must also contain the points () 2,5 and () 1,3 (note that (0, 2) is on the y-axis).

For the graph to also be symmetric with respect to the x-axis, the graph must also contain the points () 2,5 , () 1,3 , () 0,2 , () 2,5 , and

() 1,3 . Recall that a graph with two of the symmetries (x-axis, y-axis, origin) will necessarily have the third. Therefore, if the original graph with y-axis symmetry also has x-

Chapter2: Graphs 170

axis symmetry, then it will also have origin symmetry.

92. 6(2)41 6(2)82 +− ==

Section2.3: Lines

6. 12mm = ; y-intercepts; 12 1 mm⋅=−

7. 2

8. 1 2

33075 3(1025) 3(5)(5)3(5) −+= −+= −−=−

xx xx

94. 196(1)(196)14i

xx xx xx x x x −+= −=− −+=−+ −= −=± =± =±

2. 3; 2 x-intercept: 23(0)6 26 3

9. False; perpendicular lines have slopes that are opposite-reciprocals of each other.

10. d

11. c

12. b

13. a. 101 Slope 202 ==

b. If x increases by 2 units, y will increase by 1 unit.

14. a. 101 Slope 202 ==−

b. If x increases by 2 units, y will decrease by 1 unit.

15. a. 121 Slope 1(2)3 ==−

+= = = y-intercept: 2(0)36 36 2

3. True

x x x

b. If x increases by 3 units, y will decrease by 1 unit.

+= = =

y y y

16. a. 211 Slope 2(1)3 ==

b. If x increases by 3 units, y will increase by 1 unit.

17. 21 21

033 Slope 422 yy xx ===−

yx yx

=+ =+

4. False; the slope is 3 2 . 235 35 22

5. True; ()() ? ? 2124 224 44 True

+= += =

171

2016 Pearson Education, Inc.

93. 2 2 2 xxx

−=−=

95. () 2 2 2 2 840 84 816416 412 412 412 423

Section 2.3

1. undefined; 0

22.

23. 21 21

224 Slope undefined. 1(1)0 yy xx ===

24.

25. ()1,2;3Pm== ; 23(1)yx−=−

172

Pearson Education, Inc.

Chapter2: Graphs

18. 21 21 422 Slope2 341 yy xx ====−

19. 21 21 1321 Slope 2(2)42 yy xx ====−

20. 21 21 312 Slope 2(1)3 yy xx ===

21. 21 21 1(1)0 Slope0 2(3)5 yy xx ====

21 21 220 Slope0 549 yy xx ====

21 21 202 Slope undefined. 220 yy xx ===

26. ()2,1;4Pm== ; 14(2)yx−=−

30. ()2,4;0Pm=−= ; 4 y =−

27. () 3 2,4; 4 Pm==− ; 3 4(2) 4 yx−=−−

31. ()0,3; slope undefined P = ; 0 x =

28. () 2 1,3; 5 Pm==− ; 2 3(1) 5 yx−=−−

(note: the line is the y-axis)

32. ()2,0; slope undefined P =− 2 x =−

29. ()1,3;0Pm=−= ; 30 y −=

33. 4 Slope4 1 == ; point: () 1,2

If x increases by 1 unit, then y increases by 4 units.

Answers will vary. Three possible points are:

112 and 246

173

Section2.3: Lines

Education, Inc.

() () ()

2,6 213

6410 3,10 314 and 10414 4,14 xy xy xy =+==+= =+==+= =+==+=

and

34. 2 Slope2 1 == ; point: () 2,3

If x increases by 1 unit, then y increases by 2 units.

Answers will vary. Three possible points are:

211 and 325 1,5 110 and 527 0,7 011 and 729

38. 1 Slope1 1 =−= ; point: () 4,1

If x increases by 1 unit, then y decreases by 1 unit.

35. 33 Slope 22 =−= ; point: () 2,4

If x increases by 2 units, then y decreases by 3 units.

Answers will vary. Three possible points are:

and 437

Answers will vary. Three possible points are:

415 and 110 5,0

39. (0, 0) and (2, 1) are points on the line.

36. 4 Slope 3 = ; point: () 3,2

If x increases by 3 units, then y increases by 4 units.

Answers will vary. Three possible points are:

330 and 246

37. 2 Slope2 1 =−= ; point: () 2,3

If x increases by 1 unit, then y decreases by 2 units.

40.

-intercept

Chapter2: Graphs 174

() () () 211

1,5 110

0,7 011

1,9 xy xy xy =−+=−=+= =−+==+= =+==+=

and 325

and 527

and 729

() () ()

4,7 426

6,10 628

8,13 xy xy xy =+==−−=− =+==−−=− =+==−−=−

224

and 7310

and 10313

() () ()

0,6 033

3,10 336

6,14 xy xy xy =−+==+= =+==+= =+==+=

and 6410

and 10414

()

1,9 xy xy xy =−+=−=−−=− =−+==−−=− =+==−−=−

() ()

()

6,1 617

7,2 xy xy xy =+==−= =+==−=− =+==−−=−

() ()

516 and 011

and 112

101 Slope

yymxb == =+ 1 0 2 2 02 1 20 or 2 yx yx xy x yyx =+ = =− −==

202 -intercept is 0; using :

line.

(0, 0) and (–2, 1) are points on the

1011 Slope 2022

: yymxb ===− =+ 1 0 2 2 20 1 20 or 2 yx yx xy x yyx =−+ =− += +==−

0; using

===−

132 Slope1 1(1)2 Using ()yymxx −=−− −=−+ =−+ +==−+

11 2 2 or 2 yx

3 1 1(1) 3 11 1 33 14 33 14

or 33

43. 11(),2yymxxm

48. Slope = 2; containing the point (4, –3) 11() (3)2(4) 328 211 211 or 211

yymxx yx yx yx xyyx −−=− +=− =− −==−

−=−

yymxx yx yx yx xyyx −−=−− +=−+ =−− +=−=−−

−=−

Lines 175

Pearson Education, Inc.

Section2.3:

2016

−=− 11(1)

41. (–1, 3) and (1, 1) are points on the line. 11 yx yx xyyx

−=− ()

1(1)

yx yx yx yx xyyx −=−− −=+ −=+ =+ −=−=+

−=−= 32(3) 326 23 23 or 23 yx yx yx xyyx −=− −=− =− −==−

11(),1yymxxm −=−=− 21(1) 21 3 3 or 3 yx yx yx xyyx −=−− −=−+ =−+ +==−+ 45. 11 1

42. (–1, 1) and (2, 2) are points on the line. 11 2 yymxxm −=−=− 1 2(1) 2 11 2 22 15 22 15 25 or 22

211 Slope 2(1)3 Using ()yymxx yx yx yx xyyx

== −=−− −=−+ =−+ +==−+

44.

(),

46. 11(),1yymxxm −=−= 11((1)) 11 2 2 or 2 −=+ =+ −=−=+

yx yx yx xyyx

−=−−

47. Slope = 3; containing (–2, 3) 11() 33((2)) 336 39 39 or 39 −=−− −=+ =+ −=−=+

yymxx yx yx yx xyyx

−=−

49. Slope = 2 3 ; containing (1, –1) 11() 2 (1)(1) 3 22 1 33 21 33 21 231 or 33

50. Slope = 1 2 ; containing the point (3, 1) 11() 1 1(3) 2 13 1 22 11 22 11 21 or 22

yymxx yx yx yx xyyx −=− =− −==−

Chapter2: Graphs

51. Containing (1, 3) and (–1, 2)

56. x-intercept = –4; y-intercept = 4 Points are (–4, 0) and (0, 4)

52. Containing the points (–3, 4) and (2, 5)

57. Slope undefined; containing the point (2, 4) This is a vertical line.

2 No slope-intercept form. x =

58. Slope undefined; containing the point (3, 8) This is a vertical line.

3 No slope-intercept form. x =

59. Horizontal lines have slope 0 m = and take the form yb = . Therefore, the horizontal line passing through the point () 3,2 is 2 y =

60. Vertical lines have an undefined slope and take the form x a = . Therefore, the vertical line passing through the point () 4,5 is 4 x =

53. Slope = –3; y-intercept =3

61. Parallel to 2 y x = ; Slope = 2 Containing (–1, 2) 11() 22((1)) 22224 24 or 24

yymxx yx yxyx xyyx

−=− −=−− −=+→=+ −=−=+

54. Slope = –2; y-intercept = –2

55. x-intercept = 2; y-intercept = –1

62. Parallel to 3 y x =− ; Slope = –3; Containing the point (–1, 2) 11() 23((1)) 23331 31 or 31

yymxx yx yxyx xyyx

−=− −=−−− −=−−→=−− +=−=−−

176

Inc.

2311 1122 m === 11() 1 3(1) 2 11 3 22 15 22 15 25 or 22 yymxx yx yx yx xyyx −=− −=− −=− =+ −=−=+

541 2(3)5 m == 11() 1 5(2) 5 12 5 55 123 55 123 523 or 55 yymxx yx yx yx xyyx −=− −=− −=− =+ −=−=+

33 33 or 33 ymxb yx xyyx =+ =−+ +==−+

2(2) 22 or 22 ymxb yx xyyx =+ =−+− +=−=−−

are

1011 0222 m === 1 1 2 1 22 or 1 2 ymxb yx x yyx =+ =− −==−

Points

(2,0) and (0,–1)

404 1 0(4)4

m === 14 4 4 or 4 ymxb yx yx xyyx =+ =+ =+ −=−=+

63. Parallel to 22 xy−=− ; Slope = 2 Containing the point (0, 0)

69. Perpendicular to 22 xy+= ; Containing the point (–3, 0)

64. Parallel to 25xy−=− ;

Containing the point

70. Perpendicular to 25xy−=− ; Containing the point (0, 4) Slope of perpendicular = –2

65. Parallel to 5 x = ; Containing (4,2) This is a vertical line.

66. Parallel to 5 y = ; Containing the point (4, 2) This is a horizontal line. Slope = 0

67. Perpendicular to 1 4; 2 yx=+ Containing (1, –2) Slope of perpendicular = –2

71. Perpendicular to 8 x = ; Containing (3, 4) Slope of perpendicular = 0 (horizontal line) 4 y =

72. Perpendicular to 8 y = ; Containing the point (3, 4) Slope of perpendicular is undefined (vertical line). 3 x = No slope-intercept form.

73. 23yx=+ ; Slope = 2; y-intercept = 3

68. Perpendicular to 23yx=− ; Containing the point (1, –2)

74. 34yx=−+ ; Slope = –3; y-intercept = 4

Section2.3: Lines

11() 02(0) 2 20 or 2 yymxx yx yx x yyx −=− −=− = −==

() 1 Slope;

2 = 11() 11 0(0)22 1 20 or 2 yymxx yxyx xyyx −=− −=−→= −==

0,0

No slope-intercept form. x =

2 y =

11() (2)2(1) 2222 20 or 2 yymxx yx yxyx xyyx −=− −−=−− +=−+→=− +==−

1 Slope of perpendicular 2 =− 11() 1 (2)(1) 2 1113 2 2222 13 23 or 22 yymxx yx yxyx xyyx −=− −−=−− +=−+→=−− +=−=−−

of perpendicular 2

11() 0((3))113 222 13 23 or 22 yymxx yxyx xyyx −=− −=−−→=+ −=−=+

Slope

ymxb yx xyyx =+ =−+ +==−+

Chapter2: Graphs

75. 1 1 2 yx=− ; 22yx=−

Slope = 2; y-intercept = –2

79. 24xy+= ; 1 242 2 yxyx =−+→=−+

1 Slope 2 =− ; y-intercept = 2

76. 1 2 3 xy+= ; 1 2 3 yx=−+

1 Slope 3 =− ; y-intercept = 2

77. 1 2 2 yx=+ ; 1 Slope 2 = ; y-intercept = 2

80. 36xy −+= ; 1 362 3 yxyx =+→=+

1 Slope 3 = ; y-intercept = 2

81. 236 xy−= ; 2 3262 3 yxyx −=−+→=−

2 Slope 3 = ; y-intercept = –2

78. 1 2 2 yx=+ ; Slope = 2; 1 -intercept 2 y =

178

82. 326 xy+= ; 3 2363 2 yxyx =−+→=−+

3 Slope 2 =− ; y-intercept = 3

86. 1 y =− ; Slope = 0; y-intercept = –1

83. 1 xy+= ; 1 y x =−+ Slope = –1; y-intercept = 1

87. 5 y = ; Slope = 0; y-intercept = 5

88. 2 x = ; Slope is undefined y-intercept - none

84. 2 xy−= ; 2 yx=− Slope = 1; y-intercept = –2

85. 4 x =− ; Slope is undefined y-intercept - none

89. 0 yx−= ; yx = Slope = 1; y-intercept = 0

Lines 179

Education, Inc.

Section2.3:

Pearson

Chapter2: Graphs

90. 0 xy+= ; yx =−

Slope = –1; y-intercept = 0

91. 230 yx−= ; 3 23 2 yxyx =→=

3 Slope 2 = ; y-intercept = 0

92. 320 xy+= ; 3 23 2 yxyx =−→=−

3 Slope 2 =− ; y-intercept = 0

x x x

+= = =

93 a. x-intercept: () 2306 26 3

The point () 3,0 is on the graph.

y-intercept: () 2036 36 2

y y y

+= = =

The point () 0,2 is on the graph. b.

x x x

−= = =

94. a. x-intercept: () 3206 36 2

The point () 2,0 is on the graph.

y-intercept: () 3026 26 3

y y y

−= −= =−

The point () 0,3 is on the graph. b.

180

x 5 5 5 5

(0,2)

(3,0)

(0,−3)

x 5 5 5 5

(2,0)

95. a. x-intercept: () 45040

The point () 10,0 is on the graph.

y-intercept: () 40540

The point () 0,8 is on the graph.

97. a. x-intercept: () 72021

The point () 3,0 is on the graph.

+= = = The point 21 0, 2

is on the graph. b.

96. a. x-intercept: () 64024

The point () 4,0 is on the graph.

y-intercept: () 60424

The point () 0,6 is on the graph.

x x += = = The point 18 ,0

518

y y y += = =

Section2.3: Lines

440 10

x x

−= =−

−+=

540 8 y y y −+= = =

624 4

x x

−= =

424 6

y y y −= −= =−

721 3

x x x += = =

221

y-intercept: () 70221   

y y y

5   

98. a. x-intercept: () 53018

is on the graph.

318 6

y-intercept: () 50318

The point () 0,6 is on the graph.

Chapter2: Graphs

99. a. x-intercept: () 11 01 23

101. a. x-intercept: () 0.20.501

The point () 5,0 is on the graph.

The point () 2,0 is on the graph.

y-intercept: () 11 01 23

y-intercept: () 0.200.51

The point () 0,2 is on the graph. b.

102. a. x-intercept: () 0.30.401.2

The point () 4,0 is on the graph. y-intercept: () 0.300.41.2

The point () 0,3 is on the graph.

103. The equation of the x-axis is 0 y = . (The slope is 0 and the y-intercept is 0.)

104. The equation of the y-axis is 0 x = . (The slope is undefined.)

105. The slopes are the same but the y-intercepts are different. Therefore, the two lines are parallel.

182

1 1 2 2

x x

= =

1 1 3 3 y y y

= =

3 4 x x −= =

3 2 4 3 6 y y y −= −= =−

The point () 0,3 is on the graph. b. 100. a. x-intercept: ()

The point () 4,0 is on the graph. y-intercept: ()

The point () 0,6 is on the graph. b.

0.21 5

x x

= =

−=

0.51 2

y y y −= −= =−

0.31.2 4

−= =−

x x

−+=

0.41.2 3

= =

y y y −+=

106. The slopes are opposite-reciprocals. That is, their product is 1 . Therefore, the lines are perpendicular.

107. The slopes are different and their product does not equal 1 . Therefore, the lines are neither parallel nor perpendicular.

108. The slopes are different and their product does not equal 1 (in fact, the signs are the same so the product is positive). Therefore, the lines are neither parallel nor perpendicular.

109. Intercepts: () 0,2 and () 2,0 . Thus, slope = 1. 2 or 2 yxxy=+−=−

110. Intercepts: () 0,1 and () 1,0 . Thus, slope = –1. 1 or 1 yxxy =−++=

111. Intercepts: () 3,0 and () 0,1 . Thus, slope = 1 3 1 1 or 33 3 yxxy =−++=

112. Intercepts: () 0,1 and () 2,0 . Thus,

=− , () 4 4,1 P = () 12 303 1 213 m === ; 24 13 1 42 m ==− ;

() 34 12 3 1 413 m === ; () 13 20 1 11 m ==−

Opposite sides are parallel (same slope) and adjacent sides are perpendicular (product of slopes is 1 ). Therefore, the vertices are for a rectangle.

116. () 1 0,0 P = , () 2 1,3 P = , () 3 4,2 P = , () 4 3,1 P =−

12 30 3 10 m == ; 23 231 413 m ==− ; 34 12 3 34 m == ; 14 101 303 m ==−

()() 22 12 10301910 d =−+−=+=

()() 22 23 41239110 d =−+−=+=

()() 22 34 34121910 d =−+−−=+=

()() 22 14 30109110 d =−+−−=+=

Opposite sides are parallel (same slope) and adjacent sides are perpendicular (product of slopes is 1 ). In addition, the length of all four sides is the same. Therefore, the vertices are for a square.

117. Let x = number of miles driven, and let C = cost in dollars.

Total cost = (cost per mile)(number of miles) + fixed cost

0.6039Cx=+

When x = 110, ()() 0.6011039$105.00 C =+=

Since 12 1 mm⋅=− , the line segments 12PP and 23PP are perpendicular. Thus, the points 1P , 2P , and 3P are vertices of a right triangle.

When x = 230, ()() 0.6023039$177.00 C =+= .

118. Let x = number of pairs of jeans manufactured, and let C = cost in dollars.

Total cost = (cost per pair)(number of pairs) + fixed cost

8500Cx=+

When x = 400, ()()8400500$3700 C =+=

When x = 740, ()()8740500$6420 C =+=

Each pair of opposite sides are parallel (same slope) and adjacent sides are not perpendicular. Therefore, the vertices are for a parallelogram.

119. Let x = number of miles driven annually, and let C = cost in dollars.

Total cost = (approx cost per mile)(number of miles) + fixed cost

0.174462Cx=+

Section2.3: Lines 183

Education, Inc.

slope

113. () 1 2,5 P =− , () 2 1,3 P = : 1 5322 2133 m ===− () 2 1,3 P = , () 3 1,0 P =− : () 2 303 112 m ==

114. () 1 1,1 P =− , () 2 4,1 P = , () 3 2,2 P = , () 4 5,4 P = () 12 11 2 413 m == ; 24 41 3 54 m == ; 34 422 523 m == ; () 13 21 3 21 m ==

= 1 2

1 or 22 2 yxxy =−−+=−

115. () 1 1,0 P =− , () 2 2,3 P = , () 3 1,2 P

Chapter2: Graphs

120. Let x = profit in dollars, and let S = salary in dollars.

Weekly salary = (% share of profit)(profit) + weekly pay

0.05375Sx=+

121. a. 0.082115.37Cx=+ ; 0800 x ≤≤

c. For 200 kWh, 0.0821(200)15.37$31.79 C =+=

d. For 500 kWh, 0.0821(500)15.37$56.42 C =+=

e. For each usage increase of 1 kWh, the monthly charge increases by $0.0821 (that is, 8.21 cents).

122. a. 0.09077.24Cx=+ ; 01000 x ≤≤

c. For 200 kWh, () 0.09072007.24$25.38 C =+=

d. For 500 kWh, () 0.09075007.24$52.59 C =+=

e. For each usage increase of 1 kWh, the monthly charge increases by $0.0907 (that is, 9.07 cents).

123. (,)(0,32);(,)(100,212) CFCF °°=°°= 212321809 slope 10001005

=== °−=°− °−=° °=°−

FC FC CF

9 32(0) 5 9 32() 5 5 (32) 9

If 70 F °= , then 55(7032)(38) 99 21.1

C C

°=−= °≈°

124. a. º273KC=+

KF KF KF

=°−+ =−+ =+

b. 5 º(º32) 9 CF=− 5 (32)273 9 5160 º273 99 52297 º 99

125. a. The y-intercept is (0, 30), so b = 30. Since the ramp drops 2 inches for every 25 inches of run, the slope is 22 2525 m ==− . Thus, the equation is 2 30 25 yx=−+ .

b. Let y = 0.

The x-intercept is (375, 0). This means that the ramp meets the floor 375 inches (or 31.25 feet) from the base of the platform.

184

25 2 30 25 25225 30 2252 375 x x x x =−+ =  =   =

() 2 030

c. No. From part (b), the run is 31.25 feet which exceeds the required maximum of 30 feet.

d. First, design requirements state that the maximum slope is a drop of 1 inch for each 12 inches of run. This means 1 12 m ≤ Second, the run is restricted to be no more than 30 feet = 360 inches. For a rise of 30 inches, this means the minimum slope is 301 36012 = . That is, 1 12 m ≥ . Thus, the only possible slope is 1 12 m = . The diagram indicates that the slope is negative. Therefore, the only slope that can be used to obtain the 30-inch rise and still meet design requirements is 1 12 m =− . In words, for every 12 inches of run, the ramp must drop exactly 1 inch.

126. a. The year 2000 corresponds to x = 0, and the year 2012 corresponds to x = 12. Therefore, the points (0, 20.6) and (12, 9.3) are on the line. Thus, 9.320.611.3 0.942 12012 m ==−=− . The yintercept is 20.6, so b = 20.6 and the equation is 0.94220.6yx=−+

22 (,)(200,000,60,000) xA = ()

60,00040,000 slope 200,000100,000 20,0001 100,0005 1 40,000100,000

b. If x = 300,000, then () 1 300,00020,000$80,000 5 A =+=

c. Each additional box sold requires an additional $0.20 in advertising.

128. Find the slope of the line containing () , ab and () , ba : slope1 ab ba ==−

The slope of the line yx = is 1.

Since 111−⋅=− , the line containing the points (,) and (,)abba is perpendicular to the line yx =

x x x

=−+ = =

b. x-intercept: 00.94220.6 0.94220.6

21.9

y-intercept: () 0.942020.620.6 y =−+=

The intercepts are (21.9, 0) and (0, 20.6).

c. The y-intercept represents the percentage of twelfth graders in 2000 who had reported daily use of cigarettes. The x-intercept represents the number of years after 2000 when 0% of twelfth graders will have reported daily use of cigarettes.

d. The year 2025 corresponds to x = 25. () 0.9422520.62.95 y =−+=−

This prediction is not reasonable.

127. a. Let x = number of boxes to be sold, and A = money, in dollars, spent on advertising. We have the points 11 (,)(100,000,40,000); xA =

The midpoint of (,) and (,)abba is , 22 abba M ++  = 

Since the coordinates are the same, the midpoint lies on the line yx =

Note: 22 abba ++ = 129. 2 x yC−= Graph the lines:

All the lines have the same slope, 2. The lines

Section2.3: Lines 185

2016 Pearson Education, Inc.

5 1 40,00020,000 5 1 20,000 5 Ax Ax Ax = == −=− −=− =+



24 20 22

xy −=− −= −=

are parallel.

slope 1 and y-intercept (0,1). Thus, the lines are parallel with positive slopes. One line has a positive y-intercept and the other with a negative y-intercept.

134. (d)

130. Refer to Figure 47. () () ()

length of ,1 length of ,1 length of ,

OAdOAm OBdOBm ABdABmm

==+

2 1 2 2 12

Now consider the equation

If this equation is valid, then AOBΔ is a right triangle with right angle at vertex O

But we are assuming that 12 1 mm =− , so we have

Therefore, by the converse of the Pythagorean Theorem, AOBΔ is a right triangle with right angle at vertex O. Thus Line 1 is perpendicular to Line 2.

131. (b), (c), (e) and (g)

The line has positive slope and positive y-intercept.

132. (a), (c), and (g)

The line has negative slope and positive y-intercept.

133. (c)

The equation 2 xy−=− has slope 1 and yintercept (0,2). The equation 1 xy−= has

The equation 22yx−= has slope 2 and yintercept (0,2). The equation 21xy+=− has slope 1 2 and y-intercept 1 0,. 2

are perpendicular since 1 21 2 

The lines

. One line has a positive y-intercept and the other with a negative y-intercept.

135 – 137. Answers will vary.

138. No, the equation of a vertical line cannot be written in slope-intercept form because the slope is undefined.

139. No, a line does not need to have both an xintercept and a y-intercept. Vertical and horizontal lines have only one intercept (unless they are a coordinate axis). Every line must have at least one intercept.

140. Two lines with equal slopes and equal y-intercepts are coinciding lines (i.e. the same).

141. Two lines that have the same x-intercept and yintercept (assuming the x-intercept is not 0) are the same line since a line is uniquely defined by two distinct points.

142. No. Two lines with the same slope and different xintercepts are distinct parallel lines and have no points in common.

Assume Line 1 has equation 1ymxb =+ and Line 2 has equation 2ymxb =+ ,

Line 1 has x-intercept 1b m and y-intercept 1b .

Line 2 has x-intercept 2b m and y-intercept 2b

Assume also that Line 1 and Line 2 have unequal x-intercepts. If the lines have the same y-intercept, then 12bb = .

186

Chapter2: Graphs

Inc.

==+ ==−

()()() 22

+++=−

2 22 111212 mmmm

()()() 22 2 22 1212 2222 121122 2222 121122 11 112 22 mmmm mmmmmm mmmmmm +++=− +++=−+ ++=−+

() 2222 1212 2222 1212 221 22 00 mmmm mmmm ++=−−+ ++=++ =

  

−=− 

But 12 bb mm −=−  Line 1 and Line 2 have the same x-intercept, which contradicts the original assumption that the lines have unequal x-intercepts. Therefore, Line 1 and Line 2 cannot have the same y-intercept.

143. Yes. Two distinct lines with the same y-intercept, but different slopes, can have the same x-intercept if the x-intercept is 0 x =

Assume Line 1 has equation 1 ymxb =+ and Line 2 has equation 2 ymxb =+ ,

Line 1 has x-intercept 1

b m and y-intercept b

Line 2 has x-intercept 2

b m and y-intercept b

Assume also that Line 1 and Line 2 have unequal slopes, that is 12mm ≠ .

If the lines have the same x-intercept, then

Since we are assuming that 12mm ≠ , the only way that the two lines can have the same x-intercept is if 0. b =

144. Answers will vary.

145. () 21 21

4263 42 13 yy m xx ====−

It appears that the student incorrectly found the slope by switching the direction of one of the subtractions.

mm −=−

12 21 21 0 bb mm mbmb mbmb −=− −=− −+= ()2112 1212 But 00 0 or 0 mbmbbmm b mmmm −+=  −=  = −=  =

146. 23222 45453 2 28 2 28 416 1 1 xyx xyxyy xy xy x y = = ==

222 81522 16225 289 28917 hab h =+ =+ =+ = ==

() () 2 2 32549 324 324 326 326 x x x x x −+= −= −=± −=± =±

solution set is: {} 326,326 −+ .

253 3253 228 14 x x x x x −+< −< −<−< << << The solution set is: {} |14xx<< . Interval notation: () 1,4

147.

148.

The

149. 25710

add; () 2 1 2 1025 ⋅=

() 2 29 29 23 23 x x x x −= −=± −=± =± 5 or 1 xx==− The solution set is {1,5}.

Section 2.4 1.

3. False. For example, 22 2280xyxy++++= is not a circle. It has no real solutions.

4. radius

5. True; 2 93rr=→=

6. False; the center of the circle

()() 22 3213xy++−= is () 3,2 .

7. d

8. a

9. Center = (2, 1) 22

General form: 22 40 xy+−=

= =−+−==

Radiusdistance from (0,1) to (2,1) (20)(11)42

Equation: 22 (2)(1)4 xy−+−=

10. Center = (1, 2) 22

14. ()()222 x hykr −+−= 222 22 (0)(0)3 9 xy xy

−+−= +=

General form: 22 90 xy+−=

= =−+−==

Radiusdistance from (1,0) to (1,2) (11)(20)42

Equation: 22 (1)(2)4 xy−+−=

11. Center = midpoint of (1, 2) and (4, 2)

15. ()()222 x hykr −+−= 222 22 (0)(2)2 (2)4 xy xy

−+−= +−=

General form: 22 22

Equation:

12. Center = midpoint of (0, 1) and (2, 3)

Equation:

13. ()()222 x hykr −+−= 222 22 (0)(0)2 4 xy xy

−+−= +=

+−+= +−=

444 40 xyy xyy

16. ()()222 x hykr −+−= 222 22 (1)(0)3 (1)9 xy xy

−+−= −+=

Chapter2: Graphs 188

()()

++ == () 2 2 5 2

from ,2 to (4,2) 4(22)593 242 =  =−+−==  

1422 5 222,,2

Radiusdistance

2 2 59

24xy −+−= 

(2)

()

,1,2 22

 ==   () () 2 2

from

21(32)2 = =−+−=

0213

Radiusdistance

1,2 to (2,3)

() 2 2 1(2)2xy−+−=

General form: 22 22

219 280 xxy xyx

−++= +−−=

19. ()()222 x hykr −+−=

17. ()()222 x hykr −+−= 222 22 (4)((3))5 (4)(3)25 xy xy

−+−−= −++=

General form: 22 22 8166925 860 xxyy xyxy

−++++= +−+=

18. ()()222 x hykr −+−= 222 22 (2)((3))4 (2)(3)16 xy xy

−+−−= −++=

General form: 22 22 446916 4630 xxyy xyxy

−++++= +−+−=

() 222 22 (2)(1)4 (2)(1)16 xy xy

−−+−= ++−=

General form: 22 22

442116 42110 xxyy xyxy

+++−+= ++−−=

20. ()()222 x hykr −+−=

() 222 22 (5)((2))7 (5)(2)49 xy xy

−−+−−= +++=

General form: 22 22 10254449 104200 xxyy xyxy

+++++= +++−=

xy xy

−+−= 

−+=

xxy xyx

−++= +−=

11 44 0

Section2.4: Circles 189

Education, Inc.

Pearson



 

21. ()()222 x hykr −+−= 22 2 2  

11 (0) 22 11 24

General form: 22 22