Microeconomics an intuitive approach with calculus 2nd edition thomas nechyba solutions manual

ChoiceSetsandBudgetConstraints

Theeven-numberedsolutionstoend-of-chapterexercisesareprovidedforuse byinstructors. (Solutionstoodd-numberedend-of-chapterexercisesareprovidedhereaswellasinthe StudyGuide thatisavailabletostudents.)

Solutionsmaybesharedbyaninstructorwithhisorherstudentsattheinstructor’sdiscretion.

Theymaynotbemadepubliclyavailable.

Ifpostedonacourseweb-site,thesitemustbepasswordprotectedandfor useonlybythestudentsinthecourse.

Reproductionand/ordistributionofthesolutionsbeyondclassroomuseis strictlyprohibited.

Inmostcolleges,itisaviolationofthestudenthonorcodeforastudentto sharesolutionstoproblemswithpeersthattakethesameclassatalaterdate.

•Eachend-of-chapterexercisebeginsonanewpage.Thisistofacilitatemaximumflexibilityforinstructorswhomaywishtoshareanswerstosomebut notallexerciseswiththeirstudents.

•IfyouareassigningonlytheA-partsofexercisesin Microeconomics:AnIntuitiveApproachwithCalculus,youmaywishtoinsteadusethesolutionset createdforthecompanionbook Microeconomics:AnIntuitiveApproach

• SolutionstoWithin-ChapterExercisesareprovidedinthestudent StudyGuide.

Exercise2.1

AnygoodSouthernbreakfastincludesgrits(whichmywifeloves)andbacon (whichIlove).Supposeweallocate$60perweektoconsumptionofgritsandbacon, thatgritscost$2perboxandbaconcosts$3perpackage.

A: Useagraphwithboxesofgritsonthehorizontalaxisandpackagesofbacon ontheverticaltoanswerthefollowing:

(a) Illustratemyfamily’sweeklybudgetconstraintandchoice set. Answer:Thegraphisdrawninpanel(a)ofExerciseGraph2.1.

ExerciseGraph2.1:(a)Answerto(a);(b)Answerto(c);(c)Answerto(d)

(b) Identifytheopportunitycostofbaconandgritsandrelatethesetoconcepts onyourgraph.

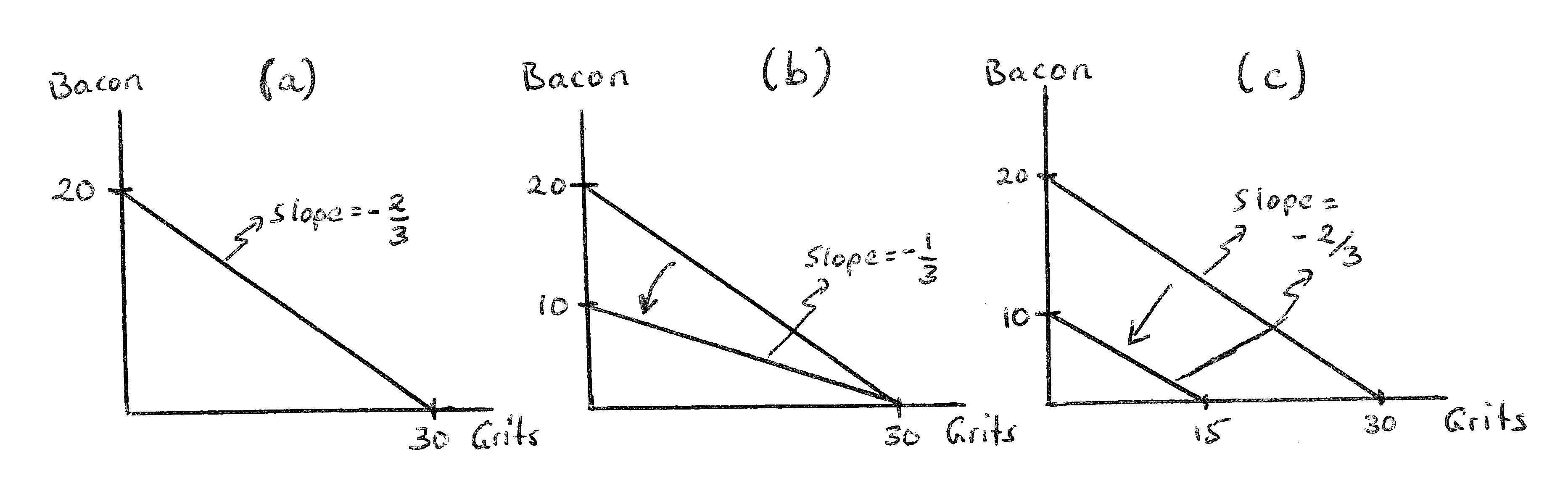
Answer:Theopportunitycostofgritsisequalto2/3ofapackageofbacon (whichisequaltothenegativeslopeofthebudgetsincegritsappearon thehorizontalaxis).Theopportunitycostofapackageofbaconis3/2of aboxofgrits(whichisequaltotheinverseofthenegativeslopeofthe budgetsincebaconappearsontheverticalaxis).

(c) Howwouldyourgraphchangeifasuddenappearanceofararehogdiseasecausedthepriceofbacontoriseto$6perpackage,andhowdoesthis changetheopportunitycostofbaconandgrits?

Answer:Thischangeisillustratedinpanel(b)ofExerciseGraph2.1.This changestheopportunitycostofgritsto1/3ofapackageofbacon,and itchangestheopportunitycostofbaconto3boxesofgrits.Thismakes sense:Baconisnow3timesasexpensiveasgrits—soyouhavetogive up3boxesofgritsforonepackageofbacon,or1/3ofapackage ofbacon for1boxofgrits.

(d) Whathappensinyourgraphif(insteadofthechangein(c))thelossofmy jobcausedustodecreaseourweeklybudgetforSouthernbreakfastsfrom $60to$30?Howdoesthischangetheopportunitycostofbacon andgrits?

ChoiceSetsandBudgetConstraints

Answer:Thechangeisillustratedinpanel(c)ofExerciseGraph2.1.Since relativepriceshavenotchanged,opportunitycostshavenotchanged. Thisisreflectedinthefactthattheslopestaysunchanged.

B: Inthefollowing,compareamathematicalapproachtothegraphicalapproachusedinpartA,usingx1 torepresentboxesofgritsandx2 torepresent packagesofbacon:

(a) Writedownthemathematicalformulationofthebudgetlineandchoice setandidentifyelementsinthebudgetequationthatcorrespondtokey featuresofyourgraphfrompart2.1A(a).

Answer:Thebudgetequationis p1 x1 + p2 x2 = I canalsobewrittenas

x2 = I p2 p1 p2 x1 (2.1.i)

With I = 60, p1 = 2and p2 = 3,thisbecomes x2 = 20 (2/3)x1 —anequationwithinterceptof20andslopeof 2/3asdrawninExerciseGraph 2.1(a).

(b) Howcanyouidentifytheopportunitycostofbaconandgritsinyourequationofabudgetline,andhowdoesthisrelatetoyouranswerin2.1A(b).

Answer:Theopportunitycostof x1 (grits)issimplythenegativeofthe slopeterm(intermsofunitsof x2).Theopportunitycostof x2 (bacon)is theinverseofthat.

(c) Illustratehowthebudgetlineequationchangesunderthescenarioof2.1A(c) andidentifythechangeinopportunitycosts.

Answer:Substitutingthenewprice p2 = 6intoequation(2.1.i),weget x2 = 10 (1/3)x1 —anequationwithinterceptof10andslopeof 1/3as depictedinpanel(b)ofExerciseGraph2.1.

(d) Repeat(c)forthescenarioin2.1A(d).

Answer:Substitutingthenewincome I = 30intoequation(2.1.i)(holdingpricesat p1 = 2and p2 = 3,weget x2 = 10 (2/3)x1 —anequation withinterceptof10andslopeof 2/3asdepictedinpanel(c)ofExercise Graph2.1.

Exercise2.2

Supposetheonlytwogoodsintheworldarepeanutbutterandjelly.

A: Youhavenoexogenousincomebutyoudoown6jarsofpeanutbutterand2 jarsofjelly.Thepriceofpeanutbutteris$4perjar,andthe priceofjellyis$6per jar.

(a) Onagraphwithjarsofpeanutbutteronthehorizontalandjarsofjellyon theverticalaxis,illustrateyourbudgetconstraint.

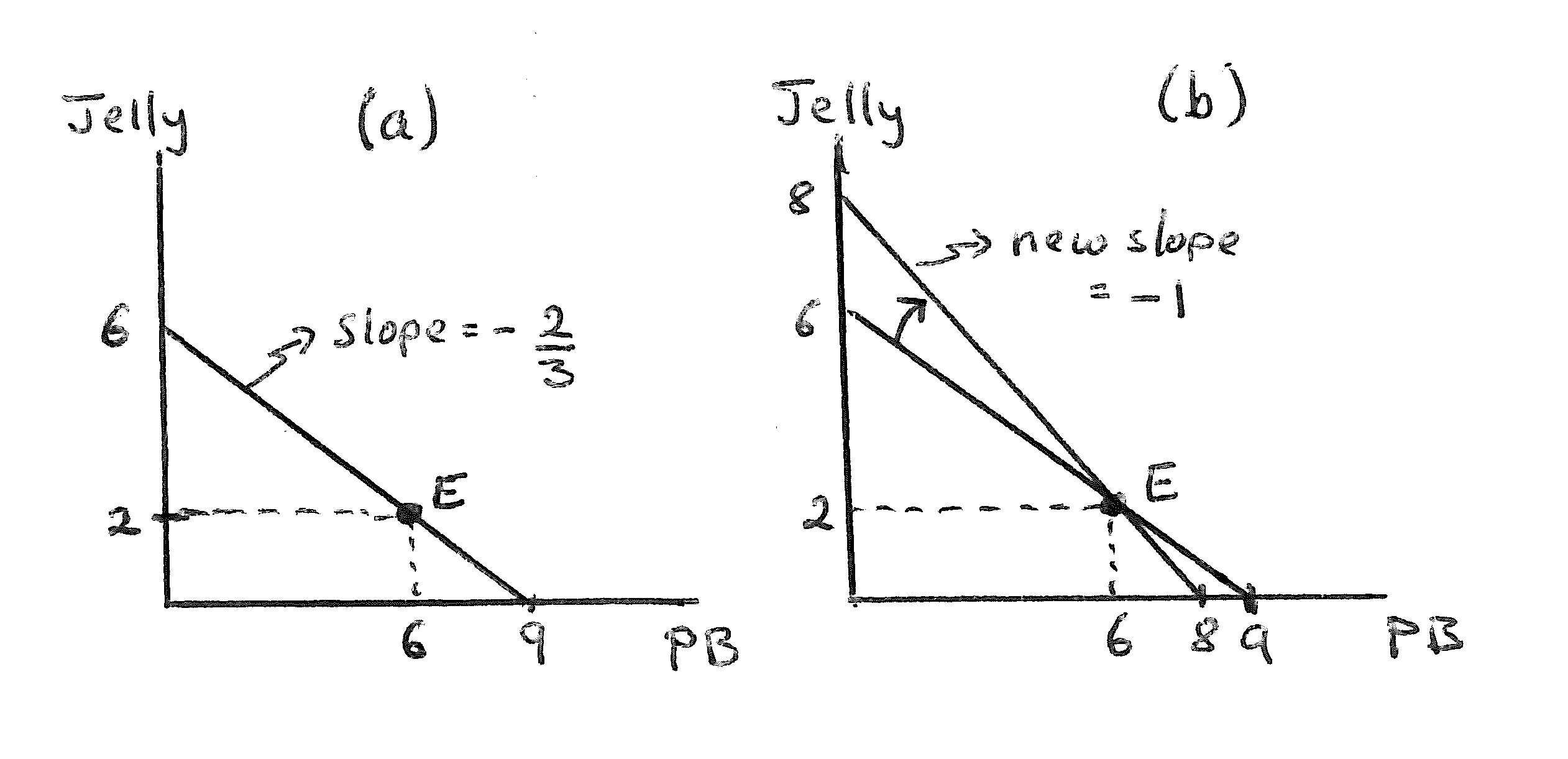
Answer:Thisisdepictedinpanel(a)ofExerciseGraph2.2.Thepoint E istheendowmentpointof2jarsofjellyand6jarsofpeanutbutter(PB). Ifyousoldyour2jarsofjelly(atapriceof$6perjar),youcouldmake $12,andwiththatyoucouldbuyanadditional3jarsofPB(attheprice of$4perjar).Thus,themostPByoucouldhaveis9,theinterceptonthe horizontalaxis.Similarly,youcouldsellyour6jarsofPBfor$24,andwith thatyoucouldbuy4additionaljarsofjellytogetyoutoamaximumtotal of6jarsofjelly—theinterceptontheverticalaxis.Theresultingbudget linehasslope 2/3,whichmakessensesincethepriceofPB($4)divided bythepriceofjelly($6)isinfact2/3.

ExerciseGraph2.2:(a)Answerto(a);(b)Answerto(b)

(b) Howdoesyourconstraintchangewhenthepriceofpeanutbutterincreases to$6?Howdoesthischangeyouropportunitycostofjelly?

Answer:Thechangeisillustratedinpanel(b)ofExerciseGraph2.2.Since youcanalwaysstillconsumeyourendowment E ,thenewbudgetmust contain E .Buttheopportunitycostshavenowchanged,withtheratioof thetwopricesnowequalto1.Thus,thenewbudgetconstraint hasslope 1andrunsthrough E .Theopportunitycostofjellyhasnowfallenfrom 3/2to1.Thisshouldmakesense:Before,PBwascheaperthanjellyand so,foreveryjarofjellyyouhadtogiveupmorethanajarofpeanutbutter.

ChoiceSetsandBudgetConstraints

Nowthattheyarethesameprice,youonlyhavetogiveuponejarofPB toget1jarofjelly.

B: Considerthesameeconomiccircumstancesdescribedin2.2A andusex1 to representjarsofpeanutbutterandx2 torepresentjarsofjelly.

(a) Writedowntheequationrepresentingthebudgetlineandrelatekeycomponentstoyourgraphfrom2.2A(a).

Answer:Thebudgetlinehastoequateyourwealthtothecostofyourconsumption.Yourwealthisequaltothevalueofyourendowment,whichis p1e1 + p2e2 (where e1 isyourendowmentofPBand e2 isyourendowment ofjelly).Thecostofyourconsumptionisjustyourspending onthetwo goods—i.e. p1 x1 + p2 x2.Theresultingequationis

Whenthevaluesgivenintheproblemarepluggedin,thelefthandside becomes4(6) + 6(2) = 36andtherighthandsidebecomes4x1 + 6x2 resultingintheequation36

1, (2.2.ii)

whichisexactlywhatwegraphedinpanel(a)ofExerciseGraph2.2—a linewithverticalinterceptof6andslopeof 2/3.

(b) Changeyourequationforyourbudgetlinetoreflectthechangeineconomiccircumstancesdescribedin2.2A(b)andshowhowthisnewequation relatestoyourgraphin2.2A(b).

Answer:Nowthelefthandsideofequation(2.2.i)is6(6) + 6(2) = 48while therighthandsideis6x1 +6x2.Theequationthusbecomes48 = 6x1 +6x2 or,when x2 istakentooneside,

x2 = 8 x1 (2.2.iii)

Thisisanequationofalinewithverticalinterceptof8andslopeof 1— exactlywhatwegraphedinpanel(b)ofExerciseGraph2.2.

Exercise2.3

Considerabudgetforgoodx1 (onthehorizontalaxis)andx2 (onthevertical axis)whenyoureconomiccircumstancesarecharacterizedbypricesp1 andp2 and anexogenousincomelevelI.

A: Drawabudgetlinethatrepresentstheseeconomiccircumstancesandcarefullylabeltheinterceptsandslope.

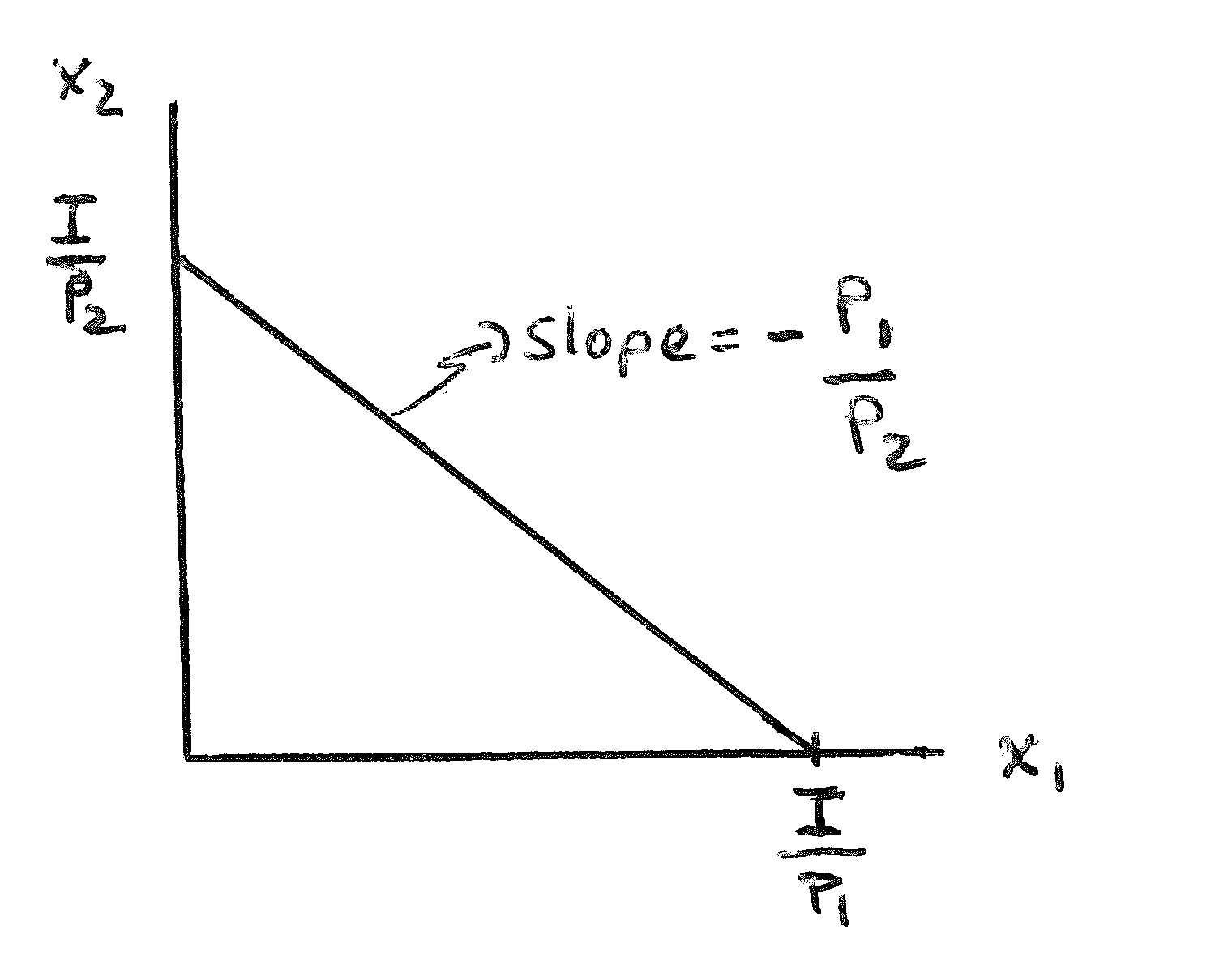
Answer:ThesketchofthisbudgetlineisgiveninExerciseGraph2.3.

ExerciseGraph2.3:Abudgetconstraintwithexogenousincome I

Theverticalinterceptisequaltohowmuchof x2 onecouldbywith I ifthat isallonebought—whichisjust I /p2 .Theanalogousistruefor x1 onthe horizontalintercept.Onewaytoverifytheslopeistorecognizeitisthe“rise” (I /p2)dividedbythe“run”(I /p1)—whichgives p1/p2 —andthatitisnegative sincethebudgetconstraintisdownwardsloping.

(a) IllustratehowthislinecanshiftparalleltoitselfwithoutachangeinI.

Answer:Inorderforthelinetoshiftinaparallelway,itmustbethat theslope p1/p2 remainsunchanged.Sincewecan’tchange I ,theonly valueswecanchangeare p1 and p2 —butsince p1/p2 can’tchange,it meanstheonlythingwecandoistomultiplybothpricesbythe same constant.So,forinstance,ifwemultiplybothpricesby2,theratioofthe newpricesis2p1/(2p2) = p1/p2 sincethe2’scancel.Wethereforehave notchangedtheslope.Butwehavechangedtheverticalinterceptfrom I /p2 to I /(2p2 ).Wehavethereforeshiftedinthelinewithoutchangingits slope.

Thisshouldmakeintuitivesense:Ifourmoneyincomedoesnotchange butallpricesdouble,thenIcanbyhalfasmuchofeverything.Thisis equivalenttopricesstayingthesameandmymoneyincomedropping byhalf.

(b) Illustratehowthislinecanrotateclockwiseonitshorizontalinterceptwithoutachangeinp2.

Answer:Tokeepthehorizontalinterceptconstant,weneedtokeep I /p1 constant.Buttorotatethelineclockwise,weneedtoincreasetheverticalintercept I /p2.Sincewecan’tchange p2 (whichwouldbetheeasiest

ChoiceSetsandBudgetConstraints

waytodothis),thatleavesusonly I and p1 tochange.Butsincewecan’t change I /p1,wecanonlychangethesebymultiplyingthembythesame constant.Forinstance,ifwemultiplybothby2,wedon’tchangethehorizontalinterceptsince2I /(2p1 ) = I /p1 .Butwedoincreasethevertical interceptfrom I /p2 to2I /p2 .So,multiplyingboth I and p1 bythesame constant(greaterthan1)willaccomplishourgoal. Thisagainshouldmakeintuitivesense:Ifyoudoublemyincomeandthe priceofgood1,Icanstillaffordexactlyasmuchofgood1ifthatisall Ibuywithmyincome.(Thustheunchangedhorizontalintercept).But, ifIonlybuygood2,thenadoublingofmyincomewithoutachangein thepriceofgood2letsmebuytwiceasmuchofgood2.Thescenariois exactlythesameasif p2 hadfallenbyhalf(and I and p1 hadremained unchanged.)

B: Writetheequationofabudgetlinethatcorrespondstoyourgraphin2.3A.

Answer: p1 x1 + p2 x2 = I ,whichcanalsobewrittenas

(a) Usethisequationtodemonstratehowthechangederivedin2.3A(a)can happen.

Answer:IfIreplace p1 with αp1 and p2 with αp2 (where α isjustaconstant),Iget

Thus,multiplyingbothpricesby α isequivalenttomultiplyingincome by1/α (andleavingpricesunchanged).

(b) Usethesameequationtoillustratehowthechangederivedin 2.3A(b)can happen.

Answer:IfIreplace p1 with βp1 and I with βI ,Iget

Thus,thisisequivalenttomultiplying p2 by1/β.Solongas β > 1,itis thereforeequivalenttoreducingthepriceofgood2(withoutchanging theotherpriceorincome).

Exercise2.4

Supposetherearethreegoodsintheworld:x1,x2 andx3

A: Ona3-dimensionalgraph,illustrateyourbudgetconstraintwhenyoureconomiccircumstancesaredefinedbyp1 = 2,p2 = 6,p3 = 5 andI = 120.Carefully labelintercepts.

Answer:Panel(a)ofExerciseGraph2.4illustratesthis3-dimensionalbudget witheachinterceptgivenby I dividedbythepriceofthegoodonthataxis.

ExerciseGraph2.4:Budgetsover3goods:Answersto2.4A,A(b)andA(c)

(a) Whatisyouropportunitycostofx1 intermsofx2?Whatisyouropportunitycostofx2 intermsofx3?

Answer:Onanysliceofthegraphthatkeeps x3 constant,theslopeofthe budgetis p1/p2 =−1/3.Justasinthe2-goodcase,thisisthentheopportunitycostof x1 intermsof x2 —since p1 isathirdof p2,onegivesup 1/3ofaunitof x2 whenonechoosestoconsume1unitof x1 .Onanyverticalslicethatholds x1 fixed,ontheotherhand,theslopeis p3 /p2 =−5/6. Thus,theopportunitycostof x3 intermsof x2 is5/6,andtheopportunity costof x2 intermsof x3 istheinverse—i.e.6/5.

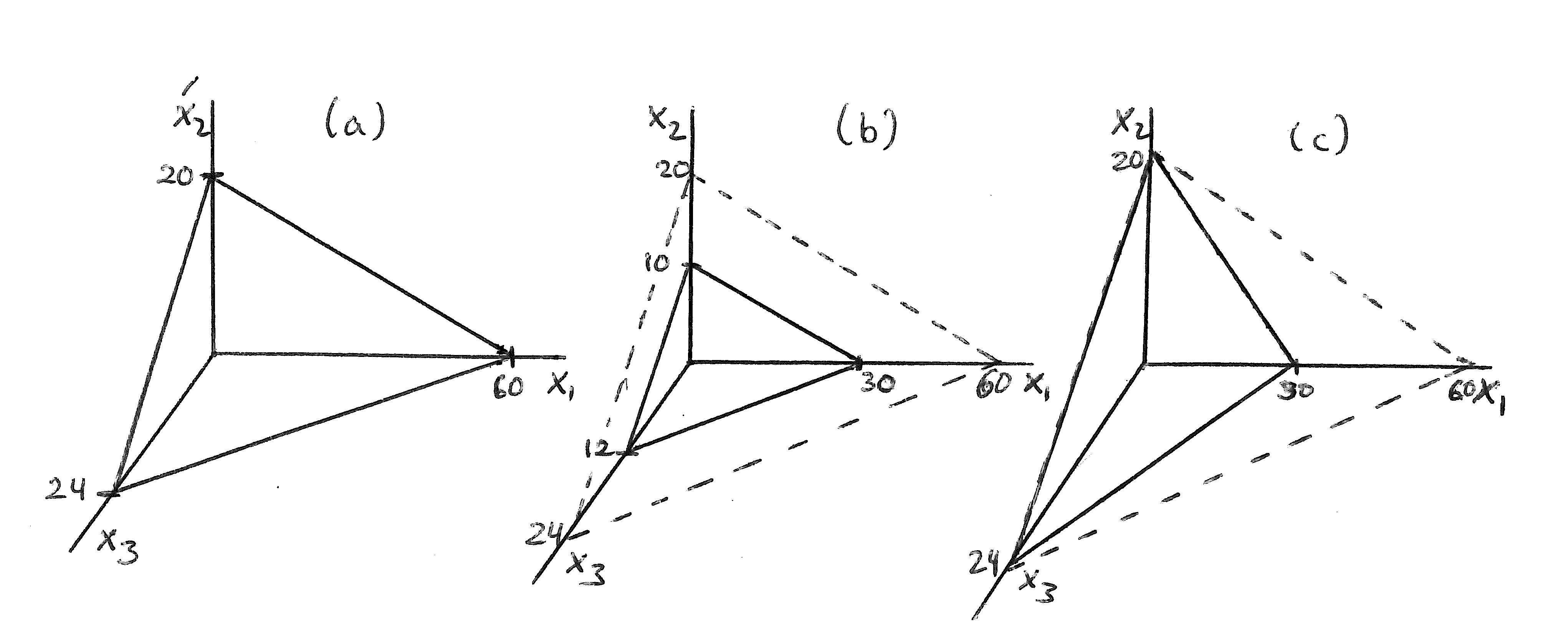
(b) IllustratehowyourgraphchangesifIfallsto$60.Doesyour answerto(a) change?

Answer:Panel(b)ofExerciseGraph2.4illustratesthischange(withthe dashedplaneequaltothebudgetconstraintgraphedinpanel (a).)The answertopart(a)doesnotchangesincenopricesandthusnoopportunitycostschanged.Thenewplaneisparalleltotheoriginal.

(c) Illustratehowyourgraphchangesifinsteadp1 risesto$4.Doesyouranswertopart(a)change?

Answer:Panel(c)ofExerciseGraph2.4illustratesthischange(withthe dashedplaneagainillustratingthebudgetconstraintfrom part(a).)Since

ChoiceSetsandBudgetConstraints

only p1 changed,onlythe x1 interceptchanges.Thischangestheslope onanyslicethatholds x3 fixedfrom 1/3to 2/3—thusdoublingthe opportunitycostof x1 intermsof x2.Sincetheslopeofanysliceholding x1 fixedremainsunchanged,theopportunitycostof x2 intermsof x3 remainsunchanged.Thismakessensesince p2 and p3 didnotchange, leavingthetradeoffbetween x2 and x3 consumptionunchanged.

B: Writedowntheequationthatrepresentsyourpicturein2.4A.Thensuppose thatanewgoodx4 isinventedandpricedat$1.Howdoesyourequationchange? Whyisitdifficulttorepresentthisnewsetofeconomiccircumstancesgraphically?

= I or, pluggingintheinitialpricesandincomerelevantforpanel

Answer:Theequationrepresentingthegraphsis

= 120.Withanewfourthgoodpricedat1,thisequationwouldbecome2x1 + 6x2 + 5x3 + x4 = 120.Itwouldbedifficulttographsincewewouldneedtoadd afourthdimensiontoourgraphs.

Exercise2.5

EverydayApplication: WatchingaBadMovie: Ononeofmyfirstdateswithmy wife,wewenttoseethemovie“Spaceballs”andpaid$5perticket.

A: Halfwaythroughthemovie,mywifesaid:“Whatonearthwereyouthinking?

Thismoviesucks!Idon’tknowwhyIletyoupickmovies.Let’s leave.”

(a) Intryingtodecidewhethertostayorleave,whatistheopportunitycostof stayingtowatchtherestofthemovie?

Answer:Theopportunitycostofanyactivityiswhatwegiveupbyundertakingthatactivity.Theopportunitycostofstayingin themovieis whateverwewouldchoosetodowithourtimeifwewerenotthere.The priceofthemovieticketsthatgotusintothemovietheaterisNOTapart ofthisopportunitycost—because,whetherwestayorleave, wedonot getthatmoneyback.

(b) Supposewehadreadasignonthewayintotheaterstating“Satisfaction Guaranteed!Don’tlikethemoviehalfwaythrough—seethemanager andgetyourmoneyback!”Howdoesthischangeyouranswertopart(a)?

Answer:Now,inadditiontogivingupwhateveritiswewouldbedoing ifweweren’twatchingthemovie,wearealsogivingupthepriceofthe movietickets.Putdifferently,bystayinginthemovietheater,wearegivinguptheopportunitytogetarefund—andsothecostoftheticketsisa realopportunitycostofstaying.

ChoiceSetsandBudgetConstraints

Exercise2.6

EverydayApplication: RentingaCarversusTakingTaxis: Supposemybrother andIbothgoonaweek-longvacationinCaymanand,whenwearriveattheairportontheisland,wehavetochoosebetweeneitherrentinga carortakingataxi toourhotel.Rentingacarinvolvesafixedfeeof$300fortheweek,witheachmile drivenafterwardsjustcosting20cents—thepriceofgasolinepermile.Takingataxi involvesnofixedfees,buteachmiledrivenontheislandduringtheweeknowcosts $1permile.

A: SupposebothmybrotherandIhavebrought$2,000onourtriptospendon “milesdrivenontheisland”and“othergoods”.Onagraphwithmilesdrivenon thehorizontalandotherconsumptionontheverticalaxis,illustratemybudget constraintassumingIchosetorentacarandmybrother’sbudgetconstraint assuminghechosetotaketaxis.

Answer:ThetwobudgetlinesaredrawninExerciseGraph2.6.Mybrother couldspendasmuchas$2,000onothergoodsifhestaysattheairportand doesnotrentanytaxis,butforeverymilehetakesataxi,hegivesup$1inother goodconsumption.Themosthecandriveontheislandis2,000 miles.Assoon asIpaythe$300rentalfee,Icanatmostconsume$1,700inothergoods,but eachmilecostsmeonly20cents.Thus,Icandriveasmuchas1700/0.2=8,500 miles.

ExerciseGraph2.6:Graphsofequationsinexercise2.6

(a) WhatistheopportunitycostforeachmiledriventhatIfaced?

Answer:Iamrentingacar—whichmeansIgiveup20centsinother consumptionpermiledriven.Thus,myopportunitycostis20 cents.My opportunitycostdoesnotincludetherentalfeesinceIpaid thatbefore evengettingintothecar.

(b) Whatistheopportunitycostforeachmiledriventhatmybrotherfaced?

Answer:Mybrotheristakingtaxis—sohehastogiveup$1inother consumptionforeverymiledriven.Hisopportunitycostistherefore$1 permile.

B: Derivethemathematicalequationsformybudgetconstraint andmybrother’s budgetconstraint,andrelateelementsoftheseequationstoyourgraphsinpart A.Usex1 todenotemilesdrivenandx2 todenoteotherconsumption.

Answer:Mybudgetconstraint,onceIpaytherentalfee,is0.2x1 + x2 = 1700 whilemybrother’sbudgetconstraintis x1 + x2 = 2000.Thesecanberewritten with x2 onthelefthandsideas

Theinterceptterms(1700formeand2000formybrother)aswellastheslopes ( 0.2formeand 1formybrother)areasinExerciseGraph2.6.

(a) Whereinyourbudgetequationformecanyoulocatetheopportunitycost ofamiledriven?

Answer:Myopportunitycostofmilesdrivenissimplytheslopeterm in mybudgetequation—i.e.0.2.Igiveup$0.20inotherconsumptionfor everymiledriven.

(b) Whereinyourbudgetequationformybrothercanyoulocatetheopportunitycostofamiledriven?

Answer:Mybrother’sopportunitycostofmilesdrivenistheslopeterm inhisbudgetequation—i.e.1;hegivesup$1inotherconsumptionfor everymiledriven.

ChoiceSetsandBudgetConstraints

Exercise2.7

EverydayApplication: DietingandNutrition: Onarecentdoctor’svisit,you havebeentoldthatyoumustwatchyourcalorieintakeandmustmakesureyou getenoughvitaminEinyourdiet.

A: Youhavedecidedthat,tomakelifesimple,youwillfromnowoneatonly steakandcarrots.Anicesteakhas250caloriesand10unitsofvitamins,anda servingofcarrotshas100caloriesand30unitsofvitaminsYourdoctor’sinstructionsarethatyoumusteat nomore than2000caloriesandconsume atleast 150 unitsofvitaminsperday.

(a) Inagraphwith“servingsofcarrots”onthehorizontalandsteakonthe verticalaxis,illustrateallcombinationsofcarrotsandsteaksthatmake upa2000calorieadaydiet.

Answer:Thisisillustratedasthe“calorieconstraint”inpanel(a)ofExerciseGraph2.7.Youcanget2000caloriesonlyfromsteakif youeat8 steaksandonlyfromcarrotsifyoueat20servingsofcarrots.Theseform theinterceptsofthecalorieconstraint.

ExerciseGraph2.7:(a)CaloriesandVitamins;(b)BudgetConstraint

(b) Onthesamegraph,illustrateallthecombinationsofcarrotsandsteaks thatprovideexactly150unitsofvitamins.

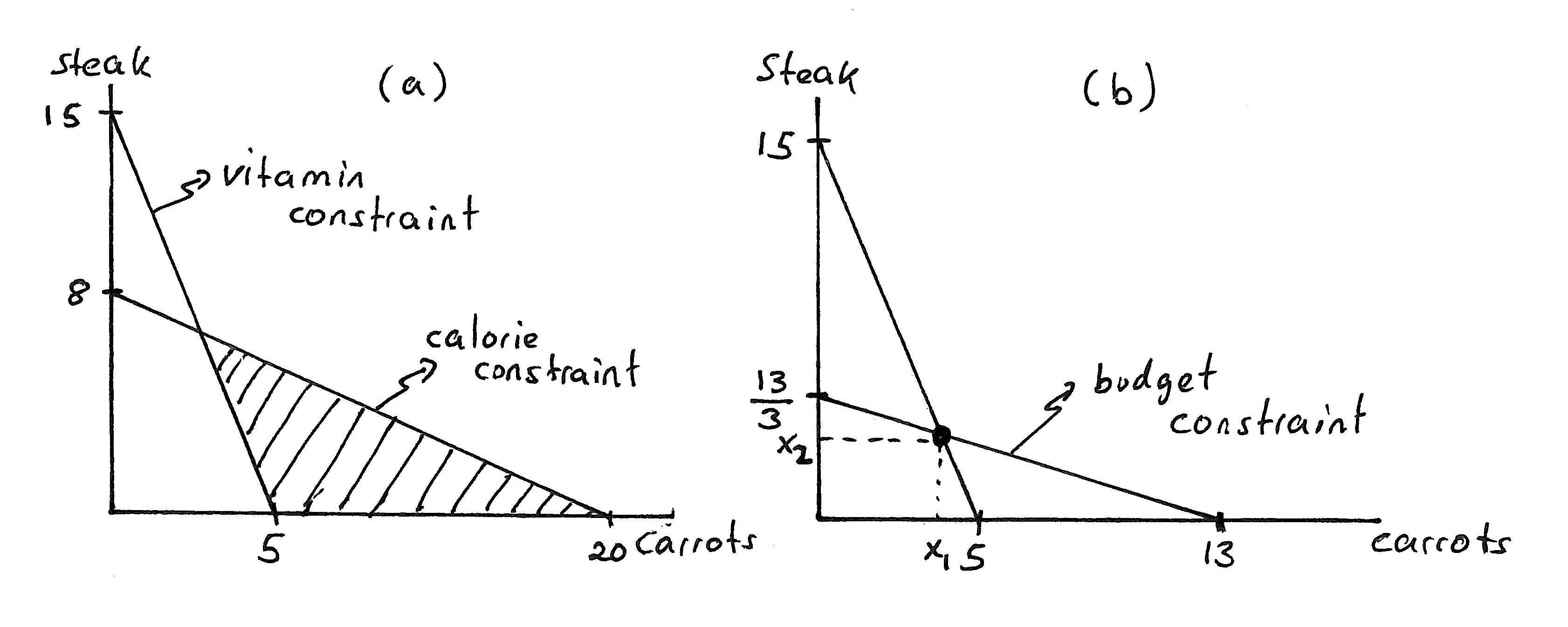
Answer:Thisisalsoillustratedinpanel(a)ofExerciseGraph2.7. Youcan get150unitsofvitaminsfromsteakifyoueat15steaksonlyorifyoueat 5servingsofcarrotsonly.Thisresultsintheinterceptsforthe“vitamin constraint”.

(c) Onthisgraph,shadeinthebundlesofcarrotsandsteaksthat satisfyboth ofyourdoctor’srequirements.

Answer:Yourdoctorwantsyoutoeatnomorethan2000calories—which meansyouneedtostayunderneaththecalorieconstraint.Yourdoctor alsowantsyoutogetatleast150unitsofvitaminE—whichmeansyou mustchooseabundle above thevitaminconstraint.Thisleavesyouwith

theshadedareatochoosefromifyouaregoingtosatisfyboth requirements.

(d) Nowsupposeyoucanbuyaservingofcarrotsfor$2andasteakfor$6.You have$26perdayinyourfoodbudget.Inyourgraph,illustrateyourbudget constraint.Ifyoulovesteakanddon’tmindeatingornoteatingcarrots, whatbundlewillyouchoose(assumingyoutakeyourdoctor’s instructions seriously)?

Answer:With$26youcanbuy13/3steaksifthatisallyoubuy,oryoucan buy13servingsofcarrotsifthatisallyoubuy.Thisformsthetwointerceptsonyourbudgetconstraintwhichhasaslopeof p1/p2 =−1/3and isdepictedinpanel(b)ofthegraph.Ifyoureallylikesteak anddon’tmind eatingcarrotsonewayoranother,youwouldwanttogetasmuchsteak aspossiblegiventheconstraintsyourdoctorgaveyouandgivenyour budgetconstraint.Thisleadsyoutoconsumethebundleattheintersectionofthevitaminandthebudgetconstraintinpanel(b) —indicated by(x1, x2)inthegraph.Itseemsfromthetwopanelsthatthisbundlealso satisfiesthecalorieconstraintandliesinsidetheshadedregion.

B: ContinuewiththescenarioasdescribedinpartA.

(a) DefinethelineyoudrewinA(a)mathematically.

(b) DefinethelineyoudrewinA(b)mathematically.

(c) Informalsetnotation,writedowntheexpressionthatisequivalenttothe shadedareainA(c).

(d) DerivetheexactbundleyouindicatedonyourgraphinA(d).

Answer:Wewouldliketofindthemostamountofsteakwecanaffordin theshadedregion.Ourbudgetconstraintis2x1 +6x2 = 26.Ourgraphsuggeststhatthisbudgetconstraintintersectsthevitaminconstraint(from equation(2.7.ii))withintheshadedregion(inwhichcasethatintersectiongivesusthemoststeakwecanaffordintheshadedregion).Tofind thisintersection,wecanplugequation(2.7.ii)intothebudgetconstraint 2x1 + 6x2 = 26toget

ChoiceSetsandBudgetConstraints

2x1 + 6(15 3x1 ) = 26, (2.7.iv) andthensolvefor x1 toget x1 = 4.Pluggingthisbackintoeitherthebudgetconstraintorthevitaminconstraint,wecanget x2 = 3.Weknowthis liesonthevitaminconstraintaswellasthebudgetconstraint.Tocheck tomakesureitliesintheshadedregion,wejusthavetomakesureitalso satisfiesthedoctor’sordersthatyouconsumefewerthan2000calories. Thebundle(x1, x2)=(4,3)resultsincaloriesof4(100) + 3(250) = 1150,well withindoctor’sorders.

Exercise2.8

EverydayApplication: SettingupaCollegeTrustFund: Supposethatyou,after studyingeconomicsincollege,quicklybecamerich—sorich thatyouhavenothing bettertodothanworryaboutyour16-yearoldniecewhocan’t seemtofocusonher future.Yourniececurrentlyalreadyhasatrustfundthatwillpayheraniceyearly incomeof$50,000startingwhensheis18,andshehasnoother meansofsupport.

A: Youareconcernedthatyourniecewillnotseethewisdomofspendingagood portionofhertrustfundonacollegeeducation,andyouwouldthereforeliketo use$100,000ofyourwealthtochangeherchoicesetinwaysthatwillgiveher greaterincentivestogotocollege.

(a) Oneoptionisforyoutoplace$100,000inasecondtrustfundbuttorestrict yourniecetobeabletodrawonthistrustfundonlyforcollegeexpensesof upto$25,000peryearforfouryears.Onagraphwith“yearlydollarsspent oncollegeeducation”onthehorizontalaxisand“yearlydollarsspenton otherconsumption”onthevertical,illustratehowthisaffectsherchoice set.

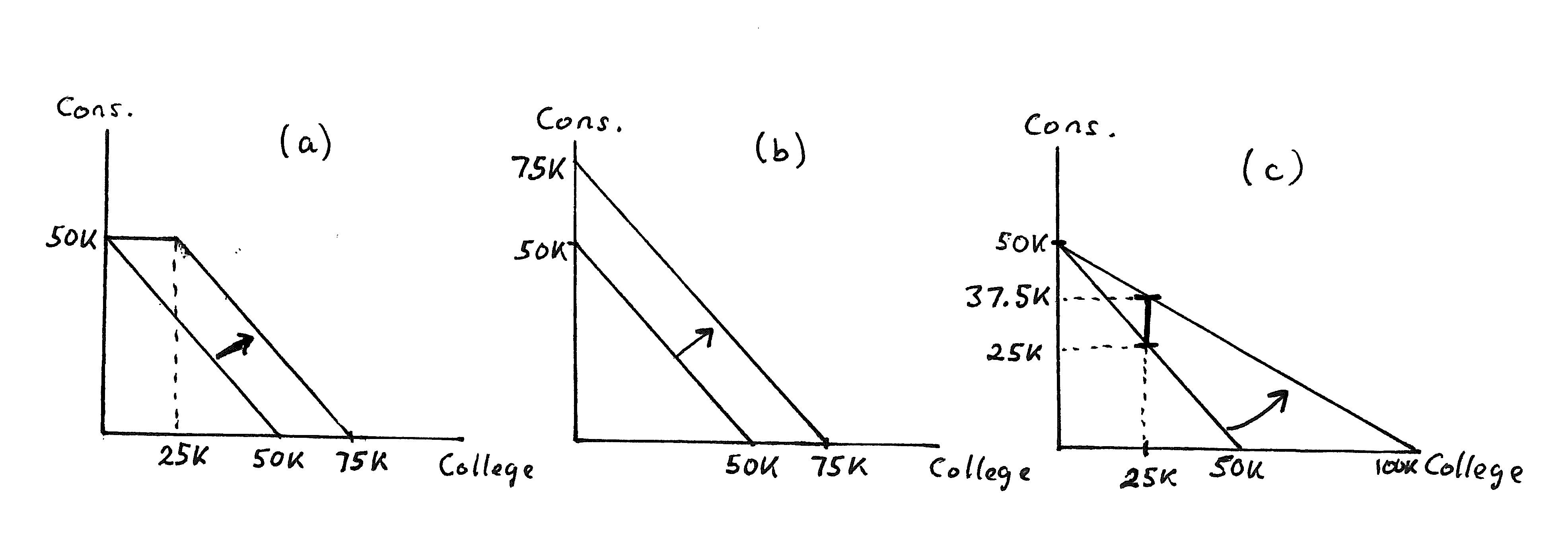
Answer:Panel(a)ofExerciseGraph2.8illustratesthechangeinthebudgetconstraintforthistypeoftrustfund.Theoriginalbudgetshiftsout by$25,000(denoted$25K),exceptthatthefirst$25,000canonlybeused forcollege.Thus,themaximumamountofotherconsumptionremains $50,000becauseofthestipulationthatshecannotusethetrustfundfor non-collegeexpenses.

ExerciseGraph2.8:(a)RestrictedTrustFund;(b)Unrestricted;(c)MatchingTrustFund

(b) Asecondoptionisforyoutosimplytellyourniecethatyouwillgiveher $25,000peryearfor4yearsandyouwilltrustherto“dowhat’sright”.How doesthisimpactherchoiceset?

Answer:Thisisdepictedinpanel(b)ofExerciseGraph2.8—itisapure incomeshiftof$25,000sincetherearenorestrictionsonhowthemoney canbeused.

ChoiceSetsandBudgetConstraints

(c) Supposeyouarewrongaboutyourniece’sshort-sightedness andshewas planningonspendingmorethan$25,000peryearfromherothertrust fundoncollegeeducation.Doyouthinkshewillcarewhether youdoas describedinpart(a)orasdescribedinpart(b)?

Answer:Ifshewasplanningtospendmorethan$25Koncollegeanyhow, thentheadditionalbundlesmadepossiblebythetrustfundin(b)arenot valuedbyher.Shewouldthereforenotcarewhetheryousetup thetrust fundasin(a)or(b).

(d) Supposeyouwererightabouther—sheneverwasgoingtospend very muchoncollege.Willshecarenow?

Answer:Nowshewillcare—becauseshewouldactuallychooseoneof thebundlesmadeavailablein(b)thatisnotavailablein(a) andwould thereforeprefer(b)over(a).

(e) Afriendofyoursgivesyousomeadvice:becareful—yourniecewillnot valuehereducationifshedoesnothavetoputupsomeofherownmoney forit.Soberedbythisadvice,youdecidetosetupadifferenttrustfundthat willrelease50centstoyourniece(tobespentonwhatevershewants)for everydollarthatshespendsoncollegeexpenses.Howwillthisaffecther choiceset?

Answer:Thisisdepictedinpanel(c)ofExerciseGraph2.8.Ifyourniece nowspends$1oneducation,shegets50centsforanythingshe would liketospenditon—so,ineffect,theopportunitycostofgetting$1of additionaleducationisjust50cents.This“matching”trustfundtherefore reducestheopportunitycostofeducationwhereasthepreviousonesdid not.

(f) Ifyourniecespends$25,000peryearoncollegeunderthetrustfundinpart (e),canyouidentifyaverticaldistancethatrepresentshowmuchyoupaid toachievethisoutcome?

Answer:Ifyourniecespends$25,000onhereducationunderthe“matching”trustfund,shewillgethalfofthatamountfromyourtrustfund—or $12,500.Thiscanbeseenastheverticaldistancebetweenthebeforeand afterbudgetconstraints(inpanel(c)ofthegraph)at$25,000ofeducation spending.

B: Howwouldyouwritethebudgetequationforeachofthethreealternatives discussedabove?

Answer:Theinitialbudgetis x1 +x2 = 50,000.Thefirsttrustfundin(a)expands thistoabudgetof

whilethesecondtrustfundin(b)expandsitto x1 + x2 = 75,000.Finally,the last“matching”trustfundin(e)(depictedinpanel(c))is0.5x1 + x2 = 50,000.

Exercise2.9

BusinessApplication: PricingandQuantityDiscounts: Businessesoftengive quantitydiscounts.Below,youwillanalyzehowsuchdiscountscanimpactchoice sets.

A: Irecentlydiscoveredthatalocalcopyservicechargesoureconomicsdepartment$0.05perpage(or$5per100pages)forthefirst10,000copiesinanygiven monthbutthenreducesthepriceperpageto$0.035foreachadditionalpage upto100,000copiesandto$0.02pereachpagebeyond100,000.Supposeour departmenthasamonthlyoverallbudgetof$5,000.

(a) Putting“pagescopiedinunitsof100”onthehorizontalaxis and“dollarsspentonothergoods”onthevertical,illustratethisbudgetconstraint. Carefullylabelallinterceptsandslopes.

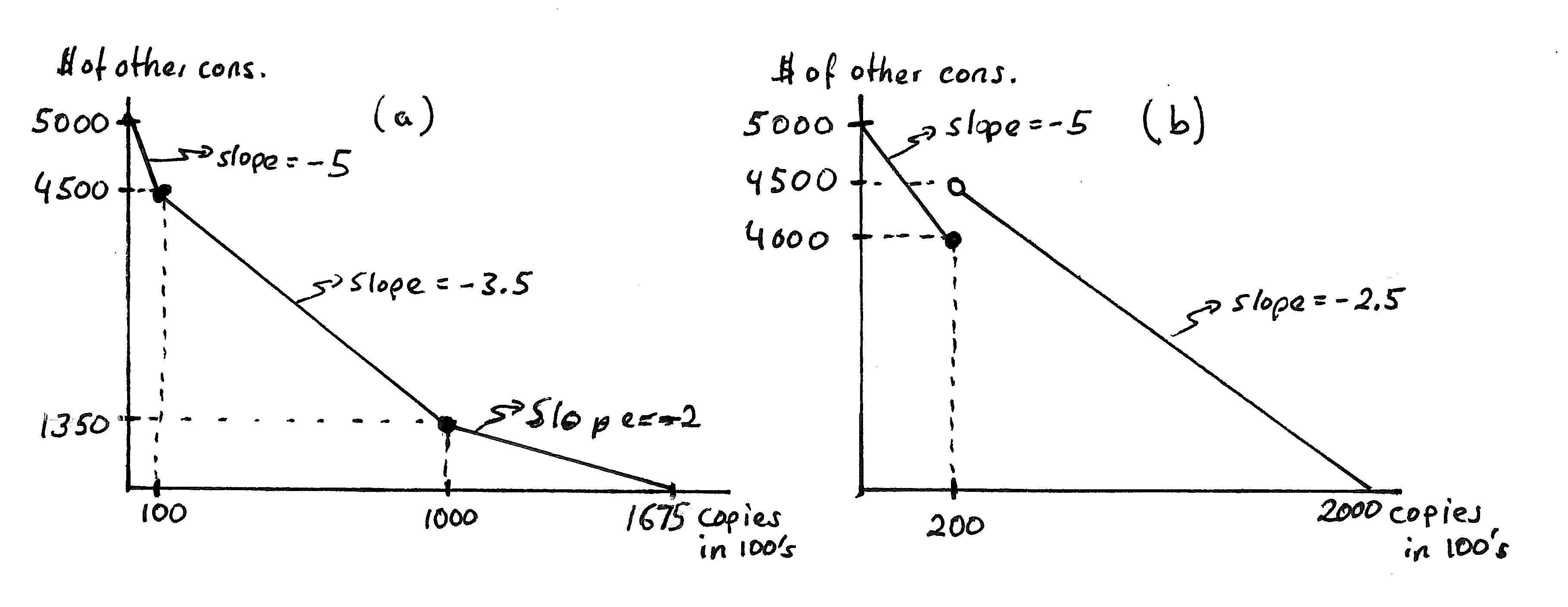
Answer:Panel(a)ofExerciseGraph2.9tracesoutthisbudgetconstraint andlabelstherelevantslopesandkinkpoints.

ExerciseGraph2.9:(a)Constraintfrom2.9A(a);(b)Constraintfrom2.9A(b)

(b) Supposethecopyservicechangesitspricingpolicyto$0.05 perpagefor monthlycopyingupto20,000and$0.025perpagefor all pagesifcopying exceeds20,000permonth.(Hint:Yourbudgetlinewillcontainajump.)

Answer:Panel(b)ofExerciseGraph2.9depictsthisbudget.Thefirst portion(beginningatthe x2 intercept)isrelativelystraightforward.The secondpartarisesforthefollowingreason:Theproblemsaysthat,ifyou copymorethan2000pages, all pagescostonly$0.025perpage—includingthefirst2000.Thus,whenyoucopy20,000pagespermonth, youtotal billis$1,000.Butwhenyoucopy2001pages,yourtotalbillis$500.025.

(c) Whatisthemarginal(or“additional”)costofthefirstpagecopiedafter 20,000inpart(b)?Whatisthemarginalcostofthefirstpagecopiedafter 20,001inpart(b)?

ChoiceSetsandBudgetConstraints

Answer:Themarginalcostofthefirstpageafter20,000is-$499.975,and themarginalcostofthenextpageafterthatis2.5cents.Toseethedifferencebetweenthese,thinkofthemarginalcostastheincreaseinthe totalphoto-copybillforeachadditionalpage.Whengoingfrom20,000to 20,001,thetotalbillfallsby$499.975.Whengoingfrom20,001to20,002, thetotalbillrisesby2.5cents.

B: Writedownthemathematicalexpressionforchoicesetsforeachofthescenariosin2.9A(a)and2.9A(b)(usingx1 todenote“pagescopiedinunitsof100” andx2 todenote“dollarsspentonothergoods”).

Answer:Thechoicesetin(a)is

Exercise2.10

BusinessApplication: Supersizing: SupposeIrunafast-foodrestaurantandI knowmycustomerscomeinonalimitedbudget.Almosteveryonethatcomesinfor lunchbuysasoft-drink.Nowsupposeitcostsmevirtuallynothingtoserveamedium versusalargesoft-drink,butIdoincursomeextracostswhenaddingitems(likea dessertoranotherside-dish)tosomeone’slunchtray.

A: Supposeforpurposesofthisexercisethatcupscomeinallsizes,notjustsmall, mediumandlarge;andsupposetheaveragecustomerhasalunchbudgetB.On agraphwith“ouncesofsoft-drink”onthehorizontalaxisand“dollarsspent onotherlunchitems”onthevertical,illustrateacustomer’sbudgetconstraint assumingIchargethesamepricepperounceofsoft-drinknomatterhowbiga cupthecustomergets.

Answer:Panel(a)ofExerciseGraph2.10illustratestheoriginalbudget,with thepriceperouncedenoted p.Thehorizontalinterceptisthemoneybudget B dividedbythepriceperounceofsoftdrink;theverticalinterceptisjust B (sincethegoodontheverticalaxisisdenominatedindollars—withtheprice of“$’soflunchitems”thereforeimplicitlysetto1.

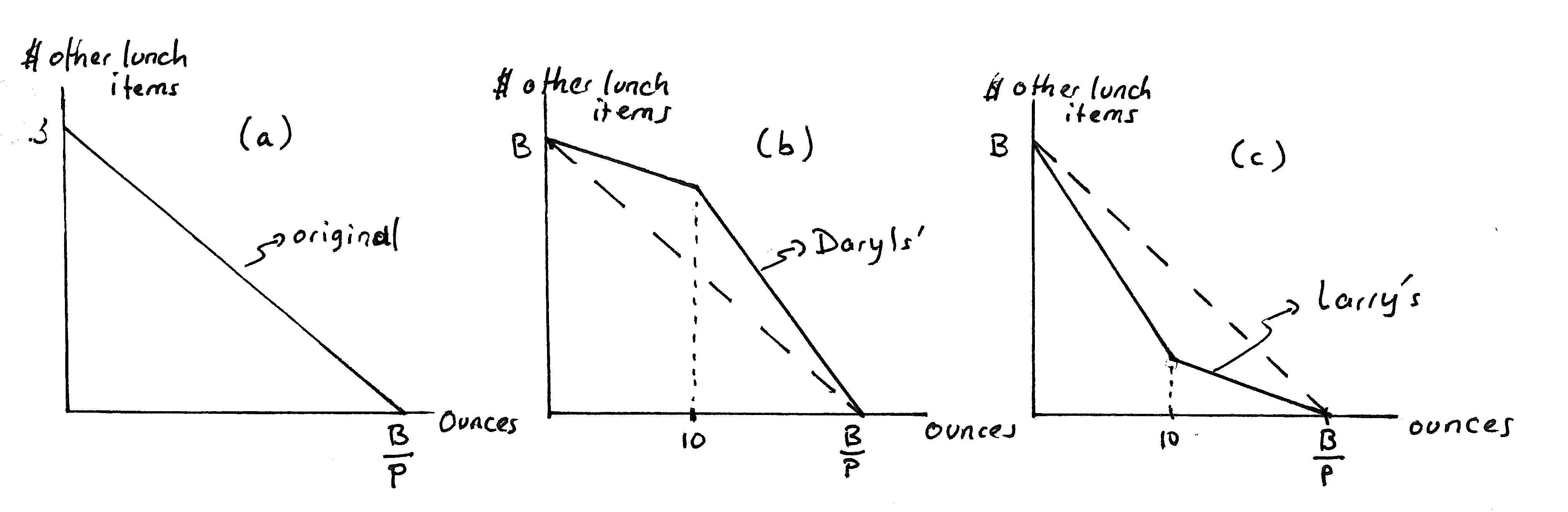
(a) Ihavethreebusinesspartners:Larry,hisbrotherDaryland hisotherbrother Daryl.TheDarylsproposethatwelowerthepriceoftheinitialouncesof soft-drinkthataconsumerbuysandthen,startingat10ounces,weincreasetheprice.Theyhavecalculatedthatouraveragecustomerwouldbe abletobuyexactlythesamenumberofouncesofsoft-drink(ifthatisall heboughtonhislunchbudget)asunderthecurrentsingleprice.Illustrate howthiswillchangetheaveragecustomer’sbudgetconstraint.

Answer:Panel(b)illustratestheDaryls’proposal.Thebudgetisinitially shallower(becauseoftheinitiallowerpriceandthenbecomessteeper at10ouncesbecauseofthenewhigherprice.)Theintercepts areunchangedbecausenothinghasbeendonetoallowtheaveragecustomer tobuymoreofnon-drinkitemsifthatisallshebuys,andbecausethe

ExerciseGraph2.10:(a)OriginalBudget;(b)TheDaryls’proposal;(c)Larry’sproposal

ChoiceSetsandBudgetConstraints

newpriceshavebeenconstructedsoastoallowcustomerstoachievethe sametotaldrinkconsumptionintheeventthattheydonotbuy anything else.

(b) LarrythinkstheDarylsareidiotsandsuggestsinsteadthat weraisethe priceforinitialouncesofsoft-drinkandthen,startingat 10ounces,decreasethepriceforanyadditionalounces.He,too,hascalculatedthat, underhispricingpolicy,theaveragecustomerwillbeabletobuyexactly thesameouncesofsoft-drinks(ifthatisallthecustomerbuysonhislunch budget).Illustratetheeffectontheaveragecustomer’sbudgetconstraint. Answer:Larry’sproposalisgraphedinpanel(c).Thereasoningissimilar tothatinthepreviouspart,exceptnowtheinitialpriceishighandthen becomeslowafter10ounces.

(c) Iftheaveragecustomerhadachoice,whichofthethreepricingsystems— thecurrentsingleprice,theDaryls’proposalorLarry’sproposal—would hechoose?

Answer:CustomerswouldsurelyprefertheDaryls’proposal—since the choicesetitformscontainsalltheotherchoicesets.

P.S:IfyoudidnotcatchthereferencetoLarry,hisbrotherDarylandhis otherbrotherDaryl,Irecommendyourentsomeoldversionsofthe1980’s BobNewhartShow.

B: Writedownthemathematicalexpressionforeachofthethree choicesetsdescribedabove,lettingouncesofsoft-drinksbedenotedbyx1 anddollarsspend onotherlunchitemsbyx2

Answer:Theoriginalbudgetsetinpanel(a)ofExerciseGraph2.10issimply px1 + x2 = B givingachoicesetof

= B px1 . (2.10.i)

IntheDaryls’proposal,wehaveaninitialprice p ′ < p forthefirst10ounces, andthenaprice p ′′ > p thereafter.Wecancalculatethe x2 interceptofthe steeperlinefollowingthekinkpointinpanel(b)ofthegraphbysimplymultiplyingthe x1 interceptof B/p bytheslope p ′′ ofthatlinesegmenttoget Bp ′′ /p ThechoicesetfromtheDaryls’proposalcouldthenbewrittenas {(

Wecouldevenbemorepreciseabouttherelationshipof p ′ , p and p ′′ .The twolinesintersectat x1 = 10,anditmustthereforebethecasethat B 10p ′ = (Bp ′′ /p) 10p ′′ .Solvingthisfor p ′ ,wegetthat p ′ = B(p p ′′ ) 10p + p ′′ (2.10.iii)

Larry’sproposalbeginswithaprice p ′′ > p andthenswitchesat10ouncesto aprice p ′ < p (wherethesepriceshavenoparticularrelationtothepriceswe justusedfortheDaryl’sproposal).Thisresultsinthechoiceset

Wecouldagainderiveananalogousexpressionfor p ′ intermsof p and p ′′

ChoiceSetsandBudgetConstraints

Exercise2.11

BusinessApplication: FrequentFlyerPerks: Airlinesofferfrequentflyersdifferentkindsofperksthatwewillmodelhereasreductionsinaveragepricespermile flown.

A: Supposethatanairlinecharges20centspermileflown.However,oncea customerreaches25,000milesinagivenyear,thepricedropsto10centsper mileflownforeachadditionalmile.Thealternatewaytotravelistodrivebycar whichcosts16centspermile.

(a) Consideraconsumerwhohasatravelbudgetof$10,000peryear,abudget whichcanbespentonthecostofgettingtoplacesaswellas“otherconsumption”whiletraveling.Onagraphwith“milesflown”onthehorizontalaxisand“otherconsumption”onthevertical,illustratethebudgetconstraintforsomeonewhoonlyconsidersflying(andnotdriving)totravel destinations.

Answer:Panel(a)ofExerciseGraph2.11illustratesthisbudgetconstraint.

ExerciseGraph2.11:(a)Airtravel;(b)Cartravel;(c)Comparison

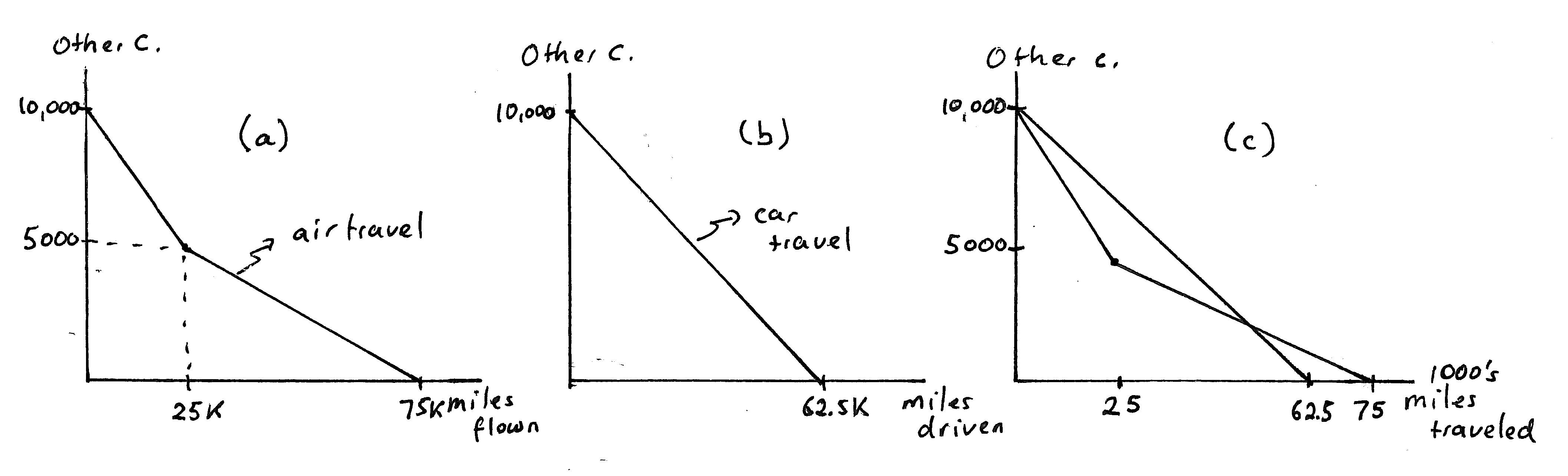
(b) Onasimilargraphwith“milesdriven”onthehorizontalaxis,illustratethe budgetconstraintforsomeonethatconsidersonlydriving(andnotflying) asameansoftravel.

Answer:Thisisillustratedinpanel(b)ofthegraph.

(c) Byoverlayingthesetwobudgetconstraints(changingthegoodonthehorizontalaxissimplyto“milestraveled”),canyouexplainhowfrequentflyer perksmightpersuadesometoflyalotmorethantheyotherwise would?

Answer:Panel(c)ofthegraphoverlaysthetwobudgetconstraints. Ifit werenotforfrequentflyermiles,thisconsumerwouldneverfly—becausedrivingwouldbecheaper.Withthefrequentflyerperks,drivingis cheaperinitiallybutbecomesmoreexpensiveperadditionalmilestraveledifatravelerfliesmorethan25,000miles.Thisparticularconsumer wouldthereforeeithernotflyatall(andjustdrive),orshewouldflya lotbecauseitcanonlymakesensetoflyifshereachestheportionofthe

air-travelbudgetthatcrossesthecarbudget.(Oncewelearnmoreabout howtomodeltastes,wewillbeabletosaymoreaboutwhetherornotit makessenseforatravelertoflyunderthesecircumstances.)

B: Determinewheretheair-travelbudgetfromA(a)intersects thecarbudget fromA(b).

Answer:Theshallowerportionoftheair-travelbudget(relevantformilesflown above25,000)hasequation x2 = 7500 0.1x1 ,where x2 standsforotherconsumptionand x1 formilestraveled.Thecarbudget,ontheotherhand,has equation x2 = 10000 0.16x1 .Todeterminewheretheycross,wecansetthe twoequationsequaltooneanotherandsolvefor x1 —whichgives x1 = 41,667 milestraveled.Pluggingthisbackintoeitherequationgives x2 = $3,333.

ChoiceSetsandBudgetConstraints

Exercise2.12

BusinessApplication: ChoiceinCallingPlans: Phonecompaniesusedtosell minutesofphonecallsatthesamepricenomatterhowmanyphonecallsacustomermade.(Wewillabstractawayfromthefactthattheychargeddifferentprices atdifferenttimesofthedayandweek.)Morerecently,phone companies,particularly cellphonecompanies,havebecomemorecreativeintheirpricing.

A: Onagraphwith“minutesofphonecallspermonth”onthehorizontalaxis and“dollarsofotherconsumption”onthevertical,drawabudgetconstraint assumingthepriceperminuteofphonecallsispandassuming theconsumer hasamonthlyincomeI.

Answer:ExerciseGraph2.12givesthisbudgetconstraintasthestraightline withverticalintercept I .

ExerciseGraph2.12:PhonePlans

(a) Nowsupposeanewoptionisintroduced:Youcanpay$Px tobuyintoa phoneplanthatoffersyouxminutesoffreecallspermonth,withanycalls beyondxcostingpperminute.Illustratehowthischangesyourbudget constraintandassumethatPx issufficientlylowsuchthatthenewbudget containssomebundlesthatwerepreviouslyunavailabletoourconsumer.

Answer:Thesecondbudgetconstraintinthegraphbeginsat I Px whichishowmuchmonthlyincomeremainsavailableforother consumptiononcethefixedfeeforthefirst x minutesispaid.Thepriceper additionalminuteisthesameasbefore—soafter x callshavebeenmade, theslopeofthenewbudgetisthesameastheoriginal.

(b) Supposeitactuallycostsphonecompaniesclosetopperminutetoprovideaminuteofphoneservicesothat,inordertostayprofitable,aphone companymustonaveragegetaboutpperminuteofphonecall.Ifallconsumerswereabletochoosecallingplanssuchthattheyalwaysuseexactly xminutespermonth,woulditbepossibleforphonecompanies tosetPx sufficientlylowsuchthatnewbundlesbecomeavailabletoconsumers?

Answer:Ifthephonecompanyneedstomakeanaverageof p perminute ofphonecalls,andifallconsumersplanaheadperfectlyand choosecallingplansunderwhichtheyusealltheirfreeminutes,thenthecompany wouldhavetoset Px = px.Butthatwouldmeanthatthekinkpointon thenewbudgetwouldoccurexactlyontheoriginalbudget—thusmakingnonewbundlesavailableforconsumers.

(c) Ifsomefractionofconsumersinanygivenmonthbuyintoacallingplan butmakefewerthanxcalls,howdoesthisenablephonecompaniestoset Px suchthatnewbundlesbecomeavailableinconsumerchoicesets?

Answer:Ifsomeconsumersdonotinfactusealltheir“freeminutes”, thenthephonecompanycouldset Px < px andstillcollectanaverageof p perminuteofphonecall.Thiswouldcausethekinkpointofthenew budgettoshifttotherightoftheoriginalbudget—makingnewbundles availableforconsumers.Consumerswhoplanaheadwellare, insome sense,receivingatransferfromconsumerswhodonotplanaheadwell.

B: Supposeaphonecompanyhas100,000customerswhocurrently buyphone minutesundertheoldsystemthatchargespperminute.Supposeitcoststhe companyctoprovideoneadditionalminuteofphoneservicebutthecompany alsohasfixedcostsFC(thatdon’tvarywithhowmanyminutesaresold)ofan amountthatissufficientlyhightoresultinzeroprofit.Supposeasecondidenticalphonecompanyhas100,000customersthathaveboughtintoacallingplan thatchargesPx = kpxandgivescustomersxfreeminutesbeforechargingpfor minutesabovex.

(a) Ifpeopleonaverageusehalftheir“freeminutes”permonth, whatisk(asa functionsofFC,p,candx)ifthesecondcompanyalsomakeszeroprofit?

Answer:Theprofitofthesecondcompanyisitsrevenueminusitscosts. Revenueis

Eachcustomeronlyuses x/2minutes,whichmeansthecostofproviding thephoneminutesis100,000(cx/2) = 50,000cx.Thecompanyalsohas tocoverthefixedcosts FC .So,ifprofitiszeroforthesecondcompany (asitisforthefirst),then

(b) Iftherewerenofixedcosts(i.e.FC = 0)buteverythingelsewasstillas statedabove,whatdoeschavetobeequaltoinorderforthefirstcompany tomakezeroprofit?Whatiskinthatcase?

Answer: c = p and k = 1/2.Thisshouldmakeintuitivesense:Underthe simplifiedscenario,thefactthatpeopleonaverageuseonly halftheir

ChoiceSetsandBudgetConstraints

“freeminutes”impliesthatthesecondcompanycansetitsfixedfeeof x minutesathalfthepricethattheothercompanywouldcharge forconsumingthatmanyminutes.

Exercise2.13

PolicyApplication: FoodStampProgramsandotherTypesofSubsidies: The U.S.governmenthasafoodstampprogramforfamilieswhoseincomefallsbelow acertainpovertythreshold.Foodstampshaveadollarvalue thatcanbeusedatsupermarketsforfoodpurchasesasifthestampswerecash,but thefoodstampscannot beusedforanythingotherthanfood.

A: Supposetheprogramprovides$500offoodstampspermonthto aparticular familythathasafixedincomeof$1,000permonth.

(a) With“dollarsspentonfood”onthehorizontalaxisand“dollarsspenton non-fooditems”onthevertical,illustratethisfamily’smonthlybudgetconstraint.Howdoestheopportunitycostoffoodchangealongthebudget constraintyouhavedrawn?

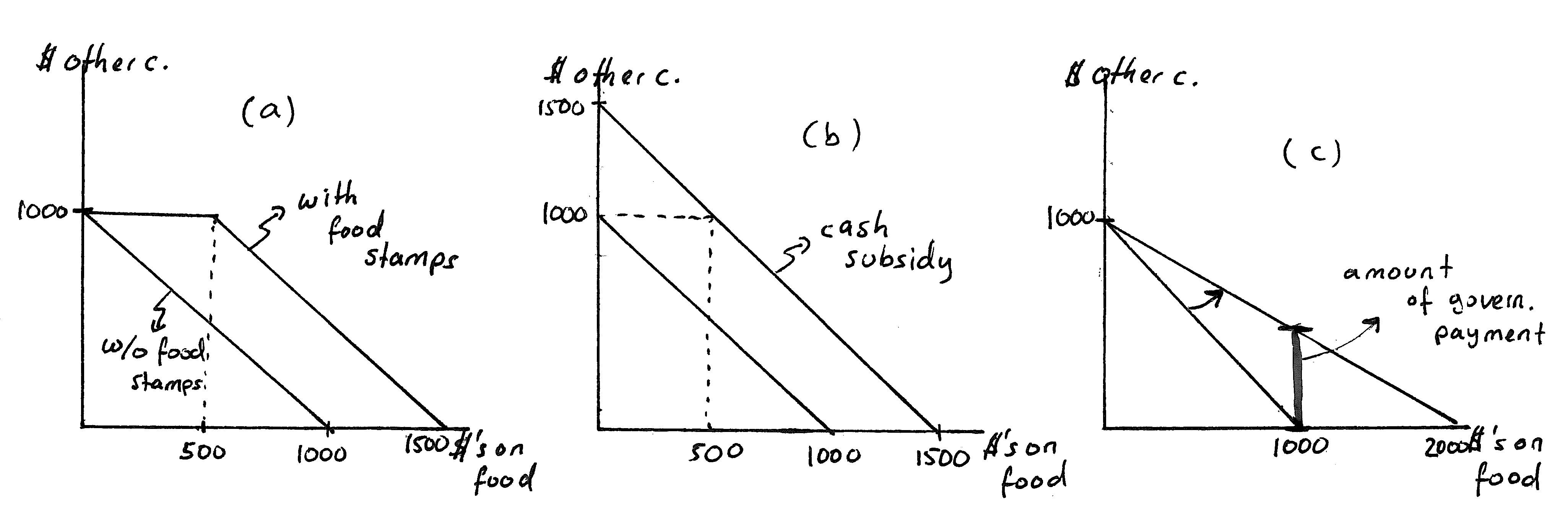
Answer:Panel(a)ofExerciseGraph2.13illustratestheoriginalbudget— withintercept1,000oneachaxis.Itthenillustratesthenewbudgetunder thefoodstampprogram.Sincefoodstampscanonlybespenton food, the“othergoods”interceptdoesnotchange—owningsomefoodstamps stillonlyallowshouseholdstospendwhattheypreviouslyhadonother goods.However,thefamilyisnowabletobuy$1,000inothergoodseven asitbuysfood—becauseitcanusethefoodstampsonthefirst$500 worthoffoodandstillhaveallitsotherincomeleftforotherconsumption.Onlyafterallthefoodstampsarespent—i.e.afterthe familyhas bought$500worthoffood—doesthefamilygiveupotherconsumptionwhenconsumingadditionalfood.Asaresult,theopportunitycost offoodiszerountilthefoodstampsaregone,anditis1after that.Thatis, afterthefoodstampsaregone,thefamilygivesup$1inother consumptionforevery$1offooditpurchases.

(b)

ExerciseGraph2.13:(a)FoodStamps;(b)Cash;(c)Re-imbursehalf

Howwouldthisfamily’sbudgetconstraintdifferifthegovernmentreplaced thefoodstampprogramwithacashsubsidyprogramthatsimplygavethis

ChoiceSetsandBudgetConstraints

family$500incashinsteadof$500infoodstamps?Whichwouldthefamilyprefer,andwhatdoesyouranswerdependon?

Answer:Inthiscase,theoriginalbudgetwouldsimplyshiftoutby$500 asdepictedinpanel(b).Ifthefamilyconsumesmorethan$500offood underthefoodstampprogram,itwouldnotseemlikeanything really changesunderthecashsubsidy.(Wecanshowthismoreformallyonce weintroduceamodeloftastes).If,ontheotherhand,thefamilyconsumes$500offoodunderthefoodstamps,itmaywellbethatit would prefertogetcashinsteadsothatitcanconsumemoreothergoodsinstead.

(c) Howwouldthebudgetconstraintchangeifthegovernmentsimplyagreed toreimbursethefamilyforhalfitsfoodexpenses?

Answer:Inthiscase,thegovernmentessentiallyreducestheprice of$1of foodto50centsbecausewhenever$1isspentonfood,thegovernment reimbursesthefamily50cents.Theresultingchangeinthefamilybudget isthendepictedinpanel(c)ofthegraph.

(d) Ifthegovernmentspendsthesameamountforthisfamilyontheprogram describedin(c)asitdidonthefoodstampprogram,howmuchfoodwill thefamilyconsume?Illustratetheamountthegovernmentis spendingas averticaldistancebetweenthebudgetlinesyouhavedrawn.

Answer:Ifthegovernmentspent$500forthisfamilyunderthisprogram, thenthefamilywillbeconsuming$1,000offoodand$500inothergoods. Youcanillustratethe$500thegovernmentisspendingasthe distance betweenthetwobudgetconstraintsat$1,000offoodconsumption.The reasoningforthisisasfollows:Ontheoriginalbudgetline,youcansee thatconsuming$1,000offoodimpliesnothingisleftoverfor“otherconsumption”.Whenthefamilyconsumes$1,000offoodunderthe newprogram,itisabletoconsume$500inothergoodsbecauseoftheprogram— sothegovernmentmusthavemadethatpossiblebygiving$500 tothe family.

B: Writedownthemathematicalexpressionforthechoicesetyoudrewin2.13A(a), lettingx1 representdollarsspentonfoodandx2 representdollarsspentonnonfoodconsumption.Howdoesthisexpressionchangein2.13A(b)and2.13A(c)?

Answer:Theoriginalbudgetconstraint(priortoanyprogram)isjust x2 = 1000 x1,andthebudgetconstraintwiththe$500cashpaymentinA(b) is x2 = 1500 x1 .Thechoicesetunderfoodstamps(depictedinpanel(a))then is

whilethechoicesetinpanel(b)underthecashsubsidyis

ChoiceSetsandBudgetConstraints

Exercise2.14

PolicyApplication: PublicHousingandHousingSubsidies: Foralongperiod,the U.S.governmentfocuseditsattemptstomeethousingneedsamongthepoorthrough publichousingprograms.Eligiblefamiliescouldgetonwaitingliststoapplyfor anapartmentinapublichousingdevelopmentandwouldbeofferedaparticular apartmentastheymovedtothetopofthewaitinglist.

A: Supposeaparticularfamilyhasamonthlyincomeof$1,500andisoffereda 1,500squarefootpublichousingapartmentfor$375inmonthlyrent.Alternatively,thefamilycouldchoosetorenthousingintheprivatemarketfor$0.50per squarefoot.

(a) Illustrateallthebundlesinthisfamily’schoicesetof“squarefeetofhousing”(onthehorizontalaxis)and“dollarsofmonthlyothergoodsconsumption”(ontheverticalaxis).

Answer:Thefullchoicesetwouldincludeallthebundlesthatareavailablethroughtheprivatemarketplusthebundlethegovernmenthasmade available.Inpanel(a)ofExerciseGraph2.14,theprivatemarketconstraintisdepictedtogetherwiththesinglebundlethatthe government makesavailablethroughpublichousing.(Thatbundlehas$1,125inother monthlyconsumptionbecausethegovernmentcharges$375forthe1,500 squarefootpublichousingapartment.)

ExerciseGraph2.14:(a)PublicHousing;(b)RentalSubsidy

(b) Inrecentyears,thegovernmenthasshiftedawayfromanemphasison publichousingandtowardprovidingpoorfamilieswithadirectsubsidyto allowthemtorentmorehousingintheprivatemarket.Suppose,insteadof offeringthefamilyinpart(a)anapartment,thegovernment offeredtopay halfofthefamily’srentalbill.Howwouldthischangethefamily’sbudget constraint?

Answer:Thechangeinpolicyisdepictedinpanel(b)ofthegraph.

(c) Isitpossibletotellwhichpolicythefamilywouldprefer?

Answer:Sincethenewbudgetinpanel(b)containsthepublichousing bundlefrompanel(a)butalsocontainsadditionalbundlesthatwerepreviouslynotavailable,thehousingsubsidymustbeatleastasgoodasthe publichousingprogramfromtheperspectiveofthehousehold.

B: Writedownthemathematicalexpressionforthechoicesetsyoudrewin2.14A(a) and2.14A(b),lettingx1 denotesquarefeetofmonthlyhousingconsumptionand x2 denotedollarsspentonnon-housingconsumption.

Answer:Thepublichousingchoiceset(whichincludestheoptionof notparticipatinginpublichousingandrentingintheprivatemarketinstead)isgiven by

ChoiceSetsandBudgetConstraints

Exercise2.15

PolicyApplication: TaxingGoods versus LumpSumTaxes: Ihavefinallyconvincedmylocalcongressmanthatmywife’stasteforgritsarenutsandthattheworld shouldbeprotectedfromtoomuchgritsconsumption.Asaresult,mycongressman hasagreedtosponsornewlegislationtotaxgritsconsumptionwhichwillraisethe priceofgritsfrom$2perboxto$4perbox.Wecarefullyobservemywife’sshopping behaviorandnoticewithpleasurethatshenowpurchases10boxesofgritspermonth ratherthanherprevious15boxes.

A: Putting“boxesofgritspermonth”onthehorizontaland“dollarsofotherconsumption”onthevertical,illustratemywife’sbudgetline beforeandafterthe taxisimposed.(YoucansimplydenoteincomebyI.)

Answer:Thetaxraisestheprice,thusresultinginarotationofthe budgetline asillustratedinpanel(a)ofExerciseGraph2.15.Sincenoindicationofan incomelevelwasgivenintheproblem,incomeissimplydenoted I

ExerciseGraph2.15:(a)TaxonGrits;(b)LumpSumRebate

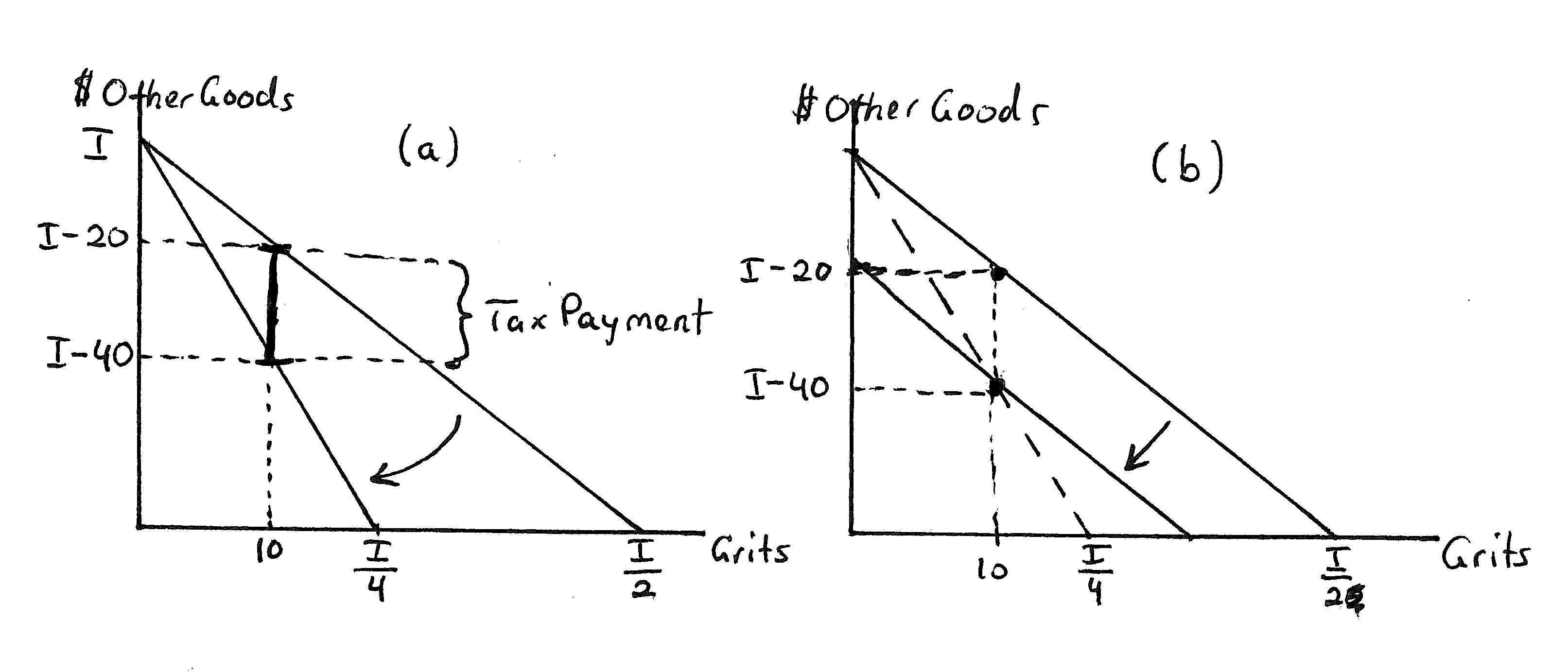
(a) Howmuchtaxrevenueisthegovernmentcollectingpermonthfrommy wife?Illustratethisasaverticaldistanceonyourgraph.(Hint:Ifyou knowhowmuchsheisconsumingafterthetaxandhowmuchinother consumptionthisleavesherwith,andifyouknowhowmuchinotherconsumptionshewouldhavehadifsheconsumedthatsamequantitybefore theimpositionofthetax,thenthedifferencebetweenthese two“otherconsumption”quantitiesmustbeequaltohowmuchshepaidintax.)

Answer:Whensheconsumes10boxesofgritsafterthetax,shepays$40 forgrits.Thisleavesherwith(I 40)tospendonothergoods.Hadshe bought10boxesofgritspriortothetax,shewouldhavepaid$20,leaving herwith(I 20).Thedifferencebetween(I 40)and(I 20)is$20— whichisequaltotheverticaldistanceinpanel(a).Youcanverifythat thisisexactlyhowmuchsheindeedmusthavepaid—thetaxis$2per

boxandshebought10boxes,implyingthatshepaid$2times10 or$20in gritstaxes.

(b) GiventhatIliveintheSouth,thegritstaxturnedouttobeunpopularin mycongressionaldistrictandhasledtothedefeatofmycongressman.His replacementwononapro-gritsplatformandhasvowedtorepealthegrits tax.However,newbudgetrulesrequirehimtoincludeanewwaytoraise thesametaxrevenuethatwasyieldedbythegritstax.Heproposestosimplyaskeachgritsconsumertopayexactlytheamountheorshe paidin gritstaxesasamonthlylumpsumpayment.Ignoringforthemoment thedifficultyofgatheringthenecessaryinformationforimplementingthis proposal,howwouldthischangemywife’sbudgetconstraint?

Answer:Inpanel(b)ofExerciseGraph2.15,thepreviousbudgetunder thegritstaxisillustratedasadashedline.Thegritstaxchangedtheopportunitycostofgrits—andthustheslopeofthebudget(asillustrated inpanel(a)).Thelumpsumtax,ontheotherhand,doesnotalteropportunitycostsbutsimplyreducesincomeby$20,theamountofgritstaxes mywifepaidunderthegritstax.Thischangeisillustratedinpanel(b).

B: StatetheequationsforthebudgetconstraintsyouderivedinA(a)andA(b), lettinggritsbedenotedbyx1 andotherconsumptionbyx2

Answer:Theinitial(before-tax)budgetwas x2 = I 2x1 whichbecomes x2 = I 4x1 aftertheimpositionofthegritstax.Thelumpsumtaxbudget constraint, ontheotherhand,is x2 = I 20 2x1

ChoiceSetsandBudgetConstraints

Exercise2.16

PolicyApplication: PublicSchoolsandPrivateSchoolVouchers: Considerasimplemodelofhoweconomiccircumstancesarechangedwhenthe governmententers theeducationmarket.

A: Supposeahouseholdhasanafter-taxincomeof$50,000andconsideritsbudgetconstraintwith“dollarsofeducationservices”onthehorizontalaxisand “dollarsofotherconsumption”onthevertical.Beginbydrawingthehousehold’s budgetline(giventhatyoucaninferapriceforeachofthegoodsontheaxes fromthewaythesegoodsaredefined)assumingthatthehouseholdcanbuyany levelofschoolspendingontheprivatemarket.

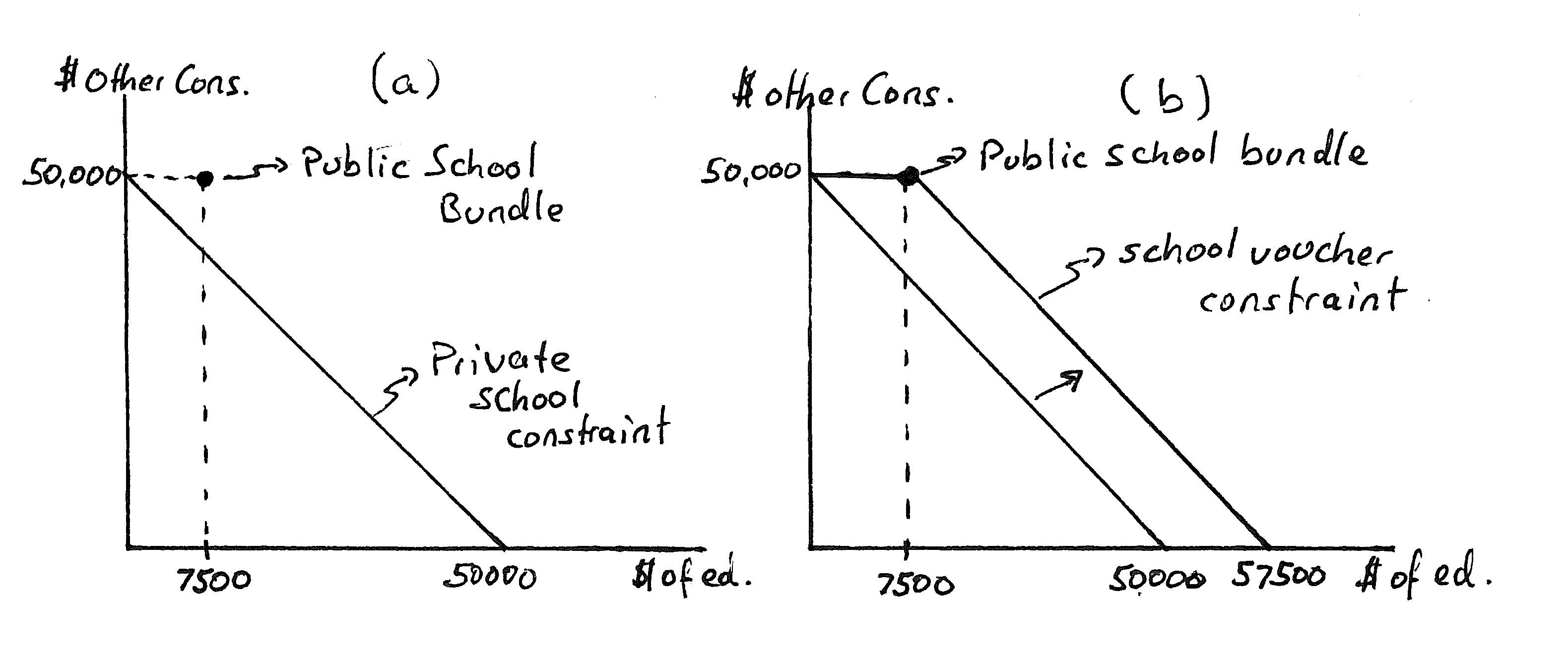
Answer:Thebudgetlineinthiscaseisstraightforwardandillustratedinpanel (a)ofExerciseGraph2.16astheconstraintlabeled“privateschoolconstraint”.

ExerciseGraph2.16:(a)PublicSchools;(b)PrivateSchool Voucher

(a) Nowsupposethegovernmentusesitsexistingtaxrevenuesto fundapublicschoolat$7,500perpupil;i.e.itfundsaschoolthatanyonecanattendforfreeandthatprovides$7,500ineducationservices.Illustratehow thischangesthechoiceset.(Hint:Oneadditionalpointwillappearinthe choiceset.)

Answer:Sincepubliceducationisfree(andpaidforfromexistingtaxrevenues—i.e.nonewtaxesareimposed),itnowbecomespossibletoconsumeapublicschoolthatoffers$7,500ofeducationalserviceswhilestill consuming$50,000inotherconsumption.Thisaddsanadditionalbundletothechoiceset—thebundle(7,500,50,000)denoted“publicschool bundle”inpanel(a)ofthegraph.

(b) Continuetoassumethatprivateschoolservicesofanyquantitycouldbe purchasedbutonlyifthechilddoesnotattendpublicschools.Canyou thinkofhowtheavailabilityoffreepublicschoolsmightcausesomechildrentoreceivemoreeducationalservicesthanbeforetheywouldintheabsenceofpublicschools?Canyouthinkofhowsomechildrenmightreceive fewereducationalservicesoncepublicschoolsareintroduced?

Answer:Ifahouseholdpurchasedlessthan$7,500ineducationservices forachildpriortotheintroductionofthepublicschool,it seemslikely thatthehouseholdwouldjumpattheopportunitytoincrease bothconsumptionofothergoodsandconsumptionofeducationservicesbyswitchingtothepubliceducationbundle.Atthesametime,ifahouseholdpurchasedmorethan$7,500ineducationservicespriortotheintroduction ofpublicschools,itisplausiblethatthishouseholdwillalsoswitchtothe publicschoolbundle—because,whileitwouldmeanlesseductionserviceforthechild,itwouldalsomeanalargeincreaseinotherconsumption.(Wewillbeabletobemorepreciseonceweintroduceamodelof tastes.)

(c) Nowsupposethegovernmentallowsanoption:eitheraparent cansend herchildtothepublicschoolorshecantakeavouchertoaprivateschool anduseitforpartialpaymentofprivateschooltuition.Assumethatthe voucherisworth$7,500peryear;i.e.itcanbeusedtopayfor upto$7,500 inprivateschooltuition.Howdoesthischangethebudgetconstraint?Do youstillthinkitispossiblethatsomechildrenwillreceivelesseducation thantheywouldifthegovernmentdidnotgetinvolvedatall(i.e.nopublic schoolsandnovouchers)?

Answer:Thevoucherbecomesequivalenttocashsolongasatleast$7,500 isspentoneducationservices.Thisresultsinthebudgetconstraintdepictedinpanel(b)ofExerciseGraph2.16.Sinceonecannotusethe vouchertoincreaseotherconsumptionbeyond$50,000,thevoucherdoes notmakeanyprivateconsumptionabove$50,000possible.However,it doesmakeitpossibletoconsumeanylevelofeducationservicebetween 0and$7,500withoutincurringanyopportunitycostinterms ofother consumption.Onlyoncethefullvoucherisusedand$7,500in educationserviceshavebeenboughtwillthehouseholdbegivingupadollarin otherconsumptionforeveryadditionaldollarineducation services. Itiseasytoseehowthiswillleadsomeparentstochoosemore education fortheirchildren(justasitwastruethattheintroduction ofthepublic schoolbundlegetssomeparentstoincreasetheeducationservicesconsumedbytheirchildren.)Butthereversenolongerappearslikely—if someonechosesmorethan$7,500ineducationservicesinthe absenceof publicschoolsandvouchers,theeffectiveincreaseinhouseholdincome impliedbythevoucher/publicschoolcombinationmakesitunlikelythat suchahouseholdwillreducetheeducationservicesgivento herchild. (Again,wewillbeabletobemorepreciseonceweintroducetastes— andwewillseethatitwouldtakeunrealistictastesforthis tohappen.)

B: Lettingdollarsofeducationservicesbedenotedbyx1 anddollarsofotherconsumptionbyx2,formallydefinethechoicesetwithjustthepublicschool(and aprivateschoolmarket)aswellasthechoicesetwithprivateschoolvouchers definedabove.

ChoiceSetsandBudgetConstraints

Answer:Thefirstchoiceset(inpanel(a)ofthegraph)isformallydefinedas

,

whiletheintroductionofvoucherschangesthechoicesetto

Exercise2.17

PolicyApplication: TaxDeductionsandTaxCredits: IntheU.S.incometax code,anumberofexpendituresare“deductible”.Formosttaxpayers,thelargest taxdeductioncomesfromtheportionoftheincometaxcodethatpermitstaxpayers todeducthomemortgageinterest(onbothaprimaryandavacationhome).This meansthattaxpayerswhousethisdeductiondonothavetopay incometaxonthe portionoftheirincomethatisspentonpayinginterestontheirhomemortgage(s). Forpurposesofthisexercise,assumethattheentireyearly priceofhousingisinterest expense.

A: TrueorFalse:Forsomeonewhosemarginaltaxrateis33%,thismeansthat thegovernmentissubsidizingroughlyonethirdofhisinterest/housepayments.

Answer:Considersomeonewhopays$10,000peryearinmortgageinterest. Whenthispersondeducts$10,000,itmeansthathedoesnothavetopaythe 33%incometaxonthatamount.Inotherwords,bydeducting$10,000inmortgageinterest,thepersonreduceshistaxobligationby$3,333.33.Thus,thegovernmentisreturning33centsforeverydollarininterestpaymentsmade—effectivelycausingtheopportunitycostofpaying$1inhomemortgageinterest tobeequalto66.67cents.Sothestatementistrue.

(a) Considerahouseholdwithanincomeof$200,000whofacesataxrateof 40%,andsupposethepriceofasquarefootofhousingis$50peryear.With squarefootageofhousingonthehorizontalaxisandotherconsumption onthevertical,illustratethishousehold’sbudgetconstraintwithandwithouttaxdeductibility.(Assumeinthisandtheremainingpartsofthequestionthatthetaxratecitedforahouseholdappliestoallofthathousehold’s income.)

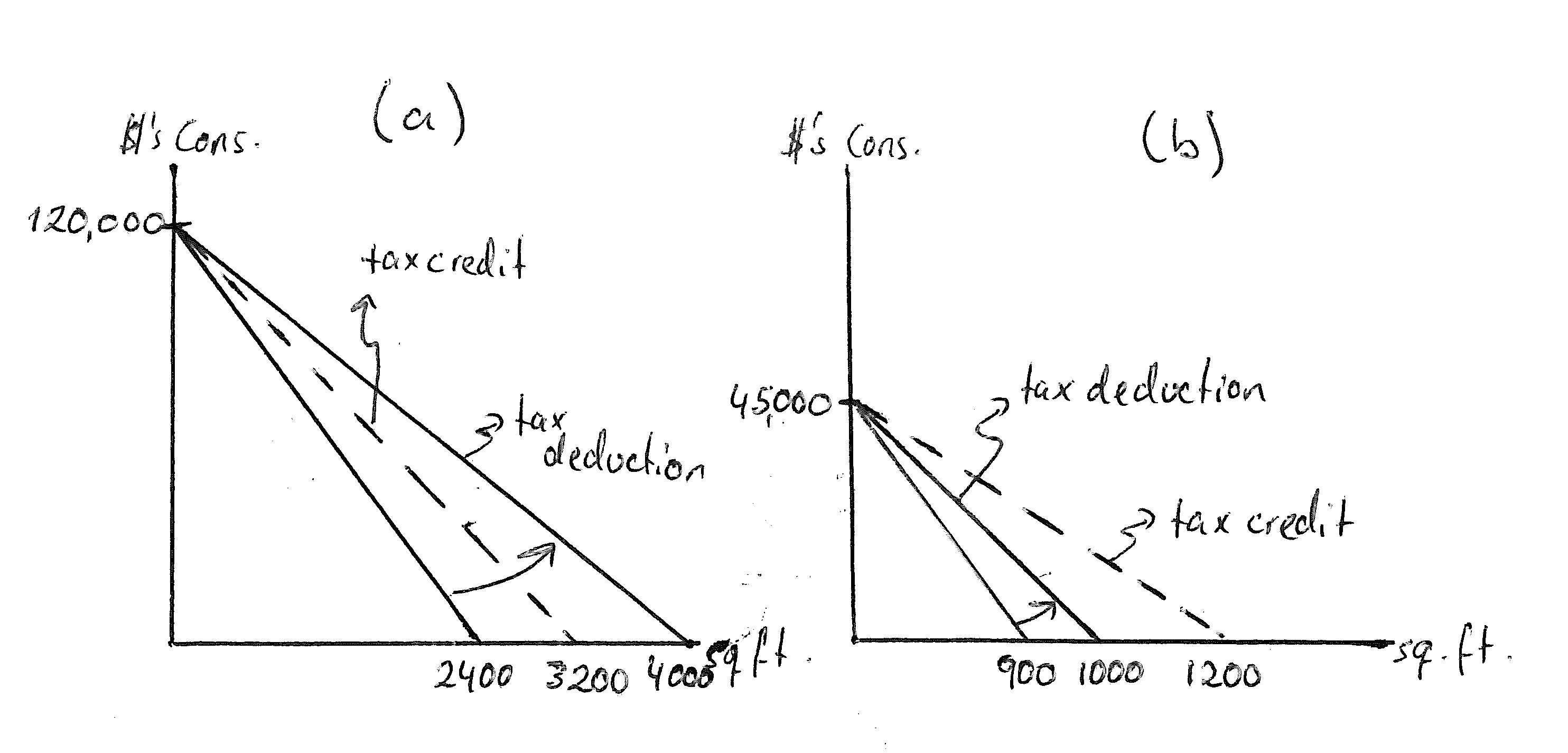
Answer:Asjustdemonstrated,thetaxdeductibilityofhomemortgage interestlowersthepriceofowner-occupiedhousing,andit doessoin proportiontothesizeofthemarginalincometaxrateonefaces.

ExerciseGraph2.17:TaxDeductionsversusTaxCredits

ChoiceSetsandBudgetConstraints

Panel(a)ofExerciseGraph2.17illustratesthisgraphicallyforthecase describedinthispart.Witha40percenttaxrate,thehouseholdcould consumeasmuchas0.6(200,000)=120,000inothergoodsifit consumed nohousing.Withapriceofhousingof$50persquarefoot,the pricefalls to(1 0.4)50 = 30undertaxdeductibility.Thus,thebudgetrotatesout tothesolidbudgetinpanel(a)ofthegraph.Withoutdeductibility,the consumerpays$50persquarefoot—whichmakes120,000/50=2,400the biggestpossiblehouseshecanafford.Butwithdeductibility,thebiggest houseshecanaffordis120,000/30=4,000squarefeet.

(b) Repeatthisforahouseholdwithincomeof$50,000whofacesa taxrateof 10%.

Answer:Thisisillustratedinpanel(b).Thehouseholdcouldconsume asmuchas$45,000inotherconsumptionafterpayingtaxes,andthedeductibilityofhousepaymentsreducesthepriceofhousingfrom$50per squarefootto(1 0.1)50 = $45persquarefoot.Thisresultsintheindicatedrotationofthebudgetfromthelowertothehighersolidlinein thegraph.Therotationissmallerinmagnitudebecausetheimpactof deductibilityontheafter-taxpriceofhousingissmaller. Withoutdeductibility,thebiggestaffordablehouseis45,000/50=900squarefeet,while withdeductibilitythebiggestpossiblehouseis45,000/45=1,000square feet.

(c) Analternativewayforthegovernmenttoencouragehomeownershipwould betoofferatax credit insteadofatax deduction.Ataxcreditwouldallow alltaxpayerstosubtractafractionkoftheirannualmortgagepayments directlyfromthetaxbilltheywouldotherwiseowe.(Note:Becareful—a taxcreditisdeductedfromtax payments thataredue,notfromthetaxable income.)Forthehouseholdsin(a)and(b),illustratehowthisalterstheir budgetifk = 0.25.

Answer:ThisisillustratedinthetwopanelsofExerciseGraph2.17 —in panel(a)forthehigherincomehousehold,andinpanel(b)forthelower incomehousehold.Bysubsidizinghousingthroughacreditratherthana deduction,thegovernmenthasreducedthepriceofhousingbythesame amount(k)foreveryone.Inthecaseofdeductibility,thegovernment hadmadethepricesubsidydependentonone’staxrate—withthose facinghighertaxratesalsogettingahighersubsidy.Thepriceofhousing howfallsfrom$50to(1 0.25)50 = $37.50—whichmakesthelargest affordablehouseforthewealthierhousehold120,000/37.5=3,200square feetand,forthepoorerhousehold,45,000/37.5=1,200squarefeet.Thus, thepoorerhouseholdbenefitsmorefromthecreditwhen k = 0.25while thericherhouseholdbenefitsmorefromthededuction.

(d) Assumingthatataxdeductibilityprogramcoststhesameinlosttaxrevenuesasataxcreditprogram,whowouldfavorwhichprogram?

Answer:Peoplefacinghighermarginaltaxrateswouldfavorthedeductibilityprogramwhilepeoplefacinglowermarginaltaxrateswouldfavorthe taxcredit.

B: Letx1 andx2 representsquarefeetofhousingandotherconsumption,and let thepriceofasquarefootofhousingbedenotedp.

(a) Supposeahouseholdfacesataxratetforallincome,andsupposetheentireannualhousepaymentahouseholdmakesisdeductible.Whatisthe household’sbudgetconstraint?

Answer:Thebudgetconstraintwouldbe x2 = (1 t )I (1 t )px1

(b) Nowwritedownthebudgetconstraintunderataxcreditasdescribedabove.

Answer:Thebudgetconstraintwouldnowbe x2 = (1 t )I (1 k)px1.