Precalculus 10th edition sullivan solutions manual by james.barone369

Precalculus 10th Edition Sullivan Solutions Manual

To download the complete and accurate content document, go to: https://testbankbell.com/download/precalculus-10th-edition-sullivan-solutions-manual/

Precalculus 10th Edition Sullivan Solutions Manual Visit TestBankBell.com to get complete for all chapters

Chapter 7 Analytic Trigonometry

Section 7.1

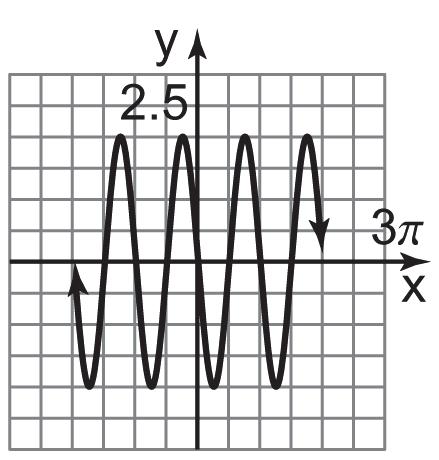
1. Domain: { } is any real number xx ; Range: { }11yy−≤≤

2. { }|1xx ≥ or { }|1xx ≤

3. [ ) 3, ∞

4. True

5. 1; 3 2

6. 1 2 ; 1

7. sin x y =

8. 0 x π ≤≤

9. x −∞≤≤∞

10. False. The domain of 1 sin yx = is 11 x −≤≤

11. True

12. True 13. d 14. a 15. 1 sin0

We are finding the angle θ , 22 θ ππ −≤≤ , whose sine equals 0.

sin0, 22 0 sin00

16. 1 cos1

We are finding the angle θ , 0 θ ≤≤π , whose

cos1,0 0 cos10

θθ

=≤≤π

17. () 1 sin1

1 sin1,

()

2 sin1 2 θθ

1 cos1,0 cos1 θθ

()

tan0

θθ

ππ =−<<

20. () 1 tan1

θθ

649

θθ

ππ =−≤≤

cosine equals 1. = =

π −=−

We are finding the angle θ , 22 θ ππ −≤≤ , whose sine equals 1

ππ =−−≤≤ π =−

18. () 1 cos1

=π −=π

We are finding the angle θ , 0 θ ≤≤π , whose cosine equals 1 .

=−≤≤π

19.

We are finding the angle θ , 22 θ ππ −<< , whose tangent equals 0. = =

tan0, 22 0 tan00

We are finding the angle θ , 22 θ ππ −<< , whose tangent equals 1 . π =− π −=−

tan1, 22 4 tan(1) 4

θ ππ =−−<<

Chapter 7: Analytic Trigonometry

21. 1 2 sin 2

2 sin, 222 4 2 sin 24

ππ =−≤≤

−<< , whose tangent equals 3 3 .

1 3 tan, 322

ππ =−<<

3 θθ

=−

3 sin, 222 3 3 sin 23 π

25. 1 3 cos 2

   

We are finding the angle θ , 0 θ ≤≤π , whose cosine equals 3 2 1 θθ θ

   

We are finding the angle θ , 22 θ ππ −≤≤ , whose sine equals 2 2

2 sin, 222 4 2 sin 24  π −=−  

650

θθ θ

We are finding the angle θ , 22 θ ππ −≤≤ , whose sine equals 2 2 1 π

= 22. 1 3 tan 3

ππ

6 3

θθ θ ππ

π = π =

We are finding the angle θ , 22 θ

tan 36

=−<<

23. 1 tan3

We are finding the angle θ , 22 θ ππ −<< , whose tangent equals 3 . 1    

tan3, 22 3 tan3

24. 1 3 sin 2

We are finding the angle θ , 22 θ ππ −≤≤ , whose sine equals 3 2 1

θθ θ  π −=−  

ππ =−−≤≤

3 cos,0 2 =−≤≤π π =  π −=  

5 6 35 cos 26

26. 1 2 sin 2

θθ

θ ππ =−−≤≤ π =−

Section 7.1: The Inverse Sine, Cosine, and Tangent Functions

follows the form of the equation () () () ()11tantan f fxxx == .

3 8 π is in the interval , 22

, we can apply the equation directly and get

follows the form of the equation () () () ()

, we can apply the equation directly and get

f fxxx == . Since 3 7 π is in the interval , 22

follows the form of the equation () () () ()11sinsin f fxxx == . Since 10 π is in the interval , 22 ππ 

, we can apply the equation directly and get

43. 1 9 sinsin 8

follows the form of the equation () () () ()11sinsin f fxxx == , but we cannot use the formula directly since 9 8 π is not in the interval , 22

for which

. We need to find an angle θ in the interval , 22

sinsin 8 π θ = . The angle 9 8 π is in quadrant III so sine is negative. The reference angle of 9 8 π is 8 π and we want θ to be in quadrant IV so sine will still be negative. Thus, we have

. Since 8 π is in the interval ,

, we can apply the equation above and get

1 sin0.10.10 ≈

≈

1 7 cos0.51 8 ≈

1 1 sin0.13 8 ≈

1 tan(0.4)0.38 −≈− 34. 1 tan(3)1.25 −≈− 35. 1 sin(0.12)0.12 −≈− 36. 1 cos(0.44)2.03 −≈ 37. 1 2 cos1.08 3 ≈ 38. 1 3 sin0.35 5 ≈ 39. 1 4 coscos 5 π   

()

11 coscos f fxxx ==

Since 4 5 π is in the interval 0, π  

we can

directly and get 1 44 coscos 55 ππ =   40. 1 sinsin 10 π       



ππ  −=−     .

1 3 tantan 8 π       

27.

28.

cos0.60.93

29.

tan51.37

30.

tan0.20.20

31.

32.

33.

follows the form of the equation

() () ()

apply the equation



sinsin 1010

41.

Since

ππ   

1 33 tantan 88 ππ  −=−    

sinsin 7 π       

11sinsin

ππ   

1 33 sinsin 77 ππ  −=−    

42. 1 3

π       

ππ      

ππ   

ππ

 

22 ππ      

11 9 sinsinsinsin

πππ =−=−  

9 sinsin 88

=−

888

Chapter 7: Analytic Trigonometry

44. 1 5 coscos 3 π        follows the form of the equation () () () () 11 coscos f fxxx == , but we cannot use the formula directly since 5 3 π is not in the interval 0, π   . We need to find an angle θ in the interval 0, π   for which 5 coscos 3 π θ  −=  . The angle 5 3 π is in quadrant I so the reference angle of 5 3 π is 3 π Thus, we have 5 coscos 33 ππ −=  . Since 3 π is in the interval 0, π   , we can apply the equation above and get 11 5 coscoscoscos 333 πππ

follows the form of the equation () () () ()11tantan f fxxx == , but we cannot use the formula directly since 4 5 π is not in the interval , 22 ππ  

. We need to find an angle

for which

. The angle 4 5 π is in quadrant

II so tangent is negative. The reference angle of 4 5 π is 5 π and we want θ to be in quadrant IV so tangent will still be negative. Thus, we have

. Since 5 π is in the interval , 22

, we can apply the equation above and get

47. 1 coscos 4 π follows the form of the equation () () () () 11 coscos f fxxx == , but we cannot use the formula directly since 4 π is not in the interval 0, π     . We need to find an angle θ in the interval 0, π   for which coscos 4 π θ −= . The angle 4 π is in quadrant IV so the reference angle of 4 π is 4 π . Thus, we have coscos 44 ππ −= . Since 4 π is in the interval 0, π     , we can apply the equation above and get 11 coscoscoscos 444

652

 −== 

 . 45. 1 4

π       



ππ   

4 tantan 5 π θ 

 



tantan 5

in the interval , 22

 

ππ   

  =−=−     46. 1 2 tantan 3 π        follows the

() () () ()11tantan f fxxx == . but we cannot use the formula directly since 2 3 π is not in the interval , 22 ππ       . We need to find an angle θ in the interval , 22 ππ       for which 2 tantan 3 π θ  −=  . The angle 2 3 π is in quadrant III so tangent is positive. The reference

2 tantan 33 ππ  −=   . Since 3 π is in the interval ,

ππ       , we can

above and get 11 2 tantantantan 333

 −==   

tantan 55 ππ  =−

4 tantantantan 555 πππ

form

the equation

angle of 2 3 π is 3

and we want θ to be in quadrant I so tangent will still be positive. Thus, we have

apply the equation

πππ

πππ −==

Section 7.1: The Inverse Sine, Cosine, and Tangent Functions

48. 1 3 sinsin 4 π follows the form of the equation () () () ()11sinsin f fxxx == , but we cannot use the formula directly since 3 4 π is not in the interval , 22

. We need to find an angle

angle of 3 2 π is 2 π . Thus, we have 3 tantan 22 ππ −= . In this case, tan 2 π is undefined so 1 tantan 2 π would also be undefined.

in the interval , 22

for which 3 sinsin 4 π θ −= . The reference angle of 3 4 π is 4 π and we want θ to be in quadrant IV so sine will still be negative. Thus, we have 3 sinsin 44 ππ −=− . Since 4 π is in the interval , 22

, we can apply the equation above and get 11 3 sinsinsinsin 444 πππ

49. 1 tantan 2 π follows the form of the equation () () () ()11tantan f fxxx == . We need to find an angle θ in the interval , 22

for which tantan 2 π θ = . In this case, tan 2 π is undefined so 1 tantan 2 π would also be undefined.

50. 1 3 tantan 2 π follows the form of the equation () () () ()11tantan f fxxx == . We need to find an angle θ in the interval , 22

for which 3 tantan 2 π θ −= . The reference

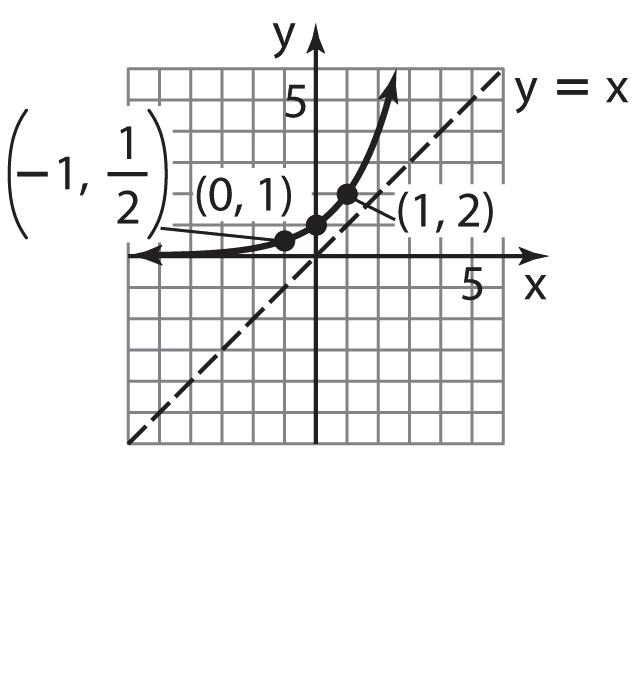
51. 1 1 sinsin 4

follows the form of the equation

() () () ()11 sinsin f fxxx == . Since 1 4 is in the interval 1,1     , we can apply the equation directly and get 1 11 sinsin 44

52. 1 2 coscos 3

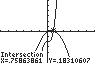
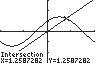
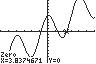
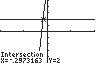
follows the form of the equation () () () ()11 coscos f fxxx ==

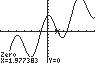
Since 2 3 is in the interval 1,1   , we can apply the equation directly and get 1 22 coscos 33

53. () 1 tantan4 follows the form of the equation

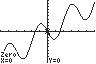
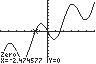
() () () ()11 tantan f fxxx == . Since 4 is a real number, we can apply the equation directly and get () 1 tantan44 = .

54. () () 1 tantan2 follows the form of the equation

() () () ()11 tantan f fxxx == . Since 2 is a real number, we can apply the equation directly and get () () 1 tantan22 −=−

55. Since there is no angle θ such that cos1.2 θ = , the quantity 1 cos1.2 is not defined. Thus, () 1 coscos1.2 is not defined.

653

  

ππ   

−=−=−

ππ

ππ      

  



 

      

  −=−    

Chapter 7: Analytic Trigonometry

56. Since there is no angle θ such that sin2 θ =− , the quantity () 1 sin2 is not defined. Thus, () () 1 sinsin2 is not defined.

57. () 1 tantan π follows the form of the equation () () () ()11 tantan f fxxx == . Since π is a real number, we can apply the equation directly and get () 1 tantan ππ = .

58. Since there is no angle θ such that sin1.5 θ =− , the quantity () 1 sin1.5 is not defined. Thus, () () 1 sinsin1.5 is not defined.

60. () 2tan3 2tan3 f xx yx

2tan3 2tan3 3 tan 2 3 tan 2

59. () 5sin2fxx=+ 5sin2yx=+ () 11

5sin2 5sin2 2 sin 5 2 sin 5

=+ =− = ==

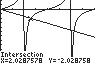
xy yx x y x yfx

The domain of () f x equals the range of

interval notation. To find the domain of () 1 f x we note that the argument of the inverse sine function is 2 5 x and that it must lie in the interval 1,1 

. That is,

The domain of () 1 f x is { }|37xx−≤≤ , or 3,7   in interval notation. Recall that the domain of a function equals the range of its inverse and the range of a function equals the domain of its inverse. Thus, the range of f is also 3,7   .

xy yx x y x yfx

=− =+ + = + ==

=− =− () 11

The domain of () f x equals the range of 1 () f x and is 22 x ππ −<< or , 22

notation. To find the domain of () 1 f x we note that the argument of the inverse tangent function can be any real number. Thus, the domain of () 1 f x is all real numbers, or () , −∞∞ in interval notation. Recall that the domain of a function equals the range of its inverse and the range of a function equals the domain of its inverse. Thus, the range of f is () , −∞∞ .

61. ()() 2cos3 f xx =−

The domain of () f x equals the range of 1 () f x and is 0 3 x π ≤≤ , or 0,

in interval notation. To find the domain of () 1 f x we note that the argument of the inverse cosine function is 2 x and that it must lie in the interval 1,1

654

x ππ −≤≤

ππ   



1 () f x and is 22

or , 22

2 11 5 525 37 x x x −≤≤ −≤−≤ −≤≤

  

ππ

in interval

()

() () () 1 11 2cos3 cos3 2 3cos 2 1 cos 32 xy x y x y x yfx =− =−  =−   =−=  

2cos3 yx =−

  

  

That is, 11 2 22 22 x x x −≤−≤ ≥≥− −≤≤ The domain of () 1 f x is { }|22xx−≤≤ , or

3 π



Section 7.1: The Inverse Sine, Cosine, and Tangent Functions

2,2   in interval notation. Recall that the domain of a function equals the range of its inverse and the range of a function equals the domain of its inverse. Thus, the range of f is 2,2  

odd function).

3sin2 sin2 3 2sin 3 1 sin 23

= = = ==

62. ()() 3sin2 f xx = ()3sin2 yx = () () ()

xy x y x y x yfx

1 11

The domain of () f x equals the range of

1 () f x and is 44 x ππ −≤≤ , or , 44 ππ 

in interval notation. To find the domain of () 1 f x we note that the argument of the inverse sine function is 3 x and that it must lie in the interval

1,1   . That is, 11 3 33

x x

−≤≤ −≤≤

The domain of () 1 f x is { }|33xx−≤≤ , or

3,3   in interval notation. Recall that the domain of a function equals the range of its inverse and the range of a function equals the domain of its inverse. Thus, the range of f is

(note here we used the fact that 1 tan y x = is an

in interval notation. To find the domain of () 1 f x we note that the argument of the inverse tangent function can be any real number. Thus, the domain of () 1 f x is all real numbers, or () , −∞∞ in interval notation. Recall that the domain of a function equals the range of its inverse and the range of a function equals the domain of its inverse. Thus, the range of f is () , −∞∞ 64. ()()cos21fxx=++ () cos21yx=++ () () () () 1 1 =++ +=− +=− =−−

cos21 2cos1 cos12 xy

cos21

The domain of () f x equals the range of 1 () f x and is 22 x π −≤≤− , or 2,2 π     in interval notation. To find the domain of () 1 f x we note that the argument of the inverse cosine function is 1 x and that it must lie in the interval 1,1     . That is, 111 02 x x −≤−≤ ≤≤

655

 

 63. ()() () tan13 tan13 fxx yx =−+− =−+− () () () () ()() 1 1 11 tan13 tan13 1tan3 1tan3 1tan3 xy yx yx yx x fx =−+− +=−− +=−− =−+−− =−−+=

3,3 

     

The domain of () f x equals the range of 1 () f x and is 11 22 x ππ −−≤≤− , or 1,1 22 ππ yx yx yx

The domain of () 1 f x is { }|02xx≤≤ , or 0,2     in interval notation. Recall that the domain of a function equals the range of its inverse and the range of a function equals the domain of its inverse. Thus, the range of f is 0,2    

Chapter 7: Analytic Trigonometry

65. ()() 3sin21fxx=+ () 3sin21yx=+

The domain of () f x equals the range of 1 () f x and is 11 2424 x ππ −−≤≤−+ , or 11 , 2424 ππ  −−−+   in interval notation. To find the domain of () 1 f x we note that the argument of the inverse sine function is 3 x and that it must lie in the interval 1,1   . That is, 11 3 33

x x

−≤≤ −≤≤ The domain of () 1 f x is { }|33xx−≤≤ , or 3,3   in interval notation. Recall that the domain of a function equals the range of its inverse and the range of a function equals the domain of its inverse. Thus, the range of f is 3,3 

66. ()() 2cos32fxx=+

()2cos32yx=+

2,2 π π π

= = == The solution set is 2 2          . 68. 1 1

The domain of () 1 f x is { }|22xx−≤≤ , or 2,2     in interval notation. Recall that the domain of a function equals the range of its inverse and the range of a function equals the domain of its inverse. Thus, the range of f is x x x

−≤≤ 4sin sin 4 2 sin 42

x x x

π π π

2cos cos 2 cos0 2

= = == The solution set is {0}

656

() () () 1

232

=+ += +=  =−    =−=  

1 11 3sin21 sin21 3 21sin

2sin1 3 11 sin

y x yfx



() () () 1 1 11 2cos32 cos32 2 32cos 2 3cos2 2 12 cos 323 xy x y x y x y x yfx =+ +=  +=    =−    =−=  

The domain of () f x equals the range of 1 () f x and is 22 333 x π −≤≤−+ , or 22 , 333 π   −−+     in interval notation. To find the domain of () 1 f x we note that the argument of the inverse cosine function is 2 x and that it must lie in the interval 1,1     . That is, 11 2 22−≤≤

x x     67. 1 1

Section 7.1: The Inverse Sine, Cosine, and Tangent Functions

75. Note that 294529.75 θ ′ =°=° a.

76. Note that 404540.75 θ ′ =°=°

77. Note that 211821.3 θ ′ =°=°

657 Copyright © 2016 Pearson Education, Inc. 69. () () 1 1 3cos22 2 cos2 3 2 2cos 3 1 2 2 1 4 x x x x x π π π = = = =− =− The solution set is 1 4    . 70. () () 1 1 6sin3 sin3 6 3sin 6 1 3 2 1 6 x x x x x π π π −= =−  =−  =− =− The solution set is 1 6    71. 1 1 3tan tan 3 tan3 3 x x x π π π = = == The solution set is { }3 . 72. 1 1 4tan tan 4 tan1 4 x x x π π π −= =−  =−=−   The solution set is {1} 73. 11 1 1 1 4cos22cos 2cos20 2cos2 cos cos1 x x x x x x π π π π π −= −= = = ==− The solution set is {1} . 74. 11 1 1 5sin22sin3 3sin sin 3 3 sin 32 xx x x x ππ π π π −=− =− =−  =−=−   The solution set is 3 2     

()

241 13.92 hours or 13 hours, 55 minutes D ππ     =⋅− π     ≈ b. () () () 1 costan0tan29.75180180 241 12 hours D ππ     =⋅− π     ≈ c. () () () 1 costan22.8tan29.75180180 241 13.85 hours or 13 hours, 51 minutes D ππ   ⋅⋅   =⋅− π     ≈

() () 1 costan23.5tan29.75180180

() () () 1 costan23.5tan40.75180180 241 14.93 hours or 14 hours, 56 minutes D ππ  =⋅− π  ≈ b. () () () 1 costan0tan40.75180180 241 12 hours D ππ  =⋅− π  ≈ c. () () () 1 costan22.8tan40.75180180 241 14.83 hours or 14 hours, 50 minutes D ππ  =⋅− π  ≈

1 costan23.5tan21.3180180 241 13.30 hours or 13 hours, 18 minutes D ππ  ⋅⋅ =⋅− π  ≈ b.

1 costan0tan21.3180180 241 12 hours D ππ  =⋅− π  ≈

. a. () () ()

() () ()

Chapter 7: Analytic Trigonometry

c. () () ()

hours or 13 hours, 15 minutes

78. Note that 611061.167 θ ′ =°≈°

a. () () ()

d. The amount of daylight at this location on the winter solstice is 24240 −= hours. That is, on the winter solstice, there is no daylight. In general, for a location at 6630' ° north latitude, it ranges from around-the-clock daylight to no daylight at all.

81. Let point C represent the point on the Earth’s axis at the same latitude as Cadillac Mountain, and arrange the figure so that segment CQ lies along the x-axis (see figure).

b. () () ()

() () ()

At the latitude of Cadillac Mountain, the effective radius of the earth is 2710 miles. If point D(x, y) represents the peak of Cadillac Mountain, then the length of segment PD is

d. There are approximately 12 hours of daylight every day at the equator.

80. Note that 663066.5 θ ′ =°=° . a. () () () 1 costan23.5tan66.5180180

b. () () () 1 costan0tan66.5180180

82.

2710 cos 2710.29 2710 cos0.01463 radians 2710.29 ==  =≈  

Finally, 2710(0.01463)39.64 miles srθ ==≈ , and 2(2710)39.64 24 t π = , so

24(39.64) 0.05587 hours3.35 minutes

2(2710) t π =≈≈

tantan11346 x x x θ  =−  . a. ()

11346

658

Education, Inc.

241 13.26

D ππ  =⋅− π  ≈

costan22.8tan21.3180180

241 18.96

D ππ  =⋅− π  ≈

costan23.5tan61.167180180

hours or 18 hours, 57 minutes

241 12 hours D ππ  =⋅− π  ≈

241 18.64

D ππ  ⋅⋅ =⋅− π  ≈

241 12 hours D ππ  =⋅− π  ≈ b.

1 costan0tan0180180 241 12 hours D ππ  =⋅− π  ≈

241 12 hours D ππ  =⋅− π  ≈

costan0tan61.167180180

c. () () ()

costan22.8tan61.167180180

hours or 18 hours,

minutes

79.

costan23.5tan0180180

() () ()

c. () () ()

costan22.8tan0180180

241 24

D ππ  =⋅− π  ≈

241 12

D ππ  =⋅− π  ≈ c. ()

1 costan22.8tan66.5180180 241 22.02

D ππ  ⋅⋅ =⋅− π  ≈

hours

() ()

hours or

hours,

minute

1 mile 1530 ft0.29 mile 5280 feet ⋅≈ . Therefore, the point (,)(2710,) Dxyy = lies on a circle with radius 2710.29 r = miles. We now have 1 x r θ θ

10tantan42.6 1010 θ  =−≈°  

Therefore, a person atop Cadillac Mountain will see the first rays of sunlight about 3.35 minutes sooner than a person standing below at sea level.

()

y x θ P Q (2 71 0 ,0 ) D () x,y C s 27 1 0 mi 2710 2710

If you sit 10 feet from the screen, then the viewing angle is about 42.6°

If you sit 15 feet from the screen, then the viewing angle is about 44.4°

If you sit 20 feet from the screen, then the viewing angle is about 42.8°

b. Let r = the row that result in the largest viewing angle. Looking ahead to part (c), we see that the maximum viewing angle occurs when the distance from the screen is about 14.3 feet. Thus,

Sitting in the 4th row should provide the largest viewing angle.

c. Set the graphing calculator in degree mode and let

85. Here we have 1 4150' α =° , 1 8737' β =−° , 2 2118' α =° , and 2 15750' β =−° . Converting minutes to degrees gives

2 6 157 β

. Substituting these values, and 3960 r = , into our equation gives 4250 d ≈ miles. The distance from Chicago to Honolulu is about 4250 miles.

(remember that S and W angles are negative)

86. Here we have 1 2118' α =° , 1 15750' β =−° , 2 3747' α =−° , and 2 14458' β =° .

Pearson Education, Inc. () 11346 15tantan44.4 1515 θ  =−≈°  

Section 7.1: The Inverse Sine, Cosine, and Tangent Functions

2016

() 11346 20tantan42.8 2020 θ  =−≈°  

53(1)14.3 53314.3 312.3 4.1 r r r r +−= +−= = =

1 346 tantan Y x x  =−  : 050 0° 90° Use MAXIMUM: 050 0° 90°

maximum

14.3 x ≈

83. a. 0 a = ; 3 b = ; The area is: 1111 tantantan3tan0 0 3 square units 3 ba π π −=− =− = b. 3 3 a =− ; 1 b = ; The area is: 1111 3 tantantan1tan 3 46 5 square units 12 ba ππ π  −=−−    =−−  = 84. a. 0 a = ; 3 2 b = ; The area is: 1111 3 sinsinsinsin0 2 0 3 square units 3 ba π π  −=−    =− = b. 1 2 a =− ; 1 2 b = ; The area is: sinsinsinsin111111 22 66 square units 3 ba ππ π  −=−−   =−−  =

The

viewing angle will occur when

feet.

() 5 1 6 41 α =° , () 37 1 60 87 β =−°

α =° ,

()

, 2 21.3

and

=−°

Chapter 7: Analytic Trigonometry

Converting minutes to degrees gives 1 21.3 α =° ,

() 5 1 6 157 β =−° , () 47 2 60 37 α =−° , and

() 29 2 30 144 β =° . Substituting these values, and 3960 r = , into our equation gives 5518 d ≈ miles. The distance from Honolulu to Melbourne is about 5518 miles. (remember that S and W angles are negative) 87.

Section 7.2

1. Domain: odd integer multiples of 2 xx

Range: { } 1 or 1 yyy

2. True

3. 15 5 5 =

4. sec x y = , 1 ≥ , 0 , π

5. cosine

6. False

7. True

8. True

9. 1 2 cossin 2

88. The function f is one-to-one because every horizontal line intersects the graph at exactly one point.

Find the angle ,, 22 θθππ −≤≤ whose sine equals 2 2

10. 1 1 sincos 2

Find the angle ,0, θθ≤≤π whose cosine equals 1 2

660

3 3 10411 107 log10log7 3log10log7 3log7 log7 3 x x x x x x += = = = = = The solution is: log7 3

89. 22 22 ()12 12 12 12 log(1)log2 log(1)log2 x x y y y fx y x x x xy =+ =+ =+ −= −= −= 2 1 2 log(1) ()log(1) xy fxx −= =− 90. 133 sincos 33224 ππ ==

π   ≠    ,

≤−≥

   

θθ θ ππ =−≤≤

=  π ==   

1 2 sin, 222 4 22 cossincos 242

  

sincossin13

θθ θ =≤≤π π = π  ==  

1 1 cos,0 2 3

232

Find

15.

equals 1 2 . 1 ππ =−−≤≤ π =−  π  −=−=− 

1 sin, 222 6 1 cotsincot3 26

() 1 csctan1

θθππ

−<<

16.

θθππ

() 1 tan3, 22 3 sectan3sec2 3 θθ θ ππ =−<< π = π ==

17. 1

θθππ

−≤≤ whose sine θθ θ

11. 1 3 tancos 2        

the angle

θθ≤≤π whose cosine equals 3 2 . 1 3 cos,0 2 5 6 353 tancostan 263 θθ θ =−≤≤π π =   π −==−      12. 1 1 tansin 2      

the angle ,, 22 θθππ −≤≤ whose sine equals 1 2 . 1 1 sin, 222 6 tansintan13 263 θθ θ ππ =−−≤≤ π =−  π  −=−=−  13. 1 1 seccos 2   

Find

,0,

Find

the angle ,0, θθ≤≤π whose cosine equals 1 2 1 1 cos,0 2 3 1 seccossec2 23 θθ θ π =≤≤π π =  ==  

1 1 cotsin 2      

14.

θθππ

Find the angle ,, 22

() 1 tan1, 22 4 csctan1csc2 4 θθ θ π ππ =−<< π = ==

Find

the angle ,, 22

whose tangent equals 1.

()

1 sectan3

sintan(1)    

Find the angle ,, 22

−<< whose tangent equals 3 .

1 tan1,

4 2 sintan(1)sin 42 θθ θ ππ =−−<< π =− π  −=−=−   

Find the angle ,, 22

−<< whose tangent equals 1 .

Chapter 7: Analytic Trigonometry

Find

662

18. 1 3 cossin 2        

the angle ,, 22 θθππ −≤≤ whose sine equals 3 2 1 3 sin, 222 3 cossincos31 232 θθ θ ππ =−−≤≤ π =−   π  −=−=        19. 1 1 secsin 2      

Find

the angle ,, 22 θθππ −≤≤ whose sine equals 1 2 . 1 1 sin, 222 6 secsinsec123 263 θθ θ ππ =−−≤≤ π =−  π  −=−=  20. 1 3 csccos 2        

the angle ,0, θθ≤≤π whose cosine equals 3 2 1 3 cos0 2 5 6 35 csccoscsc2 26 θθ θ =−≤≤π π =   π −==      21. cossincos1152 42  π  =−     Find the angle ,0, θθ≤≤π whose cosine equals 2 2 1 2 cos,0 2 3 4 53 cossin 44 θθ θ =−≤≤π π = ππ =   22. tancottan1121 3 3  π  =−     Find the angle ,, 22 θθππ −<< whose tangent equals 1 3 1 1 tan, 22 3 6 2 tancot 36 θθ θ π ππ =−−<< π =− π  =−   23. sincossin1173 62   π   −=−       Find the angle ,, 22 θθππ −≤≤ whose sine equals 3 2 1 3 sin, 222 3 7 sincos 63 θθ θ π ππ =−−≤≤ π =−  π  −=−    24. () 11 costancos1 3  π   −=−    Find the angle ,0, θθ≤≤π whose cosine equals 1 1 cos1,0 3 costan 3 θθ θ π =−≤≤π π =  π   −=   

Find

25. 1 1 tansin 3

Let 1 1 sin 3 θ = . Since 1 sin 3 θ = and 22 θ ππ −≤≤ , θ is in quadrant I, and we let

1 y = and 3 r =

Solve for x:

7.2: The Inverse Trigonometric Functions [Continued]

28. 1 2 cossin 3

Let 1 2 sin 3 θ = . Since 2 sin 3 θ = and 22 θ ππ −≤≤ , θ is in quadrant I, and we let

2 y = and 3 r =

Solve for x:

x x x

+= = =±=±

19 8 822

Since θ is in quadrant I, 22 x =

1 1122 tansintan 34 222 y x θ

26. 1 1 tancos 3

Let 1 1 cos 3 θ = . Since 1 cos 3 θ = and 0 θ ≤≤π ,

θ is in quadrant I, and we let 1 x = and 3 r =

Solve for y:

2 2

x x x

+= = =±

29 7 7

Since θ is in quadrant I, 7 x =

1 cossincos27 33 x r

19 8 822

y y y

+= = =±=±

Since θ is in quadrant I, 22 y = .

1 122 tancostan22 31 y x θ

27. 1 1 sectan 2

Since

Let 1 1 tan 2 θ = . Since 1 tan 2 θ = and 22

ππ −<< , θ is in quadrant I, and we let

2 x = and 1 y =

Solve for r: 22

21 5 5

r r r

+= = =

θ is in quadrant I.

1 15 sectansec 22 r x θ

Since

663

Section

  

 ===⋅=  

  



 

====

  



 

===

   

θ  ===   

cotsin 3             Let 1 2 sin 3 θ  =−   . Since 2 sin 3 θ =− and 22 θ ππ −≤≤ , θ is in quadrant IV, and we let

for

2 29

29. 1 2

=− and 3 r = . Solve

x: 2

x x x += = =±

1 cotsincot27214 32 22 x y θ   −===⋅=−      30. 1 csctan(2)     Let 1 tan(2) θ =− . Since tan2 θ =− and 22 θ ππ −<< , θ is in quadrant IV,

is in quadrant IV, 7 x =

and

let

x = and 2 y =− Solve for r:

2 14 5 5 r r r += = =±

csctan(2)csc





θ is in quadrant IV, 5 r = 1 55

22 r y θ

−====−

Chapter 7: Analytic Trigonometry

31. 1 sintan(3)

x = and 3 y =− . Solve for r:

x =− and 3 r = .

1 3 cotcoscot 3

−≤≤

Solve for x:

2 2

x x x

+= = =±

2025 5 5

Since θ is in quadrant I, 5 x =

θ  ====   

  

Let 1 1 tan 2 θ = . Since 1 tan 2 θ = and 22 θ ππ −<< , θ is in quadrant I, and we let 2 x = and 1 y = Solve for r: 22 2

21 5 5

r r r

+= = = θ is in quadrant I.

y θ  ====  

 ππ =−=−     

1 cot3,0 6

cot3

1 cot1,0 4 cot1 4 θθ θ =<<π π = π =

664

2 2

Let 1 tan(3) θ =− . Since tan3 θ =− and

ππ −<< , θ is in quadrant IV, and we let

19 10 10 r r r += = =±

310310

θ −== =⋅=−

       

 =−  

Since θ is in quadrant IV, 10 r = 1 sintan(3)sin

10 1010 y r

32. 1 3 cotcos 3

Let 1 3 cos 3 θ

. Since 3 cos 3 θ =− and

≤≤π

is in quadrant II, and we let

Solve for y: 2 2 39 6 6 y y y += = =±

3122 2 622

  −==      ==⋅=−

25 secsin 5    

Since θ is in quadrant II, 6 y =

x y θ

33. 1

22 θ ππ

Let 1 25 sin 5 θ = . Since 25 sin 5 θ = and

, θ is in quadrant I, and we let 25 y = and 5 r =

1 255 secsinsec5 5 5 r x

34. 1 1 csctan 2

1 15 csctancsc5 21 r

ππ =−= 

35. sincossin1132 424

36. cossincos11712 623

37. 1 cot3

6 θθ θ

π = π =

We are finding the angle ,0, θθ<<π whose cotangent equals 3 .

=<<π

38. 1 cot1

We are finding the angle ,0, θθ<<π whose cotangent equals 1.

We are finding the angle , 22 θθππ −≤≤ ,

, whose cosecant equals 1 .

We are finding the angle , 22

finding the angle ,0, θθ<<π whose cotangent equals 3 3

45. 11 1 sec4cos 4 =

We seek the angle ,0, θθπ ≤≤ whose cosine equals 1 4 . Now 1 cos 4 θ = , so θ lies in quadrant

I. The calculator yields 1 1 cos1.32 4 ≈ , which is an angle in quadrant I, so () 1 sec41.32 ≈

Section 7.2: The Inverse Trigonometric Functions [Continued] 665

39. 1 csc(1)

0 θ ≠

1 csc1,,0

2 csc(1) 2 θθθ θ ππ =−−≤≤≠ π =− π −=− 40. 1 csc2

θθππ −≤≤ , 0 θ ≠ ,

1 csc2,,0

4 csc2 4 θθθ θ ππ =−≤≤≠ π = π = 41. 1 23 sec 3

whose cosecant equals 2

θθ≤≤π

2 θ π ≠

whose

1 23 sec,0, 32 6 23 sec 36 θθθ θ π =≤≤π≠ π = π = 42. () 1 sec2

We are finding the angle ,0

secant equals 23

θθ≤≤π , 2 θ π ≠

() 1 sec2,0, 2 2 3 2 sec2 3 θθθ θ π =−≤≤π≠ π = π −= 43. 1 3 cot 3    

We are finding the angle ,0

, whose secant equals 2

1 3 cot,0 3 2 3 32 cot 33 θθ θ =−<<π π =  π −=   44. 1 23 csc 3    

are

22 θθππ −≤≤ , 0 θ ≠ , whose

equals 23 3 . 1 23 csc,,0 322 3 23 csc 33 θθθ θ ππ =−−≤≤≠ π =−  π −=−  

are

finding the angle ,

cosecant

Chapter 7: Analytic Trigonometry

46. 11 1 csc5sin 5 =

We seek the angle ,, 22 θθππ −≤≤ whose sine equals 1 5 . Now 1 sin 5 θ = , so θ lies in quadrant I. The calculator yields 1 1 sin0.20 5 ≈ , which is an angle in quadrant I, so 1 csc50.20 ≈

47. 11 1 cot2tan 2 =

We seek the angle ,0, θθπ ≤≤ whose tangent equals 1 2 . Now 1 tan 2 θ = , so θ lies in quadrant I. The calculator yields 1 1 an0.46 2 ≈ , which is an angle in quadrant I, so () 1 cot20.46 ≈

48. 11 1 sec(3)cos 3  −=−

We seek the angle ,0, θθπ ≤≤ whose cosine equals 1 3 . Now 1 cos 3 θ =− , θ lies in quadrant II. The calculator yields 1 1 cos1.91 3  −≈  , which is an angle in quadrant II, so () 1 sec31.91 −≈

49. () 11 1 csc3sin 3  −=−

We seek the angle ,, 22 θθππ −≤≤ whose sine equals 1 3 . Now 1 sin 3 θ =− , so θ lies in quadrant IV. The calculator yields 1 1 sin0.34 3

, which is an angle in quadrant IV, so () 1 csc30.34 −≈− .

50. 11 1 cottan(2)

We seek the angle ,0, θθπ ≤≤ whose tangent equals 2 . Now tan2 θ =− , so θ lies in quadrant II. The calculator yields () 1 tan21.11 −≈− , which is an angle in quadrant IV. Since θ lies in quadrant II, 1.112.03θπ≈−+≈ . Therefore,

1 1 cot2.03 2

51. () 11 1 cot5tan 5

We seek the angle ,0, θθπ ≤≤ whose tangent equals 1 5 . Now 1 tan 5 θ =− , so θ lies in quadrant II. The calculator yields

1 1 tan0.42 5

, which is an angle in quadrant IV. Since θ is in quadrant II, 0.422.72θπ≈−+≈ . Therefore,

() 1 cot52.72 −≈ .

666





 

 −≈−

 −=− 

 −≈  .

−=− 



 −≈− 

52. () 11 1 cot8.1tan 8.1  −=− 

We seek the angle ,0, θθπ ≤≤ whose tangent equals 1 8.1 . Now 1 tan 8.1 θ =− , so θ lies in quadrant II. The calculator yields

1 tan0.12 8.1

 , which is an angle in quadrant IV. Since θ is in quadrant II, 0.123.02θπ≈−+≈ . Thus, () 1 cot8.13.02 −≈

We are finding the angle ,0, θθπ ≤≤ whose tangent equals 2 3 . Now 2 tan 3 θ =− , so θ lies in quadrant II. The calculator yields 1 2 tan0.59 3

, which is an angle in quadrant IV. Since θ is in quadrant II, 0.592.55

. Thus, 1 3 cot2.55 2  −≈

56. () 11 1 cot10tan 10

We seek the angle ,, 0 22

, whose sine equals 2 3 . Now 2 sin 3 θ =− , so θ lies in quadrant IV. The calculator yields 1 2 sin0.73 3

, which is an angle in

We are finding the angle ,0, θθπ ≤≤ whose tangent equals 1 10 . Now 1 tan 10 θ =− , so θ lies in quadrant II. The calculator yields 1 1 tan0.306 10

, which is an angle in quadrant IV. Since θ is in quadrant II, 0.3062.84

57. Let 1 tan u θ = so that tan u θ = , 22 ππ θ −<< , u −∞<<∞ . Then,

We are finding the angle ,0, 2

θθπθ≤≤≠ , whose cosine equals 3 4 . Now 3 cos 4 θ =− , so θ lies in quadrant II. The calculator yields

, which is an angle in

58. Let 1 cos u θ = so that cos u θ = , 0 ≤≤θπ , 11 u −≤≤ . Then,

Section 7.2: The Inverse Trigonometric Functions [Continued] 667

 −≈−



 

53.

cscsin1132 23

−=−

 −≈− 

quadrant IV,

1 3 csc0.73 2  −≈− 

ππ θθθ −≤≤≠

1143 seccos 34  −=−  

54.

 −≈ 

quadrant II, so 1 4 sec2.42 3  −≈ 

3 cos2.42 4

 −=−  

55. cottan1132 23

 −≈− 

 

θπ≈−+≈

 −=− 

 −≈− 

θπ≈−+≈ . So, ()

cot102.84 −≈

() 1 2 22 11 costancos sec sec 11 1tan1 u u θ θ θ θ === == ++

()12 22 sincossinsin 1cos1

θθ θ == =−=−

u u

Chapter 7: Analytic Trigonometry

u u u

θ θ θ

θθ

sin tansintan cos sinsin cos1sin 1 θθ

1 22 2

1 22 2 sin tancostan cos sin1cos coscos 1 u u u θ θ θ θθ

122

θ θθθθ

u u u

cotcotcsc1 csccsccsc 1 ==⋅= === =

64. Let 1 sec u θ = so that sec u θ = , 0 ≤≤θπ and 2 π θ ≠ , 1 u ≥ . Then,

() 1 11 cosseccos sec u u θ θ ===

() 1 11 tancottan cot u u θ θ ===

66. Let 1 sec u θ = so that sec u θ = , 0 ≤≤θπ and 2 π θ ≠ , 1 u ≥ . Then,

12 2 22 1 sincotsinsin csc 11 1cot1 u u θθ θ θ === == ++

()12 22

u u

== =−=−

tansectantan sec11

θθ θ

67. 111212 cossin 1313 gf



 

x x x x

222 2 2

+= += = =±=±

1213 144169 25 255

Since θ is in quadrant I, 5 x =

1112125 cossincos 131313 x gf r θ

 ==== 

668

()

59. Let 1 sin u θ = so that sin u θ = , 22 ππ θ −≤≤ , 11 u −≤≤ . Then,

== == =

()

θθ

60. Let 1 cos u θ = so that cos u θ = , 0 ≤≤θπ , 11 u −≤≤ . Then,

== == =

()

2 2 2 2

1sec1 1 sec sec 1

u u θθθ θ θ θ ===− =−= =

61. Let 1 sec u θ = so that sec u θ = , 0 ≤≤θπ and 2 π θ ≠ , 1 u ≥ . Then,

sinsecsinsin1cos

()

62. Let 1 cot u θ = so that cot u θ = , 0 <<θπ , u −∞<<∞ . Then,

63. Let 1 csc u θ = so that csc u θ = , 22 ππ θ −≤≤ , 1 u ≥ . Then, () 1 22 2

sin coscsccoscoscotsin sin θθθ θθθ

65. Let 1 cot u θ = so that cot u θ = , 0 <<θπ , u −∞<<∞ . Then,

Let 1 12 sin 13 θ = . Since 12 sin 13 θ = and

ππ θ −≤≤ , θ is in quadrant I, and we let 12 y = and 13 r = . Solve for x:

68. 1155

sincos 1313 fg

Since

. Since 4 cos 5 θ =− and 0 ≤≤θπ , θ is in quadrant II, and we let 4 x =− and 5 r = . Solve for y: 222 2 2

(4)5 1625 9 93

y y y y

−+= += = =±=±

Since θ is in quadrant II, 3 y = . 1144 tancos 55 33 tan 44   −=−     ====−

73. 111212 costan 55 gh

 =  

222 2

r r r

=+ =+= =±=±

512 25144169 16913

Now, r must be positive, so 13 r = 1112125 costancos 5513 x gh r θ

 ==== 

74. 1155 sintan 1212 fh =

ππ θ −≤≤ , θ is in quadrant I, and we let 12 x = and 5 y = . Solve for r:

r r r

222 2

=+ =+= =±=±

125 14425169

16913

Now, r must be positive, so 13 r = .

 ==== 

11555 sintansin 121213 y fh r θ

Section 7.2: The Inverse Trigonometric Functions [Continued] 669

1 5 cos 13 θ = .

5 cos 13 θ

0 ≤≤θπ

x =

r = . Solve for y: 222

y y

+= += = =±=±

Let

= and

, θ is in quadrant I, and we let 5

and 13

2 2 513 25169 144 14412 y

115512 sincossin

θ  ====  69. 11 1 77 cossin 44 23 cos 24 gf ππ π  =    =−=    70. 11 1 55 sincos 66 3 sin 23 fg ππ π  =    =−=−    71. 1133 tansin 55 hf  −=−     Let 1 3 sin 5 θ  =−  . Since 3 sin 5 θ =− and 22 ππ θ −≤≤ , θ is in quadrant IV, and we let 3 y =− and 5 r = . Solve for x: 222 2 2 (3)5 925 16 164 x x x x +−= += = =±=±

in quadrant IV, 4 x = . 1133 tansin 55 33 tan 44 hf y x θ   −=−     ====−

hg  −=−    

Since θ is in quadrant I, 12 y =

131313 y

Since

72. 1144 tancos 55



Let 1 4 cos 5 θ  =−

hg y x θ

Let 1 12 tan 5 θ = . Since 12 tan 5 θ = and 22 ππ θ −≤≤ , θ is in quadrant I, and we let 5 x = and 12 y = . Solve for r:

 

Let 1 5 tan 12 θ = . Since 5 tan 12 θ = and 22

79. a. Since the diameter of the base is 45 feet, we have 45 22.5 2 r == feet. Thus,

1 22.5 cot31.89 14 θ  ==°

b. 1 cot cot cot

= =→=

r h r rh h

θ θθ

Here we have 31.89 θ =° and 17 h = feet. Thus, () 17cot31.8927.32 r =°= feet and the diameter is () 227.3254.64 = feet.

c. From part (b), we get cot r h θ =

The radius is 22 61 2 1 = feet. 61 37.96 cot22.5/14 r h θ ==≈ feet. Thus, the height is 37.96 feet.

80. a. Since the diameter of the base is 6.68 feet, we have 6.68 3.34 2 r == feet. Thus,

1 3.34 cot50.14 4 θ  ==°

b. 1 cot cot cot

= =→=

r h rr h h

θ θ θ

Here we have 50.14 θ =° and 4 r = feet. Thus, () 4 4.79 cot50.14 h == ° feet. The bunker will be 4.79 feet high.

c. 1 4.22 cot54.88 6 TGθ  ==°

From part (a) we have 50.14 USGAθ =° . For steep bunkers, a larger angle of repose is required. Therefore, the Tour Grade 50/50 sand is better suited since it has a larger angle of repose.

Analytic

670 Copyright © 2016 Pearson Education, Inc. 75. 11 1 44 cossin 33 3 cos 26 gf ππ π   −=−     == 76. 11 1 55 cossin 66 12 cos 23 gf ππ π   −=−      =−=   77. 1111 tancos 44 hg  −=−     Let 1 1 cos 4 θ  =−  . Since 1 cos 4 θ =− and 0 ≤≤θπ , θ is in quadrant II, and we let 1 x =− and 4 r = . Solve for y: 222 2 2 (1)4 116 15 15 y y y y −+= += = =± Since θ is in quadrant II, 15 y = 1111 tancos 44 15 tan15 1 hg y x θ   −=−     ====− 78. 1122 tansin 55 hf  −=−     Let 1 2 sin 5 θ  =−  . Since 2 sin 5 θ =− and 22 ππ θ

2 y =− and 5 r =

Solve for x: 222 2 2 (2)5 425 21 21 x x x x +−= += = =±

θ is in quadrant

21 x = . 1122 tansin 55 2221 tan 21 21 hf y x θ   −=−     ====−

Chapter 7:

Trigonometry

−≤≤ ,

is in quadrant IV, and we let

Since

IV,





 

84. 11 1 cscsinyx x ==

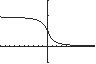
The artillery shell begins at the origin and lands at the coordinates () 6175,2450 . Thus,

The artilleryman used an angle of elevation of 22.3° b.

2.27

85 – 86. Answers will vary.

87. 42 42 22

()421100 4211000 (4)(25)0

fxxx xx xx

=+− +−= −+= 22 40 or 250 2 or 5 xx x xi −=+= =±=±

So the solution set is: {} 2,2,5,5ii

88. 32 32 ()()()() () f xxxx xxxfx −=−+−−−

So the function is not even. 32 32 ()()()() ()() f xxxx xxxfx −=−+−−−

So the function is not odd.

89. 7 315 1804 ππ = radians

90. 5 75 12 π

671

a. 2 1 2 2 cot 2 2 cot 2 x ygt x ygt θ θ = +  =   + 

Section 7.2: The Inverse Trigonometric Functions (Continued)

() () 1



 ⋅+  ≈≈°

2 1 26175 cot 2245032.22.27 cot2.43785822.3 θ 

()()

sec

2940.23 ft/sec vt x x v t θ θ = ° == = 82. Let. 11 2 cotcos 1 x yx x == + −1010 3 2 π 2 π

that the range of 1 cot y x =

0, π

so 1 1 tan x will not work. 83. 11 1 seccosyx x == 0 −5 π 5

0 0 sec 6175sec22.3

Note

is ()

−10 10 2 π 2 π

=−++≠

=−−−≠−

°= 5 6 12 5 7.85 in. 2 srθ π π = = =≈

Chapter 7: Analytic Trigonometry

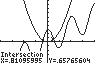
In this case, the graphs only intersect in one location, so the equation has only one solution. Rounding as directed, the solutions set is { }0.76

7. False because of the circular nature of the functions.

8. True

9. True

10. False, 2 is outside the range of the sin function.

672

Section 7.3

46 63 42 x x x x −=−+ = == The solution set is 3 2   

21 , 22

1. 351

2 450 4510 xx xx −−= −+= 450 or 10 5 or 1 4 xx xx −=+= ==− The solution set is 5 1, 4   

2 10 xx−−= ()()()() () 2 11411 21 114 2 15 2 x −−±−−− = ±+ = ± = The solution set is 1515 , 22  −+    

2 (21)3(21)40 (21)1(21)40 2(25)0 xx xx xx −−−−= −+−−= −= 20 or 250 5 0 or 2 xx xx =−= == The solution set is 5 0, 2    .

5232 x xx−=− Let 3 1 52yx=− and 2 2 yxx =− . Use INTERSECT to find the solution(s): −6 6 −6 6

3. ()()

5. [][]

2sin32 2sin1 1 sin 2 θ θ θ += =− =− 711 2 or 2, is any integer 66 kkkθθππ =+π=+π

11.

12.

13.

02 θ ≤<π , the solution set is 711 , 66 ππ    . 14. 1 1cos 2 1 1cos 2 1 cos 2 θ θ θ −= −= = 5 2 or 2, is any integer 33 kkkθθππ =+π=+π

02 θ ≤<π

5 , 33 ππ    .

, the solution set is

Section 7.3: Trigonometric Equations

15. 2sin10 2sin1 1 sin 2

+= =− =− 711 2 or 2, is any integer 66 kkkθθππ =+π=+π

θ θ θ

On 02 θ ≤<π , the solution set is 711 , 66 ππ

16. cos10 cos1 θ θ += =− 2, is any integer kk θ =π+π

On the interval 02 θ ≤<π , the solution set is {π}

17. tan10 tan1 θ θ += =− 3 , is any integer 4 kk θ π =+π

On 02 θ ≤<π , the solution set is 37 , 44 ππ

θ θ θ

+= =− =−=−

18. 3cot10 3cot1 13 cot 3 3

, is any integer 3 kk θ π =+π

On 02 θ ≤<π , the solution set is 25 , 33 ππ

θ θ θ

+=− =− =−

19. 4sec62 4sec8 sec2

242or2, is any integer 33 kkkθθππ =+π=+π

On 02 θ ≤<π , the solution set is 24 , 33 ππ

20. 5csc32 5csc5 csc1

−= = = 2, is any integer 2 kk θ π =+π

θ θ θ

On 02 θ ≤<π , the solution set is 2 π

673

θ θ θ

+=− =− =−=−

21. 32cos21 32cos3 12 cos 2 2

352or2, is any integer 44 kkkθθππ =+π=+π

On 02 θ ≤<π , the solution set is 35 , 44 ππ    

θ θ θ

+= =− =−=−

22. 4sin333 4sin23 233 sin 42

452or2, is any integer 33 kkkθθππ =+π=+π

On 02 θ ≤<π , the solution set is 45 , 33 ππ  

2 or, is any integer 33 kkkθθππ=+π=+π

On the interval 02 θ ≤<π , the solution set is 245 ,,, 3333 ππππ

24. 2 1 tan 3 13 tan 33

= =±=± 5 or , is any integer 66 kkkθθππ=+π=+π

θ θ

On the interval 02 θ ≤<π , the solution set is 5711 ,,, 6666 ππππ  

 



  

 



  



2 2

4 1

 

23.

4cos1

cos

θ θ θ = = =±





 









Chapter 7: Analytic Trigonometry

2sin10 2sin1 1 sin 2 12 sin 22

44 kkkππ θπθπ =+=+

26. 2

ππ

θπθπ =+=+



  .

32 2 2 , is any integer 23 k k k θ



kk kk

θ θ

π =+π ππ =+

kk k k

On the interval 02 θ ≤<π , the solution set is 245 ,,, 3333 ππππ   

On the interval 02 θ ≤<π , the solution set is 371115 ,,, 8888 ππππ

   .

31. 3 sec2 2 θ =− 3234 2 or 2 2323 4484 or , 9393 θπθπ ππ θθππππ

 



On the interval 02 θ ≤<π , the solution set is 4816 ,, 999 πππ  

32. 2 cot3 3 θ =−

θπ π ππ θ

=+ =+

53 , is any integer 42

On 02 θ ≤<π , the solution set is 5 4 π  



674

25. 2 θ θ θ

−= = = =±=± 3 or , is any integer

  

θ θ

On the interval 02 θ ≤<π , the solution set is 357 ,,, 4444 ππππ

2 4cos30 4cos3 3 cos 4 3 cos 2 θ

θ −= = = =± 5

or, is any integer 66 kkkθθππ =+π=+π

On the interval 02 θ ≤<π , the solution set is 5711 ,,, 6666 ππππ

ππ

27. () sin31

θ =− π =+π

 

On the interval 02 θ ≤<π , the solution set is 711 ,, 266 πππ

θ θπ

π θπ 

 

 

28. tan3 2 , is any integer

2, is any integer

On 02 θ ≤<π , the solution set is 2 3 π 

θπθπ ππ

29. () 1 cos2 2 θ =− 24 22 or 22 33 2 or , 33 =+=+

kk kk

k is any integer





30. () tan21 θ =− 3 2, is any integer 4 3 , is any integer 82

 

kk kk =+=+ =+=+

k is any integer

25 , is any integer 36

kk k k

37.

any integer. Six solutions are 513172529 ,,,,,

38.

=+π    , k is any integer

Six solutions are 59131721 ,,,,, 444444 θ ππππππ =

39. 3 tan 3 θ =−

5 6 k θθ π  =+π    , k is any integer

Six solutions are 51117232935 ,,,,, 666666 θ ππππππ =

40. 3 cos 2 θ =−

57 2 or 2 66 kk π θθθ π  =+π=+π  

, k is any integer. Six solutions are 5717192931 ,,,,, 666666 θ ππππππ = .

41. cos0 θ = 3 2 or =2 22 kkθθθ ππ  =+π+π  

, k is any integer

Six solutions are 357911 ,,,,, 222222 θ ππππππ = .

42. 2 sin 2 θ = 3 2 or 2 44 kk π θθθπ π  =+π=+  

, k is any integer

Six solutions are 39111719 ,,,,, 444444 θ ππππππ = .

675 Copyright © 2016 Pearson Education, Inc. 33. cos21 2 θ π  −=−  22 2 3 22 2 3 , is any integer 4 k k kk θ θ θ π −=π+π π =+π π =+π On 02 θ ≤<π , the solution set is 37 , 44 ππ    . 34. sin31 18 θ π +=  32 182 4 32 9 42 , is any integer 273 k k k k θ θ θ ππ +=+π π =+π ππ =+ On the interval 02 θ ≤<π , the solution set is 42240 ,, 272727 πππ    . 35. tan1 23 θ π +=  234 212 2, is any integer 6 k k kk θ θ θ ππ +=+π π =−+π π =−+π On 02 θ ≤<π , the solution set is 11 6 π    . 36. 1 cos 342 θ π  −=  5 2 or 2 343343 723 2 or 2 312312 723 6 or 6, 44 kk kk kk θθ θθ θθ ππππ −=+π−=+π ππ =+π=+π ππ =+π=+π k is any integer. On 02 θ ≤<π , the solution set is 7 4 π   

Section 7.3: Trigonometric Equations

θθπθπ  =+=+   

θ ππππππ =

1 sin 2 θ =

2 or 2 66

ππ

666666

θθ



tan1 θ = 4 k



Chapter 7: Analytic Trigonometry

43. () 1 cos2 2 θ =−

48. () 1

cos0.6 cos0.60.93 θ θ = =≈

24 22 or 22, is any integer

33 kkkθθππ =+π=+π

33 kkkθθθ ππ  =+π=+π  

2 or , is any integer

Six solutions are 24578 ,,,,, 333333 θ ππππππ =

44. () sin21 θ =−

3 22, is any integer 2 kk θ π =+π

3 , is any integer 4 kk θθ π  =+π  

Six solutions are 3711151923 ,,,,, 444444 θ ππππππ =

45. 3 sin 22 θ =−

45 2 or 2, is any integer 2323 kkkθθππ =+π=+π

810 4 or4 33 kkθθθ ππ  =+π=+π   , k is any integer. Six solutions are 81020223234 ,,,,, 333333 θ ππππππ =

46. tan1 2 θ =−

3 , is any integer 24 kk θπ π =+

3 2, is any integer 2 kk π θθπ

Six solutions are 3711151923 ,,,,, 222222 θ ππππππ = .

47. () 1

sin0.4 sin0.40.41 θ θ = =≈

0.41 θ ≈ or 0.412.73θπ≈−≈ .

The solution set is { } 0.41, 2.73

0.93 θ ≈ or 20.935.36θπ≈−≈ .

The solution set is { } 0.93, 5.36

49. () 1

tan5 tan51.37 θ θ = =≈

1.37 θ ≈ or 1.374.51θπ≈+≈

The solution set is { } 1.37, 4.51

= = 

676

≈ or 0.463.61

0.46

The solution set is { } 0.46, 3.61

The solution set is { } 2.69, 3.59 .

() 1 sin0.2 sin0.20.20



 

50. 1 =≈  

cot2 1 tan 2 1 tan0.46 2 θ

θ θ θ θπ≈+≈

=− =−≈

51.

() 1 cos0.9 cos0.92.69 θ θ

2.69 θ ≈ or 22.693.59θπ≈−≈

θ θ =− =−≈− 0.202 6.08 θπ ≈−+ ≈ or () 0.20 3.34 θπ≈−− ≈ . The solution set is { } 3.34, 6.08 53. 1 sec4 1 cos 4 1 cos1.82 4 θ θ θ =− =−  =−≈   1.82 θ ≈ or 21.824.46θπ≈−≈ . The solution set is { } 1.82, 4.46 54. 1 csc3 1 sin 3 1 sin0.34 3 θ θ θ =− =−  =−≈−   0.342 5.94 θπ ≈−+ ≈ or () 0.34 3.48 θπ≈−− ≈ The solution set is { } 3.48, 5.94

52.

Section 7.3: Trigonometric Equations

The solution set is 243 , , , 2332 ππππ

60. 2 sin10 (sin1)(sin1)0 θ θθ −= +−= sin10or sin10

61. 2 2sinsin10 (2sin1)(sin1)0 θθ

, 66

The solution set is 711 , , 266 πππ 

62. 2 2coscos10 (cos1)(2cos1)0 θθ

The solution set is 5 , , 33 ππ π

677 Copyright © 2016 Pearson Education, Inc. 55. 1 5tan90 5tan9 9 tan 5 9 tan1.064 5 θ θ θ θ += =− =−  =−≈−   1.064 2.08 θπ ≈−+ ≈ or 1.0642 5.22 θπ ≈−+ ≈ The solution set is { } 2.08, 5.22 . 56. 1 4cot5 5 cot 4 4 tan 5 4 tan0.675 5 θ θ θ θ =− =− =−  =−≈−   0.675 2.47 θπ ≈−+ ≈ or 0.6752 5.61 θπ ≈−+ ≈ . The solution set is { } 2.47, 5.61 57. 1 3sin20 3sin2 2 sin 3 2 sin0.73 3 θ θ θ θ −= = =  =≈   0.73 θ ≈ or 0.732.41θπ≈−≈ The solution set is { } 0.73, 2.41 . 58. 1 4cos30 4cos3 3 cos 4 3 cos2.42 4 θ θ θ θ += =− =−  =−≈   2.42 θ ≈ or 22.423.86θπ≈−≈ The solution set is { } 2.42, 3.86

cos(2cos1)0 θθ θθ += += cos0 or 2cos10 32cos1 , 22 1 cos 2 24 , 33 θθ θ θ θ θ =+= ππ=− = =− ππ =

59. 2 2coscos0

  

sin1sin1

θθ θθ θθ +=−= =−= ππ ==





3 22

The solution set is 3 , 22 ππ



=−= π =−= ππ

θθ −−= +−= 2sin10or sin10 2sin1 sin1 1 sin 22 711

θθ θθ θθ θ +=−=

 

cos12cos1

θθ θθ θ θ θ

=−= =π = ππ

θθ +−= +−= cos10or 2cos10

1 cos 2 5 , 33

+=−=

  

Chapter 7: Analytic Trigonometry

678

(tan1)(sec1)0 θθ−−= tan10or sec10 tan1sec1 5 0 , 44 θθ θθ θ θ −=−= == ππ = = The solution set is 5 0, , 44 ππ    . 64. 1 (cot1)csc0 2 θθ +−=   1 cot10or csc0 2 cot1 1 csc 37 2 , 44 (not possible) θθ θ θ θ +=−= =− = ππ = The solution set is 37 , 44 ππ    . 65. () ()() 22 22 2 2 sincos1cos 1coscos1cos 12cos1cos 2coscos0 cos2cos10 θθθ θθθ θθ θθ θθ −=+ −−=+ −=+ += += cos0or 2cos10 31 ,cos 222 24 , 33 θθ ππ θθ ππ θ =+= ==− = The solution set is 243 , , , 2332 ππππ    . 66. () ()() 22 22 2 2 cossinsin0 1sinsinsin0 12sinsin0 2sinsin10 2sin1sin10 θθθ θθθ θθ θθ θθ −+= −−+= −+= −−= +−= 2sin10or sin10 1sin1 sin 2 711 2 , 66 θθ θ θ π θ ππ θ +=−= = =− = = The solution set is 711 , , 266 πππ    67. () () () () ()() 2 2 2 2 sin6cos1 sin6cos1 1cos6cos6 cos6cos50 cos5cos10 θθ θθ θθ θθ θθ =−+ =+ −=+ ++= ++= cos50or cos10 cos5cos1 (not possible) θθ θθ θπ +=+= =−=− = The solution set is {π} .

() () () () () ()() 2 2 2 2 2 2sin31cos 2sin31cos 21cos31cos 22cos33cos 2cos3cos10 2cos1cos10 θθ θθ θθ θθ θθ θθ =−− =− −=− −=− −+= −−= 2cos10or cos10 1cos1 cos 2 0 5 , 33 θθ θ θ θ ππ θ −=−= = = = = The solution set is 5 0, , 33 ππ     

68.

cossin sin 1 cos tan1 5 , 44 θθ θθ θθ θ θ θ θ =−− =−− = = = ππ = The solution set is 5 , 44 ππ      .

69. () () cossin cossin

Section 7.3: Trigonometric Equations

The solution set is 53 , , 662 πππ

2 2 2 2 θθ θθ θ

cos2cos10 cos10 cos10 cos1 θθ

sin2cos2 1cos2cos2

θθ θθ

−=−= π ==

The solution set is 2 π   

θθ θ θ θ

+=−= = =−

ππ =

76. ()() 2 2cos7cos40 2cos1cos40 θθ θθ −−= +−= 2cos10orcos40 1cos4 sin 2 (not possible) 24 , 33



() () () cossin0 cossin0 cossin0 sincos sin 1 cos tan1 37 , 44 θθ θθ θθ θθ θ θ θ θ −−= −−= += =− =− =− ππ = The solution set is 37 , 44 ππ    71. tan2sin sin 2sin cos sin2sincos 02sincossin 0sin(2cos1) θθ θ θ θ θθθ θθθ θθ = = = =− =− 2cos10or sin0 10, cos 2 5 , 33 θθ θ θ θ −== =π = ππ = The solution set is 5 0, , , 33 ππ π    72. 2 tancot 1 tan tan tan1 tan1 357 ,,, 4444 θθ θ θ θ θ θ = = = =± ππππ = The solution set is 357 , , , 4444 ππππ    . 73.

1sin2(1sin) 1sin22sin 2sinsin10

θθ θθ θθ θθ θθ += +=− +=− +−= −+= 2sin10or sin10 1sin1 sin 2 3 5 2 , 66 θθ θ θ θ θ −=+= =− = π = ππ =

70.

2 2 2 2 1sin2cos

(2sin1)(sin1)0

  

74. ()

θ θ θ =+ −=+ ++= += += =− =π

The solution set is {π}

75. ()() 2 2sin5sin30 2sin3sin10 θθ θθ −+= −+= 2sin30orsin10 3 sin (not possible) 22



The solution set is 24 , 33 ππ 

Chapter 7: Analytic Trigonometry

81. 2 2

sectan0 tan1tan0

This equation is quadratic in tan θ

The discriminant is 2` 41430bac−=−=−< The equation has no real solutions.

82. sectancotθθθ =+

83. 5cos0xx+= Find the zeros (x-intercepts) of 1 5cos Yxx =+ :

680

Inc. 77. ()() 2 2 2 3(1cos)sin 33cos1cos cos3cos20 cos1cos20 θθ θθ θθ θθ −= −=− −+= −−= cos10orcos20 cos1cos2 0(not possible) θθ θθ θ −=−= == = The solution set is { }0 78. ()() 2 2 2 4(1sin)cos 44sin1sin sin4sin30 sin1sin30 θθ θθ θθ θθ += +=− ++= ++= sin10orsin30 sin1sin3 3(not possible) 2 θθ θθ π θ +=+= =−=− = The solution set is 3 2 π    . 79. 2 2 2 2 3 tansec 2 3 sec1sec 2 2sec23sec 2sec3sec20 (2sec1)(sec2)0 θθ θθ θθ θθ θθ = −= −= −−= +−= 2sec10 orsec20 1sec2 sec 2 5 , (not possible) 33 θθ θ θ θ +=−= = =− ππ = The solution set is 5 , 33 ππ    80. 2 2 2 csccot1 1cotcot1 cotcot0 cot(cot1)0 θθ θθ θθ θθ =+ +=+ −= −= cot0orcot1 35 ,, 2244 θθ θθ == ππππ == The solution set is 53 , , , 4242 ππππ   

θθ θθ += ++=

22 1sincos coscossin

cossincos

cos θθ θθθ θθ θθθ θθθ θθ θ =+ + = = = sin1 2 θ θ = π = Since sec and tan 22 ππ    do not exist, the equation has

1sincos

sincos 1

no real solutions.

−10 10 −3π 3π −10 10 −3π 3π −10 10 −3π 3π 1.31,1.98,3.84 x ≈−

Section 7.3: Trigonometric Equations

: −10 10 −3π 3π −10 10 −3π 3π −10 10 −3π 3π 2.47,0,2.47 x ≈−

2217sin3 xx−=

the intersection of 1 2217sin Yxx =− and 2 3 Y = : −5 5 −π π 0.52 x ≈

198cos2 xx+= Find the intersection of 1 198cos Yxx =+ and 2 2 Y = : −5 5 −π π 0.30 x ≈−

sincos x xx+=

the intersection of 1 sincos Yxx =+ and 2 Yx = : −3 3 −π π 1.26 x ≈

intersection

and 2 Yx = : −3 3 −π π 1.26 x ≈− 89. 2 2cos0xx−= Find the zeros (x-intercepts) of 2 1 2cos Yxx =− : −3 3 −π π −3 3 −π π 1.02,1.02 x ≈− 90. 2 3sin0xx+= Find the zeros (x-intercepts) of 2 1 3sin Yxx =+ : −3 3 −π π −3 3 −π π 1.72,0 x ≈− 91. () 2 2sin23 x xx−= Find the intersection of () 2 1 2sin2 Yxx =− and 2 3 Yx = : −3 12 −π 3π 2 −3 12 −π 3π 2 0,2.15 x ≈

84. 4sin0xx−= Find the zeros (x-intercepts) of 1 4sin Yxx =−

85.

Find

86.

87.

Find

88. sincos

xx−= Find the

of 1 sincos Yxx =−

Chapter 7: Analytic Trigonometry

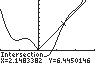
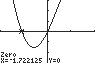
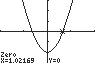
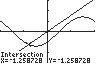
92. 2 3cos(2) x xx=+

Find the intersection of 2 1 Yx = and 2 3cos(2) Yxx =+ :

On the interval [ ] 0,2 π , the zeros of f are 245 ,,, 3333 ππππ

2π 0.62,0.81 x ≈−

93. 6sin2,0 x xex−=>

Find the intersection of 1 6sin x Yxe =− and

94. 4cos(3)1,0 x xex−=>

Find the intersection of 1 4cos(3) x Yxe =− and 2 1 Y = :

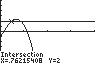
π 0.31 x ≈

95. () 2 2 2

96. () () () ()

0 2cos310 2cos31 1 cos3 2

fx x x x

x kxk kk xx

ππ ππ ππππ

=+=+ =+=+

= += =− =− 24 32 or 32 33 2242 or , 9393

k is any integer

On the interval [ ] 0, π , the zeros of f are 248 ,, 999 πππ .

97. a. () 0 3sin0 sin0

= = = 02 or 2, x kxk =+=+πππ k is any integer

fx x x

On the interval [ ] 2,4 π −π , the zeros of f are 2,,0,,2,3,4 −π−πππππ

b. () 3sin f xx =

0 4sin30 4sin3 3 sin 4 33 sin 42

fx x x x x

= −= = = =±=± 2 or 33 x kxkππ =+=+ππ , k is any integer

682

c. () 3 2 3 3sin 2 1 sin 2

= = = 5 2 or 2, 66 x kxkππ =+=+ππ k is any integer

fx x x

−5

−2π 2π −5

−2π

−6 6 0 2π −6 6 0 2π

2 Y = :

0.76,1.35 x ≈

−6 6 0

On the interval [ ] 2,4 π −π , the solution set is 11751317 ,,,,, 666666 ππππππ 

d. From the graph in part (b) and the results of part (c), the solutions of () 3 2 fx > on the interval [ ] 2,4 π −π is 117 66 xx  ππ −<<−   51317 or or 6666 xx ππππ  <<<<   .

Section 7.3: Trigonometric Equations

interval [ ] 2,4 π −π is 75 66 xx  ππ −<<−   571719 or or 6666 xx ππππ

<<<<

99. () 4tan f xx =

98. a. () 0

2cos0 cos0

fx x x

= = = 3 2 or 2, 22 x kxkππ =+=+ππ k is any integer

On the interval [ ] 2,4 π −π , the zeros of f are 3357 ,,,,, 222222 ππππππ

b. () 2cos f xx =

fx x x

=− =− =−

c. () 3 2cos3 3 cos 2

57 2 or 2, 66 x kxkππ =+=+ππ k is any integer

On the interval [ ] 2,4 π −π , the solution set is 75571719 ,,,,, 666666 ππππππ 

d. From the graph in part (b) and the results of part (c), the solutions of () 3 fx <− on the

683

fx x x 



=− =− =− , is any integer 4 xxkk π π  =−+

fx x x

<− <− <−

 

, we see that 12yy < for

or ,



xxkk π π

b. () 3 cot3 fx x

x π << or 5 0, 6 π 

 

  .

 



a. () 4 4tan4 tan1

b. () 4 4tan4 tan1

24 x ππ −<<−

24 ππ    2 π 2 π −6 6

Graphing 1 tan yx = and 2 1 y =− on the interval , 22 ππ 

100. () cot f xx =

a. () 3 cot3 fx x  

=− =− 5 , is any integer

>− >−

 

Graphing 1 1 tan y x = and 2 3 y =− on the interval () 0, π , we see that 12yy > for

Chapter 7: Analytic Trigonometry

a, d. ()()3sin22fxx=+ ; () 7 2 gx =

b. ()() () () ()

k is any integer

On [ ] 0, π , the solution set is 5 , 1212 ππ    .

c. From the graph in part (a) and the results of part (b), the solution of ()() f xgx > on

[ ] 0, π is 5 1212 xx  ππ  <<   or 5 , 1212 ππ    . 102. a, d. () 2cos3 2 x fx =+ ; () 4 gx =

b. ()() 2cos34 2 2cos1 2 1 cos 22

f xgx x x x

xxkk x kxk

=+=+ =+=+

ππ ππ ππ ππ

= += = = 5 2 or 2 2323 210 4or 4, 33

k is any integer

On [ ] 0,4π , the solution set is 210 , 33 ππ  

c. From the graph in part (a) and the results of part (b), the solution of ()() f xgx < on

[ ] 0,4 π is 210 33 xx  ππ  <<    or 210 , 33 ππ    .

103. a, d. () 4cos f xx =− ; () 2cos3gxx=+

b. ()() 4cos2cos3 6cos3 31 cos 62

= −=+ −= ==− 24 2or 2, 33 x kxkππ =+=+ππ

fxgx xx x x

k is any integer

On [ ] 0,2π , the solution set is 24 , 33 ππ   

684

−6 6 0 π

101.

2 3

2 1

= = 5 22

x kxk x kxk ππ ππ ππ

=+=+ =+=+

7 3sin22

3sin2

sin2

f xgx x x x = +=

or 22 66

or , 1212

ππ



c. From the graph in part (a) and the results of part (b), the solution of ()() f xgx > on

[ ] 0,2π is 24 33 xx ππ  << 

or 24 , 33

104. a, d. () 2sin f xx = ; () 2sin2gxx=−+

For 0 k = , 0 t = sec.

For 1 k = , 3 0.43 7 t =≈ sec.

For 2 k = , 6 0.86 7 t =≈ sec.

The blood pressure will be 100 mmHg after 0 seconds, 0.43 seconds, and 0.86 seconds.

b. Solve () 120 Pt = on the interval [ ]0,1 . 7 10020sin120 3 7 20sin20 3 7 sin1

b. ()() 2sin2sin2 4sin2 21 sin 42

= =−+ = == 5 2or 2, 66 x kxkππ =+=+ππ

fxgx xx x x

k is any integer

On [ ] 0,2π , the solution set is 5 , 66 ππ

c. From the graph in part (a) and the results of part (b), the solution of ()() f xgx > on [ ] 0,2 π is 5 66 xx  ππ  << 

() 7 10020sin 3 Ptt π 

a. Solve () 100 Pt =

interval [ ]0,1 .

The

On the interval [ ]0,1 , we get 0.03 t ≈ seconds, 0.39 t ≈ seconds, and 0.89 t ≈ seconds. Using this information, along with

Section 7.3: Trigonometric Equations 685



ππ   

 





   . 105.

 

or 5 , 66 ππ

7 10020sin100 3 7 20sin0 3 7 sin0 3

t t π π π  +=    =    =   3 7 7 , is any integer 3 , is any integer tkk tkk π π = = We need 3 7 01 k ≤≤ , or 7 3 0 k ≤≤ .

on the

3 t t t π π π  +=    =    =   () 1 2 7 2, is any integer 32 32 , is any integer 7 tkk k tk ππ π =+ + = We need () 1 2 7 1 23 111 26 111 412 32 01 7 02 2 k k k k + ≤≤ ≤+≤ −≤≤ −≤≤ For 0 k = , 3 0.21 sec 14 t =≈

blood pressure will be

after

sec

120mmHg

0.21

Pt = on the interval [ ]

1 1 7 10020sin105 3 7 20sin5 3 73 sin 34 73 sin 34 33 sin 74 t t t t t π π π π π  +=    =    =    =    =  

c. Solve () 105

0,1 .

Chapter 7: Analytic Trigonometry

the results from part (a), the blood pressure will be between 100 mmHg and 105 mmHg for values of t (in seconds) in the interval [ ] [ ] [ ] 0,0.030.39,0.430.86,0.89 ∪∪ .

106. () 125sin0.157125

a. Solve () 125sin0.157125125

0.1572, is any integer

, is any

So during the first 80 seconds, an individual on the Ferris wheel is exactly 250 feet above the ground when 20 seconds t ≈ and again when 60 seconds

So during the first 40 seconds, an individual on the Ferris wheel is exactly 125 feet above the ground when 10 seconds

and again when 30 seconds

So during the first 40 seconds, an individual on the Ferris wheel is more than 125 feet above the ground for times between about 10 and 30 seconds. That is, on the interval 1030 x << , or () 10,30

686

π 

 

2 htt

=−+

π  =−+=  

[ ] 0,40

2 125sin0.1570 2 sin0.1570 2 t t t π π π  −+=   −=   −= 

is any integer 2 0.157, is any integer 2 2 , is any integer 0.157 tkk tkk k tk π π π π π π −= =+ + = For 0 2 0, 10 seconds 0.157 kt π + ==≈ For 2 1,

0.157 kt π π + ==≈ .

2 2 2, 50 seconds 0.157 kt π π + ==≈ .

htt

on the interval

125sin0.157125125

0.157,

30 seconds

For

t ≈

t ≈ .

Solve () 125sin0.157125250 2 htt π  =−+=   on the interval [ ] 0,80 .

2 125sin0.157125 2 sin0.1571 2 t t t π π π −+=   −=   −= 

125sin0.157125250

0.157 tkk tkk k tk ππ π ππ ππ −=+ =+ + = For 0, 20 seconds 0.157 kt π ==≈ . For 2 1, 60 seconds 0.157 kt ππ + ==≈ For 4 2, 100 seconds 0.157 kt ππ + ==≈ .

integer

t ≈ .

2 htt π  =−+>   on the interval [ ] 0,40 125sin0.157125125 2 125sin0.1570 2 sin0.1570 2 t t t π π π −+>   −>   −>  Graphing 1 sin0.157 2 yx π  =−  and 2 0 y = on the interval [ ] 0,40 , we see

12yy > for 1030 x << . −1.5 0 1.5 40

Solve () 125sin0.157125125

that

107. ()()70sin0.65150dxx=+

a. ()() () () 070sin0.650150 70sin0150 150 miles

d =+ =+

b. Solve ()()70sin0.65150100dxx=+= on the interval [ ] 0,20 () () ()

+= =−

=− 1 1 5 0.65sin2 7 5 sin2 7 0.65 x k k x

min 8.44 min

++ππ

d. No, the plane is never within 70 miles of the airport while in the holding pattern. The minimum value of ()sin0.65 x is 1 . Thus, the least distance that the plane is from the airport is () 70115080 −+= miles.

108. ()() 672sin2 R θθ =

R θθ==

interval 0, 2 π       () () 1 1

672sin2450

x x x

+> >−

>−

70sin0.65150100 70sin0.6550 5 sin0.65 7

687

Section 7.3: Trigonometric Equations

π π  =−+   −+ 

kk xx k ++ππ ≈≈

6.06

≈≈ ≈≈

15.72

≈≈ ≈≈

70sin0.65150100 70sin0.6550 5 sin0.65 7 xx

x x x ≈≈ ≈≈

3.9425.942 or , 0.650.65 is any integer

For 0 k = , 3.9405.940 or 0.650.65

For

k = , 3.9425.942 or 0.650.65

min 18.11 min

++ππ

For 2 k = , 3.9445.944

or 0.650.65

25.39 min 27.78 min

So during the first 20 minutes in the holding pattern, the plane is exactly 100 miles from the airport when 6.06 minutes x ≈ , 8.44 minutes x ≈ , 15.72 minutes x ≈ , and 18.11 minutes x ≈

c. Solve ()()70sin0.65150100dxx=+> on the interval [ ] 0,20 . () () ()

Graphing () 1 sin0.65 y x = and 2 5 7

=− on

−1.5 0 1.5 20

the interval [ ] 0,20 , we see that 12yy > for 06.06 x << , 8.4415.72 x << , and 18.1120 x <<

So during the first 20 minutes in the holding pattern, the plane is more than 100 miles from the airport before 6.06 minutes, between 8.44 and 15.72 minutes, and after 18.11 minutes.

450225 sin2 672336 225 2sin2 336 225 sin2 336 2 k k θ θ θπ π θ = ==  =+    +   = 0.733722.4082 or , 22 is any integer kk k θθππ ++ ≈≈ For 0 k = , 0.73370 2 0.36685 21.02 θ + = ≈ ≈° or 2.4080 2 1.204 68.98 θ + = ≈ ≈° For 1 k = , 0.73372 2 3.508 200.99 π θ + = ≈ ≈° or 2.4082 2 4.3456 248.98 π θ + = ≈ ≈° So the golfer should hit the ball at an angle of

21.02

68.98

a. Solve ()()672sin2450

on the

either

° or

Chapter 7: Analytic Trigonometry

b. Solve ()()672sin2540 R θθ== on the interval 0, 2 π 

So, the golf ball will travel at least 480 feet if the angle is between about 22.79° and 67.21°

d. No; since the maximum value of the sine function is 1, the farthest the golfer can hit the ball is () 6721672 = feet.

109. Find the first two positive intersection points of 1 Yx =− and 2 tan Yx = .

So the golfer should hit the ball at an angle of either

c. Solve ()()672sin2480 R θθ=≥ on the interval 0, 2 π

The first two positive solutions are 2.03 x ≈ and 4.91 x

110. a. Let L be the length of the ladder with x and y being the lengths of the two parts in each hallway.

and using INTERSECT, we see that

yy ≥ when 0.39781.1730 x ≤≤

688

   () () 1 1 672sin2540 540135 sin2 672168 135 2sin2 168 135 sin2 168 2 k k θ θ θπ π θ = ==  =+    +   =

integer kk k θθππ ++ ≈≈ For 0 k = , 0.93300 2 0.46665 26.74 θ + = ≈ ≈° or 2.20830 2 1.10415 63.26 θ + = ≈ ≈° For 1 k = , 0.93302 2 3.608 206.72 π θ + = ≈ ≈° or 2.20832 2 4.246 243.28 π θ + = ≈ ≈°

0.933322.20832 or , 22 is any

26.74

° or 63.26

    . () () () 672sin2480 480 sin2 672 5 sin2 7 θ θ θ ≥ ≥ ≥ Graphing () 1 sin2 y x = and 2 5 7 y

interval 0, 2 π    

radians,

2 π −1.5 1.5 0 2 π −1.5 1.5 0

= on the

or 22.7967.21 x °≤≤°

−12 2 0 2π

2 02π

−12

≈

Lxy =+ 3 cos 3 cos x x θ θ = = 4 sin 4 sin y y θ θ = = 34 ()3sec4csc cossin L θθθ θθ =+=+ 3sectan4csccot0 θθθθ−= 3 3 3sectan4csccot sectan4 csccot3 4 tan 3 4 tan1.10064 3 47.74º θθθθ θθ θθ θ θ θ = = = =≈ ≈ b. () () () 34 47.74º cos47.74ºsin47.74º 9.87 feet L =+ ≈

c. Graph 1 34 cossin Y x x =+ and use the MINIMUM feature:

112. a. 2 (40)sin(2) 110 9.8

An angle of 47.74 θ ≈° minimizes the length at 9.87 feet

d. For this problem, only one minimum length exists. This minimum length is 9.87 feet, and it occurs when 47.74 θ ≈° . No matter if we find the minimum algebraically (using calculus) or graphically, the minimum will be the same. 111. a. () 2 (34.8)sin2 107 9.8 θ =

or 68.8º

b. The maximum distance will occur when the angle of elevation is 45° :

(40)sin2(45)

9.8

The maximum distance is approximately 163.3 meter

c. Let 2 1 (40)sin(2) 9.8 x Y = :

b. Notice that the answers to part (a) add up to 90° . The maximum distance will occur when the angle of elevation is 90245 °÷=° :

The maximum distance is 123.6 meters.

c. Let 2 1 (34.8)sin(2) 9.8 x Y =

Section

7.3: Trigonometric Equations 689 Copyright

0 20 0 90

L ≈

()

θ θ θ θ =≈ ≈ ≈ ≈

() 2 1 107(9.8) sin20.8659 (34.8) 2sin0.8659 260º or 120º 30º or 60º

()

  °=≈

() 2 (34.8)sin245 45123.6 9.8

0 125 0 90

()

40 2sin0.67375

21.2º

θ θ θ θ ⋅ =≈ ≈ ≈ ≈

θ =

2 1 1109.8 sin(2)0.67375

242.4º or 137.6º

()

[ ] 2

45163.3

R ° °=≈

0 170 0 90 d. 113. () 2 2 2 1 2 sin40 1.33 sin 1.33sinsin40 sin40 sin0.4833 1.33 sin0.483328.90 θ θ θ θ ° = =° ° =≈ =≈°

Chapter 7: Analytic Trigonometry

119. If θ is the original angle of incidence and φ is the angle of refraction, then 2 sin sin n θ φ = . The angle of incidence of the emerging beam is also φ , and the index of refraction is 2

115. Calculate the index of refraction for each:

1 n . Thus, θ is the angle of refraction of the emerging beam. The two beams are parallel since the original angle of incidence and the angle of refraction of the emerging beam are equal.

Yes, these data values agree with Snell’s Law. The results vary from about 1.25 to 1.34.

120. Here we have

The index of refraction for this liquid is about 1.56.

117. Calculate the index of refraction:

121. Answers will vary.

122. Since the range of sin yx = is 11 y −≤≤ , then 5sin yxx =+ cannot be equal to 3 when 4 x π > or x <−π since you are multiplying the result by 5 and adding x.

123.

6log x y xy=↔=

118. The index of refraction of crown glass is 1.52.

124.

The angle of refraction is about 19.20°

690

114. () 2 2 2 1 2 sin50 1.66 sin 1.66sinsin50 sin50 sin0.4615 1.66 sin0.461527.48 θ θ θ θ ° = =° ° =≈ =≈°

11 12 22 sin sin sin10º

sin8º sin20º

sin v v θ θθ θ = ≈ =≈ =≈ =≈ =≈ =

≈ =≈ =≈

10º8º1.2477

20º15º30'15.5º1.2798 sin15.5º sin30º 30º22º30'22.5º1.3066 sin22.5º sin40º 40º29º0'29º1.3259 sin29º sin50º 50º35º0'35º1.3356 sin35º sin60º 60º40º30'40.5º

1.3335 40.5º sin70º 70º45º30'45.5º1.3175 sin45.5º sin80º 80º50º0'50º1.2856 sin50º

8 1 8 2 2.99810 1.56 1.9210 v v × =≈ ×

116.

θ θθ θ ===≈

2 sin sin40º 40º,26º;1.47 sinsin26º

() 2 2 2 1 2

1.52

θ θ θ θ ≈ =° ° =≈ ≈≈°

sin30º 1.52 sin 1.52sinsin30 sin30 sin0.3289

sin0.335219.20

1 1.33 n = and 2 1.52 n = 1B2 2 1 2 1 11 2 1 sincos sin cos tan 1.52 tantan48.8 1.33 B B B B B nn n n n n n n θ θ θ θ θ = = =  ==≈°  

2 (9)(9)4(2)(8) 2(2) 98164 4 917 4 x −−±−− = ±− = ± = So the solution set is: 917917 , 44 −+

Section 7.4: Trigonometric Identities

7. False, you need to work with one side only.

691 Copyright © 2016 Pearson Education, Inc. 125. 10310 sin,cos1010 θθ =−= 10 10 sin10101 tan cos103 310 310 10 θ θ θ ===−⋅=− 111010 csc110 sin 1010 10 10 θ θ ===−=− 11101010 sec cos3 31010 310 10 θ θ ===⋅= 1 cot3 tan θ θ ==− 126. ()2sin2 yx π =− Amplitude:22 22 Period: 2 Phase Shift: 22 A T π ω φππ ω == ππ === ==

Section 7.4

1. True

2. True 3.

identity;

conditional 4. 1

0 6. True

8. True 9. c 10. b 11. sin11 tancsc cossincos θ θθ θθθ ⋅=⋅= 12. cos11 cotsec sincossin θ θθ θθθ ⋅=⋅= 13. () () 2 2 cos1sin cos1sin 1sin1sin 1sin cos1sin cos 1sin cos θθ θθ θθ θ θθ θ θ θ + + ⋅= −+ + = + =

() ()

θθ θθ θθ θ θθ θ θ θ ⋅= +− = =

()

sincos θθθθ θθ θθθθθθ θθ θθθθθθ θθ θθθθθθ θθ +− + ++− = ++− = ++− = 1 sincosθθ = 16. ()() 2 2 111cos1cos 1cos1cos1cos1cos 2 1cos 2 sin vv vvvv v v ++− += −+−+ = =

14.

2 2 sin1cos sin1cos 1cos1cos 1cos sin1cos sin 1cos sin

15.

2 22 22 sincoscossin cossin sinsincoscoscossin sincos sinsincoscoscossin sincos sincossincoscossin