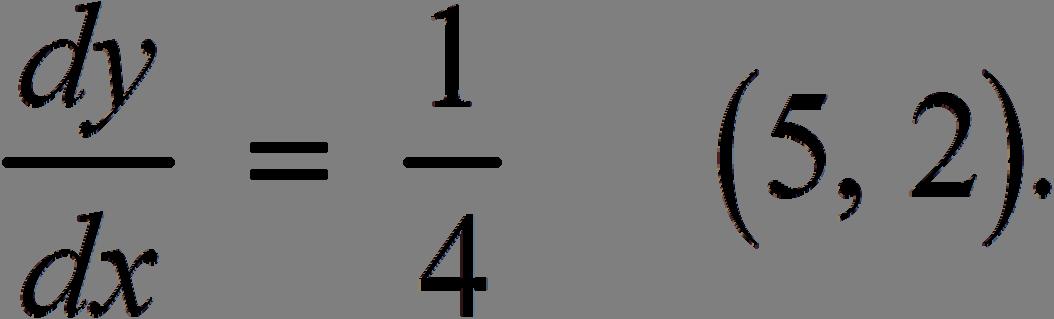Calculus of a single variable 11th edition larson solutions manual by ivy.howard597

Calculus of a Single Variable 11th Edition Larson Solutions Manual Visit to Download in Full: https://testbankdeal.com/download/calculus-of-a-single-vari able-11th-edition-larson-solutions-manual/

Differentiation Section 2.1 TheDerivativeandtheTangentLineProblem.................................114 Section 2.2 BasicDifferentiationRulesandRatesofChange .............................129 Section 2.3 ProductandQuotientRulesandHigher-OrderDerivatives.............142 Section 2.4 TheChainRule...................................................................................157 Section 2.5 ImplicitDifferentiation.......................................................................171 Section 2.6 RelatedRates......................................................................................185 Review Exercises 196 Problem Solving 204 Calculus of a Single Variable 11th Edition Larson Solutions Manual Visit TestBankDeal.com to get complete for all chapters

CHAPTER 2 Differentiation

Section 2.1 The Derivative and the Tangent Line Problem

1. Theproblemoffindingthetangentlineatapoint P is essentiallyfindingtheslopeofthetangentlineatpoint P.Todosoforafunction f,if f isdefinedonanopen intervalcontaining c,andifthelimit ()() 00 limlim Δ→Δ→

+Δ− Δ == ΔΔxx

fcxfc y m xx exists,thenthelinepassingthroughthepoint () () , Pcfc withslope m isthetangentlinetothegraphof f atthe point P

2. Somealternativenotationsfor () f x ′ are ()

3. Thelimitusedtodefinetheslopeofatangentlineisalso usedtodefinedifferentiation.Thekeyistorewritethe differencequotientsothat Δx doesnotoccurasafactor ofthedenominator.

4. Ifafunction f isdifferentiableatapoint, x c = then f iscontinuousat. x c = Theconverseisnottrue.Thatis, afunctioncouldbecontinuousatapoint,butnot differentiablethere.Forexample,thefunction yx = is continuousat0, x = butisnotdifferentiablethere.

5. At () 11,,slope0. = xy At ()

6. At ()

7. (a)–(c)

8. (a) ()() ()()

ff ff

4152 1 413 4354.75 0.25 431

== ≈= So, ()() ()() 4143 4143 ffff >

(b)Theslopeofthetangentlineat ()1,2equals ()1. f ′ Thisslopeissteeperthantheslopeoftheline through ()1,2and ()4,5.So, ()() () 41 1. 41 ff f ′ <

9. () 35 f xx =− isaline.Slope5 =−

10. () 3 21gxx=+ isaline.3 Slope2 = 11. ()

114 ©

2018

dxdx ′  

Dx y

,,,dydyfx

and [ ]

5 2

,,slope.xy

2 3

22 2 5

=−

,,slope. = xy At ()

,,slope.xy

(d) ()() ()() () () 41 11 41 3 12 3 112 1 ff yxf x x x =−+ =−+ =−+ =+

()() ()() ()() () () 0 22 0 2 0 2 0 0 22 Slopeat2,5lim 223223 lim 24435 lim 82 lim lim828 x x x x x fxf x x x xx x xx x x Δ→ Δ→ Δ→ Δ→ Δ→ +Δ− = Δ   +Δ−−−   = Δ +Δ+Δ−− = Δ Δ+Δ = Δ =+Δ= 12. () ()() () ()() ()() 0 2 0 2 0 2 0 0 33 Slopeat3,4lim lim53(4) 5964 lim 6 lim lim(6)6 x x x x x fxf x x x xx x xx x x Δ→ Δ→ Δ→ Δ→ Δ→ +Δ− −= Δ −+Δ−− = Δ −−Δ−Δ+ = Δ −Δ−Δ = Δ =−−Δ=− 13. () ()() ()() () 0 2 0 0 00 Slopeat0,0lim 30 lim lim33 t t t ftf t tt t t Δ→ Δ→ Δ→ +Δ− = Δ Δ−Δ− = Δ =−Δ= 6 5 4 3 2 123456 1 y x f (4) f (1)=3 41=3 (4,5) (1,2) f (4)=5 f (1)=2 f (4) f (1) 41 y = (x 1)+ f (1)= x +1

Section 2.1 The Derivative and the Tangent Line Problem 115 ©

Rights Reserved.

not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 14. () ()() () ()() 0 2 0 2 0 2 0 0 11 Slopeat1,5lim lim14(1)5 lim1244()5

lim(6)6 t t t t t hth t tt t ttt t tt t t Δ→ Δ→ Δ→ Δ→ Δ→ +Δ− = Δ +Δ++Δ− = Δ +Δ+Δ++Δ− = Δ Δ+Δ = Δ =+Δ= 15. () () ()() 0 0 0 7 lim 77 lim lim00 x x x fx f xxfx fx x x Δ→ Δ→ Δ→ = +Δ− ′ = Δ = Δ == 16. () () ()() () 0 0 0 3 lim 33 lim 0 lim0 x x x gx g xxgx gx x x x Δ→ Δ→ Δ→ =− +Δ− ′ = Δ = Δ == Δ 17. () () ()() ()() () 0 0 0 0 0 5 lim 55 lim 555 lim 5 lim lim55 x x x x x fxx f xxfx fx x x xx x xxx x x x Δ→ Δ→ Δ→ Δ→ Δ→ =− +Δ− ′ = Δ −+Δ−− = Δ −−Δ+ = Δ −Δ = Δ =−=− 18.

() 0 0 0 0 0 73 lim 7373 lim 77373 lim 7 lim lim77 x x x x x fxx fxxfx fx x xxx x xxx x x x Δ→ Δ→ Δ→ Δ→ Δ→ =− +Δ− ′ = Δ +Δ−−− = Δ +Δ−−+ = Δ Δ = Δ == 19. () () ()() () 0 0 0 0 2 3 3 lim 22 33 lim33 222 33 lim333 2 lim32 3 s s s s hss hsshs hs s s ss s s ss s s s Δ→ Δ→ Δ→ Δ→ =+ +Δ− ′ = Δ ++Δ−+  = Δ ++Δ−− = Δ Δ == Δ 20. () () ()() () () 0 0 0 0 0 2 5 3 lim 22 55 lim33 222 55 lim333 2 lim3 22 lim 33 x x x x x fxx fxxfx fx x x xx x x xx x x x Δ→ Δ→ Δ→ Δ→ Δ→ =− +Δ− ′ = Δ −+Δ−−  = Δ −−Δ−+ = Δ −Δ = Δ  =−=−   21. () () ()() ()() () ()() ()() () 2 0 22 0 2 22 0 2 0 0 3 lim 33 lim 233 lim 2 lim lim2121 Δ→ Δ→ Δ→ Δ→ Δ→ =+− +Δ− ′ = Δ +Δ++Δ−−+− = Δ +Δ+Δ++Δ−−−+ = Δ Δ+Δ+Δ = Δ =+Δ+=+ x x x x x fxxx fxxfx fx x xxxxxx x xxxxxxxx x xxxx x xxx

2018 Cengage Learning. All

May

lim6()()

() () ()() ()()

116 Chapter 2 Differentiation

not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 22. () () ()() () () ()() ()() () 2 0 22 0 2 22 0 2 0 0 5 lim 55 lim 255 lim 2 lim lim22 x x x x x fxx fxxfx fx x xxx x xxxxx x xxx x xxx Δ→ Δ→ Δ→ Δ→ Δ→ =− +Δ− ′ = Δ +Δ−−− = Δ +Δ+Δ−−+ = Δ Δ+Δ = Δ =+Δ= 23. () () ()() ()() ()() ()() () () 3 0 33 0 23 323 0 223 0 2 22 0 12 lim 1212 lim 33121212 lim 3312 lim lim3312312 Δ→ Δ→ Δ→ Δ→ Δ→ =− +Δ− ′ = Δ  +Δ−+Δ−−  = Δ +Δ+Δ+Δ−−Δ−+ = Δ Δ+Δ+Δ−Δ = Δ =+Δ+Δ−=− x x x x x fxxx fxxfx fx x xxxxxx x x xxxxxxxxx x xxxxxx x xxxxx 24. () () ()() ()() ()() ()() ()() () 3 0 33 0 23 333 0 223 0 22 0 2 4 lim 44 lim 33444 lim 334 lim lim334 34 Δ→ Δ→ Δ→ Δ→ Δ→ =+ +Δ− ′ = Δ  +Δ++Δ−+  = Δ +Δ+Δ+Δ++Δ−− = Δ Δ+Δ+Δ+Δ = Δ =+Δ+Δ+ =+ t t t t t gttt gttgt gt t tttttt t tttttttttt t tttttt t tttt t

Section 2.1 The Derivative and the Tangent Line Problem 117 © 2018 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 25. () () ()() ()() ()() ()() ()() () 0 0 0 0 0 2 1 1 lim 11 lim11 11 lim 11 lim 11 1 lim 11 1 1 Δ→ Δ→ Δ→ Δ→ Δ→ = +Δ− ′ = Δ +Δ−− = Δ −−+Δ− = Δ+Δ−− −Δ = Δ+Δ−− = +Δ−− =− x x x x x fx x fxxfx fx x xxx x xxx xxxx x xxxx xxx x 26. () () ()() () () () () () () 2 0 22 0 22 022 2 02 022 4 3 1 lim 11 lim lim 2 lim 2 lim 2 2 x x x x x fx x f xxfx fx x x xx x xxx xxxx xxx xxxx xx xxx x x x Δ→ Δ→ Δ→ 2 Δ→ Δ→ = +Δ− ′ = Δ +Δ = Δ −+Δ = Δ+Δ −Δ−Δ = Δ+Δ −−Δ = +Δ = =− 27. () () ()() ()() 0 0 0 0 4 lim 4444 lim 44 44 lim 44 111 lim 444424 x x x x fxx fxxfx fx x xxxxxx x xxx xxx xxxx xxxxxx Δ→ Δ→ Δ→ Δ→ =+ +Δ− ′ = Δ +Δ+−++Δ+++ =⋅   Δ +Δ+++  +Δ+−+ =  Δ+Δ+++  === +Δ+++++++ 28. () () ()() () () () () 0 0 0 0 0 2 lim 22 lim 2 lim 2 lim 2 lim 21 2 s s s s s hss hsshs hs s sss s sss s ss s s ss sss ssss sss ss Δ→ Δ→ Δ→ Δ→ Δ→ =− +Δ− ′ = Δ −+Δ−− = Δ −+Δ− +Δ+ =⋅ Δ +Δ+ −+Δ− = Δ+Δ+ = +Δ+ =−=−

118 Chapter 2 Differentiation © 2018 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 29. (a)2()3fxx=+ () ()() () () () () () 0 22 0 2 22 0 2 0 0 lim 33 lim 233 lim 2 lim lim22 Δ→ Δ→ Δ→ Δ→ Δ→ +Δ− ′ = Δ +Δ+−+ = Δ +Δ+Δ+−− = Δ Δ+Δ = Δ =+Δ= x x x x x fxxfx fx x xxx x xxxxx x xxx x xxx At ()1,4,theslopeofthetangentlineis () 212. m =−=− Theequationofthetangentlineis () 421 422 22 yx yx yx −=−+ −=−− =−+ 30. (a)2()21 fxxx=+− () ()() ()() () () () 0 22 0 2 22 0 2 0 0 lim 2121 lim 222121 lim 22 lim lim2222 Δ→ Δ→ Δ→ Δ→ Δ→ +Δ− ′ = Δ  +Δ++Δ−−+−  = Δ    +Δ+Δ++Δ−−+−    = Δ Δ+Δ+Δ = Δ =+Δ+=+ x x x x x fxxfx fx x xxxxxx x xxxxxxxx x xxxx x xxx At ()1,2,theslopeofthetangentlineis () 2124. m =+= Theequationofthetangentlineis () 241 244 42. yx yx yx −=− −=− =− (b) (c)Graphingutilityconfirms () 4at1,2. dy dx = (b) (c)Graphingutilityconfirms 3 1 8 3 (1,4) 10 4 8 8 (1,2)

At ()1,0,theslopeofthetangentlineis () 2 313. m =−=

At ()1,1,theslopeofthetangentlineis 11 212 m ==

Section 2.1 The Derivative and the Tangent Line Problem 119 © 2018 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 31. (a) () () ()() () ()() ()() () () 3 33 00 3223 0 223 0 2 22 0 limlim 33 lim 33 lim lim333 Δ→Δ→ Δ→ Δ→ Δ→ = +Δ−+Δ− ′ == ΔΔ +Δ+Δ+Δ = Δ Δ+Δ+Δ = Δ =+Δ+Δ= xx x x x fxx f xxfxxxx fx xx xxxxxx x xxxxx x xxxxx At ()2,8,theslopeofthetangentis () 2 3212. m == Theequationofthetangentlineis ()8122 81224 1216. yx yx yx −=− −=− =− 32. (a) () () ()() () () ()()() ()() 3 0 33 0 23 323 0 2 22 0 1 lim 11 lim 3311 lim lim333 x x x x fxx fxxfx fx x xxx x xxxxxxx x xxxxx Δ→ Δ→ Δ→ Δ→ =+ +Δ− ′ = Δ +Δ+−+ = Δ +Δ+Δ+Δ+−− = Δ  =+Δ+Δ= 

Theequationofthetangentlineis () 031 33. yx yx −=+ =+ 33. (a) () () ()() () () 0 0 0 0 lim lim lim 11 lim 2 Δ→ Δ→ Δ→ Δ→ = +Δ− ′ = Δ +Δ−+Δ+ =⋅ Δ +Δ+ +Δ− = Δ+Δ+ == +Δ+ x x x x fxx fxxfx fx x x xxxxx x x xx xxx xxxx xxxx

Theequationofthetangentlineis () 1 11 2 11 1 22 11 22 −=− −=− =+ yx yx yx (b) (c)Graphingutilityconfirmsat (b) (c)Graphingutilityconfirms at (b) (c)Graphingutilityconfirmsat 9 6 6 9 (1,0) 5 1 1 3 (1,1)

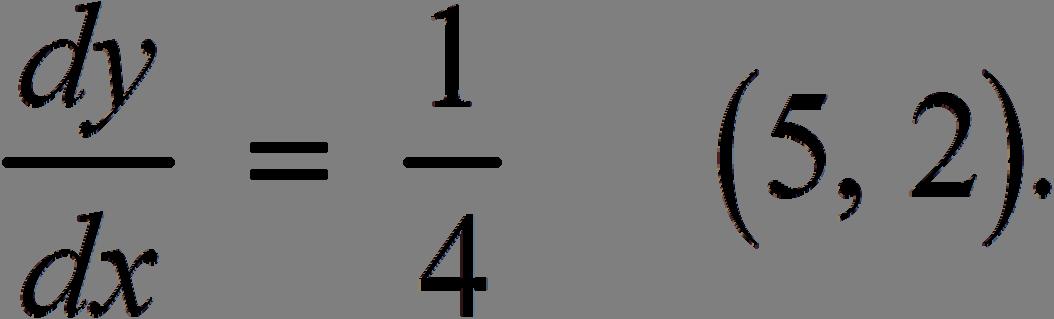
120 Chapter 2 Differentiation

be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 34. (a) () () ()() ()() () 0 0 0 0 1 lim 1111 lim 11 11 lim 11 11 lim 1121 x x x x fxx fxxfx fx x xxxxxx x xxx xxx xxxx xxxx Δ→ Δ→ Δ→ Δ→ =− +Δ− ′ = Δ +Δ−−−+Δ−+− =⋅   Δ +Δ−+−  +Δ−−− = Δ+Δ−+− == +Δ−+−− (b) At ()5,2,theslopeofthetangentlineis 11 2514 m == Theequationofthetangentlineis () 1 25 4 15 2 44 13 44 yx yx yx −=− −=− =+ 35. (a) () () ()() () ()()()() ()() ()()()() ()() ()()() ()() () () 0 0 2 0 2 3232 0 22 0 2 0 2 2 4 lim 44 lim 44 lim 24 lim 4 lim 4 lim 44 1 x x x x x x fxx x fxxfx fx x xxx xxx x x xxxxxxxxxx xxxx xxxxxxxxx xxxx xxxxx xxxx xxx xxx x xx Δ→ Δ→ Δ→ Δ→ Δ→ Δ→ =+ +Δ− ′ = Δ +Δ+−+ +Δ  = Δ +Δ+Δ+−+Δ−+Δ = Δ+Δ +Δ+Δ−−Δ−Δ = Δ+Δ Δ+Δ−Δ = Δ+Δ +Δ− = +Δ ==− 2 At ()4,5,theslopeofthetangentlineis () 2 43 1. 44 m =−= Theequationofthetangentlineis () 3 54 4 3 53 4 3 2. 4 yx yx yx +=+ +=+ =− (c)Graphingutilityconfirms at (5,2) 2 4 10 4 (b) (c)Graphingutilityconfirms at 12 10 6 12 (4,5)

4 4

37. Usingthelimitdefinitionofaderivative, () 1 2 f xx ′ =− Becausetheslopeofthegivenlineis1,youhave 1 1 2 2.

x x

−=− =

Atthepoint ()2,1,thetangentlineisparallelto 0. xy+= Theequationofthislineis ()() 112 1. yx yx

−−=−− =−+

38. Usingthelimitdefinitionofderivative, () 4. f xx ′ = Becausetheslopeofthegivenlineis–4,youhave 44 1. x x

=− =−

Atthepoint ()1,2thetangentlineisparallelto 430. xy++= Theequationofthislineis

() 241 42. yx yx

−=−+ =−−

5 (1,0)

39. FromExercise31weknowthat () 2 3. f xx ′ = Becausetheslopeofthegivenlineis3,youhave 2 33 1. x x

= =±

Therefore,atthepoints ()1,1and ()1,1thetangent linesareparallelto310. xy−+= Theselineshaveequations

()() 131and131 3232. yxyx yxyx

−=−+=+ =−=+

40. Usingthelimitdefinitionofderivative, () 2 3. f xx ′ = Becausetheslopeofthegivenlineis3,youhave 2 2

33 11. x xx

= =  =±

Therefore,atthepoints ()1,3and ()1,1thetangent linesareparallelto340. xy−−= Theselineshave equations

−=−−=+ ==+ 5

Section 2.1 The Derivative and the Tangent Line Problem 121 © 2018 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 36. (a) () () ()() ()()()() () ()()() () ()()() () () 0 0 2 0 2 3232 0 2 22 0 22 0 1 lim 11 lim lim 2 lim 2 lim 21 lim Δ→ Δ→ Δ→ Δ→ Δ→ Δ→ =− +Δ− ′ = Δ  +Δ−−−  +Δ   = Δ +Δ+Δ−−+Δ++Δ = Δ+Δ +Δ+Δ−−−Δ++Δ = Δ+Δ Δ+Δ−Δ+Δ = Δ+Δ +Δ−+ = x x x x x x fxx x fxxfx fx x xxx xxx x xxxxxxxxxxx xxxx x xxxxxxxxxx xxxx xxxxxxx xxxx xxxx x () 2 22 11 1 +Δ + ==+ xx x xx At ()1,0,theslopeofthetangentlineis ()12. mf ′ == Theequationofthetangentlineis () 021 22. yx yx

−=− =−

()() 331and131 334. yxyx yxyx (b) (c)Graphingutilityconfirms at

41. Usingthelimitdefinitionofderivative, () 1 2 fx x x ′ = Becausetheslopeofthegivenlineis1,2youhave

45. Theslopeofthegraphof f isnegativefor4, x < positivefor4, x > and0at4. x =

46. Theslopeofthegraphof f is–1for4, x < 1for 4, x > andundefinedat4. x =

42. Usingthelimitdefinitionofderivative,

47. Theslopeofthegraphof f isnegativefor0 x < and positivefor0. x > Theslopeisundefinedat0. x =

48. Theslopeispositivefor20 x −<< andnegativefor 02. x << Theslopeisundefinedat2, x =± and0at

122 Chapter 2 Differentiation

to a publicly accessible website,

part.

2018 Cengage Learning.

in whole or in

11 22 1. xx

−=−

Therefore,atthepoint

260.xy+−= Theequationofthislineis () 1 11 2 11 1 22 13 22 −=−− −=−+ =−+ yx yx yx

()1,1thetangentlineisparallelto

() ()32

() () 32 32 11 212 11 112. x x xx =− =− =−  = Atthepoint

270.xy++= Theequationofthetangentlineis () 1 12 2 1 2. 2 −=−− =−+ yx yx

1 . 21 fx

′

Becausetheslopeofthegivenlineis1,2youhave

()2,1,thetangentlineisparallelto

43. Theslopeofthegraphof f is1forall x-values. 44. Theslopeofthegraphof f is0forall x-values.

0. x = 2 2 1 3 4 212 313 f ′ y x 1 212 1 2 1 2 x y f ′ 42 6246 2 4 6 8 2 4 x y f ′ x y f ′ 123456 1 2 3 y x 1 21234 2 1 2 f ′ 1 212 1 2 1 2 f ′ y x

49. Answerswillvary. Sample answer: yx =−

Thederivativeof =− yx is1. y ′ =− So,thederivative isalwaysnegative.

50. Answerswillvary. Sample answer:32 3 yxx =−

59. ()02 f = and () 3, fxx ′ =−−∞<<∞

() 32fxx=−+

60. ()()() 04,00;0 fffx ′′ ==< for () 0,0xfx ′ <> for0 x >

Answerswillvary: Sample answer: () 24 fxx=+

Notethat () 2 3632.yxxxx ′ =−=− So,0 y ′ = at0 x = and2. x =

51. No.Forexample,thedomainof () f xx = is0, x ≥ whereasthedomainof () 1 2 fx x ′ = is0. x >

52. No.Forexample, () 3 f xx = issymmetricwithrespectto theorigin,butitsderivative, () 2 3, f xx ′ = issymmetric withrespecttothe-axis. y

53. ()45 g = becausethetangentlinepassesthrough ()4,5. () 505 4 473 g ′ ==−

54. ()14 h −= becausethetangentlinepassesthrough ()1,4. () () 6421 1 3142 h′ −===

55. () 53 f xx =− and1 c =

56. () 3 f xx = and2 c =−

57. () 2 f xx =− and6 c =

58. () 2 f xx = and9 c =

61. Let () 00 , x y beapointoftangencyonthegraphof f Bythelimitdefinitionforthederivative, () 42. f xx ′ =−

Therefore,thepointsoftangencyare ()1,3and ()3,3, andthecorrespondingslopesare2and–2.Theequations ofthetangentlinesare:

Section 2.1 The Derivative and the Tangent Line Problem 123

Rights

not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part.

Reserved. May

()() () ()() 0 0 0 000 22 0000 2 00 000 5 42 2 5242 54882 043 0131,3 y x x yxx xxxx xx xxx =− −=−− −−=−+ =−+ =−−  =

()() 522522 2129 yxyx yxyx −=−−=−− =+=−+ x 1 2 3 4 2 1 3 4 321 4234 y 1 212 3 4 1 x y 21 323 1 2 3 x y f 1 2 42 6246 2 4 6 8 10 12 x y f x 21236 2 4 3 5 7 6 1 (1,3) (3,3) (2,5) y

Theslopeofthelinethrough ()2,5and () 00

x y equalsthederivativeof f at0: x

62. Let () 00 , x y beapointoftangencyonthegraphof f.

Bythelimitdefinitionforthederivative, () 2. f xx ′ = Theslopeofthelinethrough () 1,3and () 00 , x y equals thederivativeof

(b) ()

()() () ()()() ()() () ()() () 0 33 0 23 323 0 22 0 2 22 0 lim lim 33 lim 33 lim lim333 x x x x x gxxgx gx x xxx x x xxxxxx x xxxxx x xxxxx Δ→ Δ→ Δ→ Δ→ Δ→ +Δ− ′ = Δ +Δ− = Δ +Δ+Δ+Δ− = Δ Δ+Δ+Δ = Δ =+Δ+Δ=

Therefore,thepointsoftangencyare ()3,9and ()1,1, andthecorrespondingslopesare6and–2.Theequations ofthetangentlinesare:

At () 0,00xg ′ == andthetangentlineis0. y =

At () 1,13xg ′ == andthetangentlineis

() 131or32.yxyx −=−=−

Forthisfunction,theslopesofthetangentlinesare sometimesthesame.

= +Δ− ′ = Δ +Δ− = Δ +Δ+Δ− = Δ Δ+Δ = Δ =+Δ=

+=−+=−− 2 0 22 0 2 22 0 0 0

fxx fxxfx fx x xxx x x xxxx x xxx x xxx

lim lim 2 lim 2 lim lim22

64. (a) ()03 g ′ =−

(b) ()30 g ′ =

Δ→ Δ→ Δ→ Δ→ Δ→

x x x x x

At () 1,12xf ′ =−−=− andthetangentlineis () 121or21.yxyx −=−+=−−

At () 0,00xf ′ == andthetangentlineis0. y =

At () 1,12xf ′ == andthetangentlineis 21.yx=−

(c)Because () 8 3 1, g g ′ =− isdecreasing(falling)at

1. x =

(d)Because () 7 3 4, g g ′ −= isincreasing(rising)at

4. x =−

x 6224684 2 4 4 8 6 10 (3,9) (1,3) (1,1) y 3 3 3 2 33 2 2

Forthisfunction,theslopesofthetangentlinesare alwaysdistinctfordifferentvaluesof x.

(e)Because () 4 g ′ and () 6 g ′ arebothpositive, () 6 g is greaterthan ()4, g and ()() 640.gg−>

(f)No,itisnotpossible.Allyoucansayisthat g is decreasing(falling)at2. x =

124 Chapter 2 Differentiation

be scanned, copied or duplicated, or posted to a publicly accessible website, in

or in part.

whole

f at0: x () ()() 0 0 0 000 22 000 2 00 000 3 2 1 312 322 230 3103,1 y x x yxx xxx xx xxx = −−=− −−=− −−= −+=  =−

()() 361321 6921 yxyx yxyx =−=−− 63. (a) () () ()() () ()() () ()

At () 1,13xg ′ =−−= andthetangentlineis

() 131or32.yxyx +=+=+

() ()() 00,1212,11,22 ffff ′′′′

() ()() 00,1214,11,24, ffff ′′′′

Section 2.1 The Derivative and the Tangent Line Problem 125 © 2018 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 65. () 12 2 f xx = (a)

====

()() 1212,11,22fff ′′′ −=−−=−−=− (c) (d) () ()() () ()() () 22222 0000 1111 2 2222 limlimlimlim 2 xxxx xxxxxxxx fxxfx x f x xx xxx Δ→Δ→Δ→Δ→ +Δ−+Δ+Δ− +Δ− Δ  ′ ====+=  ΔΔΔ  66. () 13 3 f xx = (a) ()

()39 f ′ = (b)Bysymmetry: () () 1214,11,ff ′′ −=−= ()()24,39ff ′′ −=−= (c) (d) () ()() () ()()() () () () 0 33 0 23 323 0 2 22 0 lim 11 lim33 11 33 lim33 1 lim 3 x x x x fxxfx fx x xxx x x xxxxxx x xxxxx Δ→ Δ→ Δ→ Δ→ +Δ− ′ = Δ +Δ− = Δ +Δ+Δ+Δ− = Δ  =+Δ+Δ=   2 66 6 y x 32 41234 2 3 4 1 2 3 4 f ′ 9 6 9 6 21 3123 1 1 2 3 4 5 x y f ′

()

(b)Bysymmetry: ()

====

x x x x →=→−∞

As 1 0,. x x x x + →=→∞

Therefore () g x isnotdifferentiableat0. x =

() 3 ,4fxc x ==

73. ()() 23 6,6fxxc=−=

fxf f x x x x

′ = ==

6 6lim 6 601 limlim. 66

x xx

() ()() () ()

→ →→

6 23 6613

Doesnotexist.

Therefore () f x isnotdifferentiableat6. x =

74. ()()13 3,3gxxc=+=−

gxg g x x x x

′ −= +− == + +

3 3lim 3 301 limlim. 33

x xx

() ()() () () ()

→− →−→−

3 13 3323

Doesnotexist.

Therefore () g x isnotdifferentiableat3. x =−

75. () 7,7hxxc=+=− () ()() () 7 77

hxh h x xx xx

′ −= +−+ == ++

7 7lim 7 707 limlim. 77

x xx

→− →−→−

Doesnotexist. Therefore ()hx isnotdifferentiableat7. x =−

76. () 6,6fxxc=−= () ()() 6 66

fxf f x xx xx

′ = ==

6 6lim 6 606 limlim. 66

x xx

→ →→

Doesnotexist. Therefore () f x isnotdifferentiableat6. x =

77. () f x isdifferentiableeverywhereexceptat4. x =− (Sharpturninthegraph)

78. () f x isdifferentiableeverywhereexceptat2. x =± (Discontinuities)

79. () f x isdifferentiableontheinterval () 1,.−∞ (At 1=− x thetangentlineisvertical.)

80. () f x isdifferentiableeverywhereexceptat0. x = (Discontinuity)

126 Chapter 2 Differentiation ©

not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 67. ()()()() () () 22424,2.12.142.13.99 3.994 20.1Exact:20 2.12 ff ff =−==−= ′′ ≈=−  =   68. () () () () () 13 222,2.12.31525 4 2.315252 23.1525Exact:23 2.12 ff ff === ′′ ≈=  =   69. () 3221,2fxxxc=++=− () ()() () () 2 32 2 2 2 22 2 2lim 2 211 lim 2 2 limlim4 2 x x xx fxf f x xx x xx x x →− →− →−→− ′ −= + ++− = + + === + 70. () 2,1gxxxc=−= () ()() () 1 2 1 1 1 1 1lim 1 0 lim 1 1 lim 1 lim1 x x x x g xg g x xx x xx x x → → → → ′ = = = == 71. () ,0gxxc== () ()() 00 0 0limlim. 0 xx x gxg g x x →→ ′ == Doesnotexist. As 1 0,.

() ()() () () () 4 4 4 4 4 33 4 4 4lim 4 lim 4 123 lim 44 34 lim 44 33 lim 416 x x x x x x fxf f x x x xx x xx x → → → → → ′ = = = = =−=−

72.

81. () 5 fxx=− isdifferentiable everywhereexceptat5. = x Thereisasharpcornerat 5. x =

82. () 4 3 x fx x = isdifferentiable everywhereexceptat3. x = f isnotdefinedat3. x = (Verticalasymptote)

83. () 25 f xx = isdifferentiable forall0. x ≠ Thereisasharp cornerat0. x =

84. f isdifferentiableforall1. x ≠ f isnotcontinuousat1. x =

85. () 1 fxx=−

Thederivativefromtheleftis

87. () () () 3 2 1,1 1,1

xx fx xx

 −≤  =  −>  

Thederivativefromtheleftis

→→ →

fxfx xx x

()() () ()

3 11 2 1

= =−=

110 limlim 11 lim10. xx x

Thederivativefromtherightis

2 11 fxfx xx x

11 = =−=

110 ++ →→ + →

Theone-sidedlimitsareequal.Therefore,

f is differentiableat1. x = () () 10 f ′ =

Thederivativefromtheleftdoesnotexist.

Similarly,thederivativefromtherightdoesnotexist becausethelimitis ∞

isnotdifferentiableat1.

()() 11

x fxf xx→→ ==−

110 limlim1. 11xx

Thederivativefromtherightis

 =

 

()() 11

110 limlim1. 11xx

x fxf xx++ →→ ==

Theone-sidedlimitsarenotequal.Therefore, f isnot differentiableat1. x =

86. () 12 f xx =−

x fxf xx x →→ →

()() () ()

+− = =+=

Thederivativefromtherightis

2435 limlimlim44. 22 xxx

fxfx xx +++ →→→ ===

()() () 222

Thederivativefromtheleftdoesnotexistbecause ()() 2 11 22 12 12

→→ → →

xx x x

110limlim 11 11 lim 11 1 lim. 1

fxf x xx x x x x x x

(Verticaltangent)

= =⋅ + =−=−∞

Thelimitfromtherightdoesnotexistsince f is undefinedfor1. x > Therefore, f isnotdifferentiableat 1. x =

Theone-sidedlimitsareequal.Therefore, f is differentiableat2. x = () () 24 f ′ =



 ≥  

1 lim223

2 2

Section 2.1 The Derivative and the Tangent Line Problem 127

to a publicly accessible

posted

website,

whole or in part.

limlim

()() () () lim10. xx x

88. ()()123 f xx =−

() 23 11 13 1 110 limlim 11 1 lim 1 →→ → = ==−∞ xx x fxfx xx x

()() ()

Therefore, f

x =



89. Notethat f iscontinuousat2. x = () 21,2 43,2 xx fx xx  +≤

−>

Thederivativefromtheleftis

2 22 2

215 limlim 22 lim24. xx x

x x fx fx → + →

1 111 7 8 6 12 15 6 3 6 5 3 5 3 4

90. () 1 22,2 2,2 xx fx xx

 +<

f isnotdifferentiableat2 = x becauseitisnot continuousat2. x = () () ()()

lim222

=+= ==

91. (a)Thedistancefrom ()3,1totheline40 mxy−+= is

(b) Thefunction d isnotdifferentiableat1. m =− Thiscorrespondstotheline4, yx=−+ whichpassesthrough thepoint ()3,1.

92. (a) () 2 f xx = and () 2 f xx ′ = (b) () 3 g xx = and () 32 g xx ′ =

(c)Thederivativeisapolynomialofdegree1lessthantheoriginalfunction.If () , hxxn = then () 1 hxnxn ′ =

() 4 , f xx = then

then () 43 f xx ′ = whichisconsistentwiththeconjecture.However,thisisnotaproofbecauseyou mustverifytheconjectureforallintegervaluesof,2. nn ≥

93. False.Theslopeis

94. False.2 yx=− iscontinuousat2, x = butisnot differentiableat2. x = (Sharpturninthegraph)

95. False.Ifthederivativefromtheleftofapointdoesnot equalthederivativefromtherightofapoint,thenthe derivativedoesnotexistatthatpoint.Forexample,if () , f xx = thenthederivativefromtheleftat0 x = is –1andthederivativefromtherightat0 x = is1.At 0, x = thederivativedoesnotexist.

96. True.SeeTheorem2.1.

2018

128 Chapter 2 Differentiation

to a publicly accessible

in part.

website,

whole or

()()

11 2222 311433 . 11 m AxByCm d ABmm −+ +++ === +++

(d)If

() ()() () ()()()() ()()() () ()()() () 0 44 0 234 4324 0 3223 23 323 00 lim lim 464 lim 464 limlim4644. x x x xx fxxfx fx x xxx x xxxxxxxxx x xxxxxxx x xxxxxx x Δ→ Δ→ Δ→ Δ→Δ→ +Δ− ′ = Δ +Δ− = Δ +Δ+Δ+Δ+Δ− = Δ Δ+Δ+Δ+Δ ==+Δ+Δ+Δ= Δ So,if () 4

, f xx

()() 0 22 lim. x fxf x Δ→ +Δ− Δ

x 2 3 1234 1 y 5 1 44 x 1234 1 3 2 4 1 3 2 f f' 4 5 3 y g g ′ x 2 1 1 3 2 1 2 1 y

98.

UsingtheSqueezeTheorem,youhave () sin1,0.xxxxx −≤≤≠ So, ()() 0 limsin100 x x xf → == and f iscontinuousat0. x = Usingthealternativeformofthederivative,youhave

0sin101 limlimlimsin. 00 xxx 

() 2sin1,0



fxfxx x xx→→→  ==

0sin101 limlimlimsin0. 00 xxx

gxgxx x xxx→→→ ===

Asyouzoomin,thegraphof211yx=+ appearstobelocallythegraphofahorizontalline,whereasthegraphof 21yx=+ alwayshasasharpcornerat ()0,1.2 y isnotdifferentiableat ()0,1.

Section 2.2 Basic Differentiat ion Rules and Rates of Change

[] 0 d c dx

1 ′ = n f xncx

(a) () 12 112 2 1 12 yx yx y = ′ = ′ = (b) () 3 32 13 yx yx y = ′ = ′ =

Section 2.2 Basic Differentiation Rules and Rates of Change 129 ©

not be

copied or duplicated, or posted to a publicly accessible website, in whole or in part.

xxx



 =  =  

2018 Cengage Learning.

May

scanned,

97. () () sin1,0 0,0

fx x

≠

()() () 000

()

0,0 xxx



 = 

 

Becausethislimitdoesnotexist( ()sin1 x oscillatesbetween–1and1),thefunctionisnotdifferentiableat0. x =

gx x

≠

UsingtheSqueezeTheoremagain,youhave () 222sin1,0.xxxxx −≤≤≠ So, ()() 2 0 limsin100 x x xg → == and g iscontinuousat0. x = Usingthealternativeformofthederivativeagain,youhave ()() () 2 000

Therefore, g isdifferentiableat () 0,00.xg ′ ==

1. Thederivativeofaconstantfunctionis0.

()

2. Tofindthederivativeof () , n f xcx = multiply n by, c andreducethepowerof x by1.

3. Thederivativeofthesinefunction, () sin, f xx = isthe cosinefunction, () cos. f xx ′ = Thederivativeofthecosinefunction, () cos, g xx = is thenegativeofthesinefunction, () sin. g xx ′ =−

(a) () 12 132 2 1 12 yx yx y = ′ =− ′ =− (b) () 1 2 11 yx yx y = ′ =− ′ =− 3 3 1 3

4. Theaveragevelocityofanobjectisthechangein distancedividedbythechangeintime.Thevelocityis theinstantaneouschangeinvelocity.Itisthederivative ofthepositionfunction.

17. () () 2 326 62 fttt ftt =−+− ′ =−+

18. 231 23 ytt yt =−+ ′ =−

19. () () 23 2

4 212 g xxx g xxx

=+ ′ =+

20. 3 2

=− ′ =−

43 49 yxx yx

21. () () 32 2

538 3103 stttt sttt

=+−+ ′ =+−

22. 32 2

261 612 yxx yxx

=+− ′ =+

y y

= ′ =

23. sin 2 cos 2

π θ π θ

() ()

72sin 742cos282cos yxx y xxxx Function Rewrite Differentiate Simplify 27. 45 45 2288 7777 ′′ ===−=− yyxyxy x x 28. () 544 5 888 58 555 ′′ ==== yyxyxyx x 29. () 34 34 661818 5125125125 yyxyxy x x ′′ ===−=− 30. () () 2 2 3 1212224 2 ′′ ==== yyxyxyx x

=+ ′ =+=+

130 Chapter 2 Differentiation

scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part.

12 0 = ′

y y

7 76

= ′ = 10. 12 1211 yx yx = ′ = 11. 5 5 6 6 1 5 5 yx x yx x == ′ =−=− 12. () 7 7 8 8 3 3 21 37 yx x yx x == ′ =−=−

x == ′ ==

8. () () 9 0 fx fx =− ′

yx yx

13. () () 919 89 89

99 fxxx fxx

34 34

x == ′ ==

14. 414

11 44 yxx yx

15. () () 11 1 fxx fx

′ =

16. () () 63 6 gxx gx =+ ′ =

24.

cos sin g tt g tt π π = ′ =−

25. 21 2

2 cos 2sin yxx yxx =− ′ =+

26. () 4 33

41. () ()

=−=− ′ =+=+

gtttt t gtttt t

42. () ()

223 3 4 4

4 4 12 2122

=+=+ ′ =−=−

3 883 6 868

f xxxx x fxx x

++ ==++

43 ′

=+− +− =

ss hssss s hssss ss s

47. ()23 2

=+=+

′ =+

=−=−

′ =−=−

48. () () 2243 322

49. () ()

50. () ()

=−=−

fxxxxx fxxx x x ′

=−+

′ =−=−

fttt fttt tt

2313 1323 1323

51. () ()

=+=+

12 12

=−=−

Section 2.2 Basic Differentiation Rules and Rates of Change 131 © 2018 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 31. () () () () 2 2 3 3 8 8,2,2 16 16 22 fxx x fxx x f == ′ =−=− ′ =− 32. () () () () 1 2 2 4 224,4,1 4 4 1 4 4 ftt t ftt t f =−=− ′ == ′ = 33. () () () () 3 2 7 11 252 21 5 ,0, 00 fxx fxx f =−+− ′ = ′ = 34. () () 4 3 23,1,1 8 18 yx yx y =−− ′ = ′ = 35. ()() ()() 2 2 41,0,1 1681 328 032088 =+ =++ ′ =+ ′ =+= yx xx yx y 36. ()()() () () 2 2 24,2,8 21632 416 28168 fxx xx fxx f =− =−+ ′ =− ′ =−=− 37. ()() () ()() 4sin,0,0 4cos1 04113 f f f θθθ θθ =− ′ =− ′ =−= 38. ()() () () 2cos5,,7 2sin 0 gtt gtt g π π =−+ ′ = ′ = 39. () () 22 3 3 53 6 262 fxxx fxxxx x =+− ′ =+=+ 40. () () 33 242 4 23 9 32932 fxxxx fxxxx x =−+ ′ =−−=−−

2 3 3

43. () ()′ =−=

33 34 34 88 1 xx f xxx x x fx xx −+ ==−+

2 2

′ =−=−

tt t

==+− ′ =−+ −+ =

44. () ()

425 425 5 858 xx hxxx x hxxxx x ++ ==++

45. () ()

121232 32 123252

52 348 348

212

3424

tt g tttt t gtttt

+−

46. () ()

1432313 13 1131343

26 26 144 2 33 1446 3

1 31 yxxxx yx

2323 8989 yxxxxx yxxxx

31213 1223 23

66 112 2 22

4 2121 3333

65cos65cos 3 35sin5sin

f xxxxx f xxxx x ′

52. () ()

=+=+ ′ =−−=−−

2 3cos23cos 22 3sin3sin 33

13 3 43 43

fxxxx x f xxxx x

53. () () 22 2 1 5cos35cos95cos 3 185sin

57. (a) () ()

== ′ =−=−

yxxxxx x yxx

=−=−=− ′ =+

54. () 3 3 4 4

=+=+ ′ =+ =−+

33 2sin2sin 28 9 2cos 8 9 2cos 8

yxxx x yxx x x

55. (a) () () 42 3

253 810 fxxx fxxx =−+− ′ =−+

At ()()()() 3 1,0:1811012 f ′ =−+=

−=− =−

Tangentline: () 021 22 yx yx

(b)and(c)

56. (a)3 2

=− ′ =−

3 33 yxx yx

At ()() 2 2,2:3239 y ′ =−=

yx yx xy

−=− =− −−=

Tangentline: ()292 916 9160

(b)and(c)

fxx x fxx x

34 43 74 74

2 2 33 22

At ()() 3 1,2:1 2 f ′ =−

Tangentline: () 3 21 2 37 22 3270

yx yx xy

−=−− =−+ +−=

(b)and(c)

58. (a) ()()232 2

236 326 yxxxxxx yxx

=−+=+− ′ =+−

At ()()() 2 1,4:312161 y ′ −=+−=−

yx yx xy

−−=−− =−− ++=

Tangentline: ()() 411 3 30

(b)and(c)

60.

yxx yxx xx xxx yx

=−+ ′ =− =− =−+ ′ =  =±

23 44 41 411 00,1

59. () ()()

42 3 2

Horizontaltangents: ()()() 0,3,1,2,1,2

=+ ′ =+>

2 310forall. yxx yxx

Therefore,therearenohorizontaltangents.

132 Chapter 2 Differentiation

a publicly accessible

part.

website,

whole or in

2 2 3 3 1 2 2cannotequalzero. yx x yx x == ′ =−=−

61.

3 33 1 (1,0) 4 3 3 5 (2,2) 7 1 2 5 (1,2) 10 55 (1,4) 10

=+ ′ ==  =

62. 29 200 yx yxx

At0,1. xy==

Horizontaltangent: () 0,9

=+≤< ′

π π  =

=−

At: x y ==ππ

xx π ππ =+≤< ′ =−= =  =

At 2233 : 33xy ππ

Horizontaltangents: 332233 ,,, 3333

′

x x

′ =− =− =− 12 233 y kk  =−−+=+

fx kx x k +=−  += =− =−

1 3 1 3 k kk kk k k

67. () 3 ,3 4 k fxyx x ==−+

x ′ =−

2 k

Section 2.2 Basic Differentiation Rules and Rates of Change 133 © 2018 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part.

63. sin,02 1cos0 cos1

yxxx yx xx =+=

Horizontaltangent: () ,

ππ

64. 32cos,02 32sin0 32 sinor 233 ==

yxxx yx

At 33 : 33xy ππ +

ππππ  +−   

() 6

=− −=− = () 2

−=− =

65. () 2,61fxkxyx=−=−+

()

2 f xx ′ =− andslopeoftangentlineis6. m =−

63117 173 8 y k k =−+=−

66. () 2,23fxkxyx==−+

() 2 f xkx ′ = andslopeoftangentlineis2. m =−

() 2 22 1  

212 3

21 3

4 m =− () 2 2 3 4 3 4 4 3 4 3 fx k x k x k x ′ =− −=− = = 334 33 443 k yx=−+=−+ 343 3 434 3 k k k k −+= =

()

andslopeoftangentlineis3

68. () ,4fxkxyx==+ () 2 k fx x ′ = andslopeoftangentlineis1. m =

74.

If f isquadratic,thenitsderivativeisalinearfunction. () () 2 2 f xaxbxc fxaxb =++ ′ =+

75. Thegraphofafunction f suchthat0 f ′ > forall x and therateofchangeofthefunctionisdecreasing (i.e.,as x increases, ′ f decreases)would,ingeneral,look likethegraphbelow.

69. ()()()() 6 g xfxgxfx ′′ =+  =

70. ()()()() 22 g xfxgxfx ′′ =  =

71. ()()()() 55 g xfxgxfx ′′ =−  =−

72. ()()()() 313 g xfxgxfx ′′ =−  =

73. If f islinearthenitsderivativeisaconstantfunction. () () f xaxb fxa =+ ′ =

76. (a)Theslopeappearstobesteepestbetween A and B

(b)Theaveragerateofchangebetween A and B is greater thantheinstantaneousrateofchangeat B (c)

134 Chapter 2 Differentiation

duplicated, or

to a publicly accessible website, in

in part.

posted

whole or

() 2 1 1 2 2 4 ′ = = = = fx k x k x k x 2 44 4 k yx=+=+ 2 22 2 2 4 42 4 42 4 4 16 4 +=⋅ −=− −=− = = kk k kk k k k

3 3 1 32112 2 x f f ′ y x 21134 1 2 3 4 f f ′ y x y x f C A B E D y

Let () 11 , x y and () 22 , x y bethepointsoftangencyon2 yx = and265, yxx=−+− respectively.

78. 1m istheslopeofthelinetangentto2 yxm = istheslopeofthelinetangentto1. yx = Because

11and.yxymyym x xx ′′ =

Thepointsofintersectionof yx = and1yx = are 1211.xxx x =  =  =±

At21,1.xm=±=− Because211,mm =− thesetangentlinesareperpendicularatthepointsofintersection.

79. () () 3sin2 3cos fxxx fxx =++ ′ =+

Because () cos1,0 xfx ′ ≤≠ forall x and f doesnot haveahorizontaltangentline.

80. () () 53 42

35 595 f xxxx fxxx =++ ′ =++

Because () 42 590,5. xxfx ′ +≥≥ So, f doesnot haveatangentlinewithaslopeof3.

Section 2.2 Basic Differentiation Rules and Rates of Change 135 © 2018 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part.

Thederivativesofthesefunctionsare: 12 12 12 22and2626 226 3 yxmxyxmx mxx xx ′′ =  ==−+  =−+ ==−+ =−+ Because2 11 yx = and222265:yxx=−+− ()() 22 21221 2 2121 65 26 xxx yy mx xxxx −+−− ===−+ () () () ()() ()() ()() 22 222 2 22 22 222222 22 2222 2 22 22 2 653 26 3 65692623 2121441818 2640 2210 1or2 xxx x xx xxxxxx xxxx xx xx x −+−−−+ =−+ −−+ −+−−−+=−+− −+−=−+− −+= −−= = 22110,2xyx =  == and14 y = So,thetangentlinethrough ()1,0and ()2,4isSo,thetangentlinethrough ()2,3and ()1,1is () 40 0144. 21 yxyx  −=−  =−   () 31 1121. 21 yxyx  −=−  =−   22123,1xyx =  == and11 y =

77.

111

 =  ==  =−  =−

5 4 3 1 1 2 2 23 x (1,0) (2,4) y 5 4 3 1 1 2 23 x (2,3) (1,1) y

() 3.9,7.7019and ()4,8:

Theslope(andequation)ofthesecantlineapproachesthatofthetangentlineat ()4,8asyouchoosepointscloserandcloserto ()4,8. (c)Asyoumovefurtherawayfrom ()4,8,theaccuracyoftheapproximation T getsworse.

136 Chapter 2 Differentiation © 2018 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 81. () () () 12 ,4,0 11 22 10 24 42 42 42 4,2 fxx fxx x y x x xxy xxx xx xy =− ′ == = += += += == Thepoint ()4,2isonthegraphof f. Tangentline: () 02 24 44 484 044 yx yx xy −=− −=− =−+ 82. () () () 2 2 ,5,0 2 fx x fx x = ′ =− 2 2 2 20 5 102 2 102 1022 410 54 , 25 y xx xxy xx x xx x xy −= −+=−  −+=−   −+=− = == Thepoint 54 , 25    isonthegraphof f.Theslopeofthe tangentlineis 58 225 f ′ =−   Tangentline:485 5252 2520820 825400 yx yx xy  −=−−  −=−+ +−= 83. (a)Onepossiblesecantisbetween

() () () 87.7019 84 43.9 82.9814 2.9813.924 yx yx ySxx −=− −=− ==− (b) () () () ()() 12 33 423 22 34834 fxxf Txxx ′′ =  == =−+=−

(d)–3–2–1–0.5–0.100.10.5123 12.8285.1966.5487.70288.3029.54611.18014.69718.520 –1256.57.788.39.5111417 2 2 12 (4,8) 20 2 2 12 T f 20

84. (a)Nearbypoint: () 1.0073138,1.0221024 () ()

1.02210241 Secantline:11 1.00731381

3.02211

yx yx

−=− =−+ (Answerswillvary.)

′ = =−+=−

(b) () ()() 32 31132 fxx Txxx

(c)Theaccuracyworsensasyoumoveawayfrom ()1,1.

(d)

TheaccuracydecreasesmorerapidlythaninExercise85because3 yx = isless“linear”than32 yx =

85. False.Let () f xx = and () 1. gxx=+ Then ()() , f xgxx ′′ == but ()() f xgx ≠

86. True.If2, a yxbx + =+ then () () () 211 22. a a dy axbaxb dx +− + =++=++

87. False.If2, y π = then0. dydx = (2 π isaconstant.)

88. True.If ()() , f xgxb =−+ then ()()() 0. f xgxgx ′′′ =−+=−

89. False.If () 0, fx = then () 0 fx ′ = bytheConstantRule.

90. False.If () 1 , n n f xx x == then () 1 1 n n n fxnx x + ′ =−=

91. () [ ]35,1,2=+ftt () 3. ′ = ft So, ()() 123.′′ ==ff

Instantaneousrateofchangeistheconstant3. Averagerateofchange: ()() 21118 3 211 == ff

=− ′ =

92. () [ ] () 27,3,3.1 2 ftt ftt

Instantaneousrateofchange: At ()() 3,2:36 f ′ = At ()() 3.1,2.61:3.16.2 f ′ =

Averagerateofchange: ()() 3.132.612 6.1 3.130.1 ff ==

1 ,1,2 1

93. () [] () 2

=− ′ =

fx x fx x

Instantaneousrateofchange: ()() () 1,111 11 2,2 24

f f

′  =  ′  =  

Averagerateofchange: ()() ()() 211211 21212 ff ==

Section 2.2 Basic Differentiation Rules and Rates of Change 137 ©

not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part.

–3–2–1–0.5–0.100.10.5123 –8–100.1250.72911.3313.37582764 –8–5–2–0.50.711.32.54710 3 3 2 (1,1) 2 3 3 2 f T 2 (1,1)

=−++=−+ ′ ==−

98. (a) () ()() 22 00 4.94.9214 9.8 sttvtst stvtt

(b) ()() 52 Averagevelocity52 91.5194.4 3 34.3m/sec

= = =−

′ =−=− ′ =−=

(d) () 2 2 2

stt t t t

=−+= = = ≈

4.92140 4.9214 214 4.9 6.61sec

(e) ()() 6.619.86.6164.8m/sec v =−≈−

99. From ()0,0to ()() () 11 22 4,2,mi/min. sttvt =  =

() () 1 26030mi/h vt == for04 t <<

Similarly, () 0 vt = for46. t << Finally,from () 6,2 to () 10,6,

()()41mi/min.60mi/h.sttvt =−  ==

(Thevelocityhasbeenconvertedtomilesperhour.) 100. ThisgraphcorrespondswithExercise101.

101. 32 ,3 dV Vss ds ==

When3 6cm,108cm dV s ds == percmchangein s

138 Chapter 2 Differentiation ©

not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 94. () () sin,0, 6 cos fxx fxx π  =   ′ = Instantaneousrateofchange: ()() 0,001 13 ,0.866 6262 f f ππ ′  =  ′  =≈   Averagerateofchange: ()() () () () 601203 0.955 6060 ff π πππ ==≈ 95. (a) () () 2 161362 32 stt vtt =−+ =−

()() 21 1298134648ft/sec 21 ss =−=−

()() 32 vtstt ′ ==−

(b)

(c)

1:132ft/sectv==−

()

tv==− (d)2 2 1613620 13621362 9.226sec 164 t tt −+= =  =≈ (e) 13621362 32 44 81362295.242ft/sec v  =−    =−≈− 96. () () () () () ()() ()() 2 2 2 1622220 3222 3118ft/sec 1622220 112heightafterfalling108ft 16221080 228270 2 232222 86ft/sec sttt vtt v sttt tt tt t v =−−+ =−− =− =−−+ = −−+= −−+= = =−− =− 97. () () ()() ()() 2 00 2 4.9 4.9120 9.8120 59.8512071m/sec 109.81012022m/sec sttvts tt vtt v v =−++ =−+ =−+ =−+= =−+=

When ()

When

2:264ft/sec

t Time(inminutes)

10 20 30 40 50 60 Velocity (in mi/h) v t 246810 2 6 10 4 8 (0,0) (4,2)(6,2) (10,6) Distance (in miles) Time(inminutes) s

246810

(b)Usingagraphingutility, () 2 0.00560.0010.04.Bvvv=++

(d)

(e)0.01120.418 dT v dv =+

For () 40,400.866vT ′ =≈

For () 80,801.314vT ′ =≈

For () 100,1001.538vT ′ =≈

(f)Forincreasingspeeds,thetotalstoppingdistance increases.

Section 2.2 Basic Differentiation Rules and Rates of Change 139 © 2018 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 102. 2,2 dA A ss ds ==

When6m, s = 12m2 dA ds = permchangein

103. (a)Usingagraphingutility, () 0.4170.02.Rvv=−

104. ()() () 2 gallonsoffuelusedcostpergallon 15,00052,200 3.48 52,200 C xx dC dxx =  ==   =− Thedriverwhogets15milespergallonwouldbenefitmore.Therateofchangeat15 x = islargerinabsolutevaluethanthat at35. x = 105. () 12 2 s tatc =−+ and () s tat ′ =− ()() ()() ()() ()()) ()() () ()() () () 22 0000 00 2222 0000 0 000 1212 Averagevelocity:2 122122 2 2instantaneousvelocityat 2 attcattc sttstt ttttt attttatttt t att atsttt t  −+Δ+−−−Δ+ +Δ−−Δ  = +Δ−−ΔΔ −+Δ+Δ+−Δ+Δ = Δ −Δ ′ ==−== Δ 106. ()() 1,008,0006.3 1,008,0006.3 3513505083.0955085$1.91 CQ Q dC dQQ CC =+ =−+ −≈−≈− When350,$1.93. dC Q dQ =≈− 120 0 0 T B R 80 x 10152025303540 C 522034802610208817401491.41305 –522–232–130.5–83.52–58–42.61–32.63

Rights

May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 107. 2 yaxbxc =++ Becausetheparabolapassesthrough ()0,1and ()1,0,youhave: ()()() ()()() 2 2 0,1:1001 1,0:01111 abcc abba =++  = =++  =−− So, () 211.yaxax=+−−+ Fromthetangentline1, yx=− youknowthatthederivativeis1atthepoint ()1,0. () ()() 21 1211 11 2 13 yaxa aa a a ba ′ =+−− =+−− =− = =−−=− Therefore,2231.yxx=−+ 108. 2 1 ,0 1 yx x y x => ′ =− At (),,ab theequationofthetangentlineis () 22 112 or. x yxay aaaa −=−−=−+ The x-interceptis () 2,0. a The y-interceptis 2 0,. a    Theareaofthetriangleis () 112 22. 22 Abha a  ===   109. 3 2 9 39 yxx yx =− ′ =− Tangentlinesthrough () 1,9: ()() () () 2 332 322 3 2 9391 993399 02323 0or yxx xxxxx xxxx xx +=−− −+=−−+ =−=− == Thepointsoftangencyare ()0,0and () 381 28,.At ()0,0,theslopeis ()09. y ′ =− At () 381 28,,theslopeis ()39 24 y ′ =− TangentLines: () ()8193 842 927 44 090and 9 9094270 −=−−+=−− =−=−− +=++= yxyx yxyx xyxy x 123 1 2 ) a,(( ,)=a b 1 a y

2018 Cengage Learning. All

Reserved.

Section 2.2 Basic Differentiation Rules and Rates of Change 141 © 2018 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 110. 2 2 yx yx = ′ = (a)Tangentlinesthrough ()0,: a () 22 2 20 2 yaxx xax ax ax −=− −= −= ±−= Thepointsoftangencyare () ,.aa±−− At (),,aa theslopeis () 2.yaa ′ −=− At (),,aa theslopeis () 2.yaa ′ −−=−− () () Tangentlines:2and2 22 yaaxayaaxa yaxayaxa +=−−−+=−−+− =−+=−−+ Restriction: a mustbenegative. (b)Tangentlinesthrough (),0:a () () 22 2 02 22 022 yxxa xxax x axxxa −=− =− =−=− Thepointsoftangencyare ()0,0and () 2 2,4. aa At ()0,0,theslopeis ()00. y ′ = At () 2 2,4, aa theslopeis ()24. yaa ′ = ()() 2 2 Tangentlines:000and442 044 yxyaaxa yyaxa −=−−=− ==−

111. () 3 2 ,2 ,2 axx fx xbx  ≤  =  +>   f mustbecontinuousat2 x = tobedifferentiableat2. x = () () () 3 22 2 22 limlim8 84 limlim484 xx xx fxaxa ab ab fxxbb →→ →→++  == =+   −= =+=+   () 2 3,2 2,2 axx fx xx  <  ′ =  >   For f tobedifferentiableat2, x = theleftderivativemustequaltherightderivative. ()() 2 1 3 4 3 3222 124 84 a a a ba = = = =−=−

Restriction: None, a canbeanyrealnumber.

112. () cos,0 ,0 xx fx axbx <  =

()() 0cos011 fbb ===  =

113. () 1sinf xx = isdifferentiableforall, x nn π ≠ an integer.

() 2sin f xx = isdifferentiableforall0. x ≠

Youcanverifythisbygraphing1 f and2 f andobserving thelocationsofthesharpturns.

114. Let () cos. f xx =

2. Tofindthederivativeofthequotientoftwodifferentiable functions f and, g where()0, gx ≠ multiplythe denominatorbythederivativeofthenumeratorminus thenumeratortimesthederivativeofthedenominator, allofwhichisdividedbythesquareofthedenominator. 3.

2 2 tansec cotcsc secsectan csccsccot d xx dx d xx dx d x xx dx d x xx dx = =− = =−

4. Higher-orderderivativesaresuccessivederivativesofa function.

115. Youaregiven: f RR → satisfying

()() ()() * f xnfx fx n +− ′ = forallrealnumbers x and allpositiveintegers n.Youclaimthat () ,,. f xmxbmbR =+∈

Forthiscase, () () [ ]mxnbmxb f xmm n  ++  −+  ′ ===

Furthermore,thesearetheonlysolutions:

Notefirstthat () ()() 21 1, 1 fxfx fx +−+ ′ += and

′

fxfxfx

Thus, ()()1. fxfx ′′ =+

Let ()()() 010.mgff ==−

constant0

()()() ()() ()()()() ()

142 Chapter 2 Differentiation

to a publicly accessible website, in

or in part.

posted

whole



() sin,0 ,0 xx fx ax −< ′ =  >  So,0. a =

ab==

 +≥

Answer:0,1

() ()() () ()

00 lim limcoscossinsincos coscos1sinlimlimsin 0sin1sin x x xx fxxfx fx x xxxxx x xx x x x x xx Δ→ Δ→ Δ→Δ→ +Δ− ′ = Δ Δ−Δ− = Δ Δ− Δ  =− ΔΔ =−=−

0 0

()()() 1. f xfxfx ′ =+− From ()*youhave ()()() ()()()() ()() f xfxfxfx fxfx

22 211 1. =+− =  +−+  +  +−    ′′ =++

Let ()()() 1. g xfxfx =+−

gxfxfx gxgm f xfxfxgxm fxmxb ′′′=+−= === ′ =+−==  =+

Let ()0. bf = Then

Section 2.3 Product and Quotient Rules and Higher-Order Derivatives

1. Tofindthederivativeoftheproductoftwodifferentiable functions f and g,multiplythefirstfunction f bythe derivativeofthesecondfunction g,andthenaddthe secondfunction g timesthederivativeofthefirst function f.

5. ()()() ()()()()() 2315 235152 1015210 2017 =−− ′ =−−+− =−++− =−+ gxxx gxxx xx x 6. ()() ()()()() 3 23 323 32 345 34353 912315 121215 yxx yxxx xxx xx =−+ ′ =−++ =−++ =−+ 7. () () () () () () 2122 12212 3232 12 32 12 22 12 11 1 21 2 11 2 22 51 22 1515 22 =−=− ′ =−+− =−+− =−+ == httttt httttt tt t t t tt t t

Section 2.3 Product and Quotient Rules and Higher-Order Derivatives 143 © 2018 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 8. () () () () () () 2122 12212 323212 32 12 2 88 1 28 2 1 24 2 54 2 58 2 gsssss gsssss sss s s s s =+=+ ′ =++ =++ =+ + = 9. () ()() () () 3 32 23 2 cos sincos3 3cossin 3cossin fxxx f xxxxx xxxx xxxx = ′ =−+ =− =− 10. () () sin 1 cossin 2 1 cossin 2 gxxx gxxxx x x xx x =  ′ =+   =+ 11. () () ()()() () () () 222 5 51155 555 x fx x xx xx fx xxx = ′ ===− 12. () () ()() ()() () () () 2 2 2 22 2 2 2 31 25 256312 25 123062 25 6302 25 t gt t ttt gt t ttt t tt t = + +−− ′ = + +−+ = + ++ = +

() () () () () () () 12 33 312122 32 33 1232 3 32 11 1 13 2 1 16 21 15 21 == ++ +− ′ = + +− = + = + xx hx xx x xxx hx x xx xx x xx 14. () 2 21 x fx x = + () ()() () () () () () () 212 2 3232 2 32 2 2 212 21 42 21 32 21 32 21 +− ′ = + +− = + + = + + = + xxxx fx x xxx x xx x xx x 15. () () ()() () 2 2 223 sin cossin2cos2sin x gx x xxxx x xx gx x x = ′ == 16. () () () () () 3 32 324 cos sincos3sin3cos t ft t tttt ttt ft t t = + ′ ==− 17. () ()() () ()() ()() () 32 322 4234322 432 4325 46232534 62428961512820 158211620 020 =++− ′ =++++−+ =+++++−++− =+++− ′ =− fxxxxx fxxxxxxx xxxxxxxxx xxxx f

13.

() x fx x xxx fx x xxx x f π π π π π π π

fxxx f

cos sincos1cossin

222

() = ′ = = ′ =   = = Function Rewrite Differentiate Simplify 23. 36 3 + = x x y 132 3 =+ yxx ()1232 3 ′ =+yx 22 ′ =+yx 24. 2 53 4 x y = 2 53 44yx=− 10 4 yx ′ = 5 2 x y ′ = 25. 2 6 7 y x = 62 7 yx = 123 7 yx ′ =− 3 12 7 y x ′ =− 26. 3 10 3 y x = 103 3 yx = 304 3 yx ′ =− 4 10 y x ′ =− 27. 432 x y x = 12 4,0yxx=> 212yx ′ = 2 ,0yx x ′ => 28. 13 2 x y x = 223yx = 413 3 yx ′ = 13 4 3 y x ′ =

() () ()()()() ()() () ()

144 Chapter 2 Differentiation

be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 18. () ()() ()()()() ()()() 2

xx f =−+ =−++− =−++−− =−− ′ −=−−−−= 19. () () ()() ()() () () () () () 2 2 2 22 2 2 2 2 4 3 3241 3 264 3 64 3 1641 1 134 x fx x xxx fx x xxx x xx x f = ′ = −−+ = −+ = −+ ′ ==− 20. () () ()()()() () () () () () 2 2 2 2 4 4 4141 4 44 4 8 4 88 3 3449 x fx x xx fx x xx x x f = + +−− ′ = + +−+ = + = + ′ == + 21.

()()()()()

4 42428

2 22 2 2 2 2 2 2 2

2394 2399443 182736162712 543812 15413811280 sin

fxxxx xxxx xxxxx cossin 63212 636 3318 336

cossin1

31. () () ()() () () () ()

Section 2.3 Product and Quotient Rules and Higher-Order Derivatives 145 © 2018 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 29. () () ()() ()() () () () () () () ()() () 2 2 22 22 2323 22 2 22 2 22 2 222 43 1 132432 1 3322862 1 363 1 321 1 313 ,1 111 xx fx x x xxxx fx x x xxxxx x xx x xx x x x xxx = ′ = −+−+−++ = −+ = −+ = ==≠ −++ 30. () () ()() ()() () () () () ()() () ()() () 2 2 22 22 3232 22 2 22 2 22 2 22 2 56 4 425562 4 2582021012 4 52020 4 544 22 52 22 5 ,2,2 2 xx fx x xxxxx fx x x xxxxx x xx x xx xx x xx x x ++ = −+−++ ′ = +−−−−− = = −++ = −+ −+ = −+ =−≠− Alternate solution: () ()() ()() 2 2 56 4 32 22 3 ,2 2 xx fx x xx xx x x x ++ = ++ = +− + =≠− () ()()()() () () 2 2 2131 2 5 2 xx fx x x −−+ ′ = =−

2 2 2 2 2



x xx x xx x

2 3 2

2 1 

 ++   +−−  ′  =+  +   +   =+  ++   +−  =  +  x fxxx xx xx x f xxx x x x xx xx xx x x 33. () () 1212 1232 32 31 3 3131 222 ==− + ′ =+= x fxxx x x fxxx x Alternate solution: () () ()() () () 12 1212 12 32 3131 1 331 2 1 31 2 31 2 ==    ′ = + = + = xx fx x x xxx fx x xx x x x 34. () () () () () 31312 13121223 1623 1623 33 11 3 23 5 6 51 6 =+=+  ′ =++  =+ =+ fxxxxx fxxxxx xx xx Alternate solution: () () () 35613 1623 1623 33 551 66 =+=+ ′ =+=+ fxxxxx fxxx x x

44 1 33 3441 1 3 6912 3 63 3

=−=− ++ +− ′ =− + ++− = + +− = + x fxxx xx xx fx

32. () () ()() () () () () () () 44 43

2 43 22

21 1 11 111 4 11 21 4 11 22

=−=

Note: Youcouldsimplifyfirst: () ()() 32 256fxxxxx=+−−

Cengage

All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 35. () () () () () ()() () () () () 2 2 22 22 22 22 2222 212121 333 322123 3 26483 3 223223 33 x xx fx x xxxx xxxx fx xx xxxx xx xxxx xx xx === ′ = −−+− = −+−−+ == 36. () () ()()()() () () () () 3 32 32232 322 54254 42 42 42 3 32 12515 1 151532 1515321510 1 532 1 532 1 x x x hx xxx x xxxxx hx xx x xxxxx xx xxx xx xx xx + + == ++ +−++ ′ = + +−−−− = + = + = + 37. () () ()() () () () () () () () () () () 4 33 34 2 2 43 2 2 2 243 2 2243 2 432 2 22 2 55 22 241 15 2 38 15 2 15238 2 154438 2 125260 2 431315 2 ss gsss ss sss gss s ss s s ssss s s ssss s sss s sss s  =−=− ++ +− ′ =− + + =− + +−+ = + ++−− = + ++ = + ++ = + 38. () () ()() () () () () 2 2 2222 222 21 2 11 121221222 2 111 x gxxx xxx xxxx xxx xx gx xxx  =−=− ++ ++−− +− ++ ′ =−== +++ 39. () ()()() () ()()() ()()() ()()() ()()()() ()() ()()() 3 233 2233 4232432423 432 2532 653225122531 656252253 656536302451025615 108211030 fxxxxx fxxxxxxxxxx xxxxxxxxx x xxxxxxxxxxxx xxxx =+−+ ′ =+−++++++− =+−−+++++− =+−−−−++++++−− =−−−−

2018

Learning.

40. () ()()() () ()()()()()()()()() ()()()()()() () () () 322 2223232 42242253 6425342 645342 64253 653 21 312121221 3521221221 352352352 222222 2242 7649 fxxxxxx fxxxxxxxxxxxxxx xxxxxxxxxxxx xxxxxxxx xxxxxx xxxxxx xxxx 2 =−++− ′ =−++−+−+−+−++ =+−+−+−+−++−+ =+−++−−−+ +−+−−+ ++−++− =++−− 42 x +

All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 58. () () ()()()() () () () 2 22 2 2 cos 1sin 1sinsincoscos 1sin sinsincos 1sin 1sin 1sin 1 1sin x fx x x xxx fx x xxx x x x x = ′ = −++ = = = (Formofanswermayvary.) 59. ()()()() () () ()() () 22 2 1csc 1csc 1csccsccot1csccsccot2csccot 1csc1csc 223 43 612 x y x xxxxxx x x y xx y π + = −−−+ ′ == ′ ==−   60. () () () tancot1 0 10 fxxx fx f == ′ = ′ = 61. () () ()()() () () () 22 22 sec sectansec1sectan1 sectan11 t ht t ttttttt ht tt h πππ π ππ = ′ == ′ == 62. ()() ()()() 22 sinsincos sincossinsincoscos sincossinsincoscos sin2cos2 sincos1 422 fxxxx f xxxxxxx x xxxxx xx f πππ =+ ′ =−++ =−++ =+ ′ =+=   63. (a) () ()()() () ()()()() ()() 3 3 332 32 412,1,4 411234 413648 4689 13;Slopeat1,4 fxxxx fxxxxx xxxxx xxx f 2 =+−−− ′ =+−+−+ =+−+−+− =−+− ′ =−− Tangentline: () 43131yxyx +=−−  =−− (b) (c)Graphingutilityconfirms3 dy dx =− at () 1,4. 64. (a) ()()() () ()()() ()() ()() 2 2 22 2 24,1,5 2241 244 344 13;Slopeat1,5 fxxx fxxxx xxx xx f =−+− ′ =−++ =−++ =−+ ′ =−− Tangentline: ()()53138yxyx −−=−  =− (b) (c)Graphingutilityconfirms3 dy dx = at () 1,5. 6 13 3 (1,4) 15 36 (1,5) 3

Learning.

68. (a) ()

sec,,2 3 sectan

Section 2.3 Product and Quotient Rules and Higher-Order Derivatives 149 © 2018 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 65. (a) () () () ()()() () () () () () 22 2 ,5,5 4 4114 44 4 54;Slopeat5,5 54 x fx x xx fx xx f =− + +− ′ == ++ ′ −==− −+ Tangentline: () 545425yxyx −=+  =+ (b)

dy dx = at ()5,5.

(a) () () () ()()()() () () () () 22 3 ,4,7 3 31316 33 6 46;Slopeat4,7 1 x fx x xx fx xx f + = −−+ ′ ==− ′ ==− Tangentline: () 764631yxyx −=−−  =−+ (b)

dy dx =− at ()4,7. 67. (a) () () 2 tan,,1 4 sec 2;Slopeat,144 fxx fxx f π ππ  =   ′ = ′ =   Tangentline:124 12 2 4220 yx yx xy π π π  −=−  −=− −−+= (b) (c)Graphingutilityconfirms2 dy dx = at,1. 4 π   

()

23;Slopeat,233 fxx fxxx f π ππ  =   ′ = ′ =  

223 3 6336230 yx xy π π  −=−  −+−= (b)

dy dx = at,2. 3 π    69. () () () ()()() () () () () () 2 2 2222 2 8 ;2,1 4 408216 44 1621 2 442 fx x xx x fx xx f = + +− ′ == ++ ′ ==− + () 1 12 2 1 2 2 240 yx yx yx −=−− =−+ +−= 70. () () ()()() () () () () () 2 2 2222 2 273 ;3, 92 9027254 99 5431 3 992 fx x xx x fx xx f  =− +  +− ′ == ++ ′ −== + () 31 3 22 1 3 2 260 yx yx yx −=+ =+ −−= 6 81 8 (5,5) 8 5 10 (4,7) 8 4 4 π (4( ,1 π π 2 6 ππ π (3( ,2

(c)Graphingutilityconfirms4

66.

(c)Graphingutilityconfirms6

Tangentline:

(c)Graphingutilityconfirms23

fx x x x

= + +− ′ = + = + () 0 fx ′ = when0. x = Horizontaltangentisat ()0,0.

x fx x xxx fx x xx xx xx

2 2 2 2 22

75. () () ()()() () () () ()

= ′ = == () 0 fx ′ = when0 x = or2. x = Horizontaltangentsareat ()0,0and ()2,4.

1 121 1 22 11

2 2 22 22 22 2 2222

4 7 7142 7 728 7 8771 77

= ′ = −−+ = −+ =−=−  

() ()() () () 22 1 1 112 11 + = −−+ ′ == x fx



x fx x xxx fx x xxx x xx xx xx () 0 fx ′ = for () () 11 1,7;1,7 214xff=== f hashorizontaltangentsat 1 1, 2    and 1 7,. 14

not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 71. () () ()()() () () () () 2 22 2222 2 168 ;2, 165 161616225616 1616 25616412 2 2025 x fx x xxx x fx xx f  =−− +  +− ′ == ++ ′ −== () 812 2 525 1216 2525 2512160 yx yx yx +=+ =− −+= 72. () () ()()() () () () 2 22 2222 2 44 ;2, 65 6442244 66 24162 2 1025 x fx x xxx x fx xx f  =  +  +− ′ == ++ ′ == () 42 2 525 216 2525 252160 yx yx yx −=− =+ −−= 73. () () () 12 2 23 3 21 2 21 22 x fxxx x x fxxx x ==− −+ ′ =−+= () 0 fx ′ = when1, x = and ()11. f = Horizontaltangentat ()1,1. 74. () () ()() ()() () () 2 2 22 22 22 1 122 1 2 1 x fx x x xxx

76. () () ()()()() () () () ()() ()

xx 1

+=  =−+ Slope: 1 2

2 2

=− −= −=± =−−== x x x xff

−=−+  =−− −=−−  =−+ 2246 4 6 6 (3,2) (1,0) 2y + x =1 2y + x =7 y x f (x)= x +1 x 1 2 64

77.

()

xx fx

263;

yxyx

() () ()()

21 12 14 12 1,3;10,32

() () 111 01 222 117 23 222 yxyx yxyx

80. () ()()() () ()()() () ()

′ == +−+ ′ == +−+ ===+

22 22

cos3sin31cossin cos2sin21cossin sin2sin35 5

xxxx x xx fx xx xxxx x xx gx xx xxxxx gxfx xx

f and g differbyaconstant.

81. (a) ()()()()()

pxfxgxfxgx pfgfg

′′′ =+  ′′′ =+=+−=  

()()()()()() 1 111111461 2

′′ ′ = ′ ==−

g xfxfxgx qx gx q

(b) () ()()()() () () ()() 2 2 31701 4 33

p xfxgxfxgx p

′′′ =+ ′ =+=

82. (a) ()()()()() () ()() 1 48104 2

g xfxfxgx qx gx q

(b) () ()()()() () () ()() 2 2 4241123 7 4164

′′ ′ = ′

(a)When (b)When (c)When Astheordersizeincreases,thecostperitemdecreases.

Section 2.3 Product and Quotient Rules and Higher-Order Derivatives 151 © 2018 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part.

′ ==

()() (),,1 xyxxx=− beapointoftangencyonthe graphof f () () () ()() () ()() ()() 2 2 2 511 11 451 111 4511 41040 1 2210,2 2 xx x x x xx x xxx xx xxx = = −+ −−=+ −+= −−=  = () () 11 1,22;4,21 22 ffff ′′ =−==−=− 

() 1 1441 2 2124 yxyx yxyx  +=−−  =−+   −=−−  =−+ 79. () ()() () () () ()()() () () () () () () () 22 22 23316 22 255416 22 54324 2 222 xx fx xx xx gx xx xxx gxfx xxx +− ′ == ++ +−+ ′ == ++ ++ ==+=+ +++

and g differbyaconstant.

78. () () () () () 22 1 11 11 x

x xx fx

Let

Twotangentlines:

===

9cm/sec 22

ttttt

Attt t ==+=+ + ′ =+=

πππ  ==+=+   () 12123 12 1332 in./sec 224 t Vttt t ππ +  ′ =+=   85. () 2 32 200 100,1 30 40030 100 30 x Cx xx dC dxx x  =+≤  +   =−+ +  x y (2,2) (1,5) 1,1 (2) 2 424 2 6 y =4x +1 y = x +4 f (x)= x x 1

83. ()() () 3212 12122 Area6565 5185

84. () () 23212 11 22

Vrhtttt

(a) () () 101.71593 2.1287 =+ =+ htt ptt

101.71593 2.1287 + = + t A t A representstheaveragehealthcareexpendituresper person(inthousandsofdollars).

(a) ()

sin

(b) ()()

152 Chapter 2 Differentiation © 2018 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 86. () () ()()()() () () () () 2 222 222 222 4 5001 50 50442200450 5005002000 505050 231.55bacteria/h t Pt t ttt tt Pt ttt P =+ +   +−  ′ === +++  ′ ≈ 87. (a) [] ()()()() () 2 1 sec cos cos01sin 1sin1sin secsectan coscoscoscoscos cos x x xx ddxx x xx dxdxxxxxx x =  ====⋅=   (b) [] ()()()() () 2 1 csc sin sin01cos 1cos1cos csccsccot sinsinsinsinsin sin x x xx ddxx x xx dxdxxxxxx x =  ===−=−⋅=−   (c) [] ()()() () 2 2 222 cos cot sin sinsincoscos

cotcsc sinsinsin sin x x x xxxx ddxxx x x dxdxxxx x 2 =  + ===−=−=−   88.

() [ ) ()() sec csc,0,2

gxx fxgx π = = ′′ = 3 3 3

=−  =−  =−  =−  =−  =− 37 , 44 x ππ = 89.

(b) (c)

90.

=−=−

cossincos1 ()

() θθθ π ′ =−⋅ ′′ °=   =−⋅=− hr hh 2300 714 3000 300 714 320 0 714 10

fxx

1sin

sectansin coscos sectancsccot111tan1tan1 1cos csccotcos sinsin

x xxx xx xxxxxx x xxx xx

(d) () 2 25,842.6 4.411205.482,369 ′ ≈ ++ At tt () A t ′ representstherateofchangeoftheaverage healthcareexpendituresperpersonforthegiven year t.

csc csccsc1 r rh rhr hrrr θ θ θθ = + +=

() csccot 30 6 40002380003mi/rad

′

fxxx fxxxx f

xxxxx xxx

fxxx fxxxx f xxxxxxxx

=− ′′

csccotcsc fxx fxxx f xxxxxx xxx = ′ =−+ ′′ =−−−− =+

102. () () ′′ =− =− = = =− =− = 104. () () () () 4 5

103. cos cossin fttt f tttt

= =−

Section 2.3 Product and Quotient Rules and Higher-Order Derivatives 153 © 2018 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 91. () () () 274 27 2 fxxx fxx fx =+− ′ =+ ′′ = 92. () () () 532 42 3 425 20610 801210 f xxxx f xxxx fxxx =−+ ′ =−+ ′′ =−+ 93. () () () 32 12 12 4 6 3 3 fxx fxx fxx x = ′ = ′′ == 94. () () () 23 4 5 5 3 29 36 2362 fxxx fxxx fxx x =+ ′ =− ′′ =+=+ 95. () () ()()() () () () () 22 3 1 1111 11 2 1 x fx x xx fx xx fx x = ′ == ′′ = 96. () () ()() ()() () () () ()() ()() () ()()() () () ()() () () () () 2 2 2 222 22 22 4 2 4 2 3 22 3 3 3 4 42331 4 25123812 4816 42881228 4 44282812 4 4282812 4 2163221624 4 56 4 xx fx x xxxx fx x xxxxxx xx x xxxxx fx x xxxxx x xxxx x xxxx x x + = −+−+ ′ = == −+ ′′ =   = = −+−++ = =

97. () () ()() =

sin cossin sincoscos sin2cos =+ ′′ =−++ =−+

98. () () ()()

cos cossin sinsincoscos2sin =−−+=−−

= ′

()

2 22 sec sectan secsectansectan secsectan fxx fxxx f xxxxxx xxx = ′ = ′′ =+ =+ 101. () () () 325 235 85 85 2 3 5 66 66 2525 fxxx fxxx fxxxx x ′ =− ′′ =− ′′′ =+=+

() () 35445 415 15 44 55 fxxx fxx x == ==

99. () () () () () 2 32 () () () () () () () () () () () () ()

csc csccot csccsccotcsccot 3 4 5 6 7 8

100. () () sin cos sin cos sin cos sin

() () () f xx f xx f xx f xx f xx f xx f xx

109. Polynomialsofdegree1 n (orlower)satisfy () () 0. n fx = Thederivativeofapolynomialofthe0th degree(aconstant)is0.

110. Todifferentiateapiecewisefunction,separatethefunctionintoitspieces,anddifferentiateeachpiece. If () , f xxx = thenon () ,0 −∞ youhave () 2 , f xx =− () 2, f xx ′ =− and () 2. fx ′′ =−

On () 0, ∞ youhave () 2 , f xx = () 2, f xx ′ = and () 2. fx ′′ = Noticethat ()() 00,00,ff ′ == but () 0 f ′′ doesnotexist(theleft-handlimitis2,whereastheright-handlimitis2).

111.

Itappearsthat f iscubic,so f ′ wouldbequadraticand f ′′ wouldbelinear.

114.

112.

Itappearsthat f isquadratic so f ′ wouldbelinearand f ′′ wouldbeconstant.

115. Thegraphofadifferentiablefunction f suchthat ()20,0ff ′ =< for2, x −∞<< and0 f ′ > for 2 x <<∞ would,ingeneral,looklikethegraph below.

113.

Onesuchfunctionis ()() 2 2. fxx=−

154 Chapter 2 Differentiation

Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 105. ()()() ()()() ()()() () 2 2 2222 224 0 f xgxhx f xgxhx fgh =+ ′′′ =+ ′′′ =+ =−+ = 106. ()() ()() ()() 4 224 fxhx fxhx fh =− ′′ =− ′′ =−=− 107. () () () () ()()()() () () ()()()() () ()()()() () 2 2 2 2222 2 2 1234 1 10 gx fx hx hxgxgxhx fx hx hggh f h = ′′ ′ =   ′′ ′ =   = =− 108. ()()() ()()()()() ()()()()() ()()()() 22222 3412 14 fxgxhx f xgxhxhxgx fghhg = ′′′ =+ ′′′ =+ =+−− =

2 2 1 211 x f y f ′ f ″ x 234 1 2 1 3 2 f f ′ f ″ y 32112345 3 4 5 1 2 3 4 x y f ′ f ″ 1 2 3 4 1 y x f ′ f ″ 2 π π2 x 1 1 2 2 3 34 4 y

116. Thegraphofadifferentiablefunction f suchthat0 f > and0 f ′ < forallrealnumbers x would,ingeneral, looklikethegraphbelow.

(b)Thespeedoftheparticleistheabsolutevalueofitsvelocity.So,theparticle’sspeedisslowing downontheintervals ()0,43and ()83,4anditspeedsupontheintervals

Section 2.3 Product and Quotient Rules and Higher-Order Derivatives 155 © 2018 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part.

117. () ()() () () 2 2 36,06 2 327m/sec 36m/sec vttt atvtt v a =−≤≤ ′ ==− = =− Thespeedoftheobjectisdecreasing. 118. () ()() ()()()() () () 22 100 215 21510010021500 215215 t vt t tt atvt tt = + +− ′ === ++ (a) () () 2 2 1500 52.4ft/sec 2515 a ==  +   (b) () () 2 2 1500 101.2ft/sec 21015 a =≈  +   (c) () () 2 2 1500 200.5ft/sec 22015 a =≈  +   119. () ()() ()() 2 8.2566 16.5066 16.50 sttt vtstt atvt =−+ ′ ==+ ′ ==− Averagevelocityon: [] [] [] [] 57.750 0,1is57.75 10 9957.75 1,2is41.25 21 123.7599 2,3is24.75 32 132123.75 3,4is8.25 43 = = = = 120. (a) s positionfunction v velocityfunction a accelerationfunction

()

()4,6. x f y t(sec)01234 s(t)(ft)057.7599123.75132 6649.53316.50 –16.5–16.5–16.5–16.5–16.5 y t 1 14567 8 4 12 16 s v a 13567 4 8 12 16 4 8 12 16 t t = t 4=4 3 t = 8 3 v speed

43,83and

124.

′′′′′′′′′′ =+++ ′′′′′′ =++

′′′′′′′′′′′′′′′′′′′′′ =+++++ =+++′′′′′′′′′′′′

′′′′′′′′′′′′′′ =++++ ()()()()

()() () ()()

g xhxgxhx gxhxgxhx gxhxgxhxgxhxgxhxgxhx 12 3 1 12

3 464 ′′′′′′ + ′′′′ ++ ′′′′′′′′′′′′ =++++ (b) () ()() () () ()()()() ()()()() () () () ()()()() ()()()()()() () () () ()()()() ()()()()()()() () () () ()()()() ()()()()() () ()() () ()() () () () () () () () () () () ()

12211221 11221212321 1221 3213421 1221 12211 !! 1!1!2!2!

′′′ =++     ′′′ ++    ′ ++    ′′′ =+++ +

nnnn n nn nnn

nnnnnn f xgxhxgxhxgxhx nnnn nnn gxhx nn nnn gxhxgxhx nn nn gxhxgxhxgxhx nn n

  () () ()() () ()() !1 1!1! nn gxhxgxhx n ′ +

′ ′  =+  ′′ ′′′′′′′ 

()()() ()()()()()() ()()()()()() 2 23 xfxxfxfx xfxxfxfxfxxfxfx xfxxfxfxfxxfxfx

= ′ =+

n nn

sin cossin

fxxx f xxxnxx

When () 1:cossin nfxxxx ′ ==+

When () 2 2:cos2sin nfxxxx ′ ==+

When () 32 3:cos3sin nfxxxxx ′ ==+

When () 43 4:cos4sin nfxxxxx ′ ==+

Forgeneral () 1 ,cossin. nn nfxxxnxx ′ =+

156 Chapter 2 Differentiation © 2018 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 121. () () ()()()()()1221! n n fxx f xnnnn = =−−= Note: ()() !1321read“factorial” nnnn =−⋅⋅ 122. () () () ()()()()()() () 11 1 112211! nn n nn fx x nnnn fx xx ++ = ==  123. ()()() f xgxhx = (a) ()()()()() ()()()()()()()()() ()()()()()() ()()()()()()()()()()()()() ()()()()()()()() () ()() () ()()()()()()() 44 2 22 33 333 fxgxhxhxgx

gxhxgxhxgxhxgxhx

fxgxhxgxhxhxgxhxgx gxhxgxhxhxgx fxgxhxgxhxgxhxgxhxhxgxhxgx

fxgxhxgxhxgxhxgxhx

′′′ =+

() () ()()()()()()() () ()() 4 44

 ′′′ ′′′′′′′′′′′′ 



Note:

() !1321nnn=−⋅⋅ (read“n factorial”)

=++=+

Ingeneral, () () () () () () 1 . n nn xfxxfxnfx =+ 

125. () () 1