Collision pulse modeling: Closed form solutions for sinusoids exponentiated to integer powers by IRJET Journal

Collision pulse modeling: Closed form solutions for sinusoids exponentiated to integer powers

Jai Singh1

1Biomechanical Engineering Analysis & Research, Inc., Thousand Oaks, California, USA

Abstract - The subject work extends the mathematical framework forthe well-established use of halfperiodand quarter period sine and sine squared functions for modeling collision pulses within the contextual fields of accident reconstruction, occupant kinematics and biomechanical engineering. The topical focus of the material presented herein is the derivation of the kinematic equations (i.e. acceleration, velocity and displacement) for the cases in which either a sine or cosine function, exponentiated to an arbitrary, positive, integer value, is used as the base function for modeling a segment of the underlying acceleration. The closed form analytic solutions presented also account for non-zero valuedinitialaccelerationoffsetsandfortheuseofpartial full periodresponsesbeyond,butinclusiveof,the quarter andhalfperiodresponses

Key Words: Collision pulse modelling, Accelerationtime history analytic modelling, Trigonometric modelling, Sine, Cosine

1. INTRODUCTION

Thesynonymous termscrashpulse andcollisionpulse, as either explicitlydefined or implicitlyused in the scientific literature, refer to the shape and characteristics of the acceleration or deceleration (referred herein as acceleration) experienced by an object or structure when subjected to an impact [1-7]. The characterization of the shapeoftheacceleration-timehistoryalongwithitsother characteristics can be applied to any event in which an objectorstructureincursanaccelerationduetotheevent. Thetermeventpulseisthuslyadoptedtoaccountforthis extension. Contextually, the literature contains evaluations of the event pulses for motor vehicles subjected to collisions [5-7, 8-12], motor vehicle seats [13], motor vehicle occupants [14-16] and coupled analysesinvolvingmultiplestructures[6,17-23].

Oneofthedeterminablecharacteristicsofanyeventpulse is the area encompassed between the abscissa and the acceleration response curve. Mathematically, this area is the first time integral of the acceleration and represents the velocity change (delta-v or v) incurred by the object orstructureduetotheevent. Withinthecontextofmotor vehicle collisions, the velocity change incurred by a vehicular collision partner, due to an impact, represents themostimportantfactorwhenitcomestopredictingthe

mortality risk for the occupants of the collision partner [24]. The scientific literature contains numerous studies that have focused on the relationship between vehicular collisionpartnercrashpulsemetrics andthe potential for occupantinjury[8,25-28].

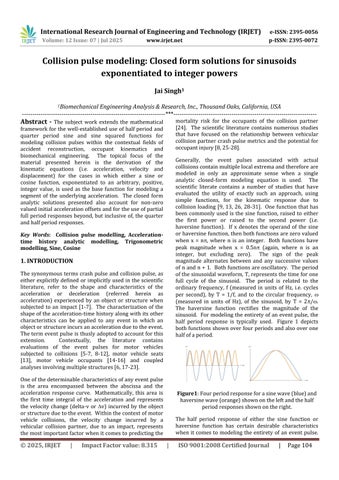
Generally, the event pulses associated with actual collisionscontainmultiplelocalextremaandthereforeare modeled in only an approximate sense when a single analytic closed-form modeling equation is used. The scientific literate contains a number of studies that have evaluated the utility of exactly such an approach, using simple functions, for the kinematic response due to collision loading [9, 13, 26, 28-31]. One function that has been commonly used is the sine function, raised to either the first power or raised to the second power (i.e. haversine function). If x denotes the operand of the sine orhaversinefunction,thenbothfunctionsarezerovalued when x = n, where n is an integer. Both functions have peak magnitude when x = 0.5n (again, where n is an integer, but excluding zero). The sign of the peak magnitude alternates between and any successive values ofnand n+1. Bothfunctionsareoscillatory. Theperiod ofthesinusoidalwaveform,T,representsthetimeforone full cycle of the sinusoid. The period is related to the ordinary frequency, f (measured in units of Hz, i.e. cycles per second), by T = 1/f, and to the circular frequency,  (measured in units of Hz), of the sinusoid, by T = 2/ The haversine function rectifies the magnitude of the sinusoid. Formodelingtheentiretyofan eventpulse, the half period response is typically used. Figure 1 depicts bothfunctionsshownoverfourperiodsandalsooverone halfofaperiod.

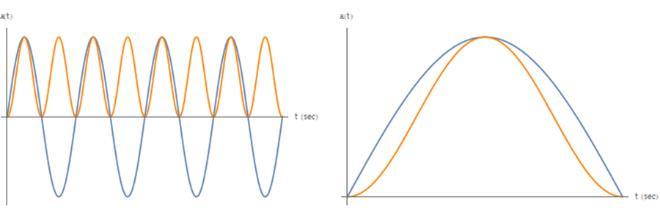
Figure1:Fourperiodresponseforasinewave(blue)and haversinewave(orange)shownontheleftandthehalf periodresponsesshownontheright.

The half period response of either the sine function or haversine function has certain desirable characteristics when it comes to modeling the entirety of an event pulse.

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056

Volume: 12 Issue: 07 | Jul 2025 www.irjet.net p-ISSN: 2395-0072

The first is that the modeled acceleration response terminates at the same value as the initial acceleration (zero as shown in Figure 1). The second is that the magnitude of peak acceleration occurs at an interior temporal value (if the initial time value is t = 0 and the eventdurationis t,thenthepeakaccelerationoccursatt = t/2). IfthepeakaccelerationisdenotedasApthenthe sine and haversine functions can be written as a(x) = Ap sin(x) and a(x) = Ap sin2(x), respectively. The operand of bothfunctions,x,isafunctionoftime(i.e.x=f(t)). Whena single sine or haversine function is used to model the entire event pulse, x = (t)/(0.5T) = (2t)/T. If the event duration is denoted as t then the relationship between the event duration and the period of the sinusoid is T = 2t. Therefore, x = t/t and the two modeled accelerationfunctions,operativeover{t:0≤t≤ t}are:

caseinwhichbothcollisionpartnersexhibitalinearforcedeflection response for both the closure and separation phases [36]. The linear force-deflection response can be deriveddirectlyfromahalfperiodsinemodel(i.e.thehalf sinemodel).

Matchingtheresultsofaphenomenologicalmodelisnota requisite study-independent requirement. Nor is there a physicalormodelingreasonastowhytheexponentiation ofthesinefunctionmustbelimitedtoeitheravalueofone or two. The subject paper, specifically, focuses on the theoretical development of the analytic closed form solutions for the case in which the power of the exponentiation, n, for a sine based event pulse, is of an integer value {n: n is an integer greater than or equal to unity}. The case of n = 0 is quite simple, with the sin0(x) reducingtounityforallvaluesofx.

2. THEORY

Thehalfsineaccelerationresponseisalsotheresponseof the simplest phenomenological model (i.e. the half period response of a single degree of freedom (SDOF) simple harmonic oscillator). Such a model consists of a single lumped mass (m) and a single massless element that developsforceasalinearfunctionofdeflection(wherekis theconstant slopeof the relationship). The model can be equivalently characterized by defining the circular frequency for the system,  = (k/m)0.5. In the case of the simpleharmonicoscillator, thekinematicresponsesatt = T/4are ofpeak accelerationmagnitude,zerovelocityand peak displacement. The kinematic responses at t = T/2 areofzeroacceleration,thenegativeoftheinitialvelocity and zero displacement. This simple model may also be usedformodelingtheresponseofavehiclesubjectedtoa full-widthengagement,collinear,axial,impactwithafixed, rigid,massivebarrier(FRMB).

The time at which the terminus of closure between the collision partners (i.e. for the case described, this is the time at which the velocity of the test vehicle is zero valued) can be used to segment the kinematic responses into a closure phase and separation phase response [29, 32-33]. This approach does not change the shape of the kinematic responses, but instead, segments them. The matching of all terminus of closure and terminus of separation phase kinematic responses is generally not achieved, when working with actual test data, secondary to the fact that the estimation of any single parameter between the set of phasic stiffnesses, phasic circular frequencies, the times at which closure or separation terminate, or the deflection at the terminus of closure, or separation analytically fixes the values of the other parameters[34]. TheSDOFmodelingapproachunderpins the most commonly utilized, closure phase only, residual damage based model [35] and has been extended to the

From the introductory material presented, it is clear that the base function of interest can be written as f(x) = sinn(x),wheren{n:1 ≤ n,nisaninteger }. Furthermore, f(x) = a(x) and because x is a function of time during the event pulse, f(x) = a(x) = a(t). The operative temporal boundarycanbedefinedasbeingbetweenandinclusiveof theindexedtimest=ti and t=tj wheretheindexj=i+ 1 (i.e.the nextindexedlocationin a series oflocations)and where{ti,tj:ti <tj}. Theoperativetemporaldurationofthe event can be written as tji = tj – ti. The accelerations at timet=ti andt=tj aredenotedasai andaj.

This approach to the symbolic terms in the problem may appeartobeanunnecessarycomplication,onfirstglance. However, if one considers even the simple problem of a two phase response (the closure and separation phases), the problem involves three critical points. These points are the start of the closure phase, the contemporaneous terminus of closure and start of separation and the terminus of the separation phase). The indexes can be numericallylabeledasone,twoandthree,respectively.

The explicit representation of the operative equations for each phase can readily be avoided (a tedious task as the number of critical points increases) by the use of the sequential alphabetic subscripts coupled with the nature ofthephasicresponsethatisbeingmodeledbetweeneach successive pair of indexed points. It should be readily apparent that t = ti will not always be zero valued. Furthermore,a(ti)willnotalwaysbezerovaluedanda(ti) =ai maygenerallynotbeequaltoa(t2)=a2. Thebaseform ofthesinefunctioncanreadilybegeneralized. Theinitial valueoffsetsof(ti,ai)canbeaccountedforbyintroducing aphaseshiftandanamplitudeshift,respectively.

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056

Volume: 12 Issue: 07 | Jul 2025 www.irjet.net p-ISSN: 2395-0072

In equation (2), the response amplitude is denoted symbolically (a), the period T is equal to 2b-1 and the phaseshiftisbti. Theconstanttermbcanbesolvedforby algebraically rearranging the definition of the period, b= (2)/T = /(0.5T). This relationship is based upon a full periodresponseandcanbegeneralizedtoapartialperiod responsebychangingthevalueoftheconstantterminthe denominator. For the case when the constant term is in thenumeratorandissetequaltoone,ratherthantwo,the relationship is based in on the half period response. For the case when the constant term is set to 0.5 (in the numerator),ratherthantwo,therelationshipisbasedona quarter period response. When the temporal domain of interestis tji (specifically,ratherthanT),thetermbmay bewrittenasb=c/tji. Rewritingequation(2):

2.2 The binomial theorem

The binomial theoremstatesthatthesum of twoterms,a and b, raised to a power, n, can be expressed in the followingform.

Where the binomial coefficient, representing the kth entry ofthenth rowinPascal’striangle,isdefinedas:

Letting z = ejx and z-1 = e-jx, equations (8) and (9) can be rewritteninthefollowingmanner:

Equation(3),writtenast=tj is:

When c is equal to 0.5, in equation (4), the sine function hasavalueofoneanda= aji Thisrepresentsthequarter periodresponse. Moregenerally:

2.1 Euler’s Formula

Euler’s formula defines the relationship between the complex exponential function and the trigonometric functionsofsineandcosine. Forallxinthereals:

Wherejisthecomplexunit(i.e.jisthesquarerootof-1). The cosine function is an even function and therefore cos(x)=cos(-x). The sinefunction isanoddfunctionand therefore sin(-x) = -sin(x). Substitution for x, by -x, in equation (6) and employing the symmetry properties of thecosineandsinefunctionsleadstothefollowing:

Summing equations (6) and (7) followed by algebraic rearrangementyieldsthefollowingsolutionforthecosine function.

Forthecaseofcosn(x):

Subtracting equation (7) from equation (6) followed by algebraic rearrangement yields the following solution for thesinefunction.

Substitution for z, in the form to the right of the last equality,leadtothefollowingresult.

Using Euler’s formula on this equation and employing the symmetry properties of the trigonometric functions leads tothefollowingresult.

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056

Volume: 12 Issue: 07 | Jul 2025 www.irjet.net p-ISSN: 2395-0072

Forthecaseofsinn(x):

Substitution for z, in the form to the right of the last equality,leadstothefollowingresult.

Whenniseven,thetotalnumberoftermssummedwillbe equalto2k+1. Theextratermoccurswhenk=0.5n. Asa result,thesummationmaybepartitioned. Thetermsfork not equal to 0.5n, representing an even number of terms, reduces to the form shown by equation (17) but with the modification for the upper limit on the summation operatorbeing0.5n–1.

Using Euler’s formula and employing the symmetry propertiesofthetrigonometricfunctions(aswasdonefor thepreviouscase)leadstothefollowingresult.

Further reduction of equation (14) and equation (16) depends upon the parity (i.e. odd or even integer valuation)oftheexponent,n.

2.3 Form of cosn(x) based on exponential parity

The summation resulting from the employment of the binomial theorem, as shown in equation (14), entails the involvement of n +1 terms. Therefore, when n is odd, there will be an even number of terms under the summation operator. Correspondingly, when n is even, there will be an odd number of terms under the summation operator. Starting with case where n is odd, the total number of terms summed will be equal to 2k. Because of symmetry this can also be viewed as being equal to the presence of pairwise terms for each k and -k {k:kisnotequaltozero}. Ifqisequalton–2k,thenthese pairwise terms will be found in the form of cos(qx) and cos(-qx)=cos(qx)andadditionally as -jsin(qx)and-jsin(qx) = jsin(qx). The summation, therefore, when n is an odd integer, eliminates the sine terms in equation (14). Thecosineterms,however,arepairwiseadditive. Thusly, when n is equal to an odd integer, equation (14) reduces tothefollowing:

2.4 Form of sinn(x) based on exponential parity

Justaswasthecasewiththecosinefunction,whennisan odd integer, the summation involves an even number of terms. Wethuslyrewriteequation(16)asfollows:

(19)

Because of the symmetry of each even row (the rows underconsiderationareevenbecausen+1isevenwhenn isodd),thefollowingholdsforthebinomialcoefficients.

(20)

Theoperandofeachtrigonometricfunctionis(n–2k)xfor k = 0 to k = 0.5 (n -1) and is equal to –(n-2k)x for k = 0.5 (n-1) + 1 to k = n. Because of the even symmetry in the cosine function, however, the corresponding pairwise terms have the same sign for the cosine function. The term(-1)n-k followsthesegmentoftherepeatingsequence of{-1,1,-1,1,…}overthedomainofk=0tok=0.5(n-1) and the negative of this sequence over the domain of k = 0.5 (n-1) + 1 to k = n. As a result, the pairwise terms, consisting of the multiplication of the cosine term and (1)n-k, associated with each value of k and n – k have oppositesigns. Becausethebinomialcoefficienttermsfor each of these pairwise terms is the same (on a pairwise basis), the summation associated with the cosine terms is zero valued. Equation (19), for any odd integer, n, becomes:

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056

Volume: 12 Issue: 07 | Jul 2025 www.irjet.net p-ISSN: 2395-0072

(21)

Using the definition of j as (-1)0.5 and reducing the terms that involve the exponentiation of (-1) leads to the followingresult.

(22)

The finding shown in equation (20), in regards to the binomial coefficient, is again noted. However, the sine function, being odd, results in the pairwise sine terms having the opposite sign. For example, for n = 3, the summation occurs over k = 0 to 3 and the corresponding valuesofn–2k are(3,1,-1,-3)respectively. Forthelast two terms, sin(-x) = -sin(x) and sin(-3x) = -sin(3x).

Accounting for this fact leads to the final form for the solutionofsinn(x):

(23)

When n is an even integer, the reduction starts by consolidating the terms in equation (19) that are exponentiatedvaluesof-1.

(24)

The previous finding of equation (20) also holds here, in regards to the binomial coefficient terms. For the summation term involvingthesinefunction, when nis an even integer, the central term (i.e. at k = 0.5 n) is zero valued. The signs of the pairwise terms at {k, n – k} are valued {1, -1}, respectively, due to the odd symmetry of the sine function. The exponentiated -1 term, for each pairwise {k, n – k} are equally valued. The result of the multiplication of the three terms under the summation operator associated with the sine function is of equal magnitudeandoppositelysignedtermsforallpairs{k,n–k} and a zero valued central term. The summation operation results in a zero valuation, resulting in the followingrelationship:

3. COLLISION PULSE MODELLING

Thegenericvariablexcanbereplacedwiththefollowing, whichbringsthesubjectformulationintothetimedomain.

3.1 Segmented acceleration response for sinn(x)

Substitution of this relationship into equation (23) and substitution of the resultant into the form of equation (3) leads to the following solution for the modeled acceleration-time response for the case in which n is an oddinteger

Equation (25) reduces following the same approach as described for cosn(x), for n being an even integer. The resultofthisreductionisthefollowing:

Substitution of equation (27) into equation (26) followed by substitution of the resultant into the form of equation (3) leads to the following solution for the modeled acceleration-time response for the case in which n is an eveninteger.

(29)

Equations (28) and (29) are operative over the temporal domain of t {t: ti less than or equal to t and t less than or equaltotj}.

3.1 Segmented acceleration response for cosn(x)

In certain cases, such as when the magnitude of acceleration is decreasing between the two indexed points,itispreferabletouseacosinefunctionratherthan asinefunction. Subtractingtheoperand,x,from0.5,and takingthecosine,yieldsthesineoftheoperand,x. Taking thesineof0.5 – xresultsinthecosineoftheoperand, x. Substitutionforx,usingthedefinitioninequation(27),in equation (17), followed by writing the resultant in the formofequation(3),leadstothefollowingsolutionforthe modeled acceleration-time response for the case in which nisanoddinteger.

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056

Volume: 12 Issue: 07 | Jul 2025 www.irjet.net p-ISSN: 2395-0072

(30)

Following the same approach leads to the following solution for the modeled acceleration-time history for the caseinwhichnisaneveninteger.

Equations (30) and (31) are operative over the temporal domain of t {t: ti less than or equal to t and t less than or equaltotj}.

3.3

Boundary value assessment

Eachofthefourequationsfortheaccelerationmustyielda response of ai at the temporal boundary of t = ti.

Substitution of t = ti into equation (28) results in the parenthetical term that multiplies a, being zero valued (the sine function is zero-valued when the operand is zero). This produces the expected result of ai = ai Substitution of t = ti into equation (29) leads to the followingresult:

The parenthetical term, for any arbitrary, positive, even, integer value of n, is unity. This leads to the result of a =

Equation(29)canthuslyberewrittenas:

The parenthetical term, for any arbitrary, positive, even, integer value of n, is zero valued. This leads to the expected results of ai = ai. Substitution of t = ti into equation(30)leadstothefollowingresult:

The terminus boundary condition requires that the accelerationhasavalueofaj att=tj. Substitutionoft=tj intoequation(30)leadstothefollowingresult:

(37)

Thetermontheleftoftheequalityinequation(37)isnot readily reducible. However, if that term is plotted as a functionofpositive,odd,integervaluesofn(from1to99) and over a domain of c {c: c is greater than equal to zero and c is less than or equal to ten}, it can be seen (see Figure 2)that the ratio of theacceleration difference, aji, totheamplitude,a,forequation(37),isconstantoverthe domain of positive, odd, integer values of n, and that it is cyclical with respect to c. For any value of n within this domain,theratioiszeroforintegervaluesofc,0.5forc= (2k+1)/2 for k {k: k is an even integer greater than or equaltozero},and-0.5fork{k:kisanoddintegergreater thanorequaltoone}.

The parenthetical term for any arbitrary, positive, odd, integervalueofn,isunity. Thisleadstotheresultthata= aij. Equation(30)canthuslyberewrittenas:

Substitution of t = ti into equation (29) leads to the followingresult:

Figure 2:Ratiooftheaccelerationdifference aji tothe amplitude,a,forthecaseofthesinefunctionraisedtoa

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056

Volume: 12 Issue: 07 | Jul 2025 www.irjet.net p-ISSN: 2395-0072

positive,odd,integervalue. Theresponsesurfaceis shownascontinuoussolelyforthepurposeofaidingthe visualization. Inactuality,theresponsesurfaceexistsat discretepositive,oddinteger,valuesofn.

Rearrangingequation(37)andsubstitutingtheresultinto equation(30)leadstothefollowingresult:

Substitution of t = tj into equation (29) leads to the followingresult.

equation (39) and substituting the result into equation (29)leadstothefollowingresult.

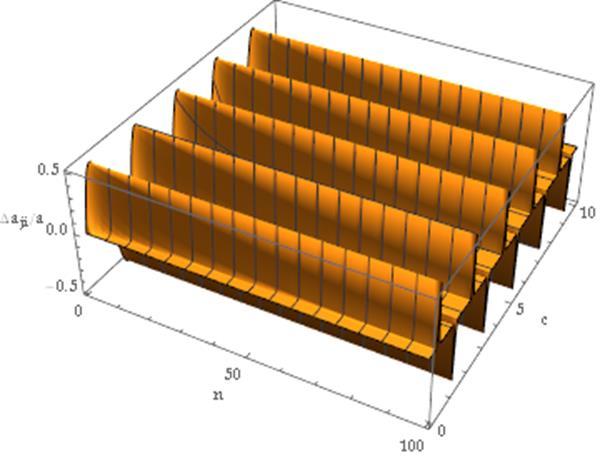
The term on the left of the equality is, again, not readily reducible. Following the same approach as for the previouscaseleadstotheresultshowninFigure3.

Figure 3:Ratiooftheaccelerationdifference aji tothe amplitude,a,forthecaseofthesinefunctionraisedtoa positive,even,integervalue. Theresponsesurfaceis shownascontinuoussolelyforthepurposeofaidingthe visualization. Inactuality,theresponsesurfaceexistsat discretepositive,eveninteger,valuesofn.

From Figure 3, it can readily be seen that the ratio of the acceleration difference, aji, to the amplitude, a, for equation (39), is constant over the domain of positive, integervalues of nandthat itiscyclical with respect to c. Foranyvalueofnwithinthisdomain,theratioiszerofor integer values of c and unity for c = k/2 {k: k is an odd integerthatisgreaterthanorequaltozero}. Rearranging

For the cosine function where n is an odd integer, substitution of t = tj into equation (30) leads to the followingresult.

The case where a = 0 is the trivial case and thusly not germane to the subject problem. Therefore, it is the parenthetical termthatiszero valued. Clearly,21-n,is not zerovaluedforpositive,odd,integervaluesofn. Thusly,it is the summation that is zero valued. For any positive, odd, integer values of n, the solution for c is ±0.5 + 2k where k is within the integers. The solution of c = 0.5 is thequarterperiodresponse.

For the case of the cosine function with n being an even integer,substitutionoft=tj intoequation(31)leadstothe followingresult.

Following the same approach used for the previous case, theinnerparentheticalmustbezerovalued. Thisleadsto thefollowing:

For any positive, even, integer value of n, the solution for equation(43)isc=±0.5.

4. TIME DIFFERENTIATION

4.1

Velocity solutions

Foragivenaccelerationfunction,a(t),thevelocitysolution canbeobtainedbyimplicitintegrationoftheacceleration.

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056

Volume: 12 Issue: 07 | Jul 2025 www.irjet.net p-ISSN: 2395-0072

(44)

The constant of integration, C1, is typically solved for by using a point in time at which both the time and velocity areknown. Iftheproblemisaninitial valueproblem,the pointisat{ti,vi}. Thisleadstothefollowingsolution:

(45)

Forthecasewhentheaccelerationisasinefunctionraised to a positive, odd, integer power, the velocity solution is thefollowing:

(48)

Forthecasewhentheaccelerationisasinefunctionraised to a positive, even, integer power, the velocity solution is thefollowing:

Finally, for the case when the acceleration is a cosine function raised to a positive, even, integer power, the velocitysolutionis:

For the case when the acceleration is a cosine function raised to a positive, odd, integer power, the velocity solution

When t = tj, the solution for the velocity, v(tj), must be equal to vj. This can be written as vj = vi + vji. For the case where the underlying acceleration is a sine function raised to a positive, odd, integer power, writing equation (46)att=tj leadstothefollowingresult.

(50)

The denominator within the parenthetical is zero valued when c is an integer. For the case where the underlying acceleration is a sine function raised to a positive, even, integer power, writing equation (47) at t = tj leads to the followingresult.

For the case when the underlying acceleration is a cosine function raised to a positive, odd, integer power, writing

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056

Volume: 12 Issue: 07 | Jul 2025 www.irjet.net p-ISSN: 2395-0072

equation (48) at t = tj and using the previously derived resultofa= aji leadstothefollowingsolution.

Forthecasewheretheunderlyingaccelerationisacosine function raised to a positive, even, integer power, writing equation (49) at t = tj and using the previously derived resultofa= aji leadstothefollowingsolution.

4.2 Displacement solutions

The displacement solution, for a given velocity function, v(t),canbeobtainedbyimplicitintegration.

Theconstantofintegration,C2,canbesolvedforbyusinga point where both the time value and displacement are known. For an initial value problem, this condition is {ti, ui}. For the case in which the acceleration is a sine function raised to a positive, odd, integer power, the displacementsolutionisgivenbythefollowing.

For the case in which the underlying acceleration is a cosine function raised to a positive, odd, integer power, thedisplacementsolutionisgivenbythefollowing:

Forthecaseinwhichtheunderlyingaccelerationisasine function raised to a positive, even, integer power, the displacementsolutionisgivenbythefollowing.

For the case in which the underlying acceleration is a cosine function raised to a positive, even, integer power, thedisplacementsolutionisgivenbythefollowing:

Thedisplacementattheterminusboundarypoint,tj,must beequaltouj. Thisdisplacementmayalsobewrittenasuj = ui + uji For the case in which the underlying acceleration is a sine function raised to a positive, odd, integerpower:

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056

Volume: 12 Issue: 07 | Jul 2025 www.irjet.net p-ISSN: 2395-0072

Forthecaseinwhichtheunderlyingaccelerationisasine functionraisedtoapositive,even,integerpower:

solutions were coded in a symbolic mathematics package (Mathematicav.12.0;WolframResearch,Inc.;Champaign, Illinois, USA). The exponential power was arbitrarily chosen as four for the even integer case and five for the odd integer case. For the sine based acceleration functions,theinitialvalueof{ti,ai}={0.1,5}alongwith tji =0.07, aji =20andc =0.19(0.095ofa full period)were arbitrarily chosen. For the cosine based acceleration functions,the valuesofti = 0.1,aj =5, tji = 0.07, aji = 20 and c = 0.5 were chosen. The value of c, for the cosine case, was not arbitrary while the values of the other parameters were arbitrary. The results from the coded equations were compared against the results based upon the solutions from direct entry of each function (in the formofai +asinn(x)oraj +acosn(x)). Theresultsforthe accelerationfunctionsareshowninFigures4and5.

For the case in which the underlying acceleration is a cosinefunctionraisedtoapositive,odd,integerpower:

For the case in which the underlying acceleration is a cosine

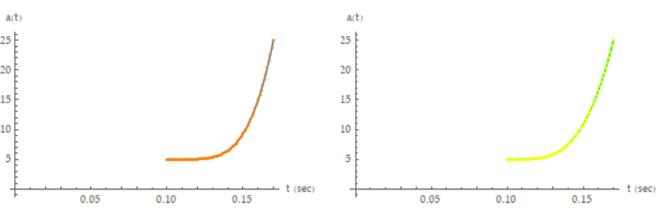
Figure 4:Accelerationresponseforthesinefunctions. Theimageontheleftshowstheoverlayforthecasewhere n=5(theresultsfromequation38areshowninbluewith thedirectentryresultsshowninorange). Theimageon therightshowstheoverlayforthecasewheren=4(the resultsfromequation40areshowningreenwiththe directentryresultsshowninyellow).

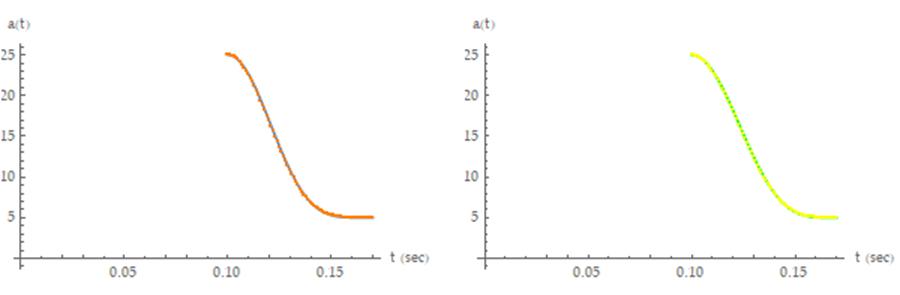
Figure 5:Accelerationresponseforthecosinefunctions. Theimageontheleftshowstheoverlayforthecasewhere n=5(theresultsfromequation34areshowninbluewith thedirectentryresultsshowninorange). Theimageon therightshowstheoverlayforthecasewheren=4(the resultsfromequation36areshowningreenwiththe directentryresultsshowninyellow).

5. SOLUTION VALIDATION

The kinematic solutions for the sine based acceleration formulationsasperequations (38)and(40),cosinebased acceleration formulations as per equations (34) and (36), and the corresponding velocity and displacement

For the velocity comparisons, an arbitrary initial velocity, vi =2,wasused. Theresultsforthevelocitycomparisons areshowninFigures6and7.

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056

Volume: 12 Issue: 07 | Jul 2025 www.irjet.net p-ISSN: 2395-0072

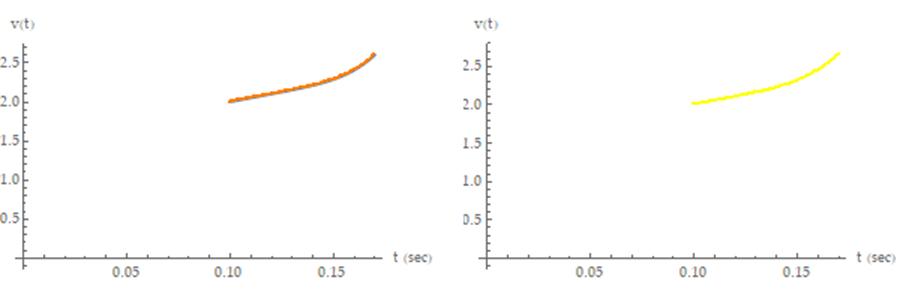
Figure 6:Velocityresponseforthesinefunctions. The imageontheleftshowstheoverlayforthecasewheren= 5(theresultsfromequation46areshowninbluewiththe directentryresultsshowninorange). Theimageonthe rightshowstheoverlayforthecasewheren=4(the resultsfromequation47areshowningreenwiththe directentryresultsshowninyellow).

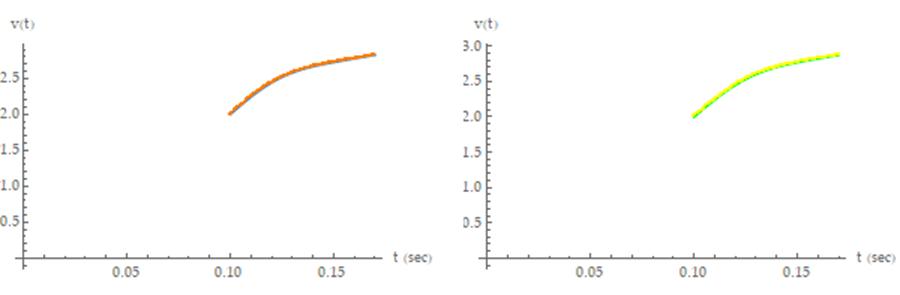
Figure 7:Velocityresponseforthecosinefunctions. The imageontheleftshowstheoverlayforthecasewheren= 5(theresultsfromequation48areshowninbluewiththe directentryresultsshowninorange). Theimageonthe rightshowstheoverlayforthecasewheren=4(the resultsfromequation49areshowningreenwiththe directentryresultsshowninyellow).

For the displacement comparisons, an arbitrary initial displacement of ui = 0.5 was used. The results for the displacementcomparisonsareshowninFigures8and9.

Figure 8:Displacementresponseforthesinefunctions. Theimageontheleftshowstheoverlayforthecasewhere n=5(theresultsfromequation55areshowninbluewith thedirectentryresultsshowninorange). Theimageon therightshowstheoverlayforthecasewheren=4(the resultsfromequation56areshowningreenwiththe directentryresultsshowninyellow).

Figure 9:Displacementresponseforthecosinefunctions. Theimageontheleftshowstheoverlayforthecasewhere n=5(theresultsfromequation57areshowninbluewith thedirectentryresultsshowninorange). Theimageon therightshowstheoverlayforthecasewheren=4(the resultsfromequation58areshowningreenwiththe directentryresultsshowninyellow).

Thesolutionsgeneratedbytheequationspresentedinthe subject work, matched, exactly, the solutions based upon directentryforthevaluesofnthatwereconsidered.

6. DISCUSSION

Theclosedformanalyticsolutionspresentedinthesubject work are certainly more complex, in appearance, than those typically found in the extant scientific literature. The basis for this increased complexity is multifactorial. Firstly, the equations presented in the subject work account for non-zero valued initial acceleration offsets. Noteveryanalysisinvolvesa situationinwhichtheinitial valueoftimeiszeroandtheinitialaccelerationiszero. An excellent example of such a situation is that in which one is evaluating the separation phase of a collision while havingtimet=0beingthetimeatwhichclosureinitiates. Secondly, for the case in which the acceleration response ismodeledusingthesinefunction,thesubjectformulation allowsfortheconsiderationoffractionalperiodresponses beyond the standard half period or quarter period responses. Historically, the half period model has been usedwhenmodelingtheentiretyofaneventandwiththe acceleration being symmetric in shape [29] whereas the quarterperiodmodelhasbeenusedwhensegregatingthe acceleration response (i.e. for a collision in regards to closure and separation) [34]. The half period model can alsobeusedforasegregatedresponseanalysis. However, thissegregationoccursinregardstothevelocityresponse while leaving the symmetric shape of the acceleration responseunchanged. Whilenotaddressedherein,thehalf period and quarter period models, as historically used, generally produce poor matches for the total set of segregatedkinematicresponseparametersfor data based upon even the simplest collision test configuration (i.e. full-width engagement, collinear, axial impact between a testvehicleandaFRMB). Thirdlyandfinally,thegreatest sourceofcomplexityinregardstotheformsofthesubject equations is the inclusion of arbitrary, positive, integer exponentiation. Equations (16) and (14) are valid

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056

Volume: 12 Issue: 07 | Jul 2025 www.irjet.net p-ISSN: 2395-0072

equations for sinn(x) and cosn(x) where {n: n is in the integers} and could have readily been used for the baseline acceleration functions. However, both equations arecomplexequationsinthemathematicalsense(i.e.they both contains terms associated with j = (-1)0.5). The separationoftheresponsesbasedonoddandeveninteger valuationavoidshavingtodeal withcomplexanalysisbut is at the expense of increasing the complexity in the appearance of the equations. Again, it should be noted that there is no underlying, uniform and ubiquitous requirement that the exponential order of the trigonometric functions employed should be limited to eitheravalueofoneortwo.

The presentation of the solutions based upon the use of the use of the cosine function might appear to be extraneous on first glance. However,suchisnotthe case. The cosine function correctly models the shape of the second quarter period response of a half period sinusoid. This can readily be seen in Figure 10, which depicts a simplehalfperiodsineresponse,thecorrespondinginitial quarter period sine response (overlayed) and the overlayed cosine and sine models for the corresponding finalquarterperiodresponse

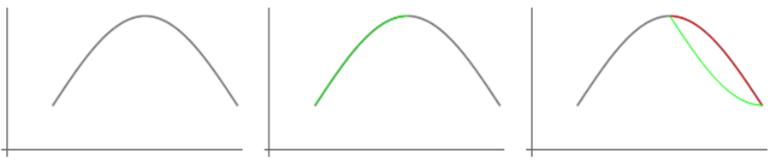
Figure 10:Asimplehalfperiodsinefunctionwithan initialoffsetandreturntotheoriginalordinatevalue (left). Themiddleimageshowsthefirstquarterperiod sineresponse(green)overlayedonthehalfperiod response. Theimageontherightshowsthecosine response(red)aswellasthesineresponse(green),forthe secondquarterperiod,overlayedonthehalfperiod response.

Theformulativenatureofthesubjectworkwasstrictlyto derivetheclosedformanalyticsolutionsforthekinematic responses of an event pulse modeled using sinusoids exponentiated to integer powers. In that regard, the equationsshown,totheauthor’sknowledgearepresented for the first time within the context of event pulse modeling. The exclusion of application examples, based upon the stated scope of the subject work, in the author’s view, does not represent an intrinsic limitation of the subject work. This choice was made due to space limitations and the necessity for the presentation, in a subsequent work, of the equations when the exponential power of the sinusoidal functions is not limited to integer powers. Exampleapplicationspredicateduponreal-world datadonotinvolveanaprioribasisofbeinglimited,inthe modeling sense, to sinusoidal functions that are raised to justintegerpowers. Theintrinsiclimitationofthesubject

work lies within the solution validation and is due to the useofsingularparametervaluesforeachcase. Thischoice was made due to the fact that the solution validation was simplymeanttoshowthattheequationspresentedherein matchtheresultsofthesolutionsbaseduponthesymbolic solutions for the case in which the exponential has a defined, ‘known’ value. The presence of derivational errorsortypographicalerrors,bothbeingaconcerngiven the complex appearance of the equations, would have beenreadilymanifestforanyarbitraryoddorevenvalued integer of choice. While not shown here, the arbitrary changingofeachexponentialvaluetootherintegervalues within each subset (i.e. odd or even) produced an equivalent result when compared with entered, symbolic, solutionsoftheformofbothsinn(x)andcosn(x).

REFERENCES

[1] Lim GG (1972) Crash data analysis. SAE Technical paperno.720496.

[2] Huang M, GP Lawson, BK Powell and JH Walker (1977) Characterization of vehicle deceleration time histories in the analysis of impact dynamics. SAE Technicalpaperno.770013.

[3] Gearhart C (2001) Recent progress in crash pulse analysis. International Journal of Vehicle Design (SpecialIssue)26(4):395-406.

[4] Gildfind D and D Rees (2002) Accelerationdisplacement crash pulse optimization – a new methodology to optimize vehicle response for multiple impact speeds. Proceedings: Young Automotive and Transport Executives Conference, Melbourne,Victoria,Australia,October29-30,2002.

[5] Locey CM, JF Garcia-Espana, A Toh, A Belwadi, KB Arbogast andMR Maltese(2012)Homogenization of vehicle fleet frontal crash pulses from 2000-2010. Proceedings:56thAAAMAnnual Conference,Seattle, Washington, October 14-17, 2012. Annals of AdvancesinAutomotiveMedicine56:299-311.

[6] TengT-L,P-HChang,C-CLiangandD-AFung(2017) Application of crash pulse on the car crashworthiness design. Advances in Mechanical Engineering9(9):1-8.

[7] Dima DS and D Covaciu (2019) Vehicles frontal impactanalysisusingcomputersimulationandcrash test. InternationalJournalofAutomotiveTechnology 20(4):655-661.

[8] Krafft M, A Kullgren and C Tingvall (1998) Crash pulse recorders in rear impacts – real life data. Proceedings: 16th International Technical Conference on the Enhanced Safety of Vehicles,

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056

Windsor, Ontario, Canada, May 31 – June 4, 1998. PaperNo.98-S6-O-10.

[9] Huang M (2002) Vehicle Crash Mechanics. Boca Raton,Florida,USA:CRCPress,pp.128-135.

[10] Gu L, RJ Yang, G Li, et al. (2005) Structural optimization for crash pulse. SAE Technical paper no.2005-01-0748.

[11] DalmotasDJ,AGermanandJ-LComeau(2009)Crash pulse analysis using event data recorders. Proceedings: 19th Canadian Multidisciplinary Road SafetyConference,Saskatoon,Saskatchewan,Canada, June8-10,2009.

[12] Park C-K and C-D Kan (2015) Objective evaluation methodofvehiclecrashpulseseverityinfrontalNew CarAssessmentProgram(NCAP)tests. Proceedings: 24th International Technical Conference on the Enhanced Safety of Vehicles, Gothenburg, Sweden, June8-11,2015. Paperno.15-0055.

[13] Insurance Institute for Highway Safety (2016) Vehicle seat/head restraint evaluation protocol dynamic criteria (version IV). IIHS, Ruckersville, Virginia. Pp.4-5.

[14] Lundell B (1984) Dynamic response of a belted dummy – a computer analysis of crash pulse variation. SAEPaperNo.840401.

[15] Evans NC, LM Furton and DA Cok (1992) Occupant energy management technique for restraint system analysis and design – theory and validation. SAE Technicalpaperno.922082.

[16] Grimes WD and FD Lee (2000) The effect of crash pulseshape on occupantsimulations. SAE Technical paperno.2000-01-0460.

[17] KatohHandRNakahama(1982)Astudyontheridedown evaluation. Proceedings: 9th International Technical Conference on Experimental Safety Vehicles,Kyoto,Japan,November1-4,1982,pp.190195.

[18] Bonello KJ (1992) Occupant energy management technique for restraint system analysis and design –understanding the physics of the system. SAE Technicalpaperno.922083.

[19] Huang M, J Laya and M Loo (1995) A study on ridedown efficiency and occupant responses in high speedcrashtests. SAEPaperNo.950656.

[20] Wu J, GS Nusholtz and S Bilkhu (2002) Optimization of vehicle crash pulses in relative displacement

domain. International Journal of Crashworthiness 7(4):397-414.

[21] Wu J, S Bilkhu and GS Nusholtz (2003) An impact pulse-restraint energy relationship and its applications. SAE Technical paper No. 2003-010505.

[22] Cao JZ, MR Koka and SE Law (2004) Vehicle pulse shapeoptimization toimprove occupant responsein frontimpact. SAETechnicalpaperno.2004-01-1625.

[23] ChengZ(2006)Optimalcrashpulseforminimization ofpeakoccupantdecelerationinfrontalimpact. SAE Technicalpaperno.2006-01-0670.

[24] Funk JR, JM Cormier and HC Gabler (2008) Effect of delta-V errors in NASS on frontal crash risk calculations. Annals of Advances in Automotive Medicine52:155-164.

[25] Linder A, M Avery, M Krafft, A Kullgren and MY Svensson (2001) Acceleration pulses and crash severity in low velocity rear impacts – real world data and barrier tests. Proceedings: 17th 18th International Technical Conference on the Enhanced SafetyofVehicles,Amsterdam,TheNetherlands,June 4-7,2001. Paperno.216.

[26] Heitplatz F, R Sferco, PA Fay, J Reim and D de Vogel (2002) Development of a generic low speed rear impactpulseforassessingsofttissueneckinjuryrisk. Proceedings: International IRCOBI Conference, Munich,Germany,September18-20,2002.

[27] Linder A, M Avery, M Krafft and A Kullgren (2003) Change of velocity and pulse characteristics in rear impact: real world and vehicle tests data. Proceedings: 18th International Technical Conference on the Enhanced Safety of Vehicles, Nagoya,Japan,May19-22,2003. PaperNo.285.

[28] SiegmundGP,BEHeinrichs,DDChimich,ALDeMarco and JR Brault (2005) The effect of collision pulse properties on seven proposed whiplash injury criteria. Accident Analysis & Prevention 37(2): 275285.

[29] Varat MS and SE Husher (2003) Crash pulse modeling for vehicle safety research. Proceedings: 18th International Technical Conference on the Enhanced Safety of Vehicles, Nagoya, Japan, May 1922,2003. Paperno.501.

[30] Singh J and J Perry (2005) Comparative analysis of FMVSS 208 sled and dynamic deceleration pulse characteristics. Proceedings: 19th International Technical Conference on the Enhanced Safety of

| Page116

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056

Vehicles,WashingtonDC,USA,June6-9,2005. Paper no.05-0028.

[31] Hynd D and C Willis (2007) Recommendations for a low-speedrearimpactsledtestpulse. DocumentNo. 166, European Enhanced Vehicle Safety Committee (EEVC)WG20Report.

[32] Singh J and J Perry (2007) Implication of symmetric sine-basedcollisionpulsemodelsonforce-deflection characteristics. Collision2(2):104-113.

[33] SinghJandJPerry(2008)Analternativeformulation for symmetric sine based collision pulse models. Collision3(1):34-43.

[34] Singh J (2013) Further developments regarding the dynamic modeling of motor vehicle collision response using the SDOF approach. Collision 8(1): 10-31.

[35] McHenry RR (1975) A comparison of results obtained with different analytical techniques for reconstruction of highway accidents. SAE Technical paperno.750893.

[36] Singh J (2013) Laplace domain analysis of the collinear vehicle-to-vehicle collision under linear force-deflection constraints coupled with net externally applied loads. Proceedings: 23rd International Technical Conference on the Enhanced Safety of Vehicles, Seoul, South Korea, May 27-30, 2013. PaperNo.13-0016.

BIOGRAPHY

Mr. Singh is a private practice engineerwithspecialtiesinthefields of motor vehicle accident reconstruction and biomechanical engineering. He holds a BS in mechanical engineering from the University of Illinois at UrbanaChampaign and a MS in biomedical engineering from the University of Southern California. He has authored numerous peer reviewed conference proceedings, technical articlesandscientificpapers.

| Page