Issuu

MATHEMATICS Deﬁnite Integration JEE

DEFINITE INTEGRATION

BUILDING UPON PRIOR KNOWLEDGE

In the preceding chapter, we delved into integration, which acts as the inverse counterpart of differentiation. Initially, integration found its roots in the need to calculate the enclosed area of regions delineated by curves, and it was identified as the culmination of a particular summation approach. Subsequently, luminaries such as Newton and Leibnitz solidified the profound connection between integration and differentiation, a renowned union known as the fundamental theorem of integral calculus. This chapter will extensively examine this theorem. We will rigorously define the definite integral as the limit of a summation, demonstrating its indispensable role in measuring the areas of specific geometric regions, thereby providing a comprehensive understanding of the intricate relationship between differentiation and integration.

• Unique Value of a Definite Integral

• Definite Integral as The Limit of a Sum

• First Fundamental Theorem of Integral Calculus

• Second Fundamental Theorem of Integral Calculus

• Properties of Definite Integral

• Differentiation under the Sign of Integration

• Inequalities

• Determination of Function using Definite Integral

• Walli’s Formula

1 | Page

The study of definite integrals in calculus serves several important objectives:

• Accumulation of Quantities: Definite integrals are used to calculate the accumulated quantity of a varying quantity over a specific interval. This is particularly useful in scenarios where you want to find the total accumulation of, for example, distance travelled, volume, or mass, given a varying rate or density.

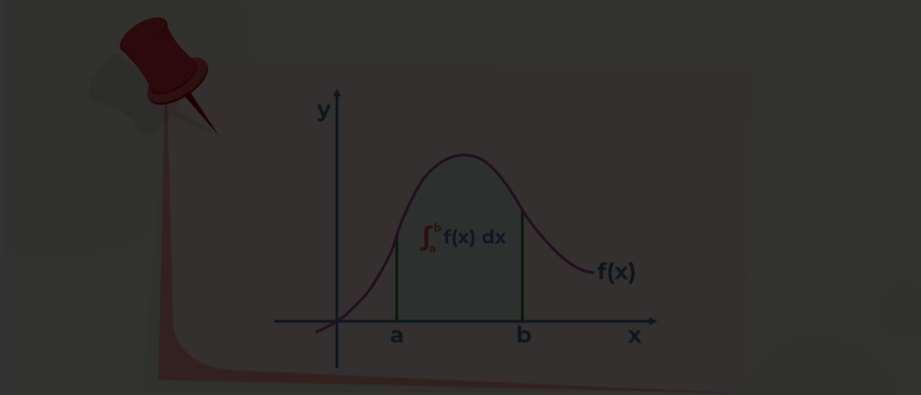
• Area under Curves: Definite integrals are employed to find the area enclosed between a curve and the x-axis over a certain interval. This is essential for various applications, such as determining the total distance travelled by an object with changing velocity or calculating the total accumulated profit from a changing revenue function.

• Physical Applications: Many real-world phenomena involve continuous changes, such as motion, fluid flow, and electromagnetic fields. Definite integrals help model and solve problems related to these processes by providing tools to calculate quantities like displacement, work, fluid volume, and more.

• Probability and Statistics: In probability theory, definite integrals are used to compute probabilities by integrating probability density functions. This is crucial in understanding the likelihood of different events and outcomes in various random processes.

• Calculation of Average: The definite integral can be used to calculate the average value of a function over a specific interval. This concept is important in various fields, including physics, engineering, and economics, where finding average values helps to understand overall trends.

• Solution of Differential Equations: Definite integrals play a significant role in solving differential equations, both ordinary and partial. They help find particular solutions by relating the derivative and integral operations, allowing us to connect the rate of change of a quantity with its accumulated value.

• Geometry and Curvilinear Motion: Definite integrals enable the calculation of arc length, surface area, and other geometric properties of curves and surfaces. These properties are important in various fields, including engineering and architecture.

• Economics and Finance: Definite integrals are used to analyse and optimize various economic and financial scenarios. For instance, they help determine total revenue, profit, or cost functions when rates are changing.

• Optimization Problems: Many real-world optimization problems involve finding the maximum or minimum values of functions. Definite integrals can be used to formulate and solve these problems by representing them as areas or accumulations.

In essence, the study of definite integrals provides a powerful mathematical tool for modelling, analysing, and solving a wide range of problems across various disciplines, making it a fundamental concept in calculus and applied mathematics.

DEFINITE INTEGRATION_XII Page | 2

1. UNIQUE VALUE OF A DEFINITE INTEGRAL

• Let F(x) be an anti-derivative of a continuous function f(x) on [a, b]. Then ()()()

Key Concept

=

Integration symbol

a = Lower Limit

b = Upper limit

f(x) = Integrand

dx = Integrating agent

Thus, ( ) b a fxdx  is read as the definite integral of f(x) with respect to x from a to b.

• The definite integral can be evaluated by using various techniques of integration studied in indefinite integrals or by using the properties of definite integrals or by writing it as a limit of a sum. In the next section, we will understand definite integration as the limit of a sum and in more detail about how an infinite series can be converted into and hence evaluated as definite integral.

2. DEFINITE INTEGRAL AS THE LIMIT OF A SUM

• In the standard part we have discussed the following in detail that,

DEFINITE INTEGRATION_XII 3 | Page

b a

 ( ) ( ) ( ) b a fxdxFbFa =− 

fxdxFbFa =−

Illustration-1 Find 0 2 22xx++  –1 dx Solution: 00 22 1122(1)1 dxdx xxx = ++++ 10 1 |tan(1)|=+ x 11 tan1tan0 4  =−=

1 01 b–a ()lim()lim()whereh= n b nn nn rr a fxdxhfarhhfarh →→ == =+=+   .

• We have, sn < area of region ABCD < Sn.

• If f(x) is a continuous function, then both the limits

exist and are equal. Then, f(x) is said to be integrable. This limit gives the area of the region ABCD (area under the curve y = f(x), above the x-axis and bounded by the lines x = a, x = b) and is written as a definite integral. Hence, we have

Infinite Series as Definite Integral

• In the standard segment, as we have discussed in short in the above segment, learnt how Definite integration can be evaluated as limit of a sum. In this part, we will learn how an Infinite Series can be expressed as Definite Integral using the following steps:

1. Express the given series in the form

2. Then the value of the limit of the sum when

can be expressed as a Definite integral following the below steps:

3. Replace r n by x and 1 n by dx and

lim

by the sign of

4. The lower and the upper limit of integration are the limiting values of r n for the first and the last term of r respectively.

DEFINITE INTEGRATION_XII Page | 4 Let sn = h  1 011 0 ()()....()() n nr r fxfxfxhfx = +++=  and Sn = h  12 1 ()()....()() n nr r fxfxfxhfx = +++=  . O x0 x1 x2 xr 1 xr xn 1 xn A P Q B D C L R S M y x

→→

lim()lim b nn nn a sfxdxS →→ == 

lims andlim n

1 r f nn     .

1 n r limf nn →    

→ , i.e.

→ 



Key Concept • 1 1 lim n n r r f nn → =     or 1 1 1 0 1 lim() n n r r ffxdx nn → =  =     • 1 1 lim() pn n r r ffxdx nn   → =  =     where 0 n r Lim n  → == (as r = 1) and n r Limp n  → == (as r = pn)

DEFINITE INTEGRATION_XII 5 | Page Illustration-2 Find 1111 1232 lim.. →  ++++  +++  n nnnn Solution: lim1111 1232 n nnnn →  ++++  +++  1 1 lim n n r rn → = = +  1 0 1 11 lim 1 1 n n r dx r nx n → = == +  +     ( ) 1 0 [ln1]ln2. x =+= Illustration-3 Find  n–1 22 r=0 1 S= 4n–r as n→. Solution: Let Sn = 1 22 0 1 4 n r nr =  = 1 2 0 1 4 n r r n n =     = 1 2 0 11 4 n r n r n =     Hence, S = lim n→ Sn = lim n→ 1 2 0 11 4 n r n r n =     = 1 2 0 4 dx x  = 1 1 2 0 sin x   = 1 sin1 2    = 6  Illustration-4 Find 2 1 1 n r n n = →  22 r lim n+r . Solution: ( ) 2 2 2 2 0 22 1 0 1/ lim151 1 1 n r rn x dxx n n x r n = ==+=− → +  +     .

DEFINITE INTEGRATION_XII Page | 6 Illustration-5 Find ( ) ( ) ( ) 222 n nnn1 lim+++....+ 49n 3+4n232+4n333+4n →      . Solution: Let S = ( ) ( ) ( ) 222lim.... 34232434 n nnn nnnnn →   +++  +++   . = ( )22 11 limlim1 3434 nn nn rr n rr rrn n nn →→ == =  + +     = ( ) 1 2 0 34 dx xx +  . Let, 3 x + 4 = t,  3 2 dxdt x = . Hence S = 7 7 2 4 4 2212111 3337414 dt t t  =−=−−=    Illustration-6 Find ( )( ) 22223333 6666 123123 123 nn n ++++++++ ++++ Solution: The given limit is n2n3 r1r1 n n6 r1 rr lim r  == → =   23 nn r1r1 6 n n r1 1r1r nnnn lim 1r nn  == → =     =      1123 00 1 6 0 xdxxdx xdx =   3411 00 1 7 0 xx11 347 34 x112 77     ===   

DEFINITE INTEGRATION_XII 7 | Page Illustration-7 Find →    1 n n n n! lim n Solution: Let 1 ! lim n n n n L n →  =   ln 1!limln n n n L n n →  =   11.2.3......limln n n n n n →  =   1123 limlnlnln...ln n n nnnnn →  =++++     1 1 limln n n r r nn → =  =    1 1 0 0 lnlnxdxxxx ==−    0 (01)limln0101 x xx + → =−−+=−−=− 1 L e = Illustration-8 Find ( )1 2 / lim n n nn C → Solution: Let ( ) 1/ 2! lim !! n n n L nn →  =    ( )( ) ( ) 1/n n!n1n2..nn L n!n!  +++ =   1/n n1n2nn 12n +++  =   1n1n2nnlnLlnlnln n12n +++  =+++  Here, r 1nr11Tln1 nrnr/n +  ==+  n n r1 11 S1 nr/n =  =+  Hence, 1 0 lnln11Ldx x =+   ( ) ( ) 1 0 ln1lnxxdx=+−  ( ) ( ) ( )   1ln11lnxxxxxx =++−+−− ( ) ( ) 1 0[1ln11ln] xxxx=++−− ( ) ( )2ln21001 =−−−− Thus, lnLln4L4 ==

DEFINITE INTEGRATION_XII Page | 8

Find ( ) 2 11 1 1 123 2 123 lim.. n n n n nn   −+  →  Solution: Let ( ) 2 11 1 1 123n 2n B Llimn123n n  −+   → = 2 1 111 lnlimlnln 2 n n k n Lnkk n n → = +  =−+    11 limln 2 n n n n → +  =−   ( ) n 2 k1 1 klnkklnnklnn n = +−+  22 11 111lnlimlnln 2 nn n kk nknnkk nnnn → == +  =−++    ( ) 2 1 111ln1limlnln 22 n n k nn nkkn n nnnn n → = + +  =−++    1 0 1n11n1lnnxlnxdxlnn 2n2n ++  =−++   1 0 1 ln. (byintegrating by 4parts). xxdx ==−  1 4 Le.= Know Yourself 1. 1111 lim... 123 n nnnn →  ++++  ++  equals (U) (a) log 2 (b) log 4 (c) 0 (d) loge 3 2. 2222 121 lim.... 12 n nn n nn → ++  +++  ++  is equal to (U) (a) log2 4  (b) 4log2 + (c) 2log2 + (d) None of these 3. 2 22 1 1 lim n n r r n nr → = +  equal to (U) (a) 12−+ (b) 15−+ (c) 15 + (d) 12 + 3. FUNDAMENTAL THEOREM OF CALCULUS 3.1 Area function

Illustration-9

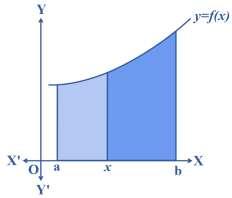
• We'veintroducedtheconceptof ( ) b a fxdx  asthemeasureofthe area enclosed by the curve defined by y = f(x), the vertical lines at x = a and x = b, and the x-axis. Consider any specific point ‘x’ within the interval [a, b]. At this chosen value 'x', ( ) x a fxdx  signifies the area encompassed by the light shaded region within the corresponding diagram. It's important to note that this discussion assumes f(x) > 0 for   , xab  , but it's worth mentioningthat thefollowing assertion remains valid for various other functions as well. The magnitude of this shaded region's area is contingent upon the specific value of ‘ x’.

• In other words, the area of this shaded region is a function of x. We denote this function of x by A(x). We call the function A(x) as Area function and is given by

• Based on this definition, following are the two basic fundamental theorems

3.2 First Fundamental Theorem of Integral Calculus

Theorem: Let f be a continuous function on the closed interval [a, b] and let A(x) be the area function. Then A(x) = f(x), for all x  [a, b].

Illustration-10

we need to use the Chain Rule

3.3 Second Fundamental Theorem of Integral Calculus

Theorem: Let f be a continuous function defined on the closed interval [a, b] and F be an antiderivative of f. Then ( ) ( ) ( ) ( ) [F]FFbb aa fxdxxba ==− .

Illustration-11

DEFINITE INTEGRATION_XII 9 | Page

( ) ( ) A x a xfxdx = 

Find 4 1 x d sectdt dx 

Let 4 ux = . Then 4 11 secsec xu ddtdttdt dxdx =  1 sect (bytheChainRule) u ddu dt dudx  =    sec du u dx = ( ) 43sec4xx=

Solution: Here

Find 2 2 0 / cos xdx   .

Solution: Now 22 1 cos2cos 2 xdxxdx =

( ) 1111cos2sin2 224 xdxxx=+=+

Illustration-12

Find 1 45 1 51 .xxdx +

Solution: Let t = x5 + 1. Then dt = 5x4 dx.

Note that, when x= –1, t = 0 and when x = 1, t = 2

Thus, as x varies from –1 to 1, t varies from 0 to 2

Therefore 12 45 10 51xxdxtdt +=

Illustration-13

DEFINITE INTEGRATION_XII Page | 10



 /2 /2 2 0 0

cossin2

  =+    1sin. 444   =+=

24 xdxxx



 2 333 222 0 22242 2022 3333 t  ==−==   

Find 1 1 2 1 1 tan xdx x +  . Solution: Let t = tan–1 x, then 2 1 1 dtdx x = + . The new limits are, when x = 0, t = 0 and when x = 1, 4 t  = . Thus, as x varies from 0 to 1, t varies from 0 to 4  . Therefore 1222 4 1 4 2 00 0 tan1 0 221632 1 xt dxtdt x    ===−=  +   Know Yourself

DEFINITE INTEGRATION_XII

11 | Page 1. /4 2 0 tan xdx   is equal (U) (a) /4 (b) 1 + (/4) (c) 1 – (/4) (d) 1 – (/2) 2. /2 0 sinsin2 d    (U) (a) /3 (b) 2/3 (c) 2/3 (d) 4/3 3. /4 0 seclog(sectan)xxxdx  +=  (U) (a) 2 1 [log(12)]2 + (b) 2[log(12)] + (c) 2 1 [log(21)]2 (d) 2[log(21)] 4. 1 (1log) e x e xxdx x +=  (U) (a) ee (b) ee – e (c) ee + e (d) None of these 5. /4 4 0 tan xdx   equals (U) (a) 2 43  + (b) 2 43  (c) 1 43  + (d) 1 43  6. /2 2222 0 cossin dx axbx  +  equals (U) (a) /ab (b) 2/ab (c) ab/ (d) /2 ab

4. PROPERTIES OF DEFINITE INTEGRAL

4.1 PROPERTY – 0

()()

Key Concept

Definite integral is independent of variable of integration.

4.2 PROPERTY – 1 ()0

4.3 PROPERTY – 2 ()()

4.4 PROPERTY – 3

()()()

where the point c may lie between a and b or it may be exterior to (a, b).

Key Concept

The Property 3 can also be extended as:

Solution: The graph of f(x) = sin–1 (sin x) is as shown in below figure.

DEFINITE INTEGRATION_XII Page | 12



bb aa fxdxftdt =

a a fxdx



ba ab

=− 

fxdxfxdx

bcb aac fxdxfxdxfxdx =+ 

3 12 121 ()()()()...()() n nn xx xx bb aaxxxx fxdxfxdxfxdxfxdxfxdxfxdx =+++++ 

Find ( ) 2 1 2  xdx  / sinsin .

Illustration-14

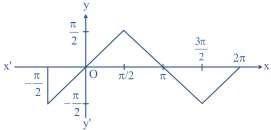
DEFINITE INTEGRATION_XII 13 | Page ( ) ( ) ( ) ( ) 202 1111 /2/20 sinsinsinsinsinsinsinsin xdxxdxxdxxdx   =++  . = Area of shaded region 111 2222222    =−+−   111 2222222    =−+−   2 8  =− Illustration-15 Find: Let ( ) 0 23 || x fxtdt =−  Then discuss continuity and differentiability of f(x) at 3 2 x = . Solution ( ) 0 |23| x fxtdt =−  ( ) ( ) ( ) 0 3/2 03/2 3 32, 2 3 3223, 2 x x tdtx tdttdtx  −   =   −+−     2, 2 3 3 2 93 3 22 xxx xxx  −   =   −+   Clearly, f(x) is continuous at 3 2 x = as 339 224ff −+  ==  3 ()32,2 3 23,2 xxx fx xx  −    =   −   33 0 22ff −+   ==   Hence, f(x) is differentiable at 3 2 x =

Illustration-16

Find: If [x] denotes the greatest integer less than or equal to x, then find the value of integral

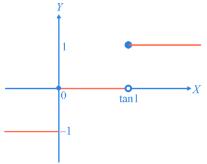
Illustration-17

Find: 10 1 0 [tan], xdx 

where [x] represents greatest integer function.

Solution: Here, y = tan–1 x is a monotonic function. So, the analytical method is advisable.

DEFINITE INTEGRATION_XII Page | 14

2 2 0 [] xxdx  . Solution:       212 222 001 xxdxxxdxxxdx =+  ( ) ( ) 1222 01 01 xdxxdx== 2 3 2 2 1 1 817 0 333 x xdx =+=== 



We have 1 0when0tan1 tan 1whentan110 x x x    =    10tan110 1 00tan1 tan01 Ixdxdxdx   ==+   10tan1  =− 4.5 PROPERTY-4 ()() bb aa fxdxfabxdx =+−

Concept 00 ()() aa fxdxfaxdx =− (replacing a by 0 and b by a).

Key

Find: 1 sin x xxdx e

Solution:

Using

Illustration-18

Adding

DEFINITE INTEGRATION_XII 15 | Page

 + 



e   = +  … (1)

Let sin 1 x x exxdx I

( ) ( ) sin sin 11 x xx xxdx exxdx I ee   == ++ … (2)

property IV, we replace x by –x

Ixx   =  or 0 sin Ixxdx  =  ( ) ( ) 00 sinsin xxdxxdxI   =−−=−  0 2sin2 ===  IxdxI   Illustration-19

For 0 2 ,       , prove that ( ) ( ) 0 1 logtantanlogsec. xdx  += 

log1tantan Ixdx   =+  ( ) ( ) 0 log1tantan xdx   =+−  2 2 0 1tan log1tantan dx x     + =  +   ( ) ( ) 2 00 log1tanlog1tantandxxdx  =+−+  = 2θ log sec θ – I  2I = 2θ log sec θ  I = θ log sec θ

Find: ( ) 3 logsectan d     Solution: Let ( ) 3 logsectan Id   =−  … (1)

equations (1) and (2), we get 2sin

Find:

Solution: ( ) 0

Illustration-20

Key Concept

DEFINITE INTEGRATION_XII Page | 16 Using the property ()(), bb aa fxdxfabxdx==+−  we get ( ) ( ) 3 logsec2tan2 Id   =−−−   .   3 logsectan d   =+  … (2) Adding equations (1) and (2), we get ( )( ) 3 2logsectansectan Id   =−+   ( ) 33 log10.0 dd    ===  4.6 PROPERTY-5 /2 00 ()[()()] aa fxdxfxfaxdx =+−

• If f (x) = f(a − x), then 2 00 ()2() a a fxdxfxdx =  • If f (x) = − f(a − x), then 0 ()0 a fxdx =  Illustration-21 Show that 22 00 11 22logsinlogcoslog xdxxdx    ==    Solution: Let 2 0 logsin Ixdx  =  … (1) But using property 4, we have 22 00 logsinlogcos 2 IxdxorIxdx    =−=    … (2) Adding equations (1) and (2), we get ( ) 2 0 2logsinlogcos Ixxdx  =+ 

Illustration-22

= sin100 xcos99 x for which f(2π – x) = f(x) or ( ) ( )

Here,

Illustration-23

Solution: Let 0 logsin Ixxdx

Now, using property 4, we have ( ) ( )

DEFINITE INTEGRATION_XII 17 | Page ( ) 2 0 logsincosxxdx  =  ( )   2 0 logsin2/2xdx  =  22 00 logsin2log2xdxdx  =−  ( )  /2 0 0 1 logsinlog2 2 x tdtx  =−  1 2, 2 Puttingxtdxdt  ==   ( ) ( ) /2 0 1 2logsin/2log252 tdtbyproperty   =−  ( ) ( ) /2 0 logsin/2log20 xdxbyproperty   =−  = I – (π/2) log 2 or 2I – I = –(π/2) log 2 Hence, ( ) /2 0 Ilogsin/2log2 xdx   ==−  11 log 22   =  

2 10099 0 sincos. xxdx  

2 10099 0 sincos Ixxdx  = 

Find:

Solution:

  =−−  (

10099 0 2sincosxxdx   =−− 

4) 10099 0 2sincosxxdx  =−  = –I or 2I = 0 or I = 0

f(x)

10099

2sincos Ixxdx

) ( )

(by property

 

Find: 0 logsin xxdx



=  … (1)



 or

 



logsin Ixxdx

 =−−

( )

logsin Ixxdx

=−

… (2)

Adding equations (1) and (2), we get 0 2logsin Ixdx   =

(by Property 5)

Illustration-24

Solution: Putting x = tan θ, dx = sec2 θ dθ, given integral becomes

DEFINITE INTEGRATION_XII Page | 18

 



or /2 0 logsin Ixdx   =  ( ) ( ) 2 11log1/2log1/222   ==  

 or /2 0 22logsin Ixdx

 



  log. dx x x x

Find: 2 0

( ) /2 2 2 0 logtancot sec 1tan Id     + = +  /2 0 logsincos cossin d      =+   ( )   /2 0 log1/sincos d   =  /2/2 00 logsinlogcosdd  =−−  1 2log2log2 2   =−−=   4.7 PROPERTY-6 0 ()[()()] aa a fxdxfxfxdx =+− Key Concept 0 2(),() () 0,() a a a fxdxiffxiseven fxdx iffxisodd   =     

Illustration-25



−+−+

371 / / cos xxxx dx x 

Solution: 953 2 2 37 ()sec cos xxxx fxx x −+− =+

  = 

[∵ sec2 x(x9 – 3x5 + 7x3 – x) is an odd function]

Illustration-26

 +−   −+    

/ /

• 0 () nT fx  dx = n 0 () T fx  dx, n  z

DEFINITE INTEGRATION_XII 19 | Page

Find: 953 4 2 4



= sec2 x (x9 – 3x5 + 7x3 – x) + sec2 x or /4/4 2 /4/4 ()sec fxdxxdx

2 0 2sec xdx  =  /4 0 2tan|2 x  ==

Find: 12 22 12 12 xx dx xx

11 2 11  +−

1/2 2 1/2 1/2 11 11 xx dx xx  +−    −+     1/2 1/2 11 . 11 xx dx xx +− =− −+  1/21/2 1/2022 44 2 11 xxdxdx xx == 1/2 22 0 44 20 11 xx dx xx  =    when 1 0 2 x     ( ) 1/2 2 0 4log1 x =−−  ( ) ( )4log3/44log4/3=−= 4.8 PROPERTY-7

Solution: Given integral

f(x)

is a periodic function with period T, then

Solution: Note that |cos x| is a periodic function with period . Hence the given integral

Illustration-29

where n is a positive integer and 0 v

DEFINITE INTEGRATION_XII Page | 20 • () anT a fx +  dx = n 0 () T fx  dx, n  z, a  R • () nT mT fx  dx = (n – m) 0 () T fx  dx, m, n  z • () anT nT fx +  dx = 0 () a fx  dx, n  z, a  R • () bnT anT fx + +  dx = () b a fx  dx, n  z, a, b  R

Find: 4 0 | cosx|dx   .

I = 0 4|cos|xdx   (using property 7) = /2 0/2 4coscosxdxxdx        = /2 0/24[sin][sin] xx     = 4 [1 + 1] = 8.

Illustration-27

5 {} 3 x e  dx,

Solution: 5 {} 3 x e  dx = 1 {} 0 (5–(–3)) x edx = 1 0 8 x edx = 1 0 8 x e   = 8 (e –1)

Illustration-28 Find:

where {.} denotes the fractional part function.

 nπ+v 0 |sinx|dx=2n+1-cosv

 Solution: 00 |sin||sin||sin| nvvnv v xdxxdxxdx  ++ =+ 

Show that ,

(where [x] and {x} and integral and fractional parts of x and n

21 | Page = 00 sin|sin| v xdxnxdx  +  = ( ) 0 0 cossin v xnxdx  −+  = – cos v + 1 + n ( ) 0 cos x  Illustration-30 Find: 163 0 / |sin|xdx   . Solution: 16/355/3 005 |sin||sin||sin|

  + =+  /3 00 5|sin||sin|xdxxdx  =+ [∵ |sin x| is

with period π] /3 00 5sinsinxdxxdx  =+ 121 521 22  =+−+=   Illustration-31 Find:   0 0     n n xdx xdx

∈ Solution:     0 0 n n xdx I xdx =     ( )   0 0 n n xxdx xdx =     0 0 1 n n xdx xdx =−     2 0 1 0 2 1 n x nxdx =−  22 1 0 22111 1 2 nn n nxdx n =−=−=− 

DEFINITE INTEGRATION_XII

xdxxdxxdx

periodic

DEFINITE INTEGRATION_XII Page | 22

1. /2 0 1sin2xdx  +  equals (U) (a) 1/2 (b) 1 (c) 2 (d) None of these 2. () bc ac fxcdx +  equals (I) (a) () b a fxcdx +  (b) () b a fxdx  (c) 2 2 () bc ac fxdx  (d) (2) b a fxcdx +  3. 1 0 |31|xdx  equals (U) (a) 5/6 (b) 5/3 (c) 10/3 (d) 5 4. 1/ |log| e e xdx =  (U) (a) e –1 – 1 (b) 2(1 – 1/e) (c) 1 – 1/e (d) None of these 5. 1 0 |sin2|xdx  is equals to (U) (a) 0 (b) –1/ (c) 1/ (d) 2/ 6. 3 2 6 3 sin 1 xx dx x +  equals (A) (a) 4 (b) 2 (c) 0 (d) None of these 7. /2 /2 2sin log 2sin d        +   equals (U) (a) 0 (b) 1 (c) 2 (d) None of these 8. 1 1 1 log 1 x dx x +     is equals to (U) (a)  (b) 1 (c) 0 (d) 2 9. () ()() b a fx dx fxfabx ++−  equals (I) (a) b – a (b) a + b (c) 1 ()2 ba (d) 1 ()2 ab +

Know Yourself

DEFINITE INTEGRATION_XII

23 | Page 10. /2 3/2 3/23/2 0 sin sincos x dx xx  +  equals (I) (a) /2 (b) /4 (c)  (d) 2 11. /4 0 log(1tan) d   +=  (U) (a) log2 4  (b) 1 log 42  (c) log2 8  (d) 1 log 42  12. 2 0 sin2 cos d ab      equals (U) (a) 1 (b) 2 (c) /4 (d) 0 13. 400 0 1cos2xdx   is equals to (U) (a) 4002 (b) 8002 (c) 0 (d) None of these 14. /2 0 logsin2xdx   equals (U) (a) (/2) log 2 (b) – (/2) log 2 (c) (/4) log 2 (d) – (/4) log 2 15. /2 0 logsec xdx   equals (U) (a)  log 2 (b) (/2) log 2 (c) –  log 2 (d) – (/2) log 2

5. DIFFERENTIATION UNDER THE INTEGRAL SIGN (LEIBNITZ THEOREM)

From the wavy curve, it is clear that f

(x) changes its sign at x =

1, 0 and hence the points of maxima are –1, 1 and of the minima are –2, 0, 2

DEFINITE INTEGRATION_XII Page | 24

• If F(x) = () () () hx gx ftdt  , then ()dFx dx = f(h(x)) h(x) – f(g(x)) g(x) Proof : Let P(t) = () ftdt   F(x) = () () () hx gx ftdt  = P(h(x)) – P(g(x))  ()dFx dx = P(h(x)) h(x) – P(g(x)) g(x) = f(h(x)) h(x) – f (g(x)) g(x) Illustration-32 If F(x) = 3 2 1 ln x x dt t  then find F (e) Solution: F(x) = 2 3 3 ln x x –2 2 ln x x = 2 ln x x –ln x x = (–1) ln xx x now F(e) = (–1) ln ee e = e(e – 1) Illustration-33 Find 0 x lim + →  2 x 4 0 sinttantdt x Solution: Applying L’ hospital rule 0 x lim + → 3 2sintan 4 xxx x  0 x lim + → 1 2 sin x x    tan x x    = 1 2

the points of maxima / minima of 2 2 0 54 2 x t tt dt e −+ +  . Solution: Let 2 2 0 54 () 2 x t tt fxdt e −+ = +  2 4254 '()20 2 x xx fxx e −+ =− + 2 (1)(1)(2)(2)2 2 x xxxxx e −+−+ = +

Illustration-34 Find





Illustration-35

Find Let F: R →R be a differentiable function having f(2) = 6. 1 2 48 () f

= . Then evaluate

Illustration-36

Find Evaluate Prove that 22 11 1818 =+  sincos //sincos, xx ytdttdt where 0 ≤ x ≤ π/2, is the equation of a straight line parallel to the x-axis. Find its equation.

Solution: Here, we have to prove that y = constant or derivative y w.r.t. x is zero. 22 sincos11 1/81/8 sin,cos xx ytdtdttdt =+

1212 sinsin2sincoscoscos(2cossin) dy xxxxxx dx =+−

= 2x sin x cos x – 2x sin x cos x = 0 for all x

Therefore, the curve in equation (1) is a straight line parallel to the x-axis. Now, since y is constant, it is independent of x. So let use select x = π/4, Then 1/21/211 1/81/8 sincos ytdttdt =+

Therefore, equation of the line is 3 16 y  =

DEFINITE INTEGRATION_XII 25 | Page



3 6 2 4 2 →  () lim. fx x t dt x Solution: () 3 3 () 6 6 22 4 limlim40 220 fx fx xx tdt t dtform xx→→  =     ( ) ( ) ( ) 3 2 4' lim 1 x fxfx → (applying L’ Hospital rule) =4(f(2))3 × f(2) ( )3 1 46 48 = = 18



 (

 1/2 1/8





) 1/2 11 1/8 sincosttdt=+

2 dt

3 16  =

Know Yourself

DEFINITE INTEGRATION_XII Page | 26

Find Evaluate If ( )   0 ()sin x yftkxtdt =−  , then prove that 2 2 2 (). dy kykfx dx += Solution: ( )   0 ()sin x yftkxtdt =−    0 ()sincossincos x ftkxktktkxdt=−  00 sin()coscos()sin xx kxftktdtkxftktdt=− …(1) ( ) ( ) 00 cos()cossincossin()sincossin xx dy kkxftktdtkxfxkxkkxftktdtkxfxkx dx =++−  00 cos()cossin()sin xx kkxftktdtkxftktdt =+ …(2)

differentiating equation (2)

    2 22 2 00 sin()coscos()coscos()sinsin()sin xx dy kkxftktdtkkxfxkxkkxfttdtkkxfxkx dx =−+++  = –k2y + kf(x) ( ) 2 2 2 dy kykfx dx +=

Illustration-37

Again

w.r.t. x, we ge

1. 2 (), x t x e fxdt t =  , then f (1) is equal to: (U) (a) e (b) 2e (c) 2e2 – 2 (d) e2 – e 2. If 2 1 (())(1sin),thenf 3 tftdtx  =−    is (U) (a) 1/3 (b) 1/3 (c) 3 (d) 3

6. INEQUALITIES

• ()|()| bb aa fxdxfxdx 

• Equality sign holds when f (x) is entirely of the same sign on [a, b].

• If f(x)  g(x) on [a, b], then ()() bb

fxdxgxdx 

. In particular, if f(x)  0, then ()0 b a fxdx

• For a given function f (x) continuous on [a, b] if we are able to find two continuous functions f1(x) and f2(x) on [a, b] such that f1(x)  f(x)  f2(x) x  [a, b], then 12

• If m and M are respectively the global minimum and global maximum of f (x) in [a, b] then m (b a) ()() b a

Since the function f (x) =

increases monotonically on the interval [1,

DEFINITE INTEGRATION_XII 27 | Page







aaa

 

()()() bbb

fxdxfxdxfxdx

fxdxMba −  Illustration-38 Prove that 4 3 3 1 3230 xdx +  . Solution:

3 3 x +

2, M = 30 , b – a = 2. Hence, 2.2 3 3 1 3230 xdx +   4 3 3 1 3230 xdx +  . Illustration-39 For x (0, 1) arrange f1(x) = 2 1 9– x , f2(x) = 2 1 92 – x and f3(x) = 23 1 9 xx in ascending order and hence prove that 1 23 0 111 25 6 9 62 n ldxln xx   Solution:  0 < x3 < x2, for all x  (0,1)  x2 < x2 + x3 < 2x2  –2x2 < – x2 – x3 < –x2  9 – 2x2 < 9 –x2 – x3 < 9 – x2  2232 111 9–9––9–2 xxxx 

3], m =

Know Yourself

DEFINITE INTEGRATION_XII Page | 28 f1(x) < f3(x) < f2(x) for x  (0, 1)  1 1 0 ()fx  dx < 1 3 0 ()fx  dx < 1 2 0 ()fx  dx  111 2232 000 9–9––9–2 dxdxdx xxxx    1 0 13 63–x n x  +   < 1 23 0 9––dx xx  < 1 0 132 3–2 62 x n x  +    1 6 n2 < 1 23 0 1 9 dx xx  < 1 62 n5

1. If f(x) is a continuous function such that f(x)  0  x  [2, 10] and 8 4 ()0,(6) fxdxthenfindf =  (A) 2. Prove that 2 2 0 5–6 1 5 9–x dx x      (A)

7. DETERMINATION OF FUNCTION USING DEFINITE INTEGRAL

Illustration-40

Find the real number a such that

Solution: Differentiating both sides of the given expression, we get

dt x t +=

⇒ 1022 x a tx  +=



⇒ 210 a =

⇒ a = 25

Hence, f(x) = x3/2 and a = 25

( ) ( )( ) 2 0 sin'2sinsin x fxxftttdt =+−  then find  =   3 ? 2 f 

Solution: Differentiating both sides w.r.t. x, we get f'(x) = cos x + f'(x) (2 sin x – sin2x)

 (1 + sin2 x – 2 sin x) f '(x) = cos x

(

== +−

(

Put 1 – sin x = t

(

31 22 f   =−  

DEFINITE INTEGRATION_XII 29 | Page

(



a ftdt

) +=

2 102. x

( ) ( ) 3/2 2 1 2.. 2 fx fxx x x ==

Substituting this value in the given relation, we get, 102 x a 

⇒ 1022xax +−= 

Illustration-41 A function f (x) satisfies

)

) 22 'coscos 1sin2sin1sin xx fx xx x

Integrating, ( ) ( )2 cos 1sin xdx fx x = 

) 2 11 1sin dt fxC tx t =−==+ 

Also, f(0) = 0, hence C = –1

) 111sinsin 1. 1sin1sin1sin xx fx xxx −+ =−==

Illustration-42

Consider a real valued continuous function f such that ( ) ( )

the maximum and minimum values of the function f.

Solution: We have ( ) ( ) ( )

Illustration-43

Let f(x) be a continuous function and c is a constant satisfying ( )

find f(x) and the value of c.

Solution: Put x = 0 in the given equation

Differentiating,

DEFINITE INTEGRATION_XII Page | 30

(

/2 /2 sinsin fxxxtftdt   =++ 

)

Find

 

 ( ) /2 /2

   =++ 

sinsin fxxxtftdt

=++

sinsinxxtftdt

 f (x) = ( + 1) sin x + A

/2 /2

  

 ( )

 



Now, ( ) ( )

1sin AttAdt

=++

21sinttdt

⇒ A= 2(π + 1)

Hence, f (x) = ( + 1) sin x + 2( + 1)  fmax. = 3( + 1) and fmin. = ( + 1).

( )

 1 2 00 x xxt ftdteceftedt then

=−

( ) 1 0 01 t cftedt=−  Let 1 c k = where ( ) 1 0 t kftedt = 

( ) 2 0 2, x xxftdte=− 

Substituting in the given equation, we get

we get f(x) = ex – 2e2x

11 2

21232

 11 32 c ke ==

Now, ( ) ( )

tttt keeedtedte =−=−=−

Hence, ( ) ( ) 2 211 . 4242 xx e e fxee e e =+

Know Yourself

DEFINITE INTEGRATION_XII 31 | Page

Illustration-44

1 0

( ) 1 0 1 Aftdt =+  and ( ) 1 0 .Btftdt =  ( ) ( ) 1 0 0 11 t tttt AAeBedtAeBe =++=+−   A = 1 + A(e1 – 1) – B(e–1 – 1)  (2 – e) A + (e–1 – 1) B = 1 (1) Now, ( ) ( ) ( ) 1 1 0 0 0 t tttttt BtAeBedtAteeBtee =+=−+−+   B = A + B(1 – 2e–1)  A – 2e–1 B = 0 ... (2) 

ee ==

If ( ) ( ) ( )

, xxx fxeeteftdt =++  find f(x). Solution: We can write f(x) = Aex + Be–x, where

From (1) and (2), we get ( ) 2 211 ,.4242 e e AB e

f(x)

f(x) > 0 for all x  0 and ( ) ( ) ( ) 101 0 1. x fxftdt =+  Find (f(101))100 (A) 2.

f (x)

( ) 0 sin x t extdt=−  and g(x) = f (x ) – f(x). Find the

(A) 3. If ( ) ( )

(

1 22 0

fxxxyxyfydy =++ 

f(x). (A) 4. If ( ) ( ) ( ) 1 0 ,fxxtxtftdt =++ 

integral ( ) 1 0 .tfxdx (A)

Let

be a continuous function such that

Let

is a derivable function satisfying f(x)

range of g(x)

( )

)

find

then find the value of the

8. WALLIS’ FORMULA

• The formula for evaluating /2 ,0 sincosmn mn Ixxdx  = where m,n are any positive integers, is called Wallis' Formula.

• First of all, let us devise a formula to evaluate a special case of the above integral i.e.

• To

let us find a reduction formula. We have

• In order to evaluate

we start with (n-1) in the numerator and go on reducing by 2 till we get either 2 or 1. Similarly we start with n in the denominator and go on reducing by 2 till we get either 2 or 1 . Further, we multiply by 2

in case n is even and by 1 if n is odd.

DEFINITE INTEGRATION_XII Page | 32

2 0 sin /n n Ixdx = .

evaluate 2 0 sin /n n Ixdx = ,

/2 0 sinn n Ixdx = 1 2 0 sincos n xx   =−+  ( ) /222 0 1sin.cos n nxxdx  − ( ) ( ) /222 0 1sin1sin n nxxdx  =−− ( ) ( ) /22 0 1sin1 n nxdxn  =−−− /2 0 sinn xdx  22 1 (1)(1). nnnnn n InInIII n  +−=−=  

the above formula repeatedly, we obtain 0 135 .. 24 n nnn II nnn  =   or 1I (respectively as n is even or odd). We know 01,1 2 II  == . Hence, In n1n3n51if n is even nn2n422 n1n3n52 1if n is odd nn2n43     =     Key Concept • 22 00 n1n3n51if n is even nn2n422 sincos n1n3n521if n is odd nn2n43 /n/nxdxxdx     ==    

Using

2 0 sin /nxdx 

2 0 cos /nxdx 



• Using the above formula repeatedly, we obtain:

DEFINITE INTEGRATION_XII 33 | Page

that /43/2 0 3 (cos2)cos 162 d    = Solution: L.H.S. = /4 3/2 0 (cos2)cos d    /4 23/2 0 (12sin)cos d   =−  Put 2sinsint = cost cosddt 2  = When  = 0then t = 0 When  = /4 then t = /2  L.H.S. 4 /2 0 cos131 422 22 t dt   =  3 162  == R.H.S. •

for /2 ,0 sincosmn mn Ixxdx  = . ( ) /21 ,0 sinsincos mn mn Ixxxdx = 111 2 /2 2 0 0 sincoscos (1)sincos 11 mnn m xxx mxxdx nn   −++ =−+−  ++  /222 0 1sincoscos 1 mn m xxxdx n   =  +  ( ) /22 0 1sincossincos 1 mnmn m xxxxdx n   =−  +  2,, 11 11mnmn mmII nn  =− ++  ,2, 11 1 11mnmn mmII nn  += ++  ,2, 1 mnmn m II mn  =  + 

Illustration-45 Prove

Now, let us develop a reduction formula

2,4,' 3 2 mnmn m II mn = +− 4,6,' 5 4 mnmn m II mn = +−

The above formulae can be combined to have the following simple formula covering all the cases:

Key Concept

or2][(n1)(n3)(n5)..1or2]K (mn)(mn2)(mn4).1or2

if both m and n are even (m,nN);  K = 1 otherwise.

The above formula is called Wallis formula.

Note: Wallis formula is applicable only when limits are 0 to 2 

Illustration-46

is 1 since the exponents are not both even.

DEFINITE INTEGRATION_XII Page | 34 ................................. 2,1, 2 3 nn II n = + if m is odd 2,0, 1 2,, nn II n = + if m is even Thus, ,1, 1352 243 mnn mmm II mnmnmnn  =  ++−+−+  if m is even (1) ,0, 1351 242 mnn mmm II mnmnmnn  =  ++−+−+  if m is even … (2) /2 1 /2 1,0 0 cos1 sincos 11 n n n Ixxdx nn   +  ===  ++ (3) /20/2 0,00sincoscos nn n Ixxdxxdx  == 1352.1ifis odd 243 1351.ifis even 2422 nnn n nnn nnn n nnn      =      ... (4)

/2 0 sin.cosmnxxdx  [(m1)(m3)..1

= ++−+− where K



(a) /257 0 sincosxxdx  (b) /268 0 sincos. xxdx 

sincos Ixxdx = 42642 K 12108642  =  K

Find

Solution: /257 5,70

120

where K

DEFINITE INTEGRATION_XII

6,8 4 5 8 20, K I = where K is π/2 since the exponents are both even

5 . 4096  =

Illustration-47

Find: 56 0 sincos. xxxdx 

Solution: Let 56 0 sincos Ixxxdx = 56 0 ()sin()cos() Ixxxdx   =−−−

56 0 sincosxxdx   =− 56 0 sincos xxxdx  

/256 0 2I2sinxcosxx d   =

Illustration-48

Find: 135 0 (1) xxdx−

Solution: Put x = 2 sin2sincos==dxd  x = 0

35 | Page

42531 I

 = 

1197531

8 I 693  =

 == 2   = 135

(

/2711

  = 642108642 2

=  642108642 18161412108642  =

0;1 x

0 (1) xxdx−

)5 /262 0 sincos2sincos d  =

0 2sincos d

18161412108642

Illustration-49

Find: 100 30 C.Iif ( ) 0 30 17 0 1. 1 I xd x x

Put x = sin2 

Know Yourself

DEFINITE INTEGRATION_XII Page | 36

/214161 0 2sincos Id  = 2(140138.2)(6058.2) 202200..2 I  =  7030 101 22(70691)2(30291) 2(101100..1) I  =  100 30 70!30!11 101100!101C ==  100 30 1 IC. 101 =

= Solution:

1. Find: 243 0 sincosxxdx   . (U) 2. Find: 246 0 sincosxxdx   (U) 3. Find: /222 /2sincos(sincos)xxxxdx   + (U) 4. Find : 62 0 sincos xxxdx  (A)

DEFINITE INTEGRATION_XII 37 | Page

Single Correct Answer Type Question

DEFINITE INTEGRATION_XII Page | 38

EXERCISE-1

1. Evaluate: 4 2 2 x dx x1 +  (a) 117 log 25    (b) 15 log 217    (c) log17 5    (d) log517    2. Evaluate: ( ) 2 4 2 xx dx 2x1 + +  (a) 5755 (b) 575 5 (c) 5755 5 + (d) 5755 5 3. Evaluate: π/4 3 0 tanxdx  (a) ( )1log2 (b) ( )1log2 + (c) ( )11log2 2 (d) ( )11log2 2 + 4. Evaluate : 1 x 0 πx esindx 4  +    (a) 224 e1 ππ +++ (b) 224 e1 ππ −−+ (c) 224 e1 ππ +−+ (d) 224 e1 ππ −+− 5. Evaluate : 2 34x 0 edx  (a) ( )53 1 ee 4 (b) ( ) 53 1 ee 4 (c) ( ) 53 1 ee 4 (d) ( )53 1 ee 4 6. The value of 2π sinx 0 dx e1 +  is (a) π (b) 0 (c) 3π (d) π 2 7. Find the value of π/2 π/2 sinxdx  (a) 0 (b) 1 (c) 2 (d) 3 8. Evaluate : ( ) 1 1 3/2 0 2 xtanx dx 1x +  (a) 4 π 22 (b) 4 π 22 + (c) 4 π 42 (d) None of these

DEFINITE INTEGRATION_XII

39 | Page 9. Evaluate: π 107 π xsinxdx  (a) 1 (b) 2 (c) 1 (d) 0 10. Evaluate:   ( ) 2 0 xxdx  (a) 0 (b) –1 (c) 1 (d) 2 11. The value of ( ) 4 2x 0 xedx +  is (a) 815e 2 + (b) 815e 2 (c) 8 e15 2 (d) 8 e15 2 12. The value of ( ) 2 32 1 4x5x6x9dx −++  equal to (a) 64 3 (b) 64 (c) 132 3 (d) 132 13. The value of integral 2x4x 1 3x 0 eedx e +  is (a) 2 e1 e (b) 2 e1 e + (c) 2 e1 e (d) 2 e1 e −+ 14. Find the value of 4 1 x5dx  is (a) 15 2 (b) 15 2 (c) 33 2 (d) 33 2 15. The value of integral 2 1 0 x dx 1x +  is equal to (a) 21 + (b) 21 (c) 21 (d) 21−+ 16. The value of integral 1 45 –1 5xx1dx +  is (a) 42 3 (b) 42 3 (c) 4 3 (d) 42 17. π/2 sinx 0 cosxedx  is equal to (a) e1 + (b) e1 (c) e (d) –e 18. The value of integral ( ) 3 1 1 dx x1logx +  is (a) log1log3 (b) log1log3 + (c) log1log2 (d) log1log2 + 19. ( ) 1 1 0 tansinxdx  equals (a) 2 (b) 0 (c) –1 (d) 1

DEFINITE INTEGRATION_XII Page | 40 20. The value of /4 0 tan xdx   is (a) log 2 (b) 1 log22 (c) log22 (d) None of these 21. 2/3 2 0 1 dx 49x +  is equal to (a) π 6 (b) π 12 (c) π 24 (d) π 4 22. The value of integral π/2 2 0 cosxdx  is (a) π 4 (b) π 4 (c) π 2 (d) π 2 23. The value of integral 2π 5 0 cosxdx  is (a) 0 (b) 1 (c) –1 (d) 2 24. The value of π 32 π sinxcosxdx  is (a) 0 (b) 1 (c) –1 (d) 2 25. ( ) ( ) ( ) 0 fxdx fxfax a +−  is equal to (a) a (b) a 2 (c) a 2 (d) 2a 26. If ( ) fxsinxcosx 1sinxcosx = + , then π fx 2    is equal to (a) f(x) (b) ( )fx (c) ( ) 1 fx (d) ( )2fx 27. If ( ) fxsinxcosx 1sinxcosx = + , then ( ) 2 0 π fxdx  is equal to (a) π 2 (b) π 4 (c) 0 (d) None 28. If ( ) ( )gxlog1tanx =+ , then π gx 4    is equal to (a) ( )log2gx (b) ( ) 1 gxlog2 2 (c) ( ) gxlog2 (d) ( ) 1log2gx2 + 29. If ( ) ( )gxlog1tanx =+ , then ( ) 4 0 π gxdx  is equal to (a) π log2 4 (b) π log2 8 (c) π log2 4 (d) π log2 8

DEFINITE INTEGRATION_XII

30. ( ) 2 fxxsinx = is a

(a) even

= , then

where [ . ] denotes greatest integer function is equal

41 | Page

(b) odd

31.

) π π fxdx 

(a) π 4 (b) 2π (c) π 2 (d) 0 32. If (

gxxsinx

π π xsinxdx 

(a) π (b) 2π (c) 3π (d) 4π 33. π/2 π/2 sinxdx 

to (a) 0 (b) 1 (c) 2 (d) 3 34. π/2 7 π/2 sinxdx 

(a) 0 (b) 1 (c) 2 (d) π 35.     bb aa xdxxdx +−

to: (a) a + b (b) b – a (c) a – b (d) 2 ab + 36. 0 1ln . x fxdx xx   +   

(c) is equal to 1 2 (d) can not be evaluated 37. ( ) 3 2 5 x dx xx = −+  (a) 1 2 (b) 1 3 (c) 1 5 (d) None of these 38. For any integer n the integral ( ) 2 cos3 0 cos21 x enxdx  +  has the value [JEE 1998] (a) 2 (b) 1 (c) 0 (d) None of these 39. ( )2 3 2 2 2 21053 x dx xx + −+  is equal to(a) 2 (b) 1 (c) 1 2 (d) 5 2 40. The value of   2 2sin xdx    ,

[ ]

(a) 5 3  (b)  (c) 5 3  (d) 2

(

is equal to f(x) = x2 sin x

)

is equal

is equal to

(a) is equal to zero (b) is equal to one

where

represents the greatest integer function is-

cos x gxtdt =

41. If ( ) 4 0

, then g(x + π) equals-

(a) g(x) + g(π) (b) g(x) – g(π) (c) g(x)g(π) (d) (

, then f’(9)

(a) is equal to 1 9 (b) is equal to 1 3 (c) is equal to 1

(d) is non existent 43. Let f : R → R be a differentiable function and f(1) = 4. Then the value of

The value of

: ([ . ] denotes greatest integer function)

is, ([ . ] denotes the greatest integer)

DEFINITE INTEGRATION_XII Page | 42



( )

g 

( )



)

42. If

cos

tdtxx  =

( ) 1 4 2 lim 1 fx x t dt x →  (a) 8 f’(1) (b)

f’(1) (c) 2 f’(1) (d) f’(1) 44.

2222

14221 x nnnn nnnnn →  ++++  ++−+  is (a) 4  (b) 2  (c) 3  (d) None of these 45. ( )   ( ) /4 2 0 tantannnxxdxx  +−  is

(a) 1 1 n (b) 1 2 n + (c) 2 1 n (d) none of these 46. 2 0 3 0 sin lim x x xdx x + → =  (a) 1/3 (b) 0 (c) 2/3 (d) does not exist 47. ( ) /2 0 sin8lncot cos2 xx dx x   is equal to: (a) π ln 2 (b) ln2 2  (c) 2 ln2  (d) zero 48. ( )2 0 cos 1sin xx dx x  +  is equal to: (a) π – 2 (b) –(2 + π) (c) zero (d) 2 – π 49.

value of   1 1 1sin1 xxdx   ++  

(a) 2 (b) 0 (c) 1 (d) none of these

lim.....

The

JEE Main Level Quetions

f(x).

cotm d

1/2

sin 2

(2, 3)

 a (b)  ax2

(c)



1/4

3 (2) T

( , 2)

none

(3, )

is equal to 1 xx++  (ax2 + bx + c) dx. Then the quadratic

DEFINITE INTEGRATION_XII 43 | Page

EXERCISE-2

(a)

/2 /4

   

(a)

(b)

(c)

(d)

   t

(a) x 

(b) x 



1. Let (a, b) and (, ) be two point on the curve y = f (x). If the slope of the tangent to the curve at (x, y) be  (x) then () a    (d)

xdx   3 2 0

 1 xx++  (ax2 + bx + c) dx = 5 2 0

 +  a b (d) none of these 2. If Im =

, then value of I4 + I2 is

1/3

none of these 3. If 2 56 xx + 2 00

x dtx



dt, then

5 ,32

of these 4. Let a, b, c be non zero numbers such that

equation

+ bx + c = 0 has

(d)

5. 2 2 2 0 2 0 lim x t x x t edt edt →       is equal to (a) 1 (b) 0 (c) –1 (d)

(a) /4 (b) 0 (c) /2 (d) none

(a) no root in (0, 3)

(b)

at least one root in (3, 5) (c) a double root in (0, 3)

two imaginary roots

none of these 6. The value of 22 sincos 11 00 sin()cos() xx tdttdt +

of these

7. Let T > 0 be a fixed real number. Suppose f is a continuous function such that for all x  R f(x + T) =

If I = 0 () T fxdx  , then the value of 33

fxdx + 

DEFINITE INTEGRATION_XII Page | 44 (a) 3 2 I (b) 2I (c) 3I (d) 6I 8. If for non-zero x, 3f (x) + 4f 11 xx  =   – 10, then 3 2 () fxdx  is equal to (a) 42 ln 73 (b) 33 ln 72 (c) 32 ln 73 (d) none of these 9. Let g (x) = sin x + cos x and f (x) = ||,0 0,0 x x x x      =  . Then the value of 2 /4 (()) fgxdx    is equal to (a) /2 (b) /4 (c)  (d) none of these 10. The value of I = 3 0 12 [] 33 xxx   ++++     dx, where [.] denotes the greatest integer function, is equal to; (a) 10 (b) 11 (c) 12 (d) none of these 11. A function is defined as f (x) = 1,0 1,0 x x    − , then the value of 1 1 [] ()1()()1()2 x xfxnxfxnxfxnxfxn nnnn −+−−+−++−++  +++    is (a) –1 3 (b) 1 4 (c) 1 (d) none of these 12. If ( )( ) 3/4/2 /4 /4 /4/2 sec sincos x edx kxdx eexx     = ++  , then the value of k is (a) 1 2 (b) 1 2 (c) 1 22 (d) –1 2 13. Suppose g(x) satisfies g(x) = x + ( ) ( ) 1 22 0 xyyxgydy +  , then g(x) is (a) 2 6180 119119 xxx ++ (b) 2 7 11 xx + (c) 2 18080 61119 xx + (d) none of these 14. Let f (x) = 2 1 (32) x xxxdx −+  , 1  x  4. Then the range of f (x) is (a) 163 , 44    (b) 1 4,2    (c) 163 , 42    (d) none of these

15. The value of

16. If f (x) =

17. Let y = f(x) be a continuous and differentiable curve. The normals at (1, f(1)), (2, f(2)) and (3, f(3)) make angles , 346 and  with positive x-axis respectively. Then value of

The value of

is equal to

n is an odd integer) then the value of S is

45 | Page

DEFINITE INTEGRATION_XII

xx   +−  

to (a)

(b)

(d)

1 2

21 tan 1 x dx

is equal

none of these

tan12 x xxe xxx x

/2 /2 ()fx    d x is equal to:

(b)

2 22 cos sinsin

then the value of

(a) 0

none of these

( ) ( ) ( ) ( ) ( ) 23 12 fxxfxdxfxfxdx ++ is equal to (a)

(2)

f(1)

(b) 2f(2) – f(1) + 1 (c) f(3)

f(2) +

(d) none of these 18.

2 0

 

(a) 22 (b) 2 (c) 4 (d) 42 19. /2 2cos 0 4 1 x dx e    +   +  is equal to (a) /3 (b) /4 (c) /6 (d) none of these 20. ( ) /4 2 /4 sin 1 x x exx dx e    is

to (a) 0 (b) 2 (c) e (d) none of these 21. If S = 1 0 1 () () n n r n r xr dx xr = =    ,

(a) 1 (b) 0 (c) –1 (d) none of these 22. /2 0 1(cot) n n dx nx  +  is

(n  N) (a) 4 n (b) 2n  (c) 4n  (d) 2 n 

f

+ 1

–

|cossin|xxdx

equal

(where

equal to

23. The value of the integral || b

(a < b) is equal to

The value of

x 

dx, where [.] is the greatest integer function, is (a) 13

The value of

(a sin3 x + b tan x3 + c2) dx is

(a) dependent on a, b, c

dependent on b and c

dx is equal to

DEFINITE INTEGRATION_XII Page | 46



(c)

(d)

(b) a

– 1 (c) a = 1, b = –1 (d) none

25.

1 1 0 (1) n r frxdx = −+ 

(a) 1 0 ()fx  dx (b) n 1 0 ()fx  dx (c) (n – 1) 0 () n fx  dx (d) 0 () n fx  dx

9 0

(b)

27.

 

x dx x

(a) b – a (b) a – b

b + a

none of these 24. If 1 3 0 32 axb dx xx + ++  = ln 3 2 , then (a) a = 1, b = 1

= 2, b =

of these

The value of

is equal to

26.

 

of these



(b)

(d)

28. If f 1 x    + x2 f (x)

 x

cos sin () ecx x fz  dz is for x  0,2     is equal to (a) 1 (b) a

The

/3 5 /61tan dx x   +  is (a) 1 (b) /12 (c) /6 (d) none of these 30. 1 2 1 {5}xxdx +−  , where {.} denotes the fractional part of x, is equal to (a) 1 + 3 5 (b) 1 6 (1 + 3 5) (c) 3 5 – 1 (d) 1 6 (1 – 3 5)



(a) 0 (b) 1 (c) 2 (d) none of these 32. 3 3 2 2 3 (3)(1) x x dx xe ++  is equal to (a) 3 3  (b) 3 3  (c) 3 3  (d) none of these

dependent on a and b

dependent on c only

= 0,

> 0, then

function of x

29.

value of the integral

31. The sum 72 22 36 tan(6)tan(1875) xdxxx −+++

DEFINITE INTEGRATION_XII



5 ln 64 x dx xx

none of these 34. ( ) 8 93295

8 sin xxdx +

The value of

100 0

2 + 8295

100

sec  log |cosec|

47 | Page

33. 2 2 2 1   

is equal to

(c)

(d)



(d)

35.

  10 10 3 3 x x



(a)

(b)

(c)

(d)

36.

(a) 50 (b) 1 (c)

(d) none

37.

 

x x  −    =  ,

( ) 2 3/2 fxdx 

(a) 11 2 (b) 7 2 (c) –6 (d) 17 2 38. 2 2 0 2 x xdx     is equal to (a) 1/2 (b) 1 (c) 0 (d) none of these 39. 0 1 coscos dx x   +  is equal to (a)

(b)

(c)

(d)

40. ( )( ) b a xabxdx 

to (a) 4  (a – b)2 (b) 2  (a – b)2 (c) 8  (a – b)2 (d) none of these

(a) ln 2 (b) – ln 2

is equal to (a) 0 (b) any number other than 0 (c) 2(8295 + 1)

is equal to

40 ln3

20 ln3

none of these

The value of  

xdx  (where {x} is the fractional part of x) is

of these

If f(x) =

35,0 2,0

then

is equal to ([.] denotes the greatest integer function)

cosec  log sec

cosec  log |sec|

none of these

is equal

Single

EXERCISE-3

JEE Advanced Level Questions

, where [x] denotes the greatest integer not exceeding x is-

DEFINITE INTEGRATION_XII Page | 48

Answer

( ) 0 sin xfxdx   is equal to(a) ( ) 0 sin xfxdx   (b) ( ) /2 0 sin 2 fxdx    (c) ( ) /2 0 cos fxdx    (d) ( ) 0 cos fxdx  

 



(a) [a] f(a) – {f(1) + f(2) +…+ f([a])} (b) [a] f([a]) – {f(1) + f(2) +…+ f(a)} (c) a f([a]) – {f(1) + f(2) +…+ f(a)} (d) a f(a) – {f(1) + f(2) +…+ f([a])} 3. Let ( ) ( ) 1 , Fxfxf x  =+   where ( ) 1 ln 1 x t Fxdt t = +  . Then F(e) equals(a) 1/2 (b) 0 (c) 1 (d) 2 4. The solution for x of the equation 2 1 12 1 x dt tt  =  is(a) 2 (b) π (c) 3 2 (d) 22 5. ( ) 2 sec 2 2 2 4 lim 16 x x ftdt x   →  equals(a) ( ) 8 2 f  (b) ( ) 2 2 f  (c) 21 2 f     (d) 8f(2) 6. /4 /4 ln1sin2xdx   +  has the value equal to: (a) ln2 4  (b) ln2 2  (c) ln2 8  (d) ln2 16 

Correct

Type Questions 1.

2. The value of

( )

',1 a xfxdxa 

11. Let a, b, c be non-zero real numbers such that:

1cos1cosxaxbxcdxxaxbxcdx+++=+++

, then the quadratic equation

ax 2 + bx + c = 0 has-

(a) no root in (0, 2) (b) atleast one root in (0, 2)

is equal to-

where a and b are integer is equal to-

14. Value of

, (where [x] and {x} are integral and fractional parts of x and n ∈ N) is:

DEFINITE INTEGRATION_XII 49 | Page

/8 00 2tan sin2 a dx d xax     = ++ 

of ‘a’

to (a > 0) (a) 3 4 (b) 4  (c) 3 4  (d) 9 16 8. The value of the integral ( ) /2 /3 sin[] xxxdx     is (where [x] denotes step up function) (a) 1 26  + (b) 11 1 22 3     (c) 3 1 26  −+ (d) 3 1 26  9. The value of the definite integral 2 1 0 1 x edx +    is(a) –1 (b) 2 (c) 1 + e–1 (d) None of these 10. For n ∈N, the value of the definite integral 0 1cos2 2 nv x dx + +  where 2 V    is(a) 2n + 1 – cos V (b) 2n – sin V (c) 2n + 2 – sin V (d) 2n + 1 – sin V

7. If

, then value

is equal

( )( ) ( )( ) 12

8282



1 0

 

(a) 0 1  (b) 1  (c) 1  (d) 2 

  

(a) –π (b)

|sin2|xdx

13. ( )2 cossinaxbx

   0 0 n n xdx xdx  

(a) 2n (b)



22. If a, b and c are real numbers then the value of

DEFINITE INTEGRATION_XII Page | 50 15. For f(x) = x4 + |x|, let ( ) 1 0 cos Ifxdx  =  and ( ) /2 2 0 sin Ifxdx  =  then 1 2 I I has the value equal to(a) 1 (b) 1/2 (c) 2 (d) 4 16. ( ) /4 3/2 0 cos2.cosxxdx  =  (a) 3 16  (b) 3 32  (c) 3 162  (d) 32 16  17. The value of ( ) 1 1 1 0 1 n n k r xrdx xk = =  +   +     equals (a) n (b) n! (c) (n + 1)! (d) n.n! 18. If the value of the integral 2 2 1 x edx  is α, then the value of 4 ln e e xdx  is(a) e4 – e – α (b) 2e4 – e – α (c) 2(e4 – e) – α (d) 2e4 – 1 – α 19. 0 2 x edx     where [x] denotes the greatest interger function is(a) 0 (b) ln 2 (c) e2 (d) 2/e 20. Let ( ) sin x fx x = , then ( ) /2 0 2 fxfxdx    −=   (a) ( ) 0 2 fxdx    (b) ( ) 0 fxdx   (c) ( ) 0 fxdx   (d) ( ) 0 1 fxdx    21.

a non-zero

11 ,5 xafxbf xx  +=−   ,

a ≠ b, then ( ) 2 1 fxdx = 

(b) 22 17 log252 b aa ab  −+  

b aa ab  −+−

 (d) None of these

( ) 1 / 0 0 1 limln1sin cx t abxdx t →  +     equals(a) abc (b) ab/c (c) bc/a (d) ca/b

If for

( )

where

(a) 22 17 log252 b aa ab  ++  + 

be a differentiable curve satisfying

DEFINITE INTEGRATION_XII 51 | Page

y = f(x)

( ) ( ) 2 2 2 2 , 2 x x x ftdttftdt =+  then ( ) /4 93 2 /4 1 cos fxxxx dx x   +−++  equals(a) 0 (b) 1 (c) 2 (d) 4 24. If y = f(x) is a linear function

relation f(xy) = f(x). f(y) ∀ x, y ∈ R, then the curve ( ) 223 0 sin, x ytatbtdtR  + +++=  cuts y = f–1(x) at(a) no point (b) exactly one point (c) atleast two points (d) infinite points 25. If 2 2 2 0 2tan1tan 2sec t z zz xedz zz  +−  =     & 2 22 2 0 1tan2tan 2sec t z zz yedz zz   =     . Then the inclination of the tangent to the curve at 4 t  = is: (a) 4  (b) 3  (c) 2  (d) 3 4  26. If 1 0 1 t e Idt t = +  then 1 1 a t a e dt ta  is equal to: (a) e –a I (b) ea I (c) –e –a I (d) –ea I One or More Correct Answer Type Questions 27. If I = /2 3 0 1sin dx x  +  , then (a) 0 < I < 1 (b) I > 22  (c) I < 2  (d) I > 2  28. 0 x   f(sin x) dx is equal to (a) 0 (sin) 2 fx    dx (b) /2 0 (sin)fx    dx (c) /2 0 2(sin) fx    dx (d) none of these 29. If 2 2 (),0 (log) x x dt fxx t =  , then f(x) is (a) monotonically increasing in (2, ) (b) monotonically decreasing in (1, 2) (c) monotonically decreasing in (2, ) (d) monotonically decreasing in (0, 1)

23. Let

satisfying the

DEFINITE INTEGRATION_XII Page | 52 30. The value of /4 2222 0 cossin dx axbx  +  is (a) 1 1 tan;(0,0) b ab aba     (b) 1 1 tan;(0,0) b ab aba     (c) ;(1,1) 4 ab  == (d) 1 11 tan a abbab  +   31. If 0 (0) 1coscossin dxA B x    =+  the values of A and B are (a) ,0 2 AB  == (b) , 44sin AB  == (c) , 6sin AB  == (d) ,sinAB    == 32. ( ) ( ) 2 0 11 x xx  ++  dx equals to: (a) 4  (b) 2  (c) is same as ( ) ( ) 2 0 11 dx xx  ++  (d) cannot be evaluated 33. The value of integral || b a x x  dx, a < b is: (a) b – a if a > 0 (b) a – b if b < 0 (c) b + a if a < 0 < b (d) | b | – | a | 34. If  n = ( ) 2 1 0 1 n dx x +  ; n  N, then which

statements hold good? (a) 2n n + 1 = 2 n + (2n 1) In (b) 2 = 1 84  + (c) 2 = 1 84  (d) 3 = 5 1648  35. The value of integral 0 (sin)xfx   dx is: (a) 2  0 (sin)fx   dx (b)  /2 0 (sin) fxdx   (c) 0 (d) 2 /4 0 (sin) fxdx  

of the following

36. If  =

sin, xdx

then

37. Given f is an odd function defined everywhere, periodic with period 2 and integrable on every interval.

x  f(t) dt. Then:

Let g(x) = 0

(a) g(2n) = 0 for every integer n

38. Let f : R → R be defined as f(x) =

(a) f(x) is periodic

39. If a, b  R+ then

(a) 1(1) ln (1) bb abaa + −+ if

g(x) is an even function

g(x) is an odd function

f(f(x)) = f(x)  x  R

f(x) is unbounded

40. Let f(x) = 3 |sin| x x

  +  (x  [0, ])

(a) f(x) is strictly increasing in this interval (b) f(x) is differentiable in this interval

(d) f(x) has a maxima at x = 3 

41. If f(x) = 2{x}, where {x} denotes the fractional part of x. Then which of the following is true?

(a) f is periodic

42. Let f(x) = 0 |23|, x tdt  then f is

(a) continuous at x = 3/2

(b) continuous at x = 3

(d) differentiable at x = 0

DEFINITE INTEGRATION_XII 53 | Page

 

 =

2 0

  (b)  = 4 /2 2 0 sin xdx  



2 2 0 cos xdx   (d)  = 8 /4 2 0 sin xdx  

(a)

sin xdx

(c)

(b)

(d)

2 11 x e dt t +  + 2 1 1 x e dt t +  , then

(b)

(d)

1 ()() n n k n Lim kankbn → = ++  is equal to



(b)

(1)

1(1) ln

ab abba + −+ if a  b

0 1 2 2 x dx



2 0 2log x dxe

 (d) 100 {} 2 0 2100log x dxe = 

(b)

{}

n =

(c)

{}

DEFINITE INTEGRATION_XII Page | 54 43. Let  n = 0 (sin), n xdx   n  N, then (a)  n is rational if n is odd (b)  n is irrational if n is even (c)  n is an increasing sequence (d)  n is a decreasing sequence 44. Let  n = 2 2 0 sin() sin nx dx x   , n  N, then (a) n+2 +  n = 2n+1 (b)  n = n+1 (c)  n = n (d) 1, 2, 3,  n are in Harmonic progression 45. Let A = 2 1 e nx dx x  , then (a) A > 2 1 – e e    (b) A < (e – 1) 1 2 e  +   (c) A > (e – 1) 1 2 e  +   (d) A < ( ) 2 –1 e 2 e 46. 1 = 2 0 sin 1cos xx dx x  +  , 2 = 3 222 0 sin , (33)(1cos) xx dx xxx  −++  then (a) 1 = 2 8  (b) 1 = 2 4  (c) 1 = 2 (d) 1 > 2 47. Let L1 = 2 0 0 sin lim, sin x x tdt xx + →  L2 = 2 0 0 sin lim, sin x x tdt xx →  then identify the correct option(s). (a) L1 = 4 (b) L1 + L2 = 8 (c) L1 + L2 = 0 (d) |L2| = |L1| 48. 222333 (123.....) lim (12.....)(12........) kkkk n n nn → ++++ ++++++ = F(k), then (k  N) (a) F(k) is finite for k  6 (b) F(5) = 0 (c) F(6) = 12 7 (d) F(6) = 5 7

1. Match the following:

EXERCISE-4

Matrix Match Type Questions

(a) (A)-(S); (B)-(P); (C)-(Q); (D)-(R) (b) (A)-(R); (B)-(Q); (C)-(P); (D)-(S)

2. Match the following:

(a) (A)-(S); (B)-(P); (C)-(Q); (D)-(R) (b) (A)-(R); (B)-(P); (C)-(Q); (D)-(S)

DEFINITE INTEGRATION_XII 55 | Page

List-I List-II

( ) ( ) ( ) /2 cossin 0 sincoscotlogxx xxxsinxdx   (P) 4 3 (B) ( ) ( ) 10 22 01 11ydyydy−+− (Q) 32 9 (C) f (x) = 2 1 x ( ) 2 4 42'() x tft  dt then ' f (4) is equal to (R) 1 (D) 0 (|sin4||cos4|)xxdx  +  is equal to (S) 4

(A)

List-I List-II (A) If 11/2/2 4444 00 (sincos)(sincos) xxdxkxx  +=+ dx, then k is (P) 1 4 (B) The value of k, if /3 0 cos 34sin x x  +  dx = k . log 323 3  +    , is (Q) 1 (C) If I1 = 5 0 (|cos|) fxdx   and I2 = 5 0 (|cos|) fxdx   then 1 2 I I is (R) 11 (D) If ( ) /2 0 logsin xdx   = k log2 2  .then k is (S) –1

3. Match the column

(a) (A)-(Q); (B)-(S); (C)-(P); (D)-(P)

4. Match the column

(b) (A)-(R); (B)-(P); (C)-(Q); (D)-(S)

(d) (A)-(R); (B)-(Q); (C)-(S); (D)-(P)

(a) (A)-(S); (B)-(P); (C)-(Q); (D)-(R) (b) (A)-(R); (B)-(R); (C)-(Q); (D)-(Q)

Integer Type Questions

where , n  N and gcd(, n) = 1, then find the value of  – 3n.

6. Let U =

min

(3sin,cos) xx dx and V = 5 2 3

x  sgn (x – 1)dx. If V = U, then find the value of .

[Note : sgn k denotes the signum function of k.]

DEFINITE INTEGRATION_XII Page | 56

Column-I Column-II (A) ( ) ( ) 10 22 01 11ydyydy−+− (P) 1 100 (B) 2 1 || x dx x =  (Q) 4 3 (C) 999999 100 12.... lim n n n → +++ = (R) 1 3

1 200 1 1 5050, xdx  =  then α = (S) 1

(D)

Column-I Column-II (A) 1 2 tan 1 3 14 x x dx = +  (P) 7 (B) ( ) 8 2 2 2 6 sin sinsin14 xdx xx = +−  (Q) 1 2 (C)   13 1 1 156 xdx =  {where [.] denotes greatest integer function} (R) 1 (D) 0 /2 1 lnsin2 ln2 xdx  

 (S)



2 23

31 (1) x dx x +



2 6

  

7. Let f(x) be a function satisfying

12. If f, g, h be continuous functions on [0, a] such that

x) = 5, then find the value

13. Let a be a real number in the interval [0, 314] such that

number of such values of a is k2, find k.

14. If f(x) = (ax + b) ex satisfies the equation :

15. ( )2 log2 log2 ln2

x x

16. The value of ( ) 22 1sincosxxxdx

is-

17. Number of values of x satisfying the equation

18. The value of

is-

57 | Page

DEFINITE INTEGRATION_XII

100 ()0. fxfx x  =   If 10 1 () 5 fx dx x =  then find the value of 100 1 () 2 fx dx x  8.

/2 0 sin2.sin d    = n 

n 9.

I1 = /4 2 0 (1tan)xdx  +  , 2 = 1 22 0 (1)(1) dx xx++  then find the value of     10.

2 1 2 0 n(21) tt ettdt +  ++     2 1 2 0 n(21) tt ettdt +  ++     11.

0 1 1 x x dx xe ++ 

equal to –nk

then find

Let

Find the value of

, then find the value of

f (a x) = f (x), g (a x) = g (x) and 3 h (x) 4

of 0 a  f (x) g (x) h (x) dx

h (a

3 ||sin 2 a a x xadx    + −+     = –16, then if

the

2 0 ()'()(1) x xyx fxefydyxxe =−−+  ,

(a2 +

find

 −=   

  

( ) 2 1 3 1 28 2 84, 3 log1 x x ttdt x   +  +    ++= +   is-

( )( ) 3 3

dxrr → +− 

lim

x x dr dr

Linked Comprehension Type Questions

According to Leibritz differentiation under the sign of integration can be performed as below:

DEFINITE INTEGRATION_XII Page | 58

If f(8 – t) = f(t) and ( ) 4 0 8, fd =  then ( ) 8 0 fd  is20. Let ( ) 4 2 1 x dt fx t = +  and g be the inverse of f. Then the value of g’(0) is21. The value of ( ) 4 2 1 lim 34 rn n r n rrn = → = +  is equal to: 22. The value of the integral 2 1 log e e e x dx x  is: 23. If ( ) cos .sin||2 2 x exforx fx Otherwise    =    Then ( ) 3 2 fxdx  (a) J (b) J (c) J (d) J 24. Let f : (0, ∞) → R and ( ) ( ) 0 x Fxftdt =  If ( ) ( ) 22 1,Fxxx =+ then f(4) equals.

19.

- 1

Comprehension

(i)     ( )     () () ()()()() x x dddftdtfxxfxx dxdxdx      =−    (ii) ( ) ( ) ( ) ( ) ()() ()() (,)(,),()(),()() xx xx ddd fxtdtfxtdtfxxxfxxx dxxdxdx       =+−    25. 3 2 2 cos x x tdt  has the derivative (a) 3x2cosx3 2xcosx2 (b) 3x2cosx6 2xcosx4 (c) cosx6 cosx4 (d) none of these 26. The points of maximum of the function 2 2 0 54 () 2 x t tt fxdt e −+ = +  (a) 2, 0, 2 (b) 1, 1 (c) 2, 2 (d) 0, 1 27. If (x) = cosx 0 ()() x xttdt   , then (x) (x) is equal to (a) sinx (b) cosx (c) sinx (d) cosx

Comprehension – 2

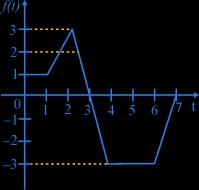
Let ( ) 0 () x gxftdt =  , where f is a function whose graph is show adjacently,

28. Maximum value of g(x) in x ∈[0,7]is-

(a) 3 (b) 9/2 (c) 3/2 (d) 6

29. Value of x at which g(x) becomes zero, is-

(a) 3 (b) 4 (c) 5 (d) 6

30. Set of values of x in [0, 7] for which g(x) is negative is-

(a) (2, 7) (b) (3, 7) (c) (4, 6) (d) (5, 7)

Comprehension – 3

Consider two curves 2 1 y x = and ( ) 1 41 y x = . ‘a’ is a number such that a > 2 & the reciprocal of the area of the figure bounded by the curves, the line x = 2 & x = a is a itself. ‘b’ is a number such that 1 < b < 2 & the area bounded by the two curves & the lines x = b & x = 2 is equal to 1 1 b .

31. The value of ln a – ln b is:

(a) positive integer

(b) negative integer

(d) irrational number

32. If ( ) ( ) ln10 0ln1 a A b − =   , then A–1 is :

(a) –A/4 (b) A (c) 4A (d) A/4

33. If z is a complex number such that z = ln(a – 1) + iln (b – 1) then arg(z) is :

(a) 4  (b) 3 4  (c) 4  (d) 3 4 

DEFINITE INTEGRATION_XII 59 | Page

DEFINITE INTEGRATION_XII Page | 60 Comprehension-4 ( ) ( ) ( ) ( ) ( ) 1 2 max.min. ,004 2 5445 6 tansin5 1237 ftft txx Considergxxxx x x xx  +     =−+−            −+     where f(x) = x2 – 4x + 3. 34. ( ) 5 2 gxdx  is equal to (a) 5/3 (b) 3 (c) 13/3 (d) 3/2 35. If ( ) ( ) 2 0 x hxgtdt =  , then complete set of values of x in the interval [0, 7] for which h(x) is decreasing, is(a) (6, 7] (b) (5, 7] (c) ( 6,7  (d) ( 6,7  36. ( ) ( ) ( ) ( ) 4 2 lim lncos4 x gxg x → is equal to(a) 0 (b) 1 (c) 2 (d) does not exist

EXERCISE-5A

Single Correct Answer Type Questions

DEFINITE INTEGRATION_XII 61 | Page

1. If 1 50100 1 0 (1) Ixdx =−  and 1 50101 2 0 (1) Ixdx =−  such that 21II  = then  equal to: [Main – 2020] (a) 5049 5050 (b) 5050 5049 (c) 5050 5051 (d) 5051 5050 2. The value of /2 sin /2 1 1 x dx e   +  is: [Main – 2020] (a) 4  (b)  (c) 2  (d) 3 2  3. Let f(x) = | x – 2) and g(x) = f(f(x)), x [0, 4]. [Main – 2020] then 3 0 (()()) gxfxdx  is equal to: (a) 1 (b) 0 (c) 1 2 (d) 3 2 4. The integral /3 3222 /6 tansin3(2secsin33tansin6) xxxxxxdx   +  is equal to: [Main – 2020] (a) 7 18 (b) 1 9 (c) 1 18 (d) 9 2 5. ||||xdx     is equal: [Main – 2020] (a) 2 2 (b) 22 (c) 2 (d) 2 2  6. If the value of the integral 1/2 2 23/2 0 (1) x dx x  is 6 k , then k is equal to [Main – 2020] (a) 23  (b) 23 + (c) 32  + (d) 32  7. If for all real triplets (a, b, c), f (x) = a + bx + cx2, then 1 0 () fxdx  is equal to: [Main – 2020] (a) 1 23(1)2 2 ff   +     (b) 11 (1)3 22 ff   +     (c) 11 (0) 32 ff   +     (d) 11 (0)(1)4 62 fff   ++    

8. The value of

sin sincos xx dx xx

is equal to:

10. If f(a + b + 1 – x) = f(x), for all x, where a and b are fixed positive real numbers, then

is equal to :

Let f : R → R be a continuously differentiable function such that f(2) = 6 and

then

is equal to:

then ( )

is equal to:

where [t] denotes the greatest integer function, is:

where g is a non-zero even function. If f(x + 5) = g(x), then

DEFINITE INTEGRATION_XII Page | 62

2 8





[Main – 2020] (a) 2 (b) 22 (c) 2 (d) 4

dx I



[Main – 2020] (a) 2 11 84 I  (b) 2 11 98 I  (c) 2 11 169 I  (d) 2 11 62 I 

1 (()(1)) b a xfxfxdx ab

+ 

[Main – 2020] (a) 1 1 () b a fxdx + +  (b) 1 1 () b a fxdx  (c) 1 1 (1) b a fxdx +  (d) 1 1 (1) b a fxdx + + + 

'(2)148 f  = If () 3 6 4(2)(), fx tdtxgx =− 

→

[Main – 2019] (a) 18 (b) 24 (c) 12 (d) 36 12.

( ) ( ) ( ) 3 6 42, fx tdtxgx =− 

→

[Main – 2019] (a) 18 (b) 24 (c) 12 (d) 36 13.

(

2 0 sin21cos3,

 +  

[Main – 2019] (a) p (b) –p (c) –2p (d) 2p 14. The value of /2 3 0 sin sincos x dx xx  +  is: [Main – 2019] (a) 2 8  (b) 1 4  (c) 2 4  (d) 1 2  15.

( ) ( ) 0

x fxgtdt



) 0 x ftdt 

[Main – 2019] (a) ( ) 5 5 x gtdt +  (b) ( ) 5 5 x gtdt +  (c) ( ) 5 5 2 x gtdt +  (d) ( ) 5 5 5 x gtdt + 

9. If

32 1 , 29124

xxx = −++

then:

11.

lim()

lim

The value of

)

xxdx

Let

(

is equals:

DEFINITE INTEGRATION_XII

16. Let f and g be continuous functions on [0, a] such that f(x) = f(a

x) and g(x) + g(a

x) =4, then

then y(x) equals: (where C is a constant)

0, if y(x) is a differentiable function such that (

63 | Page

–

( ) ( ) 0 a fxgxdx  is

to: [Main – 2019] (a) ( ) 0 4 a fxdx  (b) ( ) 0 a fxdx  (c) ( ) 0 2 a fxdx  (d) ( ) 0 3 a fxdx  17. The integral 2 1 log xx e e xe xdx ex          is equal to: [Main – 2019] (a) 11 22 e (b) 2 111 2 2 e e −+− (c) 2 311 2 2 e e (d) 2 31 2 2 e e 18. The value of the integral 2 2 2 sin 1 | 2 x dx x      (where [x] denotes the greatest integer less than or equal to x) is: [Main – 2019] (a) 0 (b) sin 4 (c) 4 (d) 4 –sin 4 19. If ( ) ( ) 1 22 0 , x x ftdtxttdt =+  then f’(1/2) is: [Main – 2019] (a) 2 (b) 22 (c) 2 (d) 4 20. The value of 3 0 cos xdx   is: [Main – 2019] (a) 0 (b) 4/3 (c) 2/3 (d) –4/3 21. If 2 11 22 12 00 cos;cos xx IexdxIexdx ==  and 3 1 3 0 ; x Iedx =  then [Main Online – 2018] (a) I2 > I3 > 11 (b) I3 > I1 > 12 (c) I2 > I1 > 13 (d) I3 > I2 > 11 22. The integral 3 4 4 1cos dx x   +  is equal to: [Main – 2017] (a) –1 (b) –2 (c) 2 (d) 4 23.

[Main – 2017] (a) 1 ,0 5    (b) 1 ,1 5    (c) 1 ,0 5    (d) 1 ,1 5    24.

≠

( ) 11



[Main Online – 2016] (a) 1 3 x cxe (b) 1 3 x Cxe (c) 1 x C e x (d) 1 3 x C e x

equal

Let ( ) 55 46 tan,1.tan, n n IxdxnIIaxbxC =+=++  where C is constant of integration, then the ordered pair (a, b) is equal to:

For x ∈R, x

) ( )

xytdtxtytdt =+

be a fixed real number suppose f is a continuous function such that for all

DEFINITE INTEGRATION_XII Page | 64 25. The integral 2 0 14sin4sin 22 xx dx  +−  equals: [Main – 2014] (a) 434 (b) 434 3  (c) 4  (d) 2 443 3  26. For 0, 2 x   the value of ( ) ( ) 22 sincos 11 00 sincos xx tdttdt +  equals: [Main Online – 2013] (a) /4 (b) 0 (c) 1 (d) –/4 27. Let f be a non-negative

[0, 1]. If ( ) ( ) ( ) 2 00 1',01, xx ftdtftdtx −= and f(0) = 0, then [Main – 2009] (a) 1111 2233fandf    (b) 1111 2233fandf    (c) 1111 2233fandf    (d) 1111 2233fandf    28. ( ) ( )   0 32 2 3331cos1 xxxxxdx ++++++  is equal to [2005S] (a) –4 (b) 0 (c) 4 (d) 6 29. The value of the integral 1 0 1 1 x dx x +  is [2004S] (a) 1 2  + (b) 1 2  (c) –1 (d) 1 30. If f(x) is differentiable and ( ) 2 5 0 2 , 5 t xfxdxt =  then 4 25 f    equals [2004S] (a) 2/5 (b) –5/2 (c) 1 (d) 5/2 31. If ( ) 2 2 2 1 , x t x fxedt + =  then f(x) increases in [2003S] (a) (–2, 2) (b) no value of x (c) (0, ∞) (d) (–∞, 0) 32. The integral   1/2 1/2 1 ln 1 x xdx x  +  +      equal to [2002S] (a) 1 2 (b) 0 (c) 1 (d) 1 2ln 2    33. Let T > 0

∈R, f(x + T) = f(x). If ( ) 0 T Ifxdx = 

valueof ( ) 33 3 2 T fxdx +  is [2002S] (a) 3/2I (b) 2I (c) 3I (d) 6I

function defined on the interval

thenthe

DEFINITE

65 | Page 34. Let ( ) 2 1 2 x fxtdt =−  .Then the real roots of the equation x 2 – f’(x) = 0 are [2002S] (a) ±1 (b) 1 2  (c) 1 2  (d) 0 and 1 35. The value of 2 cos ,0, 1 x x dxa a    +  is [2001S] (a)  (b) a (c) /2 (d) 2 36. The value of the integral 2 1 log e e e x dx x  is: [2001S] (a) 3/2 (b) 5/2 (c) 3 (d) 5 37. If ( ) cos sin,||2 2, x exforx fx otherwise    =    then ( ) 3 2 fxdx =  [2000S] (a) 0 (b) 1 (c) 2 (d) 3 38. Let ( ) ( ) 0 , x gxftdt =  where f is such that ( ) 1 1, 2 ft  for t ∈[0, 1] and ( ) 1 0, 2 ft  for t ∈[1, 2] Then g(2) satisfies the inequality [2000S] (a) 2 (b) 22 (c) 2 (d) 4 39. Let a function f: [0, 5] → R be continuous, f (1) = 3 and F be defined as: [Main – 2020] 2 1 ()(), x Fxtgtdt =  where 1 ()() x gtfudu = 

INTEGRATION_XII

(a)

(b)

of local maxima (d)

inflection. 40. 1/31/31/3 4/34/34/3 lim...(1)(2)(2) n nnn nnn →  ++ +++   is equal to: [Main – 2019] (a) 4/3 33 (2) 24 (b) 4/3 4(2)3 (c) 4/3 34 (2) 23 (d) 3/4 4(2)3 41. 212222 lim...1 1235 n nnn n nnn →  ++++  +++  is equal to: [Main – 2019] (a) 4  (b) tan–1 (3) (c) 2  (d) tan–1 (2) 42. If 1 12........1 lim 60 (1)[(2)....()] aaa a n n nnanan → +++ = ++++ [Main Online – 2017] for some positive real number a, then a is equal to (a) 7 (b) 8 (c) 15/2 (d) 17/2

Then for the function

the point x = 1 is:

a point of local minima

not a critical point

point

a point of

If (,)(1), mn lmnttdt =+

then the expression for l(m, n) in terms of l(m + 1,

Integer Type Questions

denote the fractional part of x and the greatest integer ≤ x is respectively of a real number

Let [t] denote the greatest integer less than or equal to t. Then the value of

DEFINITE INTEGRATION_XII Page | 66 43. 1 2 (1)(2)...3 lim n n n nnn n → ++    is equal to : [Main– 2016] (a) 2 9 e (b) 3 log 3 – 2 (c) 4 18 e (d) 2 27 e 44. The value of 34 0 0 1ln(1) lim 4 x n tt dt xt → + +  is [Main– 2010] (a) 0 (b) 1/12 (c) 1/24 (d) 1/64 45.

– 1)

[Main– 2003] (a) 2 (1,1) 11 n n lmn mm −+− ++ (b) 1(1,1) n lmn m +− + (c) 2 (1,1) 11 n n lmn mm ++− ++ (d) 1(1,1)m lmn n +− +



46.

[x]

x. If     00 , nn xdxxdx and ( ) ( ) 2 10,,1 nnnNn− arethreeconsecutive

a G.P.,then n is equal to _______. [Main – 2020] 47. The integral 2 0 |1||xxdx  is equal to ___________. [Main – 2020] 48.

  2 0 23xxdx  is ________. [Main – 2020] 49. The value of the integral ( ) /2 5 0 3cos cossin d     +  equals ________ [Main – 2019]

Let {x} and

terms of

Single Correct Answer Type Questions

DEFINITE INTEGRATION_XII 67 | Page

EXERCISE-5B

1. The value of 2 2 2 cos 1 x xx dx e   +  is equal to [Adv. – 2016] (a) 2 2 4  (b) 2 2 4  + (c) 2 2e   (d) 2 2e   + 2. The following integral ( ) 2 17 4 2cosec xdx    is equal to [Adv. – 2014] (a) ( ) ( )log12 16 0 2 uu eedu + +  (b) ( ) ( )log12 17 0 uu eedu + +  (c) ( ) ( )log12 17 0 uu eedu +  (d) ( ) ( )log12 16 0 2 uu eedu +  3. Lef 1 :,1 2 fR  →   (the set of all real number) be a positive, nonconstant and differentiable function such that ( ) ( ) '2 fxfx  and 1 1. 2 f  =   Then the value of ( ) 1 1/2 fxdx  lies in the interval [Adv. – 2013] (a) (2e – 1, 2e) (b) (e – 1, 2e – 1) (c) 1 ,1 2 e e    (d) 1 0, 2 e    4. The value of the integral /2 2 /2 lncos x xxdx x     +  +    is [2012] (a) 0 (b) 2 4 2  (c) 2 4 2  + (d) 2 2  5. The value of ( ) ln3 2 22 ln2 sin sinsinln6 xx dx xx +−  is [2011] (a) 13 ln 42 (b) 13 ln 22 (c) 3 ln 2 (d) 13 ln 62

6. Let f be a real-valued function defined on the interval (–1, 1) such that

One or More Correct Answer Type Questions

1) be a continuous function. Then, which of the following function(s) has (have) the value zero at some point in the interval (0, 1)?

→

DEFINITE INTEGRATION_XII Page | 68

( ) 4 0 21, x x efxtdt =++  for all x ∈(–

1),

f–1

inverse

of f. The (f–1) (2) is equal to [2010] (a) 1 (b) 1/3 (c) 1/2 (d) 1/e 7. The integral ( ) 4 2 22 2 log loglog3612 x dx xxx +−+  is equal to: [2015] (a) 1 (b) 6 (c) 2 (d) 4 8. Let 3 4 ()192 2sin x fx x  = + forall x  with 1 0 2 f  =   . If 1 1/2 () mfxdxM   , thenthe possiblevalues of m and M are [Adv. – 2015] (a) m = 13, M = 24 (b) 11 , 42 mM== (c) m = – 11, M = 0 (d) m = 1, M = 12 9. The value(s) of 1 44 2 0 (1) 1 xx dx x +  is (are) [2010] (a) 22 7  (b) 2 105 (c) 0 (d) 713 152 

and let

be the

function

10. Which of the following inequalities is/are True? [Adv. – 2020] (a) 1 0 3 cos 8 xxdx   (b) 1 0 3 sin 10 xxdx   (c) 1 2 0 1 cos 2 xxdx   (d) 1 2 0 2 sin 9 xxdx   11. If 1 98 1 1 (1) k k k k Idx xx + = + = +   , then [Adv. – 2017] (a) 1 > loge 99 (b) 1 < loge 99 (c) 49 1 50  (d) 49 1 50  12. If sin(2) 1 sin ()sin() x x fxtdt =  , then [Adv. – 2017] (a) 2 2 g    =−   (b) 2 2 g   −=  (c) 2 2 g    =   (d) 2 2 g   −=−  13.

[Adv. – 2017] (a) x9 – f(x) (b) 2 0 ()cos x xfttdt   (c) 0 ()sin x x efttdt =  (d) 2 0 ()()sin fxfttdt  + 

Let f :

(0,

17. The option(s) with the value of a and L that satisfy the following equation is(are)

18. Let f be a real-valued function defined on the interval (0, ∞) by

. Then which of the following statement(s) is (are) true? [2010]

(a) f  (x) exists for all x  (0, ∞)

fxxtdt =++

(b) f  (x) exists for all x  (0, ∞) and f is continuous on (0, ∞), but not differentiable on (0, ∞).

(d) there exists  > 0 such that |f(x) |+| f(x) |   for all x  (, ∞)

DEFINITE INTEGRATION_XII 69 | Page 14. For, a  Z [Adv. – 2019] 3 3 7/3 222 12.... lim54 111 (1)(2)() x n n ananann →   +++  =   +++   +++    Then the possible value(s) of a is/are (a) – 9 (b) 7 (c) – 6 (d) 8 15. Let 22 2222 2 ().... 2 ()lim !()... 4 x n n n nn nxnxx n fx nn nxnxx n →    +++   =    +++    , for all x > 0. Then [Adv. – 2016] (a) 1(1) 2 ff     (b) 12 33ff    (c) (2)0 f   (d) (3)(2) (3)(2) ff ff   16. Let f(x) = 7 tan8 x + 7 tan6 x – 3 tan4 x – 3 tan2 x for all , 22 x   −  . Then the correct expression9s) is (are) [Adv. – 2015] (a) /4 0 1 () 12 xfxdx  =  (b) /4 0 ()0fxdx  =  (c) /4 0 1 () 6 xfxdx  =  (d) /4 0 ()1fxdx  = 

[Adv. –

4 64 0 64 0 (sinatcosat) ? (sinatcosat) t t edt L edt   + = +   (a) 4 1 2, 1 e aL e   == (b) 4 1 2, 1 e aL e   + == + (c) 4 1 4, 1 e aL e   == (d) 4 1 4, 1 e aL e   + == +

0 ()ln1sin x



2015]

then

Let f(x) be a non-constant twice differentiable function defined on (–∞, ∞) such that f(x)

Linked Comprehension Type Questions

exists. Let this limit be g(a). In addition, it is given that the function g(a) is differentiable on (0, 1).

Given that for each a  (0, 1),

21. The value of

Passage for Questions 23 to 24 : F → be a thrice differentiable function. Suppose that F(1) = 0, F(3) = – 4 and F(x) < 0 for all

23. The correct statement(s) is (are)

DEFINITE INTEGRATION_XII Page | 70 19. If sin 0,1,2,...., (1)sin n x nx Idxn x    == + 

[2009] (a) 2 nn II + = (b) 10 21 1 10 m m I  + = =  (c) 10 2 1 0 m m I = =  (d) 1 nn II + = 20.

= f(1 – x) and 1 0 4 f  =   . Then, [2008] (a) ()fx  vanishes

[0, 1] (b) 1 0 2 f  =   (c) 1/2 1/2 1 sin0 2 fxxdx  +=   (d) 1/21 sinsin 01/2 ()(1)tt ftedtftedt  =−

at least twice on

Passage for Questions 21 to

1 1 0 lim(1) h aa h h ttdt + → 

[Adv. – 2014]

1 2 g   

(a) π (b) 2 π (c) π/2 (d) π/4

The value of 1 2 g    ’is (a) π.2 (b) π (c) – π/2 (d) 0

22.

1 ,3.2 x    Let f(x)

x  [Adv. – 2015]

= xF(x) for all

(a) f(1) <

(b) f(2) < 0 (c) f(x) ≠ 0

x  (1, 3) (d) f(x) = 0 for some x  (1, 3)

3 2 1 '()12xFxdx  =−  and 3 3 1 ()40xFxdx  = 

expression(s)

(are) (a) 9f(3) + f(1) – 32 = 0 (b) 3 1 ()12fxdx =  (c) 9f(3) – f(1) + 32 = 0 (d) 3 1 ()12fxdx =− 

for any

24. If

then the correct

DEFINITE INTEGRATION_XII

Passage for Questions 25 to 27

Consider the polynomial f(x) = 1 + 2x + 3x2 + 4x3 .

Let s be the sum of all distinct real roots of f9x) and let t = |s|.

25. The real numbers lies in the interval

26. The area bounded by the curve y = f(x) and the lines x = 0, y = 0 and x = t, lies in the interval

27. The function f

(x) is

(b) decreasing in 1 , 4 t

(d) decreasing in (– t, t)

Passage for Questions 28 to 30

and decreasing in 1 ,4

and increasing in 1 ,4

28. Which of the following is true?

29. Which of the following is true?

(a) f(x) is decreasing on (–1, 1) and has a local minimum at x = 1

(b) f(x) is increasing on (–1, 1) and has a local minimum at x = 1

(d) f(x) is decreasing on (–1, 1) but has neither a local maximum nor a local minimum at x = 1 30. Let

. Which of the following is true?

(a) g(x) is positive on (–∞, 0) and negative on (0, ∞)

(b) g(x) is negative on (–∞, 0) and positive on (0, ∞)

(d) g(x) is does not change sign on (–∞, ∞)

71 | Page

[2010]

(a) 1 ,04    (b) 3 11,4    (c) 31 , 42    (d) 1 0,4   

(a) 3 4,3    (b) 2111 , 6416    (c) (9, 10) (d) 21 0,64   



t   

  

(a) increasing in 1 ,4

  

t   

the function f : (–∞, ∞) → (–∞, ∞)

2 2 1 (),02 1 xax fxa xax −+ = ++ [2008]

Consider

defined by

(a) (2 + a)2 f (1) + (2 – a)2 f (–1) = 0 (b) (2 – a)2 f (1) – (2 + a)2 f (–1) = 0 (c) f(1) f(–1) = (2 – a)2 (d) f(1) f(–1) = –(2 + a)2

2 0 () () 1 x e ft gxdt t  = + 

Passage for Questions 31 to 33

ba fxdxfafb =+

Let the definite integral be defined by the formula ()(()()) 2

b), we can use

Matrix Match Type Questions

. For more accurate result

(B) The number of points in the interval [13,13] at which f9x)

sin(x2) + cos (x2) attains its maximum value, is

equals

(a) (A)-(R); (B)-(Q); (C)-(S); (D)-(P) (b) (A)-(Q); (B)-(R); (C)-(S); (D)-(P)

DEFINITE INTEGRATION_XII Page | 72

b a

for c 

()()()() bcb aac fxdxfxdxfxdxFc =+= so that

2 ab c + = , we get ()(()()2()) 4 b a ba fxdxfafbfc =++  [2006] 31. /2 0 sin xdx  =  (a) (12) 8  + (b) (12) 4  + (c) 82  (d) 42  32. If 3 ()(()()) 2 lim0 () x a xa xa fxdxfxfa xa →  −+   =  , then f(x) is of maximum degree (a) 4 (b) 3 (c) 2 (d) 1 33. If ()0(,) fxxab   and c

< c < b, and (c

f©)

(a) ()() fbfa ba (b) 2(()()) fbfa ba (c) 2()() 2 fbfa ba (d) 0



(a,

for

is a point such that a

is the point lying on the curve for which F(c) is maximum, then f

34. List-I List-II (A) The number of

non-negative integer

(P) 8

polynomials f(x) with

coefficients

(Q) 2 (C) 2



(R)

3 (1) x x dx e +

1/2 1/2 0

cos2log



       +         (S)

(D) 1/2

1 cos2log 1 1

1 x xdx x x xdx x

35. For each positive integer n, let

Integer Type Questions

For

, let [x] be the greatest integer less than or equal to x. If

73 | Page

DEFINITE INTEGRATION_XII

[Adv. – 2018] 1 1 (1)(2)...() n n ynnnn n =+++



n yL →

________.

: f

and (1)1 2 f = .

1 ()() x Fxftdt =  for

x  [–1, 2] and 1 ()|(())| x Gxtfftdt =  for x  [–1, 2]. If 1 lim()1 ()14 x Fx Gx → = , then the value of 1 2 f    is [Adv. – 2015] 37. Let f : R → R

f’ is continuous and f(π) = –6 If F : [0, π] → R is defined by ( ) ( ) 0 , x fxftdt =  and if ( ) ( ) ( ) 0 'cos2, fxFxxdx  +=  then the value of f(0) is _____ [Adv. 2020] 38. If ( )( ) /4 sin /4 2 , 12cos2 x dx I ex    = +−  then 27 I2 equals _______, [Adv. 2019] 39. The value of the integral ( ) ( ) ( ) 1 2 1 26 0 2 13 11 dx xx + +−  is _______. [Adv. 2018] 40. Let f : R → R be a differentiable function such that ( ) 00,3 2 ff   ==   and f’(0) = 1. If ( ) ( ) ( ) /2 'coseccotcosec x gxfttttftdt  =−   for 0,, 2 x     then ( ) 0 lim x gx → = [Adv. 2018] 41. The total number of distinct x ∈[0, 1] for which 2 4 0 21 1 x t dtx t =− +  is [Adv. 2016] 42. If ( ) 1 1 2 93tan 2 0 129 1 xx x edx x  +  + =  +   where tan–1 x takes only principal values, then the value of log|1|34 e    +−   is [Adv. 2015] 43. Let f : R → R be a function defined by ( )  , 02 xx fx x   =    where [x] is the greatest integer less than or equal to x, if ( ) ( ) 2 2 1 21 xfx Idx fx = ++  , then the value of (4I – 1) is [Adv. 2015] 44. The value of ( ) 1 2 5 32 2 0 41 d xxdx dx       is [Adv. 2014]

lim, n

= then the value of [L] is

36. Let

→ be a continuous odd function, which vanishes exactly at one pont

Suppose that

all

be a differentiable function such that its derivative

45. For any real number x, let [x] denote the largest integer less than or equal to x. Let f be a real valued function defined on the interval [

10, 10] by

46. Let f : R → R be a continuous function which satisfies

. Then the value of f

DEFINITE INTEGRATION_XII Page | 74

( )         , 1 xxifxisodd fx xxifxiseven   =  +−   . Then the value of ( ) 10 2 10 cos 10 fxxdx    is [Adv. 2010]

–

( ) ( ) 0 x fxftdt = 

(ln

[Adv. 2009]

JEE Main Level Questions

JEE Advanced Correct Answer Type Questions

DEFINITE INTEGRATION_XII 75 | Page

Exercise-1 1. (a) 2. (d) 3. (c) 4. (b) 5. (d) 6. (a) 7. (c) 8. (c) 9. (d) 10. (c) 11. (a) 12. (a) 13. (a) 14. (a) 15. (c) 16. (a) 17. (b) 18. (b) 19. (d) 20. (b) 21. (c) 22. (b) 23. (a) 24. (a) 25. (b) 26. (b) 27. (c) 28. (a) 29. (b) 30. (b) 31. (d) 32. (a) 33. (c) 34. (a) 35. (d) 36. (c) 37. (d) 38. (a) 39. (a) 40. (c) 41. (c) 42. (c) 43. (b) 44. (b) 45. (b) 46. (d) 47. (c) 48. (b) 49. (c)

ANSWER KEY

Exercise-2

1. (b) 2. (b) 3. (a) 4. (b) 5. (b) 6. (a) 7. (c) 8. (c) 9. (b) 10. (c) 11. (a) 12. (c) 13. (a) 14. (a) 15. (b) 16. (a) 17. (b) 18. (d) 19. (b) 20. (a) 21. (c) 22. (c) 23. (d) 24. (a) 25. (d) 26. (a) 27. (d) 28. (d) 29. (b) 30. (b) 31. (a) 32. (b) 33. (c) 34. (a) 35. (b) 36. (d) 37. (a) 38. (c) 39. (b) 40. (c) Exercise-3

Single Correct Answer Type Questions 1. (c) 2. (a) 3. (a) 4. (a) 5. (a) 6. (a) 7. (d) 8. (c) 9. (d) 10. (c) 11. (b) 12. (d) 13. (d) 14. (d) 15. (c) 16. (c) 17. (d) 18. (b) 19. (b) 20. (a) 21. (b) 22. (a) 23. (c) 24. (c) 25. (d) 26. (c)

DEFINITE INTEGRATION_XII Page | 76

27. (b, c) 28. (a, b) 29. (a, b) 30. (a, b, c) 31. (a, b) 32. (a, c) 33. (a, b, c, d) 34. (a, b) 35. (a, b) 36. (a, b, c) 37. (a, b, c) 38. (a ,b) 39. (b, d) 40. (b, c, d) 41. (a, b, c, d) 42. (a, b, c, d) 43. (a, b, d) 44. (a, c) 45. (b, c) 46. (b, c) 47. (a, c, d) 48. (a, b, c) Exercise-4 Matrix Match Type Questions 1. (c) 2. (b) 3. (a) 4. (b) Integer Type Questions 5. (1) 6. (8) 7. (5) 8. (4) 9. (4) 10. (2) 11. (2) 12. (0) 13. (5) 14. (5) 15. (0) 16. (0) 17. (1) 18. (1/2) 19. (16) 20. ( 17 ) 21. (1/18) 22. (5/2) 23. (2) 24. (4) Linked Comprehension Type Questions 25. (b) 26. (b) 27. (d) 28. (b) 29. (d) 30. (c) 31. (b) 32. (c) 33. (b) 34. (b) 35. (d) 36. (a) Exercise-5A Single Correct Answer Type Questions 1. (c) 2. (c) 3. (a) 4. (c) 5. (c) 6. (a) 7. (d) 8. (c) 9. (b) 10. (c) 11. (a) 12. (d) 13. (b) 14. (b) 15. (a) 16. (c) 17. (d) 18. (a) 19. (a) 20. (b) 21. (d) 22. (c) 23. (c) 24. (d) 25. (b) 26. (a) 27. (c) 28. (c) 29. (b) 30. (a) 31. (d) 32. (a) 33. (c) 34. (a) 35. (c) 36. (b) 37. (c) 38. (b) 39. (a) 40. (a) 41. (d) 42. (a) 43. (d) 44. (b) 45. (a) 46. (21) 47. (1.5) 48. (1) 49. (0.50)

One or More Correct Answer Type Questions

Exercise-5B

DEFINITE INTEGRATION_XII 77 | Page

Single Correct Answer Type Questions 1. (a) 2. (a) 3. (d) 4. (b) 5. (a) 6. (b) 7. (a) 8. (d) 9. (a) One or More Correct Answer Type Questions 10. (a, b, d) 11. (b, d) 12. (None) 13. (a, b) 14. (a, d) 15. (b, c) 16. (a, b) 17. (a, c) 18. (b, c) 19. (a, b, c) 20. (a, b, c, d) Comprehension Based Answer Type Questions 21. (a) 22. (d) 23. (a, b, c) 24. (c, d) 25. (c) 26. (a) 27. (b) 28. (a) 29. (b) 30. (b) 31. (a) 32. (d) 33. (b) 34. (d) 35. (1) 36. (7) 37. (4) 38. (4) 39. (2) 40. (2) 41. (1) 42. (9) 43. (0) 44. (2) 45. (4) 46. (0)