SYSTEM OF PARTICLES AND ROTATIONAL MOTION BUILDING UPON PRIOR KNOWLEDGE
The concepts of “System of Particles and Rotational Motion” in Class 11 physics are built upon the foundational concepts learned in previous classes, particularly in the context of classical mechanics. Here’s how these topics are linked to previous classes. In Class 9, you learned about Newton's three laws of motion. These laws form the basis for understanding how forces affect the motion of individual particles or objects. Understanding work and energy concepts from previous class (Class 9) is crucial in the context of rotational motion. Work-energy theorem helps in solving problems related to the rotational kinetic energy of objects. Momentum, which is a product of mass and velocity (p = mv), is crucial when dealing with systems of particles, which was introduced in Class 9. The conservation of linear momentum is an important concept, and it's linked to Newton’s third law of motion. You build upon the kinematics equations (s = ut + 1/2at2) learned in earlier classes by introducing rotational analogs, such as angular displacement, angular velocity, and angular acceleration. Torque is analogous to force in rotational motion and is related to the angular acceleration of an object. Moment of inertia (I), which is the rotational analog of mass, is also introduced. In summary, the topics of “System of Particles and Rotational Motion” in Class 11 physics are built upon the foundational principles of classical mechanics, including Newton’s laws of motion, work-energy concepts, and earlier introductions to linear motion and momentum. These concepts are extended to address the behaviour of systems of particles and objects undergoing rotational motion.
• Introduction
• Centre of Mass
• Motion of Centre of Mass
• Momentum Conservation
• Torque
• Couple
• Angular Momentum

• Equilibrium of Rigid Bodies
• Centre of Gravity
• Moment of Inertia
• Relation Between Torque and Momentum of Inertia
• Relation Between Angular Momentum and Momentum of Inertia
• Conservation of Angular Momentum
P – 06 – 1
KEY-TERMINOLOGY
➢ Axis of Rotation: The imaginary line around which an object rotates or spins.
➢ Moment of Inertia: A measure of an object's resistance to rotational motion, analogous to mass in linear motion.
➢ Angular Velocity: The rate of change of angular displacement with respect to time. It measures how quickly an object rotates
➢ AngularAcceleration: The rate of change of angular velocity with respect to time.
➢ Torque: A twisting force that causes an object to rotate about an axis. It is analogous to force in linear motion.
➢ Angular Momentum: A measure of the rotational motion of an object, calculated as the product of its moment of inertia and angular velocity.
➢ Centre of Mass: The point within an object where its entire mass can be considered to be concentrated for the purpose of analysing its motion.
➢ Rotational Kinetic Energy: The energy associated with the rotational motion of an object.
➢ Angular Displacement: The change in the angular position of an object, often measured in radians.
➢ Tangential Velocity: The linear velocity of an object at a point on its circular path, perpendicular to the radius.
➢ Centripetal Force: The forcedirectedtowardsthecentreofa circular paththat keepsan object moving in a circular motion.
➢ Rotational Equilibrium: When the net torque acting on an object is zero, and it is not accelerating in its rotational motion.
➢ Rolling Motion: A combination of translational and rotational motion, as seen in rolling objects like wheels.
➢ Radius of Gyration: The distance from the axis of rotation at which an object's entire mass could be concentrated to produce the same moment of inertia.
➢ Lever Arm: The perpendicular distance between the axis of rotation and the point where a force is applied.
➢ These terms should help you better understand the concepts and principles associated with the system of particles and rotational motion in physics.
Abbreviation to Comprehend Know Yourself
1. If a question is based on understanding of concept, it is being marked as [U].
2. If a question is based on information, it is marked as [I].
3. If a question is based on application of concepts, it is marked as [A].
SYSTEM OF PARTICLES AND ROTATIONAL MOTION _XI P – 06 – 2
OBJECTIVE OF STUDYING SYSTEM OF PARTICLES AND ROTATIONALMOTION
The key objectives of learning about the system of particles and rotational motion in the 11th-grade physics curriculum are to provide students with a comprehensive understanding of how objects move and behave in a rotational context. These objectives include:
➢ Understanding Particle Systems: Gain a clear comprehension of how multiple particles interact withinasystem.Learntoanalyseandpredictthemotionofsystemsofparticles,consideringbothinternal and external forces.
➢ Applying Newton's Laws: Apply Newton's laws of motion to understand the dynamics of systems of particles. Explore the principles of linear momentum and angular momentum in the context of particle systems.
➢ Grasping Rotational Motion: Understand the fundamental concepts of rotational motion, including angular displacement, angular velocity, and angular acceleration. Learn how to describe and analyse rotational motion using analogues of linear motion.
➢ Studying Moment of Inertia: Learn about the moment of inertia, which quantifies an object's resistance to rotational motion. Understand how the distribution of mass affects the moment of inertia and rotational behaviour.
➢ Examining Torque and Angular Momentum: Explore the concept of torque as a rotational analogue to force. Understand how torque influences the angular acceleration of objects and its connection to angular momentum.
➢ Exploring Equilibrium: Study conditions for translational and rotational equilibrium in both single particles and systems of particles. Learn to analyse the equilibrium of rigid bodies subjected to external forces.
➢ Analysing Rotational Kinematics: Apply rotational kinematics equations to describe the motion of rotating objects, such as wheels, pulleys, and gears.
➢ Connecting to Real-WorldApplications: Recognize the practical applications of rotational motion and systems of particles in fields like engineering, mechanics, robotics, and architecture. Explore how these principles are used in designing and optimizing machinery.
➢ Enhancing Problem-Solving Skills: Develop the ability to solve complex problems involving rotational motion and systems of particles. Apply mathematical techniques and critical thinking to analyse and solve real-world scenarios.
➢ Preparing for Advanced Physics: Lay the foundation for advanced physics topics that build upon principles of rotational motion, such as fluid dynamics, wave mechanics, and quantum physics.
By achieving these objectives, students will not only gain a deeper understanding of the mechanics of particles and rotational motion but will also acquire problem-solving skills that are crucial in various scientific and engineering disciplines. This knowledge serves as a fundamental building block for more advanced studies in physics and related fields.
SYSTEM OF PARTICLES AND ROTATIONAL MOTION_XI P – 06 – 3
1. INTRODUCTION
In the preceding chapters, our primary focus was on examining the motion of a single particle, which is conceptually represented as a point mass without physical dimensions. We extended the findings of our analysis to describe the motion of objects with finite size, assuming that the motion of such objects could be approximated by treating them as single particles.

In our daily experiences, real-world objects possess finite dimensions, and when addressing the motion of these extended bodies, the idealised model of a point particle often falls short. In this chapter, we will endeavour to surpass this limitation by delving into a deeper understanding of themotion of extended bodies. An extended body, at its core, can be viewed as a collection of particles. Our exploration will commence with the examination of the motion of the entire particle system. The concept of the centre of mass of a system of particles will play a pivotal role in our analysis, as we delve into the motion of extended bodies.
To address a wide range of problems involving extended bodies, we can simplify our approach by treating them as rigid bodies. In theory, a rigid body maintains an absolutely constant and unchanging shape, with no alteration in the distances between any pair of particles comprising it. It is important to note, however, that no actual physical body is entirely rigid since real objects may deform in response to applied forces. Nevertheless, in many practical situations involving objects such as wheels, spinning tops, steel beams, molecules, and celestial bodies like planets, the deformations are so minor that we can disregard them and treat these objects as if they were rigid.
What types of motion are possible for a rigid body?
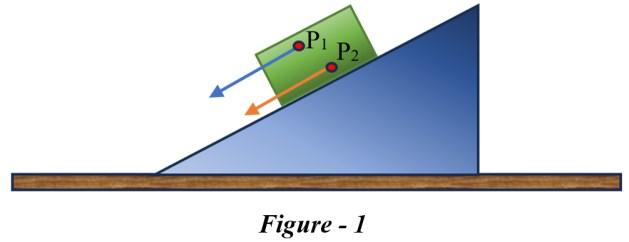
Let's examine this inquiry by considering specific instances of rigid body motion. To start, let's look at the motion of a rectangular block as it descends an inclined plane without deviating sideways.
The block is regarded as a rigid body, and as it descends the incline, all its constituent particles move in unison, maintaining the same velocity at any given moment. This results in the rigid body exhibiting pure translational motion (as depicted in Figure 1).
In pure translational motion, every particle within the body possesses identical velocity at any given instant. Now, let's consider the rolling motion of a solid metallic or wooden cylinder along the same inclined plane (as illustrated in Figure 2). In this scenario, the rigid body, which is the cylinder, progresses from the top to the bottom of the incline and appears to undergo translational motion. However, as indicated in Figure 2, not allofitsparticlesmovewithuniform velocityatanypoint intime.Consequently,thebodyisnotexperiencing pure translational motion; its motion combines translational motion with an additional component.
SYSTEM OF PARTICLES AND ROTATIONAL MOTION _XI P – 06 – 4
To comprehend this additional element, let's consider a scenario where a rigid body is deliberately restricted from undergoing translational motion. The most common method to constrain a rigid body to prevent translational motion is by securing it along a straight line. In such cases, the sole feasible type of motion for this rigid body is rotational. The specific line or fixed axis about which the body undergoes rotation is known as itsaxis ofrotation. You can readilyfind numerousinstancesofrotation about anaxisin yoursurroundings, such as a ceiling fan, a potter's wheel, a Ferris wheel at an amusement park, or a merry-go-round (as depicted in Figure 3).

Let's explore the concept of rotation and what distinguishes it. You may observe that when a rigid body rotates around a stationary axis, each particle within the body follows a circular path situated within a plane perpendicular to the axis. Additionally, the centre of these circular paths coincides with the axis itself. Figure 4 illustrates the rotational motion of a rigid body around a fixed axis (specifically, the z-axis of the frame of reference).
Consider a particle within the rigid body, denoted as P₁, which is arbitrarily selected and positioned at a distance r₁from thefixedaxis. Particle P₁traces acircular path witharadiusofr₁,and itscentre,C₁,coincides with the fixed axis. This circular path is situated within a plane that is perpendicular to the axis. The illustration also depicts another particle, P₂, within the rigid body, positioned at a distance r₂ from the fixed axis. Particle P₂ follows a circular trajectory with a radius of r₂, and its centre, C₂, is located on the same axis. It's important to note that while the circles traced by P₁ and P₂ may be situated in different planes, both of these planes are perpendicular to the fixed axis. Additionally, any particle positioned directly on the axis, such as P₃, has a radius r equal to zero. Such a particle remains motionless as the body undergoes rotation, as one would expect, given that the axis of rotation remains fixed.

OF PARTICLES AND ROTATIONAL MOTION_XI P – 06 – 5
SYSTEM
Fig. 4
In certain instances of rotational motion,theaxis of rotationmay not remain stationary. Aprominent example of such a rotational motion is seen in a spinning top that remains in a fixed position (as shown in Figure - 5). We assume here that the top does not slide or move around, thus avoiding translational motion. As observed through experience, the axis of the spinning top moves in a circular manner around the vertical line passing through its point of contact with the ground, forming a cone-shaped path, which is referred to as precession. It's important to note that the point where the top touches the ground remains fixed. At any given moment, the axis of rotation of the top passes through this fixed point. Another straightforward illustration of this type of rotational motion can be observed in oscillating table fans or pedestal fans (as depicted in Figure - 6). In these cases, you may have noticed that the axis of rotation of the fan exhibits a back-and-forth (sidewise) movement within a horizontal plane, rotating around the vertical axis at the point where it is pivoted (identified as point O in Figure - 6).


While the fan rotates and its axis experiences sidewise movement, this pivot point remains fixed. Consequently, in more general instances of rotational motion, like the rotation of a top or a pedestal fan, a single point, rather than a single line, within the rigid body is stationary. In such cases, the axis is not fixed, although it consistently passes through the stationary point. However, it's worth noting that our study primarily deals with the simpler and specific case of rotation where a single line (i.e., the axis) remains fixed.


SYSTEM OF PARTICLES AND ROTATIONAL MOTION _XI P – 06 – 6
Fig. 5 Fig. 6
Fig. 7 Motion of a rigid body which is pure translation.
Fig. 8 Motion of a rigid body which is a combination of translation and rotation.
Figures - 7 and 8 depict distinct movements of the same object. Please note that P represents an arbitrary point on the object, while O signifies the centre of mass of the object, which will be defined in the following section. At this juncture, it's sufficient to state that the paths followed by O are the translational trajectories Tr1 and Tr2 of the object. In both Figures - 7 and 8, positions O and P at different time instances are denoted as O1, O2, O3, and P1, P2, P3, respectively.
• As evident from Figure - 7, at any given moment, the velocities of any particles, such as O and P, within the object are identical during pure translation. It's worth noting that in this scenario, the orientation of OP, i.e., the angle formed by OP with a fixed reference direction (e.g., the horizontal), remains constant, represented as 1 = 2 = 3
• On the other hand, Figure - 8 illustrates a scenario where a combination of translation and rotation is occurring. In this case, the velocities of O and P differ at any instant. Furthermore, the angles α1, α2, and α3 may all be distinct.
• For our study, it's important to clarify that we will consider rotation to occur exclusively around a fixed axis unless explicitly stated otherwise. The rolling motion of a cylinder down an inclined plane, for instance, combines rotation about a fixed axis and translational motion. Thus, the " additional element " mentioned earlier in the context of rolling motion is, indeed, rotational motion. Figures - 7 and 8 provide valuable visual insights into this concept. Both figures depict motion along identical translational trajectories, with one (Figure - 7) representing pure translation and the other (Figure - 8) depicting a combination of translation and rotation. (You can try to replicate these two types of motion using a rigid object like a heavy book.)
• In summary, the key takeaways from this section are as follows: The motion of an unrestrained rigid body is either pure translation or a combination of translation and rotation. In contrast, a rigid body that is anchored or fixed in some manner undergoes rotational motion. This rotation may occur about either a fixed axis (e.g., a ceiling fan) or a moving axis (e.g., an oscillating table fan). In this chapter, our focus will be exclusively on rotational motion about a fixed axis.
Key Concept
1. In pure translation, every particle of the body moves with the same velocity at any instant of time.
2 Ideally, a rigid body is one for which the distances between different particles of the body do not change, even though there are forces on them.
3. A rigid body fixed at one point or along a line can have only rotational motion.
4. A rigid body not fixed in some way can have either pure translational motion or a combination of translational and rotational motions.
5. In rotation about a fixed axis, every particle of the rigid body moves in a circle which lies in a plane perpendicular to the axis and has its centre on the axis. Every Point in the rotating rigid body has the same angular velocity at any instant of time.

SYSTEM OF PARTICLES AND ROTATIONAL MOTION_XI P – 06 – 7
2. CENTRE OF MASS
• When the motion of a body involves rotation and vibration, we must treat it as a system of particles. In spite of complex motion of which a system is capable, there is a single point, the centre of mass (CM), whose translational motion is characteristic of the system as a whole. Here we shall discuss about location of centre of mass of a system of particles and its motion.
The centre of mass of a system of particles is that single point which moves in the same way in which a single particle having the total mass of the system and acted upon by the same external force would move.
2.1 Derivation of Expression for the Centre of Mass of a Two-Particle System
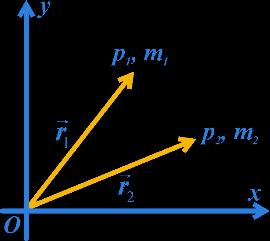
• Consider a system of two particles P1 and P2 of masses m1 and m2. Let 1r and 2r be their position vectors at any instant t with respect to the origin O, as shown in Fig. The velocity and acceleration vectors of the two particles are:
• Total force acting on particle P1 is the sum of the internal force 12F due to P2 and external force
on it. Thus according to Newton's second law of motion
• Similarly, total force acting on particle P2 is given by
• On adding equations (1) and (2), we get
• According to Newton's third law, the internal forces mutually exerted by the two particles are equal and opposite, i.e.,
12211221 or 0 FFFF=−+=
• So, equation (3) becomes 22 12 1 ext2 ext1222 drdr
where 12extextFFF =+ is the total external force acting on the system.
• Suppose the total mass of the two-particle system is M. Then M = m1 + m2
SYSTEM OF PARTICLES AND ROTATIONAL MOTION _XI P – 06 – 8
2
dt
2
111 112 and drdvdr va dtdt
===
222 222 and drdvdr va dtdt dt ===
1
F
2 1 121 ext111 2 dr FFmam dt +== ...(1)
ext
2 2 212 ext2222 dr FFmam dt +== ...(2)
22 12 12211 ext2 ext1222 drdr FFFFmm dtdt +++=+ ...(3)
22
Fmm dtdt
...(4)
FFmm dtdt +=+
12 1222 drdr
=+
• Let us assume that the total external force F acting on the system of mass M produces acceleration CMa . Then according to Newton's second law,
• From equations (4) and (5), we get
• Clearly,
• CMr is called the position vector of the centre of mass.
• This equation defines the position of the centre of mass of a system of two particles of masses m1 and m2 and having position vectors 1r and 2r . Here the entire mass of the two-particle system may be supposed to be concentrated. Clearly’, Newton’s second law, as applied to the individual particles of the system, also holds for the entire system provided the external force acts at the centre of mass as defined by the above equation.
2.2 Centre of Mass of a System of ‘N’Particles
• Consider a system of N particles having masses

rrrr with respect to the origin. The centre of mass,
• The Cartesian co-ordinates of the centre of mass are given by
N having respective position vectors
of this system is given by
Key Concept
(i) The position of centre of mass is independent of the co-ordinate system chosen.
(ii) If the origin is at the centre of mass, then the sum of the moments of the masses of the system about the centre of mass is zero i.e. Σ0 ii mr = .
SYSTEM OF PARTICLES AND ROTATIONAL MOTION_XI P – 06 – 9
CM MaF = ...(5)
22 12 1222 CM drdr Mamm dtdt =+ ( ) 22 1122 22 CMdr d Mmrmr dtdt =+ [where cm r is the position vector of centre of mass] ( ) 222 1122 112212222 12 1 CMdr ddmrmr mrmrMmm dtdtdtMmm + =+==+ +
1122 12
CM mrmr r mm + = +
.
m1, m2, m3,
m
cm r
11221 12 N ii NNi CM N mr mrmrmr r mmmM = +++ == +++
...
123,,,...., N
,
11221 12 N ii NNi N mx mxmxmx x mmmM = +++ == +++ 11221 12 N ii NNi N my mymymy y mmmM = +++ == +++ 11221 12 N ii NNi N mz mzmzmz z mmmM = +++ == +++
Illustration-1
Four particles of mass 1 kg, 2 kg, 3 kg and 4 kg are placed at the four vertices A, B, C and D of a square of side 1 m. Find the position of the centre of mass of the particles.
Solution: Assuming D as the origin, DC as x -axis and DA as y-axis, we have
m1 = 1 kg, (x1, y1) = (0, 1m)
m2 = 2 kg, (x2, y2) = (1m, 1m)
m3 = 3 kg, (x3, y3) = (1m, 0) and m4 = 4 kg, (x4, y4) = (0, 0)
Co-ordinates of their COM are
11223344 1234 COM mxmxmxmx X mmmm +++ = +++
(1)(0)2(1)3(1)4(0) 1234 +++ = +++ 51 0.5 102 mm===
Similarly,
11223344 1234 COM mymymymy Y mmmm +++ = +++
(1)(1)2(1)3(0)4(0) 1234 +++ = +++ 3 0.3 10 mm==
(xCOM, yCOM) = (0.5 m, 0.3 m)
Thus, position of COM of the four particles is as shown in figure
Illustration-2
The position vector of three particles of mass m1 = 1 kg, m2 = 2 kg and m3 = 3 kg are 1 ˆˆˆ (4)=++ rijkm , 2 ˆˆˆ ()=++ rijkm and 3 ˆˆˆ (22)=−− rijkm respectively. Find the position vector of their centre of mass.
Solution: The position vector of COM of the three particles will be given by 112233
Substituting the values, we get
SYSTEM OF PARTICLES AND ROTATIONAL MOTION _XI P – 06 – 10
r
COM 123 mmm mmm rrr
++ = ++
COM ˆˆˆˆˆˆˆˆˆˆˆˆ
1236 ijkijkijkijk r +++++++− == ++ COM 1 ˆ ˆˆ 2(3)mrijk =+−
(1)(4)(2)()(3)(2––2)933
Illustration-3
Find out the centre of mass of a system of three particles of 1 kg, 2 kg and 3 kg kept at the vertices of an equilateral triangle of side 1 m as shown
Know Yourself
1. Particle of masses 2 kg, 2 kg, 1 kg and 1 kg are placed at the corners A, B, C, D of a square of side L as showninthefigure.Findthecentre ofmass ofthe system. Take Atobetheoriginof the coordinate system. [A]
2 In the HCl molecule, the separation between the nuclei of the two atoms is about 1.27Å(1Å = 10–10 m). Find the approximate location of the CM of the molecule, given that a chlorine atom is about 35.5 times as massive as a hydrogen atom and nearly all the mass of an atom is concentrated in its nucleus [A]
SYSTEM OF PARTICLES AND ROTATIONAL MOTION_XI P – 06 – 11
O
112233 123
1 1(0)23(1)
2 1233
== ++ 112233 123
= ++ ( ) 1(0)2323(0) 3 1236 m ++ == ++
x y 1 kg 2 kg 3 kg Solution:
cm mxmxmx x mmm ++ = ++
2
m
++
cm mymymy y mmm ++
D C B A 1 Kg 1 Kg 2 Kg 2 Kg
1 kg 3 kg (1, 0) O 2 kg (½ ,3/2) x y




..................................................................................................................................
.................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. ..................................................................................................................................
.................................................................................................................................. ..................................................................................................................................
2.3 Centre of Mass of Continuous Bodies
• For calculating centre of mass of a continuous body, we first divide the body into suitably chosen infinitesimal elements. The choice is usually determined by the symmetry of body.
• Consider element dm of the body having position vector ,r the quantity ii mr in equation of CM is replaced by r dm and the discrete sum over particles ii mr M , becomes integral over the body:
• In component form this equation can be written as
• To evaluate the integral we must express the variable m in terms of spatial coordinates x, y, z or r .
Illustration-4
Show that the centre of mass of a uniform rod of mass M and length L lies at the middle point of the rod.
Solution: As shown in figure suppose the rod is placed along X-axis with its left end at the origin O. Consider a small element of thickness dx at distance x from O
Mass of the small element M dx L =
Position of the centre of mass is given by

SYSTEM OF PARTICLES AND ROTATIONAL MOTION _XI P – 06 – 12
y x dm r
1 CM rrdm M
...(1)
=
;and CMCMCM XxdmYydmZZdm MMM === ...(2)
111
0 1 L CM xxdm M = 0 1 L M xdx ML = 0 1 L xdx L = 2 0 1 22 L xL L ==
Illustration-5
Determine the position of the centre of mass of a hemisphere of radius R.

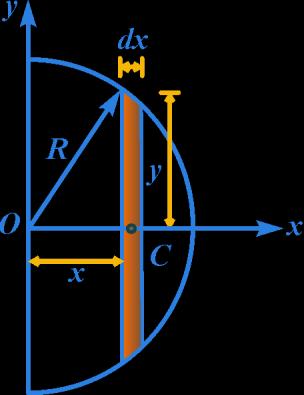
Solution: Let be the density of the material of the hemisphere. Take its centre O as the origin. The hemisphere can be assumed to be made of up a large number of co-axial discs. Consider one such elementary disc of radius y and thickness dx at a distance x from the origin.
Mass of the elementary disc = Volume density ( )
The coordinates of the centre of mass of the hemisphere can be determined as follows:
Hence the coordinates of the centre of mass of the hemisphere are 3 8,0,0 R
Key Concept
The position of centre of mass depends upon the shape of the body and distribution of mass.
SYSTEM OF PARTICLES AND ROTATIONAL MOTION_XI P – 06 – 13
dmydxRxdx ==−
222 .
( ) 22 0 11 R CM xxdmxRxdx MM ==− ( ) 24 232 0 0 24 R R xx RxxdxR MM =−=− 444 244 RRR MM =−= 4 3 3 32 2 483 3 R RMR R ===
0and 0 CMCM yydmzzdm ====
Similarly,
.
Position of Centre of Mass for Different Bodies
S.No. Body Position of Centre of Mass
a. Uniform hollow sphere Centre of sphere
b. Uniform solid sphere Centre of sphere
c. Uniform circular ring Centre of ring
d. Uniform circular disc Centre of disc
e. Uniform rod Centre of rod
f. A plane lamina (Square, Rectangle, Parallelogram)
g. Triangular plane lamina
h. Rectangular or cubical block
Point of inter section of diagonals
Point of inter section of medians
Points of inter section of diagonals
i. Hollow cylinder Middle point of the axis of cylinder
j. Solid cylinder Middle point of the axis of cylinder
k. Cone or pyramid
On the axis of the cone at point distance 3/4 from the vertex where h is the height of cone
TO UNDERSTAND THE C.O.M OF CONE & OTHER NON-SYMMETRICAL BODIES REFER TO ADVANCED MODULE.
Illustration-6
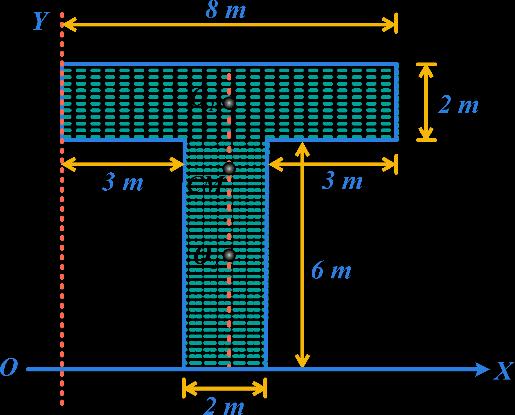
Find the position of the centre of mass of the T-shaped plate from O in Fig.
Solution: Let mass per unit area of the plate be σ
SYSTEM OF PARTICLES AND ROTATIONAL MOTION _XI P – 06 – 14
Mass of
σ = 16 σ
(4m,
Mass of vertical
×
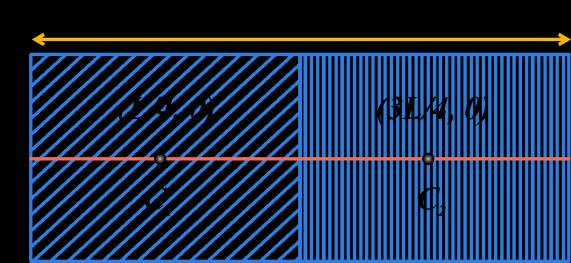
σ = 12 σ at (4m, 3m) 164124 1612 CMx + = + 112 4 28 m == 167123 1612 CMy + = 148 5.29 28 m ==
horizontal portion = 8 × 2
at
7m)
portion = 6
2
Illustration-7
Half of the rectangular plate shown in figure is made up of material of density ρ1 and the other half of density ρ2. The length of the plate is L. Locate the centre of mass of the plate.
Solution: Let C1 and C2 be the C.M. points of these two half take mid point of the left edge as origin then C.M. of the whole system lies on the line joining C1 and C2
Illustration-8
A circular disc of uniform thickness has a diameter of 56 cm. A circular disc of diameter of 42 cm is removed from one edge of the plate as shown in figure. Find the position of the centre of mass of the remaining potion.

Solution: M be the mass and C be the centre of the circular disc of diameter 56 cm
M1 be the mass and C1 be the centre of the circular disc of diameter 42 cm
M1 = π(21)2σ = 441πσ
Remaining mass M2 = M – M1 = 784πσ – 441πσ = 343πσ
Using the relation M1r1 = M2r2
(441πσ) × 7 = (343 πσ) × r2
r2 = 9 cm
MOTION_XI P – 06 – 15
SYSTEM OF PARTICLES AND ROTATIONAL
of mass 11 2 L mB = at (L/4, 0) Co-ordinate of mass 22 2 L mB = at (3L/4, 0) ( ) 12 1122 12 12 3 2424 1 22 cm LLLL BB mxmx x L mm BB + + == + + ( ) ( ) 12 12 3 4 cm L x + = +
Co-ordinate
( ) 2 2 28784 2 d M ===
Key Concept
• The centre of mass of a circular disc is within the material of the body while that of a circular ring is outside the material of the body.
• In symmetrical bodies in which the distribution of mass is homogenous, the centre of mass coincides with the geometrical centre or centre of symmetry of the body
Know Yourself
1. Find the centre of mass of a triangular lamina. [A]
2. Find the centre of mass of a uniform L-shaped lamina (a thin flat plate) with dimensions as shown. The mass of the lamina is 3 kg. [A]
3. Give the location of the centre of mass of a (i) sphere, (ii) cylinder, (iii) ring, and (iv) cube, each of uniform mass density. Does the centre of mass of a body necessarily lie inside the body. [I]

4. From a uniform disk of radius R, a circular hole of radius R/2 is cut out. The centre of the hole is at R/2 from the centre of the original disc. Locate the centre of mass of the resulting flat body. [A]

SYSTEM OF PARTICLES AND ROTATIONAL MOTION _XI P – 06 – 16




..................................................................................................................................
.................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. ..................................................................................................................................
.................................................................................................................................. ..................................................................................................................................
2.4 Motion of Centre of Mass
• Equipped with the definition of the centre of mass, we are now in a position to discuss its physical importance for a system of n particles.
Let M = m1 + m2 + …. mn = Total mass of system
Then ii cm
mr r M =
1122 rrrr cmiinn Mrmmmm ==+++ … (1)
• Differentiating the two sides of the equation with respect to time we get
12 dd dd d d d cmn n rr rr Mmmm tttdt =+++
12
or 1122 cmnn Mvmvmvmv =+++ … (2)
• where 1 1 dr v dt =
is the velocity of the second particle etc. and cm cm dr v dt
is the velocity of the first particle
is the velocity of the centre of mass. Note that we assumed the masses m1, m2, .... etc.do not changeintime.We havetherefore,treatedthem as constantsin differentiating the equations with respect to time.
• Differentiating Eq. (2) with respect to time, we obtain
or 1122 .......
is the acceleration of the first particle, 2 2 dv a dt
is the acceleration of the second particle etc. and cm cm
a
= is the acceleration of the centre of mass of the system of particles.
• Now, from Newton's second law, the force acting on the first particle is given by 111 Fma = The force acting on the second particle is given by 222 Fma = and so on. Eq. (3) may be written as
• Thus, the total mass of a system of particles times the acceleration of its centre of mass is the vector sum of all the forces acting on the system of particles.
• Note when we talk of the force 1F on the first particle, it is not a single force, but the vector sum of all the forces on the first particle; likewise for the second particle etc. Among these forces on each particle there will be external forces exerted by bodies outside the system and also internal forces exerted by theparticleson oneanother.Weknowfrom Newton's thirdlawthat theseinternal forcesoccur inequal and opposite pairs and in the sum of forces of Eq. (4), their contribution is zero. Only the external forces contribute to the equation. We can then rewrite Eq. (4) as
MOTION_XI P – 06 – 17
SYSTEM OF PARTICLES AND ROTATIONAL
2
v
=
2
dr
dt
=
12 12
dvdv dvdv d d d d cmn nMmmm tttt =+++
=
cmnn Mamamama =+++ … (3) where 1 1 dv a dt
=
dv
dt
12 cmn MaFFF =+++
… (4)
cmext
MaF = … (5)
where extF represents the sum of all external forces acting on the particles of the system. Eq. (5) states that the centre of mass of a system of particles moves as if all the mass of the system was concentrated at the centre of mass and all the external forces were applied at that point.
• Notice, to determine the motion of the centre of mass no knowledge of internal forces of the system of particles is required; for this purpose we need to know only the external forces.
• To obtain Eq. (5) we did not need to specify the nature of the system of particles. The system may be a collection of particles in which there may be all kinds of internal motions, or it may be a rigid body which has either pure translational motion or a combination of translational and rotational motion. Whatever is the system and the motion of its individual particles, the centre of mass moves according to Eq. (5).
• Instead of treating extended bodies as single particles as we have done in earlier chapters, we can now treat them as systems of particles. We can obtain the translational component of their motion, i.e. the motion of the centre of mass of the system, by taking the mass of the whole system to be concentrated at the centre of mass and all the external forces on the system to be acting at the centre of mass.
• This is the procedure that we followed earlier in analysing forces on bodies and solving problems without explicitly outlining and justifying the procedure. We now realise that in earlier studies we assumed, without saying so, that rotational motion and/or internal motion of the particles were either absent or negligible. We no longer need to do this. We have not only found the justification of the procedure we followed earlier; but we also have found how to describe and separate the translational motion of (1) a rigid body which may be rotating as well, or (2) a system of particles with all kinds of internal motion.
• Figure - 9 is a good illustration of Eq. (5). A projectile, following the usual parabolic trajectory, explodes into fragments midway in air. The forces leading to the explosion are internal forces. They contribute nothing to the motion of the centre of mass. The total external force, namely, the force of gravity acting on the body, is the same before and after the explosion. The centre of mass under the influence of the external force continues, therefore, along the same parabolic trajectory as it would have followed if there were no explosion.

SYSTEM OF PARTICLES AND ROTATIONAL MOTION _XI P – 06 – 18
Fig. 9
Key Concept
1. To determine the motion of the centre of mass of a system no knowledge of internal forces of the system is required. For this purpose we need to know only the external forces on the body.
2. If r is a position vector of centre of mass of a system then velocity of centre of mass
3. If a system of particles of masses m1, m2, m3, ..... move with velocities v
, ........ then the velocity of centre of mass
4. If a system of particles of masses m1, m2, m3, ..... move with accelerations a
, a
, a3, ....... then the acceleration of centre of mass
5. Velocity of the centre of mass of a system of particles is given by P V M = , where P is the linear momentum of the system. The centre of mass moves as if all the mass of the system is concentrated at this point and all the external forces act at it. If the total external force on the system is zero, then the total linear momentum of the system is constant
Illustration-9
The velocities of three particles of masses 20g, 30g and 50g are 10i,10j , and 10k respectively. The velocity of the centre of mass of the three particles is
(a) 25k + i+3j
(c) k + 20i+30+j5
(b) ( )k + 10i+j
(d) k + 2i+30+j50
Know Yourself
1. Two particles of mass 1 kg and 0.5 kg are moving in the same direction with speeds of 2 m/sec and 6 m/sec, respectively, on a smooth horizontal surface. Find the speed of centre of mass of the system
2. Two bodies of masses and are moving with velocities 263ijk −+ and 1 10353ijkms−+− respectively. Find the velocity of the centre of mass of the system. [A]

SYSTEM OF PARTICLES AND ROTATIONAL MOTION_XI P – 06 – 19
112233 123 cm mrmrmr drd v dtdtmmm +++ == +++
2
v3
ii cm i mv v m = .
1, v
,
1
ii cm i ma a m =
2
Solution: Velocity of centre of mass 112233 123 201030105010 235 100 cm mvmvmv ijk vijk mmm ++ ++ ===++ ++
[A]




..................................................................................................................................
.................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. ..................................................................................................................................
.................................................................................................................................. ..................................................................................................................................
3. MOMENTUM CONSERVATION AND CENTRE-OF-MASS MOTION
• Consider a system of n particles of masses m1, m2, m3, ..., mn.. Suppose the forces 123,,,, n FFFF exerted on them produce accelerations 123,,,, naaaa respectively. In the absence of any external force, or
where P is the total linear momentum of the system.
• Hence if no net external force acts on a system, the total linear momentum of the system is conserved. This is the law of conservation of linear momentum.
Illustration-10
A man of mass m is standing on a platform of mass M kept on smooth ice. If the man starts moving on the platform with a speed v relative to the platform, with what velocity relative to the ice does the platform recoil?

Solution: Consider the situation shown in figure. Suppose the man moves at a speed w towards right and the platform recoils at a speed V towards left, both relative to the ice. Hence, the speed of the man relative to the platform is V + w. By the question,
V + w = v, or w = v – V . . . (i)
Taking the platform and the man to be the system, there is no external horizontal force on the system. The linear momentum of the system remains constant. Initially both the man and the platform were at rest. Thus,
0 = MV – mw or, MV = m (v – V) [Using (i)] or, mv V Mm = +
TO UNDERSTAND ‘HOW TO USE C.O.M. FRAME REFER TO ADVANCED MODULE.
Know Yourself
1. A child sits stationary at one end of a long trolley moving uniformly with a speed V on a smooth horizontal floor. If the child gets up and runs about on the trolley in any manner, what is the speed of the CM of the (trolley + child) system? [U]
2. Two blocks of masses 3 kg and 2 kg are place on frictionless surface and connected by a spring. External kick gives a velocity of 10 m/s to the block in the direction of lighter one. Calculate velocity grained by the centre of mass [A]
SYSTEM OF PARTICLES AND ROTATIONAL MOTION _XI P – 06 – 20
tot 0 F = 123 0 n FFFF++++= 112233 0 nnmamamama ++++= 3 12 123 0 n n dvdv dvdv mmmm dtdtdtdt ++++= ( ) 112233 0 nn d mvmvmvmv dt ++++= or 112233 nnmvmvmvmv++++=
constant
Ppppp =++++=
constant or 123
n




..................................................................................................................................
.................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. ..................................................................................................................................
.................................................................................................................................. ..................................................................................................................................
4. MOMENT OF FORCE (TORQUE)
• The rotational analogue of force in linear motion is moment of force. It is also referred to as torque
• If a pivoted, hinged or suspended body tends to rotate under the action of a force, it is said to be acted upon by a torque.
• To open a door, we apply a force on its handle. The door turns on its hinges. The larger the force, the more is its turning effect. Also, we can easily notice that it is easier to open a door by applying a force near the end than near the hinges. This is because the turning effect of the same force is larger when its distance from the axis of rotation is more.

• This turning effect of force is called moment of force or torque. It depends on two factors:
(i) The magnitude of the force.
(ii) The perpendicular distance of the line of action of the force from the axis of rotation. It is called lever arm or moment arm.
• If a force acts on a single particle at a point P whose position with respect to the origin O is given by the position vector r (Fig. 11), the moment of the force acting on the particle with respect to the origin O is defined as the vector product

rF= τ
• The moment of force (or torque) is a vector quantity. The symbol stands for the Greek letter tau. The magnitude of is sinrF =
where r is the magnitude of the position vector r , i.e. the length OP, F is the magnitude of force F and is the angle between r and F as shown.
SYSTEM OF PARTICLES AND ROTATIONAL MOTION_XI P – 06 – 21
Fig. - 10
Fig. 11
• The magnitude of the moment of force may be written ( ) sin FrFr ⊥ ==
where sinrr ⊥ = is the perpendicular distance of the line of action of F from the origin.
• Torque = Force Perpendicular distance of line of action of force from origin.
• The magnitude of the moment of force may be written sin rFrF ⊥ ==
and ( ) sinFF ⊥ = is the component of F in the direction perpendicular to r.
• Torque = distance of point of action of force from origin component of force perpendicular to the position vector.
• One may note that since rF is a vector product, properties of a vector product of two vectors apply to it. If the direction of F is reversed, the direction of the moment of force is reversed. If directions of both r and F are reversed, the direction of the moment of force remains the same.
Dimensions
• Moment of force has dimensions ML2T–2. Its dimensions are the same as those of work or energy. It is, however, a very different physical quantity than work. Moment of a force is a vector, while work is a scalar.
Unit
• The SI unit of moment of force is newton metre (Nm)
4.1 Torque in Terms of Rectangular Components
• For motion in three dimensions, the position vector r , force vector F and torque vector can be written in terms of their rectangular components as follows :
j i rxyzk =++
xyz FFFFijk =++
and xyz ijk =++
• Now
rF = ( ) ( ) xyz xiyjzk k FFF ij =++++
i xyz k
j FF =
F
xyz
or ( ) ( ) ( ) xyzzyxzyx kiyFzF i jzFxFkxFy j F ++=−+−+−
• Comparing the coefficients of ad , n ijk on the two sides of the above equation, we get the rectangular components of torque as follows: ; ; .xzyyxzzyx yFzFzFxFxFyF =−−=−=−
SYSTEM OF PARTICLES AND ROTATIONAL MOTION _XI P – 06 – 22
Key Concept
1. As rF = , so = 0 if r = 0, F = 0 or = 0° or 180°. Thus, the moment of a force vanishes if either the magnitude of the force is zero, or if the line of action of the force passes through the origin.

2. The torque or moment of force is the turning effect of the force about the axis of rotation. It is measured as the product of the magnitude of the force and the perpendicular distance between the line of action of the force and the axis of rotation.

3. Torque = Force Perpendicular distance of line of action of force from origin.
4. Torque = distance of point of action of force from origin component of force perpendicular to the position vector.
Illustration-11
A particle of mass m is dropped at point A, find the torque about O.
Solution: rF = ( ) sinsin rFnrFn
bmg =
The direction of torque is directed inward the paper or in other words, rotation about O is clockwise.
Illustration-12
A force of ( ) 2–4j i +2kN acts at a point ( )3i+2j–4k metre from the origin. The magnitude of torque is
Solution: (b) ( ) ( ) 242and324FkNr i ji j i =−+=+− meter
Torque 324121416 242
i rFijk jk ==−=−−− and 222 (12)(14)(16) =−+−+−= 24.4Nm
Know Yourself
1. Find the torque of a force 735ijk +− about the origin. The force acts on a particle whose position vector is i jk−+ . [A]
SYSTEM OF PARTICLES AND ROTATIONAL MOTION_XI P – 06 – 23
==
(a) Zero (b) 24.4 Nm (c) 0.244 Nm (d) 2.444Nm.




..................................................................................................................................
.................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. ..................................................................................................................................
.................................................................................................................................. ..................................................................................................................................
5. COUPLE
• A pair of equal and opposite forces acting on a body along two different lines of action constitute a couple. A couple has a turning effect, but no resultant force acts on a body. So it cannot produce translational motion. When we steer a bicycle round a bend with our both hands on the handle-bars, we apply a couple.
5.1 Moment of a Couple:
• The moment of couple can be found by taking the moments of the two forces about any point and then adding them.
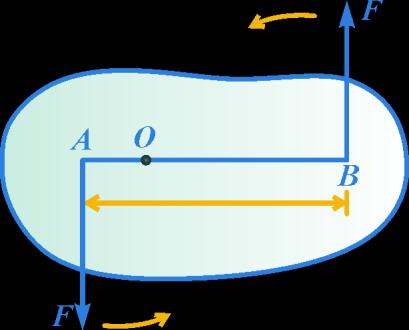
• In Figure - 12, two opposite forces, each of magnitude F act at two points A and B of a rigid body, which can rotate about point O. The turning tendency of the two forces is anticlockwise.
• Moment or torque of the couple about O is
= F × AO + F × OB
= F (AO + OB) = F × AB
= Fd [AB = d, say]
• Moment of a couple = Force × perpendicular distance between two forces.
• Hence the moment of a couple is equal to the product of either of the forces and the perpendicular distance, called the arm of the couple, between their lines of action
Know Yourself
1. Show that moment of a couple does not depend on the point about which you take the moments.[U]
Key Concept
The torque exerted by couple about O does not depend on the position of O. Hence torque or moment of a comple is intependent of the choice of the fulcrum or the point of rotation. or

The total torque on a system is independent of the origin if the total external force is zero.
SYSTEM OF PARTICLES AND ROTATIONAL MOTION _XI P – 06 – 24
Fig. 12
6. WORK DONE BY A TORQUE
• As shown in Figure - 13, suppose a body undergoes an angular displacement Δθ under the action of a tangential force F.
Fig. 13
• The work done in the rotational motion of the body or the work done by the torque is Δ distance along the arc WFPQ =
But Arc Arc Δ Radius PQ r ==
Arc PQ = r Hence W = Fr or
W =
i.e., Work done by a torque = Torque × angular displacement
• In case the torque applied is not constant, but variable, the total work done by the torque is given by 2 1 Wd =
7. POWER DELIVERED BY A TORQUE
• We know that W =
• Dividing both sides by t, we get
ΔΔ ΔΔ W tt = P = or
i.e., Power = Torque × Angular velocity
Know Yourself
1. To maintain a rotor at a uniform angular speed of 200 rads–1, an engine needs to transmit a torque of 180 N m. What is the power required by the engine? (Note: uniform angular velocity in the absence of friction implies zero torque. In practice, applied torque is needed to counter frictional torque). Assume that the engine is 100% efficient. [A]

SYSTEM
AND ROTATIONAL MOTION_XI P – 06 – 25
OF PARTICLES




..................................................................................................................................
.................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. ..................................................................................................................................
.................................................................................................................................. ..................................................................................................................................
8. ANGULAR MOMENTUM
• In linear motion, the linear momentum of a body gives a measure of its translatory motion. Analogous to it in rotational motion, the angular momentum gives a measure of the turning motion of the body.
• Consider a particle P of mass m whose position vector relative to the origin O is r . Suppose the momentum vector p of the particle makes angle with the position vector r , as shown in Fig.-
• The angular momentum L of the particle about the origin O is defined as the vector product of the vectors r and p . Thus
Lrp =
• Angular momentum is a vector quantity. The direction of angular momentum L is perpendicular to the plane of vectors r and p in the sense given by right hand rule.
• Its magnitude is given by
L = rp sin
• Draw ON perpendicular to the line of action of linear momentum p . From right angled ONP, we get sinor sin. ONd dr OPr ===
• Where d is the perpendicular distance of the line of motion of linear momentum from the point of rotation O and is called moment arm of the momentum.
• The magnitude of the angular momentum about the point O is
L = rp sin = p(r sin ) = pd
i.e., Angular momentum = Linear momentum × moment arm
= Linear momentum × its perpendicular distance from the axis of rotation.
• This is the physical meaning of angularmomentum. According to it, angularmomentum isthemoment of linear momentum and is a measure of the turning motion of the object.
• Moreover, as shown in Figure - 14, the momentum vector p can be resolved into two rectangular components:

(i) Radial component, pr along the direction of position vector r
(ii) Angular or tangential component, p perpendicular to r
Clearly, pr = p cos and p = p sin
L = (p sin ) r = pr
or Angular momentum
= Angular component of linear momentum × its distance from the axis of rotation.
SYSTEM OF PARTICLES AND ROTATIONAL MOTION _XI P – 06 – 26
Fig. 14
Dimensions:
• Dimensions of angular momentum = L × MLT–1 = [ML2 T–1]
Units:
• SI unit of angular momentum is kgm2 s –1
• CGS unit of angular momentum is gcm2 s –1 .
Special Cases.
(i) If = 0° or 180°, sin = 0
L = rp × 0 = 0
Hence the angular momentum is zero if the line of action of linear momentum passes through the point of rotation.
(ii) If If = 90°, sin 90° = 1
L = rp × 1 = rp = maximum
Hence the angular momentum is maximum and is equal to rp or mvr, if the line of action of the linear momentum is perpendicular to the position vector.
8.1 Angular Momentum in Terms of Rectangular Components.
• For motion in three dimensions, the position vector r and linear momentum vector p can be written in terms of their rectangular components as follows:
rxiyjzk =++ and xyz ppppijk =++
But angular momentum is the cross product of r and p , so
Lrp =
) ( ) xyz xiyjz k pp k p ij =++++
• Comparing the coefficients of ,andi jk on the two sides of the above equation, we obtain the rectangular components of vector L as follows:
Lx = ypz – zpy; Ly = zpx – xpz and Lz = xpy – ypx
Key Concept
1. Angular momentum is an axial vector i.e., always directed perpendicular to the plane of rotation and along the axis of rotation.
2. A particle in translatory motion always have an angular momentum unless it is a point on the line of motion.

P – 06 – 27
SYSTEM OF PARTICLES AND ROTATIONAL MOTION_XI
= or ( ) ( ) ( )
(
xyz jk xyz ppp i
xyzzyxzyx LLLiypzpjzpxk i p jk pxyp++=−+−+−
Illustration-13
An electron of mass 9 × 10–31 kg revolves in a circle of radius 0.53 A around the nucleus of hydrogen with a velocity of 2.2 × 106 ms –1 . Show that its angular momentum is equal to h/2, where h is Planck’s constant of value 6.6 × 10–34 Js.
Solution:
Here m = 9 × 10–31 kg,
r = 0.53Å = 0.53 × 10–10 m,
v = 2.2 × 106 ms –1 ,
h = 6.6 × 10–34 Js
Angular momentum,
L = mvr = 9 × 10–31 × 2.2 × 106 × 0.53 × 10–10 = 1.0494 × 10–34 Js
Also, 34 6.610 223.142 h = 34 1.050310Js=
Hence 2 h L =
Know Yourself
1. Determine the angular momentum of a car of mass 1500 kg moving in a circular track of radius 50 m with a speed of 40ms–1 [A]
2. Mass of an electron is 9.0 × 10–31 kg. It revolves around the nucleus of an atom in a circular orbit of radius 4.0Å with a speed of 6.0 × 106 ms –1. Calculate the angular momentum of the electron. [A]
3. The position of aparticle isgivenby: (2) rijk =+− andmomentum (342) Pijk =+− . The angular momentum is perpendicular to
(a) X-axis
(b) Y-axis
(c) Z-axis
(d) Line at equal angles to all the three axes [A]
4. Show that if the particle moves only in the x-y plane the angular momentum has only a z-component. [U]
SYSTEM OF PARTICLES AND ROTATIONAL MOTION _XI P – 06 – 28




..................................................................................................................................
.................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. ..................................................................................................................................
.................................................................................................................................. ..................................................................................................................................
9. RELATION BETWEEN TORQUE AND ANGULAR MOMENTUM
• The physical quantities, moment of a force and angular momentum, have an important relation between them. It is the rotational analogue of the relation between force and linear momentum. For deriving the relation in the context of a single particle, we differentiate Lrp = with respect to time, ( ) dLd rp dtdt =
• Applying the product rule for differentiation to the right hand side, ( ) ddrdp rppr dtdtdt =+
• Now, the velocity of the particle is dr v dt = and pmv =
• Because of this 0 dr v dt m pv = = , as the vector product of two parallel vectors vanishes.
• Further, since dp F dt = , dp rrF dt ==
• Hence ( ) d rp dt = or dL dt =
• Thus, the time rate of change of the angular momentum of a particle is equal to the torque acting on it. This is the rotational analogue of the equation dp F dt = , which expresses Newton's second law for the translational motion of a single particle.
10. TORQUE & ANGULAR MOMENTUM FOR A SYSTEM OF PARTICLES
• To calculate the total angular momentum of a system of particles about a specific point, we must vectoriallysum the angularmomenta of individual particles. Thus,for asystem comprising nparticles:
• The angular momentum of the ith particle is defined as:
iii Lrp =
where ir is the position vector of the ith particle with respect to a given origin and ( ) iipmv = is the linear momentum of the particle (mi being its mass and iv denoting its velocity). The total angular momentum of a system of particles can then be expressed as
• This definition is an extension of the concept of angular momentum from a single particle to a system of particles.
Using. dL dt = , we get
SYSTEM OF PARTICLES AND ROTATIONAL MOTION_XI P – 06 – 29
12 1 ...... n ni i LLLLL = =+++=
11
nn iiii ii LLrp == == ...(1)
• where i is the torque acting on the tth particle;
• The force iF on the ith particle is the vector sum of external forces ext iF acting on the particle and the internal forces int iF exerted on it by the other particles of the system.
• Consequently, we can separate the contributions of external and internal forces to the total torque as follows:
• Assuming Newton's third law of motion holds, implying that forces between any two particles within the system are equal and opposite and act along the line joining the two particles, we can deduce that the contribution of internal forces to the total torque on the system is zero, since the torque resulting from each action reaction pair of forces is zero.
• We thus have, int
= 0 and therefore ext
• Since
, it follows from Eq. (2) that
• Hence, the time rate of change of the total angular momentum of a system of particles about a specific point (considered as the origin of our frame of reference) is equal to the sum of the external torques (i.e., torques due to external forces) acting on the system, all taken about the same point. Equation (3) isanextensionoftheprincipleobservedinsingle-particlecases.Itisessentialtonotethatwhendealing with just one particle, there are no internal forces or torques. Eq.(3) is the rotational analogue of
• It applies to any system of particles, whether it's a rigid body or comprises individual particles with various internal motions.
Know Yourself
1. Twoparticles,eachofmass��andspeed��,travelinoppositedirectionsalongparallel linesseparated by a distance ��. Show that the angular momentum vector of the two particle system is the same whatever be the point about which the angular momentum is taken. [U]
SYSTEM OF PARTICLES AND ROTATIONAL MOTION _XI P – 06 – 30 ( ) i i i dL dLd L dtdtdt === ...(2)
iii rF =
11 nn iiii ii rF == == iextint =+ , where 1 n ext extii i rF = = and int 1 n int ii i rF = =
=
1 n i i = =
ext dL dt = ...(3)
ext dp F
dt =




..................................................................................................................................
.................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. ..................................................................................................................................
.................................................................................................................................. ..................................................................................................................................
11. EQUILIBRIUM OF RIGID BODIES
• When subjected to external forces, a rigid body can exhibit two types of motion:
(i) translational motion, wherein all particles move with identical velocities, and
(ii) rotational motion about an axis.
• The term ‘equilibrium’ signifies balance.
• A body may be in partial equilibrium, i.e., it may be in translational equilibrium and not in rotational equilibrium, or it may be in rotational equilibrium and not in translational equilibrium.
• Consider a light (i.e. of negligible mass) rod (AB) as shown in Fig(A). At the two ends (A and B) of which two parallel forces, both equal in magnitude and acting along same direction are applied perpendicular to the rod.

• Let C be the midpoint of AB, CA = CB = a the moment of the forces at A and B will both be equal in magnitude (aF), but opposite in sense as shown. The net moment on the rod will be zero. The system will be in rotational equilibrium, but it will not be in translational equilibrium; F0
• The force at B in Fig(A) is reversed in Fig(B). Thus, we have the same rod with two forces of equal magnitudebut actingin opposite directions appliedperpendiculartotherod, one at end A andthe other at end B. Here the moments of both the forces are equal, but they are not opposite; they act in the same sense and cause anticlockwise rotation of the rod. The total force on the body is zero; so the body is in translational equilibrium; but it is not in rotational equilibrium. Although the rod is not fixed in any way, it undergoes pure rotation (i.e. rotation without translation).

• A rigid body is deemed to be in a state of equilibrium when both its linear momentum and angular momentum remain unchanging over time. Consequently, for a body in equilibrium, the centre of mass experiences zero linear acceleration, and the rigid body exhibits zero angular acceleration about any axis.
• A body subjected to multiple forces will achieve equilibrium only if it simultaneously fulfils the following two equilibrium conditions:
(i) Translational Equilibrium: The vector sum of all external forces acting upon the body must equate to zero, as any non-zero resultant force would result in linear acceleration. Hence, for translational equilibrium,
• Applying Newton's second law,
SYSTEM OF PARTICLES AND ROTATIONAL MOTION_XI P – 06 – 31
Fig (A) Fig(B)
0 extF = or 0, 0and 0 xyz FFF ===
or Σ0 CM cxtCM dv FMaM dt === or 0or constant. CM CM dv v dt ==
• This signifies that a body experiencing translational equilibrium will either remain at rest ( v = 0) or move with constant velocity ( v = constant). If the body is stationary, it is referred to as being in a state of static equilibrium. If the body is in uniform motion along a straight path, it is considered to be in dynamic equilibrium.
(ii) Rotational Equilibrium: To achieve rotational equilibrium, the sum of torques resulting from all forces acting on the body about any chosen point must be zero. Otherwise, these torques would induce angular acceleration. Hence, for rotational equilibrium, ΣΣ0 ext extii rF ==
• In the context of rotational equilibrium, the selection of the rotation point (or fixed point) holds no significance. If the total torque sums to zero around one point,it will also sum to zero around any other point when the body is in equilibrium.
11.1 Principle of Moments
• An ideal lever can be described as a slender rod with negligible mass, hinged at a specific point along its length known as the fulcrum. A common illustration of a lever is a seesaw found on a children's playground. In this setup, two forces, denoted as F₁ and F₂, which are typically parallel and perpendiculartothelever,areappliedtotheleveratdistancesd₁andd₂,respectively,from thefulcrum, as depicted in Figure
• The lever represents a mechanical equilibrium system. Let's denote R as the reaction force from the support at the fulcrum, which is directed in the opposite direction to forces F₁ and F₂. For translational equilibrium, we have the equation:

R
F1
F2 = 0 ...(1)
• To consider rotational equilibrium, we calculate the moments about the fulcrum, and the sum of these moments must equal zero:
d1F1 – d2F2 = 0 ...(2)
• Usually, counter clockwise moments are taken as positive, while clockwise moments are considered negative. It's worth noting that R acts directly at the fulcrum itself, resulting in a zero moment about the fulcrum.
• In the context of the lever, force F1 typically represents a weight that needs to be lifted, often referred to as the load. The distance from the fulcrum to the load is called the load arm and is denoted as d1. Force F2, on the other hand, represents the effort applied to lift the load, and the distance of this effort from the fulcrum is known as the effort arm, denoted as d2 Eq. (2) can be written as
d1F1 = d2F2 or load arm × load = effort arm × effort
• The above equation expresses the principle of moments for a lever. Incidentally the ratio F1/F2 is called the Mechanical Advantage (M.A.);
SYSTEM OF PARTICLES AND ROTATIONAL MOTION _XI P – 06 – 32
–
–
12 21 M.A. Fd Fd ==
• When the effort arm, denoted as d2, exceeds the length of the load arm, it results in a mechanical advantage greater than one. A mechanical advantage greater than one signifies that a relatively small effort can be employed to raise a substantial load. There are numerous instances of levers in your surroundings aside from the seesaw. For instance, the beam of a balance operates as a lever. You can explore more examples and identify the fulcrum, effort, effort arm, load, and load arm for each lever in these cases.
• It’s worth noting that the principle of moments remains applicable even when the parallel forces F1 and F2 are not acting perpendicularly but at some angle to the lever.

Key Concept
A body is said to be in equilibrium if it simultaneously fulfils the following two equilibrium conditions:
12. CENTRE OF GRAVITY
Many of you might have had the experience of balancing a notebook on the tip of your finger. A similar experiment, as depicted in Figure - 15, is easy to carry out. You can take an irregularly shaped piece of cardboard with a mass M and a slender pointed object such as a pencil. Through trial and error, you can find a point G on the cardboard where it can be balanced on the tip of the pencil, maintaining a horizontal orientation for the cardboard. This point of balance represents the centre of gravity (CG) of the cardboard. The tip of the pencil exerts an upward force, resulting in mechanical equilibrium for the cardboard.
As illustrated in Figure - 15, the reaction at the tip is equal in magnitude but opposite in direction to Mg (the weight of the cardboard). Consequently, the cardboard is in translational equilibrium. Furthermore, it is also in rotational equilibrium; otherwise, due to an unbalanced torque, it would tilt and fall. There are torques actingonthecardboardduetothegravitationalforces,suchasm1g,m2g,andsoforth,actingontheindividual particles composing the cardboard.

SYSTEM OF
AND ROTATIONAL MOTION_XI P – 06 – 33
PARTICLES
0and Σ0extextF ==
Fig. 15
The CG of the cardboard is so located that the total torque on it due to the forces m1g, m2g .... etc. is zero. If ri is the position vector of the i th particle of an extended body with respect to its CG, then the torque about the CG, due to the force of gravity on the particle is iiirmg = . The total gravitational torque about the CG is zero, i.e.
We may therefore, define the CG of a body as that point where the total gravitational torque on the body is zero.
We notice that in Eq. (1), g is the same for all particles, and hence it comes out of the summation. This gives, since g is non-zero,
Remember that the position vectors ( r ) are taken with respect to the CG. Now, if the sum is zero, the origin must be the centre of mass of the body. Thus, the centre of gravity of the body coincides with the centre of mass in uniform gravity or gravity- free space.

We note that this is true because the body being small, g does not vary from one point of the body to the other. If the body is so extended that g varies from part to part of the body, then the centre of gravity and centre of mass will not coincide. Basically, the two are different concepts. The centre of mass has nothing to do with gravity. It depends only on the distribution of mass of the body.
Figure - 16 illustrates another way of determining the CG of an irregular shaped body like a cardboard. If you suspend the body from some point like A, the vertical line through A passes through the CG. We mark theverticalAA1.WethensuspendthebodythroughotherpointslikeBandC.Theintersectionoftheverticals gives the CG. Since the body is small enough, the method allows us to determine also its centre of mass.
Key Concept
1. The centre of gravity of an extended body is that point where the total gravitational torque on the body is zero.
2. The centre of gravity of a body coincides with its centre of mass only if the gravitational field does not vary from one part of the body to the other.

SYSTEM OF PARTICLES AND ROTATIONAL MOTION _XI P – 06 – 34
0 giiirmg === (1)
0 ii mr = … (2)
Fig. 16




..................................................................................................................................
.................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. ..................................................................................................................................
.................................................................................................................................. ..................................................................................................................................
Illustration-14
A metal bar 70 cm long and 4.00 kg in mass supported on two knifeedges placed 10 cm from each end. A 6.00 kg load is suspended at 30 cm from one end. Find the reactions at the knife-edges. (Assume the bar to be of uniform cross section and homogeneous.)
Solution: Figure shows the rod AB, the positions of the knife edges K1 and K2, the centre of gravity of the rod at G and the suspended load at P.
Note the weight of the rod W acts at its centre of gravity G. The rod is uniform in cross section and homogeneous; hence G is at the centre of the rod;
AB = 70 cm.
AG = 35 cm. AP = 30 cm, PG = 5 cm, AK1 = BK2 = 10 cm and
K1 G = K2 G = 25 cm.
Also, W= weight of the rod = 4.00 kg and W1 = suspended load = 6.00 kg; R1 and R2 are the normal reactions of the support at the knife edges. For translational equilibrium of the rod,
R1 + R2 – W1 – W = 0.
… (i)
Note W1 and W act vertically down and R1 and R2 act vertically up. For considering rotational equilibrium, we take moments of the forces. A convenient point to take moments about is G. The moments of R2 and W1 are anticlockwise (+ve), whereas the moment of R1 is clockwise (–ve).
For rotational equilibrium,
R1 (K1G) + W1 (PG) + R2 (K2 G) = 0 … (ii)
It is given that W=4.00 g N and W1 = 6.00 g N, where g = acceleration due to gravity. We take g = 9.8 m/s2
With numerical values inserted, from (i) (R1 + R2 – 4.00g – 6.00g = 0 or R1 + R2 = 10.00g N … (iii) =98.00 N
From (ii), –0.25R1 + 0.05W1 + 0.25R2 = 0 or R1 – R2 = 1.2 g N = 11.76 N. (iv)
From (iii) and (iv), R1 = 54.88 N, R2 = 43.12 N
Thus the reactions of the support are about 55 N at K1 and 43 N at K2
SYSTEM OF PARTICLES AND ROTATIONAL MOTION_XI P – 06 – 35
–
Illustration-15
A 3m long ladder weighing 20 kg leans on a frictionless wall. Its feet rest on the floor 1 m from the wall as shown in Fig. Find the reaction forces of the wall and the floor.
Solution: The ladder AB is 3 m long, its foot A is at distance AC = 1 m from the wall. From Pythagoras theorem, BC = 2√2 m. The forces on the ladder are its weight W acting at its centre of gravity D, reaction forces F1 and F2 of the wall and the floor respectively. Force F1 is perpendicular to the wall, since the wall is frictionless. Force F2 is resolved into two components, the normal reaction N and the force of friction F. Note that F prevents the ladder from sliding away from the wall and is therefore directed toward the wall.

For translational equilibrium, taking the forces in the vertical direction, N – W = 0 … (i)
Taking the forces in the horizontal direction, F – F1 = 0. … (ii)
For rotational equilibrium, taking the moments of the forces about A, 2√2 F1 – (1/2)W = 0 (iii)
Now W = 20 g = 20 × 9.8 N = 196.0 N
From (i) N = 196.0 N
From (iii) F1 = W/4√2 = 196.0/4√2 = 34.6 N
From (ii)
F = F1 = 34.6 N
F2 = √(F2 + N2) = 199.0 N
The force F2 makes an angle α with the horizontal, tan α = N/F = 4√2, α = tan–1 (4√2) ≈ 80°
SYSTEM OF PARTICLES AND ROTATIONAL MOTION _XI P – 06 – 36
Illustration-16
As shown in Fig., the two sides of a step ladder BA and CA are 1.6 m long and hinged at A. A rope DE, 0.5 m is tied half way up. A weight 40 kg is suspended from a point F, 1.2 m from B along the ladder BA Assuming the floor to be frictionless and neglecting the weight of the ladder, find the tension in the rope and forces exerted by the floor on the ladder. (Take g = 9.8 m/s2).
Solution: As shown in Fig., let NB and NC be the normal reactions of the floor at B and C respectively and T be the tension in the rope DE. Then
NB + NC = W = 40 × 9.8 N
or NB + NC = 392 N
Consider the portion AC of the ladder. Balancing torques about A, we get NC × LC = T × AG
From the geometry of the figure, we get LC = 2GE = DE = 0.5 m or GE = 0.25 m

22AGAEGE =− ( ) ( ) 220.80.25=−
0.57750.76m ==
SYSTEM OF PARTICLES AND ROTATIONAL MOTION_XI P – 06 – 37
Hence NC × 0.5 = T × 0.76 or T = 0.66 NC … (2)
Now consider the portion AB of the ladder. Balancing the torques about A, we get
NB × BL = W × JL + T × AG
But 11 0.50.125 44 JLDEm ===
BL = DE = 0.5 m, W = 392 N
∴ NB × 0.5 – 392 × 0.125 = T × 0.76 or NB × 0.5 – 392 × 0.125 = 0.66 NC × 0.76 [Using (2)]
On solving (1) and (3), we get
NB = 245 N, NC = 245 – 98 = 147 N, and T = 0.66 NC = 0.66 × 147 = 97 N
Know Yourself
1. A non-uniform bar of weight W is suspended at rest by two strings of negligible weight as shown in Fig. The angles made by the strings with the vertical are 36.9° and 53.1° respectively. The bar is 2 m long. Calculate the distance d of the centre of gravity of the bar from its left end. [A]

2. A car weighs 1800 kg. The distance between its front and back axles is 1.8 m. Its centre of gravity is 1.05 m behind the front axle. Determine the force exerted by the level ground on each front wheel and each back wheel. [A]
3. A metre stick is balanced on a knife edge at its centre. When two coins, each of mass 5 g are put one on top of the other at the 12.0 cm mark, the stick is found to be balanced at 45.0 cm. What is the mass of the metre stick? [A]
SYSTEM OF PARTICLES AND ROTATIONAL MOTION _XI P – 06 – 38




..................................................................................................................................
.................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. ..................................................................................................................................
.................................................................................................................................. ..................................................................................................................................
13. MOMENT OF INERTIA
The role of moment of inertia in rotational motion is analogous to the role of mass in linear motion. It is a property inherent to a body that resists any alteration in its state of either rest or uniform rotation. In accordance with Newton's first law of motion, every object persists in its current state, be it at rest or in uniform linear motion, unless an external force intervenes to modify that state. This inherent tendency of an object to maintain its state of rest or uniform linear motion is termed inertia. Likewise, a body that is rotating about a specific axis strives to preserve its state of uniform rotation, unless an external torque is exerted to modify that condition. This property of a body, which causes it to resist the torque's attempt to change its state of rest or uniform rotation about an axis, is known as rotational inertia or moment of inertia.

Let us try to get an expression for the kinetic energy of a rotating body. We know that for a body rotating about a fixed axis, each particle of the body moves in a circle with linear velocity given by v = rω
For a particle at a distance ri from the axis, the linear velocity is
The kinetic energy of motion of this particle is
where mi is the mass of the particle. The total kinetic energy K of the body is then given by the sum of the kinetic energies of individual particles,
Here n is the number of particles in the body. Note ω is the same for all particles. Hence, taking ω out of the sum,
If we compare this with
is the analogue of mass in rotational motion
SYSTEM OF PARTICLES AND ROTATIONAL MOTION_XI P – 06 – 39
vi = riω.
222 1 11 22iiii kmvmr ==
( ) 22 11 1 2 nn iii ii Kkmr == ==
22 1 1 2 n ii i Kmr = =
2 1 2 Kmv = 2 1 n ii i mr =
We define it a new parameter characterising the rigid body, called the moment of inertia I, given by
With this definition, 2 1 2 KI =
The moment of inertia of a rigid body about a fixed axis is defined as the sum of the products of the masses of the particles constituting the body and the squares of their respective distances from the axis of rotation.
13.1 Factors on which the Moment of Inertia Depends

The role of moment of inertia in rotational motion is analogous to the role of mass in linear motion. It is a property inherent to a body that resists any alteration in its state of either rest or uniform rotation. The moment of inertia of an object quantifies how its various components are spread out at varying distances from the axis of rotation. Unlike mass, it is not a constant value and is contingent on the position and alignment of the axis of rotation concerning the entire body. The moment of inertia of a body depends on
(i) Mass of the body
(ii) Size and shape of the body.
(iii) Distribution of mass about the axis of rotation.
(iv) Position and orientation of the axis of rotation
Key Concept
1. The moment of intertia of a rigid body about an axis is defined by the formula 2
Imr =
= where ri is the perpendicular distance of the ith point of the body from the axis. The kinetic energy of rotation is 2 1 2 KI =
2. Let m1 and m2 be two masses distant r from each-other then Moment of Inertia of two point masses about their centre of mass is
TO UNDERSTAND THIS CONCEPT REFER TO ADVANCED MODULE.
SYSTEM OF PARTICLES AND ROTATIONAL MOTION _XI P – 06 – 40
2 1 n ii i Imr = =
1
ii i
n
22 12 12 mm Irr mm == + where 12 12 mm mm = + is known as reduced mass μ < m1
μ < m2
and
Illustration-17
Three particles of masses 1 g, 2 g and 3 g are kept at points (2 cm, 0), (0, 6 cm), (4 cm, 3 cm). Find moment of inertia of all three particles (in gm- cm 2) about, (a) x- axis (b) y-axis (c) z-axis

Solution:
(a) About x-axis
123 x IIII =++
222 112233 mrmrmr=++
Here, perpendicular distance of the particle from x-axis
( )( ) ( )( ) ( )( ) 222 1 102633 I =++
2 99gcm =
(b) About y-axis =++
222 y112233 Imrmrmr
Here, r = perpendicular distance of the particle from y-axis
( )( ) ( )( ) ( )( ) 222 122034 y I =++
2 52 gcm=−
(c) About z-axis
222 112233 z Imrmrmr =++
Here, r = perpendicular distance of the particle from z-axis.
( ) ( ) 22 0 345 rcm =+=
( )( ) ( )( ) ( ) 222 122635 z I =++
2 151 gcm=−
Illustration-18
Three mass points m1, m2 and m3 are located at the vertices of an equilateral triangle of length a. What is the moment of inertia of the system about an axis along the altitude of the triangle passing through m1?
SYSTEM OF PARTICLES AND ROTATIONAL MOTION_XI P – 06 – 41
Solution: As shown in Fig, the axis of rotation passes through m1. The distances of m1, m2 and m3 from the axis of rotation are 0, a/2 and a/2 respectively.

∴ M.I. of the system about the altitude through m1 is
Know Yourself
1. Three balls of masses 1, 2 and 3 kg respectively are arranged at the corners of an equilateral triangle of side 1 m. What will be the moment of inertia of the system about an axis through the centroid and perpendicular to the plane of the triangle? [A]
2. Four particles of masses 4 kg, 2 kg, 3 kg and 5 kg are respectively located at the four corners A,B,C and D of a square of side 1 m as shown in Fig. Calculate the moment of inertia of the system about
(i) an axis passing through thepoint of intersection of the diagonals and perpendicular to the plane of the square,

(ii) the side AB, and
(iii) the diagonal BD. [A]
3. The oxygen molecule has a mass of 5.30 × 10–26 kg and a moment of inertia of 1.94 × 10–46 kg m2 about an axis through its centre perpendicular to the lines joining the two atoms. Suppose the mean speed of such a molecule in a gas is 500 m/s and that its kinetic energy of rotation is two thirds of its kinetic energy of translation. Find the average angular velocity of the molecule. [A]
SYSTEM OF PARTICLES AND ROTATIONAL MOTION _XI P – 06 – 42
222 112233 Imrmrmr =++ ( ) 22 2 123 0 22 aa mmm =++ or ( ) 2 23 4 a Imm =+




..................................................................................................................................
.................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. ..................................................................................................................................
.................................................................................................................................. ..................................................................................................................................
13.2 MOMENT OF INERTIA OF CONTINUOUS BODY
For calculating moment of inertia of a continuous body, we first divide the body into suitably chosen infinitesimal elements. The choice depends on symmetry of body. Consider an element of the body at a distance r from the axis of rotation. The moment of inertia of this element about the axis we define as (dm) r 2 and the discrete sum over particles becomes integral over the body:
13.3 Radius of Gyration
Radius of gyration of a body about a given axis is the perpendicular distance of a point from the axis, where if whole mass of the body were concentrated, the body shall have the same moment of inertia as it has with the actual distribution of mass.
When square of radius of gyration is multiplied with the mass of the body gives the moment of inertia of the body about the given axis. 2 I IMkork M
Here k is called radius of gyration.
13.4 Theorem of Perpendicular axes
The moment of inertia of a plane lamina about an axis perpendicular to its plane is equal to the sum of the moments of inertia of the lamina about any two mutually perpendicular axes in its own plane and intersecting each other at the point where the perpendicular axis passes through the lamina.
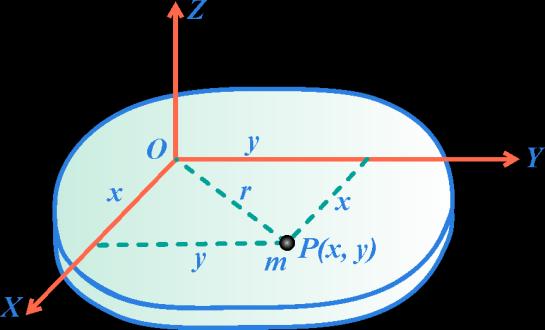
Consider a plane lamina lying in the XOY plane. It can be assumed to be made up of large number of particles. Consider one such particle of mass m situated at point P(x, y). Clearly, the distances of the particle from X, Y and Z-axes are y, x and r respectively such that
r 2 = y 2 + x2
Moment inertia of the particle about X-axis = my 2
∴ Moment of inertia of whole lamina about X-axis is
Ix = Σ my 2
Moment of inertia of whole lamina about Y-axis is
SYSTEM OF PARTICLES AND ROTATIONAL MOTION_XI P – 06 – 43
( ) 2Idmr = dm r
==
Iy = ∑ mx 2
Moment of inertia of whole lamina about Z-axis is
Iz = Σ mr 2 = Σ m(y2 + x 2)
= Σ my 2 + Σ mx 2
Iz = Ix + Iy
Key Concept
For Iz = Ix + Iy, x and y axis must be on plane lamina and z axis must be perpendicular to the plane.
13.5 Theorem of Parallel axes
The moment of inertia of a body about any axis is equal to its moment of inertia about a parallel axis through its centre of mass plus the product of the mass of the body and the square of the perpendicular distance between the two parallel axes.


Let I be the moment of inertia of a body of mass M about an axis PQ. Let RS be a parallel axis passing through the centre of mass C of the body and at distance d from PQ. Let ICM be the moment of inertia of the body about the axis RS
Consider a particle P of mass m at distance x from RS and so at distance (x + d) from PQ.
Moment of inertia of the particle about axis PQ = m(x + d)2

∴ Moment of inertia of the whole body about the axis PQ is
I = Σ m(x + d)2 = Σ m(x2 + d2 + 2xd)
= Σ mx 2 + Σ md2 + Σ 2mxd
Now Σ mx 2 = ICM
Σ md2 = (Σm)d2 = Md2
Σ 2mxd = 2d Σ mx = 2d × 0 = 0
This is because a body can balance itself about its centre of mass, so the algebraic sum of moments (∑ mx of masses of all its particles about the axis RS is zero).
Hence I = ICM + Md2
Key Concept
It is important to note that for I = ICM + Md2, ICM is the moment of Inertia about the axis passing through the centre of mass.
SYSTEM OF PARTICLES AND ROTATIONAL MOTION _XI P – 06 – 44
13.6 Moment of Inertia of a Thin Ring
(a) M.I. of a ring about an axis through its centre and perpendicular to its plane.
Consider a thin uniform circular ring of radius R and mass M. As shown in Fig. we wish to determine its moment of inertia I about an axis YY' passing through its centre O and perpendicular to it. The ring can be imagined to be made of a large number of small elements. Consider one such element of length dx.
Length of the ring = circumference = 2πR
Mass per unit length of ring
Mass of the small element
2 M R =
2 M dx R =
Moment of inertia of the small element about the axis YY',
2 22 MMR dIdxRdx R
The small elements lie along the entire circumference of the ring i.e., from x = 0 to x = 2πR. Hence the moment of inertia of the whole ring about the axis YY' will be


I
.
(b) M.I. of a ring about any diameter.
According to the theorem of perpendicular axes, the moment of inertia about an axis YY' through O and perpendicular to the ring is equal to sum of its moments of inertia about two perpendicular diameters AB and CD, as shown in Fig.
of the ring about any diameter.
MOTION_XI P – 06 – 45
SYSTEM OF PARTICLES AND ROTATIONAL
==
00 22 RR MRMR Idxdx == ( ) 2 0 20 22 R MRMR xR ==−
22
=
2
MR
IAB + ICD = IYY’ ID + ID = MR2 2 1 2 D IMR. =
ID
M.I.
Here
is the
(c) M.I. of a ring about a tangent in its plane. Let IT be the moment of inertia of the ring about the tangent EBF
Applying the theorem of parallel axes, we get IT = M.I. about diameter CD + MR2 22 1 2 MRMR=+ or 2 3 2 T IMR. =
(d) M.I. of a ring about a tangent perpendicular to its plane. Let IT be the moment of inertia of the ring about the axis PAQ tangent to the plane of the ring.

Applying the theorem of parallel axes, IPQ = IYY' + MR2 = MR2 + MR2 or
IT = 2MR2
13.7 Moment of Inertia of a Uniform Circular Disc
M.I. of a circular disc about an axis through its centre and perpendicular to its plane. As shown in Fig, consider a uniform disc of mass M and radius R. Suppose YY' is an axis passing through the centre O of the disc and perpendicular to its plane.

Area of the disc = πR2
Mass per unit area of the disc 2 M R
=
SYSTEM OF PARTICLES AND ROTATIONAL MOTION _XI P – 06 – 46
We can imagine the disc to be made up of a large number of concentric rings, whose radii vary from O to R. Let us consider one such concentric ring of radius x and width dx.
Area of the ring
= Circumference × Width = 2πx × dx
Mass of the concentric ring, 22 2 2 MMxdx mxdx RR
Moment of inertia of the concentric ring about the axis YY'

3 22 22 22 MxdxMxdx dImxx RR ===
The moment of inertia of the whole disc about the axis YY' can be obtained by integrating the above expression between the limits O to R
22 RR MxdxM Ixdx RR 22 0 42
R MxMM RR RRR ==−= 2 1 2 IMR =
Know Yourself
1. Find the Moment of Inertia of a disc about any diameter. [U]
2. Find the Moment of Inertia of a disc about a tangent perpendicular to its plane. [U]
3. Find the Moment of Inertia of a disc about a tangent in its plane. [U]
SYSTEM OF PARTICLES AND ROTATIONAL MOTION_XI P – 06 – 47
==
3 3 22 00 == 4 44 222 0




..................................................................................................................................
.................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. ..................................................................................................................................
.................................................................................................................................. ..................................................................................................................................
13.8 Moment of Inertia of a Thin Uniform Rod
M.I. of a thin uniform rod about a perpendicular axis through its centre.

Consider a thin uniform rod AB of length L and mass M, free to rotate about an axis YY' through its centre O and perpendicular to its length.
∴ Mass per unit length of rod M L =
Consider a small mass element of length dx at a distance x from O
Mass of the small element M dx L =
Moment of inertia of the small element about YY'
Themoment ofinertiaofthewholerodabouttheaxis YY' canbeobtainedbyintegratingtheaboveexpression between the limits x = –L/2 and x = +L/2
Let k be the radius of gyration of the rod about the axis YY'. Then
= or 23 L k = .
Thus, the radius of gyration of a uniform thin rod rotating about an axis passing through its centre and perpendicular to its length is 23 L/.
SYSTEM OF PARTICLES AND ROTATIONAL MOTION _XI P – 06 – 48
( )2 2 M dIMassdistancedxx L ==
2 2 2 L/ L/ M IdIxdx L + == 2 23 2 2 2 3 L/ L/ L/ L/ MMx xdx LL + + == 33 322 MLL L =−− 333 38834 MLLML LL =+= 2 12
I = Radius
ML
of Gyration
I
2 2 12 ML Mk =
2 2 12 L k
= Mk2
or
Know Yourself
1. Derive an expression for the moment of inertia of a thin uniform rod about an axis passing through its one end and perpendicular to its length. Also determine its radius of gyration about the same axis. [U]

2. Write an expression for the moment of inertia of hollow cylinder of mass M and radius R about its own axis. [U]
3. Derive an expression for the moment of inertia of solid cylinder of mass M and radius R about its own axis. [U]
4. Derive an expression for the moment of inertia of a uniform solid cylinder about an axis passing through its centre and perpendicular to its length. [A]

5. Fourthinrodsofsamemass M andsamelength l,form asquareas shownin figure.Moment of inertia of this system about an axis through centre O and perpendicular to its plane is [A]
FOR MORE INSIGHTFUL AND INTRIGUING FACTS REFER TO ADVANCED MODULE.
13.9 Moment of Inertia of a Solid Sphere about its Diameter
Consider a uniform solid sphere of mass M and radius R. We wish to determine its moment of inertia about diameter AB.
Wecanimaginethespheretobemadeupofalargenumber ofthinslicesplacedperpendiculartothediameter AB. Consider one such slice of thickness dx placed at distance x from the centre O
Radius of the elementary slice 22Rx=−
SYSTEM OF PARTICLES AND ROTATIONAL MOTION_XI P – 06 – 49
(a) 2 4 3 Ml (b) 2 3 Ml (c) 2 6 Ml (d) 2 2 3 Ml
Volume of the sphere 3 4 3 R
Mass per unit volume, 3 3 4 M R
=
=
of inertia of the thin slice about the axis AB passing through its centre and perpendicular to its plane,
The moment of inertia of the whole sphere about the diameter AB can be obtained by integrating the above expression between the limits x = 0 and x = R and multiplying the result by 2 to include both halves of the sphere.
Know Yourself
1. Derive an expression for the moment of inertia of the hollow sphere about a diameter. [U]
2. Derive an expression for the moment of inertia of the solid sphere about a tangent. [U]
3. Derive an expression for the moment of inertia of the hollow sphere about a tangent. [U]
4. A circular ring and a circular disc of the same radius have the same moment of inertia about axis passing through their centres and perpendicular to their planes. What is the ratio of their masses? [U]
SYSTEM OF PARTICLES AND ROTATIONAL MOTION _XI P – 06 – 50 Volume
× thickness ( ) ( ) 2 2222 RxdxRxdx =−=− Mass
( ) 22 3 3 4 M VolumeRxdx R ==− ( ) 22 3 3 4 MRxdx R =
( )2 1 2 dIMassradius = ( ) ( ) 22 22 3 3 1 24 MRxdx Rx R =− ( )2 22 3 3 8 MRxdx R =
of the elementary slice = Area
of the elementary slice
Moment
( )2 22 3 0 3 22 8 R MRxdx IdI R == ( )2 22 3 0 23 8 R M Rxdx R =− ( ) 4224 3 0 3 2 4 R M RRxxdx R =−+ 4224 3 000 3 2 4 RRR M RdxRxdxxdx R =−+ 35 42 3 0 00 3 2 435 RR R Mxx RxR R =−+ ( ) 35 42 3 3 0200 435 MRR RRR R =−−−+− 5 555 33 3238 435415 MRM RRR RR =−+= or 2 2 5 IMR. =




..................................................................................................................................
.................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. ..................................................................................................................................
.................................................................................................................................. ..................................................................................................................................
14. RELATION BETWEEN TORQUE & MOMENT OF INERTIA
When a torque acts on a body capable of rotation about an axis, it produces an angular acceleration in the body. If the angular velocity of each particle is then the angular acceleration, d dt = will be same for all particles of the body. The linear acceleration will depend on their distances r1, r2, …. rn from the axis of rotation.

As shown in Fig, consider a particle P of mass m1 at a distance r1 from the axis of rotation. Let its linear velocity be v1.
Linear acceleration of the first particle, a1 = r1 α
Force acting on the first particle, F1 = m1r1α
Moment of force F1 about the axis rotation is
2
11111 Frmr ==
Total torque acting on the rigid body is
But
mr 2 = I, moment of inertia of the body about the given axis
Torque = Moment of inertia × Angular acceleration
SYSTEM OF PARTICLES AND ROTATIONAL MOTION_XI P – 06 – 51
123 n =++++
112233 nn mrmrmr...mr =++++ ( ) 2222 112233 nn mrmrmr...mr =++++ ( ) 2 mr =
2222
Σ
∴ τ = Iα
Illustration-19
A wheel of mass 25 kg has a radius of 0.2 m. What force should be applied tangentially to the rim of the wheel so that it acquires an angular acceleration of 2rads–2 ?
Solution: Here M = 25 kg, R = 0.2 m, α = 2rads–2
M.I. of the wheel about its axis, ( )2 2211 250205 22 IMR..kgm ===
As torque, τ = F.R = Iα
∴ Force, 052 5 02 I. FN. R. === .
Illustration-20
A torque of 10 Nm is applied to a wheel of mass 10 kg and radius of gyration 50 cm. What is the resulting angular acceleration?
Solution: Here
τ = 10 Nm, M = 10 kg, K = 0.50 m, α = ?
As τ = Iα = MK
Illustration-21
A grindstone has a moment of inertia of 6 kg m2. A constant torque is applied and the grindstone is found to have a speed of 150 rpm, 10 seconds after starting from rest. Calculate the torque.
Solution: Here I = 6 kg m2, t = 10 s, ω0 = 0
SYSTEM OF PARTICLES AND ROTATIONAL MOTION _XI P – 06 – 52
α ( ) 2 2 2 10 4 10050
MK . ===
2
rads.
1 5 225 2 vrads === 2 0 50
rads t ===
1505 150 602 rpmrpsrps===
102
2
===
Torque, 63
INm.
Illustration-22
A cord of negligible mass is wound round the rim of a fly wheel of mass 20 kg and radius 20 cm. A steady pull of 25 N is applied on the cord as shown in Fig. The flywheel is mounted on a horizontal axle with frictionless bearings.
(a) Compute the angular acceleration of the wheel.
(b) Find the work done by the pull, when 2 m of the cord is unwound.
(c) Find also the kinetic energy of the wheel at this point. Assume that the wheel starts from rest.
(d) Compare answers to parts (b) and (c).
Solution:
(a) We use Iα = τ the torque τ = FR = 25 × 0.20 Nm (as R = 0.20 m) = 5.0Nm
I = Moment of inertia of flywheel about its axis ( )2 2 2 2002 04
α = angular acceleration

= 5.0 Nm/0.4 kg m2 = 12.5 rad s –2
(b) Work done by the pull unwinding 2 m of the cord
= 25 N × 2 m = 50 J
(c) The angular displacement θ = length of unwound string/radius of wheel = 2 m/0.2 m = 10rad since the wheel starts from rest, 0 0 = Let ω be the final angular velocity. Now, 22 0 2 , =+
SYSTEM OF PARTICLES AND ROTATIONAL MOTION_XI P – 06 – 53
===
I
22 . MR .kgm
=
2
=+=
0212.510250
(d) The answers are the same, i.e. the kineticenergy gainedby the wheel = work done by the force. There is no loss of energy due to friction.
Know Yourself
1. A cylinder of length 20 cm and radius 10 cm is rotating about its central axis at an angular speed of 100rad/s. What tangential force will stop the cylinder at a uniform rate in 10 seconds? The moment of inertia of the cylinder about its axis of rotation is 0.8 kgm2 [A]
2. A flywheel of moment of inertia 107 g cm2 is rotating at a speed of 120 rotations per minute. Find the constant breaking torque required to stop the wheel in 5 rotations. [A]
3. If a constant torque of 500Nm turns a wheel of moment of inertia 100 kg m2 about an axis through its centre, find the gain in angular velocity in 2 s. [A]
4. Torques of equal magnitude are applied to a hollow cylinder and a solid sphere, both having the same mass and radius. The cylinder is free to rotate about its standard axis of symmetry, and the sphere is free to rotate about an axis passing through its centre. Which of the two will acquire a greater angular speed after a given time. [U]
5. A rope of negligible mass is wound round a hollow cylinder of mass 3 kg and radius 40 cm. What is the angular acceleration of the cylinder if the rope is pulled with a force of 30 N ? What is the linear acceleration of the rope? Assume that there is no slipping. [A]
SYSTEM OF PARTICLES AND ROTATIONAL MOTION _XI P – 06 – 54 The kinetic energy gained 2 1 2 I = , 1 0425050 2 K.E.gained.J ==




..................................................................................................................................
.................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. ..................................................................................................................................
.................................................................................................................................. ..................................................................................................................................
15. RELATION BETWEEN L & MOMENT OF INERTIA
Consider a rigid body rotating about a fixed axis with uniform angular velocity ω The body consists of n particles of masses m1, m

situated at distance
from the axis of rotation.
The angular velocity ω of all the n particles will be same but their linear velocities will be different and are given by
Linear momentum of first particle, P
Moment of linear momentum of the first particle about the z axis,
The angular momentum of a rigid body about an axis is the sum of moments of linear momenta of all its particles about that axis. Thus
But
2 = I, moment of inertia of the body about the given axis ∴
Illustration-23
A ring of diameter 0.4 m and of mass 10 kg is rotating about its axis at the rate of 2100 rpm. Find (i) moment of inertia (ii) angular momentum and (iii) rotational K.E. of the ring.
SYSTEM OF PARTICLES AND ROTATIONAL MOTION_XI P – 06 – 55
2
r1, r2, r3 …, rn
, m3, …., mn;
v1 = r1ω, v2 = r2ω, v3 = r3 ω, …, vn = rnω
1 = m1v1 = m1r1ω
2 11111 Lprmr
==
L = L1 + L2 + L3 + … + Ln 2222 112233 nn mrmrmr...mr =++++ ( ) 2222 112233 nn mrmrmr...mr =++++ ( ) 2 mr =
Σ
L = Iω
mr
Illustration-24
Calculate the angular momentum of a planet rotating about its own axis with time period of one day. Mass of the planet = 5.98 × 1024 kg, mean radius of the planet = 6.37 × 106 m.
Solution: Here M = 5.98 × 1024 kg, R
Know Yourself
1. A body of mass 1.0 kg is rotating on a circular path of diameter 2.0 m at the rate of 10 rotations in 31.4 s. Calculate (i) angular momentum of the body and (ii) rotational kinetic energy. [A]
2. A circular ring of diameter 40 cm and mass 1 kg is rotating about an axis normal to its plane and passing through the centre with a frequency of 10 rotations per second. Calculate the angular momentum about its axis of rotation. [A]
3. A solid cylinder of mass 20 kg rotates about its axis with angular speed 100 rad s –1. The radius of the cylinder is 0.25 m. What is the kinetic energy associated with the rotation of the cylinder? What is the magnitude of angular momentum of the cylinder about its axis? [A]
SYSTEM OF PARTICLES AND ROTATIONAL MOTION _XI P – 06 – 56
Here 04 0210 2 . R.m,Mkg === 2100 210035 60 rpmrpsrps=== 1 22 235220 7 rads ==
M.I. of the ring about its axis, I = MR2 = 10 × (0.2)2 = 0.4 kg m2 .
Angular momentum, L = Iω = 0.4 × 220 = 88 kg m2 s –1
Rotational K.E. ( )2 2 11 042209680 22 I.J. ===
Solution:
(i)
(ii)
(iii)
106 m ( )2 224622 5981063710 55 IMR.. == = 2.1 × 1038 kg m2 1 222 1246060 rads Tday === Angular momentum, 38 2 2110 246060 LI. == = 1.53 × 1034 kg m2 s –1 .
= 6.37 ×




..................................................................................................................................
.................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. ..................................................................................................................................
.................................................................................................................................. ..................................................................................................................................
16. LAW OF CONSERVATION OF ANGULAR MOMENTUM
Newton's second law for rotational motion
=
So if the net external torque on a particle (or system) is zero then 0 dL dt = i.e. 123 LLLL...constant. =+++=
Angular momentum of a system (may be particle or body) remains constant if resultant torque acting on it zero.
As L = Iω so if 0 = then Iω = constant
Since angular momentum Iω remains constant so when I decreases, angular velocity ω increases and viceversa.
Examples of law of conservation of angular momentum:
(1) The angular velocity of revolution of a planet around the sun in an elliptical orbit increases when the planet come closer to the sun and vice-versa because when planet comes closer to the sun, it's moment of inertia I decreases therefore ω increases.
(2) A circus acrobat performs featsinvolving spin by bringing his arms and legs closer to his body or viceversa. On bringing the arms and legs closer to body, his moment of inertia I decreases. Hence ω increases.
(3) A person-carrying heavy weight in his hands and standing on a rotating platform can change the speed of platform. When the person suddenly folds his arms. Its moment of inertia decreases and in accordance the angular speed increase.
(4) A diver performs somersaults by Jumping from a high diving board keeping his legs and arms out stretched first and then curling his body.
Illustration-25
A small block is rotating in a horizontal circle at the end of a thread which passes down through a hole at the centre of table top. If the system is rotating at 2.5 rps in a circle of 30 cm radius, what will be the speed of rotation when the thread is pulled inwards to decrease the radius to 10 cm? Neglect friction. Solution: Here v1 = 2.5 rps, r1 = 30 cm, r2 = 10 cm, v2 = ?
SYSTEM OF PARTICLES AND ROTATIONAL MOTION_XI P – 06 – 57
dL dt
1
I
By law of conservation of angular momentum, or L1 = L2 or I1ω1 = I2ω2 22 1122 22 mrvmrv = 2 11 2 2 2 303025 225 1010 rv. v.rps. r ===
Illustration-26
A thin circular ring of mass M and radius R is rotating about its axis with a constant angular velocity ω. Four objects each of mass m, are kept gently to the opposite ends of two perpendicular diameters of the ring. The angular velocity of the ring will be
Solution: Initial angular momentum of ring = Iω = MR2 ω
If four object each of mass m, and kept gently to the opposite ends of two perpendicular diameters of the ring then final angular momentum = (MR2 + 4mR2)ω'
By the conservation of angular momentum
Initial angular momentum = Final angular momentum
Know Yourself
1. An ice skater spins with arms outstretched at 5 rps. His moment of inertia at this instant is 4 kgm2 He pulls in his arms to increase his rate of spin. If the moment of inertia is 2 kgm2 after he pulls in his arms, what is his new rate of rotation? [A]
2. A mass of 5 kg is rotating on a circular path of radius 1 m with angular velocity of 22 rad s–1. If the radius of the path becomes 2 m, what will be the value of angular velocity? [A]
3. A ball tied to a string takes 8 s to complete revolution along a horizontal circle. If, by pulling the cord, the radius of the circle is reduced to half of the previous value, then how much time the ball will take in one revolution? [A]
4. (a) A child stands at the centre of a turntable with his two arms outstretched. The turntable is set rotating with an angular speed of 40 rev/min. How much is the angular speed of the child if he folds his hands back and thereby reduces his moment of inertia to 2/5 times the initial value ?
Assume that the turntable rotates without friction. [A]
(b) Show that the child's new kinetic energy of rotation is more than the initial kinetic energy of rotation. How do you account for this increase in kinetic energy? [U]
SYSTEM OF PARTICLES AND ROTATIONAL MOTION _XI P – 06 – 58
(a) 4 + M Mm (b) ( ) 4 + Mm M (c) ( ) 4 4 + Mm Mm (d) 4 M m
( ) 222 4 4 M MRMRmR'' Mm =+= +




..................................................................................................................................
.................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. ..................................................................................................................................
.................................................................................................................................. ..................................................................................................................................
17. ROLLING OF A CYLINDER ON A ROUGH INCLINED PLANE
Consider a cylinder of mass ‘m’ and radius R rolling over an inclined plane at an angle θ. Let ‘F’ be the force of friction acting on the cylinder. If ‘a’ is the acceleration produced in the body, then mg sin

If, ‘α’ is the angular acceleration of the rotating cylinder about its axis, then,
Also,
A solid sphere rolls down two different inclined planes of the same heights but different angles of inclination. (a) will it reach the bottom with the same speed in each case? (b) Will it take longer to roll down one plane than the other? (c) If so, which one and why?
SYSTEM OF PARTICLES AND ROTATIONAL MOTION_XI P – 06 – 59
F = ma
(1)
θ –
…
τ = FR = Iα FR I = or I F R = b … (2)
a Ra R ==
the value in (ii) 2 Ia F R = 2 sin Ia Mgma R =+ 2 1 sin mgma R =+ ( ) 2 sin / mg a mIR = + ( ) 2 sin / mg RmIR = +
Put
Illustration-27
Solution: Acceleration of the rolling sphere, ( ) 22 sin 1/ g a kR = +
Velocity of the sphere at the bottom of the inclined plane, ( ) 22 2 1/ gh v kR = +
(a) Yes, the sphere will reach the bottom with the same speed v because h is same in both cases.
(b) Yes, the sphere will take longer time to roll down one plane than the other.
(c) The sphere will take larger time in case of the plane with smaller inclination because the acceleration, α ∝ sin θ
Illustration-28
A hoop of radius 2 m weighs 100 kg. It rolls along a horizontal floor so that its centre of mass has a speed of 20 cm/s. How much work has to be done to stop it?
Solution: Here R = 2 m, m = 100 kg
vcm = 20 cms–1 = 0.20 ms–1
Work required to stop the hoop = Total K.E. of the hoop = Rotational K.E. +
Illustration-29
A solid cylinder rolls up an inclined plane of angle of inclination 30°. At the bottom of the inclined plane the centre of mass of the cylinder has a speed of 5 m/s.
(a) How far will the cylinder go up the plane?
(b) How long will it take to return to the bottom?
Solution:
(a) Total initial kinetic energy of the cylinder.
SYSTEM OF PARTICLES AND ROTATIONAL MOTION _XI P – 06 – 60
Translational
( ) 2 2 222 1111 2222 cm cmcm v IMvMRMV R =+=+ = ( )2 2 1000.204 cm MvJ ==
K.E.
2211 22 icmCMKMvI =+ 2 22 2 111 222 CM CM v MvMR R =+ 222113 244CMCMCMMvMvMv=+=
Initial potential energy, Ui = 0
Final kinetic energy, Kf = 0
Final potential energy, 1 sin30 2 f UMghMgsMgs ===
where s is the distance travelled up the incline and h is the vertical height covered above the bottom. Gain in P.E. = Loss in K.E.
(b) Using equation of motion for the motion up the incline, we get 0 CM CM
Also, 22 02
Total time taken in returning to the bottom = 2 × 1.5 = 3.0 s
Illustration-30
Three bodies, a ring, a solid cylinder and a solid sphere roll down the same inclined plane without slipping. They start from rest. The radii of the bodies are identical. Which of the bodies reaches the ground with maximum velocity?
Solution: We assume conservation of energy of the rolling body, i.e., there is no loss of energy due to friction etc. The potential energy lost by the body in rolling down the inclined plane (= mgh) must, therefore, be equal to kinetic energy gained. (See Fig.) Since the bodies start from rest the kinetic energy of the bodies. From Eq.
body. Equating K and mgh,
, where v is the final velocity of (the centre of mass of ) the
P – 06 – 61
SYSTEM OF PARTICLES AND ROTATIONAL MOTION_XI
2
CM
= ( )2 2 35 3 3.8 229.8 CMv sm g ===
13 24
MgsMv
V vatora t =+=−
2 2
=
CM vas−= or 2 2 CMv a s =−
CMCMvv ts
or 223.8 1.5 5 CM s ts v ===
2 2 2 1
2
=+
1
k Kmv R
2 2 2 1 1 2 k mghmv R =+ or 2 22 2 1/ gh v kR = +
It is independent of the mass of the rolling body; For a ring, k2 = R2
2 11' ring gh v = + gh =
For a solid cylinder k2 = R2/2
2 11/2 disc gh v = + 4 3 gh = For a solid sphere k2 = 2R2/5
2 12/5 sphere gh v = + 10 7 gh =
From the results obtained it is clear that among the three bodies the sphere has the greatest and the ring has the least velocity of the centre of mass at the bottom of the inclined plane.
Illustration-31
A solid cylinder rolls down an inclined plane. Its mass is 2 kg and radius 0.1 m. If the height of the inclined plane is 4m, what is its rotational kinetic energy when it reaches the foot of the inclined plane?

Solution: Considering conservation of energy, we can write,
(Potential energy) A = (K.E.) B = [kinetic energy of translation + kinetic energy of rotational]B or
SYSTEM OF PARTICLES AND ROTATIONAL MOTION _XI P – 06 – 62
2211
=+ But vr = and 2 2 mr I = 2222111 222 mghmrmr =+ or 222222 3 244 rrr gh =+=
22 mghmvI
Know Yourself
1. A disc of mass M and radius R rolls on a horizontal surface and then rolls up an inclined plane as shown in the figure. If the velocity of the disc is v, the height to which the disc will rise will be:- [A]

2. When a body starts to roll on an inclined plane, its potential energy is converted into [U]
(a) translational kinetic energy only
(b) translational and rotational kinetic energy
(c) rotational energy only
(d) none
3. A solid cylinder rolls down an inclined plane. Its mass is 2 kg and radius 0.1 m. If the height of the inclined plane is 4 m, what is its rotational kinetic energy when it reaches the foot of the plane? Assume that the surfaces are smooth. [U]
SYSTEM OF PARTICLES AND ROTATIONAL MOTION_XI P – 06 – 63 or 2 4 3 gh r = ∴ Rotational kinetic energy at 2 2211 222 mr BI== 2 2 4 43 mrgh r = 29.84 33 mgh == = 26.13 J
(a) 2 3 2 v g (b) 2 3 4 v g (c) 2 4 v g (d) 2 2 v g




..................................................................................................................................
.................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. ..................................................................................................................................
.................................................................................................................................. ..................................................................................................................................
Illustration-32
If the angular momentum is conserved in a system whose moment of inertia is decreased, will its rotational kinetic energy be also conserved?
Solution: According to the law of conservation of angular momentum, I1 ω1 = I2 ω2 or 2222 1122 II = As 22 121122 , IIII or 22 1122 11 22 II
Thus, the rotational kinetic energy of the system increases on decreasing its moment of inertia.
Illustration-33
A planet revolves around a massive star in highly elliptical orbit. Is the angular momentum constant over the entire orbit?
Solution: A planet revolves around a star under the effect of the gravitational force, which purely radial in nature. As radial component of a force does not contribute to torque, so the angular momentum of the planet remains unaffected. As 0 dL dt == , so L = constant
Illustration-34
A cat is able to land on its feet after a fall. Why?
Solution: When a cat falls to ground from a height, it stretches its body along with the tail so that its moment of inertia becomes high. Since Iω is to remain constant, the value of angular speed ω decreases and therefore the cat is able to land on the ground gently.
Illustration-35
If earth contracts to half its radius, what would be the length of the day?
Solution: The moment of inertia 2 2 5 IMR =
of the earth about its own axis will become one fourth and so its angular velocity will become four times (L = Iω = constant). Hence the time period will reduce to one fourth (T = 2π/ω) i.e., 6 hours.
SYSTEM OF PARTICLES AND ROTATIONAL MOTION _XI P – 06 – 64
Illustration-36
The moments of inertia of two rotating bodies A and B are IA and IB and (IA > IB) and their angular momenta are equal. Which one has a greater kinetic energy? Solution: Angular
∴
Illustration-37
Light thread is wound over a cylinder which is free to rotate about its own axis. A block of mass m is attached at the free end of the thread as shown and system is released then obtain expression for
(i) acceleration with which block falls.
(ii) Tension in the thread
(iii) Torque applied by force of tension on the cylinder
(iv) angular acceleration produced in the cylinder.
Solution: Consider a cylinder of mass M and radius R. Let a massless string is would over the surface of cylinder. Let a body of mass m is attached to one free end of string. When the body moves downwards, the drum starts rotating about its own axis.
If ‘a’ is the acceleration produced in the body, then mg – T = ma … (1)
where, T is the tension produced in the string. If ‘α’ is the angular acceleration of the rotating drum about its axis, then
τ = I α = TR
Also, Rα = a
SYSTEM OF PARTICLES AND ROTATIONAL MOTION_XI P – 06 – 65
L = Iω
of rotation, 222 2 111 222 IL KI II ===
constant L, 1 K I
IA > IB
momentum,
K.E.
For
As
K
KB or KB > KA
body B has a greater rotational K.E.
A <
So
TRI T IR == … (2)
a R =
Illustration-38
The centre of mass a system of particles does not depend on:
(a) masses of the particles
(c) position of the particles
Solution: (b)
(b) forces on the partices
(d) relative distance between the particles
C.O.M→ depend on mass, position of particle, separation between particles.
Illustration-39
A particle of mass m is describing a circular path of radius r with uniform speed. If L is the angular momentum of the particle (about the axis of the circle), then the kinetic energy of the particle is

SYSTEM OF PARTICLES AND ROTATIONAL MOTION _XI P – 06 – 66 Putting the value in (ii), we get 2 Ia T R = 2 Ia mgma R −= 22 IaI mgmaamRR =+=+ ( ) 2 / mg a mIR = + ( ) 2 / amg R RmIR == + and ( ) 22 / IImg T R RmIR == + ( ) 2 Img T mRI = + τ = T × R 2 ImgR mRI = +
(a) 2 2 L mr (b) mr 2L (c) 2 2 2 L mr (d) 22Lr m
(c) 222 2222 2 11111 22222 IL KEmvmrI I mr ===== FOR TOPPLING & I.A.O.R. REFER TO ADVANCED MODULE.
Solution:




..................................................................................................................................
.................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. .................................................................................................................................. ..................................................................................................................................
.................................................................................................................................. ..................................................................................................................................

P – 06 – 67
SYSTEM OF PARTICLES AND ROTATIONAL MOTION_XI
MIND MAP

SYSTEM OF PARTICLES AND ROTATIONAL MOTION _XI P – 06 – 68
MIND MAP
EXERCISE - 1
MCQs with One Correct Answer Type
1. What is the radius of gyration of a uniform rod whose length is L and passes through the centre of mass
(a) 3 L/ (b) 2 L/ (c) 23 L/ (d) 2 12 L/
2. Two identical particles move towards each other with velocity 3v and 2v respectively. The velocity of their centre of mass is
(a) 0.5 v (b) 3 v (c) 5 v (d) 1.5 v
3. What is the angular momentum vector in an orbital motion?
(a) The vector is perpendicular to the orbital plane
(b) The vector is along the radius vector
(c) The vector is parallel to the linear momentum
(d) The vector is in the orbital plane
4. What is the acceleration of the rolling sphere at the centre of the plane with inclination, θ to the horizontal?
(a) Zero
(c) Greater than g sin θ
(b) Less than g sin θ
(d) g sin θ
5. On which of the following factor does the moment of inertia of an object not depend upon
(a) Axis of rotation
(c) Distribution of mass
(b) Angular velocity
(d) Mass of an object
6. What is the effect of frictional force on a round object with mass M and radius R which rolls down the inclined plane without slipping along the way
(a) There is a decrease in the rotational motion
(b) There is a decrease in the rotational and translational motion
(c) There is a conversion of translational motion into rotational motion
(d) Kinetic energy is converted into heat
7. When the torque acting on the system is zero, which of the following is constant?
(a) Linear impulse
(c) Force
(b) Linear momentum
(d) Angular momentum
8. Theangularmomentumofarigidbodyis L anditskineticenergyishalved.What happenstoitsangular momentum?
(a) L (b) 2 L
(c) L/2 (d) 2 L/
9. Consider two objects a disk and a sphere that has the same radius but different masses which roll down the two inclined planes with the same altitude and length. Out of the two objects, which one gets to the bottom of the plane first?
(a) It is dependent on the masses of the objects
(b) Disk
(c) Sphere
(d) Both reach at the same time
SYSTEM OF PARTICLES AND ROTATIONAL MOTION_XI P – 06 – 69
10. What does L2/2I represent?
(a) Power
(b) The torque of a particle
(c) The potential energy of a particle
(d) The rotational kinetic energy of a particle
11. The motion of planets in the solar system is an example of conservation of
(a) Energy
(c) Angular momentum
(b) Linear momentum
(d) Mass
12. When does the moment of inertia of a body come into the picture?
(a) When the motion is rotational
(b) When the motion is linear
(c) When the motion is along a curved path (d) None of the above
13. A body of M.I. 3 kg m2 rotating with an angular velocity 2 rad/s has the same K.E. as a mass of 12 kg moving with a velocity of
(a) 1 m/s (b) 2 m/s (c) 4 m/s (d) 8 m/s
14. A particle performing uniform circular motion has angular momentum L. If its angular frequency is doubled and its kinetic energy halved, then the new angular momentum is
2L
4L
15. A thin uniform, circular ring is rolling down an inclined plane of inclination 30° without slipping. Its linear acceleration along the inclined plane will be
2g/3
16. A ring of radius r and mass m rotates about an axis passing through its centre and perpendicular to its plane with angular velocity ω. Its kinetic energy is
17. The moment of inertia of a disc having mass M and radius R, about an axis passing through its centre and perpendicular to its plane is
18. If a body is rotating about an axis, passing through its centre of mass then its angular momentum is directed along its
(a) Radius (b) Tangent (c) Circumference (d) Axis of rotation
19. A solid cylinder of mass 20 kg, has length 1 metre and radius 0.5 m. then its momentum of inertia in kg m2 about its geometrical axis is
(a) 2.5 (b) 5 (c) 1.5 (d) 3
20. A particle moves on a circular path with decreasing speed. Choose the correct statement.
(a) Angular momentum remains constant.
(b) Acceleration is towards the centre.
(c) Particle moves on a spiral path with decreasing radius.
(d) The direction of angular momentum remains constant.
21. Rotational analogue of mass in linear motion is
(a) Weight (b) Moment of inertia
(c) Torque (d) Angular momentum
SYSTEM OF PARTICLES AND ROTATIONAL MOTION _XI P – 06 – 70
(b)
(c)
(a) L/2
L/4
(d)
(a) g/2 (b)
(c) g/4 (d)
g/3
(a) mrω 2 (b) 2 1 2 mr (c) Iω2 (d) 2 1 2 I
2 1 2 MR (b) MR2 (c) 2 1 2 MR (d) 2 5 4 MR
(a)
SYSTEM OF PARTICLES AND ROTATIONAL MOTION_XI
22. Which is the wrong relation from the following?
(a) τ = I a (b) F = ma (c) L = Iw (d) I = τ a
23. A solid sphere is rotating in free space. If the radius of the sphere is increased keeping mass same, which one of the following will not be affected?
(a) Moment of inertia
(b) Angular momentum
(c) Angular velocity (d) Rotational kinetic energy
24. The moment of momentum is also called as
(a) Couple (b) torque (c) impulse (d) angular momentum
25. Larger the moment arm, the greater will be the
(a) Momentum (b) Velocity (c) Torque (d) Axis of rotation
26. The angular speed of minute arm in a watch is :
(a) π/21600 rads–1 (b) π/12 rads–1 (c) π/3600 rads–1 (d) π/1800 rads–1
27. One circular ring and one circular disc both having same mass and radius. What will be the ratio of their moment of inertia about the axis passing through their centres and perpendicular to their planes?
(a) 1 : 1 (b) 2 : 1 (c) 1 : 2 (d) 12 :
28. If I, a and t are the moment of inertia, angular acceleration and torque respectively of a body rotating about any axis with angular velocity w, then
(a) t = Ia (b) t = Iw (c) I = tw (d) a = Iw
29. A dancer on ice spins faster when she folds here arms. This is due to
(a) Increases in energy and increase in angular momentum
(b) Decrease in friction at the skates
(c) Constant angular momentum and increase in kinetic energy
(d) Increase in energy an decreases in angular momentum
30. The moment of inertia of a uniform semicircular disc of mass M and radius about a line perpendicular to the plane of the disc through the centre is (a)
31. Choose the correct relation
32. For increasing the angular velocity of an object by 10%, the kinetic energy has to be increased by
33. What does a couple produce?
(a) pure rotation (b) rotation and translation
(c) no motion (d) pure translation
34. Maintaining constant velocity, a particle is travelling down a line which is parallel to X-axis (positive). What will be the angular momentum magnitude with regards to origin?
(a) zero (b) increasing along with x
(c) decreasing along with x (d) remains constant
35. A rope coils an empty cylinder whose mass and radius are 3 kg and 40 cm respectively. Determine the cylinder's angular acceleration if someone pulls the rope with 30 N force.
(a) 0.25 rads
2 (b) 25 rads–2
P – 06 – 71
(b) (1/4) Mr2 (c) (1/2)Mr2 (d) Mr2
(2/5)Mr2
(a) 0 =ij (b) =− ijk (c) = ijk (d) = ijj
(a)
(b)
(c) 10% (d) 21%
40%
20%
(c) 5 m s –2 (d) 25 m s –2
–
36. A closed vessel of cylindrical shape is partly filled with water. What happens to the moment of inertia if the vessel rotates along a horizontal plane around perpendicular bisector?
(a) increases
(c) stays constant
(b) decreases
(d) depends on rotation direction
37. One rigid body having angular momentum L is rotating, and its K.E (kinetic energy) is reduced to one fourth. What will be its angular momentum then?
(a) L (b) L2 (c) 2 L (d) L/2
38. A particle is in UCM (uniform circular motion). Its angular momentum remains intact about:
(a) middle point of circle
(c) circumference point of the circle
(b) at any point within the circle
(d) at any point exterior to the circle.
39. An object round in shape having radius R and mass M rolls down by an inclined surface but does not slip. Its frictional force:
(a) vanishes K.E as heat
(b) reduces rotational motion
(c) changes translational energy to rotational energy
(d) reduces both translational and rotational motion.
40. What will be a body's angular momentum if the time period is doubled and its moment of inertia is kept constant?
(a) remain constant
(c) doubles
(b) become half
(d) quadruples
41. Centre of mass of two particle (different masses) system lies near to
(a) heavier mass
(c) at the middle only
(b) lighter mass
(d) always outside the body
42. Find the moment of inertia if 2000Nm torque is acting on a body with 2 rad/s2 angular acceleration.
(a) 1200 kgm2
(c) 1000 kgm2
(b) 900 kgm2
(d) Cannot be determined
43. If an object's angular velocity is increased by 10 per cent, then K.E must be increased by what percentage?
(a) 40% (b) 20%
44. What is angular momentum?
(a) a scalar
(c) a polar vector
45. Choose the wrong relation to the following options.
(a) a = rα
(c) 10% (d) 21%
(b) scalar as well as vector
(d) an axial vector
46. Two discs A and B circular in shape have a uniform thickness and similar masses. But the density of disc 1 is greater than disc 2. What is the moment of inertia?
(a) I1 > I
47. Calculatetheangularmomentum of abodywhenit'sK.E andM.I are 4joules and 2kgm
respectively.
48. Raw egg and hard boiled eggs are given equal torques,
(a) Raw egg will be rotated faster (b) Hard boiled egg will be rotated faster.
(c) angular velocity will be same for both.
Can't say anything.
SYSTEM OF PARTICLES AND ROTATIONAL MOTION _XI P – 06 – 72
(b) F
(c) K.E. = L2/ω (d) rF =
= m × a
(b)
≫ I2 (c) I1 < I2 (d) I1 = I2
2
I1
2
m2/sec (b) 5 kg m2/sec (c) 6 kg m2/sec (d) 7 kg m2/sec
(a) 4 kg
(d)
49. A disc having diameter 2 m and mass 2 kg undergoes rotational motion. Consider the rotation of disc is from 300 to 600 rpm. Evaluate the work done.
(a) 1479 J (b) 14.79 J (c) 147.9 J (d) 1.479 J
50. Suppose a gymnast is sitting on a rotating chair and his arms are outstretched. If he suddenly shortens his arms, what will happen?
(a) angular velocity will decrease
(b) moment of inertia will decrease
(c) angular velocity will stay constant
(d) angular momentum will increase.
51. A particle ofmassm is moving in yz-plane with a uniform velocity v with its trajectory running parallel to +ve y-axis and intersecting z-axis at z = a in figure. The change in its angular momentum about the origin as it bounces elastically from a wall at y = constant is
52. When a disc rotates with uniform angular velocity, which of the following is not true?
(a) The sense of rotation remains same
(b) The orientation of the axis of rotation remains same
(c) The speed of rotation is non-zero and remains same
(d) The angular acceleration is non-zero and remains same
53. A uniform square plate has a small piece Q of an irregular shape removed and glued to the centre of the plate leaving a hole behind in figure. The moment of inertia about the z-axis is then,

(a) increased
(c) the same
(b) decreased
(d) changed in unpredicted manner
54. A merry-go-round, made of a ring-like platform of radius R and mass M, is revolving with angular speed ω. A person of mass M is standing on it. At one instant, the person jumps off the round, radially away from the centre of the round (as seen from the round). The speed of the round of afterwards is
55. Choose the correct alternatives
(a) For a general rotational motion, angular momentum L and angular velocity ω need to be parallel.
(b) For a rotational motion about a fixed axis, angular momentum L and angular velocity ω are always parallel.
(c) For a general translational motion, momentum p and velocity v are always parallel.
(d) For a general translational motion, acceleration a and velocity v are always parallel.
MOTION_XI P – 06 – 73
SYSTEM OF PARTICLES AND ROTATIONAL
(a) mvai (b) 2mvai (c) ymvi (d) 2ymv
(a) 2ω (b) ω (c) 2 (d) 0
56. Figure shows two identical particles 1 and 2, each of mass m, moving in opposite directions with same speed v along parallel lines. At a particular instant r1 and r2 are their respective position vectors drawn from point A which is in the plane of the parallel lines. Choose the correct options.
(a) Angular momentum I1 of particle 1 about A is ( )1 = Imvr
(b) Angular momentum I2 of particle 2 about A is 22 = Imvr
(c) Total angular momentum of the system about A is ( ) 12=+ Imvrr
(d) Total angular momentum of the system about A is ( )21 =−Imvdd
57. The net external torque on a system of particles about an axis is zero. Which of the following are compatible with it?
(a) The forces may be acting radially from a point on the axis
(b) The forces may be acting on the axis of rotation
(c) The forces may be acting parallel to the axis of rotation
(d) All of these
58. Figure shows a lamina in xy-plane. Two axes z and z' pass perpendicular to its plane. A force F acts in the plane of lamina at point P as shown. Which of the following are true? (The point P is closer to z'axis than the z-axis.)


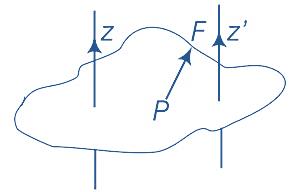
(a) Torque τ caused by F about z-axis is along
(b) Torque τ' caused by F about z'-axis is along
(c) Torque τ caused by F about z-axis is greater in magnitude than that about z-axis
(d) Total torque is given be τ = τ + τ'
59. With reference to figure of a cube of edge a and mass m, choose the following are true. (0 is the centre of the cube.)
(a) The moment of inertia of cube about z-axis is zxy III +
(b) The moment of inertia of cube about z'-axis is
II=+
z'z
(c) The moment of inertia of cube about z''-axis is
(d) xy II
SYSTEM OF PARTICLES AND ROTATIONAL MOTION _XI P – 06 – 74
2 2
ma
2 2
=+ z ma I
60. A uniform cube of mass m and side a is placed on a frictionless horizontal surface. A vertical force F is applied to the edge as shown in figure. Match the following (most appropriate choice)

Column-I

Column-II
A. mg/4 < F < mg/2 (i) Cube will move up.
B. F > mg/2 (ii) Cube will not exhibit motion.
C. F > mg (iii) Cube will begin to rotate and slip at A
D. F = mg/4 (iv) Normal reaction effectively at a/3 from A, no motion
(a) (A) → (i); (B) → (iii); (C) → (ii); (D) → (iv)
(b) (A) → (ii); (B) → (iii); (C) → (i); (D) → (iv)
(c) (A) → (iii); (B) → (ii); (C) → (i); (D) → (iv)
(d) (A) → (ii); (B) → (iii); (C) → (iv); (D) → (i)
61. A uniform sphere of mass m and radius R is placed on a rough horizontal surface (figure). The sphere is struck horizontally at a height h from the floor. Match the following

A. h = R/2
(i) Sphere rolls without slipping with a constant velocity and no loss of energy.
B. h = R (ii) Sphere spins clockwise, loses energy by friction.
C. h = 3R/2 (iii) Sphere spins anti-clockwise, loses energy by friction.
D. h = 7R/5 (iv) Sphere has only a translational motion, loses energy by friction.
(a) (A) → (iii), (B) → (iv), (C) → (ii), (D) → (i)
(b) (A) → (ii), (B) → (iv), (C) → (iii), (D) → (i)
(c) (A) → (iii), (B) → (i), (C) → (ii), (D) → (iv)
(d) (A) → (iii), (B) → (iv), (C) → (i), (D) → (ii)
62. A uniform disc of radius R and mass M, is resting on a table on its rim. The coefficient of friction between disc and table is μ (figure). Now, the disc is pulled with a force F as shown in the figure. What is the maximum value of F for which the disc rolls without slipping?
MOTION_XI P – 06 – 75
SYSTEM OF PARTICLES AND ROTATIONAL
(a) μMg (b) 2μMg (c) 3μMg (d) 4μMg
63. A force F is applied on a single particle P as shown in the figure. Here, r is the position vector of the particle. The value of torque τ is
(a) Fr (b) rF (c) rF (d) Fr
64. A force F525 =+− ˆ ˆˆ ijk acts on a particle whose position vector is r2=−+ ˆ ˆˆ ijk . What is the torque about the origin?
(a) 81012 ++ ˆ ˆˆ ijk (b) 81012 +− ˆ ˆˆ ijk (c) 8108 ˆ ˆˆ ijk (d) 1010 ˆ ˆˆ ijk
65. Newton's second law for rotational motion of a system of particle can be represented as (L for a system of particles)
(a) = ext dp dt (b) = int dL dt (c) = ext dL dt (d) =+intext dL dt
66. A point mass m is attached to a massless string whose other end is fixed at P as shown in figure. The mass is undergoing circular motion in xy-plane with centre O and constant angular speed ω. If the angular momentum of the system, calculated about O and P be L0 and LP respectively, then

(a) L0 and LP do not vary with time
(b) L0 varies with time while LP remains constant
(c) L0 remains constant while LP varies with time
(d) L0 and LP both vary with time
67. In the game of see-saw, what should be the displacement of boy B from right edge to keep the see-saw in equilibrium? (Given, M1 = 40 kg and M2 = 60 kg)


68. A disc of mass M and radius R is rotating about one of its diameter. The value of radius of gyration for the disc is
these
SYSTEM OF PARTICLES AND ROTATIONAL MOTION _XI P – 06 – 76
(a) 4 3 m (b) 1 m (c) 2 3 m (d) Zero
(a)
(b) R/2 (c) R/6 (d) None of
R/4
69. A flywheel of moment of inertia 0.4 kg-m2 and radius 0.2 m is free to rotate about a central axis. If a string is wrapped around it and it is pulled with a force of 10N, then its angular velocity after 4s will be
(a) 10 rad s–1 (b) 5 rad s–1
20 rad s–1
None of these
70. A disc of radius R is rotating with an angular speed ω0 about a horizontal axis. It is placed on a horizontal table. The coefficient of kinetic friction is μk. What was the velocity of its centre of mass before being brought in contact with the table?
(a) ω0 R (b) Zero
71. If frictional force is neglected and girl bends her hand, then (initially girl is rotating on chair)

(a) Igirl will reduce (b) Igirl will increase
ωgirl will reduce
None of the above
72. Awheelofradius R rollsonthegroundwithauniformvelocity v.Thevelocityoftopmostpointrelative to the bottommost point is (a) v (b) 2v
73. When a disc rotates with uniform angular velocity, which of the following statements is incorrect.
(a) The sense of rotation remains same.
(b) The orientation of the axis of rotation remains same.
(c) The speed of rotation is non-zero and remains same.
(d) The angular acceleration is non-zero and remains same.
74. A bicycle wheel rolls without slipping on a horizontal floor. Which one of the following statements is true about the motion of points on the rim of the wheel, relative to the axis at the wheel's centre?
(a) Points near the top move faster than points near the bottom.
(b) Points near the bottom move faster than points near the top.
(c) All points on the rim move with the same speed.
(d) All points have the velocity vectors that are pointing in the radial direction towards the centre of the wheel.
75. If radius of earth is reduced to half without changing its mass, then match the following columns and choose the correct option from the codes given below.
Column-I
Column-II
A. Angular momentum of earth (p) Will become one fourth
B. Time period of rotation of (q) Will become four times
C. Rotational kinetic energy of earth (r) No change
MOTION_XI P – 06 – 77
SYSTEM OF PARTICLES AND ROTATIONAL
(d)
(c)
(c) 0 2 R (d) 2ω0R
(d)
(c)
(c)
v/2 (d) zero
(d) p r p
Codes A B C (a) p q r (b) p q p (c) r p q
76. A circular disc is to be made by using iron and aluminum, so that it acquires maximum moment of inertia about its geometrical axis. It is possible with
(a) iron and aluminum layers in alternate order
(b) aluminum at interior and iron surrounding it
(c) iron at interior and aluminum surrounding it
(d) Either (a) or (c)
77. Three thin rods each of length L and mass M are placed along X, Y and Z-axes such that one end of each rod is at origin. The moment of inertia of this system about Z-axis is
78. For which of the following does the centre of mass lie outside the body?
(a) A pencil (b) A shotput (c) A dice (d) A bangle
79. Which of the following pointsisthelikely position of the centre ofmass of the system showninfigure?
(a) A (b) B (c) C (d) D
80. A uniform square plate has a small piece Q of an irregular shape removed and glued to the centre of the plate leaving a hole behind in figure. The center of mass of the plate is now in the following quadrant of x-y plane.
(a) I (b) II (c) III (d) IV
81. A ball kept in a closed box moves in the box making collisions with the walls. The box is kept on a smooth surface. The velocity of the centre of mass
(a) of the box remains constant
(b) of the box and the ball system remains constant

(c) of the ball remains constant
(d) of the ball relative to the box remains constant
82. The centre of gravity of a homogeneous body is the point at which the whole

(a) volume of the body is assumed to be concentrated
(b) area of the surface of the body is assumed to be concentrated
(c) weight of the body is assumed to be concentrated
(d) All of the above
SYSTEM OF PARTICLES AND ROTATIONAL MOTION _XI P – 06 – 78
(a) 2 2 3 ML (b) 2 4 3 ML (c) 2 5 3 ML (d) 2 3 ML
Very Short Answer Type Question
1. Where does the Centre of mass of a two particle system lie, if one particle is more massive than the other?
2. Give an example each for a body, where the centre of mass lies inside the body and outside the body.
3. What is a rigid body?
4. Name the rotational analogue of force. Give its SI unit.
5. Is torque a scalar or vector ? If vector, which rule is used to determine its direction?
6. Define Centre of mass of a system.
7. On what factors, does the position of Centre of mass of a rigid body depend ?
8. Where does the Centre of mass of uniform triangular lamina lie?
9. Where does the Centre of mass of a cone lie ?
10. Under what conditions, is the torque zero ?
11. A body is rotating at a steady rate. Is any torque acting on the body ?
12. Does the magnitude and direction of angular momentum depend on the choice of the origin ?
13. Does the total momentum of a system of particles depend upon the velocity of the centre of mass?
14. What is the angular momentum of a body of mass m moving in a circular path of radius r with constant speed v ?
15. Which physical quantity is conserved when a planet revolves around the sun?
16. A boat is likely to capsize if the persons in the boat stand up. Why?
17. A body is moving in a circle of radius r centimetre at a constant speed of v cm s –1. What is the angular velocity?
18. Write two factors on which centre of mass of a body does not depend.
19. Which physical quantity corresponds to moment of linear momentum ?
20. Name the constant whose dimensions are same as that of angular momentum ?
21. What is the angular velocity of the earth spinning about its own axis?
22. Two bodies move in two concentric circular paths of radii r1 and r2 in the same time. What is the ratio of their angular velocities?
23. Name the rotational analogue of linear acceleration.
24. What is the moment of inertia of a solid sphere about its diameter?
25. What is the moment of inertia of a hollow sphere about an axis passing through its centre?
26. What is the moment of inertia of a circular ring about its tangent in its plane?
27. What is the analogous of mass in rotational motion? Write unit of that physical quantity also.
28. What is the ratio of the SI unit to the CGS unit of angular momentum?
29. Is moment of inertia a scalar or a vector quantity?
30. Write an expression for the moment of inertia of a rod of mass 'M' and length 'L' about an axis perpendicular to it through one end.
31. What is the dimensional formula of radius of gyration?
32. State the factors on which radius of gyration of a body depends.
33. A circular ring and a circular disc of the same radius have the same moment of inertia about axis passing through their centres and perpendicular to their planes. What is the ratio of their masses ?
SYSTEM OF PARTICLES AND ROTATIONAL MOTION_XI P – 06 – 79
EXERCISE-2
34. Where does the centre of mass of a rectangular lamina lie?
35. What is torque ? Give its SI unit.
36. What are the factors on which the moment of inertia of a body depends ?
37. Give the physical significance of moment of inertia.
38. Define angular momentum or moment of momentum.
39. A ladder is resting with one end on a vertical wall and the other end on horizontal floor. Is it more likely to slip when a man stands near the bottom or near the top?
40. A stone of mass m tied to a string of length e is rotating along a circular path with constant speed v, what is the torque on the stone?
41. How will you distinguish between a hard boiled egg and a raw egg by spinning each on table top?
42. Name the physical quantity which has unit 'Joul-sec'.
43. Why are there two propellers in a helicopter?
44. Why are spokes fitted in a cycle wheel?
45. If earth contracts to half its radius, what would be the length of a day?
46. A ring and a disc have the same mass and radius. Find the ratio of their moment of inertia about their axis.
47. What is the moment of inertia of a disc of mass m and radius r about a line parallel to the axis of disc but lying near the boundary of it.
48. What is the moment of inertia of a uniform semicircular wire of mass M and radius R about a line perpendicular to the plane of the wire through the centre.
49. A solid spherical ball (MI = 2/5 mr2) rolls on a table. What is the ratio of rotational KE to the total kinetic energy?
50. What is rotational inertia? Explain it.
51. A solid and a hollow cylinder are allowed to roll down an inclined plane without slipping. If they have equal mass and radius which will reach the ground earlier and with higher speed. Explain the reason.
52. Three mass points m1, m2 and m3 are located at the vertices of an equilateral triangle of length 'a'. What is the moment of inertia of the system about an axis along the altitude of the triangle passing through m1,.
Short Answer Type Question
1. Write an expression for the centre of mass of a two particle system. What will be the location of centre of mass if the two particles have equal masses?
2. Discuss the motion of the centre of mass of a fire cracker that explodes in air.
3. Define centre of mass of a system. How does it differ from the centre of gravity?
4. Define a rigid body. State the factors on which the centre of mass a rigid body depends.
5. Name the physical quantity corresponding to force in rotational motion. How is it related to force ? Give its units.
6. Showthatthetotallinearmomentumofasystemofparticlesisconservedintheabsenceofanyexternal force.
7. Define a couple. Show that the moment of a couple is same irrespective of the point of rotation of a body.
8. Show that the angular momentum of a particle is the product of its linear momentum and moment arm. Also show that the angular momentum is produced only by the angular component of linear momentum. What is the physical meaning of angular momentum ?
SYSTEM OF PARTICLES AND ROTATIONAL MOTION _XI P – 06 – 80



















































































































































