Mathematical Literacy

Owned and published by Optimi, a division of Optimi Central Services (Pty) Ltd.
7 Impala Avenue, Doringkloof, Centurion, 0157 info@optimi.co.za www.optimi.co.za
© Optimi
Apart from any fair dealing for the purpose of research, criticism or review as permitted in terms of the Copyright Act, no part of this publication may be reproduced, distributed, or transmitted in any form or by any means, electronic or mechanical, including photocopying, recording, or any information storage and retrieval system without prior written permission from the publisher.
The publisher has no responsibility for the persistence or accuracy of URLs for external or third-party internet websites referred to in this publication, and does not guarantee that any content on such websites is, or will remain, accurate or appropriate.
There are instances where we have been unable to trace or contact the copyright holder. If notified, the publisher will be pleased to rectify any errors or omissions at the earliest opportunity.
Reg. No.: 2011/011959/07

Mathematical Literacy
Study Guide
Grade 10
Lesson elements




LEARNING OBJECTIVES
What you should know at the end of the lesson. Taken from CAPS.
IMPORTANT TERMINOLOGY
New terminology to improve understanding of the subject as part of the lesson.
IMPORTANT
A summary or explanation of the main concepts of a lesson.
ACTIVITY
Formative assessment to test your progress and knowledge at the end of each lesson.
Sample
Preface
Recommended books
Any additional book may be used with this study guide. It is always a good idea to refer to other textbooks to develop a broader perspective on the subject.
• The Answer Series: Grade 10 Mathematical Literacy 3 in 1
• Mathematical Literacy for the Classroom Grade 10 Learner’s Book
Assessment requirements
Note that there are constant references to TL1, TL2, TL3 and TL4 throughout this facilitator guide. These are the thinking levels required to answer the specific question asked.
The thinking levels represent the following skills
• Thinking level 1
Knowing
• Thinking level 2
Applying routine procedures in familiar contexts
• Thinking level 3
Applying multi-step procedures in a variety of contexts
• Thinking level 4
Reasoning and reflecting
When tasks, investigations and especially tests and examinations are set, the guidelines below are used to allocate a number of marks to a specific thinking level. Mark distribution according to the thinking levels
The assessment programme
Refer to Impaq’s online platform for assessment tasks, examinations and the assessment plan.
1 Numbers and calculations
2 Patterns, relationships and representations
1
– March
3 Measurement: Conversions and time 4 Finance: Financial documents and tariff systems Term 2 April – June
5 Measurement: Distance/length, weight (mass), volume and temperature 6 Mapwork
Probability
8 Finance: Income, expenditure, profit/loss, incomeand-expenditure statements, and budgets
9 Measurement: Perimeter and area 10 Instructions, assembly diagrams and packaging 11 Finance: VAT, banking, interest and bank charges Term 4
handling
Term 3 July – September
Topics
Suggested time to spend on each unit (according to CAPS)
1
Contexts focusing on Numbers and calculations
Contexts focusing on Patterns, relationships and representations
Contexts focusing on Measurement (conversions and time)
Assessment Assignment/investigation
Control test (covering Numbers and calculations, Patterns, relationships and representations, and Measurement)
Term 2
Contexts focusing on Finance (financial documents and tariff systems)
Contexts focusing on Measurement (distance/length, weight (mass), volume and temperature)
Topics
Contexts focusing on Maps, plans and other representations of the physical world (scale and mapwork)
Contexts focusing on Probability
Revision
Assessment Assignment/investigation
June examination (2 papers, 1 hour each, 50 marks each; covering Finance, Measurement, Mapwork and Probability, integrated with Numbers and Patterns)
Term 3
Contexts focusing on Finance (income, expenditure, profit/loss, incomeand-expenditure statements, and budgets)
Topics
Contexts focusing on Measurement (perimeter, area and volume)
Contexts focusing on Maps, plans and other representations of the physical world (models and plans)
Assessment Assignment/investigation
Control test (covering Finance, Measurement and Models and plans, integrated with Numbers and Patterns)
Term 4
Contexts focusing on Finance (interest, banking and taxation)
Topics
Contexts focusing on Data handling
Revision
Assessment Assignment/investigation
November examination (2 papers, 1½ hours each, 75 marks each; covering all topics in the curriculum)
Time allocation per topic serves as a guideline only and it can be adjusted to your own pace. Bear in mind that you must first complete the relevant Lessons before you will be allowed to take a test or the relevant examination.
You need to spend 4,5 hours per week on Mathematical Literacy. Take note that this time allocation per week excludes all activities, assessments and examinations; it gives an indication only of the time that must be spent on theoretical aspects. If you tend to work more slowly, the necessary adjustments must be made to ensure that you still master all the work in time.
Proposed instructional time per week:

Learning objectives
At the end of the unit, you must be able to:
• write numbers in different formats
• write numbers in words
• write words in numbers
• describe numbers used in different contexts
• do calculations using a calculator
• apply the BODMAS rule
• multiply and divide by 10, 100 and 1 000
• convert common fractions and decimal fractions
• do calculations (addition, subtraction, multiplication and division) with fractions
• round off within context
• round off to the nearest 10, 100 and 1 000
• work with percentages
• calculate the initial price of items
• do calculations with rate and proportion
• discuss the difference between direct and indirect proportion, and do calculations
Lesson 1: Number formats and conventions
CONVENTION
UNIT 1: NUMBERS AND CALCULATIONS Sample
A fixed way of doing something
FORMAT
A fixed form in which something is written down or expressed.
Number formats and conventions refer to the different ways in which we can write and use numbers.
In South Africa, it is a legal requirement to use a decimal comma in all numbers. A decimal fraction is therefore separated by a decimal comma from the rest of the number (integer). This legislation also applies to monetary amounts because cents can be written as a decimal fraction of a rand. NEVER use a decimal point, as that is NOT the convention.
In large numbers consisting of three or more digits, spaces are used to divide the digits into groups of three for the sake of legibility. In numbers with decimal fractions, the digits on either side of the decimal sign are also divides into groups by using spaces. In some countries, a comma is used to divide digits into groups of three, but in South Africa we use spaces. This spacing, indicating the separation of numbers, is called thousands separators
EXAMPLES
One million eighty-three thousand five hundred and five: 1 083 505
Two million one hundred and five thousand forty-eight: 2 105 048
Three thousand four hundred fifty-six comma nine two seven: 3 456,927
This convention facilitates the reading of numbers. Compare 400000 with 400 000.
Write the number in words: 1
426
078,389



One million four hundred twenty-six thousand seventy-eight comma three eight nine
Value of each digit:
1: one million 4: four hundred thousands 2: twenty thousands 6: six thousands 0: zero hundreds 7: seventy 8: eight 3: three tenths 8: eight hundredths 9: nine thousandths

Activity 1
Study the number in the table.
1. Write the number in words.
2. Write the number in the correct format.
3. Show the thousands separators and the decimal separator.
Lesson 2: Numbers used in different contexts
Numbers are primarily used for counting or measuring. The types of numbers we use, however, depend on the specific contexts in which they occur. Sometimes we use whole number (integers) to indicate quantities or dimensions and at other times, we use ordinal numbers to indicate sequence. We also use numbers in the form of codes to identify someone/something, e.g., an ID number.



Sample


EXAMPLES OF NUMBERS USED IN DIFFERENT CONTEXTS
• Dimensions, for example, length and mass
• Street numbers as used in a home address
• Integers, for example, the number of passengers on a plane
• Ordinal numbers, for example, Teboho winning the first prize and Sipho winning the second prize
• Numbers indicating monetary amounts
• Unemployment rate, matric pass rate, interest rate, etc., expressed as a percentage
• Numbers representing a code and having no value, for example, phone numbers, car registration numbers, and personal identification numbers (PINs)

Numbers can be represented or used in various ways.
• Natural numbers (integers): a person has 10 fingers
• Ordinal numbers: 1st place, 2nd place, 3rd place
• Indication of location: flat on floor 3, number 11 311 or street number 701 in Park Street 701 Park Street
• Whole numbers: 17 years; 1994; 33 000; 1 524 796
• Decimals: 15,3; 10,3; 0,24
• Percentages: 99%; 25%; 10,75%
• Fractions: 1 3 ; 1 4 ; 7 8
• Ratios: 1 : 4; 2 : 3
Different number conventions are used in different contexts.
• Consider the flat number 811. The number 8 refers to the floor. The number 11 refers to the position of the flat It means that flat 11 is located on the eighth floor.
• The number on your movie ticket indicates the seat number where you must sit, e.g., B12 means that you must sit in row B, seat number 12.
• On a cricket scoreboard, a number such as 14.4 means that 14 overs and 4 balls have already been bowled. Similarly, 128/6 does not mean 128 divided by 6 but rather that a team has scored 128 runs for the loss of 6 wickets.
Take note: A full stop is used in this case as it is the worldwide convention in cricket.
• Positive and negative numbers:
o Temperature: -4 °C means 4 °C below freezing point (0 °C)
0 °C means at freezing point
4 °C means 4 °C above freezing point
o Bank statements: A balance of -R329 means that your account is overdrawn and that you owe the bank money, whereas a balance of R329 means that the bank owes you money.
o Percentage: Increases and decreases in share prices, commodities and currencies are expressed in percentage, e.g., +5,4% (increase) or -2,3% (decrease).
Increase (green)
Decrease (red)

Activity 2
1. First write the numbers using the correct thousands separators and then write them in words.
2. Write the numbers.
3. In a radio advertisement, it is stated that the balloon payment on a car is ‘six seven four five seven’ rand.
3.1 Is this a large amount? Motivate your answer.
3.2 Why do you think this number is read out in digits instead of being read correctly?
4. In each case, show which one of the two numbers is the greater.
4.1 12 or -12
4.2 -7 °C or -14 °C
4.3 R2 000 or -R5 000
4.4 -800 or -794
5. The number of a flat is 1206. Discuss the possible location of the flat
Lesson 3: Operations using numbers and calculator skills
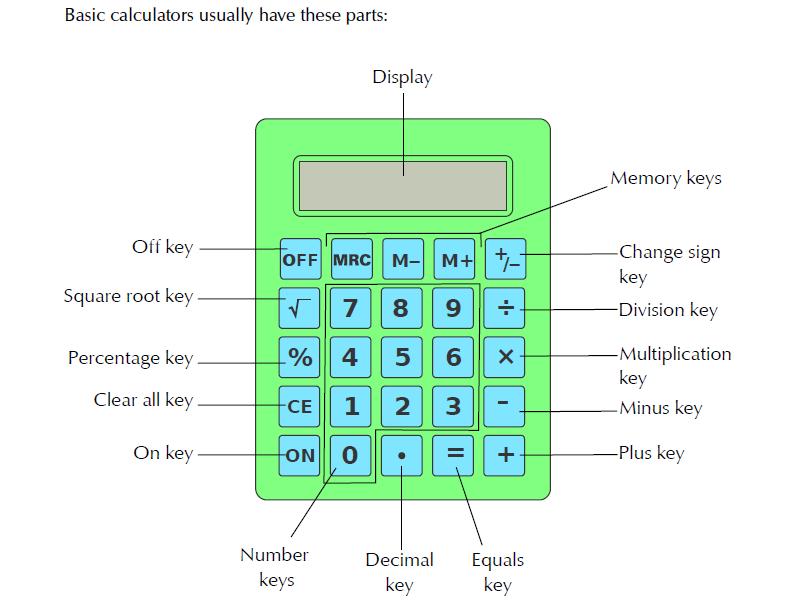
BASIC CALCULATOR A basic calculator can be used to do simple calculations quickly.

Activity 3
Use a calculator to find the solution.
1. 26 – 5 × 4
2. 5 + 6 × 62
3. 9 + 72
4. 5(10 – 4)2
5. 2 500 × (1 + 0,14 × 4)
6. 2 500(1 + 0,14)4
7. 9 + (18 – 3 × 5)3
8. �3(8 5)
9.
10.
Lesson 4: BODMAS rule (order of operations)
You must already have heard a lot about BODMAS. It is an easy method by which to remember the order of operations.
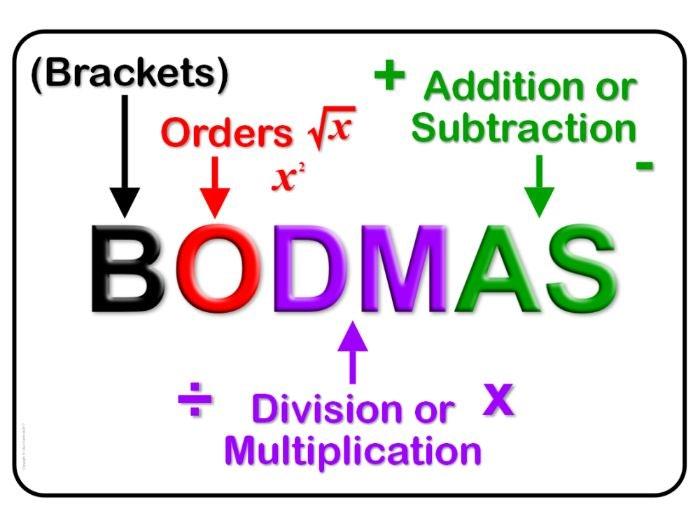
The term 'BODMAS' is explained below.
B – Brackets (...)
O – Order – exponents; roots; ‘of’, meaning multiplication
D – Divide
M – Multiply
A – Add
S – Subtract
If both division and multiplication are used, the calculation is done from left to right.

If both addition and subtraction are used, the calculation is done from left to right.

Take note that the operations in the same colour carry the same ‘weighting’. If both these operations occur in an expression, the operations are done from left to right.
EXAMPLES
1. 9 + 8 × 9 = 9 + (8 × 9) = 9 + 72 = 81
2. 122 + 4 × 9 – 10 = 144 + (36) – 10 = 170
3. 14% of R3 400 = 0,14 × R3 400 = R476

Activity 4
Use the BODMAS rule to do the calculations WITHOUT a calculator.
1. 16 – 8 × 3
2. 6 + 43
3. (3 × 6) + 5 × 7 – 10
Lesson 5: Multiplication and division by 10, 100 and 1 000
When multiplying by 10, 100 or 1 000, the number increases and the decimal comma moves to the right.
EXAMPLES
Sample
1. 28,98 × 10 = 289,8 (comma moves one place to the right)
2. 678,789 × 100 = 67 878,9 (comma moves two places to the right)
3. 67,23456 × 1 000 = 67 234,56 (comma moves three places to the right)
4. 0,345 × 1 000 = 345 (comma moves three places to the right)
When dividing by 10, 100 or 1 000, the number decreases and the decimal comma moves to the left.
EXAMPLES
1. 1 233,45 ÷ 10 = 123,345
2. 4535,678 ÷ 100 = 45,35678
3. 105 789 ÷ 1 000 = 105,789
4. 0,456 ÷ 100 = 0,00456

Activity 5
Do the calculations without a calculator and complete the table.
1. 19,57 × 10
2 125,345 × 100
3. 1 475 × 1 000
4. 0,468 × 100
5 1 234 ÷ 10
6. 125,12 ÷ 100
7 12 544 ÷ 1 000
8. 96 ÷ 100
• Comprehensive explanations of mathematical concepts in plain language.
• Practical, everyday examples.
• Activities that test learners’ knowledge application and reasoning.
• The facilitator’s guide contains step-by-step calculations and answers.
• Includes a formula sheet and an alphabetical list of mathematical terms for easy reference.
• Use in school or at home.
home classroom college workplace
