ILASCD Winter 2025 Journal

'I AM NOT A MATH PERSON"

A Letter from the President Quick Links

Amy Warke

ILASCD President

How often do we still hear someone say, “I’m not a math person!” or “I just don’t do math!”? Those words echo in classrooms and conversations alike, and they remind us how deeply our early experiences with math can shape our lifelong relationship with it.

As I reflect on my own journey, I’m reminded of the years I spent practicing math facts through drills and timed tests throughout my elementary years. Despite all that repetition, those facts didn’t truly become automatic for me until my first year of teaching, when I was teaching my own students to learn them. It was then that I began to see math differently: not as something to memorize, but as something to make sense of, to question, and to explore.

ILASCD Leaders

Amy Warke, President awarke2008@gmail.com

Scott England, Past President esengland@umes.edu

Amy MacCrindle, President-elect amaccrindle@district158.org

Sarah Cacciatore, Treasurer scacciatore@d75.org

Andrew Lobdell, Secretary lobdella@le-win.net

Debbie Poffinbarger, Media Director debkpoff@gmail.com

Ryan Nevius, Executive Director rcneviu@me.com

Bill Dodds, Associate Director dwdodds1@me.com

Task Force Leaders:

Membership & Partnerships

Denise Makowski, Amie Corso Reed

Communications & Publications

Belinda Veillon, Jacquie Duginske

Advocacy & Influence

Richard Lange, Brenda Mendoza Program Development

Jamie Bajer, Heather Bowman, Scott England, Amy MacCrindle, Terry Mootz, Amie Reed, Dee Ann Schnautz, Belinda Veillon, Amy Warke, Doug Wood

As you read through this Winter Journal edition, you’ll encounter ideas that feel familiar yet offer refreshing new perspectives on math teaching and learning. Math instruction has its base in the Eight Mathematical Principles, yet continues to evolve. Today, it’s about fostering critical and creative thinking, encouraging students to learn from mistakes, building conceptual understanding, and connecting mathematics to meaningful, real-world problem-solving.

We’re also reimagining what it means to build strong mathematical foundations. Play, storytelling, inquiry, and consistent integration into daily routines all play vital roles in making math engaging and accessible for every student. Still, we recognize that challenges—such as instructional time and structural constraints—can make implementation complex.

Our Illinois Numeracy Plan provides a strong vision for moving forward, and it

invites us to reflect together on how we can deepen our collective understanding. How can we best support teacher leaders, school teams, and district leaders as they bring this vision to life? What additional resources, professional learning, or collaborative opportunities might further strengthen that work?

Within the pages of this edition, you’ll find thought-provoking articles that challenge us to think deeply about what

math learning can be. I hope these voices inspire you—to reflect, to reimagine, and to continue your own journey of growth as a math educator and leader.

Amy Warke, Ed.D. President, IL ASCD -

A Letter from the Director

Ryan Nevius

ILASCD Executive Director

rcneviu@me.com

As we welcome a new year, I hope the holiday season offered you moments of rest, reflection, and connection. January always brings a renewed sense of purpose in our work as educators—and with it, excitement for one of the most energizing professional learning experiences in the Midwest: Pump Up Primary Conference, The 45th Annual Pre-K, Kindergarten, 1st, and 2nd Grade Conference, proudly hosted by Illinois ASCD/PD365.

Each spring, thousands of educators gather to celebrate and elevate the art of teaching our youngest learners. As we enter our 45th year, this event remains a practitioner-driven celebration of all things Pre-K through 2nd grade.

Why Attend?

With uncertain budgets, ongoing teacher shortages, and the increasing challenge of finding substitute coverage, prioritizing professional development can feel more difficult than ever. Yet these challenges make time for renewal even more essential. Pump Up Primary provides a purposeful opportunity to step back, recharge, and reinvest in your professional craft.

Attendees leave with:

• Practical, classroom-ready strategies

• Reenergized purpose and a strong sense of community connection

• Access to national experts bringing cutting-edge research and inspiration

• Tools, resources, and solutions tailored for the unique needs of early childhood and primary educators

Event Highlights for 2026

The 2026 conference—held March 5–6 at the Renaissance Schaumburg Convention Center—promises another unforgettable two-day experience. This year’s features include:

• Dynamic national keynote speakers who bring unmatched energy and expertise to early childhood and primary education

• Over 120 National and Local Speakers

• More than 225 breakout sessions designed specifically for Pre-K, Kindergarten, 1st, and 2nd grade teachers

• A high-energy Expo Hall filled with classroom resources, manipulatives, literacy and math tools, tech solutions, and hands-on demonstrations

• Dedicated transition times that ensure meaningful engagement between attendees and exhibitors

• A fantastic hotel experience with incredible food included in your registration costs.

What makes Pump Up Primary truly exceptional is its loyal, ever-growing community. Many districts send entire early learning teams to the conference, using it as a shared professional learning experience that strengthens collective practice. During the general session, we often ask participants how many years they have attended. It is not uncommon to see hands raised for 20, 25, and even 30 years—a testament to the conference’s impact and longevity. It’s no surprise that new educators often describe attending Pump Up Primary as the moment they “found their people.”

As we prepare for another record-setting year, we invite you to join us—and to encourage colleagues across Illinois to take part. Together, we can continue shaping joyful and developmentally rich classrooms for our youngest learners.

Registration is now open. We can’t wait to celebrate with you this March! Registration Details • Hotel Block Information • Vendor Applications

Ryan Nevius Illinois ASCD/PD365 Executive Director

Whole Child

Rebuilding Mathematical Identity: How Connection-Based Mathematics Classrooms Bring the Illinois Numeracy Plan to Life

If you ask a wide range of students how they feel about math, you are likely to hear some of these answers:

“I’m just not a math person.”

“I get so nervous, I can’t even think.”

“I used to like math…until the problems started getting harder. I’m just not that good at it.”

For years, math has been framed as a race to the rightor-wrong answer. The students who were good at memorizing the procedures and could then successfully apply them to quickly arrive at the correct answer were praised as “good at math,” while others were quietly deciding that math just wasn’t for them. As the Illinois Comprehensive Numeracy Plan notes, math anxiety and negative perceptions of mathematics now “compound the challenge for learners to succeed,” especially when math is seen as “an exclusive subject reserved for a few, rather than a right for all” (Illinois State Board of Education [ISBE], 2025).

We also know something about the brain: it doesn’t invest deeply in tasks that are of low interest and have a perceived low probability of success (Fitz &

Anne Paonessa

Price, 2025). When students come to math already convinced they will fail, they naturally protect themselves by disengaging. Recent research continues to confirm that math anxiety undermines achievement, often by interfering with working memory and problem-solving (Ma & Sun, 2025; Finell et al., 2022).

The new Illinois Comprehensive Numeracy Plan gives us a powerful opportunity to change that story. It redefines numeracy as far more than getting to the right answers quickly. True “numeracy” extends beyond procedural fluency to encompass reasoning, problem-solving, and the ability to communicate and apply mathematical ideas and it is grounded in equity and the belief that all students can develop the skills and confidence to thrive mathematically (ISBE, 2025, p. 4).

The question becomes: How do we bring that vision to life in everyday classrooms?

My work with the four domains of connection: Connections to Self, Others,

Learning, and Community, offers one way forward (Paonessa & Zwiers, 2025). When we align these domains with the ASCD Whole Child tenets and the Illinois Numeracy Plan, we get a roadmap for rebuilding mathematical identity for every student, as we shift away from the concept that math is only for an elite few who are “naturally” good at it (ASCD, 2013; ISBE, 2025).

True “numeracy” extends beyond procedural fluency to encompass reasoning, problemsolving, and the ability to communicate and apply mathematical ideas...

From “Right Answers” to Mathematical Identity

The Numeracy Plan acknowledges that achievement gaps in Illinois remain “significant and longstanding,” especially for students from historically marginalized groups, due in part to inequitable access to high-quality, culturally relevant math instruction (ISBE, 2025). It calls for math to become a pathway of opportunity, not a barrier, by creating conditions where students see mathematics as useful, achievable, and deeply connected to their lives (ISBE, 2025).

That vision aligns closely with emerging research on mathematical identity

and belonging. A 2024 student using international assessment data found that students’ sense of school belonging significantly predicted their math achievement, even after controlling for prior performance (Allen et al., 2018). A 2025 dissertation examining high school students’ math sense of belonging showed that students who felt they “fit” in math class reported higher confidence and more persistence with challenging tasks (Stevenson, 2025). Work on “mathematical life stories” underscores how experiences of exclusion or affirmation shape students’ long-term relationships with math (Gweshe & Brodie, 2024).

Jo Boaler’s mathematical mindset work reinforces this: students who encounter math as a creative, sense-making subject, and who see mistakes as a valuable learning opportunity, develop stronger confidence and have higher math achievement than those who treat math as a subject that they are “naturally” good or bad at (Boaler, 2022). The Illinois plan clearly leans in this direction. It emphasizes that mathematics is not culture-neutral and that communities can help students feel that mathematics belongs to them, that it is meaningful, and that these instructional shifts “align with the vision of numeracy for all” (ISBE, 2025, p. 11).

To me, that is the heart of rebuilding mathematical identity, helping each student think, “Math is a part of my world, and I belong here.” The four domains of connection offer a practical way to do exactly that (Paonessa & Zwiers, 2025).

The Four Domains of Connection in a Numeracy

Classroom

1. Connections to Self

Whole Child Tenet Lens: Healthy, Supported, Challenged

Connections to Self are centered on how students see themselves as mathematicians. Do they see themselves as capable problem solvers, or as people who just try to “get through” math? The Numeracy Plan calls for instruction where “students see themselves as capable, persistent, and confident problem solvers,” not just accurate test takers, and highlights the importance of habits of mind such as perseverance, reasoning, and reflection (ISBE, 2025, p. 2).

When we design math experiences that explicitly build on Connections to Self, we:

• Normalize and value mistakes as data for learning. Boaler’s work shows that when students see mistakes as evidence of brain growth rather than failure, they engage more deeply and persist longer (Boaler, 2022;

Sengupta-Irving, 2016).

• Give students chances to choose strategies and explain why a method makes sense to them, not just which method the teacher prefers. The Numeracy Summit and draft Numeracy Plan frame fluency as efficiency, flexibility, and accuracy, including selecting and adapting strategies, not just recalling procedures (ISBE, 2025).

• Help students name their own math strengths through reflective pauses. For example, “I’m good at visualizing fractions” or “I’m good at explaining my thinking to others,” connecting this to growth over time (Paonessa & Zwiers, 2025).

From a student’s perspective, Connections to Self sounds like: “I used to be afraid to speak up in math. Now we actually talk about mistakes in class. I can say, 'Here’s what I tried and what I learned from it,' and that feels different. I get stuck sometimes, but that doesn’t mean I’m bad at math. It just means that I’m learning.”

This directly supports the Whole Child tenets of Healthy (reducing anxiety), Supported (explicit scaffolds), and Challenged (expecting all students to engage in rich thinking) (ASCD, 2013).

2. Connections to Others

Whole Child Tenet Lens: Safe, Engaged

Connections to Others focuses on the social side of mathematics. The Numeracy Plan calls for discourse-rich classrooms where students justify reasoning, compare strategies, and engage in the Standards of Mathematical Practice (SMPs), especially constructing arguments and critiquing the reasoning of others (ISBE, 2025). Research continues to affirm that belonging and relationships are powerful predictors of math outcomes; a 2025 brief on positive conditions for math learning concluded that students achieve more when they experience strong relationships with teachers, feel a sense of belonging in the math community, and engage in highquality instruction that invites their ideas (Fitz & Price, 2025).

Connections to Others show up when:

• Design structures make thinking visible and shared. Peter Liljedahl’s Building Thinking Classrooms (2020) demonstrates that when students work in visibly random groups at vertical, non-permanent surfaces (whiteboards, windows, chart paper), more students think, talk, and revise their ideas, and they also take more intellectual risks.

• Normalize mathematical discourse as part of learning, not performance. Students regularly explain their reasoning, ask questions of peers, and build on one another’s ideas, reinforcing the Numeracy Plan’s emphasis on communication and justification (ISBE, 2025).

This domain aligns strongly with the Whole Child tenets of Safe (psychological safety to share ideas) and Engaged (active, social problem-solving) (ASCD, 2013).

...students learn best when classrooms are designed for interaction, where thinking is visible, talk is purposeful, and understanding is coconstructed rather than delivered...

3. Connections to Learning

Whole Child Tenet Lens: Engaged, Challenged

• In Essential Connection Skills, we emphasize that students learn best when classrooms are designed for interaction, where thinking is visible, talk is purposeful, and understanding is co-constructed rather than delivered (Paonessa & Zwiers, 2025).

From a student’s perspective, Connection to Others might sound like: “We don’t just sit alone doing problem sets anymore. Most days, we’re standing at the whiteboards in groups, trying to figure out a puzzle. I get to see how other people think, and sometimes my idea helps someone else. It feels like being a part of a team, and I end up understanding the math better.”

Connections to Learning is about meaningmaking, helping students understand why procedures work, when they are useful, and whether an answer is reasonable. The Numeracy Summit presentation and the Numeracy Plan offer a clear conception of fluency as the combination of efficiency, flexibility, and accuracy, including selecting appropriate strategies, adapting them, and evaluating reasonableness (ISBE, 2025). The plan calls for instruction that “blends understanding concepts (why), practicing skills (how), and applying knowledge to solve real-world problems (when and where)” (ISBE, 2025, p. 7).

Connections to Learning show up when we:

• Routinely ask students, “Does this answer make sense?” and build quick

estimation and over/under routines that make “reasonableness” a habit (National Council of Teachers of Mathematics, 2023).

• Use low-floor, high-ceiling tasks that invite multiple solution paths instead of one narrow algorithm (Boaler, 2022).

• Give students opportunities to reflect on their own learning: “What strategy did you use today? How did your thinking change?” (Paonessa & Zwiers, 2025). Current research on motivation and interest in math suggests that when students see purpose and coherence in what they are learning, they are more likely to sustain effort and develop deeper understanding (Eccles & Wigfield, 2020; National Council of Teachers of Mathematics, 2023).

From a student’s perspective, Connections to Learning might sound like: “We don’t just learn a trick and then move on. My teacher always asks us to show another way or to explain why a method works. Sometimes that’s harder, but I actually remember it now, and it’s satisfying when math actually makes sense.”

This domain clearly supports the Whole Child tenets of Engaged and Challenged, as students grapple with meaningful, coherent mathematics (ASCD, 2013).

4. Connections to Community

Whole Child Tenet Lens: Engaged, Supported

Finally, Connections to Community recognizes that math is not just a subject in school, it is a tool for understanding and shaping the world. The Numeracy Plan explicitly states that mathematics is “an important component of cultures throughout the world” and notes that ways of doing mathematics are culturally situated; communities that honor these connections help students feel that mathematics “belongs to them and is a meaningful part of their world” (ISBE, 2025, p.6).

Connections to Community show up when we:

• Use local data, such as attendance, neighborhood resources, school lunch waste, or community issues, as the context for math investigations (Turner et al., 2023; Yeh & Otis, 2019).

• Invite families and community members to share how they use math in their work and lives, affirming diverse mathematical practices (Turner et al., 2023).

• Connect projects to service-learning or real audiences, so that students experience math as civic and relational, not isolated, individual

performance (Paonessa & Zwiers, 2025).

Studies on identity and belonging in mathematics emphasize that when students see their cultures, languages, and communities reflected in math tasks, their sense of belonging and confidence grows (Burke, 2017; Gweshe & Brodie, 2024).

From a student’s perspective: “This year, we used data from our own school to make graphs and suggest changes to our bus routes. It felt like math actually mattered, not just for a test but for something real.”

This domain supports the Whole Child tenets of Engaged (real-world relevance) and Supported (acknowledging students’ full lives and identities) (ASCD, 2013).

Bringing

It Together: The Whole Child, the Four Domains of Connection, and Illinois’ Numeracy Vision

Prior IL ASCD Whole Child articles have emphasized the importance of keeping schools human-centered, particularly as instructional demands, accountability pressures, and technology continue to evolve. This body of work reinforces the need to look beyond data points alone and to intentionally design learning environments that attend to the whole child. The ASCD Framework calls on schools to ensure that each

student is Healthy, Safe, Supported, and Challenged, not as a slogan, but in daily practice (ASCD, 2013). For this to take place, we need to collaboratively plan and deliver connection- driven instruction which will positively shape our students’ learning experiences.

The Illinois Comprehensive Numeracy Plan gives us a similar invitation in mathematics. It calls on us to:

• Address math anxiety and negative perceptions that keep students from engaging (ISBE, 2025; Ma & Sun, 2025).

• Build conditions where math becomes a pathway of opportunity, particularly for students from historically marginalized groups (ISBE, 2025).

• Ensure teaching blends conceptual understanding, skill practice, and realworld application (ISBE, 2025).

• Center equity, identity, and belonging in professional learning for educators (Allen et al., 2018; Fitz & Price, 2025; ISBE, 2025).

When we see these commitments through the four domains of connection, the “how” becomes clearer:

• Connections to Self help students rebuild a sense of themselves as

capable mathematicians (Boaler, 2022; Paonessa & Zwiers, 2025)

• Connections to Others create classrooms where thinking is visible, social, and safe, aligned with Liljedahl’s thinking classrooms and the SMPs (Liljedahl, 2020; National Governors Association Center for Best Practices & Council of Chief State School Officers, 2010).

• Connections to Learning ensure instruction is coherent, sense-making, and grounded in flexible fluency (ISBE, 2025; National Council of Teachers of Mathematics, 2023).

• Connections to Community anchor math in students’ cultures, futures, and civic lives (Turner et al., 2023; Yeh & Otis, 2019).

Together, these domains serve the Whole Child: Healthy, Safe, Engaged, Supported, and Challenged, not as shown in posters on a wall, but in the lived experience of a numeracy-based math class (ASCD, 2013; ISBE, 2025).

Rebuilding mathematical identity is not an “extra” on top of the Numeracy Plan; it is the work (Allen et al., 2018; Stevenson, 2025). As we design classrooms grounded in connection, we’re not just improving test scores; we’re prioritizing something students needed all along: a

sense that they belong in mathematics and that mathematics can help them to better navigate their world (Boaler, 2022; ISBE, 2025; Paonessa & Zwiers, 2025).

References

Allen, K.A., Kern, M.L., Vella-Brodrick, D., Hattie, J., & Waters, L. (2018). What schools need to know about fostering school belonging: A meta-analysis. Educational Psychology Review, 30(1), 1-34. https://doi.org/10.1007/ s10648-016-9389-8

ASCD. (2013). Whole child tenets. https:// www.ascd.org/whole-child

Boaler, J. (2022). Mathematical mindsets: Unleashing students’ potential through creative mathematics, inspiring messages and innovative teaching. (2nd ed.). Jossey-Bass. https://eric. ed.gov/?id=ED620466

Burke, R. (2017). Language and culture in the mathematics classroom: Scaffolding learner engagement. In: Sellars, M. (Ed.), Numeracy in Authentic Contexts (pp. 91-109). Springer. https://doi.org/10.1007/978-98110-5736-6_6

Eccles, J. S., & Wigfield, A. (2020). From expectancy-value theory to situated expectancy-value theory: A developmental, social cognitive,

and sociocultural perspective on motivation. Contemporary Educational Psychology, 61, 101859. https://doi.org/10.1016/j. cedpsych.2020.101859

Finell, J., Sammallahti, E., Korhonen, J., Eklöf, H., & Jonsson, B. (2022). Working memory and its mediating role on the relationship of math anxiety and math performance: A meta-analysis. Frontiers in Psychology, 12, 798090. https:// www.frontiersin.org/journals/ psychology/articles/10.3389/ fpsyg.2021.798090/full

Fitz, J., & Price, H. (2025, June). Positive conditions for math learning: An overview of the research [Brief]. Learning Policy Institute. https:// learningpolicyinstitute.org/ product/positive-conditions-mathlearning-brief

Gweshe, L. C., & Brodie, K. (2024). Learners’ mathematical identities: Exploring relationships between high school learners and significant others. Mathematics Education Research Journal. Advance online publication. https://doi.org/10.1007/s13394023-00479-5

Illinois State Board of Education. (2025). Illinois Comprehensive Numeracy Plan

(Draft 1). Authors. https://www.isbe. net/numeracyplan

Liljedahl, P. (2020). Building thinking classrooms in mathematics, grades K-12: 14 teaching practices for enhancing learning. Corwin. https:// www.corwin.com/books/buildingthinking-classrooms-268862

Ma, H., & Sun, C. (2025). The relationship between mathematics anxiety and mathematics achievement of middle school students: The moderating effect of working memory. Behavioral Sciences, 15(11), 1566. https://doi. org/10.3390/bs15111566

National Council of Teachers of Mathematics. (2023, January). Procedural fluency in mathematics [Position statement]. https://www. nctm.org/Standards-and-Positions/ Position-Statements/ProceduralFluency-in-Mathematics/

National Governors Association Center for Best Practices, & Council of Chief State School Officers. (2010). Common Core State Standards for Mathematics. https://www.isbe. net/Documents/core_standards_ release.pdf

Paonessa, A., & Zwiers, J. (2025). Essential connection skills: Strategies for integrating social connections into

core content. Corwin. https://www. corwin.com/books/connectionskills-289436

Sengupta-Irving, T. (2016). Doing things: Organizing for agency in mathematical learning. Journal of Mathematical Behavior, 41, 210218. https://www.sciencedirect. com/journal/the-journal-ofmathematical-behavior/vol/41/ suppl/C

Stevenson, M. L. (2025). High school students’ sense of belonging in math (Doctoral dissertation, California State University, San Bernadino). https://scholarworks.lib.csusb.edu/ etd/2211/

Turner, E., Ester Mariñoso, P., Civil, M., Quintos, B., Salazar, F., & Varley Gutiérrez, M. (2023). Parents and teachers doing math together. In Lamberg, T. & Moss, D., (Eds.), Proceedings of the forty-fifth annual meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education (Vol. 2, pp. 499–507). University of Nevada, Reno. https://files.eric. ed.gov/fulltext/ED658451.pdf

Yeh, C., & Otis, B. M. (2019). Mathematics for whom: Reframing and humanizing mathematics. Occasional Paper

Series, 2019 (41). DOI: https://doi. org/10.58295/2375-3668.1276

Anne Paonessa, Ph.D., is a the coauthor of Essential Connection Skills: Strategies for Integrating Social Connections into Core Content (Corwin, 2025) with Dr. Jeff Zwiers, and she is the founder of ConnectED Classrooms, an organization focused on helping schools embed connection-driven practices into core instruction.

She serves as an adjunct professor at National Louis University, is a mentor for new principals, and is currently working as a School Improvement Specialist supporting CPS schools. With more than 20 years of experience as a teacher, principal, and district administrator, Anne partners with schools and districts to strengthen student engagement, belonging, and learning through inclusive, Whole Child-aligned instructional practices.

Book Review

Mathematics of Tabletop Games

by Aaron Montgomery

For most of the history of education, educators have used games in the classroom. Whether for physical education, as ways to break the monotony of routine instruction, or to allow students to take a break, games have long been integral to any classroom. For the last several decades, these games have included what may casually be called “board games” but are more accurately described as “tabletop games.” Tabletop games, which include games that use cards, dies, boards, pawns, spinners, tiles, miniatures, and any assortment of accessories that do not

easily fit into any category, are generally used in one of three ways:

• Engagement

• Exploration

• Experiences

Educators may use tabletop games for engagement when they want to provide students a break from traditional instruction, as a reward at the end of the week or, as I look out the window and see the 12 inches of snow from a recent early winter storm that is showing no signs of melting due to extreme cold, as a way to keep students occupied when

Click the cover to view on Amazon.

the weather prevents them from going outdoors for recess. It is not unusual to find a classroom, regardless of the gradelevel or content area, that has a ready supply of traditional board games such as Monopoly, Scrabble, Sorry, Clue, or chess/checkers, along with card games like Uno, Go Fish, or just a deck of playing cards that can be used for a wide variety of games.

Some educators, wanting to use games for more instructional purposes, may choose to incorporate them into the curriculum as a way of exploring concepts and skills. This may include “educational games” that teach academic vocabulary or math facts through flashcards or simple board games that require students to roll dice, move pawns, and then answer questions related to specific content areas. Teachers may also use traditional games to support academic concepts, such as using Monopoly to teach the basics of finances, Scrabble to practice letter-word recognition and spelling, and counting as students add up scores, or short-term simulations that have students imagine they are in a historical or non-school situation and, through prompts, challenges, and other tasks, have to reach a goal. (Consider here the classic computer game Oregon Trail, the source of deep consternation for school children throughout the 1980s and 1990s.)

A third way teachers may use games in the classroom is through experiential learning, such as full-blown classroom transformations, long-term simulations or role-playing games, or by converting the classroom itself into a game, known as a transformation or “gamification,” where students are in teams that are completing tasks, earning “experience points,” participating in “real-world” situations (such as designing a business or running a restaurant), and competing for a top position on a leaderboard.

All of these are common enough methods of incorporating tabletop games into the classroom that we hardly need to seek out citations to support this claim. Simply visit any classroom anywhere in the state, country, or even the world, and you are almost guaranteed to find evidence of games being used in at least one of these three ways.

However, there is another way that tabletop games can be used in the classroom, which is the focus of Aaron Montgomery’s Mathematics of Tabletop Games (2025), part of the AK Peters/ CRC Recreational Mathematics Series, published by CRC Press, an imprint of the Taylor & Francis Group. Dr. Montgomery presents tabletop games not just as a way to supplement the learning experience for students but also as a source for teaching students about a variety of mathematical

concepts, including combinatorics, geometry, group theory, graph theory, probability, game theory, auctions, logic, and number theory.

The purpose of this book is to link mathematics and tabletop gaming in such a way that the reader can explore ways to answer mathematical questions through games. For example, many games use a combination of cards for players. Thus the game becomes a demonstration, rather than simply discussing a concept such as the

the second collection”) can be used to determine the number of possible combinations for an opening hand in the game. The answer, incidentally, is worked out as follows: P(11,2)/2! x P212, 8)/8! = 4,869,460,249,861,350 possible opening hands (p. 8-12). And since the average game time for Ark Nova is 90150 minutes, it would take four players approximately 15,430,388 years to go through every possible opening hand combination–thus all but ensuring the impossibility of ever experiencing the same game twice!

...use games as a way of exploring and understanding mathematical vocabulary...

Combination Rule, which states that “if k selections are made from a collection of size n without replacement, and the order of selection does not matter, then there are C(n, k) ways to make those selections, where C(n, k) = P(n, k)/k! or n!/k!(n-k)!”

Dr. Montgomery shows how an instructor could use the game Ark Nova to demonstrate how this rule, combined with the Product Rule (”if there are m objects in one collection and n objects in a second collection, then there are m x n pairs of objects where the first object comes from the first collection and the second object comes from

Another way to teach mathematics through tabletop games, rather than using games as an extension of instruction, is to use games as a way of exploring and understanding mathematical vocabulary, which often has specific uses different from colloquial usage. For example, in the chapter on Group Theory, Dr. Montgomery demonstrates how games that involve placing tiles that are constrained by adjacency rules, such as Carcassone, Galaxy Truckers, and Railroad Ink, to define the following mathematical terms: group, which is defined by three properties: identity, inversion, and closure; and equivalence, which is

defined by the properties of reflexivity, symmetry, and transitivity (p. 49-50). Likewise, in chapter 9, which focuses on Number Theory, the game Codenames is used to explore the Fundamental Theory of Arithmetic, and the game Hanabi is used to demonstrate the principles of modular arithmetic.

Whether you are a fellow tabletop gaming enthusiast or just a math educator looking to teach mathematics through a non-traditional format, or are simply looking for a way to change up your traditional curriculum, Mathematics of Tabletop Games provides questions and prompts that can be used to teach mathematical concepts through gaming.

Alex T. Valencic is an educator, former small business owner, bibliophile, and geek of all things. As the Professional Learning Coordinator for Freeport SD 145, he supports the development and implementation of innovative educational practices in the classroom and leads the district mentoring leadership team. He served as FSD’s Elementary Summer Learning Administrator from 2021 to 2024, where they offered academic and enrichment classes that included robotics, 3-D art, and tabletop gaming.

Resource Corner

ANYONE CAN BE A “MATH PERSON”

“Why,” Su asks then, “don’t we approach mathematics the way that we approach art?” READ MORE...

TURNING MATH ANXIETY INTO CURIOSITY: A TEACHER’S TAKE ON GAME-BASED LEARNING

Game-based learning isn’t about replacing rigor. It’s about sparking curiosity, reducing fear and fostering a genuine love of learning. READ MORE...

JIGSAW PUZZLES HELP MAKE MATHEMATICS LEARNING MORE ACTIVE AND FUN

Using puzzles, both at home and in classrooms, can restore the often-forgotten truth that learning happens in conversation. READ MORE...

NEW MATH STRATEGY EQUALS CONFIDENCE, COMPETENCE

Vertical learning encourages students to get out of their seats and work collaboratively with their classmates to solve equations and story problems. READ MORE...

EMPOWERING EDUCATORS, FAMILIES, AND STUDENTS THROUGH MATHEMATICS Twana Young is a visionary leader deeply committed to empowering educators, families, and students through mathematics. READ THE INTERVIEW...

MATHEMATICS IS THE SENSE YOU NEVER KNEW YOU HAD | EDDIE WOO | TEDXSYDNEY High school mathematics teacher and YouTube star Eddie Woo shares his passion for mathematics, declaring that "mathematics is a sense, just like sight and touch" and one we can all embrace. WATCH THE VIDEO... Browse His

TALK NERDY TO ME:

TEACHERS WHO USE MATH VOCABULARY HELP

STUDENTS DO BETTER IN MATH

Using words like ‘factors,’ ‘denominators’ and ‘multiples’ may be part of a constellation of good math teaching practices. READ MORE...

A LITTLE PARENT MATH TALK WITH KIDS MIGHT REALLY ADD UP

Mentioning numbers during everyday activities could be more beneficial than workbooks and exercises. READ MORE...

CREATING A CLASS COOKBOOK TO INSPIRE CRITICAL THINKING IN MATH

Students get to share their favorite family recipes and practice their problemsolving strategies in this engaging math project. READ MORE...

5 MATH SKILLS YOU CAN TEACH IN THE KITCHEN

The kitchen is one of the easiest and most enjoyable places to see math in action. READ MORE...

USING LEGO TO BREAK THROUGH THE ANXIETY BARRIER IN JR. HIGH MATH

I’d love to say it was intentional but it’s really more of a happy accident that this has come to play a big role in decreasing the math anxiety in my students. READ MORE... Did You Know? Read

5 WAYS TO SHARE MATH WITH KIDS

n this playful, inspiring talk, the founder of Math for Love offers teachers and parents alike a five-step guide to sharing the beauty and playfulness of mathematical thinking with children. WATCH NOW...

James Burnett

Short on Time, Long on Understanding: Rethinking Fact Fluency

For more than a century, helping students learn basic number facts such as 9 + 6 = 15 has been a goal of elementary mathematics. Yet despite generations of effort, many students beyond Grades 3 and 4 still lack automatic recall.

We simply cannot continue relying on the same outdated pattern — a brief flurry of activities to “introduce” strategies, followed by months of repetitive practice in the hope that facts will somehow be committed to memory.

Nowhere is this issue more evident than in the United States, where structural realities make this traditional model almost certain to fail. Why do I make this claim? Because U.S. schools operate on an unusually short academic calendar, about 180 school days a year. That’s 20 days (one month) fewer than in Australia, and 40 days fewer than in Singapore. Add to that a long summer break — the perfect opportunity for students to forget what they learned — and it’s no surprise that fact fluency erodes rather than deepens over time.

And let’s not mention the number of minutes dedicated to teaching math each day and the instructional time lost to maintaining two measurement systems!

So while extending the school year may be beyond the control of most districts (and certainly teachers), there is something that can be done right now: adopt a different approach to fact fluency — one that works even when we’re short on time, because it builds long-term understanding.

In this article, I’ll share a five-stage model for teaching fact fluency. To illustrate the model, I’ll use the Make-10 addition strategy, as it is one of the most widely recognized and explicitly cited strategies in contemporary state and national mathematics standards both in the U.S. and abroad.

The Five-Stage Model for Building Fact Fluency

The visual model below illustrates the five sequential stages of fluency development: Prepare, Introduce, Reinforce, Practice, and Extend.

teachers must ensure that students possess the prerequisite knowledge and skills needed for success. For the Make10 strategy, students should:

• Have a deep conceptual understanding of addition

• Be able to read, write, and count numbers to at least 20

• Be able to subitize quantities and recognize visual number patterns

• Have had experience using fiveframes and ten-frames

While the first three are non-negotiable, the fourth is strongly recommended. A well-structured core program gives kindergarten students opportunities to fill five-frames, helping them see that five is the sub-base of ten. Over time, they use ten-frames to represent numbers greater than five.

2. Introduce

The Five-Stage Model for Building Fact Fluency

Each stage has a purpose and aligns with how children move from concrete experiences to abstract reasoning.

1. Prepare

The visual model below illustrates the five sequential stages of fluency development: Prepare, Introduce, Reinforce, Practice, and Extend.

Before introducing any new strategy,

Once readiness has been established, we move to introducing the strategy. At this stage, students use hands-on counters to physically make a ten. A meaningful context helps anchor the idea to something familiar — connecting new learning to prior experience.

For example, suppose we want to find the total cost of these two items.

teachers wish to capture students’ reasoning, the vertical alignment of the ten-frames naturally aligns with the horizontal equation that includes the equivalence symbol.

At this point, the link between action, language, and symbol begins to take shape.

ouble ten-frames and counters to represent the value of each item, as shown

uble ten-frames and counters to represent the value of each item, as shown

Students use double ten-frames and counters to represent the value of each item, as shown below.

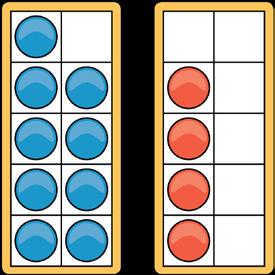
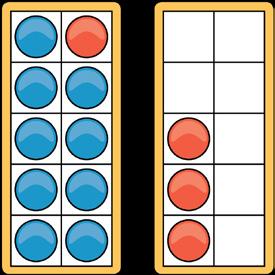
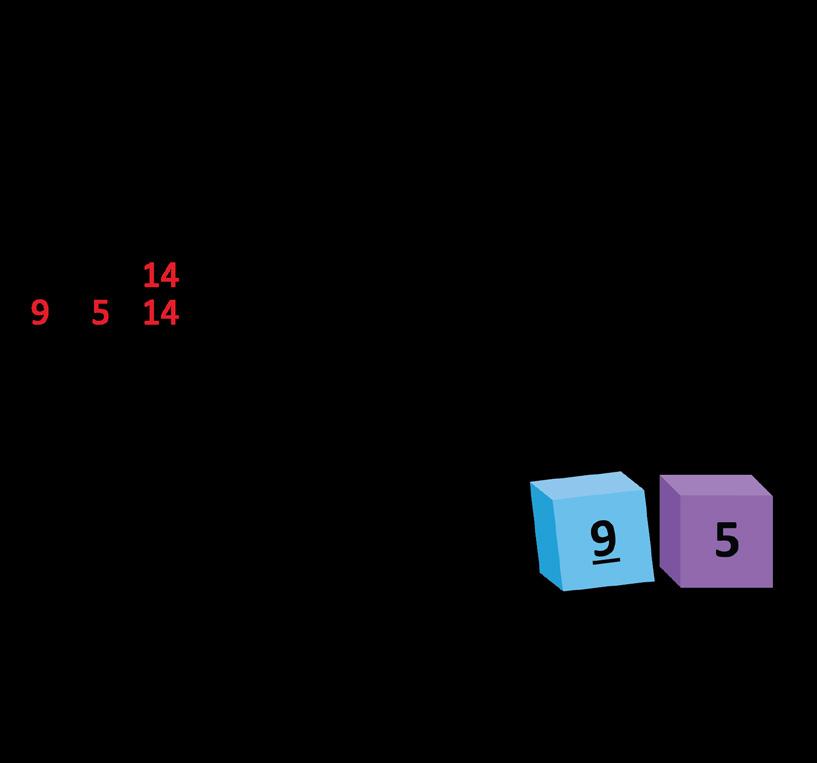
[CAPTION: 9 + 4 = 13]

[CAPTION: 9 + 4 = 13]

To see this process in action, you can view a short demonstration on my YouTube the Number from Down Under, which models how to teach the Make-10 strategy u double ten-frames and counters (watch here)

ation intentionally leverages the prior understanding that nine is five and most importantly, that nine is one less than ten. Through careful questioning, ompted to move counters to find the total value

3 Reinforce

tion intentionally leverages the prior understanding that nine is five and most importantly, that nine is one less than ten Through careful questioning, ompted to move counters to find the total value.

y As students move the counters, we wan t them to verbalize their thinking, and four is the same value as ten and three.”

nd four is the same value as ten and three ”

To see this process in action, you can view a short demonstration on my YouTube channel, the Number from Down Under, which models how to teach the Make-10 strategy using double tenframes and counters.

This stage allows students to assimilate and internalize the strategy It serves as a connecting the concrete and pictorial models of the int roductory phase with the a symbols used during practice

. As students move the counters, we want them to verbalize their thinking,

3. Reinforce

rk is required, but if teachers wish to capture students’ reasoning, the vertical

This representation intentionally leverages the prior understanding that nine is five and four more, and most importantly, that nine is one less than ten. Through careful questioning, students are prompted to move counters to find the total value.

e ten-frames naturally aligns with the horizontal equation that includes the mbol.

k is required, but if teachers wish to capture students’ reasoning, the vertical e ten-frames naturally aligns with the horizontal equation that includes the mbol

Because classroom time is precious, this stage often moves to pictorial models Th teachers from constantly distributing manipulatives while keeping the learning vi interactive

he link between action, language, and symbol begins to take shape.

e link between action, language, and symbol begins to take shape

Language is key. As students move the counters, we want them to verbalize their thinking, such as: “Nine and four is the same value as ten and three.”

This stage allows students to assimilate and internalize the strategy. It serves as a bridge — connecting the concrete and pictorial models of the introductory phase with the abstract symbols used during practice.

A simple folding card can help remind students of the thinking they developed ear counters and frames. When the card is opened, they see both parts (for example, n four). When folded, they see the ten and the remaining three visually reinforcin relationship they discovered

No written work is required, but if

Because classroom time is precious, this stage often moves to pictorial models.

These free teachers from constantly distributing manipulatives while keeping the learning visual and interactive.

A simple folding card can help remind students of the thinking they developed earlier with counters and frames. When the card is opened, they see both parts (for example, nine and four). When folded, they see the ten and the remaining three — visually reinforcing the relationship they discovered.

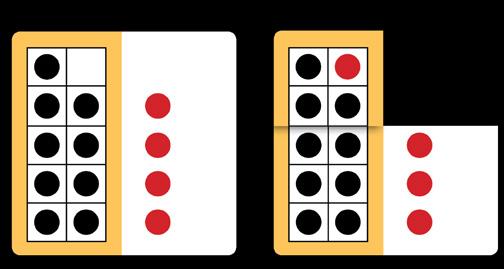
[CAPTION: “Nine

add four is the same as ten add three.”]

But it isn’t enough to use this folding card on its own. To truly reinforce the strategy, students need an activity that bridges the concrete and the abstract, like the one shown on the following page.

In this task, students write the numerals shown on the right on the six faces of two blank cubes. They roll the cubes and search their activity sheet for

the matching equation that will help them find the sum. They then record the answer for both related facts. For example, rolling a 9 and a 5 reinforces that 10 + 4 has the same value as 9 + 5.

Activities like this are not conceptual, so they cannot be part of the “Introducing” stage — but they are not yet practice either. They deliberately bridge the visual model and the symbolic representation.

We don’t provide enough of these transitional experiences, yet it’s here that students truly begin to own the strategy — moving from manipulation to mental imagery, and from guided reasoning to independent recall.

4. Practice

Only after students have grasped the underlying idea do we focus on automating recall. Practice develops accuracy and speed, but it must remain meaningful. I encourage teachers to select or design games that focus specifically on the target facts while gradually incorporating previously learned facts from the Count On and Use Doubles number fact clusters for addition.

Remember that time is critical, so practice sessions should be frequent (daily) and short (up to 5 minutes). It is better to do five 5-minute sessions a week than one 20-30 minute session on one day.

[CAPTION: “Nine

In this task, students write the numerals shown below on the six faces of two blank cubes

They roll the cubes and search their activity sheet for the matching equation that will help them find the sum They then record the answer for both related facts

The final stage—and perhaps the most overlooked—is extension: applying the same strategies to greater numbers, fractions, and decimals.

For example, rolling a 9 and a 5 reinforces that 10 + 4 has the same value as 9 + 5

Activities like this are not conceptual, so they cannot be p art of the “Introducing” stage but they are not yet practice either They deliberately bridge the visual model and the symbolic representation

If students can successfully use a strategy to calculate 9 + 4 = 13, why not encourage them to use that same thinking later to solve 29 + 15 = 44? When students view numbers as quantities, not symbols, they know they can decompose and recompose values just as they did with counters on a double ten-frame.

We don’t provide enough of these transitional experiences, yet it’s here that students truly begin to own the strategy moving from manipulation to mental imagery, and from guided reasoning to independent recall.

6 5. Extend

For instance, they can see that 15 can be broken into 14 and 1, and that moving one unit to the other addend creates 30 + 14, an easier calculation. Similarly, with 398 + 56, students who think strategically recognize that this is equivalent to 400 + 54. This is a mental adjustment that simplifies what would otherwise require a written algorithm.

The same reasoning applies as students progress into fractions and decimals. In 1 5/7 + 4/7, the strategy becomes one of making a whole rather than making ten.

Likewise, 1.95 m + 2.45 m can be seen as 2.00 m + 2.40 m, again simplifying the calculation through compensation.

In both cases, students generalize a strategy first learned in the early grades. The skill is no longer about “making ten” — it’s about making sense. When students internalize strategies this way, they build a lifelong understanding of how numbers work.

Conclusion

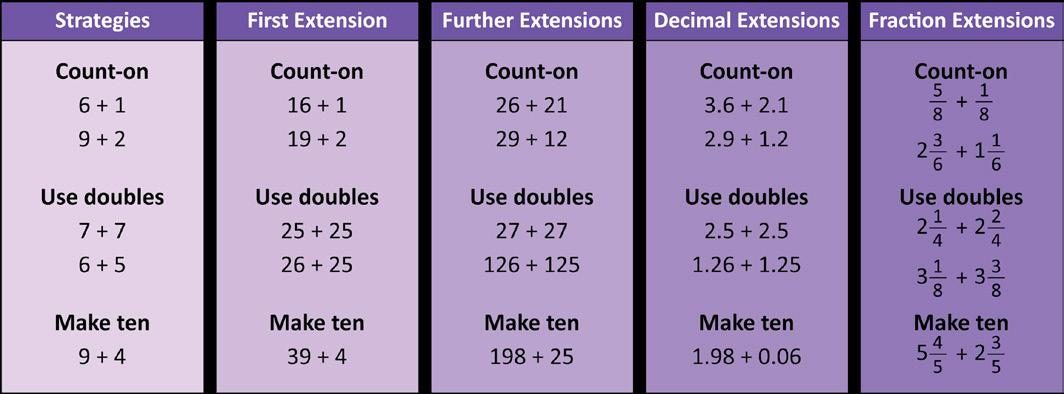
The image below shows how the basic addition strategies can be extended across the grades. Strong core programs will have these progressions naturally embedded in their developmental sequence, and effective curriculum leaders will understand why they are there.

forget their facts; it’s that we too often stop teaching for understanding too soon. When fluency is taught this way, it doesn’t fade over the summer. It endures—because it’s built on understanding.

Fact fluency is not a topic to be covered and tested — it’s a foundation to be expanded, even in classrooms short on time. The problem isn’t that students

The image below shows how the basic addition strategies can be extended across the grades. Strong core programs will have these progressions naturally embedded in their developmental sequence, and effective curriculum leaders will understand why they are there.

James Burnett is the co-founder of ORIGO Education, an award-winning mathematics education company serving schools across Australia, North America, and beyond. With more than 30 years’ experience as an educator, author, and curriculum designer, he has written and co-authored over 300 mathematics resources, including Stepping Stones, a comprehensive K–6 program. A frequent keynote presenter throughout the United States, James is recognised for helping educators make mathematics meaningful, enjoyable, and accessible for every learner. He also shares practical classroom insights through his YouTube channel, the Number from Down Under, which showcases contemporary ideas for teaching mathematics.

Beyond Right Answers: What Critical Thinking in Math Really Looks Like

When we think about mathematics instruction, it’s easy to picture problem sets, formulas, and step-by-step procedures. Yet, math classrooms that cultivate critical thinking look and sound different. In these spaces,

In these spaces, students don’t just do math; they think mathematically.

students don’t just do math; they think mathematically. It isn’t about the knowledge, but the understanding, which makes it critical thinking.

Critical thinking in math isn’t about harder problems; it’s about deeper reasoning. It’s when students move beyond the “how” to explore the “why” and the “what if.” The goal is not merely procedural fluency, but the development of flexible thinkers who can analyze, justify, and apply mathematical ideas across contexts.

Asking “Why?” and “What If?”

Students engaged in critical thinking don’t take formulas at face value. They explore where mathematical rules come from and test their limits.

Travis Mackey

“Why does this formula for area always work?”

“What happens if we double one dimension but not the other?”

This kind of inquiry transforms math from memorization to meaning-making. When students are encouraged to question, they start to see patterns, make conjectures, and build their own understanding of mathematical relationships.

Explaining Reasoning, Not Just Answers

Critical thinkers can explain their process clearly — in words, numbers, and

math is a language for reasoning, not just computation.

Evaluating Multiple Approaches

Critical thinking thrives when students compare and evaluate strategies.

“Would factoring or the quadratic formula be more efficient here?”

“Can we solve this geometrically instead of algebraically?”

When students see there is more than one valid path to a solution, they begin to appreciate the creativity inherent in

When students are encouraged to question, they start to see patterns, make conjectures, and build their own understanding of mathematical relationships.

visuals. They justify how they reached an answer and can defend it to others. Ask students, “Why do you know your answer is correct?” Hopefully, you start to get responses like, “I know my answer works because when I substitute it back, both sides of the equation balance.”

By requiring students to articulate their reasoning, teachers help them internalize mathematical structure and logic. It also allows peers to learn from multiple approaches — reinforcing that

mathematics. This comparison builds adaptability and deepens conceptual understanding.

Making Connections Across Concepts

Students who think critically connect math ideas across topics and to realworld contexts.

“This slope formula reminds me of the unit rate in proportions.”

“This geometry problem uses the same reasoning as a scale model in science.”

Connections make math stick. They help students recognize that mathematical thinking is a coherent system, not a collection of isolated rules.

Learning from Mistakes

Critical thinking also means treating errors as opportunities. Students reflect on missteps, identify misconceptions, and adjust their reasoning.

“Where did my thinking break down?”

“What assumption did I make that wasn’t true?”

When classrooms normalize this kind of reflection, they build resilience and foster a growth mindset that extends far beyond math.

Applying Math in New Situations

True mathematical understanding shows when students transfer knowledge to unfamiliar contexts.

“This problem is new, but it reminds me of how we used systems of equations in the budgeting project.”

Whether through modeling, projectbased learning, or real-world applications, these experiences ask students to synthesize what they know — the essence of critical thinking.

Collaborating and Debating Ideas

Finally, critical thinking in math is

inherently social. When students discuss, defend, and critique reasoning respectfully, they sharpen their own thinking.

“I understand your process, but does that always work?”

“Can we prove your conclusion is true for all numbers?”

Collaborative dialogue turns classrooms into communities of reasoning — places where thinking is visible and valued.

Classroom Example: Turning SurfaceLevel Work into Deep Thinking

In an Algebra I classroom, students were working on solving systems of equations. Initially, most students followed a substitution procedure without much discussion. I paused the class and asked, “Can anyone explain why substitution works?” Silence filled the room until one student replied, “Because we’re replacing one variable with what it equals.”

Pressing further, “What if we replaced it with something *not* equal what would happen?” This sparked a discussion about equivalence, balance, and maintaining equality.

By shifting from procedure to reasoning, we moved the class from doing math to thinking mathematically. Students began to see the connection between

equations, graphs, and real-world systems — the heart of critical thinking.

Final Thought

Critical thinking in math is not a new initiative or an add-on to instruction. It’s the heartbeat of meaningful learning. When we create classrooms where students question, justify, and connect ideas, we prepare them for more than exams. We prepare them for life’s complex problems that don’t come with answer keys.

Travis Mackey, a former math teacher and administrator, has 36 years of experience in education. He is passionate about integrating real-world problem-solving into math instruction. He has led district-level innovation around instructional leadership and student engagement across Illinois.

Article

Improving Students' Efficacy in Mathematics through

Progression-Based Assessment

Introduction

Mathematical literacy is an essential life skill to guide our understanding of economics, finance, science, and engineering. Mathematics influences the development of new algorithms that support the advancement of innovative fields such as artificial intelligence, robotics, and quantum science and engineering. As educators, we should strive to motivate students to continue their mathematics journey so they may be well informed, advance in these fields, and ultimately use their skills to improve the welfare of others.

As students learn mathematics throughout their education, however, they develop varying levels of confidence in whether they are a "math person" or not (Dresel et al., 2024). This happens, in part, due to the manner in which they are assessed. When they make numerous errors, students begin to believe they are not capable of understanding or performing well, and unfortunately, they perceive that they've reached a threshold for how math may be applied in their future. We believe all students are mathematical thinkers, and we need to find pathways to build efficacy.

Anderson Trimm

Evan Glazer

One approach to building efficacy is to acknowledge that students learn and show readiness at different rates. In this article, we promote a progression approach to assessment that gives students choice in the problems they

(Hemmings et al., 2011). In early grades, high performance often provides opportunities to be placed in accelerated or gifted programs. Low performance sets the stage for students to feel frustrated and doubt their potential to

The net result has been greater self-awareness, willingness to learn from mistakes and tackle new challenges, and improved efficacy, helping them believe they are capable of continuing their mathematics journey.

believe they can solve. This is an evolution of a standards-based report card where students demonstrate performance against designated standards. As an added element, we are using assessment tools with varied difficulty-levels where students respond to questions at their readiness level, and then grow at different rates to achieve different levels of progress. The net result has been greater self-awareness, willingness to learn from mistakes and tackle new challenges, and improved efficacy, helping them believe they are capable of continuing their mathematics journey.

The Woes of Assessment Practices

Past performance in mathematics paired with positive attitudes towards mathematics is a strong indicator of continued success in the subject

develop as mathematical thinkers. Ability groups intend to provide environments where students can engage in learning at their readiness level. However, even in advanced math classes, students' sense of efficacy is influenced by how well they are performing on their course assessments (Sakellariou, 2022). In essence, students’ sense of whether they are good at math is, in part, attributed to their perceived success.

The manner in which students are assessed influences students’ understanding of their success, and that can be problematic with traditional approaches to grading (Brookhart, 2017; Guskey, 2013; Willam, 2011). For example, by calculating the grade by averaging, early mistakes permanently lower a student’s course grade regardless

of whether they later mastered the same material. This often results in a lack of motivation, especially when it becomes impossible to earn an A or B, no matter how much the student improves. This can lead to test anxiety, since once points are lost, they cannot be recovered. For the same reason, there is not much motivation to learn from mistakes on a test. The points become the primary concern, as evidenced by the majority of student questions in office hours taking the form “will I get counted off if I write XYZ on a test?” or “can I get a point back on this problem?”, rather than serious questions about the content. Assessment shouldn’t be a motivation killer, but rather a feedback loop for students to want and feel like they could do better.

We believe, then, that systems of assessment should be designed so that students are showing signs of success through questions they are ready to solve rather than being measured with the same set of questions for all students. Varying the assessments is not a new phenomenon in education. Elementary educators, for example, provide different reading levels to students so they can all be engaged with their text at the appropriate challenge level (Fountas & Pinnell, 2017). We argue the same should be true for mathematics. If students can be given problems where they are successful

independently, then they should be gradually challenged further in the classroom as well as on their assessments.

Making the Switch to ProgressionBased Assessment

We endorse a progression assessment approach based on the learners’ readiness. The benefit of this approach is that it provides students the opportunity to build on their previous success rather than experiencing an unproductive struggle with content they do not fully understand. Knowing their level of success provides a fruitful opportunity for both students and educators to identify the next challenge level. The shift in thinking creates an environment where students realize they are on a learning journey of growth rather than learning trials of acceptance. Rather than feeling anxious about whether they can and cannot do math, students are rewarded by working at it until they understand. The goal is to build students' mindset of more self-confidence and to become more resilient when working through their mistakes. The following section describes Dr. Trimm’s transformation in assessment practices and the impact on student learning.

Starting in the Fall of 2022, I switched to a progression assessment approach, desiring an attitudinal shift towards greater self-awareness, motivation, and a

Progression-Based Assessment (cont.)

more positive view of mathematics. I also wanted to make sure that students were better-prepared for their future courses. In traditional grading, deficiencies in core areas can be made up for by doing well in others, so the grade averages out to a successful outcome. For instance, a student might have a failing assessment average, but earn enough points in categories for homework and participation so that they ultimately pass the course, despite serious deficiencies in their understanding. This approach does not set them up for success in future courses.

As advocated by Clark (2022) and Talbert (2022), grading should be based on

expectations by acknowledging that students can achieve different levels of success (e.g., sometimes described as “meets” or “exceeds”). There is no partial credit if the standard is not yet met – 70% is no longer “good enough.” Additionally, students have multiple opportunities to challenge themselves to their potential.

Comparing the Old with the New Approach

I have now used this progressionbased assessment system in a variety of mathematics courses ranging from Geometry to AP Calculus to post-calculus electives such as Linear Algebra and

All that matters is that a student eventually meets clearly-defined learning targets by the end of the course, and provides flexibility for how and when they get there.

abundance, rather than scarcity, where students have many opportunities to demonstrate learning and improve over time, without penalty for earlier mistakes. This acknowledges that students do not all start from the same place and do not all learn at the same rate. All that matters is that a student eventually meets clearly-defined learning targets by the end of the course, and provides flexibility for how and when they get there. Further, it also sets high

Differential Equations. My original approach was heavily influenced by that of Talbert (2022). In each of these courses, 15-20 clear learning standards are assessed multiple times throughout the semester. Each standard assessed is scored on a 4-point scale: (1) Beginning, (2) Proficient, (3) Advancing, (4) Distinguished, based on a holistic review of the student’s solution, rather than on points and partial credit.

Most assessments provide students with a choice of problems at different levels, differentiated by depth of knowledge (see Trimm, 2025, for an example). It is assumed that students will not finish the full set of questions, but rather choose the set of problems that they feel confident in solving. Students must be able to solve the more challenging questions for their solution to receive a 3 or 4. After each assessment, students are given feedback, have the opportunity to make corrections, complete targeted additional practice, and are offered an opportunity to be reassessed with a different set of questions to demonstrate understanding at a new level of proficiency. The new performance is the final score, which is different from my past practice of averaging scores, because students have demonstrated a new level of progress.

In each of these courses, I also assigned a weekly project or problem set on which students worked in pairs, mostly outside of class. These assignments synthesized different learning standards, applied them in a novel context, and/or guided an exploration deeper into the underlying theory. These assignments went into their own grading category as a separate requirement of the course, and could not be used to directly bring up progress levels as determined by solutions on timed, in-class assessments.

As advocated by French et al. (2024), I have also reframed the purpose of my final exam. Rather than think of it as solely a summative assessment of what students recall over the course, it is also one final attempt to level up on any standards on which they may have still needed more time and practice to master.

In sum, letter grades were determined at the end of the semester according to the level of success they achieved, rather than by a weighted average. All requirements for a given letter grade must be met to earn that grade; it is not possible to make up deficiencies in one area by doing well in another, which aims to avoid gaps in understanding. The threshold for passing the course was set so that the instructor could be confident that a student who passed the course would be prepared for success in the following course. Earning an A in the course required students to meet high expectations. The requirements for different letter grades were communicated to the students in the syllabus at the beginning of the semester, to make this as transparent as possible. Students know their progress on each learning standard throughout the semester, which tells them what they need to improve upon to earn the desired letter grade.

Implications and Reflections on Impact

While the switch to progression-based assessment has reaped a lot of rewards,

I have had to endure some lessons along the way. I initially thought that grading would be more work through a progression-based approach to assessment. As with trying anything new, there was additional work involved, but by now the grading workload has turned out to be about the same for me, and I find it much more meaningful. Second, my first iteration of this grading system utilized

in the allotted time. To mitigate this problem, I now split my final exam into a required part and an optional part, taken on different days, with the required part covering a subset of core learning standards, and the remaining ones covered on the optional part.

I have learned this system encourages students to take academic risks. If they

In progression-based assessment, students often ask for more assessments because they don’t think of the assessment as a test, but rather a desire to demonstrate they are getting better. Test-anxiety seems to have almost completely disappeared...

binary scoring, according to whether or not the standard had been met. While this worked well enough initially, over time, I realized that the 4-level system better communicated growth to students. Third, I have learned that some students who have historically relied on partial credit or homework participation are initially challenged to meet course standards. However, that was ok, because they ultimately became more self-aware of the progressions they need to make in order to be successful. Finally, I initially found it difficult to meet my goal of using the final exam to reassess all standards at the same level as previous assessments

make mistakes along the way, they know they will be supported and have the opportunity to improve without penalty.

In traditional grading, students are incentivized to figure out what’s on the test so they may earn their desired level of points. What’s more important is what they are learning and what they are able to demonstrate. In progression-based assessment, students often ask for more assessments because they don’t think of the assessment as a test, but rather a desire to demonstrate they are getting better. Test-anxiety seems to have almost completely disappeared, which is consistent with Emeka et al.’s findings Progression-Based

(2023) findings on the effects of secondchance assessments on anxiety levels.

I also feel like I have a better relationship with students now compared to when I used traditional grading. With traditional grading, as noted in (Clark, 2022), the teacher can at times have an adversarial relationship with students as the keeper of the points. With progression-based assessment, the relationship feels more supportive as a coach. There are transparent expectations that students can work toward throughout the semester, and I am just here to help them reach their goals. My interactions with students after handing back tests and in office hours have been completely transformed, as the discussions are now focused on the content and how to improve.

I have received overwhelmingly positive feedback from students. In my course surveys, students frequently comment on having reduced stress and anxiety, increased motivation, and better retention of what they have learned. For example, one student from first-semester BC Calculus noted,

“I put in more work than I had in almost any other math class. I did this because I knew it was going to pay off. BC1 was my second-highest math grade at IMSA because of this. It was critical for my understanding in BC2, as I was able to

remember and apply almost all of the topics from the semester before.”

Students have also frequently commented on equity. For instance, one student noted,

“I learn calculus more slowly than others, and progression-based grading allowed my grade to reflect what I understood by the end of the semester.”

Another noted,

“As a student from an underserved school, I find that, as I continue through math, the concepts IMSA expects me to know I have never been taught… Although I have grown a lot, there is no doubt that I am at a disadvantage compared to my peers. For me, progression-based grading allows me time to catch up on concepts I have never learned.”

Finally, students also describe an increased enjoyment of mathematics. As one student reflected,

“I was able to understand and apply almost every topic. I was MUCH less stressed with math and really enjoyed the class. The class that I liked the most was math… I felt more capable of understanding the work that I received instead of just finishing it to get it out of the way… I put in an insane amount of

work, and it paid off. I put in that work because the class was fun and I was able to understand.”

Perhaps most strikingly, I have been told on more than one occasion that the tests were actually “fun”!

Transforming Your Assessment Practices by Starting Small

Changing to a progression-based assessment approach to assessment requires extra work, but the impact on students’ disposition and success has been worth it. We recognize that changing practices is not easy; however, as educators, we should constantly find ways to improve learning systems for the welfare of our students’ success and enjoyment of learning mathematics. They are more mindful of how they understand mathematics than ever before. Keeping this in mind, we encourage you to sample with progression-based assessment in ways that support your workload, and then build your practice as you see success.

Here are a few ways to get started:

1. Allow student choice on homework on an extended problem set

Provide a set of problems with varied difficulty, and ask students to tackle the most challenging problems they are able to do within a given time

period. Every problem should not be completed. Don’t spend time on the problems you automatically know how to do, but rather the ones you think you know how to get started and feel you can get through with some thought.

2. Customize quiz questions

When a student hasn’t developed proficiency in an important skill area necessary for the next course, provide them with additional opportunities on future assessments. If a student desires to excel in that skill, then provide them the chance to level up with a more challenging problem. The goal is to provide students with continued opportunities to demonstrate that they understand.

3. Offer chances for revision after minimal feedback

When students take an assessment, circle the location where they make an error. Hand back the paper and ask them to make a revision. Often, they can reconcile the mistake, and that will propel them to offer a better solution.

Naturally, a teacher has to identify how much they want to vary their assessment based on their capacity, resources, and the impact they see on learning. Our intention is to challenge students at their level of understanding and help them

grow through the assessment process. We feel it is necessary to keep students engaged in learning mathematics, especially when they face setbacks, so they realize assessment is a necessary tool to support their continued learning. We desire a sense that all students belong in mathematics, and through these assessment approaches, have built a sense of efficacy for students to embrace new challenges rather than worry about what’s on the test or whether or not they are good at math.

References

Brookhart, S. M. (2017). How to use grading to improve learning. ASCD.

Clark, D. (2022). Abundance and scarcity: Spicy takes from Benjamin Bloom. Grading for Growth. https:// gradingforgrowth.com/p/ abundance-and-scarcity

Dresel, M., Daumiller, M., Spear, J., Janke, S., Dickhäuser, O., & Steuer, G. (2024). Learning from errors in mathematics classrooms: Development over 2 years in dependence of perceived error climate. British Journal of Educational Psychology, 95(1), 180–196. https://doi.org/10.1111/ bjep.12697

Emeka, C., Zilles, C., West, M., Herman, G., & Bretl, T. (2023). Second-chance testing as a means of reducing students’ test anxiety and improving outcomes. In Proceedings of the ASEE (American Society for Engineering Education) Conference. https://peer. asee.org/second-chance-testingas-a-means-of-reducing-studentstest-anxiety-and-improvingoutcomes.pdf

Fountas, I. C., & Pinnell, G. S. (2017). The Importance of Guided Reading Within a Multi-Text Approach. Fountas & Pinnell Literacy™.

French, S., Dickerson, A. & Mulder, R.A. A review of the benefits and drawbacks of high-stakes final examinations in higher education. High Educ 88, 893–918 (2024). https://doi.org/10.1007/ s10734-023-01148-z

Guskey, T. R. (2013). The case against percentage grades. Educational Leadership, 71(1), 68–72.

Hemmings, B., Grootenboer, P., & Kay, R. (2011). Predicting mathematics achievement: The influence of prior achievement and attitudes. International Journal of Science and Mathematics Education, 9(3), 691–705. https://doi.org/10.1007/s10763010-9224-5

Progression-Based Assessment (cont.)

Sakellariou, C. (2022). The reciprocal relationship between mathematics self-efficacy and mathematics performance in U.S. high school students: Instrumental variables estimates and gender differences. Frontiers in Psychology, 13, Article 941253. https://doi.org/10.3389/ fpsyg.2022.941253

Talbert, R. (2023). Grading for Growth: A Guide to Alternative Grading Practices that Promote Authentic Learning and Student Engagement in Higher Education (with D. Clark). Routledge.

Talbert, R. (2022). How specifications grading changed. Grading for Growth. https://gradingforgrowth.com/p/ how-specifications-grading-changed

Talbert, R. (2020). Building calculus learning objectives. RTalbert.org. https://www.rtalbert.org/blogarchive/index.php/2020/07/09/ building-calculus-learning-objectives

Trimm, A. (2025). Sample progressive assessment: Squeeze Theorem [Unpublished Instructional Document] Illinois Mathematics and Science Academy https://drive.google.com/ file/d/1rQ1BvlysX96NkorSdR2WO VijyLDhm1pD/view?usp=sharing

Wiliam, D. (2011). Embedded formative assessment. Solution Tree Press.

Dr. Anderson Trimm, a mathematics faculty member at the Illinois Mathematics and Science Academy (atrimm@imsa. edu), has a variety of experience teaching mathematics and physics and is particularly interested in assessment practices that support student growth, confidence, and long-term engagement in mathematics.

Dr. Evan Glazer, President, Illinois Mathematics and Science Academy (eglazer@imsa.edu), is a lifelong mathematics educator who has written books about mathematics, including RealLife Math: Everyday Use of Mathematical Concepts and Using Internet Primary Sources to Teach Critical Thinking in Mathematics. He is deeply interested in the role assessment plays to support students’ learning and their continued interest in mathematics.

Strengthening Early Math Thinking Through Daily Routines, Language & Play

Aljobori is an educator and instructional leader with experience in early childhood, multilingual and curriculum design. He works across classroom, policy, and leadership settings, serving Childhood Educator Policy Fellow with Teach Plus Illinois and a Director-at-Large with Mindfully. His work focuses on integrating language development, equity, and whole-child and he contributes to professional communities through national conference presentations for Edutopia. He holds an MBA, an MEd in Elementary Education, and ESL/Bilingual endorsements, with ongoing work supporting multilingual learners and district-level program improvement.

Early math instruction in preK through grade 3 shapes how students approach problem solving, number relationships, and reasoning for years to come. Strong instruction in the early grades builds confidence, supports cognitive development, and lays the foundation for later success in higher-level mathematics. The Illinois Comprehensive Numeracy Plan emphasizes the importance of early learning environments that promote meaningful math experiences. These experiences help students form ideas through exploration, discussion, and reflection. Daily routines, intentional language, and play can strengthen early math thinking. Here are several practical examples that educators can use in any program model, including classrooms with multilingual learners and students with diverse needs.

1. Math in Daily Routines

Young children learn best when math is embedded in tasks they already understand. Daily routines give students repeated opportunities to use math in context. These routines help children develop operational fluency, comparison skills, and logical reasoning.

• Attendance and Counting

Teachers often begin the day with attendance. This

simple activity offers several math opportunities. Students count how many children are present, how many are absent, and how the totals change throughout the week. Students compare numbers, identify more or less, and describe what they notice.

• Transitions

Transitions between activities also support math growth. Teachers can measure walking time, compare the number of steps between classroom areas, or use timers to show the duration of each task.

• Classroom Jobs

Classroom jobs introduce grouping, estimation, and problem-solving.

Students determine how many items are needed, check their count, and adjust if the number changes.

2. Building Math Language Through Discussion

Math understanding grows when students explain their thinking.

Discussion supports conceptual development, clarity, and reasoning.

• Structured Math Talk

Teachers use short prompts that guide discussion: How do you know? What changed? What stays the same?

• Supporting Multilingual Learners

Students can explain ideas in their home language during small-group conversations while still using English vocabulary during whole-group sharing.

• Using Everyday Language First

Teachers begin with familiar terms such as bigger or smaller before introducing greater than or less than.

3. Play as a Context for Math Exploration

Play supports repetition, creativity, and collaboration.

• Block Building Students compare lengths, create symmetrical designs, and explore balance.

• Sorting and Classifying Sorting builds the foundation for data analysis.

• Dramatic Play

In pretend stores, students count items, compare prices, and distribute money.

• Outdoor Play

Students compare distances, collect natural items, and group them.

4. Linking Math Across Languages and Experiences

Teachers build on what students know from home. Connecting math to family practices increases relevance and engagement.

5. Observation and Assessment in Early Math

Assessment focuses on understanding rather than speed.

• Anecdotal Notes

Short observations track growth.

• Student Work Samples

Drawings, number stories, and photographs show reasoning.

• Performance Tasks

Teachers create challenges with blocks, sorting, or estimation.

6. Practical Steps for Educators

– Integrate math into daily routines

– Use discussion prompts

– Encourage bilingual expression

– Provide play opportunities

– Use observation to plan

– Connect math to family practices

– Offer materials that support exploration

Conclusion

Early math learning depends on experiences that help students make sense of ideas. Daily routines, discussion,

and play help students build reasoning, strategy use, and confidence.

Thamir Aljobori is an educator and instructional leader with experience in early childhood, multilingual education, and curriculum design. He works across classroom, policy, and leadership settings, serving as an Early Childhood Educator and Numeracy Policy Fellow with Teach Plus Illinois and a Director-at-Large with Educating Mindfully. His work focuses on integrating language development, equity, and whole-child practices, and he contributes to professional communities through national conference presentations and writing for Edutopia. He holds an MBA, an MEd in Elementary Education, and ESL/ Bilingual endorsements, with ongoing work supporting multilingual learners and district-level program improvement.

Pre-Service Teachers in Illinois Receive FREE ILASCD/PD365 Membership!

Are you a pre-service teacher? Don’t wait until graduation to start building your professional network! By joining ILASCD/PD365, you’ll:

Connect with experienced teachers, mentors, and school leaders

A pre-ser vice teacher gains connections, career readiness, and credibility by joining IL ASCD/P D365. It’s a way to star t your professional journey early, surrounded by people and resources that will suppor t you through your first years in the classroom and beyond. What ’s in it for YOU?

Access practical resources, journals, and classroom-ready strategies

Attend exciting conferences and workshops as a volunteer!

Boost your résumé with professional memberships that set you apart

Join a statewide community committed to helping you thrive

Get published in Journals and publications

IL ASCD Area Representatives

Our “Area Reps” are a link to and from the various regions of our state. IL ASCD follows the same areas established by the Regional Offices of Education.

Our Area Reps are led by a members of our IL ASCD Board of Directors, Denise Makowski.

AREA 1: (Green)

Denise Makowski

Chicago

618.203.3993

dmkowski224@gmail.com

Amie Corso Reed

O'Fallon School District

618.203.3993

amie.corso@gmail.com

Current Area Reps

AREA 2: (Dark Blue)

AREA 3: (Yellow)

AREA 4: (Pink)

AREA 5: (Light Blue)

AREA 6: (Gold)

April Jordan

Jennifer Winters

Stacy Stewart

Jen Pollack

Chad Dougherty

Heather Bowman

Jamie Bajer

Mica Ike

Vacant

Contact information for them can be found HERE.

The roles of the IL ASCD Area Representatives are:

• Encouraging IL ASCD membership to educators in their local areas;

• Assisting with professional development;

• Attend board meetings and the annual leadership retreat, when possible;

• Disseminating information from IL ASCD board meetings or other sanctioned IL ASCD activities to local school districts or other regional members

• Being a two-way communication vehicle between the local IL ASCD members regarding IL ASCD or any educational issues.

• Keeping IL ASCD Board of Directors apprised of pertinent information regarding personnel issues (e.g., job vacancies, job promotions) and district program awards/recognition within the local area.

• Communicating regularly with IL ASCD Executive Director and the Co-Leaders of the Membership and Partnerships Focus Area.

From Gaps to Growth: How

Tahlia’s Journey Reflects the Power of Illinois’ Numeracy Plan

When Tahlia entered my classroom as a freshman in high school, she carried more than just her backpack. She had years of feeling like she “wasn’t a math person,” piles of unfinished homework, and a placement test score equivalent to that of a third-grader. Three years later, after a lot of hard work, time, and support, Tahlia looked at the score on her final exam with tears in her eyes: her first A in math. Her test score did not happen by accident, nor was it any singular change that pushed Tahlia to success. It was a strategic system of supports that included daily interweaving of number sense, lowfloor high-ceiling tasks, assessments to identify gaps in numeracy skills, and a classroom culture of perseverance.

Stories like Tahlia’s illustrate the need for Illinois to have a coherent vision for math instruction. The State Board of Education (ISBE) has taken up that call and is creating the Illinois Comprehensive Numeracy Plan, a framework designed to ensure every student has access to the kind of targeted, equitable supports that transformed Tahlia’s trajectory. As a working document, the plan offers a solid foundation with many of the elements that made Tahlia so successful. This article examines the Illinois

Comprehensive Numeracy Plan through the lens of secondary mathematics instruction, highlighting both its promising strategies and implementation challenges that the plan must address.

Key Strengths of the Numeracy Plan

The central pillar of the Numeracy Plan is to increase students' numeracy skills. At the secondary level, these skills are foundational for success in Algebra (Ronau et al, 2020), yet many students

Another of the features of the Numeracy Plan is low-floor, high-ceiling tasks for students to engage in numeric and mathematical thinking. An example of such a task is to develop a formula for the number of blocks needed for a staircase where each step uses one more block than the previous step. Students can simply count the steps to start, but eventually they recognize patterns in the sums to create an equation to find the number

In Tahlia’s class, each day began with warmup questions containing at least one number sense or proportional reasoning problem to help make incremental but impactful progress in students' numeracy skills.

still struggle. Utilizing short numbersense routines is a simple way to increase number sense in all students, regardless of ability level. In Tahlia’s class, each day began with warm-up questions containing at least one number sense or proportional reasoning problem to help make incremental but impactful progress in students' numeracy skills. These helped to fill in gaps for Tahlia, but if elementary schools adopt these practices on a wide scale as the plan recommends, fewer students will enter high school with gaps like hers in the first place, and they will be better positioned for success.

of blocks for any number of steps. (See pg. 59) These tasks are supported by the work of Stanford Professor Jo Boaler, who argues that open-ended, visually rich, and discussion-based tasks engage students and help develop mathematical mindsets (Boaler, 2016). They allow students to access grade-level coursework while simultaneously reinforcing foundational numeracy skills to help address gaps. Tasks like these were a core reason Tahlia was able to succeed, and they should continue to be a pillar of the Numeracy Plan in the final draft.

The importance of diagnostic assessments to identify gaps in students’ knowledge is also a key point in the Numeracy Plan. As the National Mathematics Advisory Panel found, gaps that begin in early education are exacerbated with age (National Mathematics Advisory Panel, 2008). By the time students reach middle or high schools, deficiencies in numeracy and content knowledge compound and create additional frustrations for struggling students. For Tahlia, this frustration resulted in a daily struggle to engage in class, as she always felt defeated. If these gaps had been addressed earlier for Tahlia, her energy could have been spent building on new

Numeracy Plan encourages diagnostic testing with larger in-depth assessments sparingly to address gaps and shorter, more frequent formatives to help address fundamental numeracy skills. While students like Tahlia rarely enjoyed these assessments, they are critical for educators to find and address essential skills for success.

Finally, one of the most important intervention systems for Talhia highlighted in the Numeracy Plan is creating an environment where productive failure is encouraged. Many teachers want to support students at the first signs of struggle, but to truly engage students in mathematical

The most crucial factor for Tahlia, and the most difficult to implement, is providing students enough time to bridge gaps in numeracy while succeeding in their gradelevel coursework.

content rather than battling the lingering effects of unfinished learning.

It is critical for educators to identify gaps in foundational algebraic topics like fractions (Siegler et al, 2013) and equations (Knuth et al., 2006) as early as possible, as these are indicators of success in the upper grade levels. The

thinking, we must let them progress on their own before utilizing direct instruction. The deepest learning comes from productive failure and unproductive success (Kapur, 2016). In my classroom, I intentionally developed this mindset in a classroom filled with students who were used to avoiding challenges. Students were encouraged to explore, make

Success in advanced coursework and placement exams depends on students having solid foundations and recall in numeracy.

conjectures, and revise their thinking before giving answers. Tahlia, who once shut down when faced with unfamiliar problems as a freshman, learned to lean into struggle and embrace it as a part of learning by her junior year.

Implementation Challenges at the Secondary Level

While these critical elements are strengths of ISBE’s Numeracy Plan draft, other key elements are missing or will be difficult for districts to implement. The most crucial factor for Tahlia, and the most difficult to implement, is providing students enough time to bridge gaps in numeracy while succeeding in their grade-level coursework. To secondary teachers, it may seem like an impossible task to adopt new practices like lowfloor high-ceiling tasks, diagnostic testing, and foundational number sense routines while also covering the required course curriculum. Without adjustments to course pacing, teachers may feel overwhelmed and return to old habits. The final draft of the Numeracy Plan should address how teachers can balance or prioritize different strategies and interventions during class time to best help students.

When I worked with Tahlia, my school helped address this problem by providing her with a “double dose” intervention course, where I had Tahlia two class periods per day for three years. This was an amazing benefit to her and her classmates, as they had the time and space to engage with math in meaningful ways. However, access to this kind of intensive support varies widely among districts and schools, and not all districts have the funding, staffing, or structural flexibility required. Some schools use co-taught classes, targeted math intervention classes, or drop-in tutoring/ support for students. For the Numeracy Plan to truly support our struggling secondary students, ISBE should offer several possible concrete solutions to help districts provide support and then support these recommendations with resources to help underfunded districts build effective intervention systems.

Finally, while the current version of the plan strongly emphasizes conceptual learning, it must be careful not to undervalue fluency in numeracy and number sense. High school students need procedural fluency and automaticity as well—the ability to utilize mental math

facts. Success in advanced coursework and placement exams depends on students having solid foundations and recall in numeracy. As Tahlia once told me, “Math is easy when you don’t have to type everything into your calculator all the time!” The goal of the plan should be to integrate conceptual understanding with mathematical fluency to produce the best results for our students.

Recommendations for Moving Forward

When the state’s vision and classroom practice align, students not only catch up; they flourish. And when students flourish, they exit high school as numerate citizens capable of solving problems, analyzing information, and contributing meaningfully to an increasingly data-driven world. The Illinois Comprehensive Numeracy Plan represents an opportunity to transform mathematics education for students across the state. Tahlia's story demonstrates what becomes possible when research-based strategies are implemented with fidelity and adequate support. As the plan continues to grow and develop, the following points are particularly important for the secondary level:

• Daily number sense routines in secondary classrooms can help to address foundational gaps while students work on grade-level content

• Low-floor, high-ceiling tasks provide access points for all students

• Diagnostic assessments, in both the elementary and secondary levels, are essential for identifying and addressing gaps before they compound

• Classroom cultures that embrace productive failure help students develop the perseverance needed for mathematical success

• Implementation requires creative scheduling solutions and additional supports

• The plan must balance conceptual understanding with procedural fluency

As ISBE continues to refine this framework, input from classroom teachers and building administrators will be essential to ensure the final plan is both ambitious and achievable. ISBE will have a second draft of the plan and hold a listening tour from February to March. The details can be found on ISBE’s webpage. Administrators and educators are strongly encouraged to participate and share their insights on what will make this plan work in real classrooms with real students. Your voice matters in shaping a framework that can help every student experience the kind of transformation Tahlia did.

References

Boaler, J. (2016). Mathematical mindsets: Unleashing students' potential through creative math, inspiring messages and innovative teaching. Jossey-Bass.

Kapur, M. (2016). Examining productive failure, productive success, unproductive failure, and unproductive success in learning. Educational Psychologist, 51(2), 289–299. https://doi.org/10.1080/00461 520.2016.1155457

Knuth, E. J., Stephens, A. C., McNeil, N. M., & Alibali, M. W. (2006). Does understanding the equal sign matter? Evidence from solving equations. Journal for Research in Mathematics Education, 37(4), 297–312. https:// doi.org/10.2307/30034852

National Mathematics Advisory Panel. (2008). Foundations for success: The final report of the National Mathematics Advisory Panel. U.S. Department of Education.

Ronau, R. N., Bay-Williams, J. M., & Van de Walle, J. A. (2020). Elementary and middle school mathematics: Teaching developmentally (10th ed.). Pearson.

Siegler, R. S., Thompson, C. A., & Schneider, M. (2013). An integrated theory of whole number and fractions

development. Psychological Review, 120(3), 559–588. https://doi. org/10.1037/a0032159

This is an image of the "low-floor highceiling task" described earlier.

If we continue to add "steps" to these stairs, how many would we have we we get to Step 5?

Sarah Murmann is a dual-credit math teacher and Robotics coach at Crystal Lake South High School in Crystal Lake, Illinois. She is also a Senior Policy Fellow for Teach Plus Illinois, where she has helped to input teacher voice in AI legislation at the state level.

Why Math Matters: Beyond Grades and Test Scores

In 2022, the United States recorded the steepest decline in math scores in three decades. According to the National Assessment of Educational Progress (NAEP), only 26% of eighth graders met proficiency standards, down from 34% in 2019 (National Center for Education Statistics [NCES], 2022). Internationally, American students continue to lag behind peers from countries such as Singapore, Japan, and Estonia on the Program for International Student Assessment (PISA) (Organisation for Economic Co-operation and Development [OECD], 2019).

For many parents and educators, these statistics are concerning primarily because of their implications for college admissions or standardized tests. However, math is far more than a set of numbers on a grade report. Learning mathematics shapes how the brain develops, strengthens critical life skills, and builds confidence in problem-solving. If we reframe how we view math—less as a hurdle to clear and more as a language and way of seeing the world—we can help today’s students reclaim their mathematical potential.

The State of Math Achievement in America

Declining math achievement is not simply an academic issue. Math proficiency is strongly correlated with college readiness, employability, and future earnings. In fact,

students with higher math achievement in high school are more likely to graduate college and secure stable, high-paying jobs, even if they pursue non-STEM careers (National Mathematics Advisory Panel [NMAP], 2008).

sulcus is central to numerical processing, while the prefrontal cortex supports logical reasoning and problemsolving (Ansari, 2008). Engaging these areas repeatedly strengthens neural connections, much like exercise

Students who regularly practice mathematics show better executive function, stronger attention control, and more effective decision-making (Park & Brannon, 2013).

The consequences extend beyond the individual. Economists warn that lagging numeracy skills weaken the U.S. workforce in a world increasingly shaped by data, algorithms, and quantitative reasoning (OECD, 2021). New studies using digital twins—AI models of brain activity—reveal the unique neural challenges faced by students with math learning disabilities and provide insights into tailoring instruction (Stanford University, 2025). Reversing the downward trend is essential not just for students’ futures, but for national competitiveness.

What Happens in the Brain When Kids Learn Math

Mathematics is one of the most cognitively demanding subjects we teach, and for good reason: it engages multiple brain regions at once. Neuroscientific research shows that the intraparietal

strengthens muscles. Stanislas Dehaene (2011) has described math as a kind of “mental gymnasium,” where working with numbers improves working memory, cognitive flexibility, and abstract thought. Importantly, these skills transfer. Students who regularly practice mathematics show better executive function, stronger attention control, and more effective decision-making (Park & Brannon, 2013).

Recent breakthroughs provide even more promising directions. Safe, non-invasive brain stimulation techniques, such as transcranial random noise stimulation (tRNS), have been shown to significantly improve math performance in young adults with weaker neural connectivity, suggesting that neuroscience-informed interventions may help struggling learners (University of Surrey, 2025). Similarly, Oxford researchers

demonstrate that, unlike AI, the human brain learns by first stabilizing activity patterns, then adjusting connections— making math learning an especially powerful tool for cognitive resilience (University of Oxford, 2024).

Number Sense as the Foundation

At the heart of math learning is number sense—the intuitive ability to understand and manipulate quantities. Think of number sense as a child’s “feel” for how numbers work: recognizing that six is more than four, estimating how many candies are in a jar, or understanding that 12 can be broken into 7 and 5. When I work with students on SAT prep, I am astounded by how many students do not understand that dividing a number by a fraction will increase the number rather than decrease it. This type of numerical sensibility is critical for being able to solve problems and navigate patterns.

Research consistently shows that early number sense is one of the strongest predictors of later math success (Libertus, Feigenson, & Halberda, 2011). Moreover, children with well-developed number sense are less likely to struggle with math disabilities such as dyscalculia (Butterworth, Varma, & Laurillard, 2011). David Geary (2013) emphasizes that preschool and early elementary years represent a critical window for strengthening these foundational skills.

More recent evidence underscores the importance of number sense for higherlevel thinking. A 2025 comparative study found that gifted students rely on more flexible, reasoning-based number sense strategies than their typically developing peers, highlighting the need to cultivate number sense not just for basic skills but for deeper problem-solving (Er & Dinç Artut, 2025). Unfortunately, as education experts note, number sense often receives less emphasis than early literacy in U.S. schools, despite its equal importance (Hechinger Report, 2025).

Math as a Language

One of the most powerful shifts we can make is to help students see math as a language. Like spoken language, mathematics has symbols, grammar, and rules of syntax. For instance, an equation such as 3x + 2 = 11 is a concise way of communicating a relationship. Learning math, then, is not just about memorizing procedures but about expressing ideas, patterns, and relationships clearly and precisely (Sarnecka & Carey, 2008).

Framing math as a language also changes how students respond to challenges. Struggling to solve a problem becomes more like learning to conjugate a verb incorrectly at first—a natural step in mastering a new form of communication. Jo Boaler (2015) argues that this mindset shift is essential for reducing

math anxiety and building persistence. When students see math as a way to communicate ideas rather than as a test of intelligence, they are more likely to stay engaged and grow.

Seeing Math in the World Around Us

For many teens, math feels disconnected from their daily lives. Yet math is everywhere: in the ratios of a recipe, the statistics of a favorite sports team, the angles of a skateboard ramp, or the symmetry of architecture. Nature itself is filled with mathematical beauty, from the spirals of sunflowers to the fractal patterns of coastlines.

Helping teens notice these patterns makes math less abstract and more relevant. The OECD (2021) notes that numeracy is also a form of life literacy: individuals with stronger math skills demonstrate better financial decisionmaking, improved health outcomes, and greater adaptability in technologydriven fields. Parents can support this by pointing out real-world examples, encouraging budgeting exercises, or linking math to a teen’s personal interests. I love to have students budget for trips or events. To have limits on the spending, a goal in mind, and put together a realistic and feasible budget. When students see math as part of their world—not just a school subject—they are more motivated to learn.

Moving Forward: How Parents and Educators Can Help

The decline in math scores is reversible, but it requires collective effort. Recent educational psychology research emphasizes that a blend of conceptual understanding and timed practice builds both deep comprehension and automaticity—a three-step process of grounding, automating, and reflecting (McNeil et al., 2025). This approach builds flexible fluency without reducing math to rote memorization.

In addition, neuroscience-driven programs are emerging as powerful supports. The MIND Research Institute’s ST Math platform, a visual, game-based system grounded in cognitive science, has shown significant improvements in student performance across diverse groups. Its new curriculum, InsightMath, continues this trend by integrating visual problem-solving with conceptual rigor (MIND Research Institute, 2025).

Practical strategies remain essential:

1. Encourage a growth mindset. Students who believe math ability is expandable through effort and strategies outperform those who believe it is fixed (Boaler, 2015).

2. Emphasize conceptual understanding. Procedural fluency

matters, but research shows that deep understanding of why math works predicts long-term achievement (NCTM, 2020).

3. Supportive environments. Schools that provide tutoring, math labs, and collaborative teacher practices see stronger outcomes (NMAP, 2008).

4. Integrate real-world math. Connect math to areas teens already care about—music, sports, video games, or social media analytics.

Conclusion

Math scores in the United States are declining, but the solution is not to double down on test prep. Mathematics is more than a school subject: it is brain training, a language, and a life skill. Learning math strengthens neural networks, fosters logical reasoning, and builds resilience. It equips students not only to succeed academically but to thrive in a world where quantitative reasoning shapes everything from personal finance to public policy.

Parents and educators play a crucial role in reshaping how teens view math. By nurturing number sense, framing math as communication, and highlighting its presence in the world, we can restore confidence and ignite curiosity. Ultimately, the goal is not simply to

raise test scores—it is to cultivate mathematically literate citizens who see math as a tool for understanding and shaping their lives.

References

Ansari, D. (2008). Effects of development and enculturation on number representation in the brain. Nature Reviews Neuroscience, 9(4), 278–291.

Boaler, J. (2015). Mathematical mindsets: Unleashing students’ potential through creative math, inspiring messages, and innovative teaching. Jossey-Bass.

Butterworth, B., Varma, S., & Laurillard, D. (2011). Dyscalculia: From brain to education. Science, 332(6033), 1049–1053.

Dehaene, S. (2011). The number sense: How the mind creates mathematics (2nd ed.). Oxford University Press.

Er, Z., & Dinç Artut, P. (2025). Comparative analysis of number sense performance in gifted vs. typically developing students. Humanities and Social Sciences Communications, 12, 1016. https://doi.org/10.1057/s41599-02505403-9

Geary, D. C. (2013). Early foundations for mathematics learning and their relations to learning disabilities.

Current Directions in Psychological Science, 22(1), 23–27.

Hechinger Report. (2025). The building blocks of math students need to excel https://hechingerreport.org/thebuilding-blocks-of-math-studentsneed-to-excel

Libertus, M. E., Feigenson, L., & Halberda, J. (2011). Preschool acuity of the approximate number system correlates with school math ability. Developmental Science, 14(6), 1292–1300.

McNeil, N., et al. (2025). What the science of learning teaches us about arithmetic fluency.

Psychological Science in the Public Interest, 26(1). https://doi. org/10.1177/1529100625123456

MIND Research Institute. (2025). 2024 Annual report: Neurosciencedriven math learning. https://2024. mindresearch.org/news/mindeducation-marks-strides-inneuroscience-driv en-mathlearning-in-2024-annual-report

National Center for Education Statistics. (2022). The Nation’s Report Card: Mathematics 2022. U.S. Department of Education.

National Council of Teachers of Mathematics. (2020). Catalyzing

change in high school mathematics: Initiating critical conversations. Author.

National Mathematics Advisory Panel. (2008). Foundations for success: The final report of the National Mathematics Advisory Panel. U.S. Department of Education.

Organisation for Economic Co-operation and Development. (2019). PISA 2018 results: What students know and can do. OECD Publishing.

Organisation for Economic Co-operation and Development. (2021). OECD skills outlook 2021: Learning for life. OECD Publishing.

Park, J., & Brannon, E. M. (2013). Training the approximate number system improves math proficiency. Psychological Science, 24(10), 2013–2019.

Sarnecka, B. W., & Carey, S. (2008). How counting represents number: What children must learn and when they learn it. Cognition, 108(3), 662–674.

Stanford University. (2025). Digital twins offer insights into brains struggling with math. https://hai.stanford.edu/ news/digital-twins-offer-insightsinto-brains-struggling-with-math and-hope-for-students

University of Oxford. (2024). New

Why Math Matters (cont.)

research shows the way the brain learns is different and better than AI. https://www.ox.ac.uk/news/202401-03-new-research-shows-waybrain-learns-different-and-b etterway-artificial-intelligence University of Surrey. (2025). Brain stimulation boosts math skills in struggling learners. PLOS Biology. https://phys.org/news/2025-06brain-boost-math-people-weaker. html

Dr. Emily Wassell is an award-winning educator and holistic college coach with more than 25 years of experience helping students thrive inside and outside the classroom. She holds a BAS, MAT, and PhD in Educational Leadership, Research, and Policy from the University of Colorado Colorado Springs. A former teacher, principal, and visiting professor, Dr. Wassell is the founder of a global coaching practice that guides ambitious teens toward their dream colleges while prioritizing wellbeing, leadership, and long-term success.

Liesl McConchie

From Students' Hearts to Brains – How Math Identity Improves Math Achievement

Ask any teacher what’s getting in the way of students learning math today, and you’ll hear a variety of responses: lack of motivation, debates around explicit vs. inquiry-based instruction, or a general “checked-out” attitude that wasn’t nearly as common a decade ago. We tend to respond with new strategies for instruction, curriculum, or assessment. But in my 25+ years as a classroom teacher, school leader, and translator of cognitive neuroscience, one truth keeps rising to the top:

A student’s emotional relationship with math is foundational to their cognitive relationship with math. Students don’t walk into our classrooms as blank slates. They enter with years of experience, feelings, messages, and beliefs that shape how they see themselves as math learners. In neuroscience, we call this an “identity-shaping neural network.” It is a tapestry of past experiences, future expectations, sociocultural messages, and personal efficacy judgments. In schools, we simply call it their math identity.

And teachers don’t need a degree in neuroscience to leverage it. Below are four high-impact, low-prep activities you can use in any classroom to strengthen students’ math identities. Each activity is paired with a

“Nugget of Neuroscience” to help you understand why these strategies work.

1. Mathland

Every student carries a story about their past experiences with math— great teachers, discouraging moments, proud successes, bruised attempts, and everything in between. Those experiences shape how they show up academically today.

To surface these stories, invite students to draw their version of Mathland—a fictitious place ruled by mathematics— and place themselves in it. It could be a faraway planet with non-human species, or a hidden civilization somewhere on Earth. Give students full creative license to draw their vision of this place where math rules everything. Their artwork will reveal their relationship with math more than any survey ever will. This can be the starting point of future conversations with each student as you journey with them through their own emotional landscape of Mathland.

Figures 1, 2, and 3 show three different depictions of middle school students’ Mathland art. Ask yourself "If this is how they perceive themselves and math, how might that impact their ability to learn math?"

1: A depiction of Mathland that includes candy, flowers, sunshine, and a river of hearts as the line of symmetry.

3: A depiction of Mathland that positions learning math in school, similar to a prison sentence.

Figure

Figure 2: A student who feels “lost in the forest” of math.

Figure

Nugget of Neuroscience

Emotions and cognition are inseparable partners in learning. The brain systems we rely on in school—attention, motivation, memory, and decisionmaking—are all highly influenced by emotional states. When negative emotions like anxiety or uncertainty activate the amygdala, they block access to the prefrontal cortex, limiting students’ ability to think, plan, and learn. In contrast, positive emotional states such as curiosity, confidence, and hope release hormones and neurotransmitters that strengthen memory formation and deeper learning (Ahmed et al., 2013). In short, how students feel directly shapes how well they can think.

2. Belonging Bios

Students are quick to label themselves as a “math person” or “not a math person.” These labels have lasting impacts on their brain and their capacity to learn mathematics. On a neurological level, belonging isn’t soft. It’s survival. When students feel excluded or unsure of their place in math environments, the brain is flooded with increased cortisol levels, which interfere with attention, working memory, and executive functioning (Quaedflieg & Schwabe, 2018).

Students need to see people like them being successful in math spaces.

Once a week, introduce a Belonging Bio:

• a math teacher who shares their family background

• a mathematician who looks like them

• a community member using STEM in meaningful ways

Keep each bio short, just a few minutes. Over time, patterns shift. Students begin thinking, “If they can do it, maybe I can too.”

Nugget of Neuroscience

Feeling like part of the classroom “in-group” protects students against the neurological impact of chronic stress. When students feel excluded, the amygdala (the brain’s uncertainty detector) activates, pulling attention away from learning and toward social survival (Stanley & Adolphs, 2013). By diversifying who students see as successful math learners, we biologically reduce the stress placed on minoritized students.

3. Math Media Moments

Students are swimming in messages about what it means to be “good at math” or who is good at math. Many of these messages come from media— TikTok videos joking about hating math, movies showing “genius” as rare and socially awkward, or influencers glorifying speed over depth.

These messages accumulate in the brain as unconscious beliefs.

Once a week, lead a Math Media Moment:

1. Show a 15–30 second clip:

• a commercial

• a line from a show

• a meme

• a screenshot of an online comment

2. Ask students:

• What message is being communicated?

• Is it true? Where do we see evidence?

3. Replace the message with an accurate one.

This takes a couple of minutes but can undo years of internalized stereotypes.

Nugget of Neuroscience

The brain strengthens neural pathways that fire frequently and with emotional intensity. This is Hebb’s Law, often summarized as “neurons that fire together, wire together” (Langille & Brown, 2018). Media messages, especially humorous or emotionally charged ones, “fire” often, making them neurologically sticky. Talking about them interrupts automatic wiring and rewires healthier beliefs.

4. Math Gremlins

Every student has an inner voice that whispers unhelpful things. For students learning math, it could sound like:

• “You’re slower than everyone else.”

• “Everyone understands this but you.”

• “You’re doing it different than everyone else. That means you’re wrong.”

These internal messages become part of students’ personal efficacy—their belief about what they can or cannot do in math spaces.

To interrupt this, invite students to draw their Math Gremlin—the little figure on their shoulder whispering discouraging thoughts.

Giving your Math Gremlin its own shape and color helps externalize these unhelpful thoughts, creating distance from the student’s identity.

Once students have separated themselves from this invisible gremlin,

Figure 4: A Math Gremlin drawn by an elementary-aged student.

invite them to create a comeback phrase: Gremlin: “You’re not smart enough.” Response: “I’m learning. My brain changes every day.”

When you see a student shutting down, a quiet “What’s your gremlin saying today? And what can you say back?” can shift a student’s beliefs about their math ability.

Nugget of Neuroscience

A student’s emotional state directly influences whether the learning regions of the brain “turn on” or “shut down.” Negative states like anxiety or hopelessness activate the amygdala, which blocks the prefrontal cortex—the center of complex thinking, planning, and problem-solving (McGarry & Carter, 2016). Externalizing the negative voice reduces its emotional power and reopens cognitive functioning.

Putting It All Together

These four activities align with the four main variables that build one’s math identity:

1. Past experiences with math (Mathland)

2. Future vision of self in math spaces (Belonging Bios)

3. Socio-cultural influences regarding who is good at math, and what it means to be a “math person” (Math Media Moments)

4. Personal efficacy, one’s level of confidence and competence with math (Math Gremlins)

For more activities and a deeper understanding of the brain science behind our math identities, check out my newest book, Building a Positive Math Identity: A Brain Science Approach.

Building strong math learners requires strengthening the relationship students have with math itself. When students heal from their past, believe they belong, and rewire unhelpful messages, the academic gains follow organically. In other words, every micro-interaction in the classroom influences whether a student moves toward or away from a stronger math identity.

This isn’t extra work.

This is the work that makes the rest achievable.

References

Ahmed, W., Van der Werf, G., Kuyper, H., & Minnaert, A. (2013). Emotions, selfregulated learning, and achievement in mathematics: a growth curve analysis. Journal of educational psychology, 105(1), 150.

Langille, J. J., & Brown, R. E. (2018).

The synaptic theory of memory: a historical survey and reconciliation of recent opposition. Frontiers in systems neuroscience, 12, 52.

McGarry, L. M., & Carter, A. G. (2016). Inhibitory gating of basolateral amygdala inputs to the prefrontal cortex. Journal of Neuroscience, 36(36), 9391-9406.

Quaedflieg, C. W., & Schwabe, L. (2018). Memory dynamics under stress. Memory, 26(3), 364-376.

Stanley, D. A., & Adolphs, R. (2013). Toward a neural basis for social behavior. Neuron, 80(3), 816-826.

Liesl McConchie is an international expert on how the brain learns, author of Building

a Positive Math Identity: A Brain Science Approach, and co-author of the bestselling book Brain-Based Learning with Dr. Eric Jensen. She has been published in multiple education journals, including ASCD's Educational Leadership journal and NCTM’s Mathematics Teacher. With over 25 years of experience in education, Liesl bridges her knowledge of how the brain best learns with her experience of teaching across the K-12 spectrum to create tangible strategies to support teachers and schools across the globe. She has a rich background in education that includes creating new schools, leading wholeschool reforms, delivering workshops to educators, and speaking at conferences. Liesl brings the highest quality of research, professionalism, and engagement to all her contributions to the field of education.

The Skills-Based Classroom: Rethinking Assessments to Refocus Learning

Keenan Clark Introduction

In our high school mathematics classrooms, we began to notice patterns that didn’t sit right with us. Students with solid conceptual understanding weren’t always earning the grades they deserved, while others with significant gaps were still walking away with A’s or B’s. Homework was losing its value—students copied, skipped it entirely, or increasingly turned to apps like Photomath and AI tools to generate answers. Makeup work consumed hours each week, and students who needed more time to learn rarely had meaningful chances to show improvement.

We knew these were not isolated challenges but symptoms of outdated assessment practices. During the summer of 2022, we committed to rethinking our approach. What emerged was a hybrid model we now call The Skills-Based Classroom. This is a system that blends the core ideas of Standards-Based Grading with our district’s traditional 100-point scale. It’s not radical, but it is transformative. And more importantly, it works.

Identifying the Problems

1. Unreliable Grades

Our grading system was skewed by compliance.

Jake Towers

Completed homework, extra credit, and effort-based tasks often outweighed actual understanding. Grades were misleading and did not tell an accurate story of what students knew.

2. The Homework Dilemma

Math has long been synonymous with homework, but many students were no longer engaging authentically with it. Copying from peers or apps inflated grades but left gaps in learning, and homework checks consumed precious instructional time.

3. Makeup Work Overload

Daily assignments, weekly quizzes, and chapter tests created a maze of deadlines and makeups. Students with absences (excused or not) found themselves in a perpetual cycle of catching up, and teachers had to choose between hours of managing the logistics or disregarding antiquated school policies.

4. Student Learning Variability

Our pacing was guided by isolated instructional units and left some students racing to keep up and others bored, unchallenged, or unmotivated. The structure offered little room for remediation or evidence of growth once an assessment window closed.

The Skills-Based Classroom

To confront these challenges, we redesigned nearly every aspect of our instructional and assessment system.

At the heart of this model is performance-based communication on a 1–4 scale:

1 – Insufficient Evidence

2 – Basic Understanding

3 – Strong Understanding

4 – Mastery

These levels communicate learning more clearly than points or percentages ever could.

The biggest structural change, however, is our weekly routine. Every student meets with us individually to review progress, discuss misconceptions, and set goals. These short conversations have become one of the most powerful tools we use. They create accountability, build relationships, and shift the classroom culture from “What’s my grade?” to “Where am I at right now?”

We still track and calculate a traditional percentage at semester’s end, but compliance and learning are separated, allowing us to see a clearer picture of true mathematical proficiency. Surprisingly, our workload has decreased, and student ownership has skyrocketed.

The Skills Assessment

Central to our model is a reimagined approach to assessment. Traditional vehicles such as homework for practice, quizzes for checks, and tests for summative grading often blurred together in confusing and inequitable ways. We combined them into one tool: The Skills Assessment.

Structure and Frequency

A Skills Assessment:

• includes approximately four test-like questions

• is given about twice per week

• takes 8–12 minutes

• focuses on a tightly aligned set of skills that summarizes a unit

These brief, targeted assessments allow us to monitor learning in real time instead of waiting until the end of a chapter. They serve as both formative checks and summative evidence.

Feedback and Revision

Students receive written and verbal feedback every week. During one class period, we conduct one-on-one feedback conferences that rely on a discussion between the teacher and student. These conversations help students identify errors, revisit rules, and see patterns in their thinking. Concurrently, the rest of the class works on independent practice related to the current learning unit.

Multiple Attempts Without Penalty

No two assessments are identical, but each version samples the same breadth of content. Students must take at least four assessments per skill, and we always average a student’s best four scores. This approach:

• encourages persistence

• reduces anxiety

• allows students to demonstrate growth

• avoids grade inflation because rigor remains consistent

Instruction still moves forward traditionally from unit to unit, but students can request reassessments on any prior skill at any time. When a student demonstrates mastery, they shift their focus to the next skill.

Measuring Impact

To understand whether this new system truly improved learning, we compared outcomes from our Algebra II classes from 2014–2019 to those from 2022–2024. The results were striking.

Keep in mind, the same curriculum was used both before and after the switch to the Skills-Based Classroom strategy. In fact, the final exam covered the same topics and was written to be almost

identical to exams prior to the change.

• Semester exam grades improved proportionally to final semester averages.

• Students earning a final semester average of an A increased from 17% to 49%.

• Over 80% of students earned an 80% or higher class average.

• Students earning a final semester failing grade dropped from 5% to 0%. Yes, not one student has failed one of our classes in the past 3 years.

• Students displayed stronger confidence, fewer gaps, and far more ownership over their progress.

We also examined broader school-wide data.

State Performance

Beginning in 2022, the majority of our juniors, which includes the non-advancedtrack students, entered skills-based math classrooms. In 2023, our school’s SAT average exceeded the state average by 27.3 points, compared to 25.2 and 19.5 in the two years prior to implementation.

In 2024-2025, when Illinois transitioned from SAT to ACT, our students continued to outperform state averages by a large margin. With the ACT only being in effect for one year, longitudinal data does not yet exist.

Statewide Recognition

For the fourth consecutive year, our high school earned an Exemplary designation for the 2024–2025 school year. Not only was Carterville High School Exemplary, but its raw score has it currently placed as the 6th highest rated high school in the state of Illinois

Advanced Placement Success

Initially uncertain about applying this approach to advanced-track students, we piloted the Skills-Based Classroom in AP Calculus during the 2023–2024 school year. Homework and quizzes were eliminated; students relied solely on skills assessments and retakes to demonstrate mastery. AP Calculus enrollment typically ranges from 22 to 28 students.

Results spoke for themselves:

• Before implementation (2022 - 2023): 43% scored a 3 or higher.

• After implementation (2023 - 2024): 81% scored a 3 or higher. This exceeded both the state average (64.8%) and the global average (64.3%).

• More than 60% of our students scored a 4 or higher.

• In 2024 – 2025, an incredible 89.3% of AP Calculus students scored a 3 or higher and once again obliterated the state and global average.

Returning to Our Original Problems

Unreliable Grades

By removing homework and other compliance tasks from grading, our assessments now reflect only the knowledge students demonstrate in supervised settings.

Homework Dilemmas

Practice remains essential, but we no longer collect or grade it. Students quickly realized that their success on skills assessments, not points from worksheets, determined their grade.

Conclusion

The Skills-Based Classroom is not a departure from sound mathematics instruction; we have simply refined our approach to assessments. If you walk into our classroom on any random school day, what you will likely see is the same as in any other math classroom. We still rely on daily lessons, independent practice, group work, and meaningful teacher-student interactions. What has changed is the lens through which we view assessment.

Grades now reflect knowledge rather than compliance, and students who once felt left behind are finding pathways to mastery.

Makeup Assignments

With fewer traditional assessments, the burden of late work disappeared. Skills assessments offer flexible, lowstakes opportunities for students to demonstrate learning, eliminating the need for extensive makeup policies.

Student Learning Variations

Students can reassess at any time, allowing those who need more time to learn deeply while enabling advanced learners to move forward at an appropriate pace. Growth is built into the structure, not treated as an exception.

By focusing on skills, feedback, and growth, we have witnessed students take greater responsibility for their learning, engage more deeply with mathematics, and experience more equitable opportunities to succeed. Grades now reflect knowledge rather than compliance, and students who once felt left behind are finding pathways to mastery.

Most importantly, the Skills-Based Classroom doesn’t require a new curriculum, expensive software, or permission to overhaul the grading system. It simply requires a willingness to rethink assessment in the service of student learning.

Keenan Clark has been a dedicated educator in the Carterville school district since 1998. His career journey includes teaching junior high (1998–2003), followed by nearly two decades as a high school teacher (2003–2021). He also served as an Assistant Principal at the 4-6 Intermediate School (2020–2022) before returning to Carterville High School in 2022 to focus on Algebra II instruction.

He is a proud co-creator of the Skills Based Classroom (SBC) teaching strategy (www.skillsbasedclassroom.com), a framework dedicated to improving student mastery through focused, transparent skill development and assessment. His instructional work prioritizes deep understanding and practical application of mathematical concepts, moving beyond traditional chapter-based instruction. At CHS, Keenan is also a longtime coach, and he shares his commitment to education with his wife, Kaci, who serves as the Social Studies Department Chair at CHS. They are the parents of four children.

Jake Towers has been teaching mathematics at Carterville High School for eight years. He graduated from Southern Illinois University Carbondale in 2018 with a bachelor's degree in mathematics education, and Iater earned his master's degree in educational leadership from Eastern Illinois University in 2022. In addition to teaching, he also coaches football and basketball within the district.

Kathleen Meyer

What's the Story?

When thinking about math instruction, the thought of infusing stories and literacy skills with different mathematical topics is often something not considered. However, the demands of the state-level tests and other tests that students regularly take require a strong literacy background. Schmidtke et al. (2025) shared that when students have poor levels of reading fluency, these students generally become frustrated and tend to avoid tasks that involve reading (Schmidtke et al., 2025). What happens when students have the skills in math but cannot solve the problems that stare back at them? What can be done to support the linguistic needs of these students in a math class while moving forward with the requirements of a math curriculum?

A few summers ago, I found myself with a bunch of other educators from around the country at a STEAM in the PARK camp in the New River Gorge National Park and Preserve. Our evening conversation topics ranged from the beauty of the New River flowing right outside of the lodge at Camp Brookside to grant writing. Our conversation eventually drifted to some of the new Artificial Intelligence (AI) programs that were emerging and changing the landscape of education.

As a long-time special education teacher with stops along the way to teach math, STEM, and language arts, while

supporting a group of students who were also English language learners, I knew that a lot of my students not only struggled with the math but also with working through lengthy word problems where the purpose of the problem was often unclear. When a student is reading several grade levels below and then needs to work through math word problems, the situation becomes daunting. The question becomes, how can math become more accessible to all students while supporting the linguistic needs of these students?

The Main Tools - MagicSchool.ai and ChatGPT

The environmental implications of using AI tools are immense, and this needs to be acknowledged. However, as a teacher who is constantly trying to adapt lessons

2024). AI provides the ability to quickly create the skeletons of a lesson that can be fleshed out to meet the needs of many different types of learners in a matter of minutes instead of the hours the same task once took. These tools also allow for creative ways to embed literacy, problem-solving, and interest into various math topics.

Readers’ Theatre

Finding ways to introduce a math topic can be a challenge. What happens when the topic is introduced by an assortment of characters that the students came together to name and to adopt as a chapter mascot? Suddenly, students have materials to work with when working through new math concepts that are not as intimidating. Jones (2025) also shared that there is a wide range of

These tools also allow for creative ways to embed literacy, problem-solving, and interest into various math topics.

to meet the needs of my students, creating several assignments that meet the various needs of my students each week was just not feasible. Handley and Donnelly (2024) explained that if meaningful and sustainable change is to happen, educators need to be equipped with the tools necessary to take tasks off their plates (Handley and Donnelly,

benefits of students using readers’ theatre in class, including improved fluency, increased comprehension through text engagement, oral language skills, increased vocabulary, and creating a collaborative learning environment (Jones, 2025). Students are working together and experiencing the math lesson through a story using characters

that may experience math in real-world settings. Through an engaging lesson, student participation increases, and the students also learn how to talk about math through a script that they can use later to explain what they have learned.

memorable (Frommert, 2023). By asking one of the AI tools to create a story about a given math topic that includes key vocabulary, real-life examples, set in a certain location, with specific characters, and practice problems, students are

Developing language-rich supplemental activities becomes increasingly important for all levels of students, especially students who are struggling with the academic language in a course.

Stories

How long does it take to write a story that is mathematically accurate, interesting, and ready to use? A few hours, if everything goes as planned. This task can be done using an AI tool like ChatGPT or MagicSchool in a matter of minutes. Is it perfect? No. However, often the elements and details are created, and it takes the expertise of the teacher to make it something special for the class.

Stories can be used to introduce a unit or as a review for a test. Frommert (2023) shared that storytelling has been embedded in the humanities subjects as it captures the attention of the learners and allows the learners to see how different concepts are interconnected. Stories have been shared for generations because they are meaningful and

more engaged with the paths that the characters take, and helping the characters to successfully navigate the math. When math concepts become less intimidating, they also become more accessible to students.

Vocabulary and Academic Language

Students need to be able to understand and apply the math vocabulary for a given unit to effectively convey their understanding of a topic. Espinas and Fuchs (2022) explained that when the academic language in a content area, such as math, is limited, the student will often struggle to solve word problems (Espinas and Fuchs, 2022). Developing language-rich supplemental activities becomes increasingly important for all levels of students, especially students who are struggling with the academic language in a course. AI

provides anything from vocabulary lists, vocabulary games, and strategies to interject vocabulary development activities into lessons. If a student can practice the vocabulary consistently and then apply the vocabulary to different situations, when it comes time for the extended response type questions, not only will the students be confident in answering the questions, but the students will also have the mathematical terminology to answer the questions accurately.

Conclusion

There is no perfect way to teach math. Some students thrive on the routines of algorithms. Other students require creativity. Some students simply need a reason to be engaged with the topic. When the students and the teacher can come together to create something unique to the class that covers the topic, not only does math get taught, but the classroom community becomes stronger. Peanut the Squirrel and Waddles the Duck may mean nothing to students outside of my classroom, but to my students, they are the characters who are making math meaningful and accessible.

References

Espinas, D. R., & Fuchs, L. S. (2022). The effects of language instruction on math development. Child development perspectives, 16(2), 69–75. https:// doi.org/10.1111/cdep.12444

Frommert, C. (2023). Using stories beyond word problems to teach math: Stories can help students recall key math concepts and make the subject more relevant to them. Edutopia. https:// www.edutopia.org/article/mathclass-using-storytelling/

Handley, J. & Donnelly, L. (2024). What Can I Take Off Your Plate? A Structural-and Sustainable-- Approach to Countering Teacher Burnout. ASCD.

Jones, S. (2025). Bringing readers’ theatre to life: The power of readers’ theatre. Town End Research School. https:// researchschool.org.uk/town-end/ news/bringing-reading-to-life-thepower-of-readers-theatre

Schmidtke, D., Yamada, S. & Moro, A.L. Bridging to academic success: The impact of reading gains in an English bridging program on GPAs. Read Writ 38, 195–224 (2025). https://doi. org/10.1007/s11145-024-10514-x

Kathleen Meyer is currently a sixth-grade general education mathematics teacher and an eighth-grade special education resource teacher at Indian Trail Junior High School in Addison, Illinois. She has been in the Addison School District #4 for almost two decades. She has taught a wide range of subjects, including STEM, language arts, math intervention, instructional math, instructional language arts, and has cotaught math, language arts, science, and social science. Kathleen is also a regular participant in the STEAM in the PARK program through Expeditions in Education, which allows her to collaborate with educators from all over the country while exploring different National Parks.

The concept of being a lifelong learner is something that Kathleen takes seriously. She earned her bachelor’s degree from Butler University, where she studied history, education, music, and geography. She then completed a master’s degree in effective teaching with a concentration in special education at Butler University. She continued her graduate education at Concordia University and earned a second master’s degree in curriculum and instruction with a focus on supporting English language learners. Just to keep things exciting, she also earned her bilingual certification in Spanish. She is pursuing another degree through the American College of Education in curriculum and instruction.

Everyone's a Math Person

It is common to hear someone say, “I’m not a math person.” Many people go through life thinking they are consigned to not being able to make sense of math. In fact, there’s the old story from the 1990’s when A&W Restaurants offered a ⅓ pound burger for the same price as most fast food restaurants were charging for a ¼ pound burger. The “Third is the Word” campaign failed terribly because most Americans did not understand that ⅓ pound is actually larger than ¼ pound (Green, 2014). Many Americans were taught that being good at math meant being good at memorizing math facts and the order in which to perform a procedure. If that was difficult, there was no way around it and no hope for becoming better at math. Using a cognitive science lens on the teaching and learning of math shows that no one should think they are unable to become a math person.

Using a lens of cognitive science means making instructional decisions based on how the brain learns. It begins with having a foundational understanding of the architecture of what is happening when the brain is exposed to new information and what needs to happen in order for that information to be retained in a useful way.

Key attributes of lessons that cognitive science show maximize the learning include:

• Directing the learner’s attention

• Connecting new learning to prior learning

• Managing the amount of new information, and

• Providing time and opportunities to think deeply about the new information.

The conventional picture of most math classes is one where the teacher is at the board, demonstrating a problem stepby-step while the students are frantically trying to write down all of the things the teacher is doing. The teacher is doing all the talking, and many students may not know what question to ask in the moment if they missed a step in the procedure. If a student missed copying down a step, that student may not know what to do, especially if they had to do the homework after class, on their own. In that “typical” setting, there are multiple daily opportunities for a student to fall behind, each time reinforcing the

This type of classroom scenario has been in play for decades, aiding and abetting the conventional wisdom that most Americans are not “math people.” In fact, American students have lagged behind their international peers for decades; the country’s current 8th-grade Math NAEP scores are only 5 points (out of a 500-point scale) higher than they were in the 1970s (Petrilli, 2024).

Paying attention to cognitive science in the design and implementation of any lesson, but especially in a math lesson, will increase the likelihood that the information transmitted will not only be retained but will also be used in connecting more knowledge. The key instructional moves missing in the traditional math lesson are small but important and, unfortunately, easy to overlook.

When thinking of the tenets of cognitive science, key instructional moves a teacher will need to specifically plan for

Processing can look like students reflecting on what was just explained, restating the information, comparing with their peers, or examining how this new concept compares to their current understanding.

idea that the student will never be able to be proficient at math.

are: “Who is doing the thinking?” and “How often is that person getting the

opportunity to do that thinking?” When a teacher is explaining a new concept or a new procedure, and students are copying down the information from the board,

typically is (Brown, Roediger III, McDaniel, 2014). This simple change in the daily work of a mathematics classroom can go a long way towards increasing student

These connections are important for students to see explicitly..

the teacher needs to stop often—twenty to thirty seconds after new information is given—to allow students time to process that information. Processing can look like students reflecting on what was just explained, restating the information, comparing with their peers, or examining how this new concept compares to their current understanding. The key is the frequency and depth of this processing. If the teacher asks one deep question every ten minutes, there has not been sufficient processing time for new knowledge to stick.

In math classes, whether they are utilizing “traditional” or “new math” philosophies, every student needs to be thinking deeply about the concepts, spurred by regular, frequent questions specifically designed to help students see the connections between their current understanding and the new understanding of the teacher’s lesson. In order to make these lessons stickier in students’ brains, the material needs to be practiced significantly more often than it

retention of materials, regardless of whether the level of mathematics instruction is primary or advanced high school coursework.

The practice of regular reflection and practice in the classroom is a small tweak with big benefits. Additionally, there are other teacher moves that can increase the effectiveness of the lesson. Math concepts build upon each other. Teachers are very familiar with the concepts that they are teaching and see the connections between individual concepts. As teachers, our mathematical knowledge has been connected and solidified to the point that the connections between strategies or procedures are obvious to us. Oftentimes, teachers forget to make these clear to the students because they are already clear to the teacher. These connections are important for students to see explicitly—to connect the new learning to previously built understanding. The teacher needs to lead students from where they started

in their previous learning to the day’s new learning, making sure that students are able to make those connections and build upon the math foundation that has already been laid.

Instructional moves are critical to the teaching of math. However, encouraging enough practice for work to become automatic and memorized is still a critical component. Good instructional strategies will help students develop conceptual fluency, leading to a strong number sense that will help students gain more access to increasingly difficult concepts and procedures (Huinker, 2018). As teachers plan their lessions, they need to ensure that they are creating opportunities for students to develop and build fluency. Having good conceptual fluency will allow students to have more cognitive space.

References

Brown, P. C., Roediger III, H. L., & McDaniel, M. A. (2014). Make it stick: The science of successful learning. Harvard University Press.

Green, E. (2014). Why do Americans stink at math? The New York Times MM22, July 27.

Huinker, D. (2018). Principles to Actions:

Moving to a framework for teaching mathematics. Teaching Children Mathematics, 25(3), 133-136.

Kirschner, P., Hendrick, C., & Heal, J. (2022). How teaching happens: Seminal works in teaching and teacher effectiveness and what they mean in practice. Routledge.

Petrilli, M. (2024, July 2). When was the golden age of American K-12 education? and how can we tell?

– The 74. The 74. https://www. the74million.org/article/when-wasthe-golden-age-of-american-k-12education-and-how-can-we-tell/

Dr. Emmie Pawlak is the Director of Math, Science, and Accelerated Pathways in Cicero School District 99. Her professional work is creating and supporting systems that elevate instructional practices, including helping staff measure their impact quantitatively and qualitatively and use those measurements to further student growth and achievement. Dr. Pawlak is also a language learner. Learning a second (or third) language has helped her support dual language learning environments. A core value of hers is that students should be not just biliterate but also "bi-numerate" and be able to use their whole linguistic repertoire to explain their math thinking!

Upcoming Events

Empowering Visionary Curriculum Leadership Cohort

Jan.-May | 9:00am - 3:00pm

10701 S. Kilpatrick Ave

Explore learning with education leaders who deliver valid research-based learning approaches.

26 27

MORE INFORMATION

AI with Intention - Catch Them

Learning: Supporting Academic Integrity in an ERA of AI presented by Tony Frontier

Jan. 27 | 8:30am - 3:00pm

Medinah Shrine Banquets or Online

3

Explore practical, research-based solutions to support academic integrity, deter cheating, and help students take ownership for their learning.

MORE INFORMATION

My Kids Can't Write presented by Paul Emerich France

Feb. 10 | 9:00am - 12:00pm

NIU Naperville or Online

28

Learn to use cognitive writing as a means for writing across the disciplines, building students' stamina for on-demand writing tasks, and generating studentdriven evidence of learning.

MORE INFORMATION

4

Beyond the Numbers: Understanding Absenteeism and Building Bridges to Engagement presented by Jennifer Ciok

10

Feb. 5 | 9:00am - 12:00pm Live Online or On-Demand

Using evidence-based research and data, we will uncover key trends and drivers behind attendance barriers and equip attendees with actionable insights to foster solutions.

MORE INFORMATION

Grading Visible Learners presented by Dave Nagel

Feb. 12 | 9:00am - 3:00pm

NIU Naperville

5

Gain access to evidence-based approaches that empower educators to refine grading practices, fostering a vibrant culture of deeper student engagement and meaningful learning experiences.

12 17

MORE INFORMATION

11

Decision Science as a School Leader presented by Jason Major

Feb. 18 | 9:00am - 3:00pm

NIU Naperville

In this interactive workshop, Major will increase awareness of four domains from The Alliance for Decision Education: Valuing and Applying Rationality, Thinking Probabilistically, Structuring

18 19

29 30 1 Oct

Decisions, and Recognizing and Resisting Cognitive Biases.

MORE INFORMATION

Next Generation Science presented by Jeff Spencer

Feb. 19th - Champaign

March 16th - Oak Lawn

9:00am - 3:00pm In-person

6

to equip educators, administrators, and support staff with the skills and confidence needed to navigate the Individualized Education Program (IEP) process.

MORE INFORMATION

7

Learn what the Next Generation Science Standards are and what an NGSS-aligned classroom looks like.

MORE INFORMATION

Pump Up Primary Conference - PreK thru 2nd

March 4 - 6

Renaissance Hotel

13

45th annual Pre-K, Kindergarten, 1st and 2nd grade conference.

MORE INFORMATION

IEP Toolkit: Mastering Writing, Accommodations, Data Collection, and Understanding Behavior presented by Shelley Kenow

March 11 | 9:00am - 12:00pm

Live Online or On-Demand

20

This comprehensive webinar is designed

Solutions In Action: A National Virtual Conference

8

March 17-19 | 9:00am - 3:00pm Online or 90-Days for On-Demand

Teaching and Learning (Classroom Management, Data, Innovative Teaching Methods). Leading (Recruitment and Retention, Pipeline, Professional Development)

MORE INFORMATION

14

15

Every Graduate Future Ready: Delivering Employability Skills

Presented by Chapman & Simons

April 14 | 9:00am - 3:00pm Oak Lawn, Online or On-Demand

School-based teams will design a grades 6–12 scope and sequence that builds college, career, and civic readiness for all learners.

21

MORE INFORMATION

22

Empowering Small Group Instruction in Reading and Writing presented by Jennifer Serravallo

April 15 | 9:00am - 3:00pm Online or On-Demand

Regardless of your literacy curriculum or approach, you will be empowered to bring truly responsive small group teaching to your classroom for better outcomes in both reading and writing.

MATH THERAPY Featuring Vanessa Vakharia

26 27

MORE INFORMATION

Building School-Wide Systems of Care and Belonging presented by Ricky Robertson

28

April 22 | 9:00am - 3:00pm Medinah Shrine Center, Online or OnDemand

You’ll leave this session with practical, no-nonsense tools to turn those “I can’t do math” students into “I can do this” students!

4

5

3

April 21 & May 5 | 8:30am - 3:30pm

Medinah Shrine Center, Online or OnDemand

Through guided reflection and actionable strategies, you will leave equipped to foster a culture where you and staff will feel valued, safe, and supported in your essential work.

MORE INFORMATION

10

11

18

12

MORE INFORMATION

OUR MISSION

“To build the capacity of educational leaders to enhance the quality of teaching and learning”

EXECUTIVE COMMITTEE

President—Amy Warke (Bolingbrook)

President-Elect—Amy MacCrindle (Huntley Community SD158)

Past-President—Scott England (University of Maryland Eastern Shore)

Treasurer—Sarah Cacciatore (Mundelein SDs 75 & 120)

Secretary—Andrew Lobdell (Lena-Winslow SD 202)

FOCUS AREA LEADERS

Membership and Partnerships

Denise Makowski (Chicago)

Amie Corso Reed (O'Fallon SD 90)

Communications and Publications

Belinda Veillon (Nippersink SD 2 & Richmond Burton SD 157)

Jacquie Duginske (McHenry SD15)

Advocacy and Influence

Richard Lange (National Louis University)

Brenda Mendoza (West Aurora SD 129)

Program Development

Jamie Bajer (ROE 9), Heather Bowman (Washington GSD 52), Scott England (University of Maryland Eastern Shore), Amy MacCrindle (Huntley CSD 158), Terry Mootz (Crystal Lake), Amie Reed (O'Fallon SD 90), Dee Ann Schnautz (SIU), Belinda Veillon (Nippersink SD 2 & Richmond Burton SD 157) Amy Warke (Bolingbrook), Doug Wood (Springfield)

JOIN OUR ONLINE COMMUNITY!

Get involved with our social media: