


Increase Your Chord
Complete Guide For Building Chords Anywhere On The Guitar Fretboard
Music Guitar
Guitarists
Vocabulary The
Robert Sinclair BA Hons App.
Lessons Meath EssentialChordTheoryFor
The Chromatic Scale
In western music the equal temperament tuning system is utilised creating 12 equal distances or intervals between each note at a distance of a Semi-tone. The letters A to G are used in identifying these notes of differing pitches; this results in seven notes each defined by a letter. After reaching the seventh note the letters simply repeat this is termed as the next octave, the same is true when moving in the reverse direction. So after G comes A and Before A comes G, if we start on any letter for example C and follow the same sequence when we hit C again we have covered a complete octave.
The smallest distance between any two notes is a semi-tone which is one fret on the guitar two frets give a tone, or in other words, another way of understanding this is half-tone and full-tone.
Western music is divided into 12 equal pitches each a semi-tone apart this creates the chromatic scale -a scale is just an ordered set of pitches- the chromatic scale forms the basis for all music and all musical instruments, every other scale is built from the chromatic scale. This type of tuning is called the ‘equal temperament tuning system’.
The distance between any two notes is a whole tone with the exception of B-C and E-F which are semi-tones. When a note is moved forward by one semi-tone, this note is termed as being sharpened and indicated by the ♯ symbol. When a note is moved in reverse by one sem-tone this is note is now flattened, and detailed by the symbol ♭.
Depending on the direction travelled the note is either sharpened or flattened; so moving forward one semi-tone from C creates a C sharp (C♯) going backwards from D will give a D flat (D♭) in practice and pitch wise C♯ and D♭ are the same note and will sound exactly the same. This is known as an ‘Enharmonic Equivalent’ (EQ) the same is true for all other EQ – D♯ and E♭, F♯ and G♭ etc.
How does this apply to the guitar? In standard tuning guitars have six strings in open position set at different pitches E1 B2 G3 D4 A5 E6. By starting on open E and placing a finger on the first fret the note E is raised by one semi-tone to F, placing a finger on the second fret of the same string raises F by one semi-tone to F# and so the same applies to all other strings e.g. G fret one is G#, G on fret two is A and so on. This method can be applied to all strings and depending on the starting point going forward raises the note, going backwards flattens the note.
Chord Construction © Guitar Lessons Meath 2018
A♯ C♯ D♯ F♯ G♯ A - B-C - D - E-F - G - A B♭ D♭ E♭ G♭ A♭
Chord Construction
The Major Scale
The distance between notes can be expressed in terms of frets, steps, tones, or intervals. Frets are an acceptable term to use when dealing with other guitarists. Steps are a general musical term, used and understood by all musicians. Thinking of the distance between any two notes as intervals, however, is the most concise and universal way. This allows the distance between notes to be thought of as an independent unit of measure rather than a series of frets or steps.
Music’s Little Ruler
The major scale is used to measure the distance between notes. For example, the distance between the first and second notes of the major scale is two frets, one Whole Tone, Two Sem-Tones, or a “major second” interval. The distance between the first and third notes of the major scale is four frets, Two Whole Tones, Four SemTones or a “major third” interval. There are seven notes in the major scale and thus seven intervals. An eighth term, octave, refers to a higher or lower occurrence of the same note.
The Major scale is made up from a fixed set of intervals or pitches this being:
This formula when applied to any note of the Chromatic Scale produces a Major Scale. For Example:
Because the distance between E & F, B & C is only a Semitone when this formula is applied to other pitches of the Chromatic scale sharps and flats are produced. Let’s look at the G major Scale for example.
This is where key signatures originate from (a scale with one sharp F♯ indicates G Major) but more on that later.
© Guitar Lessons Meath 2018
Tone – Tone – Semi-tone – Tone – Tone – Tone – Semi-tone
C Major 1 2 3 4 5 6 7 8 C D E F G A A B C T T ST T T T ST
G Major 1 2 3 4 5 6 7 8 G A B C D A E F♯ G T T ST T T T ST
Chord Construction
As can be seen there are various ways of naming notes, measuring the distance between notes and identifying the position of notes in relation to each other and their root or tonic. When notes are arranged in a certain fashion we refer to these as been set in a particular scale or key the formula for each scale and key is a fixed set of intervals as with the Major scale:
Tone – Tone – Semi-tone – Tone – Tone – Tone – Semi-tone
When notes are stacked on top of each other and played at the same time this is referred refer to as a ‘Chord’ a chord is also a fixed set of intervals or notes stacked in thirds.
From each degree of the major scale we can develop a chord and as the major scale is a fixed set of intervals so the chords of the major scale follow a fixed pattern.
Major – minor – minor – Major – Major – minor – Diminished
Each chord takes its name from the degree of the major scale to which it relates or originates. Chords are numbered using roman numerals; upper case for major, and lower case for minor and diminished. So chord (iii) is always minor and chord (IV) always major and so on. To see how this works in practice the following table outlines the degrees of the C major scale, and the notes of this scale stacked in 3rds on top of each degree.
For Example: C Major chord taken from the first degree of the C Major scale the next note a 3rd apart is E and a 3rd from E is G stack these notes together one on top of the other and it produces a C Major chord.
C Major Scale
So the seven main triads (3 note chords) we get in C major are as follows:
C Major – D minor – E minor – F Major – G Major – A minor – B diminished
By applying the formula 1 3 5 from every degree of a scale, this produces a triad chord (a chord of three notes). Each chord is specifically related to this scale, we refer to these chords as “Diatonic” belonging to a particular scale. As such the scale fits perfectly with each chord. This relationship is called the Scale/Chord relationship.
© Guitar Lessons Meath 2018
I ii iii IV V VI vii° Root C D E F G A B Third E F G A B C D Fifth G A B C D E F
Some of these chords are minor, some major, some diminished and others augmented, so what defines these chords and gives them their particular characteristics? What makes a chord minor or major? This lesson will show how chords are constructed To begin with we will use the basic C major scale. Each note in this scale is numbered, the numbers are important it is from these numbers that we create our formulas.
Major Chord Construction
C Major Scale
Chords are constructed by stacking notes with an interval of a third on top of each other 1 = root.
3 = 3rd above root.
5 = 3rd above 3 or a 5th above root.
There are two kinds of thirds or 3rds - minor 3rds and major 3rds
Minor Third Interval of 3 semi-tones Symbol = ♭3
Major Third Interval of 4 semi-tones Symbol = 3
It is the type of third used in a chord that defines whether it is Major or Minor; a major chord uses the major 3rd above the root, and a minor chord uses a minor 3rd above the root.
Chord Construction © Guitar Lessons Meath 2018
1 2 3 4 5 6 7 C D E F G A B
Chord Construction
By stacking 3rds on top of the Root or the 1 - including the 1st note the notes given are C E G
This creates a C major chord or a C major triad (a 3 note chord)
From C to E is a major 3rd (4 semi-tones)
From E to G is a minor 3rd (3 semi-tones)
Every major chord has this structure: first a major third, then a minor third. A chord like this is called major because there is a major 3rd (4 semi-tones) between the root and the 3rd.
The formula for a major chord = 1 3 5
Minor Chord Construction
By stacking thirds on top of the second note “D” the number (2) of the C major scale. This second note of the major scale now becomes “1”, because it the root of our new chord:
© Guitar Lessons Meath 2018
1 3 5
C E G
1 ♭3 5 D F A
Chord Construction
This creates a D minor chord or a D minor triad (a 3 note chord)
From D to F is a minor 3rd (3 semi-tones)
From F to A is a major 3rd (4 semi-tones)
Every minor chord has this structure: first a minor third, then a major third. A chord like this is called minor because there is a minor 3rd (3 semi-tones) between the root and the 3rd.
The formula for a minor chord = 1 ♭3 5
It is important to note that a ♭3 is one semi-tone lower than a 3rd unless indicated a 3rd is always counted as a “Major 3rd”.
Diminished Chord Construction
The next type of chord is the “Diminished Chord” which gets its name from the inclusion of the flattened fifth or in other words “Diminished 5th” The diminished chord is a type of minor chord, as it also includes the “Minor 3rd” This chord is built from the seventh degree of the “Major Scale”
By stacking thirds on top of the seventh note “B” the number (7) of the C major scale. This seventh note of the major scale now becomes “1”, because it the root of our new chord:
This creates a B diminished chord or a B diminished triad (a 3 note chord)
From B to D is a minor 3rd (3 semi-tones)
From D to F is a minor 3rd (3 semi-tones)
© Guitar Lessons Meath 2018
1 ♭3 ♭5 B D F
Chord Construction
Every diminished chord has this structure: first a minor third, then a minor third. A chord like this is called diminished because there is a minor 3rd (3 semi-tones) between the root and the 3rd and a minor 5th or ♭5 between root and the 5th.
The formula for a diminished chord = 1 ♭3 ♭5
As the “Major Scale” is a fixed pattern, or a fixed set of intervals, so the chords created from each degree are also fixed. The following table details this fixed set of chords. This is the same for all major scales the only thing that changes is the name of the scale, and the note from which the scale starts. This is known as the “Root or Tonic”. All the chords that relate to a particular scale are termed as “Diatonic” or belonging to this scale.
©
Guitar Lessons Meath 2018
Notes Formula Chord Name Chord Symbol 1 C 1 3 5 C Major C 2 D 1 ♭3 5 D Minor Dm or Dmin or D3 E 1 ♭3 5 E Minor Em or Emin or E4 F 1 3 5 F Major F 5 G 1 3 5 G Major G 6 A 1 ♭3 5 A Minor Am or Amin or A7 B 1 ♭3 ♭5 B Diminished Bdim or B°
Finding Chord Tones
There are two methods for constructing chords. The first method is explained here, the second (more practical) method, will be looked at a later in this lesson:
The first method starts from the “Major Scale” and involves 3 steps:
1. Find the major scale of a given key. If you’re not sure how to do this, you need to refer back to the study Major Scale Introduction Parts I and II
Example 1: to find the notes of an Em chord, firstly find the notes of the E major scale:
2. Construct the Major Chord using the chord formula
3. Apply the Minor Chord Formula to the major chord. The chord formula for all minor chords is 1
By applying this formula the 3rd of the E Major Chord (E G♯ B) has to be lowered by 1 semi-tone. This would mean that the G♯ has to be lowered to G ; the other notes of the chord don’t change, so these are the notes of the E minor chord:
Guitar Lessons Meath 2018
©
Chord Construction
E
1 2 3 4 5 6 7 E F♯ G♯ A B C♯ D♯
Major Scale
1 3 5 1 3 5 E G♯ B
3
♭
5
To visualise how this looks on the guitar fretboard the following diagrams detail an E major triad built from the 7th fret on the 5th string, by lowering the 3rd (G♯) by 1 sem-tone to (G

) E Major is changed to E minor
Maj7 Chord Construction
Seventh chords are chords that contain 4 or more notes
To build a seventh chord using the C Major scale as an example:
C Major Scale
Chord Construction ©
1 ♭3 5 E G B
Guitar Lessons Meath 2018
2
6
C D E F G A B
1
3 4 5
7
The construction of seventh chords follows the same principle as constructing triads; that is by stacking thirds on top of each other. Triads were made by stacking 2 thirds on top of the root. Seventh chords are constructed by stacking 3 thirds on top of the root.
This creates a C major7th chord (Cmaj7) or a C major triad with an added major 3rd (a 4 note chord)
From C to E is a major 3rd (4 semi-tones)
From E to G is a minor 3rd (3 semi-tones)
From G to B is a major 3rd (4 semi-tones)
Every major 7th chord has this structure: first a major third, then a minor third, then a major third A chord like this is called major because there is a major 3rd (4 semi-tones) between the root and the 3rd. The addition of the major 7th is also a major 3rd (4 semi-tones) above the 5th.
The formula for a maj7 chord = 1 3 5 7
Minor 7 Chord Construction
By applying the same principal to the second note “D” the number (2) of the C major scale. This second note of the major scale now becomes “1”, because it the root of our new chord:
Chord Construction © Guitar Lessons Meath 2018
1 3 5 7 C E G B
1 ♭3 5 ♭7
This creates a D minor 7 chord (Dmin7) or a D minor triad with an added minor 3rd (a 4 note chord)
From D to F is a minor 3rd (3 semi-tones)
From F to A is a major 3rd (4 semi-tones)
From A to C is a minor 3rd (3 semi-tones)
Every minor 7 chord (min7) has this structure: first a minor third, then a major third, and then a minor third A chord like this is called minor because there is a minor 3rd (3 semi-tones) between the root and the 3rd.The seventh is also minor, or flattened. Every minor chord can be developed in this way – II – III – VI degrees of the major scale.
The formula for a minor chord = 1 ♭3 5♭7
Dominant 7 Chord Construction
Although seventh chords can be constructed from every degree of the major scale, the next important chord is the Dominant 7th. This is developed from the 5th Degree of the major scale and is often indicated by V7. By applying the same principal to the 5th note “G” the number (5) of the C major scale. This note of the major scale now becomes “1”, because it the root of the new chord:
This creates a D dominant 7 chord (G7) or a G major triad with an added minor 3rd (a 4 note chord)
Chord Construction ©
D F A C
Guitar Lessons Meath 2018
1 3 5 ♭7 G B D F
Chord Construction
From G to B is a major 3rd (4 semi-tones)
From B to D is a minor 3rd (3 semi-tones)
From D to F is a minor 3rd (3 semi-tones)
Every dominant 7 chord (dom7) has this structure: first a major third, then a minor third, and then a minor third A chord like this is called Dominant because it is built from the 5th degree of the major scale. This degree is also named the dominant. It is constructed from a major triad with an added minor 3rd (3 semi-tones) between the fifth and the 7th. The seventh is also minor, or flattened. This can also be applied to the SubDominant which is taken from the 4th degree of the major scale.
The formula for a Dominant 7 chord = 1 3 5♭7
m7♭5 or half diminished Chord Construction
From the seventh degree of the major scale the minor7 flat5 (m7♭5) or half diminished chord is developed, by stacking 3rds on top of the 7th degree. This kind of diminished chord is called ½ diminished due to the fact that a full diminished chord contains a ♭♭7 and is developed from the 7th note of the harmonic minor scale.
Applying the same principal to the 7th note “B” the number (7) of the C major scale a m7♭5 chord is created This note of the major scale now becomes “1”, because it the root of the new chord:
This creates a Bm7♭5 chord (B ø7) or a B diminished triad with an added major 3rd (a 4 note chord)
From B to D is a minor 3rd (3 semi-tones)
From D to F is a minor 3rd (3 semi-tones)
From F to A is a major 3rd (4 semi-tones)
© Guitar Lessons Meath 2018
1 ♭3 ♭5 ♭7 B D F A
Chord Construction
Every minor 7 chord flat 5 (m7♭5) has this structure: first a minor third, then a minor third, and then a major third. A chord like this is called a Half Diminished and is built from the 7th degree of the major scale. This degree is also named the Leading Note as it leads back to the Tonic or Root as such it creates a strong pull or tension to the root. It is constructed from a diminished triad with an added major 3rd (4 semi-tones) between the fifth and the 7th. The seventh is also minor, or flattened.
The formula for a m7
♭
5 chord = 1
♭3 ♭5♭
7
Below is a summary of the Diatonic Seventh chords.
© Guitar Lessons Meath 2018
Notes Formula Chord Name Chord Symbol 1 C 1 3 5 7 C Major 7 Cmaj7 2 D 1 ♭3 5 ♭7 D Minor 7 Dm7 or Dmin7 or D-7 3 E 1 ♭3 5 ♭7 E Minor 7 Em7 or Emin7 or E-7 4 F 1 3 5 7 F Major 7 Fmaj7 5 G 1 3 5 ♭7 G dominant 7 G7 6 A 1 ♭3 5 ♭7 A Minor 7 Am7 or Amin7 or A-7 7 B 1 ♭3 ♭5 ♭7 B half dim 7 Bm7♭5 or B
The next logical progression in developing chords is the use of Extensions or Tensions these are extended notes of the major scale that are not Chord Tones again the same principal applies as before – these extensions are notes stacked in thirds. They are not called chord tones, that is; 1 3 5 7 as the progression has now moved into the next Octave (after the 7th note).
Using the C Major scale again as an example:
C Major Scale
The first extension is the Ninth – 9th outside of the chord tones 1 3 5 7 there are 3 notes left in the major scale that are not chord tones: 2, 4 and 6.
Adding these tones to the chord; they become known as tensions. Normally these tensions are added at an octave higher than chord tones as they otherwise get in the way, and have the effect of making the chord sound “muddy”. Tensions are also notated in the next octave as such;
2 becomes 9 7 + 2 = 9
4 becomes 11 7 + 4 = 11
6 becomes 13 7 + 6 = 13
By adding the second note “D” of the major scale, only an octave higher which now becomes a ninth, to a C maj7 chord – C maj9 is created.
There are some note combinations that should be avoided when creating Seventh Chords; the reason here is that they clash with each other. The two remaining notes of the major scale 4 and 6 tend to sound dissonant when used in combination with the seventh degree of the major scale, whether this degree is flattened or not.
Guitar Lessons Meath 2018
Chord Construction ©
1 2 3 4 5 6 7
D E
C
F G A B
1 3 5 7 9 C E G
B D
Chord Construction
As such special rules are applied here. This does not mean that in the right context that they can’t be used together, but under normal circumstances they are generally avoided.
The 4th degree of the C major scale “F” is a semi-tone above the “E” (the 3rd of Cmaj7). When E and F are combined together in the same octave they sound dissonant, so the 4th degree – in this case being the note “F” is generally avoided for Cmaj7 and is not often used with this chord.
The 6 degree is also a special case when used in combination with major chords. Most of the time when we add a 6th to a major chord, the 7th is omitted and there is no octave added to the 6th. This is because the 6th and 7th also clash and get in each other’s way.
Adding a 6th to a C major chord creates the chord C6 as can be seen below.
The same rule applies when adding the 6th in combination with minor chords: the ♭7 is omitted. By adding the 6th to Dm7 this creates Dm6. Note that the 6th is no longer A as in the C6 example above because the root of the chord has now changed to D. This will now make the 6th a B - (D E F G A B C) as detailed below.
© Guitar Lessons Meath 2018
1 3 5 6 C E G A
1 ♭3 5 6 D F A B
With minor chords the 4th does not clash, the 4th when used in combination with minor chords, because it is two semi- tones above the ♭3 and not one semi- tone the effect is more consonant, therefore the 4th degree works well with minor seventh chords.
When you add the 4 degree of the major scale to Dm7, this creates a Dm11 chord:
NB: theoretically the 9th should also be included within the “11th” chord, this is keeping with the logic that chords are stacked in 3rds.
The 4th degree also has a special relationship when used in conjunction with Dominant Chords in this case the 3rd can be omitted, and just as when the 4th degree was added to any major chords they were called Sus4, so too when the 4th degree is added to dominant 7th chords they are termed as Sus4. For example “D7sus4” the 4th often serves as a precursor, or delay for the main chord it is built from, and so the term Suspension is used. This creates the sense that resolution is needed, and the over whelming effect is of coming home 9th’s and 7th’s are often used in conjunction with 4th’s – below is an example of G9sus4.
G C B F A
There are other Extensions or Tensions which can be applied, but these are taken from the Harmonic minor scale, and are a study which is outside this basic Diatonic or Major scale chord tone study. These are referred as Altered Tensions these would include ♭9, ♯9, ♭5, ♭13 scale tones, including the ♯11 taken from the dominant Lydian scale.
Chord Construction © Guitar Lessons Meath 2018
1 ♭3 5 ♭7 11
F A C G
D
1 4 5 ♭7 9
The above table is a summary of the chord extensions, or tensions covered so far.
© Guitar Lessons Meath 2018
Chord Type Extension Symbol Major 9/2 Cmaj9 4 ♯11/♯4 / Cmaj7♯11 avoid note ♯11 taken from the Lydian scale 6 C6 7th is omitted Minor 9th/2nd C9 11/4 Cm11 6 Cm6 ♭7 is omitted Dominant 9/2 C9 ♭9/♭2 C7♭9 ♭9 is taken from the altered scale, or the 5th mode of the harmonic minor scale ♯9/♯2 C7♯9 ♯9 is taken from the altered scale 4 C7sus4 13/6 C13 ♭13/♭6 C7♭13 ♭9 is taken from the altered scale, or the 5th mode of the harmonic minor scale
Chord Construction
Diatonic Tensions
The table below details the most common basic chord type and formulas much of which has been covered so far, comparing these formulas is a useful tool in understanding how chords are developed, and their relationship to each other, also what can be clearly seen is the power of the 3rd in defining each chord. In their fundamental state chords are either major, or minor in construction with the addition of the 5th and 7th, including further extensions chords can be coloured and defined in many ways.
©
Chord Construction
Guitar Lessons Meath 2018
Chord Formula Major Triad 1 3 5 Minor Triad 1 ♭3 5 Diminished Triad 1 ♭3 ♭5 Augmented Triad 1 3 ♯5 Major 7 1 3 5 7 Minor 7 1 ♭3 5 ♭7 Dominant 7 1 3 5 ♭7 Half Diminished 7 1 ♭3 ♭5 ♭7 Diminished 7 1 ♭3 ♭5 ♭♭7 Augmented 7 1 3 ♯5 ♭7 Suspended 4 1 3 4 ♭7 Minor/Major 7 1 ♭3 5 ♭7
Chord Type
Chord Construction 2
There is another method that can be applied in constructing chords, and possibly a more practical means. Understanding the first method though gives a more rounded approach, and will give greater understanding when using this method.
The first step is to commit to memory the chord tones, and their formulas for the C major scale. It will be necessary to be able to picture these chord types, tones and formulas. The above table details seventh chords of the C major scale.
The following examples will show how to apply this information when developing chords:
Example 1: to find the chord tones of Cm7:
1. You know the chord tones of Cmaj7: C E G B
2. You know the chord formula of Cmaj7: 1 3 5 7
3. You know the chord formula of minor 7: 1 b3 5 b7
4. Adapt the chord tones of Cmaj7 to the formula of minor 7: bring the 3 and the 7 a half step down.
5. Conclusion: the chord tones of Cm7 are: C Eb G Bb
By simply comparing and adapting the chord tones of the C maj7 chord and applying the formula for the minor 7th chord, the chord tones of the Cmaj7 chord can be altered to create the Cm7 chord.
© Guitar Lessons Meath 2018
Chord Construction
Cmaj7 CEGB 1357 Dm7 DFAC 1♭35♭7 Em7 EGBD 1♭35♭7 Fmaj7 FACE 1357 G7 GDBF 135♭7 Am7 ACEG 1♭35♭7 Bm7♭5 BDFA 1♭3♭5♭7
Example 2: the chord tones of Ddim7:
1. You know the chord tones of Dm7: D F A C
2. You know the formula of Dm7: 1 b3 5 b7
3. You know the formula of diminished 7: 1 b3 b5 bb7
4. Adapt the chord tones of Dm7 to the formula of diminished 7: bring the 5 and the 7 a half step down
5. Conclusion: the chord tones of Ddim7 are: D F Ab B
By simply comparing and adapting the chord tones of the Dm7 chord and applying the formula for the diminished chord, the chord tones of the Dm7 chord can be altered to create the Ddim7 chord.
Example 3: the chord tones of F#7:
1. You know the chord tones of Fmaj7: F A C E
2. To find the chord tones of F#maj7 you just have to raise each chord tone a half step: F# A# C# E#
3. You know the formula of major 7: 1 3 5 7
4. You know the formula of dominant 7: 1 3 5 b7
5. Adapt the chord tones of F#maj7 to the formula of dominant 7: bring the 7 a half step down
6. Conclusion: the chord tones of F#7 are: F# A# C# E
By simply comparing and adapting the chord tones of the F maj7 chord and applying the formula for the dominant 7th chord, the chord tones of the Fmaj7 chord can be altered to create the F♯7 chord.
Chord Construction © Guitar Lessons Meath 2018
Placing Chords on the Guitar Fretboard
The first thing to know when placing chords on the guitar fretboard is that not every chord tone is required or equally important:

Tones 3 and 7 are the most important notes of any chord as they determine the chord type. They also are important for voice leading. When moving from chord to chord chords will flow smoothly when correct voice leading is applied, instead of bouncing all around the guitar neck. Each note of a chord is a voice; voice leading is moving individual chord voices smoothly from one chord to the next.
Voice leading is also useful in single note improvisations voice leading can function as the framework with which to base melodic, and harmonic lines on.
The 1 tone is the least important note, because usually it is played by the bass player. The 5 tone is also not as important these can sometimes make harmony sound muddy
Tensions add colour and interest to a chord, so these have greater importance than 1 and 5 chord tones. As can be seen how a chord is configured and the tones that are selected serve a much greater purpose than just choosing a chord from a chord book.
The nest to know is that 1 sem-tone is equivalent to one fret on the guitar fretboard
To illustrate this we can take a basic D major chord played using an (A shape) with its root on the 5th fret of the fifth string.
X15135: D
Identifying the notes from left to right (from low E string to high E string) the following is played:
X: the low E-string is not played
1: the 1 or root of the chord is played on the A-string
5: the 5th of the chord is played on the D-string
1:the root again, but now on the G-string
3: the third is played on the B-string
5: the 5th is played again, but this time on the high E-string
It is OK to duplicate chord tones, like the 1 and the 5 in the above example.
©
Chord Construction
Guitar Lessons Meath 2018
As a basic major chord this chord sounds quite blocky and lacks life, to spice this chord up a colour tone, tension note can be added.

Replacing the 1 on the G-string with the 7: the chord Cmaj7 (1 3 5 7) has been created instead of duplicating the root on the G-string, it was just exchanged for the 7 of the chord.
Adding further tension or colour brings greater life, as can be seen the 5 tone has now been omitted and the 9 tone has been added to create a Cmaj9 chord (1 3 5 7 9) This Cmaj9 would be a great choice if playing Bossa Nova, solo guitar or in duo setting, but if playing with a bass player the root note tends to get in the way, it is better to omit the root and to play on the higher strings only:
Chord Construction © Guitar Lessons Meath 2018
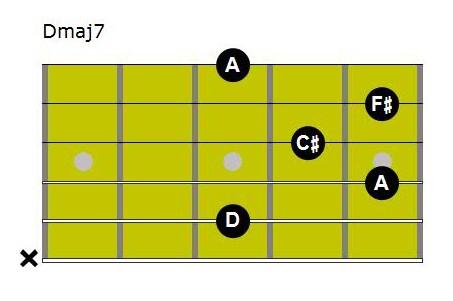
X15735: Dmaj7
X1379X: Dmaj9
This arrangement would be a far better choice when playing with a bass player, removing the root from the chord allows the bass player to have more freedom. This type of chord is what is termed as an inversion; the 3rd is in the bass instead of the root. This arrangement is also an example of choosing one chord voicing over another to follow good voice leading.
An Inversion is basically any chord that does not have its root in the bass
There are three types of chord inversions:
Root Position: the root is in the bass
First inversion: the 3rd in the bass.
Second inversion: the 5th in the bass.
Third inversion: the 7th in the bass.
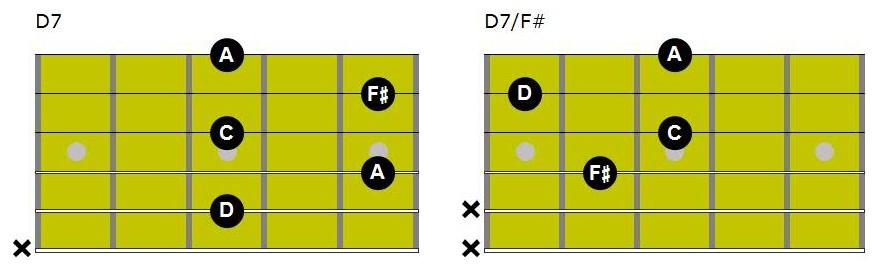
The following are an example of a D7 chord in root position and this chord’s three inversions:
Chord Construction © Guitar Lessons Meath 2018
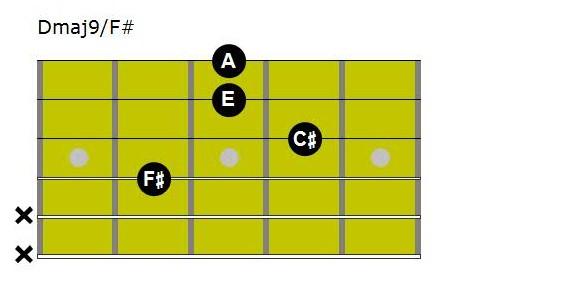
XX3795: Dmaj9/F♯
X15♭735: D7 XX3♭715
Identifying the notes from left to right in example 1(from low E string to high E string) the following is played:
X: the low E-string is not played
1: the 1 or root of the chord is played on the A-string
5: the 5th of the chord is played on the D-string
♭7: the ♭7 on the chord is played on the G-string
3: the third is played on the B-string
5: the 5th is played again, but this time on the high E-string
The second example shows the 3rd F♯ is now played in the bass, or lowest note, in this arrangement all four notes of the D7 are played. Simply moving the D note to F♯ on the 7th fret of the B string will remove the root note D from this chord voicing.
The third example shows the 5th in the bass, and the root has been omitted, while the final example shows the root in the highest position on the 3rd fret of the B string. Placing the root at the highest point in a chord voicing tends not to interfere with the bass player.
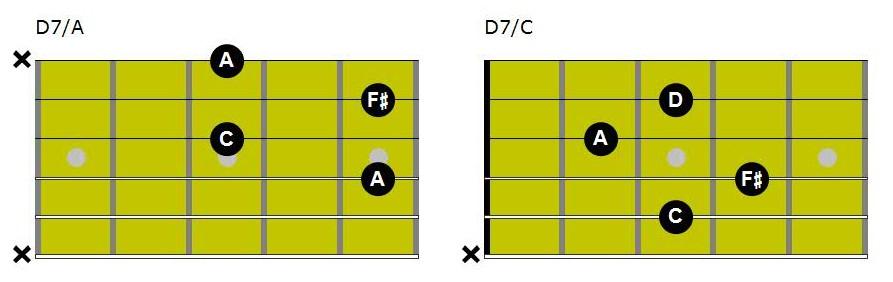
Chord Construction © Guitar Lessons Meath 2018
X15♭735: D7
XX3♭715
Voice Leading
Voice leading is a discipline that deserves a separate study and investigation in its own right, but since it has been mentioned in passing a simple explanation is warranted, the chord diagrams below detail such an example The harmonic passage shown here implies an ii-V-I movement in the key of C major, before transitioning to the key of B♭ major via the Cm9 chord. In simple terms voice leading is the practice of moving harmony with small adjustments, or movements of chordal tones. The Dm9/F is chord ii of C major – the F note here is ♭3 of this chord. This then becomes ♭7 of the next chord, G13/F the other chord tones have moved no more than a full tone. The G13/F is chord V of C major; moving to the - I chord in C major, C9/E has been has been applied. The movement from V-I has been achieved by changing the F (♭7) of the G13 chord to E which has now become the 3rd of C9/E. The remaining chord tones have also followed good voice leading in that the G which was already present as the root of the G13 chord has now become the 5th of the C9 chord, The D note that has been introduced to create tension or colour in the C chord, is in fact also the 5th of the G13 chord, and the B note has only dropped a semi-tone to create B♭, which is the ♭7 of the C9 chord. The next movement implies a key change – to B♭ major, it can be clearly seen here that the only chord tone that is moved is the E to E♭, both of these notes are the 3rd of each chord; there is no movement required with the remaining notes.
All of these chords have been created between the 3rd and 5th frets. The movements within all four chords are either semi-tone or tone steps, as result the harmonic movement is smooth.
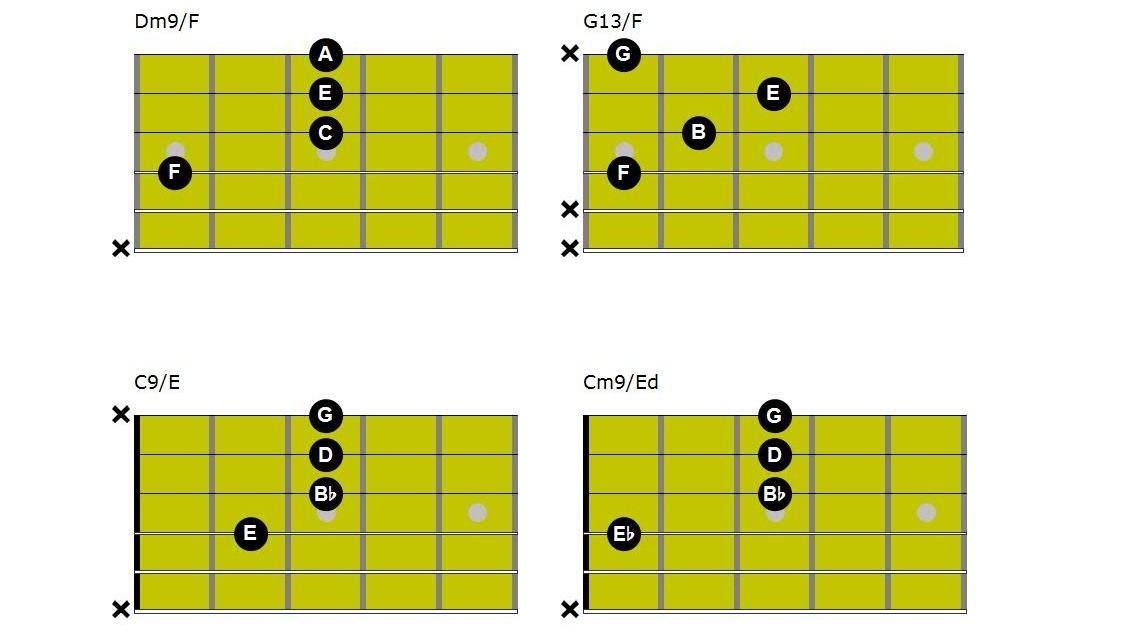
Chord Construction © Guitar Lessons Meath 2018
This investigation has shown that chord construction is simply the process of stacking notes predominantly in thirds, except for the 2nd or 4th which have a special relationship to the tonic, on top of each other. The inclusion of other notes from the tonic scale, or from the chromatic scale creates tension and colour. This tension implies movement as the pull of resolution is created. It is the relationship to the tonic which sets tension in motion.
The diagrams below detail the relationship each note of the chromatic scale has in relation to the root, in this instance our root is “C” which is taken from the 3rd fret on the 5th string.
This pattern of notes in relationship to the root is better defined as “intervals” or in other words the distance each note is from the root. This pattern is fixed and in standard tuning can be moved up and down the neck. Of course as the root is moved the actual pitch names will change, however one semi-tone up from the root will produce a “flat 9th or ♭2nd, and 2 whole tones from the root will produce a 3rd 5 semi-tones will produce a perfect 4th 7 semi-tones will produce a perfect 5th , and so on.
As previously seen in this study of the “major scale” another way of naming the notes of a scale is by using intervals, and universally this is the most precise way of naming notes in relationship to the root.
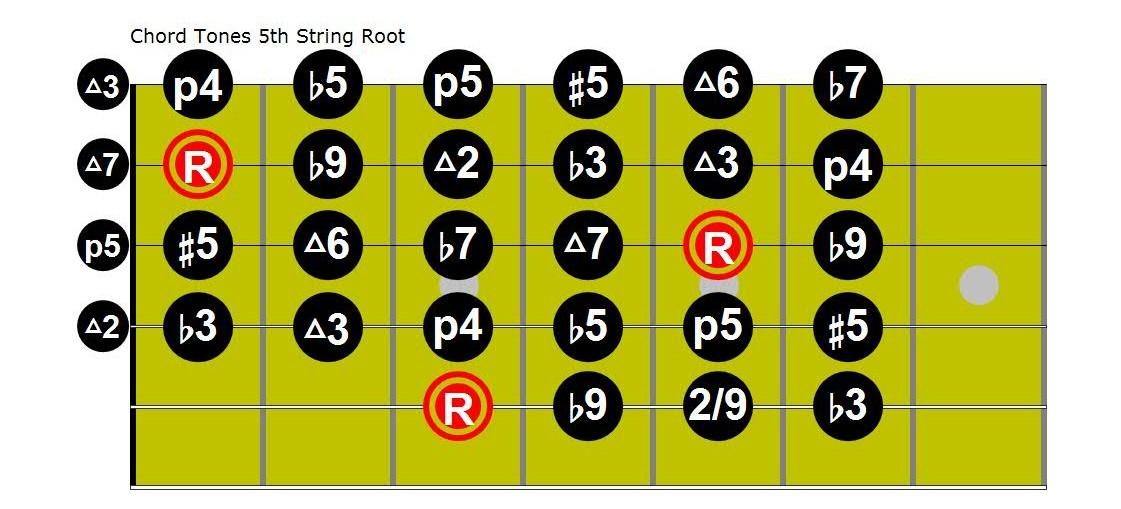
Chord Construction © Guitar Lessons Meath 2018
C C♯ D♭ D D♯ E♭ E F F♯ G♭ G G♯ A♭ A A♯ B♭ B C root ♭♭♭9 ♭♭9 9/2 ♯9 ♭10 3 4/11 ♯4/♯11 ♭5 5 ♯5 ♭13 6/13 ♭7 ♭7 7 octave
In the above table, and fretboard diagram the same logic is applied to the note “G” this time taken from the 3rd fret of the 6th string, this table also includes enharmonic equivalents (notes that sound exactly the same, but are notated differently). To show that it is the distance between the root and the next note that gives the interval its name or quality the fretboard diagram has highlighted the root notes in red; it can be taken that the root is 1. It can also be noted that some pitches, or notes have two ways of being identified as intervals, for example a 9th and a 2nd these are technically the same note only placed at different intervals from the root. In the musical alphabet there are only seven notes, after which time they just repeat. Still using the note “G” as our root note the musical alphabet from here would be;
G-A-B-C-D-E-F-G the intervallic distance between G to G is a perfect 8th or an octave, so G to A is a 2nd or major 2nd however G to A in the next octave would be a 9th it is the position of the note A within the chord in relationship to the root that will indicate whether the note “A” is identified as a 2nd or a 9th , thus a 4th in the next octave is an 11th and a 6th in the next octave is a 13th. This is where the names for various chords originate. The following table gives some of the main examples of chord types, how they would be notated, and the chord tones used to create them.

Chord Construction © Guitar Lessons Meath 2018 G G♯ A♭ A A♯ B♭ B C C♯ D♭ D D♯ E♭ E F F♯ G♭ G root ♭♭♭9 ♭♭9 9/2 ♯9 ♭10 3 4/11 ♯4/♯11 ♭5 5 ♯5 ♭13 6/13 ♭7 7 7 octave
Chord Construction
Chord Type Notation Scale Tones Major 1, 3, 5 Minor m 1, ♭3, 5 Diminished dim, o, m♭5 1, ♭3, ♭5 Diminished 7th dim7, o7, dim 1, ♭3, ♭5, ♭♭7 Half Diminished M7♭5, 1, ♭3, ♭5, ♭7 Augmented aug 1, 3, ♯5 5th or Power Chord 5 1, 5 Dom7th 7 1, 3, 5, ♭7 Minor 7th m7 1, ♭3, 5 Major 7th maj7 1, 3, 5, 7 Minor/Major 7th m/maj7 1, ♭3, 5, 7 Suspended 4th sus4 1, 4, 5 Suspended 2nd sus2 1, 2, 5 7th suspended 4th 7sus4 1, 4, 5, ♭7 7th suspended 2nd 7sus2 1, 2, 5, ♭7 Added 2nd add2 1, 2, 3, 5 Added 9th add9 1, 3, 5, 9 Added 4th add4 1, 3, 4, 5 Major 6th 6 1, 3, 5, 6 Minor 6th m6 1, ♭3, 5, 6 Major 6/9 6/9 1, 3, 5, 6, 9 Minor 6/9 m6/9 1, ♭3, 5, 6, 9 Dom9th 9 1, 3, 5, ♭7, 9 Minor 9th m9 1, ♭3, 5, ♭7, 9 Major 9th maj9 1, 3, 5, 7, 9 Dom11th 11 1, 3, 5, ♭7, 9, 11 Minor 11th m11 1, ♭3, 5, ♭7, 9, 11 Major 11th maj11 1, 3, 5, 7, 9, 11 Dom13th 13 1, 3, 5, ♭7, 9, 11, 13 Minor 13th m13 1, ♭3, 5, ♭7, 9, 11, 13 Major 13th maj13 1, 3, 5, 7, 9, 11, 13 Dom7th# 9th 7♯9, 7+9 1, 3, 5, ♭7, ♯9 Dom7th flat 9th 7♭9, 7-9 1, 3, 5, ♭7, ♭9 Dom7th sharp 5th 7♯5, 7+5 1, 3, ♯5, ♭7 Dom7th flat 5th 7♭5, 7-5 1, 3, ♭5, ♭7
© Guitar Lessons Meath 2018
All this knowledge would be useless unless it is applied in a practical and usable fashion, it is not just the understanding of music that creates music, it is however, the application of this knowledge upon a given instrument that binds this understanding together and underpins the concept of harmony. No better example can be given of how tones and pitches react one with the other than to play them together as a block, this is in essence what a chord is, groups of notes played simultaneously. When this is done consonance or dissonance, colour and tension, resolution and implied movement are created within the sonic realms. In the words of Claude Debussy (1862-1918) “when it comes to music there is only one rule need apply, the rule of the ear”
In this next section fourth, fifth and sixth string root chords in movable shapes are created and shown in the following fretboard diagrams, by moving these shapes along the fretboard it will be possible to play each shape from every root note of the chromatic scale this will give a total of 1,044 different chords. By comparing each shape one with the other in its associated group it can be seen that in most cases just the movement of one chord tone or finger position will create a new chord. Further comparison can serve as a template for voice leading applications and harmonic structure.
Using the above table and applying it to the relevant string the root note of each chord can be moved along the fretboard. This will create a new chord; the structure will however remain the same, in other the whole harmony block as indicated in the following chord diagrams will simply be moved to a new position. For example if Cmaj7 (which has its root on the 3rd fret of the fifth string) as a block were moved two frets toward the sound hole of the guitar, the new chord will take its name from the note on the 5th fret of the fifth string, namely D, the new chord will then be named Dmaj7. This can also be done with all the chord shapes that take their roots on the 4th and 6th string.
Roots on the 5th string; using chords with roots 5th string work well for sequences, and are particularly effective when combined with those that are based on a 6th string root. Chords with a 5th string root often have adjacent outer or inner strings that are not played. The player should prevent these unused strings from ringing by letting the side of the fingers rest naturally against them.
Roots on the 6th string; building chords from a 6th string root enables a guitarist to play low register chords, as well as full-sounding 5 and 6 string voicing’s
Roots on the 4th string; on the four upper strings of the guitar the range of chordal possibilities is more limited. Eleventh and thirteenth chords can be constructed, but with only four voices; they lack some of the important notes that give certain chords their harmonic character. The upper sting chords are ideal for supporting melody, their bright clear sound; good separation and high register make them useful for chord fills in group playing.
© Guitar Lessons Meath 2018
Chord Construction
Fret 0 1 2 3 4 5 6 7 8 9 10 11 12 6th E F F♯/G♭ G G♯/A♭ A A♯/B♭ B C C♯/D♭ D D♯/E♭ E 5th A A♯/B♭ B C C♯/D♭ D D♯/E♭ E F F♯/G♭ G G♯/A♭ A 4th D D♯/E♭ E F F♯/G♭ G G♯/A♭ A A♯/B♭ B C C♯/D♭ D
Chord Construction
Fifth Sting Root Chords
 © Guitar Lessons Meath 2018
© Guitar Lessons Meath 2018
Chord Construction
 © Guitar Lessons Meath 2018
© Guitar Lessons Meath 2018
Chord Construction
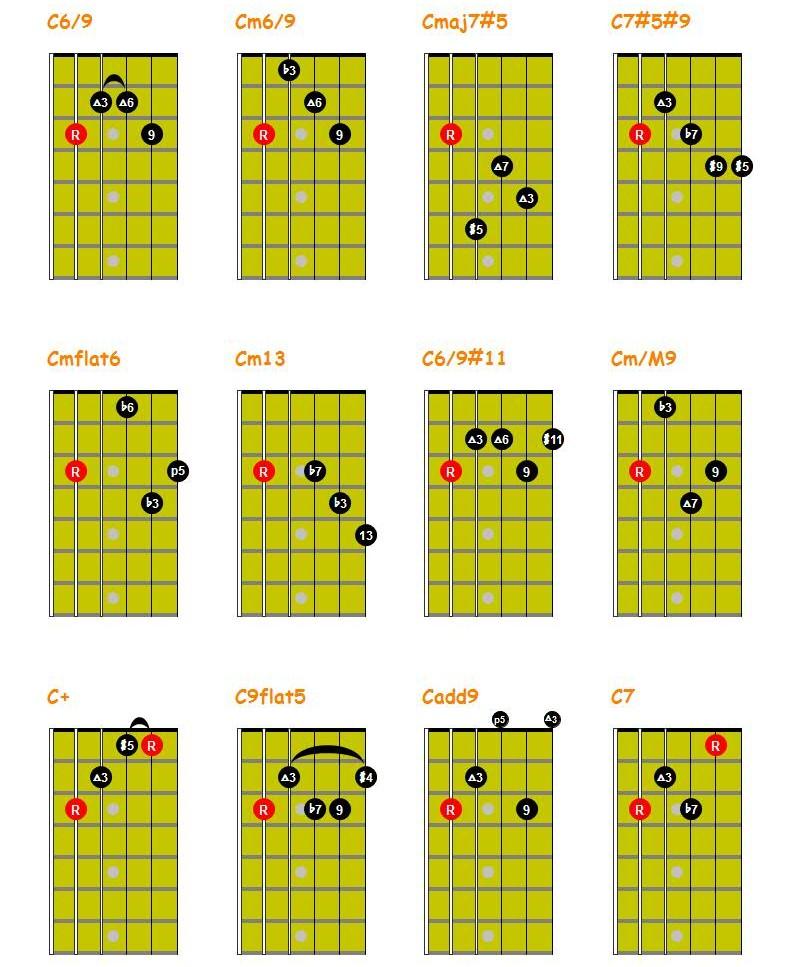 © Guitar Lessons Meath 2018
© Guitar Lessons Meath 2018
Chord Construction
Sixth String Root Chords
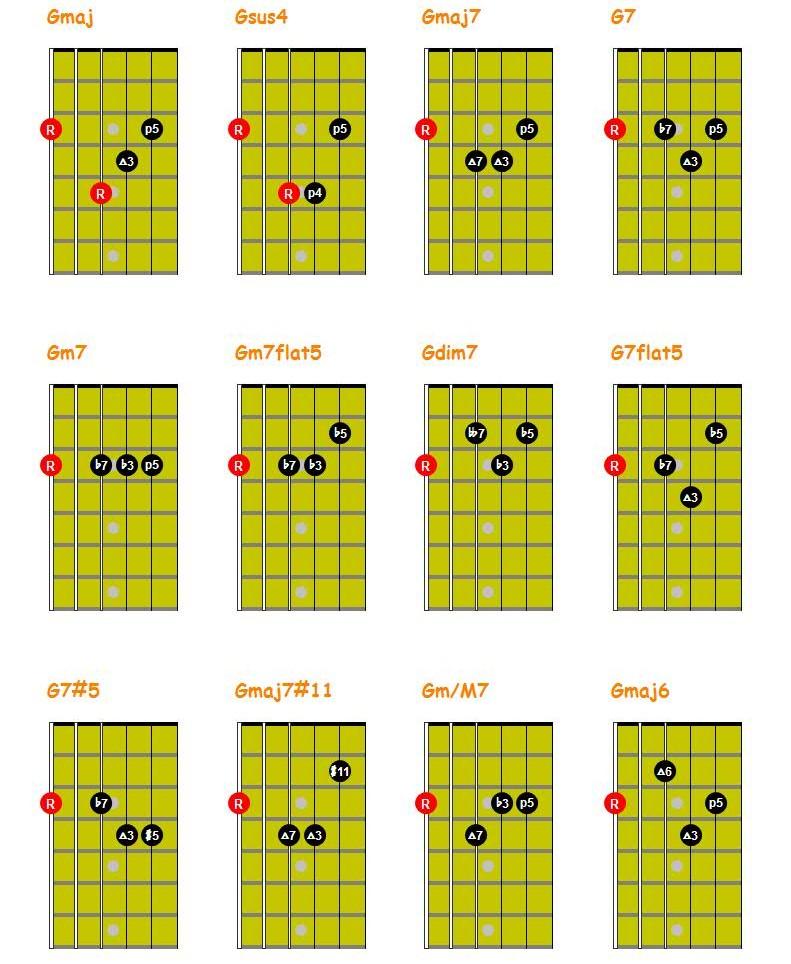 © Guitar Lessons Meath 2018
© Guitar Lessons Meath 2018
Chord Construction
 © Guitar Lessons Meath 2018
© Guitar Lessons Meath 2018
Chord Construction
 © Guitar Lessons Meath 2018
© Guitar Lessons Meath 2018
Chord Construction
Fourth String Root Chords
 © Guitar Lessons Meath 2018
© Guitar Lessons Meath 2018
Chord Construction
 © Guitar Lessons Meath 2018
© Guitar Lessons Meath 2018
Chord Construction
Scale Tone Chords
With so many different chord types it can be confusing when trying to place chords in their relevant keys, and learning the function each has one with the other. The twelve keys each contain an extensive series of chord types and they all have specific functions; this function is dictated by each chords position and relationship to the tonic. Previously it has been shown that chords are created from each degree of the major scale, the notes of the major scale are used as the root for each of these chords, and that is where each chord gets its name. The chords of each key are assigned Roman Numerals and this places them in positions relative to the tonic, or root note of each key. Their use and level of development depend on the style and form of the music and on the requirement for certain types of harmonic colour, or tension. Chords are developed by adding further scale tone notes on top of the basic triad these main types of developments are; Sixth; Seventh; Ninth; Eleventh; and Thirteenth. The following tables detail the position of each of these developments in relation to the tonic, by comparing chords from other keys it can be seen that one chord type on a root also occurs in different keys only its position and function has changed, for example Dm7 is chord II of C major, it is also chord VI of F major and chord III of B♭ major. This difference of function can be applied as a useful tool when transitioning from one key to another or introducing a key change within a song.
C Major
G Major
© Guitar Lessons Meath 2018
I II III IV V VI VII I Sixth C maj6 D min6 F maj6 G maj6 C maj6 Seventh C maj7 D min7 E min7 F maj7 G7 A min7 B min7♭5 C maj7 Ninth C maj9 D min9 F maj9 G9 A min9 C maj9 Eleventh D min11 E min11 F maj7♯11 G11 A min11 B min11♭5 Thirteenth D min13 G13
I II III IV V VI VII I Sixth G maj6 A min6 C maj6 D maj6 G maj6 Seventh G maj7 A min7 B min7 C maj7 D7 E min7 F♯ min7♭5 G maj7 Ninth G maj9 A min9 C maj9 D9 E min9 G maj9 Eleventh A min11 B min11 C maj7♯11 D11 E min11 F♯ min11♭5 Thirteenth A min13 D13
Chord Construction
© Guitar Lessons Meath 2018 D Major I II III IV V VI VII I Sixth D maj6 E min6 G maj6 A maj6 D maj6 Seventh D maj7 E min7 F♯ min7 G maj7 A7 B min7 C♯ min7♭5 D maj7 Ninth D maj9 E min9 G maj9 A9 B min9 D maj9 Eleventh E min11 F♯ min11 G maj7♯11 A11 B min11 C♯ min11♭5 Thirteenth E min13 A13 A Major I II III IV V VI VII I Sixth A maj6 B min6 D maj6 E maj6 A maj6 Seventh A maj7 B min7 C♯ min7 D maj7 E7 F♯ min7 G♯ min7♭5 A maj7 Ninth A maj9 B min9 D maj9 E9 F♯ min9 A maj9 Eleventh B min11 C♯ min11 D maj7♯11 E11 F♯ min11 G♯ min11♭5 Thirteenth B min13 E13
Major I II III IV V VI VII I Sixth E maj6 F♯ min6 A maj6 B maj6 E maj6 Seventh E maj7 F♯ min7 G♯ min7 A maj7 B7 C♯ min7 D♯ min7♭5 E maj7 Ninth E maj9 F♯ min9 A maj9 B9 C♯ min9 E maj9 Eleventh F♯ min11 G♯ min11 A maj7♯11 B11 C♯ min11 D♯ min11♭5 Thirteenth F♯ min13 B13
E
© Guitar Lessons Meath 2018 B Major I II III IV V VI VII I Sixth maj6 min6 maj6 maj6 maj6 Seventh maj7 min7 min7 maj7 7 min7 min7♭5 maj7 Ninth maj9 min9 maj9 9 min9 maj9 Eleventh min11 min11 maj7♯11 11 min11 min11♭5 Thirteenth min13 13 D♭ Major I II III IV V VI VII I Sixth maj6 min6 maj6 maj6 maj6 Seventh maj7 min7 min7 maj7 7 min7 min7♭5 maj7 Ninth maj9 min9 maj9 9 min9 maj9 Eleventh min11 min11 maj7♯11 11 min11 min11♭5 Thirteenth min13 13 A♭ Major I II III IV V VI VII I Sixth maj6 min6 maj6 maj6 maj6 Seventh maj7 min7 min7 maj7 7 min7 min7♭5 maj7 Ninth maj9 min9 maj9 9 min9 maj9 Eleventh min11 min11 maj7♯11 11 min11 min11♭5 Thirteenth min13 13
Chord Construction
© Guitar Lessons Meath 2018 E♭ Major I II III IV V VI VII I Sixth maj6 min6 maj6 maj6 maj6 Seventh maj7 min7 min7 maj7 7 min7 min7♭5 maj7 Ninth maj9 min9 maj9 9 min9 maj9 Eleventh min11 min11 maj7♯11 11 min11 min11♭5 Thirteenth min13 13 B♭ Major I II III IV V VI VII I Sixth maj6 min6 maj6 maj6 maj6 Seventh maj7 min7 min7 maj7 7 min7 min7♭5 maj7 Ninth maj9 min9 maj9 9 min9 maj9 Eleventh min11 min11 maj7♯11 11 min11 min11♭5 Thirteenth min13 13 F Major I II III IV V VI VII I Sixth maj6 min6 maj6 maj6 maj6 Seventh maj7 min7 min7 maj7 7 min7 min7♭5 maj7 Ninth maj9 min9 maj9 9 min9 maj9 Eleventh min11 min11 maj7♯11 11 min11 min11♭5 Thirteenth min13 13
Chord Construction
Chord Construction
Harmonic Resolution
After developing an understanding of how chords are constructed, and a knowledge base of the position each chord has along with its function in relation to the tonic, the next logical step is the practical application of these chords. Harmonic Resolution is the act, or movement of a note or chord from dissonance (an unstable sound) to a consonance (a more final or stable sounding one). Harmonic resolution adds closure, or implied movement to any harmonic progression.
The movement from a dominant chord (V) to the tonic (I) chord is an important part of chordal harmony. It is the central mechanism in jazz music. Although V-I is a resolution with a full close sound used for endings, it is also treated as part of a flowing movement of chordal harmony. It is frequently preceded by a II chord of the related key
Harmonic resolution is a study that deserves to be looked at in its own right, and to explore it completely would take its own publication, however to have brief understanding of how it works will complete this study of chord construction. Using an example from the key of C major chord I and chord V G major the following explanation will be given.
The table below details the notes that create the chord of C major, it can be seen that this chord also has the note of G in its formation.
C major
The following table details the notes that create the chord of G major, it can be seen that the note G is now the root of this chord 1 3 5 G B D
G major
There is another feature at work here that creates a strong tension or pull, the 3rd of G major is the note B the note B is also the 7th or leading note of the C major scale. The seventh note of the C major scale, the leading
©
Guitar Lessons Meath 2018
1 3
C
5
E G
note, B resolves naturally to the C or the tonic of C major. It is the movement from B to C that is heard in the V-I resolution when the 3rd of the dominant chord of G major resolves to the root note of the tonic C major.
When the dominant chord V is extended to a V7 by the addition of the note F this resolution or tension is even greater.

If the two tables above are compared the 3rd of G7- B moves to C the root of C major, and the 7th of G7-F moves to E the 3rd of C major, when the V-I resolution is complete.
The effect of the addition of the note F to the G major chord can be heard more clearly when using two note chords. The musical example below shows G major being played, and then followed by the addition of the note F before resolving to a two note chord C major.
© Guitar Lessons Meath
Chord Construction
2018
1 3 5 ♭7 G B D F
1 3 5 C E G
G7 or G dominant 7
C major
By converting the I chord to a dominant seventh the V-I movement can also be used as a transpositional device V-I7 this implies movement instead of closure, this movement or tension is toward the IV chord F major.
Again the same devices are at work only producing a different result, by comparing both the C7 and the F7 it can be seen that they both have the note C in common, also the ♭7 of C7 is the 5th note in the F major scale, and the 3rd of F major A is the 6th note of the C major scale. The chord C7 is the dominant V7 in the key of F major. This V-I connection can be used to work harmonically around the circle of fourths on a never ending loop, only bringing complete closure when the I chord is played without the addition of the 7th. This is a very useful device to create a natural key change within music. The following musical example details this sense of movement without closure. Starting on V7 – G7 of C major it then moves to I7 – C7 of C major, which is also V7 of F major, F7 is also the IV7 of C major. The harmony then moves to I7 – F7 of F major, which is also IV7 of B♭ major, the movement then from F major to B♭ major is accomplished again by a V-I relationship in that F is the V chord of B♭ the movement however is created by travelling through a sequence of 4ths. The movement then from B♭ major to E♭ is accomplished in the same manner, in that E♭ is the IV chord of B♭ major and that B♭ is chord V of E♭ major. Finally applying the same approach the harmony is transposed to A♭ major, with A♭ being the IV chord of E♭ major, and E♭ being chord V of A♭ major It is only with the 7th note removed in the A♭ major chord that the movement concludes with any sense of finality.
©
Chord Construction
Guitar Lessons Meath 2018
1 3 5 ♭7 C E G B♭ C7 or C dominant 7 1 3 5 ♭7 F A C E♭ F7 or F dominant 7
All this discussion of one chord being the 5th of the preceding key, and then being the 4th of the following key can seem a little confusing, however when this information is collated into the following diagram, the circle of 4th’s – 5th’s it becomes a little clearer. Travelling clockwise the harmony moves in a circle of 5ths, in the opposite direction – counter clockwise the harmonic movement is through a cycle of 4th’s.


This direction is travelling in 4ths
This direction is travelling in 5ths
Circle of 4th’s – 5th’s
The inner circle of the diagram of the circle of 4th’s – 5th’s also includes the relative minor of each key, the relative minor is taken from the 6th degree of each major scale.
Chord Construction © Guitar Lessons Meath 2018
Chord Construction
© Guitar Lessons Meath 2018














 © Guitar Lessons Meath 2018
© Guitar Lessons Meath 2018
 © Guitar Lessons Meath 2018
© Guitar Lessons Meath 2018
 © Guitar Lessons Meath 2018
© Guitar Lessons Meath 2018
 © Guitar Lessons Meath 2018
© Guitar Lessons Meath 2018
 © Guitar Lessons Meath 2018
© Guitar Lessons Meath 2018
 © Guitar Lessons Meath 2018
© Guitar Lessons Meath 2018
 © Guitar Lessons Meath 2018
© Guitar Lessons Meath 2018
 © Guitar Lessons Meath 2018
© Guitar Lessons Meath 2018



