matematika
Page 1 : Cover
Page 2 : Overview
Page 3- 8 : Trigonometric Functions
Page 9-12 : Finding the Trigonometric Ratios with Missing Side
Page 13-15 : Special Angles
Page 16-19 : Angle of Elevation and Depression
Page 20-26 : Tangents and Secants of a Circle
Page 27 : Formative Assessment
Page 28 : Answer Key
Page 29 : Cover
The Trigonometric Functions
Lesson Proper: Introduction of the lesson
First of all, do you guys have any idea or have you heard about Trigonometric?

Trigonometric is from the Greek word "Trigonometria" and it means triangles measurements. A Trigonometric is made by an acute right triangle that is 180° and it bedside to measure a distance that cannot be directly measured
There are 2 types of triangles: The Right Triangle which measured 30°-60°-90° and Isosceles Right Triangle which measured 45°-45°-90°. Trigonometric functions can be used in either of the two right triangles. Before you do the trigonometric function you need to know about the point of reference from which to work which is called the the Reference Angle
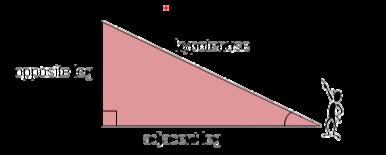
This is the image of a Right triangle it has 3 sides The Hypotenuse, Opposite side, and Adjacent side Always remember that labeling changes when the Reference angle location changes so it means the position of the 3 is not permanent it depends on the position of the Reference Angle.
Lesson Proper:
Introduction of the lesson
The 2 Acute Right Triangle has 2 formulas the SIN-COS-TAN For the 30°-60°-90° and CSC-SEC-COT for 45°-45°-90°
Sin: SOH = O/H
Cos: CAH = A/H
Tan: TOA = O/A
Csc: CHO = H/O
Sec: SHA = H/A
Cot: CAO = A/O
Here is an example of a Trigonometric function:
Example 1:
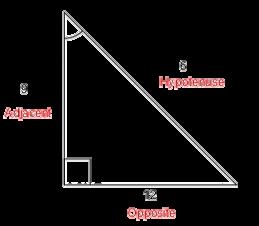
Sin = 12/6
Cos = 9/6
Tan = 12/9
Csc = 6/12
Sec = 6/9
Cot = 9/12
Lesson Proper:
Introduction of the lesson
Here is an example of a Trigonometric function:
Example 2:

Sin = 5/15
Cos = 10/15
Tan = 5/10
Csc = 15/5
Sec = 15/10
Cot = 10/5
Now that you know the basic labeling of Trigonometric Functions, try answering the activities in the next page!

Lesson Proper:
Activities:
Try This!
1.)
sin = csc =
cos = sec =
tan = cot =
2.)
sin = csc =
cos = sec = tan = cot =
Lesson Proper:
This!

sin = csc =
cos = sec =
tan = cot =

sin = csc =
cos = sec = tan = cot =
- ProductionFinding trigonometric ratios with missing sides
Lesson Proper:
Introduction of the lesson
As you guys can see one of our sides is missing so we need to find it by using the Pythagorean Theorem
FORMULA:
A = √c2 - b2 (If adjacent is missing.)
B = √c2- a2 (If the opposite angle is missing in our sample given.)
C = √a2 +b2 (If the hypotenuse is missing.)

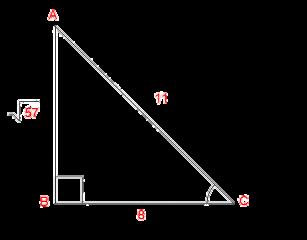
In our give the opposite side is the one that is missing when the opposite is missing we subtract the hypotenuse and opposite.
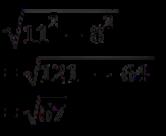
Since 57 doesn't have any square root that's already the final answer.
Take note: If your denominator is radical, you need to rationalizeit.
Example of rationalization:
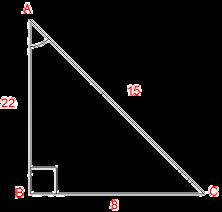
Sin C = 57/11
Cos C = 8/11
Tan C = 57/8
Csc C = 11 / √57 x √57 /
√57 = 11√57/57
Sec C = 11/8
Cot C = 8/√57 x
√57 / √57 = 85757
Lesson Proper:
Introduction of the lesson
Another example:
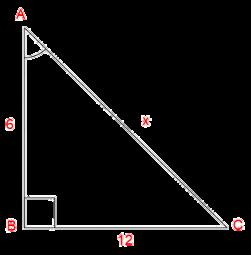
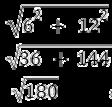
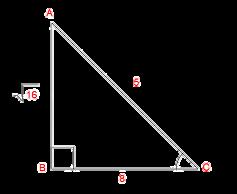
Since 180 doesn't have any square root that already has the value of x
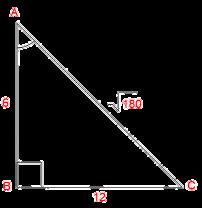
Sin A = 12/√ 180 x √ 180 / √ 180 = 12√180 /180
Cos A = 6/√180 x √180 / √ 180 = 6√ 180/180
Tan A = √ 180/12
Csc A = √180/12
Sec A = √180/6
Cot A = 12/6
Lesson Proper:
Try This! 1.)
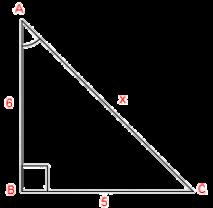
SIN A = CSC A =
COS A = SEC A = TAN A = COT A =
2.)
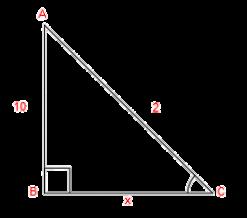
SIN C = CSC C =
COS C = SEC C =
TAN C = COT C =
sPECIAL ANGLES
Lesson Proper:
Introduction of the lesson
Theorem 30-60-90 in the first theorem the length of the hypotenuse is equal to twice the length of the opposite side of the 30 angles, The length of the longer leg which is the opposite of 60 is the adjacent 3.
Theorem 45-45-90 is the second triangle and it is an isosceles right triangle, the hypotenuse is 2 then the opposite and adjacent are the same 1
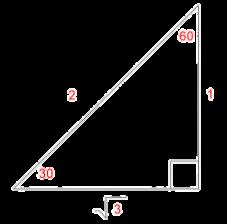
Theorem 1
Theorem 2
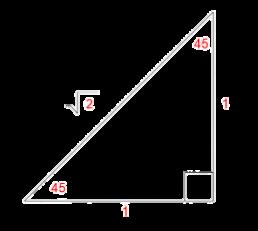
Example:
1.) Cos 30 + Tan 45
2.) Csc 60 + Cos 45
1.) You need to multiply the 2 denominator Steps: 2 ) after that do the butterfly method
*THIS FORMULA IS for the SHORT cut METHOD
Lesson Proper:
Introduction of the lesson and activities
Example:
3.) Cot 30 + Tan 60

Steps:
1.) Find the LCD of the denominator
2.) After that the LCD of the denominator is used to divide the denominator
3.) The answer that you got in the 2nd step multiplied by the numerator Try this!
*THIS FORMULA IS for the long METHOD
1.) Csc 45 + Toa 60
2.) Tan 45 + Sec 30
3.) Cos 60 + Sin 45
 By: Noventa y Uno - Production
By: Noventa y Uno - Production
Angle of Elevation and Depression
Lesson Proper:
Introduction of the lesson
The angle of Elevation is above the horizontal line and line of sight of the observer The angle of depression is the opposite of Elevation if the horizontal is above the depression Is below the line of sight and the horizontal line.
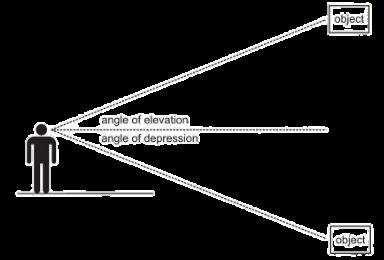
Examples of word problems:
1.) Angle is standing at the top of the building which is 86ft and Angel is looking at Mark. The angle of elevation to the mark is 50°. What is the distance of Mark to the building?
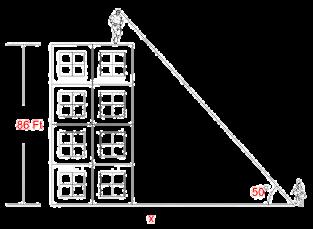
Because our Hypotenuse is missing we will not use all the trigonometrics that have hypotenuses So here we will use “Tan”
Lesson Proper:
Introduction of the lesson
Formula:
= 72.16 ft
72 .16 is the distance of the mark to the building.
*In calculating this problem you need a calculator. type 86÷tan(50) in your calculator.
2.) Karla is standing in front of the plane that just landed. The distance of Karla to the plane is 65m and the height of the plane to the window of the cockpit is 125 ft. What is the angle of elevation starting from the base of the ground?
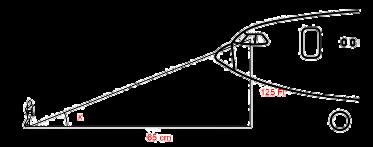
=27
In this Given, we are just finding the angle to get that, press shift then tan, put (65 ÷ 125) after you got the answer, press °’” then the first number is the answer.
Lesson Proper: activities:
Try This!
1.) Renren is in his room on the second floor of the hotel, And Andrei looking at Renren at a distance of 76 ft on the hotel the angle of elevation is 45°. What is the Height Of the Building?
2.) Dave is Staring at the bridge At a distance of 80 ft away from the bridge and the height of the bridge 180 ft. What is the angle of elevation?
3.) ABCD is a quadrilateral with AB = 10 cm, BC = 5 cm, CD = 10 cm, and AD = 5 cm. Is ABCD a square? If not, what type of quadrilateral is it?
4.) A Ferris wheel casts a shadow of 12 meters when the angle of elevation of the sun is 60 degrees. What is the height of the Ferris wheel?
5.) From the top of a 50-meter lighthouse, the angle of depression to a point on the ground is 30 degrees. How far is the point from the base of the lighthouse?
By: Noventa y Uno - Productiontangents and secants of a circle
other lesson
Lesson Proper:
Introduction of the lesson
In geometry, a tangent to a circle is a line that meets the circle precisely once, known as the point of tangency. In contrast, a secant is a line that crosses a circle at two locations. These principles are frequently employed in issues that include circles and angles.
LET’S TRY THIS!
1.) What is the line called that touches a circle at exactly one point?
A. Tangent
B. Cosine
Answer: A
C. Sine
D. All of the Above
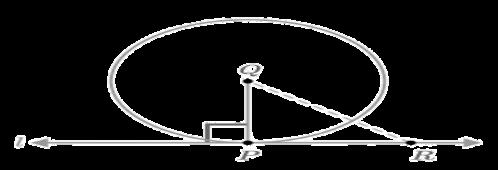
When a line meets a circle at exactly one place, it is referred to as tangent to the circle or tangent to the circle. Below, line L is tangential to the circle at point P. This point is known as the point of tangency.
Theorems on Tangents to a Circle
Theorem: The tangent at any point on a circle is perpendicular to the radius through the point of contact.
2.) What shape is associated with the tangent in the theorem?
A. BOX
B. Square
C. Circle
D. Triangle
Answer: C
The shape associated with the tangent in the theorem is a circle. You're most likely talking to the Tangent Theorem, which asserts that the tangent to a circle is perpendicular to the radius drawn to the point of tangency.
Lesson Proper:
Introduction of the lesson
Converse of Tangent Theorem
Let's show that if a line is drawn across the endpoint of a radius and perpendicular to it, it is tangent to the circle.
Theorem: A line drawn perpendicular to the endpoint of a radius is tangent to the circle.
Given: a circle with center A. AP is the radius, and L is the line that passes through P.
To demonstrate: the line L is the tangent to the circle at point P.
To construct: select a point (R) on the line L that is not P. Participate in AR.
Proof R is a point on the line I, other than the point of contact P. R lies outside the circle
Since, AP ⊥ line L
AP is the shortest distance between the line's center (A) and all other points (excluding P).
⇒ AP < AR
⇒ AR > AP
Point R is outside the circle. Thus, every point on the line L, except for P, is outside the circle. The line L only joins the circle at point P. Hence, the line L is a tangent to the circle at point P.
3.) Where is point R with reference to the circle?
A. Outside the circle
B. Inside the circle
C. At the center of the circle
D. At the side of the circle
Answer: A
Without a graphic or further information, it is hard to definitely establish where the point is in relationship to the circle. However, if you've examined a diagram and concluded that point is outside the circle.
Lesson Proper:
Introduction of the lesson
Two Tangent Theorem
NOTE!
A circle can have just one tangent drawn at a point on it. Two tangents can be made to a circle from a point outside of it.
Given: A circle with center A. CP and CQ are two tangents drawn to this circle, from an exterior point C
To prove:
i. CP = CQ
ii. angle PAC = angle QAC
iii. angle PCA = angle QCA
Construction: Join AC, AP and AQ
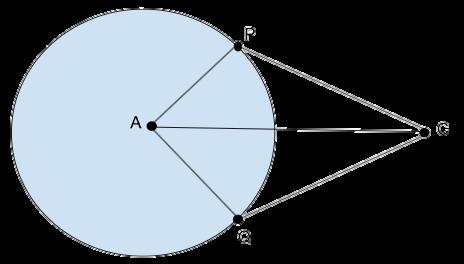
Next step; Proof: In △ CPA and △ CQA,
As per the proof above, overline AC ≅ AC by the reflexive property and PA ≅ QA because they are both radii of the circle. This means that △ APC ≅ △ AQC by R.H.S. ≅ PC ≅ QC because the segments are corresponding parts of congruent triangles.
PC and QC are known as tangent segments. In general, two tangent segments to a circle from the same point outside the circle will always be congruent.
Lesson Proper:
Introduction of the lesson
From point C, both lines I and m are tangent to circle A. Show that ∠PAQ and ZPCQ are supplementary. What does this mean in general?
ZAQC is a straight angle because line m is tangential to circle A at point Q. A quadrilateral's internal angles add up to 360 degrees. This signifies that.

Therefore, ∠PAQ and ∠PCQ are supplementary.
In general, the angle formed by two lines tangent to a circle from the same point is additional to the central angle established by the two tangent lines.
m∠PAQ + m∠AQC + m∠PCQ +m∠CPA = 360°. m∠PAQ + m∠PCQ = 360 deg - 90 deg - 90 deg = 180 degLesson Proper:
Introduction of the lesson
4. What are the lengths of two tangents taken from an exterior point to a circle?
A. Same point
B. Same degree
C. Equal
D. Not equal
Answer: C
The two tangents drawn from an exterior point to a circle are the same/equal length. This is an essential feature of circles and tangents. So, if you draw two tangents from the same exterior point to a circle, their lengths will be identical.
LET’S TRY THIS!
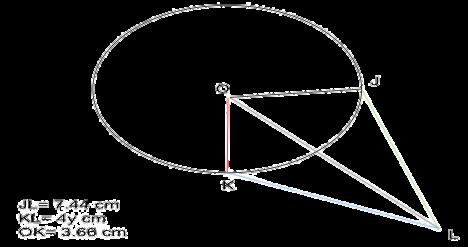
Place the red point L inside the red circle N. Note that KL has a length of 4y cm. What is the value of y?
A. 3.66 cm
C. 0.5 cm
B. 5.93 cm D. 1.5 cm
The answer is D.
Lesson Proper:
Introduction of the lesson
2. Is it feasible for tangential segments JL and KL to exist if point L is on circle O's circumference? Why, or why not?
A. Yes, they just pass through the circle.
B. No, tangential segments cannot be traced to the same point on the circle.
C. No, they are too short to be called tangent lines. The answer is B.
If point L is on the circle's circumference, then so are points J and K. There is only one unique point, hence no tangential segment can be drawn because each segment requires two distinct points to be identified.
3. Is the line overlining JL perpendicular to any line(s)?
A. OL
B. OK
C. OJ
D. KL
The answer is C.
FORMATIVE ASSESSMENT
1. What is the angle between a line and the radius drawn to the point of tangency if a line is tangent to a circle at that particular point?
A. 180 degrees
B. 45 degrees
C. 30 degrees
D. 90 degrees
2. The measure of the angle generated when two secant lines cross outside of a circle is equal to half the difference between the measurements of the intercepted arcs.
A. True
B. False
3. The measure of each angle created in a circle is half the measure of its interception if a secant and a tangent meet at the point of tangency?
4. When two tangents are traced from an outside point to a circle, they are
A. Parallel
B. Congruent
C. Intersecting
D. None of the above
5. The product of the lengths of the secant and its exterior segment equals the square of the length of the tangent when a secant and a tangent of a circle are drawn from a point outside the circle.
A. True
B. False
ANSWER KEY
A tangent and a radius drawn to the point of tangency always form a 90 degree angle. Thus, the right response is d. 1. Half of the total measure of the intercepted arcs equals the measure of the angle created. So the answer is B. 2. "ARC" is the right answer. Each produced angle has a measure equal to half of its intercepted arc.
3. Tangents from an outside point that are drawn to a circle are congruent. So, B is the right answer.
5.
4. The correct answer is "A." This is referred to as the Power of a Point Theorem.
