Solution manual for dynamics of structures 4 e 4th edition 0132858037 by geraldine.roberson709

Solution Manual for Dynamics of Structures, 4/E 4th Edition :

0132858037

Download full chapter at: https://testbankbell.com/product/solution-manual-for-dynamics-ofstructures-4-e-4th-edition-0132858037/

CHAPTER 3

© 2012 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photoco1pying, recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.

Problem 3.1 From the given data, k = ω2 = (2π f )2 = (8π)2 = 64π2 (a) m n n k = (ω′)2 = (2π f ′)2 = (6π)2 = 36π2 m + Δm n n (b) Dividing Eq. (a) by Eq. (b) gives 1 + Δm m = 16 9 m = 9 Δm = 9 5 = 6.43 lbs g (c) 7 From Eq. (a), 7 g g k = 64π 2 m = 64π2 6.43 g = 10 52 lbs in (d)

Problem 3.2

At ω = ω n , from Eq. (3.2.15), 1

o = (ust )o 2ζ = 2 (a)

At ω = 0 1ω n, from Eq. (3.2.13),

uo ≈ (ust )o = 0 2

Substituting (ust )o = 0 2 in Eq. (a) gives

ζ = 0.05

© 2012 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photoco2pying, recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.

Assuming that damping is small enough to justify the approximation that the resonant frequency is ω n and the resonant amplitude of Rd is 1 2ζ, then the given data implies:

0.0576

of small damping implied in Eq. (a) is reasonable; otherwise we would have to use the exact resonant frequency

and exact resonant

© 2012 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photoco3pying, recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.

) n n n n ⎝

Problem 3.3

(uo )ω = ω = (u ) 1 st o 2ζ (a) (uo )ω = 12ω 1 = (ust )o 2 2 1 (ω ωn )2 + 2ζω ω n = (ust )o [1 1 (1 2)2 ]2 + [2ζ (1 2)]2 (b) Combining Eq. (a) and Eq. (b): 2 ⎛ 2 ⎞ 1 ⎜ (uo )ω=1 2ωn ⎟ 1 For (2ζ )2 ⎜ (uo 2 ⎟ ω=ωn ⎠ = ( 0.44)2 +(2.4ζ )2 (c) (uo )ω = 12ω = 1 (uo )ω = ω 4 Equation

64ζ2

5 76ζ2 ⇒ ζ

= ω n 1 ⎡ 2ζ2 2 ⎤

amplitude = (u st ) o ⎢ ⎣2ζ 1 2ζ .

= 0.1935 +

Assumption

Problem 3.4

(a) Machine running at 20 rpm

(d) Summarizing these results together with given data:

The isolator is effective at ωω n = 0.9; it reduces the deformation amplitude to 39% of the response without

isolators. At ωω = 0 1 or 3, the isolator has essentially

n no influence on reducing the deformation.

© 2012 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photoco4pying, recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.

ωω n (uo )ζ = 0 (uo )ζ=0.25 0.1 0.2 0.1997 0.9 1.042 0.4053 3.0 0.0248 0.0243 st o 2

ω = ω n 20 200 = 0.1 (u ) uo = (a) 1 (ω ω n ) or

0 2 = (ust )o ⇒ (u ) = 0 1980 in

1 (0 1)2 st o

For ζ = 0 25 and ωω n = 0 1, 1 uo = (ust )o 2 2 2 (b) 1 (ω ωn ) + 2ζωωn or uo = 0.1980 [1 1 (0 1)2]2 + [2 (0 25) (0 1)]2 = 0 1997 in

ω = ωn 180 200 = 0 9 From Eq. (a), (u ) 1 042 = st o ⇒ (ust )o = 0 1980 in 1 (0.9)2 For ζ = 0 25 and ωω n = 0 9, Eq. (b) reads 1 uo = 0.1980 2 2 1 = 0 4053 in (0 9)2 + 2 (0 25)(0 9)

(b) Machine running at 180 rpm

ω = ωn 600 = 3 200

Eq. (a),

From

Inc.,

NJ. All rights

This publication

from the publisher prior to any prohibited reproduction, storage in a retrieval system,

in any form or by any

electronic, mechanical, photoco5pying, recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458. (u ) 0.0248 = st o ⇒ (ust )o = 0.1980 in. 1 (3)2

0 25 and ωωn = 3, Eq. (b) reads 1 uo = 0.1980 [1 (3)2 ]2 + [2 (0.25)(3)]2 = 0.0243 in.

Upper Saddle River,

reserved.

is protected by

should

obtained

or transmission

means,

For

Problem

© 2012 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photoco6pying, recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.

3.5

= 1200 lbs, E = 30 × 106 psi, I = 10 in 4 , L = 8 ft; ζ = 1% ⎛300⎞ po = 60 lbs; ω = ⎜ ⎟ 2π = 10πrads sec

of two beams: ⎝ 60 ⎠ k = 2 ⎜ 48 ⎟ = 32,552 lbs in. ⎛ EI ⎞ ⎝ L3 ⎠ Natural frequency: k k 32,552 ωn = = = = 102 3 rads sec m w g 1200 386 Steady state response: 1 Rd = 2 2 1 (ω ωn )2 + 2ζω ω n where ωωn = 10π102.3 = 1 Rd = 0.3071. Therefore, = 1 104 [1 0 0943]2 + [2 × 0 01 × 0 3071]2 Displacement: p uo = (ust )o Rd = o Rd k = 60 32,552 × 1.104 = 2.035 × 10 3 in Acceleration amplitude: 2 2 3 u && o = ω uo = (10π) 2.035 × 10 = 2 009 in sec 2 = 0 0052g

Given: w

Stiffness

Problem 3.6

In Eq. (3.2.1) replacing the applied force by po cosωt and dividing by m we get

u && + 2ζω nu & + ω 2 u = po cosωt m (a)

(a) The particular solution is of the form:

u p (t) = C sinωt + D cosω t (b)

Differentiating once and then twice gives

u & p (t) = Cω cosωt Dω sinωt (c)

u && p (t) = Cω 2 sinωt Dω 2 cosωt (d)

Substituting Eqs. (b)-(d) in Eq. (a) and collecting terms: 2 2 (ω n ω ) C 2ζω nω D

sinωt p + 2ζω n ω C + (ω n ω ) D cosωt = o cosωt m

Equating coefficients of sin ωt and of cosωt on the two sides of the equation:

Solving Eqs. (e) and (f) for C and D gives

(ωn ω ) + (2ζωnω)

(g)

Substituting Eqs. (g) and (h) in Eq. (b) gives u (t) = po 1 (ωωn ) cos ωt + 2ζωω n sin ωt k 1 (ω ω )2 2 + 2ζω ω 2 n n

(b) Maximum deformation is uo =

Substituting for C and D gives C2 + D2

© 2012 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photoco7pying, recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.

n n 2

C = D =

2 2

(ω n ω ) C (2ζωnω) D = 0 p (e)

ζωnω) C + (ω

ω2 ) D = o m (f)

2 2 2 2

p ω2 ω2 o n 2 2 2 2

ζωnω

(h)

(ωn ω ) + (2ζωnω)

u = po 1

This is same as Eq (3 2 11) for the amplitude of deformation due to sinusoidal force.

© 2012 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photoco8pying, recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.

o k 2 2 1 (ω ωn )2 + 2ζω ω n

Problem 3.7

(a) The displacement amplitude in given by Eq. (3.2.11):

where β = ωω n Resonance occurs at β when uo is maximum, i.e., duo respect to β gives

= 0. Differentiating Eq. (a) with

(b) Substituting Eq. (b) in Eq. (a) gives the resonant amplitude:

© 2012 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photoco9pying, recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.

2 2 2 1 2 uo

ust

o (1 β ) + (2ζβ

(a)

= (

)

1 2 2 2 3 2 (1 β ) 2 + (2ζβ) × 2(1 β 2 ) ( 2β) + 2 (2ζβ) 2ζ = 0 or 4 (1 or β 2) β + 8ζ 2β = 0 1 β 2 = 2ζ 2 ⇒ β = 1 2ζ 2 (b) Resonant frequency: ω r = ω n 1 2ζ 2

uo = (ust )o (2ζ2 )2 1 + 4ζ2 (1 2ζ2 ) or uo = (ust )o 2ζ 1 1 ζ 2 (c)

Problem 3.8

(a) From Eq. (3.2.19) the acceleration amplitude is

where β = ωω n Resonance occurs at β where u && o is maximum, i.e., du && o dβ = 0 Differentiating Eq. (a) with respect to β and setting the result equal to zero gives

(b) Dividing both the numerator and denominator of Eq (a) by

© 2012 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photoco10pying, recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.

⎜ ω 2 ⎧ 2 o ⎟ ⎜ ⎟

u && o = po 1

m 2ζ 1 ζ2 po u & = R 2 = po ⎛ ω ⎞ o m a Rd m ⎝ n ⎠ p β= 2 = o (a) m (1 β2 )2 1 2 + (2ζβ)

1 (1 β 2)2 +(2ζβ )2 ⎨2β ⎩ [(1 β 2)2 + (2ζβ )2 ]1 2 ⎜β ⎟ [(1 β 2)2 + (2ζβ )2] 1 2[ 4β (1 β 2) + 8ζ 2β] =0 ⎛ 2 ⎞ ⎜ ⎟ ⎬ ⎝ ⎠ ⎪ ⎭ Multiplying the numerator by [(1 and dividing it by β

β 2)2 + (2ζβ)2 ] 1 2 2 (1 β 2)2 + 4ζ 2β 2 β= 2 2 4 (1 β 2) + 8ζ 2 = 0 or 1 2β 2 + β 4 + 4ζ 2β 2 + β 2 β 4 2ζ 2β 2 = 0 or 1 = β 2 (1 2ζ 2) ⇒β = 1 (b) 1 2ζ2 Resonant frequency: ω r = ωn (c) 1 2ζ 2

gives

β 2

u & o p 1 = 1 2 (d)

gives:

Substituting Eq. (b) in Eq. (d) gives the resonant amplitude:

© 2012 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photoco11pying, recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.

⎝ 2 ⎠ m ⎡⎛ 1 ⎞2 4ζ 2 ⎤ ⎢⎜ 1⎟ + ⎥ ⎢⎜β 2 ⎟ ⎣ β 2 ⎥ ⎦

p 1 u && o = o m ( 2ζ2 )2 + 4ζ2 (1 1 2 2ζ )

(a) From Eq (3.2.17), the velocity amplitude is

0. Differentiating Eq. (a) with respect to β and setting the derivative equal to zero gives

Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458. ⎟R 2 2 2 3/2 2 ⎜ Problem 3.9

0 0 ⎛ω ⎞ p u &0 = p Rv = ⎜ ω ⎟ d km km ⎝ n ⎠ = p0 β km [(1 β2)2 + (2ζβ)2]1/ 2 (a) where β=ω/ω n Resonance occurs

u & is maximum, i.e., du &

/ dβ =

[(1 β 2 )2 +(2ζβ)2] 1/2 β[(1 β ) +(2ζβ) ] [2(1 β )( 2β)+2(2ζβ)2ζ ]=0 2 Multiplying the numerator by [(1 β 2 )2 +(2ζβ)2 ]3/2 gives [(1 β2)2 +(2ζ β)2] β[2(1 β2)( 2β)+2(2ζβ)(2ζ )]=0 2 or 1 2β 2 +β 4 +4ζ 2β 2 β ( 2β+2β 3 +4ζ 2β) = 0 or β 4 =1⇒ β=1 (b) Resonant frequency: ω r =ω n (b) Substituding Eq. (b) into Eq. (a)

where

gives

© 2012 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photoco9pying, recording, or likewise. For information regarding permission(s), write to:

Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.

Problem 3.10

We assume that the structure has no mass other than the roof mass.

From Eq. (3.3.4),

At ω = ω n , Ra = 1 2ζ and Eq (a) gives

ζ = 1 me e ω2 (b)

2u && o m

Given:

me = 2 × 50 g = 100 lbs g = 0.1kips g

m = 500 kips g

e = 12 in

ω n = 2π fn = 2π × 4 = 8π 2

u && o = 0.02g = 7.72 in. sec

Substituting the above data in Eq (b) gives

ζ = 1 01 (12) (8π)2 2 (7.72) 500 = 0.0982 = 9.82%

© 2012 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photoco1p0ying, recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.

m ω

m e ω2 Fω I 2

&& o = e n Ra

n (a)

Problem 3.11

The given data is plotted in the form of the frequency response curve shown in the accompanying figure:

(a) Natural frequency

The frequency response curve peaks at fn = 1 487 Hz

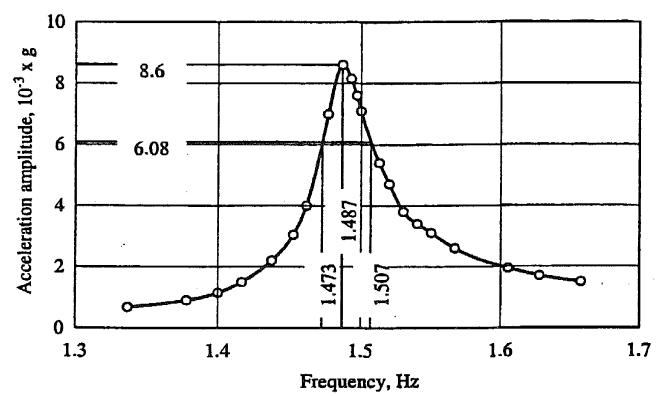
Assuming small damping, this value is the natural frequency of the system

(b) Damping ratio

The acceleration at the peak is rpeak = 8.6 ×10 3 g. 3 Draw a horizontal line at rpeak ÷ 2 = obtain fa and fb in Hz: 6 08 × 10 g to fa = 1 473 Hz fb = 1 507 Hz

© 2012 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photoco1p1ying, recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.

Then, ζ = fb fa = 2 fn 1 507 1 473 2 (1 487)

= 1.14%

= 0.0114

Problem 3.12

(a) Transmissibility is given by Eq. (3.5.3) with ζ = 0. Thus the force transmitted is

The negative value is invalid. Therefore,

© 2012 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photoco1p2ying, recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.

2 st

1 ( fT)o = po 1 (ω ω n ) where ω n = g δst and ω 1 = 2π f .

( fT)o = po 4π2 2 (a) 1 f g δ st (b) For ( fT)o 0 1 = = 0 1 po and f =

(a)

1 ⇒ 1 (4π 2 386)(20)2 δ 4π 2 2 1 (20) 386 δst = ±10 ⇒ 4π 2 2(20) δst = 9 or 11 386

Therefore

20, Eq.

gives

δst =

(4π 2

(20)2 =

386)

0 269 in

Problem 3.13

The equation governing the deformation u(t) in the suspension system is

mu&& + cu & + ku = mu&& g (t) (a)

where ug (t) = ugo sinωt and ω = 2π v L

Substituting in Eq. (a) gives

mu&& + cu & + ku = mω 2 ugo sinωt (b)

The amplitude of deformation is

uo = (ust )o Rd

= 2 u = Rd k

The amplitude of the spring force is

Numerical calculations:

k = 800 lbs in.; m = 4000 386 lb-sec

ugo = 3 in.

ω n = 8 768 rads sec; ω = 3 686 rads sec

ωω n = 0.420

Thus Eq. (d) gives

Substituting ωn and Rd in Eq. (c) gives

fSo = 4000 386 (3.686)2 3(1124) = 474 8 lbs

© 2012 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photoco1p3ying, recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.

2 fSo

where Rd = kuo = mω ugoRd 1 2 2 (c) (d) 1 (ω ωn )2 + 2ζω ω n

2 ]2 1

= [1 (0 42)

+ [2 (0.4)(0.42)]

= 1.124

Spring force: f S = ku

The resonant frequency for f S is the same as that for uo , which is the resonsnat frequency for Ra (from section 3.2.5):

Resonance occurs at this forcing frequency, which implies a speed of

10.655g100 =1696 ft /sec =116 mph

© 2012 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photoco1p4ying, recording, or likewise. For information regarding permission(s), write

o d 2 2

ug btg= ugo sinωt ⇒ u && g btg= ω ugo sinω t peff btg= mu && g btg= mω ugo sinωt ≡ po sinωt mω ugo Fω I u0 =bust g R = 2 2 Rd = ugo Rd = ugo Ra k ω n

to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.

Problem 3.14

res = ωn 1 2ζ 2 =

/ sec 1 2(0.4)2

8786 =10655 rads

= ωL = b

2π 2π

Problem 3.15

Given: w = 2000 lbs, f = 1500 cpm = 25 Hz, and TR = 0 10

For an undamped system, TR = 1

= 0.1

For TR < 1, ωω n > 2 and the equation becomes

11 6 kips in

(47 31) 2000 386

© 2012 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photoco1p5ying, recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.

1 (ω ωn )

1 (ω ω )2

⇒ 1 (ω ω )2 =

⇒ ωω =

n n ω = ω = 2πf = 2π

= n 3 32 3.32 47.31rads

3.32 2 2 2 k = ωnm = ωn w g =

= 0.1

3 32

(25)

sec

Problem 3.16

The excitation is

The equation of motion is mu&& where

+ cu & + ku = peff (t) (b) peff (t) = m u && g (t) = ω m ugo sinωt (c)

The deformation response is given by Eq. (3.2.10) with po replaced by ω2 m ugo :

2 m u

(t) = go R sin (ωt φ) (d)

where Rd and φ are defined by Eqs. (3.2.11) and (3.2.12), respectively.

The total displacement is

Substituting Eqs. (a), (d), (3.2.11) and (3.2.12) gives

Equation (e) is of the form u t (t) = C sin

hence uo = C

+ D . Substituting for C and D gives

Equation (f) is the same as Eq. (3.6.5).

© 2012 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photoco1p6ying, recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.

a f a f 2 | V 2 2 2 = |

ug (t) = ugo sinωt or u && g (t) =

ugo sinωt (a)

k d

u t (t) = u(t) +

(

aω ωf2 u u t (t)= u go sinω n t + 1 aω ω n f n go 2 2 2 + 2ζω ω n × n 1 aω ω n f sinω n t 2ζ ω ω n cosω ts 1 aω ω n f u go 2 2 2 + 2ζω ω n × { 1 aω ω n f + 4ζ aω ω n f sinω n t 2ζaω ω n f cosω t} 2 2 2 3

t 2 2

U1/2 t | 1+b2ζωωn g

uo = ugo S T 1 bω ω n g2 2 2 + 2ζωω n W (f)

ωt (e) + D cos

t ;

Problem 3.17

The accelerometer properties are fn = 50 cps and ζ = 0 7; and the excitation is

u && g (t) = 0 1g sin (2π f t); f = 10, 20 and 40 Hz (a)

Compare the excitation with the measured relative displacement

( 1 ω2 ) R u && g (t φ ω)

(b)

(c)

Table

P3.17

© 2012 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photoco1p7ying, recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.

n d n

Rd =

2 2 1

ωωn )2

ζω ω n and ⎡ 2ζ ωω ⎤ φ = tan 1 ⎢ n ⎥ (d) 1

u(t) = where ωω n )2

(

+ 2

(

t) = Rd u && g (t φ ω)

Because the instrument has been calibrated at low excitation frequencies, after separating the instrument constant 1 ω2 , the recorded acceleration is

(

(e)

For a given f (or ω), ωω n is computed and substituted in Eqs. (c) and (d) to calculate Rd and φ With Rd and φ known for a given excitation frequency, the recorded acceleration is given by Eq. (e).

f (Hz) ωω n Rd φ ω, sec % error in Rd 10 0.2 1 0.0045 0 20 0.4 0.991 0.0047 0.9 40 0.8 0.850 0.0050 15

The computed amplitude Rd and time lag φ ω agrees with Fig. 3.7.3. The difference between Rd and 1 is the error in measured acceleration (Table P3.17).

We want to bound Rd as follows:

The relevant condition is Rd ≤ 1 01 because we are interested in a continuous range of frequencies over which the error is less than 1%. Therefore, impose

This publication

the

prior to any prohibited reproduction, storage in a retrieval system,

1p8ying,

For information regarding

write to: Rights and Permissions Department,

Upper

River,

07458. n d g n 2 Problem 3.18 From Eq. (3.7.1), ω2 u(t) = R u && (t φ ω) f ≤ 4 86 Hz = Rd u && go sin (2π f t and therefore, 2 φ) ω nuo = R u&& d = 1 2 2 (a) go 1 (ω ωn )2 + 2ζω ω n Equation (a) is plotted for ζ = 0 6, the accelerometer damping ratio: 1 5 1 01 ω 2 uo & u&go 1 0 5 0 194 0 723 0 0 0 5 1 1 5 2 Error < 1% f fn or ωωn

is protected by Copyright and written permission should be obtained from

publisher

or transmission

any form or by any means, electronic, mechanical, photoco

recording,

likewise.

permission(s),

Pearson Education, Inc.,

Saddle

0 99 ≤ Rd ≤ 1 01 (b)

1 = 1 01 (c) 1 (ω ω )2 2 + 2ζω ω 2 Defining β n n ≡ ωωn , Eq. (c) can be rewritten as (1 β 2 )2 + (2ζβ)2 = ⎜ 1 ⎟ ⇒ ⎛ ⎞ β4 0 56β2

Choose β = 0 194 frequency range: (see figure) which gives the desired

© 2012 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photoco1p9ying, recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.

+ 1 = ⎝ 1.01⎠ 0.980 3 ⇒ β4 0.56β2 + 0 0197 = 0 ⇒ β

2 = 0 0377, 0 5223 ⇒ β = 0 194,

723

f ≤

⇒

0 194 fn = 0 194 (25)

We want to bound Rd as follows 0.99

The relevant condition is 0 99 ≤ Rd because Rd is always smaller than 1.01 in this case. Therefore, impose

which gives the desired frequency range:

in a

2 2 2

retrieval system, or transmission in any form or by any means, electronic, mechanical, photoco1

10ying, recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.

Problem 3.19

From Eq. (3.7.1), f ≤ 0.405 fn = 0 405(50) ⇒ ω n u(t) = Rd u&& g (t φ ω) f ≤ 20 25 Hz = Rd u && go sin (2π f t and therefore, 2 φ) ω nuo = R u&& d = 1 2 2 (a) go 1 (ωωn )2 + 2ζω ω n Equation (a) is plotted for ζ = 0 7, the accelerometer damping ratio: 1 5 ω n uo &u&go 1 0 5 0 99 0 405 0 0 0 5 1 1 5 2 Error < 1% f f n or ωω n

≤ R

≤ 1 01 (b)

1 = 0 99 (c) 1 (ω ω )2 2 + 2ζω ω 2 Defining β ≡ n n ωωn , Eq. (c) can be rewritten as (1 β 2 )2 + (2ζ β)2 = ⎜ 1 ⎟ ⇒ ⎛ ⎞

0.99

β 4 004β 2 + 1 = 10203 ⇒

β 4 0.04β 2 0.0203 = 0 ⇒

β 2 = 0.1239, 01639

Take only the positive value:

β 2 = 01639 ⇒ β = 0405

© 2012 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photoco1p11ying, recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.

⎝

⎠

Problem 3.20

From Eq. (3.7.3),

For maximum accuracy, uo ugo = 1; this condition after using Eqs. (3.2.20) and (3.2.11) for Ra gives

© 2012 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photoco2p0ying, recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.

uo = Ra ugo (a)

(ωω n )2 = 1 (b) 2 2 1 (ωωn )2 + 2ζω ω n Squaring, simplifying and defining β = ωω n : (1 β 2)2 + (2ζβ)2 = β 4 ⇒ 1 2β 2 + 4ζ 2β 2 = 0 ⇒ ζ 2 = 1 1 2 4β 2 For ωω n >> 1 (β >> 1), ζ 2 = 1 ⇒ ζ = 0 707 2

Problem 3.21

From Eq. (3.7.3),

Equation (a) is plotted for ζ = 0 6, the instrument damping ratio:

We want to bound Ra as follows (see figure) Ra ≤ 1 01 (b)

Therefore imposing Ra = 1 01 which, after defining

, gives

Squaring this equation gives

1.383, 5149

Choose β = 5.149 frequency range: (see figure) which gives the desired

© 2012 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photoco2p1ying, recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.

⎜ ⎠

u (ω ω )2 o = Ra = n (a) ugo

ω ω

2ζω ω 2 n n

1 (

)2 2 +

1 5 1 Ra 0 5 1 01 1 383 5 149 Error < 1% 0 0 1 2 3 4 5 6 f fn or ωω n

β ≡ ωωn

β 2

101 (1 β 2)2 + (2ζβ)2

2 ⎛ β 2 ⎞ (1 β 2)2 + (2ζβ)2 =⎜ ⎝ ⎟ ⇒ 1.01⎟ 1 2β 2 + β 4 + 144β 2 = 0.9803β 4 ⇒ 0.0197β 4 0.56β 2 + 1 = 0 ⇒ β

2 = 1.914, 26.51 ⇒ β =

© 2012 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photoco2p2ying, recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458. f ≥ 5.149 fn = 5 149 (0 5) ⇒ f ≥ 2 575 Hz

Problem 3.22

From Eq. (3.7.3),

Equation (a) is plotted for ζ = 0 7, the instrument damping ratio:

Since Ra is always smaller than 1.01, we want to bound Ra as follows

Therefore imposing Ra = 0.99 (b) which, after defining

Squaring this equation gives

Take only the positive value:

© 2012 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photoco2p3ying, recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.

u (ω ω )2 o = Ra = n (a) ugo 1 (ω ω )2 2 + 2ζω ω 2 n n

1 5 1 0 99 0 5 Error < 1% 2 470 0 0 1 2 3 4 5 6 f f n or ω ωn

a ≥ 0.99

β ≡ ωω

β 2

0.99 (1 β 2)2

(2ζβ)2

n , gives

2 ⎛ ⎞ (1 β 2 )2 + (2ζβ)2 = ⎜β ⎟ ⇒ ⎜ 0.99⎟ 1 2β 2 + β 4 ⎝ + 196β 2 ⎠ = 10203β 4 ⇒ 0.0203

0.04β 2 1 = 0 ⇒ β 2

= 8073, 6.102

β2 = 6.102 ⇒ β = 2 470

which gives the desired frequency range:

f ≥ 2 470 fn = 2.470 (0.5) ⇒

f ≥ 1.235 Hz

© 2012 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photoco2p4ying, recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.

Problem 3.23

From Eq. (3.8.1),

ED where

= 2πζ (ω ω n ) ku2 (a)

u = po R (b)

o k d

In Eq (a) substituting Eq (b) and Eq (3 2 11) for Rd gives

π p 2 2ζωω

o 2

E = o n k 1 (ω ω )2 + 2ζωω 2 n n

© 2012 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photoco2p5ying, recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.

Problem 3.24

From Eq. (3.8.9) the loss factor is

(a)

where ED =πcω u 2 and ESo = k u 2 2. Substituting these in Eq. (a) gives

© 2012 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photoco2p6ying, recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.

o o

1 ED 2π ESo

ξ =

ξ = c ω k (b)

Based on equivalent viscous damping, the displacement amplitude is given by

© 2012 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photoco2p7ying, recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.

o T 2 g

Problem 3.25

uo = {1 [(4 π) (F p )]2 }1 2 (a) (ust ) o From the given data 1 (ω ω n ) F po ω ω n = 50 = 100 = Tn = T 1 2 0 25 = 0.3 0 833 Substituting these data in Eq. (a) gives uo = (u st ) o Now, {1 [(4 π) (1 2)]2 }1 2 1 (0 833)2 = 2 52 (u where st )o = po k po = 100 kips 2 ⎛ π⎞ w k = ω 2 m = ⎜ 2 ⎟ = (8π)2 500 n ⎜ ⎟ ⎝ n ⎠ 386 = 818kips in. Thus (ust )o = 100 818 = 0.1222 in. and uo = 2

= 0

1222)

308

Because of the j4 in the denominator of the series, two

terms are enough to obtain reasonable convergence of the

or transmission in any form or by any means, electronic, mechanical, photoco2p6ying, recording, or likewise.

to:

o T 0 0 0 u T T 0 0T | Problem 3.26 where (ust )o = po k and β j = jω0 ω n . Equation (f) is (a) p(t) is an even function: indeterminate when β j = 1; corresponding values of T0 are T n , 3T n , 5T n , etc. p(t) = ⎛ 2 ⎞ p o ⎜1 t ⎟ 0 ≤ t ≤ T0 2 (a) (c) For T T = 2, β = jω ω = j T T = j 2 and ⎜ ⎟ 0 n j 0 n n 0 ⎝ T0 ⎠ T 2 T 2 Eq. (f) becomes ∞ 1 2 ⎛ 2 ⎞ u(t) 1 16 1 2πjt a = p(t)dt = p ⎜1 t ⎟ dt = + 2 ∑ 2 2 cos ( ) 0 T ∫ T ∫ o ⎜ T ⎟ (u ) 2 π j (4 j ) T 0 p = 2 T T0 2 z 0 0 ⎝ cos ω 0 ⎠ (b) st o j =1,3,5,L 0 1 two terms 2 a j = T0 2pbtg b j 0tgdt 0.8 0.6 three terms 0 T0 2 u (t ) = 4 p T0 z 2F 2 t I cos b jω tgdt ( ) st o 0.4 0 H G1 0 0 0 0 = p0 R ω b jω tg T 2 z t b jω tgdt U 0.2 0 4 1 0 2 T0 2 T0 | T j 0 8 0 z sin 0 0 F 2π I cos 0 W 0 0.2 0.4 0.6 0.8 1 t T T = p0 2 0 t jt dt 2 cos T 0 0 0 4 p = L Mt F 2πj I t T0 2 T L F 2πj IO t T0 2

a retrieval system,

For information regarding permission(s), write

Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.

SN M sin J KQ P + 0 McosG JP V

π j

(b) The steady-state response of an undamped system is obtained by substituting Eqs. (b), (c) and

to any prohibited reproduction, storage in a retrieval system,

electronic, mechanical, photoco2p6

For information

to:

and Permissions Department,

Education, Inc.,

N 0 b g = t Q 2 ∞ 2 ∞ T | T T 2π j M N H T KP Q W | series solution. 0 0 0 0 0 L OT0 2 2 p0 M F2π j I P = cos 2 j2 T π 0 0 2 p = cos π j 1 π 2 j2 ⎧ 4 po ∴a j ⎪ ⎨ π j 2 ⎪ j = 1,3,5,L (c) ⎩ 0 j = 2,4,6,L bn = 0 because p(t)is an even function (d) Thus the Fourier series representation of p(t) is p(t) = po + 4 po ∑ 1 cos ( jω0t) (e) 2 2 2 π j =1,3,5,L j

or transmission in any form or by any means,

ying, recording,

likewise.

regarding permission(s), write

Rights

Pearson

Upper Saddle River, NJ 07458.

u(t) = 1 + 4 ∑ 1 2 2 cos ( jω0t) (ust )o 2 π j =1,3,5,L j (1 β j ) (f)

(d) in Eq (3.13.6)

obtain