Introducción
En el presente trabajo vamos a observar todos los temas que estuvimos viendo en el semestre en el curso de matemáticas discreta ya que está unido todo en un solo documento de todos los temas ya que cada tema nos va servir para nuestro futuro.
Protafolio Matematica discreta.
Principios Fundamentales del Conteo: El principio básico o fundamental de conteo se puede utilizar para determinar los posibles resultados cuando hay dos o más características que pueden variar.
Ejemplo: El helado puede venir en un cono o una tasa y los sabores son chocolate, fresa y vainilla.

Principio de la suma
Si un evento o suceso “A” ocurre de n maneras y otro “B” ocurre de m maneras, entonces existen n+m maneras en que puede ocurrir el evento A o el evento B si y solo si los eventos no suceden en simultaneo.
Ejemplo: La biblioteca de la Universidad tiene 40 libros de programación y 50 de lógica ¿Cuántas formas de aprender un curso tiene un estudiante?
Puede elegir 40+50= 90 libros de texto y aprender alguno de estos cursos
Principio de la multiplicación

Si un evento A ocurre de n maneras diferentes seguido de otro evento B que ocurre de m maneras distintas, entonces existen n*m maneras en que puede ocurrir el evento A o el evento B si y solo si los eventos ocurren uno a continuación del otro.
Ejemplo: En una obra de teatro ensayan 6 hombres y 8 mujeres para integrar los papeles principales (masculino, femenino) ¿Cuántas formas distintas tiene el director para elegir la pareja principal?
El director puede tener 6*8= 48 formas distintas de elegir la pareja principal PRINCIPOS FUNDAMENTALES DEL CONTEO PERMUTACIONES
Regla de la Suma y del Producto: Si sumamos o restamos una expresión algebraica a los dos miembros de la ecuación, la ecuación resultante es equivalente a la primera
Permutaciones.
Refiere al procedimiento y el resultado de permutar, define los posibles ordenamientos de aquellos elementos que forman parte de un conjunto no infinito.
Tipos de Permutaciones

1. Permutaciones con repetición
Si tienes n cosas para elegir y eliges r de ellas, las permutaciones posibles son: n × n × ... (r veces) = nr donde n es el número de cosas que puedes elegir, y eliges r de ellas (Se puede repetir, el orden importa)

2. Permutaciones sin repetición
De un conjunto o evento dado se reduce el número de opciones en cada paso, su cálculo se realiza a través de su factorial (n!)

Combinaciones
Refiere al acto o consecuencia de combinar algo, es decir, unir, complementar o ensamblar cosas diversas para lograr un compuesto.
• EXISTEN DOS TIPOS DE COMBINACIONES.
1.COMBINACIONES SIN REPETICIÓN:
Son las distintas formas en que se puede hacer una selección de elementos de un conjunto
COMBINACIONES CON REPETICIÓN


Son las distintas formas en que se puede hacer una selección de elementos de un conjunto dado, permitiendo que las selecciones puedan repetirse.
Teoría de conjuntos.
Un conjunto es una colección o clase de objetos bien definidos y diferenciables entre sí, llamados elementos del conjunto.
Diagrama de Venn
Es una representación gráfica, normalmente óvalos o círculos, que nos muestra las relaciones existentes entre los conjuntos. Cada óvalo o círculo es un conjunto diferente.


Conjuntos iguales.
Dos conjuntos A y B son iguales (A = B) si tienen los mismos elementos o la misma propiedad característica.


Operaciones entre conjuntos
Intersección
La intersección de los conjuntos A y B, que representamos por A ∩ B, es el conjunto formado por los elementos de A y de B, es decir:
A ∩ B = {x : x ∈ A ∧ x ∈ B }

Unión
La unión de dos conjuntos A y B, que representamos por A ∪ B, es el
conjunto formado por los elementos de A o de B o de ambos, es decir:
A ∪ B = {x : x ∈ A ∨ x ∈ B}
Diferencia
Sean los conjuntos A y B. Llamamos conjunto diferencia de A y B y lo representamos por A ‐ B, al conjunto formado por todos los elementos que están en A pero no en B:
A ‐ B = {x: (x ∈ A) ∧ (x ∉ B)}

Complementario

Sea el conjunto A. El complementario de A, que se escribe A’, es el conjunto de todos los elementos que no pertenecen a A, o que pertenecen a la diferencia U ‐ A (U conjunto universal fijado de antemano).

Leyes de Teoría de conjuntos

TEORÍA DE CONJUNTOS Conteo, Producto Cartesiano y Relaciones

PRODUCTO CARTESIANO

El producto cartesiano de AxB Considerando dos conjuntos A y B, llamamos producto cartesiano de A y B al conjunto formado por todos los pares ordenados (a; b) de tal manera que la primera componente “a” pertenece al conjunto A y la segunda componente “b” pertenece al conjunto B

RELACIONES EN TEORÍA DE CONJUNTOS
Una relación entre dos conjuntos A y B es un subconjunto del producto cartesiano AxB, donde las parejas (x,y) cumplen una condición específica.
INDUCCIÓN MATEMÁTICA Teorema Fundamental de la Aritmética, Algoritmo de la División

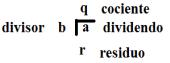
Algoritmo de la división
Teorema que asegura que el proceso habitual de división entre números enteros puede llevarse a cabo y que el resultado además es único. Es un método efectivo que produce un cociente y un residuo.
Proceso habitual de la división
Algoritmo de división:
Dados enteros a, b con b ≠ 0 existen enteros q y r tales que a = b q + r y 0<= r <|b| a = dividendo b = divisor. q = cociente r = residuo.

INDUCCIÓN MATEMÁTICA

Teorema Fundamental de la Aritmética, Máximo común Divisor Algoritmo de la División y el de Euclides
Teorema Fundamental de la Aritmética
Afirma que todo entero positivo se puede representar de forma única como producto de factores primos:
Máximo Común Divisor
Consiste en el mayor número que divide a todos los Z+ exactamente.
Procedimiento:
a. Se descomponen cada Z+ en factores primos
b. Se toman los factores comunes con menor exponente y se multiplican dichos factores y el resultado obtenido es el MCD.
Algoritmo de Euclides Permite expresar el MCD como una combinación lineal entre dos números.
Procedimiento
a. Se divide el número mayor entre el menor
- Si la división es exacta el divisor es el MCD
Si la división no es exacta, dividimos el divisor entre el residuo obtenido y se continua de esa forma hasta obtener una división exacta siendo el ultimo divisor el MCD.

Teoría de Grafos
¿Qué es un Grafo?
En matemáticas y en ciencias de la computación, la teoría de grafos (también llamada teoría de las gráficas) estudia las propiedades de los grafos (también llamadas gráficas).

¿Por qué se estudian Grafos?
Porque permiten estudiar interrelaciones entre elementos que interactúan unos con otros. Dado un escenario donde ciertos objetos se relacionan se puede “modelas el grafo” y luego aplicar algoritmos para resolver diversos problemas.
¿Dónde son Aplicables?
Ingeniería de Sistemas
Modelado de Redes
Ingeniería Industrial, Electrónica
etc.


¿Qué podemos representar con un Grafo? Red de Computadoras Conexiones de vuelo de una aerolínea Carreteras que unen ciudades Actividades de un Proyecto Circuitos electrónicos Representación de un mapa
Tipos de Grafos











Trayectorias en Grafos

Camino / recorrido
Un camino P desde u hasta v en el grafo G es una secuencia finita de vértices que empieza en u y acaba en v.
• Cada par de vértices consecutivos son adyacente
Puentes de Königsberg
El problema consiste en recorrer toda la ciudad partiendo de cualquier lugar (A, B, C o D) caminando sobre cada puente exactamente una vez y regresar a la posición inicial.

Caminos y Ciclos de Euler
Camino de Euler Recorre TODOS los ARCOS sin repetirlos
Los vértices se pueden repetir

Ciclo de Euler
Recorre TODOS los ARCOS sin repetirlos Los vértices se pueden repetir Inicia y termina en el mismo vértice
Ciclo Hamiltoniano
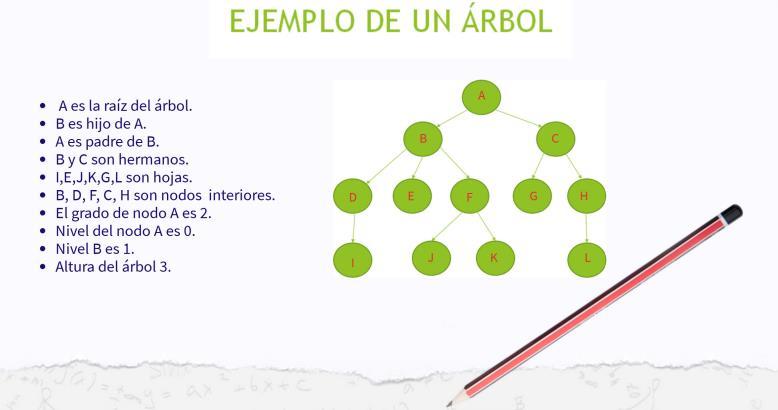
Arboles

Propiedades de un árbol


Características de un árbol
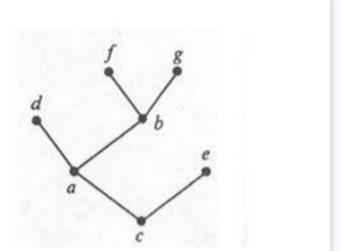
Árbol libre